图的表达
Graph Embedding可用于可视化、结点分类、链接预测link prediction、推荐等任务中。- 网络表示学习
network representation learning :NRL:将网络的每个顶点编码到一个统一的低维空间中。
一、DeepWalk[2014]
network representation的稀疏性既是优点、也是缺点。稀疏性有助于设计高效的离散算法,但是会使统计学习中的泛化变得更加困难。network中的机器学习应用(例如network classification、内容推荐、异常检测、缺失链接预测)必须能够处理这种稀疏性才能生存。在论文
《DeepWalk: Online Learning of Social Representations》中,作者首次将深度学习(无监督特征学习)技术引入到网络分析network analysis中,而深度学习技术已经在自然语言处理中取得了成功。论文开发了一种算法(DeepWalk),它通过对短short的随机游走流a stream of short random walks进行建模,从而学习图顶点的社交表示social representation。social representation是捕获邻域相似性neighborhood similarity和社区成员关系community membership的顶点的潜在特征。这些潜在representation在低维的、连续的向量空间中对社交关系social relation进行编码。DeepWalk将神经语言模型推广为处理由一组随机生成的游走walks组成的特殊语言。这些神经语言模型已被用于捕获人类语言的语义结构semantic structure和句法结构syntactic structure,甚至是逻辑类比logical analogies。DeepWalk将图作为输入,并生成潜在representation作为输出。论文的方法应用于经过充分研究的空手道网络
Karate network,其结果如下图所示。Karate network通常以force-directed布局呈现,如图a所示。图b展示了论文方法的输出,其中具有两个潜在维度。除了惊人的相似性之外,我们注意到(图b)的线性可分部分对应于通过输入图(图a)中的modularity maximization发现的clusters(以不同顶点颜色表示)。下图中,注意输入图中的社区结构和embedding之间的对应关系。顶点颜色表示输入图的modularity-based clustering。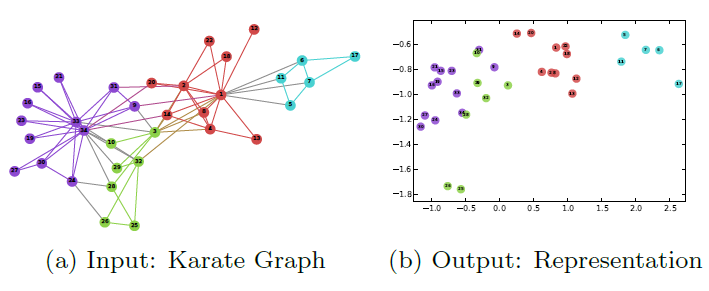
为了展示
DeepWalk在现实世界场景中的潜力,论文评估了它在大型异质图large heterogeneous graph中具有挑战性的multi-label network classification问题的性能。在关系分类relational classification问题中,特征向量之间的链接links违反了传统的独立同分布的假设。解决这个问题的技术通常使用近似推断技术approximate inference technique来利用依赖信息dependency information从而改善分类结果。论文通过学习图的label-independent representation来远离这些方法。论文的representation质量不受标记顶点选择的影响,因此它们可以在任务之间共享。DepWalk在创建社交维度social dimensions方面优于其它潜在representation方法,尤其是在标记顶点稀疏的情况下。论文的representation可以通过非常简单的线性分类器(例如逻辑回归)获得强大的性能。论文的representation是通用的,可以与任何分类方法(包括迭代式推断方法iterative inference method)结合使用。DeepWalk实现了所有的这些,同时是一种可简单并行的在线算法。论文的贡献如下:
- 我们引入深度学习作为分析图的工具,从而构建适用于统计建模的鲁棒的
representation。DeepWalk学习短的随机游走中存在的结构规律structural regularity。 - 我们在多个社交网络上广泛评估了我们在多标签分类任务上的表现。在标签稀疏的情况下,我们展示了显著提高的分类性能。在最稀疏的问题上,我们获得了
Micro F1的5% - 10%的提升。在某些情况下,即使训练数据减少60%,DeepWalk的representation也可以胜过其它竞争对手。 - 我们通过使用并行实现
parallel implementation来构建web-scale图(例如YouTube) 的representation,从而证明了我们算法的可扩展性。此外,我们描述了所需的最小修改从而构建我们方法的streaming版本。
- 我们引入深度学习作为分析图的工具,从而构建适用于统计建模的鲁棒的
DeepWalk是一种学习网络中顶点潜在representation的新方法。这些潜在representation在连续向量空间中编码社交关系social relation,从而很容易被统计模型所利用。DeepWalk推广了语言模型和无监督特征学习(或深度学习)从单词序列到graph的最新进展。DeepWalk使用从截断的随机游走中获得的局部信息,通过将随机游走视为等价的sentence来学习潜在representation。DeepWalk也是可扩展scalable的。它是一种在线学习算法online learning algorithm,可以构建有用的增量结果,并且可以简单地并行化。这些品质使其适用于广泛的现实世界application,例如network classification和异常检测。DeepWalk与以前的工作之间的主要区别可以总结如下:DeepWalk学习潜在的social representation,而不是计算中心统计量centrality statistics(如《Leveraging label-independent features for classification in sparsely labeled networks: An empirical study》)、或者分区统计量partitioning statistics(如《Leveraging social media networks for classification》)。DeepWalk不尝试扩展分类程序本身(通过集体推断collective inference如《Collective classification in network data》,或者graph kernel如《Diffuusion kernels on graphs and other discrete input spaces》)。DeepWalk提出了一种仅使用局部信息的、可扩展的、在线方法。大多数方法需要全局信息、并且是离线的。DeepWalk将无监督representation learning应用于图。
接下来,我们讨论
network classification和无监督feature learning方面的相关工作。相关工作:
关系学习
Relational Learning:关系分类relational classification(或者集体分类collective classification)方法使用数据item之间的链接links作为分类过程的一部分。集体分类问题中的精确推断exact inference是NP-hard问题,其解决方案主要集中在近似推断算法。这些近似推断算法可能无法保证收敛。与我们的工作最相关的关系分类算法包括:学习
clusters(《Leveraging relational autocorrelation with latent group models》)、在附近节点之间添加边(《Using ghost edges for classification in sparsely labeled networks》)、使用PageRank(《Semi-supervised classification of network data using very few labels》)、通过扩展关系分类来考虑额外的特征(《Multi-label relational neighbor classification using social context features》),通过这些方法从而合并社区信息community information。我们的工作采取了截然不同的方法。我们提出了一种学习网络结构
representation的程序,而不是新的近似推断算法,然后可以由现有的推断程序inference procedure(包括迭代式推断程序)来使用。人们还提出了很多从图中生成特征的技术。和这些技术相比,我们将特征创建过程构建为
representation learning问题。人们也 提出了
graph kernel(《Graph kernels》) ,从而将关系数据用作分类过程的一部分。但是,除非近似(《Fast random walk graph kernel》),否则它的速度非常慢。我们的方法与graph kernel是互补的:我们没有将结构编码为核函数kernel function的一部分,而是学习一种representation,从而允许该representation直接用于任何分类方法的特征。无监督特征学习
Unsupervised Feature Learning:人们已经提出分布式representation learning来建模概念之间的结构关系structural relationship。这些representation通过反向传播和梯度下降来进行训练。由于计算成本和数值不稳定,这些技术被放弃了十几年。最近,分布式计算允许训练更大的模型,并且用于无监督学习的数据出现增长。分布式
representation通常通过神经网络进行训练,这些神经网络在计算机视觉、语音识别、自然语言处理等不同领域取得了进步。
DeepWalk可以挖掘图 的局部结构,但是无法挖掘图 的整体结构。
1.1 模型
1.1.1 问题定义
考虑社交网络成员的分类问题。正式地,令 ,其中 为图中所有的顶点(也称为网络的成员
member), 为所有的边。给定一个部分标记的social network,其中:- 特征 , 为属性空间的维度, 为顶点数量。
- , 为
label空间, 为分类类别数量。
在传统的机器学习分类
setting中,我们的目标是学习将 的元素映射到标签集合 的假设hypothesis。在我们的例子中,我们可以利用嵌入在 结构中的样本依赖性example dependence的重要信息,从而实现卓越的性能。在文献中,这被称作关系分类relational classification(或者集体分类collective classification)问题。关系分类的传统方法提出将问题作为无向马尔科夫网络
undirected Markov network中的推断inference,然后使用迭代式近似推断算法(例如迭代式分类算法《Iterative classi fication in relational data》、吉布斯采样《Stochastic relaxation, gibbs distributions, and the bayesian restoration of images》、或者标签松弛算法《On the foundations of relaxation labeling processes》)来计算给定网络结构下标签的的后验分布。我们提出了一种不同的方法来捕获网络拓扑信息
network topology information。我们没有混合label空间从而将其视为特征空间的一部分,而是提出了一种无监督方法,该方法学习了捕获独立于label分布的、图结构的特征。结构表示
structural representation和标记任务labeling task的这种分离避免了迭代式方法中可能发生的级联错误cascading error。此外,相同的representation可以用于与该网络有关的多个分类任务(这些分类任务有各自不同的label)。我们的目标是学习 ,其中 是一个较低的潜在维度。这些低维
representation是分布式的,意味着每个社交概念social concept都由维度的某个子集来表达,每个维度都有助于低维空间所表达的一组社交概念的集合。使用这些结构特征
structural feature,我们将扩充属性空间从而帮助分类决策。这些结构特征是通用的,可以与任何分类算法(包括迭代式方法)一起使用。然而,我们相信这些特征的最大效用是:它们很容易与简单的机器学习算法集成。它们在现实世界的网络中可以适当地scale,正如我们在论文中所展示的。
1.1.2 基础知识
我们寻求具有以下特性的
learning social representation:- 适应性
adaptability:真实的社交网络在不断演变,新的社交关系不应该要求一遍又一遍地重新训练整个网络。 - 社区感知
community aware:潜在维度之间的距离应该能够代表评估网络成员之间社交相似性social similarity的指标。 - 低维
low dimensional:当标记数据稀疏时,低维模型泛化效果更好,并且加快收敛和推断速度。 - 连续
continuous:除了提供社区成员community membership的精细的视图之外,continuous representation在社区之间具有平滑的决策边界,从而允许更鲁棒的分类。
我们满足这些要求的方法从短期随机游走的
stream中学习顶点的representation,这是最初为语言建模而设计的优化技术。在这里,我们首先回顾随机游走和语言建模language modeling的基础知识,并描述了它们的组合如何满足我们的要求。- 适应性
随机游走
random walk:我们将以顶点 为root的随机游走表示为 。 是一个随机游走过程,其中包含随机变量 。 是一个顶点,它是从顶点 的邻居中随机选中的。随机游走已被用作内容推荐
content recommendation和社区检测community detection中各种问题的相似性度量similarity measure。随机游走也是一类输出敏感算法output sensitive algorithm的基础,这类算法使用随机游走来计算局部社区结构信息local community structure,并且计算时间复杂度为input graph规模的亚线性sublinear。正是这种与局部结构的联系促使我们使用短的随机游走流
stream of short random walks作为从网络中提取信息的基本工具。除了捕获社区信息之外,使用随机游走作为我们算法的基础还为我们提供了另外两个理想的特性:- 首先,局部探索很容易并行化。多个随机游走器
random walkers(在不同的线程、进程、或者机器中)可以同时探索同一个图的不同部分。 - 其次,依靠从短的随机游走中获得的信息,可以在不需要全局重新计算的情况下适应图结构的微小变化。我们可以使用新的随机游走,从图变更的区域游走到整个图,从而以亚线性时间复杂度来更新已经训练好的模型。
- 首先,局部探索很容易并行化。多个随机游走器
幂律
power law分布:选择在线随机游走作为捕获图结构的原语primitive之后,我们现在需要一种合适的方法来捕获这些图结构信息。如果连通图的
degree分布遵循幂律分布power law(也叫作Zipf定律),那么我们观察到顶点出现在短随机游走中的频率也遵循幂律分布。自然语言中的单词遵循类似的分布,语言模型language modeling技术解释了这种分布行为。为了强调这种相似性,我们在下图中展示了两个不同的幂律分布:第一个来自一个图上的一系列短随机游走,第二个来自于英文维基百科的100,000篇文章的文本。图a给出了short random walk中,顶点出现频次的分布。图b给出了英文维基百科的10万篇文章中,单词的频次分布。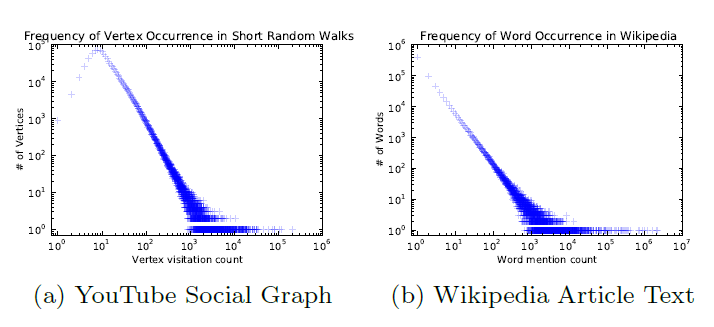
我们工作的一个核心贡献是这样的一种思想:用于建模自然语言(其中单词频率遵循幂律分布)的技术也可以复用于建模网络中的社区结构。
接下来我们将回顾语言建模中不断发展的工作,并将其转换为学习满足我们标准的顶点
representation。
1.1.3 语言模型
语言模型的目标是估计特定单词序列在语料库
corpus中出现的可能性。正式地,给定一个单词序列 ,其中 ( 为词典vocabulary),我们希望在整个训练语料库上最大化 。最近在
representation learning方面的工作聚焦于使用概率神经网络probabilistic neural network来构建单词的general representation,从而将语言建模的范围扩展到其原始目的之外。在这项工作中,我们提出了语言建模的泛化,以通过短随机游走流
stream来探索图。这些随机游走可以被认为是一种特殊语言的短句short sentence和短语short phrase。我们进行直接的类比,从而在随机游走中,给定到目前为止访问的所有顶点序列来估计观察到顶点 的可能性,即 。我们的目标是学习潜在
representation,而不仅仅是节点共现node co-occurrence的概率分布,因此我们引入一个映射函数 。该映射函数 将图中每个顶点 映射到一个潜在的social representation。即:我们想要的是顶点
representation,而不是预估这个随机游走序列出现的概率。实际上,我们使用
free parameters的矩阵 来表达 ,这在稍后将被用作我们的 。然后,问题变成了似然估计:然而,随着游走序列长度的增加,计算这个目标函数变得不可行。
因为
sentence越长,它出现的频次越低,样本过于稀疏。最近,在语言模型中的放松条件使得这个预测问题得到了解决。
- 首先,我们不是使用上下文来预测缺失单词
missing word,而是使用一个单词来预测上下文。 - 其次,上下文由出现在给定单词左侧和右侧的单词组成。
- 最后,我们消除了对问题的顺序约束
ordering constraint。即,模型需要最大化任何单词出现在上下文中的概率,而无需知道上下文与目标单词的偏移量。
应用到顶点建模中,这得到了优化问题:
其中 为上下文窗口尺寸。
我们发现这些放松条件对于
social representation learning是特别理想的。- 首先,顺序独立性假设
order independence assumption更好地捕获了随机游走的nearness的sense。 - 其次,这种松弛条件对于通过构建一大批小模型来加速训练非常有用,因此一次给定一个顶点。
解决上式中的优化问题将得顶点
representation,这些representation捕获了顶点之间在局部图结构local graph structure中的相似性。具有相似邻域的顶点将获得相似的representation(编码了co-citation相似性),并允许对机器学习任务进行泛化。- 首先,我们不是使用上下文来预测缺失单词
通过结合截断的随机游走和神经语言模型,我们制定了一种满足我们所有期望特性的方法。
- 该方法生成低维的社交网络
representation,并存在于连续向量空间中。 - 该方法生成的
representation对社区成员的潜在形式latent form进行编码。 - 并且,由于该方法输出有用的
intermediate representation,因此它可以适应不断变化的网络拓扑结构。
- 该方法生成低维的社交网络
1.1.4 DeepWalk
与任何语言建模算法一样,
DeepWalk唯一需要的输入是语料库和词表 。DeepWalk将一组截断的短随机游走视为语料库,将图的顶点视为词表() 。虽然在训练之前知道随机游走中顶点集合 和顶点的频率分布是有益的,但是DeepWalk在不知道顶点集合的情况下也可以工作。DeepWalk算法主要由两部分组成:随机游走生产器、更新过程。随机游走生成器
random walk generator:以图 作为输入并均匀随机采样一个顶点 作为随机游走 的root。随机游走从最近访问的顶点的邻域中均匀采样,直到游走序列长度达到最大长度 。虽然在我们的实验中,随机游走序列的长度设置为固定的(固定为 ),但是理论上没有限制它们都是相同的长度。这些随机游走可能会重启(即返回
root的传送概率teleport probability),但是我们的初步结果并为表明使用重启能带来任何优势。更新过程:基于
SkipGram语言模型来更新参数 。SkipGram是一种语言模型,可最大化在一个句子中出现在窗口 内的单词之间的共现概率。在随机游走中,对于出现在窗口 中的所有上下文,我们最大化给定当前顶点 的
representation的条件下,上下文顶点 出现的概率。
DeepWalk算法:输入:
- 图
- 上下文窗口尺寸
embedding size- 每个节点开始的随机游走序列数量
- 每条随机游走序列长度
输出:顶点
representation矩阵算法步骤:
representation初始化:从均匀分布中采样,得到初始的 。从 构建一颗二叉树
binary tree建立二叉树是为了后续
SkipGram算法采用Hierarchical Softmax遍历,,遍历过程:
随机混洗顶点:
每次遍历的开始,随机混洗顶点。但是这一步并不是严格要求的,但是它可以加快随机梯度下降的收敛速度。
对每个顶点 :
- 利用随机游走生成器生成随机游走序列:
- 采用
SkipGram算法来更新顶点的representation:
SkipGram算法:输入:
- 当前的顶点
representation矩阵 - 单条随机游走序列
- 上下文窗口尺寸
- 学习率
- 当前的顶点
输出:更新后的顶点
representation矩阵算法步骤:
对每个顶点 :
对窗口内每个顶点 :
Hierarchical Softmax: 计算 是不容易的,因为这个概率的分母(归一化因子)计算代价太高(计算复杂度为 )。如果我们将顶点分配给二叉树的叶节点,那么预测问题就变为最大化树中特定路径的概率。如果到顶点 的路径由一系列树节点 ( 为root,)标识,则有:现在 可以通过分配给节点 的父节点的二分类器来建模。这降低了计算 的复杂度,计算复杂度从 降低到 。
我们可以通过为随机游走中的高频顶点分配树中更短的路径来进一步加快训练过程。霍夫曼编码用于减少树中高频元素的访问次数。
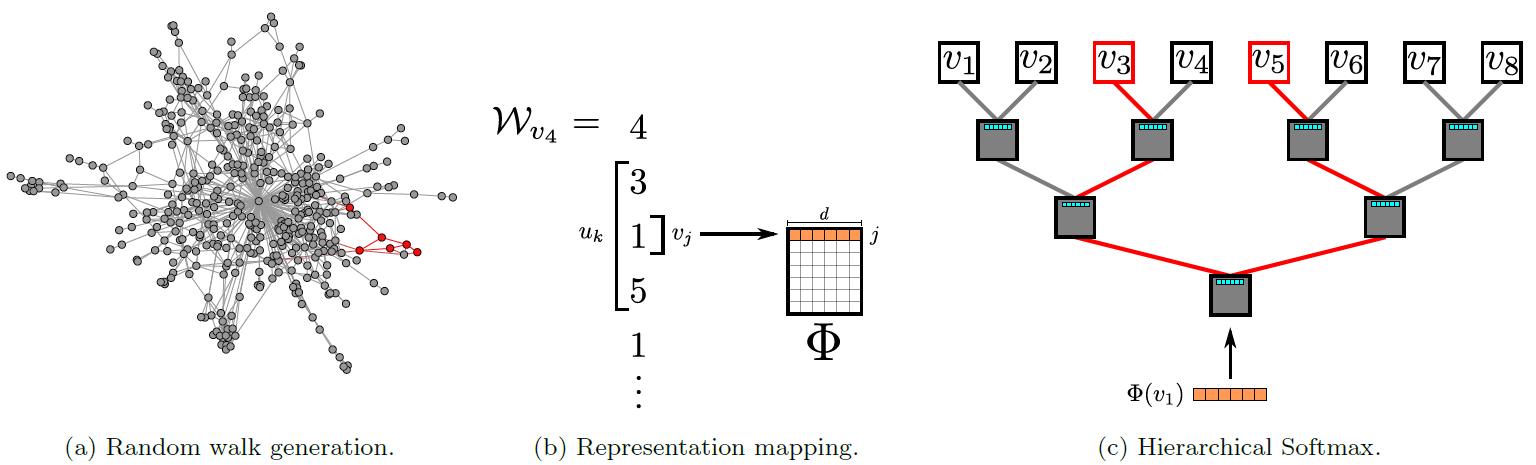
DeepWalk模型参数规模为 ,并且使用随机梯度下降来优化这些参数。导数是通过反向传播算法来估计的。SGD的学习率在最初时设置为0.025,然后随着目前为止看到的顶点数量呈线性下降。DeepWalk算法整体如下图所示。图
a:短随机游走序列的生成过程。图
b:在随机游走 上滑动一个长度为 的窗口,将中心顶点 映射到它的representation。图
c:Hierarchical Softmax在对应于从root到 的路径上的概率序列来分解 。 也是类似的。representation被更新从而最大化中心顶点 与它的上下文 共现的概率。
1.1.5 并行化
社交网络随机游走中的顶点频率分布和语言中的单词分布都遵循幂律分布。这会导致低频顶点的长尾效应,因此,对 的更新本质上将是稀疏的(即,同时对同一个顶点进行更新的概率很低)。 这将允许我们在多个
worker的情况下使用随机梯度下降的异步版本ASGD。鉴于我们的更新是稀疏的,并且我们没有利用锁来访问模型共享参数,
ASGD将实现最佳收敛速度。虽然我们在单台机器上使用多线程进行实验,但是已经证明了ASGD具有高度可扩展性,可用于非常大规模的机器学习。下图展示了并行化
DeepWalk的效果。结果表明:随着我们将worker数量增加到8,处理BlogCatalog和Flickr网络的加速是一致的。结果还表明,与串行执行DeepWalk相比,并行化DeepWalk的预测性能没有损失。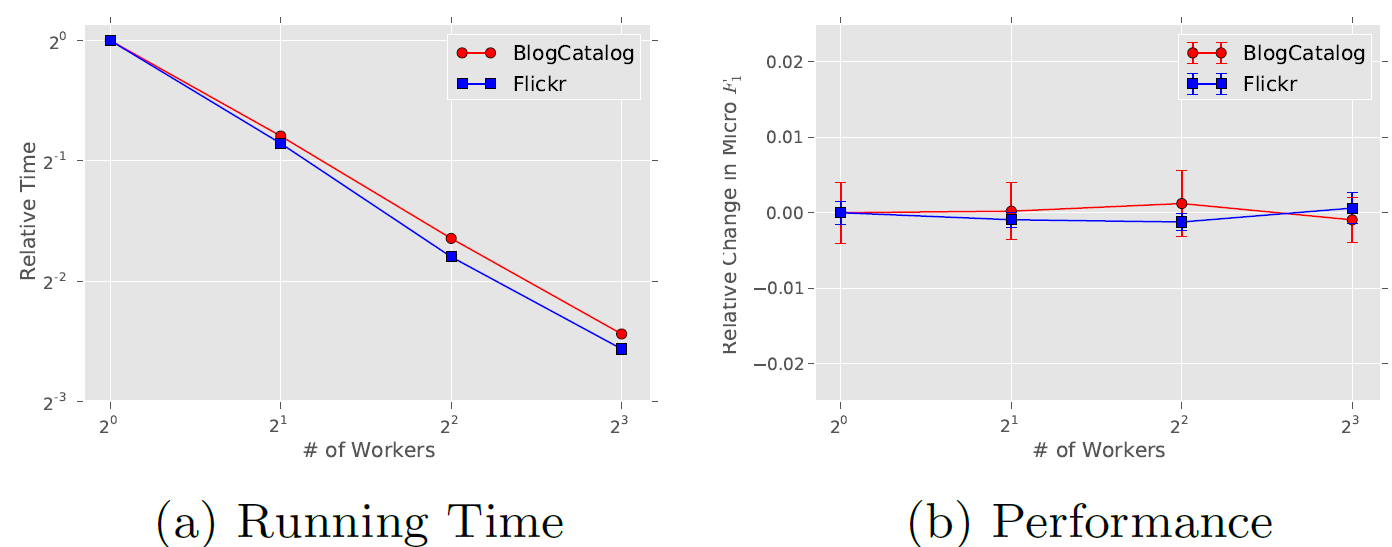
1.1.6 变体
这里我们讨论我们方法的一些变体,我们认为这些变体可能会引起人们的兴趣。
流式
streaming:我们方法的一个有趣变体是流式方法,它可以在不了解整个图的情况下实现。在这个变体中,来自图中的短随机游走直接传递给representation learning代码,并直接更新模型。这里需要对学习过程进行一些修改:
- 首先,不再使用衰减的学习率。相反,我们可以将学习率 初始化为一个小的常量。这需要更长的时间来学习,但是在某些
application中可能是值得的。 - 其次,我们不能再构建参数树
tree of parameters。如果 的基数cardinality是已知的(或者有界),我们可以为这个最大值构建Hierarchical Softmax tree。当首次看到顶点时,可以将它分配给剩余的叶节点之一。如果我们有能力估计顶点分布的先验,我们仍然可以使用霍夫曼编码来减少高频元素的访问次数。
- 首先,不再使用衰减的学习率。相反,我们可以将学习率 初始化为一个小的常量。这需要更长的时间来学习,但是在某些
非随机的游走:有些图是用户与一系列元素(如网站上页面的导航)交互的副产品而创建的。当通过这种非随机游走的
stream来创建图时,我们可以使用这个过程直接为建模阶段提供游走数据。以这种方式采样的图不仅会捕获与网络结构相关的信息,还会捕获与路径遍历频率相关的信息。以我们的观点来看,这个变体还包括语言建模。
sentence可以被视为经过适当设计的语言网络的、有目的的游走,而像SkipGram这样的语言模型旨在捕获这种行为。这种方法可以与流式变体结合使用,从而在不断演化的网络上训练特征,而无需显式地构建整个图。使用这种技术维护的
representation可以实现web-scale的分类,而无需处理web-scale图的麻烦。
1.2 实验
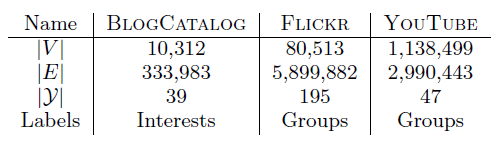
数据集:
BlogCatalog数据集:由博客作者提供的社交关系网络。标签代表作者提供的主题类别。Flickr数据集:Flickr网站用户之间的关系网络。标签代表用户的兴趣组,如“黑白照片”。YouTube数据集:YouTube网站用户之间的社交网络。标签代表用户的视频兴趣组,如“动漫、摔跤”。
baseline方法:为了验证我们方法的效果,我们和一些baseline方法进行比较。谱聚类
SpectralClustering:从图 的normalized graph Laplacian矩阵 中计算到的 个最小的特征向量,构成图的representation。使用 的特征向量隐含地建设图割graph cuts对分类有用。Modularity:从图 的Modularity计算得到top-d个特征向量,构成了图的representation。 的特征向量编码了关于 的modular graph partition信息。使用它们作为特征假设modular graph partition对于分类有用。EdgeCluster:基于k-means聚类算法对图 的邻接矩阵进行聚类。事实证明它的性能可以和Modularity相比,并且可以扩展到那些超大规模的图,这些图太大而难以执行谱分解spectral decomposition。wvRN:weighted-vote Relational Neighbor是一个关系分类器relational classi er。给定顶点 的邻居 ,wvRN通过邻居结点的加权平均来预估 :其中 为归一化系数。
该方法在实际网络中表现出惊人的良好性能,并被推荐为优秀的关系分类
relational classification的baseline。Majority:选择训练集中出现次数最多的标签作为预测结果(所有样本都预测成一个值)。
评估指标:对于多标签分类问题
multilabel classi cation,我们采用Macro-F1和Micro-F1作为评估指标。Macro-F1:根据整体的混淆矩阵计算得到的 值。micro-F1:先根据每个类别的混淆矩阵计算得到各自的 值,然后对所有 值取平均。
另外我们采用模型提取的特征训练
one-vs-rest逻辑回归分类器,根据该分类器来评估结果。我们随机采样一个比例为 的带标签顶点作为训练集,剩余标记节点作为测试集。我们重复该过程
10次,并报告Macro-F1的平均性能和Micro-F1的平均性能。注意,
DeepWalk是无监督的representation learning方法,因此训练过程是无需label数据的。这里的标记数据是在无监督学习之后,利用学到的顶点representation进行有监督分类,分类算法为逻辑回归,从而评估顶点representation的效果。实验配置:
- 对所有模型,我们使用由
LibLinear实现的one-vs-rest逻辑回归进行分类。 DeepWalk的超参数为 。- 对于
SpectralClustering, Modularity, EdgeCluster等方法,我们选择 。
- 对所有模型,我们使用由
1.2.1 实验结果
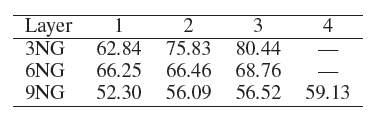
BlogCatalog数据集:我们评估 的结果。结果如下表,粗体表示每一列最佳结果。结论:
DeepWalk性能始终优于EdgeCluster,Modularity,wvRN。事实上当
DeepWalk仅仅给出20%标记样本来训练的情况下,模型效果优于其它模型90%的标记样本作为训练集。虽然
SpectralClustering方法更具有竞争力,但是当数据稀疏时DeepWalk效果最好:对于Macro-F1指标, 时DeepWalk效果更好;对于Micro-F1指标, 时DeepWalk效果更好。当仅标记图中的一小部分时,
DeepWalk效果最好。因此后面实验我们更关注稀疏标记图sparsely labeled graph。
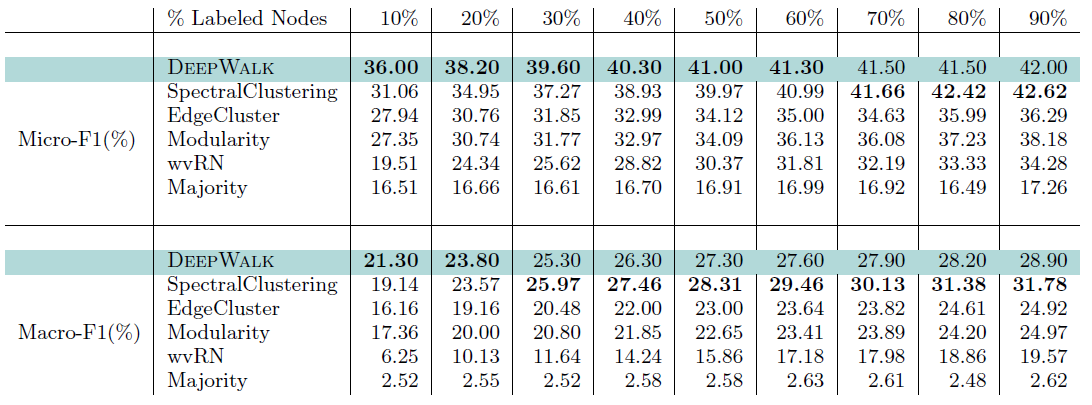
Flickr数据集:我们评估 的结果。结果如下表,粗体表示每一列最佳结果。结论与前面的实验一致。- 在
Micro-F1指标上,DeepWalk比其它基准至少有3%的绝对提升。 - 在
Micro-F1指标上,DeepWalk只需要3%的标记数据就可以打败其它方法10%的标记数据,因此DeepWalk的标记样本需求量比基准方法少60%。 - 在
Macro-F1指标上,DeepWalk性能接近SpectralClustring,击败了所有其它方法。

- 在
YouTube数据集:我们评估 的结果。结果如下表,粗体表示每一列最佳结果。由于
YouTube规模比前面两个数据集大得多,因此我们无法运行两种基准方法SpecutralClustering, Modularity。DeepWalk性能远超EdgeCluster基准方法:- 当标记数据只有
1%时,DeepWalk在Micro-F1指标上相对EdgeCluster有14%的绝对提升,在Macro-F1指标上相对EdgeCluster有10%的绝对提升。 - 当标记数据增长到
10%时,DeepWalk提升幅度有所下降。DeepWalk在Micro-F1指标上相对EdgeCluster有3%的绝对提升,在Macro-F1指标上相对EdgeCluster有4%的绝对提升。
- 当标记数据只有
DeepWalk能扩展到大规模网络,并且在稀疏标记环境中表现出色。

1.2.2 参数敏感性
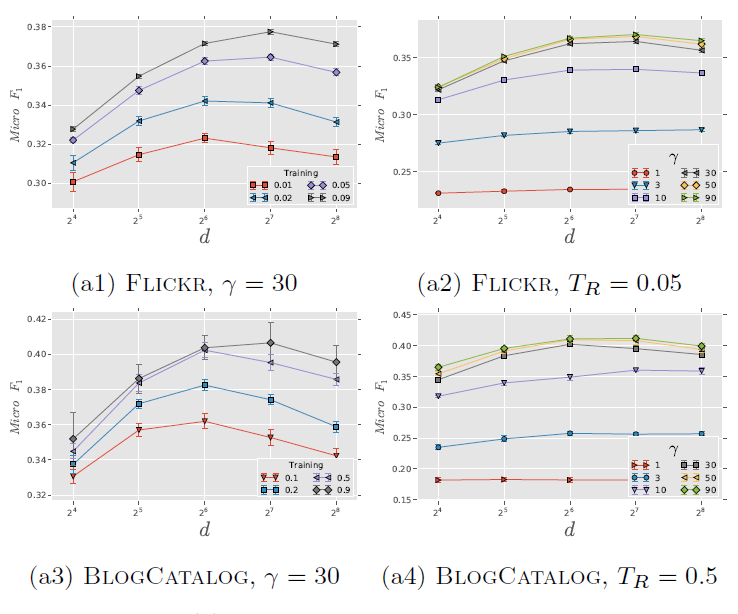
为评估超参数的影响,我们在
Flickr和BlogCatalog数据集上进行实验。我们固定窗口大小 和游走长度 。然后我们改变潜在维度 、每个顶点开始的随机游走数量 、可用的训练数据量 ,从而确定它们对于网络分类性能的影响。考察不同 的效果:
图
a1和 图a3考察不同 和不同 的效果。Flickr和BlogCatalog数据集上模型的表现一致:模型最佳尺寸 取决于训练样本的数量。注意:
Flickr的1%训练样本和BlogCatalog的10%训练样本,模型的表现差不多。图
a2和图a4考察不同 和不同 的效果。在不同 取值上,模型性能对于不同 的变化比较稳定。- 从 开始继续提高 时模型的效果提升不大,因此 几乎取得最好效果。继续提升效果,计算代价上升而收益不明显。
- 不同的数据集中,不同 值的性能差异非常一致,尽管
FLICKR包含边的数量比BLOGCATALOG多一个数量级。
这些结论表明:我们的方法可以得到各种size 的有用模型。另外,模型性能取决于模型看到的随机游走数量,模型的最佳维度取决于可用的训练样本量。
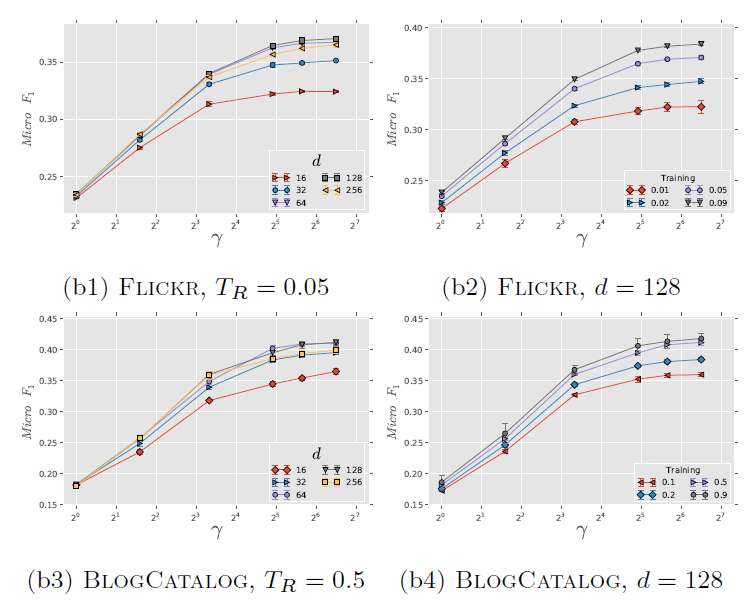
考察不同 的影响。图
b1和b3考察不同 的效果,图b2和b4考察了不同 的效果。实验结果表明,它们的表现比较一致:增加 时开始可能有巨大提升,但是当 时提升效果显著下降。
这些结果表明:仅需要少量的随机游走,我们就可以学习有意义的顶点潜在表示。
二、LINE[2015]
信息网络
information network在现实世界中无处不在,例如航空网络、出版物网络、社交网络、通信网络、以及万维网。这些信息网络的规模从数百个节点到数百万、甚至数十亿个节点不等。分析大型信息网络已经引起学术界和工业界越来越多的关注。论文《LINE: Large-scale Information Network Embedding》研究了将信息网络嵌入到低维空间中的问题,其中每个顶点都表示为一个低维向量。这种低维embedding在各种application中非常有用,例如可视化visualization、节点分类node classi fication、链接预测link prediction、推荐recommendation。机器学习文献中已经提出了各种
graph embedding方法。它们通常在较小的网络上表现良好。当涉及现实世界的信息网络时(这些网络通常包含数百万节点、数十亿条边),这个问题变得更具挑战性。例如,2012年Twitter的followee-follower网络包含1.75亿活跃用户、大约200亿条边。大多数现有的graph embedding算法无法针对这种规模的网络进行扩展。例如,MDS、IsoMap、Laplacian eigenmap等经典graph embedding算法的时间复杂度至少是顶点数量的二次方,这对于具有数百万个节点的网络来说是不可行的。尽管最近的一些工作研究了大规模网络的
embedding,但是这些方法要么采用了不是为网络而设计的间接方法(如《Distributed large-scale natural graph factorization》),要么缺乏为网络embedding量身定制的、明确的目标函数(如《Deepwalk: Online learning of social representations》)。论文《LINE: Large-scale Information Network Embedding》预计:具有精心设计的、保持图属性的目标函数和有效优化技术的新模型,应该可以有效地找到数百万个节点的embedding。因此在该论文中,作者提出了一种称为LINE的network embedding模型,它能够扩展到非常大的、任意类型的网络:无向/有向图、无权/有权图。该模型优化了一个目标函数,该目标函数同时保持了局部网络结构local network structure和全局网络结构global network structure。局部网络结构(一阶邻近性):自然地,局部网络结构由网络中观察到的链接来表示,它捕获顶点之间的一阶邻近性
first-order proximity。大多数现有的graph embedding算法都旨在保持这种一阶邻近性,例如IsoMap、Laplacian eigenmap,即使这些算法无法扩展。全局网络结构(二阶邻近性):作者观察到:在现实世界的网络中,实际上很多合法的链接都未被观测到。换句话讲,在现实世界数据中观察到的一阶邻近性不足以保持全局网络结构。作为补充,作者探索了顶点之间的二阶邻近性
second-order proximity,这是通过顶点的共享邻域结构shared neighborhood structure来确定的,而不是通过观察到的直接连接强度来确定。二阶邻近性的通用概念可以解释为:具有共享邻居的节点之间可能是相似的。这种直觉可以在社会学和语言学的理论中找到。例如:在社交网络中,“两个人的社交网络的重叠程度与他们之间的联系强度相关”(
the degree of overlap of two people's friendship networks correlates with the strength of ties between them);在文本网络中,“一个词的意思是由它的使用环境所形成的”(You shall know a word by the company it keeps)。确实,有很多共同好友的人很可能有相同的兴趣并成为朋友,而与许多相似词一起使用的单词很可能具有相似的含义。下图展示了一个说明性的例子,其中边越粗权重越大:
- 由于顶点
6和顶点7之间的边的权重很大,即顶点6和顶点7具有较高的一阶邻近性,因此它们的representation应该在embedding空间中彼此靠近。 - 另一方面,虽然顶点
5和顶点6之间没有直接链接,但是它们共享了许多共同的邻居,即它们具有很高的二阶邻近性,因此它们的representation应该在embedding空间中彼此靠近。
论文期望对二阶邻近性的考虑能够有效地补充一阶邻近性的稀疏性,从而更好地保持网络的全局结构。在论文中,作者将展示精心设计的目标函数,从而保持一阶邻近性和二阶邻近性。
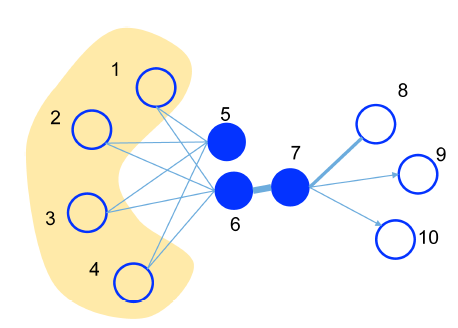
- 由于顶点
即使找到了一个合理的目标函数,为一个非常大的网络优化该目标函数也是具有挑战性的。近年来,引起大家关注的一种优化方法是随机梯度下降。然而,论文表明:直接部署随机梯度下降对现实世界的信息网络是有问题的。这是因为在许多网络中,边是加权的,并且权重通常呈现高方差
high variance。考虑一个单词共现网络word co-occurrence network,其中word pair的权重(共现)可能从 “一” 到 “几十万” 不等。这些边的权重将乘以梯度,导致梯度爆炸从而影响模型性能。因为
LINE的目标函数是加权的交叉熵,权重为word pair共现次数。为了解决这个问题,论文提出了一种新的边采样方法
edge-sampling method,该方法提高了推断的效率efficiency和效果effectiveness。作者以与边权重成正比的概率对边进行采样,然后将采样后的边视为用于模型更新的二元边binary edge。通过这个采样过程,目标函数保持不变,边的权重不再影响梯度。这可能会导致数据稀疏性问题:即一些权重很小的边未被采样到。
LINE非常通用,适用于有向/无向图、加权/未加权图。论文使用各种真实世界的信息网络(包括语言网络language network、社交网络social network、引文网络citation network)来评估LINE的性能。论文在多个数据挖掘任务中评估了学到的embedding的有效性,包括单词类比word analogy、文本分类text classification、节点分类node classification。结果表明,LINE模型在效果和效率方面都优于其它竞争baseline。LINE能够在几个小时内在单台机器上学习具有数百万个节点、数十亿条边的网络的embedding。总而言之,论文主要贡献:
- 论文提出了一个叫做
LINE的、新的network embedding模型,该模型适用于任意类型的信息网络,并可轻松地扩展到数百万个节点。该模型有一个精心设计的目标函数,可以同时保持一阶邻近性和二阶邻近性。 - 论文提出了一种边采样算法来优化目标函数,该算法解决了经典随机梯度下降的局限性,提高了推断的效率和效果。
- 论文对现实世界的信息网络进行了广泛的实验,实验结果证明了
LINE模型的效率和效果。
相关工作:
我们的工作通常与
graph embedding或降维的经典方法有关,例如多维缩放multidimensional scaling: MDS、IsoMap、LLE、Laplacian Eigenmap。这些方法通常首先使用数据点data point的特征向量feature vector构建affinity graph,例如数据的K-nearest neighbor graph,然后将affinity graph嵌入到低维空间中。然而,这些算法通常依赖于求解
affinity matrix的top-n eigenvectors,其复杂度至少是节点数量的二次方,使得它们在处理大规模网络时效率很低。最近的文献中有一种叫做图分解
graph factorization(《Distributed large-scale natural graph factorization》) 的技术。该方法通过矩阵分解找到大规模图的低维embedding,并使用随机梯度下降进行优化。这是可行的,因为图可以表示为affinity matrix。然而,矩阵分解的目标不是为网络设计的,因此不一定保持了全局网络结构。直觉上,图分解预期具有较高一阶邻近性的节点的
representation彼此靠近。相反,LINE模型使用了一个专门为网络设计的目标函数,该目标函数同时保持了一阶邻近性和二阶邻近性。另外,图分解方法仅适用于无向图,而LINE方法适用于无向图和有向图。与我们最相关的、最新的工作是
DeepWalk,它通过截断的随机游走truncated random walk来学习社交网络的embedding。尽管在经验上是有效的,但是DeepWalk并为提供明确的目标来阐明保持哪些网络属性。直觉上,DeepWalk期望具有较高二阶邻近性的节点产生相似的低维representation,而LINE同时保持一阶邻近性和二阶邻近性。DeepWalk使用随机游走来扩展顶点的邻域,这类似于深度优先搜索depth-first search: DFS。LINE使用广度优先搜索breadth- first search: BFS策略,这是一种更合理的二阶邻近性方法。另外,DeepWalk仅适用于无权图,而LINE适用于加权图和无权图。
在实验中,我们使用各种真实世界的网络来评估
LINE和这些方法的效果。
2.1 模型
2.1.1 问题定义
信息网络
information network的定义:一个信息网络定义为 ,其中:为顶点集合,每个元素代表一个数据对象
data object。为边集合,每个元素代表两个数据对象之间的关系。
每条边 是一个有序的
pair,它关联一个权重 表示关系的强度。- 如果 是无向图,则有 且 ;如果 是有向图,则有 且 。
- 如果 是无权图,则 ,这种边称作二元边
binary edge,权重表示相连/不相连;如果 是带权图,则 则边的取值是实数,这种边表示连接的紧密程度。
这里所有权重都是非负的,并不考虑负权重。
在实践中,信息网络可以是有向的(如引文网络),也可以是无向的(如
Facebook的用户社交网络)。边的权重可以是二元binary的,也可以是任何实际值。注意,虽然边的权重理论上也可以是负的,但是这里我们仅考虑非负的权重。例如,在引文网络和社交网络中, 是二元的。在不同共现网络中, 可以取任何非负值。某些网络中的边的权重方差可能很大,因为某些对象会多次共现、而其它对象可能很少共现。将信息网络嵌入到低维空间在各种
application中都很有用。为了进行embedding,网络结构必须被保持。第一个直觉是必须保持局部网络结构,即顶点之间的局部pairwise邻近性。我们将局部网络结构定义为顶点之间的一阶邻近性。一阶邻近性
first-order proximity的定义:网络中的一阶邻近性是两个顶点之间的局部pairwise邻近性。对于边 连接的顶点pair,边上的权重 表示顶点 和顶点 之间的一阶邻近性。如果在顶点 和顶点 之间没有观察到边,则它们之间的一阶邻近性为0。一阶邻近性通常意味着现实世界网络中两个节点的相似性
similarity。例如:在社交网络中彼此成为好友的人往往有相似的兴趣,在万维网中相互链接的网页倾向于谈论相似的话题。由于这种重要性,许多现有的graph embedding算法(如IsoMap、LLE、Laplacian eigenmap、graph factorization)都以保持一阶邻近性为目标。然而,在现实世界的信息网络中,观察到的链接仅是一小部分,还有许多其他链接发生了缺失
missing。缺失链接上的顶点pair之间的一阶邻近性为零,尽管它们本质上彼此非常相似。因此,仅靠一阶邻近性不足以保持网络结构,重要的是寻找一种替代的邻近性概念来解决稀疏性问题。一个自然的直觉是:共享相似邻居的顶点往往彼此相似。例如:在社交网络中,拥有相同朋友的人往往有相似的兴趣,从而成为朋友;在单词共现网络中,总是与同一组单词共现的单词往往具有相似的含义。因此,我们定义了二阶邻近性,它补充了一阶邻近性并保持了网络结构。二阶邻近性
second-order proximity的定义:网络中一对顶点 之间的二阶邻近性是它们的邻域网络结构之间的相似性。数学上,令 为顶点 和所有顶点的一阶邻近性向量,然后顶点 和顶点 之间的二阶邻近性由 和 的相似性来确定。如果没有任何顶点同时与 和 相连,则 和 之间的二阶邻近性为0。我们研究了
network embedding的一阶邻近性和二阶邻近性,定义如下。大规模信息网络嵌入
Large-scale Information Network Embedding:给定一个大型网络 ,大规模信息网络嵌入的问题旨在将每个顶点 映射到一个低维空间 中,即学习一个函数 ,其中 。在空间 中,顶点之间的一阶邻近性和二阶邻近性都可以得到保持。现实世界信息网络的理想
embedding模型必须满足几个要求:- 首先,它必须能够同时保持顶点之间的一阶邻近性和二阶邻近性。
- 其次,它必须针对非常大的网络可扩展,比如数百万个顶点、数十亿条边。
- 第三,它可以处理具有任意类型边的网络:有向/无向、加权/无权的边。
这里,我们提出了一个叫做
LINE的新型network embedding模型,该模型满足所有这三个要求。我们首先描述了LINE模型如何分别保持一阶邻近性和二阶邻近性,然后介绍一种简单的方法来组合这两种邻近性。
2.1.2 保持一阶邻近性的 LINE
一阶邻近性是指网络中顶点之间的局部
pairwise邻近性。为了对一阶邻近性建模,对于每条无向边 ,我们定义顶点 和 之间的联合概率为:其中 为顶点 的低维
representation向量。上式定义了 空间上的一个概率分布 ,它的经验概率
empirical probability定义为:其中 为所有边权重之和。
为了保持一阶邻近性,一个直接的方法是最小化以下目标函数:
其中 为两个概率分布之间的距离。这里我们选择
KL散度作为距离函数,因此有:注意,上述一阶邻近性仅适用于无向图,而无法适用于有向图。
通过最小化 从而得到 ,我们可以得到每个顶点在 维空间中的
representation。读者注:
- 上式的物理意义为:观测边的加权负对数似然,每一项权重为边的权重。
- 上式并不是严格的
KL散度,它用到的是两个非归一化概率 和 。 - 最小化
KL散度等价于最小化交叉熵:
其中省略了常数项 。
2.1.3 保持二阶邻近性的 LINE
二阶邻近性适用于有向图和无向图。给定一个网络,不失一般性,我们假设它是有向的(一条无向边可以被认为是两条方向相反、权重相等的有向边)。二阶邻近性假设:共享邻域的顶点之间彼此相似。
在这种情况下,每个顶点也被视为一个特定的 “上下文”(
context)。我们假设:如果两个顶点的上下文相似,则这两个顶点是相似的。因此,每个顶点扮演两个角色:顶点本身、以及其它顶点的特定上下文。我们引入两个向量 和 ,其中 为顶点 作为顶点本身时的
representation, 为顶点 作为其它顶点的特定上下文时的representation。对于每条有向边 ,我们首先定义由顶点 生成上下文顶点 的概率为:其中 为顶点集合的大小。
对于每个顶点 ,上式实际上定义了上下文(即网络上整个顶点集合)中的条件分布 。如前所述,二阶邻近性假设具有相似上下文分布的顶点之间彼此相似。为了保持二阶邻近性,我们应该使得由低维
representation指定的上下文条件分布 接近经验分布 。因此,我们最小化以下目标函数:其中:
为顶点 的重要性。由于网络中顶点的重要性可能不同,我们在目标函数中引入了 来表示顶点 在网络中的重要性。 可以通过顶点的
degree来衡量,也可以通过PageRank等算法进行估计。注意:目标函数 中并未引入顶点重要性,而目标函数 中引入了顶点重要性。这里引入顶点重要性是为了得到 的一个简洁的公式。
是两个概率分布之间的距离。
经验分布 定义为 ,其中 是边 的权重, 是顶点 的出度
out-degree,即 , 为顶点 的out-neighbors。
在本文中,为简单起见,我们将 设为顶点 的
out-degree,即 。这里我们也采用KL散度作为距离函数。忽略一些常量,则我们得到:通过最小化 从而得到 ,我们可以得到顶点 在 维空间中的
representation。读者注:
- 上式的物理意义为:条件概率的加权负对数似然,每一项权重为边的权重。
- 与 相反,这里是严格的
KL散度,它用到的是两个归一化概率 和 。 - 同样地,最小化
KL散度等价于最小化交叉熵。 - 二阶邻近性
LINE类似于上下文窗口长度为1的DeepWalk,但是DeepWalk仅用于无权图而LINE可用于带权图。
2.1.4 组合一阶邻近性和二阶邻近性
为了通过同时保持一阶邻近性和二阶邻近性来嵌入网络,我们在实践中发现一种简单的、有效的方法是:分别训练一阶邻近性
LINE模型、二阶邻近性LINE模型;然后对于每个顶点,拼接这两种方法得到的embedding。实验部分作者提到:需要对拼接后的向量各维度进行加权从而平衡一阶
representation向量和二阶representation向量的关系。在监督学习任务中,可以基于训练数据自动得到权重;在无监督学习任务中,无法配置这种权重。因此组合一阶邻近性和二阶邻近性仅用在监督学习任务中。组合一阶邻近性和二阶邻近性的更合理的方法是联合训练目标函数 和 ,我们将其留作未来的工作。
2.1.5 模型优化
负采样:优化目标函数 的计算量很大,在计算条件概率 时需要对整个顶点集合进行求和。为了解决这个问题,我们采用了负采样方法,它对每条边 根据一些噪声分布
noisy distribution来负采样多条负边negative edge。具体而言,我们为每条边 指定以下目标函数:其中:
- 为
sigmoid函数。 - 为期望。
- 为噪声分布。
注意:目标函数 中的概率 不涉及对整个顶点集合进行求和。
第一项对观察到的边进行建模,第二项对从噪声分布中采样的负边进行建模, 是负边的数量。我们根据
Word2Vec的建议设置 ,其中 为顶点 的出度out-degree。- 为
对于目标函数 ,存在一个平凡解
trivial solution:此时 ,使得 取最小值。
为了避免平凡解,我们也可以利用负采样方法,对于每条边 :
第一项对观察到的边进行建模,第二项对从噪声分布中采样的负边进行建模, 是负边的数量。
注意这里没有上下文顶点,因此没有 。
2.1.6 边采样
我们采用异步随机梯度算法
ASGD来优化目标函数。在每一步中,ASGD算法采样了一个mini-batch的边,然后更新模型参数。假设采样到边 ,则顶点 的embedding向量 被更新为:注意,梯度将乘以边的权重。当边的权重具有高方差时,这将成为问题。例如,在一个单词共现网络中,一些词会共现很多次(例如,数万次),而另一些词只会共现几次。在这样的网络中,梯度的
scale不同,很难找到一个好的学习率:- 如果我们根据权重小的边选择较大的学习率,那么权重大的边上的梯度将会爆炸。
- 如果我们根据权重大的边选择较小的学习率,那么权重小的边上的梯度会非常小。
基于边采样
edge-sampling的优化:解决上述问题的直觉是,如果所有边的权重相等(例如,具有二元边binary edge的网络),那么如何选择合适的学习率将不再成为问题。因此,一个简单的处理是将加权边展开为多个二元边。例如,将权重为 的边展开为 条二元边。虽然这能够解决问题,但是会显著增加内存需求,尤其是当边的权重非常大时,因为这显著增加边的数量。为此,可以从原始边中采样,并将采样后的边视为二元边,采样概率与原始边的权重成正比。通过这种边采样处理,整体目标函数保持不变。问题归结为如何根据权重对边进行采样。
令 为边权重的序列。
- 首先,简单地计算权重之和 。
- 然后,在 范围内随机采样一个值,看看这个随机值落在哪个区间 。
该方法需要 的时间来采样,当边的数量 很大时,其代价太高。我们使用
alias table方法来根据边的权重来采样。当从相同的离散分布中重复采样时,其平摊的时间复杂度为 。从
alias table中采样一条正边需要 时间。此外,负采样优化需要 时间,其中 为负采样数量。因此,每个step都需要 时间。在实践中,我们发现用于优化的
step数量通常与边的数量 成正比。因此,LINE的整体时间复杂度为 ,与边的数量 成线性关系,而不依赖于顶点数量 。边采样在不影响效率的情况下提高了随机梯度下降的效果。
2.1.7 讨论
我们讨论了
LINE模型的几个实际问题。低度
low degree顶点 :一个实际问题是如何准确地嵌入degree较小的顶点。由于此类顶点的邻居数量非常少,因此很难准确地推断其representation,尤其是使用严重依赖于 “上下文” 数量的二阶邻近性方法。一种直觉的解决方案是通过添加更高阶的邻居(如邻居的邻居)来扩展这些顶点的邻居。在本文中,我们只考虑向每个顶点添加二阶邻居,即邻居的邻居。顶点 和它的二阶邻居 之间的权重被设置为:
其中:
- 为顶点 的一阶邻居集合。
- 为顶点 的二阶邻居集合。
实践中,只能添加与
low degree顶点 具有最大邻近性 的二阶邻居顶点子集 。新顶点:另一个实际问题是如何找到新顶点的
representation。对于一个新顶点 ,如果它与现有顶点存在链接,则我们可以获得新顶点在现有顶点上的经验分布 。为了获得新顶点的
embedding,根据目标函数 和 ,一个直接方法是最小化以下目标函数之一:我们更新新顶点的
embedding,并保留现有顶点的embedding。注意,对于有向边的图,需要考虑新顶点到已有顶点的链接、以及已有顶点到新顶点的链接,一共两个方向。
如果新顶点和现有顶点之间不存在链接,则我们必须求助于其它信息,如顶点的文本信息。我们将其留作我们未来的工作。
未来工作:
- 研究网络中一阶邻近性和二阶邻近性以外的高阶邻近性。
- 研究异质信息网络的
embedding,例如具有多种类型的顶点。
2.2 实验
我们通过实验评估了
LINE的效果和效率。我们将LINE应用于几个不同类型的、大型的现实世界网络,包括一个语言网络language network、两个社交网络social network、两个引文网络citation network。数据集:
- 语言网络
Language Network数据集:我们从整个英文维基百科页面构建了一个单词共现网络。我们选择滑动窗口为5,并认为滑动窗口内的单词是共现的。出现频次小于5的单词被过滤掉。 - 社交网络
Social Network数据集:和DeepWalk一致,我们也采用Flickr和Youtube数据集。Flickr网络比Youtube网络更稠密。 - 引文网络
Citation Network数据集:使用DBLP数据集构建的作者引文网络author citation network、论文引用网络paper citation network。作者引文网络记录了一位作者撰写、并被另一位作者引文的论文数量。
这些数据集的统计见下表,其中:
- 所有这些网络囊括了有向图/无向图,带权图/无权图。
- 每个网络至少包含
50万顶点和数百万条边,最大的网络包含200万顶点和十亿条边。

- 语言网络
baseline方法:我们将LINE模型与几种现有的graph embedding方法进行比较,这些方法能够扩展到非常大的网络。我们没有与一些经典的graph embedding算法(如MDS、IsoMap、Laplacian eigenmap)进行比较,因为这些算法无法处理如此规模的网络。Graph Factorization:GF:一个信息网络可以表示为一个亲和度矩阵affinity matrix,并通过矩阵分解来获取每个顶点的低维representation。GF方法通过随机梯度下降法进行优化,因此可以处理大型网络。但是它仅适合无向图。DeepWalk:DeepWalk是最近提出的、一种用于社交网络embedding的方法,它仅适用于无权网络。对每个顶点,DeepWalk使用从该顶点开始的截断随机游走来获取上下文信息,基于上下文信息建模来获取每个顶点的低维表达。因此,该方法仅利用二阶邻近性。LINE-SGD:直接通过SGD来优化目标函数的LINE模型。在优化过程中并没有使用边采样策略,因此对于采样到的正边,我们需要将边的权重直接乘以梯度。该方法有两个变种:
LINE-SGD(1st):LINE-SGD的一阶邻近模型,它的优化目标是 。该模型仅适用于无向图。LINE-SGD(2nd):LINE-SGD的二阶邻近模型,它的优化目标是 。该模型可用于无向图和有向图。
LINE:标准的LINE模型。在优化过程中使用了边采用策略。该方法也有两个变种,分别为:
LINE(1st):LINE的一阶邻近模型,它的优化目标是 。该模型仅适用于无向图。LINE(2nd):LINE的二阶邻近模型,它的优化目标是 。该模型可用于无向图和有向图。
LINE(1st+2nd):同时拼接了LINE(1st)和LINE(2nd)学到的representation向量,得到每个顶点的一个拼接后的、更长的representation向量。需要对拼接后的向量各维度进行加权从而平衡一阶
representation向量和二阶representation向量的关系。在监督学习任务中,可以基于训练数据自动得到权重;在无监督学习任务中,无法配置这种权重。因此LINE(1st+2nd)仅用在监督学习任务中。
参数配置:
所有方法都统一的配置:
- 随机梯度下降的
batch-size = 1,即每个批次一个样本。因此迭代的样本数量就等于更新的step数量。 - 学习率 ,其中: 为初始化学习率; 表示第 个更新
step; 为总的更新step数量。 - 所有得到的
embedding向量都进行归一化: 。 - 为公平比较,语言网络数据集的
embedding向量维度设为200(因为word2vec方法采用该配置);其它网络数据集的embedding向量维度默认设为128。
- 随机梯度下降的
对于
LINE及其变种,负采样比例 。对于
LINE(1st)、LINE(2nd)及其变种,总迭代步数 等于100亿 ;对于GF,总迭代步数 等于200亿。对于
DeepWalk窗口大小win=10,游走序列长度t=40,每个顶点出发的序列数量 。
2.2.1 语言网络
语言网络:语言网络数据集包含
200万顶点和10亿条边。我们使用两个任务来评估学到的embedding的有效性:单词类比word analogy、文档分类document classification。单词类比
word analogy:给定一对单词(a,b)和一个单词c,该任务的目标是寻找单词d,使得c和d的关系类比于a和b的关系。记作:如:“(中国,北京 )” 对应于 “(法国,?)” ,这里的目标单词为 “巴黎”。
因此给定单词
a,b,c的embedding向量,该任务的目标是寻找单词 ,使得该单词的embedding尽可能与 相似:在这个任务中使用了两种类型的单词类比:语义
semantic、句法syntactic。在维基百科语言网络上的单词类比结果如下表所示。其中:
- 对
GF方法,边的权重定义为单词共现次数的对数,这比直接采用单词共现次数更好的性能。 - 对
DeepWalk方法,尝试使用不同的截断阈值从而将网络权重二元化binarize。最终当所有边都被保留下来时,模型性能最好。 SkipGram直接从原始维基百科页面内容文本而不是语言网络来学习词向量。窗口大小设置为5。- 所有模型都是在单机上运行
16个线程来计算,机器配置:1T内存、2.0GHZ的40个CPU。
结论:
LINE(2nd)优于所有其它方法。LINE(2nd)优于GF,LINE(1st)等一阶方法。这表明:和一阶邻近性相比,二阶邻近性更好的捕获了单词的语义。因为如果单词
a和b的二阶邻近性很大,则意味着可以在相同上下文中可以相互替换单词a和b。这比一阶邻近性更能说明相似语义。虽然
DeepWalk也探索了二阶邻近性,但是其性能不如LINE(2nd),甚至不如一阶方法的GF,LINE(1st)。这是因为
DeepWalk忽略了单词共现次数的原因,事实上语言网络中单词共现频次非常重要。这个解释不通。单词共现次数隐含在随机游走过程中:单词共现次数越大,则随机游走被采样到的概率越大。
在原始语料上训练的
SkipGram模型也不如LINE(2nd),原因可能是语言网络比原始单词序列更好的捕获了单词共现的全局信息。
采用
SGD直接优化的LINE版本效果要差得多。这是因为语言网络的边的权重范围从个位数到上千万,方差很大。这使得最优化过程受到严重影响。在梯度更新过程中进行边采样处理的
LINE模型有效解决了该问题,最终效果要好得多。LINE(1st)和LINE(2nd)的训练效率很高,对于两百万顶点、十亿边的网络只需要不到3个小时。LINE(1st),LINE(2nd)训练速度比GF至少快10%,比DeepWalk快5倍。LINE-SGD版本要稍慢,原因是在梯度更新过程中必须应用阈值截断技术防止梯度爆炸。

- 对
文档分类:另一种评估
word embedding质量的方法是使用word embedding来计算document representation,然后通过文档分类任务评估效果。为了获得文档向量,我们选择了一种非常简单的方法,即选取该文档中所有单词的word embedding的均值。这是因为我们的目标是将不同方法得到的word embedding进行对比,而不是寻找document embedding的最佳方法。我们从维基百科种选择
7种不同的类别 “艺术、历史、人类、数学、自然、技术、体育”,对每个类别随机抽取1万篇文章,其中每篇文章都只属于单个类别(如果文章属于多个类别就丢掉)。所有这些文章及其类别就构成了一个带标记的多类别语料库。我们随机抽取不同百分比的标记文档进行训练,剩余部分进行评估。所有文档向量都使用
LibLinear package训练one-vs-rest逻辑回归分类器。我们报告了分类结果的Micro-F1和Macro-F1指标。在维基百科语言网络上的文本分类结果如下表所示。其中我们分别抽取
10%~90%的标记样本作为训练集,剩余部分作为测试集。对每一种拆分我们随机执行10轮取平均结果。结论:
GF方法优于DeepWalk,因为DeepWalk忽略了单词共现次数。LINE-SGD性能较差,因为边权重方差很大所以LINE-SGD的梯度更新过程非常困难。采用边采样的
LINE模型优于LINE-SGD,因为梯度更新过程中使用边采样能解决边权重方差很大带来的学习率选择问题。LINE(1st) + LINE(2nd)性能明显优于其它所有方法,这表明一阶邻近度和二阶邻近度是互补的。注意,对于监督学习任务,拼接了
LINE(1st)和LINE(2nd)学到的embedding是可行的。
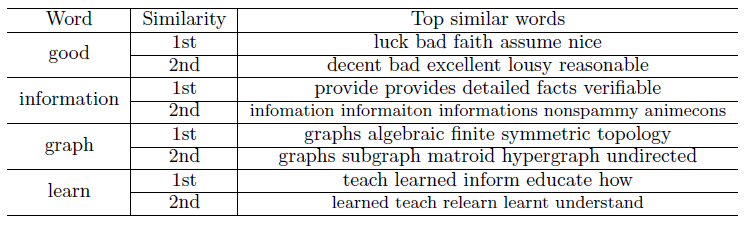
为了更深入地了解一阶邻近性和二阶邻近性,下表对给定单词,分别采用一阶邻近性模型和二阶邻近性模型召回其最相似的
top单词。可以看到:- 二阶邻近度召回的最相似单词都是语义相关的单词。
- 一阶邻近度召回的最相似单词是语法相关、语义相关的混合体。
2.2.2 社交网络
相比语言网络,社交网络更为稀疏,尤其是
YouTube网络。我们通过多标签分类任务来评估每个模型的embedding效果。多标签分类任务将每个顶点分配到一个或者多个类别,每个类别代表一个社区community。最终评估分类结果的Micro-F1和Macro-F指标。我们分别抽取
10%~90%的标记样本作为训练集,剩余部分作为测试集。对每一种拆分随机执行10轮取平均结果。Flickr Network数据集:我们选择最热门的5个类别作为分类的类别,评估结果如下表。LINE(1st)模型优于GF模型,这表明LINE(1st)模型比GF模型具有更好的一阶邻近性建模能力。LINE(2nd)模型优于DeepWalk模型,这表明LINE(2nd)模型比DeepWalk模型具有更好的二阶邻近性建模能力。LINE(1st)模型略微优于LINE(2nd)模型,这和语言网络的结论相反。原因有两个:- 社交网络中,一阶邻近性比二阶邻近性更重要,因为一阶关系表明两个顶点的关系更紧密。
- 当网络非常稀疏并且顶点的平均邻居数太小时,二阶邻近性可能不太准确。
LINE(1st) + LINE(2nd)性能明显优于其它所有方法,这表明一阶邻近性和二阶邻近性是互补的。
YouTube数据集:YouTube网络非常稀疏,每个顶点的平均degree小于5。对该数据集的评估结果如下表。- 在不同规模训练集上,
LINE(1st)一致性的优于LINE(2nd)。这和Flickr数据集一致。
- 在不同规模训练集上,
由于极度稀疏性,
LINE(2nd)性能甚至不如DeepWalk。- 在
128维或256维上,LINE(1st) + LINE(2nd)优于DeepWalk。这表明一阶邻近性和二阶邻近性是互补的,并能够缓解网络稀疏问题。
考察
DeepWalk是如何通过截断的随机游走来解决网络稀疏性问题的。随机游走类似于深度优先搜索,这种方式可以通过引入间接邻居来迅速缓解邻域稀疏的问题。但是这种方式也可能引入距离较远的顶点,距离较远意味着相关性不大。一种更合理的方式是采用广度优先搜索策略来扩展每个稀疏顶点的邻域,如二阶邻域策略。下表中,括号中的指标是二阶邻域策略的表现。其中我们对邻居数量少于
1000的顶点扩展其二阶邻域,直到扩展邻域集合规模达到1000。我们发现添加超过1000个顶点并不会进一步提高性能。采用二阶邻域策略的网络称作重构网络reconstructed network。可以看到:采用二阶邻域策略之后
GF,LINE(1st),LINE(2nd)的性能都得到提升,其中LINE(2nd)的性能提升最为明显。采用二阶邻域策略之后
LINE(2nd)大多数情况下都优于DeepWalk。采用二阶邻域策略之后
LINE(1st+2nd)性能并没有提升太多。这意味着原始网络的一阶邻近性和二阶邻近性组合已经捕获了大部分信息。因此,
LINE(1st+2nd)是一个非常有效的Graph Embedding方式,适用于dense网络和sparse网络。
注意:二阶邻域策略中,新增邻域顶点的权重需要重新计算,并且优先添加权重最大的顶点。

- 在
2.2.3 引文网络
引文网络数据集包括作者引文网络、论文引用网络,它们都是有向图。由于
GF和LINE(1st)都无法应用于有向图,因此这里仅仅比较DeepWalk和LINE(2nd)。我们还通过多标签分类任务评估顶点
embedding的效果。我们选择7个热门的会议(AAAI,CIKM,ICML,KDD,NIPS,SIGIR,WWW)作为分类类别,在会议中发表的作者或者论文被标记为对应类别。最终评估分类结果的Micro-F1和Macro-F指标。我们分别抽取
10%~90%的标记样本作为训练集,剩余部分作为测试集。对每一种拆分随机执行10轮取平均结果。作者引用网络数据集的评估结果如下表所示。
- 由于网络稀疏,因此
DeepWalk性能优于LINE(2nd)。 - 通过二阶邻域策略重构网络,邻域规模的阈值设定为
500,最终LINE(2nd)性能大幅提升并且优于DeepWalk。 LINE-SGD(2nd)性能较差,因为边权重方差很大所以LINE-SGD的梯度更新过程非常困难。

- 由于网络稀疏,因此
论文引用网络数据集的评估结果如下所示。
LINE(2nd)的性能明显优于DeepWalk。这是由于在论文引用网络中的随机游走只能沿着引用路径来游走,这使得一些时间比较久远的、相关性不大的论文被作为上下文。相比之下,
LINE(2nd)的上下文都是最近的、密切相关的参考文献,因此更为合理。通过二阶邻域策略重构网络,邻域规模的阈值设定为
200,最终LINE(2nd)性能得到进一步提升。

2.2.4 可视化
graph embedding的一个重要用途是输出有意义的Graph可视化。我们选择作者引文网络数据集来可视化,选择了三个领域的不同会议:数据挖掘data mining领域的WWW,KDD会议、机器学习machine learning领域 的NIPS,IML 会议、计算机视觉computer vision领域的CVPR,ICCV会议。作者引用网络基于这些会议公开发表的文章来构建,丢弃
degree < 3的作者(表明这些作者不怎么重要),最终得到一个包含18561个顶点、207074条边的网络。可视化这个作者引文网络非常具有挑战性,因为这三个研究领域彼此非常接近。我们首先通过不同的模型来得到
graph embedding,然后将顶点的embedding向量通过t-SNE进行可视化。下图中不同颜色代表不同的领域:红色代表数据挖掘,蓝色代表机器学习,绿色代表计算机视觉。GF模型的可视化结果不是很有意义,因为不同领域的顶点并没有聚集在一起。DeepWalk模型的可视化结果要好得多,但是很多不同领域的顶点密集的聚集在中心区域,其中大多数是degree较高的顶点。这是因为:
DeepWalk使用基于截断随机游走的方式来生成顶点的邻居,由于随机性这会带来很大的噪声。尤其是degree较高的顶点,因为对于degree较高的顶点和大量其它顶点共现。LINE(2nd)模型的可视化结果更好、更具有意义。

2.2.5 网络稀疏性
以社交网络为例,我们分析了模型性能和网络稀疏性的影响。
我们首先研究网络的稀疏性如何影响
LINE(1st)和LINE(2nd)。图a给出了Flickr网络链接的百分比和LINE模型性能的关系。选择Flickr的原因是它比YouTube网络更密集。我们从原始网络中随机采样不同比例的链接从而构建具有不同稀疏性的网络。可以看到:- 一开始网络非常稀疏时,
LINE(1st)的性能好于LINE(2nd)。 - 当网络逐渐密集时,
LINE(2nd)的性能超越了LINE(1st)。
这表明:当网络极其稀疏时二阶邻近性模型受到影响;当每个顶点附近有足够的邻居时,二阶邻近性模型优于一阶邻近性模型。
- 一开始网络非常稀疏时,
图
b给出了YouTube数据集原始网络和二阶邻域策略重构网络中,顶点degree和模型性能指标的关系。我们将顶点根据degree来分组:: 。然后评估每个分组的顶点分类结果指标。可以看到:- 总体而言,当顶点的
degree增加时,所有模型的效果都得到提升。
- 总体而言,当顶点的
在原始网络中除第一个分组之外,
LINE(2nd)的性能始终优于LINE(1nd)。这表明二阶邻近性模型不适用于degree较小的点。- 在重构网络中,
LINE(1st)和LINE(2nd)都得到了改善,尤其是LINE(2nd)。 - 在重构网络中,
LINE(2nd)始终优于DeepWalk。
- 在重构网络中,

2.2.6 参数敏感性
我们在重建的
Youtube网络上考察了不同的embedding维度 和LINE模型性能的关系,以及样本数量和模型收敛速度的关系。图
a给出了不同维度 时模型的性能。可以看到:当 过大时,LINE(1st)和LINE(2nd)性能有所下降。图
b给出了LINE和DeepWalk在优化过程中收敛速度和样本数量的关系。可以看到:LINE(2nd)始终优于LINE(1st)和DeepWalk,并且LINE(1st)和LINE(2nd)收敛速度都快于DeepWalk。注意:这里的样本量指的是模型训练过程中见过的总样本量,包括重复的样本。由于
batch-size = 1,因此每个sample需要一个迭代step,因此样本数量也等于迭代step。

2.2.7 可扩展性
最后,我们研究了采用边采样和异步随机梯度下降法的
LINE模型的可扩展性scalability。我们部署了多线程进行优化。- 图
a给出了在YouTube数据集上的线程数及其加速比。可以看到线程加速比接近线性。 - 图
b给出了使用多线程进行模型更新时,模型性能的波动。可以看到采用多线程训练模型时,模型的最终性能保持稳定。
这两个结果表明:
LINE模型具有很好的可扩展性(即并行度)。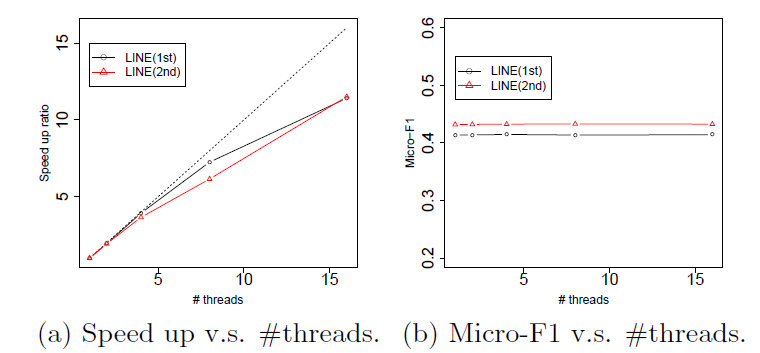
- 图
三、GraRep[2015]
在许多实际问题中,信息通常是使用图来组织的。例如,在社交网络研究中,基于社交图
social graph将用户分类为有意义的社交群组social group在很多实际application中有用,例如用户搜索user search、定向广告targeted advertising、以及推荐recommendation。因此,从图中准确地学习有用的信息至关重要。一种策略是学习图的graph representation:图中的每个顶点都用一个低维向量来表达,这个低维向量可以准确地捕获图所传达的语义信息semantic information、关系信息relational information、以及结构信息structural information。最近,人们对从数据中学习
graph representation的兴趣激增。例如,最近的一个模型DeepWalk使用均匀采样(也称作截断的随机游走truncated random walk)将图结构转换为由顶点组成的线性序列的样本集合。SkipGram模型最初设计用于从线性序列中学习word representation,也可用于从此类样本(即顶点组成的线性序列的样本)中学习顶点的representation。尽管这种方法在经验上是有效的,但是人们并不清楚在学习过程中所涉及的、图上定义的、确切exact的损失函数是什么。在论文
《GraRep: Learning Graph Representations with Global Structural Information》中,作者首先提出了在图上定义的SkipGram模型的显式损失函数。论文表明:本质上,我们可以使用SkipGram模型以不同的 值来捕获图中每个顶点与其k-step邻居之间的k-step关系()。SkipGram模型的一个缺陷是:它将所有这些k-step关系信息投影到一个公共子空间中。论文认为,这种简单的处理可能会导致潜在的问题。通过在不同的子空间中保存不同的k-step关系信息,论文提出的模型GraRep克服了上述限制。最近人们提出的另一个工作是
LINE,它有一个损失函数来同时捕获1-step局部关系信息local relational information和2-step局部关系信息。为了捕获此类局部信息中的某些复杂关系,他们还从此类数据中学习非线性变换(LINE用到了sigmoid函数,但是本质上LINE是广义线性函数)。虽然他们的模型不能很容易地扩展到捕获k-step()关系信息来学习他们的graph representation,但是他们提出了一个重要策略来提高模型的效果:对于degree较小的顶点,考虑高阶邻域。这一策略在某种程度上隐式地将某些k-step信息捕获到他们的模型中。GraRep的作者相信:对于不同的k值,不同顶点之间的k-step关系型信息揭示了与图相关的、有用的全局结构信息,并且在学习良好的graph representation时显式地充分利用这一点至关重要。在论文
《GraRep: Learning Graph Representations with Global Structural Information》中,作者提出了GraRep,这是一种为知识管理knowledge management学习graph representation的新模型。该模型通过操作在图中定义的、不同的全局转移矩阵global transition matrix,直接从图中的顶点中捕获具有不同 值的、不同k-step关系信息,而不涉及缓慢slow的、复杂complex的采样过程。与现有工作不同,GraRep模型定义了不同的损失函数来捕获不同的k-step局部关系信息(即不同的 )。论文使用矩阵分解matrix factorization技术优化每个模型,并通过组合从不同模型中学到的不同representation来构建每个顶点的全局representation。这种学到的全局represetnation可以用作下游任务的特征。论文对
GraRep模型进行了正式的处理formal treatment,并展示了GraRep模型与之前几个模型之间的联系。论文还通过实验证明了学到的representation在解决几个现实世界问题中的有效性。具体而言,论文对语言网络聚类任务、社交网络多标签分类任务、以及引文网络可视化任务进行了实验。在所有这些任务中,GraRep优于其它graph representation方法,从而证明了GraRep学到的全局representation可以有效地用作聚类、分类、可视化等任务的特征。并且,GraRep可以简单地并行化。论文贡献如下:
论文引入了一种新模型来学习图上顶点的潜在
representation,该模型可以捕获与图相关的全局结构信息。论文从概率的角度提供了对
DeepWalk中用于学习graph representation的均匀采样方法的理解,该均匀采样方法将图结构转换为线性序列。此外,论文在图上显式定义了
DeepWalk的损失函数,并将其扩展为支持加权图。论文正式分析了带有负采样
SkipGram模型(skip-gram model with negative sampling: SGNS)相关的缺陷。论文的模型定义了一个更准确accurate的损失函数,该损失函数允许集成不同局部关系信息的非线性组合。
相关工作:
线性的序列
representation方法Linear Sequence Representation Method:由单词的stream组成的自然语言语料库可以视为一种特殊的图结构,即线性链linear chain。目前,学习word representation有两种主流方法:神经嵌入neural embedding的方法、基于矩阵分解matrix factorization based的方法。神经嵌入方法采用固定长度的滑动窗口捕获当前单词的
context words。人们提出了像SkipGram这样的模型,这些模型提供了一种学习word representation的有效方法。虽然这些方法可能会在某些任务上产生良好的性能,但是它们不能很好地捕获有用的信息,因为它们使用独立的、局部的上下文窗口,而不是全局共现计数global co-occurrence count。另一方面,矩阵分解方法可以利用全局统计。先前的工作包括潜在语义分析
Latent Semantic Analysis: LSA,该方法分解term-document矩阵从而产生潜在语义representation。《Producing high-dimensional semantic spaces from lexical co-occurrence》提出了Hyperspace Analogue to Language: HAL,它分解一个word-word共现计数矩阵来生成word representation。《Extracting semantic representations from word co-occurrence statistics: A computational study》提出了用于学习word representation的、shifted positive Pointwise Mutual Information: PMI矩阵的矩阵分解,并表明带负采样的SkipGram模型(Skip-Gram model with Negative Sampling: SGNS)可以视为隐式的这样的一个矩阵。
图表示
Graph Representation方法:存在几种学习低维graph representation的经典方法,如多维缩放multidimensional scaling: MDS、IsoMap、LLE、Laplacian Eigenmaps。最近,
《Relational learning via latent social dimensions》提出了学习图的潜在representation向量的方法,然后可以用于社交网络分类。《Distributed large-scale natural graph factorization》提出了一种图分解方法,该方法使用随机梯度下降来优化大型图中的矩阵。《Deepwalk:Online learning of social Representations》提出了DeepWalk方法,该方法通过使用截断的随机游走算法将图结构转换为多个线性的顶点序列,并使用SkipGram模型生成顶点的representation。《Line: Large-scale information network embedding》提出了一种大规模信息网络的embedding,它优化了一个损失函数从而可以在学习过程中同时捕获1-step关系信息和2-step关系信息。
3.1 模型
3.1.1 图及其 Representation
给定一个图 ,其中 为顶点集合, 为顶点数量, 为边集合。路径
path定义为连接一个顶点序列的边序列。邻接矩阵:定义邻接矩阵为 。
- 对于无权图,如果顶点 到 之间存在边,那么 ,否则 。
- 对于带权图, 为顶点 到 之间边的权重。
尽管边的权重可以为负值,但是这里我们仅考虑正的权重。
度矩阵
degree matrix:定义度矩阵degree matrix为 ,其中:转移概率矩阵
probability transition matrix:假设我们想要捕获从一个顶点到另一个顶点的转移,并假设顶点 转移到顶点 的概率正比于 ,则定义转移概率矩阵probability transition matrix: 。其中 定义了从顶点 经过一步转移到顶点 的概率,因此也称为一阶转移概率矩阵。显然 可以认为是对 按 ”行“ 进行的归一化。
带全局结构信息的
graph representation:给定一个图 ,学习带全局结构信息的graph representation的任务旨在学习图的全局represetation矩阵 ,其中第 行 为图 中顶点 的 维向量,并且这些representation向量可以捕获图的全局结构信息global structural information。在本文中,全局结构信息有两个功能:捕获两个不同顶点之间的长距离关系、根据不同的转移
steps考虑不同的链接。我们将在后面进一步地说明。正如我们之前讨论过的,我们认为在构建这样的全局
graph representation时需要从图中捕获k-step(具有不同的 )的关系信息。为了验证这一点,下图给出了一些说明性的示例,展示了需要在两个顶点A1和A2之间捕获的、k-step(其中 ) 的关系信息的重要性。图中,粗线表示两个顶点之间的关系较强、细线表示两个顶点之间的关系较弱。在
(a)和(e)中显示了捕获彼此直接连接的、顶点之间简单的1-step信息的重要性,其中(a)具有较强的关系,(e)具有较弱的关系。在
(b)和(f)中显示了2-step信息,其中(b)中两个顶点A1和A2共享许多共同的邻居,而(f)中两个顶点A1和A2仅共享一个邻居。显然,
2-step信息对于捕获两个顶点之间的连接强度很重要:顶点之间共享的共同邻居越多,则它们之间的关系就越强。在
(c)和(g)中显示了3-step信息。具体而言:- 在
(g)中,尽管A1和B之间的关系很强,但是由于连接B和C、以及C和A2的两条较弱的边,A1和A2之间的关系可能会减弱。 - 相比之下,在
(c)中,A1和A2之间的关系仍然很强,因为B和A2之间有大量的共同邻居,这加强了它们的关系。
显然,在学习具有全局结构信息的良好
graph representation时,必须捕获此类3-step信息。- 在
类似地,如
(d)和(h)所示,4-step信息对于揭示图的全局结构特性也至关重要。在(d)中,A1和A2之间的关系明显很强。而在(h)中,A1和A2明显不相关,因为从一个顶点到另一个顶点之间不存在路径。在缺乏4-step关系信息的情况下,无法捕获这种重要的区别important distinction。

我们还认为:在学习
graph representation时,必须区别对待不同的k-step信息。我们在下图的(a)中展示了一个简单的例子。让我们专注于学习图中顶点A的representation。可以看到,A在学习其representation时接收到两种类型的信息:来自顶点B的1-step信息、以及来自顶点C的2-step信息。我们注意到,如果我们不区分这两种不同类型的信息,我们可以构建如图
(b)所示的替代品,其中顶点A接受与(a)完全相同的信息。但是,图(b)具有完全不同的结构。这意味着如何使用
k-step信息很重要,它们位于不同的子空间,应该区别对待。
在本文中,我们提出了一种用于学习准确
graph representation的新的框架,它集成了各种k-step信息,这些信息共同捕获了与图相关的全局结构信息。
3.1.2 图上的损失函数
我们将在这里讨论用于学习具有全局结构信息的
graph representation的损失函数。对于图 ,考虑两个顶点 和 。为了学习全局representation来捕获它们之间的关系,我们需要了解这两个顶点之间的连接强度。让我们从几个问题开始。是否存在从顶点 到顶点 的路径?如果存在,那么假设我们随机采样一条从顶点 开始的路径,我们到达顶点 的可能性有多大?
为了回答这些问题,我们首先令 表示从顶点 刚好通过 步到达顶点 的转移概率。我们已经知道了
1-step转移概率(即矩阵 ),为了计算k-step转移概率,我们引入k-step转移概率矩阵probability transition matrix:可以看到 表示从顶点 刚好通过 步到达顶点 的转移概率。这直接得到 ,其中 为矩阵 的第 行、第 列的元素。
现在考虑一个给定的 。给定一个图 ,考虑从顶点 开始到顶点 结束、并且长度为
k-step的所有路径的集合。这里我们称 为current vertex、 为context vertex。我们的目标旨在最大化:这些pair来自图中的概率、以及其它pair不来自图中的概率。受到
SkipGram模型的启发,我们采用了《Noise-contrastive estimation of unnormalized statistical models, with applications to natural image statistics》提出的噪声对比估计noise contrastive estimation: NCE来定义我们的目标函数。遵循《Neural word embedding as implicit matrix factorization》中提出的类似讨论,我们首先介绍我们在图上定义的k-step损失函数为:其中:
- 描述了顶点 和顶点 之间的
k-step关系,即从顶点 到顶点 的k-step转移概率。 - 为
sigmoid函数,定义为 。 - 表示顶点 作为
current vertex时的representation, 表示顶点 作为context vertex时的representation。二者采用了不同的representation矩阵。 - 为超参数,表示负样本的数量。
- 为
k-step负采样分布, 表示当 服从分布 时的期望值, 是从负采样中获得的负样本。
上式物理意义:
- 第一项为 “正样本” 的加权对数似然,权重为
k-step转移概率,“正样本”为从顶点 所有经过k-step能够到达的顶点集合。 - 第二项为 “负样本”的对数似然。这里负样本没有加权。
和
DeepWalk相比,GraRep的重要区别在于它对正样本进行了加权。期望部分可以重写为:
因此对于特定的顶点
pair对 ,定义其局部损失函数local loss为:其物理意义为:
- 对于从 经过
k-step到达的顶点 ,其损失为作为正样本的加权对数似然(权重为k-step转移概率),加上作为负样本的加权对数似然(权重为k-step采样概率)。 - 对于从 无法经过
k-step到达的顶点 ,其损失为作为负样本的加权对数似然(权重为k-step采样概率)。
k-step负采样分布 可以计算为:其物理意义为:以概率 随机选择一个顶点,然后经过
k-step转移到顶点 的概率。这里 是选择 作为路径中第一个顶点的概率,我们假设它服从均匀分布,即 。因此得到:则
k-step损失函数为:为最小化 则只需要最小化每个成分,即求解: 。令 ,求解:
得到最优解:
其中 。
可以得到结论:我们本质上需要将矩阵 分解为两个矩阵 和 ,其中 的每一行和 的每一行分别由顶点 和顶点 的向量
representation组成。其中矩阵 的元素定义为:现在我们已经定义了我们的损失函数,并表明优化该损失函数本质上涉及到矩阵分解问题。
- 描述了顶点 和顶点 之间的
在这项工作中,我们为每条路径设置最大长度。换句话讲,我们假设 。实际上,当 足够大时,转移概率会转移到某些固定值。
3.1.3 矩阵分解的最优化
遵从
《Neural word embedding as implicit matrix factorization》的工作,为了降低噪音,我们将 中的所有负数都替换为0。因为若存在负数,则图中存在的 阶顶点pair对的概率 。这使得我们得到一个正的k-step概率矩阵 ,其中:虽然存在各种矩阵分解技术,但是在这项工作中,由于其简单性,我们将重点放在流行的奇异值分解
singular value decomposition: SVD方法上。SVD已经在多个矩阵分解任务中取得成功,被认为是可用于降维的重要方法之一。对于矩阵 ,
SVD分解为:其中:
- 均为正交矩阵。
- 为对角矩阵,对角线元素为按降序排列的矩阵奇异值。
我们可以用 来近似原始的矩阵 ,即:
其中: 为最大的 个奇异值, 为 的前 列, 为 的前 列。它们的物理意义为: 、 最大的
d个特征值对应的特征向量。通过这种方式,我们可以分解我们的矩阵 为:
其中 。 的每一行给出了各顶点作为当前顶点的
representation向量, 的每一行给出了各顶点作为上下文顶点的representation向量。最终我们返回矩阵 作为顶点的 维representation,它在图中捕获了k-step全局结构信息。在我们的算法中,我们考虑所有 阶转移,其中 是预定义的常数。我们在学习
graph representation时整合了所有这些k-step信息,这将在接下来讨论。注意,这里我们实际上是在寻找从 的行空间到具有低秩的 的行空间的投影。因此,也可以利用流行的
SVD以外的替代方法,包括incremental SVD、独立成分分析independent component analysis: ICA、神经网络DNN。 我们这项工作的重点是学习graph representation的新模型,因此矩阵分解技术不是我们的重点。事实上,如果在这一步使用诸如稀疏自编码器之类的替代方法,则相对难以证明我们
representation的实验效果是由于我们的新模型、还是由于降维步骤引入的任何非线性。为了保持与《Neural word embedding as implicit matrix factorization》工作的一致性,这里我们只使用了SVD。
3.1.4 GraRep 算法
这里我们详细介绍我们的学习算法。通常,
graph representation被提取为其它任务的特征,例如分类、聚类。在实践中,编码k-step representation的一种有效方法是将k-step representation拼接起来作为每个顶点的全局特征,因为每个不同的step representation反映了不同的局部信息。GraRep算法:算法输入:
- 图的邻接矩阵
- 最大转移阶数
- 对数偏移系数
- 维度
算法输出:顶点的
representation矩阵算法步骤:
计算 阶转移概率矩阵 。计算流程:
首先计算 ,然后依次计算 。
对于带权图, 是一个实数矩阵;对于无权图, 是一个
0-1矩阵。算法都能够处理。对 迭代计算每个顶点的
k-step representation,计算流程:获取正的对数概率矩阵 :
首先计算 ,其中 ;然后计算:
计算
representation矩阵 :
拼接所有的 阶表达:
未来工作:
- 研究矩阵操作有关的近似计算和在线计算。
- 研究通过深度架构代替
SVD矩阵分解来学习低维representation。
3.1.5 SkipGram 作为 GraRep 特例
GraRep旨在学习grap representation,并且我们基于矩阵分解来优化损失函数。另一方面,SGNS已被证明在处理线性结构(如自然语言的句子)方面是成功的。GraRep和SGNS之间有内在的联系吗?这里我们将SGNS视为GraRep模型的一个特例。
a. 图 SkipGram 模型的损失函数
SGNS旨在以线性序列的方式来表达单词,因此我们需要将图结构转换为线性结构。DeepWalk揭示了一种均匀采样(截断的随机游走)的有效方法。该方法首先从图中随机均匀采样一个顶点,然后随机游走到它的一个邻居并重复这个随机游走过程。如果顶点序列长度达到某个预定值,则停止随机游走并开始生成新的序列。该过程可用于从图中生成大量序列。本质上,对于无权图,这种均匀采样的策略是有效的。但是对于加权图,需要一种基于边权重的概率性采样方法,而
DeepWalk中没有采用这种方法。在本文中,我们提出了一种适用于加权图的增强型SGNS方法Enhanced SGNS: E-SGNS。我们还注意到,DeepWalk优化了一个不同于负采样的、替代的损失函数alternative loss function(即hierarchical softmax)。首先,我们考虑图上的、所有
K-step的损失 :其中 为一个线性函数: 。
我们关注特定于
pair的损失,它们是图中第 个顶点和第 个顶点。定义 ,其中 。这里 为 步之内的概率转移矩阵, 表示从顶点 不超过 步转移到顶点 的概率。
则损失函数重写为:
同样的推导过程可以解得最优解:
其中其中 。
定义矩阵 ,其中:
则 为
E-SGNS的被分解矩阵factorized matrix。E-SGNS和GraRep模型的区别在于 的定义:E-SGNS可以认为是K-step loss的线性组合,每个loss的权重相等。E-SGNS和SGNS的主要区别在于对正样本的加权:E-SGNS的正样本权重为 ,即从顶点 不超过 步转移到顶点 的概率。我们的
GraRep模型没有做出如此强的假设,但允许在实践中从数据中学习它们的关系(比如,潜在的非线性关系)。直觉上,不同的
k-step转移概率应该有不同的权重。对于异质网络数据heterogeneous network dat,这些损失的线性组合可能无法达到理想的效果。
b. 采样与转移概率之间的内在联系
在我们的方法中,我们使用转移概率来衡量顶点之间的关系。这合理吗?在这里,我们阐明了采样了转移概率之间的内在联系。
在随机游走生成的序列中,我们假设顶点 一共出现的次数为:
其中 是与 相关的变量。
我们将顶点 视为当前顶点,则顶点 为 直接邻居(
1-step距离)的次数的期望为:这对于无权图的均匀采样、或者对于加权图的非均匀采样都成立。
进一步地,顶点 为 二阶邻居(
2-step距离)的次数的期望为:其中 为连接顶点 和 的任意其它顶点,即 为顶点 和 的共享邻居。
类似地,我们可以推导出 的方程:
然后,我们将它们相加并除以 ,得到:
其中 为顶点 和顶点 在 步内共现的期望次数。
根据 的定义,我们有: 。
现在,我们可以计算将顶点 作为上下文顶点的期望次数 为: ,其中我们考虑从所有可能顶点 到顶点 的转移。
最后,我们将所有这些期望计数代入 的方程,得到:
定义数据集中所有观察到的
pair的集合为 ,则 ,因此有:矩阵 变得与
《Neural word embedding as implicit matrix factorization》中描述的SGNS完全相同。这表明
SGNS本质上是我们GraRep模型的一个特殊版本,它可以处理从图中采样的线性序列。我们的方法相比缓慢的、昂贵的采样过程有若干优点,并且采样过程通常涉及几个要调整的超参数,例如线性序列的最大长度、每个顶点开始的序列数量等等。
3.2 实验
这里我们通过实验评估
GraRep模型的有效性。我们针对几个不同的任务在几个真实世界数据集上进行了实验,并与baseline算法进行了比较。数据集和任务:为了证明
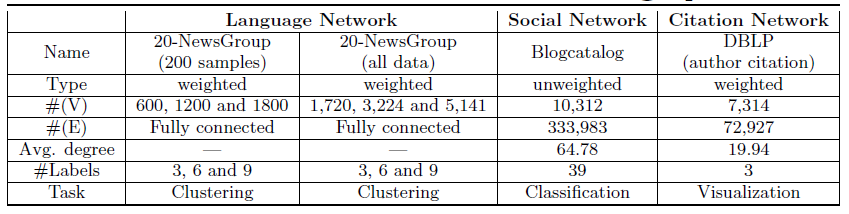
GraRep的性能,我们在三种不同类型的图上进行了实验,社交网络social network、语言网络language network、引文网络citation network,其中包括加权图和无权图。我们对三种不同类型的任务进行了实验,包括聚类clustering、分类classification,、以及可视化visualization。正如我们前面提到的,我们工作的重点是提出一个新的框架,用于学习具有全局结构信息的、图的良好representation,旨在验证我们提出的模型的有效性。因此,除了SVD之外,我们不采用其它更有效的矩阵分解方法,并重点关注以下三个真实世界的数据集:语言网络数据集
20-Newsgroup:包含2万篇新闻组文档,并分类为20个不同的组。每篇文档由文档内单词的tf-idf组成的向量来表示,并根据余弦相似度计算得到文档的相似度。根据文档的这些相似度构建语言网络,该网络是一个全连接的带权图,用于聚类效果的评估。为验证模型的鲁棒性,论文分别从
3/6/9个不同的新闻组构建了三个更小规模的语言网络(NG代表Newsgroups):3-NG:由comp.graphics, comp.graphics and talk.politics.guns这三个新闻组的文档构成。6-NG:由alt.atheism, comp.sys.mac.hardware, rec.motorcycles, rec.sport.hockey, soc.religion.christian and talk.religion.misc这六个新闻组的文档构成。9-NG:由talk.politics.mideast, talk.politics.misc, comp.os.ms- windows.misc, sci.crypt, sci.med, sci.space, sci.electronics, misc.forsale, and comp.sys.ibm.pc.hardware这九个新闻组的文档构成。
这些小网络分别使用所有文档
all data,以及每个主题随机抽取200篇文档两种配置。每个文档上的topic label被认为是ground truth。这些
toplic label被认为是聚类的真正cluster id。社交网络数据集
Blogcatalog:它是一个社交网络,每个顶点表示一个博客作者,每条边对应作者之间的关系。每个作者都带有多个标签信息,标签来自39种主题类别。该网络是一个无权图,用于多标签分类效果的评估。我们的模型以及
baseline算法生成的graph representation被视为特征。引文网络数据集
DBLP Network:它是一个引文网络,每个顶点代表一个作者,边代表一个作者对另一位作者的引用次数。我们选择六个热门会议并分为三组:数据挖掘
data mining领域的WWW,KDD会议、机器学习machine learning领域 的NIPS,IML 会议、计算机视觉computer vision领域的CVPR,ICCV会议。我们使用可视化工具
t-SNE来可视化所有算法学到的representation,从而提供学到的representation的定性结果和定量结果。
总而言之,我们对加权图和无权图、稀疏图和稠密图进行了实验,其中执行了三种不同类型的学习任务。这些数据集的更多细节如下表所示。
baseline方法:我们使用以下graph representation方法作为baseline。LINE:LINE是最近提出的一种在大规模信息网络上学习graph representation的方法。LINE根据顶点之间的1-step和2-step关系信息定义了一个损失函数。一种提升small degree顶点的性能的策略是:扩展它们的邻域使得图更稠密。如果将1-step关系信息的representation和2-step关系信息的representation拼接起来,并调节邻域最大顶点的阈值,则LINE将获得最佳性能。DeepWalk:DeepWalk是一种学习社交网络representation的方法。原始模型仅适用于无权图。对于每个顶点,截断的随机游走用于将图结构转换为线性序列。带hierarchical softmax的SkipGram模型用作损失函数。E-SGNS:SkipGram是一种有效的模型,可以学习大型语料库中每个单词的representation。对于这个增强版本,我们首先对无权图使用均匀采样、对加权图使用与边权重成正比的概率性采样(即随机游走),从而生成顶点序列。然后引入SGNS进行优化。这种方法可以视为我们模型的一个特例,其中每个
k-step信息的不同representation向量进行均值池化。Spectral Clustering:谱聚类是一种合理的baseline算法,旨在最小化归一化割Normalized Cut:NCut。与我们的方法一样,谱聚类也对矩阵进行分解,但是它侧重于图的不同矩阵:拉普拉斯矩阵Laplacian Matrix。本质上,谱聚类和E-SGNS的区别在于它们的损失函数不同。
参数配置:
对于
LINE模型:batch-size=1,学习率为0.025,负采样系数为5,迭代step总数为百亿级。我们还还将
1-step关系信息representation和2-step关系信息representation拼接起来 ,并针对degree较小的顶点执行重构策略来达到最佳性能。对于
DeepWalk和E-SGNS模型:窗口大小为10,序列最长长度为40,每个顶点开始的游走序列数量为80。正则化:
LINE,GraRep模型进行 正则化可以达到最佳效果,DeepWalk,E-SGNS模型没有正则化也能达到最佳效果。embedding维度 :为公平比较,Blogcatalog和DBLP数据集的 ,而20-NewsGroup数据集的 。GraRep模型: ;Blogcatalog和DBLP数据集的 ,20-NewsGroup数据集的 。
3.3.1 语言网络
我们通过在
k-means算法中使用学到的representation,通过聚类任务在语言网络上进行实验。为了评估结果的质量,我们报告了每个算法在10次不同运行中的平均归一化互信息Normalized Mutual Information (NMI)得分。为了理解不同维度 在最终结果中的影响,我们还展示了
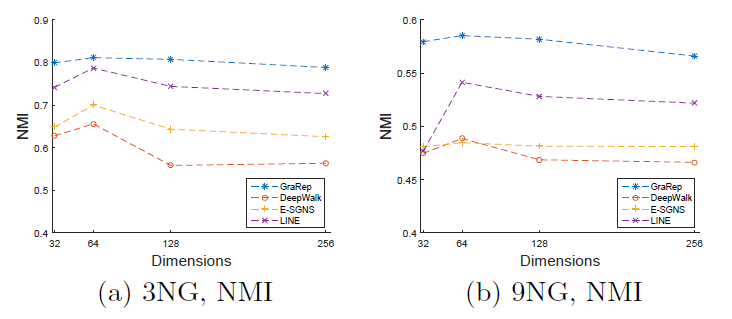
DeepWalk、E-SGNS、Spectral Clustering在 的结果(除了 之外)。对于LINE模型这里采用了重构策略,邻居数量阈值分别设定为k-max = 0,200,500,1000取最佳阈值(最佳阈值为200)。最终结果如下表所示,每列的最佳结果用粗体突出显示。结论:
GraRep模型在所有实验中都优于其它baseline方法。- 对于
DeepWalk, E-SGNS和Spectral Clustering,增加维度 似乎并不能有效提高性能。我们认为:较高的维度并不会为representation提供额外的补充信息。
- 对于
对于
LINE模型采用重建策略确实有效,因为它可以捕获图的额外结构信息,例如超出1-step、2-step的局部信息。- 值得一提的是,
GraRep和LINE模型在很小的Graph上就可以得到良好的性能。我们认为:即使在图很小的条件下,这两个模型也可以捕获丰富的局部关系信息。 - 此外,对于标签较多的任务,例如
9GN,GraRep和LINE可以提供比其它方法更好的性能。 - 一个有趣的发现是:当 时
Spectral Clustering达到最佳性能,但是对其它算法 达到最佳性能。
由于篇幅所限,我们没有报告所有
baseline方法在 时的详细结果,也没有报告LINE的k-max=500, 1000以及没有重建策略的结果。因为这些结果并不比下表的效果更好。后面的实验会进一步探究参数敏感性问题。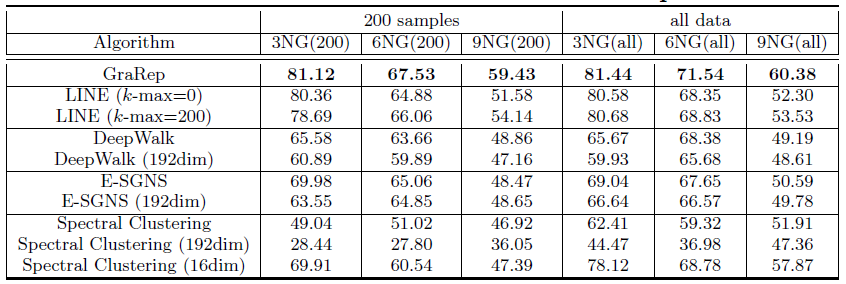
- 值得一提的是,
3.3.2 社交网络
在这个实验中,我们专注于社交网络上的监督任务。我们将学到的
representation视为特征,通过多标签分类任务评估不同算法得到的graph representation的有效性。我们使用
LibLinear package来训练one-vs-rest逻辑回归分类器。我们将这个过程运行10轮并报告平均Micro-F1和Macro-F1指标。对于每一轮,我们随机采样10%~90%的顶点来训练,剩下的顶点作为测试集 。 这里LINE模型采用了重构策略,邻居数量阈值分别设定为k-max = 0,200,500,1000取最佳阈值(最佳阈值为500)。最终结果如下表所示,每列的最佳结果用粗体突出显示。结论:总体上
GraPep性能远超过其它方法,尤其是仅使用10%样本训练。这表明
GraRep学到的不同类型的、丰富的局部结构信息可以相互补充从而捕获到全局结构信息。在与现有的baseline相比具有明显的优势,尤其是在数据稀疏时。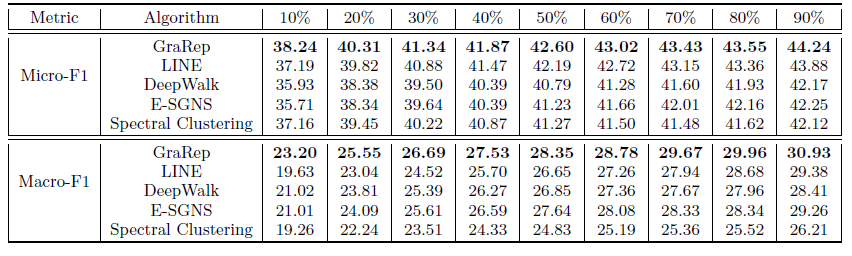
3.3.3 引文网络
在这个实验中,我们专注于通过检查一个真实的引文网络
DBLP来可视化学到的representation。我们将学到的graph representation输入到t-SNE工具中来lay out图,其中来自同一个研究领域的作者使用相同的颜色,绿色表示数据挖掘、紫色表示计算机视觉、蓝色表示机器学习。结论:
使用谱聚类的效果一般,因为不同颜色的顶点相互混合。
DeepWalk和E-SGNS结果看起来好得多,因为大多数相同颜色的顶点似乎构成了分组,但是分组的边界似乎不是很明显。LINE和GraRep结果中,每个分组的边界更加清晰,不同颜色的顶点出现在明显可区分的区域中。与
LINE相比GraRep的结果似乎更好,每个区域的边界更清晰。

引文网络可视化的
KL散度如下表所示。其中KL散度捕获了 ”成对顶点的相似度” 和 “二维投影距离” 之间的误差。更低的KL散度代表更好的表达能力。可以看到:GraRep模型的顶点representation效果最好。
3.3.4 参数敏感性
这里我们讨论参数敏感性,具体而言我们评估了最大步长 、维度 对于模型效果的影响。
值:下图给出
Blogcatelog数据集上不同 值对应得Micro-F1和macro-F1得分。为阅读方便,这里仅给出 的结果。因为实验发现: 的结果略好于 ,而 的效果与 相当。可以看到:
比 有明显改善,而 的性能进一步优于 。
这表明:不同的 阶信息可以学到互补的局部信息。
的结果并不比 好多少。
这是因为当 足够大时,学到的 阶信息会减弱并趋于一个稳定的分布。

值:下图给出了
3NG和9NG在不同 配置下不同模型的NMI得分。可以看到:GraRep模型结果始终优于其它模型。- 几乎所有算法都在 时取得最佳性能,当 从
64继续增加到更大值时所有算法效果都开始下降。
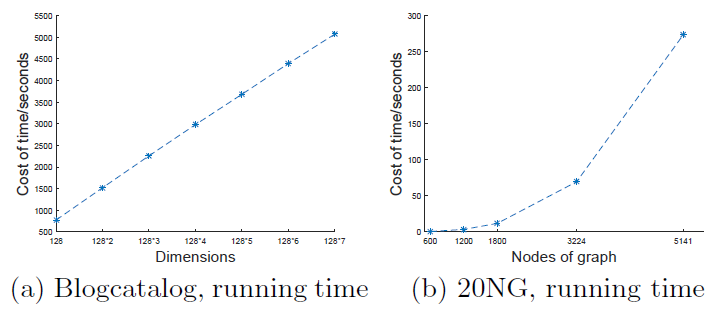
运行时间:下图给出不同总维度和不同图大小时模型的运行时间。总维度等于 ,它代表最终
GraRep拼接得到的representation向量。图
a给出了 且 时,模型在Blogcatalog数据集上的模型训练时间。可以看到:模型训练时间随着总维度的增加而几乎线性增加。
图
b给出了在20-NewsGroup数据集不同规模的网络上训练的时间。可以看到:随着
Graph规模的增长,模型训练时间显著增加。原因是随着Graph增长,矩阵幂运算 和矩阵SVD分解涉及到时间复杂度较高的运算。后续可以考虑采用深度学习来替代
SVD技术来做矩阵分解。
四、TADW[2015]
网络在我们的日常生活中无处不在,例如
Facebook用户之间的友谊或学术论文之间的引用。近年来,研究人员广泛研究了网络中许多重要的机器学习应用,例如顶点分类vertex classification、标签推荐tag recommendation、异常检测anomaly detection、链接预测link prediction。数据稀疏data sparsity是这些任务面临的常见问题。为了解决数据稀疏性问题,network representation learning: NRL在统一的低维空间中编码和表达每个顶点。NRL有助于我们更好地理解顶点之间的语义相关性semantic relatedness,并进一步缓解稀疏性带来的不便。NRL中的大多数工作从网络结构中学习representation。例如,social dimensions是计算网络的拉普拉斯Laplacian矩阵或modularity矩阵的特征向量eigenvectors。最近,NLP中的word representation模型SkipGram被引入,用于从社交网络中的随机游走序列中学习顶点的representation,称作DeepWalk。social dimensions和DeepWalk方法都将网络结构作为输入来学习network representation,但是没有考虑任何其它信息。在现实世界中,网络中的顶点通常具有丰富的信息,例如文本内容和其它元数据
meta data。例如,维基百科文章相互连接并形成网络,每篇文章作为一个顶点都包含大量的文本信息,这些文本信息可能对NRL也很重要。因此,论文《Network Representation Learning with Rich Text Information》提出了同时从网络结构和文本信息中学习network representation的想法,即text-associated DeepWalk: TADW。- 一种直接的方法是:分别独立地从文本特征和网络特征中学习
representation,然后将两个独立的representation拼接起来。然而,该方法没有考虑网络结构和文本信息之间复杂的交互interaction,因此通常会导致效果不佳。 - 在现有的
NRL框架中加入文本信息也不容易。例如,DeepWalk在网络中的随机游走过程中,无法轻松地处理附加信息。
幸运的是,给定网络 ,论文证明
DeepWalk实际上是分解矩阵 ,其中每一项 是顶点 以固定steps随机游走到顶点 的平均概率的对数。下图(a)展示了MF风格的DeepWalk:将矩阵 分解为两个低维矩阵 ,其中 。DeepWalk将矩阵 作为顶点representation。我们将在后面进一步详细介绍。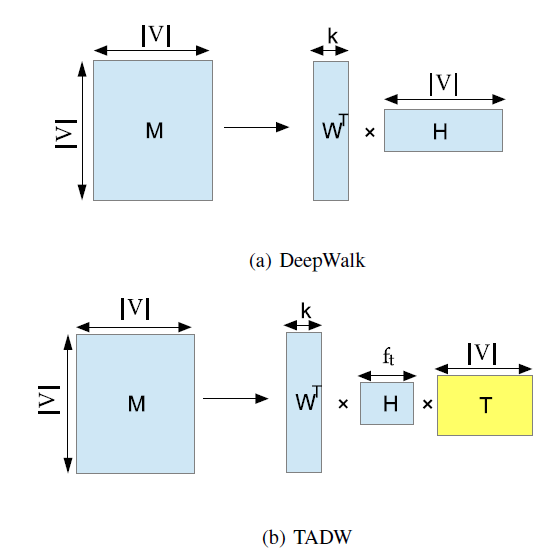
DeepWalk的矩阵分解视角启发了作者将文本信息引入到NRL的MF中。如上图(b)展示了论文方法的主要思想:将矩阵 分解为三个矩阵的乘积: ,其中 为文本特征矩阵。然后论文拼接 和 作为每个顶点的 维的representation。论文在三个数据集上针对多个
baseline测试了TADW算法。当训练集比率training ratio在10% ~ 50%的范围内时,TADW的representation的分类准确率比其它baseline高达2% ~ 10%。当训练集比率小于10%时,论文还使用半监督分类器Transductive SVM: TSVM测试这些方法。TADW在1%的训练集比率下,相比其它baseline方法提升了5% ~ 20%,尤其是在网络信息包含噪音的情况下。论文主要贡献:
- 论文证明了
DeepWalk算法实际上分解了一个矩阵 ,并找出了 的封闭形式closed form。 - 论文将文本特征引入
NRL,并相比其它baseline获得了5% ~ 20%的优势,尤其是在训练集比率较小的情况下。
- 一种直接的方法是:分别独立地从文本特征和网络特征中学习
相关工作:
representation learning广泛应用于计算机视觉、自然语言处理、knowledge representation learning。一些研究集中在NRL,但它们都无法泛化来处理顶点的其它特征。据作者所知,很少有工作致力于考虑NRL中的文本信息。有一些主题模型
topic model,如NetPLSA,在主题建模时同时考虑了网络和文本信息,然后可以用主题分布topic distribution来表示每个顶点。在本文中,作者以NetPLSA作为baseline方法。
4.1 模型
4.1.1 DeepWalk 作为矩阵分解
公式化
NRL:给定网络 ,我们希望为每个顶点 构建一个低维representation向量 ,其中 。作为一种稠密的real-valued representation, 可以缓解邻接矩阵等network representation的稀疏性。我们可以将 视为顶点 的特征,并将这些特征应用到许多机器学习任务中,如顶点分类。这些特征可以方便地提供给许多分类器,例如逻辑回归、SVM。注意,representation不是特定于任务task-specific的,可以在不同任务之间共享。我们首先介绍
DeepWalk,然后给出DeepWalk和矩阵分解之间的等价证明。
a. DeepWalk
DeepWalk首次将应用广泛的分布式word representation方法SkipGram引入到社交网络的研究中,从而根据网络结构来学习vertex representation。DeepWalk首先生成短的随机游走short random walk(短的随机游走也被用作相似性度量)。给定一条由随机游走生成的顶点序列 ,我们将顶点 视为中心顶点 的上下文,其中 为窗口大小window size。遵循SkipGram的思想,DeepWalk旨在最大化随机游走顶点序列 中所有vertex-context pair的平均对数概率average log probability:其中 以
softmax函数的方式来定义:其中 :
- 为顶点 作为
center vertex时的represetation向量。 - 为顶点 作为
context vertex时的representation向量。
即,每个顶点 有两个
representation向量:当 作为center vertex时的 、当 作为context vertex时的 。之后,
DeepWalk使用SkipGram和Hierarchical Softmax从随机游走生成的序列中学习顶点的representation。注意,Hierarchical Softmax是用于加速的softmax的变体。- 为顶点 作为
b. 等价性证明
假设一个
vertex-context集合 是从随机游走序列中生成,其中每个元素为一个vertex-context pair。定义vertex集合为 ,定义context集合为 ,并且大多数情况下 。DeepWalk将一个vertex嵌入到一个 维向量 。另外,一个context被嵌入到一个 维向量 。令 为所有vertex embedding组成的矩阵,其中第 行表示顶点 的vertex representation。令 为 所有context embedding组成的矩阵,其中第 行表示顶点 的context representation。我们的目标是找出矩阵 的封闭形式closed form,其中 。现在我们考虑一个
vertex-context pair。定义 为 出现在 中的次数, 为vertex出现在 中的次数, 为context出现在 中的次数。《Neural word embedding as implicit matrix factorization》已经证明:当维度 足够大时,带负采样的SkipGram(SkipGram with Negative Sampling: SGNS) 相当于隐式地分解word-context矩阵 。其中 的元素为:其中 为每个
word-context pair的负样本数量。可以解释为
word-context pair的Pointwise Mutual Information: PMI的 偏移。类似地,我们可以证明带
softmax的SkipGram相当于分解矩阵 ,其中:我们现在讨论
DeepWalk中的 代表什么。显然,vertex-context pair的采样方法会影响矩阵 。假设网络是连通connected和无向undirected的,窗口大小为 。我们将基于DeepWalk算法的理想ideal的采样方法来讨论 ,,以及 :- 首先我们生成一条足够长的随机游走序列 。令 表示随机游走序列 上位置 的顶点。
- 然后我们将
vertex-context pair添加到 中,当且仅当 。
就是顶点 在随机游走中出现的频率,也就是 的
PageRank值。 为在 的左侧或右侧 个邻居中观察到 的期望次数。现在我们尝试基于这种理解来计算 。将
PageRank中的转移矩阵表示为 。令 为顶点 的degree,则有:我们使用 来表示一个 维的行向量,其中除了第 项为
1之外其它项均为零。假设我们从顶点 开始随机游走并使用 表示初始状态。那么 是所有顶点的分布,它的第 项是顶点 随机游走到顶点 的概率。因此, 的第 项是顶点 以恰好 步随机游走到顶点 的概率,其中 是矩阵 的 次幂。因此, 的第 项是 出现在 的右侧 个邻居中的期望次数。因此我们有:上述证明也适用于有向图。因此,我们可以看到 为顶点 在 步中随机游走到顶点 的平均概率的对数。
通过证明
DeepWalk等价于矩阵分解,我们提出融合丰富的文本信息到基于DeepWalk派生的矩阵分解中。
4.1.2 TADW
- 这里我们首先简要介绍低秩矩阵分解,然后我们提出从网络和文本信息中学习
representation的方法。
a. 低秩矩阵分解
矩阵是表示关系型数据
relational data的常用方法。矩阵分析的一个有趣主题是通过矩阵的一部分项来找出矩阵的内在结构。一个假设是矩阵 可以用低秩 的另一个矩阵来近似,其中 。然后我们可以在这个假设下用这样一个低秩近似来补全complete矩阵 的缺失值。然而,求解秩约束优化rank constraint optimization始终是NP难的。因此,研究人员求助于寻找矩阵 和 ,从而最小化损失函数 ,并且带有迹范数的约束trace norm constraint(这个约束可以通过在损失函数中添加一个惩罚项从而进一步地移除)。在本文中,我们使用平方损失函数。低秩分解:形式上,令矩阵 的观察集为 。我们希望找到矩阵 和 ,从而最小化损失函数:
其中 表示矩阵的
Frobenius范数, 为正则化系数。归纳矩阵补全:低秩矩阵分解仅基于 的低秩假设来补全矩阵 。如果矩阵 中的
item具有附加特征additional feature,那么我们可以应用归纳矩阵补全inductive matrix completion来利用它们。归纳矩阵补全通过融合两个特征矩阵feature matrix到目标函数中从而利用更多行单元row unit和列单元column unit的信息。假设我们有特征矩阵 和 ,其中 分别为两个矩阵列向量的维度。我们的目标是求解矩阵 和 ,从而最小化:
注意,归纳矩阵补全最初是为了补全具有基因特征和疾病特征的 “基因-疾病”矩阵,其目标与我们的工作有很大不同。受归纳矩阵补全思想的启发,我们将文本信息引入
NRL。
b. TADW
给定一个网络 以及它对应的文本特征矩阵 ,我们提出了文本相关的
DeepWalk(text-associated DeepWalk: TADW)从网络结构 和文本特征 中学习每个顶点 的representaion。回想一下,
DeepWalk分解矩阵 ,其中 。 当 较大时,准确地计算 的计算复杂度为 。实际上,DeepWalk使用基于随机游走的采样方法来避免显式地、精确地计算矩阵 。当DeepWalk采样更多的随机游走序列时,性能会更好,但是计算效率会更低。在
TADW中,我们找到了速度和准确性之间的tradeoff:分解矩阵 。在这里,为了计算效率,我们分解矩阵 而不是 。原因是 比 具有更多的非零项,并且具有平方损失的矩阵分解的复杂度与矩阵 中非零元素的数量成正比。由于大多数现实世界的网络都是稀疏的,即 ,因此计算矩阵 需要 的时间。如果网络是稠密的,我们甚至可以直接分解矩阵 。即使是 的计算复杂度,对于百万甚至亿级顶点的网络而言,这个计算复杂度仍然无法接受。
我们的任务是求解矩阵 和 ,从而最小化:
为了优化 和 ,我们交替最小化 和 ,因为它是 或 的凸函数。虽然
TADW可能收敛到局部最小值而不是全局最小值,但我们的方法在实践中效果很好,如我们的实验所示。也可以直接应用随机梯度下降法来优化。
不同于低秩矩阵分解
low-rank matrix factorization和归纳矩阵补全inductive matrix completion(它们聚焦于补全矩阵 ),TADW的目标是结合文本特征从而获得更好的network representation。此外,归纳矩阵补全直接从原始数据中获得矩阵 ,而我们从MF风格的DeepWalk的推导中人为地构建矩阵 。由于从
TADW获得的 和 都可以视为顶点的低维representation,因此我们可以通过拼接它们为network representation构建一个统一的、 维的矩阵。在实验中,我们将证明统一的representation显著优于将network representation和文本特征(即矩阵 ) 的简单组合。复杂度分析:在
TADW中,计算 的过程需要 的时间。我们使用《Large-scale multi-label learning with missing labels》引入的快速过程来求解TADW的优化问题。最小化 和 的每次迭代的复杂度为 ,其中
nnz(.)为矩阵非零元素的个数。作为比较,传统矩阵分解的复杂度(即低秩矩阵分解的优化问题) 为 。在我们的实验中,优化在10次迭代中收敛。未来工作:针对大规模网络数据场景的
TADW在线学习和分布式学习。另外,还可以研究矩阵分解的其它技术,例如matrix co-factorization,从而包含来自其它来源的丰富信息。
4.2 实验
我们使用顶点分类问题来评估
NRL的质量。正式地,我们得到顶点的低维representation作为顶点特征,然后我们的任务是基于顶点特征用标记顶点集合 来预测未标记顶点集合 的label。机器学习中的许多分类器可以处理这个任务。我们分别选择
SVM和transductive SVM从而进行监督的、半监督的学习和测试。注意,由于representation learning过程忽略了训练集中的顶点label,因此representation learning是无监督的。我们使用三个公开可用的数据集,并使用
representation learning的五种baseline方法来评估TADW。我们从文档之间的链接或引用,以及这些文档的term frequency-inverse document frequency: TF-IDF矩阵(即矩阵 )中学习representation。数据集:
Cora数据集:包含来自七个类别的2708篇机器学习论文。论文之间的链接代表引用关系,共有5429个链接。每篇文档映射为一个1433维的binary向量,每一位为0/1表示对应的单词是否存在。Citeseer数据集:包含来自六个类别的3312篇公开发表出版物。文档之间的链接代表引用关系,共4732个链接。每篇文档映射为一个3703维的binary向量,每一位为0/1表示对应的单词是否存在。Wiki数据集:包含来自十九个类别的2405篇维基百科文章。文章之间的链接代表超链接,共17981个链接。我们移除了没有任何超链接的文档。每篇文章都用内容单词的TFIDF向量来表示,向量维度为4973维。
Cora和Citeseer数据集从标题、摘要中生成短文本作为文档,并经过停用词处理、低频词处理(过滤文档词频低于10个的单词),并将每个单词转化为one-hot向量。Cora、Citeseer数据集平均每篇文档包含18~32个单词,数据集被认为是有向图。Wiki数据集是长文本,平均每篇文档包含640个单词,数据集被认为是无向图。baseline方法及其配置:TADW:通过SVD分解TFIDF矩阵到200维的文本特征矩阵 ,这是为了降低矩阵 的规模。我们也将文本特征矩阵 视为一个content-only的baseline。对于
Cora,Citeseer数据集 ;对于Wiki数据集 。注意:最终每个顶点的
representation向量的维度为 。DeepWalk:DeepWalk是一种network-only representation learning方法。我们选择参数为:窗口尺寸 ,每个顶点的游走序列数量 。对于Cora,Citeseer数据集维度 ,对于Wiki数据集维度 ,这些是在50 ~200之间选择的性能最佳的维度。我们还通过求解“低秩分解”方程并将 和 拼接起来作为顶点
representation从而评估MF-style DeepWalk的性能。结果与DeepWalk相比差不多,因此我们仅报告了原始DeepWalk的性能。pLSA:我们使用PLSA通过将每个顶点视为一个文档来从TF-IDF矩阵训练主题模型。因此,PLSA是content-only baseline方法。PLSA通过EM算法估计文档的主题分布和主题的word分布。我们使用文档的主题分布作为顶点representation。Text Features:使用文本特征矩阵 作为每篇文档的200维representation,这也是一种content-only baseline方法。Naive Combination:直接拼接DeepWalk的embedding向量和文本特征向量。对于Cora,Citeseer数据集这将得到一个300维向量;对于Wiki数据集这将得到一个400维向量。NetPLSA:NetPLSA将文档之间的链接视为网络正则化来学习文档的主题分布,存在链接的文档应该共享相似的主题分布。我们使用网络增强的文档主题分布作为network representation。NetPLSA可以视为一种兼顾网络和文本信息的NRL方法。我们将Cora,Citeseer数据集主题数量设置为160,将Wiki数据集主题数量设置为200。
评估方式:对于监督分类器,我们使用由
Liblinear实现的linear SVM。对于半监督分类器,我们使用SVM-Light实现的transductive SVM。我们对TVSM使用线性核。我们为每个类别训练一个one-vs-rest分类器,并选择linear SVM和transductive SVM中得分最高的类别。我们将顶点的
representation作为特征来训练分类器,并以不同的训练比率training ratio来评估分类准确性。训练比率从linear SVM的10% ~ 50%,以及从TSVM的1% ~ 10%不等。对于每个训练比率,我们随机选择文档作为训练集,剩余文档作为测试集。我们重复试验10次并报告平均准确率。实验结果:下表给出了
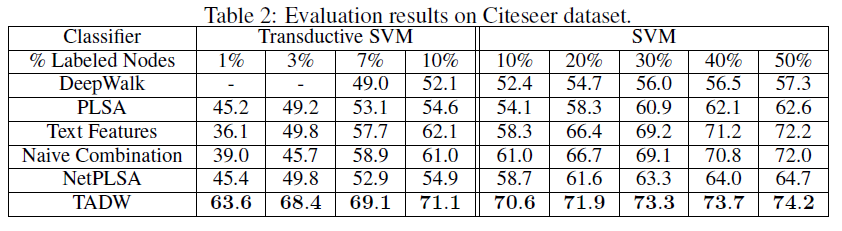
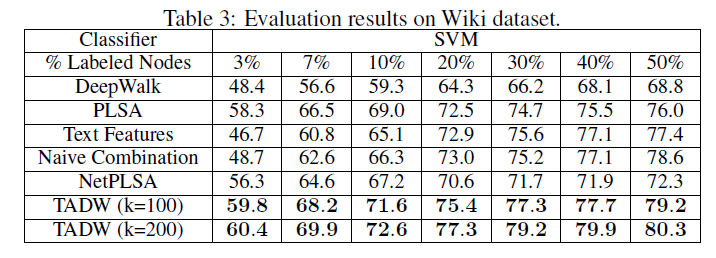
Cora数据集、Citeseer数据集、Wiki数据集的分类准确率。这里-表示TSVM不能在12小时内收敛,因为representation的质量较低(对于TADW,TADM总是可以在5分钟内收敛)。我们没有在Wiki数据集上展示半监督学习的结果,因为监督SVM已经在这个数据集上以较小的训练比率获得了有竞争力的、甚至更好的性能。因此,我们仅报告Wiki数据集的有监督SVM的结果。Wiki数据集的类别要比其它两个数据集多得多,这需要更多的数据来进行足够的训练,因此我们将最小训练比率设为3%。从这些表中我们可以看到:
TADW在所有三个数据集上始终优于所有其它baseline。此外,TADW可以在Cora数据集和Citeseer数据集上减少50%的训练数据从而击败其它baseline。这些实验证明TADW是有效且鲁棒的。TADW对于半监督学习有更显著的提升。TADW的表现优于最佳的baseline(即naive combination),在Cora数据集上提升4%、在Citeseer数据集上提升10% ~ 20%。这是因为在Citeseer上的network representation质量很差,而TADW从噪音的数据中学习比naive combination更鲁棒。TADW在训练比率较小时有更好的表现。大多数baseline的准确率随着训练比率的降低而迅速下降,因为它们的vertex representation对于training和testing而言非常noisy和inconsistent。相反,由于TADW从网络和文本信息中联合学习representation,因此representation具有更少的噪音并且更加一致。
这些观察结果证明了
TADW生成的高质量representation。此外,TADW不是task-specific的,representation可以方便地用于不同的任务,例如链接预测、相似性计算、顶点分类等等。TADW的分类准确性也与最近的几种collective分类算法相媲美,尽管我们在学习representation时没有对任务执行特别的优化。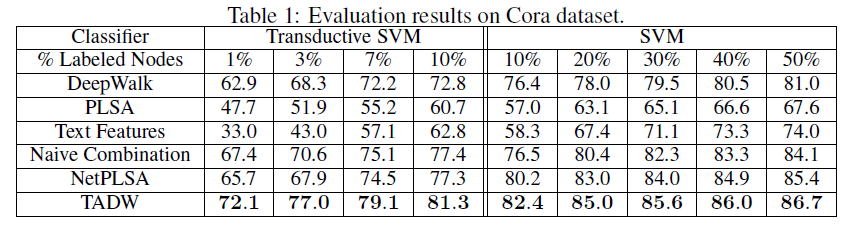
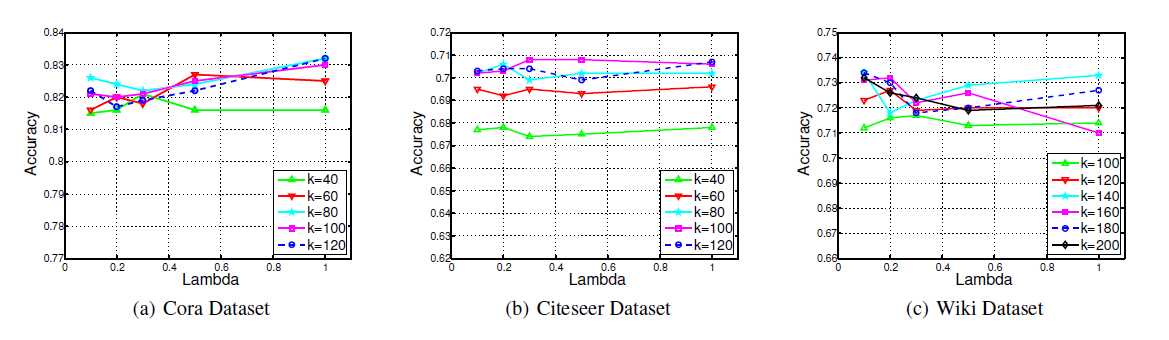
参数敏感性:
TADW有两个超参数:维度 和正则化系数 。我们将训练比率固定为10%,并使用不同的 和 测试分类准确率。对于Cora数据集和Citeseer数据集,我们让 在40 ~ 120之间变化,而 在0.1 ~ 1之间变化。对于Wiki数据集,我们让 在100 ~ 200之间变化,而 在0.1 ~ 1之间变化。下图显示了不同 和 下分类准确率的变化。可以看到:
- 对于
Cora, Citeseer, Wiki上的固定 ,不同 对应的准确率分别在1.5%, 1%, 2%的波动范围内。 - 当
Cora和Citeseer上的 、Wiki上的 时,准确率具有竞争性competitive。因此,当 和 在合理范围内变化时,TADW可以保持稳定。
- 对于
案例研究:为了更好地理解
NRL文本信息的有效性,我们在Cora数据集中提供了一个案例。document标题为Irrelevant Features and the Subset Selection Problem(不相关特征和子集选择问题)。我们将这篇论文简称为IFSSP。IFSSP的类别标签为Theory。如下表所示,使用DeepWalk和TADW生成的representation,我们找到了5篇最相似的论文,并基于余弦相似度来排序。我们发现,所有这些论文都被
IFSSP引用。然而,DeepWalk发现的5篇论文中有3篇具有不同的类别标签,而TADW发现的前4篇论文具有相同的类别标签Theory。这表明:与单纯的基于网络的DeepWalk相比,TADW可以借助文本信息学到更好的network representation。DeepWalk发现的第5篇论文也展示了仅考虑网络信息的另一个限制。《MLC Tutorial A Machine Learning library of C classes》(简称MLC)是一个描述通用toolbox的论文,可以被不同主题的许多论文引用。一旦其中一些论文也引用了IFSSP,DeepWalk将倾向于给IFSSP一个与MLC类似的representation,即使它们具有完全不同的主题。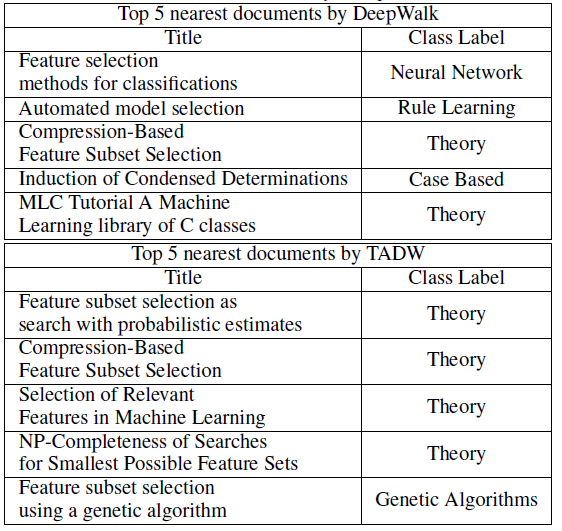
五、DNGR[2016]
图是许多现实世界问题中用于信息管理的常见表达。例如,在
protein-protein interaction网络中挖掘蛋白质复合物在同源蛋白质功能多样性的描述中起着重要作用,并提供有价值的演化洞察,这本质上是一个聚类问题。因此,开发自动化算法以从图中提取有用的深层信息至关重要。组织这类信息(它与潜在的大且复杂的图相关)的有效方法之一是学习graph representation,它为图的每个顶点分配一个低维的稠密的向量representation,从而对图传达的有意义的信息进行编码。最近,人们对学习
word embedding的工作产生了浓厚的兴趣。他们的目标是从大量自然语言文本中,根据上下文为每个自然语言单词学习一个低维的向量representation。这些工作可以被视为线性序列的learning representation,因为语料库由自然语言序列构成的线性结构组成。由此产生的紧凑的、低维的向量representation被认为能够捕获丰富的语义信息,并被证明可用于各种自然语言处理任务。虽然已经确定了学习线性结构的良好representation的有效方法,但是处理具有丰富拓扑的、通用的图结构更为复杂。为此,一种自然的方法是确定一种有效的转化方法:将学习通用图结构的vertex representation的任务转化为学习线性结构的representation的任务。DeepWalk提出了一种思想,它通过称作截断的随机游走truncated random walk的均匀采样方法将无权图转换为线性序列的集合。在他们的方法中,采样的顶点序列刻画了图中顶点之间的连接。这一步可以理解为将通用的图结构转化为线性结构集合的过程。接下来,他们利用了SkipGram模型从这种线性结构中学习顶点的低维representation。学到的顶点representation在一些任务中是有效的,并且优于先前的几种方法,如谱聚类spectral clustering、以及modularity方法。虽然这种学习无权图的顶点
representation的方法是有效的,但是仍然有两个重要问题有待回答:- 首先,对于加权图,如何更准确、更直接地捕获到图结构信息?
- 其次,是否有更好的方法来表达线性结构的顶点?
为了回答第一个问题,论文
《Deep Neural Networks for Learning Graph Representations》设计了一个适合加权图的随机冲浪模型random surfing model,它可以直接产生一个概率共现矩阵probabilistic co-occurrence matrix。这样的矩阵类似于通过从图中采样线性序列获得的共现矩阵,但是我们的方法不需要采样过程。使用带重启的
PageRank来计算转移概率,并不具备创新性。为了回答第二个问题,论文
《Deep Neural Networks for Learning Graph Representations》首先回顾了一种用于学习线性结构的顶点representation的现有方法。最近的一项研究《Neural word embedding as implicit matrix factorization》表明:使用负采样的SkipGram的目标函数,与分解由单词和它们上下文组成的一个shifted positive pointwise mutual information: PPMI矩阵有内在关系。具体而言,他们表明可以使用标准的奇异值分解SVD方法对PPMI矩阵进行因式分解,从而从分解的矩阵中导出vertex/word representation。最近的方法GraRep已被证明在学习graph representation的任务上取得了良好的实验结果。然而,该方法采用SVD来执行线性降维,而没有探索更好的非线性降维技术。在论文
《Deep Neural Networks for Learning Graph Representations》中,作者对《Neural word embedding as implicit matrix factorization》的工作给出了一个新的视角。作者认为:原始PPMI矩阵本身是图的显式representation矩阵,而SVD步骤本质上起到了降维toolbox的作用。虽然用于产生最终word representation的SVD步骤被证明是有效的,但是《Improving distributional similarity with lessons learned from word embeddings》也证明了使用PPMI矩阵本身作为word representation的有效性。有趣的是,正如《Improving...》的作者所展示的,从SVD方法学到的representation不能完全胜过PPMI矩阵本身的representation。由于我们的最终目标是学习能够有效捕获图信息的良好顶点representation,因此必须研究从PPMI矩阵中得到顶点representation的更好方法,其中可以捕获不同顶点之间潜在的、复杂的非线性关系。深度学习揭示了非线性的复杂现象建模的路径,它在不同领域有许多成功的应用,例如语音识别和计算机视觉。深度神经网络
DNN,例如堆叠自编码器stacked autoencoder,可以被视为从低级特征学习高级抽象的有效方法。该过程本质上执行降维,将数据从高维空间映射到低维空间。与基于SVD的降维方法不同(它通过线性投影从原始representation空间映射到具有较低秩的新空间),堆叠自编码器等深度神经网络可以学习高度非线性的投影。事实上,
《Learning deep representations for graph clustering》在聚类任务中使用稀疏自编码器sparse autoencoder来代替谱聚类spectral clustering的特征值分解eigenvalue decomposition步骤,并取得了显著的改进。受他们工作的启发,论文《Deep Neural Networks for Learning Graph Representations》还研究了使用基于深度学习的替代方法从原始数据representation中学习低维representation的有效性。与他们的工作不同,这里的目标是学习通用图的顶点representation,而不是专门关注聚类任务。作者将深度学习方法应用于PPMI矩阵,而不是他们模型中使用的拉普拉斯矩阵。DeepWalk已经证明前者有可能比后者产生更好的表现。为了增强模型的鲁棒性,作者还使用了堆叠降噪自编码器来学习多层representation。仅仅用非线性投影代替线性投影,并不具有创新性。
作者称提出的模型为
deep neural networks for graph representation: DNGR。学到的representation可以视为能够输入到其它任务中的输入特征,例如无监督聚类任务和有监督分类任务。为了验证模型的有效性,作者进行了将学到的representation用于一系列不同任务的实验,其中考虑了不同类型和拓扑的现实世界网络。为了在考虑更简单、但是更大规模的实际图结构时证明DNGR模型的有效性,作者将DNGR模型应用于一个非常大的语言数据集,并在word similarity任务上进行了实验。在所有这些任务中,DNGR模型优于其它learning graph representation方法,而且DNGR模型也可以简单地并行化。论文的主要贡献在两个方面:
- 从理论上讲,作者认为深度神经网络的优势在于能够捕获图传递的非线性信息,而许多广泛使用的、传统的线性降维方法无法轻易地捕获此类信息。此外,作者认为论文的随机冲浪模型可用于取代广泛使用的传统采样方法来直接捕获图结构信息。
- 根据实验,作者证明
DNGR模型能够更好地学习加权图的低维顶点representation,其中可以捕获图的有意义的语义信息semantic information、关系信息relational information、以及结构信息structural information。作者表明,得到的representation可以有效地用作不同下游任务的特征。
5.1 背景和相关工作
这里我们首先展示
DeepWalk中提出的无权图的随机采样,从而说明将顶点representation转换为线性representation的可行性。然后我们考虑两种word represenation方法:带负采样的SkigGram、基于PPMI矩阵的矩阵分解。这些方法可以视为从线性结构数据中学习word representation的线性方法。背景:给定加权图 ,其中 为顶点集合, 为边集合,边 由两个顶点组成。在无权图中,二元的边权重表示两个顶点之间是否存在关系。相比之下,加权图中的边权重是个实数,表示两个顶点之间的相关程度。尽管加权图中的边权重可能为负,但是我们在本文中仅考虑非负权重。
为了符号方便,我们在全文中也使用 和 来表示顶点。我们试图通过捕获图 的深层结构信息来获得顶点的
representation矩阵 。DeepWalk:DeepWalk提供了一种有效的方法,称作截断的随机游走truncated random walk,从而将无权的图结构信息转换为表示顶点之间关系的线性序列。所提出的随机游走是一种适用于无权图的均匀采样方法:- 首先从图中随机选择一个顶点 ,并将其标记为当前顶点。
- 然后从当前顶点 的所有邻居中随机选择下一个顶点 。现在,将这个新选择的顶点 标记为当前顶点并重复这样的顶点采样过程。
当一条序列中的顶点数量达到 (称作游走长度
walk length)的预设数时,算法终止。重复上述过程 次(称作游走次数total walk)后,我们得到线性序列的集合。虽然截断的随机游走是一种使用线性序列表达无权图结构信息的有效方法,但是该过程涉及缓慢的采样过程,并且超参数 和 不易确定。我们注意到:
DeepWalk基于采样的线性序列产生了一个共现矩阵co-occurrence matrix。在下文中,我们描述了我们的随机冲浪模型random surfing model,该模型直接从加权图中构建概率共现矩阵,从而避免了昂贵的采样过程。SkipGram with negative sampling: SGNS:自然语言语料库由线性序列的streams of words组成。最近,神经嵌入方法neural embedding method和基于矩阵分解的方法已广泛应用于学习word representation。《Distributed representations of words and phrases and their compositionality》提出的SkipGram模型已被证明是一种有效且高效的学习word representation的方法。改进SkipGram模型的两种值得注意的方法是负采样skip-gram with negative sampling: SGNS、以及hierarchical softmax。在本文中,我们选择使用前一种方法。在
SGNS中,采用噪声对比估计noise contrastive estimation: NCE方法(《A Fast and Simple Algorithm for Training Neural Probabilistic Language Models》)的简化变体来增强SkipGram模型的鲁棒性。SGNS根据经验的unigram word distribution随机创建negative pairs,并尝试使用低维向量表示每个单词 和每个上下文单词 。SGNS的目标函数旨在最大化positive pairs和最小化negative pairs:其中:
- 为
sigmoid函数 。 - 为负样本数量。
- 为当负样本 从分布 中采样时的期望。分布 为均匀分布,
#(c)为上下文顶点 在数据集 中出现的次数, 为数据集规模。 - 为顶点 的
representation向量, 为上下文顶点 的context representation向量。
- 为
PPMI矩阵和SVD:学习graph representation(尤其是word representation)的另一种方法是基于矩阵分解技术。这种方法基于全局共现计数global co-occurrence counts的统计数据来学习representation,并且在某些预测任务中可以优于基于单独的局部上下文窗口local context windows的神经网络方法。矩阵分解方法的一个例子是超空间模拟分析
hyperspace analogue analysis,它分解word-word共现矩阵从而产生word representation。这种方法和相关方法的一个主要缺点是:语义信息相对较小的高频词(例如停用词stop words)对生成的word representation产生不成比例的影响disproportionate effect。《Word association norms, mutual information, and lexicography》提出了pointwise mutual information: PMI矩阵来解决这个问题,并且已经被证明可以提供更好的word representation:其中: 表示数据集 中出现的次数, 为所有
pair的总样本量。进一步提高性能的方法是将每个负值调整为
0(详细信息参考论文《Neural word embedding as implicit matrix factorization》),从而形成PPMI矩阵:其中 为
PPMI矩阵。尽管
PPMI矩阵是一个高维矩阵,但是使用截断的SVD方法truncated SVD method执行降维会产生关于L2损失的最佳秩 的分解。我们假设矩阵 可以分解为三个矩阵: ,其中 为正交矩阵, 为对角矩阵(奇异值从大到小排列)。换言之:其中: 为 的最左侧的 列, 为 的最左侧的 列, 为 最左侧的 个奇异值(也是最大的 个奇异值)。根据
《Improving distributional similarity with lessons learned from word embeddings》,word representation矩阵 可以为:PPMI矩阵 是word representation矩阵和context矩阵的乘积。SVD过程为我们提供了一种从矩阵 中找到矩阵 的方法,其中 的行向量是word/vertex的低维representation,并且 的行向量可以通过 给出的高维representation的线性投影获得。我们认为这种投影不一定是线性投影。在这项工作中,我们研究了使用非线性投影方法通过使用深度神经网络来代替线性SVD的方法。深度神经网络:可用于学习
multiple level的feature representation的深度神经网络在不同领域取得了成功。训练这样的网络被证明是困难的。一种有效的解决方案是使用贪心的逐层无监督预训练greedy layer-wise unsupervised pre-training。该策略旨在一次学习一层的有用的representation。然后将学到的low-level representation作为下一层的输入,用于后续的representation learning。神经网络通常采用非线性激活函数(例如sigmoid或tanh)来捕获从输入到输出的复杂非线性投影。为了训练涉及多层
feature representation的深层架构,自编码器autoencoder已经成为常用的building block之一。自编码器执行两个操作:编码encoding、解码decoding。- 在编码步骤中,函数 应用于输入空间中的向量,并将其转换到新的特征空间。在这个过程中通常会涉及一个激活函数来对两个向量空间之间的非线性进行建模:输入向量空间,以及潜在向量
representation的空间。 - 在解码步骤中,重构函数 用于从潜在
representation空间重构原始输入向量。
让我们假设 ,以及 ,其中: 为非线性激活函数, 为编码器的参数, 为解码器的参数。这里 是转换输入空间的线性映射的权重, 为线性映射的
bias向量。我们的目标是通过找到 和 来最小化以下重构损失函数:其中 为数据集, 为单个样本的损失函数。
堆叠自编码器
stacked autoencoder是由多层的此类自编码器组成的多层深度神经网络。堆叠自编码器使用逐层训练方法来提取基本规律,从数据中逐层捕获不同level的抽象,其中更高层传递来自数据的更高level的抽象。- 在编码步骤中,函数 应用于输入空间中的向量,并将其转换到新的特征空间。在这个过程中通常会涉及一个激活函数来对两个向量空间之间的非线性进行建模:输入向量空间,以及潜在向量
5.2 模型
现在我们详细介绍我们的
DNGR模型。如下图所示,该模型由三个主要步骤组成:- 首先,我们引入随机场冲浪模型
random surfing model来捕获图结构信息并生成概率共现矩阵probabilistic co-occurrence matrix。 - 接下来,遵从
《Extracting semantic representations from word co-occurrence statistics: A computational study》,我们根据概率共现矩阵计算PPMI矩阵。 - 最后,我们使用堆叠降噪自编码器
stacked denoising autoencoder来学习低维的vertex representation。
下图的
SDAE结构中, 对应于输入数据、 对应于第一层学到的representation, 对应于第二层学到的representation。临时破坏的节点(例如 ) 以红色突出显示。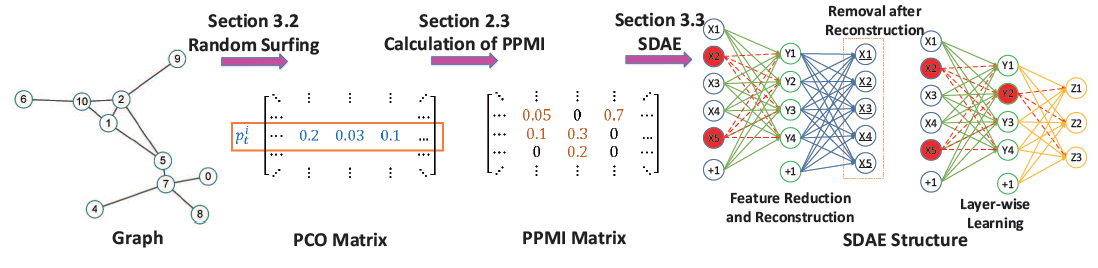
- 首先,我们引入随机场冲浪模型
5.2.1 随机冲浪和上下文加权
虽然有效,但是将图结构转换为线性序列的采样方法有一些弱点:
- 首先,采样序列的长度是有限的。这使得很难为出现在采样序列边界处的顶点捕获正确的上下文信息。
- 其次,确定某些超参数(例如游走长度 、游走次数 )难以简单地确定,尤其对于大图。
为了解决这些问题,我们考虑使用由
PangeRank模型启发的随机冲浪模型andom surfing model,其中PageRank模型原本用于ranking任务。我们首先对图中的顶点进行随机排序。我们假设当前的顶点是第 个顶点,并且有一个转移矩阵 来捕获不同顶点之间的转移概率transition probability。我们引入一个行向量 ,它的第 项表示经过 步转移之后达到第 个顶点的概率。 为初始的
1-hot向量,它的第 项为1而其它所有项为0。我们考虑一个带重启的随机冲浪模型random surfing model with restart:在每次,继续随机冲浪过程的概率为 ,返回原始顶点并重新开始的概率为 ,其中 。这将导致以下递推关系:如果我们假设过程中没有随机重启,则在恰好 步转移之后到达不同顶点的概率由以下公式指定:
如果我们考虑所有顶点开始的随机冲浪(而不仅仅是顶点 开始的),则有:
设最大的转移步数为 ,则通过这种方式我们得到
PMI矩阵:直觉上,两个顶点之间的距离越近,它们的关系就应该越紧密。因此,根据上下文节点和当前节点的相对距离来衡量上下文节点的重要性是合理的。在
word2vec和GloVe中都实施了此类加权策略,并且发现对于获得良好的实验结果很重要(《Improving distributional similarity with lessons learned from word embeddings》)。基于这一事实,我们可以看到,理想情况下,第 个顶点的representation应该以如下方式构建:其中 是一个单调递减函数(称作权重函数
weighting function),满足 。注意:
PMI的转移概率向量也可以视为顶点的某种representation。我们认为,基于上述随机冲浪过程构建顶点
representation的以下方式(即 )实际上满足了上述条件。事实上,可以证明:其中 。则 中 的系数为:
当满足 时, 是一个单调递减函数。
另外,
SkipGram中的 函数为:而
GloVe中的 函数为:如下图所示,所有权重函数 都是单调递减的。图中纵轴是分配给上下文节点的权重,横轴是上下文顶点和当前顶点之间的距离。
因此,与
word2vec和GloVe类似,我们的模型还允许根据上下文到target的距离从而对上下文信息进行不同的加权。这在之前被证明对于构建良好的word representation很重要。我们将通过实验评估这方面的重要性。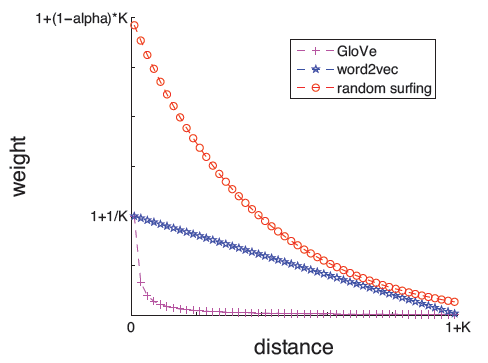
5.2.2 堆叠降噪自编码器
我们的研究旨在钻研从
PPMI矩阵构建顶点的高质量低维向量representation,其中PPMI矩阵传递了图的基本结构信息。SVD过程虽然有效,但是它本质上只产生从PPMI矩阵所包含的高维向量representation到最终低维向量representation的线性变换。我们相信可以在两个向量空间之间构建潜在的非线性映射。因此,我们使用堆叠降噪自编码器stacked denosing autoencoder(一种用于深度学习的流行模型)从原始高维顶点向量representation生成压缩的低维顶点向量representation。我们首先初始化神经网络的参数,然后我们使用贪心的逐层训练
greedy layer-wise training策略来学习每一层的high-level抽象。为了增强DNN的鲁棒性,我们使用了堆叠降噪自编码器stacked denoising autoencoder: SDAE。与传统的自编码器不同,降噪自编码器会在进行训练之前部分破坏输入数据。具体而言,我们通过将输入向量中的一些位置以一定概率设置为0来随机破坏每个输入样本 (它是一个向量)。这个想法类似于在矩阵补全matrix completion任务中对缺失项进行建模,其目标是利用数据矩阵中的规律性在某些假设下有效地恢复完整矩阵。与标准的自编码器类似,我们从潜在representation中重建数据。换句话讲,我们对以下目标感兴趣:其中 是 的破坏的版本, 为标准的平方误差。
SDAE算法:输入:
PPMI矩阵SDAE层数
输出:顶点的
representation矩阵算法步骤:
初始化第一层的
input贪心逐层训练,步骤为: :
- 基于
input来构建单隐层的SDAE - 学习隐层
representation - 隐层的输出作为
- 基于
最后一层隐层的
representation作为顶点的representation矩阵 。
5.2.3 DNGR 模型的讨论
这里我们分析以下
DNGR的优势,其实验有效性将在实验部分介绍。随机冲浪策略:如前所述,随机冲浪过程克服了以前工作中的采样程序相关的限制,并且为我们提供了某些所需的属性。这些属性是以前的
embedding模型 (例如word2vec和GloVe)所具备的。随机冲浪策略涉及计算
PMI矩阵,其计算复杂度太高()。堆叠策略:堆叠结构提供了一种平滑的降维方式。我们相信在深度架构的不同层上学习的
representation可以为输入数据提供不同level的有意义的抽象。降噪策略:高维输入数据通常包含冗余信息和噪声。我们相信降噪策略可以有效地降低噪声并增强鲁棒性。
效率:根据之前的分析,
DNGR中使用自编码器来推断,在顶点数量方面,比基于SVD的矩阵分解方法具有更低的时间复杂度。SVD的时间复杂度至少是顶点数量的二次方。然而,DNGR的推断时间复杂度与图中的顶点数量呈线性关系。但是在训练效率方面,
DNGR和SVD都需要计算PPMI矩阵,二者都是 计算复杂度。
5.3 实验
为了评估
DNGR模型的性能,我们在真实数据集上进行了实验。除了展示graph representation的结果以外,我们还评估了从自然语言语料库(它由线性序列组成)中学习的word embedding的有效性。数据集:
语言网络数据集
20-Newsgroup:包含2万篇新闻组文档,并按照20个不同的组分类。每篇文档由文档内单词的tf-idf组成的向量表示,并根据余弦相似度计算得到文档的相似度。根据文档的这些相似度构建语言网络,该网络是一个全连接的带权图,用于聚类效果的评估。为验证模型的鲁棒性,我们分别从
3/6/9个不同的新闻组构建了三个更小规模的语言网络(NG代表Newsgroups):3-NG:由comp.graphics, comp.graphics and talk.politics.guns这三个新闻组的文档构成。6-NG:由alt.atheism, comp.sys.mac.hardware, rec.motorcycles, rec.sport.hockey, soc.religion.christian and talk.religion.misc这六个新闻组的文档构成。9-NG:由talk.politics.mideast, talk.politics.misc, comp.os.ms- windows.misc, sci.crypt, sci.med, sci.space, sci.electronics, misc.forsale, and comp.sys.ibm.pc.hardware这九个新闻组的文档构成。
这些小网络分别对每个主题随机抽取
200篇文档。Wine数据集:包含意大利同一地区种植的三种不同品种的葡萄酒化学分析的13种成分的数量(对应13个特征及其对应取值),数据包含178个样本。我们将样本作为顶点、采用不同样本之间的余弦相似度作为边来构建
Graph。维基百科语料库:包含
2010年4月的快照作为训练集,包含2000万条文章和9.9亿个token。由于SVD算法复杂性,我们选择1万个最常见的单词构建词典。为了评估每个算法生成的
word representation的性能,我们在四个数据集上进行了word similarity实验,包括流行的WordSim353、WordSim Similarity、WordSim Relatedness、MC四个数据集。所有这四个数据集都有word pairs以及人工分配的相似性。
注意,这里得到的
graph都是根据节点相似性来构建的,因此并不是天然的图结构。这种数据集作为benchmark可能不太科学,因为稍微不同的图构建方式可能导致完全不同的评测结果。baseline方法:我们考虑以下四个baseline方法:DeepWalk:使用截断的随机游走truncated random walk将图结构转化为线性结构,然后使用hierarchical softmax的SkipGram模型处理序列。SGNS:使用带负采样的SkipGram模型。它已被证明是从理论上和经验上学习word representation的有效模型。PPMI:是信息论中经常使用的度量。该方法直接基于单词的共现来构建PPMI矩阵,并用顶点的PPMI信息构建顶点的稀疏、高维representation。SVD:是一种常用的矩阵分解方法,用于降维或提取特征。我们使用SVD来压缩PPMI矩阵从而获取顶点的低维representation。
参数配置:
随机游走序列长度 ,每个顶点开始的序列数量为 。
对于
DeepWalk, SGNS,负采样个数 ,上下文窗口大小为 。对于
DNGR:使用
dropout缓解过拟合,dropout比例通过调参来择优。所有神经元采用
sigmoid激活函数。堆叠式降噪自编码器的层数针对不同数据集不同。

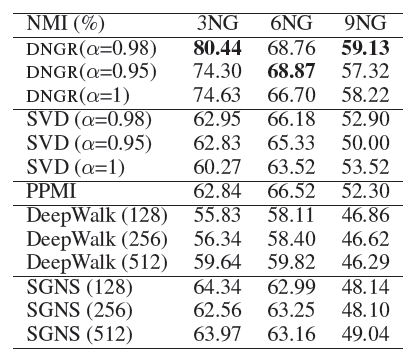
20-NewsGroup数据集上的聚类任务:该任务通过K-means对每个算法生成的顶点representation向量进行聚类,并以归一化互信息normalized mutual information: NMI作为衡量指标。每种算法随机执行10次并报告平均结果。为了验证不同维度的影响,下面还给出了DeepWalk,SGNS在维度为128、512时的结果。结论:
我们的
DNGR模型明显优于其它baseline方法,尤其是当 时。当 时,上下文信息不会根据它们的距离进行加权,我们得到较差的结果。这证明了前面讨论的上下文加权策略的重要性。
在
DeepWalk和SGNS中,增加维度使得效果先提升后下降。比较
DNGR和PPMI,效果的提升证明了对于高维稀疏矩阵降维并提取有效信息的好处。在相同的 设置下,
DNGR始终比SVD效果更好。这为我们之前的讨论提供了实验证据:DNGR是一种比SVD更有效的降维方法。
Wine数据集上的可视化任务:该任务采用t-SNE将DNGR,SVD,DeepWalk,SGNS输出的顶点representation映射到二维空间来可视化。在二维空间中,相同类型的葡萄酒以相同颜色来展示。在相同设置下,不同类型葡萄酒之间具有更清晰边界的聚类意味着更好的representation。结论:
DeepWalk和SGNS的可视化显示不清晰的边界和分散的簇。DNGR()要好得多。虽然SVD优于DNGR(),但是在结果中我们可以看到绿色的点仍然与一些红色的点混合在一起。DNGR()效果最好。我们可以看到不同颜色的点出现在3个独立的区域,并且大多数相同颜色的点聚集在一起。

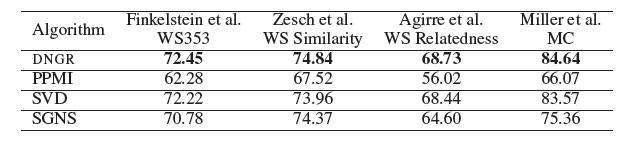
Word Similarity任务:我们在维基百科语料库上执行单词相似度任务,该任务直接从训练语料库中计算word-context组合因此不需要随机冲浪模型来生产PPMI矩阵。我们采用Spearman’s rank correlation coefficient来评估算法的结果。为了获得最佳结果,我们将SGNS,DNGR,SVD负采样的样本数分别设置为5,1,1。结论:
DNGR的性能优于其它baseline方法。SVD,DNGR都比PPMI效果更好,这表明降维在该任务中的重要性。DNGR超越了SVD和SGNS,这表明学习representation时捕获非线性关系的重要性,并说明了使用我们的深度学习方法学习更好抽象的能力。
深度结构的重要性:为了理解深层结构的必要性,我们进一步度量了
20-NewsGroup数据集的layerwise NMI值。对于3NG和6NG,我们使用3层神经网络,对于9NG我们使用4层神经网络。从结果中我们可以看到:从浅层到深层,这三个网络的性能总体而言都在提升。这证明了深层结构的重要性。
六、Node2Vec[2016]
网络分析中的许多重要任务涉及对节点和边的预测。
- 在典型的节点分类任务中,我们需要预测网络中每个节点最可能的标签。例如,在社交网络中我们预测用户的兴趣标签,在
protein-protein interaction网络中我们预测蛋白质的功能标签。 - 类似地,在链接预测中,我们希望预测网络中的一对节点之间是否应该存在一条边。链接预测在各个领域都很有用。例如,在基因组学
genomics中它可以帮助我们发现基因之间的、新的interaction,在社交网络中它可以识别现实世界中的朋友。
任何有监督的机器学习算法都需要一组信息丰富
informative的、有区分力discriminating的、独立independent的特征。在网络的预测问题中,这意味着必须为节点和边构建特征的向量representation。典型的解决方案涉及基于专家知识的、人工的、领域特定domain-specific的特征。即使不考虑特征工程所需的繁琐工作,这些特征通常也是为特定任务设计的,并且不会在不同的预测任务中泛化。另一种方法是通过解决优化问题来学习feature representation。feature learning的挑战在于定义目标函数,这涉及计算效率和预测准确性的trade-off:- 一方面,人们可以致力于找到一种直接优化下游预测任务性能的
feature representation。虽然这种监督的过程具有良好的准确性,但是由于需要估计的参数数量激增,因此需要以高的训练时间复杂度为代价。 - 另一方面,目标函数可以定义为独立于下游预测任务,并且可以通过纯粹的无监督的方式学习
representation。这使得优化过程的计算效率较高,并且具有精心设计的目标函数。但是该目标函数产生了与任务无关的特征,这些特征无法达到task-specific方法的预测准确性。
然而,当前的技术未能令人满意地定义和优化网络中的合理目标函数,从而支持可扩展的无监督
feature learning。基于线性降维技术和非线性降维技术的经典方法,例如主成分分析
Principal Component Analysis: PCA、多维缩放Multi-Dimensional Scaling: MDS及其扩展方法,它们优化一个目标函数,该目标函数变换transform网络的代表性的数据矩阵representative data matrix从而最大化data representation的方差(原始数据在低维空间representation的方差,即数据尽可能分散)。因此,这些方法总是涉及对应矩阵的特征分解eigen decomposition,而特征分解对于大型现实世界网络而言是代价昂贵的。此外,所得到的潜在representation在网络上的各种预测任务中表现不佳。或者,我们可以设计一个旨在保留节点的局部邻域
local neighborhood的目标函数(最大化保留节点的网络邻域network neighborhood的可能性)。我们可以使用随机梯度下降stochastic gradient descent: SGD来有效优化目标函数。最近一些工作在这个方向上进行了尝试,但是它们依赖于网络邻域network neighborhood的严格概念,这导致这些方法在很大程度上对网络特有的连接模式connectivity pattern不敏感。具体而言,网络中的节点可以根据它们所属的社区community(即同质性homophily)进行组织,也可以根据它们的结构角色structural role(即结构相等性structural equivalence)来组织。例如,下图中,我们观察到节点 和 都属于同一个紧密结合的节点社区,而两个不同社区中的节点 和 共享相同的结构角色(即中心节点
hub node的角色)。现实世界的网络通常表现出这种相等性的混合体。因此,重要的是允许灵活的算法从而可以学习遵守这两个准则的node representation:能够学习将来自同一个网络社区的节点紧密地嵌入在一起的representation,也能够学习共享相似结构角色的节点具有相似embedding的representation。这将允许feature learning算法在广泛的领域和预测任务中推广。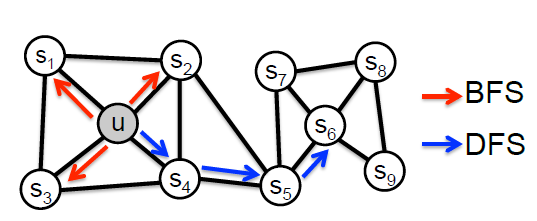
为此,论文
《node2vec: Scalable Feature Learning for Networks》提出了node2vec,一种用于网络中可扩展的feature learning的半监督算法。论文使用SGD优化graph-based自定义的目标函数,其灵感来自于自然语言处理的先前工作(《Efficient estimation of word representations in vector space》)。直观而言,论文的方法返回的feature representation可以最大化在低维特征空间中保留节点的网络邻域的可能性。论文使用二阶随机游走方法为节点生成(或采样)网络邻域。论文的主要贡献是定义了节点的网络邻域
network neighborhood的灵活概念。通过选择适当的邻域概念,node2vec可以学习根据节点的网络角色、和/或它们所属的社区而组织的representation。论文通过开发一系列有偏biased的随机游走来实现这一点,它可以有效地探索给定节点的多样化diverse的邻域。与先前工作中的严格搜索过程相比,由此产生的算法是灵活的,可以对超参数进行调优。因此,论文的方法推广了先前的工作,并且可以对网络中观察到的所有相等性equivalence进行建模。控制搜索策略的超参数有一个直观的解释,并且使得随机游走偏向于不同的网络探索策略。这些超参数也可以通过半监督的方式使用一小部分标记数据直接学习。论文还展示了如何将单个节点的
feature representation扩展到节点pair对(即edge)。为了生成边的feature representation,论文使用简单的binary operator组合学习到的各个节点的feature representation。这种组合性compositionality使得node2vec可用于涉及节点预测任务和边预测任务。论文的实验聚焦于网络中的两个常见预测任务上:多标签分类任务,其中每个节点都被分配一个或者多个类别标签;链接预测任务,在给定一对节点的情况下预测边是否存在。作者将
node2vec的性能与state-of-the-art的feature learning算法进行了对比。作者对来自不同领域的几个真实世界的网络进行了实验,例如社交网络social network、信息网络information network、以及来自系统生物学的网络。实验表明:node2vec在多标签分类任务上的性能优于state-of-the-art的方法高达26.7%,在链接预测任务上的性能优于state-of-the-art的方法高达12.6%。node2vec即使在10%的标记数据下也表现出有竞争力的性能,并且对噪声或者链接缺失的扰动也具有鲁棒性。
在计算上,
node2vec的主要阶段是可并行化的,它可以在几个小时内扩展到具有数百万个节点的大型网络。总体而言,论文做出了以下贡献:
- 论文提出了
node2vec,这是一种用于网络中feature learning的高效可扩展算法,可使用SGD有效优化新颖的、网络感知network-aware的、邻域保留neighborhood preserving的目标函数。 - 论文展示了
node2vec如何符合网络科学中的既定准则,为发现符合不同相等性equivalence的representation提供了灵活性。 - 论文扩展了
node2vec和其它基于邻域保留的目标函数的feature learning方法,从节点到节点pair对,从而用于edge-based预测任务。 - 论文根据经验评估了
node2vec在几个真实世界数据集上的多标签分类和链接预测任务。
- 在典型的节点分类任务中,我们需要预测网络中每个节点最可能的标签。例如,在社交网络中我们预测用户的兴趣标签,在
相关工作:机器学习社区在各种领域对特征工程
feature engineering进行了广泛的研究。在网络中,为节点生成特征的传统范式paradigm基于特征提取技术feature extraction technique,该技术通常涉及一些基于网络属性的、手工制作的特征。相比之下,我们的目标是通过将特征提取作为representation learning问题来自动化整个过程。在这种情况下,我们不需要任何手工设计的特征。无监督
feature learning方法通常利用图的各种矩阵representation的谱特性spectral property,尤其是图拉普拉斯矩阵Laplacian matrix和图邻接矩阵adjacency matrix。在这种线性代数的视角下,这些方法可以被视为降维技术。人们已经提出了几种线性降维技术(如PCA)以及非线性降维技术(如IsoMap)。这些方法同时存在计算性能缺陷和统计statistical性能缺陷。- 首先,在计算效率方面,数据矩阵的特征分解
eigen decomposition是代价昂贵的,因此这些方法很难扩展到大型网络。 - 其次,这些方法优化的目标函数对于网络中观察到的多样化模式
diverse pattern(例如同质性homophily和结构相等性structural equivalence)不是鲁棒的,并且对底层网络结构和预测任务之间的关系做出假设。例如,谱聚类spectral clustering做出了一个强烈的同质性假设,即图割graph cut对分类有用。这种假设在许多场景下都是合理的,但是在有效地推广到不同的网络方面并不令人满意。
自然语言处理中
representation learning的最新进展为离散对象(如单词)的feature learning开辟了新途径。具体而言,SkipGram模型旨在通过优化邻域保留neighborhood preserving的似然目标函数likelihood objective来学习单词的continuous feature representation。该算法的过程如下:首先扫描文档的单词,然后embedding每个单词使得该单词的特征能够预测附近的单词(即,该单词某个上下文窗口内的其它单词)。单词的feature representation是通过使用带负采样的SGD来优化似然目标函数likelihood objective来学习的。SkipGram的目标函数基于分布式假设distributional hypothesis,该假设指出:相似上下文中的单词往往具有相似的含义。即,相似的单词往往出现在相似的word neighborhood中。受
SkipGram模型的启发,最近的研究通过将网络表示为文档document来建立网络的一个类比analogy。就像文档是一个有序的单词序列一样,我们可以从底层网络中采样节点序列,并将网络变成一个有序的节点序列。然而,节点有多种可能的采样策略,导致学到的feature representation不同。事实上,正如我们将要展示的,没有明确的、最好的采样策略从而适用于所有网络和所有预测任务。这是先前工作的一个主要缺点:无法为网络中的节点采样提供任何灵活性。node2vec算法通过设计一个灵活的目标函数来克服这个限制,这个目标函数不依赖于特定的采样策略,并提供超参数来调整探索的搜索空间。最后,对于
node-based预测任务和edge-based预测任务,最近有大量基于现有的graph-specific深度网络架构的监督feature learning工作,和新颖的graph-specific深度网络架构的监督feature learning工作。这些架构使用多层非线性变换直接最小化下游预测任务的损失函数,从而获得高准确性,但是由于高训练时长的要求从而以可扩展性scalability为代价。- 首先,在计算效率方面,数据矩阵的特征分解
6.1 模型
我们将网络中的
feature learning形式化为最大似然优化问题。令 为一个给定的网络。我们的分析是通用的,适用于任何有向/无向、加权/无权的网络。令 是一个从节点到
feature learning的映射函数,其中feature learning用于下游预测任务。这里 为一个超参数,指定我们的feature representation的维度。换个说法, 是一个大小为 的参数矩阵,记作 。即 和 是同一个函数的不同表现形式。给定节点 , 为 的第 行。对于每个源节点 ,我们将 定义为通过邻域采样策略
neighborhood sampling strategy生成的节点 的网络邻域network neighborhood。我们继续将SkipGram框架扩展到网络。我们寻求优化以下目标函数,该目标函数最大化在给定节点 的feature representation的条件下,观察到一个网络邻域 的对数概率:为了使优化问题易于处理,我们做出两个标准假设:
条件独立
conditional independence:我们假设在给定源节点的feature representation的条件下, 观察到一个邻域节点的可能性独立于其它任何邻域节点。即:特征空间中的对称性
symmetry:源节点source node和邻域节点neighborhood node在特征空间中相互对称。因此,我们将每个source-neighborhood节点pair的条件似然建模为一个softmax单元,通过其特征向量的内积来参数化:
通过上述假设,则我们的最优化方程简化为:
其中 为逐节点的分区函数
per-node partition function。对于大型网络, 计算代价昂贵,为此我们使用负采样来近似它。我们使用随机梯度上升来优化上述方程。本质上是一个期望,是否可以通过均匀采样来近似?这是与负采样近似不同的另一种近似方法。
基于
SkipGram框架的feature learning方法最初是在自然语言的背景下开发的。鉴于文本的线性特性,邻域的概念可以使用连续单词上的滑动窗口sliding window自然地定义。然而,网络不是线性的,因此需要更丰富的邻域概念。为了解决这个问题,我们提出了一个随机程序,它对给定源节点 的许多不同的邻域进行采样。邻域 不仅局限于直接邻域,还可以根据采样策略 得到截然不同的各种邻域结构。
6.1.1 经典搜索策略
我们将源节点的邻域采样
sampling neighborhood问题视为一种局部搜索形式local search form。下图展示了一个graph,其中给定一个源节点 ,我们的目标是采样其邻域 。更重要的是,为了能够公平地比较不同的采样策略 ,我们将邻域 的大小限制为 个节点,然后为单个节点 采样多个邻域。通常,生成 个节点的邻域 有两种极端的采样策略:
- 广度优先采样
Breadth-first Sampling: BFS:邻域 仅限于与源节点 直接相邻的节点。例如在图中,对于节点 的大小为 的邻域,BFS采样节点为 。 - 深度优先采样
Depth-first Sampling: DFS:通过以距离递增顺序采样的节点组成了邻域。
广度优先采样和深度优先采样代表了搜索的极端场景,对学到的
representation产生了有趣的影响。具体而言,网络中节点的预测任务经常在两种相似性之间切换:同质性homophily和结构相等性structural equivalence。在同质性的假设下,高度互联且属于相似的网络簇
network cluster或网络社区network community的节点应该紧密地嵌入在一起。例如,图中的节点 和 属于同一个网络社区。相比之下,在结构相等性的假设下,在网络中具有相似结构角色
structural role的节点应该紧密地嵌入在一起。例如,图中的节点 和 作为各自社区的hub角色。重要的是,与同质性不同,结构相等性并不强调连通性
connectivity:节点可以在网络中相距很远,但是仍然具有相同的结构角色structural role。
在现实世界中,这些相等性概念
equivalence notion并不是互斥的:网络通常表现出两种行为,其中一些节点表现出同质性,而另一些节点则表现出结构相等性。
- 广度优先采样
我们观察到
BFS策略和DFS策略在生成反映上述任何一个相等性的representation中起着关键作用。具体而言:BFS采样的邻域导致embedding与结构相等性密切对应。直观地,我们注意到,为了确定结构相等性,准确地刻画局部邻域通常就足够了。例如,仅通过观察每个节点的直接邻域就可以推断出基于网络角色(例如bridge和hub)的结构相等性。通过将搜索限制在附近节点,BFS实现了这种刻画并获得了每个节点邻域的微观视图microscopic view。此外,在BFS中,被采样邻域中的节点往往会重复多次。这也很重要,因为它减少了源节点1-hop邻域的方差。然而,对于任何给定的邻域大小 ,
BFS仅探索了图中的很小一部分。DFS的情况正好相反,它可以探索网络的更大部分,因为它可以远离源节点。在DFS中,被采样的节点更准确地反映了邻域的宏观视图macro-view,这对于基于同质性的社区推断inferring community至关重要。然而,
DFS的问题在于:首先,不仅要推断网络中存在哪些
node-to-node的依赖关系,而且还要刻画这些依赖关系的确切性质(比如1-hop、2-hop等等)。鉴于我们限制了邻域规模,并且探索的邻域空间很大,这会导致高方差,因此这很难。高方差的意思是:从源节点 的每次
DFS采样都可能得到不同的结果。其次,切换到更大的深度(即更大的邻域大小 )会导致复杂的依赖关系,因为被采样的节点可能远离源节点并且可能不太具有代表性
less representative。
6.1.2 node2vec
鉴于上述观察,我们设计了一个灵活的邻域采样策略
neighborhood sampling strategy,使得我们能够在BFS和DFS之间平滑地进行插值interpolate。我们通过开发一个灵活的有偏随机游走biased random walk程序来实现这一点,该程序可以通过BFS的方式和DFS的方式探索社区。随机游走:正式地,给定一个源节点 ,我们模拟一个固定长度为 的随机游走。令 为随机游走中的第 个节点,其中 为随机游走的起始节点。节点 根据以下概率分布生成:
其中:
- 为节点 和 之间的未归一化的转移概率
unnormalized transition probability。 - 为归一化常数。
- 为节点 和 之间的未归一化的转移概率
search bias:有偏随机游走最简单的方法是根据静态的边权重 对下一个节点进行采样,即 。在无权图中, 。然而,这不允许我们考虑网络结构并指导我们的搜索过程来探索不同类型的网络邻域。此外,与分别适用于结构相等性、同质性的极端采样范式BFS和DFS不同,我们的随机游走应该适应这样一个事实,即:这些相等性概念equivalence notation不是相互竞争的、也不是互斥的,现实世界的网络通常表现出二者的混合。我们使用两个超参数 和 定义了一个二阶随机游走,它指导游走过程:考虑一个刚刚经过边 ,并且现在停留在节点 处的随机游走(如下图所示)。游走过程现在需要决定下一步,因此它评估从 开始的边 上的非归一化转移概率 。
我们将非归一化的转移概率设置为 ,其中:
其中 表示从节点 到节点 的最短路径距离
shortest path distance。注意: 的取值必须为{0, 1, 2},因此这两个超参数 对于指导随机游走是必要且充分的。如下图所示,edge上的文字表示search biases。
直观而言,超参数 和 控制着游走过程探索和离开起始节点 的邻域的速度。具体而言,这些超参数允许我们的搜索过程在
BFS和DFS之间进行近似approximately地插值,从而反映对节点的不同相等性概念的affinity。返回参数
return parameter:超参数 控制在游走过程中立即重访已有节点的可能性。- 将其设为较高的值()可以确保我们在接下来的两步中不太可能对已经访问过的节点进行采样(除非游走过程中的下一个节点没有其它邻居)。该策略鼓励适度探索并避免采样中的
2-hop冗余redundancy。 - 另一方面,如果 值较低(),则它将导致游走过程回退一步,这将使得游走过程局部地
local靠近起始节点 。
控制着返回上一个已访问节点 的概率。 越小,则返回的概率越大。
- 将其设为较高的值()可以确保我们在接下来的两步中不太可能对已经访问过的节点进行采样(除非游走过程中的下一个节点没有其它邻居)。该策略鼓励适度探索并避免采样中的
in-out parameter:超参数 允许搜索区分向内inward的节点和向外outward的节点。如上图所示:- 如果 ,则随机游走偏向于靠近节点 的节点。此时我们的
samples由小的局部small locality内的节点组成,这种游走过程获得了近似于BFS行为(以起始节点开始)的、底层图的局部视图local view。 - 相反,如果 ,则随机游走更偏向于远离节点 的节点。这种行为反映了鼓励向外探索的
DFS。然而,这里的一个本质区别是:我们在随机游走框架内实现了类似于DFS的探索。因此,采样节点与给定源节点 的距离并不是严格增加的。但是反过来,我们受益于易于处理的preprocessing、以及随机游走的卓越采样效率。
控制着远离上一个已访问节点 的概率。 越小,则远离的概率越大。
- 如果 ,则随机游走偏向于靠近节点 的节点。此时我们的
注意,通过将 设置为游走过程中前一个节点 的函数,随机游走过程是二阶马尔科夫的。
随机游走的好处:和单纯的
BFS/DFS方法相比,随机游走同时在空间复杂度和时间复杂度方面的效率较高。对于图中的所有节点,存储它们直接邻域的空间复杂度为 。对于二阶随机游走,存储所有节点的邻居之间的互联
interconnection是有帮助的,这会产生 的空间复杂度,其中 为图的平均degree并且在现实世界中通常很小。与经典的基于搜索的
BFS/DFS采样策略相比,随机游走的另一个关键优势是它的时间复杂度。具体而言,通过在sample generation过程中施加了图的连通性graph connectivity,随机游走提供了一种方便的机制,通过跨不同源节点reuse samples来提高采样效率:由于随机游走的马尔科夫性质,通过模拟长度为 的随机游走,我们可以一次性为 个源节点生成随机游走序列,即 条随机游走序列,每条随机游走序列的长度为 。因此,每个采样节点的有效时间复杂度为 。例如,下图中,我们采样了一条长度为 的随机游走序列 ,这将导致 ,其中 。注意,
sample reusing可能会在整个过程中引入一些bias,但是我们发现它大大提高了效率。
Node2Vec算法主要包含两个过程:Learn Feature过程、node2vecWalk过程。Learn Feature过程:输入:
- 图
- 维度
- 每个源节点开始的随机游走序列数量
- 每条随机游走序列长度
- 上下文尺寸
- 超参数
输出:每个节点的低维
representation步骤:
预处理权重 ,重新构造新的图
这是计算转移概率,并将转移概率设置为边的权重。但是这里转移概率是二阶马尔科夫的,如何设置为一阶的边权重?具体可能要看源代码。
初始化列表 为空:
迭代 次,对每个节点生成以该节点为起点、长度为 的 条随机游走序列。迭代过程为::
对每个节点 执行:
执行随机梯度下降 。
返回求解到的每个节点的
representation。
node2vecWalk过程:输入:
- 修改后的图
- 源节点
- 随机游走序列长度
输出:长度为 的一条随机游走序列
步骤:
初始化列表
迭代 ,迭代过程为:
- 获取当前节点
- 获取当前节点的邻居节点
- 采样下一个节点
- 将 添加到序列:
返回列表
Node2Vec算法的node2vecWalk过程中,由于源节点 的选择导致引入了隐式的bias。由于我们需要学习所有节点的representation,因此我们通过模拟从每个节点开始的、长度固定为 的 条随机游走序列来抵消该bias。另外在
node2vecWalk过程中,我们根据转移概率 来采样。由于二阶马尔可夫转移概率 可以提前计算好,因此可以通过AliasTable技术在 时间内高效采样。node2vec的三个阶段:即计算转移概率的预处理、随机游走模拟、以及使用SGD的优化,按顺序依次进行。每个阶段都是可并行化和异步执行的,有助于node2vec的整体可扩展性。
6.1.3 边的representation
node2vec算法提供了一种半监督方法来学习网络中节点的丰富特征representation。 然而,我们经常对涉及节点pair,而不是单个节点的预测任务感兴趣。例如,在链接预测中,我们预测网络中两个节点之间是否存在链接。由于我们的随机游走天然地基于底层网络中节点之间的连接结构connectivity structure,因此我们在单个节点的特征representation上使用bootstrapping的方法从而将它们扩展到节点pair。node2vec的训练是无监督的,但是可以使用下游任务的、少量的监督样本来选择最佳的超参数 ,从而实现半监督学习。给定两个节点 和 ,我们在相应的特征向量 和 上定义二元算子 ,从而生成
representation使得 ,其中 为pair的representation维度。我们希望我们的算子可以为任何一对节点进行定义,即使这对节点之间不存在边,因为这样做使得
representation对于链接预测有用,其中我们的测试集同时包含true edge(即存在边)和false edge(即不存在边)。我们考虑了算子 的几种选择,使得 ,如下所示:- 均值操作符
Average: Hadamard操作符:L1操作符Weighted-L1:L2操作符Weighted-L2:
- 均值操作符
6.1.4 总结
本文中我们将网络中的
feature learning作为search-based优化问题进行研究。这种观点为我们提供了多种优势:它可以在
exploration-exploitation trade-off的基础上解释经典的搜索策略。此外,当应用于预测任务时,它为学到的
representation提供了一定程度上的可解释性。- 例如,我们观察到
BFS只能探索有限的邻域,这使得BFS适用于刻画依赖于节点直接局部结构immediate local structure的网络中的结构相等性。 - 另一方面,
DFS可以自由探索网络邻域,这对于以高方差为代价发现同质社区homophilous community很重要。
- 例如,我们观察到
DeepWalk和LINE都可以视为严格的网络搜索策略。DeepWalk提出使用均匀的随机游走进行搜索。这种策略的明显限制是它使得我们无法控制已经探索的邻域explored neighborhood。即倾向于
exploration。LINE主要提出了BFS策略,并且独立地在1-hop邻域和2-hop邻域上采样节点和优化似然likelihood。这种探索的效果更容易刻画,但是它的限制是:无法灵活地探索更深的节点。即倾向于
exploitation。
相比之下,通过超参数 和 探索网络邻域,
node2vec中的搜索策略既灵活又可控。虽然这些搜索超参数具有直观的解释,但是当我们可以直接从数据中学习它们时,我们在复杂网络上获得了最佳结果。从实用角度来看,node2vec具有可扩展性并且对扰动具有鲁棒性。未来工作:
- 探索
Hadamard算子比其它算子效果更好的背后原因。 - 基于搜索超参数为边建立可解释的相等性概念。
- 将
node2vec应用到特殊结构的网络,如异质信息网络heterogeneous information network、具有节点特征的网络、具有边特征的网络。
- 探索
6.2 实验
6.2.1 案例研究:悲惨世界网络
如前所述,我们观察到
BFS和DFS策略代表了节点嵌入的两个极端:基于同质性(即网络社区)、以及基于结构相等性(即节点的结构角色)。我们现在的目标是凭经验证明这一事实,并表明node2vec实际上可以发现同时符合这两个准则的embedding。我们用一个网络来描述小说《悲惨世界》中的角色,边代表角色之间是否共同出现过。网络共有
77个节点和254条边。我们设置 并利用node2vec学习网络中每个节点的feature representation,然后通过k-means算法对这些feature representation聚类。最后我们在二维空间可视化原始网络,节点根据它们的cluster分配相应的颜色,节点大小代表节点的degree。- 上半图给出了 的结果,可以看到
node2vec挖掘出小说中的社区community:有密切交互关系的人的相似度很高。即representation结果和同质性homophily有关。 - 下半图给出了 的结果,可以看到
node2vec挖掘出小说中的角色:角色相同的人的相似度很高。即representation结果和结构相等性有关。如:node2vec将蓝色节点嵌入在一起,这些节点代表了小说不同场景之间切换的桥梁bridge的角色;黄色节点代表小说中的边缘角色。
人们可以为这些节点
cluster解释以不同的语义,但关键是node2vec不依赖于特定的相等性概念。正如我们通过实验表明的那样,这些相等性概念通常出现在大多数现实世界的网络中,并且对预测任务学到的representation的性能产生重大影响。
- 上半图给出了 的结果,可以看到
6.2.2 实验配置
baseline:我们的实验在标准的监督学习任务上评估了feature representation(通过node2vec获得的):节点的多标签分类任务multilabel classification、边的链接预测link prediction任务。对于这两个任务,我们将node2vec和下面的算法进行对比:谱聚类
spectral clustering:这是一种矩阵分解方法,其中我们将图 的归一化拉普拉斯矩阵normalized Laplacian matrix的top d特征向量eigenvector作为节点的feature vector representation。DeepWalk:这种方法通过模拟均匀随机游走来学习 维feature representation。DeepWalk中的采样策略可以视为 的node2vec的一个特例。LINE:这种方法在两个独立的phase中学习 维的feature representation。- 在第一种
phase,它保持节点的一阶邻近性来学习 维的representation。 - 在第二种
phase,它保持节点的二阶邻近性来学习另一个 维的representation。
- 在第一种
我们剔除了其它已经被证明不如
DeepWalk的矩阵分解matrix factorization方法。我们还剔除了最近的一种方法GraRep,它将LINE推广为保持节点的高阶邻近性,但是它无法有效地扩展到大型网络。配置:与先前工作中用于评估
sampling-based的feature learning算法的配置相比,我们为每种方法生成相同数量的samples,然后在预测任务中评估获得的特征的质量。因此,在采样阶段sampling phase,DeepWalk, LINE, node2vec的参数设置为:在runtime时生成相同数量的samples。例如,如果 是总的采样预算,那么node2vec的超参数满足: 。在优化阶段
optimization phase,所有这些算法都使用SGD进行了优化,其中我们纠正了两个关键性差异:- 首先,
DeepWalk使用hierarchical softmax来近似softmax概率,其目标函数类似于node2vec使用的目标函数。然而,与负采样相比,hierarchical softmax效率低下。因此对于DeepWalk我们切换到负采样并保持其它一切不变,这也是node2vec和LINE中实际使用的approximation。 - 其次,
node2vec和DeepWalk都有一个超参数,用于优化上下文邻域节点的数量,数量越大则需要迭代的轮次越多。对于LINE,该超参数设置为单位数量(即1),但是由于LINE比其它方法更快地完成单个epoch,我们让它运行 个epoch。
node2vec使用的超参数设置与DeepWalk和LINE使用的典型值一致。具体而言,我们设置 ,并且优化了一个epoch。我们选择10个随机数种子初始化并重复我们的实验,并且我们的结果在统计上显著,p-value小于0.01。最佳的
in-out超参数 和return超参数 是在10%标记数据上使用10-fold交叉验证进行网格搜索来找到的,其中 。- 首先,
6.2.3 多标签分类任务
多标签分类任务中,每个节点属于一个或者多个标签,其中标签来自于集合 。在训练阶段,我们观察到一定比例的节点上的所有标签。任务是预测剩余节点上的标签。当标签集合 很大时,多标签分类任务非常有挑战性。
数据集:
BlogCatalog:该数据集包含BlogCatalog网站上博客作者之间的社交关系,标签代表通过元数据推断出来的博主兴趣。网络包含10312个节点、333983条边、39种不同标签。Protein-Protein Interactions:PPI:该数据集包含蛋白质和蛋白质之间的关联,标签代表基因组。我们使用智人PPI网络的子图。网络包含3890个节点,76584条边,50种不同标签。Wikipedia:该数据集包含维基百科dump文件的前一百万字节中的单词共现,标签代表单词的词性Part-of-Speech:POS(由Standford POS-Tagger生成)。网络包含4777个节点,184812条边,40种不同标签。
所有这些网络都同时呈现同质性和结构相等性。如:
- 博主的社交网络呈现出很强的同质性,但是可能还有一些 “熟悉的陌生人”:博主之间没有关联但是兴趣相同。因此它们在结构上是等效的节点。
- 蛋白质-蛋白质的相互作用网络中,当蛋白质和邻近蛋白质功能互补时,它们呈现出结构相等性;而在其他时候,它们基于同质性组织从而协助相邻蛋白质执行相似的功能。
- 在单词共现网络中,当相邻的单词具有相同
POS标签时,它们呈现出同质性;当相邻单词呈现某种语法模式,如 “限定词+名词“、”标点符号 + 名词” ,它们呈现结构相等性。
实验结果:每个模型输出的节点
representation输入到一个 正则化的one-vs-rest逻辑回归分类器中,采用Macro-F1作为评估指标。Micro-F1和准确率的趋势与Macro-F1类似,因此并未给出。训练数据和测试数据均拆分为10个随机实例。结论:
node2vec探索邻域时的灵活性使得它超越了其它算法。在
BlogCatalog中,可以设置较低的 和 值来较好的融合同质性的结构相等性,在Macro-F1分数中比DeepWalk提高22.3%、比LINE提高229.2%。LINE的表现低于预期,这可能是因为它无法reuse samples,而基于随机游走的策略可以reuse samples。即使在我们的其它两个网络中(这两个网络也存在混合的相等性),
node2vec的半监督特性也可以帮助我们推断feature learning所需的适当的探索程度。- 在
PPI网络中,最佳探索策略 () 结果证明与DeepWalk的均匀探索() 几乎没有区别,但是node2vec通过高 值避免了重复访问已访问节点的冗余性,使得node2vec相比DeepWalk略有优势。而node2vec在Macro-F1分数上相比LINE高出23.8%。 - 然而,通常而言,均匀随机游走可能比
node2vec的探索策略差得多。正如我们在Wikipedia单词共现网络中看到的那样,均匀随机游走不能导致最佳的采样,因此node2vec比DeepWalk提高了21.8%,比LINE提高了33.2%。
- 在
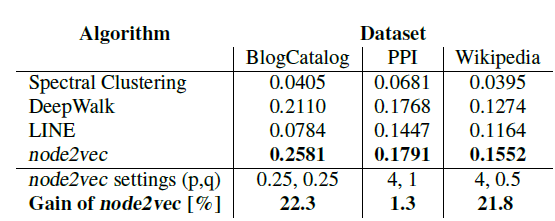
数据稀疏性:为了进行更细粒度的分析,我们将
train-test拆分比例从10%~90%,超参数 在10%的数据上学习。结果表明:- 所有方法都明显超越了谱聚类,
DeepWalk优于LINE。 node2vec始终超越了LINE,并且最差情况也等价于DeepWalk、最好情况相比DeepWalk有巨大提升。例如在70%的标记数据中,我们在BlogCatalog上相比DeepWalk提升了26.7%。

- 所有方法都明显超越了谱聚类,
参数敏感性:
node2vec算法涉及许多超参数,我们在BlogCatalog数据集上评估这些超参数的影响。我们使用标记数据和未标记数据之间的50 - 50拆分。除了待评估的参数外其它参数均为默认值( 的默认值均为1)。我们的评估指标为Macro-F1。结论:随着 的减小
node2vec性能将有所提高,这是因为更小的 将达到预期的同质性和结构相等性。低 虽然鼓励向外探索,但是由于低 的平衡作用可以确保随机游走距离源点不会太远。
提高维度 可以提升性能,但是一旦维度达到
100左右,性能提升将趋于饱和。增加源点的游走序列数量 可以提升性能,增加序列的长度 也可以提升性能。
这两个参数表明更大的采样预算
sampling budget,因此它们对于性能有较大的影响。上下文大小 以优化时间的增加为代价来提升性能,但是性能提升不明显。

扰动分析:对于许多现实世界的网络,我们无法获得有关网络结构的准确信息。我们进行了一项扰动研究,分析了
node2vec在BlogCatalog网络中的、边结构edge structure的两个不完美信息场景imperfect information scenario下的性能。第一个场景:我们评估缺失边
missing edge比例(相对于完整网络)对性能的影响。缺失边是随机选择的,但是存在连接的节点总数是固定的。如上半图所示,随着缺失边比例上升网络性能大致呈现线性下降,但是下降的斜率较小。在图随时间演变的情况下(例如,引文网络)或网络建设成本较高的情况下(例如,生物网络),网络对于缺失边的鲁棒性尤其重要。
第二个场景:我们在网络中随机选择的节点对之间添加噪声边
noisy edge。如下半图所示,与缺失边相比这种情况的网络性能下降速度稍快,但是斜率趋于放缓。同样地,
node2vec对假边false edge的鲁棒性在多种情况下很有用,例如传感器网络sensor network其中传感器的值有噪声。

可扩展性:为测试可扩展性我们用
node2vec学习Erdos-Renyi网络的节点representation。所有参数为默认值,网络规模从100到 一百万,每个节点的平均degreee固定为10。可以看到:
node2vec随着节点数量的增加,其收敛时间基本呈线性关系,在不到四个小时即可生成一百万节点的representation。采样过程包括:为我们随机游走计算转移概率的预处理
perprocessing(时间成本小到可以忽略不计)、以及随机游走的模拟simulation。我们使用负采样和异步SGD使得优化阶段变得高效。在
node2vec的训练过程我们采用了很多优化技巧:如随机游走过程中的sample reusing重用技巧、Alias Table技巧。虽然我们可以根据底层任务和领域自由地设置搜索超参数,但是学习搜索超参数的最佳设置会增加开销。然而,正如我们的实验所证实的,这种开销很小,因为node2vec是半监督的,因此可以用很少的标记数据有效地学习这些超参数。
6.2.4 链接预测任务
在连接预测任务中,我们给定一个删除了一定比例边的网络,希望模型能够预测这些被删除的边。数据集的生成方式为:
- 网络中随机删除
50%的边,剩下的所有边的节点pair对作为正样本。但是,要确保删除边之后的残差网络是连通的。 - 从网络中随机选择相同数量的、不存在边的节点
pair对作为负样本。
由于之前还没有针对链接预测的特征学习算法,因此我们将
node2vec和一些流行的启发式方法进行对比。这些启发式方法通过评估节点 的邻居集合 和节点 的邻居集合 的某种得分,然后根据该得分来判断 之间是否存在边。
- 网络中随机删除
数据集:
FaceBook数据集:包含FaceBook用户之间的社交关系,节点代表用户、边代表好友关系。网络一共包含4039个节点和88234条边。Protein-Protein Interactions: PPI数据集:在智人的PPI网络中,节点代表蛋白质,边代表蛋白质和蛋白质之间的关联。网络一共包含19706个节点、390633条边。arXiv ASTRO-PH数据集:包含arXiv网站上发表论文的作者之间的关联,节点代表作者、边代表两个作者共同参与同一篇论文写作。网络一共包含18722个节点、198110条边。
实验结果:我们经过超参数优化选择最佳的 ,优化过程这里不做讨论。下图给出了
node2vec的不同operator,以及不同启发式算法的结果,指标为auc。图中:a表示均值算子operator,b表示Hadamard积算子,c表示WeightedL1算子,d表示WeightedL2算子。结论:
通过
feature learning学习节点pair对特征(如node2vec, LINE, DeepWalk, Spectral Clustering等等)的效果明显优于启发式方法。在所有
feature learning的算法中,node2vec的效果最佳。当我们单独查看算子时,除了
Weighted-L1和Weighted-L2之外(这两种算子中LINE最佳),其它算子中node2vec超越了DeepWalk和LINE。Hadamard算子与node2vec一起使用时非常稳定stable,在所有网络中平均提供最佳性能。

七、WALKLETS[2016]
社交网络本质上是分层
hierarchical的。例如,在人类社交网络中,每个人都是若干个社区community的成员,这些社区从小型(例如家庭、朋友)到中型(例如学校、企业)到大型(例如民族、国家)。随着这些关系的尺度scale发生变化,关系的拓扑结构也会发生变化。例如,考虑社交网络上某个大学的一名大学生(如下图所示):Friends尺寸:他可能与朋友或直系亲属非常紧密地联系在一起,并与这些人(朋友或直系亲属)形成紧密的图结构。Classmates尺寸:然而,他与同一座大学内的其它学生的关系更加松散。事实上,他与大多数学生没有直接的社交关系。Society尺度:最后,他与本国其他人的联系相对较少,但是由于共同的文化,他仍将与本国其他人共享很多属性。
尺度在预测任务中也起着重要作用,因为这些任务也从与特定的用户属性相关(如用户的电影兴趣)到与用户所属社区的、更通用的属性相关(如用户所属的学校)。
在搜广推领域,尺度在刻画
user/item特征上也是很重要的。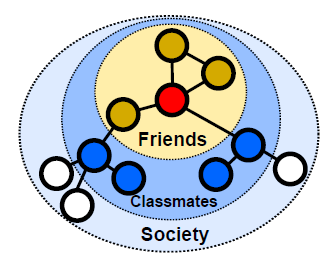
大多数关于
network representation learning的先前工作都使用 “一刀切” 的方法来处理这个问题,其中每个用户都使用单个network representation来进行预测,因此无法显式捕获节点在网络中具有的多尺度关 系multiscale relationship。在论文《Don’t Walk, Skip! Online Learning of Multi-scale Network Embeddings》的作者看来,最好有一组representation从而捕获用户的、所有尺度的社区成员关系。在论文
《Don’t Walk, Skip! Online Learning of Multi-scale Network Embeddings》中,作者研究了大型图中node embedding问题,其中该embedding捕获了节点所属的所有社区的潜在层次结构latent hierarchy。这些潜在的multiscale representation对于社交网络中的预测任务很有用。在预测时,可以利用(单独的、或者组合的)representation来提供更全面的、用户的隶属关系affiliation。下面的左图和右图说明了不同尺度上representation相似性之间的差异。中心的红色顶点表示源点,顶点颜色代表该顶点和源点的距离:距离越近颜色越红,距离越远颜色越蓝。- 左图给出了细粒度
representation相似度的结果。在这一尺度下,只有源点的直系邻居才是相似的。 - 右图给出了粗粒度
representation相似度的结果。在这一尺度下,源点附近的很多顶点都是相似的。
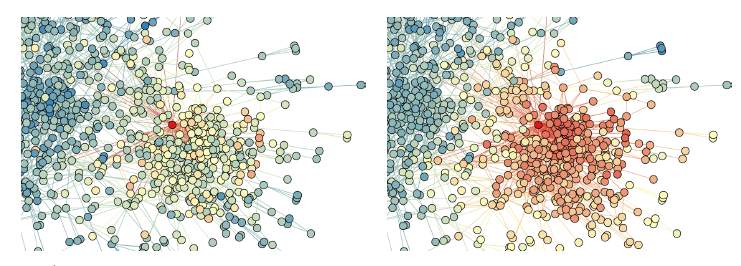
最近,人们对社交网络
representation learning的兴趣激增,主要是基于神经矩阵分解neural matrix factorization。这些方法在半监督网络分类问题上展示了强大的任务性能。尽管它们在任务中的表现很强,但是作者发现这些方法还有很多不足之处。首先,最初的工作只是间接地解决了在多个尺度上学习
representation的问题,或者作为学习过程的产物(《Deepwalk: Online learning of social representations》)、或者通过不同目标函数的不直观的组合(《Line: Largescale information network embedding》)。最近,
《GraRep: Learning graph representations with global structural information》提出了一种学习多尺度representation的方法,但是它的计算复杂度使得它对于大多数真实世界的图而言都难以处理。其次,这些方法中的大多数都依赖于
network representation learning的“一刀切”方法,它掩盖了图的每个单独尺度上存在的细微差别的信息。
论文
《Don’t Walk, Skip! Online Learning of Multi-scale Network Embeddings》提出了一种用于学习网络中顶点的、多尺度multiscale的representation的新方法:WALKLETS。这是一种用于学习社交representation的在线算法,它的representation以一种可推导derivable的方式显式编码多尺度的顶点关系。与现有工作不同,WALKLETS的维度具有意义,允许进行信息网络分类informed network classification以及被捕获关系的可视化。该方法本身是可扩展的,并且可以在具有数百万个顶点的图上运行。WALKLETS通过在图的顶点上对短的随机游走short random walk进行子采样subsampling来生成这些多尺度关系multiscale relationship。通过在每个随机游走中跳过某些step,论文的方法生成了一个由顶点pair组成的语料库,其中这些顶点pair可以通过固定长度的路径到达。然后可以使用该语料库来学习一系列潜在representation,每个潜在representation都从邻接矩阵中捕获更高阶的关系。具体而言,论文的贡献如下:
- 多尺度
representation learning:论文提出了一种graph embedding方法,它显式地捕获了多尺度关系multiple scale relationship。 - 评估:论文在多个社交网络(如
BlogCatalog, DBLP, Flickr, YouTube, Arxiv)上广泛评估WALKLETS的representation在多标签分类任务上的表现。在Micro-F1指标上,WALKLETS比DeepWalk等几个具有挑战性的baseline要高出多达5%。 - 可视化和分析:
WALKLETS保留了潜在representation的多个尺度,作者用它来分析大型图中存在的多尺度效应multiscale effect。
最后,
WALKLETS是一种在线算法,可以轻松扩展到具有数百万个顶点和边的graph。相关工作:相关工作分为三类:无监督
feature learning、多尺度graph clustering、graph kernel。无监督
feature learning:最近提出的社交representation learning(DeepWalk, LINE, node2vec, Graph Likelihood)使用Word2Vec提出的神经网络损失来学习representation从而编码顶点相似性vertex similarity。与我们的工作不同,这些方法没有显式保留网络中发生的多尺度效应。与我们最接近的相关工作
GraRep是通过随机游走转移矩阵random walk transition matrix上的SVD来显式建模网络中的多尺度效应。我们的工作使用采样sampling和在线学习来操作更大规模的语料库。此外,我们的工作保留了多个尺度的representation,这可以提供更好的任务性能的modeling insight。人们还提出了分布式
representation来对不同领域的结构关系进行建模,如计算机视觉、语音识别、自然语言处理。多尺度社区检测:人们已经提出了很多用于检测图中多尺度离散社区的技术。一般而言,与我们的方法不同,这些方法试图返回一个描述图中社交层级结构的硬聚类
hard clustering。Graph Kernel:Graph Kernel是一种方法,它使用关系数据作为分类程序的一部分,但是通常速度很慢。最近的工作已经应用神经网络来学习graph kernel的子图相似性subgraph similarity。
7.1 模型
7.1.1 基础知识
基本概念:定义网络 ,其中 为网络的成员集合, 表示成员之间的链接集合,其中 。我们将 的邻接矩阵称作 ,当且仅当存在边 时,元素 是非零的。给定具有邻接矩阵 的图 ,我们将其在尺度 处的视图
view定义为由 定义的图。我们将
representation定义为映射 ,它将每个顶点 映射到低维空间 中的 维向量。在实践中,我们以参数矩阵 来表示映射 ,该矩阵通常从数据中估计。最后,令 表示部分标记
partially labeled的社交网络,其中特征为 ,标记为 , 为特征空间的维度, 为标签集合。多尺度
Representation Learning:给定网络 ,多尺度学习的目标是学习一组 个逐渐粗化coarser的社交representation,其中 捕获了 在尺度 处的视图view。直观而言,每个
representation都编码了不同视图的社交相似性social similarity,对应于不同尺度的潜在社区的成员关系membership。预测性学习任务
predictive learning task:给定一个representation或一组representation,任务的目标是学习将 映射到标签集合label set的假设hypothesis。这将允许泛化generalization,即推断 中无标签顶点的标签。Representation Learning:representation learning的目标是学习一个映射函数 ,它将图中每个顶点 映射到相关的潜在社交representation。在实践中,我们用自由参数free parameter的矩阵 来表示映射 。DeepWalk引入了一个概念:将顶点建模为截断随机游走truncated random walk中节点共现node co-occurrence的函数。这些截断随机游走序列捕获了图中每个每个顶点周围的扩散过程diffusion process,并对局部社区结构local community structure进行了编码。因此,DeepWalk的目标是估计顶点 与其局部邻域local neighborhood共现co-occurring的可能性:其中 为顶点 的
representation。然而,随着随机游走序列长度的增加,计算这个条件概率变得不可行。为解决这个问题,人们提出通过忽略相邻顶点的顺序来放松
relax这个问题:不是使用上下文context来预测目标顶点,而是使用目标顶点来预测其局部结构。就vertex representation建模而言,这得到了最优化问题:有趣的是,这个优化目标直接等价于学习邻接矩阵 的低秩近似
low-rank approximation。神经矩阵分解
Neural Matrix Factorization:一种常用的方法建模节点 和 共现的概率是,使用softmax将pairwise similarity映射到概率空间,即:其中: 为节点 的
input representation, 为节点 的output representation。不幸的是,上式分母的计算量很大。为此,人们提出了噪声对比估计
noise-contrastive estimation: NCE作为上式的松弛relaxation。NCE将节点共现pair的概率建模为:可以看出,这两个概率模型都对应于隐式分解邻接矩阵的某种变换
transformation。为了启发我们的方法,我们简要讨论一些矩阵,先前关于学习社交
representation的工作就是隐式分解了这些矩阵。具体而言,我们讨论了我们最接近的相关工作DeepWalk。如《GraRep: Learning graph representations with global structural information》、《Comprehend deepwalk as matrix factorization》所述,描述由DeepWalk执行的隐式矩阵分解的闭式解是可能的。他们推导出了一个带Hierarchical Softmax的DeepWalk(DeepWalk with Hierarchical Softmax: DWHS) 公式,表明DeepWalk正在分解一个矩阵 ,该矩阵包含高达 阶的随机游走转移矩阵random walk transition matrix。换句话讲,元素 是从节点 到节点 的、长度不超过 的路径的数量的期望。注:这意味着邻接矩阵 为
0-1矩阵,即图 为无权图。其中:
- 是计数函数,它统计随机游走中 的共现次数; 统计随机游走中 的出现次数。
- 为一个
one-hot的行向量,它的第 个元素为1、其它元素都为0。 - 表示选择向量的第 个元素。
7.1.2 多尺度神经矩阵分解
这里我们介绍用于创建多尺度
network representation的算法。我们首先描述我们用于捕获不同尺度的representation的模型。我们接着讨论一些重点,如搜索策略和优化optimization。最后,我们对一个小型的、真实世界的引文网络进行了案例研究,说明了通过我们方法捕获不同尺度的network representation。这里我们在
Neural Matrix Factorization的基础上,正式扩展了先前在社交representation learning中的方法,从而显式地建模现实世界网络中表现出的多尺度效应。如等式 所示,
DeepWalk隐式分解一个矩阵,该矩阵的元素包含 ,其中 为随机游走的窗口大小。 的每个幂次 都代表不同尺度的网络结构。回想一下, 表示节点 和 之间的、路径长度为 的路径数量。有趣的是,
DeepWalk已经隐式地对多尺度的依赖关系进行了建模。这表明学到的representation能够捕获社交网络中节点之间的短距离依赖关系和长距离依赖关系。尽管DeepWalk的表达能力足以捕获这些representation,但是它的多尺度属性有局限性:不保证多尺度:多尺度
representation不一定被DeepWalk捕获,因为多尺度没有被目标函数显式地保留。事实上,由于DeepWalk来自 的条目entry总是比来自 ()的条目更多,因此它倾向于保持最小尺度(即 的最低幂次)的representation。为看清这一点,注意观察给定任何长度为 的随机游走序列,来自 的条目数量最多为 ,而来自 的条目最多为 。当大尺度(即高阶幂次)是网络上机器学习任务的适当
representation时,这种小尺度bias是一个根本性的弱点。例如,当对大尺度的图结构相关的特征进行分类时(例如,社交网络上的语言检测),与保留单个edge的、更细粒度的representation相比,更粗粒度的representation可以提供更好的性能。仅全局
representation:DeepWalk学习了一种全局representation,它融合了所有可能尺度的网络关系。因此,不同尺度的representation是不可能独立地访问的。这是不可取的,因为每个单独的学习任务都需要从全局representation中解码相关尺度的相似度信息similarity information。实际上,社交关系的理想representation将跨越多个尺度,每个尺度依次捕获更大范围的潜在社区成员关系community membership。然后,每个学习任务都能够利用最佳level的社交关系来完成该任务。正如我们将在实验部分中展示的那样,可以通过不同尺度的社交representation来最大化每个学习任务的性能。比如线性组合或者非线性组合多个尺度的
representation,从而最优化目标任务的性能。
多尺度随机游走
WALKLETS:基于迄今为止讨论的观察结果,我们提出扩展DeepWalk引入的模型从而显式地建模多尺度依赖关系multiscale dependency。我们的方法通过分解邻接矩阵 的幂来操作,使用最近提出的算法来学习representation。与
DeepWalk类似,我们通过从每个节点开始的一系列截断的随机游走truncated random walk从而对网络进行建模。正如DeepWalk中所讨论的,这些截断的随机游走中两个顶点的共现可以建模网络中的扩散速度diffusion rate。然而,我们对采样程序进行了更关键的修改。具体而言,我们选择跳过随机游走中的一些节点。通过这种方式,我们形成了一组关系relationship,这些关系是从 的连续的、更高的幂次中采样到的。我们用 来表示从邻接矩阵的幂次 导出的WALKLETS。的每个不同幂次都构成了一个语料库,这一系列 个语料库分别对网络中的特定距离依赖性
specific distance dependency进行建模。采样过程如下图所示,其中不同颜色代表不同的 值采样的edge(意味着原始图中距离为 的路径)。
在根据尺度采样的关系进行分区之后,我们对观察样本顶点 和顶点 之间的概率进行建模。这意味着以下目标函数可以学习每个节点 的
representation:其中 为尺度 生成的随机游走
pair构成的语料库。寻求最大化 和上下文节点 共现的对数似然。这个目标通常称作
SkipGram,在《Efficient estimation of word representations in vector space》中首次被提出从而用于语言建模,并在DeepWalk中首次扩展到network representation learning。损失函数优化:我们使用具有随机梯度下降的标准反向传播算法优化上述损失函数。除非另有说明,我们使用默认的学习率
0.025、默认的embedding size。这可以很容易地扩展到加权图(通过调整与权重成比例的梯度),边采样技术(在
LINE中被提出)也可以适用于我们的方法。隐式矩阵分解的视角:通过以这种方式采样,我们可以表明我们学习了不同尺度的
representation。在skipped random walk上使用DeepWalk,其中skip factor设置为 (我们对彼此距离为 的节点进行采样),我们隐式地考虑了从 派生的矩阵。WALKLETS必须预先计算每个顶点 的、距离为 的顶点集合。论文的方法是:在常规的随机游走过程中,连续跳过 个随机游走。另一种简单的方法是计算 ,但是计算复杂度太高。观察到在
skip factor为 的skipped random walk中,每个连续的node pair和 都可以通过长度刚好为 的路径到达,因此它代表从 采样的边。当我们为DeepWalk提供的随机游走中,当前后节点之间的距离为 时,在 中仅有 对应的项存在。因此,我们隐式地分解从 派生的矩阵。搜索策略:
DeepWalk、LINE、node2vec分别提出不同的搜索策略,从而根据图中的边生成不同的社交关系。广度优先策略从源节点依次扩展并检查其所有邻居,这对于局部邻居而言效果很好,但是随着更高level的扩展(即邻居的邻居)而面临状态空间爆炸state space explosion。深度优先策略使用随机游走,它编码更远距离的信息,可能更适合学习更高阶的network representation。我们的方法通过随机游走采样
random walk sampling来观察多尺度关系,我们认为这将更具有可扩展性。值得一提的是,由于node2vec引入了一种有偏的随机游走方案,可以视为是对DeepWalk的扩展,我们的skipping算法也可以应用于node2vec生成的随机游走。另一种搜索策略(可能适用于较小的图)是直接计算 (即任何一对节点之间的路径距离为 ),并使用它来采样节点
pair。
案例研究
Cora:为了说明network representation在多尺度上的影响,我们可视化了一个小的引用网络Cora,它有2708个节点、5429条边。下图展示了从特定节点() 到每个其它节点的社交representation的距离的直方图。当我们依次检查更深层的社交representation时,我们看到随着尺度的加大,越来越多的节点(如箭头标识)靠近 。这些节点是 所属的、更大的论文社区的一部分,具体而言是遗传算法领域。如果我们在Cora中进行分类任务,网络结构的这种清晰可分离clear separation可以导致更容易的泛化。
下图也说明了这种现象,该图展示了覆盖在原始网络结构上的、到节点 (如箭头标识)距离的热力图(经过
t-SNE二维可视化)。距离越近颜色越红、距离越远颜色越蓝。注意不同尺度的网络representation的距离如何编码连续的、更大社区的成员关系。
7.2 实验
这里我们将我们的方法应用于几个在线社交网络,从而实验性地分析我们的方法。具体而言,我们的实验有两个主要目标:首先,我们试图描述不同现实世界社交网络中表现出的各种多尺度效应。其次,我们评估了我们的方法在捕获底层网络结构方面的效果。
数据集:
BlogCatalog:该数据集包含BlogCatalog网站上博主之间的社交关系,标签代表通过元数据推断出来的博主兴趣类别。网络包含10312个顶点、333983条边、39种不同标签。DBLP Network:该数据集包含学者之间的论文合作关系。每个顶点代表一个作者,边代表一个作者对另一位作者的引用次数,标签代表学者的研究领域。网络包含29199个顶点、133664条边、4种不同标签。Flickr数据集:Flickr网站用户之间的关系网络。标签代表用户的兴趣组,如“黑白照片”。网络包含80513个顶点、58999882条边、195种不同标签。YouTube数据集:YouTube网站用户之间的社交网络。标签代表用户的视频兴趣组,如“动漫、摔跤”。网络包含1138499个顶点、2990443条边、47种不同标签。
由于我们的方法以无监督的方式学习社交网络中节点的潜在
representation,因此这些representation通常应该作为各种学习任务的有用特征。因此,我们在社交网络的多标签分类multi-label classification任务上评估我们的方法。这项任务的动机是:观察到网络中的节点隶属于多个社区成员。例如,社交网络中的人是多个圈子(家庭、学校、公司、共同爱好)的成员。对这些不同的社区成员进行建模和预测,不仅对于理解现实世界的网络至关重要,而且还有几个重要的商业应用(例如更有效的广告targeting)。baseline方法:我们考虑三个最近提出的、代表state-of-the-art的社交representation learning模型。DeepWalk:该方法使用截断的随机游走序列来学习顶点的representation,学到的representation捕获了多尺度社区成员关系的线性组合。LINE:类似于DeepWalk,该方法使用SkipGram目标函数学习节点representation。但是这里我们仅仅LINE 1st方法,它只考虑 。GraRep:该方法通过显式的计算 并执行SVD分解来产生多尺度的representation。本质上该方法和WALKLET是类似的,但是它不是在线学习方法,且无法扩展到大型网络。
任务配置:我们使用
DeepWalk中描述的相同实验程序来评估我们的方法。我们随机抽取标记节点的 比例,并将它们作为训练数据,剩余部分作为测试数据。这个过程重复10次,然后报告平均MICRO-F1得分。我们不包括其它评估指标(如准确率和MACRO-F1)的结果,因为这些指标都遵循相同的趋势。这使得我们能够轻松地将我们的方法和其它相关baseline进行比较。在所有情况下,我们都会学习一个逻辑回归分类模型(基于
one vs rest策略)。我们使用 的默认L2正则化系数,并使用由Liblinear实现的优化算法。对于
WALKLETS,我们仅使用尺度为{1, 2, 3}的随机游走生成的representation。在所有情况下,每个节点开始的随机游走数量为
1000,每条随机游走序列的长度为11。在所有情况下,embedding size为 。这些设置也用于baseline。在多尺度
representation的情况下,我们拼接所有多个尺度的特征并使用PCA将它们投影到128维。PCA本质上是线性映射,因此这里是将多尺度representation进行线性组合。
通过这些方法,我们可以控制训练数据大小的差异、以及超参数的差异,这些超参数控制了
representation的容量capacity。这允许我们与其它方法和baseline进行可解释的比较。实验结果:下表显示了我们算法的性能相对于其它两种
baseline(即DeepWalk和LINE)的增益。我们没有比较GraRep,因为它不是在线算法,也无法扩展到大型图(如Flickr和Youtube)。BlogCatalog:下表显示了BlogCatalog上多标签分类的结果。我们观察到使用 特征的WALKLETS在Micro-F1上优于所有baseline。当标记数据稀疏时(仅10%的节点被标记),Micro-F1的差异在0.001水平上具有统计意义(比DeepWalk提升8.9%,比LINE提升58.4%)。我们在10次不同运行上使用paired t-test来得到统计显著性statistical significance。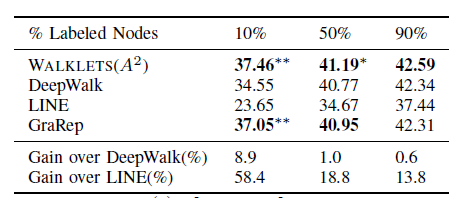
DBLP:DBLP的实验结果如下表所示。我们注意到,与DeepWalk和LINE相比, 的representation在Micro-F1上提供了统计上的显著提升。在标记节点为1%的情况下,WALKLETS() 相对于DeepWalk和LINE的增益分别为10.1%和34.3%。这些更粗的representation为作者发表的主题领域提供了更好的编码。然而,我们注意到,在这项任务中
WALKLETS未能超越GraRep学到的多尺度representation。我们将此归因于DBLP表现良好的事实。- 首先,它表现出高度同质化的行为,因为
co-authorship保证了相似的属性(两位作者之间的共同出版物必须在同一个研究领域)。 - 其次,图中的
co-authorship边表明高度相似性(更难创建虚假的边)。
当这些条件成立时,
GraRep对随机游走转移矩阵的直接计算可以产生很高的性能增益。然而,我们注意到GraRep的技术需要处理一个稠密矩阵,这本质上是不可扩展unscalable的。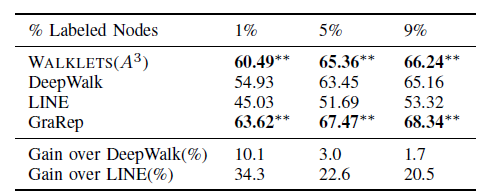
- 首先,它表现出高度同质化的行为,因为
Flickr:下表显示了Flickr数据集的结果。在这个数据集上,我们看到 派生的特征在Micro-F1指标上提供了最佳性能,显著优于所有baseline。具体而言,我们观察到,当只有1%数据被标记为训练数据时,WALKLETS在Micro-F1分数上比DeepWalk高4.1%、比LINE高29.6%。我们注意到,最具竞争力的
baselineGraRep由于内存不足而无法在该数据集(仅80513个顶点)上运行。相反,我们的方法可以轻易地处理如此大型的网络,同时产生有竞争力的结果。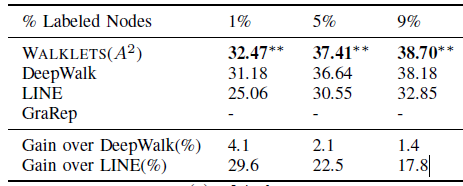
YouTube:YouTube的结果如下表所示。再一次地,我们的方法优于所有baseline方法。有趣的是,组合的representation提供了最佳性能,在p=0.05水平上显著优于DeepWalk和LINE。YouTube包含更多的顶点,因此GraRep再次耗尽内存也就不足为奇了。我们注意到WALKLETS的在线设置允许学习具有数百万个顶点的图的representation。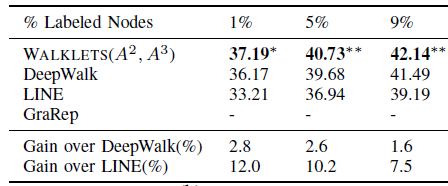
分类任务中的多尺度效应:前面的实验结果表明,没有哪个单一尺度的
representation在所有任务上都取得最佳性能。我们可以显式地提供各尺度的representation,从而解决其它baseline方法未能在多个尺度上显式编码信息的共同限制。在
Micro-F1指标上, 的特征在两个图(BlogCatalog, Flickr)上的所有训练数据变体(包括不同训练集比例)中表现最好。这表明长度为2的路径是合适的社交依赖性,从而建模共享的用户兴趣。在 中捕获的neighbor-of-neighbor信息对于处理缺失信息missing information的网络而言特别有用。发生这种情况的一个重要case是冷启动问题,其中一个节点刚刚加入网络并且还没有机会进行所有的连接。有趣的是,从 和 派生的
representation分别在DBLP和YouTube上提供了最佳的任务性能。在这些图上,分类性能随着representation尺度的增加而单调增加。我们可以推测:这些图中的分类任务确实表现出层次结构hierarchical structure,并且通过我们的方法创建的 、distinct的高阶representation允许利用图的层次结构和任务标签之间的相关性。我们在此强调:
WALKLETS显式地对社交网络中存在的多尺度效应进行建模,从而能够全面分析哪些尺度能够对给定学习任务提供最多的信息。而这是其它的一些方法无法实现的,例如DeepWalk和LINE使用全局的representation。GraRep也能够分析各个尺度,但是它无法扩展到大型图。可扩展性:
WALKLETS是一种在线算法,它对从图中以不同依赖性水平dependency level采样的顶点进行操作。这种在线方法使用采样sampling来逼近高阶的转移矩阵ransition matrix,这允许扩展到具有数百万个顶点的大型图。这和最接近的相关方法GraRep形成鲜明对比,GraRep需要操作稠密矩阵(如果图是连通的并且edge分布遵从幂律分布,那么随着 的增加, 会迅速失去稀疏性)。GraRep需要计算转移矩阵的连续幂,并且进一步需要显式计算SVD,这些都无法扩展到大型网络。采样分析:这里我们通过将我们的方法和
GraRep进行的显式和精确计算进行比较,从而分析我们提出的随机游走采样程序的有效性。给定一个图 ,我们使用GraRep显式计算它分解的矩阵 。然后,我们使用WALKLETS用到的随机游走来估计WALKLETS要分解的矩阵 。我们通过 来估计我们的近似值和精确值之间的接近程度。随机游走的超参数如前所述。我们在
DBLP和BlogCatlog数据集上评估了Err的平均误差,结果表明:两个图上的多尺度随机游走足以逼近显式计算的转移矩阵。我们观察到我们的近似值在各个尺度上的平均误差和标准差都很低,这表明我们的方法捕获了随机游走转移矩阵的合理近似值。增加sample size(通过增加更多的随机游走)将导致越来越好的近似值。
八、SDNE[2016]
如今,网络无处不在,并且许多现实世界的
application需要挖掘这些网络中的信息。例如,Twitter中的推荐系统旨在从社交网络中挖掘用户偏好的推文,在线广告targeting通常需要将社交网络中的用户聚类到某些社区。因此,挖掘网络中的信息非常重要。这里的一个基本问题是:如何学习有用的network representation?一种有效的方法是将网络嵌入到低维空间中,即学习每个顶点的
vector representation,目的是在学到的embedding空间中重建网络。因此,网络中的信息挖掘,如信息检索information retrieval、分类classification、聚类clustering,都可以直接在低维空间中进行。学习
network representation面临以下巨大挑战:- 高度非线性:网络的底层结构是高度非线性的,因此如何设计一个模型来捕获高度非线性的结构是相当困难的。
- 结构保持
structure-preserving:为了支持分析网络的application,需要network embedding能够保持网络结构。然而,网络的底层结构非常复杂。顶点的相似性取决于局部网络结构local network structure和全局网络结构global network structure。因此,如何同时保持局部结构和全局结构是一个棘手的问题。 - 稀疏性:许多现实世界的网络通常非常稀疏,以至于仅利用非常有限观察到的链接不足以达到令人满意的性能。
在过去的几十年中,人们已经提出了许多浅层模型的
network embedding方法,如IsoMap、Laplacian Eigenmaps: LE、LINE。然而,由于浅层模型的表达能力有限,它们很难捕获到高度非线性的网络结构。尽管一些方法采用了核技巧kernel technique,但是核方法也是浅层模型,也无法很好地捕获高度非线性的结构。为了很好地捕获高度非线性的结构,在论文《Structural Deep Network Embedding》中,作者提出了一种新的深度模型来学习网络的vertex representation。这是由深度学习最近的成功所推动的。深度学习已经被证明具有强大的表达能力来学习数据的复杂结构,并在处理图像数据、文本数据、音频数据方面取得了巨大成功。具体而言,在论文提出的模型中,作者设计了一个由多个非线性函数组成的多层架构。多层非线性函数的组合可以将数据映射到高度非线性的潜在空间中,从而能够捕获到高度非线性的网络结构。为了解决深度模型中的结构保持、以及稀疏性问题,作者进一步提出在学习过程中联合利用一阶邻近性
first-order proximity和二阶邻近性second-order proximity。一阶邻近性是仅在由edge连接的顶点之间的局部pairwise相似性,它刻画了局部网络结构。然而,由于网络的稀疏性,许多合法的链接(即未观测到的链接)发生缺失missing,结果导致一阶邻近性不足以表达网络结构。因此,作者进一步提出二阶邻近性来表示顶点邻域结构的相似性,从而捕获全局网络结构。通过一阶邻近性和二阶邻近性,我们可以分别很好地刻画局部网络结构和全局网络结构。顶点邻域也是一种局部网络结构,并不是全局网络结构。只是顶点邻域的 “ 局部” 要比顶点
pairwise的范围更大。为了在深度模型中同时保留局部网络结构和全局网络结构,论文提出了一种半监督架构,其中无监督组件
unsupervised component重建二阶邻近性从而保留全局网络结构,而监督组件supervised component利用一阶邻近性作为监督信息从而保留局部网络结构。因此,学到的representation可以很好地保留局部网络结构和全局网络结构。此外,如下图所示,具有二阶邻近性的vertex pair的数量,要比具有一阶邻近性的vertex pair的数量要多得多。因此,二阶邻近性的引入能够在刻画网络结构方面提供更多的信息。因此,论文的方法对稀疏网络具有鲁棒性。
论文在五个真实世界的网络数据集和四个真实世界的
application上进行了实验。结果表明:和baseline相比,论文方法生成的representation可以显著更好地重建原始网络,并在各种任务和各种网络(包括非常稀疏的网络)上取得相当大的收益。这表明SDNE在高度非线性空间中学到的representation可以很好地保持网络结构,并且对稀疏网络具有鲁棒性。综上所述,论文的贡献如下:
- 论文提出了一种
Structural Deep Network Embedding方法(即SDNE)来执行network embedding。该方法能够将数据映射到高度非线性的潜在空间从而保留网络结构,并且对稀疏网络具有鲁棒性。据作者所知,他们是最早使用deep learning来学习network representation的人之一。 - 论文提出了一种新的、具有半监督架构的深度模型,它同时优化了一阶邻近性和二阶邻近性。结果,学到的
representation同时保留了局部网络结构和全局网络结构,并且对稀疏网络具有鲁棒性。 - 作者在五个真实数据集和四个应用场景上广泛评估了
SDNE方法。结果证明了该方法在多标签分类、网络重建、链接预测、可视化等方面的优异性能。具体而言,当标记数据稀缺时,论文的方法相比baseline得到显著提升(20%)。
相关工作:
Deep Neural Network: DNN:representation learning长期以来一直是机器学习的一个重要问题,许多工作旨在学习样本的representation。深度神经网络的最新进展见证了它们具有强大的表达能力,并且可以为多种类型的数据生成非常有用的representation。例如《Imagenet classification with deep convolutional neural networks》提出了一个七层卷积神经网络来生成representation从而用于图像分类。然而,据我们所知,处理
network的deep learning工作很少,尤其是学习network representation。《A non-iid framework for collaborative filtering with restricted boltzmann machines》采用受限玻尔兹曼机进行协同过滤,《Learning deep representations for graph clustering》采用深度自编码器进行graph clustering,《Heterogeneous network embedding via deep architectures》提出了一种异质深度模型来进行异质数据的embedding。我们在两个方面与这些工作不同:- 首先,目标不同。我们的工作重点是学习低维的、结构保留的
representation,从而可以在各种下游任务之间使用。 - 其次,我们同时考虑顶点之间的一阶邻近性和二阶邻近性,从而同时保留局部网络结构和全局网络结构。但是他们仅关注单个阶次的信息。
- 首先,目标不同。我们的工作重点是学习低维的、结构保留的
Network Embedding:我们的工作是解决network embedding问题,旨在学习网络的representation。一些早期的工作,如
Local Linear Embedding: LLE、IsoMAP首先基于特征向量feature vector构建affinity graph,然后将主要的特征向量leading eigenvector作为network representation。最近,
LINE设计了两个损失函数,试图分别捕获局部网络结构和全局网络结构。此外,GraRep将工作扩展到利用高阶信息。尽管这些network embedding方法取得了成功,但是它们都采用了浅层模型。正如我们之前所解释的,浅层模型很难有效地捕获到底层网络中的高度非线性结构。此外,尽管他们中的一些人尝试使用一阶邻近性和高阶邻近性来保留局部网络结构和全局网络结构,但是他们分别独立地学习保留局部结构的representation和保留全局结构的representation并简单地拼接起来。显然,与在统一框架中同时建模并捕获局部网络结构和全局网络结构相比,他们的做法是次优的。DeepWalk结合了随机游走和SkipGram来学习network representation。尽管在经验上是有效的,但是它缺乏明确的目标函数来阐明如何保持网络结构。它倾向于仅保留二阶邻近性。然而,我们的方法设计了一个明确的目标函数,旨在通过同时保留一阶邻近性和二阶邻近性,从而同时保留局部结构和全局结构。
8.1 模型
- 这里我们首先定义问题,然后介绍
SDNE半监督深度模型,最后对模型进行一些分析和讨论。
8.1.1 问题定义
定义图 ,其中 为顶点集合, 为边集合。边 关联一个权重 。如果顶点 和 之间不存在链接,则 ,如果存在链接则对于无权图 、对于带权图 。
network embedding旨在将graph data映射到一个低维的潜在空间中,其中每个顶点都表示为一个低维向量。正如我们前面所解释的,局部结构和全局结构都必须同时被保留。接下来我们定义一阶邻近性,它刻画了局部网络结构。一阶邻近性
First-Order Proximity:一阶邻近性描述了顶点之间的pairwise邻近性。给定任何一对顶点 ,如果 ,则 和 之间存在正的一阶邻近性;否则 和 之间的一阶邻近性为零。自然地,
network embedding有必要保持一阶邻近性,因为这意味着:如果现实世界网络中的两个顶点存在链接,那么它们总是相似的。例如,如果一篇论文引用了另一篇论文,那么它们应该包含一些共同的主题。然而,现实世界的数据集通常非常稀疏,以至于观察到的链接仅占一小部分。存在许多彼此相似、但是不被任何edge链接的顶点。因此,仅捕获一阶邻近性是不够的,因此我们引入二阶邻近性来捕获全局网络结构。二阶邻近性
Second-Order Proximity:一对顶点之间的二阶邻近性描述了它们邻域结构neighborhood structure的邻近性。令 为顶点 和其它所有顶点的一阶邻近性,那么顶点 和 的二阶邻近性由 和 的相似性来决定。直观地讲,二阶邻近性假设:如果两个顶点共享许多共同的邻居
common neighbor,那么这两个顶点往往是相似的。这个假设已经在许多领域被证明是合理的。例如,在语言学中,如果两个单词总是被相似的上下文包围,那么这两个单词将是相似的(《Context and contextual word meaning》)。如果两个人之间有很多共同的好友,那么这两个人就会成为朋友(《Structure of growing social networks》)。二阶邻近性已经被证明是定义顶点相似性的一个很好的指标,即使这对顶点之间不存在链接,因此可以高度丰富顶点之间的关系。因此,通过引入二阶邻近性,我们能够刻画全局网络结构并缓解数据稀疏问题。通过一阶邻近性和二阶邻近性,我们研究了如何在执行
network embedding时集成二者,从而同时保持局部结构和全局结构。Network Embedding:给定图 ,network embedding旨在学习映射函数 ,其中 为embedding维度。该映射函数的目标是使得 和 之间的相似性显式地、同时地保留 和 的一阶邻近性和二阶邻近性。
8.1.2 SDNE 模型
在本文中,我们提出了一种半监督深度模型来执行
network embedding,其整体框架如下图所示。具体而言,为了捕获高度非线性的网络结构,我们提出了一种由多个非线性映射函数组成的深度架构,它将输入数据映射到高度非线性的潜在空间中从而捕获网络结构。此外,为了解决结构保持
structure-preserving问题和稀疏性问题,我们提出了一个半监督模型来同时利用二阶邻近性和一阶邻近性。- 对于每个顶点,我们能够获取它的邻域。因此,我们设计了无监督组件
unsupervised component,通过重建每个顶点的邻域结构来保持二阶邻近性。 - 同时,对于部分顶点
pair对(因为并不是所有顶点pair对之间都存在边),我们可以获得它们的成对相似性,即一阶邻近性。因此,我们设计监督组件supervised component,从而利用一阶邻近性作为监督信息来refine潜在空间中的representation。
通过在所提出的半监督深度模型中联合优化无监督组件和监督组件,
SDNE可以很好地保持高度非线性的局部网络结构和全局网络结构,并且对稀疏网络具有鲁棒性。接下来我们将详细介绍如何实现半监督深度模型。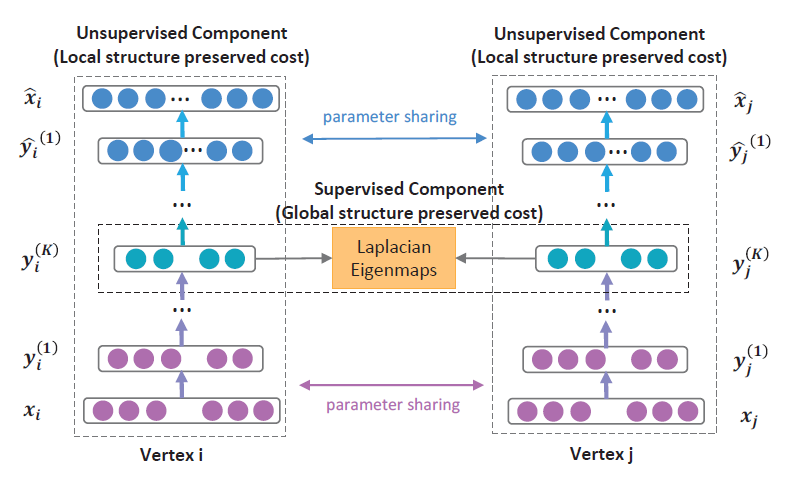
- 对于每个顶点,我们能够获取它的邻域。因此,我们设计了无监督组件
我们首先描述无监督组件如何利用二阶邻近性来保持全局网络结构。二阶邻近性是指一对顶点的邻域结构有多么相似。因此,为了对二阶邻近性进行建模,首先需要建模每个顶点的邻域。给定一个网络 ,我们可以获得它的邻接矩阵 ,它包含 个实例
instance。每个实例 描述了顶点 的邻域结构,因此 提供了每个顶点的邻域结构信息。利用 ,我们扩展了传统的深度自编码器deep autoencoder从而保持二阶邻近性。这里我们简要回顾深度自编码器的关键思想。深度自编码器是一个无监督模型,它由编码器
encoder和解码器decoder两部分组成。编码器由多个非线性函数组成,它将输入数据映射到representation空间。解码器也由多个非线性函数组成,它将representation空间中的representation映射到重建空间reconstruction space。然后,给定输入 ,每一层的hidden representation如下所示:其中:
- 为非线性激活函数。
- 为编码器第 层的权重参数矩阵, 为编码器第 层的
bias参数向量。 - 为编码器第 层的
hidden representation, 为编码器的层数。
得到 之后,我们可以通过编码器的逆过程(即解码器)得到输出 。自编码器的目标是最小化输出和输入的重建误差
reconstruction error。损失函数如下所示:正如
《Semantic hashing》所证明的,尽管最小化重建损失reconstruction loss并不能显式保留样本之间的相似性,但是重建准则reconstruction criterion可以平滑地捕获数据流形data manifold,从而保留样本之间的相似性。然后考虑我们的情况,如果我们使用邻接矩阵 作为自编码器的输入,即 ,由于每个实例 都刻画了顶点 的邻域结构,因此重建过程将使具有相似邻域结构的顶点具有相似的潜在
representation。如果网络规模较大,比如一千万个顶点,则 的维度高达千万维,这对于深度自编码器是一个严重的挑战。
然而,由于网络的某些特定属性,这种重建过程不能直接应用于我们的问题。
- 在网络中,我们可以观察到一些链接,但同时无法观察到许多合法链接
legitimate link(即理论上应该存在但是由于各种原因导致观察缺失),这意味着:顶点之间观察到链接确实表明顶点的相似性similarity,但是没有观察到链接不一定表明顶点的不相似性dissimilarity。 - 此外,由于网络的稀疏性, 中非零元素的数量远远少于零元素的数量。那么,如果我们直接使用 作为传统自编码器的输入,那么更容易重构 中的零元素。然而,这不是我们想要的。
为了解决这两个问题,我们对非零元素的重构误差施加了比零元素更大的惩罚。修改后的目标函数为:
一方面,对零元素的重建损失施加更小的惩罚,从而放松零元素的重建损失。另一方面,对非零元素的重建损失施加更大的惩罚,从而收紧非零元素的重建损失。
其中:
- 表示
Hadamard积(逐元素乘积)。 - 表示每个元素的惩罚系数。当 时 ;当 时 。 由 按行组成。
- 由 按行组成, 由 按行组成。
现在通过使用以邻接矩阵 作为输入的、修正后的深度自编码器,具有相似邻域结构的顶点将被映射到
representation空间相近的位置,这将由重建准则reconstruction criterion所保证。换句话讲,我们模型的无监督组件unsupervised component可以通过重建顶点之间的二阶邻近性来保留全局网络结构。如前所述,我们不仅需要保留全局网络结构,还必须捕获局部网络结构。我们使用一阶邻近性来表示局部网络结构。一阶邻近性可以视为监督信息,从而约束一对顶点之间潜在
representation的相似性。因此,我们设计了监督组件supervised component来利用一阶邻近性。这个监督组件的损失函数定义为:该损失函数借鉴了
Laplacian Eigenmaps的思想,即相似的顶点映射到embedding空间中很远的地方时会产生惩罚。我们将这个思想融入到深度模型中,从而使得观察到链接的顶点映射到embedding空间中相近的位置。结果,该模型保留了一阶邻近性。但是 “不相似” 的顶点映射到
embedding空间中很近的地方时不会产生惩罚。这在network embedding中是合理的,因为网络中未观察到链接的顶点之间可能是相似的,未观察到链接是因为链接缺失missing。为了同时保持一阶邻近性和二阶邻近性,我们提出了一个半监督模型,它结合了 和 并联合最小化了以下目标函数:
其中:
为一个
L2正则化项,用于防止过拟合:为超参数,用于平衡各部分损失之间的重要性。
换个角度来看,这是一个多任务学习,主任务为保持一阶邻近性的监督学习任务,辅助任务为保持二阶邻近性的无监督学习任务。
为了优化上述损失函数,我们采用随机梯度下降
stochastic gradient descent: SGD来求解。注意,由于模型的高度非线性,它在参数空间中存在许多局部最优解。因此,为了找到一个好的参数区域,我们首先使用深度信念网络Deep Belief Network对参数进行预训练,这在《Why does unsupervised pre-training help deep learning?》中已被证明是深度学习参数的基础初始化方法。
8.1.3 分析和讨论
这里我们对提出的
SDNE半监督深度模型进行一些分析和讨论。新顶点:
network embedding的一个实际问题是如何学习新顶点的representation。对于一个新的顶点 ,如果它和现有顶点的链接已知,那么我们可以得到它的邻接向量 ,其中 表示新顶点 和现有顶点 之间的边权重。然后我们可以简单地将 输入到我们的深度模型中,并使用经过训练的参数来获取 的representation。这一过程的复杂度是 。这里直接使用训练好的模型来推断,而没有继续训练的过程。
如果 和现有顶点之间都不存在链接,那么我们的方法和其它
state-of-the-art的network embedding方法都无法处理。为了处理这种情况,我们可以求助于其它辅助信息,如顶点的内容特征,我们将其留待未来的工作。训练复杂度:不难看出我们模型的训练复杂度为 ,其中: 为顶点数量, 为隐层的最大维度, 为网络的
average degree, 为迭代的次数。超参数 通常与
embedding向量的维度有关,但是与顶点数量无关。超参数 也独立于顶点数量。对于超参数 ,在实际应用中通常可以视为一个常数,例如在社交网络中,一个人的最大朋友数量总是有界的。因此, 与 无关,因此整体的训练复杂度与网络中的顶点数量成线性关系。
8.2 实验
这里我们在几个真实世界的数据集和
application上评估我们提出的方法。实验结果表明我们的方法比baseline有显著提升。数据集:为了全面评估
representation的有效性,我们使用了五个网络数据集,包括三个社交网络social network、一个引文网络citation network、一个语言网络language network,并用于三个实际application,即多标签分类任务、链接预测任务、可视化任务。考虑到这些数据集的特性,对于每个application,我们使用一个或多个数据集来评估性能。社交网络数据集
BLOGCATALOG, FLICKR, YOUTUBE:它们是在线用户的社交网络,每个用户至少标记为一种类别。BlogCatalog:该数据集包含BlogCatalog网站上博主之间的社交关系,标签代表通过元数据推断出来的博主兴趣。网络包含39种不同标签。Flickr数据集:Flickr网站用户之间的关系网络。标签代表用户的兴趣组,如“黑白照片”。网络包含195种不同标签。YouTube数据集:YouTube网站用户之间的社交网络。标签代表用户的视频兴趣组,如“动漫、摔跤”。网络包含47种不同标签。
这些标签类别可以用作每个顶点的真实
label,因此它们可以在多标签分类任务上进行评估。ARXIV GR-QC数据集:这是一个论文协同网络paper collaboration network, 包括了arXiv上广义相对论General Relativity和量子力学Quantum Cosmology领域的论文。每个顶点代表一个作者,边代表两个作者共同撰写了论文。因为我们没有顶点类别信息,因此该数据集用于链接预测任务。20-NEWSGROUP:该数据集包含两万个新闻组文档,每篇文档都标记为20个类别之一。我们用单词的tf-idf向量表示文档,用余弦相似度表示文档之间的相似性。我们可以根据这样的相似性来构建网络,网络中每个顶点代表一篇文档,边代表文档之间的相似性。我们选择以下三类标签的文档来执行可视化任务:
comp.graphics, rec.sport.baseball, talk.politics.gums。
总而言之,这些数据集分别代表了加权图/无权图、稀疏图/稠密图、小型图/大型图。因此,数据集可以全面反映
network embedding方法的特点。数据集的相似统计如下表: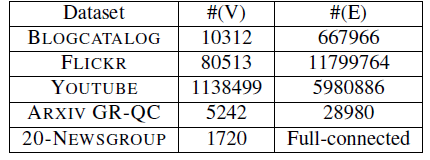
baseline方法:我们使用以下五种方法作为baseline。前四种是network embedding方法,最后一种Common Neighbor直接预测网络上的链接。Common Neighbor已被证明是执行链接预测的有效方法。DeepWalk:使用截断的随机游走和SkipGram模型来生成network representation。LINE:分别定义损失函数来保留一阶邻近性和二阶邻近性。在优化损失函数之后,它将一阶邻近性representation和二阶邻近性representation拼接起来 。GraRep:扩展到高阶邻近性并基于SVD分解来求解模型。它也是拼接了一阶邻近性representation和高阶邻近性representation作为最终的representation。Laplacian Eigenmaps:通过分解邻接矩阵的拉普拉斯矩阵来生成network representation,它仅仅保留了网络的一阶邻近性。Common Neighbor:它仅使用共同邻居的数量来衡量顶点之间的相似性。该方法仅在链接预测任务中作为baseline方法。
评估指标:在我们的实验中,我们分别执行重建任务、链接预测任务、多标签分类任务、可视化任务。
对于重建和链接预测,我们使用
precision@k和Mean Average Precision: MAP来评估性能。它们的定义如下:precision@k:其中: 为顶点集合; 为预测结果中顶点 在所有顶点预测结果中排名,得分越高排名越靠前; 表示顶点 和 中确实存在边。
该指标的物理意义为:预测结果的
top k顶点中,和顶点 真实存在边的顶点比例。Mean Average Precision: MAP:和precision@k相比,MAP更关注排名靠前的结果的表现。其计算公式为:
对于多标签分类任务,我们采用
micro-F1和macro-F1指标。macro-F1:给每个类别相等的权重,其定义为:其中: 为所有类别的取值空间集合, 为类别 的
F1指标。micro-F1:给每个样本相等的权重,其定义为:其中: 为所有类别的取值空间集合, 为类别 的
true positive, 为类别 的false positive, 为类别 的false negative。
参数配置:我们在本文中提出了一种多层深度结构
multi-layer deep structure,层数随着数据集的不同而变化。每一层的维度如下表所示。BLOGCATALOG, ARXIV GR-QC, 20-NEWSGROUP数据集为三层结构,FLICKR, YOUTUBE数据集为四层结构。如果我们使用更深的模型,则性能几乎保持不变甚至变得更差。
- 对于我们的方法,超参数 是通过在验证集上使用网格搜索来调优的。
baseline的超参数也被调优为最佳值。 - 随机梯度下降的
mini-batch size设为1。学习率的初始值设为0.025。每个正样本采样的负样本数量设为5,样本总数为100亿(包括负采样的)。 - 此外,根据
LINE的原始论文,当拼接1-step representation和2-step representation并对最终embedding向量执行L2归一化时,LINE会产生更好的结果。我们按照原始论文的方法来获取LINE的结果。 - 对于
DeepWalk,我们将窗口大小设为10,将walk length设为40,将每个顶点开始的游走数量设为40。 - 对于
GraRep,我们将最高的转移矩阵阶次设为5。
- 对于我们的方法,超参数 是通过在验证集上使用网格搜索来调优的。
8.2.1 实验结果
这里我们首先评估重建性能,然后我们报告不同
embedding方法生成的network representation在三个经典的数据挖掘和机器学习application(即多标签分类、链接预测、可视化)上的泛化结果。结果中,最佳性能以粗体突出显示。
**表示0.01的统计显著性,*表示0.05的统计显著性(成对的t-test)。网络重建
Network Reconstruction:在继续评估我们的方法在实际application中的泛化性能之前,我们首先对不同network embedding方法的网络重建能力进行基本的评估。这个实验的原因是:一个良好的network embedding方法应该确保学到的embedding能够保留原始的网络结构。我们使用语言网络
ARXIV GR-QC和社交网络BLOGCATALOG作为代表。给定一个网络,我们使用不同的network embedding方法来学习network representation,然后预测原始网络的链接。由于原始网络中的现有链接是已知的并且可以作为ground-truth,因此我们可以评估不同方法的重建性能,即训练集误差。注意:这里的误差是训练误差,而不是测试误差。
我们使用
precision@k和MAP作为评估指标,实验结果如下图所示。可以看到:SDNE在两个数据集上MAP指标始终超越其它baseline。当 增加时,SDNE在两个数据集上precision@k始终最高。这表明我们的方法(即SDNE)能够很好地保持网络结构。具体而言,在
ARXIV GR-QC数据集上,一直到 ,我们方法的precision@k都可以达到100%并保持在100%左右。这表明我们的方法几乎可以完美地重建该数据集中的原始网络,特别是考虑到该数据集中的链接总数为28980。尽管
SDNE和LINE都利用了一阶邻近性和二阶邻近性来保留网络结构,但是SDNE效果超越了LINE,原因可能有两个:LINE采用浅层结构,因此难以捕获底层网络的高度非线性结构。LINE直接将一阶邻近性representation和二阶邻近性representation拼接在一起,这比SDNE直接联合优化一阶邻近性和二阶邻近性要差。
SDNE和LINE均优于仅利用一阶邻近性来保持网络结构的LE,这表明引入二阶邻近性可以更好的保留网络结构。
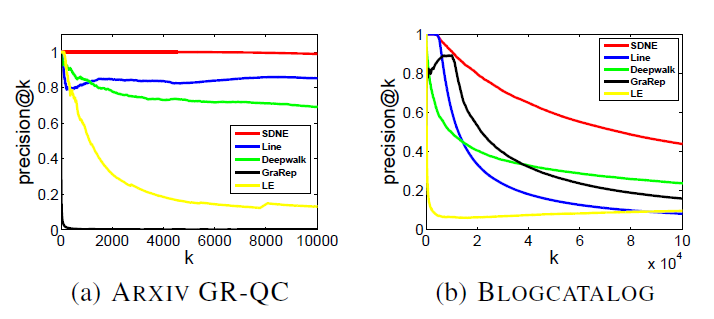

多标签分类
Multi-label Classification:我们在本实验中通过多标签分类任务来评估不同network representation的效果。顶点的representation是从network embedding方法生成的,然后作为顶点分类任务中的顶点特征。具体而言,我们采用
LIBLINEAR package来训练分类器。在训练分类器时,我们随机抽取一部分标记顶点作为训练集、剩余顶点作为测试集。对于BLOGCATALOG我们随机抽取10%到90%的顶点作为训练集,剩余顶点作为测试集;对于FLICKR,YOUTUBE我们随机抽取1%到10%的顶点作为训练集,剩余顶点作为测试集。另外我们删除YOUTUBE中没有任何类别标签的顶点。我们重复这样的过程5次并报告平均的Micro-F1和Macro-F1指标。BLOGCATALOG结果如下: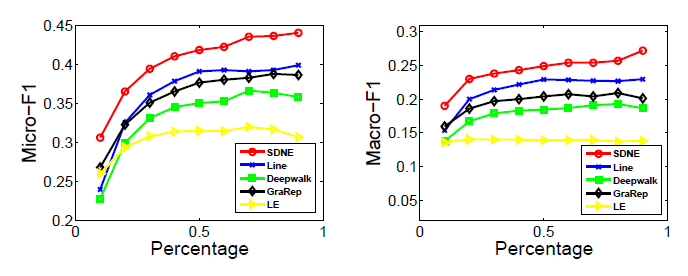
FLICKR结果如下: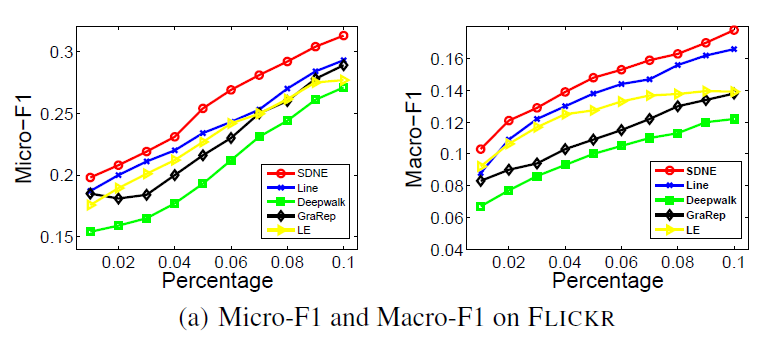
YOUTUBE结果如下: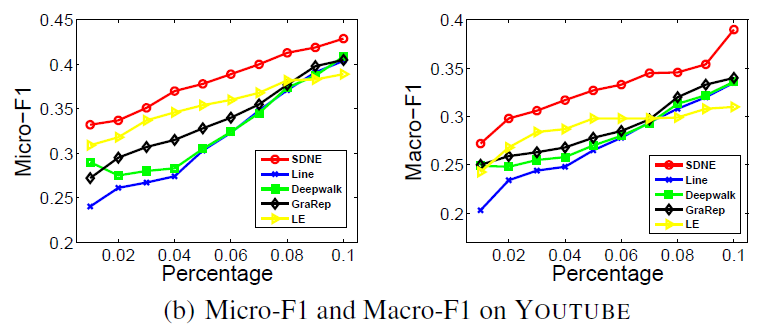
可以看到:
SDNE的效果始终超越baseline方法,证明SDNE学到的network representation相比baseline可以更好地泛化到分类任务中。在
BLOGCATALOG数据集中,当训练数据比例从60%降低到10%时,我们的方法相对于baseline的提升幅度更加明显。这表明:当标记数据有限时,我们的方法可以实现比baseline更显著的提升。这种优势对现实世界的application尤为重要,因为标记数据通常是稀缺的。大多数情况下,
DeepWalk的效果是所有network embedding方法中最差的。这有两个原因:- 首先,
DeepWalk没有显式的目标函数来捕获网络结构。 - 其次,
DeepWalk使用随机游走来产生顶点的邻居。由于随机性这会引入很多噪音,尤其对于degree很高的顶点。
- 首先,
链接预测
Link Prediction:在这里我们聚焦于链接预测任务并进行两个实验:第一个实验评估整体性能,第二个实验评估网络的不同稀疏性如何影响不同方法的性能。我们在这里使用数据集
ARXIV GR-QC。为了在网络中进行链接预测任务,我们随机隐藏一部分现有链接并使用剩余网络来训练network embedding模型。训练之后,我们可以获得每个顶点的representation,然后使用获得的representation来预测未观察到的链接。与重建任务不同(预测训练期间已知的链接),该任务预测训练期间未知的链接,而不是重建现有的链接。因此,该任务可以展示不同network embedding方法的预测能力。此外,我们在该任务中添加了Common Neighbor方法,因为它已被证明是进行链接预测的有效方法。对于第一个实验,我们随机隐藏
15%的现有链接(大约4000个链接),并使用precision@k作为预测隐藏链接的评估指标。我们逐渐将 从2增加到10000,并在下表中报告结果。可以看到:- 当 增加时,
SDNE方法始终优于其它network embedding方法。这证明了SDNE学到的representation对于未观察到的链接具有很好的预测能力。 - 当 时,
SDNE的precision仍然高于0.9,而其它方法的precision掉到0.8以下。这表明SDNE对于排名靠前的链接预测的比较准。对于某些实际application,如推荐和信息检索,这种优势非常重要。因为这些应用更关心排名靠前的结果是否准确。

- 当 增加时,
在第二个实验中,我们通过随机删除原始网络中的一部分链接来改变网络的稀疏性,然后按照上述流程报告不同
network embedding方法的结果。结果如下图所示。可以看到:- 当网络更稀疏时,
LE和SDNE/LINE模型之间的差距增大。这表明:二阶邻近性的引入使得学到的representation对于稀疏网络鲁棒性更好。 - 当删除
80%链接时,SDNE仍然比所有其它方法好。这表明:SDNE在处理稀疏网络时能力更强。
- 当网络更稀疏时,
可视化
Visualization:network embedding的另一个重要application是在二维空间上生成网络的可视化。因此,我们可视化在20-NEWSGROUP网络学到的representation。我们使用t-SNE工具可视化不同network embedding方法学到的低维network embedding。结果,每篇文档都被映射到二维空间的一个点,不同类别的文档采用不同颜色:rec.sport.baseball为蓝色、comp.graphics为红色、talk.politics.guns为绿色。因此,一个好的可视化结果是相同颜色的点彼此靠近。可视化结果如下图所示。除了可视化结果,我们还使用Kullback-Leibler: KL散度作为定量的评估指标。KL散度越低,可视化性能越好。结论:
LE和DeepWalk的效果较差,因为不同类别的顶点彼此混合。LINE虽然不同类别形成了簇,但是中间部分不同类别的文档依然彼此混合。GraRep效果更好,但是簇的边界不是很清晰。SND在簇的分组以及簇的边界上表现最佳。SDNE方法的KL散度最低,定量地证明了我们的方法在可视化任务中的优越性。


8.2.2 参数敏感性
我们在本节中研究参数敏感性。具体而言,我们评估不同的
embedding维度 、不同超参数 、不同超参数 值如何影响结果。我们在ARXIV-GRQC的数据集上报告precision@k指标。embedding维度 :我们在下图展示embedding维度 如何影响性能。可以看到:- 最初,当
embedding维度增加时效果先提升。这是因为更大的维度可以容纳更多的有效信息。 - 但是,继续增加
embedding维度将导致效果缓缓下降。这是因为太大的维度会引入更多的噪音,从而降低性能。
总体而言
embedding维度 很重要,但SDNE对此超参数不是特别敏感。
- 最初,当
超参数 :超参数 平衡了一阶邻近性损失和二阶邻近性损失的权重,实验结果如下所示。可以看到:
- 当 时,模型性能完全取决于二阶邻近性。当 越大,模型越关注一阶邻近性。
- 当 或者 时模型性能最佳。这表明:一阶邻近性和二阶邻近性对于刻画网络结构都是必不可少的。
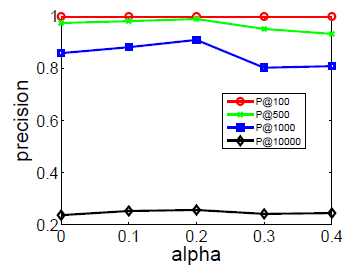
超参数 :超参数 控制了 中非零元素的重建。我们展示了 的值如何影响性能, 越大模型越倾向于重构非零元素。实验结果如下所示。可以看到:
当 时效果不佳。因为 表示模型重构 时认为零元素和非零元素都是同样重要的。
如前所述,虽然两个顶点之间没有链接不一定表示两个顶点不相似,但是两个顶点之间存在链接一定表明两个顶点的相似性。因此非零元素应该比零元素更加重要。所以 在零元素的重构中引入大量噪声,从而降低模型性能。
当 太大时性能也较差。因为 很大表示模型在重构中几乎忽略了 的零元素,模型倾向于认为每一对顶点之间都存在相似性。事实上 之间的很多零元素都表明顶点之间的不相似。所以 太大将忽略这些不相似,从而降低模型性能。
这些实验表明:我们应该更多的关注 中非零元素的重构误差,但是也不能完全忽略 中零元素的重构误差。
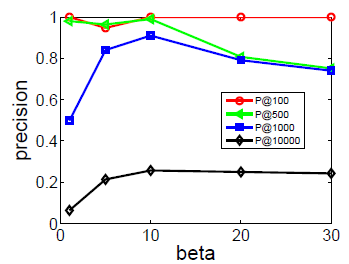
九、CANE[2017]
network embedding: NE(即network representation learning: NRL)旨在根据顶点在网络中的结构角色structural role,从而将网络的顶点映射到低维空间中。network embedding提供了一种高效efficient且有效effective的方法来表达和管理大型网络,缓解了传统基于符号的representation的计算问题和稀疏性问题。因此,近年来network embedding吸引了人们的许多研究兴趣,并在包括链接预测、顶点分类、社区检测在内的许多网络分析任务上取得了可喜的表现。在现实世界的社交网络中,一个顶点在与不同的邻居顶点交互时可能表现出不同的方面
aspect,这是很直观的。例如,研究人员通常与各种合作伙伴就不同的研究主题进行合作(如下图所示),社交媒体用户与分享不同兴趣的各种朋友联系,一个网页出于不同目的链接到多个其它网页。然而,现有的大多数network embedding方法只为每个顶点安排一个single embedding向量,并产生以下两个问题:这些方法在与不同邻居交互时,无法灵活转换不同的方面
aspect。在这些模型中,一个顶点倾向于迫使它的所有邻居之间的
embedding彼此靠近,但事实上并非一直如此。例如下图中,左侧用户和右侧用户共享较少的共同兴趣,但是由于他们都链接到中间用户,因此被认为彼此接近。因此,这使得顶点embedding没有区分性。即:“朋友的朋友“ 不一定是朋友。
为了解决这些问题,论文
《CANE: Context-Aware Network Embedding for Relation Modeling》提出了一个Context-Aware Network Embedding: CANE框架,用于精确建模顶点之间的关系。更具体而言,论文在信息网络information network上应用CANE。信息网络的每个顶点还包含丰富的外部信息,例如文本text、标签label、或者其它元数据meta-data。在这种场景下,上下文的重要性对network embedding更为关键。在不失一般性的情况下,论文在基于文本的信息网络中实现了CANE,但是CANE可以很容易地扩展到其它类型的信息网络。在传统的
network embedding模型中,每个顶点都表达为一个静态的embedding向量,即context-free embedding。相反,CANE根据与当前顶点交互的不同邻居,从而将动态的embedding分配给当前顶点,称为context-aware embedding。以一个顶点 为例:当与不同的邻居交互时, 的context-free embedding保持不变;而当面对不同的邻居时, 的context-aware embedding是动态的。CANE类似于GAT,其中不同邻域顶点的attention权重是不同的。在CANE中,注意力权重是hard的(0或者1);在GAT中,注意力权重是soft的(0到1之间)。当顶点 与它的邻居顶点 交互时,它们彼此相关的
context embedding分别来自它们的文本信息。对于每个顶点,我们可以轻松地使用神经模型neural model,例如卷积神经网络和循环神经网络来构建context-free embedding和text-based embedding。为了实现context-aware text-based embedding,论文引入了selective attention方案,并在这些神经模型中建立了 和 之间的互注意力mutual attention。mutual attention预期引导神经模型强调那些被相邻顶点focus的单词,并最终获得context-aware embedding。每个顶点的context-free embedding和context-aware embedding都可以通过使用现有的network embedding方法学到(如DeepWalk,LINE,node2vec)并拼接起来。论文对不同领域的三个真实数据集进行了实验。与其它
state-of-the-art方法相比,链接预测的实验结果展示了论文框架的有效性。结果表明,context-aware embedding对于网络分析至关重要,特别是对于那些涉及顶点之间复杂交互的任务,如链接预测。论文还通过顶点分类和案例研究来探索论文框架的性能,这再次证实了CANE模型的灵活性和优越性。CANE在链接预测方面比state-of-the-art方法取得了显著的提升,在顶点分类方面与state-of-the-art方法的性能相当。相关工作:随着大型社交网络的快速增长,
network embedding(即network representation learning)已被提出作为网络分析任务的关键技术。近年来,人们已经提出了大量的
network embedding模型来学习有效的顶点embedding。例如:DeepWalk在网络上执行随机游走,并引入了一种有效的word representation learning模型SkipGram来学习network embedding。LINE优化大型网络中edge的联合概率和条件概率,从而学习顶点representation。node2vec将DeepWalk中的随机游走策略修改为有偏的随机游走biased random walk,从而更有效地探索网络结构。
然而,这些
network embedding模型中的大多数仅将结构信息编码为顶点embedding,而没有考虑现实世界社交网络中伴随顶点的异质信息heterogeneous information。为解决这个问题,研究人员努力将异质信息整合到传统的network embedding模型中。例如:text-associated Deep-Walk: TADW使用文本信息改进了基于DeepWalk的矩阵分解。max-margin DeepWalk: MMDW利用顶点的labeling信息来学习network representation。group enhanced network embedding: GENE整合了NE中存在的group信息。context-enhanced network embedding: CENE将文本内容视为一种特殊的顶点,并同时利用结构信息和文本信息来学习network embedding。
据我们所知,所有现有的
network embedding模型都聚焦于学习context-free embedding,但是忽略了顶点和其它顶点交互时的不同角色。相比之下,我们假设一个顶点根据与它交互的不同顶点而具有不同的embedding,并提出CANE来学习context-aware embedding。
9.1 模型
9.1.1 问题定义
我们首先给出一些基本的符号和定义。给定信息网络
information network,其中 为顶点集合, 为边集合, 为顶点的文本信息。每条边 表示顶点 之间的关系,并且关联一个权重 。这里顶点 的文本信息表达为单词序列 ,其中 为序列 的长度。network representation learning旨在根据网络结构和关联信息(如文本和label)为每个顶点 学习低维embedding,其中 为representation空间的维度。Context-free Embedding的定义:传统的network representation learning模型为每个顶点学习context-free embedding。这意味着顶点的embedding是固定的,并且不会根据顶点的上下文信息(即与之交互的另一个顶点)而改变。Context-aware Embedding的定义:与现有的、学习context-free embedding的network representation learning模型不同,CANE根据顶点不同的上下文来学习该顶点的各种embedding。具体而言,对于边 ,CANE学习context-aware embedding和 。CANE的模型容量要比传统的network representation learning模型容量大得多。传统network representation learning模型只需要计算 个embedding,而CANE模型需要计算 个embedding。更大的模型容量可能会导致严重的过拟合。此外,
CANE模型中每个顶点有可变数量的embedding,在顶点分类任务中,如何利用这些embedding是个难点。
9.1.2 模型
整体框架:为了充分利用网络结构和关联的文本信息,我们为顶点 提供了两种类型的
embedding:基于结构structure-based的embedding、基于文本text-based的embedding。structure-basedembeding可以捕获网络结构中的信息,而text-based embedding可以捕获关联文本信息中的文本含义textual meaning。使用这些embedding,我们可以简单地拼接它们并获得顶点embedding为 ,其中 为拼接算子。CANE并不是独立建模structure-basedembeding和text-based embedding,而是联合优化它们。注意,
text-based embedding可以是context-free的、也可以是context-aware的,这将在后面详细介绍。当 是context-aware时,整个顶点embedding也将是context-aware。通过上述定义,
CANE旨在最大化所有edge上的目标函数,如下所示:这里每条
edge的目标函数 由两部分组成:其中: 表示基于结构的目标函数
structure-based objective, 表示基于文本的目标函数text-based objective。接下来我们分别对这两个目标函数进行详细介绍。CANE仅建模一阶邻近性(即观察到的直接链接),并没有建模高阶邻近性,因为CANE隐含地假设了 “朋友的朋友“ 不一定是朋友。仅建模一阶邻近性会遇到数据稀疏的不利影响。基于结构的目标函数:不失一般性,我们假设网络是有向的,因为无向边可以被认为是两个方向相反、且权重相等的有向边。因此,基于结构的目标函数旨在使用
structure-based embedding来衡量观察到一条有向边的对数似然log-likelihood,即:遵从
LINE,我们将上式中的条件概率定义为:基于文本的目标函数:现实世界社交网络中的顶点通常伴随着关联的文本信息。因此,我们提出了基于文本的目标函数来利用这些文本信息,并学习
text-based embedding。基于文本的目标函数 可以通过各种度量指标来定义。为了与 兼容,我们将 定义如下:
其中:
为对应部分的重要性,为超参数。
如果仅仅最小化 ,则只需要两个超参数即可。但是由于需要和 相加,因此 需要三个超参数。
定义为:
这里构建了
structure-based embedding、text-based embedding之间的桥梁,使得信息在结构和文本之间流动。
上式中的条件概率将两种类型的顶点
embedding映射到相同的representation空间中,但是考虑到它们自身的特点,这里并未强制它们相同。类似地,我们使用softmax函数来计算概率,如公式 所示。structure-based embedding被视为parameter,与传统的network embedding模型相同。但是对于text-based embedding,我们打算从顶点的关联文本信息中获取它们。此外,text-based embedding可以通过context-free的方式、或者context-aware的方式获取。接下来我们将详细介绍。Context-Free Text Embedding:有多种神经网络模型可以从单词序列word sequence中获取text embedding,如卷积神经网络CNN、循环神经网络RNN。在这项工作中,我们研究了用于文本建模的不同神经网络,包括CNN、Bidirectional RNN、GRU,并采用了性能最好的CNN。CNN可以在单词之间捕获局部语义依赖性local semantic dependency。CNN以一个顶点的单词序列作为输入,通过lookup、卷积、池化这三层得到基于文本的embedding。lookup:给定一个单词序列 ,lookup layer将每个单词 转换为对应的word embedding,并且获得embedding序列 ,其中 为word embedding的维度。卷积:
lookup之后,卷积层提取输入的embedding序列 的局部特征local feature。具体而言,它使用卷积矩阵 在长度为 的滑动窗口上进行卷积操作,如下所示:表示 个卷积核,每个卷积核的尺寸为 。 为卷积核数量,也称作输出通道数。
其中:
- 为第 个滑动窗口内所有
word embedding拼接得到的矩阵。 - 为
bias向量。
注意,我们在单词序列的边缘添加了零填充向量。
- 为第 个滑动窗口内所有
最大池化:为了获得
text embedding,我们对 进行最大池化和非线性变换,如下所示:其中:
max是在embedding维度上进行的,tanh为逐元素的函数。
Context-Aware Text Embedding:如前所述,我们假设顶点在与其它顶点交互时扮演不同的角色。换句话讲,对于给定的顶点,其它不同的顶点与它有不同的焦点,这将导致context-aware text embedding。为了实现这一点,我们采用
mutual attention来获得context-aware text embedding。mutual attention使CNN中的池化层能够感知edge中的顶点pair,从而使得来自一个顶点的文本信息可以直接影响另一个顶点的text embedding,反之亦然。加权池化,权重来自于当前顶点文本内容和另一个顶点文本内容的相关性。
如下图所示,我们说明了
context-aware text embedding的生成过程。给定一条边 和两个对应的文本序列 和 ,我们可以通过卷积层得到矩阵 和 。这里 表示 的长度, 表示 的长度。通过引入一个注意力矩阵attentive matrix,我们计算相关性矩阵correlation matrix如下:注意, 中的每个元素 表示两个隐向量(即 )之间的
pair-wise相关性得分correlation score。然后,我们沿 的行和列进行池化操作从而生成重要性向量importance vector,分别称作行池化row-pooling和列池化column-pooling。根据我们的实验,均值池化的性能优于最大池化。因此,我们采用如下的均值池化操作:其中:
- 表示行池化向量,它就是 的重要性向量。
- 表示列池化向量,它就是 的重要性向量。
接下来,我们使用
softmax函数将重要性向量 和 转换为注意力向量attention vector和 ,其中:即:对重要性向量进行
softmax归一化。最后,顶点 和 的
context-aware text embedding计算为:现在,给定一条边 ,我们可以获得
context-aware embedding,它是structure embedding和context-aware text embedding的拼接:其中 为拼接算子。
CANE优化过程:如前所述,CANE旨在最大化若干个条件概率。直观而言,使用softmax函数优化条件概率在计算上代价太大。因此,我们使用负采样,并将目标函数转换为以下形式:其中: 为负采样比例, 为
sigmoid函数, 为负顶点的采样分布, 为顶点 的out-degree。之后,我们使用
Adam来优化新的目标函数。注意,CANE通过使用训练好的CNN来为新顶点生成text embedding,从而完全能够实现zero-shot场景。
9.2 实验
为了研究
CANE对顶点之间关系建模的有效性,我们在几个真实世界的数据集上进行了链接预测实验。此外,我们还使用顶点分类任务来验证顶点的context-aware embedding是否可以反过来组成高质量的context-free embedding。数据集:我们选择如下所示的、真实世界的三个数据集。
Cora:一个典型的论文引用网络数据集。在过滤掉没有文本信息的论文之后,网络中包含2277篇机器学习论文,涉及7个类别。HepTh:另一个论文引用网络数据集。在过滤掉没有文本信息的论文之后,网络中包含1038篇高能物理方面的论文。Zhihu:一个大型的在线问答网络,用户可以相互关注并在网站上回答问题。我们随机抽取了10000名活跃用户,并使用他们关注主题的描述作为文本信息。
这些数据集的详细统计信息如下表所示。

baseline方法:我们采用以下方法作为baseline:仅考虑网络结构:
Mixed Membership Stochastic Blockmodel: MMB: 是关系数据的一个传统图模型,它允许每个顶点在形成边的时候随机选择一个不同的topic。DeepWalk:使用截断的随机游走将图结构转化为线性结构,然后使用层次softmax的SkipGram模型处理序列从而学习顶点embedding。LINE:分别定义损失函数来保留一阶邻近性和二阶邻近性来求解一阶邻近representation和二阶邻近representation,然后将二者拼接一起作为representation。Node2Vec:通过一个有偏随机游走过程biased random walk procedure来将图结构转化为线性结构,然后使用层次softmax的SkipGram模型处理序列。
同时考虑结构和文本:
Naive Combination:用两个模型分别计算structure embedding和text embedding,然后简单地将structure embedding和text embedding拼接起来。TADW:采用矩阵分解的方式将顶点的文本特征融合到network embedding中。CENE:将文本内容视为一种特殊的顶点来利用结构和文本信息,并优化异质链接的概率。
评估指标:对于链接预测任务,我们采用标准的评估指标
AUC。对于顶点分类任务,我们采用L2正则化的逻辑回归来训练分类器,并评估分类准确率指标。训练配置:
为公平起见,我们将所有方法的
embedding维度设为200。对于
LINE方法,负采样系数设置为5。一阶embedding和 二阶embedding维度都是100维,使得拼接后的向量有200维。对于
node2vec方法,我们使用网格搜索并选择最佳的超参数。对于
CANE方法,我们通过超参数搜索选择最佳的 。为了加速训练过程,我们选择负采样系数 。为了说明文本
embedding以及注意力机制的效果,我们设计了三个版本:CANE with text only:仅包含context-aware text embedding。CANE without attention:包含structure embedding以及context-free text embedding。CANE:完整的CANE模型。
链接预测实验:我们分别移除了
Cora,HepTh,Zhihu等网络不同比例的边,然后评估预测的AUC指标。注意,当我们仅保留5%的边来训练时,大多数顶点是孤立的,此时所有方法的效果都较差而且毫无意义。因此我们不考虑5%以下比例的情况。Cora的结果如下,其中 。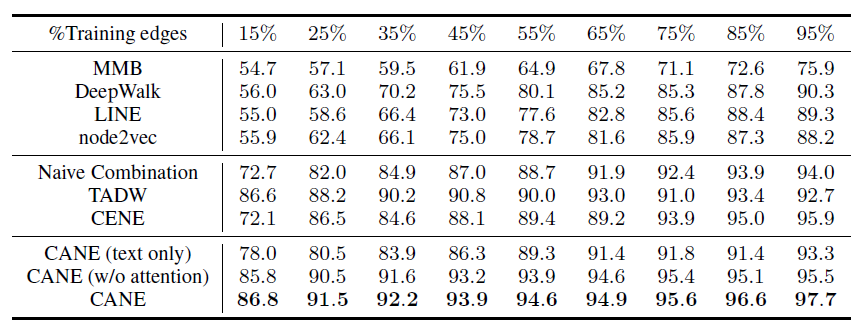
HepTh的结果如下,其中 。
Zhihu的结果如下,其中 。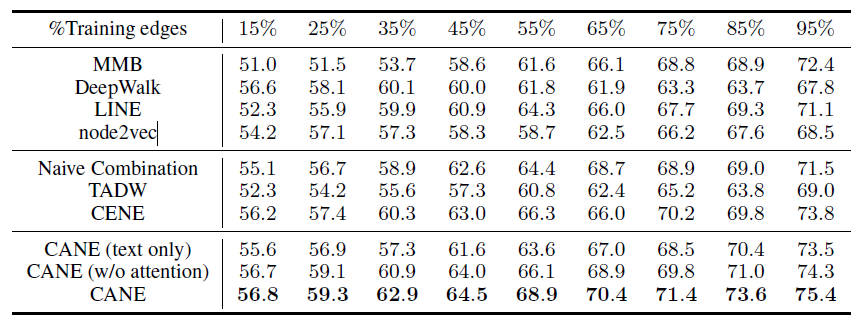
从链接预测任务的实验结果可以看到:
CANE在所有训练集、所有训练比例都取得最好的效果,这表明CANE在链接预测任务中的有效性,验证了CANE具备精确建模顶点之间关系的能力。在不同的训练比例下,
CENE和TADW的效果不稳定。具体而言:CENE在训练比例较小时效果比TADW较差,因为相比TADW,CENE使用了更多的参数(如卷积核和word embedding),因此CENE需要更多的训练数据。- 与
CENE不同,TADW在较小的训练比例时表现得更好,因为基于DeepWalk的方法即使在边有限的情况下也可以通过随机游走很好地探索稀疏网络结构。然而,由于它的简单性和bag-of-words假设的局限性,TADW在较大的训练比例时表现不佳。 CANE在各种情况下,效果都很稳定。这展示了CANE的灵活性和鲁棒性。
通过引入注意力机制,学到的
context-aware embedding比没有注意力的embedding效果更好。这验证了我们的假设:顶点和其它顶点交互时应该扮演不同的角色,从而有利于相关的链接预测任务。
综上所述,以上所有实验结果表明:
CANE可以学习高质量的context-aware embedding,这有利于精确估计顶点之间的关系。此外,实验结果也表明了CANE的有效性和鲁棒性。实验可以看到:引入顶点的文本信息可以更好地提升
network embedding的质量。因此,CANE应该和带文本信息的baseline方法进行比较。如果CANE和DeepWalk/LINE/node2vec等纯结构的network embedding方法比较,则不太公平。顶点分类实验:网络分析任务(如顶点分类和聚类)需要得到该顶点的整体
embedding,而不是顶点的很多个context-aware embedding。为了得到整体embedding,我们简单的将每个顶点的所有context-aware embedding取平均,如下所示:其中 为顶点 的
context-aware embedding数量。使用生成的整体
embedding,我们在Cora数据集上执行顶点分类任务,采用2-fold交叉验证并报告平均准确率。实验结果如下图所示,可以看到:CANE的性能与state-of-the-art的CENE相当。这表明:学到的context-aware embedding可以通过简单的取平均操作转化为高质量的context-free embedding,并进一步应用于其它网络分析任务。- 通过引入
mutual attention机制,CANE的性能比没有注意力的版本得到较大的提升。这与链接预测的结果是一致的。
综上所述,实验结果表明
CANE可以灵活地完成各种网络分析任务。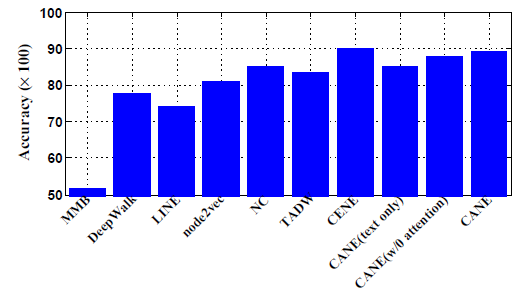
案例研究:为了说明
mutual attention机制从文本信息中选择有意义特征的重要性,我们可视化了两个顶点的热力度。图中,每个单词都带有各种背景色,颜色越深该单词的权重越大。每个单词的权重根据注意力权重来计算,计算方式为:- 首先,对于每对顶点
pair,我们获取其单词序列每个卷积窗口的注意力权重 。 - 然后,在这个窗口内我们为每个单词分配注意力权重(窗口内的多个单词对应于该窗口的权重)。
- 最后,考虑到一个单词可能会出现在多个窗口内(单个顶点的单词序列包含很多个窗口),我们将该单词的多个权重相加,得到单词的注意力权重。
我们提出的注意力机制使得顶点之间的关系明确且可解释。如下图所示,我们选择
Cora数据集存在引用关系的三篇论文A,B,C。可以看到:尽管论文B,C和论文A存在引用关系,但是论文B和论文C关注的是论文A的不同部分:Edge #1在论文A上重点关注reinforcement learning。Edge #2在论文A上重点关注machine learning, supervised learning algorithms,complex stochastic models。
另外,论文
A中的所有这些关键元素都可以在论文B和论文C中找到对应的单词。这些关键元素对引用关系给出了准确的解释,这很直观。这些挖掘出的顶点之间显著的相关性,反应了mutual attention机制的有效性,同时也表明CANE精确建模关系的能力。
- 首先,对于每对顶点
十、EOE[2017]
数据点之间的各种显式交互
explicit interaction和隐式交互implicit interaction(例如friendship, co-authorship, co-concurrence)使得network无处不在。因此,network representation在许多数据挖掘application中是难以避免的。一方面,许多数据挖掘application都是为网络而设计的,例如社区检测community detection、链接预测link prediction。另一方面,其它数据挖掘application也可以从网络分析中受益,例如collective classification和降维dimension reduction。以上所有
application都依赖于对网络交互network interaction或者edge的分析。如今,network embedding越来越多地用于辅助网络分析,因为它可以有效地学习潜在特征latent feature从而编码链接信息。network embedding的基本思想是通过在潜在空间中保持相连顶点pair对,从而保持网络结构network structure。潜在特征是有益的,因为它比edge具有更强的表达能力,并且可以直接被现有的机器学习技术所使用。尽管之前人们已经提出了各种network embedding方法,但是这些方法仅设计用于在单网络single network上学习representation。此外,在大数据时代,不同类型的相关信息往往是可用的,并且可以融合在一起形成耦合异质网络
coupled heterogeneous network,其中每种类型的信息都可以表示为一个独立的同质网络homogeneous network。我们将耦合异质网络定义为由两个不同的、但是相关的子网sub-network构成的网络。这些子网通过跨网链接inter-network link来连接,例如:author and word network:author可以通过他们之间的交互而联系起来,例如co-authorship。单词可以通过共现co-concurrence关系联系起来。author可以和他们在paper中使用的单词联系起来。social network user and word network:用户可以通过他们之间的好友关系而联系起来。单词可以通过共现co-concurrence关系联系起来。用户可以和他们使用的单词联系起来。customer and movie network:消费者可以通过他们之间的好友关系而联系起来。电影可以通过共同演员或者共同导演关系而联系起来。消费者可以和他们看过的电影联系起来。gene and chemical compound network:基因可以通过gene-gene相互作用而联系起来。化合物可以通过具有相同本体ontology的方式联系起来。基因可以通过binding关系从而和化合物联系起来。
为了直观地说明这个概念,下图给出了
author and word network的一个例子,其中author通过co-authorship联系起来,并且在同一个标题中的同时出现被定义为单词之间的co-concurrence关系。我们从DBLP数据集中对网络进行采样。被采样的co-authorship网络由2000年到2003年期间在两个数据挖掘会议KDD和ICDM、以及两个数据库会议SIGMOD和VLDB上发表paper的author组成。结果表明,author构成了两个簇cluster,单词也构成了两个簇,这些簇可以通过社区检测算法来生成。而且,数据挖掘专家对数据挖掘领域的单词相比数据库领域的单词有更多的链接,而数据库专家对数据库领域的单词相比数据挖掘领域的单词有更多的链接。
为了学习
author的潜在特征,同一个领域的author应该在潜在空间中彼此靠近。可以看出,author和单词之间的edge可以在已经存在author edge的情况下作为补充信息complementary information。这是因为同一个领域的author更有可能在其领域的单词上存在edge,这可以用来使得仅从author edge学习的潜在特征更加全面和准确。当author edge不存在时,补充信息更为重要,这可以称之为冷启动问题cold-start problem。学习单词潜在特征的情况也是类似的。author network和word network都有可用的embedding方法。然而,将现有的、用于single network的embedding方法扩展到耦合异质网络并不简单。主要挑战来自于两个不同网络的异质特性heterogeneous characteristics,这将导致两个异质潜在空间heterogeneous latent space。因此,不同网络的潜在特征无法直接匹配。为了应对这一挑战,论文《Embedding of Embedding (EOE) : Joint Embedding for Coupled Heterogeneous Networks》提出了一种叫做embedding of embedding: EOE的方法,该方法通过引入一个调和harmonious的embedding矩阵,从而进一步将embedding从一个潜在空间嵌入到另一个潜在空间。在EOE中,潜在特征不仅编码网内边intra-network edge,还编码跨网边inter-network edge。具体而言,论文提出的EOE可以通过乘以适当设计的调和embedding矩阵,将潜在特征从一个空间转换到另一个空间。有了这个调和embedding矩阵,不同网络的潜在特征之间的计算就没有障碍了。作为一种embedding方法,论文提出的EOE还使得那些被edge链接的顶点能够在潜在空间中紧密靠近。EOE与现有single network的embedding方法的主要区别在于:两个网络对应着三种类型的边、以及两种类型的潜在空间。此外,必须同时学习两个网络的潜在特征,因为任何一方都可以通过跨网边inter-network edge向另一方提供补充信息。很容易得出
EOE的学习目标learning objective中需要优化的变量有三类:两个网络对应的两类潜在特征、以及调和embedding矩阵。因此,论文提出了一种交替优化算法alternating optimization algorithm,其中学习目标单次仅针对一种类型的变量进行优化,直到算法收敛。这种交替优化算法可以用一系列更容易的优化来代替对三个变量的、困难的联合优化。EOE模型和优化算法将在正文部分详细介绍。本文主要贡献如下:
- 据作者所知,该论文是第一个研究耦合网络联合
embedding问题的人。论文提出了一个联合embedding模型EOE,该模型结合了一个调和embedding矩阵,从而进一步嵌入仅编码网内边intra-network edge的embedding。 - 论文提出了一种交替优化算法来解决
EOE的学习目标,其中学习目标单次仅针对一种类型的变量进行优化,直到算法收敛。 - 论文对各种现实世界的耦合异质网络进行了全面的实验评估,从而展示联合学习在耦合网络上的优势。所提出的
EOE在包括可视化visualization、链接预测prediction、多类别分类multi-class classification、多标签分类multi-label classification在内的四个application中优于baseline。 - 这项工作表明将耦合异质网络作为来自不同信息源的、融合信息的有效
representation,其中每个信息源都表示为单独的同质网络,并且inter-network link捕获了异质网络顶点之间的关系。
相关工作:我们提出的
EOE模型与常规的graph embedding或network embedding方法密切相关,这些方法用于学习graph或者network顶点的潜在representation。人们之前已经提出了一些
graph embedding方法或network embedding方法,但是它们最初是为已有特征的降维而设计的。具体而言,他们的目标是学习已有特征的低维潜在representation,从而显著降低特征维度带来的学习复杂度learning complexity。在我们的场景中,不存在网络顶点的特征,而是网络的edge信息。另一种称作
graph factorization(《Distributed large-scale natural graph factorization》)的graph embedding方法通常利用网络edge来学习潜在特征。它将graph表示为矩阵,其中矩阵元素对应于顶点之间的边,然后通过矩阵分解来学习潜在特征。但是graph factorization方法仅在潜在空间中表示具有交互interaction的顶点pair对。我们提出的EOE模型不仅将存在edge的顶点紧密靠近,而且还将不存在edge的顶点彼此远离。后一种规则很重要,因为它将保留某些顶点不太可能交互的信息,这也是网络结构信息的一部分。最近一种叫做
DeepWalk的network embedding模型嵌入了从随机游走获得的局部链接信息local link information。它的动机是网络的degree分布和自然语言词频word frequency分布之间的联系。基于这一观察,自然语言模型被重用于对网络社区结构进行建模。然而,随机游走可能会跨越多个社区,这对于保持网络结构的目标而言是不希望看到的。此外,DeepWalk仅能处理无权网络unweighted network,而我们提出的EOE模型同时适用于加权网络weighted network和无权网络。state-of-the-art的、相关的模型是用于大规模信息网络embedding的LINE。LINE保留了交互信息和非交互信息,这与我们提出的EOE类似。但是我们提出的EOE模型在代价函数的公式上与LINE不同。此外,我们提出的EOE是为嵌入耦合异质网络而设计的。包括LINE在内的现有方法都无法处理耦合异质网络。而耦合异质网络在现实世界中很常见,并且EOE有利于耦合异质网络中每个子网的embedding。
10.1 模型
10.1.1 基本概念
耦合异质网络
coupled heterogeneous network的定义:耦合异质网络由两个不同的、但是相关的子网络sub-network组成,这些子网络通过inter-network edge相连。术语 “不同” 指的是两个子网络的顶点属于不同的类型。术语 “相关” 意味着两个子网络的顶点具有特定类型的交互或关系。给定两个子网络 、 ,耦合异质网络表示为 ,其中:
- 为第一个子网络的顶点集合, 为第二个子网络的顶点集合。
- 为第一个子网络的边集合, 为第二个子网络的边集合, 为连接 和 的
inter-network edge集合。 分别代表这些边的权重。所有这些边都可以是加权的/无权的、有向的/无向的。
为了学习 和 的潜在特征,
EOE利用网络edge从而作为embedding方法。具体而言,具有edge的顶点pair对在潜在空间中紧密靠近。如果一对顶点之间存在边的概率相当高(理想情况下为
100%),则它们在潜在空间中是紧密靠近的。这个概率由以下公式来定义:其中 分别是子网络 中顶点 和顶点 的
embedding向量。上述方程是 在潜在空间中度量的,对于 其概率公式也是类似的。但是,上述方程无法计算来自 的顶点和来自 的顶点之间存在边的概率,因为这个概率涉及到两个不同的潜在空间。为了调和两个潜在空间的异质性,我们引入了一个调和
embedding矩阵,从而进一步将embedding从一个潜在空间嵌入到另一个潜在空间。调和
embedding矩阵harmonious embedding matrix是一个实值矩阵 ,其中 为 的潜在特征维度、 为 的潜在特征维度。使用调和embedding矩阵之后,衡量来自不同网络的顶点之间紧密程度的概率如下所示:其中 是子网络 中顶点 的
embedding向量, 是子网络 中顶点 的embedding向量。
10.1.2 EOE
基于前述的定义,我们现在提出
EOE模型。EOE模型不仅将存在edge的顶点紧密靠近,还将不存在edge的顶点彼此远离。后一种规则很重要,因为它将保留某些顶点不太可能交互的信息,这也是网络结构信息的一部分。要将这两个规则都转换为优化问题,则应该惩罚存在
edge的顶点pair对的小概率、以及不存在edge的顶点pair对的大概率。惩罚前者的损失函数如下所示:其中:
表示顶点 和 之间存在边的权重。
为 中所有顶点的
embedding向量构成的embedding矩阵, 为 中所有顶点数量, 为embedding向量的维度。为待定义的惩罚函数。乘以 是反映权重所表示的关系强度。如果网络是无权的,则 是一个常数,例如
1。
作为一个合适的惩罚函数, 必须是单调递减的,并且当概率接近
1.0时递减到0.0。单调递减保证对较大概率的链接给予较小的惩罚。这个属性是必要的,因为我们只希望惩罚存在链接但是预估概率却很小的case。此外,为了便于优化, 应该是凸函数并且是连续可微的。该属性使得上述损失函数可以通过常用的梯度下降算法求解,并确保全局最优解。具有这两个属性的简单函数是负的对数似然,因此上式改写为:类似地,对于不存在
edge的顶点pair对的惩罚函数 也是以这种方式定义的,只是必要的属性被调整为单调递增,并且在概率接近零时惩罚函数接近零。因此,惩罚预估概率很大但是却不存在链接的损失函数定义为:其中 是不存在
edge的一对顶点, 是存在edge的一对顶点。在本文的剩余部分,我们以这种方式来表示存在edge的顶点pair对、以及不存在edge的顶点pair对。在处理大规模网络时,在所有不存在
edge的顶点pair对上计算该损失函数是不切实际的。从计算规模上考虑,我们对不存在edge的顶点pair对进行采样,使得其规模仅比存在edge的顶点pair对的数量大几倍。的损失函数和来自不同子网络的顶点
pair对都以这种方式进行衡量。所有这些损失函数都应该联合优化,因为每个子网络都可以通过inter-network edge向另一个子网络提供补充信息。组合所有这些损失函数的一种直接方法是将它们直接相加。我们将更复杂的组合方式留待未来的工作。在添加
L2正则化项和L1正则化项从而避免过拟合之后,嵌入了耦合异质网络 的整体损失函数为:其中:
- , , 。
- 为正则化系数。
调和
embedding矩阵的L1正则化用于执行特征选择来协调两个潜在空间,因为这会引入稀疏性。
10.1.3 优化算法
最小化损失函数 是一个凸优化问题,因此我们可以使用基于梯度的算法来执行优化。 的梯度为 , 的梯度为 。但是,损失函数 对于 的零元素是不可微的,因此我们对 采用
sub-gradient梯度,这可以通过以下公式获得:其中 为 为第 行第 列, 定义为:
对于 不可微的,但是考虑到 在实际中很少会刚好为
0,因此如果 在梯度下降过程中穿越零点,则我们将其设置为零。这称作lazy update,因此将鼓励 成为稀疏矩阵。有了这些梯度,我们提出了一种基于梯度的交替优化算法
gradient-based alternating optimization algorithm。在该优化算法中,损失函数每次针对一种类型的变量最小化,直到收敛。这种交替优化算法可以用一系列更容易的优化来代替对三个变量的、困难的联合优化。关于变量的交替时机,直到特定于当前变量的最小化收敛时才执行。这是因为每种类型的变量都会影响其它两种类型的变量,如果当前变量没有很好地优化,则它可能会传播负面影响
negative influence。一个直观的例子是,如果存在边的两个相似单词在交替author之前在潜在空间中不接近,则由于co-author而应该接近的两个author可能会彼此远离,远离的原因仅仅是因为这两个author分别与前述单词存在边。EOE交替优化算法:输入:
- 耦合异质网络 ,
embedding维度 - 正则化系数
- 耦合异质网络 ,
输出: 的
embedding,调和embedding矩阵算法步骤:
全零初始化 的
embedding参数,以及矩阵预训练顶点集合 ,循环迭代直到算法收敛。迭代步骤为:
- 对 里的所有顶点计算梯度 ,其中 为仅仅考虑子图 的损失函数
- 线性搜索找到学习率
- 更新参数: ,其中 为迭代次数
预训练顶点 ,循环迭代直到算法收敛。迭代步骤为:
- 对 里的所有顶点计算梯度 ,其中 为仅仅考虑子图 的损失函数
- 线性搜索找到学习率
- 更新参数: ,其中 为迭代次数
循环直到收敛,迭代步骤为:
- 固定 和 的
embedding参数,利用梯度下降算法优化 - 固定 的
embedding参数和 ,利用梯度下降算法优化 的embedding参数 - 固定 的
embedding参数和 , 利用梯度下降算法优化 的embedding参数
- 固定 和 的
最终返回顶点 的
embedding向量以及调和embedding矩阵
在
EOE交替优化算法中,我们分别对 和 进行预训练从而学习 和 的潜在特征,这也是为了不将负面影响传播到其它变量。损失函数 之前未给出,它是仅包含 的损失。我们使用回溯线性搜索
backtracking line search来为每次迭代学习一个合适的学习率。判断是否整体收敛的条件:当前迭代和上一轮迭代之间的相对损失小于一个相当小的值,如0.001。EOE交替优化算法的复杂度和顶点embedding梯度、调和embedding梯度的复杂度成正比。这些梯度的复杂度处于同一个水平,即 ,其中 是存在边的顶点pair对的数量, 是 的顶点embedding维度, 是 的顶点embedding维度。因此,上述算法的复杂度为 ,其中 为迭代次数。因此,我们提出的EOE交替优化算法可以在多项式时间内求解。未来工作:将
EOE模型扩展到两个以上的网络,从而融合多个信息源。
10.2 实验
我们在可视化、链接预测、多分类、多标签分类等常见的数据挖掘任务上,评估
EOE模型学到的潜在特征的有效性。baseline方法:谱聚类
spectral clustering: SC:该方法使用谱聚类来学习顶点的潜在特征。具体而言,它使用归一化的拉普拉斯矩阵的top d个特征向量作为embedding向量。DeepWalk:通过截断的随机游走和SGNS来学习顶点的embedding向量。由于
DeepWalk仅适用于未加权的边,因此所有边的权重设置为1。LINE:它是为了嵌入大规模信息网络而提出的,适用于有向/无向图、加权/无权图。我们提出的EOE也适用于大规模网络,因为它可以在多项式时间内求解。此外,EOE也适用于所有类型的网络(有向/无向、加权/无权)。LINE分别定义损失函数来保留一阶邻近性和二阶邻近性来求解一阶邻近representation和二阶邻近representation,然后将二者拼接一起作为representation。LINE有两个变体:LINE-1st仅保留一阶邻近性,LINE-2nd仅保留二阶邻近性。而我们提出的EOE模型仅保留一阶邻近性。由于如何合理的结合
LINE-1st和LINE-2nd尚不清楚,因此我们不与LINE(1st+2nd)进行比较。
注:这些方法都是同质图的
embedding方法,仅能捕获单个图的信息。而EOE可以同时捕获多个图的信息,因此这种比较不太公平(EOE有额外的输入信息,因此理论上效果更好)。EOE的实验配置:- 设置
embedding size为128(DeepWalk和LINE的embedding size也是128)。 - 无边的顶点
pair数量相对有边的顶点pair的比例为5。 backtracking line search采用常用设置。- 正则化项的所有系数为
1。 - 采用
0.001作为相对损失的阈值,从而判断梯度下降算法是否收敛。
- 设置
10.2.1 可视化
embedding在二维空间上的可视化是network embedding的一个重要应用。如果学到的embedding很好地保留了网络结构,则可视化提供了一种生成网络布局network layout的简单方法。我们用author and word network来说明这一点。数据集:我们从
DBLP数据集中采样了一个较大的网络。具体而言,我们选择了来自四个研究领域的热门会议,即:数据库领域的SIGMOD,VLDB,ICDE,EDBT,PODS,数据挖掘领域的KDD,ICDM,SDM,PAKDD, 机器学习领域的ICML,NIPS,AAAI,IJCAI,ECML,信息检索领域的SIGIR,WSDM,WWW,CIKM,ECIR。我们选择了
2000到2009年发表的论文,过滤掉论文数量少于3篇的author,并过滤掉停用词(如where,how)。过滤后的author network包含4941位author、17372条链接(即co-authorship)。过滤后的word network有6615个单词、78217条链接(即co-concurrence)。过滤后的author到word的链接有92899条。所有
baseline都分别独立学习author embedding和word embedding。EOE通过联合推断来学习这些embedding。所有方法生成的embedding维度为128。我们使用t-SNE工具将它们映射到二维空间中,如下图所示。其中:绿色为数据库领域、浅蓝色为信息检索领域、深蓝色为数据挖掘领域、红色为机器学习领域。下图的第二排第一图应该为
SpectralClustering Word Network,这个是作者原图的标示错误。author子网络和word子网络应该显示四个聚类的混合,因为所选的四个研究领域密切相关。谱聚类的结果不符合预期,因为谱聚类的学习目标不是保留网络结构。
尽管
DeepWalk和LINE在某种程度上表现更好,但是它们无法同时展示四个不同的聚类。DeepWalk的问题可能在于:随机游走跨越了多个研究领域,结果导致来自不同领域的数据点被分布在一起。LINE也有类似的问题,因为author可能具有来自不同领域的其它author的链接。
EOE的结果最符合预期,因为EOE可以通过补充的文本信息来克服上述问题。具体而言,即使某些author和很多不同领域的其它author存在链接,author的论文中的单词也能够提供该author研究领域的补充信息。单词网络的情况也类似。

10.2.2 链接预测
链接预测问题是指通过测量顶点之间的相似性来推断网络顶点之间新的交互。我们部署了两种链接预测场景来评估潜在特征:未来链接预测
future link prediction、缺失链接预测missing link prediction。未来链接预测问题是推断未来会发生的交互。在未来链接预测中,我们采用
DBLP的2000到2009年发表的论文作为训练集,然后预测2010年、2010~2011年、2011~2012年、2010~2012年这四个时期的链接。在这四个时期,我们除了直接得到正样本( 存在co-authorship关系的author) 之外,我们还通过计算来间接得到负样本:通过随机生成数量与正样本相同、没有co-authorship关系的author pair对。通过负样本来评估模型检测负样本的能力。我们通过以下概率来预测新的
co-authoreship相似性:其中 为两个顶点的
embedding向量。我们使用
AUC来评估二类分类器的预测能力,结果如下。结果表明:- 所有的神经网络模型都优于谱聚类,这表明神经网络
embedding对于学习顶点潜在特征的有效性。 EOE方法在四个时间都优于其它模型,这表明EOE方法捕捉的信息更全面、准确。
为了从实验的角度研究
EOE性能优异的原因,我们研究这些方法如何针对测试样本进行预测。我们给出两个具有代表性的测试样本。这两个测试样本是发生在CVPR'10和SIGIR'10会议的两个co-authorship关系。- 所有的
baseline方法都低估这两个未来链接发生的概率。 EOE通过author之间共享相似的研究方向的信息(通过common word给出)给出了最佳的预测。LINE(2nd)给出的预测结果被忽略,因为它对所有测试样本(包括不存在co-authorship的author pair对)预测的概率都接近100%。我们不知道原因,并且其背后的原因也不在本文讨论范围之内。但是我们知道LINE(2nd)的学习目标是保留二阶邻近度,而推断新的链接是预测一阶邻近度,二者不匹配。

- 所有的神经网络模型都优于谱聚类,这表明神经网络
缺失链接预测问题是推断未观察到的现有交互。对于缺失链接预测,我们部署了其它三个任务,即论文引用预测、社交网络的
friendship预测、基因交互预测。- 对于论文引用预测,我们采用
Embedding可视化任务相同的数据集,但是这里考虑的是论文引用paper citation关系,而不是co-authorship关系。我们采用2000~2009年的论文,过滤掉该时间段内未发表的参考文献,并且过滤掉词频小于5的单词。最终论文引文子网络包含6904篇论文、19801个引用关系(链接),单词子网络包含8992个单词、118518条链接,论文和单词之间有59471条链接。 - 对于基因交互预测,我们从
SLAP数据集构建gene and chemical compound network,该数据集包含基因以及化合物之间的关系。基因子网络包含基因和基因之间的相互作用,化合物子网络包含化合物之间是否具有相同的本体,两个子网络之间包含基因和化合物之间的作用。最终化合物子网络有883个顶点、70746个链接,基因子网络有2472个基因、4396条链接,基因和化合物之间存在1134条链接。 - 对于社交网络
friendship预测,我们从BlogCatalog构建user and word network。我们选择四种热门类型(艺术、计算机、音乐、摄影)的用户,这包含5009个用户,用户之间存在28406条链接。我们基于这些用户的博客来构建单词子网络,词频小于8的单词被过滤掉。我们采用窗口大小为5的滑动窗口来生成单词共现关系。最终得到的单词子网络包含9247个单词、915655条链接。用户和单词之间存在350434条链接。
我们开展了
10次实验,分别对训练集中的链接保留比例从0%~90%。其中,0%的保留比例即丢弃所有链接,这将导致冷启动问题。- 目前任何
baseline模型都无法解决冷启动问题,因为所有baseline模型都依赖于已有的链接来学习潜在特征,而EOE可以通过补充信息来解决冷启动问题。 - 在所有比例的情况下,
EOE仍然优于基准方法,这说明了EOE针对耦合异质网络联合学习embedding的优势。
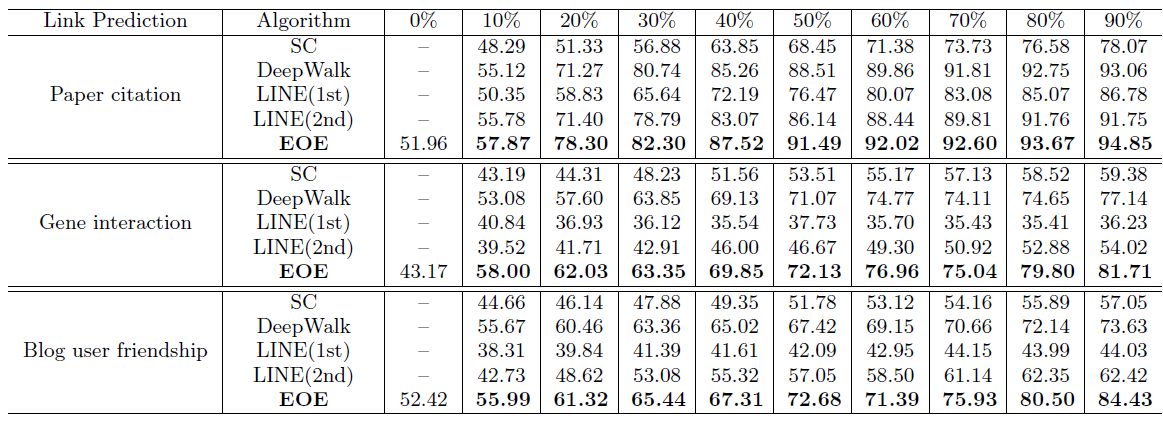
- 对于论文引用预测,我们采用
10.2.3 多分类
多分类任务需要预测每个样本的类别,其中类别取值有多个,每个样本仅属于其中的某一个类别。这里使用论文引用预测任务(
Paper citation)中使用的paper and word network。具体而言,分类任务是预测每篇论文的研究领域,可以是数据库、数据挖掘、及其学习、信息检索四个领域之一。我们开展了
10次实验,分别对训练集中的链接保留比例从10%~100%。一旦学到潜在特征,我们使用具有线性核的SVM来执行分类任务。我们采用10-fold交叉验证的平均准确率作为评估指标,结果如下:EOE在所有比例的情况下,始终优于其它baseline模型。- 当链接比例越少(如
10%~20%),EOE相比于baseline模型的提升越明显。这是因为论文的摘要中包含了大量的关于论文研究领域的信息,EOE可以很好的利用这些信息。

10.2.4 多标签分类
多类分类任务需要预测每个样本的类别,其中每个样本可以属于多个类别。
我们使用可视化中的
author and word network来预测author的领域,一些author可能是多个领域的专家,因为他们在多个领域的会议上发表论文。此外,链接预测任务中使用的BlogCatalog user and word network也用于该实验,因为用户注册的博客可以属于多个类别。我们开展了
5次实验,分别对训练集中的链接保留比例从20%~100%。一旦学到潜在特征,我们对学到的author representation执行二元SVM从而进行多领域预测任务。我们采用10-fold交叉验证的Micro-F1和Macro-F1作为评估指标,结果如下:EOE在所有任务中都超越了baseline模型。- 当链接比例越少(如
20%),EOE相比于baseline模型的提升越明显。

结合可视化任务、链接预测任务、多分类任务、多标签分类人任务的实验结果,这表明
inter-networks edge提供的互补信息是有益的,因为这些互补信息可以使得从intra-network edge学到的潜在特征更加全面和准确,并且在遇到冷启动问题时更为重要。从可视化任务、链接预测任务、多类分类任务、多标签分类任务可以看到:多个子网络之间的链接提供的额外补充信息是有益的,因为它可以使得学到的潜在特征更加准确、全面,这在解决冷启动问题时尤为重要。
10.2.5 参数探索
EOE模型有两种主要的超参数:正则项的系数、潜在特征维度。在所有之前的实验中,这两个超参数都固定为常数,正则化系数设置为1.0,潜在特征维度为128。这里我们将正则化系数分别设置为0.1,0.5,1.0,2.0,5.0,10.0、将潜在特征维度分别设置为32,64,128,256,512,然后观察这些超参数的影响。注意:研究潜在特征维度时,正则化系数固定为
1.0;研究正则化系数时,潜在特征维度固定为128。我们的训练数据集为DBLP co-authorship数据集。潜在特征维度:可以看到
EOE对于潜在特征维度不是特别敏感,只要该值不是太小。最佳性能出现在潜在特征维度为128时。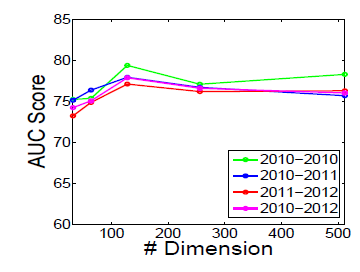
正则化系数:可以看到
EOE对于正则化系数更为敏感,当正则化系数为1.0时模型效果最好。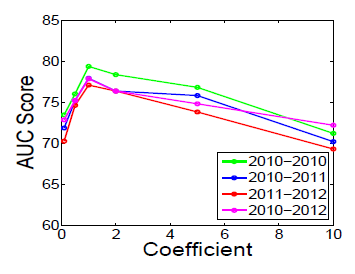
十一、metapath2vec[2017]
基于神经网络的模型可以表达潜在
embedding,这些embedding可以捕获跨各种模式(如图像、音频、语言)的丰富、复杂数据的内部关系。社交网络social network和信息网络information network同样是丰富、复杂的数据,它们对人类交互human interaction的动态性dynamic和类型type进行编码,并且同样适用于使用神经网络的representation learning。具体而言,通过将人们选择好友和保持联系的方式映射为social language,我们可以将NLP的最新进展自然地应用于network representation learning,尤其是著名的NLP模型word2vec。最近的一些研究提出了word2vec-based network representation learning框架,例如DeepWalk、LINE、node2vec。这些representation learning方法不是手工设计的网络特征,而是能够从raw network中自动发现有用的、且有意义的latent特征。然而,到目前为止,这些工作都集中在同质网络
homogeneous network(只有单一类型的节点、单一类型的关系)的representation learning上。但是,大量的社交网络和信息网络本质上是异质heterogeneous的,涉及多种类型的节点、以及多种类型的关系。这些异质网络heterogeneous network提出了独特的挑战,而这些挑战是专门为同质网络设计的representation learning模型所无法处理的。以异质学术网络heterogeneous academic network为例:我们如何在作者author、论文paper、会议venue、组织organization等多种类型的节点之间有效地保留word-context概念?随机游走(如DeepWalk和node2vec中所使用的的)能否可以应用于多种类型节点的网络?我们可以直接将面向同质网络的embedding架构(如skip-gram)应用于异质网络吗?通过解决这些挑战,
latent heterogeneous network embedding可以进一步应用于各种网络挖掘任务,如节点分类、节点聚类、相似节点搜索。与传统的meta-path-based方法相比,潜在空间representation learning的优势在于它能够在没有connected meta-path的情况下对节点之间的相似性进行建模。例如,如果两个author从未在同一个venue上发表过论文(假设一个人在NIPS上发表了10篇论文,另一个人在ICML上发表了10篇论文),则他们基于APCPA的Path-Sim相似度将为零。 但是,通过network representation learning可以自然地克服相似度为零这一缺点。论文
《metapath2vec: Scalable Representation Learning for Heterogeneous Networks》形式化了异质网络representation learning问题,其目标是同时学习多种类型节点的低维潜在的embedding。论文介绍了metapath2vec框架及其扩展metapath2vec++框架。metapath2vec的目标是最大化同时保留给定异质网络的结构structure和语义semantic的可能性。在metapath2vec中,论文首先提出了异质网络中meta-path based随机游走,从而针对各种类型的节点生成具有网络语义network semantic的异质邻域heterogeneous neighborhood。其次,论文扩展了skip-gram模型从而促进空间临近geographically close节点和语义临近semantically close节点的建模。最后,论文开发了一种基于异质负采样heterogeneous negative sampling的方法,称作metapath2vec++,可以准确有效地预测节点的异质邻域。论文提出的
metapath2vec和metapath2vec++模型不同于传统的network embedding模型,后者专注于同质网络。具体而言,传统模型对不同类型的节点和不同类型的关系进行相同的处理,导致异质节点无法产生可区分的representation,正如论文在实验中所证明的那样。此外,metapath2vec和metapath2vec++模型在几个方面也与Predictive Text Embedding: PTE模型不同。- 首先,
PTE是一种半监督学习模型,它结合了文本数据的label信息。 - 其次,
PTE中的异质性来自于text network,其中包含word-word链接、word-document链接、word-label链接。本质上,PTE的原始输入是单词,输出是每个单词的embedding,因此PTE并不是多种类型的对象。
论文在下表中总结了这些方法的差异,其中列出了算法的输入,以及
《Pathsim: Meta path-based top-k similarity search in heterogeneous information networks》中使用的相同两个query在DBIS网络的top 5相似搜索结果(每一列是一个query的结果)。通过对异质邻域建模并进一步利用异质负采样技术,metapath2vec++能够为两种类型的query实现最佳的top 5相似结果。
下图展示了
16个CS会议和每个领域的相应知名学者学到的embedding(128维)的2D投影(基于PCA)可视化。值得注意的是,论文发现metapath2vec++能够自动组织这两种类型的节点并隐式学习它们之间的内部关系,这由链接每个pair的箭头的相似方向和距离所展示。例如,metapath2vec++学习J. Dean -> OSDI以及C. D. Manning -> ACL。metapath2vec也能够将每个author-conference pair紧密分组,例如R. E. Tarjan和FOCS。所有这些属性都无法从传统的network embedding模型中发现。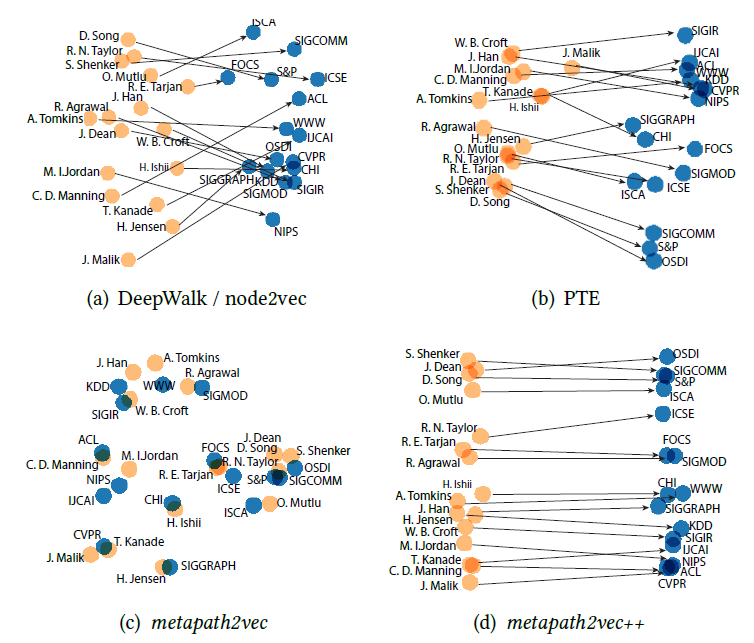
总而言之,论文工作的贡献如下:
- 形式化异质网络
representation learning的问题,并确定由网络异质性带来的独特挑战。 - 开发有效
effective的、高效efficient的network embedding框架metapath2vec & metapath2vec++,用于同时保留异质网络的结构相关性structural correlation和语义相关性semantic correlation。 - 通过广泛的实验,证明了论文提出的方法在各种异质网络挖掘任务中的有效性和可扩展性,例如节点分类(相对于
baseline提升35% ~ 219%)和节点聚类(相对于baseline提升13% ~ 16%)。 - 演示了
metapath2vec & metapath2vec++自动发现异质网络中不同节点之间的内部语义关系,而这种关系现有工作无法发现。
- 首先,
相关工作:
network representation learning可以追溯到使用潜在因子模型进行网络分析和图挖掘任务,例如factorization model在推荐系统、节点分类node classification、关系挖掘relational mining、角色发现role discovery中的应用。这一丰富的研究领域侧重于分解网络的matrix/tensor格式(例如,邻接矩阵),从而为网络中的节点或边生成潜在特征。然而,分解大型matrix/tensor的计算成本通常非常昂贵,并且还存在性能缺陷,这使得它对于解决大型网络中的任务既不实用、也不有效。随着深度学习技术的出现,人们致力于设计基于神经网络的
representation learning模型。例如Mikolov等人提出了word2vec框架(一个两层神经网络)来学习自然语言中word的分布式representation。DeepWalk在word2vec的基础之上提出,节点的context可以通过它们在随机游走路径中的共现co-occurrence来表示。形式上,DeepWalk将随机游走walker放在网络上从而记录walker的游走路径,其中每条随机游走路径都由一系列节点组成。这些随机游走路径可以被视为文本语料库中的sentence。最近,为了使节点的邻域多样化,Node2Vec提出了有偏随机游走walker(一种广度优先breadth-first和宽度优先width-first混合的搜索过程),从而在网络上产生节点路径。随着节点路径的生成,这两项工作都利用word2vec中的skip-gram架构来对路径中节点之间的结构相关性进行建模。此外,人们已经提出了几种其它方法来学习网络中的
representation。特别地,为了学习network embedding,LINE将节点的context分解为一阶邻近性(friend关系)、二阶邻近性(friend’ friend关系),这进一步发展为用于嵌入文本数据的半监督模型PTE。我们的工作通过设计
metapath2vec和metapath2vec++模型来进一步研究这个方向,从而捕获具有多种类型节点的大型异质网络所表现出的结构相关性和语义相关性。这是以前的模型所无法处理的,并且我们将这些模型应用于各种网络挖掘任务。
11.1 模型
11.1.1 问题定义
异质网络
Heterogeneous Network定义:异质网络是一个图 ,其中每个节点 和每条边 分别关联一个映射函数:其中 表示节点类型, 表示边的类型,且满足 。
例如可以用作者
author:A、论文paper:P、会议venue:V、组织organization:O作为节点类型来表示下图中的学术网络academic network。其中边可以表示coauthor合作者关系A-A、publish发表关系A-P,P-V、affiliation附属关系O-A,reference引用关系P-P。黄色虚线表示coauthor关系,红色虚线表示引用关系。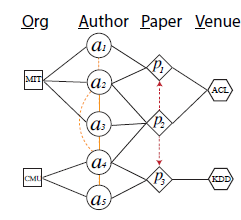
异质网络
representation learning问题:给定一个异质网络 ,任务的目标是学习一个 维的latent representation,其中 ,使得该representation能够捕获网络的结构关系以及语义关系。任务的输出是一个低维矩阵 ,其第 行对应一个 维向量 ,即顶点 的embedding。注意,尽管 中存在不同类型的节点,但是各种类型节点的
embedding都被映射到相同的潜在空间中。学到的节点embedding可以应用于各种异质网络挖掘任务,如节点分类、节点聚类、相似节点搜索等。问题的挑战来自于网络异质性,其中很难直接应用同质的
language embedding方法和同质的network embedding方法。network embedding模型的基本假设是:在embedding空间保持节点及其邻域(上下文context)之间的邻近性。但是在异质网络中,如何定义和建模node–neighborhood的概念?另外,我们如何优化embedding模型,其中该模型有效维护多种类型节点和关系的结构和语义?
11.1.2 metapath2vec
我们提出了一个通用框架
metapath2vec,从而在异质网络中学习所需要的的node representation。metapath2vec的目标是在考虑多种类型的节点和边的情况下最大化网络概率network probability。同质的
network embedding:首先考虑word2vec模型及其在同质network embedding任务中的应用。给定一个文本语料库,Mikolov等人提出word2vec来学习语料库中单词的分布式representation。受此启发,DeepWalk和node2vec旨在将文本语料库中的word-context概念映射到network中。这两种方法都利用随机游走来实现这一点,并利用skip-gram模型来学习node representation,这有助于在同质网络中预测节点的结构上下文structural context(即局部邻域local neighborhood)。通常,给定网络 ,模型的目标是根据局部结构local structure来最大化网络概率:其中:
- 为网络 中节点 的邻域,它可以由不同的定义方式,如 的直接相连的顶点集合。
- 定义了给定节点 的条件下,上下文 出现的条件概率。
为了对顶点的异质邻域建模,
metapath2vec引入了异质skip-gram模型Heterogeneous Skip-Gram。为了将异质网络结构融合到异质skip-gram模型中,metapath2vec引入了基于meta-path的随机游走。异质
skip-gram模型:在metapath2vec中,给定异质网络 ,其中 表示节点类型, 表示边的类型,。我们通过最大化给定节点 的条件下,异质上下文 的条件概率,使得skip-gram能够学习异质网络 的有效node representation:通常由一个
softmax函数定义:其中: 为 的第 行,是节点 的
embedding向量; 为异质上下文 的embedding向量。注意:
- 这里
node embedding和context embedding都是在同一个embedding空间中,它们共享embedding矩阵 。 - 由于 与顶点类型 无关,仅仅和节点
pair有关,如果我们将 合并为 ,则上式就是DeepWalk的目标函数。因此metapath2vec的目标函数和metapath2vec的目标函数是相同的,而且区别在于随机游走的方式不同。
表示节点 的第 种类型的邻域节点。考虑下图的学术网络,其中
author节点 的邻域可以为:author邻域 ,venue邻域 ,organization邻域 ,paper邻域 。
为了有效优化目标函数,
Milkolov等人引入了负采样,它从网络种随机采样相对较小的一组节点来代替softmax。metapath2vec也采用了相同的负采样技术。给定一个负采样大小 ,则定义:其中:
- 为
sigmoid函数。 - 为预定义的节点分布函数,根据该分布来采样 个负采样节点 。
metapath2vec无视节点类型来构建节点的频率分布frequency distribution。
- 这里
基于
meta-path的随机游走:如何有效的将网络结构转化为skip-gram?在DeepWalk和node2vec中,这是通过将random walker在网络上结合一个邻域函数来遍历的节点路径来实现的。我们也可以将
random walker放到异质网络中,从而生成多种类型节点的路径。在随机游走的第 步,我们定义转移概率 为:在节点 的邻域上的归一化概率分布,其中忽略节点类型。然后将生成的游走序列作为node2vec和DeepWalk的输入。但是,《Pathsim: Meta path-based top-k similarity search in heterogeneous information networks》证明了:异质随机游走偏向于高度可见的节点类型(即那些在路径中频繁出现的节点类型),以及中心节点(即那些出现频繁出现在关键路径中的节点)。有鉴于此,我们设计了基于meta-path的随机游走,从而生成能够捕获不同类型节点之间语义相关性和结构相关性的随机游走序列,从而有助于我们将异质网络结构转化为异质skip-gram。形式化地,一个
meta-path范式 定义为一个路径:其中:
- 为类型为 的节点集合, 定义了类型为 的节点和类型为 的节点之间的关系。
- 定义节点类型 之间关系的一个组合。
以下图为例:
meta-path: APA代表两个author(类型为A) 在同一论文(类型为P) 上的co-author关系,meta-path: APVPA代表两个author(类型为A)在同一个会议(类型为V)的不同论文(类型为P)上的co-venue关系。
先前的工作表明:异质信息网络中的许多数据挖掘任务都可以通过
meta-path建模受益。这里我们展示如何利用meta-path来指导异质random walker。给定一个异质网络 以及一个meta-path范式 ,在随机游走的第 步的转移概率定义为:其中: 表示第 步的节点; 表示顶点 的、类型为 的邻域节点。
即,下一个节点仅在类型为 的邻域节点中选择。
由于 ,这意味着
random walker必须根据预定义的meta-path来游走。此外,通常meta-path都是对称的,如 ,因此有:基于
meta-path的随机游走策略可以确保不同类型节点之间的语义关系可以正确的合并到skip-gram中。如下图所示,假设上一个节点为CMU,当前节点为 。在传统的随机游走过程中,下一个节点可能是 周围的节点 。但是在meta-path的范式OAPVPAO下,下一个节点倾向于论文类型的节点 (类型为P),从而保持路径的语义。总体而言,
metapath2vec和node2vec都是在DeepWalk基础上针对随机游走策略的改进。
11.1.3 metapath2vec ++
metapath2vec在创建点 的邻域 时,根据上下文节点的类型来区分节点 的上下文节点,但是它忽略了softmax函数中的节点类型信息。即:在给定节点 的条件下,为了推断来自邻域 中给定类型的上下文 ,metapath2vec实际上采用了所有类型的负样本,包括相同类型 的负样本,以及其它类型的负样本。异质负采样
heterogeneous negative sampling:我们进一步提出metapath2vec++框架,其中softmax根据上下文 的类型进行归一化。具体而言, 根据指定的节点类型 来调整:其中 为类型为 的节点集合。
这样做时,
metapath2vec++为skip-gram模型输出层中的每种邻域类型定义一组softmax分布。回想一下,在metapath2vec、node2vec、DeepWalk中,输出softmax分布的维度等于网络的节点数量 。但是在metapath2vec ++中,输出softmax分布的维度由类型为 的节点数量 决定。如下图所示给定节点 ,metapath2vec ++输出四组softmax分布,每一组分布对应于不同的邻域节点类型:会议V、作者A、组织O、论文P。 给出了类型为 的节点集合, 。 给出了节点邻域中类型为 的邻居节点数量(也是窗口大小), 。注意,这里对每种类型顶点指定各自不同的窗口大小。
受到
PTE的启发,metapath2vec在负采样过程中同样可以根据邻居节点 的类型进行调整,因此有目标函数:其中 为类型为 的顶点的分布函数。
上式的物理意义为:负采样仅在上下文 类型相同的节点集合 中进行,而不是在全部节点集合 中进行。
目标函数的梯度为:
其中 为一个示性函数,用于指示 是否为邻域上下文节点 ,并且当 时 。
最终可以通过随机梯度下降算法来对模型进行优化求解。
metapath2vec++算法:输入:
- 异构网络
- 一个
meta-path范式 - 每个顶点开始的游走序列的数量
- 每条游走序列的长度
embedding维度- 邻域大小 (即窗口大小)
输出:顶点的
embedding矩阵算法步骤:
初始化
迭代 ,迭代步骤为:
遍历图 中的每个顶点 ,执行:
返回
MetaPathRandomWalk算法:输入:
- 异构网络
- 一个
meta-path范式 - 当前顶点
- 每条游走序列的长度
输出:一条
meta-path随机游走序列算法步骤:
初始化:
迭代 ,迭代过程为:
根据 采样顶点 ,并记录
返回
HeterogeneousSkipGram算法:输入:
- 当前的
- 邻域大小
- 随机游走序列 ,以及它的长度
输出:更新后的
算法步骤:
迭代 ,迭代步骤为:
取出当前顶点 , 对左侧的 个顶点、右侧的 个顶点共计 个顶点进行更新:
其中 为学习率。
下图给出了异质学术网络
heterogeneous academic network,以及学习该网络embedding的metapath2vec/metapath2vec ++的skip-gram架构。- 图
a的黄色虚线表示co-author关系,红色虚线表示论文引用关系。 - 图
b表示metapath2vec在预测 的上下文时,使用的skip-gram架构。其中 为节点数量, 的邻居顶点包括 ,窗口大小 。 - 图
c表示metapath2vec ++在预测 的上下文时,使用的skip-gram架构。metapath2vec++中使用异质skip-gram。在输出层中,它不是为邻域中所有类型的节点指定一组多项式分布,而是为邻域中每种类型的节点指定各自的一组多项式分布。 给出了类型为 的节点集合, 。 给出了节点邻域中类型为 的邻居节点数量(也是窗口大小), 。
注:我们可以指定多个
metapath,针对每个metapath学到对应的embedding,最后将所有embedding聚合起来从而进行metapath ensemble。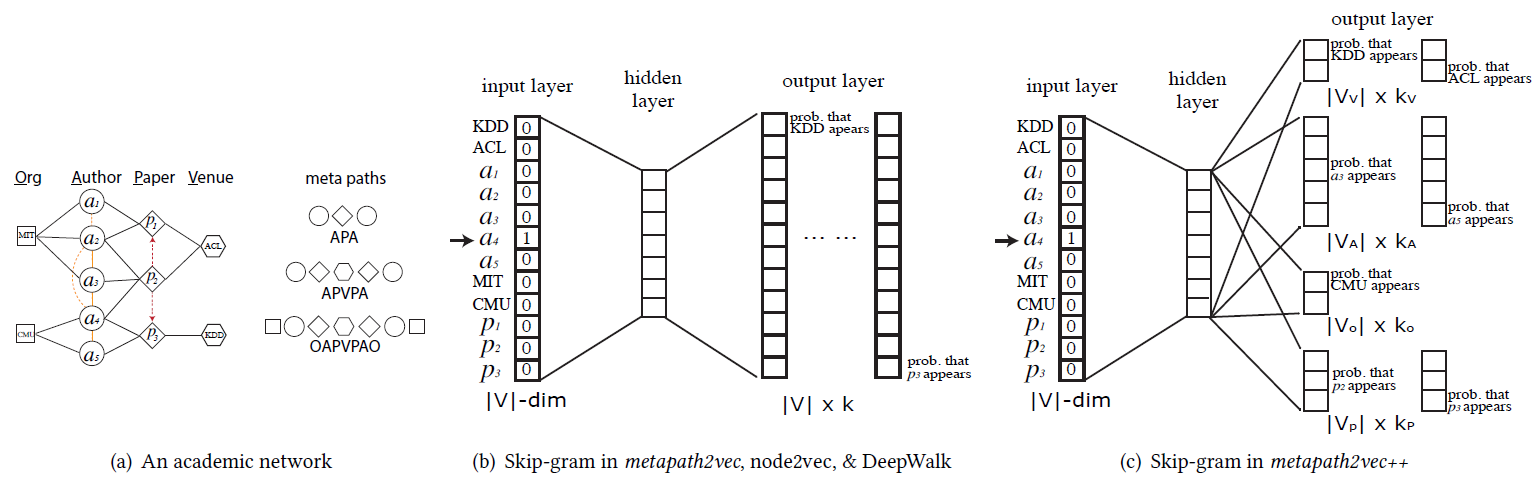
- 图
未来方向:
metapath2vec/metapath2vec++模型和DeepWalk/node2vec一样,在对网络采样生成大量随机游走路径时,面临大量中间临时输出数据的挑战。因此识别和优化采样空间是一个重要方向。- 和所有基于
meta-path异质网络挖掘方法一样,可以通过自动学习有意义的meta-path来进一步改善metapath2vec/metapath2vec++。 - 扩展模型从而融合演变中的异质网络的动态性
dynamic。 - 将模型泛化到不同风格
genre的异质网络。
11.2 实验
这里我们展示了
metapath2vec/metapath2vec ++用于异质网络representation learning的效果和效率。我们评估了经典的三种异质网络挖掘任务,包括:节点分类问题、节点聚类问题、相似节点搜索问题。另外,我们还通过
tensorflow的embedding可视化来观察异质学术网络中学到的节点embedding。数据集:我们使用以下两个异质网络,它们都是公开的:
AMiner Computer Science(CS) dataset:包含2016年之前j举行的3883个计算机科学venue(包含会议conference和期刊journal)的9323739名计算机科学家,以及3194405篇论文。我们构建了一个异质网络,该网络包含三种类型的节点:author:A、paper:P、venue:V。不同类型节点之间的链接代表不同的关系。Database and Information Systems(DBIS) dataset:包含464个会议,以及其中top-5000个作者,以及对应的72902篇论文。我们也构建了一个异质网络,该网络包含三种类型的节点:author:A、paper:P、venue:V。
baseline方法:我们将metapath2vec/metapath2vec ++和以下几种最近的网络representation learning方法进行比较:DeepWalk/node2vec:在相同的随机游走序列输入下,我们发现DeepWalk的hierarchical softmax和 的node2vec的负采样之间并未产生显著差异,因此我们这里采用 的node2vec。LINE:我们使用同时采用了1阶邻近性和2阶邻近性的LINE模型。PTE:我们构建了三个异质二部图A-A, A-V, V-V,并将其作为无监督embedding学习方法的约束。- 谱聚类
Spectral Clustering/图因子分解Graph Factorization:因为早前的研究表明DeepWalk和LINE的性能超越了它们,因此这里并不考虑这两种方法。
参数配置:对于所有模型,我们使用以下相同的参数:
- 每个顶点开始的随机游走序列数量 。
- 每个随机游走序列长度 。
- 隐向量维度 。注意:对于
LINE模型,其一阶embedding和 二阶embedding的维度都是128。 - 邻域
size。 - 负采样
size - 对于
metapath2vec/metapath2vec ++,我们还需要指定meta-path范式来指导随机游走的生成。我们调查了大多数基于meta-path的工作,发现异质学术网络中最常用和有效的meta-path范式是APA和APVPA。注意,APA表示co-author语义,即传统同质网络的collaboration关系;APVPA代表两个author在同一个venue发表了论文(可以是不同的论文)的异质语义。我们的实验表明:meta-path范式APVPA产生的节点embedding可以泛化到各种异质学术网络的挖掘任务中。
最后,在参数敏感性实验中,我们对参数中的一个进行变化,同时固定其它参数来观察 metapath2vec/metapath2vec ++ 的效果。
11.2.1 节点分类
我们使用第三方的
label来确定每个顶点的类别。首先将
Google Scholar中的八个会议的研究类别与AMiner数据中的会议进行匹配:1Computational Linguistics, Computer Graphics, Computer Networks & Wireless Communication, Computer Vision & Pattern Recognition, Computing Systems, Databases & Information Systems, Human Computer Interaction, Theoretical Computer Science每种类别
20个会议。在这160个会议中,有133个已经成功匹配并进行相应的标记。每篇论文标记为它所属会议的类别。然后,对于这
133个会议的论文的每位作者,将他/她分配给他/她大部分论文的类别,如果论文类别分布均匀则随机选择一个类别。最终有246678位作者标记了研究类别。
我们从完整的
AMiner数据集中学到节点的embedding,然后将上述节点标记以及对应的节点embedding一起作为逻辑回归分类器的输入。我们将训练集规模从标记样本的
5%逐渐增加到90%,并使用剩下顶点进行测试。我们将每个实验重复十轮,并报告平均的macro-F1和micro-F1。下表给出了
Venue类型顶点的分类结果。
下表给出了
Author类型顶点的分类结果: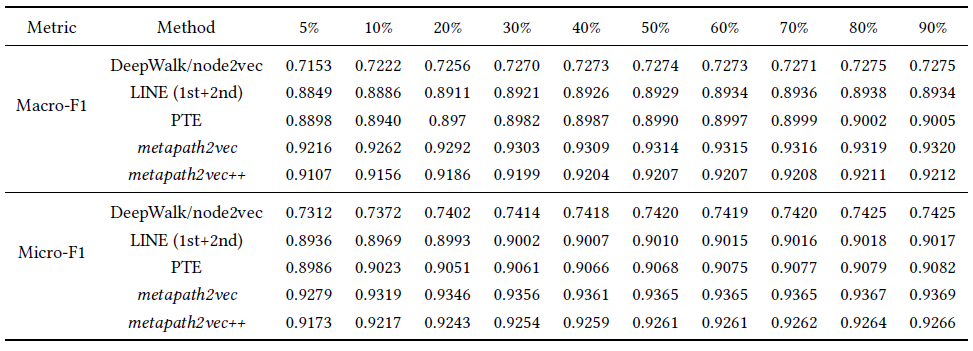
结论:
metapath2ve/metapath2vec ++模型始终一致且明显的优于所有其它基准方法。- 在预测
Venue类型节点的类别时,在训练数据量较小的情况下,metapath2vec/metapath2vec ++的优势特别明显。例如,给定5%的节点作为训练集,相对于DeepWalk/node2vec, LINE, PTE,metapath2vec/metapath2vec++在Macro-F1方面实现了0.08 ~ 0.23的绝对提升(相对提升35% ~ 319%),在Micro-F1方面实现了0.13 ~ 0.26的绝对提升(相对提升39% ~ 145%)。 - 在预测
Author类型节点的类别时,每种方法的性能在不同训练集规模情况下都相对稳定metapath2vec/metapath2vec ++相对LINE和PTE稳定提升2% ~ 3%、比DeepWalk/node2vec稳定提升~20%。
总之,通过多分类性能评估,
metapath2vec/metapath2vec++学到的异质node embedding比当前state-of-the-art的方法要好得多。metapath2vec/metapath2vec++方法的优势在于它们对网络异质性挑战(包含多种类型节点和多种类型边)的适当考虑和适应。我们接下来对
metapath2vec ++的几个通用参数进行超参数敏感性分析。我们变化其中的一个超参数,然后固定其它的超参数。结论:
从图
a和b可以看到,参数 和 对于author节点的分类性能是正向的,其中 、 左右,author节点分类性能提到到峰值附近。但是令人惊讶的是, 对于
venue节点的分类性能无关。从图
c和d可以看到,embedding尺寸 和邻域大小 与venue节点分类性能无关。而 对于author节点分类性能至关重要,下降的曲线表明较小的邻域大小对于author节点能够产生更好的embedding表示。这和同质图完全不同。在同质图中,邻域大小 通常对节点分类显示出正向影响,而这里是负向影响。根据分析,
metapath2vec++对这些参数并不严格敏感,并且能够在cost-effective超参数选择的条件下(选择范围越小则效率越高)达到高性能。此外,我们的结果还表明,这些通用的超参数在异质网络中表示出和同质网络中不同的效果,这表明对于异质网络representation learning需要采用不同的思路和解决方案。
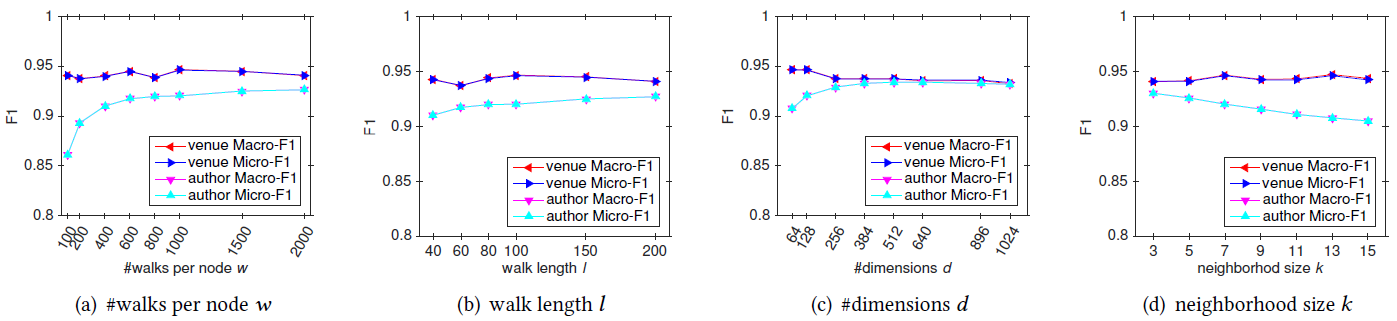
11.2.2 节点聚类
我们采用与上述分类任务中使用的相同的八个类别的
author节点和venue节点(AMiner CS数据集),我们针对这些节点的embedding进行聚类。这里我们使用k-means聚类算法,并通过归一化的互信息NMI来评估聚类效果。给定随机变量 ,则归一化的互信息定义为:
所有聚类实验均进行十次,并报告平均性能,结果如下表所示。结论:
- 总体而言,
metapath2vec和metapath2vec ++优于其它所有方法。 - 从
venue节点聚合结果可以看到,大多数方法(除了DeepWalk/node2vec)的NMI都较高,因此该任务相对容易。但是我们的方法比LINE和PTE高2% ~ 3%。author节点聚类指标都偏低,因此任务更难。但是我们的方法相比最佳baseline(LINE和PTE)上获得更显著的增益:大约提升13% ~ 16%。
总之,和
baseline相比,metapath2vec和metapath2vec ++为网络中不同类型的节点生成了更合适的embedding,这表明它们能够捕获和整合异质网络中各种类型节点之间的底层结构关系和语义关系。
- 总体而言,
和分类实验的步骤相同,我们研究了聚类任务中
metapath2vec ++的参数敏感性,衡量指标为NMI。从图
a和b可以看到,author节点和venue节点在 时可以在效果和计算效率之间取得平衡。增加 和 对author节点的聚类结构正向影响,但是对venue节点影响不大。从图
c和d可以看到,对于author节点, 和 与聚类性能呈负面影响;而对于venue节点, 也与聚类性能负面影响,但是 增加时聚类NMI先增加后减小。所有这些意味着对于
author节点和venue节点,当 时,生成的embedding可以得到较好的聚类结果。
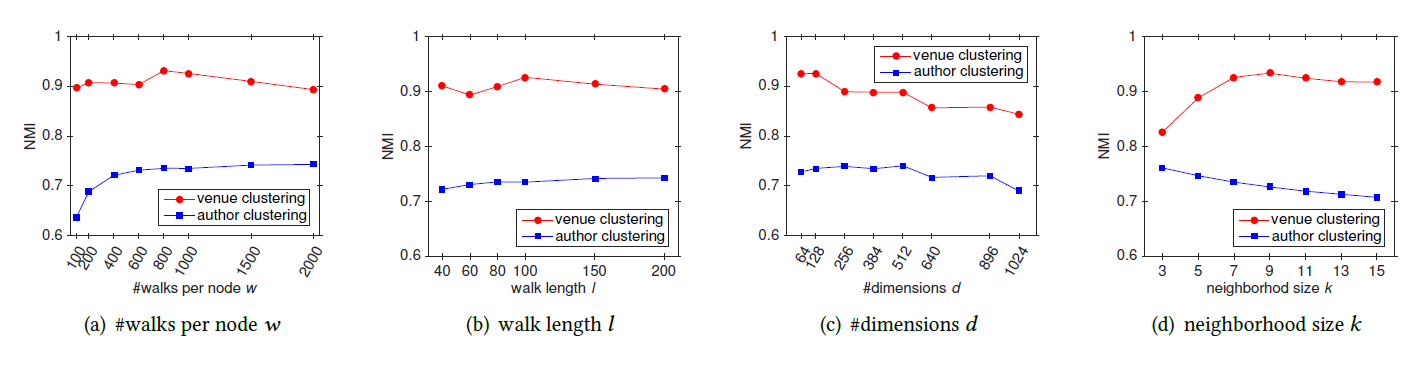
11.2.3 相似节点搜索
我们从
AMiner数据集选择16个不同领域的顶级CS会议,然后通过余弦相似度选择这些会议节点的top 10相似度结果。结论:对于
query节点ACL,metapath2vec++返回的venue具有相同的主题NLP,如EMNLP(1st)、NAACL(2nd)、Computational Linguistics(3rd)、CoNLL(4th)、COLING(5th)等等。其它领域的会议的
query也有类似的结果。大多数情况下,
top3结果涵盖了和query会议声望类似的venue。例如theory理论领域的STOC和FOCS、system系统领域的OSDI和SOSP、architecture架构领域的HPCA和ISCA、security安全领域的CCS和S&P、human-computer interaction人机交互领域的CSCW和CHI、NLP领域的EMNLP和ACL、machine learning机器学习领域的ICML和NIPS、web领域的WSDM和WWW、artificial intelligence人工智能领域的AAAI和UCAI、database数据库领域的PVLDB和SIGMOD等等。
类似的,我们从
DBIS数据中选择另外的5个CS会议,然后通过余弦相似度选择这些会议节点的top 10相似度结果。结论也类似。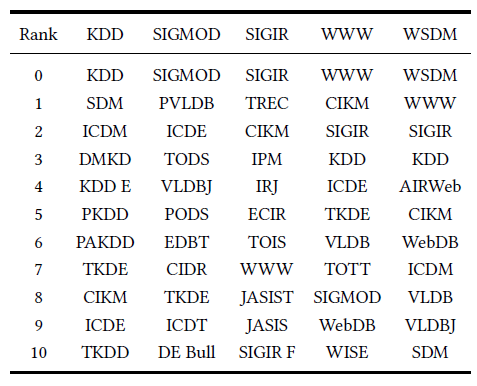
我们从
DBIS数据中选择一个会议节点、一个作者节点,然后比较不同embedding方法找出的top-5相似度的结果。结果如下表所示,其中metapath2vec ++能够针对不同类型的query节点获得最佳的top-5相似节点。
11.2.4 可视化
我们使用
tensorflow embedding2维PCA来进一步可视化模型学到的节点embedding。我们从AMiner CS数据集选择16个不同领域的顶级CS会议,以及对应的顶级作者进行可视化。从图
d可以看到,metapath2vec++能自动组织这两种类型的节点,并隐式学习它们的内部关系。这种内部关系可以通过连接每对节点的箭头的方向和距离表示,如J.Dean --> OSDI,C.D.Manning --> ACL,R.E.Tarjan --> FOCS,M.I.Jordan --> NIPS等等。这两类节点位于两个独立的“列”中,很显然图
a和b的embedding无法达到同样的效果。从图
c可以看到,metapath2vec能够将每对author-venue pair对进行紧密的分组,而不是将两种类型的节点分类两列。如R.E.Tarjan + FOCS、H.Jensen + SIGGRAPH、H.Ishli + CHI、R.Agrawal + SIGMOD等等。 常规的embedding方法也无法达到这种效果。metapath2vec/metapath2vec++都可以将来自相似领域的节点放在一起、不同领域的节点相距较远。这种分组不仅反映在venue节点上,也反映在author节点上。
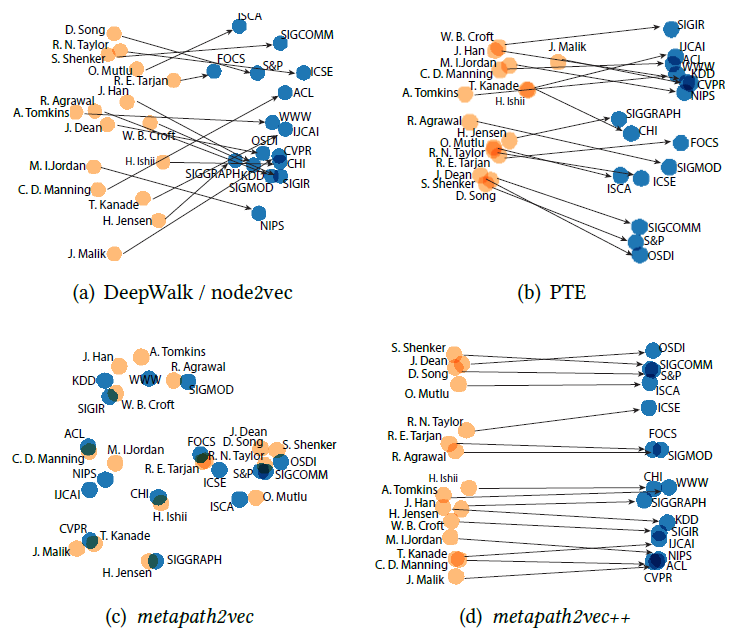
下图通过
t-SNE可视化了metapath2vec++学到的AMiner数据集不同领域的顶级CS会议,一共48个会议、16个领域,每个领域3个会议。- 可以看到:来自同一个领域的会议彼此聚在一起,并且不同组之间的间隔比较明显。这进一步验证了
metapath2vec++的embedding能力。 - 另外,异质
embedding能够揭示不同领域的节点之间的相似性。如,右下角的Core CS领域的几个簇(计算机系统簇OSDI、计算机网络簇SIGCOMM、计算机安全簇S&P、计算机架构簇ISCA)、右上角的Big AI领域的几个簇(数据挖掘簇KDD、信息检索簇SIGIR、AI簇AI、机器学习簇NIPS、NLP簇ACL、计算机视觉簇CVPR)。
因此,这些可视化结果直观地展示了
metapath2vec++的新能力:发现、建模、以及捕获异质网络中多种类型节点之间的底层结构关系和语义关系。
- 可以看到:来自同一个领域的会议彼此聚在一起,并且不同组之间的间隔比较明显。这进一步验证了
11.2.5 可扩展性
metapath2vec/metapah2vec ++可以使用和word2vec/node2vec中相同的机制来并行化。我们对AMiner数据集进行实验,实验在Quad 12(48) core 2.3 GHz Intel Xeon CPUs E7-4850上进行。我们实现不同的线程数{1,2,4,8,16,24,32,40},每个线程使用一个CPU core。下面给出了
metapath2vec/metapath2vec++的加速比。最佳加速比由虚线 表示。我们的这两种方法都可以达到能够接受的亚线性加速比,它们都接近于虚线。具体而言,在使用16个core时,它们可以实现11-12倍的加速比;使用40个core时,它们可以实现24-32倍加速比。在使用
40个core时,metapath2vec ++的学习过程只需要9分组即可训练整个AMS CS网络的embedding,该网络由900万以上的作者、3300多个venue、300万篇论文组成。总体而言,对于具有数百万个节点的大规模异质网络,metapath2vec/metapath2vec++是高效的且scalable的。
十二、GraphGAN[2018]
graph representation learning(也被称作network embedding)旨在将图(或者network)中的每个顶点表达为一个低维向量。graph representation learning可以促进对顶点和边的网络分析和预测任务。学到的embedding能够使广泛的实际application受益,例如链接预测、节点分类、推荐、可视化、知识图谱representation、聚类、text embedding、社交网络分析。最近,研究人员研究了将representation learning方法应用于各种类型的图,例如加权图weighted graph、有向图directed graph、有符号图signed graph、异质图heterogeneous graph、属性图attributed graph。此外,先前的一些工作也试图在学习过程中保留特定的属性,例如全局结构global structure、社区结构community structure、分组信息group information、非对称传递性asymmetric transitivity。总的来讲,大多数现有的
graph representation learning方法可以分为两类。- 第一类是生成式
graph representation learning模型。类似于经典的生成模型generative model(例如高斯混合模型Gaussian Mixture Model: GMM或潜在狄利克雷分配Latent Dirichlet Allocation: LDA),生成式graph representation learning模型假设:对于每个顶点 ,存在一个底层的真实的连通性分布underlying true connectivity distribution,它给出了 对图中所有其它顶点的连通性偏好connectivity preference(或者相关性分布relevance distribution)。因此,图中的边可以被视为由这些条件分布生成的观察样本observed sample,并且这些生成模型通过最大化图中边的可能性来学习顶点embedding。例如,DeepWalk使用随机游走对每个顶点的上下文顶点进行采样,并尝试最大化观察给定顶点的上下文顶点的对数似然。node2vec通过提出有偏随机游走过程进一步扩展了这个想法,这个有偏随机游走过程在为给定顶点生成上下文时提供了更大的灵活性。 - 第二类是判别式
graph representation learning模型。与生成模型不同的是,判别式graph representation learning模型不会将边视为从底层条件分布生成的,而是旨在学习一个分类器来直接预测边的存在。通常,判别模型discriminative model将两个顶点 和 共同视为特征,并根据图中的训练数据预测两个顶点之间存在边的概率,即 。例如,SDNE使用顶点的稀疏邻接向量sparse adjacency vector作为每个顶点的原始特征,并应用自编码器在边存在edge existence的监督下提取顶点的低维稠密特征。PPNE直接通过对正样本(连接的顶点pair对)和负样本(未连接的顶点pair对)的监督学习来学习顶点embedding,同时在学习过程中也保留了顶点的固有属性。
尽管生成模型和判别模型通常是
graph representation learning方法的两个不相交的类别,但是它们可以被视为同一枚硬币的两个方面。事实上,LINE已经对于隐式地结合这两个目标(一阶邻近性和二阶邻近性)进行了初步的尝试。最近,生成对抗网络Generative Adversarial Net: GAN受到了极大的关注。通过设计一个博弈论game-theoretical的minimax游戏来结合生成模型和判别模型,GAN及其变体在各种应用中取得了成功,例如图像生成image generation、序列生成sequence generation、对话生成dialogue generation、信息检索information retrieval、领域适应domain adaption。受
GAN的启发,论文《GraphGAN: Graph Representation Learning with Generative Adversarial Nets》提出了一种新颖的框架GraphGAN,它统一了graph representation learning的生成式思维和判别式思维。具体而言,框架的目标是在GraphGAN的学习过程中训练两个模型:- 生成器
generator,它试图拟合底层的真实的连通性分布 ,生成最有可能与 连接的顶点。 - 判别器
discriminator,它试图区分well-connected的顶点pair对和ill-connected的顶点pair对,并计算顶点 和 之间存在边的概率。
在提出的
GraphGAN中,生成器 和判别器 在minimax游戏中充当两个参与者:生成器试图在判别器提供的指导下产生最难以区分的 “假” 顶点,而判别器试图在ground truth和 “假” 顶点之间划清界限从而避免被生成器愚弄。这场博弈中的竞争促使它们双方都提高自己的能力,直到生成器(代表模型学到的条件分布)与真实的连通性分布true connectivity distribution无法区分。在
GraphGAN框架下,论文研究了生成器和判别器的选择。不幸的是,作者发现传统的softmax函数(及其变体)不适用于生成器,有两个原因:- 对于给定的顶点,
softmax会同等对待图中的所有其它顶点,缺乏对图结构和邻近性信息proximity information的考虑。 softmax的计算涉及图中的所有顶点,耗时且计算效率低。
为了克服这些缺陷,论文在
GraphGAN中提出了一种新的、针对生成器的softmax实现,称作Graph Softmax。Graph Softmax为图中的连通性分布提供了新的定义。论文证明了Graph Softmax满足规范化normalization、图结构感知graph structure awareness、以及计算效率computational efficiency的理想特性。据此,论文为生成器提出了一种基于随机游走的在线生成策略online generating strategy,该策略与Graph Softmax的定义一致,可以大大降低计算复杂度。论文在五个真实世界的图结构数据集上将
GraphGAN应用于三个真实世界场景,即链接预测、节点分类、推荐。实验结果表明:与graph representation learning领域的state-of-the-art的baseline相比,GraphGAN取得了可观的收益。具体而言,在准确率指标上,GraphGAN在链接预测中的性能优于baseline0.59% ~ 11.13%,在节点分类中的性能优于baseline0.95% ~ 21.71%。此外,GraphGAN在推荐任务上将Precision@20至少提高了38.56%、Recall@20至少提高了52.33%。作者将GraphGAN的优越性归因于其统一的对抗性学习框架以及邻近性感知proximity-aware的Graph Softmax设计。其中,Graph Softmax可以自然地从图中捕获结构信息。- 第一类是生成式
12.1 模型
- 这里我们首先介绍
GraphGAN的框架,并讨论了生成器和判别器的实现和优化细节。然后,我们展示了作为生成器实现的Graph Softmax,并证明了它优于传统softmax函数的性能。
12.1.1 GraphGAN 框架
令图 ,其中 为顶点集合, 为边集合。对于给定顶点 ,定义 为 直接相连的顶点集合(即,直接邻域),通常该集合的规模远远小于全量顶点集合 。
我们定义顶点 的底层真实连通性分布
underlying true connectivity distribution为条件概率 ,它反映了 对 中所有其它顶点的连通性偏好connectivity preference。从这个角度来看, 可以视为从 中抽取的一组观测样本observed sample。给定图 ,我们的目标是学习以下两个模型:
- 生成器
generator:它的目标是逼近 ,然后针对 生成最有可能和它连接的顶点。更准确的说,是从 中选择和 最有可能连接的顶点。 - 判别器
discriminator:它的目标是判断顶点pair对 之间的连通性connectivity。它输出一个标量,代表顶点 和 之间存在边的概率。
生成器 和判别器 充当两个对手:
- 生成器 试图完美拟合 ,然后生成 “假” 顶点。这些生成的顶点和 真实连接的邻居顶点相似,从而欺骗判别器 。
- 判别器 试图检测这些顶点是否是 的真实邻居,还是由生成器 生成的 ”假“ 顶点。
形式化地,生成器 和判别器 正在参与具有以下值函数
value function的双人minimax游戏:其中生成器和判别器的参数可以通过交替最大化和最小化值函数 来学习。
第一项要求判别器 尽可能给 ”真邻居” 以较高的预估概率,第二项要求判别器 尽可能给 “假邻居” 以较低的预估概率。
- 生成器
GraphGAN整体框架如下图所示。每次迭代过程中,我们使用来自 的正样本(绿色顶点)和来自生成器 的负样本(带蓝色条纹的顶点)来训练判别器 ,并在 的指导下使用策略梯度更新生成器 。和 之间的竞争促使它们都改进自己的参数,直到 与 无法区分。

判别器
Discriminator:给定从底层真实连通性分布而来的正样本,以及从生成器而来的负样本,判别器 的目标是最大化将正确label分配给正样本和负样本的概率的对数。如果判别器 是可微的,则可以通过针对 的梯度上升来解决。在
GraphGAN中,我们简单地定义判别器 为两个输入顶点的embedding内积的sigmoid函数。理论上SDNE等任何判别式模型都可以用作判别器 ,我们将如何选择合适的判别器作为未来的研究。因此,这里的判别器为:其中 分别是判别器 中顶点 和 的 维
representation向量, 。注意到这里仅包含 和 ,这意味着给定一对样本 ,我们仅仅需要通过对应的梯度上升来更新 和 :
即,没必要更新全量顶点的
embedding。生成器
Generator:和判别器相比,生成器 的目标是,使得判别器 区分由 生成的 “假” 顶点的概率最小化。即,生成器通过调整参数 来移动其近似的连通性分布approximated connectivity distribution,从而增加其生成的 “假” 顶点在判别器 中的得分。由于生成器采样的顶点 是离散的,因此遵循
《Gradient estimation using stochastic computation graphs》和《Irgan: A minimax game for unifying generative and discriminative information retrieval models》的做法,我们建议通过策略梯度policy gradient计算 对 的梯度:其中 为生成器采样的顶点数量。
考虑到 与 无关,以及 ,因此有:
则有:
梯度 的物理意义为: 的加权和,权重为 。
- 当 更容易被判别器 识别时, 得分较小,则加权的权重较大。
- 当 更不容易被判别器 识别时, 得分较大,则加权的权重较小。
这表明:当我们对 应用梯度下降时,更容易被判别器 区分的 “假” 顶点将“拉扯”生成器,使其得到一个较大的更新。
生成器 最简单直接的实现方式是通过
softmax函数来实现:其中 为分别是生成器 中顶点 和 的 维
representation向量, 。为了在每轮迭代中更新 ,我们首先基于 计算近似的连通性分布
approximated connectivity distribution,然后根据该分布随机采样一组样本 ,然后通过随机梯度下降法来更新 。注意,采样“假”顶点时采用更新前的生成器,然后通过随机梯度下降得到更新后的生成器。
12.1.2 Graph Softmax
在生成器中应用
softmax有两个限制:- 计算 的
softmax函数时涉及到图中的所有顶点,这意味着对于每个生成的样本 ,我们需要计算梯度 ,并更新所有顶点。这在计算上是低效的,尤其是对于具有数百万个顶点的真实世界的大型Graph。 - 图结构信息编码了顶点之间丰富的邻近性信息,但是
softmax函数完全忽略了来自图的结构信息,因为它不加区分地对待所有顶点。
最近
hierarchical softmax和负采样技术是softmax的流行替代方案。尽管这些方法可以在一定程度上减少计算量,但是它们也没有考虑图的结构信息,因此应用于graph representation learning时也无法获得令人满意的性能。- 计算 的
为解决
softmax的问题,在GraphGAN中我们提出了一个新颖的Graph Softmax,其关键思想是:重新对生成器 定义一个满足下面三个属性的、理想的softmax方法:- 归一化
normalized:生成器 应该是一个有效的概率分布。即: 。 - 图结构感知
graph structure aware:生成器 应该利用图的结构信息。直观而言,对于图中的两个顶点,它们的连通性概率应该随着它们之间最短路径距离shortest distance的增加而下降。 - 计算高效
computationally efficient:和计算全量softmax不同,计算 应该仅仅包含图中的一小部分顶点。
- 归一化
Graph Softmax:为计算 ,我们首先从顶点 开始对原始图 进行广度优先搜索Breadth First Search: BFS,这得到一棵以 为根的BFS树 。给定 ,我们将 表示为 中 的邻居的集合,即和 直连的顶点,包括 的直系父顶点和直系子顶点。注意: 既依赖于顶点 ,又依赖于顶点 。如果根顶点 不同,则
BFS树 也不同,则 的邻居集合也不同。另外,这里仅包含直接相连的顶点(直系父顶点、直系子顶点)。对于给定的顶点 及其邻居顶点 ,我们定义给定 的条件下 的概率为:
这其实是定义在 上的一个
softmax函数。定义的是路径概率:给定树 和顶点 ,下一步选择其父顶点或子顶点的路径概率。这个概率并不是 “假” 顶点的生成概率。
注意到 中的每个顶点 可以从根节点 通过唯一的一条路径达到,定义该路径为 ,其中 。则
Graph Softmax定义为:其中 由上式定义。最后一项因子 是为了归一化从而得到概率分布。
可以证明这种定义的
Graph Softmax满足归一性、结构感知、计算高效等性质。定理一:
Graph Softmax满足 。证明见原始论文。定理二:在原始图中如果 和 的最短路径增加,则 下降。
证明:由于 是通过广度优先
BFS得到的,因此路径 同时也定义了一条从 到 的最短路径,该路径长度为 。随着最短路径增加,则 中的概率乘积越多,因此 越小。定理三:计算 依赖于 个顶点,其中 是所有顶点的平均
degree, 为所有顶点的大小。证明:计算 依赖于两种类型的顶点:
- 在路径 上的顶点。路径的最长长度为 ,它是
BFS树的深度。 - 路径上顶点直接相连的顶点。路径上每个顶点平均有 个邻居顶点相连。
- 在路径 上的顶点。路径的最长长度为 ,它是
12.1.3 算法和讨论
在线生成策略
online generating strategy:生成器 生成 “假” 顶点的一个简单方法是:为所有的 顶点计算 ,然后根据这个近似的连通性概率执行随机采样。这里我们提出一种在线的顶点生成方法,该方法计算效率更高并且与
Graph Softmax的定义一致。为了生成一个顶点,我们从 中的根节点 开始,根据转移概率 执行随机游走。在随机游走过程中,如果 首次需要访问 的父节点(即在路径上反向),则选择 作为生成的顶点。因为
Graph Softmax的定义中包含 到 的一条路径,并且还包含 到 的父节点的反向。下图给出了 “假” 顶点的在线生成过程,以及
Graph Softmax计算过程。蓝色数字表示概率 ,蓝色实线箭头表示随机游走的方向,蓝色条纹顶点是被采样的顶点。最后一幅图的带颜色顶点(绿色、橙色、蓝色、蓝色带条纹)是需要更新参数的顶点。我们将当前访问的顶点记作 ,前一个访问的顶点记作 (即父节点)。- 在每个随机游走步通过概率 随机选择当前顶点 的一个邻居顶点(标记为蓝色)。
- 一旦 ,则将 作为采样顶点并返回(标记为蓝色带条纹)。
- 然后根据 对路径 上的所有路径顶点、以及它们直接相连的顶点的参数进行更新。
生成器 在线生成算法最多执行 个迭代步,因为随机游走路径最迟会在到达叶结点时终止。类似于
Graph Softmax,在线生成方法的计算复杂度为 ,这大大低于离线生成方法的 。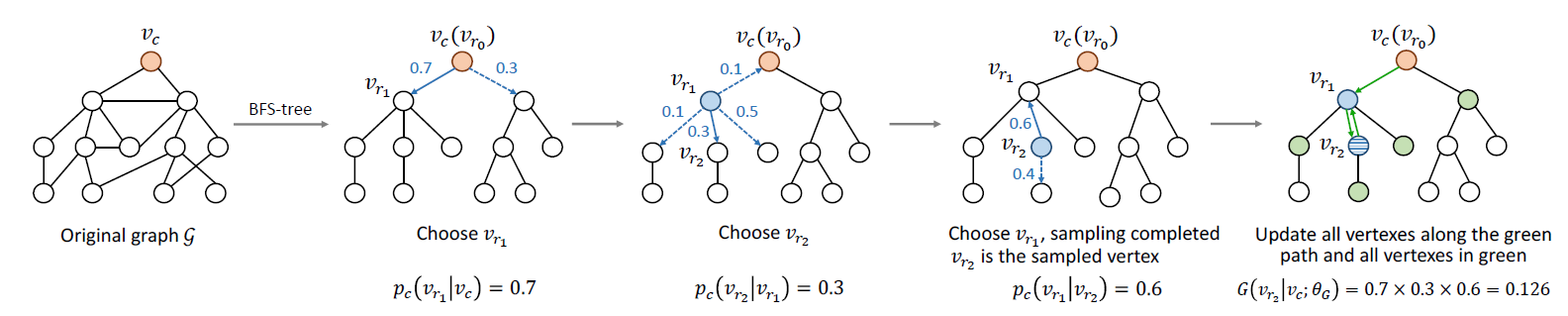
生成器 在线生成算法:
输入:
- 图
BFS树- 顶点的
embedding
输出:生成的顶点
算法步骤:
初始化:
- 根据概率 随机选择一个顶点
- 如果 ,则 ,直接返回
- 否则
GraphGAN算法:输入:
embedding维度- 生成样本数
- 判别样本数
输出:
- 生成器
- 判别器
算法步骤:
初始化和预训练 以及
对每个顶点 ,构建
BFS树 。迭代直到
GraphGAN收敛,迭代步骤为:- 根据生成器在线生成算法,生成器 对每个顶点 采样 个顶点
- 根据 更新
- 对每个顶点 ,从真实邻居顶点中采样 个正样本,从 中采样 个负样本。
- 根据 来更新
返回
由于构建每棵
BFS树的算法复杂度为 ,则构建所有BFS树的计算复杂度 。其中 为顶点的平均degree。在
G-steps,每一行的算法复杂度都是 ;在D-steps,第一行的算法复杂度为 ,第二行的算法复杂度为 。由于 都是常数,因此GraphGAN每次迭代的算法复杂度为 。因此总的算法复杂度为 ,由构建
BFS树的部分决定。读者注:论文将生成器的
embedding作为顶点的最终embedding,而并没有采用判别器的embedding。这是因为在链接预测任务的实验中表明:生成器embedding的效果要比判别器embedding的效果更好。理论上也可以尝试拼接生成器的
embedding和判别器的embedding从而得到顶点的最终embedding。
12.2 实验
我们评估
GraphGAN在一系列真实数据集上的性能,包括链接预测、节点分类、推荐等三个任务。数据集:
arXiv-AstroPh数据集:来自arXiv上天文物理领域的论文,包含了作者之间的co-author关系。顶点表示作者,边表示co-author关系。该图包含18772个顶点、198110条边。arXiv-GrQc数据集:来自arXiv上广义相对论与量子宇宙学领域的论文,包含了作者之间的co-author关系。顶点表示作者,边表示co-author关系。该图包含5242个顶点、14496条边。BlogCatalog数据集:来自BlogCatelog网站上给出的博主的社交关系网络。顶点标签表示通过博主提供的元数据推断出来的博主兴趣。该图包含10312个顶点、333982条边、39个不同的标签。Wikipedia数据集:来自维基百科,包含了英文维基百科dump文件的前 个字节中的单词co-occurrence网络。顶点的标签表示推断出来的单词词性Part-of-Speech:POS。该图包含4777个顶点、184812条边、40个不同的标签。MovieLens-1M数据集:是一个二部图,来自MovieLens网站上的大约100万个评分(边),包含6040位用户和3706部电影。
baseline方法:DeepWalk:通过随机游走和skip-gram来学习顶点embedding。LINE:保留了顶点的一阶邻近性和二阶邻近性。Node2Vec:是DeepWalk的一个变种,通过一个biased有偏的随机游走来学习顶点embedding。Struct2Vec:捕获了图中顶点的结构信息。
参数配置:
所有方法的
embedding的维度 。所有
baseline模型的其它超参数都是默认值。在所有任务上,
GraphGAN的学习率都是0.001, , 为测试集的正样本数,然后分别执行G-steps和D-steps30次。这些超参数都是通过交叉验证来选取的。最终学到的顶点
embedding为生成器的 (而不是判别器的 ) 。
12.2.1 连通性分布
我们首先实验了图中连通性分布的模式,即:边的存在概率如何随着图中最短路径的变化而变化。
我们首先分别从
arXiv-AstroPh和arXiv-GrQc数据集中随机抽取100万个顶点pair对。对于每个选定的顶点pair对,我们删除它们之间的连接(如果存在),然后计算它们之间的最短距离。我们计算所有可能的最短距离上边存在的可能性,如下图所示。显然,顶点
pair对之间存在边的概率随着它们最短路径的增加而急剧下降。从对数概率曲线几乎为线性可以看出,顶点
pair对之间的边存在概率和它们最短距离的倒数成指数关系。这进一步证明了Graph Softmax捕获了真实世界Graph的本质。这进一步证明了
Graph Softmax捕获了真实世界Graph的结构信息。
12.2.2 链接预测
在链接预测任务中,我们的目标是预测两个给定顶点之间是否存在边。因此该任务显式了不同的
graph representation learning方法预测链接的能力。我们随机将原始图中
10%的边作为测试集,并在图上删掉这些边,然后用所有的顶点和剩下的边来训练模型。训练后,我们根据所有顶点训练得到的embedding向量,然后用逻辑回归来预测给定顶点pair对之间存在边的概率。测试集包含原始图中删掉的10%条边作为正样本,并随机选择未连接的相等数量的pair对作为负样本。我们使用
arXiv-AstroPh和arXiv-GrQc作为数据集,并在下表报告准确率和Macro-F1的结果。结论:LINE和struct2vec的性能在链接预测方面相对较差,因为它们不能完全捕获图中链接存在的模式。DeepWalk和node2vec的性能优于LINE和struct2vec,这可能优于DeepWalk和node2vec都利用了基于随机游走的skip-gram模型,该模型在提取顶点之间邻近性方面表现更好。GraphGAN优于所有baseline方法。具体而言,GraphGAN将arXiv-AstroPh的预测准确率提升1.18% ~ 4.27%、将arXiv-GrQc的预测准确率提升0.59% ~ 11.13%。我们认为,与baseline方法的单个模型训练相比,对抗训练为GraphGAN提供了更高的学习灵活性。
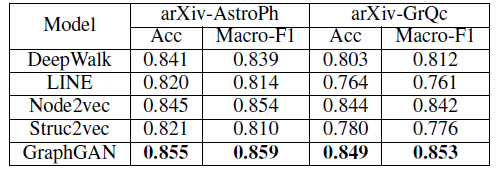
为直观了解
GraphGAN学习的稳定性,我们进一步给出了生成器和判别器在arXiv-GrQc上的学习曲线learning curve。可以看到:GraphGAN中的minimax game达到了平衡,其中生成器在收敛后表现出色,而判别器的性能首先增强然后逐渐降到0.8以下。注意,判别器不会降级到随机盲猜的水平,因为在实践中生成器仍然提供很多真正的负样本。结果表明,与
IRGAN不同,Graph Softmax的设计使得GraphGAN中的生成器能够更有效地采样顶点和学习顶点embedding。这个实验表明生成器
embedding要比判别器embedding效果更好。
12.2.3 节点分类
在节点分类中,每个顶点被分配一个或者多个标签。在我们观察到一小部分顶点及其标签之后,我们的目标是预测剩余顶点的标签。因此,顶点分类的性能可以揭示不同
graph representation learning方法下顶点的可分性。我们在BlogCatalog和Wikipedia数据集上执行顶点分类任务。我们在整个图上训练模型,然后将顶点embedding作为逻辑回归分类器的输入。其中训练集、测试集按照9:1的比例进行拆分。我们报告了测试集的准确率和Macro-F1结果。可以看到:
GraphGAN性能在这两个数据集上都优于所有基准模型。例如,GraphGAN在这两个数据集的准确率上分别实现了1.75% ~ 13.17%以及0.95% ~ 21.71%的增益。这表明:尽管GraphGAN设计用于建模顶点之间的连通性分布,但是它仍然可以有效的将顶点信息编码到顶点embedding中。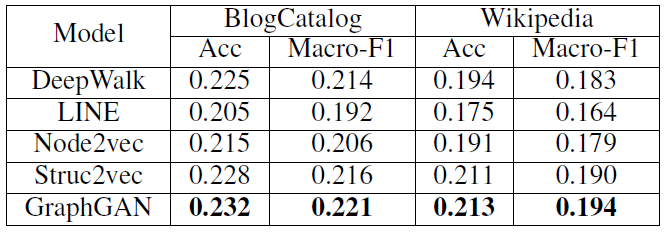
12.2.4 推荐
我们使用
Movielens-1M作为推荐数据集,我们的目标是对每个用户向该用户推荐一组尚未观看、但是可能被用户喜欢的电影。我们首先将所有的
4星和5星评级视为边,从而得到一个二部图。然后将原始图的10%边随机隐藏作为测试集,并为每个用户构建BFS树。注意:和之前的两个任务不同,在之前任务中,对于给定的顶点我们定义了它与所有其它顶点的连通性分布。但是推荐任务中,一个用户的连接概率仅定义在图中的一小部分电影顶点上(用户顶点之间不存在连接、电影顶点之间也不存在连接)。因此我们在用户的BFS树中,对于除根顶点之外的所有用户顶点,我们将它们和位于当前BFS树中的电影顶点添加直连边来shortcut。在训练并获得用户和电影的
embedding之后,对于每个用户,我们基于user embeding和电影embedding的相似度来挑选 个用户未观看的电影来作为推荐结果。我们给出测试集上的Precision@K和Recall@K指标。可以看到:GraphGAN始终优于所有基准方法,并在两个指标上均有显著改进。以Precision@20为例,GraphGAN比DeepWalk, LINE, node2vec, struct2vec分别高出38.56%、58.60%、124.95%、156.85%。因此,我们可以得出结论:GraphGAN在ranking-based任务中保持了更出色的性能。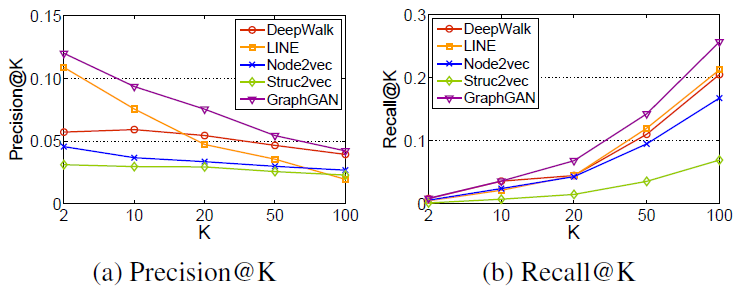
十三、struc2vec[2017]
在几乎所有网络中,节点往往具有一种或多种功能,这些功能极大地决定了节点在系统中的作用。例如,社交网络
social network中的个体具有社会角色social role或社会地位social position,而protein-protein interaction(PPI) network中的蛋白质发挥特定功能。直观而言,这些网络中的不同节点可能执行类似的功能,例如公司的社交网络中的实习生、细胞的PPI网络中的催化剂。因此,节点通常可以根据它们在网络中的功能划分为等价的类别equivalent class。尽管此类功能的识别通常利用节点的属性和边的属性,但是当节点功能仅由网络结构定义时,会出现更具挑战性和更有趣的场景。在这种情况下,甚至节点的
label都不重要,而只需要节点与其它节点(或者边)的关系。事实上,自1970年代以来,数学社会学家mathematical sociologist一直在研究这个问题,定义和计算社交网络中个体的结构身份structural identity。除了社会学之外另一个例子是,识别网页在web-graph中的结构身份(如hub、authority),正如Kleinberg的著名著作《Authoritative sources in a hyperlinked environment》所定义的那样。结构身份是一种对称性概念,其中节点是基于网络结构来识别的。这个概念与网络中节点所扮演的功能或角色密切相关。确定节点结构身份的最常见实用方法是基于距离或者递归。
- 在基于距离的方法中,我们利用节点邻域的距离函数从而测量所有节点
pair对之间的距离,然后执行聚类clustering或匹配matching从而将节点放入等价的类别。 - 在基于递归的方法中,我们构造一个关于相邻节点的递归,然后迭代展开
iteratively unfold直到收敛,节点上的最终值final value用于确定等价的类别。
虽然这些方法有优点和缺点,但论文
《struc2vec: Learning Node Representations from Structural Identity》提供了一种替代方法,一种基于无监督representation learning的方法用于识别节点的结构身份。最近在学习网络中节点的潜在
representation方面的努力在执行分类和预测任务方面非常成功。具体而言,这些努力使用广义的节点邻域作为上下文context(例如,随机游走的 步、或者具有共同邻居的节点集合),从而对节点进行编码。简而言之,具有相似邻域的节点应该具有相似的潜在representation。但是,邻域是由网络中的一些邻近性概念notion of proximity定义的局部概念local concept。因此,如果两个节点的邻域表现出结构相似但是相距很远,那么这两个节点将不会具有相似的潜在representation。下图说明了这个问题,其中节点 和 扮演相似的角色(即,具有相似的局部结构local structure),但是这两个节点在网络中相距很远。由于它们的邻域没有交集,因此最新的方法无法捕获它们的结构相似性structural similarity。
值得注意的是,为什么最近学习
node representation的方法,如DeepWalk和node2vec在分类任务中成功,但是在结构等价性任务structural equivalence task中往往失败。关键是在大多数真实网络中,许多节点特征都表现出强烈的同质性,例如具有相同政治倾向political inclination的两个博客存在连接的可能性相比随机的两个博客要大得多。具有给定特征的节点,其邻居更有可能具有相同的特征。因此,在网络和潜在representation中,“靠近” (close)的两个节点将倾向于有相似的representation。同样地,“远离”(far)的两个节点将倾向于有不同的representation,而与节点的局部结构无关。因此,潜在representation将无法正确地捕获结构等价性structural equivalence。然而,如果分类任务更多地依赖于结构身份的特征而不是同质性的特征,那么捕获结构等价性的方法将超越最近的这些方法。论文
《struc2vec: Learning Node Representations from Structural Identity》的主要贡献是一个灵活的、称作struc2vec的框架,用于学习节点结构身份的潜在representation。该框架是基于潜在representation来研究结构身份的强大工具。struc2vec的关键思想是:- 独立于节点属性、边属性、以及节点和边在网络中的位置来评估节点之间的结构相似性
structural similarity。因此,具有相似局部结构的两个节点被认为是相似的,而无关于节点在网络中的位置和节点的label。并且该方法也不需要网络是连通的,可以在不同的连通分量connected component中识别结构相似的节点。 - 建立一个层级
hierarchy来衡量结构相似性,从而允许更严格的结构相似性的的概念。具体而言,在hierarchy的底部,节点之间的结构相似性仅取决于它们的degree;而在hierarchy的顶部,节点之间的结构相似性取决于整个网络(从节点的角度来看)。 - 为节点生成随机上下文。该上下文是结构相似的节点序列,通过遍历一个多层图
multilayer graph(而不是原始网络)的加权随机游走而观察到的。因此,经常出现在相似上下文中的两个节点可能具有相似的结构。语言模型利用了这种上下文来学习节点的潜在representation。
论文实现了一个
struc2vec实例,并通过对toy网络和真实网络的实验展示了struc2vec的潜力,并将struc2vec的性能与DeepWalk、node2vec、RolX等方法进行比较。DeepWalk和node2vec是用于学习节点潜在representation的两种state-of-the-art技术,RolX是一种识别节点角色的最新方法。论文的实验结果表明:
DeepWalk和node2vec未能捕获到结构身份的概念,而struc2vec在这项任务上表现出色,即使原始网络受到很强的随机噪声(随机地移除边)的影响。struc2vec在那些节点标签更多地依赖于结构身份的分类任务中表现出色,例如航空交通网络air-traffic network。
- 在基于距离的方法中,我们利用节点邻域的距离函数从而测量所有节点
相关工作:在过去的几十年中,在空间(例如欧式空间)中嵌入网络节点受到了不同社区的广泛关注。
embedding技术有助于帮助机器学习应用程序利用网络数据,因为node embedding可以直接用于分类和聚类等任务。在自然语言处理中,为稀疏数据生成稠密的
embedding具有悠久的历史。最近,人们提出SkipGram作为一种有效的技术来学习文本数据的embedding。学到的语言模型将语义相似的单词在embedding空间中彼此靠近。DeepWalk首先提出从network中学习语言模型。它使用随机游走从网络中生成节点序列,然后将节点序列视为句子sentence并应用SkipGram。直观而言,网络中靠近的节点往往具有相似的上下文,因此具有彼此靠近的embedding。node2vec后来扩展了这一思想,并提出有偏biased的二阶随机游走模型,从而在生成节点上下文时提供了更大的灵活性。具体而言,node2vec通过设计边权重(边权重会导致有偏的随机游走)从而尝试同时捕获节点同质性vertex homophily和结构等价性structural equivalence。然而,这里存在一个基本限制:如果节点的距离(hop数)大于SkipGram窗口,那么结构相似的节点将永远不会共享相同的上下文。struc2vec也是基于DeepWalk框架的,只是struc2vec生成随机游走序列的方式不同。subgraph2vec是最近提出的另一种学习有根子图rooted subgraph的embedding的方法。与以前的技术不同,它不使用随机游走来生成上下文。相反,节点的上下文仅由其邻居定义。此外,subgraph2vec通过将具有相同局部结构local structure的节点嵌入到空间中的同一个点来捕获结构等价性。尽管如此,结构等价性的概念是非常严格的,因为它被定义为由Weisfeiler-Lehman同构测试规定的二元属性binary property(0/1代表是否某个子结构)。因此,结构上非常相似(但是未通过Weisfeiler-Lehman同构测试)并且具有非重叠邻居non-overlapping neighbor的两个节点在空间上可能不会靠近。与
subgraph2vec类似,最近人们在学习网络节点更丰富的representation方面做出了相当大的努力。然而,构建显式捕获结构身份的representation是一个相对正交的问题,尚未受到太多关注。这是struc2vec的重点。最近一种仅使用网络结构来显式识别节点角色的方法是
RolX。这种无监督方法的思想为:- 枚举节点的各种结构特征。
- 为这个联合特征空间找到更合适的基向量。
- 为每个节点分配一个已识别角色(即基向量)的分布。
这允许每个节点跨多个角色从而得到混合成员关系
mixed membership。在未显式考虑节点相似性或节点上下文的情况下,RolX很可能会遗漏结构上等价的节点pair对。
13.1 模型
考虑捕获网络中节点结构身份的
representation learning问题。一个成功的方法应该有两个预期的属性:- 节点的潜在
representation之间的距离应该与其结构相似性structural similarity强相关。因此,具有相同结构身份的两个节点应该具有相同的潜在representation,而具有不同结构身份的节点应该相距很远。 - 节点的潜在
representation不应该依赖于任何节点属性或边属性,包括节点label。因此,结构相似的节点应该具有靠近的潜在representation,独立于其邻域中节点属性和边属性。节点的结构身份必须独立于节点在网络中的 “位置”。
鉴于这两个属性,我们提出了
struc2vec框架。这是一个用于学习节点潜在representation的通用框架,由四个部分组成:结构相似性度量:基于不同的邻域大小,为图中每对节点
pair对之间定义结构相似性。这在节点之间的结构相似性度量中引入了hierarchy,为评估hierarchy中每个level的结构相似性提供了更多信息。每个邻域大小定义了一组节点
pair相似性。
- 节点的潜在
加权
multilayer graph:构造一个加权的multilayer graph,其中每个layer都包含原始图的所有节点,并且每个layer对应于hierarchy中的某个level(对应于不同的邻域大小)。此外,layer内每个节点pair对之间边的权重与结构相似性成反比。- 上下文生成:使用
multilayer graph为每个节点生成上下文。具体而言,使用multilayer graph上的有偏随机游走来生成节点序列。这些序列可能包含结构上更相似的节点。 - 学习
embedding:采用一种技术(如SkipGram)从节点序列给出的上下文中学习潜在representation。
注意,
struc2vec非常灵活,它不要求任何特定的结构相似性度量或者representational learning框架。struc2vec的核心思想是构建任意一对顶点之间的结构相似性。这个结构相似性有多个level,由1阶到k阶邻域来决定。而邻域之间的结构相似性根据邻域节点degree序列的相似性来计算。- 上下文生成:使用
13.1.1 结构相似性
struc2vec的第一步是在不使用任何节点属性或边属性的情况下确定两个节点之间的结构相似性。此外,这种相似性度量应该是层次的hierarchical,即随着邻域大小不断增加而捕获更精细的结构相似性概念。直观而言,具有相同degree的两个节点在结构上相似。但是如果它们的邻居也具有相同的degree,则这两个节点在结构上会更相似。设 为一个无向无权图, 为节点集合, 为边集合, 为所有节点数量。设 为图的直径(节点
pair对之间距离的最大值)。定义 为图中与节点 距离为 的节点的集合, 。根据该定义, 表示 的直接邻居节点的集合, 表示和 距离为 的环
ring上的节点集合。定义 为节点集合 的有序degree序列ordered degree sequence。通过比较节点 和 的距离为 (一个环
ring上的节点)的有序degree序列,我们可以得到节点 和 的相似性。根据不同的距离 ,我们可以得到一个hierarchy相似性。具体而言,定义 为节点 和 的 阶结构距离(考虑节点 和 的k-hop邻域,即距离小于或等于 的所有节点它们之间的边),我们递归定义为:其中 衡量了两个有序
degree序列 的距离,且 。的物理意义为:节点 的 阶结构距离等于它们的 阶结构距离加上它们的第 阶环之间的距离。
根据定义有:
- 是随着 递增,并且只有当 各自都存在距离等于 的邻域节点时才有定义。
- 将比较节点 和 各自距离为 的环的有序
degree序列。 - 如果 和 的 阶邻域是
isomorphic同构的,则有 。
最后一步是确定某个函数来比较两个
degree序列,即函数 。考虑到两个有序degree序列 和 可能具有不同的长度(因为对于不同节点,其 阶环的size不同),且它们的元素是位于 之间的任意整数(可能有重复的整数),则如何选择合适的距离函数是一个问题。我们采用
Dynamic Time Warping: DTW算法来衡量两个有序degree序列的距离,该算法可以有效地处理不同长度的序列并宽松地loosely比较序列模式sequence pattern。非正式地,
DTW算法寻找两个序列 和 之间的最佳对齐alignment。给定序列元素的距离函数 ,DTW的目标是匹配每个元素 到 ,使得被匹配的元素之间的距离之和最小。由于序列 和 的元素是节点的degree,因此我们采用以下距离函数:注意:
- 当 时,。因此,两个相同的有序
degree序列将具有零距离。 - 采用这种距离,
degree 1和degree 2之间的距离,相比degree 101和degree 102之间的距离,二者差异悬殊。这恰好是度量节点degree之间距离所需的属性。
最后,虽然我们使用
DTW来评估两个有序degree序列之间的相似性,但是我们的框架可以采用任何其它函数。- 当 时,。因此,两个相同的有序
DTW算法:假设 ,则DTW算法需要寻找一条从 出发、到达 的最短路径。假设路径长度为 ,第 个节点为 ,则路径需要满足条件:- 边界条件:
- 连续性性:对于下一个节点 ,它必须满足 。即数据对齐时不会出现遗漏。
- 单调性:对于下一个节点 ,它必须满足 。即数据对齐时都是按顺序依次进行的。
- 路径最短: ,其中 为单次对齐的距离。
如下图所示,根据边界条件,该路径需要从左下角移动到右上角;根据单调性和连续性,每一步只能选择右方、上方、右上方三个方向移动一个单位。该问题可以通过动态规划来求解。

13.1.2 构建 context graph
我们构建了一个
multilayer加权图来编码节点之间的结构相似性。定义 为一个multilayer图,其中layer()根据节点的 阶结构相似性来定义。layer是一个包含节点集合 的带权无向完全图complete graph(完全图表示任意一对节点之间存在边),即包含 条边。每条边的权重由节点之间的 阶结构相似性来决定:- 仅当 有定义时,
layer中节点 之间的边才有定义。 layer中边的权重与结构距离(即 阶结构相似性)成反比。layer中边的权重小于等于1,当且仅当 时权重等于1。- 和节点 结构相似的节点将在 的各层中都具有更大的权重。
由于 是随着 的增加单调增加的,因此同一对节点 从
multilayer图的底层到高层,边的权重是逐渐降低的。- 仅当 有定义时,
对于
multilayer图的不同层之间,我们使用有向边进行连接。每个节点可以连接上面一层、下面一层对应的节点。假设节点 在layer记作 ,则 可以通过有向边分别连接到 。对于跨
layer的边,我们定义其边的权重为:其中 为
layer中, 的所有边中权重大于该层平均边的权重的数量。即:因此 衡量了在
layer,顶点 和其它顶点的相似性(超出平均水平的、相似的节点数量)。这里采用对数函数,因为节点 超过层内平均权重的边的数量取值范围较大,通过对数可以压缩取值区间。如果 在当前层拥有很多结构相似的节点,则应该切换到更高层进行比较,从而得到更精细的上下文。
根据定义有 ,因此每个每个节点连接更高层的权重不小于连接更低层的权重。
通过向上移动一层,相似节点的数量只会减少。
因为同一对节点 从
multilayer图的底层到高层,结构相似性是逐渐降低的。
具有 层,每一层有 个节点,层内有 条边,层之间有 条边。因此
multilayer图有 条边。接下来我们会讨论如何优化从而降低生成 的计算复杂度,以及存储 的空间复杂度。
13.1.3 生成节点上下文
我们通过
multilayer图 来生成每个节点 的结构上下文。注意: 仅仅使用节点的结构信息,而没有采用任何额外信息(如节点属性或节点label)来计算节点之间的结构相似性。和之前的工作一样,我们也采用随机游走来生成给定节点的上下文。具体而言,我们考虑有偏的随机游走:根据 中边的权重来在 中随机游走。假设当前
layer位于第 层:首先以概率 来决定:是在当前
layer内游走还是需要切换layer游走。即以概率 来留在当前layer,以概率 来跨层。为一个超参数。
layer内游走:当随机游走保留在当前layer时,随机游走从节点 转移到节点 的概率为:其中分母是归一化系数。
因此随机游走更倾向于游走到与当前节点结构更相似的节点,避免游走到与当前节点结构相似性很小的节点。最终节点 的上下文中包含的更可能是和 结构相似的节点,与它们在原始网络 中的
label和位置无关。层间游走:如果需要切换
layer,则是移动到更上一层、还是移动到更下一层,这由层之间的有向边的权重来决定:跨层概率正比于层之间的有向边的权重。
最后,对于每个节点 ,我们从第 层开始进行随机游走。每个节点生成以它为起点的 条随机游走序列,每条随机游走序列的长度为 。
我们通过
SkipGram来从随机游走序列中训练节点embedding,训练的目标是:给定序列中的节点,最大化其上下文的概率。其中上下文由中心窗口的宽度 来给定。- 为了降低计算复杂度,我们采用
Hierarchical Softmax技巧。 - 这里也可以不使用
SkipGram,而采用任何其它的文本embedding技术。
- 为了降低计算复杂度,我们采用
13.1.4 优化
为了构建 ,我们需要计算每一层每对节点之间的距离 ,而 需要基于
DTW算法在两个有序degree序列上计算。经典的DTW算法的计算复杂度为 ,其快速实现的计算复杂度为 ,其中 为最长序列的长度。令 为网络中的最大
degree,则对于任意节点 和layer,degree序列的长度满足 ,其中 表示 的 次幂,它随着 的增加而很快接近 。由于每一层有 对节点,因此计算第 层所有距离的计算复杂度为 。最终构建 的计算复杂度为 。接下来我们介绍一系列优化来显著减少计算复杂度和空间复杂度。优化一:降低有序
degree序列的长度。为了降低对比长序列距离的代价,我们对有序
degree序列进行压缩:对序列中出现的每个degree,我们保存它出现的次数。压缩后的有序degree序列由该degree,以及它出现的次数构成的元组来组成。由于网络中很多节点往往具有相同的degree,因此压缩后的有序degree序列要比原始序列小一个量级。注意:压缩后的有序
degree序列也是根据degree进行排序。令 为压缩后的有序
degree序列,它们的元素都是元组的形式。则我们在DTW中的距离函数 修改为:其中 , 都是
degree, 都是degree对应出现的次数。注意:使用压缩的
degree序列会使得具有相同degree的原始序列片段之间的比较。原始的DTW算法是比较每个degree,而不是比较每个degree片段,因此上式是原始DTW的近似。由于DTW现在在 上计算,而它们要比 短得多,因此可以显著加速DTW的计算速度。优化二:降低成对节点相似性计算的数量。
在第 层,显然没有必要计算每对节点的相似性。考虑
degree相差很大的一对节点(如degree=2和degree=20),即使在 层它们的结构距离也很大。由于节点之间的结构距离随着 的增大而增大,因此当 时它们的结构距离更大。因此这样的一对节点在 中的边的权重很小,则随机游走序列不太可能经过这种权重的边,因此在 中移除这类边不会显著改变模型。我们将每一层需要计算结构相似性的节点数量限制为:每个节点最多与 个节点计算相似性。令节点 需要计算相似性的邻居节点集合为 ,则 需要包含那些在结构上和 最相似的节点,并且应用到所有
layer。我们选取和 的
degree最相似的节点作为 :- 首先对全网所有节点的有序
degree序列进行二分查找,查找当前节点 的degree。 - 然后沿着每个搜索方向(左侧、右侧)获取连续的 个节点。
计算 的计算复杂度为 ,因为我们需要对全网节点根据
degree进行排序。现在 每一层包含 条边 ,而不是 条边。- 首先对全网所有节点的有序
优化三:降低层的数量。
中的层的数量由网络直径 来决定。然而,对于许多网络,直径可能远远大于平均距离。此外,实际上当 的值足够大时,评估两个节点之间的结构相似性就没有任何意义。因为当 接近 时, 和 这两个序列都非常短,这使得 和 几乎相等。
当 较大时,和目标节点 或 距离刚好为 的环非常稀疏。
因此我们可以将 的层的数量限制为一个固定的常数 ,从而仅仅采用最重要的一些层来评估结构相似性。这显著减少了构建 的计算需求和内存需求。
尽管上述优化的组合会影响节点的结构
embedding,但是我们实验证明:这些优化的影响是微不足道的,甚至是有益的。因此降低模型计算量和内存需求的好处远远超出了它们的不足。最后,我们还提供了struc2vec的源代码:https://github.com/leoribeiro/struc2vec。
13.2 实验
13.2.1 杠铃图
我们定义 为
(h,k)-barbell图:- 杠铃图包含两个完全图 和 ,每个完全图包含 个节点。
- 杠铃图包含一个长度为 的路径 ,其节点记作 ,该路径连接两个完全图。
- 两个节点 和 作为
bridge,我们连接 到 、 到 。
杠铃图中包含大量结构身份相同的顶点。
- 定义 ,则所有的节点 为结构等价的。
- 顶点对之间也是结构等价的。
- 这对
bridge也是结构等价的。
下图给出了 杠铃图,其中结构等价的顶点以相同的颜色表示。
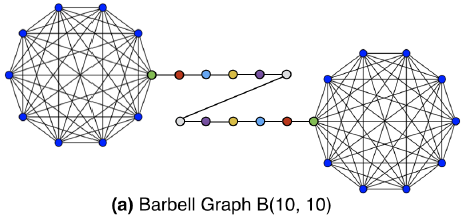
我们期望
struc2vec能够学习捕获上述结构等价的节点representation。结构等价的每个节点都应该具有相似的潜在representation。此外,学到的representation还应该捕获结构层次structural hierarchy:虽然节点 和节点 不等价,但是我们可以清楚地看到,从结构的角度来看,节点 和 更相似(它们的degree更接近)。我们使用
DeepWalk,node2vec,struc2vec等模型学习杠铃图中节点的embedding。这些模型都采用相同的参数:每个节点开始的随机游走序列数量20、每条游走序列长度80、SkipGram窗口大小为5。对于node2vec有 。下图给出了各模型针对 杠铃图学到的
embedding。DeepWalk无法捕获结构等价性。这是符合预期的,因为DeepWalk并不是为结构等价性而设计的。node2vec也无法捕获结构等价性。实际上它主要学习图距离graph distance,将图中距离相近的节点放到embedding空间中相近的位置。node2vec的另一个限制是:SkipGram的窗口大小使得 和 中的节点不可能出现在相同的上下文中。DeepWalk也存在这样的问题。
struc2vec能够学到正确分离的等效类别embedding,从而将结构等价的节点放在embedding空间中相近的位置。例如, 和 靠近 和 中节点的representation,因为它们是bridge。我们提出的三个优化并未对
embedding的质量产生任何重大影响。实际上“优化一”的embedding中,结构等价的节点甚至更加靠近。- 图
b给出了RolX的结果。模型一共确定了六个角色(从左到右依次编号为0 ~ 5),其中一些角色精确地捕获了结构等价性(角色1和3)。然而,结构上等价的节点(在 和 中)被放置在三个不同的角色(角色0,2,5)中,而角色4包含路径中的所有剩余节点。因此,尽管RolX在为节点分配角色时确实捕获了一些结构等价性的概念,但struct2vec更好地识别和分离了结构等价性。
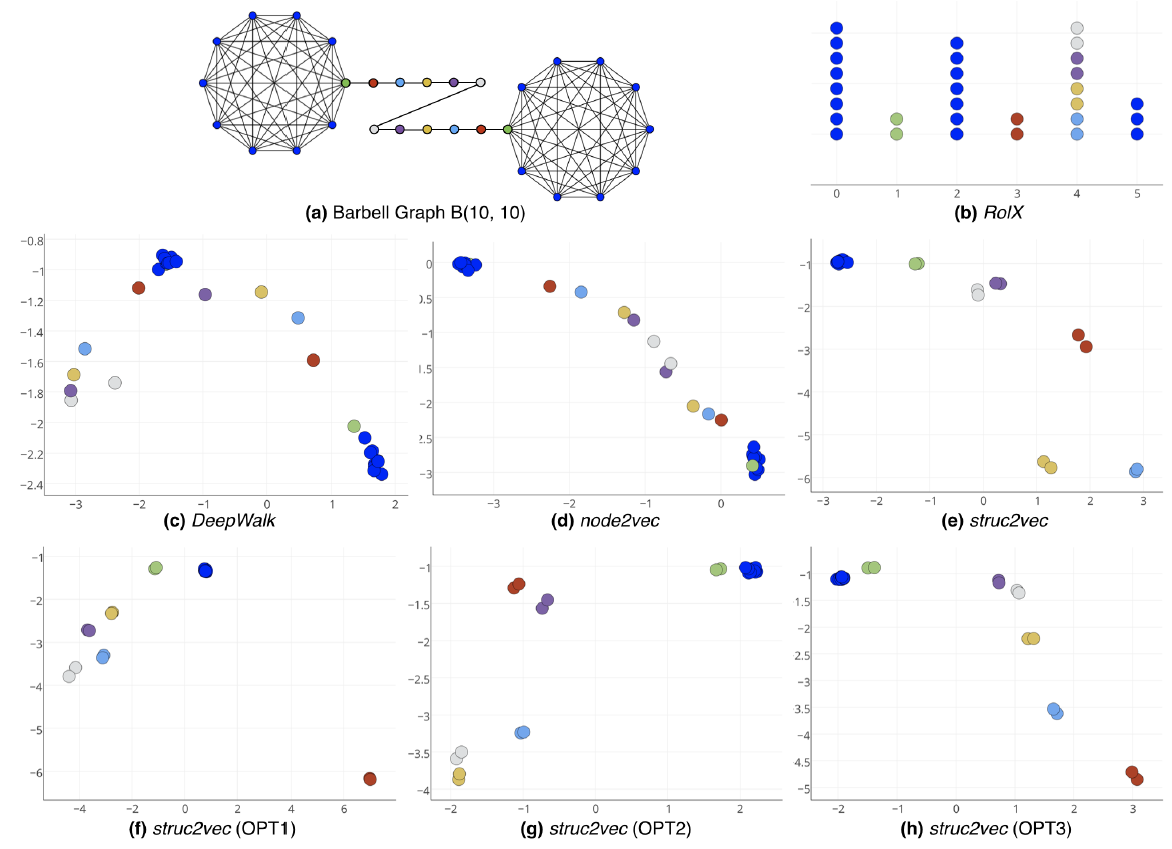
- 图
13.2.2 Karate 网络
Zachary's Karate Club是一个由34个节点、78条边组成的网络,其中每个节点代表俱乐部成员、边表示两个成员是否在俱乐部以外产生互动,因此边通常被解释为成员之间的好友关系。我们的网络由该网络的两个拷贝 组成,其中 都有一个镜像节点 。我们还通过在镜像节点对
(1,37)之间添加一条边来连通 。尽管struc2vec可以建模分离的连通分量,但是DeepWalk和node2vec无法训练。为了与DeepWalk/node2vec基准方法进行公平的比较,我们添加了这条边。下面给出了镜像网络,其中结构身份相等的节点采用相同的颜色表示。
我们使用
DeepWalk,node2vec,struc2vec等模型学习镜像图中节点的embedding。这些模型都采用相同的参数:每个节点开始的随机游走序列数量5、每条游走序列长度15、SkipGram窗口大小为3。对于node2vec有 。DeepWalk和node2vec学习的embedding可视化结果如下图所示。可以看到,它们都未能在潜在空间中对结构等效的节点进行分组。struc2vec再次正确地学到能够捕获节点结构身份的特征。镜像节点pair对在embedding空间中距离很近,并且节点以一个复杂的结构层级structural hierarchy聚合在一起。例如,节点
1和34(及其对应的镜像节点37和42)在网络中具有类似领导者leader的角色,struc2vec成功捕获了它们的结构相似性,即使它们之间不存在边。潜在空间中的另一个簇由节点
2/3/4/33以及它们的镜像节点组成。这些节点在网络中也具有特定的结构身份:它们具有很高的degree,并且至少连接到一个leader。最后,节点26和25具有非常接近的representation,这与它们的结构角色一致:二者都具有低degree,并且距离leader 34有2跳。struc2vec还捕获了non-trivial的结构等价性。注意,节点7和50(粉红色和黄色)映射到潜在空间中靠近的点。令人惊讶的是,这两个节点在结构上是等价的:图中存在一个自同构automorphism将一个节点映射到另一个节点。一旦我们注意到节点6和7在结构上也是等效的,并且节点50是节点6的镜像版本(因此在结构上也是等价的),就可以更容易地看到这一点。RolX一共识别出28个角色。注意:节点1和34被分配到不同角色中,节点1和37也被分配到不同角色中,而34的镜像节点(节点42)被放置在与节点34相同的角色中。34对镜像节点pair对中仅有7对被正确分配角色。然而,还发现了一些其它结构相似性。例如,节点6和7是结构等价的,并且被分配了相同的角色。同样地,RolX似乎捕获到了节点之间结构相似性的一些概念,但是struc2vec可以用潜在representation更好地识别和分离结构等价性。
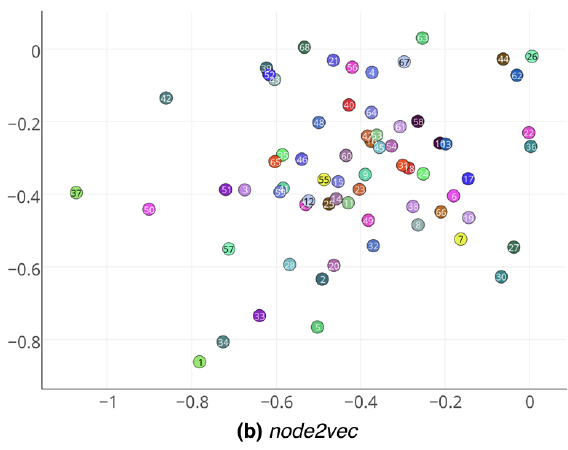


我们测量了每个节点和它的镜像节点之间的
representation距离、每个节点和子图内其它节点的representation距离,下图给出node2vec和struc2vec学到的embedding的这两种距离分布。横轴为距离,纵轴为超过该距离的节点对的占比。对于
node2vec,这两个分布几乎相同。这表明node2vec并未明显的区分镜像节点pair对和非镜像节点pair对,因此node2vec无法很好识别结构等价性。对于
struc2vec,这两个分布表现出明显的差异。94%的镜像pair对之间的距离小于0.25,而68%的非镜像pair对之间的距离大于0.25。此外,非镜像
pair对的平均距离是镜像pair对平均距离的5.6倍,而node2vec这一比例几乎为1。
为了更好地刻画结构距离和
struc2vec学到的潜在representation距离的关系,我们评估所有节点对之间的距离(通过 来衡量),以及它们在embedding空间中的距离(通过欧式距离来衡量)的相关性。我们分别计算Spearman相关系数和Pearson相关系数,结果如下图所示。这两个系数表明:对于每一层这两个距离都存在很强的相关性。这表明
struc2vec确实在潜在空间中捕获了结构相似性。
13.2.3 鲁棒性
为了说明
struc2vec对噪音的健壮性,我们从网络中随机删除边从而直接修改其网络结构。给定图 ,我们以概率 随机采样图 中的边从而生成新的图 ,这相当于图 的边以概率 被删除。我们使用 再次重复该过程从而生成另一个新的图 。因此, 和 通过 在结构上相关,而 控制结构相关性的程度。注意,当 时, 和 是同构的;当 时,所有的结构身份都丢失了。我们从
Facebook网络中随机采样,该网络包含224个节点、3192条边,节点degree最大为99最小为1。我们采用不同的 来生成两个新的图 和 ,我们重新标记 中的节点从而避免 和 中存在相同编号的节点。我们将 和 的并集视为我们框架的输入网络。注意,合并后的图至少有两个连通分量(分别对应于 和 ),并且 中的每个节点在 中都有对应的镜像。下图给出了不同的 值,
struc2vec学到的所有节点pair对之间embedding的距离分布。其中x标记的是镜像节点pair对之间的距离,+标记的是所有节点pair对之间的距离。当 时,两个距离分布明显不同。所有节点
pair对之间的平均距离要比镜像节点pair对之间的平均距离大21倍。当 时,两个距离分布仍然非常不同。进一步减小 不会显著影响所有节点
pair对的距离分布,但是会缓缓改变镜像节点pair对的距离分布。即使在 时,这意味着原始边同时出现在 和 中的概率为
0.09,struc2vec仍然会将镜像节点pair对进行很好的区分。这表明即使在存在结构噪音(通过随机移除边)的情况下,
struc2vec在识别结构身份方面仍然具有很好的鲁棒性。


13.2.4 分类任务
网络节点潜在
representation的一个常见应用是分类。当节点label与其结构身份相关时,可以利用struc2vec来完成节点分类任务。为了说明这种潜力,我们考虑一个空中交通网络。空中交通网络是一个无权无向图,每个节点表示机场,每条边表示机场之间是否存在商业航班。我们根据机场的活跃水平来分配label,其中活跃水平根据航班流量或者人流量为衡量。数据集:
- 巴西空中交通网络
Brazilian air-traffic network:包含2016年1月到2016年12月从国家民航局ANAC收集的数据。该网络有131个顶点、1038条边,网络直径为5。机场活跃度是通过对应年份的着陆总数与起飞总数来衡量的。 - 美国空中交通网络
American air-traffic network:包含2016年1月到2016年10月从美国运输统计局收集的数据。该网络有1190个顶点、13599条边,网络直径为8。机场活跃度是通过对应年份的人流量来衡量的。 - 欧洲空中交通网络
European air-traffic network:包含2016年1月到2016年11月从欧盟统计局收集的数据。该网络包含399个顶点、5995条边,网络直径为5。机场活跃度是通过对应年份的着陆总数与起飞总数来衡量的。
对于每个机场,我们将其活跃度的标签分为四类:对每个数据集我们对活跃度的分布进行取四分位数从而分成四组,然后每一组分配一个类别标签。因此每个类别的样本数量(机场数量)都相同。另外机场类别更多地与机场角色密切相关。
- 巴西空中交通网络
我们使用
struc2vec和node2vec来学习每个网络的顶点embedding,其中我们通过grid search来为每个模型选择最佳的超参数。注意,该步骤不使用任何节点标签信息。然后我们将学到的
embedding视为特征来训练一个带L2正则化的one-vs-rest逻辑回归分类器。我们还考虑直接将顶点的degree作为特征来训练一个逻辑回归分类器,从而比较使用原生特征和embedding特征的区别。因为节点的degree捕获了一个非常基础basic的结构身份概念。由于每个类别的规模相同,因此我们这里使用测试准确率来评估模型性能。我们将分类模型的数据随机拆分为
80%的训练集和20%的测试集,然后重复实验10次并报告平均准确率。结论:
struc2vec模型学到的embedding明显优于其它方法,并且其优化几乎没有产生影响。对于巴西网络,struc2vec相比node2vec,其分类准确率提高了50%。- 有趣的是,在巴西网络中,
node2vec模型学到的embedding的平均性能甚至略低于直接使用节点degree,这表明在这个分类任务中,节点的结构身份起到了重要作用。
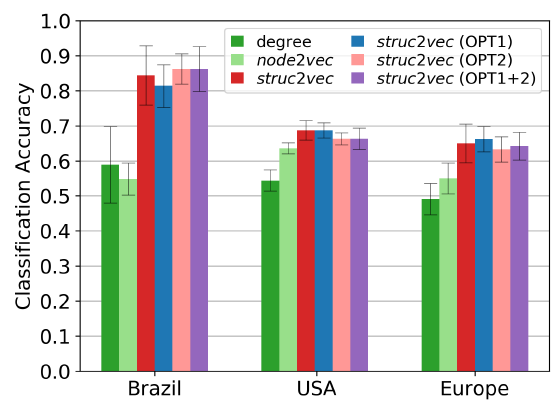
13.2.5 可扩展性
为了说明
struc2vec的可扩展性,我们将采用优化一、优化二的struc2vec应用于Erd¨os-R´enyi随机图。我们对每个节点采样10个随机游走序列,每个序列长度为80,SkipGram窗口为10,embedding维度为128。为加快训练速度,我们使用带负采样的SkipGram。为评估运行时间,我们在顶点数量从
100到100万、平均degree为10的图上训练struc2vec。每个实验我们独立训练10次并报告平均执行时间。其中training time表示训练SkipGram需要的额外时间。下图给出了
log-log尺度的训练时间,这表明struc2vec是超线性的,但是接近 (虚线)。因此尽管struc2vec在最坏情况下在时间和空间上都是不利的,但是实际上它仍然可以扩展到非常大的网络。的时间复杂度对于千万级甚至亿级的大型图而言仍然是难以接受的,其计算复杂度是线性复杂度的成千上万倍。
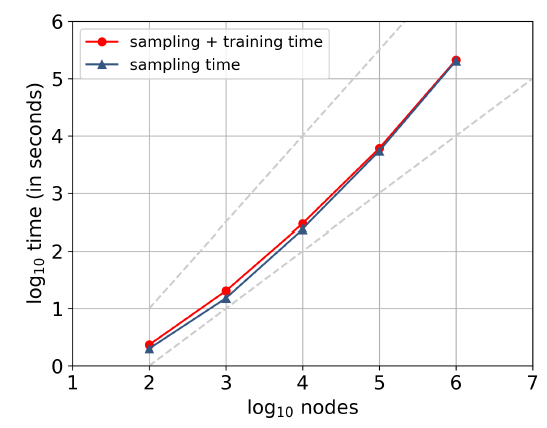
十四、GraphWave[2018]
图中的结构角色发现
structural role discovery侧重于识别具有相似拓扑网络邻域的节点,这些节点可能位于网络中相距遥远的区域。如下图所示,尽管节点 和 在图中相距甚远,但它们具有相似的结构角色structural role。直观而言,具有相似结构角色的节点在网络中执行相似的功能,例如公司社交网络中的manager、或者细胞分子网络中的酶。这种节点相似性的定义与传统的定义非常不同。传统的节点相似性定义假设图上一定程度的平滑性smoothness,因此网络中距离较近的节点是相似的。这种关于节点结构角色的信息可用于各种任务,包括作为机器学习问题的输入、识别系统中的关键节点(如社交网络中的核心 “影响者”、传染图中的关键hub)。
当在离散空间上定义节点的结构角色时,这些结构角色对应于局部网络邻域
local network neighborhood的不同拓扑,例如链条上的节点、星形的中心、两个簇之间的bridge。然而,这种离散角色必须预定义pre-defined,并且需要领域内的专业知识和人工探查图结构。一种用于识别结构相似性的更强大、更鲁棒的方法是,以无监督的方式学习每个节点 的结构embedding向量 。这启发了根据拓扑embedding的邻近性对结构相似性structural similarity的自然定义:对于任意 ,如果 则节点 被定义为ϵ-structurally similar的。因此这种方法必须引入适当的embedding方法以及一个合适的距离函数dist()。虽然已有几种方法来学习图中节点的结构
embedding(structural embedding) ,但是现有方法对拓扑中的小扰动极为敏感,并且缺乏对所学到embedding特性的数学理解。此外,它们通常需要人工标记拓扑特征(《RolX: structural role extraction & mining in large graphs》)、依赖于不可扩展non-scalable的启发式方法(《struc2vec: Learning node representations from structural identity》)、和/或返回单个相似性得分而不是多维结构embedding(《Scalable and axiomatic ranking of network role similarity》,《Axiomatic ranking of network role similarity》)。在论文
《Learning Structural Node Embeddings via DiffusionWavelets》中,作者通过开发GraphWave来解决图上的结构学习structure learning问题。基于图信号处理graph signal processing技术,论文的方法基于以节点为中心的谱图小波的扩散diffusion of a spectral graph wavelet,从而为每个节点学习多维连续的结构embedding。直观而言,每个节点在图上传播一个能量单位a unit of energy,并根据网络对该探针probe的响应response来刻画其邻域拓扑neighboring topology。论文正式证明了这个小波wavelet的系数与图拓扑性质直接相关。因此,这些系数包含恢复结构相似节点的所有必要信息,而无需对特征进行显式地人工标记hand-labeling。然而,根据设计,小波在图上是局部的。因此如果两个节点相距较远,则它们之间的小波是无法进行比较的。这时需要为每对节点指定一个一对一的映射,从而使得一对节点之间的小波可以进行直接比较,如计算每对顶点的小波之间的相关系数或者计算 距离。这种节点对之间的一一映射计算量太大,因此是难以实现的。所以这些小波方法从未被用于学习结构
embedding。为了克服这一挑战,论文提出了一种新的方法从而将小波视为图上的概率分布。这样,结构信息包含在 “
diffusion如何在网络上传播”,而不是“diffusion在网络上传播到哪里”。为了提供embedding,论文使用经验特性函数empirical characteristic function来嵌入这些小波分布wavelet distribution。经验特性函数的优点是它们捕获给定分布的所有矩(包括高阶矩)。正如论文在数学上证明的那样,这允许GraphWave对局部边结构local edge structure中的小扰动具有鲁棒性。GraphWave的计算复杂度在edge数量上是线性的,因此可以扩展到大型(稀疏的)网络。最后,论文在真实数据集和人工合成数据集上,将GraphWave与几个state-of-the-art基准进行比较,获得了137%的提升。论文还展示了GraphWave如何成为图中结构embedding的有效工具。论文的主要贡献如下:
- 论文通过将谱图小波
spectral graph wavelet视为概率分布,并使用经验特性函数来刻画这个分布,从而提出了谱图小波的新用途。 - 论文利用这些洞察开发了一种可扩展的方法
GraphWave,该方法基于图中结构相似性来学习节点embedding,并优于现有的state-of-the-art基准方法。 - 论文在数学上证明
GraphWave准确地恢复了结构相似structurally similar和结构等价structurally equivalent的节点。
- 论文通过将谱图小波
相关工作:关于挖掘相似结构角色节点的先前工作通常依赖于节点的显式特征。在基于这种启发式
heuristic representation计算节点相似性之前,这些方法生成每个节点的局部拓扑属性local topological property的详尽列表,例如节点degree、节点参与的三角形数量、k-clique数量、PageRank得分。这些方法中的一个值得注意的例子是RolX,它是一种基于矩阵分解的方法,旨在使用递归的特征抽取recursive feature extraction从而将节点的软聚类softclustering恢复为预定数量的 个不同角色。类似地,struc2vec使用启发式方法构建基于拓扑指标topological metric的multilayer graph,并在图上模拟随机游走从而捕获结构信息。相比之下,我们的方法不依赖于启发式(因为我们在数学上证明了我们方法的有效性),并且不需要显式的人工特征工程、或人工超参数调优。最近的神经表示学习
neural representation learning方法(structure2vec、neural fingerprint、graph convolutional network: GCN、message passing network等等)是相关的研究方向。然而,这些graph embedding方法不适用于我们的setting,因为它们解决了监督的图分类任务、和/或嵌入了整个graph。相比之下,我们的方法是无监督的,并且仅嵌入单个节点。另一类相关工作是
graph diffusion kernel(《Diffusion maps》),该方法已被用于各种图建模任务。然而,据我们所知,我们的论文是第一个应用graph diffusion kernel来确定图中结构角色的论文。kernel已被证明可以有效地捕获几何属性,并已成功用于图像处理社区中的形状检测shape detection。然而,与形状匹配shape-matching问题相比,GraphWave将这些kernel视为真实世界的图上的概率分布。这是因为我们考虑的图是高度不规则的(与欧式图Euclidean graph和流形图manifold graph相反)。因此,传统的小波方法通常分析以规则和可预测的模式发生的、特定节点上的节点扩散node diffusion,这种方法并不适用于我们的场景。相反,GraphWave刻画了扩散的形状diffusion shape,而不是扩散发生的特定节点。这一关键洞察使我们能够发现结构embedding,从而进一步发现结构相似的节点。
14.1 模型
给定无向图 ,其中 为节点集合, 为边集合, 为节点数量。令邻接矩阵为 ,它是二元的或者带权重的。定义度矩阵 ,其中 。
节点的结构
embedding问题为:对于每个节点 ,我们希望在一个连续的多维空间中学得一个embedding来表示它的结构角色structural role。我们将这个问题构建为基于谱图小波spectral graph wavelet的无监督学习问题,并开发了一种称为GraphWave的方法。该方法从数学上保证了所学到结构embedding的最优性能。
14.1.1 谱图小波
令 为未归一化的拉普拉斯矩阵,令 为 的特征向量
eigenvector组成的特征矩阵,则有:其中 , 为 的特征值
eigenvalue。图拉普拉斯矩阵的性质:
- 图拉普拉斯矩阵是半正定矩阵,因此有 。
- ,因为拉普拉斯矩阵每一行的和均为零。
- 特征值中
0出现的次数就是图连通区域的个数。对于单连通图,有 。 - 最小非零特征值是图的代数连通度,通常记作 。
令 为一个
scaling参数为 的滤波器核filter kernel,这里我们采用热核heat kernel,但是我们的结论适用于任何类型的scaling wavelet。另外,这里我们假设 是给定的,后续会讨论如何选择一个合适的 值。图信号处理
graph signal processing将与 相关的谱图小波spectral graph wavelet定义为:以顶点 为中心的狄拉克信号的频域响应。因此谱图小波 定义为:其中 是顶点 的
one-hot向量:顶点 对应的位置为1,其它位置为0。因此节点 的第 个小波系数为 。谱图矩阵 ,它的第 列就是 ,它的第 列第 行就是 。
的物理意义为:节点 处的狄拉克信号在节点 处的响应。并且该系数是对称的,即 。
可以看到在谱图小波中,核 调制
modulate了特征谱eigenspectrum,使得响应信号位于空域的局部区域以及频域的局部区域。如果我们将拉普拉斯矩阵和信号系统中的 ”时域-频域“ 进行类比,则发现:- 较小特征值对应的特征向量携带变化缓慢的信号,从而鼓励邻居节点共享相似的信息。
- 较大特征值对应的特征向量携带迅速变化的信号,从而使得邻域节点之间区别较大。
因此低通滤波器核
low-pass filter kernel可以看作是一种调制算子modulation operator,它降低了较高的特征值并在图中平滑了信号的变化。
14.1.2 GraphWave
我们首先描述
GraphWave算法,然后对其进行分析。对于每个节点 ,GraphWave返回表示其结构embedding的一个2d维的向量 ,使得局部网络结构相似的节点拥有相似的embedding。算法中,我们首先应用谱图小波来获取每个顶点的
diffusion pattern, 然后收集到矩阵 中,其中第 列的列向量是以节点 为中心的heat kernel产生的谱图小波。现有的工作主要研究将小波系数视为
scaling参数 的函数,而这里我们将小波系数视为局部网络结构的函数:小波系数随着节点 的局部网络结构的变化而变化。具体而言,每个小波系数都由节点来标识,并且都有深刻的物理意义: 表示节点 从节点 接收到的能量的大小(由于对称性,它也表示节点 从节点 接收到的能量的大小)。我们将小波系数视为概率分布,并通过经验特性函数来刻画该分布。我们将证明:具有相似网络邻域结构的节点 和 将具有相似的谱图小波系数分布 和 。这是一个关键的洞察,这使得GraphWave可以通过谱图小波学习节点的结构embedding。更准确地说,我们通过计算每个节点的小波系数 的特性函数,并将其在 个均匀间隔的空间点采样,从而将谱图小波系数分布
spectral graph wavelet coefficient distribution嵌入到 维的空间。概率分布 的特性函数定义为:它完全刻画了分布 ,因为它捕获了关于分布 的所有矩的信息。将它进行泰勒展开得到:
给定节点 和
scale s, 的经验特性函数定义为:理论上我们需要计算足够多的点来描述 ,但是这里我们采样了 个均匀间隔的点,即 。最终得到:
注意到我们在经验特性函数 上均匀采样了 个点,这创建了一个大小为 的
embedding,因此embedding的维度和图的大小无关。GraphWave核心思想:节点空域的局部结构相似性问题,转变为频域的小波相似性问题。它并没有采用最优化过程来优化某个代价函数,因此也没有梯度下降法来迭代求解。GraphWave算法:输入:
- 图
scale参数- 个均匀分布的采样点
输出:节点的结构
embedding向量算法步骤:
计算拉普拉斯矩阵 ,并进行特征分解: 。
计算图谱小波 。
对 ,计算 为 的
column-wise逐列均值。对于节点 ,将 的实部和虚部分配给 ,其中 为 的第 个元素。每个节点拼接 个实部和 个虚部,则得到一个
2d维的向量。
结构
embedding之间的距离:GraphWave的输出为图中每个节点的结构embedding。我们可以将结构embedding之间的距离定义为 距离,即节点 和 之间的结构距离定义为:根据函数的定义,这相当于在小波系数分布上比较不同阶次的矩。
scaling参数:scaling参数 确定每个节点 周围的网络邻域的半径。- 较小的 会使用较小半径的邻域来确定节点的结构
embedding。 - 较大的 会使得扩散过程在网络上传播得更远,从而导致使用较大半径的邻域来确定节点的结构
embedding。
GraphWave还可以采用 的不同取值来集成多尺度结构embedding,这是通过拼接 个不同的embedding来实现的,每个embedding都和一个scale相关,其中 。我们接下来提供一个理论上的方法来找到合适的 。在多尺度版本的
GraphWave中,最终节点 聚合的结构embedding为:- 较小的 会使用较小半径的邻域来确定节点的结构
计算复杂度:我们使用切比雪夫多项式来计算 ,拉普拉斯算子的每个幂具有 的计算成本,从而产生 的整体计算复杂度,其中 表示切比雪夫多项式逼近的阶数。因此
GraphWave的整体计算复杂度是edge数量的线性的,这使得GraphWave可以扩展到大型稀疏网络。
14.1.3 理论分析
这里我们为基于谱图小波的模型提供了理论动机。我们首先通过理论分析表明:谱图小波系数刻画了局部网络领域的拓扑结构。然后我们理论上证明:结构等价/相似的节点具有几乎相等/近似的
embedding,从而为GraphWave的最优性能提供了数学保证。谱图小波和网络结构:我们首先建立节点 的谱图小波和节点 的局部网络结构之间的关系。具体而言,我们证明了小波系数 提供了节点 和节点 之间网络连通性
network connectivity的度量。由于图拉普拉斯算子的谱是离散的,并且位于区间 之间,根据
Stone-Weierstrass定理可知:核 在区间 上可以通过一个多项式来逼近。记这个多项式为 ,则这个多项式逼近是紧的tight,其误差是一致有界的uniformaly bounded。即:其中 为多项式逼近的阶数, 为多项式系数, 为残差。
我们可以将顶点 的谱图小波以多项式逼近的形式重写为:
由于 是单位正交矩阵, 是一致有界的,因此我们可以通过
Cauchy-Schwartz不等式将等式右侧的第二项进行不等式变换 :其中等式左边为 的第 个元素, (因为 为单位正交矩阵), 以及:
因此每个小波 可以由一个 阶多项式逼近,该多项式捕获了有关顶点 的 阶邻域信息。这表明谱图小波主要受到顶点的局部拓扑结构影响,因此小波包含了生成顶点结构
embedding所必须的信息。结构等价节点的
embedding:然后我们证明局部邻域结构相同的顶点具有相似的embedding。假设顶点 和 的 阶邻域相同,其中 是一个小于图的直径的整数。这意味着顶点 和 在结构上是等价的。我们现在证明 和 在GraphWave中具有ϵ-structurally similar embedding。我们首先将 根据泰勒公式在零点展开到 阶:
然后对于每个特征值 ,我们使用
Taylor-Lagrange等式来确保存在 ,使得:如果我们选择 使得满足:
则可以保证绝对残差 对于任意 成立。这里 是一个参数,可以根据结构等效的顶点的
embedding期望的接近程度来指定,因此也称作ϵ-structurally similar。另外 越小则可以选择 更小,使得上界越紧。注意,这里采用 是因为最小的特征值 。
由于顶点 和 的邻域是相同的,因此存在一个
one-to-one映射 ,它将 的 阶邻域 映射到 的 阶邻域 ,使得 。通过随机映射剩余的顶点( 的 阶邻域以外的顶点),我们将 作用到整个图 上。利用图拉普拉斯矩阵的 阶多项式近似,我们有:
考虑第二行的第一项。由于顶点 和 的 阶邻域是等价的,以及拉普拉斯算子
K阶幂的局部性(表示路径为K的路径)则有:因此这一项可以约掉。
第二个等式为零,这是因为 不在节点 的 阶邻域内,因此也就不存在从节点 到 的、长度为 的路径。
考虑第二行的第二项、第三项。使用前面的残差分析可以得到它们都有一个一致的上界 ,因此有:
即: 中的每个小波系数和它对应的 中的小波系数的距离不超过 。
考虑到我们使用经验特性函数来描述分布,因此这种分布的相似性就转换为
embedding的相似性。因此如果选择合适的scale,则结构上等价的节点具有ϵ-structurally similar embedding。
结构相似节点的
embedding:接着我们证明局部邻域结构相似的顶点具有相似的embedding。设顶点 的 阶领域为 , 为顶点 的一个扰动的 阶邻域,这是通过对顶点 的原始 阶邻域重新调整边来得到。假设扰动后的图拉普拉斯矩阵为 ,接下来我们证明:如果顶点邻域的扰动很小,则顶点的小波系数的变化也很小。
假设扰动很小,即: 。我们使用核 的 阶泰勒公式在零点展开来表示扰动图的小波系数:
我们使用
Weyl定理将图结构中的扰动与图拉普拉斯算子的特征值变化联系起来。特别地,图的小扰动导致特征值的小扰动。即,对于每个 , 和原始的 接近:其中 表示 的一个无穷小量, 为一个常数。
综合所有因素,则有:
因此在
GraphWave中,结构相似的顶点具有相似的embedding。
14.1.4 scale 参数
我们开发了一个自动的方法来为
heat kernel中的scale参数 找到合适的取值范围,该方法将在GraphWave的多尺度版本中使用。我们通过分析热扩散
heat diffusion小波的方差来指定 和 来作为区间边界。直观而言:- 较小的 值使得热传播的时间较短,从而使得热扩散的小波分布没有意义,因为此时只有很少的几个小波系数是非零,绝大多数小波系数都是零。
- 较大的 值使得热传播的时间较长,热扩散的小波分布也没有意义,因为此时网络收敛到所有顶点都处于能量为 的同温状态。这意味着扩散分布
diffusion distribution与数据无关,因此没有信息。
这里我们证明两个命题,从而为热扩散小波分布的方差和收敛速度提供洞察
insight。然后我们使用这些结论来选择 和 。命题一:热扩散小波 中非对角线的系数的方差与以下指标成正比:
其中 随着 的增加单调递减。这是因为 ,它随着 的增加单调递减。
注意,,因此 。
证明:令小波 的非对角线系数均值为 。考虑到 为一个概率分布,因此有 。
根据方差的定义有:
命题一证明了小波系数的方差是 的函数,因此为了最大化方差我们必须分析 。为了确保小波系数的分布具有足够大的容量(即分布的多样性足够大),我们需要最大化方差。
因此我们选择区间 来使得 足够大,从而使得
diffusion既有足够长的时间来扩散、又不至于太长以至于到达网络的收敛状态(所有顶点的温度都相同)。注意, “足够大”并不意味着最大化这个变量。
命题二:热扩散小波系数 的收敛上下界为:
证明:对于非负的 有:
第一个不等式是因为 ,因此 。这里用到了不变式: 。
对应的有:
因此有:
对于任意的 ,我们采用数学归纳法可以证明有:
由于 是 的连续递增函数,因此我们选择大于等于零且满足条件的 进行向下、向上取整。
选择 :我们选择 使得小波系数被局限在局部邻域上(即不能收敛到同温状态)。根据命题二:
- 当大部分特征值倾向于 时, 倾向于 (命题二的下界)。
- 当大部分特征值倾向于 时, 倾向于 (命题二的上界)。
如果 高于给定阈值 (其中 ),则扩散是局部的。事实上这确保了 最多收缩到其初始值 的 (因为 随着 的增加而单调递减 ),并产生如下形式的边界:
这个边界意味着 或者 。为了在两种收敛场景之间找到一个中间地带,我们将 设为 和 的几何平均值。与算术平均值相比,几何平均值在 范围内保持相等的权重, 中的 的变化与 的 的变化具有相同的效果。因此,我们选择 为:
其中 为超参数, 越接近
1则 越小, 越接近0则 越大。选择 :我们选择 使得每个小波都有足够长的时间来扩散,即限定:
同样的分析我们有 。因此我们选择:
其中超参数 , 参数越接近
1则 越小, 参数越接近0则则 越大。为覆盖适当的
scale区间,论文建议设置 以及 。
14.2 实验
GraphWave的embedding独立于下游任务,因此我们在不同任务中对其进行评估,从而证明它在捕获网络结构角色方面的潜力。baseline方法:我们将GraphWave和两个结构嵌入的state-of-the-art基准方法struc2vec、RolX进行评估。struc2vec:struc2vec通过在multilayer graph上的一系列随机游走来发现不同尺度的结构嵌入。RolX:RolX基于节点特征(如degree、三角形数量)的矩阵的非负矩阵分解的方法,该方法基于给定的一组潜在特征来描述每个节点。注意,GraphWave和struc2vec在连续频谱上学习embedding,而不是在离散的类别中学习。- 我们还将
GraphWave和最近的两种无监督节点representation learning方法node2vec、Deepwalk方法进行比较,以强调这些方法与我们基于结构相似性方法之间的差异。
对于所有
baseline,我们使用这些模型的默认参数。对于GraphWave模型,我们使用多尺度版本,并设置 ,以及使用 内均匀间隔的采样点 。我们再次注意到,
graph embedding方法(structure2vec、neural fingerprint、GCN等等)不适用于这些setting,因为它们嵌入了整个graph,而我们嵌入了单个节点。
14.2.1 杠铃图
我们首先考虑一个杠铃图。杠铃图由两个长链组成的稠密团构成,该图包含
8个不同类别的结构等价节点,如图A的颜色所示。我们通过PCA可视化了不同模型学到的embedding,相同的embedding具有相同的投影,这使得图B~D上的点发生重叠。- 从图
D可以看出,GraphWave可以正确学习结构等价顶点的embedding,这为我们的理论提供了支撑(相同颜色的顶点几何完全重叠)。
- 从图
相反,
struc2vec和RolX都无法准确的识别结构等价性(相同颜色的节点并未重叠)。对于struc2vec,投影与预期的顺序不一致:黄色节点比红色节点离绿色节点更远。相比之下,RolX产生高度相似的节点embedding,其投影聚集成三个high-level的分组,这意味着RolX可以识别杠铃图中八个结构类别中的三个。- 所有方法都能识别杠铃图的稠密团的(紫色)的结构,但是只有
GraphWave能够准确识别杠铃图的链上节点的结构角色。
- 所有方法都能识别杠铃图的稠密团的(紫色)的结构,但是只有
14.2.2 结构等价的图
我们在人工合成的图上评估这些方法。我们开发了一个程序来生成合成图,这些合成图可以植入结构等价的子图,并且给出每个节点角色的真实标签。我们的目的是通过这些真实的角色标签来评估这些方法的性能。
我们的合成图由不同类型的基础形状给出,这些形状类型包括
house,fan,star,它们沿着长度为30的圆环规则地放置。我们一共评估四种网络结构配置:- 在
house配置中,我们选择将4个house放置在一个长度为30的圆环上。 - 在
varied配置中,我们对每个类型的形状选择8个,并随机放置在一个长度为40的圆环上,从而生成具有更丰富、更复杂结构角色的合成图。 - 在
noise配置中,我们随机添加边来增加扰动(最多10%),从而评估house perturbed, varied perturbed的鲁棒性。
我们对这四种网络结构
house, varied, house perturbed, varied perturbed分别构造一个图,然后在这些构造的图上运行不同方法来得到节点embedding。- 在
我们通过两种
setting来评估每个embedding算法的性能:无监督评估
setting:我们评估每种embedding方法将具有相同结构角色的节点嵌入到一起的能力。我们使用agglomerative聚类算法(采用single linkage)来对每种方法学到的embedding进行聚类,然后通过以下指标来评估聚类质量:同质性
homogeneity:给定聚类结果的条件下,真实结构角色的条件熵。它评估聚类结果和真实结果的差异。完整性
completeness:在所有真实结构角色相等的节点中,有多少个被分配到同一个聚类。即评估聚类结果的准确性。轮廓系数
silhouette score:它衡量簇内距离和簇间距离的关系。即评估样本聚类的合理性。对于样本 ,假设它到同簇类其它样本的平均距离为 ,则 越小说明该样本越应该被聚到本簇,因此定义 为簇内不相似度。假设它到其它簇 的平均距离为 ,则定义簇间不相似度为 。定义轮廓系数为:
xxxxxxxxxx11> 当 $s(i)$ 越接近 `1` ,则说明样本 $v_i$ 聚类合理;当 $s(i)$ 越接近 `-1` ,则说明样本 $v_i$ 聚类不合理。
- 监督评估估
setting:我们将学到的节点embedding作为特征来执行节点分类,类别为节点的真实结构角色。我们使用kNN模型,对所有样本进行10折交叉验证。对于测试集的每个节点,我们根据它在训练集中最近邻的4个节点来预测该节点的结构角色,其中”近邻” 是通过embedding空间的距离来衡量。最终我们给出分类的准确率和F1得分作为评估指标。
所有两种策略的每个实验都重复执行25 次,并报告评估指标的均值。
模型
embedding的效果比较如下图所示。- 对于无监督和有监督的
setting,GraphWave都优于其它四种方法。 - 所有实验中,
node2vec、DeepWalk的效果都很差,其得分显著低于基于结构等价的方法。这是因为这两个方法的重点都是学习节点的邻近关系,而不是节点的结构相似性。 GraphWave的效果始终优于struc2vec,在每种setting下的指标都获得更高的得分。- 虽然
RolX在部分实验中效果强于GraphWave,但是GraphWave整体效果较好。 - 轮廓系数
silhouette score表明:GraphWave发现的簇往往更聚集并且簇之间的间隔更好。
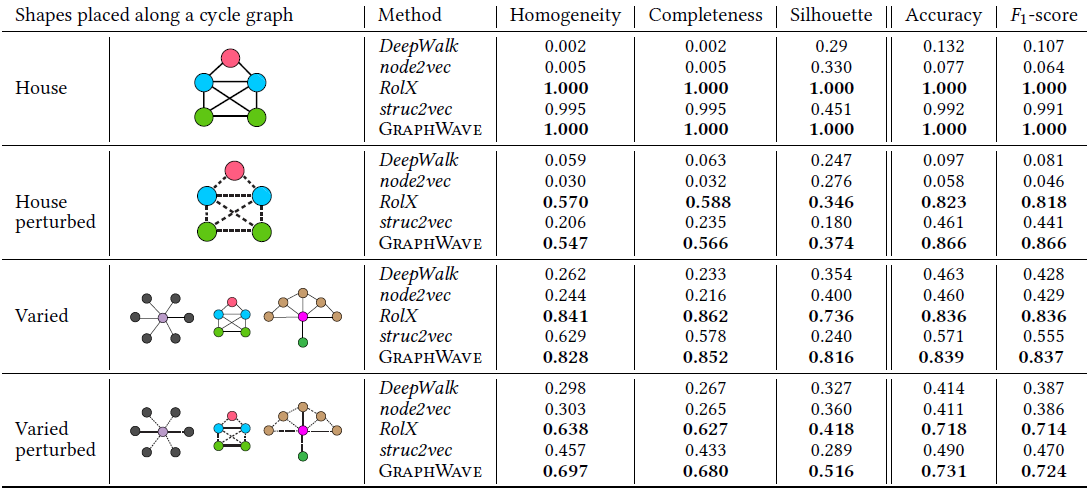
- 对于无监督和有监督的
我们将
GraphWave学到的embedding进行可视化,这提供了一种观察节点之间结构角色差异的方法。如图
A表示一个带house的环,图B是它的GraphWave学到的embedding的2维PCA投影。这证明了GraphWave可以准确区分不同结构角色的节点。图
C给出了特性函数 ,不同颜色对应不同结构角色的节点。其物理意义为:- 位于图外围的节点难以在图上扩散信号,因此派生出的小波具有很少的非零系数。因此这类节点的特性函数是一个较小的环状
2D曲线。 - 位于图核心(稠密区域)上的节点趋向于将信号扩散得更远,并在相同 值下到达更远的节点。因此这类节点的特性函数在 轴和 轴上具有更远的投影。
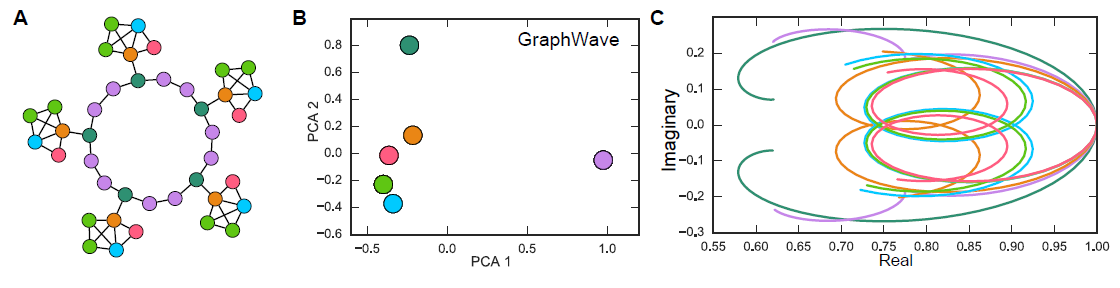
- 位于图外围的节点难以在图上扩散信号,因此派生出的小波具有很少的非零系数。因此这类节点的特性函数是一个较小的环状
14.2.3 跨图的 Embedding 泛化
我们分析
embedding如何识别位于不同图上的节点的结构相似性,这是为了评估embedding能否识别跨图的结构相似性。我们通过以下过程来生成
200个具有真实顶点结构角色标签的图。- 首先以
0.5的概率来选择环形图或者链式图,从而确定了图的骨架。 - 然后通过均匀随机选择环的大小或者链的长度来决定骨架的大小。
- 最后随机选择一定数量的小图挂载到骨架上,这些小图以
0.5的概率从5个节点的house或者5个节点的chain中选取。
为了在噪音环境中评估
embedding方法,我们还在节点之间随机添加10个随机边,然后训练每个节点的embedding。接着用学到的embedding来预测每个节点的真实结构角色。- 首先以
为了评估每个方法在跨图上的泛化能力,我们使用
10折交叉验证,并且对于测试集中的节点我们选择训练集中和它最近邻(通过embedding来计算距离)的4个邻居节点来预测该测试节点的标签。注意:所选择的4个邻居节点可能位于不同的图上。最后我们评估预测的准确率和F1得分,评估结果如下。结果表明:GraphWave方法在两个分类指标上均优于所有其它方法,这表明了GraphWave具有学习结构特征的能力,这种结构特征对于不同的图都有重要意义,且具有很高的预测能力。
最近的无监督节点
representation learning方法表现不佳,而表现第二好的方法是RolX。
14.2.4 可扩展性和鲁棒性
这里我们分析
GraphWave的可扩展性以及它对输入图中噪声的敏感性。为评估
GraphWave的可扩展性我们逐渐扩大了合成图的节点数量,我们给出了这些合成图上运行GraphWave的时间和节点数量的关系,如下图所示。GraphWave的训练时间是边数量的线性函数,因此它是一种快速算法,可以使用稀疏矩阵表示sparse matrix representation来有效地实现。GraphWave的潜在瓶颈是通过经验特性函数将小波系数的分布转换成embedding向量。这里利用了小波系数的稀疏性。小波系数通常是稀疏的,因为
GraphWave通过合理的选择scale参数 使得小波不会被传播得太远。这种稀疏性可以降低embedding过程的计算量,因为这里是一组稀疏矩阵相乘,并且在非零元素上应用element-wise函数。相比之下,
struc2vec无法应用到大图上,对于仅包含100个顶点的图,它都需要高达260秒来学习顶点的embedding。而RolX可以扩展到类似大小的图上。
接下来我们评估
GraphWave对噪音的鲁棒性。我们将噪音采取与varied perturbed相同的方式注入到图中,噪音水平由随机扰动的边占原始边的百分比给出。对于每个图,我们首先使用
GraphWave学习节点embedding,然后使用affinity propagation聚类算法对embedding进行聚类。最后我们根据节点的真实结构角色来评估聚类质量。注意,affinity propagation算法不需要簇的数量作为输入,而是自动生成簇。这在实验中很重要,因为每个簇的含义可能受到high level的噪音而难以理解。除了同质性、完整性指标之外,我们还报告检测到的聚类的数量,从而衡量
GraphWave发现的角色的丰富程度,我们随机运行10次并报告平均结果。结果如下图所示。结果表明:即使存在强烈的噪音,
GraphWave的性能也是缓慢地降低。
14.2.5 真实数据集
镜像
Karate网络:我们首先考虑一个镜像Karate网络,并使用与struc2vec中相同的实验设置。镜像Karate网络是通过获取karate网络的两个副本,并添加给定数量的随机边而创建的。这些随机边中的每条边连接来自不同副本的镜像节点,代表karate俱乐部的同一个人,即镜像边mirrored edge。该实验的目标是通过捕获结构相似性来识别镜像节点。对于每个节点,我们基于节点
embedding利用kNN寻找结构最相似的节点,然后评估这些结构最相似节点中真实结构等价的比例。我们添加镜像边的数量从1到25不等,实验结果非常一致。GraphWave的平均准确率为83.2%(最低为75.2%、最高为86.2%)、struc2vec平均准确率为52.5%(最低为43.3%、最高为59.4%)。此外,node2vec和DeepWalk的准确率都不会高于8.5%,因为它们是基于邻近性而不是结构相似性进行嵌入的。安然
email网络:我们考虑对安然公司员工之间的电子邮件通信网络进行学习,由于公司存在组织架构,因此我们预期结构GraphWave能够学到这种工作职位上的结构等价性。该网络中每个节点对应于安然的员工,边对应于员工之间的
email通信。员工的角色有七种,包括CEO、总裁president、经理manager等。这些角色给出了网络节点的真实标签。我们用不同模型学习每个节点的embedding,然后计算每两类员工之间的平均L2距离,结果如下所示。GraphWave捕获到了安然公司的复杂组织结构。如CEO和总裁在结构上与其它角色的距离都很远。这表明他们在电子邮件网络中的独特位置,这可以通过他们与其他人截然不同的局部连接模式来解释。另一方面,trader交易员看起来离总裁很远、离董事director更近。- 相比之下,
struc2vec的结果不太成功,每个类别之间的距离几乎均匀分布。
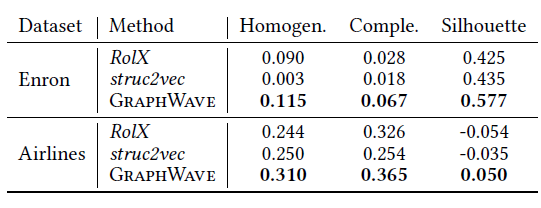
欧洲航空网络:接下来我们分析一系列航空公司网络,这些网络编码了不同航空公司运营的、机场之间的直飞航班。我们考虑六家在欧洲机场之间运营的航空公司:四家商业航空公司、两家货运航空公司。每家航空公司对应一个
Graph,其中顶点表示机场/目的地、边表示机场之间的直飞航班。这里一共有
45个机场,我们对其标记为枢纽机场hub airport、区域枢纽、商业枢纽、重点城市等几个类别,这些类别作为节点的真实结构角色。对每个Graph我们学习图中每个机场的embedding,然后将来自不同Graph的同一个机场的embedding进行拼接,然后使用t-SNE可视化。我们还将拼接后的embedding作为agglomerative聚类的输入,然后评估同质性、完整性、轮廓系数。我们衡量了每个簇中的机场与
ground-truth结构角色的对应程度(如上表所示)。从上表可以看到,GraphWave在所有三个聚类指标上都优于替代方法。下图展示了机场
embedding的t-SNE可视化。结果如下所示:struc2vec学习的embedding捕获了不同的航空公司,可以看到各航空公司的节点几乎各自聚在一起。这表明struc2vec无法在不同的航空公司网络之间泛化,因此无法识别那些结构等价、但是不属于同一个航空公司的机场。RolX学到的embedding的t-SNE投影几乎没有任何明显的模式。GraphWave可以学到节点的结构等价性,即使这些节点位于不同的图上。这表明GraphWave能够学到针对真实世界网络有意义的结构嵌入。
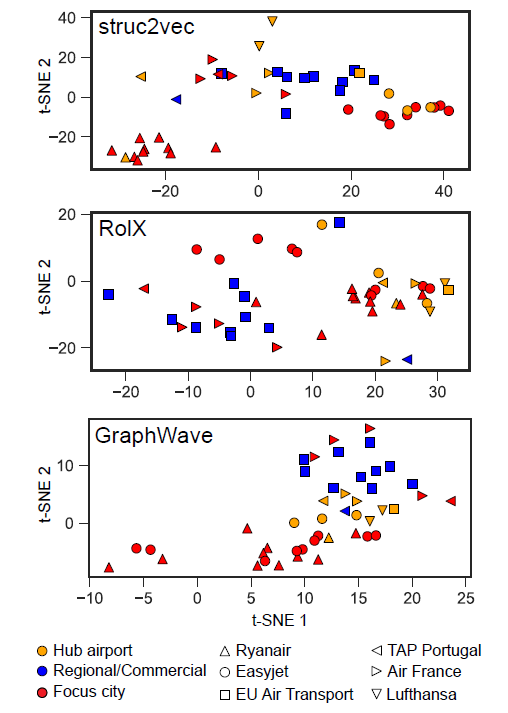
十五、NetMF[2017]
传统的网络挖掘、网络学习的范式通常从对网络结构属性
structural property的显式探索而开始。但是许多这类的属性(如中介中心度betweenness centrality、三角计数triangle count、模度modularity)由人工制作,并且需要广泛的领域知识和昂贵的计算代价。鉴于这些问题,以及最近出现的representation learning所提供的机会,人们广泛研究了学习网络的潜在representation(也就是network embedding),以便自动发现网络的结构属性并将其映射到一个潜在的空间。形式上,
network embedding的问题通常形式化如下:给定一个无向带权图 ,其中 为顶点集合、 为边集合、 为邻接矩阵,任务的目标是学习一个映射 ,该映射将每个顶点映射到一个能够捕获该顶点结构属性的 维向量。输出的representation可以用于各种网络科学任务、网络learning algorithm的输入,例如标签分类、社区检测。解决这个问题的尝试可以追溯到谱图理论
spectral graph theory和社交维度学习social dimension learning。该问题最近的进展很大程度上受到SkipGram模型的影响。SkipGram模型最初是为word embedding所提出的,其输入是由自然语言中的句子组成的文本语料库,输出是语料库中每个单词的latent vector representation。值得注意的是,受到该setting的启发,DeepWalk通过将网络上随机游走所遍历的顶点路径视为句子,并利用SkipGram来学习潜在的节点representation,从而开创了network embedding的先河。随着DeepWalk的出现,人们后续已经开发了很多network embedding模型,例如LINE、PTE、node2vec。到目前为止,上述模型已经被证明非常有效。然而,它们背后的理论机制却鲜为人知。人们注意到,用于
word embedding的、带负采样的SkipGram模型已经被证明是某个word-context矩阵的隐式分解,并且最近有人努力从几何角度从理论上解释word embedding模型。但是,目前尚不清楚word-context矩阵与网络结构之间的关系。此外,早期人们尝试从理论上分析DeepWalk的行为,然而他们的主要理论结果和原始DeepWalk论文的setting并不完全一致。此外,尽管DeepWalk, LINE, PTE, node2vec之间存在表面上的相似性,但是对它们的底层联系缺乏更深入的了解。在论文
《Network Embedding as Matrix Factorization: Unifying DeepWalk, LINE, PTE, and node2vec》中,作者提供了关于几种基于SkipGram的network embedding方法的理论结果。具体而言:- 论文首先表明这里提到的模型(即
DeepWalk, LINE, PTE, node2vec)在理论上执行隐式矩阵分解。论文为每个模型推导出矩阵的封闭形式closed form。例如,DeepWalk(图上的随机游走加上SkipGram)本质上是对一个随机矩阵进行因子分解,并且随着随机游走的长度趋于无穷大,该矩阵在概率上收敛到这个的闭式矩阵。 - 其次,从它们矩阵的闭式形式观察,作者发现有意思的是,
LINE可以视为DeepWalk的一个特例:当SkipGram中的上下文窗口大小 时。此外,作者证明了PTE作为LINE的扩展,实际上是多网络的联合矩阵joint matrix的隐式分解。 - 第三,作者发现了
DeepWalk的隐式矩阵implicit matrix和图拉普拉斯矩阵graph Laplacian之间的理论联系。基于这种联系,作者提出了一种新算法NetMF来逼近DeepWalk隐式矩阵的封闭形式。通过使用SVD显式分解该矩阵,论文在四个网络(在DeepWalk和node2vec论文中所采用的)中的广泛实验证明了NetMF相比于DeepWalk和LINE的出色性能(相对提升高达50%)。
论文的理论价值高于
NetMF实用的价值,实际上NetMF很难应用到工业环境中,因为NetMF的时间复杂度和空间复杂度都太高。- 论文首先表明这里提到的模型(即
论文展示了所有上述带负采样的模型都可以统一到具有封闭形式
closed form的矩阵分解框架中。论文的分析和证明表明:DeepWalk经验性empirically地产生了网络归一化拉普拉斯矩阵的低秩变换low-rank transformation。LINE理论上是DeepWalk的一个特例:当顶点的上下文size为1时。- 作为
LINE的扩展,PTE可以视为多个网络的拉普拉斯矩阵的联合分解。 node2vec正在分解与二阶随机游走的平稳分布、转移概率张量等相关的矩阵。
这项工作为基于
SkipGram的network embedding方法奠定了理论基础,从而更好地理解了潜在的network representation learning。相关工作:
network embedding的故事来源于谱聚类Spectral Clustering。谱聚类是一种数据聚类技术,它选择数据的亲和矩阵affinity matrix的特征值eigenvalue/特征向量eigenvector从而获得representation,从而进一步用于聚类或嵌入到低维空间。谱聚类已广泛应用于社区检测和图像分割等领域。近年来,人们对
network embedding越来越感兴趣。继SocDim和DeepWalk等一些开创性工作之后,越来越多的文献试图从不同的角度解决这个问题,例如heterogeneous network embedding、半监督network embedding、具有丰富顶点属性的network embedding、具有高阶结构的network embedding、有符号的network embedding、有向的network embedding、通过神经网络的network embedding等等。在上述研究中,一种常用的技术是为每个顶点定义context,然后训练一个预测模型来进行上下文预测。例如,DeepWalk, node2vec, metapath2vec分别通过基于一阶的随机游走、基于二阶的随机游走、基于metapath的随机游走来定义顶点的上下文。利用上下文信息的思想很大程度上是由带负采样的
SkipGram模型skip-gram model with negative sampling: SGNS所推动的。最近,人们一直在努力理解这个模型。例如:《NeuralWord Embedding as Implicit Matrix Factorization》证明了SGNS实际上是进行隐式矩阵分解,这为我们提供了分析上述network embedding模型的工具。《A latent variable model approach to pmi-based word embeddings》提出生成模型RAND-WALK来解释word embedding模型。《Word embeddings as metric recovery in semantic spaces》将word embedding框架作为度量学习问题。
基于隐式矩阵分解的工作,我们从理论上分析了流行的、基于
SkipGram的network embedding模型,并将它们与谱图理论联系起来。
15.1 模型
- 这里我们首先介绍四种流行的
network embedding方法(LINE, PTE, DeepWalk, node2vec)的详细理论分析和证明,然后提出我们的NetMF方法。
15.1.1 LINE
给定一个带权无向图 ,二阶邻近性的
LINE(即LINE(2nd))的任务是学到两个representation矩阵 :vertex represetation矩阵 :第 行 为顶点 作为vertex时的embedding向量。context representation矩阵 :第 行 为顶点 作为contex时的embedding向量。
LINE(2nd)的目标函数为:其中: 为
sigmoid函数, 为负采样系数, 为用于产生负样本的noise分布。在LINE原始论文中使用经验分布 ,其中 为顶点 的加权degree。LINE(2nd)的目标函数为 (即 ),考虑到 时 以及负采样,则得到上述目标函数。这也是为什么 中 不仅作用在“正边”、也作用在 “负边” 上的原因。本文我们选择 ,因为这种形式的经验分布将得到一个闭式解
closed form solution。定义 为所有顶点的加权degree之和,则有 。我们重写目标函数为:我们在图 的所有顶点上计算,从而得到期望为:
因此有:
则对于每一对顶点
(i,j),其局部目标函数local objective function为:定义 ,根据
《NeuralWord Embedding as Implicit Matrix Factorization》的结论:对于一个足够大的embedding维度, 每个 之间可以认为是相对独立的。因此我们有:为求解目标函数极大值,我们令偏导数为零,则有:
这个方程有两个闭式解:
- :其解为虚数,不予考虑。
- :有效解。
因此有:
则
LINE(2nd)对应于矩阵分解:其中对角矩阵 。
15.1.2 PTE
PTE是LINE(2nd)在异质文本网络heterogeneous text network中的扩展。我们首先将我们对LINE(2nd)的分析调整到二部图网络。考虑一个二部图网络 ,其中 和 是两个不相交的顶点集合, 是边集合, 为二部图网络的邻接矩阵。定义图 的volume为 。则PTE的目标是学习每个节点 的节点representation、以及学习每个节点 的节点representation。则LINE(2nd)的目标函数为:这里 内节点和 内节点互为上下文,因此没必要引入 上下文的
embedding变量、 上下文的embedding变量。与
LINE相同的分析过程,我们可以发现最大化 等价于因子分解:其中 为 各行之和构成的对角矩阵, 为 各列之和构成的对角矩阵, 为全
1的向量。当二部图是无向图时, (无向图的出边就是入边),则 。
基于上述分析,接下来我们考虑
PTE中的异质文本网络。假设单词集合为 ,文档集合为 ,标签集合为 ,我们将文本网络分为三个子网络:word-word子网 :每个word是一个顶点,边的权重为两个word在大小为T的窗口内共现的次数。假设其邻接矩阵为 ,定义 为 第 行的元素之和, 定义 为 第 列的元素之和。定义对角矩阵 , ,它们分别由 的各行之和、各列之和组成。word-document子网 :每个word和document都是一个顶点,边的权重是word出现在文档中的次数。同样地我们定义对角矩阵 , ,它们分别由 的各行之和、各列之和组成。word-label子网 :每个word和label都是一个顶点,边的权重为word出现在属于这个label的文档的篇数。同样的我们定义对角矩阵 , ,它们分别由 的各行之和、各列之和组成。
PTE的损失函数为:其中 分别为三个子网中的量, 为三个超参数来平衡不同子网的损失, 为负采样系数。根据
PTE论文, 需要满足: ,这是因为PTE在训练期间执行边采样,其中边是从三个子网中交替采样得到。根据前面的结论有:
令:
则有 ,且有:
.
15.1.3 DeepWalk
DeepWalk首先通过在图上执行随机游走来产生一个corpus,然后在 上训练SkipGram模型。这里我们重点讨论带负采样的SkipGram模型skipgram with negative sampling:SGNS。整体算法如下所示:输入:
- 图
- 窗口大小
- 随机游走序列长度
- 总的随机游走序列数量
输出:顶点的
embedding矩阵算法步骤:
迭代: ,迭代过程为:
根据先验概率分布 随机选择一个初始顶点 。
在图 上从初始顶点 开始随机游走,采样得到一条长度为 的顶点序列 。
统计顶点共现关系。对于窗口位置 :
考虑窗口内第 个顶点 :
- 添加
vertex-context顶点对 到 中。 - 添加
vertex-context顶点对 到 中。
- 添加
然后在 上执行负采样系数为 的
SGNS。
根据论文
《NeuralWord Embedding as Implicit Matrix Factorization》,SGNS等价于隐式的矩阵分解:其中: 为语料库大小; 为语料库 中
vertex-context共现的次数; 为语料库中vertex出现的总次数; 为语料库中context出现的总次数; 为负采样系数。这个矩阵 刻画了图结构的什么属性?目前并没有相关的分析工作。此外,这里是否可以去掉
log、是否可以去掉log b,也没有理论的解释。接下来的分析依赖于一些关键的假设:
- 假设图 为无向的
undirected、连接的connected、non-bipartite的,这使得 为一个平稳分布。 - 假设每个随机游走序列的第一个顶点从这个平稳分布 中随机选取。
对于 ,定义:
,即 为 的子集,它的每个
context顶点 都在每个vertex顶点 的右侧 步。另外定义 为 中vertex-context共现的次数。, 即 为 的子集,它的每个
context顶点 都在每个vertex顶点 的左侧 步。另外定义 为 中vertex-context共现的次数。定义 , ( 个 相乘),其中对角矩阵 , ,。定义 为 的第 行、第 列。
事实上 定义了一个概率转移矩阵, 定义了从顶点 经过一步转移到 的概率; 定义了从顶点 经过 步转移到 的概率。
另外考虑到对称性,我们有 。
- 假设图 为无向的
定理一:定义,则当 时有:
其中: 表述依概率收敛。
证明:
首先介绍
S.N. Bernstein大数定律:设 为一个随机变量的序列,其中每个随机变量具有有限的期望 和有限的方差 ,并且协方差满足:当 时, 。则大数定律law of large numbers:LLN成立。考虑只有一条随机游走序列(即 ): 。给定一个
vertex-context,定义随机变量 为事件 发生的指示器indicator。我们观察到:
, 。因此有:
基于我们对图的假设和随机游走的假设,则有: 发生的概率等于 的概率乘以 经过 步转移到 的概率。即:
基于我们对图的假设和随机游走的假设,则有:当 时有:
其中:第一项为 采样到 的概率;第二项为从 经过 步转移到 的概率;第三项为从 经过 步转移到 得概率;第四项为从 经过 步转移到 的概率。
则有:
当 时,从 经过 步转移到 的概率收敛到它的平稳分布,即 。即:
因此有 。因此随机游走序列收敛到它的平稳分布。
应用大数定律,则有:
类似地,我们有:
当 时,我们定义 为事件 的指示器,同样可以证明相同的结论。
事实上如果随机游走序列的初始顶点分布使用其它分布(如均匀分布),则可以证明:当 时,有:
因此定理一仍然成立。
定理二:当 时,有:
证明:
注意到 ,应用定理一有:
进一步的,考察 的边际分布和 的边际分布,当 时,我们有:
当 不大时,单边的、间隔 的
vertex-context数量是固定的,为全体vertex-context数量的 。定理三:在
DeepWalk中,当 时有:因此
DeepWalk等价于因子分解:证明:
利用定理二和
continous mapping theorem,有:写成矩阵的形式为:
事实上我们发现,当 时,
DeepWalk就成为了LINE(2nd), 因此LINE(2nd)是DeepWalk的一个特例。
15.1.4 node2vec
node2vec是最近提出的graph embedding方法,其算法如下:输入:
- 图
- 窗口大小
- 随机游走序列长度
- 总的随机游走序列数量
输出:顶点
算法步骤:
构建转移概率张量
迭代: ,迭代过程为:
根据先验概率分布 随机选择初始的两个顶点 。
在图 上从初始顶点 开始二阶随机游走,采样得到一条长度为 的顶点序列 。
统计顶点共现关系。对于窗口位置 :
考虑窗口内第 个顶点 :
- 添加三元组 到 中。
- 添加三元组 到 中。
然后在 上执行负采样系数为 的
SGNS。
注意:这里为了方便分析,我们使用三元组 ,而不是
vertex-context二元组。
node2vec的转移概率张量 采取如下的方式定义:首先定义未归一化的概率:
其中 表示在 的条件下, 的概率。
然后得到归一化的概率:
类似
DeepWalk,我们定义:这里 为
previous顶点。定义 为 出现在 中出现的次数;定义 为 出现在 中出现的次数。
定义二阶随机游走序列的平稳分布为 ,它满足: 。根据
Perron-Frobenius定理,这个平稳分布一定存在。为了便于讨论,我们定义每个随机游走序列的初始两个顶点服从平稳分布 。定义高阶转移概率矩阵 。
由于篇幅有限,这里给出
node2vec的主要结论,其证明过程类似DeepWalk:因此
node2vec有:尽管实现了
node2vec的封闭形式,我们将其矩阵形式的公式留待以后研究。注意:存储和计算转移概率张量 以及对应的平稳分布代价非常高,使得我们难以对完整的二阶随机游走动力学过程建模。但是最近的一些研究试图通过对 进行低秩分解来降低时间复杂度和空间复杂度:
由于篇幅限制,我们这里主要集中在一阶随机游走框架
DeepWalk上。
15.1.5 NetMF
根据前面的分析我们将
LINE,PTE,DeepWalk,node2vec都统一到矩阵分解框架中。这里我们主要研究DeepWalk矩阵分解,因为它比LINE更通用、比node2vec计算效率更高。首先我们引用了四个额外的定理:
定理四:定义归一化的图拉普拉斯矩阵为 ,则它的特征值都是实数。
而且,假设它的特征值从大到小排列 ,则有:
进一步的,假设该图是连通图 (
connected),并且顶点数量 ,则有: 。证明参考:
《Spectral graph theory》。定理五:实对称矩阵的奇异值就是该矩阵特征值的绝对值。
证明参考:
《Numerical linear algebra》。定理六:假设 为两个对称矩阵,假设将 的奇异值按照降序排列,则对于任意 ,以下不等式成立:
其中 为对应矩阵的奇异值根据降序排列之后的第 个奇异值。
证明参考:
《Topics in Matrix Analysis》。定理七:给定一个实对称矩阵 ,定义它的瑞利商为:
假设 的特征值从大到小排列为 ,则有:
证明参考:
《Numerical linear algebra》。
考察
DeepWalk的矩阵分解:忽略常量以及
element-wise的log函数,我们关注于矩阵: 。实对称矩阵 存在特征值分解 ,其中 为正交矩阵、 为特征值从大到小构成的对角矩阵。根据定理四可知, ,并且 。
考虑到 ,因此有:
我们首先分析 的谱。显然,它具有特征值:
这可以视为对 的特征值 进行一个映射 。这个映射可以视为一个滤波器,滤波器的效果如下图所示。可以看到:
- 滤波器倾向于保留正的、大的特征值。
- 随着窗口大小 的增加,这种偏好变得更加明显。
即:随着 的增加,滤波器尝试通过保留较大的、正的特征值来近似低阶半正定矩阵。
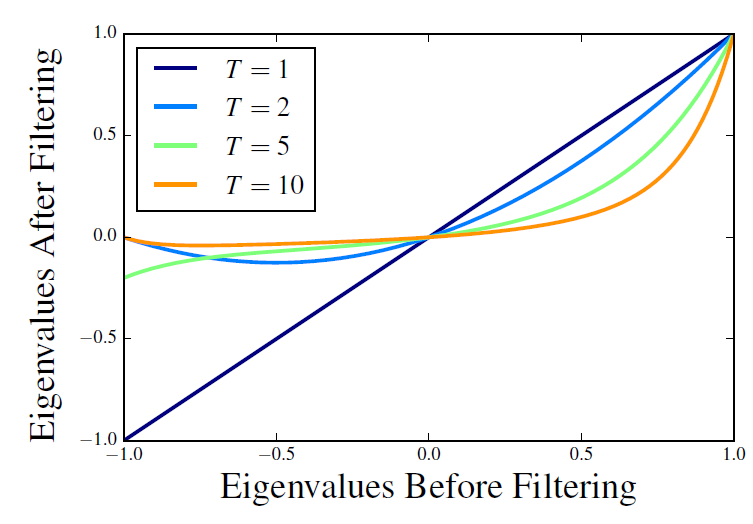
然后我们分析 的谱。
根据定理五,矩阵 的奇异值可以根据其特征值的绝对值得到。我们将 进行降序排列,假设排列的顺序为 ,则有:
考虑到每个 都是正数,因此我们可以将 的奇异值根据特征值 降序排列。假设排列的顺序为 ,则有:
特别的, 为最小的
degree。通过应用两次定理六,我们可以发现第 个奇异值满足:
因此 的第 个奇异值的上界为 。
另外,根据瑞利商,我们有:
应用定理七,我们有:
为了说明滤波器 的效果,我们分析了
Cora数据集对应的引文网络。我们将引文链接视为无向边,并选择最大连通分量largest connected component。我们分别给出了 、 以及 按照降序排列的特征值,其中 。对于 ,最大的特征值为 ,最小特征值为 。
对于 ,我们发现:它的所有负特征值以及一些小的正特征值都被过滤掉了
filtered out。对于 ,我们发现:
- 它的奇异值(即特征值的绝对值)被 的奇异值所限制
bounded。 - 它的最小特征值的被 的特征值所限制
bounded。
- 它的奇异值(即特征值的绝对值)被 的奇异值所限制
基于前面的理论分析,我们提出了一个矩阵分解框架
NetMF,它是对DeepWalk和LINE的改进。为表述方便,我们定义:
因此 对应于
DeepWalk的矩阵分解。对于很小的 ,我们直接计算 并对 进行矩阵分解。考虑到直接对 进行矩阵分分解难度很大,有两个原因:当 时 的行为未定义; 是一个巨大的稠密矩阵,计算复杂度太高。
受到
Shifted PPMI启发,我们定义 。这使得 中每个元素都是有效的,并且 是稀疏矩阵。然后我们对 进行奇异值分解,并使用它的top奇异值和奇异向量来构造embedding向量。对于很大的 ,直接计算 的代价太高。我们提出一个近似算法,主要思路是:根据 和归一化拉普拉斯矩阵之间的关系来近似 。
首先我们对 进行特征值分解,通过它的
top个特征值和特征向量来逼近 。由于只有top个特征值被使用,并且涉及的矩阵是稀疏的,因此我们可以使用Arnoldi方法来大大减少时间。大型稠密矩阵的特征值分解的代价太高,实际是不可行的。
然后我们通过 来逼近 。
NetMF算法:输入:
- 图
- 窗口大小
输出:顶点的
embedding矩阵算法步骤:
如果 较小,则计算:
如果 较大,则执行特征值分解: 。然后计算:
执行 维的
SVD分解: 或者 。返回 作为网络
embedding。
对于较大的 ,可以证明 逼近 的误差上界,也可以证明 逼近 的误差上界。
定理八:令 为矩阵的
Frobenius范数,则有:证明:
第一个不等式:可以通过
F范数的定义和前面的定理七来证明。第二个不等式:不失一般性我们假设 ,则有:
第一步成立是因为: 对于 有 ;第二步成立是因为: 。因此有 。
另外,根据 和 的定义有:
因此有: 。
15.2 实验
这里我们在在多标签顶点分类任务中评估
NetMF的性能,该任务也被DeepWalk, LINE, node2vec等工作所采用。数据集:
BlogCatalog数据集:在线博主的社交关系网络,标签代表博主的兴趣。Flickr数据集:Flickr网站用户之间的关系网络,标签代表用户的兴趣组,如“黑白照片”。Protein-Protein Interactions:PPI:智人PPI网络的子集,标签代表标志基因组和代表的生物状态。Wikipedia数据集:来自维基百科,包含了英文维基百科dump文件的前一百万个字节中的单词共现网络。顶点的标签表示通过Stanford POS-Tagger推断出来的单词词性Part-of-Speech:POS。
这些数据集的统计信息如下表所示。
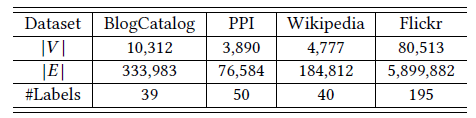
Baseline模型和配置:我们将NetMF(T=1)、NetMF(T=10)和LINE(2nd), DeepWalk进行比较。- 所有模型的
embedding维度都是128维。 - 对于
NetMF(T=10),我们在Flickr数据集上选择 ,在其它数据集上选择 。 - 对于
DeepWalk,我们选择窗口大小为10、随机游走序列长度40、每个顶点开始的随机游走序列数量为80。
我们重点将
NetMF(T=1)和LINE(2nd)进行比较,因为二者窗口大小都为1;重点将NetMF(T=10)和DeepWalk进行比较,因为二者窗口大小都为10。- 所有模型的
和
DeepWalk相同的实验步骤,我们首先训练整个网络的embedding,然后随机采样一部分标记样本来训练一个one-vs-rest逻辑回归分类模型,剩余的顶点作为测试集。在测试阶段,one-vs-rest模型给出label的排名,而不是最终的label分配。为了避免阈值效应,我们假设测试集的label数量是给定的。对于
BlogCatalog,PPI,Wikipedia数据集,我们考察分类训练集占比10%~90%的情况下,各模型的性能;对于Flickr数据集,我们考察分类训练集占比1%~10%的情况下,各模型的性能。我们评估测试集的Micro-F1指标和Macro-F1指标。为了确保实验结果可靠,每个配置我们都重复实验10次,并报告测试集指标的均值。完成的实验结果如下图所示。可以看到:
NetMF(T=1)相对于LINE(2nd)取得了性能的提升(它们的上下文窗口T=1),NetMF(T=10)相对于DeepWalk也取得了性能提升(它们的上下文窗口T=10)。在
BlogCatalog,PPI,Flickr数据集中,我们提出的NetMF(T=10)比Baseline性能更好。这证明了我们提出的理论基础在network embedding的有效性。在
Wikipedia数据集中,窗口更小的NetMF(T=1)和LINE(2nd)效果更好。这表明:短期依赖足以建模Wikipedia网络结构。这是因为Wikipedia网络是一个平均degree为77.11的稠密的单词共现网络,大量单词之间存在共现关系。如下表所示,大多数情况下当标记数据稀疏时,
NetMF方法远远优于DeepWalk和LINE。DeepWalk尝试通过随机游走采样,从而用经验分布来逼近真实的vertex-context分布。尽管大数定律可以保证这种方式的收敛性,但是实际上由于真实世界网络规模较大,而且实际随机游走的规模有限(随机游走序列的长度、随机游走序列的数量),因此经验分布和真实分布之间存在gap,从而对DeepWalk的性能产生不利影响。NetMF通过直接建模真实的vertex-context分布,从而得到比DeepWalk更好的效果。

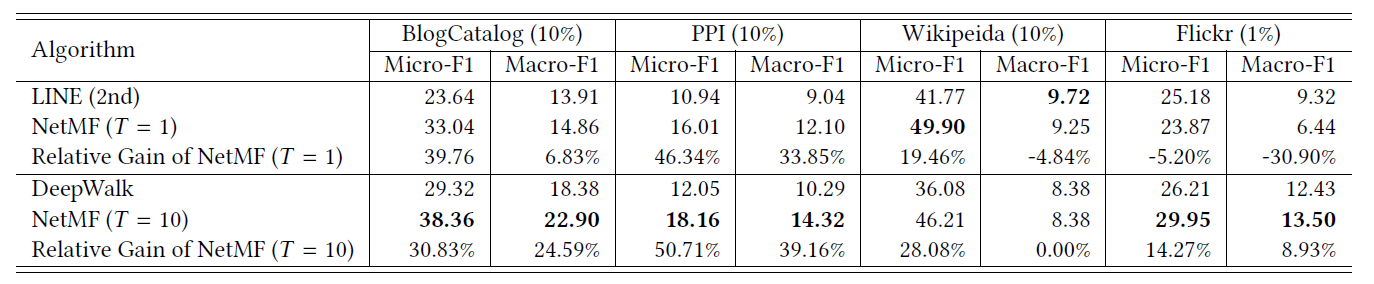
十六、NetSMF[2019]
近年来
network embedding为图和网络建模提供了革命性的范式。network embedding的目标是自动学习网络中对象(例如顶点、边)的潜在representation。重要的研究表明:潜在representation能够捕获网络的结构特性,促进各种下游网络应用,例如顶点分类任务、链接预测任务。在
network embedding发展过程中,DeepWalk, LINE, node2vec模型通常被认为是评估network embedding研究的强大基准方案。LINE的优势在于它对大规模网络的可扩展性,因为它仅对一阶邻近性和二阶邻近性建模。也就是说,LINE的embedding没有对网络中的multi-hop依赖。另一方面,DeepWalk和node2vec利用图上的随机游走和具有较大context size的SkipGram来对更远的节点(即全局结构)进行建模。因此,DeepWalk和node2vec处理大规模网络的计算成本更高。例如,使用默认参数设置的DeepWalk需要几个月的时间来嵌入一个由6700万顶点、8.95亿条边组成的学术协作网络academic collaboration network。而执行高阶随机游走的node2vec模型比DeepWalk需要更多时间来学习embedding。最近的一项研究表明,
DeepWalk和LINE方法都可以看作是一个闭式closed-form矩阵的隐式分解。在这个理论的基础上,该研究提出了NetMF方法来显式分解这个矩阵,从而实现比DeepWalk和LINE更有效的embedding。不幸的是,待分解的矩阵是一个 的稠密矩阵,其中 为网络中的顶点数量,这使得直接构造和分解大规模网络的成本过高。鉴于现有方法的这些局限性(如下表中的总结),论文
《NetSMF: Large-Scale Network Embedding as Sparse Matrix Factorization》建议研究大规模网络的representation learning,目标是达到高效率、捕获全局结构上下文global structural context、并具有理论上的保证。论文的思想是找到一个稀疏矩阵,该矩阵在谱上逼近由DeepWalk隐式分解的、稠密的NetMF矩阵。稀疏矩阵需要较低的构造成本和分解成本。同时,使其在谱上逼近原始NetMF矩阵可以保证网络的谱信息spectral information保持不变,并且从稀疏矩阵中学到的embedding与从稠密NetMF矩阵中学到的embedding一样强大。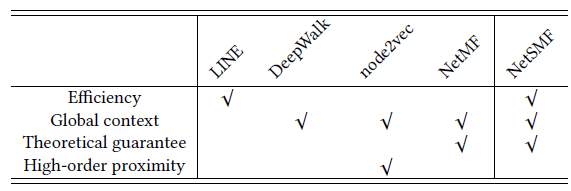
在这项工作中,论文提出了作为稀疏矩阵分解的
network embedding learning方法NetSMF。NetSMF包含三个步骤:首先,它利用谱图稀疏化技术pectral graph sparsification technique为网络的随机游走矩阵多项式random-walk matrix-polynomial找到稀疏化器sparsifier。然后,它使用这个稀疏化器来构造一个非零元素数量明显少于原始NetMF矩阵、但是在谱上逼近原始NetMF矩阵的矩阵。最后,它执行随机奇异值分解randomized singular value decomposition以有效地分解稀疏的NetSMF矩阵,从而产生网络的embedding。通过这种设计,
NetSMF保证了效率和效果,因为稀疏矩阵的逼近误差approximation error在理论上是有界的。论文在代表不同规模和类型的五个网络中进行实验。实验结果表明:对于百万级或更大的网络,NetSMF比NetMF实现了数量级上的加速,同时保持了顶点分类任务的有竞争力的性能competitive performance。换句话讲,NetSMF和NetMF都优于公认的network embedding基准方法(即DeepWalk, LINE, node2vec),但是NetSMF解决了NetMF面临的计算挑战。总而言之,论文引入了通过稀疏矩阵分解来产生
network embedding的思想,并提出了NetSMF算法。NetSMF算法对network embedding的贡献如下:- 效率:
NetSMF的时间复杂度和空间复杂度显著低于NetMF。值得注意的是,NetSMF能够在24小时内在单台服务器上为包含6700万个顶点、8.95亿条边的大型学术网络academic network生成embedding,而DeepWalk和node2vec将花费数月时间。另外在相同的硬件上,NetMF在计算上是不可行的。 - 效果:
NetSMF学到的embedding能够保持与稠密矩阵分解的解决方案相同的表达能力。在网络中的多标签顶点分类任务中,NetSMF始终优于DeepWalk和node2vec高达34%、始终优于LINE高达100%。 - 理论保证:
NetSMF的效率和效果在理论上得到了保证。稀疏的NetSMF矩阵在谱上逼近于精确的NetMF矩阵,并且逼近误差是有界的,从而保持了NetSMF学到的embedding的表达能力。
- 效率:
相关工作:这里我们回顾了
network embedding、大规模embedding算法、谱图稀疏化spectral graph sparsification等相关的工作。network embedding:network embedding在过去几年中得到了广泛的研究。network embedding的成功推动了许多下游网络应用network application,例如推荐系统。简而言之,最近关于network embedding的工作可以分为三类:- 受
word2vec启发的、基于SkipGram的方法,如LINE, DeepWalk, node2vec, metapath2vec, VERSE。 - 基于深度学习的方法,如
《Semi-Supervised Classification with Graph Convolutional Networks》、《Graph Convolutional Neural Networks for Web-Scale Recommender Systems》。 - 基于矩阵分解的方法,如
GraRep, NetMF。其中,NetMF通过将一系列基于SkipGram的network embedding方法统一到一个矩阵分解框架中来连接第一类工作和第三类工作。
在这项工作中,我们利用了
NetMF的优点并解决了它在效率方面的局限性。在文献中,
PinSage是一个用于十亿规模网络的network embedding框架。NetSMF和PinSage的主要区别在于:NetSMF的目标是以无监督的方式预训练通用的network embedding;而PinSage是一种有监督的图卷积方法,既结合了推荐系统的目标,也结合了现有的节点特征。话虽如此,NetSMF学到的embedding也可以被PinSage用于下游的网络应用。- 受
large-scale embedding learning:一些研究试图优化embedding算法从而用于大型数据集。其中的一部分专注于改进SkipGram模型,另一部分则聚焦于改进矩阵分解模型。分布式
SkipGram模型:受word2vec的启发,大多数现代的embedding learning算法都基于SkipGram模型。有一系列工作试图在分布式系统中加速SkipGram模型。例如,《Parallelizing word2vec in shared and distributed memory》在多个worker上复制embedding矩阵并定期同步synchronize它们。《Network-efficient distributed word2vec training system for large vocabularies》将embedding矩阵的列(维度)分配给多个executor,并将它们与一个parameter server进行同步。负采样
negative sampling是SkipGram的关键步骤,它需要从噪声分布noisy distribution中采样负样本。《Distributed Negative Sampling for Word Embeddings》专注于通过使用别名方法alias method的分层采样算法hierarchical sampling algorithm代替了roulette wheel selection从而优化负采样。最近,
《Billion-scale Commodity Embedding for E-commerce Recommendation in Alibaba》提出了一个十亿规模的network embedding框架。该框架通过启发式地将输入图划分为小的子图,然后并行地、单独地处理这些子图。然而,该框架的性能高度依赖于图划分graph partition的质量。另外,基于分区partition-based的embedding learning的缺点是:在不同子图中学到的embedding不共享相同的潜在空间,因此无法跨子图比较节点。高效的矩阵分解:隐式分解
NetMF矩阵(例如LINE, DeepWalk)或显式分解NetMF矩阵(例如NetMF算法)会遇到两个问题:首先,即使对于中等的上下文窗口大小(例如T=10),该矩阵的稠密程度也会使得计算变得昂贵。其次,非线性变换(即,逐元素的矩阵对数)很难近似approximate。LINE通过设置T=1解决了这个问题。通过这种简化,LINE以预测性能为代价实现了良好的可扩展性。NetSMF通过有效地稀疏化稠密的NetMF矩阵来解决这个问题,其中这个稀疏化过程具有理论上有界的近似误差。
spectral graph sparsification:谱图稀疏化在图论中已经研究了几十年。谱图稀疏化的任务是通过一个稀疏图来近似并代替一个稠密图。我们的NetSMF模型是第一个将谱图稀疏化算法纳入network embedding的工作。NetSMF提供了一种强大而有效的方法来近似和分析NetMF矩阵中的随机游走矩阵多项式random-walk matrix-polynomial。
16.1 模型
16.1.1 基本概念
通常,
network embedding问题形式化如下:给定一个带权无向图 ,其中 为 个顶点组成的顶点集合, 为 条边组成的边集合, 为邻接矩阵。network embedding学习任务的目标是学习函数 ,从而将每个顶点 映射到一个 维的embedding向量 ,其中 。这个embedding向量捕获了网络的结构属性structural property,例如社区结构。顶点的embedding向量可以提供给下游应用程序使用,例如链接预测任务、顶点分类任务等等。DeepWalk模型是network embedding的开创性工作之一,并且在过去几年中一直被认为是一个强大的基准。简而言之,DeepWalk模型分为两个步骤:首先,DeepWalk通过网络中的随机游走过程生成一些顶点序列;然后,DeepWalk在生成的顶点序列上应用SkipGram模型来学习每个顶点的潜在representation。通常,SkipGram使用上下文窗口大小 和负采样比例 进行参数化。最近,《Network Embedding as Matrix Factorization: Unifying DeepWalk, LINE, PTE,and node2vec》的理论分析研究表明:DeepWalk本质上分解了从随机游走过程中派生出derived的矩阵。更正式地讲,该论文证明了当随机游走序列的长度达到无穷大时,DeepWalk隐式且渐进地分解以下矩阵:其中:
- 为每个顶点的
embedding向量组成的embedding矩阵, 为每个顶点作为context时的embedding矩阵。 - 为矩阵的逐元素
log。 - 为顶点 的
degree, 为所有顶点的degree组成的对角矩阵, 为所有顶点degree的和。 也称作图的volume,
这种矩阵形式提供了基于
SkipGram的network embedding方法的另一种观点(即,矩阵分解的观点)。此外,该论文还提出了一种叫做NetMF的显式矩阵分解方法来学习embedding。该论文表明:基于NetMF的embedding在顶点分类任务上的准确率要优于基于DeepWalk或LINE的embedding。注意,如果在
T hop中存在一对无法到达的顶点,那么上述等式中的矩阵将是未定义ill-defined的,因为 。因此,遵循《NeuralWord Embedding as Implicit Matrix Factorization》,NetMF使用截断的对数,即 。因此,NetMF的目标是分解矩阵:在这项工作的其余部分,我们将这个矩阵称作
NetMF矩阵。- 为每个顶点的
然而,在实践中利用
NetMF矩阵时存在一些挑战。首先,距离 内的每一对顶点几乎都对应于NetMF矩阵中的一个非零项。回想一下,许多社交网络social network和信息网络information network都表现出小世界smallworld的属性,即大多数顶点之间可以通过少量step而相互抵达。例如,截至2012年,Facebook的可达顶点对reachable pair,92%的距离小于等于5。因此,即使设置一个中等的上下文窗口大小(例如,DeepWalk中的默认设置T=10),NetMF矩阵也将是具有 个非零元素的稠密矩阵。这种矩阵的精确构造和精确分解对于大型网络而言是不切实际的。更具体而言,计算矩阵 时涉及到 复杂度的矩阵幂次运算,另外对稠密的NetMF矩阵进行矩阵分解也很耗时。为了降低构造成本,
NetMF使用top特征值和特征向量来近似 。然而这个近似矩阵approximated matrix仍然是稠密的,使得这种策略无法处理大型网络。在这项工作中,我们旨在解决NetMF的效率和可扩展性的缺陷,同时保持其效果优势。计算
NetMF的top特征值和特征向量也是耗时的。
16.1.2 NetSMF
在本节中,我们将
network embedding开发为稀疏矩阵分解sparse matrix factorization(即NetSMF)。我们提出了NetSMF方法来构造和分解一个稀疏矩阵,这个稀疏矩阵逼近了稠密 的NetMF矩阵。我们利用的主要技术是随机游走矩阵多项式稀疏化random-walk matrix-polynomial sparsification。我们首先介绍谱相似度
spectral similarity的定义和随机游走多项式稀疏化定理。谱相似度
Spectral Similarity:假设有两个带权无向图 和 ,令 和 分别为它们的拉普拉斯矩阵。如果下面的关系成立,我们就说 和 是 谱相似的spectrally similar:定理(随机游走多项式的谱稀疏化器
Spectral Sparsifier):对于随机游走多项式random-walk molynomial其中 ,则可以在 时间复杂度内构造一个
spectral sparsifier,其中 具有 个非零项。对于无权图,时间复杂度可以进一步降低到 。证明参考:
《Efficient sampling for Gaussian graphical models via spectral sparsification》、《Spectral sparsification of random-walk matrix polynomials》。为构建一个包含 个非零项的
sparsifier,该稀疏化算法包含两步:- 第一步获得一个针对 的初始化
sparsifier,它包含 个非零项。 - 第二步使用标准的谱稀疏化算法
spectral sparsification algorithm来进一步降低非零项到 。
本文我们仅仅应用第一步,因为一个包含 个非零项的稀疏矩阵已经足够可用,所以我们并没有采用第二步,这能够避免额外的计算。下面讲到的所有随机游走多项式稀疏化算法都仅包含第一步
- 第一步获得一个针对 的初始化
我们取 ,因此有:
我们定义:
因此有: 。
采用 的稀疏化版本 ,我们定义 。可以发现 也是一个稀疏矩阵,其非零元素的规模和 非零元素规模相当。最终我们可以分解这个稀疏矩阵从而获得每个顶点的
embedding:我们正式给出
NetSMF算法,该算法包含三个步骤:随机游走多项式的稀疏化:我们首先构建一个网络 ,它具有和 相同的顶点但是不包含任何边。然后我们重复
Path-Sampling路径采样算法 次,从而得到 条边,这些边构成了 的非零项。在每一次迭代过程中:首先均匀随机选择一条边 ,均匀随机选择一个路径长度 。
然后从顶点 开始进行 步随机游走,得到顶点序列 ;从顶点 开始进行 步随机游走,得到顶点序列 。这一过程产生了一个长度为 的路径 。同时我们计算:
然后我们向图 中添加一条新的边 ,其权重为 。如果边已经存在,则相同的边进行合并(只需要将权重相加即可)。
这条新的边代表了图 中一条长度为 的随机游走序列,权重就是转移概率。其中 。
最终我们计算 的未归一化的拉普拉斯矩阵 ,它具有 个非零项。
这个被构造出的图的未归一化拉普拉斯矩阵与 产生联系。
NetMF稀疏器sparsifier的构造:即计算 。这一步并未改变非零项的规模。截断的奇异值分解:对 执行 维的
RandomizedSVD分解。即使稀疏矩阵仅有 个非零元素,执行精确的
SVD仍然非常耗时。这里我们使用Randomized SVD进行分解。由于篇幅有限我们无法包含更多细节,简而言之,该算法通过高斯随机矩阵将原始矩阵投影到低维空间,然后在 维的小矩阵上执行经典的SVD分解即可。采用
SVD的另一个优势是:我们可以通过使用诸如Cattell’s Scree test来确定embedding的维度。在测试中,我们绘制奇异值并选择一个rank,使得奇异值幅度显著下降或者奇异值开始趋向于平衡的位置。实际上自动选择一个
rank d需要对 进行奇异值分解,这对于大型网络而言是不可行的。
NetSFM算法:输入:
- 图
- 非零项的数量
embedding维度
输出:顶点
embedding矩阵算法步骤:
初始化 ,即只有顶点没有边。
迭代 ,迭代步骤为:
均匀随机选择一条边 。
均匀随机选择一个长度 。
随机采样一条路径:
添加边 到 中,边的权重为 。
如果有多条边相同则合并成一个,将权重直接相加即可。
计算 的未归一化的拉普拉斯矩阵 。
计算 。
对 执行 维的
RandomizedSVD分解,得到 。返回 。
PathSampling算法:输入:
- 图
- 边
- 采样的路径长度
输出:路径的初始顶点 、结束顶点 、路径 值
算法步骤:
均匀随机采样一个整数 。
从顶点 开始执行 步随机游走,采样到的顶点记作 。
从顶点 开始执行 步随机游走,采样到的顶点记作 。
计算整条路径的路径 值:
返回 。
Randomized SVD算法:输入:
- 一个稀疏的对称矩阵 。我们以行优先的方式存储矩阵,从而充分利用对称性来简化计算。
- 目标维度
输出:
SVD矩阵分解的步骤:
- 采样一个高斯随机矩阵 作为投影矩阵。
- 计算映射后的矩阵 。
- 对矩阵 进行正交归一化。
- 计算矩阵 。
- 采样另一个高斯随机矩阵 作为投影矩阵。
- 计算映射后的矩阵 。
- 对矩阵 进行正交归一化。
- 计算矩阵 。
- 对 执行
Jacobi SVD分解: 。 - 返回 。
PathSampling算法的说明:引理:给定一个长度为 的路径 ,则
PathSampling算法采样到该路径的概率为:其中:
引理:假设采样到一个长度为 的路径 ,则新的边 的权重应该为:
根据上述引理,则添加到 中的边的权重为:
对于无向图,则 ,则权重简化为 。
NetMF和NetSMF之间的主要区别在于对目标矩阵的近似策略。NetMF使用了一个稠密矩阵来近似,从而带来了时间和空间上的挑战;NetSFM基于谱图稀疏化理论和技术,使用了一个稀疏矩阵来近似。
16.1.3 复杂度
算法复杂度:
第一步:我们需要调用
PathSampling算法 次,每次PathSampling都需要在网络 上执行 步随机游走。对于无权无向图,随机游走采样一个顶点的计算复杂度为 ;对于带权无向图,可以使用roulette wheel selection从而随机游走采样一个顶点的计算复杂度为 。另外我们需要 的空间存储 ,以及额外的 空间来存储算法的输入。
第二步:我们需要 的时间来计算 以及 。
另外我们需要 空间来存储
degree矩阵 , 的空间来存储 。第三步:我们需要 时间来计算一个稀疏矩阵和一个稠密矩阵的乘积,以及 来执行
Jacobi SVD,以及 来计算Gram-Schmidt正交化 。

示例:假设网络 的顶点数量 ,边的数量为 ,上下文窗口大小 ,逼近因子
approximation factor。NetSMF调用PathSampling算法次数为 次,得到一个稀疏矩阵大约 个非零值,稠密度大约为 。然后我们在
randomized SVD中计算sparse-dense矩阵乘积,近似矩阵的稀疏性可以大大加快计算速度。NetMF必须构建一个稠密矩阵,它包含 个非零元素,这比NetSMF大一个量级。
通过一个更大的 我们可以进一步降低
NetSMF中近似矩阵的稀疏性,而NetMF缺乏这种灵活性。并行化:
NetSMF的每个步骤都可以并行化,从而scale到非常大的网络。NetSMF的并行化设计如下图所示。第一步:我们可以同时启动多个
PathSampling worker来独立的、并行的采样多个路径,每个worker负责采样一批路径。这里,我们要求每个worker能够有效访问网络数据集 。有很多选择可以满足这一要求,最简单的方法是将网络数据的副本拷贝到每个worker的内存中。但是如果网络非常大(例如万亿规模),或者worker内存受限时,应该采用图引擎来支持随机游走等图操作。在这一步结束时,我们设计了一个
reducer来合并平行边并汇总它们的权重。第二步:我们可以简单直接地并行计算 和 。
第三步:我们可以将稀疏矩阵组织为行优先的格式,这种格式可以在稀疏矩阵和稠密矩阵之间进行高效的乘法运算。其它稠密矩阵的算子(如高斯随机矩阵生成、
Gram-Schmidt正交归一化、Jacobi SVD)可以通过使用多线程或者常见的线性代数库来轻松加速。

16.1.4 近似误差分析
我们假设逼近因子 。我们假设顶点的
degree是降序排列: 。 我们令 为矩阵从大到小排列的奇异值中的第 个奇异值。我们首先证明一个结论:令 ,以及 ,则有:
证明:
它是某个图的归一化的拉普拉斯矩阵,因此有特征值 。
由于 是矩阵 的
spectral sparsifier,因此有:令 ,则有:
其中最后一个不等式是因为 。
根据瑞利商的性质有: 。
根据奇异值和特征值的关系,我们有: 。
定理: 的奇异值满足:
证明:
根据奇异值的性质,我们有:
定理:令 为矩阵的
Frobenius范数,则有:证明:很明显 函数满足是
1- Lipchitz的。因此我们有:上述界限是在未对输入网络进行假设的情况下实现的。如果我们引入一些假设,比如有界的 、或者特定的随机图模型(如
Planted Partition Model或者Extended Planted Partition Model),则有望通过利用文献中的定理来探索更严格的边界。
16.2 实验
数据集:我们使用五个数据集,其中四个规模(
BlogCatalog, PPI, Flickr, YouTube)相对较小但是已被广泛用于network embedding的论文,剩下一个是大规模的academic co-authorship network。BlogCatalog数据集:在线博主的社交关系网络。标签代表博主的兴趣。Flickr数据集:Flickr网站用户之间的关系网络。标签代表用户的兴趣组,如“黑白照片”。Protein-Protein Interactions:PPI:智人PPI网络的子图。顶点标签是从标志基因组hallmark gene set中获取的,代表生物状态。Youtube数据集:YouTube网站用户之间的社交网络。标签代表用户的视频兴趣组,如“动漫、摔跤”。Open Academic Graph:OAG数据集:一个学术网络,顶点标签位每个作者的研究领域,共有19种不同的标签。每位作者可以研究多个领域,所以有多个标签。
这些数据集的统计信息如下表所示。

baseline和配置:我们将NetSMF与NetMF, LINE, DeepWalk, node2vec等方法进行比较。- 所有模型的
embedding维度设置为 。 - 对于
NetSMF/NetMF/DeepWalk/node2vec,我们将上下文窗口大小设为 ,这也是DeepWalk, node2vec中使用的默认设置。 - 对于
LINE我们仅使用二阶邻近度,即LINE(2nd),负样本系数为5,边采样的数量为100亿。 - 对于
DeepWalk,随机游走序列的长度为40,每个顶点开始的随机游走序列数量为80,负采样系数为5。 - 对于
node2vec,随机游走序列的长度为40,每个顶点开始的随机游走序列数量为80,负采样系数为5。参数 从 中进行grid search得到。 - 对于
NetMF,我们在BlogCatalog,PPI,Flickr数据集中设置 。 - 对于
NetSMF,我们在PPI,Flickr,YouTube数据集中设置采样数量 ;我们在BlogCatalog数据集中设置采样数量 ;我们在OAG数据集中设置采样数量 。 - 对于
NetMF和NetSMF,我们设置负采样系数 。
- 所有模型的
和
DeepWalk相同的实验步骤执行多标签顶点分类任务:我们首先训练整个网络的embedding,然后随机采样一部分标记样本来训练一个one-vs-rest逻辑回归分类模型(通过LIBLINEAR实现),剩余的顶点作为测试集。在测试阶段,one-vs-rest模型产生标签的排序,而不是精确的标签分配。为了避免阈值效应,我们采用在DeepWalk, LINE, node2vec中所作的假设,即给定测试数据集中顶点的label数量。我们评估测试集的Micro-F1指标和Macro-F1指标。为了确保实验结果可靠,每个配置我们都重复实验10次,并报告测试集指标的均值。所有实验均在配备Intel Xeon E7-8890 CPU(64核)、1.7TB内存、2TB SSD硬盘的服务器上进行。对于
BlogCatalog,PPI数据集,我们考察分类训练集占比10%~90%的情况下,各模型的性能;对于Flickr,YouTube,OAG数据集,我们考察分类训练集占比1%~10%的情况下,各模型的性能。完成的实验结果如下图所示。对于训练时间超过
1周的模型,我们判定为训练失败,此时并未在图中给出结果。第二张图给出了模型训练时间,-表示模型无法在周内完成训练(时间复杂度太高);x表示模型因内存不足无法训练(空间复杂度太高)。我们首先重点对比
NetSMF和NetMF,因为NetSMF的目标是解决NetMF的效率和可扩展性问题,同时保持NetMF的效果优势。从结果可以看到:- 在训练速度上:对于大型网络 (
YouTube,OAG),NetMF因为空间复杂度和时间复杂度太高而无法训练,但是NetSMF可以分别在4h内、24h内完成训练;对于中型网络(Flickr),二者都可以完成训练,但是NetSMF的速度要快2.5倍;对于小型网络,NetMF的训练速度反而更快,这是因为NetSMF的稀疏矩阵构造和分解的优势被pipeline中其它因素抵消了。 - 在模型效果上:
NetSMF和NetMF都能产生最佳的效果(和其它方法相比)。在BlogCatlog中,NetSMF的效果比NetMF稍差;在PPI中,两种方法性能难以区分、在Flicker中,NetSMF的效果比NetMF更好。这些结果表明:NetSMF使用的稀疏谱近似sparse spectral approximation,其性能不一定比稠密的NetMF效果更差。
总之,
NetSMF不仅提高了可扩展性,还能保持足够好的性能。这证明了我们谱稀疏化近似算法的有效性。我们还将
NetSMF与常见的graph embedding基准(即DeepWalk, LINE, node2vec)进行了比较。对于
OAG数据集,DeepWalk和node2vec无法在一周内完成计算,而NetSMF仅需要24小时。根据公开报道的SkipGram运行时间,我们预计DeepWalk和node2vec可能需要几个月的时间来为OAG数据集生成embedding。在
BlogCatalog中,DeepWalk和NetSMF需要差不多的计算时间。而在Flickr, YouTube, PPI中,NetSMF分别比DeepWalk快2.75倍、5.9倍、24倍。在所有数据集中,
NetSMF比node2vec实现了4 ~ 24倍的加速。此外,
NetSMF的性能在BlogCatalog, PPI, Flickr中显著优于DeepWalk。在YouTube中,NetSMF取得了与DeepWalk相当的结果。与node2vec相比,NetSMF在BlogCatalog, YouTube上的性能相当,在PPI, Flickr上的性能显著更好。总之,NetSMF在效率和效果上始终优于DeepWalk和node2vec。LINE在所有五种方法中是效率最高的,然而它的预测效果也最差,并且在所有数据集上始终以很大的差距输给其它方法。总之,LINE以忽略网络中的multi-hop依赖性作为代价从而实现了效率,而所有其它四种方法都支持这些依赖,这证明了multi-hop依赖性对于学习network representation的重要性。更重要的是,在除了
LINE以外的四种方法之间,DeepWalk既没有达到效率上的优势,也没有达到效果上的优势。node2vec以效率为代价实现了相对较好的性能。NetMF以显著增加的时间和空间成本为代价实现了更好的效果。NetSMF是唯一同时实现了高效率和高效果的方法,使得它能够在一天内在单台服务器上为数十亿规模的网络(例如9亿条边的OAG网络)学习有效的embedding。
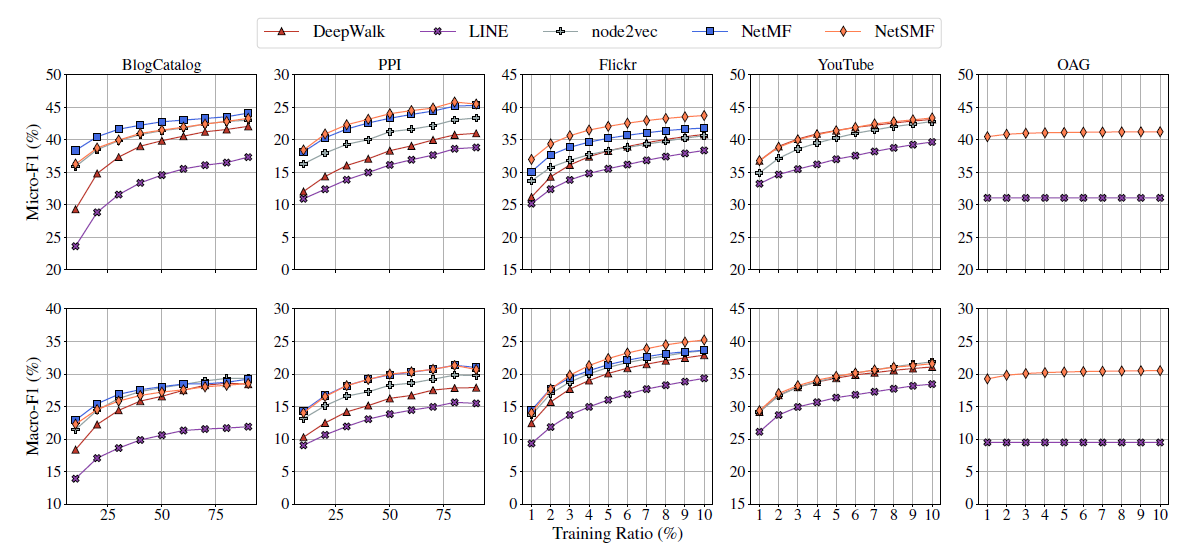
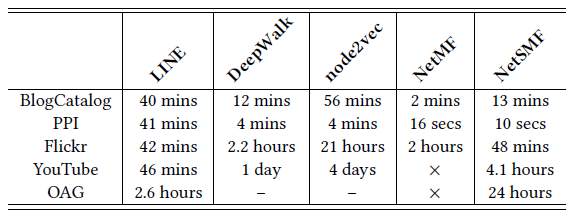
- 在训练速度上:对于大型网络 (
这里我们讨论超参数如何影响
NetSMF的效率和效果。我们用Flickr数据集的10%标记顶点作为训练集,来评估NetSMF超参数的影响。维度 :我们使用
Cattell Scree测试。首先从大到小绘制奇异值,然后再图上找出奇异值突变或者趋于均匀的点。从Flickr数据的奇异值观察到:当 增加到100时,奇异值趋近于零(图b所示)。因此我们在实验中选择 。我们观察 时测试集的指标,可以看到确实当 时模型效果最好。这表明了
NetSMF可以自动选择最佳的embedding维度。NetSMF能够自动选择选择最佳embedding维度的前提是计算矩阵 的奇异值。对于大型网络,计算奇异值是不可行的。非零元素数量:理论上 ,当 越大则近似误差越小。不失一般性我们将 设置为 ,其中 ,我们研究随着 的增大模型性能的影响。
如图
c所示,当增加非零元素数量时,NetSMF效果更好,因为更大的 带来更小的误差。但是随着 的增加,预测性能提升的边际收益在递减。可以看到当 时,NetSMF的效率和效果得到平衡。并行性:我们将线程数量分别设置为
1、10、20、30、60,然后考察NetSMF的训练时间。如图
d所示,在单线程时NetSMF运行了12个小时,在30个线程时NetSMF运行了48分钟,这实现了15倍的加速比(理想情况30倍)。这种相对较好的亚线性加速比使得NetSMF能够扩展到非常大规模的网络。
