GNN
一、GNN[2009]
数据可以在许多应用领域中自然地用图结构
graph structure来表达,包括蛋白质组织学proteomics、图像分析、场景描述、软件工程、自然语言处理。最简单的图结构包括单节点single node、序列sequence。但是在一些应用中,信息被组织成更复杂的图结构,如树、无环图、带环图。传统上,数据关系探索一直是归纳式逻辑编程inductive logic programming的社区中许多研究的主题。最近,数据关系探索data relationships exploitation这个研究主题已经朝着不同的方向发展,这也是因为统计statistics和神经网络中的相关概念在这些领域中的应用。在机器学习中,结构化数据通常与(有监督的或者无监督的)
learning的目标相关联,例如一个函数application通常可以分为两大类,分别称作graph-focused应用、node-focused应用 。在
graph-focused应用中,函数此时每个图具有一个
representation,并且每个图具有一个target。例如,可以用一个图
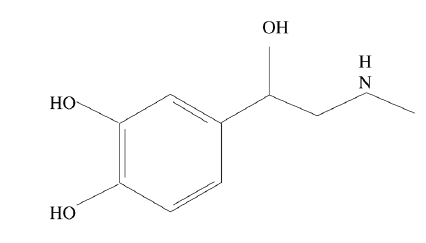
在下图中,图片由区域邻接图
region adjacency graph来表达,其中节点表示均匀图片强度的区域,边代表这些区域的邻接关系。在这种情况下,可以根据图片的内容通过
在
node-focused应用中,函数此时每个节点具有一个
representation,并且每个节点具有一个target。例如目标检测
application包括检查图片中是否包含给定的对象,如果是,则定位给定对象的位置。这个问题可以通过一个函数1、否则0。
另一个例子来自于网页分类。
web可以通过一个图来表达,其中节点代表网页,边代表网页之间的超链接,如下图所示。可以利用web connectivity以及网页内容来实现多种目的purposes,,如页面的主题分类。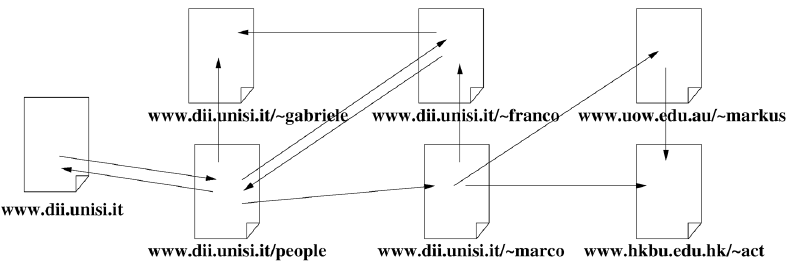
传统的机器学习
application通过使用预处理preprocessing阶段来处理图结构化数据graph structured data,该阶段将图结构化信息映射到更简单的representation,如实值向量。换句话讲,预处理步骤首先将图结构化数据 "挤压squash" 为实数向量,然后使用list-based数据处理技术来处理preprocessed的数据。然而,在预处理阶段,一些重要的信息(如每个节点的拓扑依赖性topological dependency)可能会丢失,并且最终结果可能以不可预知的方式unpredictable manner取决于预处理算法的细节。最近,有各种方法试图在预处理阶段尽可能地保留数据的图结构特性,其思想是:使用图节点之间的拓扑关系对底层的图结构化数据进行编码,以便在数据正式处理步骤(即预处理步骤之后的模型处理阶段)中融合图结构化信息。这组技术包括
recursive neural network: RNN、马尔科夫链Markov chain: MC,并且通常可以同时应用于graph-focused问题和node-focused问题。论文《The Graph Neural Network Model》提出的方法扩展了这两种方法(即RNN和马尔科夫链),因为该方法可以直接处理图结构化信息。现有的
RNN是以有向无环图directed acyclic graph作为输入的神经网络模型。该方法估计函数node-focused application中,此时,图必须经过预处理阶段。类似地,采用预处理阶段之后,我们可以处理某些类型的带环图。RNN已被应用于多个问题,包括逻辑术语分类logical term classification、化合物分类、logo识别、网页评分、人脸定位face localization。RNN也与支持向量机有关,其中支持向量机采用特殊的kernel对图结构化数据进行操作,其中:diffusion kernel是基于热扩散方程heat diffusion equation。《Marginalized kernels between labeled graphs》和《Extensions of marginalized graph kernels》中提出的kernel利用了图随机游走生成的向量。《Convolution kernels for natural language》、《Kernels for structured natural language data》、《Convolution kernels with feature selection for natural language processing tasks》中设计的kernel使用了一种计算两棵树的公共子结构数量的方法。
事实上,类似于支持向量机方法,
RNN自动将输入的图编码为内部representation。然而,在RNN中内部编码是模型自动学到的,而在支持向量机中内部编码是由用户手动设计的。另一方面,马尔科夫链模型可以建模事件之间的因果关系,其中因果关系由图来表达。最近,针对特定种类马尔科夫链模型的随机游走理论已成功应用于网页排名
ranking算法的实现。互联网搜索引擎使用排名算法来衡量网页的相对重要性。这类度量值通常与其它页面特征一起被搜索引擎所利用,从而对用户query返回的URL进行排序。人们已经进行了一些尝试来扩展这些具有学习能力的模型,以便可以从训练样本中学习模型参数。这些模型能够泛化结果从而对集合中的所有网页进行评分。更一般地,人们已经提出了几种其它统计方法,这些方法假设数据集由模式pattern、以及模式之间的关系relationship组成。这些技术包括:随机场random field、贝叶斯网络、统计关系学习、transductive learning、用于图处理的半监督方法。
在论文
《The Graph Neural Network Model》中,作者提出了一种有监督的神经网络模型,该模型同时适用于graph-focused application和node-focused application。该模型将这两个现有模型(即RNN和马尔科夫链)统一到一个通用框架中。论文将这种新颖的神经网络模型称作图神经网络graph neural network: GNN。论文将证明GNN是RNN和随机游走模型的扩展,并且保留了它们的特性characteristics。GNN模型扩展了RNN,因为GNN可以处理更通用的图,包括带环图、有向图、无向图,并且无需任何预处理步骤即可处理node-focused application。GNN方法通过引入learning算法、以及扩大可建模过程的种类从而扩展了随机游走理论。
GNN基于信息扩散机制information diffusion mechanism。图由一组单元unit来处理,每个单元对应于图上的一个节点,这些节点根据图的连通性进行链接。这些单元更新它们的状态并交换信息,直到它们到达稳定的平衡stable equilibrium。然后,基于单元的状态unit state计算每个节点的输出。扩散机制是受约束constrained的,从而确保始终存在唯一的稳定平衡。这种实现机制已经在细胞神经网络、
Hopfield神经网络中使用。在那些神经网络模型中,连通性是根据预定义的图来指定的,网络连接本质上是循环recurrent的,神经元状态是通过松弛relaxation到平衡点equilibrium point来计算的。GNN与那些神经网络不同之处在于:GNN可以处理更加通用的图,并且采用更通用的扩散机制。在论文
《The Graph Neural Network Model》中,作者将介绍一种学习算法,该算法在一组给定的训练样本上估计GNN模型的参数。此外,参数估计算法的计算代价需要被考虑。还值得一提的是,《Computation capabilities of graph neural networks》已经证明了GNN展示出一种普遍的逼近特性,并且在不严厉的条件下,GNN可以逼近图上大多数实际有用的函数
1.1 模型
定义图
节点和边可能含有额外的信息,这些信息统称为标签信息(它和监督学习中的标记
label不是一个概念),并以实值向量的形式来表示。- 定义节点
- 定义
all标签向量。 - 标签向量的符号遵循更一般的
scheme:如果
注意,这里的符号定义与大多数论文的符号定义不同。
- 定义节点
节点标签通常包含节点的特征,边标签通常包含节点之间关系的特征。如下图中:节点标签可能代表区块的属性,如:面积、周长、颜色的平均强度。边标签可能代表区块
region之间的相对位置,如:重心之间的距离、轴线之间的角度。我们未对边作出任何假设,有向边和无向边都是允许的。但是,当不同类型的边共同存在于同一个图
图
positional的、或者是nonpositional的。nonpositional graph是前面所讲的那些图。positional graph与之不同,节点unique的整数标识符,从而指示每个邻居的逻辑位置logical position。 形式上,对于positional graph中的每个节点,存在一个映射函数positionregion adjacency graph(如上图所示) :可以用注意,位置信息可以通过对邻居节点分配位置编号来显式地给出,也可以通过对邻居节点进行排序从而隐式地给出。
本文考虑的领域是
(graph, node) pair的集合graph的集合,graph的节点集合的集合,即:其中:
desired target(可能为向量也可能为标量),有趣的是,
unique的、断开的大图,因此可以将pairdomain仅由一个图组成,如大部分的web网络(如下图所示)。
1.1.1 思想
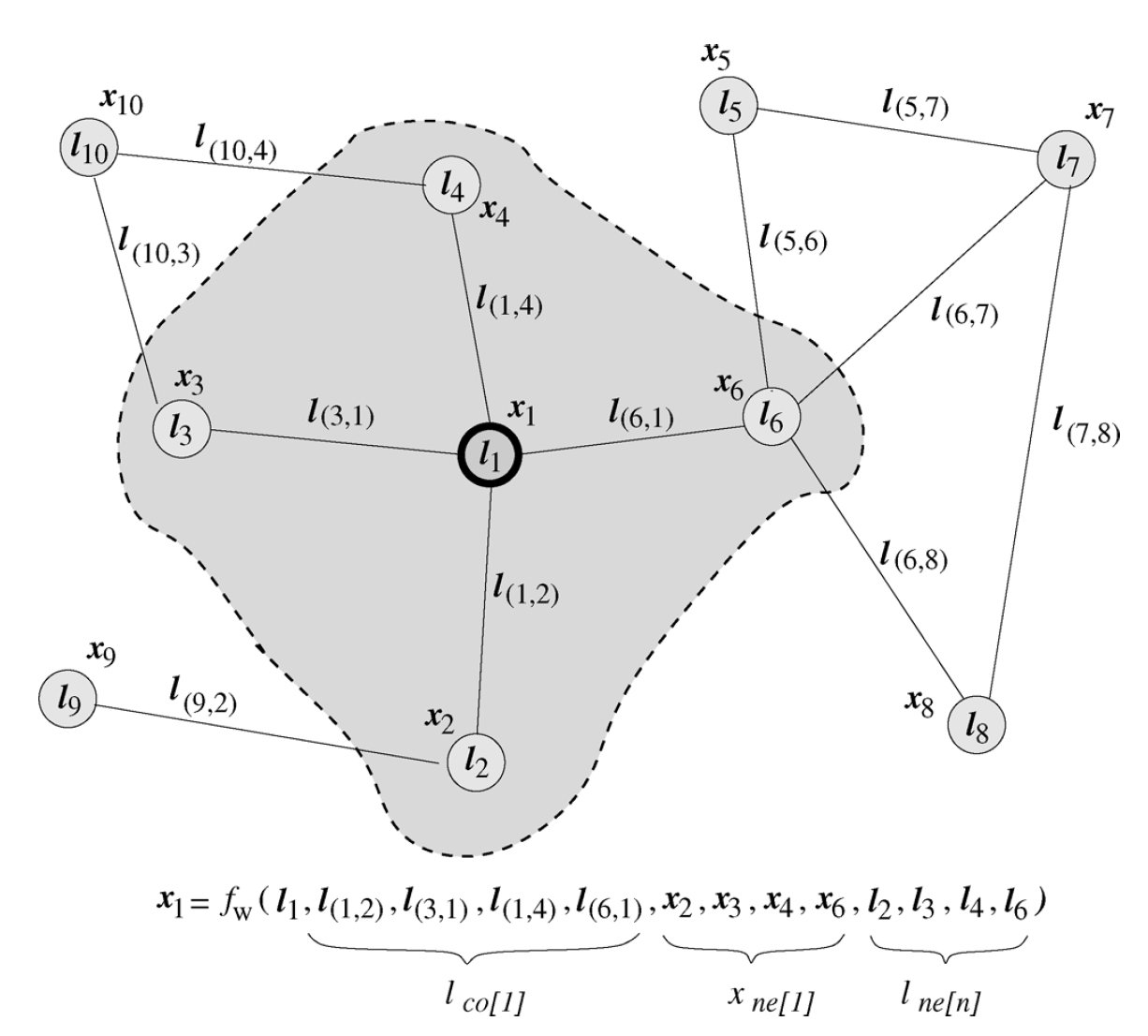
我们所提出方法的直观想法是:图中的节点代表对象或概念,而边代表它们之间的关系。每个概念自然地由它的特征和相关的概念来定义。因此,我们可以可以将一个状态向量
state vectorrepresentation,并可用于产生输出令
parametric的函数,称之为局部转移函数local transition function,用于表示节点对其邻域的依赖性。令local output function,用于描述如何产生输出。那么其中:
注意:这里有递归定义,其中节点
注意:这里的邻域依赖性使得计算状态向量所依赖的节点规模迅速膨胀。假设平均邻域大小为
10个节点,如果最多依赖于5阶邻域,那么计算每个状态向量需要依赖于5阶邻域内的10万个邻域节点。备注:
备注一:可以采用不同的邻域概念。例如,人们可能希望删除标签
2-hop或者多个hop的节点。备注二:上式用于无向图。在处理有向图时,函数
本文中为了保持符号紧凑,我们使用无向图的形式。然而,除非特殊说明,否则本文中提出的所有结果也适用于有向图、以及混合有向与无向的图。
备注三:通常而言,转移函数
parameters可能都依赖于节点然而为了简单起见,我们对所有节点共享相同的转移函数和输出函数(包括它们的参数)。
如果没有参数共享则模型的容量太大导致难以训练且很容易过拟合。
令
其中:
global transition fucntion,它由global output function,它由
令图和节点的
pair对的集合为Banach不动点理论fixed point theorem为上述方程解的存在性和唯一性提供了理论依据。根据Banach不动点理论,当contraction map。即存在其中
本文中我们假设
GNN模型中,这个条件是通过适当的选择转移函数来实现的。上述公式能够同时处理位置图
positional graph和非位置图nonpositional graph。对于位置图,
null值。例如:其中:
即:如果
null值
对于位置无关的图,我们可以将
其中
nonpositional form,而原始形式被称作positional form。注意,这里对邻居节点采用
sum聚合。也可以采用max聚合或者attention聚合。
为实现
GNN模型,我们必须解决以下问题:求解以下方程的算法:
从训练集中学习
1.1.2 方程求解算法
Banach不动点理论不仅保证了解的存在性和唯一性,还给出了求解的方式:采用经典的迭代式求解:其中
对于任意初始值
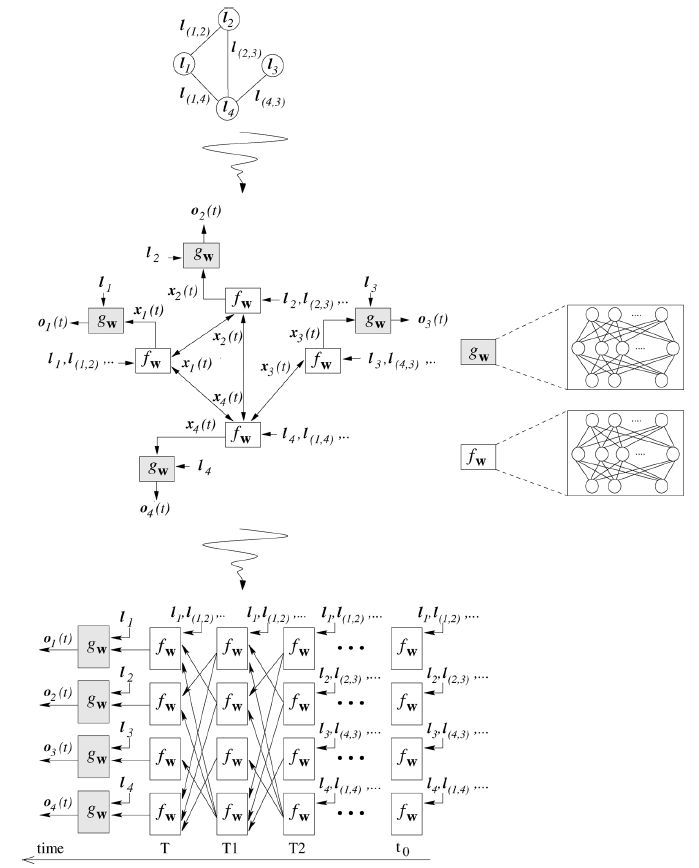
这可以解释为由很多处理单元
unit组成的神经网络,每个处理单元通过encoding network,它类似于RNN的编码网络。在编码网络中,每个单元根据邻居单元的状态、当前节点的信息、邻居节点的信息、边的信息,通过当
RNN,其中神经元之间的连接可以分为内部连接internal connection和外部连接external connection:内部连接由实现处理单元的神经网络架构(如前馈神经网络)决定,外部连接由图的边来决定。如下图所示:上半图对应一个图
Graph,中间图对应于编码网络,下半图对应于编码网络的展开图unfolding graph。在展开图中,每一层layer代表一个时间步,layer之间的链接(外部连接)由图的连接性来决定,layer内神经元的链接(内部连接)由神经网络架构决定。内部连接决定
1.1.3 参数学习算法
假设训练集为:
其中:
target(可能为标量可能为向量),- 对于
graph-focused任务,可以引入一个和任务目标相关的、特殊的节点,只有该节点包含监督信息,即 - 对于
node-focused任务,每个节点都可以包含监督信息。
假设采用平方误差,则训练集的损失函数为:
其中
也可以在损失函数中增加罚项从而对模型施加约束。
- 对于
我们可以基于梯度下降算法来求解该最优化问题,求解方法由以下几步组成:
通过下面的迭代公式求解求解
其解接近
注意:这一步要求
求解梯度
通过梯度来更新参数
梯度
GNN中发生的扩散过程diffusion process以非常高效的方式进行。这种扩散过程与RNN中发生的扩散过程非常相似,而后者是基于backpropagation-through-time: BPTT算法计算梯度的。在这种情况下,编码网络从时刻unfold到初始时刻unitBPTT是在展开图上执行传统的反向传播算法。 首先计算时间步BPTT要求存储每个单元在每个时间步Almeida-Pineda算法提出了一个非常高效的处理方式:由于我们假设状态向量BPTT算法仅需要存储下面两个定理表明这种简单直观方法的合理性:
定理(可微性
Differentiability):如果全局转移函数其证明见原始论文。值得注意的是,对于一般动力学系统而言该结论不成立。对于这些动力学系统而言,参数的微小变化会迫使其从一个固定点转移到另一个固定点。而
GNN中的定理:如果全局转移函数
则序列
更进一步有:
其中
GNN的不动点,证明见论文原文。
第一项表示输出函数
layer时计算这一项。第二项表示转移函数layer时计算这一项。
GNN参数学习算法包含三个部分:FORWARD前向计算部分:前向计算部分用于计算状态向量BACKWARD反向计算部分:反向计算部分用于计算梯度MAIN部分:该部分用于求解参数。该部分更新权重
FORWARD部分:输入:图
输出:不动点
算法步骤:
随机初始化
循环迭代,直到满足
- 计算
- 令
- 计算
返回
BACKWARD部分:输入:图
输出:梯度
算法步骤:
定义:
随机初始化
循环迭代,直到满足
- 更新
- 令
- 更新
计算梯度:
返回梯度
Main部分:输入:图
输出:模型参数
算法步骤:
随机初始化参数
通过前向计算过程计算状态:
循环迭代,直到满足停止条件。循环步骤为:
- 通过反向计算过程计算梯度:
- 更新参数:
- 通过新的参数计算状态:
- 通过反向计算过程计算梯度:
返回参数
Main部分采用预定义的学习率GNN只能通过梯度下降算法求解,非梯度下降算法目前还未解决,这是未来研究的方向。实际上编码网络仅仅类似于静态的前馈神经网络,但是编码网络的
layer层数是动态确定的(类似于RNN),并且网络权重根据输入图的拓扑结构来共享。因此为静态网络设计的二阶学习算法、剪枝算法、以及逐层学习算法无法直接应用于GNN。
1.1.4 转移函数和输出函数
局部输出函数
GNN中,另一方面,局部转移函数
GNN中起着关键作用,它决定了不动点的存在性和唯一性。GNN的基本假设是:全局转移函数nonpositional form,positional form也可以类似地实现。nonpositional linear GNN线性GNN:其中
GNN的参数。更准确的说:转移网络
transition network是一个前馈神经网络,它用于生成设该神经网络为一个映射
其中:
因此
这里的转移矩阵
tanh),使得神经网络的输出满足某些性质,从而使得约束网络
forcing network是另一个前馈神经网络,它用于生成设该神经网络为一个映射
因此,
这里
假设有:
tanh激活函数),则很容易满足该假设。根据其中:
其中:
- 如果
- 如果
- 如果
由于
则有:
因此对于任意的参数
nonpositional nonlinear GNN非线性GNN:注意,这里针对关于
其中:
超参数
更一般地,罚项可以是关于
1.2 模型分析
GNN和RNN:事实上,GNN是其它已知模型的扩展,特别地,RNN是GNN的特例。当满足以下条件时,GNN退化为RNN:- 输入图为有向无环图(例如最简单的有向的、线性的链式图)。
- 一个超级源点
graph-focused任务的输出
实现
cascade correlation、自组织映射self-orgnizing map。在RNN中,编码网络采用多层前馈神经网络。这个简化了状态向量的计算。GNN和随机游走:当选择GNN模型还捕获了图上的随机游走过程。定义节点的状态
其中:
事实上
当所有的
其中:
可以很容易的验证
马尔可夫理论认为:如果存在
因此假设存在
GNN的一个特例,其中constant stochastic matrix,而不是由神经网络产生的矩阵。当输入图为无向图时,将
读者注:
GNN的核心是不动点理论,通过节点的消息传播使得整张图的每个节点的状态收敛,然后在收敛的状态基础上预测。这里存在一个局限:基于不动点的收敛会导致节点之间的状态存在较多的消息共享,从而导致节点状态之间过于光滑
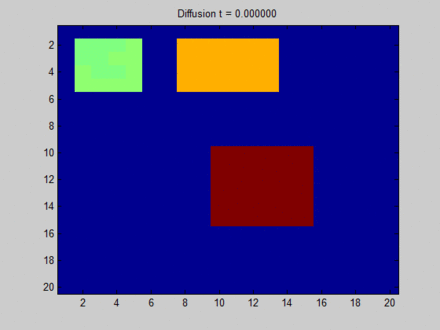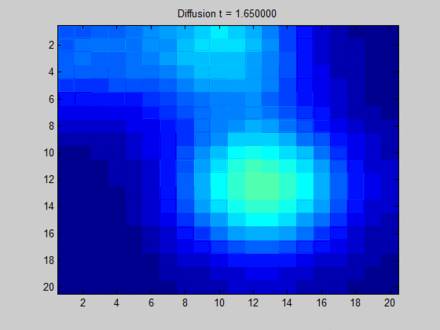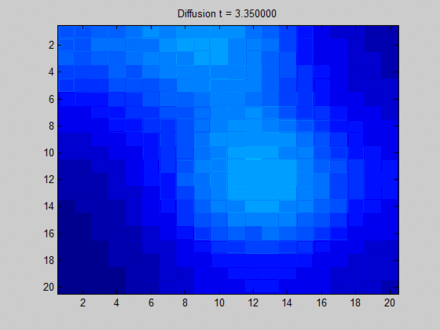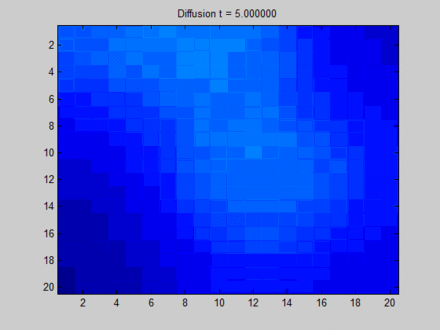
over smooth,这将使得节点之间缺少区分度。如下图所示,每个像素点和它的上下左右、以及斜上下左右八个像素点相邻。初始时刻蓝色没有信息量,绿色、黄色、红色各有一部分信息。
- 开始时刻,不同像素点的区分非常明显。
- 在不动点的收敛过程中,所有像素点都趋向于一致,最终整个系统的信息分布比较均匀。
- 最终,虽然每个像素点都感知到了全局信息,但是我们已经无法根据每个像素点的最终状态来区分它们。
1.3 计算复杂度
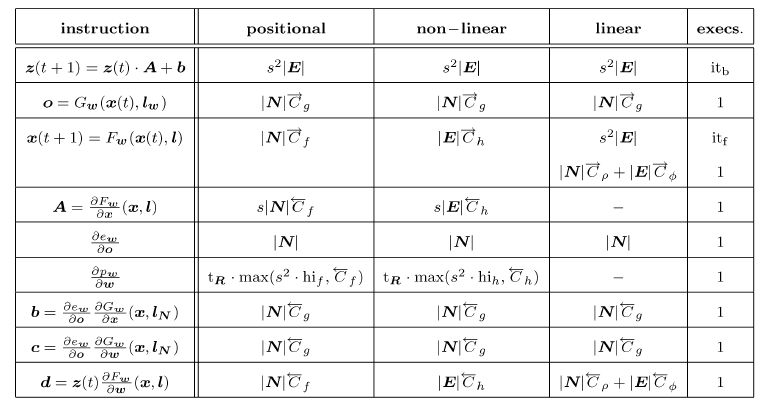
我们关心三种类型的
GNN模型:positional GNN(其中nonpositional linear GNN、nonpositional nonlinear GNN。训练过程中一些复杂运算的计算复杂度见下表。为方便表述,我们假设训练集仅包含一张图。这种简化不影响结论,因为训练集所有的图总是可以合并为一张大图。另外,复杂度通过浮点运算量来衡量。
具体推导见论文。其中:
instruction表示具体的运算指令,positional/non-linear/linear分别给出了三类GNN模型在对应运算指令的计算复杂度,execs给出了迭代的次数。epoch数量,epoch的反向迭代次数(BACKWARD过程中的循环迭代次数),epoch的前向迭代次数(FORWARD过程中的循环迭代次数)。令雅克比矩阵
其中:
定义
当
GNN模型训练完成之后,其推断速度也很快。- 对于
positional GNN,其推断的计算复杂度为: - 对于
nonpositional nonliear GNN,其推断的计算复杂度为: - 对于
nonpositional linear GNN,其推断的计算复杂度为:
推断阶段的主要时间消耗在计算状态
GNN是一个例外。线性GNN的单次迭代成本是状态维度的二次关系。状态向量的收敛速度取决于具体的问题。但是
Banach定理可以确保它是以指数级速度收敛。实验表明:通常5到15次迭代足以逼近不动点。- 对于
在
positional GNN中转移函数需要执行nonpositional nonliear GNN中转移函数需要执行positional GNN和nonpositional nonlinear GNN的推断计算复杂度是相近的,这是因为positional GNN中的nonpositional nonliear GNN中的- 在
positional GNN中,实现 - 在
nonpositonal nonliear GNN中,实现
只有在节点的邻居数量高度可变的图中才能注意到明显的差异,因为
null)。- 在
另一方面,观察到在
linear GNN中,每次迭代仅使用一次FNN,因此每次迭代的复杂度为注意到,当
FNN实现时,GNN的训练阶段要比推断阶段消耗更多时间,主要在于需要在多个epoch中重复执行forward和backward过程。实验表明:forward阶段和backward阶段的时间代价都差不多。forward阶段的时间主要消耗在重复计算- 类似于
forward阶段,backward阶段的时间主要消耗在重复计算
训练过程中,每个
epoch的计算代价可以由上表中所有指令的计算复杂度的加权和得到,权重为指令对应的迭代次数。所有指令的计算复杂度基本上都是输入图的维度(如:边的数量)的线性函数,也是前馈神经网络隐单元维度的线性函数,也是状态维度
有几个例外,如计算
最耗时的指令是
nonpositional nonlinear GNN中计算实验表明,通常
epoch中1~5之间。因此对于较小的状态维度理论上,如果
1.4 实验
这里我们展示了在一组简单问题上获得的实验结果,这些问题是为了研究
GNN模型的特性,并证明该方法可以应用于相关领域的相关应用。这些问题包括:子图匹配、诱变mutagenesis、网页排名,因为这些问题特别适合挖掘模型的属性并且与重要的现实应用相关。值得一提的是,GNN模型已经成功应用于更大的应用,包括图像分类、图像中的物体定位、网页排名web page ranking、关系学习relational learning、XML分类。除非另有说明,以下事实适用于每个实验。
- 根据
RNN的已有经验,nonpositional转移函数效果要优于positional转移函数,因此这里测试了nonpositional linear GNN和nonpositional nonlinear GNN。 - 所有
GNN中涉及到的函数,如nonpositional linear GNN中的nonpositional nonlinear GNN中的sigmoid激活函数。 - 报告的结果是五次不同运行的均值。在每次运行中,数据集是由以下过程构建的随机图的集合:每对节点之间以一定的概率
- 根据
数据集划分为训练集、验证集和测试集。
- 如果原始数据仅包含一张大图
- 如果原始数据包含多个图
在每次试验中,训练最多执行
5000个epoch,每20个epoch在验证集上评估GNN。在验证集上实现最低损失函数的GNN被认为是最佳模型,并应用于测试集。测试集性能评估指标为分类准确率或回归相对误差。
对于分类问题,
对于回归问题,
- 如果原始数据仅包含一张大图
算法在
Matlab 7上实现,在配备了2-GHz PowerPC处理器的Power Mac G5上进行。
1.4.1 子图匹配问题
子图匹配
subgraph matching问题:在更大的图如下图所示,图
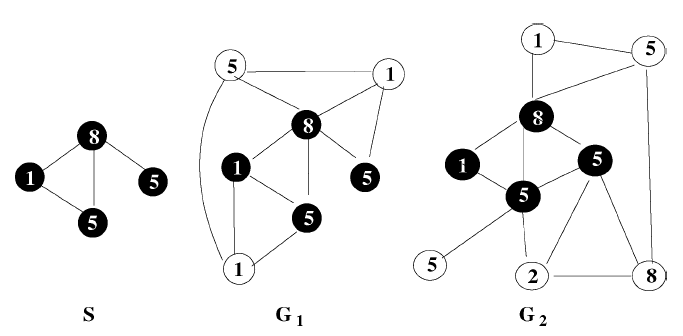
子图匹配问题有很多实际应用,如:物体定位、化合物检测。子图匹配问题是评估图算法的基准测试。实验表明
GNN模型可以处理该任务。- 一方面
GNN模型解决子图匹配问题的结果可能无法与该领域的专用方法相比,后者的速度更快、准确率更高。 - 另一方面
GNN模型是一种通用算法,可以在不经修改的情况下处理子图匹配问题的各种扩展。如:同时检测多个子图、子图的结构和标签信息向量带有噪音、待检测的目标图
- 一方面
数据集:由
600个随机图组成(边的连接概率为每个节点包含整数标签,取值范围从
[0,10]。我们使用一个均值为0、标准差为0.25的高斯噪声添加到标签上,结果导致数据集中每个图对应的注意添加噪声之后,节点的标签仍然为整数,因此需要四舍五入。
为了生成正确的监督目标
GNN配置:- 所有实验中,状态向量的维度
- 所有实验中,
GNN的所有神经网络的隐层为三层,隐层维度为5。我们已经测试过更多的网络架构,结果是类似的。
为评估子图匹配任务中,标签信息和子图连通性的相对重要性,我们还应用了前馈神经网络
FNN作为baseline。FNN有一个输出单元、20个隐单元、一个输入单元。FNN仅使用标签信息- 所有实验中,状态向量的维度
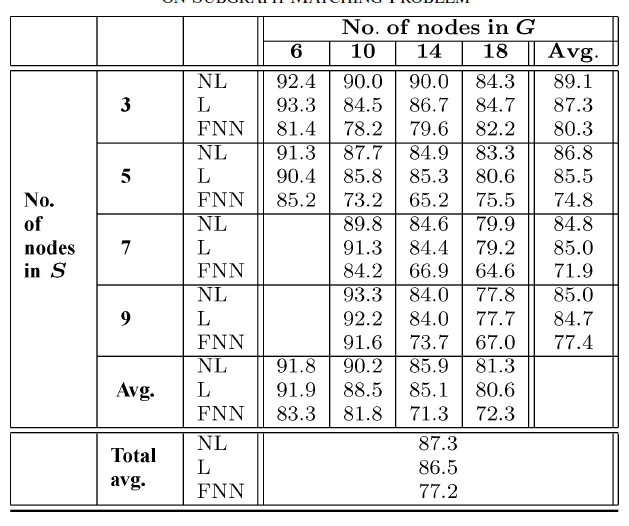
实验结果如下图所示,其中
NL表示nonpositional nonlinear GNN,L表示nonpositional linear GNN,FNN表示前馈神经网络。评估指标为测试集准确率。结论:
正负节点的比例影响了所有方法的效果。
- 当
- 当
事实上,在后一种情况下,数据集是完全平衡的,并且更难以猜测正确的目标。
- 当
子图规模
因为标签只能有
11种不同取值,当GNN总是优于FNN,这表明GNN可以同时利用标签内容和图的拓扑结构。非线性
GNN略优于线性GNN,这可能是因为非线性GNN实现了更为通用的模型,它的模型容量更大。最后,可以观察到
FNN的总体平均误差比GNN增加大约50%。GNN和FNN之间的相对错误率(衡量了拓扑结构的优势)随着实际上,
GNN使用信息扩散机制information diffusion mechanism来决定节点是否属于子图。当
为评估
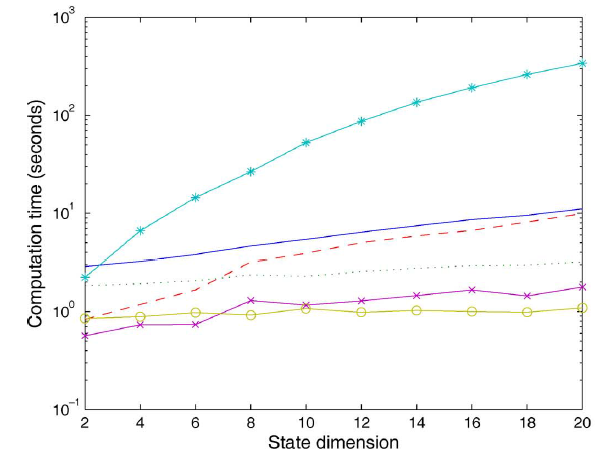
GNN的计算复杂度和准确性,我们评估了不同节点数、不同边数、不同隐层维度、不同状态向量维度的效果。在基准情况下:训练集包含10个随机图,每个图包含20个节点和40条边;GNN隐层维度为5,状态向量维度为2。GNN训练1000个epoch并报告十次实验的平均结果。如预期的一样,梯度计算中需要的CPU时间随着节点数量、边的数量、隐层维度呈线性增长,随着状态向量维度呈二次增长。下图为节点数量增加时,梯度计算花费的
CPU时间。实线表示非线性GNN,虚线表示线性GNN。
下图为状态向量维度增加时,梯度计算花费的
CPU时间。实线表示非线性GNN,虚线表示线性GNN。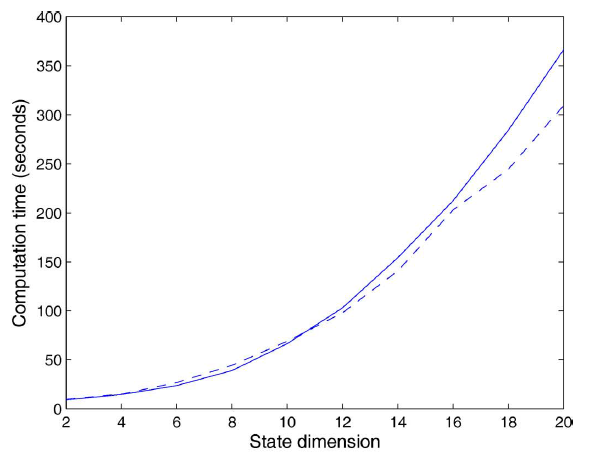
非线性
GNN中,梯度和状态向量维度的二次关系取决于计算雅可比矩阵线条
-o-给出了计算-*-给出了计算雅可比矩阵-x-给出了计算...和给出了剩下的前向计算的时间代价;虚线---给出了剩下的反向计算的时间代价;实线表示剩下的计算梯度的时间代价。可以看到:
下图给出每个
epoch中4。另外下图也给出计算稳定状态下图给出的是迭代次数或
x轴)的分布(y轴表示出现次数)。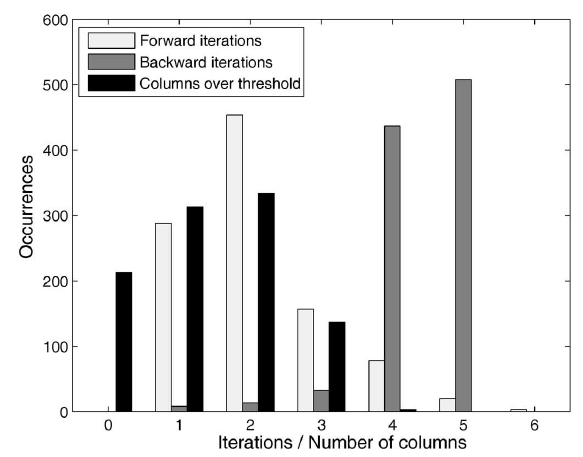
1.4.2 Mutagenesis问题
Mutagenesis数据集:一个小型数据集,经常作为关系学习relational learning和inductive logic programming中的基准。它包含230种硝基芳香族化合物的数据,这些化合物是很多工业化学反应中的常见中间副产品。任务目标是学习识别
mutagenic诱变化合物。我们将对数诱变系数log mutagenicity的阈值设为0,因此这个任务是一个二类分类问题。数据集中的每个分子都被转换为一张图:
节点表示原子、边表示原子键
atom-bond:AB。平均的节点数量大约为26。边和节点的标签信息包括原子键
AB、原子类型、原子能量状态,以及其它全局特征。全局特征包括:chemical measurement化学度量C(包括lowest unoccupied molecule orbital, the water/octanol partition coefficient)、precoded structural预编码结构属性P\mathbf S。另外原子键可以用于定义官能团
functional groups: FG。在每个图中存在一个监督节点:分子描述中的第一个原子。如果分子为诱变的则该节点的期望输出为
1,否则该节点的期望输出为-1。
在这
230个分子中,有188个适合线性回归分析,这些分子被称作回归友好regression friendly。剩下的42个分子称作回归不友好regression unfriendly。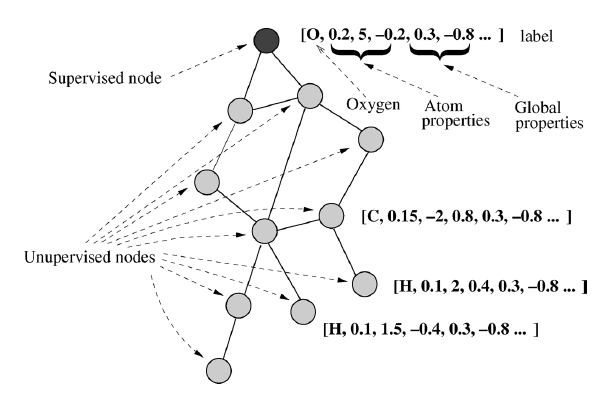
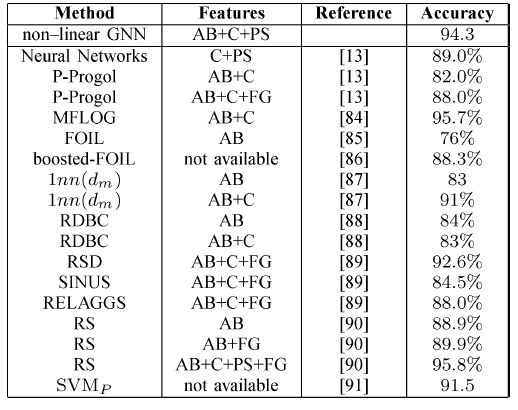
GNN在诱变化合物问题上的结果如下表所示。我们采用十折交叉验证进行评估:将数据集随机拆分为十份,重复实验十次,每次使用不同的部分作为测试集,剩余部分作为训练集。我们运行5次十折交叉,并取其均值。在回归友好分子上的效果:
在回归不友好分子上的效果:

在所有分子上的效果:
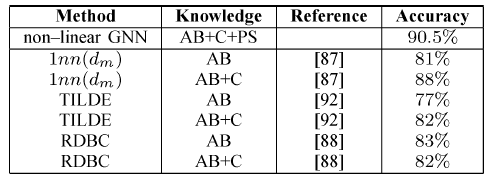
结论:
GNN在回归不友好分子和所有分子上的效果都达到最佳,在回归友好分子上的效果接近state of the art水平。- 大多数方法在应用于整个数据集时,在回归友好分子上(相比较于回归不友好分子)显示出更高的准确率。但是
GNN与此相反。这表明GNN可以捕获有利于解决问题但是在回归友好分子、回归不友好分子这两部分中分布不均的模式特征。
1.4.3 Web PageRank
受到谷歌的
PageRank启发,这里我们的目标是学习一个网页排名。网页其中:
out-degree,damping factor,图
5000个节点。训练集、验证集、测试集由图的不同节点组成,其中50个节点作为训练集、50个节点作为验证集、剩下节点作为测试集。每个节点
需要拟合的目标
target为:这里我们使用线性
GNN模型,因为线性GNN模型很自然的类似于PageRank线性模型。转移网络和约束网络forcing network都使用三层前馈神经网络,隐层维度为5。状态向量维度为输出函数为:
5。下图给出了
GNN模型的结果。其中图(a)给出了仅属于一个主题的网页的结果,图(b)给出了其它网页的结果。红色实线表示目标
GNN模型的输出。横轴表示测试集的节点数量,纵轴表示目标得分GNN在这个问题上表现得非常好。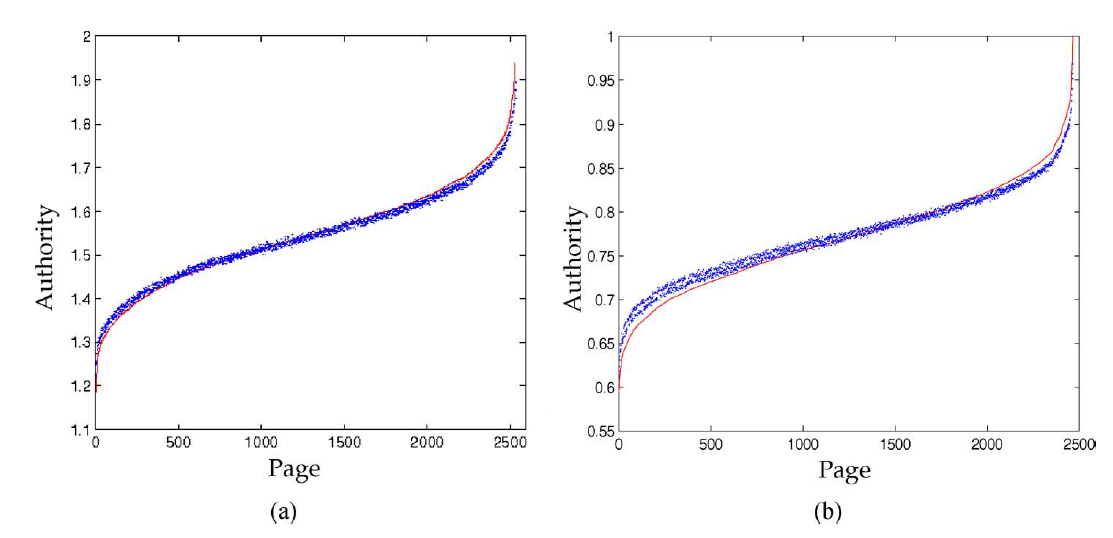
下图给出学习过程中的误差。红色实线为训练集的误差,蓝色虚线是验证集的误差。注意:两条曲线总是非常接近,并且验证集的误差在
2400个epoch之后仍在减少。这表明尽管训练集由5000个节点中的50个组成,GNN仍然未经历过拟合。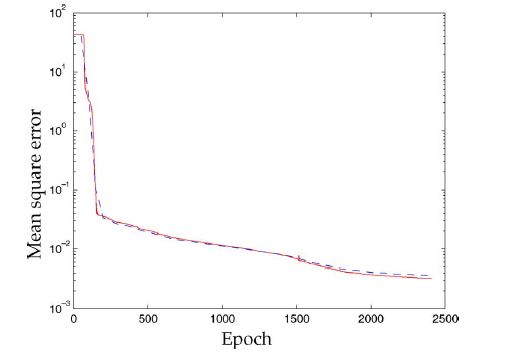
二、Spectral Networks & Deep Locally Connected Networks [2013]
卷积神经网络
Convolutional Neural Networks: CNNs在机器学习问题中非常成功,其中底层数据representation的坐标具有网格结构grid structure(一维、二维、或三维的网格),并且在这些坐标中,这些待研究的数据相对于该网格具有平移相等translational equivariance性或平移不变性translational invariance。语音、图像、视频就是属于这一类问题的著名的例子。在常规网格上,
CNN能够利用多种结构来很好地协同工作,从而大大减少系统中的参数数量:- 平移结构
translation structure:它允许使用filter而不是通用的线性映射,从而实现权重共享weight sharing。 - 空间局部性:
filter的尺寸通常都远远小于输入信号的尺寸。 - 多尺度:通过步长大于一的卷积或者池化操作来减少参数,并获得更大的感受野
receptive field。
然而在许多情况下,数据并不是网格结构,如社交网络数据,因此无法在其上应用标准的卷积网络。图
graph提供了一个自然框架来泛化网格结构,并扩展了卷积的概念。在论文《Spectral Networks and Deep Locally Connected Networks on Graphs》中,作者将讨论在除了常规网格之外的图上构建深度神经网络。论文提出了两种不同的结构:- 基于空域的卷积构建
Spatial Construction:通过将空间局部性和多尺度扩展到通用的图结构,并使用它们来定义局部连接和池化层,从而直接在原始图结构上执行卷积。 - 基于谱域的卷积构建
Spectral Construction:对图结构进行傅里叶变换之后,在谱域进行卷积。
论文主要贡献如下:
- 论文表明,从给定的图结构输入,可以获得参数为
- 论文介绍了一种使用
harmonic analysis problem的联系。
- 平移结构
2.1 基础概念(读者补充)
2.1.1 拉普拉斯算子
散度定义:给定向量场
当
其中
散度的物理意义为:在向量场中从周围汇聚到该点或者从该点流出的流量。
旋度定义:给定向量场
当
在三维空间中,上式等于:
旋度的物理意义为:向量场对于某点附近的微元造成的旋转程度,其中:
- 旋转的方向表示旋转轴,它与旋转方向满足右手定则。
- 旋转的大小是环量与环面积之比。
拉普拉斯算子定义:给定函数
梯度的物理意义为:函数值增长最快的方向。
梯度的散度为拉普拉斯算子,记作:
- 由于所有的梯度都朝着
- 拉普拉斯算子也能够衡量函数的平滑度
smoothness:函数值没有变化或者线性变化时,二阶导数为零;当函数值突变时,二阶导数非零。
- 由于所有的梯度都朝着
图拉普拉斯矩阵:假设
二阶导数为二阶差分:
一维函数其自由度可以理解为
2,分别是+1和-1两个方向。因此二阶导数等于函数在所有自由度上微扰之后获得的增益。推广到图结构
令
函数
signal。对于节点
其中:
degree matrix,考虑所有的节点,则有:
定义拉普拉斯矩阵
上述结果都是基于
假设图的节点数量为
- 对称矩阵一定有
- 半正定矩阵的特征值一定是非负的。
- 对称矩阵的特征向量相互正交,即:所有特征向量构成的矩阵为正交矩阵。
因此有拉普拉斯矩阵的谱分解:
其中
解得:
- 对称矩阵一定有
根据
根据特征方程:
在
PCA降维也是同样原理,把协方差矩阵特征分解后,取top K个特征值对应的特征向量作为新的特征空间。 如下图所示为包含25个节点的图,其25维空间中,最大特征值、第12大特征值、次小特征值(因为最小特征值为零,因此第24大特征值就是次小的)对应特征向量1的向量(或者乘以常数倍),这意味着该特征向量在所有节点上取值相等(所以变化为零),即频率为零的分量。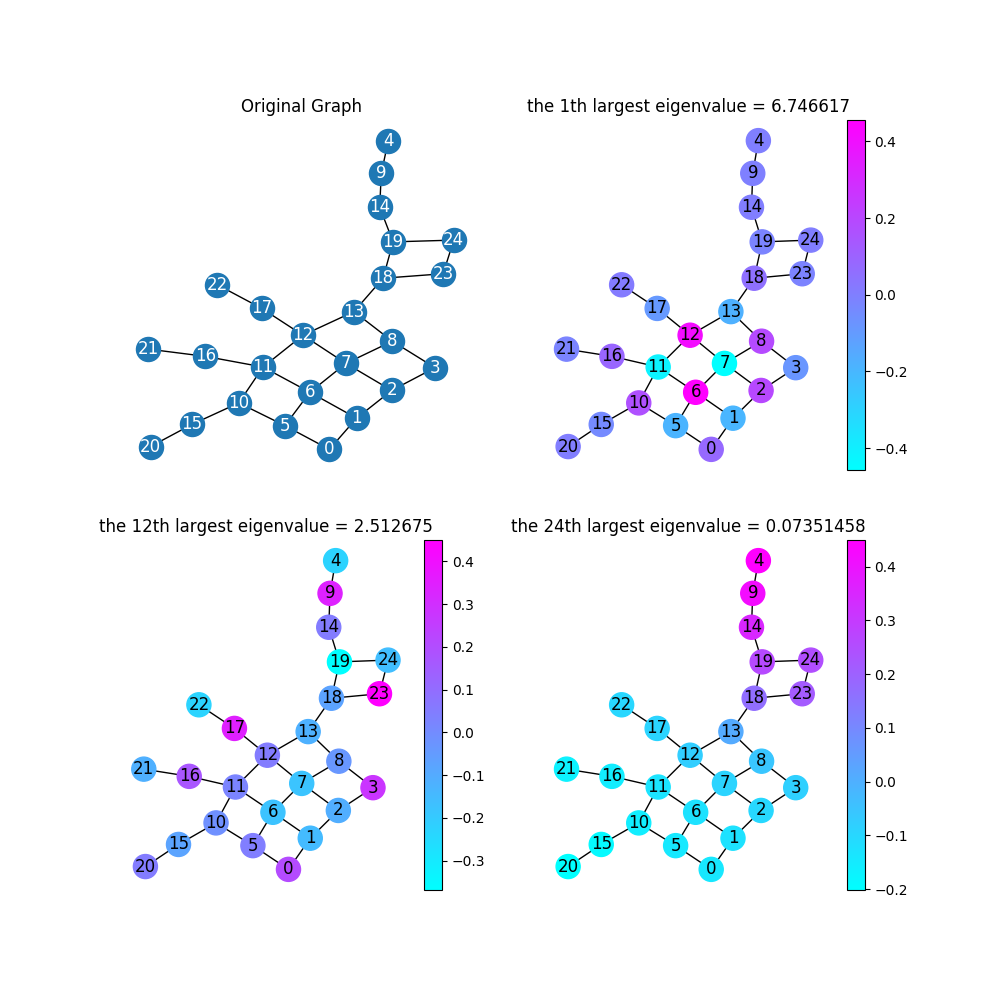
2.1.2 卷积
给定函数
其中
fouries basis。可以证明:
如果将傅里叶变换推广到图上,则有类比:
拉普拉斯算子对应于拉普拉斯矩阵
频率
傅里叶基
傅里叶系数
写成矩阵形式为:
其中:
传统的傅里叶逆变换
其中
卷积定理:两个函数在时域的卷积等价于在频域的相乘。
对应于图上有:
其中:
这里将逐元素乘积转换为矩阵乘法。
图卷积神经网络的核心就是设计卷积核,从上式可知卷积核就是
我们并不关心
2.2 空域构建 Spatial Construction
2.2.1 基本概念
在通用的图结构上针对
CNN最直接的推广是考虑多尺度的、局部的感受野。为此,我们使用一个加权图这里的权重指的是图中边的权重,而不是神经网络的权重。
基于
locality:可以很容易地在图结构中推广局部性的概念。实际上,图中的权重决定了局部性的概念。例如,在其中
在执行卷积时,我们可以仅仅考虑将感受野限制在这些邻域上的
sparse filter,从而获得局部连接的网络locally connected network,从而将卷积层的参数数量减少到每个节点需要
图的多分辨率
multiresolution分析:CNN通过池化pooling层和降采样subsampling层来减少feature map的尺寸,在图结构上我们同样可以使用多尺度聚类multiscale clustering的方式来获得多尺度结构。在图结构上如何进行多尺度聚类仍然是个开发的研究领域,我们这里根据节点的邻域进行简单的聚类。图的邻域结构天然地代表了某种意义上的聚类。比如,社交网络的一阶邻域代表用户的直接好友圈子,以一阶邻域来聚类则代表了一个个的”小团体“。基于这些 ”小团体“ 进行聚类得到的高阶聚类可能包含了国家的信息,比如”中国人“被聚合在一个高阶聚类中,”美国人“被聚合在另一个高阶聚类中。
下图给出了多尺度层次聚类的示意图(两层聚类)。原始的
12个节点为灰色。第一层有6个聚类,聚类中心为彩色节点,聚类以彩色块给出。第二层有3个聚类,聚类以彩色椭圆给出。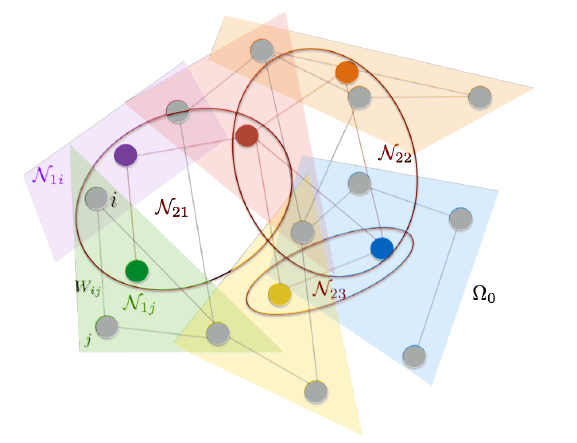
2.2.2 深度局部连接网络 Deep Locally Connected Networks
空域构建
spatial construction从图的多尺度聚类开始,并且我们考虑scale。定义第0个尺度表示原始图,即feature map,feature map有了这些之后我们现在可以定义神经网络的第
real signal(即标量值) ,我们设第filter数量为正式地,假设第
其中:
feature map。feature。
则第
其中:
信号的每一维度表示一个通道,因此
sum聚合而来。filter),它表示应用于第即:当节点
filter的待学习的参数。这意味着在线性投影时,节点
cluster id,列表示节点id,矩阵中的元素表示每个节点对应于聚类中心的权重:如果是均值池化则就是1除以聚类中的节点数,如果是最大池化则是每个聚类的最大值所在的节点。
初始化:
根据对
对于
然后按行进行归一化:
根据
如下图所示
12个节点(灰色),信号为一个通道(标量)。6个节点,输出信号四个通道(四个filter)。3个节点,输出信号六个通道(六个filter)。
每一层卷积都降低了空间分辨率
spatial resolution,但是增加了空间通道数。
假设
实际应用中我们可以使得
为什么这么做?论文并未说明原因。
空域构建的实现非常朴素,其优点是不需要对图结构有很高的规整性假设
regularity assumption。缺点是无法在节点之间实现权重共享。
2.3 谱域构建 Spectral Construction
可以通过图拉普拉斯算子来探索图的全局结构,从而推广卷积算子。
假设构建一个
feature map其中:
实际应用中,通常仅仅使用拉普拉斯矩阵的最大
regularity以及图的节点数量。此时上式中的filter。一般而言我们选择filter我们将在后文看到如何将图的全局规整性和局部规整性结合起来,从而产生具有
谱域构建可能受到以下事实的影响:大多数图仅在频谱的
top(即高频部分)才具有有意义的特征向量。即使单个高频特征向量没有意义,一组高频特征向量也可能包含有意义的信息。然而,我们的构建方法可能无法访问这些有意义的信息,因为我们使用对角线形式的卷积核,在最高频率处它是对角线形式因此仅包含单个高频特征向量(而不是一组高频特征向量)。
傅里叶变换是线性变换,如何引入非线性目前还没有很好的办法。
具体而言,当在空域执行非线性变换时,如何对应地在谱域执行前向传播和反向传播,目前还没有很好的办法,因此我们必须进行昂贵的
为了降低参数规模,一个简单朴素的方法是选择一个一维的排列
arrangement(这个排列的顺序是根据拉普拉斯特征值的排序得到)。此时第filter其中:
假设采样步长正比于节点数量,即步长
2.4 实验
- 我们对
MNIST数据集进行实验,其中MNIST有两个变种。所有实验均使用ReLU激活函数以及最大池化。模型的损失函数为交叉熵,固定学习率为0.1,动量为0.9。
2.4.1 降采样 MNIST
我们将
MNIST原始的28x28的网格数据降采样到400个像素,这些像素仍然保留二维结构。由于采样的位置是随机的,因此采样后的图片无法使用标准的卷积操作。采样后的图片的示例,空洞表示随机移除的像素点。

空域层次聚类的可视化,不同的颜色表示不同的簇,颜色种类表示簇的数量。图
a表示b表示
谱域拉普拉斯特征向量的可视化(谱域特征向量每个元素就是对应于每个节点的取值)。图
a表示b表示
不同模型在
MNIST上分类的结果如下。基准模型为最近邻模型kNN,FCN表示带有N个输出的全连接层,LRFN表示带有N个输出的空域卷积层,MPN表示带有N个输出的最大池化层,SPN是带有N个输出的谱域卷积层。- 基准模型
kNN(第一行)的分类性能比完整的(没有采样的)MNIST数据集的2.8%分类误差率稍差。 - 两层全连接神经网络(第二行)可以将测试误差降低到
1.8%。 - 两层空域图卷积神经网络(第三行的下面部分)效果最好,这表明空域卷积层核池化层可以有效的将信息汇聚到最终分类器中。
- 谱域卷积神经网络表现稍差(第四行),但是它的参数数量最少。
- 采用谱域平滑约束(选择
top的

- 基准模型
由于
MNIST中的数字由笔画组成,因此具有局部性。空域卷积通过filterfilter上添加平滑约束可以改善分类结果,因为filter被强制具有更好的空间局部性。- 图
(a),(b)表示同一块感受野在空域卷积的不同层次聚类中的结果。 - 图
(c),(d)表示谱域卷积的两个拉普拉斯特征向量,可以看到结果并没有空间局部性。 - 图
(e),(f)表示采用平滑约束的谱域卷积的两个拉普拉斯特征向量,可以看到结果有一定的空间局部性。
- 图
2.4.2 球面 MNIST
我们将
MNIST图片映射到一个球面上,构建方式为:- 首先从单位球面上随机采样
4096个点 - 然后考虑三维空间的一组正交基
- 对原始
MNIST数据集的每张图片,我们采样一个随机方差PCA的一组基
由于数字
6和9对于旋转是等价的,所以我们从数据集中移除了所有的9。下面给出了两个球面
MNIST示例: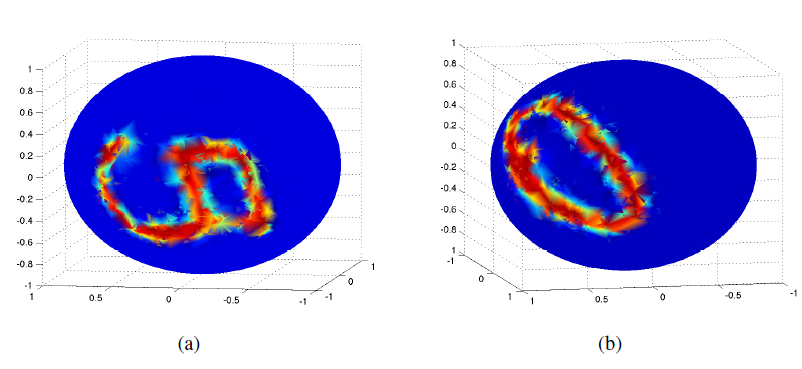
下面给出了谱域构建的图拉普拉斯矩阵的两个特征向量的可视化。图
a表示b表示
- 首先从单位球面上随机采样
首先考虑“温和”的旋转:
- 基准的
kNN模型的准确率比上一个实验(随机采样MNIST)差得多。 - 所有神经网络模型都比基准
KNN有着显著改进。 - 空域构建的卷积神经网络、谱域构建的卷积神经网络在比全连接神经网络的参数少得多的情况下,取得了相差无几的性能。

- 基准的
不同卷积神经网络学到的卷积核(即
filter)如下图所示。- 图
(a),(b)表示同一块感受野在空域卷积的不同层次聚类中的结果。 - 图
(c),(d)表示谱域卷积的两个拉普拉斯特征向量,可以看到结果并没有空间局部性。 - 图
(e),(f)表示采用平滑约束的谱域卷积的两个拉普拉斯特征向量,可以看到结果有一定的空间局部性。
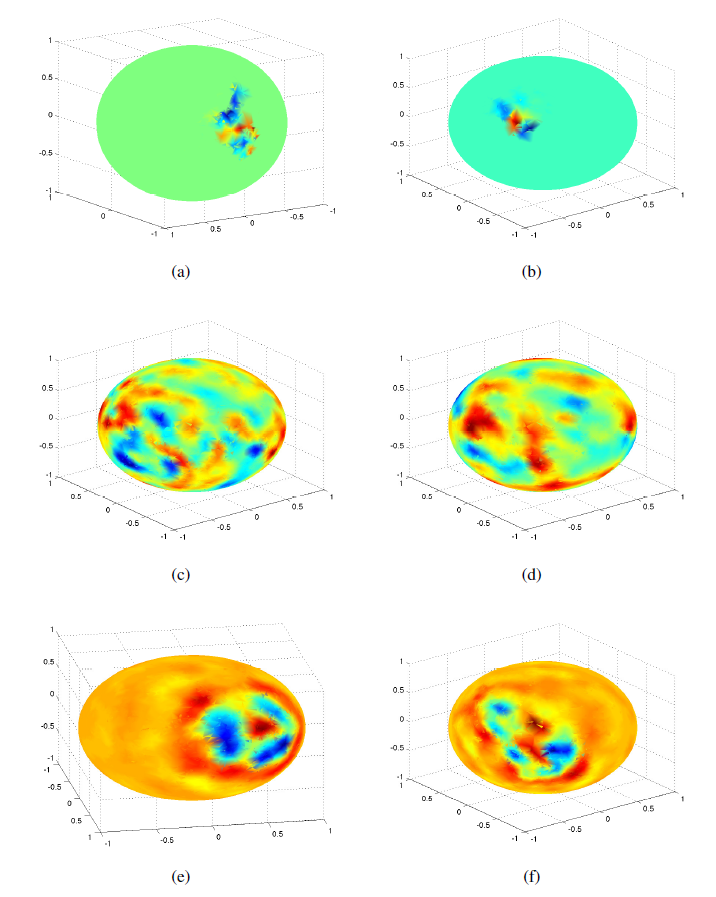
- 图
最后我们考虑均匀旋转,此时
三、Fast Localized Spectral Filtering On Graph[2016]
卷积神经网络提供了一种有效的架构,可以在大规模的、高维的数据集中抽取非常有意义的统计模式
statistical pattern。CNN学习局部静态结构local stationary structure并将它们组合成多尺度的multi-scale、分层hierarchical的模式,并导致了图像识别、视频识别、声音识别等任务的突破。准确地说,CNN通过揭示跨数据域data domain共享的局部特征来抽取输入数据(或输入信号)的局部平稳性local stationarity。这些相似的特征通过从数据中学到的局部卷积滤波器localized convolutional filter(或局部卷积核localized convolutional kernel)来识别。卷积滤波器是平移不变translation-invariant的,这意味着它们能够独立于空间位置来识别相同的特征identical feature。局部核localized kernel(或紧凑支持的滤波器compactly supported filter)指的是独立于输入数据大小并抽取局部特征的滤波器,它的支持度support大小可以远小于输入大小。社交网络上的用户数据、电信网络上的日志数据、或
word embedding上的文本文档,它们都是不规则数据的重要例子,这些数据可以用图graph来构造。图是异质pairwise关系的通用表达universal representation。图可以编码复杂的几何结构,并且可以使用强大的数学工具进行研究,如谱图理论spectral graph theory。将
CNN推广到图并不简单,因为卷积算子和池化算子仅针对规则网格regular grid才有定义。这使得CNN的扩展在理论上和实现上都具有挑战性。将CNN推广到图的主要瓶颈(也是论文《Convolutional Neural Networks on Graphs with Fast Localized Spectral Filtering》的主要目标之一),是定义可以有效评估和学习的局部图滤波器localized graph filter。准确地说,论文《Convolutional Neural Networks on Graphs with Fast Localized Spectral Filtering》的主要贡献如下:谱公式
spectral formulation:基于图信号处理graph signal processing: GSP中已有的工具,论文建立了图上CNN的谱图spectral graph理论公式。严格局部的滤波器:可以证明,论文提出的谱滤波器
spectral filter严格限定在半径为K hops。这是对《Spectral Networks and Deep Locally Connected Networks on Graphs》的增强。低的计算复杂度:论文提出的滤波器的
evaluation复杂度与滤波器尺寸degree。这使得计算复杂度与输入数据大小此外,论文的方法完全避免了傅里叶基
Fourier basis,因此避免了计算傅里叶基所需要的特征分解eigenvalue decomposition所需的计算量,也避免了存储傅里叶基的内存需求(一个GPU内存有限时尤其重要。除了输入数据之外,论文的方法只需要存储拉普拉斯算子,它是一个包含高效的池化:论文提出了一种有效的、图上的池化策略,该策略在将顶点重排为二叉树结构之后,采用类似于一维信号的池化。
实验结果:论文进行了多个实验,最终表明所提出的公式是:一个有效的模型、计算效率高、在准确性和复杂性上都优于
《Spectral Networks and Deep Locally Connected Networks on Graphs》中介绍的spectral graph CNN。论文还表明,所提出的图公式在
MNIST上的表现与经典CNN相似,并研究了各种图构造graph construction对于性能的影响。
相关工作:
图信号处理
graph signal processing: GSP:GSP的新兴领域旨在弥合信号处理和谱图理论之间的gap,是图论graph theory和谐波分析harmonic analysis之间的融合。一个目标是将信号的基本分析操作从规则网格推广到不规则的图结构。诸如卷积、平移、滤波filtering、膨胀dilatation、调制modulation、降采样downsampling等等网格上的标准操作不会直接扩展到图,因此需要新的数学定义,同时保持原有的直观概念。在这种情况下,已有工作重新审视了图上小波算子wavelet operator的构建,并提出了在图上执行mutli-scale pyramid transform。也有一些工作重新定义了图上的不确定性原理,并表明虽然可能会丢失直观的概念,但是可以导出增强的局部性准则localization principle。非欧几里得
Non-Euclidean域的CNN:图神经网络框架《The Graph Neural Network Model》(在《Gated Graph Sequence Neural Networks》中被简化)旨在通过RNN将每个节点嵌入到一个欧氏空间,并将这些embedding用作节点/图的分类/回归的特征。一些工作引入了构建局部感受野
local receptive field的概念从而减少学习参数的数量。这个想法是基于相似性度量将特征组合在一起,例如在两个连续层之间选择有限数量的连接。虽然该模型利用局部性假设locality assumption减少了参数的数量,但是它并没有尝试利用任何平稳性,即没有权重共享策略。《Spectral Networks and Deep Locally Connected Networks on Graphs》的作者在他们的graph CNN的spatial formulation中使用了这个想法。他们使用加权图来定义局部邻域,并为池化操作计算图的多尺度聚类multiscale clustering。然而,在空域构造spatial construction中引入权重共享具有挑战性,因为当缺少problem-specific ordering(如空间顺序、时间顺序等等)时,它需要选择select并对邻域内的节点进行排序。《Geodesic convolutional neural networks on riemannian manifolds》中提出了CNN到3D-mesh的空间推广,其中3D-mesh是一类平滑的、低维的非欧氏空间。作者使用测地线极坐标geodesic polar coordinate来定义mesh patch上的卷积,并定制了一个深度学习架构从而允许在不同的流形manifold之间进行比较。他们对3D形状识别获得了state-of-the-art结果。第一个谱公式由
《Spectral Networks and Deep Locally Connected Networks on Graphs》提出,它将滤波器定义为:control point向量。他们后来提出了一种从数据中学习图结构的策略,并将该模型应用于图像识别、文本分类、生物信息学(《Deep Convolutional Networks on Graph-Structured Data》)。然而,由于需要乘以图傅里叶基scale。此外,由于它们依赖于傅里叶域中的平滑性smoothness(即,通过样条参数化得到)来实现空间域的局部性,因此他们的模型无法提供精确的控制从而使得kernel支持局部性,而这对于学习局部的滤波器至关重要。我们的技术利用了这项工作,并展示了如何克服这些限制以及其它限制。
3.1 模型
- 将卷积推广到图上需要考虑三个问题:如何在图上设计满足空域局部性的卷积核、如何执行图的粗化
graph coarsening(即,将相似顶点聚合在一起)、如何执行图池化操作。
3.1.1 快速的局部性的谱滤波器
定义卷积滤波器有两种策略,可以从空间方法
spatial approach来定义,也可以从谱方法spectral approach来定义。通过构造
construction,空间方法可以通过有限大小的kernel提供filter localization。然而,从空间角度来看,图上的平移没有唯一的数学定义。另一方面,谱方法通过在谱域
spectral domain实现的Kronecker delta卷积在图上提供了一个定义明确的局部性算子localization operator。然而,在谱域定义的滤波器不是天然局部化的,并且由于和图傅里叶基乘法的计算复杂度为然而,通过对滤波器参数化
filter parametrization的特殊选择,我们可以克服这两个限制(即,滤波器的天然局部化,以及计算复杂度)。
图傅里叶变换
Graph Fourier Transform:给定无向图spectral graph analysis中最基础的算子是图拉普拉斯算子,combinatorial Laplacian定义为normalized Laplacian定义为degree矩阵(一个对角矩阵)并且论文并没有提到是用哪个拉普拉斯矩阵,读者猜测用的是任意一个都可以,因为后续公式推导对两种类型的拉普拉斯矩阵都成立。
由于
graph Fourier mode),以及与这些特征向量相关的有序实数非负特征值graph frequency)。图拉普拉斯矩阵Fourier basis傅里叶变换将信号
filtering。图信号的谱域滤波
spectral filtering:由于我们无法在顶点域vertex domain中表达有意义的平移算子translation operator,因此图上的卷积算子Fourier domain,即:其中:
Hadamard乘法,因此,图上的信号
non-parametric filter(即参数都是自由的滤波器)定义为:其中参数
Fourier coefficient组成的向量。用于局部滤波器
localized filter的多项式参数化:然而,non-parametric filter有两个限制:它们在空间域不是局部化localized的、它们学习的复杂度是polynomial filter来解决:其中:参数
以顶点
它的物理意义是:一个
delta脉冲信号根据
《Wavelets on Graphs via Spectral Graph Theory》的引理5.2,spectral filter恰好是K-localized的。此外,它的学习复杂度为CNN的复杂度相同。快速滤波
fast filtering的递归公式:虽然我们已经展示了如何学习具有localized filter,但是由于还需要与傅里叶基一种这样的多项式是
Chebyshev展开(传统上,它在GSP中被用于近似kernel,如小波wagelet)。另一种选择是Lanczos算法,它构造了Krylov子空间的正交基Lanczos算法看起来似乎有吸引力,但是它更加复杂,因此我们留待未来的工作。回想一下,
这些多项式构成
其中:
- 参数
[-1,+1]之间。
滤波操作可以协作:
其中:
定义
整个滤波操作
- 参数
学习
filter:假设第feature map) 。 第feature map为:其中:
layer的待训练参数。总的参数规模为假设
mini-batch样本的损失函数为其中:
mini-batch size。上述三种计算中的每一种都归结为
最后,
3.1.2 图粗化 Graph Coarsening
池化操作需要在图上有意义的邻域上进行,从而将相似的顶点聚类在一起。对多个
layer执行池化等价于保留局部几何结构的图多尺度聚类multi-scale clustering。然而,众所周知,图聚类graph clustering是NP-hard的并且必须使用近似算法。虽然存在许多聚类算法(例如流行的谱聚类spectral clustering),但是我们最感兴趣的还是multi-level聚类算法。在multi-level聚类算法中,每个level都会生成一个更粗coarser的图,其中这个图对应于不同分辨率看到的数据域data domain。此外,在每个level将图的大小减少两倍的聚类技术提供了对粗化coarsening和池化大小的精确控制。在这项工作中,我们利用了
Graclus multi-level聚类算法的粗化阶段。Graclus multi-level聚类算法已被证明在对各种图进行聚类时非常有效。图上的代数多重网格algebraic multigrid技术、以及Kron reduction是未来工作中值得探索的两种方法。建立在
Metis上的Graclus使用贪心算法来计算给定图的连续更粗successive coarser的版本,并且能够最小化几个流行的谱聚类目标spectral clustering objective。在这些谱聚类目标中,我们选择归一化割the normalized cut。Graclus的贪心规则为:在每个
coarsening level,选择一个未标记unmarked的顶点local normalized cut然后标记
mark并粗化coarsen这对匹配的顶点持续配对,直到所有顶点都被探索(这样就完成了一轮粗化)。
这其中可能存在部分独立顶点,它不和任何其它顶点配对。
这种粗化算法非常块,并且每轮粗化都将顶点数除以
2从而从一个level到下一个更粗的level。
3.1.3 图信号的快速池化
池化操作将被执行很多次,因此该操作必须高效。粗化之后,输入图的顶点及其粗化版本没有以任何有意义的方式排列
arrange。因此,直接应用池化操作将需要一个table来存储上一个level的顶点与到下一个level的顶点(更粗化的版本)之间的对应关系。这将导致内存效率低下、读取速度慢、并且难以并行化。然而,我们可以排列顶点,使得图池化
graph pooling操作变得与一维池化一样高效。我们分为两步进行:创建一棵平衡的二叉树、重排顶点。粗化之后,每个节点要么有两个子节点(如果它是在更精细的
level被匹配到的);要么没有(如果它在更精细的level未被匹配到),此时该节点是一个singleton,它只有一个子节点。从最粗的level到最细的level,我们为每个singleton节点添加一个fake节点作为子节点,这样每个节点就都有两个子节点。fake节点都是断开disconnected的。这种结构是一棵平衡二叉树:一个节点要么包含两个常规子节点(如下图中的
level 1节点0),要么包含一个singletons子节点和一个fake子节点(如下图中的level 2节点0) 。fake节点总是包含两个fake子节点,如下图中的level 1节点1。注意,下图中从上到下依次是level 0, level 1, level 2。输入信号在
fake节点处使用neutral value初始化,如当使用ReLU激活函数时为0。因为这些fake节点是断开的,因此滤波不会影响到初始的neutral value。虽然这些fake节点确实人为地增加了维度从而增加了计算成本,但是我们发现在实践中,Graclus留下的singleton节点数量非常少。我们在最粗
coarsest的level上任意排列节点,然后将这个次序传播到最精细finest的level,即节点level产生规则的次序regular ordering。规则的意思是相邻节点在较粗的level上层次地合并。池化如此一个重排的图信号,类似于池化一个常规的一维信号(以步长为2)。下图显示了整个池化过程的示例。这种规则排列
regular arrangement使得池化操作非常高效,并且满足并行架构(如GPU),因为内存访问是局部的,即不需要fetch被匹配的节点。池化的本质是:对每个节点多大范围内的邻域进行池化。
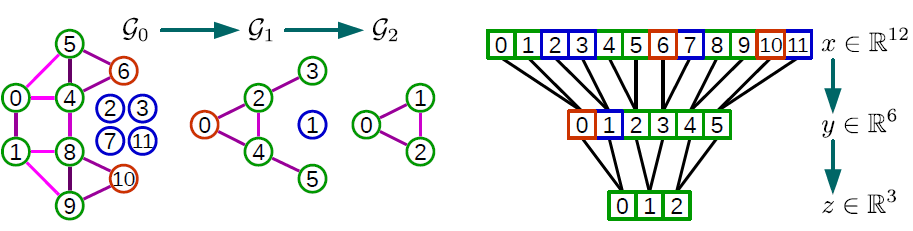
一个池化的例子如下图。带颜色的链接表示配对,红色圆圈表示未能配对顶点,蓝色圆圈表示
fake顶点。考虑图
4。level,它拥有4的池化,我们需要执行2次粗化操作(因为每次粗化都将顶点数除以2):Graclus第一次粗化产生图Graclus第二次粗化产生图level。
因此我们设置
fake节点(蓝色)添加到1个fake节点)、4个fake节点),从而与singelton节点(橙色)配对,这样每个节点正好有两个子节点。然后其中信号分量
neutral value。
3.2 实验
我们将
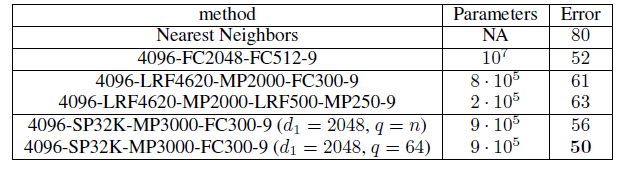
non-parametric和non-localized的filter称作Non-Param(即《Spectral Networks and Deep Locally Connected Networks on Graphs》中提出的filter称作Spline(即filter称作Chebyshev(即我们总是采用
Graclus粗化算法,而不是《Spectral Networks and Deep Locally Connected Networks on Graphs》中提出的简单聚集算法agglomerative method。我们的动机是比较学到的filter,而不是比较粗化算法。我们在描述网络架构时使用以下符号:
FCk表示一个带Pk表示一个尺寸和步长为GCK表示一个输出feature map的图卷积层graph convolutional layer,Ck表示一个输出feature map的经典卷积层。所有的
FCk,GCk,Ck都使用ReLU激活函数。最后一层始终是softmax回归。损失函数FCk层权重的l2正则化。mini-batch sizeMNIST实验:我们考虑将我们的方法应用于基准的MNIST分类数据集,它是欧氏空间的case。MNIST分类数据集包含70000张数字图片,每张图片是28 x 28的2D网格。对于我们的图模型,我们构建了一个2D网格对应的8层图神经网络,它产生了192个fake节点),以及k-NN similarity graph的权重(即人工构建的input graph中,每条边的权重)计算为:其中
2D坐标。模型配置为(来自于
TensorFlow MNIST tutorial):LeNet-5-like的网络架构,并且超参数为:dropout rate = 0.5,正则化系数为0.03,学习率衰减系数0.95,动量0.9。标准卷积核的尺度为5x5,图卷积核的20个epoch。本实验是我们模型的一项重要的健全性检查
sanity check,它必须能够在任何图上抽取特征,包括常规的2D grid。下表显示了我们的模型与具有相同架构的经典CNN模型的性能非常接近。性能的差距可以用谱域滤波器的各向同性的特性
isotropic nature来解释,即常规graph中的边不具有方向性,但是MNIST图片作为2D grid具有方向性(如像素点的上下左右)。这是优势还是劣势取决于具体的问题。性能差距的其它解释是:我们的模型缺乏架构设计经验,以及需要研究更合适的优化策略或初始化策略。

20NEWS数据集的文本分类:为了验证我们的模型可应用于非结构化数据,我们将我们的技术应用于20NEWS数据集上的文本分类问题。20NEWS数据集包含18846篇文档,分为20个类别。我们将其中的11314篇文档用于训练、7532篇文档用于测试。我们从所有文档的93953个单词中保留最高频的一万个单词。每篇文档使用词袋模型bag-of-word model提取特征,并根据文档内单词的词频进行归一化。为了测试我们的模型,我们构建了
16层图神经网络,图的构建方式为:其中
word2vec embedding。每篇文档对应一张图,它包含word2vec embedding是在当前数据集上训练的?还是在更大的、额外的数据集上训练的?论文未说明。所有模型都由
Adam优化器训练20个epoch,初始学习率为0.001。该架构是GC32。结果如下图所示,在这个小数据集上,虽然我们的模型未能超越Multinomial Naive Bayes模型,但是它超越了所有全连接神经网络模型,而这些全连接神经网络模型具有更多的参数。
效果比较:我们在
MNIST数据集上比较了不同的图卷积神经网络架构的效果,其中Spline以及需要Non-Param。
为了给出不同
filter的收敛性,下图给出训练过程中这几种架构的验证集准确率、训练集损失,横轴表示迭代次数。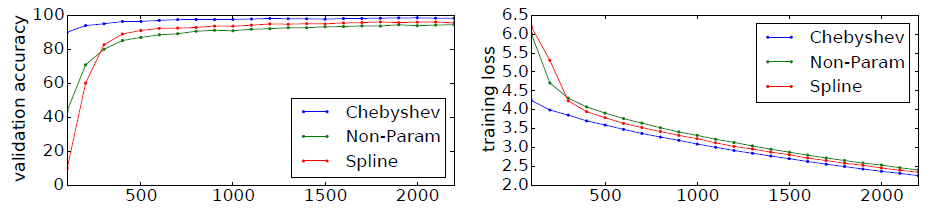
效率比较:我们在
20NEWS数据集上比较了不同网络架构的计算效率,其中《Spectral Networks and Deep Locally Connected Networks on Graphs》的计算复杂度为step数(即每个mini-batch的处理时间,其中batch-size = 100)。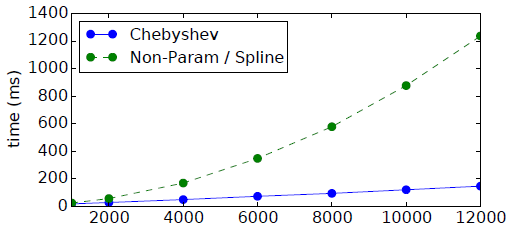
我们在
MNIST数据集上验证了不同网络架构的并行性。下表显式了从CPU迁移到GPU时,我们的方法与经典CNN类似的加速比。这体现了我们的模型提供的并行化机会。我们的模型仅依赖于矩阵乘法,而矩阵乘法可以通过NVIDA的cuBLAS库高效的支持。
图质量的影响:要使任何
graph CNN成功,数据集必须满足一定条件:图数据必须满足局部性locality、平稳性stationarity、组合性compositionality的统计假设。因此,学到的滤波器的质量及其分类性能关键取决于图的质量。从MNIST实验我们可以看到:从欧式空间的网格数据中基于kNN构建的图,这些图数据质量很高。我们基于这些图数据采用graph CNN几乎获得标准CNN的性能。并且我们发现,kNN中k的值对于图数据的质量影响不大。作为对比,我们从
MNIST中构建随机图,其中顶点之间的边是随机的。可以看到在随机图上,图卷积神经网络的准确率下降。在随机图中,数据结构发生丢失,因此卷积层提取的特征不再有意义。但是为什么丢失了结构信息之后,准确率还是那么高?读者猜测是有一些非结构性的因素在生效,例如某些像素点级别的特性。

图像可以通过网格图来构成,但是必须人工地为
bag-of-word表示的文档来构建feature graph。我们在这里研究三种表示单词one-hot向量、通过word2vec从数据集中学习每个单词的embedding向量、使用预训练的单词word2vec embedding向量。对于较大的数据集,可能需要approximate nearest neighbor: ANN算法(因为当图的顶点数量较大时找出每个顶点的kNN顶点的计算复杂度太大),这就是我们在学到的word2vec embedding上尝试LSHForest的原因。下表报告了分类结果,这突出了结构良好的图的重要性。其中:bag-of-words表示one-hot方法,pre-learned表示预训练的embedding向量,learned表示从数据集训练embedding向量,approximate表示对learned得到的embedding向量进行最近邻搜索时使用LSHForest近似算法,random表示对learned得到的embedding向量采用随机生成边而不是基于kNN生成边。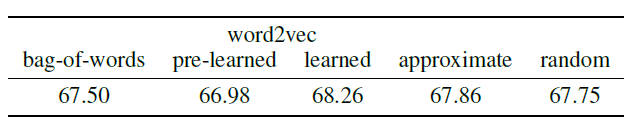
四、GCN[2016]
考虑在
graph(如,引文网络citation network)中对节点(如,文档)进行分类的问题,其中仅一小部分节点有label信息。这个问题可以被定义为基于图的半监督学习graph-based semi-supervised learning,其中label信息通过某种形式的explicit graph-based regularization在图上被平滑smoothed,例如在损失函数中使用图拉普拉斯正则化graph Laplacian regularization项:其中:
无向图
其中:
正则化项的物理意义为:
- 如果两个节点距离较近(即
label应该比较相似(即 - 如果两个节点距离较远(即
label可以相似也可以不相似。
- 如果两个节点距离较近(即
因此上述损失函数
graph中相连的节点很可能共享相同的label。然而,这种假设会限制模型的表达能力,因为图中的边不一定编码节点相似性,边也可能包含其它信息。在论文
《SEMI-SUPERVISED CLASSIFICATION WITH GRAPH CONVOLUTIONAL NETWORKS》中,作者直接使用神经网络模型distribute梯度信息,并使得模型能够学习带标签节点的representation和不带标签节点的representation。论文有两个贡献:
- 首先,论文为直接在图上运行的神经网络模型引入了一个简单且表现良好的
layer-wise传播规则propagation rule,并展示了它是如何从谱图卷积spectral graph convolution的一阶近似中启发而来。 - 其次,论文展示了这种形式的基于图的神经网络模型如何用于对图中节点进行快速且可扩展的半监督分类。对多个数据集的实验表明,论文的模型在分类准确性和效率(以
wall-clock time衡量)方面与state-of-the-art的半监督学习方法相比具有优势。
相关工作:相关工作:我们的模型主要受到
graph-based半监督学习领域、最近在图上的神经网络等工作的启发。接下来我们简要概述了这两个领域的相关工作。graph-based半监督学习:近年来人们已经提出了大量使用graph representation的半监督学习方法,其中大多数分为两类:使用某种形式的显式的图拉普拉斯正则化方法,以及基于graph embedding的方法。图拉普拉斯正则化的突出例子包括标签传播
label propagation、流形正则化manifold regularization、以及深度半监督embedding。最近,人们的注意力已经转移到
graph embedding模型,其中graph embedding模型受skip-gram模型所启发。DeepWalk通过预测节点的局部邻域local neighborhood来学习embedding,其中局部邻域是通过图上的随机游走采样而来。LINE和node2vec使用更复杂的随机游走方案来扩展了DeepWalk。然而,对于所有这些方法,都需要一个包含随机游走生成和半监督训练的
multistep pipeline,其中每个step都必须单独优化。Planetoid通过在学习embedding的过程中注入label信息来缓解这个问题。
图上的神经网络:
《A new model for learning in graph domains》曾经介绍在图上运行的神经网络。《The graph neural network model》将图神经网络作为循环神经网络的一种形式。他们的框架需要重复应用收缩映射contraction map作为传播函数propagation function,直到node representation达到稳定的不动点fixed point。后来,《Gated graph sequence neural networks》通过将循环神经网络的现代实践引入到原始图神经网络框架中,从而缓解了这种限制。《Convolutional networks on graphs for learning molecular fingerprints》在图上引入了一种类似卷积的传播规则和方法,从而用于graph-level分类。他们的方法需要学习node degree-specific的权重矩阵,这些权重矩阵无法扩展到具有宽泛wide的node degree分布的大型图。相反,我们的模型每层使用单个权重矩阵,并通过对邻接矩阵进行适当的归一化从而处理变化的node degree。《Diffusion-convolutional neural networks》最近引入了graph-based神经网络来进行节点分类。他们报告了《Learning convolutional neural networks for graphs》引入了一个不同但是相关related的模型,他们将图局部locally地转换为序列,然后馈入传统的一维卷积神经网络,而这需要在预处理步骤中定义节点排序node ordering。- 我们的方法基于谱图卷积神经网络
spectral graph convolutional neural network,该模型在《Spectral networks and locally connected networks on graphs》被引入,并由《Convolutional neural networks on graphs with fast localized spectral filtering》通过快速局部卷积fast localized convolution进行了扩展。
与这些工作相比,我们在此考虑在大型网络中进行
transductive的节点分类任务。我们表明,在这种情况下,可以将《Spectral networks and locally connected networks on graphs》和《Convolutional neural networks on graphs with fast localized spectral filtering》的原始框架进行一些简化,从而提高大型网络的可扩展性和分类性能。
4.1 模型
4.1.1 图上卷积的快速近似
这里我们提供本文模型的理论动机。我们考虑具有以下
layer-wise传播规则的一个多层Graph Convolutional Network: GCN:其中:
接下来我们将展示这种传播规则可以通过图上局部谱滤波器
localized spectral filters的一阶近似所启发而来。上式物理意义:第
representation可以这样得到:- 首先,将邻域内节点(包含它自身)在第
representation进行加权和,加权的权重为边的归一化权重(即 - 然后,将这个加权和通过一个单层前馈神经网络,网络权重为
a. 谱图卷积
我们考虑图上的普卷积
spectral convolution,它定义为信号其中:
对于信号
graph Fourier transform。注意,这里的信号
则
- 按行解读:第
- 按列解读:第
- 按行解读:第
我们可以将
计算
《Aavelets on graphs via spectral graph theory》等人提出,truncated expansion(其中:
[-1,+1]之间),
回到我们对信号
其中:
上式成立是因为我们很容易证明:
注意,这个表达式现在是
K-localized的,因为它是拉普拉斯矩阵的K step的节点(即,《Convolutional neural networks on graphs with fast localized spectral filtering》使用这种K-localized卷积来定义图上的卷积神经网络。
4.1.2 Layer-wise 线性模型
可以通过堆叠多个
layer后跟随一个point-wise non-linearity。现在,假设我们将layer-wise卷积操作限制为通过这种方式,我们仍然可以通过堆叠多个这种
layer来恢复recover丰富类型的卷积滤波器函数,但是我们不限于由诸如切比雪夫多项式给出的显式参数化。对于具有非常宽泛wide的node degree分布的图(如社交网络、引文网络、知识图谱、以及许多现实世界其它的图数据集),我们直观地期望这样的模型可以缓解图的局部邻域结构local neighborhood structure的过拟合问题。此外,对于固定的计算预算computational budget,这种layer-wise线性公式允许我们构建更深的模型。众所周知,更深的模型在很多领域可以提高模型容量。在
GCN的这个线性公式中,我们进一步近似scale的变化。为什么选择
2?因为原始公式中有系数在这些近似下,
它包含两个自由参数
free parametersuccessive application可以有效地对节点的在实践中,进一步限制参数的数量从而解决过拟合问题、并最小化每层的操作数量(如矩阵乘法)可能是有益的。因此我们进一步简化,令
为什么要凑成这个形式?假设
则根据
renormalization技巧,我们有:注意,
[0, 2]。因此,当在深度神经网络模型中重复应用该算子时,会导致数值不稳定和梯度爆炸/消失。为了缓解这个问题,我们引入以下renormalization技巧:我们可以将这个定义推广到具有
feature map):其中:
signal matrix。
该卷积操作的计算复杂度为
4.2 半监督节点分类
引入了一个简单而灵活的模型
graph-based半监督学习。我们希望该setting在邻接矩阵citation link、或者知识图谱中的关系relation。整个模型是一个用于半监督学习的多层GCN,如下图所示。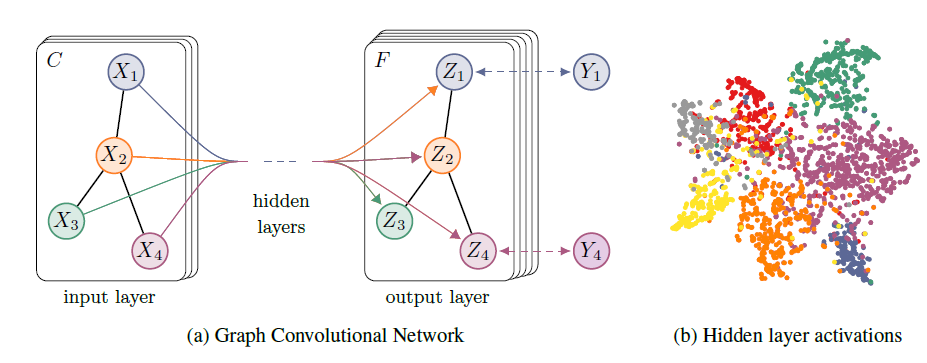
接下来我们考虑在具有对称的邻接矩阵
GCN。我们首先在预处理步骤中计算 :然后我们的前向计算采用简单的形式:
其中:
feature map隐层的input-to-hidden的权重矩阵,hidden-to-output的权重矩阵。softmax激活函数定义为:
对于半监督多类分类,我们评估所有标记节点的交叉熵:
其中:
label的节点索引集合。神经网络权重
batch gradient descent。只要数据集能够适合fit内存,这就是一个可行的选择。当邻接矩阵dropout引入随机性。我们将mini-batch随机梯度下降这个memory-efficient扩展留待未来工作。在实践中,我们采用
TensorFlow使用sparse-dense矩阵乘法来高效地基于GPU实现
4.3 和 WL 算法的关系
4.3.1 WL 算法
理想情况下图神经网络模型应该能够学到图中节点的
representation,该representation必须能够同时考虑图的结构和节点的特征。一维
Weisfeiler-Lehman:WL-1算法提供了一个研究框架。给定图以及初始节点标签,该框架可以对节点标签进行唯一分配unique assignment。注意,这里的“标签”不仅包括节点上的监督
label信号,也包括节点上的属性信息。WL-1算法:令输入:初始节点标签
输出:最终节点标签
算法步骤:
初始化
迭代直到
循环遍历
返回每个节点的标签。
如果我们采用一个神经网络来代替
hash函数,同时假设其中:
vector of activations;我们定义
degree,则上式等价于我们GCN模型的传播规则。因此我们可以将GCN模型解释为图上WL-1算法的微分化differentiable的和参数化parameterized的推广。
4.3.2 随机权重的 node embedding
通过与
WL-1算法的类比,我们可以认为:即使是未经训练的、具有随机权重的GCN模型也可以充当图中节点的一个强大的特征提取器。如:考虑下面的一个三层GCN模型:其中权重矩阵是通过
Xavier初始化的:我们将这个三层
GCN模型应用于Zachary的karate club network,该网络包含34个节点、154条边。每个节点都属于一个类别,一共四种类别。节点的类别是通过modularity-based聚类算法进行标注的。如下图所示,颜色表示节点类别。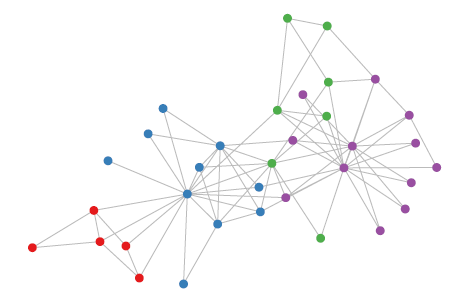
我们令
ID之外不包含任何其它特征。另外节点的ID是随机分配的,也不包含任何信息。我们选择隐层的维度为4、输出层的维度为2,因此输出层的输出下图给出了未经训练的
GCN模型(即前向传播)获得的node embedding,这些结果与从DeepWalk获得的node embedding效果相当,而DeepWalk使用了代价更高的无监督训练过程。因此可以将随机初始化的
GCN作为graph embedding特征抽取器来使用,而且还不用训练。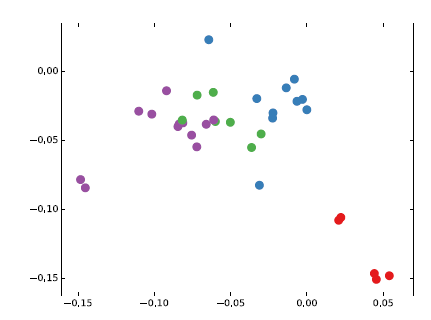
4.3.3 半监督 node embedding
在
karate club network数据集上,我们观察半监督分类任务期间node embedding如何变化。这种可视化效果提供了关于GCN模型如何利用图结构从而学到对于分类任务有益的node embedding。训练配置:
- 在上述三层
GCN之后添加一个softmax输出层,输出节点属于各类别的概率。 - 每个类别仅使用一个带标签的节点进行训练,一共有四个带标签的节点。
- 使用
Adam优化器,初始化学习率为0.01。采用交叉熵损失函数。迭代300个step。
下图给出多轮迭代中,
node embedding的演变。图中的灰色直线表示图的边,高亮节点(灰色轮廓)表示标记节点。可以看到:模型最终基于图结构以及最少的监督信息,成功线性地分离出了簇团。
- 在上述三层
4.4 实验
我们在多个任务中验证模型性能:在引文网络中进行半监督文档分类、在从知识图谱抽取的二部图中进行半监督实体分类。然后我们评估图的各种传播模型,并对随机图的
rum-time进行分析。数据集:
引文网络数据集:我们考虑
Citeseer,Cora,Pubmed三个引文网络数据集,每个数据集包含以文档的稀疏bag-of-word: BOW特征向量作为节点,文档之间的引文链接作为边。我们将引文链接视为无向边,并构造一个二元的对称邻接矩阵每个文档都有一个类别标签,每个类别仅包含
20个标记节点作为训练样本。NELL数据集:该数据集是从《Toward an architecture for never-ending language learning》引入的知识图谱中抽取的数据集。知识图谱是一组采用有向的、带标记的边链接的实体。我们为每个实体对relation node,它们之间不存在边。最终我们得到55864个关系节点和9891个实体节点。实体节点
entity node通过稀疏的特征向量来描述。我们为每个关系节点分配唯一的one-hot向量从而扩展NELL的实体特征向量,从而使得每个节点的特征向量为61278维稀疏向量。对于节点
在节点的半监督分类任务中,我们为每个类别标记一个节点作为训练集,因此属于非常极端的情况。
随机图:我们生成各种规模的随机
Graph数据集,从而评估每个epoch的训练时间。对于具有
- 随机均匀分配
- 令
id之外没有任何特征,且节点id是随机分配的。 - 每个节点标签为
- 随机均匀分配
各数据集的整体统计如下表所示。标记率
label rate:表示监督的标记节点数量占总的节点数量的比例。
模型设置:除非另有说明,否则我们的
GCN模型就是前面描述的两层GCN模型。我们将数据集拆分为
labled数据、unlabled数据、测试数据。其中我们在labled数据和unlabled数据上学习,在测试数据上测试。我们选择测试数据包含1000个节点。注意,训练期间模型能够“看到”所有节点,但是无法知道测试节点的
label信息。另外我们还使用额外的
500个带标签的节点作为验证集,用于超参数优化。这些超参数包括:所有层的dropout rate、第一个GCN层的注意:验证集的标签不用于训练。
对于引文网络数据集,我们仅在
Cora数据集上优化超参数,并对Citeseer和Pubmed数据集采用相同的超参数。所有模型都使用
Adam优化器,初始化学习率为0.01。所有模型都使用早停策略,早停的
epoch窗口为10。即:如果连续10个epoch的验证损失没有下降,则停止继续训练。所有模型最多训练200个epoch。我们使用
Xavier初始化策略:我们对输入的特征向量进行按行的归一化
row-normalize(即每个样本输入特征向量归一化为范数为1)。在随机图数据集上,我们选择隐层维度为
32,并省略正则化:既不进行dropout,也不进行
Baseline模型:我们比较了《Revisiting semi-supervised learning with graph embeddings》相同的baseline方法,即:标签传播算法label propagation: LP、半监督embedding算法semi-supervised embedding: SemiEmb、流形正则化算法manifold regularization: MainReg、基于skip-gram的图嵌入算法DeepWalk。我们忽略了TSVM算法,因为它无法扩展到类别数很大的数据集。我们进一步与
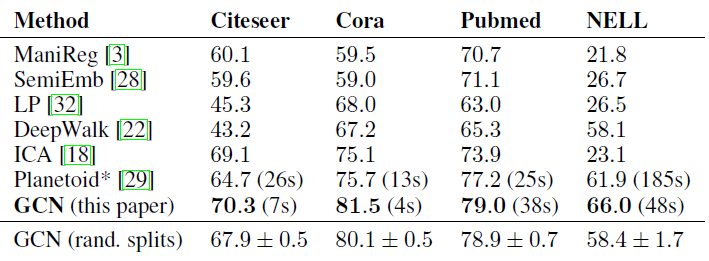
《Link-based classification》中提出的iterative classification algorithm: ICA进行比较。我们还还比较了Planetoid算法, 我们总是选择他们表现最好的模型变体(transductive vs inductive)作为baseline。模型比较结果如下表所示。对于
ICA,我们随机运行100次、每次以随机的节点顺序训练得到的平均准确率。 所有其它基准模型的结果均来自于Planetoid论文,Planetoid*表示论文中提出的针对每个数据集的最佳变体。我们在与
《Revisiting semi-supervised learning with graph embeddings》相同的数据集拆分上训练和测试了我们的模型,并报告随机权重初始化的100次的平均准确率(括号中为平均训练时间)。我们为Citeseer,Cora,Pubmed使用的超参数为:dropout rate = 0.5、16;为NELL使用的超参数为:dropout rate = 0.1,64。最后我们报告了
10次随机拆分数据集,每次拆分的labled数据、unlabled数据、测试数据比例与之前相同,然后给出GCN的平均准确率和标准差(以百分比表示),记作GCN(rand. splits)。前面七行是针对同一种数据集拆分,最后一行是不同的数据集拆分。
我们在引文网络数据集上比较了我们提出的逐层传播模型的不同变体,实验配置和之前相同,结果如下表所示。
我们原始的
GCN模型应用了renormalization技巧(粗体),即:其它的
GCN变体采用Propagation model字段对应的传播模型。- 对于每一种变体模型,我们给出执行
100次、每次都是随机权重初始化的平均分类准确率。 - 对于每层有多个权重
Chebyshev filter, 1st-order model),我们对第一层的所有权重执行

- 对于每一种变体模型,我们给出执行
我们在随机图上报告了
100个epoch的每个epoch平均训练时间。我们在Tensorflow上比较了CPU和GPU实现的结果,其中*表示内存溢出错误Out Of Memory Error。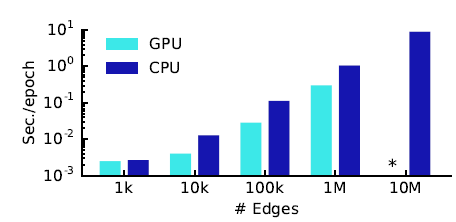
最后我们考虑模型的深度对于性能的影响。这里我们报告对
Cora,Citeseer,Pubmed数据集进行5折交叉验证的结果。除了标准的
GCN模型之外,我们还报告了模型的一种变体:隐层之间使用了残差连接:在
5折交叉验证的每个拆分中,我们训练400个epoch并且不使用早停策略。我们使用Adam优化器,初始学习率为0.01。我们对第一层和最后一层使用dropout rate = 0.5,第一层权重执行正则化系数为GCN的隐层维度选择为16。结果如下图所示,其中标记点表示
5折交叉验证的平均准确率,阴影部分表示方差。可以看到:
- 当使用两层或三层模型时,
GCN可以获得最佳效果。 - 当模型的深度超过七层时,如果不使用残差连接则训练会变得非常困难,表现为训练准确率骤降。因为每个节点的有效上下文会随着层深的增加而扩大。
- 当模型深度增加时,模型的参数数量也会增加,此时模型的过拟合可能会成为问题。
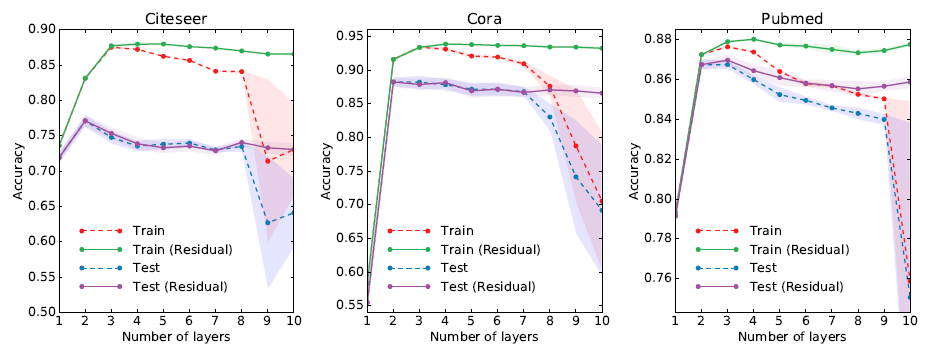
- 当使用两层或三层模型时,
4.5 讨论
半监督模型:在这里展示的实验中,我们的半监督节点分类方法明显优于最近的相关方法。
- 基于图拉普拉斯正则化的方法很可能受到限制,因为它们假设边仅仅编码了节点的相似性。
- 另一方面,基于
skip-gram的方法受限于它们难以优化的multi-step pipeline这一事实。 - 我们提出的模型可以客服这两个限制,同时在效率(以
wall-clock time衡量)方面仍然优于相关方法。与仅聚合label信息的ICA等方法相比,在每一层中从相邻节点传播feature信息提高了分类性能。 - 我们进一步证明,与使用切比雪夫多项式的朴素的一阶模型
局限性和未来方向:我们的
Semi-GCN模型存在一些局限,我们计划在将来克服这些局限性。内存需求局限性:在
full-batch梯度下降算法中,内存需求随着数据集的大小线性增长。一种解决方式是:采用
CPU训练来代替GPU训练。这种方式我们在实验中得到验证。另一种解决方式是:采用
mini-batch随机梯度下降算法。但是
mini-batch随机梯度下降算法必须考虑GCN模型的层数。因为对于一个GCN模型,其
边类型的局限性:目前我们的模型不支持边的特征,也不支持有向图。
通过
NELL数据集的实验结果表明:可以通过将原始的有向图转化为无向二部图来处理有向图以及边的特征。这通过额外的、代表原始图中的边的节点来实现。假设的局限性:我们的模型有两个基本假设:
假设
GCN依赖于locality。假设自链接和邻居链接同样重要。
在某些数据集中,我们可以引入一个折衷
trade-off:平衡了自链接和邻居链接的重要性,它可以通过梯度下降来学习(也可以作为超参数来调优)。
五、神经图指纹[2015]
在材料设计领域的最新工作已经将神经网络用于材料筛选,其任务是通过学习样本来预测新型分子的特性。预测分子特性通常需要将分子图作为输入,然后构建模型来预测。在分子图中节点表示原子,边表示化学键。这个任务的一个难点在于:输入的分子图可以具有任意大小和任意形状,而大多数机器学习模型只能够处理固定尺寸、固定形状的输入。目前
state of the art的方法是通过hash函数对分子图进行预处理从而生成固定尺寸的指纹向量fingerprint vector,该指纹向量作为分子的特征灌入后续的模型中。在训练期间,分子指纹molecular fingerprint被视为固定fixed的(即,固定指纹)。论文
《Convolutional Networks on Graphs for Learning Molecular Fingerprints》提出了神经图指纹neural graph fingerprint模型,该模型用一个可微的神经网络代替了分子指纹部分。神经网络以原始的分子图作为输入,采用卷积层来抽取特征,然后通过全局池化来结合所有原子的特征。这种方式使得我们可以端到端的进行分子预测。相比较传统的固定指纹的方式,神经图指纹具有以下优势:
预测能力强:通过实验比较可以发现,神经图指纹比传统的固定指纹能够提供更好的预测能力。
模型简洁:为了对所有可能的子结构进行编码,固定指纹的必须维度非常高。而神经图指纹只需要对相关特征进行编码,模型的维度相对而言低得多,这降低了下游的计算量和正则化需求。
可解释性:传统的固定指纹对每个片段
fragment进行不同的编码,片段之间没有相似的概念。在神经图指纹中,每个特征都可以由相似但是不同的分子片段激活,这使得特征的representation更具有意义。即,相似的片段具有相似的特征,相似的特征也代表了相似的片段。
相关工作:这项工作在精神上类似于神经图灵机
neural Turing machine: NTM,从某种意义上讲,我们采用现有的离散计算架构,并使每个部分可微从而进行gradient-based的优化。卷积神经网络:卷积神经网络已被用于对图像、语音、时间序列进行建模。然而,标准卷积架构使用固定的、网格的
graph数据结构,这使得它很难应用于具有不同尺寸或结构的对象(如分子)。最近《A convolutional neural network for modelling sentences》开发了一种卷积神经网络架构,可用于对不同长度的句子进行建模。神经指纹
neural fingerprint:最密切相关的工作是《Deep architectures and deep learning in chemoinformatics: the prediction of aqueous solubility for drug-like molecules》,它构建了一个具有graph-valued输入的神经网络。它的方法是删除所有的环cycle并将graph构建为tree结构,选择一个原子作为root,然后从叶节点到root节点运行RNN从而产生固定尺寸的representation。因为具有graph有root,所有需要构建graph。最终的descriptor是所有不同的图计算的representation的sum。这种方法的计算成本为定量构效关系
quantitative structure-activity relationship: QSAR的神经网络:预测分子性质的现代标准是结合圆形指纹circular fingerprint以及全连接神经网络(或者其它回归方法)。《Multi-task neural networks for QSAR predictions》使用圆形指纹作为神经网络、高斯过程、随机森林的输入。《Massively multitask networks for drug discovery》使用圆形指纹(深度为2)作为多任务神经网络的输入,并表明多任务有助于提高性能。
fixed graph上的神经网络:《Spectral networks and locally connected networks on graphs》在图结构固定的情况下在图上引入卷积网络,每个训练样本的不同之处仅在于:在同一个图的不同节点具有不同的特征。相比之下,我们的网络解决了每个训练样本都是不同图的情况。input-dependent graph上的神经网络:《The graph neural network model》提出了一种用于图的、具有一个有趣训练过程的神经网络模型。前向传播包括运行消息传递方案message-passing scheme从而达到平衡,这一事实(即,不动点)允许在不存储整个前向计算的情况下计算反向梯度。他们将他们的模型应用于预测分子化合物的诱变性、以及网页排名。《Neural network for graphs: A contextual constructive approach》还提出了一种用于图的神经网络模型。该模型具有一个learning scheme,其内循环优化的不是训练损失,而是每个新提出newly-proposed的向量与训练误差残差之间的相关性。他们将他们的模型应用于150种分子化合物的沸点数据集上。
我们的论文建立在这些思想的基础上,具有以下区别:我们的方法用简单的、
gradient-based的优化代替了复杂的训练算法,推广了现有的圆形指纹计算,并将这些神经网络应用于现代的QSAR pipeline上下文中(这些pipeline在指纹特征之上使用神经网络来增加模型容量)。被展开
unrolled的推断算法:《Deep unfolding: Model-based inspiration of novel deep architectures》和其他人已经注意到迭代式的推断过程有时类似于RNN的前馈计算。这些想法的一个自然扩展是参数化每个inference step,并训练神经网络从而仅使用少量迭代来近似地match精确推断的输出。从这个角度来看,神经指纹类似于原始图上被展开的消息传递算法。
5.1 模型
5.1.1 圆形指纹算法
分子指纹
molecular fingerprint的最新技术是扩展连接性圆形指纹extended-connectivity circular fingerprints: ECFP。ECFP是对Morgan算法的改进,旨在以无关于原子标记顺序atom-relabling的方式来识别分子中存在哪些子结构substructure。ECFP通过对前一层邻域的特征进行拼接,然后采用一个固定的哈希函数来抽取当前层的特征。哈希函数的结果视为整数索引,然后对节点feature vector在索引对应位置处填写1(即,登记某个特定的子结构是否出现) 。不考虑
hash冲突,则指纹向量的每个索引都代表一个特定的子结构。索引表示的子结构的范围取决于网络深度,因此网络的层数也被称为指纹的“半径”。ECFP类似于卷积网络,因为它们都在局部采用了相同的操作,并且在全局池化中聚合信息。ECFP的计算框架如下图所示:首先通过分子结构构建分子图,其中节点表示原子、边表示化学键。在每一层,信息在邻域之间流动。图的每个节点在一个固定的指纹向量中占据一个bit。其中这只是一个简单的示意图,实际上每一层都可以写入指纹向量。
指纹向量
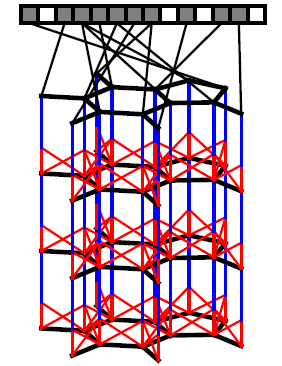
圆形指纹算法:
输入:
- 分子结构
- 半径参数
- 指纹向量长度
输出:指纹向量
算法步骤:
初始化指纹向量:
遍历每个原子
遍历每一层。对于第
遍历分子中的每个原子
- 获取节点
- 拼接节点
- 执行哈希函数得到节点
- 执行索引函数:
- 登记索引:
- 获取节点
最终返回
5.1.2 分子指纹GCN算法
我们选择类似于现有
ECFP的神经网络架构,用可微函数来代替ECFP中的每个离散操作:哈希操作
Hashing:在ECFP算法中,应用于每一层的哈希函数的目的是为了组合关于每个原子及其邻域子结构的信息。这确保了fragment中的任何修改,无论多么小,都将导致激活不同的指纹索引fingerprint index。我们利用单层神经网络代替哈希运算。当分子的局部结构发生微小的变化时(神经网络是可微的,因此也是平滑的),这种平滑函数可以得到相似的激活值。
索引操作
Indexing:在ECFP算法中,每一层采用索引操作的目的是将每个原子的特征向量组合成整个分子指纹。每个原子在其特征向量的哈希值确定的索引处,将指纹向量的单个比特位设置为1,每个原子对应一个1。这种操作类似于池化,它可以将任意大小的graph转换为固定大小的向量。当分子图比较小而指纹长度很大时,最终得到的指纹向量非常稀疏。我们使用
softmax操作视作索引操作的一个可微的近似。本质上这是要求将每个原子划分到一组类别的某个类别中。所有原子的这些类别向量的sum得到最终的指纹向量。其操作也类似于卷积神经网络中的池化操作。规范化
Canonicalization:无论原子的邻域原子的顺序如何变化,圆形指纹是不变的。实现这种不变性的一种方式是:在算法过程中,根据相邻原子的特征和键特征对相邻原子进行排序。我们尝试了这种排序方案,并且还对局部邻域的所有可能排列应用了局部特征变换。另外,一种替代方案是应用排序不变函数
permutation-invariant, 如求和。为了简单和可扩展性,我们选择直接求和。
神经图指纹算法:
输入:
分子结构
半径参数
指纹长度
隐层参数
对不同的键数量,采用不同的隐层参数
即,不同邻域大小使用不同的隐层参数
输出:指纹向量
算法步骤:
初始化指纹向量:
遍历每个原子
遍历每一层。对于第
遍历分子中的每个原子
- 获取节点
- 池化节点
- 执行哈希函数:
- 执行索引函数:
- 登记索引:
- 获取节点
最终返回
设指纹向量的长度为
上述
ECFP算法和神经图指纹算法将每一层计算得到的指纹叠加到全局指纹向量中。我们也可以针对每一层计算得到一个层级指纹向量,然后将它们进行拼接,而不是相加。以神经图指纹算法为例:- 在第
- 最终将所有层的索引拼接:
- 在第
ECFP圆形指纹可以解释为具有较大随机权重的神经图指纹算法的特殊情况。- 在较大的输入权重情况下,当
- 在较大的输入权重情况下,
softmax函数接近一个one-hot的argmax操作,这类似于索引操作。
- 在较大的输入权重情况下,当
5.1.3 限制
计算代价:神经图指纹在原子数、网络深度方面与圆形指纹具有相同的渐进复杂度,但是由于在每一步都需要通过矩阵乘法来执行特征变换,因此还有附加的计算复杂度。
假设分子的特征向量维度为
在实践中,在圆形指纹上训练一个单隐层的神经网络只需要几分钟,而对神经图指纹以及指纹顶部的单隐层神经网络需要一个小时左右。
每层的计算限制:从网络的一层到下一层之间应该采取什么结构?本文采用最简单的单层神经网络,实际上也可以采用多层网络或者
LSTM结构,这些复杂的结构可能效果更好。图上信息传播的限制:图上信息传播的能力受到神经网络深度的限制。对于一些规模较小的图如小分子的图,这可能没有问题;对于一些大分子图, 这可能受到限制。最坏情况下,可能需要深度为
为了缓解该问题,
《Spectral networks and locally connected networks on graphs》提出了层次聚类,它只需要NLP领域的相关技术。无法区分立体异构体
stereoisomers:神经图指纹需要特殊处理来区分立体异构体,包括enantomers对映异构体(分子的镜像)、cis/trans isomers顺/反异构体(绕双键旋转)。大多数圆形指纹的实现方案都可以区分这些异构体。
5.2 实验
5.2.1 随机权重
分子指纹的一个用途是计算分子之间的距离。这里我们检查基于
ECFP的分子距离是否类似于基于随机的神经图指纹的分子距离。我们选择指纹向量的长度为
2048,并使用Jaccard相似度来计算两个分子的指纹向量之间的距离:我们的数据集为溶解度数据集,下图为使用圆形指纹和神经图指纹的成对距离散点图,其相关系数为
图中每个点代表:相同的一对分子,采用圆形指纹计算到的分子距离、采用神经图指纹计算得到的分子距离,其中神经图指纹模型采用大的随机权重。距离为
1.0代表两个分子的指纹(圆形指纹或神经图指纹)没有任何重叠,距离为0.0代表两个分子的指纹圆形指纹或神经图指纹)完全重叠。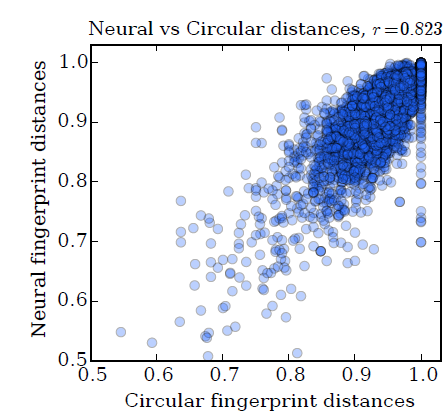
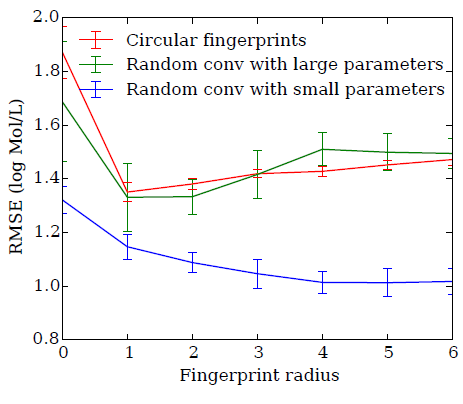
我们将圆形指纹、随机神经图指纹接入一个线性回归层,从而比较二者的预测性能。
圆形指纹、大的随机权重的随机神经图指纹,二者的曲线都有类似的轨迹。这表明:通过大的随机权重初始化的随机神经图指纹和圆形指纹类似。
较小随机权重初始化的随机神经图指纹,其曲线与前两者不同,并且性能更好。
这表明:即使是未经训练的神经网络,它相对平滑的激活值也能够有助于模型的泛化。
5.2.2 可解释性
圆形指纹向量的特征(即某一组
bit的组合)只能够通过单层的单个fragment激活(偶然发生的哈希碰撞除外),神经图指纹向量的特征可以通过相同结构的不同变种来激活,从而更加简洁和可解释。为证明神经图指纹是可解释的,我们展示了激活指纹向量中每个特征对应的子结构类别。
溶解性特征:我们将神经图指纹模型作为预测溶解度的线性模型的输入来一起训练。下图展示了对应的
fragment(蓝色),这些fragment可以最大程度的激活神经图指纹向量中最有预测能力的特征。- 上半图:激活的指纹向量的特征与溶解性具有正向的预测关系,这些特征大多数被包含亲水性
R-OH基团(溶解度的标准指标)的fragment所激活。 - 下半图:激活的指纹向量的特征与溶解性具有负向的预测关系(即:不溶解性),这些特征大多数被非极性的重复环结构所激活。
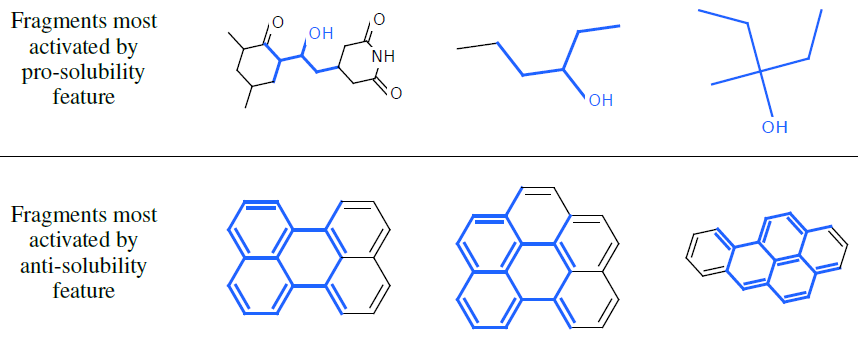
- 上半图:激活的指纹向量的特征与溶解性具有正向的预测关系,这些特征大多数被包含亲水性
毒性特征:我们用相同的架构来预测分子毒性。下图展示了对应的
fragment(红色),这些fragment可以最大程度的激活神经图指纹向量中最有预测能力的特征。- 上半图:激活的指纹向量的特征与毒性具有正向的预测关系,这些特征大多数被包含芳环相连的硫原子基团的
fragment所激活。 - 下半图:激活的指纹向量的特征与毒性具有正向的预测关系,这些特征大多数被稠合的芳环(也被称作多环芳烃,一种著名的致癌物)所激活。
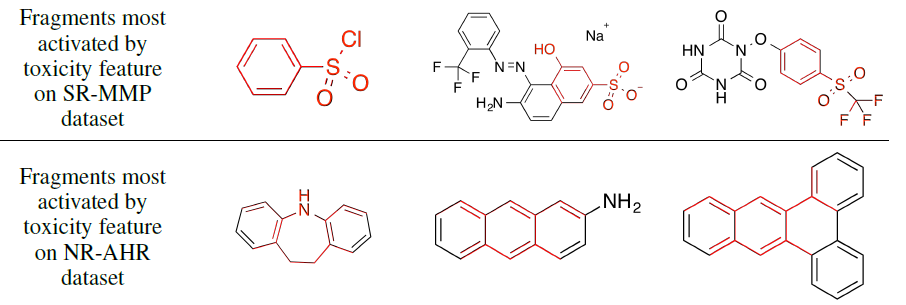
- 上半图:激活的指纹向量的特征与毒性具有正向的预测关系,这些特征大多数被包含芳环相连的硫原子基团的
5.2.3 模型比较
数据集:我们在多个数据集上比较圆形指纹和神经图指纹的性能:
- 溶解度数据集:包含
1144个分子,及其溶解度标记。 - 药物功效数据集:包含
10000个分子,及其对恶行疟原虫(一种引发疟疾的寄生虫)的功效。 - 有机光伏效率数据集:哈佛清洁能源项目使用昂贵的
DFT模拟来估算有机分子的光伏效率,我们从该数据集中使用20000个分子作为数据集。
- 溶解度数据集:包含
配置:我们的
pipeline将每个分子编码的SMILES字符串作为输入,然后使用RDKit将其转换为graph。我们也使用RDKit生成的扩展圆形指纹作为baseline。这个过程中,氢原子被隐式处理。我们的
ECFP和神经网络中用到的特征包括:- 原子特征:原子元素类型的
one-hot、原子的度degree、连接氢原子的数量、隐含价implicit valence、极性指示aromaticity indicator。 - 键特征:是否单键、是否双键、是否三键、是否芳族键、键是否共轭、键是否为环的一部分。
- 原子特征:原子元素类型的
我们采用
Adam优化算法,训练步数为10000,batch size = 100。我们还使用了batch normalization技术。我们还对神经网络进行了
tanh和relu激活函数的对比实验,我们发现relu在验证集上一直保持优势并且优势不大。我们还对神经网络进行了
drop-connect实验,它是dropout的一个变种,其中权重被随机设置为零(而不是隐单元被随机设置为零)。我们发现这会导致更差的验证误差。我们使用
Random-Search来优化以下超参数:学习率的对数 、初始权重的对数、所有超参数使用
50次。我们比较了两种情况下圆形指纹和神经图指纹的性能:
- 第一种情况:一个线性层使用指纹向量作为输入来执行预测,即
linear layer。 - 第二种情况:一个单隐层的神经网络使用指纹向量作为输入来执行预测,即
neural net。
结果如下图所示。可以看到在所有实验中,神经图指纹均达到或者超过圆形指纹的性能,并且使用神经网络层的方式(
neural net)超过了线性层的方式(linear layer)。
- 第一种情况:一个线性层使用指纹向量作为输入来执行预测,即
六、GGS-NN[2016]
许多实际应用都建立在图结构数据
graph-structured data之上,因此我们经常希望执行以graph为输入的机器学习任务。解决该问题的标准方法包括:设计关于输入图的自定义的特征工程feature engineering、graph kernel、以及根据图上的随机游走来定义graph feature的方法。与论文《Gated Graph Sequence Neural Networks》的目标更密切相关的是在图上学习特征的方法,包括图神经网络Graph Neural Networks、谱网络spectral networks、以及最近的用于学习化学分子graph representation来执行分类的graph fingerprint的工作。论文
《Gated Graph Sequence Neural Networks》的主要贡献是输出序列的图神经网络的扩展。之前的用于图结构输入的feature learning的工作主要聚焦于在产生单一输出的模型上,例如graph-level分类,但是graph input的许多问题都需要输出序列。例如,图上的path、具有所需属性的graph nodes的枚举。作者觉得现有的graph feature learning工作不适合这个问题。论文的motivating application来自于程序验证program verification,该应用需要输出逻辑公式,作者将其表述为序列输出sequential output问题。论文的第二个贡献是:强调图神经网络(以及作者在这里开发的进一步扩展)是一类广泛有用的神经网络模型,适用于当前该领域面临的很多问题。
图上的
feature learning有两种setting:- 学习输入图
input graph的representation。 - 在产生一系列输出的过程中学习内部状态
internal state的representation。
在这里,第一种
setting是通过之前关于图神经网络的工作来实现的。作者对该框架进行了一些小的修改,包括将其更改为使用围绕RNN的现代实践。第二种
setting很重要,因为我们需要图结构问题的、不仅仅是单个分类的输出。在这些情况下,挑战在于如何学习图上的特征,从而编码已经产生的部分输出序列(例如,如果是输出path,那么就是到目前为止的path)、以及仍然需要产生的部分输出序列(例如,剩余的path)。论文将展示GNN框架如何适配这些setting,从而产生一种新的、graph-based的神经网络模型,作者称之为Gated Graph Sequence Neural Networks: GGS-NN。论文在
bAbI任务、和阐明模型能力的graph algorithm learning任务的实验中说明这个通用模型的各个方面。然后作者提出一个application来验证计算机程序。当试图证明诸如内存安全(即,程序中不存在空指针解引用)等属性时,一个核心问题是找到程序中使用的数据结构的数学描述。遵循《Learning to decipher the heap for program verification》,作者将其表述为一个机器学习问题,其中论文将学习从一组输入图(代表内存状态)映射到已实例化的数据结构的逻辑描述logical description。《Learning to decipher the heap for program verification》依赖于大量的手工设计的特征,而论文表明该系统可以用GGs-NN来替代,而不会降低准确性。- 学习输入图
相关工作:
最密切相关的工作是
GNN,我们在文中详细讨论。另一个密切相关的模型是《Neural network for graphs: A contextual constructive approach》,它与GNN的主要区别在于输出模型。GNN已在多个领域得到应用,但它似乎并未在ICLR社区中广泛使用。我们在这里的部分目标是将GNN宣传为一种有用的、且有趣的神经网络变体。我们从
GNN到GG-NN的适配,与《Parameter learning with truncated message-passing》到《Empirical risk minimization of graphical model parameters given approximate inference, decoding, and model structure》在结构化预测setting中的工作之间可以进行类比。信念传播belief propagation(必须运行到接近收敛才能获得良好的梯度)被替代为截断的信念传播更新truncated belief propagation updates,然后对模型进行训练使得truncated iteration在固定数量的迭代之后产生良好的结果。类似地,RNN扩展到Tree LSTM,类似于我们在GG-NN中使用GRU更新而不是标准的GNN递归,目的是改善信息在图结构中的长期传播long-term propagation。本文所表达的将特定问题的神经网络组装
assembling成学习组件learned components的思想具有悠久的历史,至少可以追溯到1988年的《Representing part-whole hierarchies in connectionist networks》关于根据一个family tree结构来组装神经网络的工作,以便预测人与人之间的关系。类似的思想出现在《Neural methods for non-standard data》和《From machine learning to machine reasoning》中。graph kernel可用于具有图结构输入的各种kernel-based learning任务,但是我们没有发现关于学习kernel并且输出序列的工作。《Deepwalk: Online learning of social representations 》通过在图上进行随机游走将图转换为序列,然后使用sequence-based方法来学习node embedding。《Supervised neural networks for the classification of structures》将图映射到graph vector,然后使用一个output neural network进行分类。有几种模型利用图结构上
node representation的类似的propagation。《Spectral networks and locally connected networks on graphs》将卷积推广到图结构。他们的工作与GNN之间的差异类似于卷积网络和循环网络之间的差异。《Convolutional networks on graphs for learning molecular fingerprints》也考虑了对图的类卷积convolutional like操作,构建了一个成功的graph feature的可学习learnable、可微differentiable的变体。《Deep architectures and deep learning in chemoinformatics: the prediction of aqueous solubility for drug-like molecules》将任意无向图转换为许多具有不同方向的不同DAG,然后将node representation向内传播到每个root,并训练许多模型的一个ensemble。
在上述所有内容中,重点是
one-step问题。GNN和我们的扩展具有许多与指针网络pointer network(《Pointer networks》)相同的理想特性。当使用节点选择的输出层node selection output layer时,可以选择输入中的节点作为输出。有两个主要区别:- 首先,在
GNN中,图结构是显式的,这使得模型不太通用,但可能提供更强的泛化能力。 - 其次,指针网络要求每个节点都具有属性(如,空间中的位置),而
GNN可以表达仅由它们在图中的位置所定义的节点,这使得GNN更加通用。
- 首先,在
GGS-NN在两个方面与soft alignment and attentional models相关:- 首先,
graph representation使用上下文将注意力集中在哪些节点对当前决策很重要。 - 其次,在程序验证示例
program verification example中的节点注解node annotation会跟踪到目前为止已经解释了哪些节点,这提供了一种明确的机制来确保输入中的每个节点都已在producing an output的序列中使用。
- 首先,
6.1 模型
6.1.1 GNN 回顾
GNN是根据图结构pair对。我们聚焦于有向图,因此GNN框架可以很容易地适配无向图。节点
node embedding记做node label,其中节点node label为edge label,其中边edge label为在原始
GNN论文中状态向量记作RNN保持一致,这里记作定义节点集合
node embedding集合为edge label集合为定义
predecessor node集合。定义successor node集合。节点incoming edge和outgoing edge)定义为在原始
GNN论文中,邻居节点仅仅考虑前驱节点集合,即指向节点GNN论文仅考虑入边。GNN通过两个步骤来得到输出:- 首先通过转移函数
transition function得到每个节点的representationpropagation step,其中转移函数也被称作传播模型propagation model。 - 然后通过输出函数
output function得到每个节点的输出output model。
该系统是端到端可微的,因此可以利用基于梯度的优化算法来学习参数。
- 首先通过转移函数
传播模型:我们通过一个迭代过程来传播节点的状态。
节点的初始状态
其中
non-positional form和posistional form、线性和非线性。 原始GNN论文建议按照non-positional form进行分解:其中
其中
GNN的参数。输出模型:模型输出为
为处理
graph-level任务,GNN建议创建一个虚拟的超级节点super node,该超级节点通过特殊类型的边连接到所有其它节点,因此可以使用node-level相同的方式来处理graph-level任务。GNN模型是通过Almeida-Pineda算法来训练的,该算法首先执行传播过程并收敛,然后基于收敛的状态来计算梯度。其优点是我们不需要存储传播过程的中间状态(只需要存储传播过程的最终状态)来计算梯度,缺点是必须限制参数从而使得传播过程是收缩映射contraction map。转移函数是收缩映射是模型收敛的必要条件,这可能会限制模型的表达能力。当
其中
超参数
事实上一个收缩映射很难在图上进行长距离的信息传播。
考虑一个包含
1,即隐状态为标量。假设在每个时间步
令
则有:
记
即:
如果选择
1、其它位置为零) ,则有扩展
考虑到
GNN无法在图上进行长距离的信息传播。事实上,当
其中
这意味着函数
证明:考虑两个向量
则有
其中
当
当
考虑到时刻
现在考虑
当
0。这意味着一个节点对另一个节点的影响将呈指数级衰减,因此GNN无法在图上进行长距离的信息传播。当
6.1.2 GG-NN 模型
- 门控图神经网络
Gated Graph Neural Networks:GG-NN对GNN进行修改,采用了门控循环单元GRU,并对固定的back propagation through time: BPTT算法来计算梯度。这比Almeida-Pineda算法需要更多的内存,但是它消除了约束参数以确保收敛的必要性。我们还扩展了底层的representation和output model。
a. node annotation
在
GNN中节点状态的初始化值没有意义,因为不动点理论可以确保不动点独立于初始化值。但是在GG-NN模型中不再如此,节点的初始化状态可以作为额外的输入。为了区分节点的初始化状态和其它类型的节点标签信息,我们称初始化状态为节点的注解node annotation,以向量节点的初始化状态可以视为节点的标签信息的一种。
节点的注解向量就是后来广泛使用的
node feature vector。注解向量的示例:对于给定的图,我们希望预测是否存在从节点
注解向量使得节点
即:
传播模型很容易学得将节点
1。这将使得1。最终查看是否存在某个节点的状态向量前两维为
[1,1],即可判断从
b.传播模型
初始化状态向量:
信息传递:
如下图所示
(a)表示一个图,颜色表示不同的边类型(类型B和类型C);(b)表示展开的一个计算步;(c)表示矩阵sparsity structure和参数绑定parameter tying如下图所示。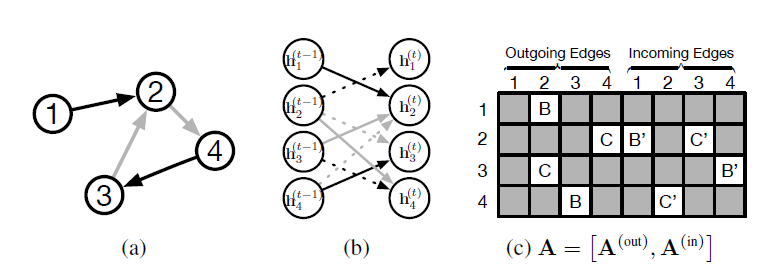
GRU更新状态:这里采用类似
GRU的更新机制,基于节点的历史状态向量和所有边的激活值来更新当前状态。sigmoid函数,我们最初使用普通的
RNN来进行状态更新,但是初步实验结论表明:GRU形式的状态更新效果更好。更新时使用了当前节点的历史信息
GG-NN可以视为:以邻域聚合信息GRU。
c. 输出模型
我们希望在不同的情况下产生几种类型的
one-step输出。node-level输出:对每个节点softmax函数来得到每个节点在各类别的得分。graph-level输出:定义graph-level的representation向量为:其中:
soft attention机制的作用,它决定哪些节点和当前的graph-level任务有关。sigmoid函数(attention系数取值是0 ~ 1之间)。
注意:这里的
GG-NN给出的是非序列输出,实际上GG-NN支持序列输出,这就是下面介绍的GGS-NN模型。
6.1.3 GGS-NN 模型
门控图序列神经网络
Gated Graph Sequence Neural Networks :GGS-NN使用若干个GG-NN网络依次作用从而生成序列输出定义所有节点的注解向量组成矩阵
定义所有节点的输出向量组成矩阵
我们使用两个
GG-NN网络output step每个
其中
我们也可以选择
annotation output模型,它用于从其中
sigmoid函数。
整个网络的结构如下图所示,如前所述有
节点注解充当
LSTM中input feature的作用,只不过节点注解可能是预测得到的(也可能是直接收集到的)。GGS-NN可以理解为:把图GG-NN,后一个GG-NN的input由前一个GG-NN来生成。
GGS-NNs的训练有两种方式:仅仅给定
我们将
指定所有的中间注解向量:
考虑一个图的序列输出任务,其中每个输出都仅仅是关于图的一个部分的预测。为了确保图的每个部分有且仅被预测一次,我们需要记录哪些节点已经被预测过。我们为每个节点指定一个
bit作为注解,该比特表明节点到目前为止是否已经被“解释”过。因此我们可以通过一组注解来捕获输出过程的进度。此时,我们可以将注解的
label信息(即GGS-NN模型中,GG-NN和给定的注解是条件独立的。- 训练期间序列输出任务将被分解为单个输出任务,并作为独立的
GG-NN来训练。 - 测试期间,第
- 训练期间序列输出任务将被分解为单个输出任务,并作为独立的
6.2 实验
bAbI任务旨在测试AI系统应该具备的推理能力。在bAbI suite中有20个任务来测试基本的推理形式,包括演绎、归纳、计数和路径查找。我们定义了一个基本的转换过程
transformation procedure从而将bAbI任务映射成GG-NN或者GGS-NN任务。我们使用已发布的
bAbI代码中的--symbolic选项从而获取仅涉及entity实体之间一系列关系的story故事,然后我们将每个实体映射为图上的一个节点、每个关系映射为图上的一条边、每个story被映射为一张图。Question问题在数据中以eval来标记,每个问题由问题类型(如has_fear)、问题参数(如一个或者多个节点)组成。我们将问题参数转换为初始的节点注解,第1。如问题
eval E > A true,则:问题类型为>,问题参数为E, A,节点的注解向量为:问题的监督标签为
true。bAbI任务15(Basic Deduction任务)转换的符号数据集symbolic dataset的一个示例:xxxxxxxxxxD is AB is EA has_fear FG is FE has_fear HF has_fear AH has_fear AC is Heval B has_fear Heval G has_fear Aeval C has_fear Aeval D has_fear F- 前
8行描述了事实fact,GG-NN将基于这些事实来构建Graph。每个大写字母代表节点,is和has_fear代表了边的label(也可以理解为边的类型)。 - 最后
4行给出了四个问题,has_fear代表了问题类型。 - 每个问题都有一个输入参数,如
eval B has_fear H中,节点B为输入参数。节点B的初始注解为标量1(只有一个元素的向量就是标量)、其它节点的初始注解标量为0。
- 前
某些任务具有多个问题类型,如
bAbI任务4具有四种问题类型:e,s,w,n。对于这类任务,我们为每个类型的任务独立训练一个GG-NN模型。论文训练四个二元分类模型,而不是单个多分类模型。实际上也可以训练单个多分类模型。
在任何实验中,我们都不会使用很强的监督标签,也不会给
GGS-NN任何中间注解信息。
我们的转换方式虽然简单,但是这种转换并不能保留有关
story的所有信息,如转换过程丢失了输入的时间顺序。这种转换也难以处理三阶或者更高阶的关系,如 “昨天John去了花园” 则难以映射为一条简单的边。注意:将一般化的自然语言映射到符号是一项艰巨的任务,因此我们无法采取这种简单的映射方式来处理任意的自然语言。
即使是采取这种简单的转化,我们仍然可以格式化描述各种
bAbI任务,包括任务19(路径查找任务)。我们提供的baseline表明:这种符号化方式无助于RNN/LSTM解决问题,但是GGS-NN可以基于这种方式以少量的训练样本来解决问题。bAbI任务19为路径查找path-finding任务,该任务几乎是最难的任务。其符号化的数据集中的一个示例:xxxxxxxxxxE s AB n CE w FB w Eeval path B A w,s- 开始的
4行描述了四种类型的边,s,n,w,e分别表示东,南,西,北。在这个例子中,e没有出现。 - 最后一行表示一个路径查找问题:
path表示问题类型为路径查找;B, A为问题参数;w,s为答案序列,该序列是一个方向序列。该答案表示:从B先向西(到达节点E)、再向南可以达到节点A。
- 开始的
我们还设计了两个新的、类似于
bAbI的任务,这些任务涉及到图上输出一个序列。这两个任务包括:最短路径问题和欧拉回路问题。最短路径问题需要找出图中两个点之间的最短路径,路径以节点的序列来表示。
我们首先生成一个随机图并产生一个
story,然后我们随机选择两个节点A和B,任务是找出节点A和B之间的最短路径。为了简化任务,我们限制了数据集生成过程:节点
A和B之间存在唯一的最短路径,并且该路径长度至少为2(即A和B的最短路径至少存在一个中间结点)。如果图中的一个路径恰好包括每条边一次,则该路径称作欧拉路径。如果一个回路是欧拉路径,则该回路称作欧拉回路。
对于欧拉回路问题,我们首先生成一个随机的、
2-regular连接图,以及一个独立的随机干扰图。然后我们随机选择两个节点A和B启动回路,任务是找出从A到B的回路。为了增加任务难度,这里添加了干扰图,这也使得输出的回路不是严格的“欧拉回路”。
正则图是每个节点的
degree都相同的无向简单图,2-regular正则图表示每个节点都有两条边。
对于
RNN和LSTM这两个baseline,我们将符号数据集转换为token序列:xxxxxxxxxxn6 e1 n1 eol n6 e1 n5 eol n1 e1 n2 eol n4 e1 n5 eol n3 e1 n4eol n3 e1 n5 eol n6 e1 n4 eol q1 n6 n2 ans 1其中
n<id>表示节点、e<id>表示边、q<id>表示问题类型。额外的token中,eol表示一行的结束end-of-line、ans代表答案answer、最后一个数字1代表监督的类别标签。我们添加
ans从而使得RNN/LSTM能够访问数据集的完整信息。训练配置:
本节中的所有任务,我们生成
1000个训练样本(其中有50个用于验证,只有950个用于训练)、1000个测试样本。在评估模型时,对于单个样本包含多个问题的情况,我们单独评估每个问题。
由于数据集生成过程的随机性,我们为每个任务随机生成
10份数据集,然后报告了这10份数据集上评估结果的均值和标准差。我们首先以
50个训练样本来训练各个模型,然后逐渐增加训练样本数量为100、250、500、950(最多950个训练样本)。由于
bAbI任务成功的标准是测试准确率在95%及其以上,我们对于每一个模型报告了测试准确率达到95%所需要的最少训练样本,以及该数量的训练样本能够达到的测试准确率。在所有任务中,我们展开传播过程为
5个时间步。对于
bAbI任务4、15、16、18、19,我们的GG-NN模型的节点状态向量4、5、6、3、6。对于最短路径和欧拉回路任务,我们的
GG-NN模型的节点状态向量20。对于所有的
GGS-NN,我们简单的令所有模型都基于
Adam优化器训练足够长的时间,并使用验证集来选择最佳模型。
6.2.1 bAbI 任务
单输出任务:
bAbI的任务4(Tow Argument Relations)、任务15(Basic Deduction)、任务16(Basic Induction)、任务18(Size Reasoning) 这四个任务都是单输出任务。对于任务
4、15、16,我们使用node-level GG-NN;对于任务18我们使用graph-level GG-NN。所有
GG-NN模型包含少于600个参数。我们在符号化数据集上训练
RNN和LSTM模型作为baseline。RNN和LSTM使用50维的embedding层和50维的隐层,它们在序列末尾给出单个预测输出,并将输出视为分类问题。这两个模型的损失函数为交叉熵,它们分别包含大约
5k个参数(RNN)和30k个参数 (LSTM)。
预测结果如下表所示。对于所有任务,
GG-NN仅需要50个训练样本即可完美的预测(测试准确率100%);而RNN/LSTM要么需要更多训练样本(任务4)、要么无法解决问题(任务15、16、18)。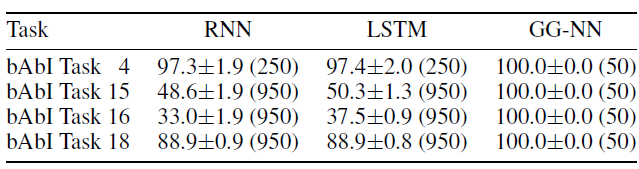
对于任务
4,我们进一步考察训练数据量变化时,RNN/LSTM模型的性能。可以看到,尽管RNN/LSTM也能够几乎完美的解决任务,但是GG-NN可以使用更少的数据达到100%的测试准确率。
序列输出任务:所有
bAbI任务中,任务19(路径查找任务)可以任务是最难的任务。我们以符号数据集的形式应用GGS-NN模型,每个输出序列的末尾添加一个额外的end标签。在测试时,网络会一直预测直到预测到end标签为止。另外,我们还对比了最短路径任务和欧拉回路任务。
下表给出了任务的预测结果。可以看到
RNN/LSTM都无法完成任务,GGS-NN可以顺利完成任务。另外GGS-NN仅仅利用50个训练样本就可以达到比RNN/LSTM更好的测试准确率。
为什么
RNN/LSTM相对于单输出任务,在序列输出任务上表现很差?欧拉回路任务是
RNN/LSTM最失败的任务,该任务的典型训练样本如下:xxxxxxxxxx3 connected-to 77 connected-to 31 connected-to 22 connected-to 15 connected-to 77 connected-to 50 connected-to 44 connected-to 01 connected-to 00 connected-to 18 connected-to 66 connected-to 83 connected-to 66 connected-to 35 connected-to 88 connected-to 54 connected-to 22 connected-to 4eval eulerian-circuit 5 7 5,7,3,6,8这个图中有两个回路
3-7-5-8-6和1-2-4-0,其中3-7-5-8-6是目标回路,而1-2-4-0是一个更小的干扰图。为了对称性,所有边都出现两次,两个方向各一次。对于
RNN/LSTM,上述符号转换为token序列:xxxxxxxxxxn4 e1 n8 eol n8 e1 n4 eol n2 e1 n3 eol n3 e1 n2 eol n6 e1 n8 eoln8 e1 n6 eol n1 e1 n5 eol n5 e1 n1 eol n2 e1 n1 eol n1 e1 n2 eoln9 e1 n7 eol n7 e1 n9 eol n4 e1 n7 eol n7 e1 n4 eol n6 e1 n9 eoln9 e1 n6 eol n5 e1 n3 eol n3 e1 n5 eol q1 n6 n8 ans 6 8 4 7 9注意:这里的节点
ID和原始符号数据集中的节点ID不同。RNN/LSTM读取整个序列,并在读取到ans这个token的时候开始预测第一个输出。然后在每一个预测步,使用ans作为输入,目标节点ID(视为类别标签) 作为输出。这里每个预测步的输出并不会作为下一个预测步的输入。我们的
GGS-NN模型使用相同的配置,其中每个预测步的输出也不会作为下一个预测步的输入,仅有当前预测步的注解RNN/LSTM的比较仍然是公平的。这使得我们的GGS-NN有能力得到前一个预测步的信息。一种改进方式是:在
RNN/LSTM/GGS-NN中,每个预测步可以利用前一个预测步的结果。实际上对于
BERT等著名的模型,解码期间可以利用前一个预测步的结果。这个典型的样本有
80个token,因此我们看到RNN/LSTM必须处理很长的输入序列。如第三个预测步需要用到序列头部的第一条边3-7,这需要RNN/LSTM能够保持长程记忆。RNN中保持长程记忆具有挑战性,LSTM在这方面比RNN更好但是仍然无法完全解决问题。该任务的另一个挑战是:输出序列出现的顺序和输入序列不同。实际上输入数据并没有顺序结构,即使边是随机排列的,目标节点的输出顺序也不应该改变。
bAbI任务19路径查找、最短路径任务也是如此。GGS-NN擅长处理此类“静态”数据,而RNN/LSTM则不然。实际上RNN/LSTM更擅长处理动态的时间序列。如何将GGS-NN应用于动态时间序列,则是将来的工作。
6.2.2 Program Verification
我们在
GGS-NN上的工作受到程序验证program verification中的实际应用的启发。自动程序验证的一个关键步骤是推断程序不变量program invariant,它逼近approximate程序执行中可达到的程序状态program state的集合。寻找关于数据结构的不变量是一个悬而未决的问题。具体实验细节参考原始论文。
6.2.3 讨论
思考
GG-NN正在学习什么是有启发性的。为此我们观察如何通过逻辑公式解决bAbI任务15。为此考虑回答下面的问题:xxxxxxxxxxB is EE has_fear Heval B has_fear要进行逻辑推理,我们不仅需要对
story里存在的事实进行逻辑编码,还需要将背景知识编码作为推理规则。如:我们对任务的编码简化了将
story解析为Graph的过程,但是它并不提供任何背景知识。因此可以将GG-NN模型视为学习背景知识的方法,并将结果存储在神经网络权重中。论文中的结果表明:
GGS-NN在一系列具有固有图结构的问题上有理想的归纳偏置inductive bias,我们相信在更多情况下GGS-NN将是有用的。然而,需要克服一些限制才能使得它们更广泛地使用。 我们之前提到的两个限制是bAbI任务翻译不包含输入的时序temporal order、也不包含三阶或更高阶的关系。我们可以想象解除这些限制的几种可能性,如拼接一系列的GG-NN,其中每条边都有一个GG-NN并将高阶关系表示为因子图factor graph。一个更重大的挑战是如何处理
less structured的input representation。例如,在bAbI任务中,最好不要使用symbolic形式的输入。一种可能的方法是在我们的GGS-NN中融合less structured的输入和latent vector。但是,需要进行实验从而找到解决这些问题的最佳方法。当前的
GG-NN必须在读取所有fact事实之后才能回答问题,这意味着网络必须尝试得出所见事实的所有后果,并将所有相关信息存储到其节点的状态中。这可能并不是一个理想的形式,最好将问题作为初始输入,然后动态地得到回答问题所需要的事实。我们对
GGS-NN的进一步应用保持乐观态度。我们对继续开发端到端的可学习系统特别感兴趣,这些系统可以学习程序的语义属性,可以学习更复杂的图算法,并将这些思想应用于需要对知识库和数据库进行推理的问题。更一般而言,我们认为这些图神经网络代表了迈向如下模型的一步:这些模型可以将结构化的representation与强大的深度学习算法相结合,目的是在学习和推断inferring如何推理reason和扩展这些representation的同时利用已知结构。
七、PATCHY-SAN[2016]
论文
《Learning Convolutional Neural Networks for Graphs》的目标是:让卷积神经网络能够解决一大类graph-based的学习问题。我们考虑以下两个问题:- 给定
graph的一个集合,学习一个函数,该函数可用于针对unseen graph的分类问题或回归问题。任意两个graph之间的结构不一定是相同的。例如,graph集合中每个graph都可以建模一种化合物,输出可以是一个函数从而将unseen的化合物映射到它们对癌细胞活性抑制的level。 - 给定一个大型的
graph,学习graph的representation,该representation可用于推断unseen的图属性(如节点类型、或missing edge)。
该论文提出了一个用于有向图或无向图的
learning representation框架。graph可能具有离散属性或连续属性的节点和边(甚至有多个属性),并且可能具有多种类型的边。类似于图像的卷积神经网络,论文从输入图input graph构建局部连接locally connected的邻域。这些邻域是有效生成的,并且作为卷积架构的感受野receptive field,从而允许框架学习有效的graph representation。所提出的方法建立在用于图像的卷积神经网络的概念之上,并将卷积神经网络扩展到任意的
graph。下图说明了用于图像的CNN的局部连接感受野。如下图所示,黑色/白色节点表示不同的像素值(黑色像素值为1、白色像素值为0),红色节点表示当前卷积核的中心位置。(a)图给出了一个3x3卷积核在一个4x4图像上的卷积过程,其中步幅为1、采用非零填充。图像可以表示为正方形的网格图square grid graph,其节点代表像素。现在,可以将CNN视为遍历节点序列(如下图(a)中的节点1,2,3,4),并为每个节点生成固定大小的邻域子图neighborhood subgraph(如下图(b)中的3x3网格)。邻域子图用作感受野从而读取像素值。由于像素的隐式空间顺序implicit spatial order,节点序列(如下图(a)中的节点1,2,3,4)从左到右、从上到下是唯一确定的。对于NLP问题也是如此,其中每个句子(及其解析树parse-tree)确定了单词序列。然而,对于许多graph集合,缺少特定于问题的顺序problem-specific ordering(空间的、时间的、或其它的顺序),并且graph的节点不存在对应关系(即,两个graph之间的结构不相等)。在这种情况下,必须解决两个问题:确定节点序列,其中我们要对序列中的节点创建邻域子图。
计算邻域子图的归一化,即从
graph到排序空间的唯一映射unique mapping。子图的归一化指的是对子图节点进行某种特定顺序的排序。
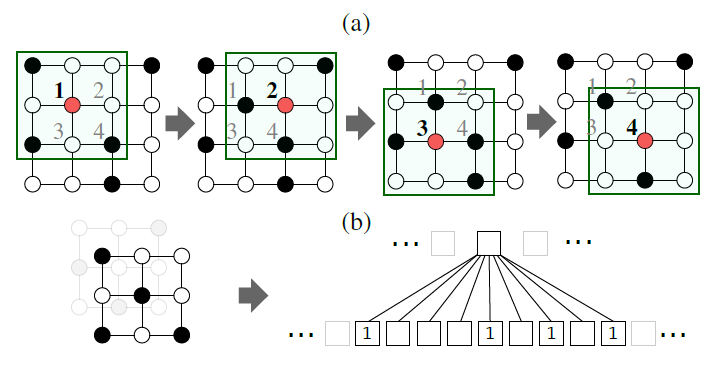
所提出的方法,称作
PATCHY-SAN,解决了任意graph的这两个问题:- 对于每个输入
graph,PATCHY-SAN首先确定需要创建邻域子图的节点(及其访问顺序)。 - 对于这些节点中的每一个,
PATCHY-SAN抽取和归一化一个刚好由fixed linear order的空间。归一化的邻域子图用作所考虑节点的感受野。 - 最后,
feature learning组件(如卷积层、稠密层)与归一化的邻域子图(作为CNN的感受野)相结合。
下图说明了
PATCHY-SAN的架构,其中红色节点表示节点序列中的节点,邻域子图大小
PATCHY-SAN与现有方法相比具有几个优点:- 首先,它高效、可并行化,并且适用于大型
graph。 - 其次,对于很多
application(从计算生物学到社交网络分析),可视化学到的网络主题network motif很重要。PATCHY-SAN支持特征可视化feature visualization,从而提供对图结构属性structural property的洞察。 - 第三,
PATCHY-SAN无需制作另一个graph kernel,而是学习application dependent的特征而无需进行特征工程。
论文的理论贡献是:
- 定义
graph上的归一化问题normalization problem,以及该问题的复杂度。 - 一种用于
graph集合的方法,该方法对比了graph labeling方法。 - 实验结果表明,
PATCHY-SAN推广了用于图像的CNN。在标准的benchmark数据集上,论文证明与state-of-the-art的graph kernel相比,学到的用于graph的CNN既高效efficient又有效effective。
- 给定
相关工作:
graph kernel:graph kernel允许kernel-based的学习方法,如直接在graph上工作的SVM。graph上的kernel最初被定义为single graph上的节点的相似函数similarity function。两类具有代表性的kernel是skew spectrum kernel和kernel based on graphlet。后者与我们的工作有关,因为它基于固定大小的子图来构建kernel。这些子图,通常被称作motif或graphlet,反映了功能性的网络的属性functional network property。然而,由于子图枚举subgraph enumeration的组合复杂性combinatorial complexity,graphlet kernel仅限于具有少量节点的子图。Weisfeiler-Lehman (WL) kernel是一类有效的graph kenerl。然而,WL kernel仅支持离散特征,并且在测试阶段使用与训练样本数量成线性关系的内存(而不是与测试样本数量成线性关系)。PATCHY-SAN使用WL作为一种可能的labeling过程来计算感受野。deep graph kernel和graph invariant kernel根据诸如最短路径shortest path、graphlet、子树subtree、以及其它的图不变量graph invariant等小型子结构的存在或数量来比较图compare graph。相反,PATCHY-SAN从graph数据中学习子结构,并且不限于预定义predefined的一组主题motif。此外,所有
graph kernel的训练复杂度至少是graph数量的二次方关系,这对于大型graph而言是不可行的,但是PATCHY-SAN的训练复杂度是graph数量的线性关系。graph neural network: GNN:GNN是图上定义的循环神经网络recurrent neural network: RNN架构。GNN将循环神经网络应用于图结构上的游走walk,传播node representation,直到达到一个不动点fixed point。然后将生成的node representation用作分类和回归问题中的特征。GNN仅支持离散特征,并在每次学习迭代过程中执行与图的边和节点数量一样多的反向传播操作。注:
GNN理论上也支持连续特征。Gated Graph Sequence Neural Network: GGSNN修改GNN以使用门控循环单元gated recurrent unit: GRU并输出序列。最近的工作将
CNN扩展到不同于低维网格结构的拓扑。然而,所有这些方法都假设一个全局的图结构,即,跨graph的节点的对应关系correspondence。《Convolutional networks on graphs for learning molecular fingerprints》对graph执行卷积类型的操作,开发了一个specific graph feature的可微变体differentiable variant。
7.1 基础概念
7.1.1 CNN
CNN受到早期工作的启发,该工作表明:动物的视觉皮层包含复杂的细胞排列,它们负责检测视野visual field的小局部区域small local region中的光。CNN是在1980年代开发的,并已应用于图像、语音、文本、以及药物发现问题。CNN的前身是Neocognitron。典型的CNN由卷积层、稠密层dense layer组成。第一个卷积层的目的是提取在输入图像的局部区域内发现的常见模式。CNN对输入图像利用学到的filter执行卷积运算,并将卷积结果输出为张量,输出的depth是filter的数量。
7.1.2 Graph Kernel(读者补充)
目前现有的大多数
Graph Kernel算法都是基于R-Convolution理论构建而来,其理论思想是:设计一种图的分解算法,两个图的核函数和图分解后的子结构的相似程度有关。给定两个图
基于该子结构,则
其中:
因此,任意一种图的分解方式
Graph Kernel,常见的主要分为三类:- 基于游走的
Graph Kernel,如Random Walk Kernel。 - 基于路径的
Graph Kernel,如Shortest-Path Kernel。 - 基于子树
subtree或者子图subgraph的Graph Kernel,如Weisfeiler-Lehman Subtree Kernel。
另外,除了
R-Convolution系列之外,还有其它的Graph Kernel。- 基于游走的
Random Walk Kernel:随机游走Kernel的基本思想是:统计两个输入图中相同的随机游走序列的数量。给定输入图
label为direct product graph其中:
label,label。注意,这里的label其实是属性,而不是监督学习中的监督信号。label的节点组成的pair对。label的边组成的pair对,且边的对应节点的label分别相同。
在
label。- 起点背后的两个子节点,在各自图中具有相同的
label。 - 终点背后的两个子节点,在各自图中具有相同的
label。 - 起点和终点背后的两对子边,在各自图中具有相同的
label。
定义图
kernel定义为:其中
label序列完全相同、路径的边label序列完全相同。Shortest-Path Kernel:随机游走Kernel的基本思想是:统计两个输入图中相同标签之间的最短路径。给定输入图
首先通过
Floyd成对最短路径生成算法,构建每个图的节点之间的最短路径,得到新的图计算:
其中
1的edge walk上的正定核。
Weisfeiler-Lehman Subtree Kernel:它基于Weisfeiler-Lehman算法。节点
label更新:对于图hash函数得到节点label:其中
label,label集合。更新后的新
label包含了其直接邻域的节点信息。因此如果两个节点更新后的label相同,我们可以认为其邻域结构是同构的。更新图的所有节点 、重复更新最多
每一轮更新后,节点
label就包含了更大规模的邻域的节点信息,最终每个节点的label编码了图的全局结构信息。对于输入图
Weisfeiler-Lehman算法,最终根据label集合的相似性(如Jaccard相似性)来得到核函数:其中
label集合。
一旦定义了
Graph Kernel,则我们可以使用基于核技巧的方法,如SVM来直接应用在图上。
7.2 模型
给定图
定义图的邻接矩阵
每个节点以及每条边可以包含一组属性,这些属性可以为离散的,也可以为连续的。这里我们用 “属性” 而不是 “标签” 来避免概念的混淆。
定义一个游走序列
walk是由连续的边组成的一个节点序列。定义一条路径path是由不重复节点构成的walk。定义
定义
Labeling and Node Partitions:PATCHY-SAN利用了graph labeling对节点进行排序。graph labeling:如果图的节点自带label, 则我们可以直接用该label。如果节点没有label,则我们可以通过一个graph labeling函数label,其中graph labeling过程计算输入图的graph labeling。graph labeling的例子包括:通过节点的度degree计算label、通过节点的中介中心性between centrality计算label。一个节点ranking:一个排序ranking(或者染色coloring)是一个函数graph labeling引入一个排序函数,使得当且仅当label越大则排名越靠前。如果图labeling其中节点
行代表节点,列代表排名。
划分
partition:graph labeling引入节点集合label的取值类别数。节点Weisfeiler-Lehman算法是一种划分图节点的过程,它也被称作color refinement和naive vertex classification。该算法在机器学习社区中引起了相当广泛的兴趣,因为它可以应用于图模型的加速推断、以及作为一种计算graph kernel的方法。
PATCHY-SAN使用这些graph labeling过程来对图的节点施加顺序,从而替代缺失的、application-dependent的顺序(如时间顺序,空间顺序)。同构和规范化
Isomorphism and Canonicalization:在很多应用领域存在的一个计算问题是:确定两个图是否是同构曲面。图同构问题graph isomorphism (GI) problem是NP的,但是不知道是属于P还是NP-hard。在一些温和的限制下,图同构问题是P的,例如对于有界degree的图。图
isomorphism class。在实践中,图规范化工具NAUTY表现出了卓越的性能。当
CNN应用于图像时,感受野(正方形网格)以特定的步长在图像上移动。感受野为每个通道读取一次像素值,并为每个通道创建一批数值。由于图像的像素具有隐式排列(即,空间顺序),因此感受野总是从左到右、从上到下移动。此外,空间顺序唯一地确定了每个感受野的节点以及这些节点映射到排序空间方式。因此,当且仅当像素的结构角色structural role(它们在感受野内的空间位置)相同时,使用两个不同绝对位置的感受野读取到的两个像素值被分配到同一个相对位置。为了展示
CNN和PATCHY-SAN之间的联系,我们把图像上的CNN视为一种框架:首先识别正方形网格图(代表图像)中的节点序列,然后为该序列中的每个节点建立一个归一化的邻域子图neighborhood graph(即,感受野)。对于缺少
application-dependent节点顺序并且任何两个图的节点尚未对齐的图集合,我们需要为每个图确定:- 一个节点序列,其中我们即将为序列中的每个节点创建邻域子图。
- 从图结构到向量
representation的唯一映射,使得相似的邻域子图具有相似的向量representation。
我们通过
graph labeling过程来解决这些问题。如果来自两个不同图的节点在图中的结构角色相似,那么它们被分配到各自邻接矩阵中的相似的相对位置。给定一组图,PATCHY-SAN对每个图执行以下操作:- 采用
Node Sequence Selection算法从图中选择一个固定长度的节点序列。 - 采用
Neighborhood Assembly算法为节点序列中的每个节点组装一个固定大小的邻域。 - 通过
Graph Normalization对每个邻域子图进行归一化处理,从而将无序的图转换为有序的、长度固定的节点序列。 - 利用
CNN学习邻域的representation。
7.2.1 Node Sequence Selection
节点序列选择
node sequence selection是为每个输入图识别需要创建感受野的节点序列的过程。首先,输入图的节点根据给定的
graph labeling进行排序。其次,使用给定的步幅
feature map的尺寸,它对应于一维CNN中的序列长度。
步幅
graph labeling进行深度优先遍历。类比一维卷积的运算,那么
Select Node Sequence算法:算法输入:
graph labeling函数- 输入图
- 步幅
算法输出:被选择的节点序列,以及对应的感受野
算法步骤:
根据
top初始化:
迭代,直到
如果
将
因为节点的特征可能是一个向量,表示多维度属性。
更新:
返回访问到的节点序列,以及创建的感受野序列。
7.2.2 Neighborhood Assembly
对于被选择的节点序列,必须为其中的每个节点构建一个感受野。创建感受野的算法首先调用邻域组装算法来构建一个局部邻域,邻域内的节点是感受野的候选节点。
给定节点
BFS来探索与节点BFS过程),直到即,广度优先搜索
另外,最终得到的
Neighborhood Assembly算法:算法输入:当前节点
算法输出:节点
算法步骤:
初始化:
BFS遍历到的节点。注意,节点
迭代,直到
- 获取当前
BFS遍历节点的一阶邻域: - 合并
BFS遍历到的节点:
- 获取当前
返回
7.2.3 Graph Normalization
子图归一化是对邻域子图的节点施加一个顺序,使得节点从无序的图空间映射到线性顺序的排序空间。子图归一化的基本思想是利用
graph labeling,对于不同子图中的节点,当且仅当节点在各自子图中的结构角色相似时,才给它们分配到各自邻接矩阵中的相似的相对位置similar relative position。为了形式化该思想,我们定义了一个
Optimal Graph Normalization问题,该问题的目标是找到给定的图集合的最佳labeling。Optimal Graph Normalization问题:令graph labeling过程。令即:从
图的最优归一化问题是经典的图规范化问题
graph canonicalization problem的推广。但是经典的labeling算法仅针对同构图isomorphic graph最佳,对于相似但是不同构的图可能效果不佳。相比之下,最优归一化问题的期望值越小,则labeling过程将具有相似结构角色的节点进行对齐的效果越好。这里结构相似度由关于图的最优归一化问题,这里给出了两个定理:
定理一:图的最优归一化问题是
NP-hard。证明:通过从子图同构进行规约
reduction。PATCHY-SAN无法完全解决图的最优归一化问题,它只是比较了不同的graph labeling方法,然后选择其中表现最好的那个。定理二:设
如果
graph labeling。证明见论文。该定理使得我们通过比较估计量
graph labeling。我们可以简单的选择使得graph labeling。当我们在图上选择编辑距离
edit distance、在矩阵另外,上述结论不仅对无向图成立,对于有向图也成立。
图的归一化问题,以及针对该问题的合适的
graph labeling方法是PATCHY-SAN算法的核心。我们对节点label:任意两个其它节点1(即排名最靠前)。注意,
PATCHY-SAN中应用了两种graph labeling函数:- 第一种
graph labeling函数Select Node Sequence算法。 - 第二种
graph labeling函数就是这里的距离函数,用于图的归一化问题,即Graph Normalization算法。
由于大多数
labeling方法不是单射的,因此有必要打破same-label节点之间的联系。为此,我们使用NAUTY。NAUTY接收先验的node partition作为输入,并通过选择字典顺序最大的邻接矩阵来打破剩余的联系remaining ties。注意,节点
graph labeling函数不是单射的。众所周知,对于有界
degree的图的同构问题可以在多项式时间求解,由于邻域子图的规模为graph labeling的过程仅产生一个微不足道的开销。- 第一种
Graph Normalization算法:算法输入:
- 节点
graph labeling函数Select Node Sequence算法中的graph labeling函数- 感受野尺寸
- 节点
输出:归一化的邻域子图
算法步骤:
对
如果
ranking取top k个节点,对所选择的节点再执行一次labeling以及ranking的过程。这里必须使用
labeling分布。如果
根据这
下图为对红色根节点
graph labeling对节点进行排序,然后创建归一化的邻域。归一化还包括裁剪多余的节点和填充虚拟节点。节点的不同属性对应于不同的输入通道。不仅可以针对节点创建感受野,还可以针对边创建感受野,边的感受野尺寸为
正如前面的评论所说,最终得到的
或者,如后文所述,也可以直接采用边的感受野(尺寸为

创建感受野的
Create Receptive Field算法:算法输入:节点
算法输出:节点
算法步骤:
- 计算节点
- 归一化邻域子图:
- 返回
- 计算节点
我们可以将
PATCHY-SAN与图像的CNN相关联。定理:在图像中得到的一个像素序列上应用
PATCHY-SAN,其中感受野尺寸为1-WL归一化,则这等效于CNN的一个感受野大小为证明:如果输入图为一个正方形网格,则为节点构造的
1-WL归一化的感受野始终是具有唯一节点顺序的正方形网格。
7.2.4 PATCHY-SAN 架构
PATCHY-SAN既能处理节点,也能处理边;它既能处理离散属性,也能处理连续属性。PATCHY-SAN对每个输入图我们可以将这两个张量
reshape为一个CNN的组件。另外我们可以利用融合层来融合来自节点的卷积输出feature map和来自边的卷积输出feature map。
7.2.5 算法复杂度
PATCHY-SAN的创建感受野算法非常高效。另外,由于这些感受野的生成是相互独立的,因此感受野生成过程原生支持并行化。定理:令
graph labeling过程的计算复杂度。则PATCHY-SAN最坏情况下的计算复杂度为证明见论文。
当采用
Weisfeiler-Lehman算法作为graph labeling算法时,它的算法复杂度为PATCHY-SAN的复杂度为
7.3 实验
7.3.1 运行时分析
我们通过将
PATCHY-SAN应用于实际的图来评估其计算效率,评估指标为感受野的生成速度。我们将PATCHY-SAN生成感受野的速度,与state-of-the-art的CNN执行学习的速度进行比较。数据集:所有输入图都来自
Python模块GRAPHTOOL。torus图:具有10k个节点的周期性晶格。random图:具有10个节点的随机无向图,节点的度的分布满足:power图:美国电网拓扑网络。polbooks:2004年美国总统大选期间出版的有关美国政治书籍的co-purchasing网络。preferential:一个preferential attachment network,其中最新添加的节点的degree为3。astro-ph:天体物理学arxiv上作者之间的co-authorship网络。email-enron:一个由大约50万封已发送email生成的通信网络。
我们的
PATCHY-SAN采用1-dimensional Weisfeiler-Lehman:1-WL算法来归一化邻域子图。下图给出了每个输入图每秒产生感受野的速度。所有实验都是在单台2.8 GHZ GPU、64G内存的机器上执行。- 对于感受野尺寸
email-eron上的速度为600/s和320/s之外,在其它所有图上PATCHY-SAN创建感受野的速度超过1000/s。 - 对于最大的感受野尺寸
PATCHY-SAN创建感受野的速度至少为100/s。
对于一个经典的带两层卷积层、两层
dense层的CNN网络,我们在相同机器上训练速度大概是200-400个样本/秒,因此PATCHY-SAN感受野的生成速度足以使得下游CNN组件饱和。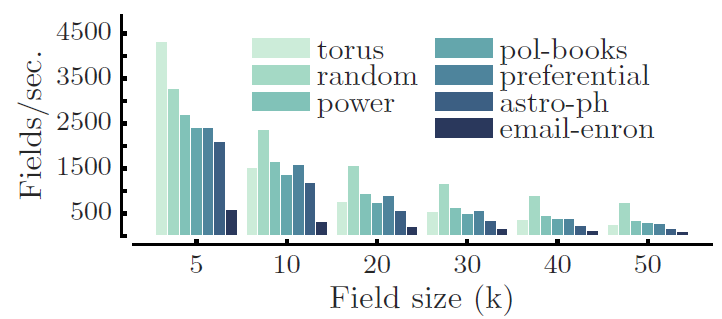
- 对于感受野尺寸
7.3.2 可视化
可视化实验的目的是定性研究
restricted boltzman machine: RBM等流行模型是否可以与PATCHY-SAN结合从而用于无监督特征学习。我们将PATCHY-SAN学到的尺寸为9的归一化感受野使用restricted boltzman machine:RBM进行无监督学习,RNM所学到的特征对应于重复出现的感受野模式。其中:PATCHY-SAN采用1-WL算法进行邻域子图归一化。- 采用单层
RBM,隐层包含100个隐单元。 RBM采用对比散度算法contrastive divergence: CD训练30个epoch,学习率设为0.01。
下图给出了从四张图中得到的样本和特征。我们将
RBM学到的特征权重可视化(像素颜色越深,则对应权重重大)。另外我们还采样了每种模式对应的三个节点的归一化邻域子图,黄色节点表示当且节点(排序为1)。左上角为
torus周期性晶格图、左下角为preferential attachment图、右上角为co-purchasing图、右下角为随机图。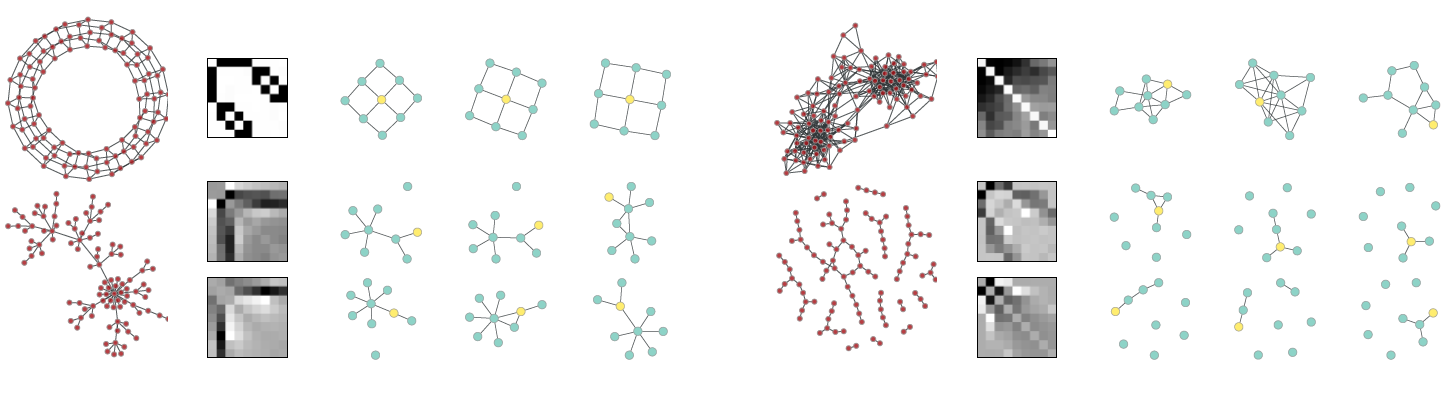
7.3.3 图的分类
图分类任务是将每个图划分到若干类别之一。我们采用
6个标准benchmark数据集来比较不同图分类模型的分类准确性和运行时间。MUTAG数据集:由188种硝基化合物组成的数据集,其类别表明该化合物是否对细菌具有诱变mutagenic作用。PTC数据集:由344种化合物组成的数据集,其类别表明是否对老鼠具有致癌性。NCI1和NCI109数据集:筛选出的抑制non-small肺癌细胞和卵巢癌细胞活性的化合物。PROTEIN:一个图的数据集,其中图的节点表示次级结构元素secondary structure element, 边表示氨基酸序列中的相邻关系,或者三维空间中的氨基酸相邻关系。其类别表示酶或者非酶。D&D:由1178种蛋白质组成的数据集,其类别表明是酶还是非酶。
我们将
PATCHY-SAN和一组核方法比较,包括shortest-path kernel: SP、random walk kernel: RW、graphlet count kernel: GK,以及Weisfeiler-Lehman sbutree kernel: WL。对于核方法,我们使用
LIB-SVM模型来训练和评估核方法的效果。我们使用10折交叉验证,其中9-fold用于训练,1-fold用于测试。我们重复10次并报告平均准确率和标准差。类似之前的工作,我们设置核方法的超参数为:
WL的高度参数设置为2,GK的尺寸参数设置为7,RW的衰减因子从对于
PATCHY-SAN: PSCN方法,我们使用1-dimensional WL归一化,设置所有
PSCN都使用了具有两个卷积层、一个dense层、一个softmax层的网络结构。其中:- 第一个卷积层有
16个输出通道,第二个卷积层有8个输出通道,步长 dense层有128个隐单元(relu激活函数),采用dropout = 0.5的dropout。我们采用一个较小的隐单元数量以及dropout从而避免模型在小数据集上过拟合。
所有卷积层和
dense层的激活函数都是reLU。 模型的优化算法为RMSPROP优化算法,并基于Keras封装的Theno实现。所有
PSCN需要优化的超参数为epoch数量以及batch-size。当
PATCHY-SAN抽取的感受野应用一个逻辑回归分类器PSLR。- 第一个卷积层有
实验结果:这些模型在
benchmark数据集上的结果如下表所示。其中前三行给出了各数据集的属性,包括图的最大节点数Max、图的平均节点数Avg、图的数量Graphs。我们忽略了NCI109的结果,因为它几乎和NCI1相同。- 尽管使用了非常普通的
CNN架构,PSCN的准确率相比现有的graph kernel方法具有很强的竞争力。在大多数情况下,采用PSCN具有最佳的分类准确性。 PSCN这里的预测方差较大,这是因为:benchmark数据集较小,另外CNN的一些超参数(epoch和batch-size除外)没有针对具体的数据集进行优化。与图像和文本数据的体验类似,我们预期PATCHY-SAN在大型数据集上的表现更好。PATCHY-SAN的运行效率是graph kernel中最高效的WL方法的2到8倍。我们预计具有大量graph的数据集上,PATCHY-SAN的性能优势会更加明显。PATCHY-SAN+ 逻辑回归的效果较差,这表明PATCHY-SAN更适合搭配CNN。CNN学到了归一化感受野的非线性特征组合,并在不同感受野之间共享权重。- 采用中介中心性归一化
betweeness centrality normalization结果也类似(未在表中体现),除了它的运行时间大约增加了10%。
融合节点的感受野和边的感受野的
PSCN k=10,这表明保留邻域子图的距离信息的有效性。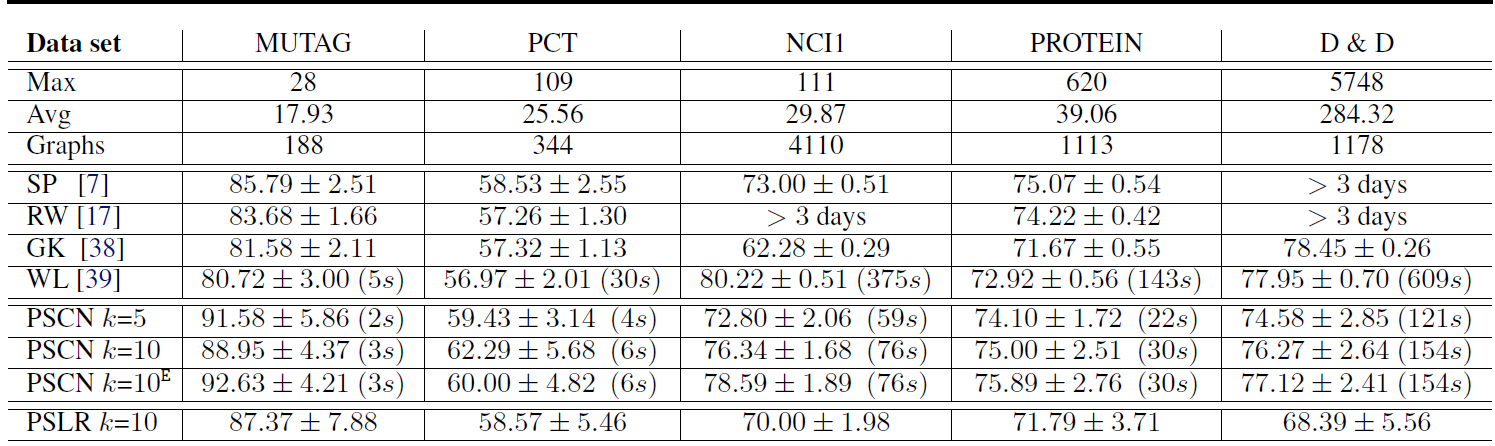
- 尽管使用了非常普通的
我们在较大的社交网络图数据集上使用相同的配置进行实验,其中每个数据集最多包含
12k个图,每个图平均400个节点。我们将PATCHY-SAN和之前报告的graphlet count: GK、deep graplet count kernel: DGK结果相比。我们使用归一化的节点
degree作为节点的属性,这突出了PATCHY-SAN的优势之一:很容易地包含连续特征。可以看到
PSCN在六个数据集的四个中明显优于其它两个核方法,并且在剩下两个数据集也取得了很好的性能。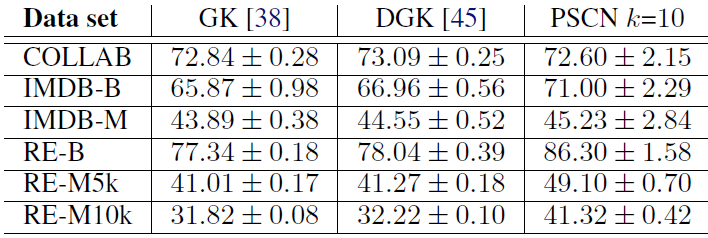
八、GraphSAGE[2017]
在大型图中节点的低维向量
embedding已被证明作为特征输入非常有用,可用于各种预测和图分析graph analysis任务。node embedding方法背后的基本思想是:使用降维技术将关于节点的graph neighborhood的高维信息蒸馏成稠密的、低维的向量embedding。然后可以将这些node embedding馈入到下游机器学习系统,并帮助完成节点分类、节点聚类、以及链接预测等任务。然而,以前的工作集中在从单个固定图
a single fixed graph上的节点的embedding,许多实际application需要为unseen的节点、或全新的图快速生成embedding。这种归纳能力inductive capability对于高吞吐量、生产型的机器学习系统至关重要,其中这些机器学习系统在不断演变的图上运行并不断遇到unseen的节点(如Reddit上的帖子、Youtube上的用户和视频)。生成node embedding的归纳方法inductive approach还有助于跨具有相同形式特征的图进行泛化:例如,可以在源自模型器官model organism的protein-protein交互图上训练一个embedding generator,然后使用经过训练的embedding generator轻松地为在新器官上收集的数据生成node embedding。与直推式配置
transductive setting相比,归纳式inductive的node embedding问题特别困难,因为泛化到unseen的节点需要将新观察到的子图observed subgraph与算法已经优化的node embedding进行对齐aligning。归纳式框架inductive framework必须学会识别节点领域的结构属性,这些属性揭示了节点在图中的局部角色local role及其全局位置global position。大多数现有的生成
node embedding的方法本质上都是直推式的。这些方法中的大多数使用基于矩阵分解的目标直接优化每个节点的embedding,并且无法自然地泛化到unseen的数据,因为它们在单个固定图上对节点进行预测。这些方法可以被修改从而在归纳式配置中运行,但是这些修改往往在计算上代价很大,需要额外的梯度下降轮次才能作出新的预测。最近还有一些使用卷积算子来学习图结构的方法,这些方法提供了作为embedding方法的承诺(《Semi-supervised classification with graph convolutional networks》)。到目前为止,图卷积网络graph convolutional network: GCN仅应用于具有固定图fixed graph的直推式配置。在论文《Inductive Representation Learning on Large Graphs》中,作者将GCN泛化到归纳式无监督学习的任务,并提出了一个框架,该框架泛化了GCN方法从而使用可训练的聚合函数(超越了简单的卷积)。《Semi-supervised classification with graph convolutional networks》提出的GCN要求在训练过程中已知完整的图拉普拉斯算子,而测试期间unseen的节点必然会改变图拉普拉斯算子,因此该方法也是直推式的。论文的工作:
作者提出了一个通用框架,称作
GraphSAGE(SAmple and aggreGatE),用于归纳式node embedding。与基于矩阵分解的embedding方法不同,GraphSAGE利用节点特征(如,文本属性、节点画像node profile信息、节点degree)来学习一个embedding函数,该embedding函数可以泛化到unseen的节点。通过在学习算法中加入节点特征,GraphSAGE同时学习了每个节点邻域的拓扑结构、以及该邻域内节点特征的分布。虽然GraphSAGE聚焦于特征丰富的graph(如,具有文本属性的引文数据,具有功能标记/分子标记的生物数据),但是GraphSAGE还可以利用所有图中存在的结构特征(如,节点degree)。因此,GraphSAGE也可以应用于没有节点特征的图。GraphSAGE不是为每个节点训练一个distinct的embedding向量,而是训练一组聚合器函数aggregator function,这些函数学习从节点的局部邻域来聚合特征信息(如下图所示)。每个聚合器函数聚合来自远离给定节点的不同hop数(或搜索深度)的信息。在测试或推断时,GraphSAGE通过应用学到的聚合函数为unseen的节点生成embedding。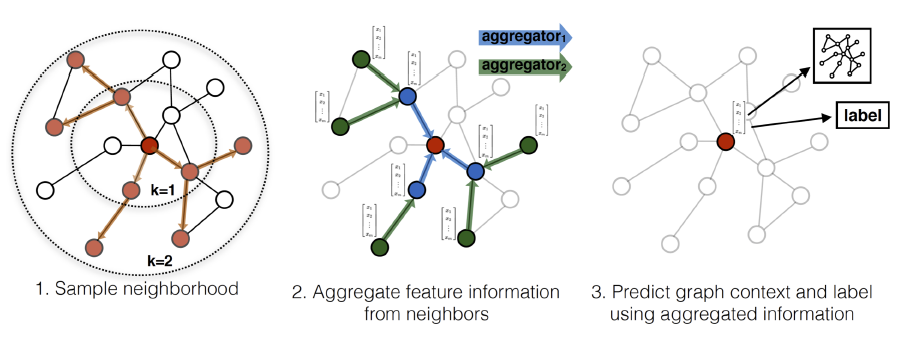
遵从之前的
node embedding工作,作者设计了一个无监督损失函数,允许在没有task-specific监督信息的情况下训练GraphSAGE。作者还表明GraphSAGE可以通过完全监督的方式进行训练。作者在三个关于节点/图分类
benchmark上评估GraphSAGE,这些benchmark测试了GraphSAGE在unseen数据上生成有效embedding的能力。作者使用基于引文数据和Reddit帖子数据(分别预测论文类别和帖子类别)的两个不断演变的文档图,以及基于protein-protein交互的数据集(预测蛋白质功能)的多图泛化multigraph generalization实验。使用这些
benchmark,作者表明GraphSAGE能够有效地为unseen的节点生成representation,并大大优于相关baseline:跨所有这些不同的领域,与单独使用节点特征相比,GraphSAGE的监督方法将分类F1分数平均提高了51%,并且GraphSAGE始终优于强大的直推式的baseline,并且该baseline需要100轮迭代甚至更长的时间才能预测unseen的节点。作者还表明,与受图卷积网络(
《Semi-supervised classification with graph convolutional networks》)启发的聚合器相比,论文提出的新聚合器架构提供了显著的增益(平均增益7.4%)。最后,作者探讨了
GraphSAGE的表达能力expressive capability,并通过理论分析表明:GraphSAGE能够学到有关节点在图中的角色的结构信息,尽管它本质上是基于特征的。
相关工作:我们的算法在概念上与之前的
node embedding方法、图上学习的通用监督方法general supervised approache、以及将卷积神经网络应用于图结构数据的最新进展等等相关。基于分解的
embedding方法:最近有许多node embedding方法使用随机游走统计和基于矩阵分解的学习目标来学习低维embedding(GraRep, node2vec, Deepwalk, Line, SDNE)。这些方法还与更经典的谱聚类spectral clustering方法、多维缩放multi-dimensional scaling、以及PageRank算法密切相关。由于这些
embedding算法直接为单个节点individual node训练node embedding,因此它们本质上是直推式的,并且至少需要昂贵的额外训练(如,通过随机梯度下降)来对unseen节点进行预测。此外,对于大多数这些方法,目标函数对于embedding的正交变换是不变的,这意味着embedding空间不会自然地在图之间泛化,并且在re-training期间可能会漂移drift。因为这些方法是基于矩阵分解的,而矩阵分解的内积函数
embedding空间的正交不变的,即:将embeddign空间旋转任意角度,原始内积函数和新内积函数的结果是相等的。这一趋势的一个显著例外是
Planetoid-I算法,它是一种归纳式的、基于embedding的半监督学习方法。但是,Planetoid-I在推断过程中不使用任何图结构信息,相反,它在训练期间使用图结构信息作为正则化的一种形式。与先前的这些方法不同,我们利用特征信息来训练模型从而为
unseen节点生成embedding。图上的监督学习:除了
node embedding方法之外,还有大量关于图结构数据的监督学习的工作。这包括各种各样的kernel-based方法,其中图的特征向量来自于各种graph kernel。最近还有许多神经网络方法可以对图结构数据进行监督学习。我们的方法在概念上受到大多数这些算法的启发。然而,这些方法试图对整个图(或子图)进行分类,但是我们这项工作的重点是为每个节点生成有用的representation。图卷积网络:近年来,人们已经提出了几种用于图上学习的卷积神经网络架构。这些方法中的大多数无法扩展到大型图、或者设计用于整个图的分类。然而,我们的方法与
《Semi-supervised classification with graph convolutional networks》提出的图卷积网络graph convolutional network: GCN密切相关。原始的GCN算法是为直推式setting的半监督学习而设计的,确切exact的算法要求在训练期间知道整个图的拉普拉斯算子。我们算法的一个简单变体可以视作GCN框架对归纳式setting的扩展,我们将在正文部分重新讨论这一点。
8.1 模型
- 我们方法背后的关键思想是:我们学习如何从节点的局部邻域聚合特征信息(如,邻域节点的
degree或文本属性)。我们首先描述GraphSAGE的embedding生成(即,前向传播)算法,该算法在假设GraphSAGE模型参数已经学到的情况下为节点生成embedding。然后,我们描述了如何使用标准随机梯度下降和反向传播技术来学习GraphSAGE模型参数。
8.1.1 前向传播
这里我们将描述前向传播算法(也叫
embedding生成算法),其中假设模型已经训练好并且参数是固定的。具体而言,假设我们已经学到了layer层数。GraphSAGE的embedding生成算法为:输入:
- 图
- 非线性激活函数
- 图
输出:节点的
embedding向量算法步骤:
初始化:
对每一层迭代,迭代条件为:
遍历每个节点
其中
concat()表示向量拼接。这里是拼接融合,也可以考虑其它类型的融合方式。
对每个节点
GraphSAGE前向传播算法的背后直觉是:在每次迭代或搜索深度,节点都会聚合来自其局部邻域的信息;并且随着这个过程的迭代,节点将从图的更远范围逐渐获取越来越多的信息。在算法的外层循环中的每个
step如下进行,其中current step(也叫做搜索深度),step中的node representation:首先,每个节点
representationnode representation(即representation被定义为节点输入特征邻域
representation可以通过各种聚合器架构(以AGGREGATE占位符来表达)来完成,接下来我们会讨论不同的架构选择。然后,在聚合邻域特征向量之后,
GraphSAGE将节点的当前representationstep要用到的representation,即大多数节点
embedding方法将学到的embedding归一化为单位向量,这里也做类似处理。
为了记号方便,我们将第
final representation记做
a. mini-batch 训练
为了将算法扩展到
mini-batch setting,给定一组输入节点,我们首先前向采样forward sample所需要的邻域集合(直到深度representation(而不是所有节点的representation)。为了使用随机梯度下降算法,我们需要对
GraphSAGE的前向传播算法进行修改,从而允许mini-batch中每个节点能够执行前向传播、反向传播。即:确保前向传播、反向传播过程中用到的节点都在同一个
mini-batch中。GraphSAGE mini-batch前向传播算法(这里representation的节点):算法输入:
- 图
- 非线性激活函数
- 图
输出:节点的
embedding向量算法步骤:
初始化:
迭代
- 遍历
初始化:
对每一层迭代,迭代条件为:
遍历每个节点
这里用
对每个节点
mini-batch前向传播算法的主要思想是:首先采样所有所需的节点。集合representation的节点所依赖的节点集合。由于representation的节点更少,这避免计算不必要的节点。然后计算目标节点的
representation,这一步和batch前向传播算法相同。mini-batch前向传播和batch前向传播的主要区别在于:mini-batch前向传播还有一个前向采样的步骤。我们使用
random walk采样。这里我们使用均匀采样,并且当节点邻域节点数量少于指定数量时采用有放回的采样,否则使用无放回的采样。有一些算法聚焦于如何更好地进行采样,从而优化最终效果。
mini-batch算法的采样过程在概念上与batch算法的迭代过程是相反的。我们从需要以深度representation的节点开始,然后我们对它们的邻域进行采样(即,深度在
batch算法中,我们在在
mibi-batch算法中,我们在这样才能保证我们的目标
mibi-batch所需要计算的所有节点。
b. 和 WL-Test 关系
GraphSAGE算法在概念上受到图的同构性检验的经典算法的启发。在前向传播过程中,如果令hash函数来作为聚合函数,同时移除非线性函数,则该算法是Weisfeiler-Lehman:WL同构性检验算法的一个特例,被称作naive vertex refinement。如果算法输出的
node representationWL-test算法认为这两个子图是同构的。虽然在某些情况下该检验会失败,但是大多数情况下该检验是有效的。GraphSAGE是WL test算法的一个continous近似,其中GraphSAGE使用可训练的神经网络聚合函数代替了不连续的哈希函数。虽然GraphSAGE的目标是生成节点的有效embedding而不是检验图的同构性,但是GraphSAGE和WL test之间的联系为我们设计学习节点邻域拓扑结构的算法提供了理论背景。可以证明:即使我们提供的是节点特征信息,
GraphSAGE也能够学到图的结构信息。参考 “理论分析” 部分。
c. 邻域定义
在
GraphSAGE中我们并没有使用完整的邻域,而是均匀采样一组固定大小的邻域,从而确保每个batch的计算代价是固定的。因此我们定义如果对每个节点使用完整的邻域,则每个
batch的内存需求和运行时间是不确定的,最坏情况为batch的时间和空间复杂度固定为
8.1.2 模型学习
为了在完全无监督的环境中学习有用的、预测性的
representation,我们将一个graph-based损失函数应用于output representationgraph-based损失函数鼓励临近的节点具有相似的representation,同时迫使不相近的节点具有高度不相似的representation:其中:
random walk上共现的节点。sigmoid(.)为sigmoid函数。negative node,
重要的是,与之前的
embedding方法不同,GraphSAGE中的节点representationembedding look-up而生成的。可以看到,
GraphSAGE和DeepWalk类似,也依赖于图上的随机游走过程。为了提高训练效率,通常在训练之前执行一次随机游走过程(避免在训练的每轮迭代中进行随机游走)。以无监督方式学到的节点
embedding可以作为通用service来服务于下游的机器学习任务。但是如果仅在特定的任务上应用,则可以简单地将特定于任务的监督学习损失替代或增强原始的无监督损失。通过结合监督损失和无监督损失,那么可以同时利用
labeled数据和unlabeled数据,即半监督学习。
8.1.3 聚合函数
和网格型数据(如文本、图像)不同,图的节点之间没有任何顺序关系,因此算法中的聚合函数必须能够在无序的节点集合上运行。理想的聚合函数是对称的,同时可训练并保持较高的表达能力。这种对称性可以确保我们的神经网络模型可以用于任意顺序的节点邻域的训练和测试。
对称性是指:对于给定的一组节点集合,无论它们以何种顺序输入到聚合函数,聚合后的输出结果不变。
聚合函数有多种形式,我们检查了三种主要的聚合函数:均值聚合函数
mean aggregator、LSTM聚合函数LSTM aggregator、池化聚合函数pooling aggregator。mean aggregator:简单的使用邻域节点的特征向量的逐元素均值来作为聚合结果。这几乎等价于直推式GCN框架中的卷积传播规则。具体而言,如果我们将前向传播:
替换为:
则这得到直推式
GCN的一个inductive变种,我们称之为基于均值聚合的卷积mean-based aggregator convolutional。它是局部谱卷积localized spectral convolution的一个粗糙的线性近似。GCN的前向传播为:其中:
degree矩阵。因此有:
注意,
GCN的embedding look-up而生成的(而不是输入特征这个卷积聚合器与我们提出的其它聚合器之间的一个重要区别在于:它并未执行拼接操作(即,将
GraphSAGE算法的不同search depth(或layer)之间的skip connection的一种简单形式,它可以显著提高性能。事实上其它聚合器在拼接操作之后执行了带非线性激活函数的投影,因此破坏了这种
skip connection。是否修改为以下形式更好?LSTM aggregator:和均值聚合相比,LSTM具有更强大的表达能力。但是LSTM原生的是非对称的(即,LSTM不是permutation invariant的),它依赖于节点的输入顺序。因此我们通过简单地将LSTM应用于邻域节点的随机排序,从而使得LSTM可以应用于无序的节点集合。pooling aggregator:池化聚合器是对称的、可训练的。在这种池化方法中,邻域每个节点的特征向量都通过全连接神经网络独立馈入,然后通过一个逐元素的最大池化来聚合邻域信息:其中
max表示逐元素的max运算符,理论上可以在最大池化之前使用任意深度的多层感知机,但是我们这里专注于简单的单层网络结构。直观上看,可以将多层感知机视为一组函数,这组函数为邻域集合内的每个节点
representation计算特征。通过将最大池化应用到这些计算到的特征上,模型可以有效捕获邻域集合的不同方面aspect。理论上可以使用任何的对称向量函数(如逐元素均值)来替代
max运算符。但是我们在实验中发现最大池化和均值池化之间没有显著差异,因此我们专注于最大池化。
8.1.4 理论分析
这里我们将探讨
GraphSAGE的表达能力,以便深入了解GraphSAGE如何学习图结构,即使它本质上是基于特征的。作为案例研究,我们考虑GraphSAGE是否可以学习预测节点的聚类系数clustering coefficient,即:在节点的1-hop邻域内,闭合的三角形占所有三角形(闭合的和未闭合的)的比例。聚类系数是衡量节点局部邻域聚类程度的常用指标,它可以作为许多更复杂的结构主题structural motif的building block。可以证明:GraphSAGE算法能够将聚类系数逼近到任意精度。定理:令
GraphSAGE算法针对图compact subset。假设存在一个固定的正的常数pairsettingGraphSAGE算法在其中:
GraphSAGE算法的final output值,注意,这里假设
output representation是一维的。上述定理指出:对于任意的图,
GraphSAGE算法都存在一个参数setting,如果每个每个节点的特征都是不同的(并且如果模型足够高维),那么算法可以将图的聚类系数逼近到任意精度。证明见原始论文。注意:作为该定理的推论,
GraphSAGE可以了解局部图结构,即使节点特征输入是从连续随机分布中采样的(因此特征输入与图结构无关)。证明背后的基本思想是:如果每个节点都有一个
unique的特征,那么我们可以学习将节点映射到indicator向量并识别节点邻域。定理的证明依赖于池化聚合器的一些属性,这也提供了为什么GraphSAGE-pool优于GCN、以及mean-based聚合器的洞察。
8.2 实验
我们在三个
benchmark任务上检验GraphSAGE的效果:Web of Science Citation数据集的论文分类任务、Reddit数据集的帖子分类任务、PPI数据集的蛋白质分类任务。前两个数据集是对训练期间
unseen的节点进行预测,最后一个数据集是对训练期间unseen的图进行预测。数据集:
Web of Science Cor Collection数据集:包含2000年到2005年六个生物学相关领域的所有论文,每篇论文属于六种主题类别之一。数据集包含302424个节点,节点的平均degree为9.15。其中:Immunology免疫学的标签为NI,节点数量77356。Ecology生态学的标签为GU,节点数量37935。Biophysics生物物理学的标签为DA,节点数量36688。Endocrinology and Metabolism内分泌与代谢的标签为IA,节点数量52225。Cell Biology细胞生物学的标签为DR,节点数量84231。Biology(other)生物学其它的标签为CU,节点数量13988。
任务目标是预测论文主题的类别。我们根据
2000-2004年的数据来训练所有算法,并用2005年的数据进行进行测试(其中30%用于验证)。我们使用节点
degree和文章的摘要作为节点的特征,其中节点摘要根据Arora等人的方法使用sentence embedding方法来处理文章的摘要,并使用Gensim word2vec的实现来训练了300维的词向量。Reddit数据集:包含2014年9月Reddit上发布帖子的一个大型图数据集,节点标签为帖子所属的社区。我们采样了50个大型社区,并构建一个帖子到帖子的图。如果一个用户同时在两个帖子上发表评论,则这两个帖子将链接起来。数据集包含232965个节点,节点的平均degree为492。为了对社区进行采样,我们按照每个社区在
2014年的评论总数对社区进行排名,并选择排名在[11,50](包含)的社区。我们忽略了最大的那些社区,因为它们是大型的、通用的默认社区,会严重扭曲类别的分布。我们选择这些社区上定义的最大连通图largest connected component。任务的目标是预测帖子的社区
community。我们将该月前20天用于训练,剩下的天数作为测试(其中30%用于验证)。我们使用帖子的以下特征:标题的平均
embedding、所有评论的平均embedding、帖子评分、帖子评论数。其中embedding直接使用现有的300维的GloVe CommonCral词向量,而不是在所有帖子中重新训练。PPI数据集:包含Molecular Signatures Dataset中的图,每个图对应于不同的人类组织,节点标签采用gene ontology sets,一共121种标签。平均每个图包含2373个节点,所有节点的平均degree为28.8。任务的目的是评估模型的跨图泛化的能力。我们在
20个随机选择的图上进行训练、2个图进行验证、2个图进行测试。其中训练集中每个图至少有15000条边,验证集和测试集中每个图都至少包含35000条边。注意:对于所有的实验,验证集和测试集是固定选择的,训练集是随机选择的。我们最后给出测试图上的micro-F1指标。我们使用
positional gene sets、motif gene sets以及immunological signatures作为节点特征。我们选择至少在10%的蛋白质上出现过的特征,低于该比例的特征不被采纳。最终节点特征非常稀疏,有42%的节点没有非零特征(即,42%的节点的特征全是空的),这使得节点之间的链接非常重要。
Baseline模型:- 随机分类器。
- 基于节点特征的逻辑回归分类器(完全忽略图的结构信息)。
- 代表因子分解方法的
DeepWalk算法+逻辑回归分类器(完全忽略节点的特征)。 - 拼接了
DeepWalk的embedding以及节点特征的方法(融合图的节点特征和结构特征)。
我们使用了不同聚合函数的
GraphSAGE的四个变体。由于卷积的变体是GCN的inductive扩展,因此我们称其为GraphSAGE-GCN。我们使用了
GraphSAGE的无监督版本,也直接使用分类交叉熵作为损失的有监督版本。模型配置:
GrahSage:- 所有
GraphSAGE模型都在Tensorflow中使用Adam优化器实现, 而DeepWalk在普通的随机梯度优化器中表现更好。 - 为防止
GraphSAGE聚合函数的效果比较时出现意外的超参数hacking,我们对所有GraphSAGE版本进行了相同的超参数配置:根据验证集的性能为每个版本提供最佳配置。 - 对于所有的
GraphSAGE版本设置 - 对于所有的
GraphSAGE,我们对每个节点执行以该节点开始的50轮长度为5的随机游走序列,从而得到pair节点对。我们的随机游走序列生成完全基于Python代码实现。 - 由于节点
degree分布的长尾效应,我们将GraphSAGE算法中所有图的边执行降采样预处理。经过降采样之后,使得没有任何节点的degree超过128。由于我们每个节点最多采样25个邻居,因此这是一个合理的权衡。
- 所有
为公平比较,所有模型都采样相同的
mini-batch迭代器、损失函数(当然监督损失和无监督损失不同)、邻域采样器。对于原生特征模型,以及基于无监督模型的
embedding进行预测时,我们使用scikit-learn中的SGDClassifier逻辑回归分类器,并使用默认配置。在所有配置中,我们都对学习率和模型的维度以及
batch-size等等进行超参数选择:除了
DeepWalk之外,我们为监督学习模型设置初始学习率的搜索空间为最初实验表明
DeepWalk在更大的学习率下表现更好,因此我们选择DeepWalk的初始学习率搜索空间为我们测试了每个
GraphSAGE模型的big版本和small版本。- 对于池化聚合函数,
big模型的池化层维度为1024,small模型的池化层维度为512。 - 对于
LSTM聚合函数,big模型的隐层维度为256,small模型的隐层维度为128。
注意,这里设置的是聚合器的维度,而不是
hidden representation的维度。- 对于池化聚合函数,
所有实验中,我们将
GraphSAGE每一层的256。所有的
GraphSAGE以及DeepWalk的非线性激活函数为ReLU。对于无监督
GraphSAGE和DeepWalk模型,我们使用20个负采样的样本,并且使用0.75的平滑参数对节点的degree进行上下文分布平滑。对于监督
GraphSAGE,我们为每个模型运行10个epoch。我们对
GraphSAGE选择batch-size = 512。对于DeepWalk我们使用batch-size=64,因为我们发现这个较小的batch-size收敛速度更快。
硬件配置:
DeepWalk在CPU密集型机器上速度更快,它的硬件参数为144 core的Intel Xeon CPU(E7-8890 V3 @ 2.50 GHz),2T内存。- 其它模型在单台机器上实验,该机器具有
4个NVIDIA Titan X Pascal GPU(12 Gb显存,10Gbps访问速度),16 core的Intel Xeon CPU(E5-2623 v4 @ 2.60GHz),以及256 Gb内存。
所有实验在共享资源环境下大约进行了
3天。我们预期在消费级的单GPU机器上(如配备了Titan X GPU)的全部资源专用,可以在4到7天完成所有实验。DeepWalk测试阶段:对于
Reddit和引文数据集,我们按照Perozzi等人的描述对DeepWalk执行oneline训练。对于新的测试节点,我们进行了新一轮的SGD优化,从而得到新节点的embedding。现有的
DeepWalk实现仅仅是word2vec代码的封装,它难以支持embedding新节点以及其它变体。这里我们根据tensorflow中的官方word2vec教程实现了DeepWalk。为了得到新节点的embedding,我们在保持已有节点的embedding不变的情况下,对每个新的节点执行50个长度为5的随机游走序列,然后更新新节点的embedding。我们还测试了两种变体:一种是将采样的随机游走“上下文节点”限制为仅来自已经训练过的旧节点集合,这可以缓解统计漂移;另一种是没有该限制。我们总数选择性能最强的那个。
尽管
DeepWalk在inductive任务上的表现很差,但是在transductive环境下测试时它表现出更强的竞争力。因为在该环境下DeepWalk可以在单个固定的图上进行持续的训练。我们观察到在inductive环境下DeepWalk的性能可以通过进一步的训练来提高。并且在某种情况下,如果让它比其它方法运行的时间长1000倍,则它能够达到与无监督GraphSAGE(而不是有监督GraphSAGE)差不多的性能。但是我们不认为这种比较对于inductive是有意义的。在
PPI数据集中我们无法应用DeepWalk,因为在不同的、不相交的图上运行DeepWalk算法生成的embedding空间可以相对于彼此任意旋转。参考最后一小节的证明。
GraphSAGE及baseline在这三个任务上的表现如下表所示。这里给出的是测试集上的micro-F1指标,对于macro-F1结果也有类似的趋势。其中Unsup表示无监督学习,Sup表示监督学习。GraphSAGE的性能明显优于所有的baseline模型。根据
GraphSAGE不同版本可以看到:与GCN聚合方式相比,可训练的神经网络聚合函数具有明显的优势。注意,这里的
GraphSAGE-mean是将GraphSAGE-pool的max函数替换为mean得到。尽管
LSTM这种聚合函数是为有序数据进行设计而不是为无序set准备的,但是通过随机排列的方式,它仍然表现出出色的性能。和监督版本的
GraphSAGE相比,无监督GraphSAGE版本的性能具有相当竞争力。这表明我们的框架无需特定于具体任务就可以实现强大的性能。
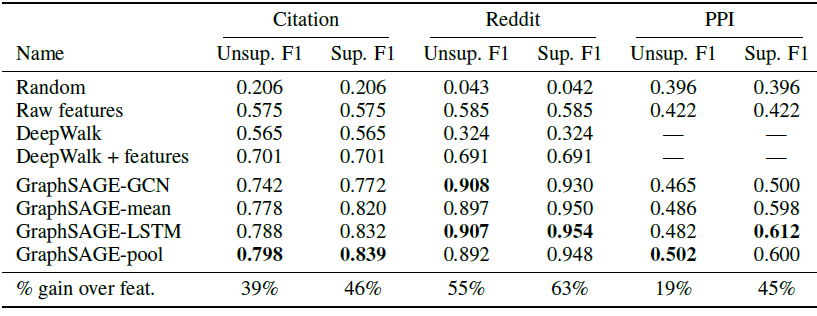
通过在
Reddit数据集上不同模型的训练和测试的运行时间如下表所示,其中batch size = 512,测试集包含79534个节点。可以看到:- 这些方法的训练时间相差无几,其中
GraphSAGE-LSTM最慢。 - 除了
DeepWalk之外,其它方法的测试时间也相差无几。由于DeepWalk需要采样新的随机游走序列,并运行多轮SGD随机梯度下降来生成unseen节点的embedding,这使得DeepWalk在测试期间慢了100~500倍。
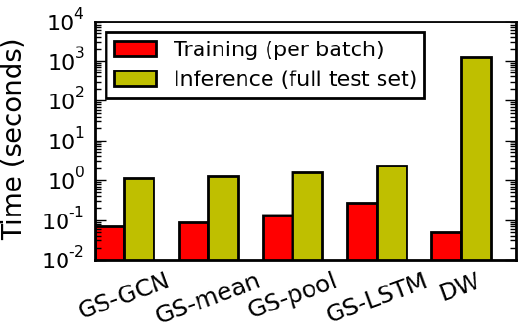
- 这些方法的训练时间相差无几,其中
对于
GraphSAGE变体,我们发现和10%~15%。但是当2以上时会导致性能的回报较低(0~5%) ,但是运行时间增加到夸张的10~100倍,具体取决于采样邻域的大小。另外,随着采样邻域大小逐渐增加,模型获得的收益递减。因此,尽管对邻域的采样引起了更高的方差,但是
GraphSAGE仍然能够保持较强的预测准确性,同时显著改善运行时间。下图给出了在引文网络数据集上GraphSAGE-mean模型采用不同邻域大小对应的模型性能以及运行时间,其中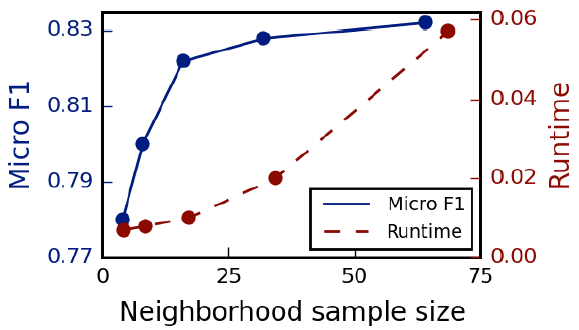
总体而言我们发现就平均性能和超参数而言,基于
LSTM聚合函数和池化聚合函数的表现最好。为了定量的刻画这种比较优势,我们将三个数据集、监督学习/无监督学习两种方式一共六种配置作为实验,然后使用Wilcoxon Signed-Rank Test来量化不同模型的性能。结论:
- 基于
LSTM聚合函数和池化聚合函数的效果确实最好。 - 基于
LSTM聚合函数的效果和基于池化聚合函数的效果相差无几,但是由于GraphSAGE-LSTM比GraphSAGE-pool慢得多(大约2倍),这使得基于池化的聚合函数总体上略有优势。
- 基于
8.3 DeepWalk Embedding 旋转不变性
DeepWalk,node2vec以及其它类似的node embedding方法的目标函数都有类似的形式:其中:
node embedding(通过embedding的look up得到)。pair对。
事实上这类方法可以认为是一个隐式的矩阵分解
embedding。
这类方法的一个重要结果是:
embedding可以通过任意单位正交矩阵变换,从而不影响矩阵分解:其中
embedding空间在训练过程中可以自由旋转。embedding矩阵可以在embedding空间可以自由旋转带来两个明显后果:如果我们在两个单独的图
A和B上基于embedding方法,如果没有一些明确的惩罚机制来强制两个图的节点对齐,则两个图学到的embedding空间将相对于彼此可以任意旋转。因此,对于在图A的节点embedding上训练的任何节点分类模型,如果直接灌入图B的节点embedding,这这等效于对该分类模型灌入随机数据。如果我们有办法在图之间对齐节点,从而在图之间共享信息,则可以缓解该问题。研究如何对齐是未来的方向,但是对齐过程不可避免地在新数据集上运行缓慢。
而
GraphSAGE完全无需做额外地节点对齐,它可以简单地为新节点生成embedding信息。如果在时刻
A基于embedding方法,然后在学到的embedding上训练分类器。如果在时刻A添加了一批新的节点,并通过运行新一轮的随机梯度下降来更新所有节点的embedding,则这会导致两个问题:- 首先,类似于上面提到的第一点,如果新节点仅连接到少量的旧节点,则新节点的
embedding空间实际上可以相对于原始节点的embedding空间任意旋转。 - 其次,如果我们在训练过程中更新所有节点的
embedding,则相比于我们训练分类模型所依赖的原始embedding空间相比,我们新的embedding空间可以任意旋转。
- 首先,类似于上面提到的第一点,如果新节点仅连接到少量的旧节点,则新节点的
这类
embedding空间旋转问题对于依赖成对节点距离的任务(如通过embedding的点积来预测链接)没有影响。因为不管
embedding空间怎么旋转,节点之间的距离不变(如通过内积的距离,或通过欧式距离的距离)。缓解这类统计漂移问题(即
embedding空间旋转)的一些方法为:- 为新节点训练
embedding时,不要更新已经训练的embedding。 - 在采样的随机游走序列中,仅保留旧节点为上下文节点,从而确保
skip-gram目标函数中的每个点积操作都是一个旧节点和一个新节点。
我们尝试了这两种方式,并始终选择效果最好的
DeepWalk变体。- 为新节点训练
从经验来讲,
DeepWalk在引文网络上的效果要比Reddit网络更好。因为和引文网络相比,Reddit的这种统计漂移更为严重:Reddit数据集中,从测试集链接到训练集的边更少。在引文网络中,测试集有96%的新节点链接到训练集;在Reddit数据集中,测试集只有73%的新节点链接到训练集。
九、GAT[2017]
卷积神经网络
Convolutional Neural Network: CNN已经成功应用于图像分类、语义分割以及机器翻译之类的问题,其底层数据结构为网格状结构grid-like structure。这些架构通过将它们应用于所有的input position从而有效地reuse具有可学习参数的局部滤波器local filter。然而,许多人们感兴趣的任务涉及的数据无法以网格状结构来表达,而是位于不规则域
irregular domain。例如,3D mesh、社交网络、电信网络、生物网络、脑连接组brain connectome等等。这些数据通常可以通过graph的形式来表达。有一些文献尝试扩展神经网络从而处理任意结构的图。
早期的工作使用递归神经网络
recursive neural network: RNN来处理graph domain中表示为有向无环图的数据。《A new model for learning in graph domains》和《The graph neural network model》提出了图神经网络Graph Neural Network: GNN作为RNN的泛化,从而可以直接处理更通用的graph类型,如:循环图、有向图、无向图。GNN包含一个迭代过程,该迭代过程传播节点状态直到达到平衡。然后是一个神经网络,它根据每个节点的状态为每个节点生成一个输出。这个思想被
《Gated graph sequence neural networks》所采纳和改进,该方法提出在传播过程中使用门控循环单元gated recurrent unit: GRU。
然而,人们将卷积推广到
graph domain的兴趣越来越大。这个方向的进展通常分为谱方法spectral approach和非谱方法non-spectral approach。一方面,谱方法与图的谱表示
spectral representation一起工作,并已成功应用于节点分类的context中。- 在
《Spectral networks and locallyconnected networks on graphs》中,卷积运算是通过计算图拉普拉斯矩阵graph Laplacian的特征分解eigen decomposition从而在傅里叶域Fourier domain中定义的,这导致潜在的稠密计算以及非空间局部化的滤波器non-spatially localized filter。 这些问题在随后的工作中得到解决。 《Deep convolutional networks on graph-structured data》引入了具有平滑系数的谱滤波器spectral filter的参数化parameterization,使得滤波器在空间上局部化。- 后来,
《Convolutional neural networks on graphs with fast localized spectral filtering》提出通过图拉普拉斯矩阵的切比雪夫展开来近似滤波器,从而无需计算图拉普拉斯矩阵的特征向量从而生成空间局部化的滤波器。 - 最后,
《Semi-supervised classification with graph convolutional networks》通过限制滤波器仅操作每个节点周围的1-step邻域内来简化之前的方法。
然而,在所有上述谱方法中,学到的滤波器依赖于拉普拉斯矩阵的特征基
Laplacian eigenbasis,而这个特征基依赖于图结构。因此,在特定图结构上训练的模型无法直接应用于具有不同结构的其它的图。- 在
另一方面,我们有非谱方法,该方法直接在图上定义卷积从而操作空间近邻的节点集合。这些方法的挑战之一是:定义一个与不同规模的邻域一起工作,并能保持
CNN的权重共享属性的算子。在某些情况下,这需要为每个节点
degree学习一个特定的权重矩阵(《Convolutional networks on graphs for learning molecular fingerprints》),或者需要使用转移矩阵transition matrix的幂来定义邻域并同时针对每个输入通道和邻域degree来学习权重(《Diffusion-convolutional neural networks》),或者需要抽取和归一化邻域从而包含固定数量节点(《Learning convolutional neural networksfor graphs》)。《Geometric deep learning on graphs and manifolds using mixture model cnns》提出了mixture model CNN(MoNet),这是一种空间方法,可以将CNN架构统一泛化到图。最近,
《representation learning on largegraphs》提出了GraphSAGE,这是一种以归纳式的方式计算node representation的方法。该技术通过对每个节点采样固定尺寸邻域,然后该邻域执行特定的聚合器(如,均值池化聚合器,或LSTM聚合器)。GraphSAGE在多个大规模归纳式benchmark中取得了令人印象深刻的性能。GAT无需对邻域进行采样,能够处理可变邻域。
在许多
sequence-based任务中,注意力机制几乎已经成为事实上的标准。注意力机制的好处之一是:注意力机制允许处理可变尺寸的输入,并聚焦于输入中最相关的部分从而作出决策。当使用注意力机制来计算单个序列的representation时,它通常被称作self-attention或intra-attention。与RNN或卷积一起,self-attention已被证明对机器阅读、sentence representation学习等任务很有用。而且,《Attention is all you need》表明:self-attention不仅可以改进基于RNN或卷积的方法,而且足以构建一个强大的模型并且在机器翻译任务上获得state-of-the-art的性能。受最近这项工作的启发,论文
《GRAPH ATTENTION NETWORKS》引入了一种attention-based架构来执行图结构数据的节点分类。基本思想是:遵从self-attention策略,可以通过attend节点的邻居来计算图中每个节点的hidden representation。注意力架构有几个有趣的特性:- 操作是高效的,因为它可以跨
node-neighbor pair进行并行化。 self-attention通过给邻居赋予可学习的、任意的权重,从而可以应用于具有不同degree的图节点。- 该模型直接适用于归纳式的学习问题,包括模型必须泛化到完全
unseen的图的任务。
作者在四个具有挑战性的
benchmark上验证了所提出的方法,实现或接近state-of-the-art的结果。实验结果凸显了attention-based模型在处理任意结构的图时的潜力。注:
inductive learning和transductive learning的区别:inductive learning是从具体样本中总结普适性规律,然后泛化到训练中unseen的样本。transductive learning是从具体样本中总结具体性规律,它用于预测训练集中已经出现过的unlabelled样本,常用于半监督学习。
相关工作:
正如
《Semi-supervised classification with graph convolutional networks》和《Diffusion-convolutional neural networks》一样,我们的工作也可以重新表述为MoNet的一个特定实例。此外,我们跨
edge共享神经网络计算neural network computation的方法让人联想起关系网络relational network(《A simple neural network module for relational reasoning》)和VAIN(《Vain: Attentional multi-agent predictive modeling》)的公式,其中object或agent之间的relation是通过采用一种共享机制来pair-wise聚合的。同样地,我们提出的注意力模型可以与
《One-shot imitation learning》和《Programmable agents》等工作联系起来,它们使用邻域注意力操作neighborhood attention operation来计算环境中不同对象之间的注意力系数。其它相关方法包括局部线性嵌入
locally linear embedding: LLE、记忆网络memory network。LLE在每个data point周围选择固定数量的邻居,并为每个邻居学习一个权重系数,从而将每个point重构为其邻居的加权和。然后第二步优化是抽取point的feature embedding。memory network也与我们的工作有一些联系。具体而言,如果我们将节点的邻域解释为memory,那么该memory被用于通过attendmemory的values来计算node feature(READ过程),然后通过将新的特征存储在node对应的位置从而进行更新(WRITE过程)。
9.1 模型
- 这里我们介绍用于构建任意
graph attention network: GAT的building block layer(通过堆叠该层),即graph attentional layer: GAL。然后我们概述与神经图处理neural graph processing领域的先前工作相比,这种layer的理论和实践上的优势和局限性。
9.1.1 Graph Attentional Layer
我们将从描述单个
graph attentional layer: GAL开始,其中GAL作为我们实验中使用的GAT架构中使用的唯一一种layer。我们使用的特定的attentional setup与《Neural machine translation by jointly learning to align and translate》的工作密切相关,但是GAT框架与注意力机制的特定选择无关。GAL的输入为一组节点特征:representation维度。GAL输出这些节点的新的representation:representation维度(可能与为了获得足够的表达能力
expressive power从而将input feature转化为higher-level feature,至少需要一个可学习的线性变换。为此,作为初始的step,我们首先对所有节点应用一个共享权重的线性变换,权重为self-attentionattentional mechanism) :attention系数:其中
理论上讲,我们允许每个节点关注图中所有其它的节点,因此这可以完全忽略所有的图结构信息。实际上,我们采用
masked attention机制将图的结构信息注入到attention机制:对于节点attention系数注意:这里
为使得系数可以在不同节点之间比较,我们使用
softmax函数对所有的在我们的实验中,注意力机制
LeakyReLU激活函数,其中负轴斜率其中:
注意:这里的节点
query,邻域key。query节点representation和每个key的representation进行拼接。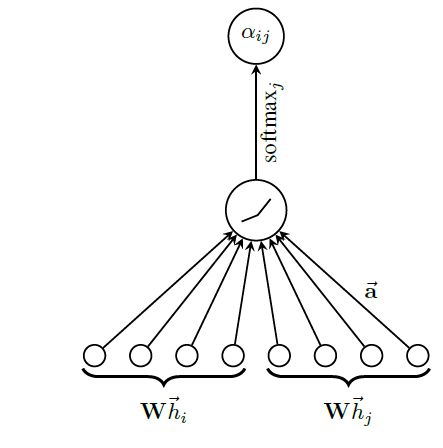
一旦得到归一化的注意力得分,我们就可以用它对相应的邻居节点的特征进行加权线性组合,从而得到每个节点的
final output feature:其中
理论上也可以使用不同的
我们使用
multi-head attention来稳定self-attention的学习过程。我们采用head,然后将它们的输出拼接在一起:其中:
head的归一化的注意力得分。head的权重矩阵。
最终的输出
但是,如果
GAL是网络最后一层(即输出层),我们对multi-head的输出不再进行拼接,而是直接取平均,因为拼接没有意义。同时我们延迟使用最后的非线性层,对分类问题通常是softmax或者sigmoid:理论上,最后的
GAL也可以拼接再额外接一个输出层。例如,实验部分作者就在最后一层使用attention head。如下图所示为
multi head = 3,当且节点head。
9.1.2 和相关工作的比较
GAL解决了现有的、基于神经网络对图结构数据建模的方法的问题。GAL计算高效:self-attentional layer的操作可以跨所有edge并行化,输出特征的计算可以跨所有节点并行化。即,单个
self-attention内部的、计算self-attention也可以并行化。不需要特征分解
eigen decomposition或类似的昂贵矩阵计算。单个
attention head计算baseline方法(如GCN)差不多。- 首先计算所有节点的
- 再计算所有的
- 再计算所有的
degree,则
最终计算复杂度为
- 首先计算所有节点的
应用
multi-head attention将存储需求和参数需求乘以head的计算是完全独立的并且可以并行化。
GCN:和GCN相比,GAT模型允许为同一个邻域内的节点分配不同的重要性,从而实现模型容量model capacity的飞跃。另外,和机器翻译领域一样,对学到的注意力权重进行分析可能会带来可解释性的好处。注意力机制以共享的方式应用于图的所有边,因此它不需要预先得到整个图结构或者所有节点(这是许多现有技术的局限性)。这有几个理想的含义:
- 图可以是有向图,也可以是无向图。如果边
GAT可以直接应用到归纳式学习inductinve learning:模型可以预测那些在训练期间中unseen的图。
- 图可以是有向图,也可以是无向图。如果边
GraphSAGE:最近发表的归纳式方法GraphSAGE对每个节点采样固定大小的邻域,从而保持计算足迹computational footprint的一致性。这使得模型无法在测试期间访问整个邻域。注意:由于训练期间训练多个
epoch,则GraphSAGE可能访问到节点的整个邻域。此外,当使用
LSTM-based邻域集合器时,GraphSAGE取得了一些最强的结果。LSTM假设在邻域之间存在一致的节点排序,并且作者通过向LSTM持续地提供随机排序的序列来使用LSTM。GAT没有这两个问题:GAT作用在完整的邻域上,并且不假设邻域内有任何节点的排序。注意:虽然
GAT作用在完整的领域上,但是在大型图的训练过程中可能还需要对邻域进行采样。因为对于大型图,对于每个mini-batchGAT有如果使用完整的邻域,那么每个
mini-batch所需要的节点可能就是整个大图。这对于大型图而言是无法接受的(空间复杂度太高)。MoNet:如前所述,GAT可以重写表述为MoNet的特定实例。更具体而言:- 设定伪坐标函数
pseudo-coordinate function为MLP变换而来), - 设定权重函数为
softmax。
此时,这种
MoNet的补丁算子patch operator将类似于我们的方法。然而,应该注意的是:与这个
MoNet实例相比,我们的模型使用节点特征来计算相似性,而不是节点的结构属性(假设预先知道图结构)。- 设定伪坐标函数
我们可以使用一种利用稀疏矩阵操作的
GAL层,它可以将空间复杂度下降到节点和边的线性复杂度,从而使得模型能够在更大的图数据集上运行。但是我们的tensor计算框架仅支持二阶tensor的稀疏矩阵乘法,这限制了当前版本的batch处理能力,特别是在具有很多图的数据集上。解决该问题是未来一个重要的方向。另外,根据现有图结构的规律,在稀疏矩阵的情况下,GPU的运算速度并不会比CPU快多少因此无法提供主要的性能优势。还应该注意的是,我们模型的感受野
receptive field的大小是网络深度的上限(类似于GCN或类似的模型)。然而,诸如skip connection之类的技术可以解决该问题,从而允许GAT使用更深的网络。最后,跨图中所有
edge的并行化,尤其是以分布式方式,可能会涉及大量冗余计算,因为图中邻域通常高度重叠。
9.1.3 未来工作
一些有待改进的点:
- 如何处理更大的
batch size。 - 如何利用注意力机制对模型的可解释性进行彻底的分析。
- 如何执行
graph-level的分类,而不仅仅是node-level的分类。 - 如何利用边的特征,而不仅仅是节点的特征。因为边可能蕴含了节点之间的关系,边的特征可能有助于解决各种各样的问题。
- 如何处理更大的
9.2 实验
9.2.1 Transductinve Learning
数据集:三个标准的引文网络数据集
Cora, Citeseer,Pubmed。每个节点表示一篇文章、边(无向)表示文章引用关系。每个节点的特征为文章的
BOW representation。每个节点有一个类别标签。Cora数据集:包含2708个节点、5429条边、7个类别,每个节点1433维特征。Citeseer数据集:包含3327个节点、4732条边、6个类别,每个节点3703维特征。Pubmed数据集:包含19717个节点、44338条边、3个类别,每个节点500维特征。
对每个数据集的每个类别,我们使用
20个带标签的节点来训练,然后在1000个测试节点上评估模型效果。我们使用额外的500个带标签节点作为验证集(与GCN论文中使用的相同)。注意:训练算法可以利用所有节点的结构信息和特征信息,但是只能利用每个类别
20个节点的标签信息。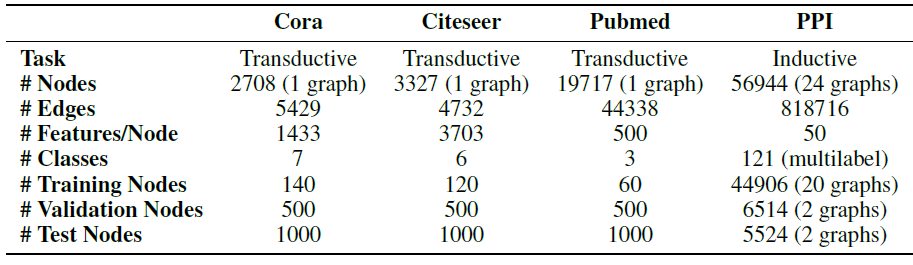
Baseline模型:- 我们对比了论文
《Semi-supervised classification with graph convolutional networks》中指定的相同的baseline。包括:标签传播模型label propagation: LP、半监督嵌入模型semi-supervised embedding: SemiEmb、流型正则化模型manifold regularization: ManiReg、基于SkipGram的graph embeding模型(如DeepWalk)、迭代式分类算法模型iterative classification algorithm: ICA,Planetoid模型。 - 我们也直接对比了
GCN模型、利用高阶切比雪夫的图卷积模型Chebyshev filter-based(《Convolutional neural networks on graphs with fast localized spectral filtering》)、以及MoNet模型。 - 我们还提供了每个节点共享
MLP分类器的性能,该模型完全没有利用图的结构信息。
- 我们对比了论文
参数配置:
我们使用一个双层的
GAT模型,它的架构超参数已经在Cora数据集上进行了优化,然后被Citeseer复用。- 第一层包含
attention head,每个head得到64个特征。第一层后面接一个exponential linear unit: ELU非线性激活层。 - 第二层用作分类,采用一个
attention head计算softmax激活函数。
- 第一层包含
当处理小数据集时,我们在模型上施加正则化:
- 我们采用
- 两个层的输入,以及
normalized attention coefficient都使用了dropout。即每轮迭代时,每个节点需要随机采样邻居(因为有些邻居被dropout了)。
- 我们采用
对于
60个样本的Pubmd数据集,我们需要对GAT架构进行微调:- 输出为
attention head,而不是一个。
除此之外都和
Cora/Citeseer的一样。- 输出为
所有模型都采用
Glorot初始化方式来初始化参数,优化目标为交叉熵,使用Adam SGD优化器来优化。初始化学习率为:Pubmed数据集为0.01,其它数据集为0.005。我们在所有任务上执行早停策略,在验证集上的交叉熵和
accuracy如果连续100个epoch没有改善,则停止训练。
我们报告了
GAT随机执行100次实验的分类准确率的均值以及标准差,也使用了GCN和Monet报告的结果。对基于切比雪夫过滤器的方法,我们提供了
我们进一步评估了
GCN模型,其隐层为64维,同时尝试使用ReLU和ELU激活函数,并记录执行100次后效果最好的那个(实验表明ReLU在所有三个数据集上都最佳),记作GCN-64*。结论:
GAT在Cora和Citeseer上超过GCN分别为1.5%, 1.6%,这表明为邻域内节点分配不同的权重是有利的。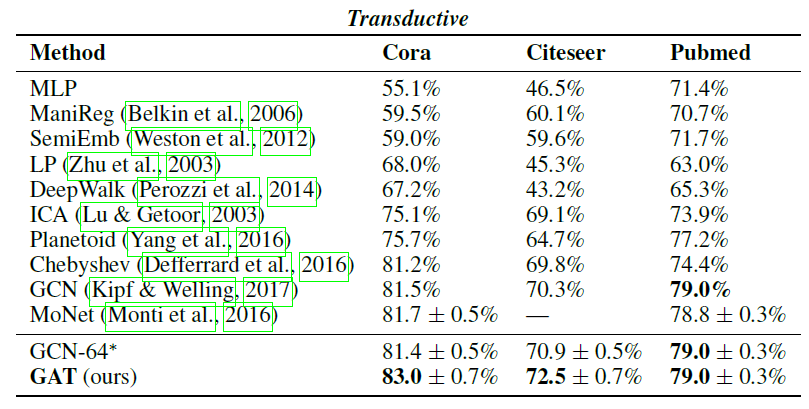
9.2.2 Inductinve learning
数据集:
protein-protein interaction: PPI数据集,该数据集包含了人体不同组织的蛋白质的24个图。其中20个图为训练集、2个图为验证集、2个图为测试集。至关重要的是,这里测试的图在训练期间完全未被观测到。我们使用
GraphSAGE提供的预处理数据来构建图,每个图的平均节点数量为2372个,每个节点50维特征,这些特征由positional gene sets, motif gene sets, immunological signatures组成。从
Molecular Signatuers Database收集到的gene ontology有121种标签,这里每个节点可能同时属于多个标签。
Baseline模型:我们对比了四个不同版本的监督GraphSAGE模型,它们提供了多种方法来聚合采样邻域内的节点特征:GraphSAGE-GCN:将图卷积方式的操作扩展到归纳式setting。GraphSAGE-mean:取特征向量的逐元素均值来聚合。GraphSAGE-LSTM:通过将邻域特征馈入LSTM来聚合。GraphSAGE-pool:采用共享非线性多层感知机转换后的特征向量的逐元素最大池化来聚合。
剩下的
transductinve方法要么完全不适用于inductive的情形,要么无法应用于在训练期间完全看不到测试图的情形,如PPI数据集。我们还提供了每个节点共享
MLP分类器的性能,该模型完全没有利用图的结构信息。参数配置:
我们使用一个三层
GAT模型:第一层包含
attention head,每个head得到1024个特征。第一层后面接一个exponential linear unit:ELU非线性激活层。第二层和第一层配置相同。
第三层为输出层,包含
attention head,每个head得到121个特征。我们对所有
head取平均,并后接一个sigmoid激活函数。
由于该任务的训练集足够大,因此我们无需执行
dropout。我们在
attention layer之间应用skip connection。训练的
batch size = 2,即每批2个graph。为评估
attention机制的效果,我们提供了一个注意力得分为常数的模型进行对比(所有模型都采用
Glorot初始化方式来初始化参数,优化目标为交叉熵,使用Adam SGD优化器来优化。初始化学习率为:Pubmed数据集为0.01,其它数据集为0.005。我们在所有任务上执行早停策略,在验证集上的交叉熵和
micro-F1如果连续100个epoch没有改善,则停止训练。
我们报告了模型在测试集(两个从未见过的
Graph)上的micro-F1得分。我们随机执行10轮 “训练--测试”,并报告这十轮的均值。对于其它基准模型,我们使用GraphSAGE报告的结果。具体而言,由于我们的setting是有监督的,我们将与有监督的GraphSAGE方法进行比较。为了评估聚合整个邻域的好处,我们进一步提供了
GraphSAGE架构的最佳结果,记作GraphSAGE*。这是通过一个三层GraphSAGE-LSTM得到的,三层维度分别为[512,512,726],最终聚合的特征为128维。最后,我们报告常数的注意力系数为
Const-GAT的结果。结论:
GAT在PPI数据集上相对于GraphSAGE的最佳效果还要提升20.5%,这表明我们的模型在inductive任务中通过观察整个邻域可以获得更大的预测能力。- 相比于
Const-GAT,我们的模型提升了3.9%,这再次证明了为不同邻居分配不同权重的重要性。
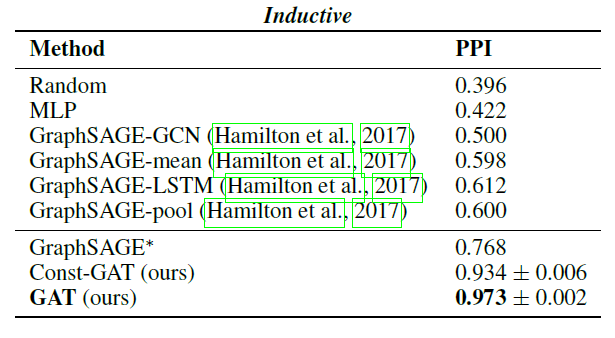
注意:这里作者并未给出超参数研究的实验分析,包括:
GAT层数、multi-head数量、是否使用skip connection等等。
9.2.3 可视化
学到的
feature representation也可以进行定性研究。为此,我们采用t-SNE对学到的特征进行可视化。我们对Cora数据集训练的GAT模型的第一层的输出进行可视化,该representation在投影到的二维空间中表现出明显的聚类。这些簇对应于数据集的七种类别,从而验证了模型的分类能力。此外我们还可视化了归一化注意力系数的相对强度(在所有
8个attention head上的均值)。如何正确的解读这些系数需要有关该数据集的进一步的领域知识。下图中:颜色表示节点类别,线条粗细代表归一化的注意力系数均值:
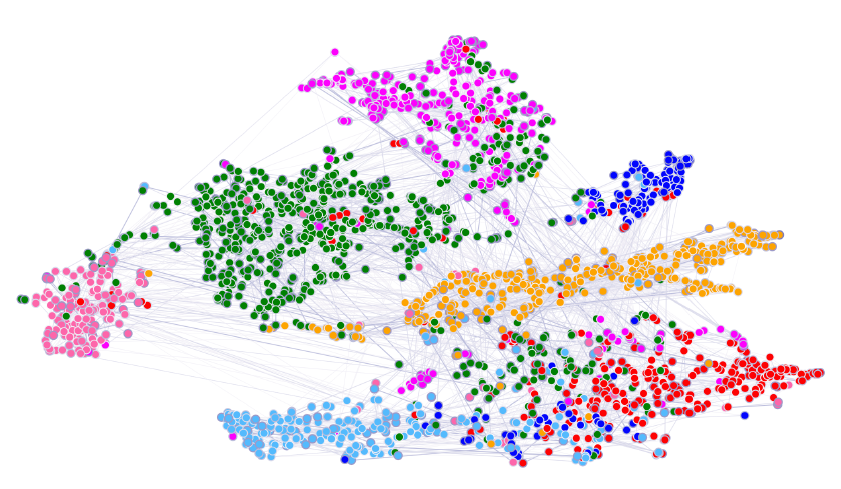
十、R-GCN[2017]
知识库
knowledge base组织和存储事实知识factual knowledge,支持包括问答question answering和信息检索在内的多种应用。尽管在维护上投入了巨大的努力,即使是最大的知识库(如DBPedia, Wikidata, Yago)仍然是不完整incomplete的, 并且覆盖度coverage的缺失会损害下游应用application。预测知识库中的缺失信息是统计关系学习statistical relational learning: SRL的主要关注点。遵从之前关于
SRL的工作,我们假设知识库存储形式为三元组(subject, predicate, object)的集合。例如,考虑三元组(Mikhail Baryshnikov, educated at, Vaganova Academy),我们将Baryshnikov和Vaganova Academy称作实体entity,将educated at称作关系relation。此外,我们假设实体标有类型(如,Vaganova Academy被标记为大学)。将知识库表示为有向的、带标签的multigraph很方便,其中实体对应于节点,而三元组被labled edge所编码。如下图所示,红色的标签以及边代表缺失信息,是需要我们推断的。。
考虑两个基本的
SRL任务:链接预测(缺失三元组missing triple的恢复recovery)、实体分类(为实体分配类型或离散属性)。在这两种情况下,许多缺失的信息都可以预期存在于通过邻域结构neighborhood structure编码的图中。例如,知道Mikhail Baryshnikov在Vaganova Academy接受教育,这同时意味着Mikhail Baryshnikov应该有标签person、以及三元组(Mikhail Baryshnikov, lived in, Russia)必须属于知识图谱knowledge graph。遵循这个直觉,论文《Modeling Relational Data with Graph Convolutional Networks》为关系图relational graph中的实体开发了一个编码器模型,并将其应用于这两个任务。论文的实体分类模型与
GCN类似,并在图中的每个节点处使用softmax分类器。分类器采用relational graph convolutional network: R-GCN提供的node representation来预测label。模型是通过优化交叉熵损失来学习的。论文的链接预测模型可以被视为一个自编码器
autoencoder,它由一个encoder和一个decoder组成,其中:encoder:一个R-GCN,它用于产生实体的latent feature representation。decoder:一个张量分解模型,它利用这些实体的representation来预测edge label。尽管原则上任何类型的因子分解模型(或者任何评分函数)都可以作为解码器,但是这里作者使用最简单、最有效的因子分解方法:DistMult。
作者观察到,论文的方法在标准
benchmark上取得了有竞争力的结果,优于直接的因子分解模型(如普通的DistMult)。当我们考虑更具挑战性的FB15k-237数据集时,这种改进尤其大。这些结果表明:在R-GCN中对邻域进行显式建模有利于恢复知识库中的missing fact。论文的贡献如下:
- 首先,据作者所知,这是第一个证明
GCN框架可以应用于建模关系数据relational data(尤其是链接预测和实体分类任务)的人。 - 其次,作者介绍了参数共享和强制稀疏约束
enforce sparsity constraint的技术,并使用它们来将R-GCN应用于具有大量关系的multigraph。 - 最后,作者展示了分解模型(以
DistMult为例)的性能可以通过使用编码器模型来显著提高,其中该编码器在关系图relational graph中执行多个信息传播step。
相关工作:
关系建模:我们用于链接预测的
encoder-decoder方法依赖于解码器中的DistMult,这是RESCAL分解的一种特殊且更简单的情况,在multi-relational knowledge base的背景下比原始的RESCAL更高效。人们在
SRL的背景下已经提出和研究了许多替代的分解模型,包括线性分解模型和非线性分解模型,其中许多方法可以被视为经典的张量分解方法(如CP或Tucker)的修改或特殊情况。对于张量分解模型的全面综述,推荐阅读论文《Tensor decompositions and applications》。合并实体之间的
path到知识库中最近受到了相当大的关注。我们可以将先前的工作分为三个方向:- 创建辅助三元组
auxiliary triple的方法,然后该方法将辅助三元组添加到分解模型的目标函数中。 - 在预测
edge时使用path(或walk)作为特征的方法。 - 同时采用这两个方法。
第一个方向在很大程度上与我们的方向正交,因为我们也预期通过向我们的损失函数中添加类似的项来改善(即,扩展我们的解码器)。
第二个方向更具有可比性,
R-GCN为这些基于path的模型提供了一种计算成本更低的替代方案。直接比较有些复杂,因为path-based方法使用不同的数据集(如,来自知识库的walk的sub-sampled子集)。- 创建辅助三元组
graph上的神经网络:我们的R-GCN编码器模型与graph上神经网络领域的许多工作密切相关。R-GCN编码器的主要动机是:对先前的GCN工作的适配,使其适用于大规模和高度multi-relational的数据(这是真实世界知识库的特点)。该领域的早期工作包括
《The graph neural network model》的GNN。人们后续对原始GNN提出了许多扩展,最值得注意的是《Gated graph sequence neural networks》和《Column networks for collective classification》,它们都利用了门控机制来促进优化过程。R-GCN可以进一步被视为消息传递神经网络(《Neural message passing for quantum chemistry》)的一个子集,基于可微的消息传递解释。其中,消息传递神经网络包含许多先前的、用于图的神经网络,包括GCN。
10.1 模型
- 定义一个有向
directed、带标签labeled的multi-graph为relation,其中
10.1.1 R-GCN
我们的模型主要受到
GCN所启发,并将基于局部图邻域local graph neighborhood的GCN扩展到大规模的关系数据。GCN相关的方法(如图神经网络)可以理解为简单的、可微的消息传递框架:其中:
incoming message的集合,它通常等于传入边incoming edge的集合(即每条边代表一条消息)。- 输入的消息按照
message-specific的、类似于神经网络的函数或者仅仅是线性变换
事实证明,这类变换非常有效地从局部的、结构化邻域中累积和编码特征,并在诸如图形分类、图半监督学习领域带来显著改进。
受此类架构的影响,我们在
relational multi-graph中定义了以下简单的消息传播模型:其中:
这里采用单个
representationproblem-specific正则化常数。它可以从数据中学习,也可以预先选择,如attention机制来学习。为了确保可以直接通过节点
skip-connection。这里
one-hot编码(不需要引入embedding layer,因为这种情况下图神经网络的第一层就是embedding layer)。
直观来看,上式累加了相邻节点的特征向量并进行归一化。与常规的
GCN不同,这里我们引入特定于具体关系edge的类型和方向。- 也可以选择更灵活的函数来替代这里简单的线性变换,如多层神经网络(但是计算代价会更高)。我们把它留待未来的工作。
- 上式在每个节点的每一层
layer执行,实践中通常采用稀疏矩阵乘法来有效实现,从而避免对邻域进行显式求和。 - 可以堆叠多个层,从而允许跨多个关系链的依赖性。
我们将这个图编码器模型称作关系图卷积网络
R-GCN,R-GCN模型中单个节点的更新计算图如下所示。红色节点为待更新的节点,蓝色节点为邻域节点。我们首先收集来自不同类型的相邻节点以及自身的消息,对每种类型的消息在变换之后归一化求和得到绿色的
representation。最后将不同类型的representation相加并通过激活函数,从而得到节点更新后的representation。可以在整个图上共享参数,从而并行地计算每个节点的更新。
整个
R-GCN模型就是堆叠大量的这种层,其中上一层的输出作为下一层的输入。如果实体没有特征,则可以将每个节点的one-hot作为第一层的输入。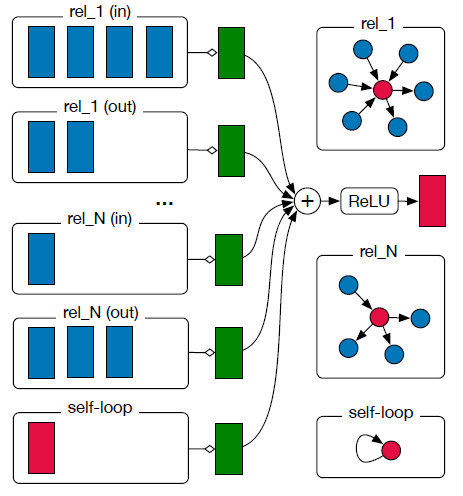
10.1.2 正则化
如果关系类型数量非常庞大,则
R-GCN模型的参数数量爆炸性增长。实际上,这很容易导致模型对稀疏关系的过拟合,并且模型非常庞大。为解决该问题,我们引入两种不同的方法来正则化
R-GCN:basis-decomposition基分解,以及block-diagonal-decomposition块对角分解。basis-decomposition:每个权重其中
这里
block-diagonal-decomposition:令其中
基分解可以视为不同关系类型之间共享权重的一种方式;块对角分解可以视为每种关系类型权重矩阵的稀疏性约束。块分解结构认为:可以将潜在特征分组,使得组内的特征相比组外的特征更为紧密地耦合。
这两种分解都减少了高度
multi-relational的数据(如知识库)所需要的参数数量。同时,我们期望基分解能够缓解稀疏关系的过拟合,因为稀疏关系和非稀疏关系共享基变换矩阵。然后,整个
R-GCN模型堆叠one-hot编码作为模型的输入。虽然我们在这项工作中仅考虑了这种无特征
featureless的方法,但是我们注意到GCN的工作表明:这类模型可以使用预定义的特征向量(如,节点的描述文本的bag-of-words)。
10.1.3 实体分类
在节点分类任务中,我们将
R-GCN最后一层(假设有softmax层。我们最小化所有标记节点的交叉熵(忽略所有未标记节点):其中:
定义好目标函数之后,我们使用随机梯度下降来训练模型。
- 虽然我们在目标函数中仅使用了标记节点,但是这并不意味着算法未使用非标记节点。因为在计算
- 此外,我们还可以在目标函数中显式添加
LINE算法之类的非监督损失,从而迫使相邻的节点具有相似的embedding。
10.1.4 链接预测
在链接预测任务中,我们的目标是给定可能的链接
普通的链接预测任务需要只需要预测二元组
为解决该问题,我们引入一个图自编码器模型,该模型由一个节点编码器和一个评分函数(解码器)组成。
- 编码器将每个实体
- 解码器根据节点的
representation来重建图的边。换句话说,它通过一个评分函数(subject, relation, object)打分:
可以在此框架下解释大多数现有的链接预测方法,但是我们工作的关键区别在于编码器。之前大多数方法直接在训练中优化每个节点
representation向量R-GCN编码器来学到整体架构如下图所示。其中:
- 图
(a)表示节点分类的R-GCN模型,每个节点具有一个损失函数。 - 图
b表示链接预测模型,包含R-GCN编码器,以及DistMult作为解码器,每条边具有一个损失函数。
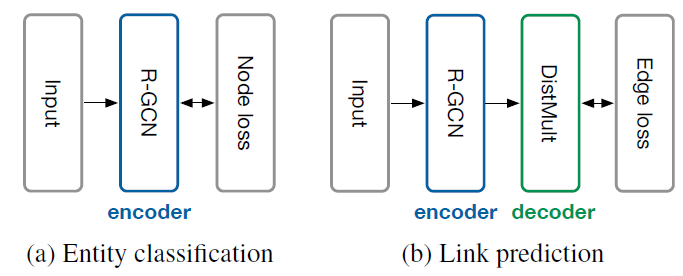
- 编码器将每个实体
在链接预测任务中,我们使用
DistMult因子分解作为解码器(评分函数),该方法独立地应用于标准链接预测baseline时表现良好。在
DistMult方法中,每个关系和之前的矩阵分解工作一样,我们使用负样本来训练模型。对于每个观察到的“正边”,我们随机采样
(subject, predicate, object),我们通过随机选择不同的subject或者不同的object来采样。我们选择交叉熵作为损失函数,目标是最大化“正边”概率、最小化“负边”概率:
其中:
10.2 实验
10.2.1 实体分类
数据集:我们评估了四个数据集,它们以
Resource Description Framework: RDF格式来描述。数据集中的关系不一定要编码为有向的subject-object关系,也可以编码为给定实体之间存在或者不存在某个指定的属性。在每个数据集中,要分类的目标是一组实体的属性。我们删除了用于创建
label的信息,如:AIFB的雇员和从属关系、MUTAG的is Mutagenic关系、BGS的hasLithogenesis关系、AM的objectCategory和material关系。数据集的统计信息见下表,其中
Labeled表示那些带标签的、用于分类的节点,它是所有节点的子集。我们采用
《A collection of benchmark datasets for systematic evaluations of machine learning on the semantic web》的benchmark训练集、测试集拆分的方式,并在训练集的基础上继续拆分20%样本作为验证集从而进行超参数调优。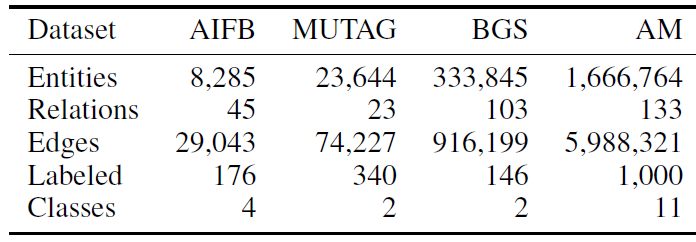
Baseline方法:我们对比了最近的state-of-the-art方法:RDF2VEC embedding、Weisfeiler-Lehman kernel: WL、人工设计的特征提取器Feat。Feat根据每个节点的入度in-degree、出度out-degree来拼接每个节点的特征向量,即feature-based方法。RDF2VEC在图上执行随机游走,然后基于SkipGram模型来从随机游走序列中学习节点embedding,然后该embedding用于下游的分类任务。
配置:
- 我们的
R-GCN模型采用两层隐层,隐层维度为16维(AM数据集的隐层维度为10),并采用基分解的正则化方式。 - 我们使用
Adam优化器训练50个epoch,学习率为0.01。 - 最后,我们选择归一化常数为
- 所有实体分类实验均在具有
64GB内存的CPU节点上运行。
- 我们的
评估指标:测试集的
accuracy。实验效果如下表所示,结论:我们的模型在
AIFB和AM上取得最好的效果,在MUTAG和BGS数据集上效果较差。为了探究
R-GCN模型为什么在MUTAG和BGS数据集上效果较差,我们深入洞察了这些数据集的性质。MUTAG是分子图的数据集,后来被转换为RDF格式,图中的关系要么表示原子键、要么表示某个属性是否存在。BGS是具有分层特征描述hierarchical feature description的岩石rock的类型,这些描述类似地转换为RDF格式,图中的关系编码了特定属性是否存在、或者属性的层级关系。
MUTAG和BGS中的标记节点仅仅通过编码了某种特征的high-degree的中心节点所连接。我们推测:采用固定的归一化常数对于degree很高的节点可能会成为问题,这导致了我们的模型在MUTAG/BGS数据集上效果不佳。克服该问题的一种潜在解决方案是:引入一种注意力机制
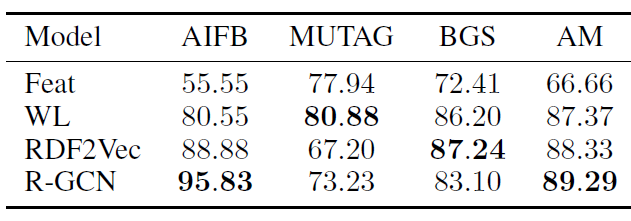
10.2.2 链接预测
数据集:链接预测任务通常在
FB15k(关系数据库Freebase的子集)和WN18(WordNet的子集)上评估。但是在《Observed versus latent features for knowledge base and text inference》中,这两个数据集都观察到严重的缺陷:训练集中的三元组LinkFeak,其效果都很大程度上优于现有的方法。LinkFeak仅仅是将观察到的关系作为特征向量(该特征向量非常稀疏)作为输入,然后采用线性分类器进行分类。为解决该问题,
《Observed versus latent features for knowledge base and text inference》提出了一个简化的数据集FB15k-237,它删除了所有这些逆三元组。因此我们选择FB15k-237作为我们的主要评估数据集。由于FB15k和WN18仍被广泛使用,因此我们也包含这些数据集的结果。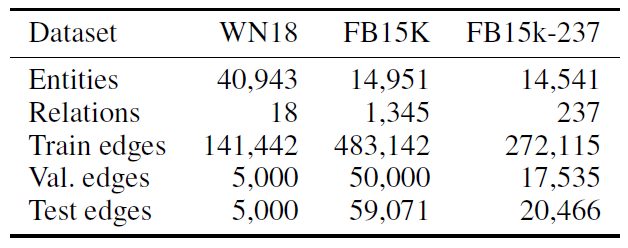
baseline方法:DistMult:对每个节点直接优化embedding,而不是R-GCN编码器。LinkFeat:《Observed versus latent features for knowledge base and text inference》提出的简单的基于邻域的方法。ComplEx:将DistMult泛化为复数域来提升对非对称关系的建模。HoIE:利用circular correlation代替了vector-matrix的乘积。
最后,我们还包含了两种经典算法的比较:
CP(《The expression of a tensor or a polyadic as a sum of products》)和TransE(《Translating embeddings for modeling multi-relational data》)。我们使用两种常用的评估指标:
mean reciprocal rank: MRR、Hits at n: H@n。我们报告了raw MRR, filtered MRR,以及n=1,3,10时的filtered Hits。filtered MRR指的是:对于排名差于n,其排名倒数置为零。配置:
我们通过验证集来选择
R-GCN的超参数。我们发现归一化常数设定为
对于
FB15k和WN18,我们使用具有两个基矩阵的基分解正则化,以及使用200维的单层编码器。对于
FB15k-237,我们发现块对角分解正则化的效果最好,block的大小为5 x 5,同时我们使用500维的两层编码器。我们对编码器执行
dropout正则化,dropout位置在normalization之前,dropout比例为:对于self-loop为0.2,对于其它边为0.4。使用dropout正则化使得我们的训练目标类似于降噪自编码器。我们对解码器执行
0.01。我们使用
Adam优化器,学习率为0.01。
对于
baseline模型,我们从《Complex embeddings for simple link prediction》中的参数(除了FB15k-237数据集上的维度)。为了使得不同方法具有可比性,我们对不同方法采用相同的负样本采样比例(如
对所有的模型,我们使用
full-batch优化。
我们给出了
FB15k数据集上,R-GCN和DistMult在不同degree上的表现。这里的degree表示三元组中subject, object节点的degree均值。在FB15k上,与R0GCN模型的设计形成对比的是,逆关系inverse relation形式的局部上下文local context将主导dominate分解的性能。可以发现:
R-GCN在上下文丰富的节点上(即degree较高)表现良好,而DistMult在上下文稀疏的节点上表现较好。我们观察到这两种模型是互补的,因此可以将这两种模型的优势结合在一起,成为一个新的模型,我们称之为R-GCN+:其中
FB15k的验证集来选择的。
我们给出不同模型在
FB15k和WN18上的表现,其中标记*的结果来自于《Complex embeddings for simple link prediction》, 标记**的结果来自于《Holographic embeddings of knowledge graphs》。R-GCN和R-GCN+均超越了DistMult。但是,和LinkFeat相比,R-GCN和R-GCN+方法均表现不佳。这突出了逆关系的贡献。有意思的是:在
FB15k上R-GCN+超越了CompIEx,尽管R-GCN并未显式建模非对称关系而CompIEx显式建模了非对称关系。这表明:将
R-GCN编码器与CompIEx的解码器相结合,可能是未来工作的一个有前景的方向。解码器的选择和编码器的选择是相互独立的,原则上可以使用任何模型作为解码器,因此可以考虑使用ComIEx作为解码器从而在R-GCN+中显式建模非对称关系。

在
FB15k-237数据集上逆关系被删除,此时LinkFeat效果非常差。而我们的R-GCN比DistMult提升29.8%,这显示了编码器模型的重要性。另外R-GCN/R-GCN+优于所有其它方法。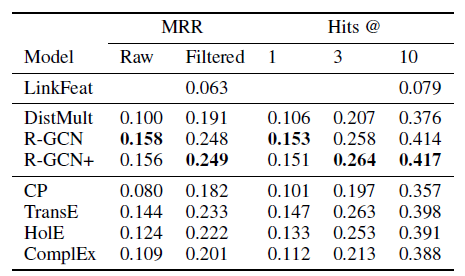
十一、 AGCN[2018]
尽管卷积神经网络
CNN在很多机器学习任务上取得极大成功,但是它要求输入数据为张量。例如,图像和视频分别建模为2-D张量和3-D张量。然而在实际任务中,很多数据都是不规则的图结构,如化学分子数据、点云数据、社交网络数据。这些数据被组织为图结构而不是规则形状的张量,并且不再满足平稳性stationarity和组合性compositionality(这两个性质允许执行grid上的kernel-based卷积),因此无法应用卷积操作。因此,有必要在图结构上重新构造卷积算子。然而将
CNN从规则的网格推广到不规则的图,并非易事。早期的
Graph CNN(《Spectral networks and locally connected networks on graphs》,《Deep convolutional networks on graphstructured data》)通常假设数据是低维的(即degree较低),因为卷积器根据节点的degree来独立地处理节点。另外,卷积核也过度局部化
over-localized,很难从复杂的图结构中学到hierarchical representation。某些情况下(如点云
point cloud的分类),图的拓扑结构要比节点特征包含更多信息。但是,现有的Graph CNN无法利用图的结构特性,因为无法设计一个匹配各种各样邻域结构的空域卷积核spatial kernel。GraphSAGE或GAT其实可以匹配各种邻域结构,因为它们是inductive的。而transductive的GCN无法匹配各种邻域结构。此外,考虑到图结构的灵活性以及模型参数规模,为数据集中每个图学习定制化
customized的、保留拓扑结构的空域卷积核是不现实的。这里我们假设数据包含很多图(比如分子图),每个图的结构都各不相同。
除了在图上进行空域卷积之外,还可以在经过傅里叶变换之后的图的频域上进行谱卷积。
类似经典的
CNN,图的谱卷积也假设样本之间(不同的图)共享卷积核。因此,为了确保卷积层输出的维度统一,卷积层的输入必须重新调整尺寸,这也是传统CNN的限制。但是,对图数据进行这种预处理可能会破坏图数据的完整性。例如,对分子图的粗化
coarsening在化学意义来看很难证明其合理性,粗化后的图很可能丢失了使得当前分子和其它分子有区分的关键子结构。如下图所示为有机化合物3, 4-亮氨酸(C7H9N)及其图结构,移除了任何一个碳原子都会破坏苯环。因此,如果
Graph CNN可以接受不同图结构的原始数据样本(而不是粗化处理的)作为输入,则非常有意义。
最后,我们提供给
Graph CNN的数据要么具有本征intrinsic的图结构(例如分子图),要么可以通过聚类来构建一个图结构(如点云数据)。在之前的
Graph CNN模型中,初始的图结构在训练过程中是固定不变的。但是,很难评估本征图或者无监督聚类产生的图是否适合于当前的任务。以化合物为例,SMILES序列给出的本征图无法说明化合物的毒性,仅靠本征图很难了解毒性的有意义的表示。尽管已有人提出了使用全连接网络的有监督的图的构建方法,但是由于训练参数规模巨大,这种方法仅适用于较小的图。另外,无法保证通过网络学到的图结构很好地作用于
Graph CNN。
因此,当前
Graph CNN的瓶颈包括:严格的graph degree限制、要求输入之间共享相同的图结构、固定构造且无需训练的图结构、无法从拓扑结构中学习。论文
《Adaptive Graph Convolutional Neural Networks》中提出了一种新的频域图卷积神经网络,该网络以原始数据的不同图结构作为输入,例如由不同数量苯环组成的有机分子。为实现这一点,作者不使用共享的谱卷积核,而是为每个图(数据集中每个样本代表一个图)定制化图拉普拉斯矩阵,这些拉普拉斯矩阵客观地描述了每个图独特的拓扑结构。一个定制化的图拉普拉斯矩阵导致一个定制化的谱滤波器,该滤波器根据图的拓扑结构来组合邻域特征。有意思的是,什么样的图结构最适合目标监督学习任务?一些图数据具有本征图结构,例如,化学键自然地生成化合物的分子图,即本征图
intrinsic graph。这些化学键已经通过化学实验被证明是正确的。但是,无法保证卷积器convolver能够提取到本征图中所有有意义的特征,因为本征图的图结构不一定和任务目标紧密相关。因此,AGCN训练了一个所谓的残差图residual graph,从而发现本征图中未能包含的残差子结构。此外,为了确保残差图是目标任务的最佳补充,作者设计了一个方案从而在训练Graph CNN的同时来学习残差图。假设训练集中有
Mahalanobis distance,则可以将学习单个图拉普拉斯矩阵的参数数量降低到metric parameter在不同样本之间共享,则数据集的参数数量也降低到在经典
CNN中,反向传播通常会更新kernel weight从而分别调整每个维度上相邻节点之间的关系。然后它聚合来自所有滤波器的信号从而构建hidden layer的activation。为了赋予Graph CNN类似的能力,作者提出使用额外变换additional transform来对feature domain进行重参数化re-parameterization。最后,卷积层中总的
distance metric,、以及节点的特征变换feature transform。给定训练好的metric、以及变换后的特征空间,我们可以构建更新后的残差图。在九个图数据集上进行的大量实验表明,
AGCN在训练速度和预测效果上都有很大的提升。论文主要贡献:
为每个样本学习图拉普拉斯矩阵:为每个样本学习残差图的拉普拉斯矩阵,并将学到的残差图的拉普拉斯矩阵添加到初始图(由本征图或聚类图给出)上。
学习度量矩阵:通过学习最佳的距离度量参数(这些参数在数据之间共享),图的拓扑结构随着训练的过程和不断更新。度量矩阵学习的算法复杂度为
这个度量矩阵用于构建残差图。
卷积中的
feature embedding:在执行图上的卷积之前,先完成节点特征的变换。灵活的输入图:由于前面的第一点和第二点,
AGCN可以接受不同结构和大小的图作为输入,并且没有图degree的限制。
相关工作:
谱图卷积
Spectral Graph Convolution:《Spectral networks and locally connected networks on graphs》首次尝试在图上应用类似CNN的方法。具体而言,空间卷积聚合了由图邻接矩阵finite-size有限尺寸的并且过度局部化。卷积层简化为类似全连接层的结构,但是使用由sparse transform matrix。空间卷积具有原生的困难:无法匹配各种各样的邻域结构。因此,如果不对图的拓扑结构加以限制,则图上的空间卷积核无法定义。谱图理论
spectral graph theory使得频域上定义卷积核成为可能。并且频域乘子multiplier的平滑性带来空间局部性spatial locality。本文的baseline方法建立在《Convolutional neural networks on graphs with fast localized spectral filtering》的基础上,并且将one-hop的local kernel扩展为带来最多K-hop connection的kernel。根据图傅里叶变换,如果graph Fourier basis,那么:其中:
《Convolutional neural networks on graphs with fast localized spectral filtering》还利用契比雪夫多项式及其近似评估方案来降低计算成本并实现局部化的滤波。《Semi-supervised classification with graph convolutional networks》展示了契比雪夫多项式的一阶近似作为graph filter spectrum,从而导致更少的训练参数。
尽管如此,人们已经开始构建更强调拓扑结构的定制化的
graph,甚至解除了对input graph的维度约束。然而,设计一个灵活的graph CNN仍然是一个悬而未决的问题。分子图
Molecular Graph上的神经网络:对有机分子化学性质的预测通常通过人工抽取特征以及feature embedding来处理。由于分子自然地被建模为图,因此人们已经成功地在原始分子上构建神经网络来学习representation。但是,由于空间卷积的局限性,这些网络无法充分利用原子的连通性connectivity(即一些原子组成的亚结构),这些连通性要比少数的化学键特征更能提供信息。最近,人们完成了对
progressive network、多任务学习、以及low-shot/one-shot学习的探索。目前为止,分子图上的state-of-the-art网络仍然使用无法充分利用空间信息的non-parameterized的spatial kernel。此外,拓扑结构可以作为有判别力
discriminative的特征的丰富来源。
11.1 模型
11.1.1 SGC-LL
为了使得谱卷积
spectral convolution能够适用于各种类型的图结构,我们对距离度量进行了参数化,使得图拉普拉斯矩阵本身是可训练的。通过训练好的度量函数,我们可以为不同形状和大小的输入图动态构建各自的动态图,并在这个动态图上执行卷积(而不是原始图上进行谱卷积)。可以学习图拉普拉斯矩阵的新的谱卷积层称作
Spectral Graph Convolution layer with graph Laplacian Learning : SGC-LL。
a. 学习图拉普拉斯矩阵
给定图
显然
node-wise连通性(由邻接矩阵degree(由由于
eigen-decomposition特征分解:其中 :
类似于欧式空间中的傅里叶变换,图上的信号
图上的一个信号定义了一个一维特征,该特征在图上每个节点都有取值。
傅里叶逆变换为:
由于图的拉普拉斯矩阵的谱为
《Spectral graph theory》表明:平滑的频域谱会产生localized局部化的空间卷积核。在
《Convolutional neural networks on graphs with fast localized spectral filtering》中定义了一个多项式卷积核:这定义了一个
多项式卷积核平滑了频谱,而参数
K的节点呈圆形分布。这种做法限制了卷积核的灵活性。更重要的是:两个节点之间的相似性不仅和距离相关,更主要的是取决于所选的距离度量函数、节点的特征。对于在非欧几何种的数据,无法保证欧式距离是衡量相似性的最佳指标。因此,两个相连的节点之间的相似性,可能会比两个未连接节点之间的相似性更低。有两个可能的原因:
- 图是在
raw feature domain原始特征领域构建的,没有经过任何特征抽取和变换,因此基于距离的相似性没有考虑特征信息。 - 图结构是
intrinsic本征的,它仅表示物理意义上的连接,如分子中的化学键,因此距离近不一定代表着相似。
- 图是在
为解决卷积核的这种限制,我们提出了一个新的谱滤波器,该滤波器对拉普拉斯矩阵
给定原始的图拉普拉斯矩阵
这个新的图拉普拉斯矩阵定义了一个新的动态图,我们在这个新的动态图上进行谱卷积。
新的滤波器为:
则对于输入信号
由于存在稠密矩阵的乘法
注意,这里的
transductive的。
b. 度量的训练
对于图结构,欧式距离不再是衡量节点相似性的很好指标。因此,距离度量在训练过程中适应目标任务、节点特征。在度量学习的论文中,算法分为监督学习和非监督学习。监督学习的最佳度量最小化监督损失,无监督学习的最佳度量最小化簇内距离(也是最大化簇间距离)。
给定节点
如果
在
AGCN中,我们选择一个对称的半正定矩阵:SGC-LL layer学习的参数。因此上式为:因此,
然后我们使用新的距离来计算高斯核:
在归一化
这个新的邻接矩阵定义了一个新的图拉普拉斯矩阵,就是前文中描述的
构建
c. 特征变换上的重参数化
在经典的
CNN中,卷积层的输出特征是来自最后一层的所有特征图的sum和,而这些特征图feature map是由独立的滤波器计算的。这意味着新特征不仅依赖于相邻节点,也依赖于其它内部节点。但是在图卷积中,为同一个图上的不同节点特征创建和训练独立的拓扑结构是不可解释的(对应于独立的滤波器)。为了构建同时包含节点内特征和节点间特征的映射,在
SGC-LL层我们引入了一个特征变换矩阵以及一个bias向量作用于层输出上:假设有
SGC-LL层,则在第SGC-LL层的计算复杂度为degree无关。在下一个
SGC-LL层,谱滤波器将建立在另一个具有不同度量的feature domain中。
d. 残差图的拉普拉斯矩阵
某些图数据具有本征的图结构,如分子。分子被建模为以原子为节点、以化学键为边的分子图。这些化学键可以通过化学实验来证明。但是,大多数数据天然地不具备图结构,因此我们必须在将图输入网络之前首先构建好图。
除了以上两种情况之外,最有可能的情况是:以无监督方式创建的图无法充分地为特定任务来表达所有有意义的拓扑结构。以化合物为例,
SMILES序列给出的本征图并不能说明化合物的毒性。仅仅依赖本征图,很难学到刻画毒性的有意义的representation。由于缺乏距离度量的先验知识,通常我们会随机初始化度量矩阵
即:原始的图拉普拉斯算子
因此,我们并不直接学习
SGC-LL层算法:输入:
- 输入节点特征
- 拉普拉斯矩阵
- 参数
- 输入节点特征
输出:输入特征
算法步骤:
根据下式计算新的邻接矩阵
将
计算残差图的拉普拉斯矩阵:
其中
计算新的图拉普拉斯矩阵:
计算卷积输出:
读者注:
从
transductive变为inductive:
GCN使用针对的参数化(并共享 ),参数的数量为 ,依赖于图大小,因此无法适用于各种不同大小的图。 - 而
SGC使用针对距离度量的马氏矩阵的参数化(并共享 ),参数的数量为 ,不依赖于图大小,因此适用于各种不同大小的图。 根据卷积公式:
,传统的 GCN主要参数化,而 SGC可以视为参数化(残差图改变了特征分解的基向量)。 我们可以把
SGC和GraphSAGE等基于消息传播机制的方法结合起来:首先,学习自适应图;然后,在自适应图上应用GraphSAGE。唯一的局限性在于:自适应图是稠密的(时间复杂度和空间复杂度都是
),因此可以采用剪枝从而使其稀疏化。
11.1.2 AGCN
我们提出的网络称为自适应图卷积网络
Adaptive Graph Convolution Network:AGCN,因为SGC-LL层能够根据数据和目标任务有效地学习自适应的图拓扑结构。除了
SGC-LL层之外,AGCN还有图最大池化层graph max pooling layer、图聚合层graph gather layer。
a. Graph Max Pooling
图最大池化层是
feature-wise的最大池化。假设节点即:池化层将
b.Graph Gather
图聚合层逐元素地将所有节点的特征向量求和,从而作为图的
graph-level representation。聚合层的输出向量用于
graph-level预测,也可以没有聚合层从而训练AGCN并将其作为vertex-level预测。
c. Bilateral Filter
在
AGCN中使用双边滤波器层bilateral filter layer用于防止过拟合。学到的残差图拉普拉斯矩阵自适应地适配训练集,但是可能会存在过拟合风险。为了缓解过拟合,我们引入修正的双边滤波器层,通过增加
SGC-LL层的输出。我们还引入了
BN层来加快训练速度。
d. Network Configure
AGCN由多个连续的layer combo组合而成,其核心为SGC-LL层。每个layer combo包含一个SGC-LL层、一个BN层、一个图最大池化层,如下图所示。每个
SGC-LL层都训练一个残差图的拉普拉斯矩阵。在随后的BN层、最大池化层中使用自适应图adaptive graph(原始图 + 残差图),直到下一个SGC-LL层。由于
SGC-LL层会转换特征,因此下一个SGC-LL层需要重新训练新的残差图。每一层都需要重新计算
input的残差图,然后在后续层中固定使用这个残差图?在通过组合层之后,我们将批量更新图结构(因为每次训练一批样本,每个样本代表一个图)。
本文中我们评估的是
graph-wise任务,因此在回归器之前还有一个graph-gather层。
对于像有机化合物这类数据,一些小的子结构对于特定的化学性质(如毒性)具有决定性作用。如:芳烃通常具有毒性,而如果氢原子被甲基取代,则毒性大大降低。
因此,如果进行图粗化或者特征平均都会损害那些信息丰富的局部结构的完整性,因此我们选择最大池化,并且不跳过卷积中的任何节点。
11.1.3 Batch 训练
图数据结构上进行卷积的最大挑战之一是难以匹配训练样本(每个样本代表一个图)的各种各样局部拓扑结构:
- 这带来设计卷积核的额外困难,因为在图上不满足核的不变性,而且节点的顺序有时也很重要
- 对于某些数据(如分子),对图进行粗化(即调整图大小)或者调整图的形状都是不合理的(破坏分子结构)
与在张量上进行经典卷积的网格数据不同,对于图上的卷积必须兼容多种拓扑结构。为此,我们提出了
SGC-LL层,它训练了自适应的图拉普拉斯矩阵,从而保留了数据的所有局部拓扑结构。我们发现在构建图结构时真正重要的是特征空间和距离度量,因此
SGC-LL层要求每个batch的样本共享相同的特征变换矩阵和距离度量。此外,训练参数的数量仅取决于特征的维度AGCN可以进行batch训练,每个batch可以包含具有不同拓扑结构和大小的原始图。注意:在训练之前需要构造原始图的拉普拉斯矩阵,这会带来额外的
RAM开销。但是我们仍然需要保留初始拉普拉斯矩阵从而更新自适应的拉普拉斯矩阵。但是,这是可以接受的,因为图拉普拉斯矩阵是稀疏的。
11.2 实验
数据集:
回归任务:
Delaney数据集:包含1144种小分子量化合物的aequeous solubility等效溶解度数据。数据集中最大的化合物包含492个原子,最小的化合物仅有3个原子。NCI数据集:包含大约2万种化合物,以及60个从药物反应到临床药理学研究的预测任务。Az-LogD数据集:来自ADME数据集的4200种化合物渗透率的logD数据。Hydration-free energy数据集:我们提供的包含642个化合物的小型数据集,用于无水合能量研究。
我们使用
5折交叉验证,并给出每个数据集中的平均RSME和标准差。分类任务:
Tox21数据集:包含12篇论文中7950种化合物及其label,用于毒性分析。但是额外的困难来自于这12项任务中缺少部分标签。对于那些缺少标签的样本,我们将其从损失函数的计算中剔除,但是仍将其保留在训练集中。ClinTox数据集:包含1451种化合物的公开数据集,用于临床病理学研究。该数据集同时包含两个任务的标签。Sider数据集:包含1392种药物及其27种不同副作用或不良反应的标签。Toxcast数据集:另一个病毒学研究数据集,包含8599个SMILES以及用于617个预测任务的标签。
对于
N-task预测,图模型将构建为具有task-specific逻辑回归输出层。点云数据:
Velodyne HDL-64E LIDAR点云数据集:包含澳大利亚悉尼的Velodyne HDL-64E LIDAR扫描的街道对象。由于对象的实际大小和形状存在很大差异,因此不同对象的点数也不同。如下图所示:
1表示自行车,有124个点;2表示卡车,有615个点;3表示行人,有78个点。
baseline方法:GraphConv:《Spectral networks and locally connected networks on graphs》使用由线性双样条插值构建的谱滤波器实现卷积。NFP:神经网络指纹Neural Fingerprint:NFP,它在空域中构建滤波器实现卷积。GCN:使用《Convolutional neural networks on graphs with fast localized spectral filtering.》提出的K阶局部化的谱卷积核来实现卷积。
我们首先来验证
SGC-LL层的效果。SGC-LL层的滤波器基于自适应图adaptive graph来构建,而自适应图由原始图加残差图residual graph组成。原始图可以是数据直接给出的本征图intrinsic graph(比如分子结构),或者是通过聚类得到的聚类图。网络以原始图作为输入,这使得AGCN能够直接读取不同结构和大小的图。由于在网络训练期间会更新距离度量以及特征变换矩阵,因此在训练期间会不断更新自适应图(原因是残差图被不断更新)。实验证明:更新后的自适应图与模型的效果密切相关。
如下图所示为化合物
C20N2O5S的节点相似度矩阵(一个28x28的矩阵,以自适应图来构建的相似度矩阵)的热力度。左图为训练之前的相似度矩阵(记作0),右图为训练了20个epoch之后的相似度矩阵。从放大的细节种我们明显发现在20个epoch之后,节点的相似性发生了显著变化。这意味着由于距离度量在训练中更新,化合物的自适应图的结构也发生了变化。
同时,平均
RMSE以及加权的L2损失函数在前20个epoch急剧下降。另外和baseline方法相比,AGCN在收敛速度、预测准确性方面都呈现压倒性优势。我们将这些提升归因于SGC-LL层的自适应图以及残差图的拉普拉斯矩阵的学习。
首先我们对比不同的模型在回归任务上的表现。可以看到:
AGCN在Delaney数据集上的RMSE降低了31%~40%,在Az-logD数据集上的RMSE降低了15%,在NCI数据集上降低了2%,在Hydration-free数据集上降低了35%。 看似来似乎当数据更为稀疏时,AGCN更为有效。
然后我们对比这些模型在多任务分类上的效果。可以看到
AGCN提升了所有数据集上的效果。对于Toxcast的617项任务,AGCN效果比SOA仍然提升了3%。
由化学式给出的分子图是化合物的本征图,这些本征图从图的结构到图的大小多种多样。
GraphConv的谱卷积核只能连接1阶邻居(通过边直接相连的邻居),因此它over-localized过于局部化。当处理分子图时这是一个问题,因为分子图的某些重要子结构无法被这种过于局部化的卷积核所覆盖。
GCN中的K阶邻域卷积核不存在过于局部化的问题,但是它假设卷积核在不同样本之间共享(每个样本代表一个分子图)。如果训练集中的样本分子共享了很多常见的子结构,如
OH(羟基)、C6H6(苯基),则这种共享效果很好(如下图所示)。如果训练集中的样本分子来自于各种类别的化合物,则它们的子结构千差万别。这时
GCN效果很差。尤其是当某些类别的样本数据不足时。这也可能是为什么
GCN在大型数据集 (如Sider)上具有和AGCN差不多的性能,但是在小型数据集(如Delaney和Clintox)上效果很差的原因。
AGCN能够以更好的方式处理分子数据。自适应图允许每个输入分子图具有不同的结构和大型,因此我们可以为AGCN提供原始数据而不会丢失任何信息。此外,
SGC-LL层针对任务目标来训练距离度量函数和其它变换参数。因此当模型收敛时,对于每层SGC-LL我们都将找到最适合的特征空间和距离度量来构建最适合的自适应图。最终学到的自适应图可能包含原始分子图中不存在的新的边。
下图为不同
Graph CNN模型的卷积比较,其中红点为卷积核的中心,橙点为卷积核的卷积范围。边的颜色代表谱卷积核的权重。- 图
(1)为2维网格上的经典3x3的CNN卷积核。 - 图
(2)为GraphConv/NFP卷积核,可以看到它过于局部化。 - 图
(3)为GCN卷积核,它时K阶局部化的,并且在所有输入图上共享。 - 图
(4)为AGCN卷积核,它也是K阶局部化的,但是它作用在自适应图上(原始图 + 残差图)。学到的残差图的边以虚线表示。
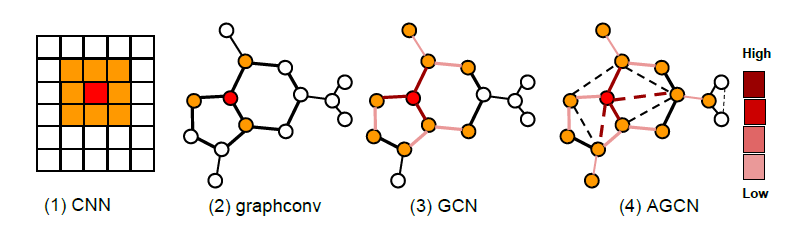
最后我们考察点云数据集上的表现。初始的点云图是通过
agglomerative聚类来构建的。- 在将点云数据馈入
Gaph CNN之前,通常需要经过降采样来统一大小,这必然会丢失部分结构信息。而AGCN通过接受不同大小的原始点云图从而克服了该问题。 - 如果使用
GCN,则GCN的卷积核在不同输入之间共享。这种共享的卷积核可能会混淆点云上的特征,而不考虑点之间的实际距离。而AGCN能够根据空间关系精确地进行卷积。 - 点云识别的
SOA方法为PointNet,但是它无法处理大小变化的点云数据。
我们采用
5折交叉验证并报告了不同模型在测试集上的平均ROC-AUC得分。可以看到,AGCN在All Classes上超越了所有其它方法。- 在大型对象(如建筑物)上,我们的
AUC得分接近1.0。其它Graph CNN模型效果较差,因为它们必须首先降采样。 - 对于重要的道路物体(如交通信号灯),
AGCN将ROC-AUC的效果提升了至少10%。
数据表明:
AGCN在点云图上可以提取比其他Graph CNN更多有意义的特征。另外,AGCN输入信息的完整性也有利于提升性能。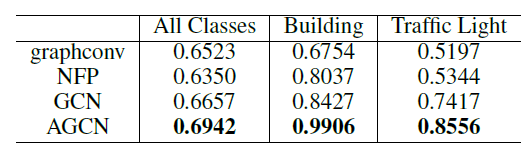
- 在将点云数据馈入
十二、FastGCN[2018]
图是
pairwise relationship的universal representation。许多现实世界的数据自然而然地以graph的形式展现,如社交网络、基因表达网络、知识图谱。为了提高graph-based学习任务的性能,最近人们努力将已有的网络架构(包括RNN和CNN)推广到graph数据。虽然学习
graph的feature representation是一个重要主题,但是这里我们重点关注节点的feature representation。在这方面,《Semi-supervised classification with graph convolutional networks》提出的GCN是最接近CNN架构的工作。借助针对图片像素的卷积滤波器的概念,或者信号的linear array的概念,GCN使用图的连通性结构connectivity structure作为滤波器进行邻域混合neighborhood mixing。该架构可以用总结为:其中:
embedding组成的embedding矩阵(按行)。
与许多图算法一样,邻接矩阵编码了训练数据和测试数据中的
pairwise relationship。模型的学习和embedding是同时在训练数据和测试数据上进行的,至少根据作者的建议而言。然而,对于许多应用程序而言,测试数据可能并不容易获得,因为图可能会不断扩展新的节点(如,社交网络的新成员、推荐系统的新产品、以及用于功能测试的新药物)。这样的场景需要一个归纳式的方案inductive scheme,该方案仅从训练数据中学习模型并且可以很好地泛化到测试数据。因为
GCN是transductive的,因此需要在训练期间就知道测试数据,并同时针对测试数据进行训练。GCN面临的一个更严峻的挑战是:跨层的邻域递归扩展会在batched training中产生昂贵的计算。尤其是对于稠密图dense graph和幂率图powerlaw graph,单个节点的邻域扩展会迅速填满图的大部分。然后,即使是一个很小的batch size,每个mini-batch训练都涉及到大量数据。因此,GCN难以推广到大型稠密图。为解决这两个挑战,
《FASTGCN: FAST LEARNING WITH GRAPH CONVOLUTIONAL NETWORKS VIA IMPORTANCE SAMPLING》从另一个角度考察图卷积,并将图卷积解释为概率测度下embedding函数的积分变换。这种观点为归纳式学习inductive learning提供了一种从损失函数的公式到梯度的随机版本的原则性的机制principled mechanism。具体来讲,论文将图节点解释为某种概率分布的独立同分布
iid样本,并将损失函数以及每个卷积层视为节点embedding函数的积分。然后通过对积分进行蒙特卡洛模拟来求解,从而得到损失函数和梯度(损失函数和梯度中包含了embedding函数的积分)。也可以进一步改变蒙特卡洛模拟中的采样分布(如,重要性采样)来减少积分近似的方差。论文所提出的方法称作
FastGCN,该方法不仅是inductive的,并且每个batch的计算成本可控。在撰写该论文时,作者注意到新发表的作品GraphSAGE,其中GraphSAGE提出使用采样来减少GCN的计算代价。相比而言,FastGCN的方法代价更低。实验表明,FastGCN的每个batch计算速度比GraphSAGE快一个量级以上,并且分类准确性相差无几。相关工作:在过去的几年中,出现了几种
graph-based的卷积网络模型,它们用于解决图结构数据的应用,如分子的representation(《Convolutional networks on graphs for learning molecular fingerprints》)。一个重要的工作方向是建立在谱图理论上的。它们受到傅里叶变换的启发,在谱域中定义了参数化的滤波器。这些方法学习整个图的
feature representation,并可用于图分类。另一个工作方向是学习
graph vertex的embedding。《Graph embedding techniques, applications, and performance: A survey》是最近的一项综述,全面涵盖了几类方法。- 一个主要的类别包括基于分解的算法,这些算法通过矩阵分解来产生
embedding。这些方法共同学习训练数据和测试数据的representation。 - 另一类方法基于随机游走,通过探索邻域来计算
node representation。LINE就是这样的一种技术,它的动机是保留一阶邻近性和二阶邻近性。 - 同时,也出现了一些深度神经网络架构,它们可以更好地捕获图中的非线性,如
SDNE。
如前所述,我们的工作是基于
GCN模型的。- 一个主要的类别包括基于分解的算法,这些算法通过矩阵分解来产生
与我们工作最相关的工作是
GraphSAGE,它通过聚合邻域信息来学习node representation。作者还承认所提出的聚合器之一采用了GCN架构。作者还承认GCN的内存瓶颈,因此提出了一种临时采样方案ad hoc sampling scheme来限制邻域大小。我们的采样方法基于一个不同的、更有原则的公式。主要区别是我们采样节点而不是邻域。
12.1 模型
GCN和许多标准神经网络架构之间的一个显著区别是:样本损失之间缺乏独立性。诸如随机梯度下降SGD以及它的batch版本等训练算法是基于损失函数相对于独立数据样本的可加性来设计的。另一方面,对于图,每个节点都与它的所有邻居进行卷积,因此定义一个计算计算高效的样本梯度非常简单。具体而言,考虑标准的随机梯度下降
SGD,其中损失函数是某个函数其中
通常数据分布
其中
iid样本。在
SGD的每一步中,梯度近似为step都会朝向着样本损失对于图,利用样本独立性并通过递归地丢弃邻域节点及其邻域信息来计算样本梯度
对于给定的图
iid样本。为解决图卷积的损失函数缺乏独立性问题,我们将卷积层定义为节点的
embedding的函数,不同节点关联了相同的概率测度,但是节点之间相互独立。注意,这里每个节点代表一个随机变量。
具体而言,考虑
GCN体系架构:从函数泛化的角度,我们改写为:
第一个积分是对邻域聚合的替代,第二个积分是对损失函数求均值的替代。
其中:
函数
embedding函数。第embedding为第embedding的卷积,并通过积分变换来公式化卷积。其中卷积核注意:积分不是通常的
Riemann–Stieltjes积分,因为随机变量embedding矩阵,每个节点占据一行。最终的损失函数是对
我们通过蒙特卡洛模拟来求解上述积分,从而得到
batch训练算法,并很自然地得到inductive learning。对于第
其中
embeding函数。最终的损失函数估计为:
原理是以蒙特卡洛模拟来执行 “期望公式 -- 积分” 之间的替代,即:“原始公式(期望视角) --> 积分 --> 新公式(期望视角)”。
要保证结果正确的核心是:大数定理。例如,样本邻域不能太稀疏,否则计算
定理:如果
1收敛到证明见原始论文,其中依赖于大数定律、连续函数理论(要求激活函数
实际应用中,给定一个图
bootstrap采样从而获得一致的估计。给定一个
batch,我们从图注意:在第
batch(注意:这里是划分,而不是采样)。我们使用节点batch的节点,因此得到batch loss:其中:
该公式可以理解为:基于采样的消息传播机制。其中,消息为
注意:这里激活函数
GCN原始的矩阵形式和我们的embedding积分形式之间的归一化差异。可以通过在每个
batch梯度,最终我们得到了batch损失以及batch梯度。理论上讲,如果跨
batch共享,那么训练速度会更快,但是效果可能会更差。论文这里选择batch之间独立地采样,即,不共享。下图给出了
GCN的两种观点。- 左图:图卷积的观点。每个圆圈表示图中的一个节点。在连续的两行上,如果图中两个节点存在连接,则对应的圆圈以灰线相连(其中部分灰线被橙线覆盖)。卷积层利用图的连接性来融合图的节点特征或者
embedding。 - 右图:积分变换的观点。下一层
embedding函数为前一层embedding函数的积分变换,用橙色扇形表示。
在
FastGCN中,所有积分(包括损失函数)都是通过蒙特卡洛模拟采样进行评估的。对应于图中,FastGCN从每一层进行有放回的节点采样从而近似卷积。采样部分由蓝色实体圆圈,以及橙线来表示。例如:- 输出层(第二层)的一个
batch包含三个节点 - 第一层有放回地随机采样三个节点,通过这三个节点来求解输出层的
embedding - 第零层有放回地随机采样三个节点,通过这三个节点来求解第一层三个节点的
embedding
每个
batch采样的节点集合(即,输出节点)不同、相同batch每一层采样的节点集合不同。
- 左图:图卷积的观点。每个圆圈表示图中的一个节点。在连续的两行上,如果图中两个节点存在连接,则对应的圆圈以灰线相连(其中部分灰线被橙线覆盖)。卷积层利用图的连接性来融合图的节点特征或者
FastGCN的batch训练算法(一个epoch):输入:
- 图
- 学习率
- 图
输出:更新后的参数
算法步骤:
迭代每个
batch,迭代过程:对每一层
对每一层
参数更新:
12.2 重要性采样
根据前文所述,
embedding函数的方差。考虑第
- 这里我们并未考虑单个函数
- 我们考虑的是非线性之前的
embedding函数embedding函数
- 这里我们并未考虑单个函数
为表述方便,我们修改某些符号。
- 对于第
- 对于第
在随机变量
- 对于第
推论:
其中:
其中向量的平方
证明见原始论文。
可以看到,
- 第一部分
- 第二部分(双重积分)取决于
当前结果是使用概率测度
importance sampling重要性采样,从而改变采样分布来减少具体而言,我们使用新的概率测度
以及新的均值:
当然,无论新的测度
- 第一部分
定理:如果:
其中
则该方差为所有可选分布
其中
证明见原始论文。
考虑
embedding矩阵作为折衷方案,我们考虑
推论:如果
证明见原始论文。
使用
实际应用过程中,我们为图中所有节点定义了概率质量函数:
其中
然后我们根据这个概率分布来采样
即,根据邻域连接强度的平方之和为概率来采样。因此,
degree较高的节点更有可能被采样。从
使用
batch损失其中:
它和前述
- 新的
- 旧的
可以通过在每个
batch梯度,最终我们得到了batch损失以及batch梯度。为什么选择这样的
- 新的
基于重要性采样的
FastGCN batch训练算法(一个epoch):输入:
- 图
- 学习率
- 图
输出:更新后的参数
算法步骤:
对每个节点
迭代每个
batch,迭代过程:对每一层
这里根据邻域连接强度的平方和作为概率,而不是均匀采样。
对每一层
参数更新:
这里虽然使用了邻接矩阵
inductive的。
12.3 讨论
inference:前述的采样方法清晰地将训练数据和测试数据分开,因此这种方法是inductive的,而不是transductive。本质是将图的节点集合转换为独立同分布的iid样本,以便学习算法可以使用损失函数的一致估计量的梯度来执行参数更新。在测试过程中,可以使用完整的
GCN架构来计算新节点的embedding,也可以使用在训练过程中通过采样来近似的方法。通常,使用完整GCN来inference更容易实现。与
GraphSAGE的比较:GraphSAGE通过聚合邻域信息来生成节点embedding。由于递归邻域扩展,它和GCN一样都存在内存瓶颈。为减少计算量,作者建议限制每一层的直接邻域大小。- 在
GraphSAGE中,如果在第 - 而在
FastGCN中,在每一层中,我们对节点进行采样,而不是对每个节点的邻居进行采样,因此涉及的节点数量为GraphSAGE。实验表明,FastGCN这种方式可以大幅度提高训练速度。
事实上
FastGCN训练算法(包括重要性采样的训练算法)并不完全遵循SGD的现有理论,因为尽管梯度的估计量是一致的,但是这个估计量是有偏的。论文证明了即使梯度估计量是有偏的,学习算法仍然是收敛的。FastGCN主要聚焦于提升邻域采样方法的效率,这种做法也可以应用到GraphSAGE等方法。方法实现很简单,但是作者这里给了理论上的说明。- 在
12.4 实验
数据集:
Cora引文数据集:数据集包含以文档(具有稀疏BOW特征向量)作为节点,文档之间的引文链接作为边。共包含2708个节点、5429条边、7个类别,每个节点1433维特征。Pubmed学术论文数据集:数据集包含以文档(具有稀疏BOW特征向量)作为节点,文档之间的引文链接作为边。共包含19717个节点、44338条边、3个类别,每个节点500维特征。Reddit数据集:包含2014年9月Reddit上发布帖子的一个大型图数据集,节点标签为帖子所属的社区。
我们调整了
Cora, Pubmed的训练集、验证集、测试集划分,从而与监督学习的场景相一致。具体而言,训练集中所有标签都用于训练,而不是半监督学习使用训练集中非常少量的标签。这种方式与GraphSage工作中使用的Reddit一致。这里没有给出平均
degree信息,读者猜测:FastGCN对于degree较小的长尾节点不利。
Baseline方法:GCN:《Semi-supervised classification with graph convolutional networks》提出的GCN方法。原始的GCN无法在非常大的图上(例如Reddit),因此我们只需要在FastGCN中移除采样即可将其修改为batch版本。如,我们在每个batch使用所有节点,而不是在每个batch中在每一层随机采样一些节点。对于较小的图(如
Cora和Pubmed),我们还将batch版本的GCN和原始GCN进行比较。GraphSAGE:为比较训练时间,我们使用GraphSAGE-GCN,它使用GCN作为聚合器,这也是所有聚合器中最快的版本。为进行准确性比较,我们还将它与
GraphSAGE-mean进行比较。
实验配置:
所有模型的学习率在
{0.01, 0.001, 0.0001}中选择。所有模型都采用两层网络(包括
FastGCN, GCN, GraphSAGE)。- 对于
GraphSAGE,这两层的邻域采样大小分别为S1=25, S2=10,隐层维度为128。 - 对于
FastGCN,Reddit数据集的隐层维度为128,其它两个数据集的隐层维度为16。
- 对于
对于
batch训练的模型(FastGCN, GCN-batch, GraphSAGE) ,Reddit, Cora数据集的batch size = 256,Pubmed数据集的batch size = 1024。GraphSAGE, GCN的代码是从原作者的网站上下载,使用原始论文的实现。FastGCN的inference是通过完整的GCN网络来完成。FastGCN使用Adam优化器。FastGCN在Cora, Pubmed, Reddit三个数据集上采样的节点数量数量分别为400, 100, 400。硬件配置:
4核2.5GHz Intel Core i7,16G Ram。
12.4.1 超参数研究
首先我们观察不同采样规模对
FastGCN的影响。下表左侧(Sampling列)给出了随着采样数量增加,对应的训练时间(单位s/epoch)、分类准确性(以F1衡量)的变化。该数据集为Pubmed数据集,batch size = 1024。为便于说明,我们将网络两层的采样数量都设为同一个值。可以看到:随着采样数量的增加,每个
epoch训练时间也会增加,但是准确性也会提高。我们观察到一个有趣的事实:在给定输入特征
我们给出预计算的结果(右侧
Precompute列),可以看到:使用预计算后,训练时间大幅降低,但是预测准确性却相当。因此后续实验我们都使用预计算。
然后我们考察
FastGCN中均匀采样和重要性采样的区别。三个图依次为Cora, Pubmed, Reddit数据集的结果。可以看到:基于重要性采样的FastGCN始终比基于均匀采样的FastGCN效果更好。我们这里使用的是折衷的重要性采样
因此,后续实验将使用重要性采样。
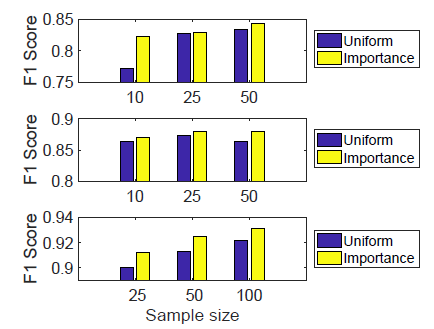
12.4.2 Baseline 比较
最后我们对比了
FastGCN和Baseline方法的训练速度和分类效果。左图以对数坐标给出了每个batch的训练时间,单位为s。注意:在训练速度比较中,
GraphSAGE指的是GraphSAGE-GCN,它和其它聚合器(如GraphSAGE-mean)是差不多的。GCN指的是GCN-batched版本,而不是GCN-original版本。GCN-original在大的图(如Reddit) 上内存溢出。可以看到:
GraphSAGE在大型和稠密的图(Reddit)上训练速度比GCN快得多,但是在小数据集上(Cora, Pubmed) 要比GCN更慢。FastGCN训练速度最快,比第二名(除Cora之外)至少提高了一个量级,比最慢的提高了大约两个量级。- 除了训练速度优势之外,
FastGCN的准确性和其它两种方法相比相差无几。
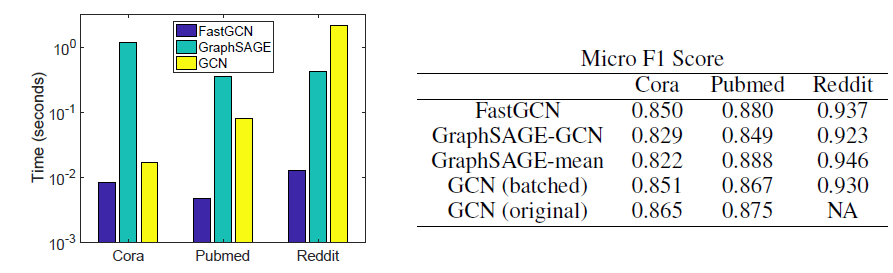
上面比较了单个
batch的训练速度。实际上总的训练时间除了受到batch训练速度的影响之外,还受到收敛性的影响(决定了需要训练多少个batch)。这里我们给出总的训练时间,单位为秒。注意:收敛性受到学习率、batch size、sample size等因素的影响。可以看到:尽管收敛速度使得
FastGCN拖慢了最终训练速度(整体训练速度的提升比例低于单个batch的提升比例),但是FastGCN整体训练速度仍然保持巨大优势。注意:即使
GCN-original的训练速度比GCN-batched更快,但是由于内存限制导致GCN-original无法扩展。因此这里我们仅比较了GCN-batched版本。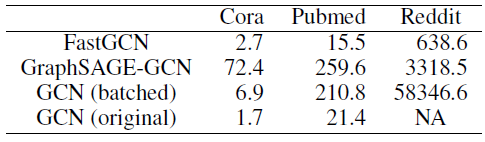
我们还给出了随着训练的进行,预测准确性的变化。下图从左到右依次为
Cora,Pubmed,Reddit数据集。
在讨论期间,
GraphSAGE的作者提供了时间优化的版本,并提醒说GraphSAGE更适合于大图。原因是:对于小图,采样大小(它等于各层样本数量的乘积)和图的大小相差无几,因此改善的程度很小。此外,采样的开销可能会对训练时间有不利影响。为公平比较,
GraphSAGE的作者保留了采样策略,但是通过消除对采样节点的冗余计算,改进了原始代码的实现。可以看到:
GraphSAGE现在在小图Cora上的训练速度快得多。注意,这种实现方式不会影响大图(Reddit) ,并且我们的FastGCN仍然比它快一个量级。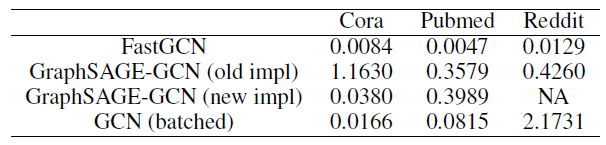
在前面评估过程中,我们增加了
Cora,Pubmed数据集中训练标签数量,从而与Reddit监督学习的训练集比例保持一致。作为参考,这里我们给出使用原始数据集拆分,从而使用更少的训练标签的结果。此外我们还给出
FastGCN的transductive版本,它同时使用训练节点、测试节点学习,这个过程中仅使用少量训练节点的标签信息(而不使用任何测试节点的标签信息)。可以看到:
GCN的结果和《Semi-supervised classification with graph convolutional networks》报告的结果一致。由于训练标记数据稀疏,GCN训练速度非常快。FastGCN仅在Pubmed数据集上超越GCN的训练速度。- 由于训练标记数据稀疏,
FastGCN的准确性也比GCN更差。 transductive版本的FastGCN和GCN的准确性相差无几,比inductive的FastGCN更好。但是其训练时间也更长(训练节点更多)。GraphSAGE的结果有些奇怪,其F1值非常低。我们怀疑模型严重过拟合,因为它的训练准确性为1.0,非常完美。- 注意到这里的
GCN-original要比前面报告给出的GCN-original更慢。这时因为我们这里使用和《Semi-supervised classification with graph convolutional networks》工作中相同的超参数,而前面给出的GCN-original使用调参之后的学习率(因为数据集拆分发生变化,所以需要调参)。
下表中的
Time单位为s/batch。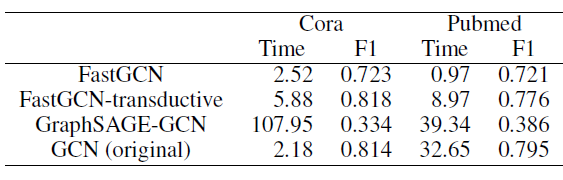
十三、PinSage[2018]
深度学习方法在推荐系统应用中发挥着越来越重要的作用,并被用于学习图像、文本、甚至单个用户的有用的低维
embedding。使用深度模型学到的representation可以用于补充甚至替代传统的推荐算法,如协同过滤。这些学到的representation具有很高的实用价值,因为它们可以在各种推荐任务中重复使用。例如,使用深度模型学到的item embedding可用于item-item推荐,也可用于被推荐主题的集合(如,playlists或者feed内容)。近年来推荐领域取得了一些重大进展,尤其是随着图结构数据上的一些新的 深度方法的研发,这对于推荐
application而言至关重要,如利用user-item交互的二部图、利用社交网络。在这些图的
deep learning方法中,最突出的就是图卷积神经网络GCN相关的deep learning架构。GCN背后的核心思想是:学习如何利用神经网络从图的local graph neighborhood局部邻域iteratively迭代地聚合节点的特征信息。一次 “卷积” 运算就可以转换和聚合节点直接邻域(直接相连的邻居)中的特征信息。并且,通过堆叠这种卷积操作,信息可以向图的更远处进行传播。和单纯的content-based深度模型(如RNN)不同,GCN会同时利用内容信息以及图结构信息。虽然基于
GCN的方法为无数推荐系统的benchmark设置了新的基准,但是benchmark上的这些任务的增益并未转换为实际生产任务的增益。主要挑战是GCN难以扩展到十亿节点、百亿边的大型图。GCN的scale非常困难,因为在大型图中违背了GCN设计过程中的诸多核心假设:- 首先,所有现有的基于
GCN的推荐系统都需要在训练过程中对完整的图拉普拉斯矩阵进行操作,当底层的图具有数十亿节点时,计算和空间复杂度太高。 - 其次,当图结构不断演变时,图的拉普拉斯矩阵发生变化,依赖于图拉普拉斯矩阵的
GCN模型无法应用。
为解决这些问题,论文
《Graph Convolutional Neural Networks for Web-Scale Recommender Systems》提出了一个叫做PinSage的highly-scalable的GCN框架,该框架是在Pinterest的生产环境中开发和部署的。PinSage框架是基于随机游走的GCN,应用在30亿节点、180亿边的大规模图上。这种规模的图比GCN的典型任务大了10000倍。PinSage利用几个关键洞察insight来显著提高GCN的可扩展性:动态卷积
On-the-fly convolution:传统的GCN算法通过将特征矩阵乘以完整的图拉普拉斯矩阵的幂来执行图卷积。相反,PinSage算法通过对节点周围的邻域进行采样,并从该采样的邻域中动态构建计算图来执行高效的局部卷积localized convolution。类似于
GraphSAGE的思想。这些动态构造的计算图指定了如何对特定节点执行局部卷积,从而缓解了训练期间对整个图进行操作的需求。
注意:这里的计算图是原图的子图,而不是
tensorflow的计算图。“生产者--消费者”
mini-batch构建:PinSage设计了一种 “ 生产者--消费者” 体系结构来构建mini-batch,从而确保模型训练期间最大限度地利用GPU。- 生产者:一个基于
CPU的、超大内存的生产者高效地对节点的邻域进行采样来动态生成计算图,然后提取局部卷积需要的特征。 - 消费者:一个基于
GPU的消费者(tensorflow模型)使用生产者动态生成的计算图以及节点特征,从而有效地执行随机梯度下降。
- 生产者:一个基于
高效的
MapReduce推断:给定一个训练好的GCN模型,PinSage设计了一种高效的MapReduce pipeline,它可以利用训练好的模型来为十亿级节点生成embedding,并最大程度地减少重复计算。这意味着
item embedding是离线计算的,而不是online学习的。
除了可扩展性这方面的提升之外,作者还使用了新的训练技术以及创新算法从而提高了
PinSage模型的效果,从而在下游推荐任务中显著提升了性能:基于随机游走的卷积:对节点的整个邻域进行卷积会产生巨大的计算图,因此
PinSage求助于邻域采样。但是随机采样的结果是次优的suboptimal,因此PinSage开发了一种基于short random walk采样来生成动态计算图。基于随机游走的卷积的另一个好处是:随机游走过程为每个邻域节点分配了一个
importance score,这个得分可以稍后应用于池化pooling层。重要性池化
importance pooling:图卷积的一个核心component是对局部邻域特征信息的聚合,即池化pooling。PinSage通过随机游走来对邻域节点进行加权,从而引入基于重要性的池化。该策略使得离线效果评估指标提升46%。attention-based聚合也是一种重要性池化方法。curriculum training:PinSage设计了一个curriculum训练方案,该方案在训练过程中向算法不断提供越来越难区分的样本。该策略使得模型性能提高12%。
目前
PinSage已经部署在Pinterest上用于各种推荐任务。Pinterest是一个流行的内容发现和管理的web服务,它为用户提供大量的pin(在线内容可视化的标签,如用户想要烹饪的食谱、用户想要购买的衣服)。用户可以和这些pin进行互动,如将这些pin保存到board中。每个board包含用户认为主题相关的一组pin,如都是食谱主题或者运动主题。总之Pinterest是世界上最大的用户精选user-curated的图,包含超过20亿去重的pin、以及10亿个board。通过离线指标评估、用户调研评估、以及在线
A/B test,论文证明了 相比其它scalable的content-based深度学习推荐算法,PinSage在item推荐任务中和homefeed推荐任务中取得了state-of-the-art性能:- 在离线的
ranking指标中,PinSage比表现最好的baseline提高了40%以上。 - 在
head-to-head的人工评估中,PinSage的推荐在大约60%的时间里更受欢迎。 - 在
A/B test中,在各种setting下,用户互动提高了30%到100%。
据作者所知,这时迄今为止
deep graph embedding最大的应用,这为基于图卷积神经网络的新一代web-scale推荐系统指明了方向。这是一篇典型的工业界的论文,这类论文的一个重要问题是:效果没办法复现。一方面,其它研究者无法获完整的数据;另一方面,算法的训练和部署要求工业级的基础设施;第三,算法和业务强烈耦合。
- 首先,所有现有的基于
相关工作:我们的工作建立在图结构数据深度学习方法的一些最新进展之上。
《A new model for learning in graph domains》首先概述了用于图数据的神经网络的概念,而《The graph neural network model》做了进一步的阐述。然而,这些在图上进行深度学习的初始方法需要运行昂贵的message-passing算法来收敛,并且在大型图上过于昂贵。《Gated graph sequenceneural networks》提出的Gated Graph Sequence Neural Network: GGSNN解决了一些局限性,它采用了现代循环神经架构,但是计算成本仍然很高,并且主要用于小于1万个节点的图。最近,人们提出了很多的、依赖于
GCN概念的方法。这些方法起源于《Spectral networks and locally connected networks on graphs》,该论文提出了一个基于谱图理论spectral graph thery的图卷积版本。遵从这项工作,许多作者提出了对谱卷积的改进、扩展、以及近似,从而在节点分类、链接预测、以及推荐系统任务等benchmark上产生了新的state-of-the-art结果。这些方法一直优于基于矩阵分解或基于随机游走的技术(如,node2vec和DeepWalk)。并且,由于这些方法的成功,因此吸引了人们对将GCN-based方法应用到从推荐系统到药物设计的应用的兴趣。《Representation Learning on Graphs: Methods and Applications》和《Geometric deep learning: Going beyond euclidean data》对最近的进展进行了全面的综述。然而,尽管
GCN算法取得了成功,但是以前没有任何工作能够将它们应用到具有数十亿节点和边的大型图数据。一个局限性是,传统的GCN方法需要在训练期间对整个图拉普拉斯算子进行操作。这里,我们填补了这一空白,并表明GCN可以扩展从而在涉及数十亿节点的production-scale的推荐系统setting中运行。我们的工作还展示了GCN在现实环境中对推荐性能的重大影响。在算法设计方面,我们的工作和
GraphSAGE以及FastGCN密切相关。GraphSAGE是GCN的inductive变体,从而避免在整个图拉普拉斯矩阵上进行操作。我们通过使用高效的随机游走来采样节点的邻域子图,从而消除了将整个图存储到GPU内存中的限制,从而从根本上改进了GraphSAGE。我们还引入了许多新的训练技术来提高性能,并引入MapReduce pipelie来扩展到数十亿节点的inference。最后,经典的
graph embedding方法(如node2vec, DeepWalk)无法应用到此处。- 首先这些方法是无监督方法,而
Pinterest包含大量的监督信息(用户保存了哪些pin是监督信息) - 其次,这些方法无法使用节点特征信息,如
pin的视觉特征、文本特征。 - 最后,这些方法直接学习节点的
embedding,因此模型参数规模和图的规模呈线性关系,这对于Pinterest是过于昂贵的。
还有,这些方法是
transductive的,因此无法应用到unseen的item。- 首先这些方法是无监督方法,而
13.1 模型
Pinterest的graph包含20亿个去重的pin、10亿个board,以及180亿条边。每条边包含一个pin节点、一个board节点。我们的任务是生成可用于推荐的高质量embedding。我们将
Pinterest建模为一个二部图pin集合为board集合为每个
pinpin的元数据(如degree)或者内容信息(如视觉特征或文本特征)。这里我们将pin与富文本和图像特征相关联。我们的目标是利用这些输入属性以及二部图的结构来生成高质量的
embedding。这些embedding然后通过最近邻查找用于推荐候选item的生成(召回阶段),或者作为机器学习系统中的特征来对候选item进行排名(排序阶段)。
13.1.1 模型架构
- 我们使用局部卷积模块为节点生成
embedding。我们从输入节点特征开始,然后学习神经网络,该神经网络在图上转换和聚合特征从而计算node embedding。
a. 前向传播算法
我们考虑为节点
embeddingPinSage的关键是局部图卷积localized graph convolution。为了生成
node embedding,我们应用了多个卷积模块(即,局部图卷积模块),这些模块从节点的局部图邻域来聚合特征信息(如,视觉特征、文本特征)。每个模块都学习如何从一个小的图邻域来聚合信息,并且通过堆叠多个这样的模块,我们的方法可以获得有关局部网络拓扑的信息。更重要的是,这些局部图卷积的参数在所有节点之间共享,使得我们方法的参数复杂度和输入图的规模无关。
局部图卷积操作
localized convolution operation的基本思想是:- 通过全连接层对
representation - 然后对变换的结果应用池化函数
vector representation - 最后将节点
representationrepresentationPinSage效果的显著提升。
此外,可以通过对结果进行归一化从而使得训练过程更为稳定,并且归一化的
embedding执行近似的最近邻搜索approximate nearest neighbor search更为有效 。- 通过全连接层对
PinSage局部图卷积算法convolve:输入:
- 节点
embedding - 节点
embedding集合 - 节点
- 池化函数
- 节点
输出:节点
embedding算法步骤:
计算局部邻域
计算节点
embedding:其中
@表示常规矩阵乘法。执行归一化:
返回节点
embedding
b. Importance-based 邻域
我们方法的一项重要创新是如何定义节点
GCN方法仅检查k阶邻域,而PinSage定义了基于重要性的邻域:节点具体而言,我们模拟从节点
这种基于重要性的邻域具有两个优点:
首先,选择固定数量的邻域节点进行聚合,使得我们在训练过程中可以控制内存消耗。
其次,它允许局部卷积算法在聚合邻域向量时考虑不同邻居节点的重要性。
具体而言,我们将
importance pooling。
c. 堆叠卷积
每次我们应用局部图卷积操作时,我们都会得到节点的一个新的
representation。我们可以堆叠多层局部图卷积,从而得到节点representation就是节点的输入特征向量。注意:前述局部卷积算法中的模型参数
PinSage mini-batch前向传播算法:输入:
mini-batch节点集合- 卷积堆叠层数
- 邻域函数
输出:节点的
embedding算法步骤:
采样
mini-batch节点的邻域:初始化:
迭代:
- 合并
生成节点
embedding:初始化第零层的
representation:迭代:
对
- 获取节点
representation集合: - 计算卷积输出:
- 获取节点
通过全连接层计算最终
embedding:对每个节点
在
PinSage mini-batch前向传播算法中,算法首先计算每个节点的各层邻域,然后应用representation。最后将最终卷积层的输出馈入到全连接层,从而得到final embedding- 模型需要学习的参数是每层卷积层的权重和偏置
- 局部邻域
embeddingembedding维度也是
- 模型需要学习的参数是每层卷积层的权重和偏置
PinSage整体结构如下图所示:左图:一个小尺寸输入图的示例。
右图:一个两层卷积层的
PinSage用于计算节点A的embedding。底图:一个两层卷积层的
PinSage用于计算所有节点的embedding。尽管每个节点的计算图都不同,但是它们都共享相同的网络参数(即
其中,具有阴影图案的阴影框共享相同的参数;
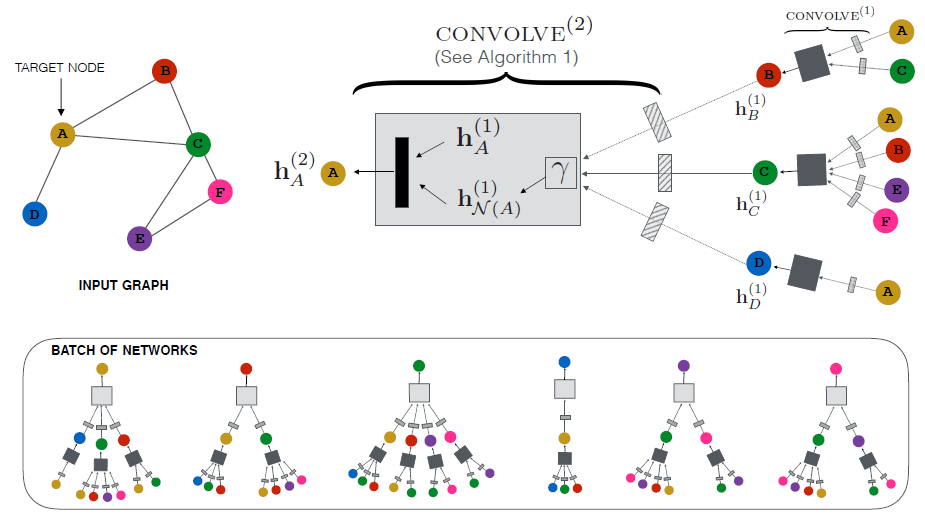
13.1.2 模型训练
我们首先详细描述我们的
margin-based损失函数。然后我们概述了我们开发的几种技术,这些技术可以提高PinSage的计算效率和收敛速度,使得我们能够在十亿级节点的图以及数十亿个训练样本上进行训练。最后,我们描述了我们的课程学习方案curriculum-training scheme,该方案提高了整体的推荐质量。损失函数:我们使用
max-margin ranking损失函数来以监督学习的方式来训练PinSage。我们根据用户历史行为数据来构造样本。每个样本都由一组pin pair对query pin:- 如果
label为1,表示正样本。postive pin。 - 如果
label为0,表示负样本。negative pin。
如果用户对
pinpinmax-margin ranking损失函数的基本思想是:希望最大化正样本的embedding内积、并且确保负样本embedding的内积比正样本embedding内积少一个预定义的margin。因此,给定一个正样本的pin pair对其中:
margin,它是一个正的超参数。query pin
注意:在目标函数中我们仅考虑
pin节点(因为label是定义在pin节点上的),不考虑board节点。但是在PinSage的模型中,我们考虑所有类型的节点(包括pin和board)。- 如果
大型
mini-batch的多GPU训练:为了在单台机器上充分利用多GPU进行训练,我们以multi-tower的方式(multi-tower是tensorflow利用多GPU训练的一种模式,默认情况下tensorflow使用单个GPU训练)进行前向传播和反向传播。对于多
GPU,我们首先将每个mini-batch划分为相等大小的部分,然后每个GPU使用mini-batch的一部分进行计算(即数据并行)。每个GPU使用相同的一组参数进行数据并行。在反向传播阶段,所有GPU上各个参数的梯度会汇聚在一起,并在每个迭代步执行同步SGD。由于需要训练数十亿样本,因此我们采用了较大的batch size,从512到4096。为处理较大的
batch size,我们使用类似于《Accurate, Large Minibatch SGD: Training ImageNet in 1Hour》等人提出的gradual warmup procedure技术,从而确保在保持准确性的条件下实现快速收敛:学习率从一个较小的值逐渐线性增加到峰值,然后指数下降。为什么要
warm up?因为刚开始训练时模型的权重是随机初始化的,此时如果选择一个较大的学习率可能带来模型的不稳定(震荡)。选择warm up预热学习率的方式,可以使得开始训练的前几个epoch或者step内的学习率较小,模型因此可以慢慢趋于稳定。等模型稳定之后再使用预先设置的学习率进行训练,使得模型收敛速度更快,模型效果更佳。上述这种
warm up是constant warm up,不足之处在于:从一个很小的学习率突然变为较大的学习率可能会导致训练误差突然增加。于是18年Facebook提出了gradual warmup来解决这个问题,即学习率从一个较小的值逐渐增加到峰值,然后指数下降。“生产者 -- 消费者”
mini-batch构建:在训练期间,数十亿个节点的邻接表以及特征矩阵的规模太大,因此只能被放在CPU内存中。但是在PinSage卷积过程中,每个GPU进程都需要访问节点邻域,以及邻域中节点的特征信息。从
GPU访问CPU内存中的数据的效率不高,为解决该问题我们使用re-indexing技术来重建一个子图mini-batch节点(及其邻域节点)。另外我们还提取了当前mini-batch计算相关节点的特征,重建了一个较小的特征矩阵,矩阵的顺序和mini-batch迭代开始的时候都被馈送到GPU中,因此在卷积过程中不再需要GPU和CPU之间进行通信,从而大幅提升了GPU的利用率。训练过程交替使用
CPU和GPU:模型运算在GPU中进行;特征提取、reindexing、负采样可以在CPU中进行。另外我们通过tensorflow的multi-tower模式来并行化GPU计算,通过OpenMP来并行化CPU计算。最后我们还设计了一个 “生产者 -- 消费者” 模式:当
GPU在计算当前迭代的运算时,CPU同时在计算下一轮迭代需要的特征提取、reindexing、负采样等等。该策略使得PinSage训练时间进一步降低近一半。负样本采样:为提高较大
batch size的训练效率,对于mini-batch中的每个正样本500个负样本从而在所有正样本之间共享负样本。和每个节点独立地负采样相比,这种共享负样本的方式可以大大节省每个训练
step需要计算的embedding数量。从经验上讲,我们并未观察到这两种方式之间的性能差异。最简单的负采样方式是均匀采样,但是这种方式采样的负样本过于简单,无法为模型提供足够区分度的负样本。考虑到我们有
20亿个去重的pin,我们的推荐算法需要在20亿个pin中推荐1000个和query pinpin,即在200万个pin中识别出1个pin,即模型分辨率为1/200万。但是,如果是500个随机负样本(以及一个正样本),则模型的分辨率resolution仅为1/501。因此,如果我们从20亿个pin中随机抽取500个负样本,则这些负样本与mini-batch中任何一个query pin相关的可能性都非常小。即:这些负样本都过于简单,没有足够的区分度。为解决上述问题,对于每个正样本
hard负样本,如和query pinpostive pinpin集合,我们称之为hard negative pin。这些hard negative pin是根据针对query pinPersonalized PageRank得分进行排序,然后挑选排序在2000 - 5000的pin被随机采样为hard negative pin的。Personalized PageRank用于计算所有节点相对于out degree均匀分布。这样经过多轮游走之后,每个节点被访问的概率趋于稳定。Personalized PageRank和常规PageRank区别在于:前者在重新游走(即,重启)时总是从节点1、其它节点初始化化为0,后者均匀初始化。如下图所示,相比随机负样本,
hard negative pin和query pin更相似,因此对模型的ranking能力提出了挑战,从而迫使模型学会更精细化地区分不同的pin。hard负样本没有选择最相关的(排序在top 2000的pin)。
课程学习方案:一旦使用
hard negative pin,则训练收敛需要的epoch会翻倍。为加快训练的收敛速度,我们制定了课程学习方案:在训练的第一个
epoch,我们不使用任何hard negative pin,因此算法可以快速找到参数空间中损失函数相对较小的区域。在随后的训练
epoch中,我们逐渐添加更多的hard negative pin,迫使模型学习如何区分高度相关的postive pin和稍微相关的negtive pin。在训练的第
epoch,我们对每个query pinhard negative pin。
学习过程由易到难。
13.1.3 MapReduce Pipeline
利用训练好的模型为所有
pin(包括训练期间未见过的pin)生成embedding仍然是一项挑战。直接应用PinSage mini-batch前向传播算法 会导致大量的重复计算,因为mini batch中的各个节点的邻域会相互重叠。当为不同目标节点生成embedding时,会在很多层重复计算很多节点,如下图所示。
为了进行高效的
inference,我们开发了一种MapReduce方法,该方法无需重复计算即可执行model inference。node embedding的inference非常适合MapReduce计算模型,下图给出了pin-board二部图上embedding inference的数据流。第零层为输入层,这一层的节点为
pin节点;第一层节点为board节点。MapReduce pipeline包含两个关键部分:- 一个
MapReduce作业将所有pin投影到低维embedding空间。 - 另一个
MapReduce作业通过将board内的pin的embedding进行池化,得到board的embedding。
我们的方法避免了冗余计算,并且每个节点的潜在
embedding仅计算一次。在获得了
board embedding之后,我们采用上述类似的方式,使用另外两个MapReduce作业来计算pin的第二层embedding,并持续迭代最多
- 一个
13.1.4 高效的最近邻检索
PinSage生成的embedding可用于下游推荐任务。在许多场景中我们可以通过在学到的embedding空间中执行最近邻检索来提供推荐。即:给定query pinembedding空间中检索pin作为推荐列表。- 可以通过
locality sensitive hashing:lsh来高效地获得近似的kNN(Approximate KNN) 。如果PinSage模型是离线训练好的,并且所有node embedding都是通过MapReduce pipeline计算并保存到数据库中,则approximate KNN可以使得系统在线提供推荐服务。
13.2 实验
为证明
PinSage的效率和效果,我们对整个Pinterest Graph进行了全面的实验,包括离线实验、在线A/B test、用户调研user study。我们评估了两个任务:
相关
pin的推荐related-pin recommendation:选择query pin最近邻的我们使用离线
ranking指标,以及用户调研来评估推荐的效果。首页
feeds流的推荐:选择用最近互动的pin的最近邻的我们使用在线
A/B test来评估PinSage部署在生产系统上的效果。
数据集:我们通过
Pinterest用户历史行为数据来构建训练数据集。如果用户与pinpinpin pair对总而言之,我们构建了
12亿个正样本。此外,我们为每个mini-batch负采样了500个共享的负样本,以及每个query pin进行hard负采样了6个hard negative pin。最终我们一共得到了75亿个训练样本。考虑到
PinSage是inductive learning,因此我们仅在Pinterest的一个子图上进行训练,然后使用MapReduce pipeline为整个图生成embedding。我们从整个
PinSage图中随机采样一个子图作为训练集,它包含20%的board节点(以及这些board包含的所有pin节点),并且包含子图中70%的正样本。我们将子图中剩余的10%正样本作为验证集进行超参数调优;并将子图中剩余的20%正样本作为测试集,用于推荐效果的离线评估。注意:在测试期间我们对整个
PinSage图进行inference从而计算所有20亿个pin的embedding。而验证期间,我们只考虑训练集中出现的节点。使用整个图的子集来训练可以大大降低训练时间,而对最终的效果影响几乎可以忽略不计。总体而言,用于训练和验证的数据集大小约为
18TB,而完整的输出embedding为4TB。节点特征:
Pinterest的每个pin都和一副图片以及一组文本(标题、描述)相关联。对于每个pinembedding(4096维)、文本embedding(256维)、pin的log degree拼接起来作为- 视觉
embedding:使用VGG-16架构的的图像分类网络的第6层全连接层的输出。 - 文本
embedding:使用word2vec-based模型训练的文本embedding,其中上下文为每个pin关联的其它文本(如标题、描述性文字)。
视觉
embedding和文本embedding由已在Pinterest上部署的state-of-the-art deep learning content-based系统生成。- 视觉
baseline方法:包括content-based方法、graph-based方法以及deep learning based方法。content-based方法:Visual:基于视觉embedding最近邻检索的推荐。Annotation:基于文本embedding最近邻检索的推荐。Combined:拼接视觉embedding和文本embedding,然后使用两层的全连接层来得到一个同时捕获了视觉特征和文本特征的embedding。最后基于这个新的embedding最近邻检索的推荐。
graph based方法:Pixie:使用有偏的随机游走,通过模拟从query pinranking score。然后将排名最高的pin作为推荐列表。尽管这种方法不会产生
pin embedding,但是对某些推荐任务来讲它是Pinterest上的state-of-the-art技术,因此是一种很好的baseline。
deep learning based方法:因为Pinterest规模太大,因此我们并未与任何deep learning based方法进行比较。
我们也未考虑其它生成
pin embedding的非深度学习方法,因为其它工作已经证明了在推荐任务中生成embedding的深度学习方法是state-of-the-art的。最后我们评估了
PinSage的几种变体从而进行消融研究:max-pooling:使用最大池化hard negative pin。mean-pooling:使用均值池化hard negative pin。mean-pooling-xent:使用均值池化hard negative pin,且使用交叉熵损失函数。mean-pooling-hard:使用均值池化hard negative pin。PinSage:使用本文中介绍的所有优化,包括在卷积过程中使用重要性池化。
最大池化和交叉熵的
setting是GraphSAGE的GCN模型的最佳扩展。其它变体在测试中效果更差,因此这里不再讨论。所有的
Pinsage及其变体使用emebddingembedding维度硬件配置:
PinSage采用tensorflow实现,并在单台机器上训练,机器配置为32 core,16个Tesla K80 GPU。为确保快速获取
pin的视觉特征和文本特征,我们将视觉特征、文本特征和Graph一起放到内存中,并使用Linux HugePages将虚拟内存页的大小从4KB增加到2MB。训练过程中使用的内存总量为500GB。在
inference阶段的MapReduce pipeline运行在Amazon AWS hadoop2集群上,集群配置为378个d2.8 x large节点。
13.2.1 离线评估
评估指标:
Hit Rate: HR:为评估related-pin推荐任务,我们定义了命中率hit-rate的概念。对于测试集中的每个正样本query pin,然后从采样的500万个测试pin中挑选出top K个最近邻的pin集合query pinhit了。总的命中的
query pin占所有query pin的比例为命中率。该指标衡量了推荐列表中包含query pin相关的pin的可能性。在我们的实验中,我们选择Mean Reciprocal Rank: MRR:除了命中率之外,我们还评估了均值倒数排名MRR指标,该指标考虑了query pinpin其中:
postive pinquery pin
由于有大量的候选
pin(约20亿),因此我们对排名进行缩小,缩小比例为100倍。这是为了确保排名在1000和2000之间的候选pin的差异仍然很明显。
不同模型在
related-pin推荐任务中的效果如下表所示。可以看到:PinSage达到了最佳的67%命中率,以及0.59的MRR。在命中率的绝对值上超越了baseline 40%(相对值150%),在MRR的绝对值上超越了baseline 22%(相对值60%)。- 将视觉信息和文本信息组合起来,要比单独使用任何一种信息都要好得多。
Combined方法比单独的Visual或者Annotation改进了60%(相对值)。
这里对比的
baseline太弱了,没有和经典推荐模型(如基于矩阵分解的模型)进行对比,也没有和深度推荐模型(如Wide & Deep)进行对比,因此不知道GCN-based推荐模型和其它推荐模型之间的差异如何。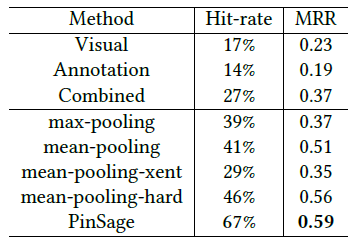
embedding similarity分布:学到的embedding的另一个有效性指标是embedding随机pair对的距离的分布是否广泛。如果所有pin的距离大致相同(即,距离上紧密聚集),则embedding空间没有足够的分辨率来区分不同相关性的pin。下图给出了使用视觉
embedding、文本embedding、PinSage embedding绘制的随机pin pair对之间距离的分布,距离采用embedding的余弦相似度。可以看到:
PinSage具有最广泛的分布,这证明了Pinsage embedding的有效性。尤其是PinSage embedding随机pin pair距离分布的kurtosis峰度为0.43,而文本embedding峰度为2.49、视觉embedding峰度为1.20。随机变量
PinSage embedding随机pin pair距离分布具有这种广泛分布的另一个优点是:它降低了后续LSH算法的冲突概率,从而提高了推荐期间检索最近邻pin的效率。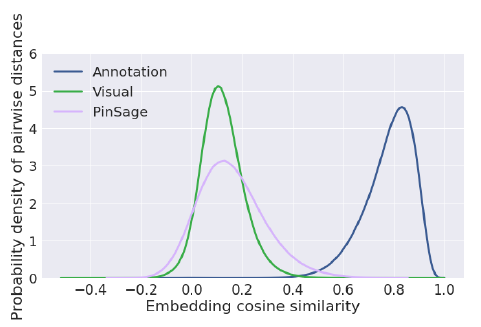
13.2.2 用户调研
我们还通过对不同方法学到的
embedding进行head-to-head比较来研究PinSage的有效性。在用户研究中,我们向用户展示
query pin的图片,以及通过两种不同推荐算法检索到的两个pin。然后要求用户选择两个候选的pin中哪个和query pin更相关。用户可以考虑各种的相关性,如视觉外观、图像的类别(比如动物、植物等等)、各自的标识等等。如果两个候选的pin看起来都相关,则用户可以选择equal。在同一个query pin问题上,如果有2/3的用户没有达成共识,则我们认为结果是不确定的。最终
PinSage和baseline方法之间的head-to-head对比结果如下。最终PinSage的推荐结果平均超越了baseline大约60%(相对值)。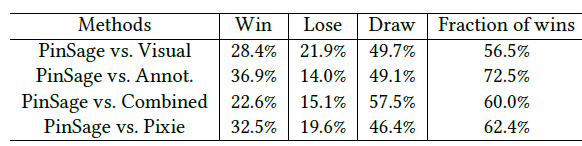
给定一些
query pin,我们给出了不同推荐的一些典型case,如下图所示。左图代表query pin,右图代表不同方法得到的embedding检索的最相似的top 3 pin。 可以看到:基于视觉
embedding通常可以很好地预测pin的类别和pin的视觉相似性,但是它们有时在图像语义方面会犯错。如下图中,由于具有相似的图像样式和外观,因此基于视觉的
embedding混淆了 “植物” 和 “食物“、”砍伐树木“ 和 ”战争“。基于图的
Pixie方法利用了pin-to-board的图关系,正确地识别了query为plant的类别,并推荐了该类别中的pin。但是,该方法找不到最相关的pin。结合了视觉信息、文本信息以及图结构,
PinSage能够找到在视觉、文本以及拓扑结构都和给定query更相似的pin。
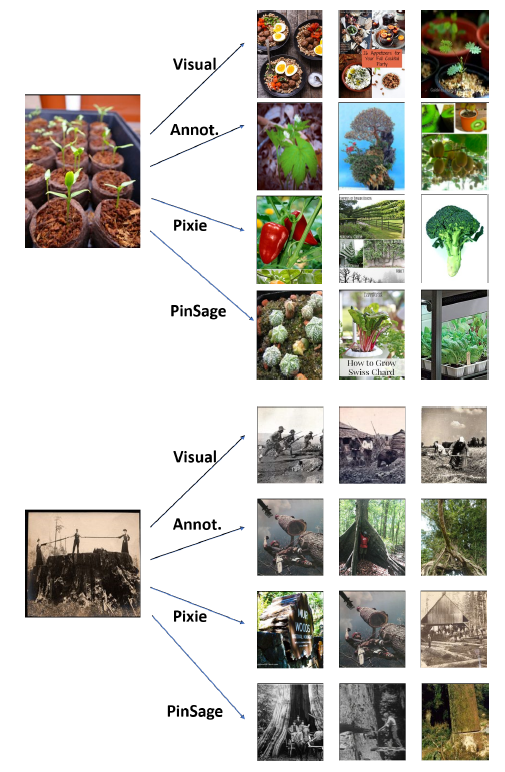
我们从
PinSage embedding中随机选择10000个pin,基于2D t-SNE来可视化embedding空间。我们观察到:相似内容的
pin之间的embedding距离很近,并且相同类别的item也被嵌入到相同的区间。注意:视觉上不同但是主题相同的
pin在embedding空间中也彼此靠近,如图的底部给出了时尚主题的、视觉上不同的一些pin。
13.2.3 A/B Test
最后我们还报告了在线
A/B test实验的结果。我们将PinSage和其它的基于内容的deep learning推荐系统在Pinterest首页信息流上的推荐效果进行比较。我们通过观察用户互动的提升来评估推荐效果。评估指标是
repin rate,它衡量的是首页信息流中,被用户保存到board中的pin的占比。每个保存行为代表一次用户的互动。这意味着当前时间给用户推荐的pin是用户感兴趣的,因此用户将这个pin保存到他们的board中,从而方便用户以后查阅。我们发现
PinSage推荐始终比其它方法具有更高的repin rate。在特定的配置下,我们发现PinSage相比文本embedding和视觉embedding有10% ~30%的repin rate的提升。
13.2.4 速度
PinSage的一个优势是它是inductive的,因此在inference阶段我们可以为训练过程中未见过的pin计算embedding。这使得我们可以在子图上进行训练,然后为剩下的节点计算embedding。另外,随着时间推移不断有新节点加入到图中,为这些新节点生成
embedding也很简单。通过验证集的实验表明,对包含
3亿个pin的子图上进行训练,即可在命中率上取得最佳性能。进一步增加子图的大小似乎对测试结果影响不大。和训练整个
Pinterest相比,训练这个3亿pin的子图可以将训练时间减少6倍。下面我们考察
batch size对训练过程的影响。我们使用mean-pooling-hard变体,结果如下:batch size越大,则每个mini-batch的计算时间越高,模型收敛需要的迭代数量越少。- 不同
batch size训练时间不同,batch size = 2048时训练效率最高,训练时间最少。
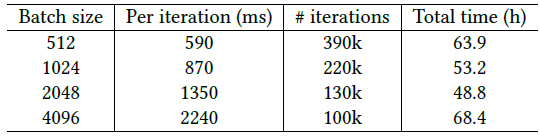
在使用重要性池化时,邻域大小
PinSage的训练时间和训练效果。我们发现随着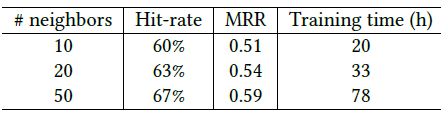
训练完成后,由于高效的
MapReduce inference pipeline,为30亿个pin生成embedding可以在不到24个小时内完成。