数值计算

一、数值稳定性

1. 在计算机中执行数学运算需要使用有限的比特位来表达实数，这会引入近似误差。

   近似误差可以在多步数值运算中传递、积累，从而导致理论上成功的算法失败。因此数值算法设计时要考虑将累计误差最小化。

2. 当从头开始实现一个数值算法时，需要考虑数值稳定性。当使用现有的数值计算库（如tensorflow ）时，不需要考虑数值稳定性。

1.1 上溢出、下溢出

1. 一种严重的误差是下溢出underflow：当接近零的数字四舍五入为零时，发生下溢出。

   许多函数在参数为零和参数为一个非常小的正数时，行为是不同的。如：对数函数要求自变量大于零，除法中要求除数非零。

2. 一种严重的误差是上溢出overflow：当数值非常大，超过了计算机的表示范围时，发生上溢出。

3. 一个数值稳定性的例子是softmax函数。

   设 $\mathbf{\vec x}=(x_1,x_2,\cdots,x_n)^{T}$，则softmax函数定义为：

   $$\text{softmax}(\mathbf{\vec x})=\left(\frac{\exp(x_1)}{\sum_{j=1}^{n}\exp(x_j)},\frac{\exp(x_2)}{\sum_{j=1}^{n}\exp(x_j)},\cdots,\frac{\exp(x_n)}{\sum_{j=1}^{n}\exp(x_j)}\right)^{T}$$

   当所有的 $x_i$ 都等于常数 $c$ 时，softmax函数的每个分量的理论值都为 $\frac 1n$ 。

   • 考虑 $c$ 是一个非常大的负数（比如趋近负无穷），此时 $\exp( c)$ 下溢出。此时 $\frac{\exp(c )}{\sum_{j=1}^{n}\exp(c )}$ 分母为零，结果未定义。
   • 考虑 $c$ 是一个非常大的正数（比如趋近正无穷），此时 $\exp( c)$ 上溢出。 $\frac{\exp(c )}{\sum_{j=1}^{n}\exp(c )}$ 的结果未定义。

4. 为了解决softmax函数的数值稳定性问题，令 $\mathbf{\vec z}=\mathbf{\vec x}-\max_i x_i$，则有 $\text{softmax}(\mathbf{\vec z})$ 的第 $i$ 个分量为：

   $$\text{softmax}(\mathbf{\vec z})_i=\frac{\exp(z_i)}{\sum_{j=1}^{n}\exp(z_j)}=\frac{\exp(\max_k x_k)\exp(z_i)}{\exp(\max_k x_k)\sum_{j=1}^{n}\exp(z_j)}\\ =\frac{\exp(z_i+\max_k x_k)}{\sum_{j=1}^{n}\exp(z_j+\max_k x_k)}\\ =\frac{\exp(x_i)}{\sum_{j=1}^{n}\exp(x_j)}\\ =\text{softmax}(\mathbf{\vec x})_i$$
   • 当 $\mathbf{\vec x}$ 的分量较小时， $\mathbf{\vec z}$ 的分量至少有一个为零，从而导致 $\text{softmax}(\mathbf{\vec z})_i$ 的分母至少有一项为 1，从而解决了下溢出的问题。
   • 当 $\mathbf{\vec x}$ 的分量较大时，$\text{softmax}(\mathbf{\vec z})_i$ 相当于分子分母同时除以一个非常大的数 $\exp(\max_i x_i)$ ，从而解决了上溢出。

5. 当 $\mathbf{\vec x}$ 的分量 $x_i$ 较小时， $\text{softmax}(\mathbf{\vec x})_i$ 的计算结果可能为 0 。此时 $\log \text{softmax}(\mathbf{\vec x})$ 趋向于负无穷，因此存在数值稳定性问题。

   • 通常需要设计专门的函数来计算 $\log\text{softmax}$ ，而不是将 $\text{softmax}$ 的结果传递给 $\log$ 函数。
   • $\log\text{softmax}(\cdot)$ 函数应用非常广泛。通常将 $\text{softmax}$ 函数的输出作为模型的输出。由于一般使用样本的交叉熵作为目标函数，因此需要用到 $\text{softmax}$ 输出的对数。

6. softmax 名字的来源是hardmax。

   • hardmax 把一个向量 $\mathbf{\vec x}$ 映射成向量 $(0,\cdots,0,1,0,\cdots,0)^T$ 。即：$\mathbf{\vec x}$ 最大元素的位置填充1，其它位置填充0。
   • softmax 会在这些位置填充0.0~1.0 之间的值（如：某个概率值）。

1.2 Conditioning

1. Conditioning刻画了一个函数的如下特性：当函数的输入发生了微小的变化时，函数的输出的变化有多大。

   对于Conditioning较大的函数，在数值计算中可能有问题。因为函数输入的舍入误差可能导致函数输出的较大变化。

2. 对于方阵 $\mathbf A\in \mathbb R^{n\times n}$ ，其条件数condition number为：

   $$\text{condition number}=\max_{1\le i,j\le n,i\ne j}\left|\frac{\lambda_i}{\lambda_j} \right|$$

   其中 $\lambda_i,i=1,2,\cdots,n$ 为 $\mathbf A$ 的特征值。

   • 方阵的条件数就是最大的特征值除以最小的特征值。
   • 当方阵的条件数很大时，矩阵的求逆将对误差特别敏感（即： $\mathbf A$ 的一个很小的扰动，将导致其逆矩阵一个非常明显的变化）。
   • 条件数是矩阵本身的特性，它会放大那些包含矩阵求逆运算过程中的误差。

二、梯度下降法

1. 梯度下降法是求解无约束最优化问题的一种常见方法，优点是实现简单。

2. 对于函数： $f:\mathbb R^{n} \rightarrow \mathbb R$，假设输入 $\mathbf{\vec x}=(x_1,x_2,\cdots,x_n)^{T}$，则定义梯度：

   $$\nabla _{\mathbf{\vec x}} f(\mathbf{\vec x})=\left(\frac{\partial}{\partial x_1}f(\mathbf{\vec x}),\frac{\partial}{\partial x_2}f(\mathbf{\vec x}),\cdots,\frac{\partial}{\partial x_n}f(\mathbf{\vec x})\right)^{T}$$

   函数的驻点满足： $\nabla _{\mathbf{\vec x}} f(\mathbf{\vec x})=\mathbf{\vec 0}$ 。

3. 沿着方向 $\mathbf{\vec u}$ 的方向导数directional derivative定义为：

   $$\lim_{\alpha\rightarrow 0}\frac{f(\mathbf{\vec x}+\alpha\mathbf{\vec u})-f(\mathbf{\vec x})}{\alpha}$$

   其中 $\mathbf{\vec u}$ 为单位向量。

   方向导数就是 $\frac{\partial}{\partial \alpha}f(\mathbf{\vec x}+\alpha\mathbf{\vec u})$。根据链式法则，它也等于 $\mathbf{\vec u}^{T}\nabla _{\mathbf{\vec x}} f(\mathbf{\vec x})$ 。

3. 为了最小化 $f$，则寻找一个方向：沿着该方向，函数值减少的速度最快（换句话说，就是增加最慢）。即：

   $$\min_{\mathbf{\vec u}} \mathbf{\vec u}^{T}\nabla _{\mathbf{\vec x}} f(\mathbf{\vec x})\\ s.t.\quad ||\mathbf{\vec u}||_2=1$$

   假设 $\mathbf{\vec u}$ 与梯度的夹角为 $\theta$，则目标函数等于：$||\mathbf{\vec u}||_2||\nabla _{\mathbf{\vec x}} f(\mathbf{\vec x})||_2 \cos\theta$ 。

   考虑到 $||\mathbf{\vec u}||_2=1$，以及梯度的大小与 $\theta$ 无关，于是上述问题转化为：

   $$\min_\theta \cos\theta$$

   于是： $\theta^{*}=\pi$，即 $\mathbf{\vec u}$ 沿着梯度的相反的方向。即：梯度的方向是函数值增加最快的方向，梯度的相反方向是函数值减小的最快的方向。

   因此：可以沿着负梯度的方向来降低 $f$ 的值，这就是梯度下降法。

4. 根据梯度下降法，为了寻找 $f$ 的最小点，迭代过程为：$\mathbf{\vec x}^{\prime}= \mathbf{\vec x}-\epsilon\nabla _{\mathbf{\vec x}} f(\mathbf{\vec x})$ 。其中：$\epsilon$ 为学习率，它是一个正数，决定了迭代的步长。

   迭代结束条件为：梯度向量 $\nabla _{\mathbf{\vec x}} f(\mathbf{\vec x})$ 的每个成分为零或者非常接近零。

5. 选择学习率有多种方法：

   • 一种方法是：选择 $\epsilon$ 为一个小的、正的常数。

   • 另一种方法是：给定多个 $\epsilon$，然后选择使得 $f(\mathbf{\vec x}-\epsilon\nabla _{\mathbf{\vec x}} f(\mathbf{\vec x}))$ 最小的那个值作为本次迭代的学习率（即：选择一个使得目标函数下降最大的学习率）。

     这种做法叫做线性搜索line search 。

   • 第三种方法是：求得使 $f(\mathbf{\vec x}-\epsilon\nabla _{\mathbf{\vec x}} f(\mathbf{\vec x}))$ 取极小值的 $\epsilon$，即求解最优化问题：

     $$\epsilon^{*}=\arg\min_{\epsilon,\epsilon \gt 0 }f(\mathbf{\vec x}-\epsilon\nabla _{\mathbf{\vec x}} f(\mathbf{\vec x}))$$

     这种方法也称作最速下降法。

     • 在最速下降法中，假设相邻的三个迭代点分别为： $\mathbf{\vec x}^{<k>},\mathbf{\vec x}^{<k+1>},\mathbf{\vec x}^{<k+2>}$，可以证明： $(\mathbf{\vec x}^{<k+1>}-\mathbf{\vec x}^{<k>})\cdot (\mathbf{\vec x}^{<k+2>}-\mathbf{\vec x}^{<k+1>})=0$。即相邻的两次搜索的方向是正交的！

       证明：

       $$\mathbf{\vec x}^{<k+1>}=\mathbf{\vec x}^{<k>}-\epsilon^{<k>}\nabla _{\mathbf{\vec x}} f(\mathbf{\vec x}^{<k>})\\ \mathbf{\vec x}^{<k+2>}=\mathbf{\vec x}^{<k+1>}-\epsilon^{<k+1>}\nabla _{\mathbf{\vec x}} f(\mathbf{\vec x}^{<k+1>})$$

       根据最优化问题，有：

       $$\epsilon^{<k>}=\arg\min_{\epsilon,\epsilon \gt 0 }f(\mathbf{\vec x}^{<k+1>})$$

       将 $\mathbf{\vec x}^{<k+1>}=\mathbf{\vec x}^{<k>}-\epsilon\nabla _{\mathbf{\vec x}} f(\mathbf{\vec x}^{<k>})$ 代入，有：

       $$f(\mathbf{\vec x}^{<k+1>})=f(\mathbf{\vec x}^{<k>}-\epsilon\nabla _{\mathbf{\vec x}} f(\mathbf{\vec x}^{<k>}))$$

       为求 $f(\mathbf{\vec x}^{<k+1>})$ 极小值，则求解： $\frac{\partial f(\mathbf{\vec x}^{<k>}-\epsilon\nabla _{\mathbf{\vec x}} f(\mathbf{\vec x}^{<k>})) }{\partial \epsilon}\mid_{\epsilon=\epsilon^{<k>}}=0$ 。

       根据链式法则：

       $$\frac{\partial f(\mathbf{\vec x}^{<k>}-\epsilon\nabla _{\mathbf{\vec x}} f(\mathbf{\vec x}^{<k>})) }{\partial \epsilon}= \nabla _{\mathbf{\vec x}} f(\mathbf{\vec x}^{<k>}-\epsilon\nabla _{\mathbf{\vec x}} f(\mathbf{\vec x}^{<k>}))\cdot[- \nabla _{\mathbf{\vec x}} f(\mathbf{\vec x}^{<k>})] = 0$$

       即：$\nabla _{\mathbf{\vec x}} f(\mathbf{\vec x}^{<k+1>})\cdot \nabla _{\mathbf{\vec x}} f(\mathbf{\vec x}^{<k>})=0$ 。则有：$(\mathbf{\vec x}^{<k+2>}-\mathbf{\vec x}^{<k+1>})\cdot (\mathbf{\vec x}^{<k+1>}-\mathbf{\vec x}^{<k>}) =0$ 。

     • 此时迭代的路线是锯齿形的，因此收敛速度较慢。

6. 某些情况下如果梯度向量 $\nabla _{\mathbf{\vec x}} f(\mathbf{\vec x})$ 的形式比较简单，则可以直接求解方程：$\nabla _{\mathbf{\vec x}} f(\mathbf{\vec x})=\mathbf{\vec 0}$ 。

   此时不用任何迭代，直接获得解析解。

7. 梯度下降算法：

   • 输入：

     • 目标函数 $f(\mathbf {\vec x})$
     • 梯度函数 $g(\mathbf {\vec x})=\nabla f(\mathbf {\vec x})$
     • 计算精度 $e$

   • 输出： $f(\mathbf {\vec x})$ 的极小点 $\mathbf {\vec x}^*$

   • 算法步骤：

     • 选取初始值 $\mathbf {\vec x}^{<0>}\in \mathbb R^{n}$，置 $k=0$ 。

     • 迭代，停止条件为：梯度收敛或者目标函数收敛。迭代步骤为：

       • 计算目标函数 $f(\mathbf {\vec x}^{<k>})$，计算梯度 $\mathbf {\vec g}_k=g(\mathbf {\vec x}^{<k>})$ 。

       • 若梯度 $|\mathbf {\vec g}_k| \lt e$，则停止迭代，$\mathbf {\vec x}^*=\mathbf {\vec x}$ 。

       • 若梯度 $|\mathbf {\vec g}_k| \ge e$，则令 $\mathbf {\vec p}_k=-\mathbf {\vec g}_k$，求 $\epsilon_k$ ： $\epsilon_k =\min_{\epsilon \le 0}f(\mathbf {\vec x}^{<k>}+\epsilon \mathbf {\vec p}_k)$ 。

         通常这也是个最小化问题。但是可以给定一系列的$\epsilon_k$的值，如：[10,1,0.1,0.01,0.001,0.0001] 。然后从中挑选使得目标函数最小的那个。

       • 令 $\mathbf {\vec x}^{<k+1>} = \mathbf {\vec x}^{<k>}+\epsilon_k \mathbf {\vec p}_k$，计算 $f(\mathbf {\vec x}^{<k+1>})$ 。

         • 若 $|f(\mathbf {\vec x}^{<k+1>})-f(\mathbf {\vec x}^{<k>})| \lt e$或者 $|\mathbf {\vec x}^{<k+1>}-\mathbf {\vec x}^{<k>}| \lt e$ 时，停止迭代，此时 $\mathbf {\vec x}^*=\mathbf {\vec x}$ 。
         • 否则，令 $k=k+1$ ，计算梯度 $\mathbf {\vec g}_k=g(\mathbf {\vec x}^{<k>})$ 继续迭代。

     

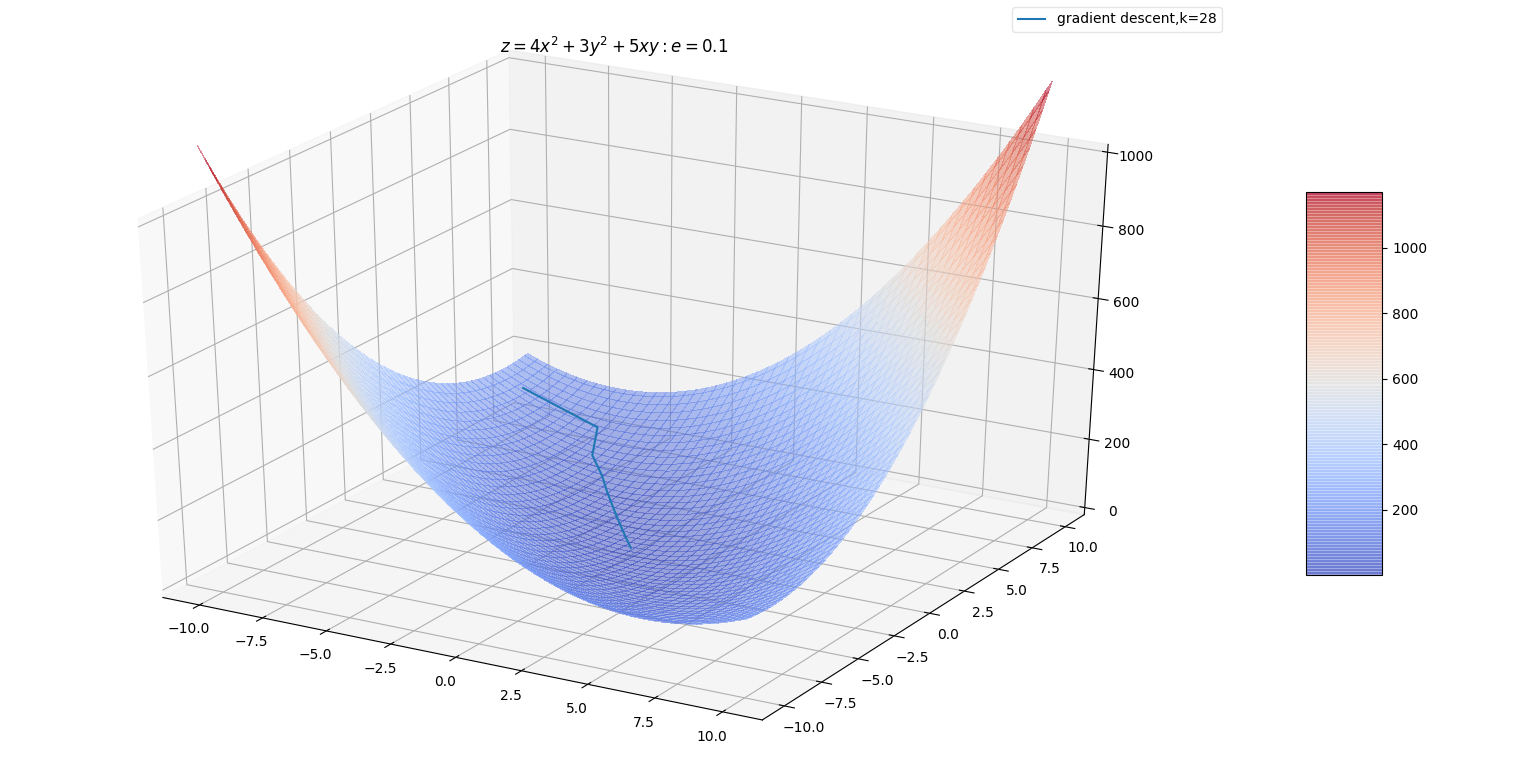
8. 当目标函数是凸函数时，梯度下降法的解是全局最优的。通常情况下，梯度下降法的解不保证是全局最优的。

9. 梯度下降法的收敛速度未必是最快的。

三、二阶导数与海森矩阵

3.1 海森矩阵

1. 二阶导数 $f^{\prime\prime}(x)$ 刻画了曲率。假设有一个二次函数（实际任务中，很多函数不是二次的，但是在局部可以近似为二次函数）：

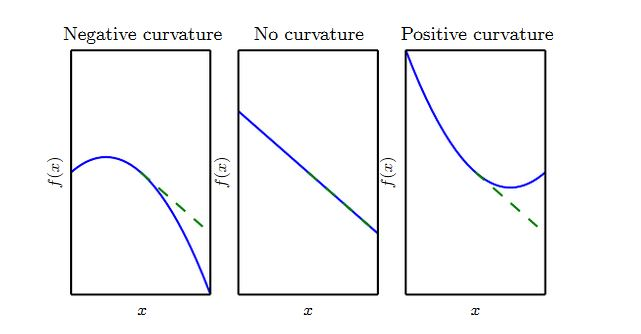
   • 如果函数的二阶导数为零，则它是一条直线。如果梯度为 1，则当沿着负梯度的步长为 $\epsilon$ 时，函数值减少 $\epsilon$ 。
   • 如果函数的二阶导数为负，则函数向下弯曲。如果梯度为1，则当沿着负梯度的步长为 $\epsilon$ 时，函数值减少的量大于 $\epsilon$ 。
   • 如果函数的二阶导数为正，则函数向上弯曲。如果梯度为1，则当沿着负梯度的步长为 $\epsilon$ 时，函数值减少的量少于 $\epsilon$ 。

2. 当函数输入为多维时，定义海森矩阵：

   $$\mathbf H(f)(\mathbf{\vec x}) =\begin{bmatrix} \frac{\partial^{2}}{\partial x_1\partial x_1}f&\frac{\partial^{2}}{\partial x_1\partial x_2}f&\cdots&\frac{\partial^{2}}{\partial x_1\partial x_n}f\\ \frac{\partial^{2}}{\partial x_2\partial x_1}f&\frac{\partial^{2}}{\partial x_2\partial x_2}f&\cdots&\frac{\partial^{2}}{\partial x_2\partial x_n}f\\ \vdots&\vdots&\ddots&\vdots\\ \frac{\partial^{2}}{\partial x_n\partial x_1}f&\frac{\partial^{2}}{\partial x_n\partial x_2}f&\cdots&\frac{\partial^{2}}{\partial x_n\partial x_n}f \end{bmatrix}$$

   即海森矩阵的第 $i$ 行 $j$ 列元素为：$\mathbf H_{i,j}=\frac{\partial^{2}}{\partial x_i\partial x_j}f(\mathbf{\vec x})$ 。

3. 当二阶偏导是连续时，海森矩阵是对称阵，即有： $\mathbf H=\mathbf H^{T}$ 。

   在深度学习中大多数海森矩阵都是对称阵。

4. 对于特定方向 $\mathbf{\vec d}$ 上的二阶导数为：$\mathbf{\vec d}^T\mathbf H \mathbf{\vec d}$ 。

   • 如果 $\mathbf{\vec d}$ 是海森矩阵的特征向量，则该方向的二阶导数就是对应的特征值。
   • 如果 $\mathbf{\vec d}$ 不是海森矩阵的特征向量，则该方向的二阶导数就是所有特征值的加权平均，权重在 (0,1)之间。且与 $\mathbf{\vec d}$ 夹角越小的特征向量对应的特征值具有更大的权重。
   • 最大特征值确定了最大二阶导数，最小特征值确定最小二阶导数。

3.2 海森矩阵与学习率

1. 将 $f(\mathbf{\vec x})$ 在 $\mathbf{\vec x}_0$ 处泰勒展开：$f(\mathbf{\vec x}) \approx f(\mathbf{\vec x}_0)+(\mathbf{\vec x}-\mathbf{\vec x}_0 )^{T}\mathbf{\vec g}+\frac 12(\mathbf{\vec x}-\mathbf{\vec x}_0)^{T}\mathbf H (\mathbf{\vec x}-\mathbf{\vec x}_0)$ 。其中： $\mathbf{\vec g}$ 为 $\mathbf{\vec x}_0$ 处的梯度； $\mathbf H$ 为 $\mathbf{\vec x}_0$ 处的海森矩阵。

   根据梯度下降法：$\mathbf{\vec x}^{\prime}= \mathbf{\vec x}-\epsilon\nabla _{\mathbf{\vec x}} f(\mathbf{\vec x})$ 。

   应用在点 $\mathbf{\vec x}_0$，有：$f(\mathbf{\vec x}_0-\epsilon\mathbf{\vec g})\approx f(\mathbf{\vec x}_0)-\epsilon\mathbf{\vec g}^{T}\mathbf{\vec g}+\frac 12\epsilon^{2}\mathbf{\vec g}^{T}\mathbf H \mathbf{\vec g}$ 。

   • 第一项代表函数在点 $\mathbf{\vec x}_0$ 处的值。
   • 第二项代表由于斜率的存在，导致函数值的变化。
   • 第三项代表由于曲率的存在，对于函数值变化的矫正。

2. 注意：如果 $\frac 12\epsilon^{2}\mathbf{\vec g}^{T}\mathbf H \mathbf{\vec g}$ 较大，则很有可能导致：沿着负梯度的方向，函数值反而增加！

   • 如果 $\mathbf{\vec g}^{T}\mathbf H \mathbf{\vec g} \le 0$ ，则无论 $\epsilon$ 取多大的值， 可以保证函数值是减小的。

   • 如果 $\mathbf{\vec g}^{T}\mathbf H \mathbf{\vec g} \gt 0$， 则学习率 $\epsilon$ 不能太大。若 $\epsilon$ 太大则函数值增加。

     • 根据 $f(\mathbf{\vec x}_0-\epsilon\mathbf{\vec g}) - f(\mathbf{\vec x}_0) \lt 0$ ，则需要满足：$\epsilon \lt \frac{\mathbf{2\vec g}^{T}\mathbf{\vec g}}{\mathbf{\vec g}^{T}\mathbf H\mathbf{\vec g}}$ 。若 $\epsilon \ge \frac{\mathbf{2\vec g}^{T}\mathbf{\vec g}}{\mathbf{\vec g}^{T}\mathbf H\mathbf{\vec g}}$ ，则会导致沿着负梯度的方向函数值在增加。

     • 考虑最速下降法，选择使得 $f$ 下降最快的 $\epsilon$ ，则有：$\epsilon^{*}=\arg\min_{\epsilon,\epsilon \gt 0 }f(\mathbf{\vec x}_0-\epsilon\mathbf{\vec g})$ 。求解 $\frac{\partial }{\partial \epsilon} f(\mathbf{\vec x}_0-\epsilon\mathbf{\vec g})=0$ 有：$\epsilon^{*}=\frac{\mathbf{\vec g}^{T}\mathbf{\vec g}}{\mathbf{\vec g}^{T}\mathbf H\mathbf{\vec g}}$ 。

       根据 $\mathbf{\vec g}^{T}\mathbf H \mathbf{\vec g} \gt 0$ ，很明显有： $\epsilon^{*} \lt \frac{\mathbf{2\vec g}^{T}\mathbf{\vec g}}{\mathbf{\vec g}^{T}\mathbf H\mathbf{\vec g}}$ 。

3. 由于海森矩阵为实对称阵，因此它可以进行特征值分解。假设其特征值从大到小排列为：$\lambda_1\ge \lambda_2\ge\cdots\ge\lambda_n$ 。

   海森矩阵的瑞利商为： $R(\mathbf{\vec x})=\frac{\mathbf{\vec x}^{T}\mathbf H\mathbf{\vec x}}{\mathbf{\vec x}^{T}\mathbf{\vec x}},\mathbf{\vec x} \ne \mathbf{\vec 0}$ 。可以证明：

   $$\lambda_n \le R(\mathbf{\vec x}) \le \lambda_1\\ \lambda_1=\max_{\mathbf{\vec x}\ne \mathbf{\vec 0}} R(\mathbf{\vec x})\\ \lambda_n=\min_{\mathbf{\vec x}\ne \mathbf{\vec 0}} R(\mathbf{\vec x})$$

   根据 $\epsilon^{*}=\frac{\mathbf{\vec g}^{T}\mathbf{\vec g}}{\mathbf{\vec g}^{T}\mathbf H\mathbf{\vec g}}=\frac{1}{R(\mathbf{\vec g})}$ 可知：海森矩阵决定了学习率的取值范围。最坏的情况下，梯度 $\mathbf{\vec g}$ 与海森矩阵最大特征值 $\lambda_1$ 对应的特征向量平行，则此时最优学习率为 $\frac {1}{\lambda_1}$ 。

3.3 驻点与全局极小点

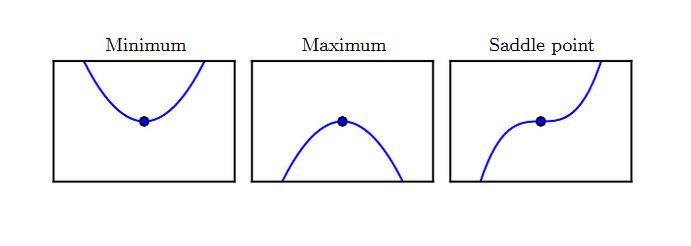
1. 满足导数为零的点（即 $f^{\prime}(x)=0$ ）称作驻点。驻点可能为下面三种类型之一：

   • 局部极小点：在 $x$ 的一个邻域内，该点的值最小。
   • 局部极大点：在 $x$ 的一个邻域内，该点的值最大。
   • 鞍点：既不是局部极小，也不是局部极大。

   

2. 全局极小点：$x^{*}=\arg\min_x f(x)$。

   • 全局极小点可能有一个或者多个。

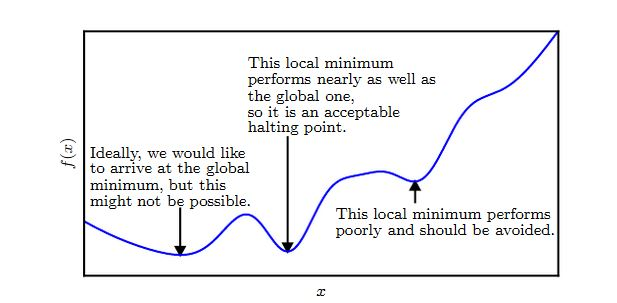
   • 在深度学习中，目标函数很可能具有非常多的局部极小点，以及许多位于平坦区域的鞍点。这使得优化非常不利。

     因此通常选取一个非常低的目标函数值，而不一定要是全局最小值。

3. 二阶导数可以配合一阶导数来决定驻点的类型：

   • 局部极小点：$f^{\prime}(x)=0,f^{\prime\prime}(x)\gt 0$ 。
   • 局部极大点：$f^{\prime}(x)=0,f^{\prime\prime}(x)\lt 0$ 。
   • $f^{\prime}(x)=0,f^{\prime\prime}(x)= 0$ ：驻点的类型可能为任意三者之一。

4. 对于多维的情况类似有：

   • 局部极小点：$\nabla _{\mathbf{\vec x}} f(\mathbf{\vec x})=0$，且海森矩阵为正定的（即所有的特征值都是正的）。

     当海森矩阵为正定时，任意方向的二阶偏导数都是正的。

   • 局部极大点：$\nabla _{\mathbf{\vec x}} f(\mathbf{\vec x})=0$，且海森矩阵为负定的（即所有的特征值都是负的）。

     当海森矩阵为负定时，任意方向的二阶偏导数都是负的。

   • $\nabla _{\mathbf{\vec x}} f(\mathbf{\vec x})=0$，且海森矩阵的特征值中至少一个正值、至少一个负值时，为鞍点。

   • 当海森矩阵非上述情况时，驻点类型无法判断。

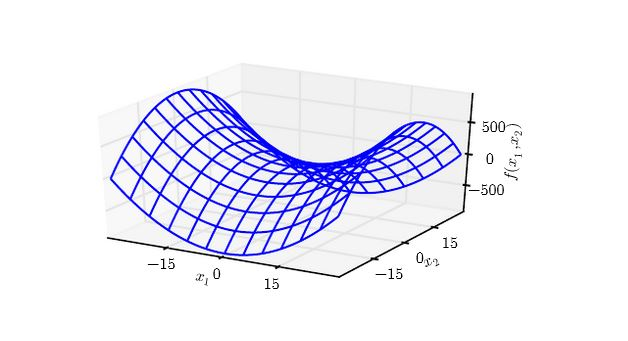
   下图为 $f(\mathbf{\vec x})=x_1^{2}-x_2^{2}$ 在原点附近的等值线。其海森矩阵为一正一负。

   • 沿着 $x_1$ 方向，曲线向上弯曲；沿着 $x_2$ 方向，曲线向下弯曲。
   • 鞍点就是在一个横截面内的局部极小值，另一个横截面内的局部极大值。

   

四、牛顿法

1. 梯度下降法有个缺陷：它未能利用海森矩阵的信息。

   • 当海森矩阵的条件数较大时，不同方向的梯度的变化差异很大。

     • 在某些方向上，梯度变化很快；在有些方向上，梯度变化很慢。

     • 梯度下降法未能利用海森矩阵，也就不知道应该优先搜索导数长期为负或者长期为正的方向。

       本质上应该沿着负梯度方向搜索。但是沿着该方向的一段区间内，如果导数一直为正或者一直为负，则可以直接跨过该区间。前提是：必须保证该区间内，该方向导数不会发生正负改变。

   • 当海森矩阵的条件数较大时，也难以选择合适的步长。

     • 步长必须足够小，从而能够适应较强曲率的地方（对应着较大的二阶导数，即该区域比较陡峭）。
     • 但是如果步长太小，对于曲率较小的地方（对应着较小的二阶导数，即该区域比较平缓）则推进太慢。

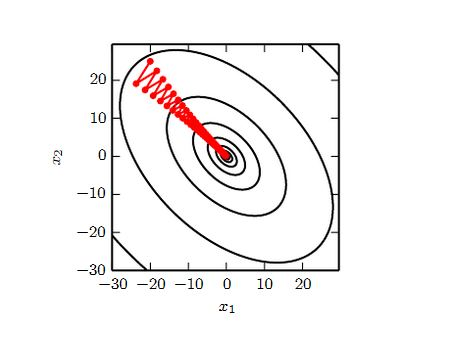
2. 下图是利用梯度下降法寻找函数最小值的路径。该函数是二次函数，海森矩阵条件数为 5，表明最大曲率是最小曲率的5倍。红线为梯度下降的搜索路径。

   它没有用最速下降法，而是用到线性搜索。如果是最速下降法，则相邻两次搜索的方向正交。

   

3. 牛顿法结合了海森矩阵。

   考虑泰勒展开式：$f(\mathbf{\vec x}) \approx f(\mathbf{\vec x}_0)+(\mathbf{\vec x}-\mathbf{\vec x}_0 )^{T}\mathbf{\vec g}+\frac 12(\mathbf{\vec x}-\mathbf{\vec x}_0)^{T}\mathbf H (\mathbf{\vec x}-\mathbf{\vec x}_0)$ 。其中 $\mathbf{\vec g}$ 为 $\mathbf{\vec x}_0$ 处的梯度； $\mathbf H$ 为 $\mathbf{\vec x}_0$ 处的海森矩阵。

   如果 $\mathbf{\vec x}$ 为极值点，则有： $\frac{\partial}{\partial \mathbf{\vec x}}f(\mathbf{\vec x})=\mathbf{\vec 0}$，则有：$\mathbf{\vec x}^{*}=\mathbf{\vec x}_0 -\mathbf H^{-1}\mathbf{\vec g}$ 。

   • 当 $f$ 是个正定的二次型，则牛顿法直接一次就能到达最小值点。
   • 当 $f$ 不是正定的二次型，则可以在局部近似为正定的二次型，那么则采用多次牛顿法即可到达最小值点。

4. 一维情况下，梯度下降法和牛顿法的原理展示：

   

   • 梯度下降法：下一次迭代的点 $\mathbf {\vec x}^{<k+1>}=\mathbf {\vec x}^{<k>}-\epsilon_k \nabla f(\mathbf {\vec x})$。

     对于一维的情况，可以固定 $\epsilon_k=\eta$ 。由于随着迭代的推进，$f^{\prime}(x)$ 绝对值是减小的（直到0），因此越靠近极值点，$\Delta(x)$ 越小。

   • 牛顿法：目标是 $\nabla f(\mathbf {\vec x})=0$。

     在一维情况下就是求解 $f^\prime (x)=0$。牛顿法的方法是：以 $x=x^{<k>}$ 做 $y=f^{\prime}(x)$ 切线，该切线过点 $(x^{<k>},f^{\prime}(x^{<k>}))$。该切线在 $x$ 轴上的交点就是： $x^{<k+1>}=x^{<k>}-\frac {f^{\prime}(x^{<k>})}{f^{\prime\prime}(x^{<k>})}$ 。

     推广到多维情况下就是：$\mathbf {\vec x}^{<k+1>}=\mathbf {\vec x}^{<k>}-\mathbf H_k^{-1}\mathbf {\vec g}_k$ 。

5. 当位于一个极小值点附近时，牛顿法比梯度下降法能更快地到达极小值点。

   如果在一个鞍点附近，牛顿法效果很差，因为牛顿法会主动跳入鞍点。而梯度下降法此时效果较好（除非负梯度的方向刚好指向了鞍点）。

6. 仅仅利用了梯度的优化算法（如梯度下降法）称作一阶优化算法，同时利用了海森矩阵的优化算法（如牛顿法）称作二阶优化算法。

7. 牛顿法算法：

   • 输入：

     • 目标函数 $f(\mathbf {\vec x})$
     • 梯度 $g(\mathbf {\vec x})=\nabla f(\mathbf {\vec x})$
     • 海森矩阵 $\mathbf H(\mathbf {\vec x})$
     • 精度要求 $e$

   • 输出： $f(\mathbf {\vec x})$ 的极小值点 $\mathbf {\vec x}^*$

   • 算法步骤：

     • 选取初始值 $\mathbf {\vec x}^{<0>}\in \mathbb R^{n}$, 置 $k=0$ 。

     • 迭代，停止条件为：梯度收敛。迭代步骤为：

       • 计算 $\mathbf {\vec g}_k=g(\mathbf {\vec x}^{<k>})$ 。

       • 若 $|\mathbf {\vec g}_k| \lt e$， 则停止计算，得到近似解 $\mathbf {\vec x}=\mathbf {\vec x}^*$ 。

       • 若 $|\mathbf {\vec g}_k| \ge e$， 则：

         • 计算 $\mathbf H_k=\mathbf H(\mathbf {\vec x}^{<k>})$，并求 $\mathbf {\vec p}_k$，使得：$\mathbf H_k \mathbf {\vec p}_k=-\mathbf {\vec g}_k$ 。
         • 置 $\mathbf {\vec x}^{<k+1>}=\mathbf {\vec x}^{<k>}+\mathbf {\vec p}_k$ 。
         • 置 $k=k+1$ ，继续迭代。

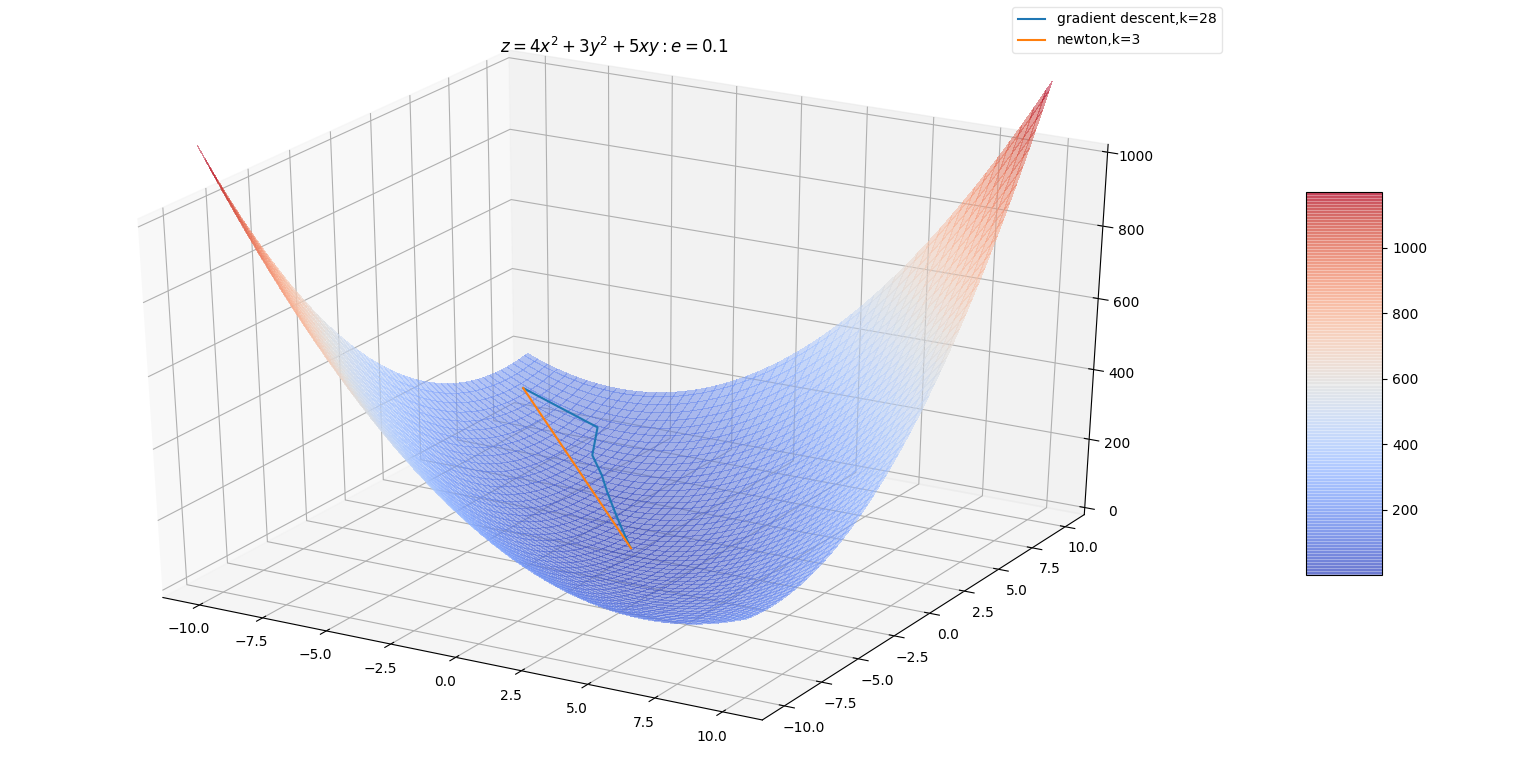
8. 梯度下降法中，每一次 $\mathbf {\vec x}$ 增加的方向一定是梯度相反的方向 $- \epsilon_k \nabla_k$ 。增加的幅度由 $\epsilon_k$ 决定，若跨度过大容易引发震荡。

   而牛顿法中，每一次 $\mathbf {\vec x}$ 增加的方向是梯度增速最大的反方向 $- \mathbf H_k^{-1} \nabla_k$（它通常情况下与梯度不共线）。增加的幅度已经包含在 $\mathbf H_k^{-1}$ 中（也可以乘以学习率作为幅度的系数）。

   

9. 深度学习中的目标函数非常复杂，无法保证可以通过上述优化算法进行优化。因此有时会限定目标函数具有Lipschitz连续，或者其导数Lipschitz连续。

   • Lipschitz连续的定义：对于函数 $f$，存在一个Lipschitz常数 $\mathcal L$，使得：
   $$\forall \mathbf{\vec x},\forall \mathbf{\vec y}, |f(\mathbf{\vec x})-f(\mathbf{\vec y})| \le \mathcal L ||\mathbf{\vec x}-\mathbf{\vec y}||_2$$

   • Lipschitz连续的意义是：输入的一个很小的变化，会引起输出的一个很小的变化。

     与之相反的是：输入的一个很小的变化，会引起输出的一个很大的变化

10. 凸优化在某些特殊的领域取得了巨大的成功。但是在深度学习中，大多数优化问题都难以用凸优化来描述。

    凸优化的重要性在深度学习中大大降低。凸优化仅仅作为一些深度学习算法的子程序。

五、拟牛顿法

5.1 原理

1. 在牛顿法的迭代中，需要计算海森矩阵的逆矩阵 $\mathbf H^{-1}$，这一计算比较复杂。

   可以考虑用一个 $n$ 阶矩阵 $\mathbf G_k=G(\mathbf {\vec x}^{<k>})$ 来近似代替 $\mathbf H^{-1}_k=H^{-1}(\mathbf {\vec x}^{<k>})$。

2. 先看海森矩阵满足的条件：$\mathbf {\vec g}_{k+1}-\mathbf {\vec g}_k=\mathbf H_k (\mathbf {\vec x}^{<k+1>}-\mathbf {\vec x}^{<k>})$ 。

   • 令 $\mathbf {\vec y}_k=\mathbf {\vec g}_{k+1}-\mathbf {\vec g}_k, \vec \delta_k=\mathbf {\vec x}^{<k+1>}-\mathbf {\vec x}^{<k>}$ 。则有：$\mathbf {\vec y}_k=\mathbf H_k \vec \delta_k$，或者 $\mathbf H_k^{-1}\mathbf {\vec y}_k=\vec \delta_k$。

     这称为拟牛顿条件。

   • 根据牛顿法的迭代： $\mathbf {\vec x}^{<k+1>}=\mathbf {\vec x}^{<k>}-\mathbf H_k^{-1}\mathbf {\vec g}_k$，将 $f(\mathbf {\vec x})$ 在 $\mathbf {\vec x}^{<k>}$ 的一阶泰勒展开：

     $$f(\mathbf {\vec x}^{<k+1>})=f(\mathbf {\vec x}^{<k>})+f'(\mathbf {\vec x}^{<k>})(\mathbf {\vec x}^{<k+1>}-\mathbf {\vec x}^{<k>})\\ =f(\mathbf {\vec x}^{<k>})+\mathbf {\vec g}_k^{T}(-\mathbf H_k^{-1}\mathbf {\vec g}_k)=f(\mathbf {\vec x}^{<k>})-\mathbf {\vec g}_k^{T}\mathbf H^{-1}_k\mathbf {\vec g}_k$$

     当 $\mathbf H_k$ 是正定矩阵时，总有 $f(\mathbf {\vec x}^{<k+1>})<f(\mathbf {\vec x}^{<k>})$，因此每次都是沿着函数递减的方向迭代。

3. 如果选择 $\mathbf G_k$ 作为 $\mathbf H_k^{-1}$ 的近似时，$\mathbf G_k$ 同样要满足两个条件：

   • $\mathbf G_k$ 必须是正定的。

   • $\mathbf G_k$ 满足拟牛顿条件：$\mathbf G_{k+1}\mathbf {\vec y}_k=\vec \delta_k$ 。

     因为 $\mathbf G_0$ 是给定的初始化条件，所以下标从 $k+1$ 开始。

   按照拟牛顿条件，在每次迭代中可以选择更新矩阵 $\mathbf G_{k+1}=\mathbf G_k+\Delta \mathbf G_k$ 。

4. 正定矩阵定义：设 $\mathbf M$ 是 $n\times n$ 阶方阵，如果对任何非零向量$\mathbf {\vec x}$ ，都有 $\mathbf {\vec x}^{T} \mathbf M \mathbf {\vec x} \gt 0$，就称 $\mathbf M$正定矩阵。

   • 正定矩阵判定：

     • 判定定理1：对称阵 $\mathbf M$ 为正定的充分必要条件是：$\mathbf M$ 的特征值全为正。
     • 判定定理2：对称阵 $\mathbf M$ 为正定的充分必要条件是：$\mathbf M$ 的各阶顺序主子式都为正。
     • 判定定理3：任意阵 $\mathbf M$ 为正定的充分必要条件是：$\mathbf M$ 合同于单位阵。

   • 正定矩阵的性质：

     • 正定矩阵一定是非奇异的。奇异矩阵的定义：若 $n\times n$ 阶矩阵 $\mathbf M$ 为奇异阵，则其的行列式为零，即 $|\mathbf M|=0$。
     • 正定矩阵的任一主子矩阵也是正定矩阵。
     • 若 $\mathbf M$ 为$n\times n$ 阶对称正定矩阵，则存在唯一的主对角线元素都是正数的下三角阵 $\mathbf L$，使得 $\mathbf M=\mathbf L\mathbf L^{T}$，此分解式称为 正定矩阵的乔列斯基（Cholesky）分解。
     • 若 $\mathbf M$ 为 $n\times n$ 阶正定矩阵，则 $\mathbf M$ 为 $n\times n$ 阶可逆矩阵。

   • 正定矩阵在某个合同变换下可化为标准型， 即对角矩阵。

   • 所有特征值大于零的对称矩阵也是正定矩阵。

5. 合同矩阵：两个实对称矩阵 $\mathbf A$ 和 $\mathbf B$ 是合同的，当且仅当存在一个可逆矩阵 $\mathbf P$ ，使得 $\mathbf A=\mathbf P^{T}\mathbf B\mathbf P$

   • $\mathbf A$ 的合同变换：对某个可逆矩阵 $\mathbf P$，对 $\mathbf A$ 执行 $\mathbf P^{T}\mathbf A\mathbf P$。

5.2 DFP 算法

1. DFP算法( Davidon-Fletcher-Powell) 选择 $\mathbf G_{k+1}$ 的方法是：

   假设每一步迭代中 $\mathbf G_{k+1}$ 是由 $\mathbf G_k$ 加上两个附加项构成：$\mathbf G_{k+1}=\mathbf G_k+\mathbf P_k+\mathbf Q_k$，其中 $\mathbf P_k,\mathbf Q_k$ 是待定矩阵。此时有：$\mathbf G_{k+1}\mathbf {\vec y}_k=\mathbf G_k\mathbf {\vec y}_k+\mathbf P_k\mathbf {\vec y}_k+\mathbf Q_k\mathbf {\vec y}_k$。

   为了满足拟牛顿条件，可以取：$\mathbf P_k\mathbf {\vec y}_k=\vec \delta_k,\quad \mathbf Q_k\mathbf {\vec y}_k =-\mathbf G_k\mathbf {\vec y}_k$。

   这样的$\mathbf P_k,\mathbf Q_k$ 不止一个。例如取 ：

   $$\mathbf P_k=\frac{\vec \delta_k\vec \delta_k^{T}}{\vec \delta_k^{T}\mathbf {\vec y}_k},\quad \mathbf Q_k=-\frac{\mathbf G_k\mathbf {\vec y}_k \mathbf {\vec y}_k^{T} \mathbf G_k}{\mathbf {\vec y}_k^{T}\mathbf G_k \mathbf {\vec y}_k}$$

   则迭代公式为：

   $$\mathbf G_{k+1}=\mathbf G_k+\frac{\vec \delta_k\vec \delta_k^{T}}{\vec \delta_k^{T}\mathbf {\vec y}_k}-\frac{\mathbf G_k\mathbf {\vec y}_k \mathbf {\vec y}_k^{T} \mathbf G_k}{\mathbf {\vec y}_k^{T} \mathbf G_k \mathbf {\vec y}_k}$$

   可以证明：如果初始矩阵 $\mathbf G_0$ 是正定的，则迭代过程中每个矩阵 $\mathbf G_k$ 都是正定的。

2. DFP算法：

   • 输入：

     • 目标函数 $f(\mathbf {\vec x})$
     • 梯度 $g(\mathbf {\vec x})=\nabla f(\mathbf {\vec x})$
     • 精度要求 $e$

   • 输出： $f(\mathbf {\vec x})$ 的极小值点 $\mathbf {\vec x}^*$

   • 算法步骤：

     • 选取初始值 $\mathbf {\vec x}^{<0>}\in \mathbb R^{n}$, 取 $\mathbf G_0$ 为正定对称矩阵，置 $k=0$ 。

     • 迭代，停止条件为：梯度收敛。迭代步骤为：

       • 计算 $\mathbf {\vec g}_k=g(\mathbf {\vec x}^{<k>})$ 。

       • 若 $|\mathbf {\vec g}_k| \lt e$， 则停止计算，得到近似解 $\mathbf {\vec x}=\mathbf {\vec x}^*$。

       • 若 $|\mathbf {\vec g}_k| \ge e$， 则：

         • 计算 $\mathbf {\vec p}_k=-\mathbf G_k\mathbf {\vec g}_k$ 。
         • 一维搜索：求 $\epsilon_k$： $\epsilon_k=\min_{\epsilon \ge 0}f(\mathbf {\vec x}^{<k>}+\epsilon\mathbf {\vec p}_k)$ 。
         • 设置 $\mathbf {\vec x}^{<k+1>}=\mathbf {\vec x}^{<k>}+\epsilon_k\mathbf {\vec p}_k$ 。
         • 计算 $\mathbf {\vec g}_{k+1}=g(\mathbf {\vec x}^{<k+1>})$。若 $|\mathbf {\vec g}_{k+1}| \lt e$， 则停止计算，得到近似解 $\mathbf {\vec x}=\mathbf {\vec x}^*$ 。
         • 否则计算 $\mathbf G_{k+1}$，置 $k=k+1$，继续迭代。

3. DFP算法中，每一次 $\mathbf {\vec x}$ 增加的方向是 $-\mathbf G_k \nabla_k$ 的方向。增加的幅度由 $\epsilon_k$ 决定，若跨度过大容易引发震荡。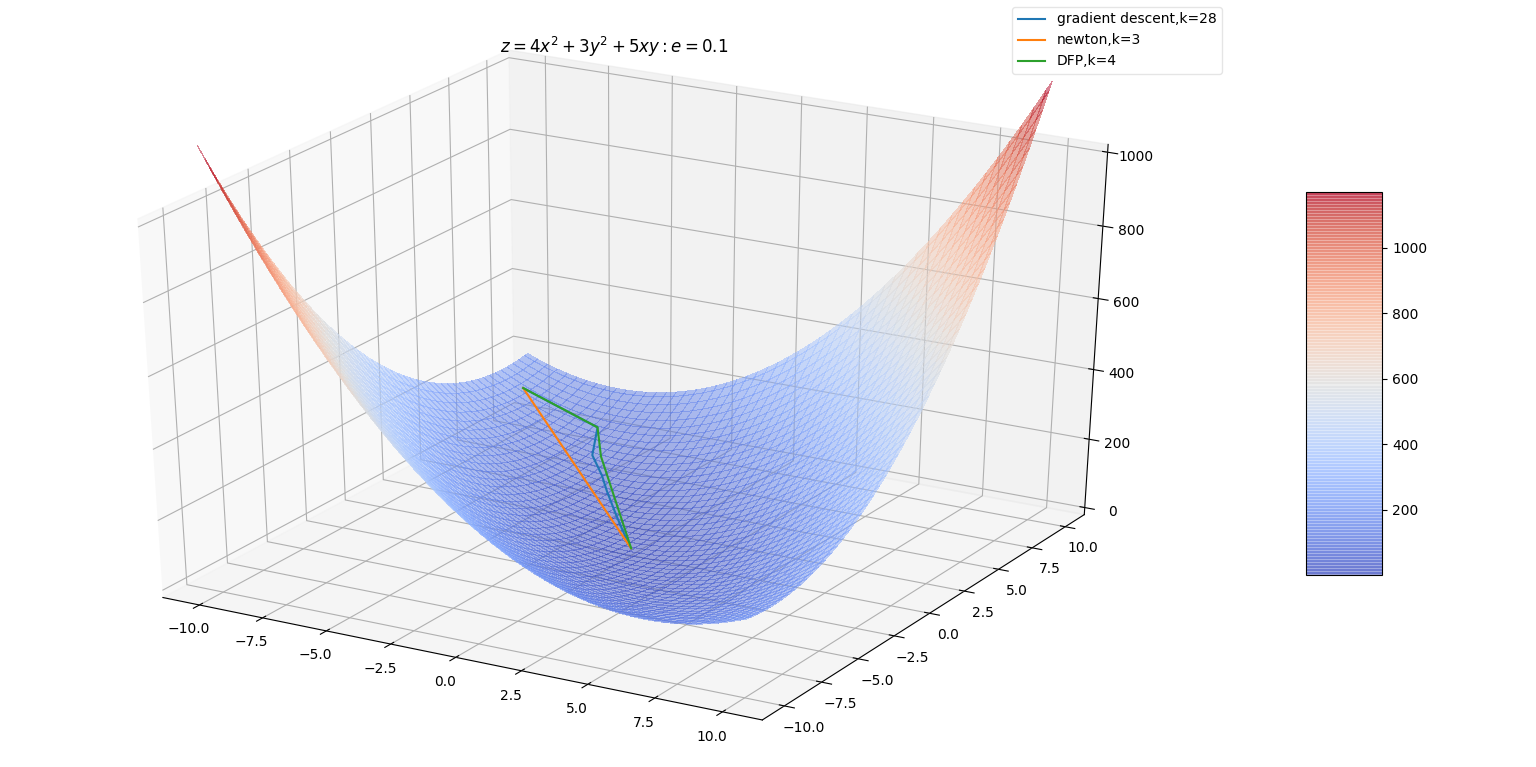

   

5.2 BFGS 算法

1. BFGS是最流行的拟牛顿算法。 DFP算法中，用 $\mathbf G_k$ 逼近 $\mathbf H^{-1}$。换个角度看，可以用矩阵 $\mathbf B_k$ 逼近海森矩阵 $\mathbf H$。此时对应的拟牛顿条件为： $\mathbf B_{k+1}\vec \delta_k=\mathbf {\vec y}_k$。

   因为 $\mathbf B_0$ 是给定的初始化条件，所以下标从 $k+1$ 开始。

2. 令： $\mathbf B_{k+1}=\mathbf B_k+\mathbf P_k+\mathbf Q_k$，有： $\mathbf B_{k+1}\vec \delta_k=\mathbf B_k\vec \delta_k+\mathbf P_k\vec \delta_k+\mathbf Q_k\vec \delta_k$ 。

   可以取 $\mathbf P_k\vec \delta_k=\mathbf {\vec y}_k,\mathbf Q_k\vec \delta_k=-\mathbf B_k\vec \delta_k$ 。寻找合适的 $\mathbf P_k,\mathbf Q_k$ ，可以得到 BFGS 算法矩阵的 $\mathbf B_{k+1}$ 的迭代公式：

   $$\mathbf B_{k+1}=\mathbf B_k+\frac{\mathbf {\vec y}_k\mathbf {\vec y}_k^{T}}{\mathbf {\vec y}_k^{T}\vec \delta_k}-\frac{\mathbf B_k\vec \delta_k\vec \delta_k^{T}\mathbf B_k}{\vec \delta_k^{T}\mathbf B_k\vec \delta_k}$$

   可以证明，若 $\mathbf B_0$ 是正定的，则迭代过程中每个矩阵 $\mathbf B_k$ 都是正定的。

3. BFGS算法：

   • 输入：

     • 目标函数 $f(\mathbf {\vec x})$
     • 梯度 $g(\mathbf {\vec x})=\nabla f(\mathbf {\vec x})$
     • 精度要求 $\ e$

   • 输出： $f(\mathbf {\vec x})$ 的极小值点 $\mathbf {\vec x}^*$

   • 算法步骤：

     • 选取初始值 $\mathbf {\vec x}^{<0>}\in \mathbb R^{n}$, 取 $\mathbf B_0$ 为正定对称矩阵，置 $k=0$ 。

     • 迭代，停止条件为：梯度收敛。迭代步骤为：

       • 计算 $\mathbf {\vec g}_k=g(\mathbf {\vec x}^{<k>})$ 。

       • 若 $|\mathbf {\vec g}_k| \lt e$， 则停止计算，得到近似解 $\mathbf {\vec x}=\mathbf {\vec x}^*$ 。

       • 若 $|\mathbf {\vec g}_k| \ge e$， 则:

         • 由 $\mathbf B_k\mathbf {\vec p}_k=-\mathbf {\vec g}_k$ 求出 $\mathbf {\vec p}_k$ 。

           这里表面上看需要对矩阵求逆。但是实际上 $\mathbf B_k^{-1}$ 有迭代公式。根据Sherman-Morrison 公式以及 $\mathbf B_k$ 的迭代公式，可以得到 $\mathbf B_k^{-1}$ 的迭代公式。

         • 一维搜索：求 $\epsilon_k$： $\epsilon_k=\min_{\epsilon \ge 0}f(\mathbf {\vec x}^{<k>}+\epsilon\mathbf {\vec p}_k)$ 。

         • 设置 $\mathbf {\vec x}^{<k+1>}=\mathbf {\vec x}^{<k>}+\epsilon_k\mathbf {\vec p}_k$ 。

         • 计算 $\mathbf {\vec g}_{k+1}=g(\mathbf {\vec x}^{<k+1>})$。若 $|\mathbf {\vec g}_{k+1}| \lt e$ ， 则停止计算，得到近似解 $\mathbf {\vec x}=\mathbf {\vec x}^*$ 。

         • 否则计算 $\mathbf B_{k+1}$ ，置 $k=k+1$ ，继续迭代。

4. BFPS 算法中，每一次 $\mathbf {\vec x}$ 增加的方向是 $-\mathbf B_k^{-1} \nabla_k$ 的方向。增加的幅度由 $\epsilon_k$ 决定，若跨度过大容易引发震荡。

   

5.3 Broyden 类算法

1. 若记 $\mathbf G_k=\mathbf B_k^{-1},\mathbf G_{k+1}=\mathbf B_{k+1}^{-1}$，则对式子：

   $$\mathbf B_{k+1}=\mathbf B_k+\frac{\mathbf {\vec y}_k\mathbf {\vec y}_k^{T}}{\mathbf {\vec y}_k^{T}\vec \delta_k}-\frac{\mathbf B_k\vec \delta_k\vec \delta_k^{T}\mathbf B_k}{\vec \delta_k^{T}\mathbf B_k\vec \delta_k}$$

   使用两次Sherman-Morrison公式可得：

   $$\mathbf G_{k+1}=(\mathbf I-\frac{\vec \delta_k\mathbf {\vec y}_k^{T}}{\vec \delta_k^{T}\mathbf {\vec y}_k})\mathbf G_k(\mathbf I-\frac{\vec \delta_k\mathbf {\vec y}_k^{T}}{\vec \delta_k^{T}\mathbf {\vec y}_k})^{T}+\frac{\vec \delta_k\vec \delta_k^{T}}{\vec \delta_k^{T}\mathbf {\vec y}_k}$$

2. 令 DFP 算法获得的 $\mathbf G_{k+1}$ 的迭代公式记作：

   $$\mathbf G^{DFP}=\mathbf G_k+\frac{\vec \delta_k\vec \delta_k^{T}}{\vec \delta_k^{T}\mathbf {\vec y}_k}-\frac{\mathbf G_k\mathbf {\vec y}_k \mathbf {\vec y}_k^{T} \mathbf G_k}{\mathbf {\vec y}_k^{T} \mathbf G_k \mathbf {\vec y}_k}$$

   由 BFGS 算法获得的 $\mathbf G_{k+1}$ 的迭代公式记作 ：

   $$\mathbf G^{BFGS}=(\mathbf I-\frac{\vec \delta_k\mathbf {\vec y}_k^{T}}{\vec \delta_k^{T}\mathbf {\vec y}_k})\mathbf G_k(\mathbf I-\frac{\vec \delta_k\mathbf {\vec y}_k^{T}}{\vec \delta_k^{T}\mathbf {\vec y}_k})^{T}+\frac{\vec \delta_k\vec \delta_k^{T}}{\vec \delta_k^{T}\mathbf {\vec y}_k}$$

   他们都满足拟牛顿条件，所以他们的线性组合：$\mathbf G_{k+1}= \alpha \mathbf G^{DFP}+(1- \alpha)\mathbf G^{BFGS}$ 也满足拟牛顿条件，而且是正定的，其中 $0 \le \alpha \le 1$ 。

   这样获得了一族拟牛顿法，称为 Broyden 类算法。

3. Sherman-Morrison公式：假设 $\mathbf A$ 是 $n$ 阶可逆矩阵， $\mathbf {\vec u},\mathbf {\vec v}$ 是 $n$ 维列向量，且 $\mathbf A+\mathbf {\vec u}\mathbf {\vec v}^{T}$ 也是可逆矩阵，则：

   $$(\mathbf A+\mathbf {\vec u}\mathbf {\vec v}^{T})^{-1}=\mathbf A^{-1}-\frac{\mathbf A^{-1}\mathbf {\vec u}\mathbf {\vec v}^{T}\mathbf A^{-1}}{1+\mathbf {\vec v}^{T}\mathbf A^{-1}\mathbf {\vec u}}$$

   .

六、 约束优化

1. 在有的最优化问题中，希望输入 $\mathbf {\vec x}$ 位于特定的集合 $\mathbb S$ 中，这称作约束优化问题。

   集合$\mathbb S$ 内的点 $\mathbf {\vec x}$ 称作可行解。集合 $\mathbb S$ 也称作可行域。

2. 约束优化的一个简单方法是：对梯度下降法进行修改，每次迭代后，将得到的新的 $\mathbf {\vec x}$ 映射到集合 $\mathbb S$ 中。

   如果使用线性搜索：则每次只搜索那些使得新的 $\mathbf {\vec x}$ 位于集合 $\mathbb S$ 中的那些 $\epsilon$ 。

   • 另一个做法：将线性搜索得到的新的 $\mathbf {\vec x}$ 映射到集合 $\mathbb S$ 中。
   • 或者：在线性搜索之前，将梯度投影到可行域的切空间内。

3. 在约束最优化问题中，常常利用拉格朗日对偶性将原始问题转换为对偶问题，通过求解对偶问题而得到原始问题的解。

4. 约束最优化问题的原始问题：假设 $f(\mathbf {\vec x}),c_i(\mathbf {\vec x}),h_j(\mathbf {\vec x})$ 是定义在 $\mathbb R^{n}$ 上的连续可微函数。考虑约束最优化问题：

   $$\min_{\mathbf {\vec x} \in \mathbb R^{n}}f(\mathbf {\vec x})\\ s.t. \quad c_i(\mathbf {\vec x}) \le 0,i=1,2,\cdots,k \;;\quad h_j(\mathbf {\vec x})=0,j=1,2,\cdots,l$$

   可行域由等式和不等式确定：$\mathbb S=\{\mathbf {\vec x} \mid c_i(\mathbf {\vec x}) \le 0,i=1,2,\cdots,k \;;\quad h_j(\mathbf {\vec x})=0,j=1,2,\cdots,l\}$ 。

6.1 原始问题

1. 引入拉格朗日函数：

   $$L(\mathbf {\vec x},\vec \alpha,\vec\beta)=f(\mathbf {\vec x})+\sum_{i=1}^{k}\alpha_ic_i(\mathbf {\vec x})+\sum_{j=1}^{l}\beta_jh_j(\mathbf {\vec x})$$

   这里 $\mathbf {\vec x}=(x_1,x_2,\cdots,x_n)^{T} \in \mathbb R^{n}, \alpha_i,\beta_j$ 是拉格朗日乘子， $\alpha_i \ge 0$ 。

   $L(\mathbf {\vec x}, \vec \alpha,\vec\beta)$ 是 $\mathbf {\vec x}, \vec \alpha,\vec \beta$ 的多元非线性函数。

2. 定义函数：

   $$\theta_P(\mathbf {\vec x})=\max_{\vec \alpha,\vec\beta\;:\;\alpha_i \ge 0}L(\mathbf {\vec x},\vec \alpha, \vec\beta)$$

   其中下标 $P$ 表示原始问题。则有：

   $$\theta_P(\mathbf {\vec x})= \begin{cases} f(\mathbf {\vec x}), & \text{if $\mathbf {\vec x}$ statisfy original problem's constraint} \\ +\infty, & \text{or else.} \end{cases}$$

   • 若 $\mathbf {\vec x}$ 满足原问题的约束，则很容易证明 $L(\mathbf {\vec x},\vec \alpha,\vec\beta)=f(\mathbf {\vec x})+\sum_{i=1}^{k}\alpha_ic_i(\mathbf {\vec x}) \le f(\mathbf {\vec x})$ ，等号在 $\alpha_i=0$ 时取到。

   • 若 $\mathbf {\vec x}$ 不满足原问题的约束：

     • 若不满足 $c_i(\mathbf {\vec x}) \le 0$ ：设违反的为 $c_{i_0}(\mathbf {\vec x}) \gt 0$，则令 $\vec \alpha_{i_0} \rightarrow \infty$，有：$L(\mathbf {\vec x},\vec \alpha,\vec\beta)=f(\mathbf {\vec x})+\sum_{i=1}^{k}\alpha_ic_i(\mathbf {\vec x}) \rightarrow \infty$ 。
     • 若不满足 $h_j(\mathbf {\vec x}) = 0$ ： 设违反的为 $h_{j_0}(\mathbf {\vec x}) \ne 0$，则令 $\vec\beta_{j_0}h_{j_0}(\mathbf {\vec x}) \rightarrow \infty$，有：$L(\mathbf {\vec x},\vec \alpha,\vec\beta)=f(\mathbf {\vec x})+\sum_{i=1}^{k}\alpha_ic_i(\mathbf {\vec x})+\vec\beta_{j_0}h_{j_0}(\mathbf {\vec x}) \rightarrow \infty$ 。

3. 考虑极小化问题：

   $$\min_{\mathbf {\vec x}} \theta_P(\mathbf {\vec x})=\min_{\mathbf {\vec x}}\max_{\vec \alpha,\vec\beta\;:\;\alpha_i \ge 0}L(\mathbf {\vec x},\vec \alpha, \vec\beta)$$

   则该问题是与原始最优化问题是等价的，即他们有相同的问题。

   • $\min_{\mathbf {\vec x}}\max_{\vec \alpha,\vec\beta\;:\;\alpha_i \ge 0}L(\mathbf {\vec x},\vec \alpha, \vec\beta)$ 称为广义拉格朗日函数的极大极小问题。
   • 为了方便讨论，定义原始问题的最优值为：$p^{*}=\min_{\mathbf {\vec x}}\theta_P(\mathbf {\vec x})$ 。

6.2 对偶问题

1. 定义 $\theta_D(\vec \alpha,\vec\beta)=\min_\mathbf {\vec x} L(\mathbf {\vec x},\vec \alpha,\vec\beta)$，考虑极大化 $\theta_D(\vec \alpha,\vec\beta)$，即：

   $$\max_{\vec \alpha,\vec\beta\;:\;\alpha_i \ge 0}\theta_D(\vec \alpha,\vec\beta)=\max_{\vec \alpha,\vec\beta\;:\;\alpha_i \ge 0} \min_{\mathbf {\vec x}}L(\mathbf {\vec x},\vec \alpha, \vec\beta)$$

   问题 $\max_{\vec \alpha,\vec\beta\;:\;\alpha_i \ge 0} \min_{\mathbf {\vec x}}L(\mathbf {\vec x},\vec \alpha, \vec\beta)$ 称为广义拉格朗日函数的极大极小问题。它可以表示为约束最优化问题：

   $$\max_{\vec \alpha,\vec\beta\;:\;\alpha_i \ge 0}\theta_D(\vec \alpha,\vec\beta)=\max_{\vec \alpha,\vec\beta\;:\;\alpha_i \ge 0} \min_{\mathbf {\vec x}}L(\mathbf {\vec x},\vec \alpha, \vec\beta)\\ s.t. \alpha_i \ge 0, i=1,2,\cdots,k$$

   称为原始问题的对偶问题。

   为了方便讨论，定义对偶问题的最优值为：$d^*=\max_{\vec \alpha,\vec\beta\;:\;\alpha_i \ge 0}\theta_D(\vec \alpha,\vec\beta)$ 。

2. 定理一：若原问题和对偶问题具有最优值，则：

   $$d^{*}=\max_{\vec \alpha,\vec\beta\;:\;\vec \alpha_i \ge 0}\min_{\mathbf {\vec x}}L(\mathbf {\vec x},\vec \alpha, \vec\beta) \le \min_{\mathbf {\vec x}}\max_{\vec \alpha,\vec\beta\;:\;\vec \alpha_i \ge 0}L(\mathbf {\vec x},\vec \alpha, \vec\beta)=p^{*}$$

   • 推论一：设 $\mathbf {\vec x}^{*}$ 为原始问题的可行解，且 $\theta_P(\mathbf {\vec x}^{*})$ 的值为 $p^{*}$ ； $\vec \alpha^{*},\vec\beta^{*}$ 为对偶问题的可行解， $\theta_D(\vec \alpha^{*},\vec\beta^{*})$ 值为 $d^{*}$。

     如果有 $p^{*}=d^{*}$，则 $\mathbf {\vec x}^{*},\vec \alpha^{*},\vec\beta^{*}$ 分别为原始问题和对偶问题的最优解。

3. 定理二：假设函数 $f(\mathbf {\vec x})$ 和 $c_i(\mathbf {\vec x})$ 为凸函数， $h_j(\mathbf {\vec x})$ 是仿射函数；并且假设不等式约束 $c_i(\mathbf {\vec x})$ 是严格可行的，即存在$\mathbf {\vec x}$ ，对于所有 $i$ 有 $c_i(x) \lt 0$。则存在 $\mathbf {\vec x}^{*},\vec \alpha^{*},\vec\beta^{*}$ ，使得： $\mathbf {\vec x}^{*}$ 是原始问题 $\min_{\mathbf {\vec x}}\theta_P(\mathbf {\vec x})$ 的解，$\vec \alpha^{*},\vec\beta^{*}$ 是对偶问题 $\max_{\vec \alpha,\vec\beta\;:\;\alpha_i \ge 0}\theta_D(\vec \alpha,\vec\beta)$ 的解，并且 $p^{*}=d^{*}=L(\mathbf {\vec x}^{*},\vec \alpha^{*},\vec\beta^{*})$ 。

4. 定理三：假设函数 $f(\mathbf {\vec x})$ 和 $c_i(\mathbf {\vec x})$ 为凸函数， $h_j(\mathbf {\vec x})$ 是仿射函数；并且假设不等式约束 $c_i(\mathbf {\vec x})$ 是严格可行的，即存在$\mathbf {\vec x}$ ，对于所有 $i$ 有 $c_i(x) \lt 0$。则存在 $\mathbf {\vec x}^{*},\vec \alpha^{*},\vec\beta^{*}$ ，使得 $\mathbf {\vec x}^{*}$ 是原始问题 $\min_{\mathbf {\vec x}}\theta_P(\mathbf {\vec x})$ 的解，$\vec \alpha^{*},\vec\beta^{*}$ 是对偶问题 $\max_{\vec \alpha,\vec\beta\;:\;\alpha_i \ge 0}\theta_D(\vec \alpha,\vec\beta)$ 的解的充要条件是：$\mathbf {\vec x}^{*},\vec \alpha^{*},\vec\beta^{*}$ 满足下面的 Karush-kuhn-Tucker(KKT) 条件：

   $$\nabla_\mathbf {\vec x}L(\mathbf {\vec x}^{*},\vec \alpha^{*},\vec\beta^{*})=0\\ \nabla_\vec \alpha L(\mathbf {\vec x}^{*},\vec \alpha^{*},\vec\beta^{*})=0\\ \nabla_\vec\beta L(\mathbf {\vec x}^{*},\vec \alpha^{*},\vec\beta^{*})=0\\ \vec \alpha^{*}_ic_i(\mathbf {\vec x}^{*})=0,i=1,2,\cdots,k\\ c_i(\mathbf {\vec x}^{*})\le 0,i=1,2,\cdots,k\\ \vec \alpha^{*}_i \ge 0,i=1,2,\cdots,k\\ h_j(\mathbf {\vec x}^{*})= 0,j=1,2,\cdots,l$$

5. 仿射函数：仿射函数即由1阶多项式构成的函数。

   一般形式为 $f(\mathbf {\vec x}) = \mathbf A \mathbf {\vec x} + b$。这里：$\mathbf A$ 是一个 $m\times k$ 矩阵，$\mathbf {\vec x}$ 是一个 $k$ 维列向量，$b$ 是一个 $m$ 维列向量。

   它实际上反映了一种从 $k$ 维到 $m$ 维的空间线性映射关系。

6. 凸函数：设 $f$ 为定义在区间 $\mathcal X$ 上的函数，若对 $\mathcal X$ 上的任意两点 $\mathbf {\vec x}_1,\mathbf {\vec x}_2$ 和任意的实数 $\lambda \in (0,1)$，总有 $f(\lambda \mathbf {\vec x}_1+(1-\lambda)\mathbf {\vec x}_2) \ge \lambda f(\mathbf {\vec x}_1)+(1-\lambda)f(\mathbf {\vec x}_2)$ ，则 $f$ 称为 $\mathcal X$ 上的凸函数 。