隐马尔可夫模型
一、隐马尔可夫模型HMM
隐马尔可夫模型(
Hidden Markov model,HMM)是可用于序列标注问题的统计学模型,描述了由隐马尔可夫链随机生成观察序列的过程,属于生成模型。隐马尔可夫模型:隐马尔可夫模型是关于时序的概率模型,描述由一个隐藏的马尔可夫链随机生成不可观测的状态随机序列,再由各个状态生成一个观察而产生观察随机序列的过程。
- 隐藏的马尔可夫链随机生成的状态的序列称作状态序列。
- 每个状态生成一个观测,而由此产生的观测的随机序列称作观测序列。
- 序列的每一个位置又可以看作是一个时刻。
1.1 基本概念
设 是所有可能的状态的集合, 是所有可能的观测的集合,其中 是可能的状态数量, 是可能的观测数量。
- 是状态的取值空间, 是观测的取值空间 。
- 每个观测值 可能是标量,也可能是一组标量构成的集合,因此这里用加粗的黑体表示。状态值的表示也类似。
设 是长度为 的状态序列, 是对应的观测序列。
- 是一个随机变量,代表状态 。
- 是一个随机变量,代表观测 。
设 为状态转移概率矩阵
其中 ,表示在时刻 处于状态 的条件下,在时刻 时刻转移到状态 的概率。
设 为观测概率矩阵
其中 ,表示在时刻 处于状态 的条件下生成观测 的概率。
设 是初始状态概率向量: 是时刻 时处于状态 的概率。
根据定义有: 。
隐马尔可夫模型由初始状态概率向量 、状态转移概率矩阵 以及观测概率矩阵 决定。因此隐马尔可夫模型 可以用三元符号表示,即 : 。其中 称为隐马尔可夫模型的三要素:
- 状态转移概率矩阵 和初始状态概率向量 确定了隐藏的马尔可夫链,生成不可观测的状态序列。
- 观测概率矩阵 确定了如何从状态生成观测,与状态序列一起确定了如何产生观测序列。
从定义可知,隐马尔可夫模型做了两个基本假设:
齐次性假设:即假设隐藏的马尔可夫链在任意时刻 的状态只依赖于它在前一时刻的状态,与其他时刻的状态和观测无关,也与时刻 无关,即:
观测独立性假设,即假设任意时刻的观测值只依赖于该时刻的马尔可夫链的状态,与其他观测及状态无关,即:
.
1.2 生成算法
隐马尔可夫模型可以用于标注问题:给定观测的序列,预测其对应的状态序列。 如:词性标注问题中,状态就是单词的词性,观测就是具体的单词。在这个问题中:
状态序列:词性序列 。
观察序列:单词序列 。
生成方式:
- 给定初始状态概率向量 ,随机生成第一个词性。
- 根据前一个词性,利用状态转移概率矩阵 随机生成下一个词性。
- 一旦生成词性序列,则根据每个词性,利用观测概率矩阵 生成对应位置的观察,得到观察序列。
一个长度为 的观测序列的
HMM生成算法:输入:
- 隐马尔可夫模型
- 观测序列长度
输出:观测序列
算法步骤:
按照初始状态分布 产生状态 。
令 ,开始迭代。迭代条件为: 。迭代步骤为:
- 按照状态 的观测概率分布 生成 , 。
- 按照状态 的状态转移概率分布 产生状态 。
- 令 。
二、 HMM 基本问题
隐马尔可夫模型的 3 个基本问题:
概率计算问题:给定模型 和观测序列 ,计算观测序列 出现的概率 。即:评估模型 与观察序列 之间的匹配程度。
学习问题:已知观测序列 ,估计模型 的参数,使得在该模型下观测序列概率 最大。即:用极大似然估计的方法估计参数。
预测问题(也称为解码问题):已知模型 和观测序列 , 求对给定观测序列的条件概率 最大的状态序列 。即:给定观测序列,求最可能的对应的状态序列 。
如:在语音识别任务中,观测值为语音信号,隐藏状态为文字。解码问题的目标就是:根据观测的语音信号来推断最有可能的文字序列。
2.1 概率计算问题
给定隐马尔可夫模型 和观测序列 ,概率计算问题需要计算在模型 下观测序列 出现的概率 。
最直接的方法是按照概率公式直接计算:通过列举所有可能的、长度为 的状态序列 ,求各个状态序列 与观测序列 的联合概率 ,然后对所有可能的状态序列求和,得到 。
状态序列 的概率为:
给定状态序列 ,观测序列 的条件概率为:
和 同时出现的联合概率为:
对所有可能的状态序列 求和,得到观测序列 的概率:
上式的算法复杂度为 ,太复杂,实际应用中不太可行。
2.1.1 前向算法
给定隐马尔可夫模型 ,定义前向概率:在时刻 时的观测序列为 , 且时刻 时状态为 的概率为前向概率,记作:
根据定义, 是在时刻 时观测到 ,且在时刻 处于状态 的前向概率。则有:
:为在时刻 时观测到 ,且在时刻 处于状态 ,且在 时刻处在状态 的概率。
:为在时刻 观测序列为 ,并且在时刻 时刻处于状态 的概率。
考虑 ,则得到前向概率的地推公式:
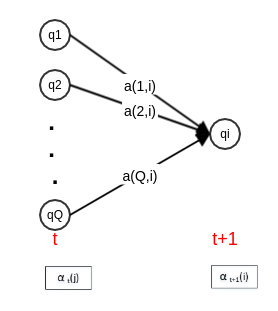
观测序列概率的前向算法:
输入:
- 隐马尔可夫模型
- 观测序列
输出: 观测序列概率
算法步骤:
计算初值: 。
该初值是初始时刻的状态 和观测 的联合概率。
递推:对于 :
终止: 。
因为 表示在时刻 ,观测序列为 ,且状态为 的概率。对所有可能的 个状态 求和则得到 。
前向算法是基于
状态序列的路径结构递推计算 。- 其高效的关键是局部计算前向概率,然后利用路径结构将前向概率“递推”到全局。
- 算法复杂度为 。
2.1.2 后向算法
给定隐马尔可夫模型 ,定义后向概率:在时刻 的状态为 的条件下,从时刻 到 的观测序列为 的概率为后向概率,记作: 。
在时刻 状态为 的条件下,从时刻 到 的观测序列为 的概率可以这样计算:
考虑 时刻状态 经过 转移到 时刻的状态 。
- 时刻状态为 的条件下,从时刻 到 的观测序列为观测序列为 的概率为 。
- 时刻状态为 的条件下,从时刻 到 的观测序列为观测序列为 的概率为 。
考虑所有可能的 ,则得到 的递推公式:
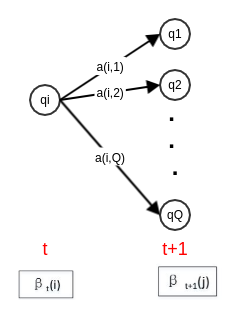
观测序列概率的后向算法:
输入:
- 隐马尔可夫模型
- 观测序列
输出: 观测序列概率
算法步骤:
计算初值:
对最终时刻的所有状态 ,规定 。
递推:对 :
终止:
为在时刻 1, 状态为 的条件下,从时刻 2 到 的观测序列为 的概率。对所有的可能初始状态 (由 提供其概率)求和并考虑 即可得到观测序列为 的概率。
2.1.3 统一形式
利用前向概率和后向概率的定义,可以将观测序列概率统一为:
当 时,就是后向概率算法;当 时,就是前向概率算法。
其意义为:在时刻 :
- 表示:已知时刻 时的观测序列为 、 且时刻 时状态为 的概率。
- 表示:已知时刻 时的观测序列为 、 且时刻 时状态为 、且 时刻状态为 的概率。
- 表示: 已知时刻 时的观测序列为 、 且时刻 时状态为 、且 时刻状态为 的概率。
- 表示:已知观测序列为 、 且时刻 时状态为 、且 时刻状态为 的概率。
- 对所有可能的状态 取值,即得到上式。
根据前向算法有: 。则得到:
由于 的形式不重要,因此有:
给定模型 和观测序列 的条件下,在时刻 处于状态 的概率记作:
根据定义:
根据前向概率和后向概率的定义,有: ,则有:
给定模型 和观测序列 ,在时刻 处于状态 且在 时刻处于状态 的概率记作:
根据
考虑到前向概率和后向概率的定义有: ,因此有:
一些期望值:
在给定观测 的条件下,状态 出现的期望值为: 。
在给定观测 的条件下,从状态 转移的期望值: 。
- 这里的转移,表示状态 可能转移到任何可能的状态。
- 假若在时刻 的状态为 ,则此时不可能再转移,因为时间最大为 。
在观测 的条件下,由状态 转移到状态 的期望值: 。
2.2 学习问题
根据训练数据的不同,隐马尔可夫模型的学习方法也不同:
- 训练数据包括观测序列和对应的状态序列:通过监督学习来学习隐马尔可夫模型。
- 训练数据仅包括观测序列:通过非监督学习来学习隐马尔可夫模型。
2.2.1 监督学习
假设数据集为 。其中:
- 为 个观测序列; 为对应的 个状态序列。
- 序列 , 的长度为 ,其中数据集中 之间的序列长度可以不同。
可以利用极大似然估计来估计隐马尔可夫模型的参数。
转移概率 的估计:设样本中前一时刻处于状态 、且后一时刻处于状态 的频数为 ,则状态转移概率 的估计是:
观测概率 的估计:设样本中状态为 并且观测为 的频数为 ,则状态为 并且观测为 的概率 的估计为:
初始状态概率的估计:设样本中初始时刻(即: )处于状态 的频数为 ,则初始状态概率 的估计为: 。
2.2.2 无监督学习
监督学习需要使用人工标注的训练数据。由于人工标注往往代价很高,所以经常会利用无监督学习的方法。
隐马尔可夫模型的无监督学习通常使用
Baum-Welch算法求解。在隐马尔可夫模型的无监督学习中,数据集为 。其中:
- 为 个观测序列。
- 序列 的长度为 ,其中数据集中 之间的序列长度可以不同。
将观测序列数据看作观测变量 , 状态序列数据看作不可观测的隐变量 ,则隐马尔可夫模型事实上是一个含有隐变量的概率模型: 。其参数学习可以由
EM算法实现。E步:求Q函数(其中 是参数的当前估计值)将 代入上式,有:
- 在给定参数 时, 是已知的常数,记做 。
- 在给定参数 时, 是 的函数,记做 。
根据 得到:
其中: 表示第 个序列的长度, 表示第 个观测序列的第 个位置。
M步:求Q函数的极大值:极大化参数在
Q函数中单独的出现在3个项中,所以只需要对各项分别极大化。:
将 代入,有:
将 代入,即有:
考虑到 ,以及 , 则有:
其物理意义为:统计在给定参数 ,已知 的条件下, 的出现的频率。它就是 的后验概率的估计值。
:同样的处理有:
得到:
考虑到 ,则有:
其物理意义为:统计在给定参数 ,已知 的条件下,统计当 的情况下 的出现的频率。它就是 的后验概率的估计值。
:同样的处理有:
得到:
其中如果第 个序列 的第 个位置 ,则 。
考虑到 ,则有:
其物理意义为:统计在给定参数 ,已知 的条件下,统计当 的情况下 的出现的频率。它就是 的后验概率的估计值。
令,其物理意义为:在序列 中,第 时刻的隐状态为 的后验概率。
令 ,其物理意义为:在序列 中,第 时刻的隐状态为 、且第 时刻的隐状态为 的后验概率。
则
M步的估计值改写为:其中 为示性函数,其意义为:当 的第 时刻为 时,取值为 1;否则取值为 0 。
Baum-Welch算法:输入:观测数据
输出:隐马尔可夫模型参数
算法步骤:
初始化:,选取 ,得到模型
迭代,迭代停止条件为:模型参数收敛。迭代过程为:
求使得
Q函数取极大值的参数:判断模型是否收敛。如果不收敛,则 ,继续迭代。
最终得到模型 。
2.3 预测问题
2.3.1 近似算法
近似算法思想:在每个时刻 选择在该时刻最有可能出现的状态 ,从而得到一个状态序列 ,然后将它作为预测的结果。
近似算法:给定隐马尔可夫模型 ,观测序列 ,在时刻 它处于状态 的概率为:
在时刻 最可能的状态: 。
近似算法的优点是:计算简单。
近似算法的缺点是:不能保证预测的状态序列整体是最有可能的状态序列,因为预测的状态序列可能有实际上不发生的部分。
- 近似算法是局部最优(每个点最优),但是不是整体最优的。
- 近似算法无法处理这种情况: 转移概率为 0 。因为近似算法没有考虑到状态之间的迁移。
2.3.2 维特比算法
维特比算法用动态规划来求解隐马尔可夫模型预测问题。
它用动态规划求解概率最大路径(最优路径),这时一条路径对应着一个状态序列。
维特比算法思想:
根据动态规划原理,最优路径具有这样的特性:如果最优路径在时刻 通过结点 , 则这一路径从结点 到终点 的部分路径,对于从 到 的所有可能路径来说,也必须是最优的。
只需要从时刻 开始,递推地计算从时刻 1 到时刻 且时刻 状态为 的各条部分路径的最大概率(以及取最大概率的状态)。于是在时刻 的最大概率即为最优路径的概率 ,最优路径的终结点 也同时得到。
之后为了找出最优路径的各个结点,从终结点 开始,由后向前逐步求得结点 ,得到最优路径 。
定义在时刻 状态为 的所有单个路径 中概率最大值为:
它就是算法导论中《动态规划》一章提到的“最优子结构”
则根据定义,得到变量 的递推公式:
定义在时刻 状态为 的所有单个路径中概率最大的路径的第 个结点为:
它就是最优路径中,最后一个结点(其实就是时刻 的 结点) 的前一个结点。
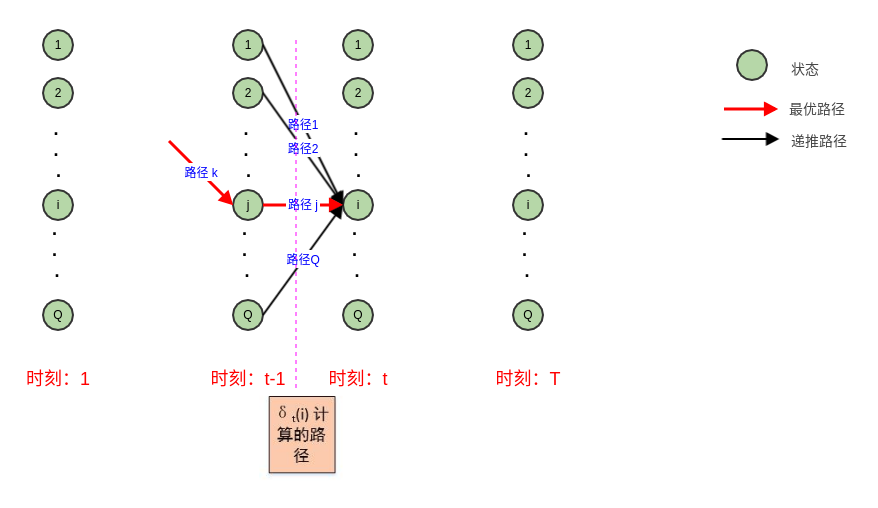
维特比算法:
输入:
- 隐马尔可夫模型
- 观测序列
输出:最优路径
算法步骤:
初始化:因为第一个结点的之前没有结点 ,所以有:
递推:对
终止: 。
最优路径回溯:对 : 。
最优路径 。
三、 最大熵马尔科夫模型MEMM
HMM存在两个基本假设:- 观察值之间严格独立。
- 状态转移过程中,当前状态仅依赖于前一个状态(一阶马尔科夫模型)。
如果放松第一个基本假设,则得到最大熵马尔科夫模型
MEMM。最大熵马尔科夫模型并不通过联合概率建模,而是学习条件概率 。
它刻画的是:在当前观察值 和前一个状态 的条件下,当前状态 的概率。
MEMM通过最大熵算法来学习。根据最大熵推导的结论:
这里 就是当前观测 和前一个状态 ,因此: 。这里 就是当前状态 ,因此: 。因此得到:
MEMM的参数学习使用最大熵中介绍的IIS算法或者拟牛顿法,解码任务使用维特比算法。标注偏置问题:
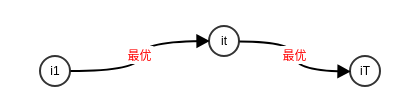
如下图所示,通过维特比算法解码得到:
可以看到:维特比算法得到的最优路径为 。
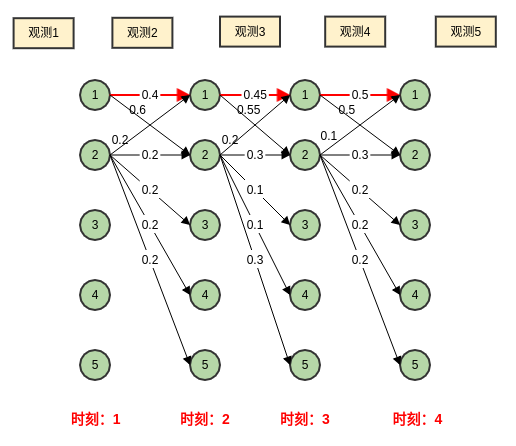
实际上,状态 倾向于转换到状态 ;同时状态 也倾向于留在状态 。但是由于状态 可以转化出去的状态较多,从而使得转移概率均比较小。
而维特比算法得到的最优路径全部停留在状态 1 ,这样与实际不符。
MEMM倾向于选择拥有更少转移的状态,这就是标记偏置问题。
标记偏置问题的原因是:计算 仅考虑局部归一化,它仅仅考虑指定位置的所有特征函数。
如上图中, 只考虑在 这个结点的归一化。
- 对于 ,其转出状态较多,因此每个转出概率都较小。
- 对于 ,其转出状态较少,因此每个转出概率都较大。
CRF解决了标记偏置问题,因为CRF是全局归一化的:它考虑了所有位置、所有特征函数。