一、FM [2011]

《Fast Context-aware Recommendations with Factorization Machines》

1. 推荐系统中的评级预测（rating prediction）主要依赖于以下信息：who（哪个用户）对 what（哪个 item，如电影、新闻、商品）如何 how 评级。有很多方法可以考虑关于 who （关于用户的人口统计信息，如年龄、性别、职业）、what （关于item 属性的信息，如电影类型、产品描述文本的关键词）的附加数据。

   除了有关评级事件（rating event）中涉及的实体的此类数据之外，还可能存在有关评级事件发生当前情况的信息，例如当前位置（location）、时间、周边的人、用户当前心情等等。这些场景信息通常称作上下文 （context）。因为从决策心理学知道一个人的环境和情绪确实会影响他们的行为，所以在推荐系统中利用上下文信息是可取的。上下文感知评级预测（context-aware rating prediction）依赖于谁（who）在何种上下文（context）下如何（how）评价什么（what）的信息。

   经典的推荐系统方法不考虑上下文信息。一些方法执行数据的预处理（pre-processing）或后处理（post-processing），使得标准方法具有上下文感知能力。虽然这种临时解决方案可能在实践中起作用，但是它们的缺点是过程中的所有步骤都需要监督和微调。

   将各种输入数据统一到一个模型中的方法在这方面更为实用，理论上也更为优雅。目前，在预测准确性方面最灵活和最强的方法是 Multiverse Recommendation ，它依赖于 Tucker 分解并允许使用任何离散型上下文（categorical context）。然而，对于现实世界的场景，它的计算复杂度 $O(d^K)$$O(d^K)$ 太高了，其中 $d$$d$ 是因子分解的维度，$K$$K$ 是所涉及变量的数量。

   在论文 《Fast Context-aware Recommendations with Factorization Machines》 中，作者提出了一种基于分解机 （Factorization Machine: FM）的上下文感知评级预测器。FM 包括并可以模拟推荐系统中最成功的方法，包括矩阵分解（matrix factorizion: MF）、SVD++、PITF 。

   • 作者展示了 FM 如何应用于各种上下文字段，包括离散型（categorical）字段、离散集合（set categorical）字段、实值（real-valued）字段。相比之下， Multiverse Recommendation 模型只适合于离散型（categorical）上下文变量。

   • 除了建模的灵活性之外，FM 的复杂度在 $d$$d$ 和 $K$$K$ 上都是线性的（即 $O(dK)$$O(dK)$），这允许使用上下文感知数据进行快速预测和学习。相比之下， Multiverse Recommendation 模型的复杂度是 $P(d^K)$$P(d^K)$ ，在 $d$$d$ 上是多项式的。

   • 为了学习 FM 模型的参数，论文提出了一种基于交替最小二乘法（alternating least squares: ALS）的新算法。新算法在给定其它参数的情况下找到一个参数的最优解，并且在几次迭代之后找到所有参数联合最优解。

     和随机梯度下降（stochastic gradient descent: SGD）一样，新算法单次迭代的复杂度为 $O(|\mathbb{S}|dK)$$O(|\mathbb S|dK)$，其中 $|\mathbb{S}|$$|\mathbb S|$ 为训练样本的数量。

     和 SGD 相比，新算法的主要优点是无需确定学习率。这在实践中非常重要，因为 SGD 学习的质量在很大程度上取决于良好的学习率，因此必须进行代价昂贵的搜索。这对于 ALS 来讲不是必需的。

   • 最后，论文的实验表明：上下文感知 FM 可以捕获上下文信息并提高预测准确性。此外 FM 在预测质量和运行时间方面都优于 SOTA 的方法 Multiverse Recommendation 。

1.1 相关工作

1. 推荐系统的大多数研究都集中在仅分析 user-item 交互的上下文无关方法上。在这里，矩阵分解（matrix factorization: MF）方法非常流行，因为它们通常优于传统的 knn 方法。

   也有研究将用户属性或 item 属性等元数据结合到预测中，从而扩展了矩阵分解模型。然而，如果存在足够的反馈数据，元数据对评分预测的强 baseline 方法通常只有很少或者没有改善。这种用户属性/item 属性和上下文之间的区别在于：属性仅仅被附加到 item 或者用户（例如，给电影附加一个流派的属性），而上下文被附加到整个评级事件（如，当评级发生时用户当时的心情）。

   和关于标准推荐系统的大量文献相比，上下文感知推荐系统的研究很少。最基本的方法是上下文预过滤（pre-filtering）和后过滤 （post-filtering），其中应用标准的上下文无关推荐系统，并在应用推荐器（recommender）之前基于感兴趣的上下文对数据进行预处理、或者对结果进行后处理。更复杂的方法是同时使用所有上下文和 user-item 信息来进行预测。

   也有人建议将上下文视为动态的用户特征，即可以动态变化。另外有一些关于 item 预测的上下文感知推荐系统的研究，将推荐视为一个排序任务，而本文将推荐视为回归任务。

2. Multiverse Recommendation 基于Tucker 分解技术来直接分解用户张量、item 张量、所有离散上下文变量的张量，从而求解该问题。它将原始的评分矩阵分解为一个小的矩阵 $\mathbf{B}$$\mathbf B$ 和 $K$$K$ 个因子矩阵 ${\mathbf{V}}^{(k)}$$\mathbf V^{(k)}$ ：

   $$\hat{y}=f(u,i,c_3,\cdots ,c_K)=\sum _{l_1=1}^{d_1}\cdots \sum _{l_K=1}^{d_K}{b}_{l_1,\cdots ,l_K}\times [v_{u,l_1}^{(U)}\times v_{i,l_2}^{(I)}\times \prod _{k=3}^K{v}_{c_k,l_k}^{(C_k)}]$$

   其中：

   $$\begin{array}{c}\mathbf{B}\in {\mathbb{R}}^{d_1\times d_2\times \cdots \times d_K}\\ {\mathbf{V}}^{(U)}\in {\mathbb{R}}^{M\times d_1},{\mathbf{V}}^{(I)}\in {\mathbb{R}}^{N\times d_2},{\mathbf{V}}^{(C_k)}\in {\mathbb{R}}^{|{\mathbb{C}}_k|\times d_k}\end{array}$$

   这种方式存在三个问题：

   • 计算复杂度太高：假设每个特征的维度都是 $d$$d$ ，则计算复杂度为 $O(d^K)$$O(d^K)$ 。一旦上下文特征数量 $K$$K$ 增加，则计算复杂度指数型增长。

   • 仅能对离散型（categorical）上下文特征建模：无法处理数值型特征、离散集合型（categorical set）特征。

   • 交互特征高度稀疏：这里执行的是 K 路特征交互（前面的 POLY2 模型是两路特征交互），由于真实应用场景中单个特征本身就已经很稀疏，K 路特征交互使得数据更加稀疏，难以准确的预估模型参数。

3. Attribute-aware Recommendation：与通用上下文感知方法的工作对比，对属性感知或专用推荐系统的研究要多得多。有一些工作可以处理用户属性和 item 属性的矩阵分解模型的扩展，还有一些关于考虑时间效应的工作。然而，所有这些方法都是为特定问题设计的，无法处理我们在本工作中研究的上下文感知推荐的通用设置。

   当然，对于特定的和重要的问题（如时间感知推荐或属性感知推荐），专用模型的研究是有益的。但是另一方面，研究上下文感知的通用方法也很重要，因为它们提供了最大的灵活性，并且可以作为专用模型的强 baseline 。

4. Alternating Least Square Optimization：对于矩阵分解模型，Bell 和 Koren 提出了一种交替优化所有 user factor 和所有 item factor 的 ALS 方法。由于所有user/item 的整个 factor matrix 是联合优化的，因此计算复杂度为 $O(d^3)$$O(d^3)$ 。标准 ALS 的这种复杂度问题是 SGD 方法在推荐系统文献中比 ALS 更受欢迎的原因。

   Pilaszy 等人提出一个接一个地优化每个user/item 中的 factor，这导致 ALS 算法复杂度为 $O(d)$$O(d)$ ，因为避免了矩阵求逆。一次优化一个factor 的思路与我们将 ALS 算法应用于FM 的思路相同。

   这两种方法仅适用于矩阵分解，因此无法处理任何上下文，例如我们提出的对所有交互进行建模的 FM 中的上下文。此外，我们的 ALS 算法还学习了全局bias 和基本的 1-way 效应。

1.2 模型

1. FM 模型是一个通用模型，它包含并可以模拟几个最成功的推荐系统，其中包括矩阵分解（matrix factorization: MF）、SVD++、PITF。我们首先简要概述了 FM 模型，然后详细展示了如何将其应用于上下文感知数据，以及在 FM 中使用这种上下文感知数据会发生什么。最后我们提出了一种新的快速 alternating least square: ALS 算法，和 SGD 算法相比它更容易应用，因为它不需要学习率。

1.2.1 FM 模型

1. 推荐系统面临的问题是评分预测问题。给定用户集合 $\mathbb{U}=\{u_1,u_2,\cdots ,u_M\}$$\mathbb U=\{u_1,u_2,\cdots,u_M\}$ 、物品集合 $\mathbb{I}=\{i_1,i_2,\cdots ,i_N\}$$\mathbb I = \{i_1,i_2,\cdots,i_N\}$ ，模型是一个评分函数：

   $$f:\mathbb{U}\times \mathbb{I}\to \mathbb{R}$$

   $y=f(u,i)$$y=f(u,i)$ 表示用户 $u$$u$ 对物品 $i$$i$ 的评分。

   其中已知部分用户在部分物品上的评分：$\mathbb{S}\in \mathbb{U}\times \mathbb{I},\mathrm{\forall }(u,i)\in \mathbb{S},\tilde{y}=f(u,i)$$\mathbb S \in \mathbb U\times \mathbb I, \forall (u,i)\in \mathbb S,\tilde y=f(u,i)$ 。目标是求解剩余用户在剩余物品上的评分：

   $$\hat{y}=f(u,i),\mathrm{\forall }(u,i)\in {\complement }_{\mathbb{S}}$$

   其中 ${\complement }_{\mathbb{S}}$$\complement_\mathbb S$ 为 $\mathbb{S}$$\mathbb S$ 的补集。

   • 通常评分问题是一个回归问题，模型预测结果是评分的大小。此时损失函数采用MAE/MSE 等等。

     也可以将其作为一个分类问题，模型预测结果是各评级的概率。此时损失函数是交叉熵。

   • 当评分只有 0 和 1 时，这表示用户对商品 “喜欢/不喜欢”，或者 “点击/不点击”。这就是典型的点击率预估问题。

2. 事实上除了已知部分用户在部分物品上的评分之外，通常还能够知道一些有助于影响评分的额外信息。如：用户画像、用户行为序列等等。这些信息称作上下文（ context）。

   对每一种上下文，我们用变量 $c\in \mathbb{C}$$c \in \mathbb C$ 来表示，$\mathbb{C}$$\mathbb C$ 为该上下文的取值集合。假设所有的上下文为 ${\mathbb{C}}_3,\cdots ,{\mathbb{C}}_K$$\mathbb C_3,\cdots,\mathbb C_K$ ，则模型为：

   $$f:\mathbb{U}\times \mathbb{I}\times {\mathbb{C}}_3\times \cdots \times {\mathbb{C}}_K\to \mathbb{R}$$

   上下文的下标从 3 开始，因为可以任务用户 $u$$u$ 和商品 $i$$i$ 也是上下文的一种。

   如下图所示为评分矩阵，其中：

   $$\begin{array}{c}\mathbb{U}=\{\text{A},\text{B},\text{C}\},\mathbb{I}=\{\text{TI},\text{NH},\text{SW},\text{ST}\}\\ {\mathbb{C}}_3=\{\text{S},\text{N},\text{H}\},{\mathbb{C}}_4=\{\text{A},\text{B},\text{C}\}\\ y\in \{1,2,3,4,5\}\end{array}$$

   所有离散特征都经过one-hot 特征转换。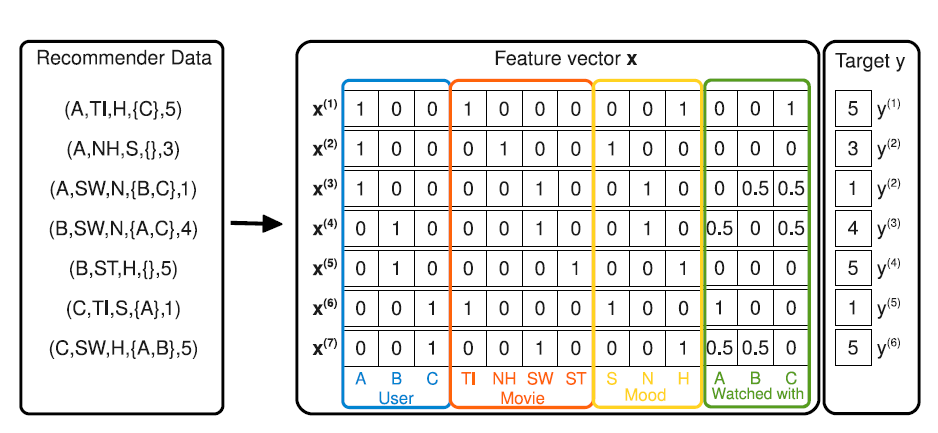

   

3. 上下文特征（context）类似属性（property）特征，它和属性特征的区别在于：

   • 属性特征是作用到整个用户（用户属性）或者整个物品（物品属性），其粒度是用户级别或者物品级别。

     如：无论用户 “张三” 在在评分矩阵中出现多少次，其性别属性不会发生改变。

   • 上下文特征是作用到用户的单个评分事件上，粒度是事件级别，包含的评分信息更充足。

     如：用户 ”张三“ 在评价某个电影之前已经看过的电影，该属性会动态改变。

   事实上属性特征也称作静态画像，上下文特征也称作动态画像。业界主流的做法是：融合静态画像和动态画像。

   另外，业界的经验表明：动态画像对于效果的提升远远超出静态画像。

4. 和 POLY2 相同FM也是对二路特征交互进行建模，但是FM 的参数要比 POLY2 少得多。

   将样本重写为：

   $$\overrightarrow{\mathbf{x}}=(x_1,x_2,x_3,\cdots ,x_K{)}^T=(u,i,c_3,\cdots ,c_K{)}^T$$

   则 FM 模型为：

   $$\hat{y}(\overrightarrow{\mathbf{x}})=w_0+\sum _{i=1}^K{w}_i\times x_i+\sum _{i=1}^K\sum _{j=i+1}^K{\hat{w}}_{i,j}\times x_i\times x_j$$

   其中 ${\hat{w}}_{i,j}$$\hat w_{i,j}$ 是交互特征的参数，它由一组参数定义：

   $${\hat{w}}_{i,j}=<{\overrightarrow{\mathbf{v}}}_i,{\overrightarrow{\mathbf{v}}}_j>=\sum _{l=1}^d{v}_{i,l}\times v_{j,l}$$

   即：

   $$\begin{array}{c}\hat{\mathbf{W}}=\left[\begin{array}{cccc}{\hat{w}}_{1,1}& {\hat{w}}_{1,2}& \cdots & {\hat{w}}_{1,K}\\ {\hat{w}}_{2,1}& {\hat{w}}_{2,2}& \cdots & {\hat{w}}_{2,K}\\ ⋮& ⋮& \ddots & ⋮\\ {\hat{w}}_{K,1}& {\hat{w}}_{K,2}& \cdots & {\hat{w}}_{K,K}\end{array}\right]={\mathbf{V}}^T\mathbf{V}=\left[\begin{array}{c}{\overrightarrow{\mathbf{v}}}_1^T\\ {\overrightarrow{\mathbf{v}}}_2^T\\ ⋮\\ {\overrightarrow{\mathbf{v}}}_K^T\end{array}\right]\left[\begin{array}{cccc}{\overrightarrow{\mathbf{v}}}_1& {\overrightarrow{\mathbf{v}}}_2& \cdots & {\overrightarrow{\mathbf{v}}}_K\end{array}\right]\end{array}$$

   模型待求解的参数为：

   $$\begin{array}{c}{w}_0\in \mathbb{R},\overrightarrow{\mathbf{w}}\in {\mathbb{R}}^K\\ \mathbf{V}=({\overrightarrow{\mathbf{v}}}_1,\cdots ,{\overrightarrow{\mathbf{v}}}_K)\in {\mathbb{R}}^{d\times K}\end{array}$$

   其中：

   • $w_0$$w_0$ 表示全局偏差。

   • $w_i$$w_i$ 用于捕捉第 $i$$i$ 个特征和目标之间的关系。

   • ${\hat{w}}_{i,j}$$\hat w_{i,j}$ 用于捕捉 $(i,j)$$(i,j)$ 二路交互特征和目标之间的关系。

   • ${\overrightarrow{\mathbf{v}}}_i$$\mathbf{\vec v}_i$ 代表特征 $i$$i$ 的representation vector，它是 $\mathbf{V}$$\mathbf V$ 的第 $i$$i$ 列。

5. FM 模型的计算复杂度为 $O(K\times K\times d)=O(K^{2}d)$$O(K\times K\times d) = O(K^2d)$ ，但是经过数学转换之后其计算复杂度可以降低到 $O(Kd)$$O(Kd)$ ：

   $$\begin{array}{c}\sum _{i=1}^K\sum _{j=i+1}^K{\hat{w}}_{i,j}\times x_i\times x_j=\sum _{i=1}^K\sum _{j=i+1}^K\sum _{l=1}^d{v}_{i,l}\times v_{j,l}\times x_i\times x_j\\ =\sum _{l=1}^d(\sum _{i=1}^K\sum _{j=i+1}^K(v_{i,l}\times x_i)\times (v_{j,l}\times x_j))\\ =\sum _{l=1}^d\frac{1}{2}({(\sum _{i=1}^K{v}_{i,l}\times x_i)}^2-\sum _{i=1}^K{v}_{i,l}^2\times x_i^2)\end{array}$$

   因此有：

   $$\hat{y}(\overrightarrow{\mathbf{x}})=w_0+\sum _{i=1}^K{w}_i\times x_i+\frac{1}{2}\sum _{l=1}^d({(\sum _{i=1}^K{v}_{i,l}\times x_i)}^2-\sum _{i=1}^K{v}_{i,l}^2\times x_i^2)$$

   其计算复杂度为 $O(Kd)$$O(Kd)$ 。

6. 将 FM 模型和标准的矩阵分解模型进行比较，可以看到：FM 也恰好包含这种分解 $<{\overrightarrow{\mathbf{v}}}_i,{\overrightarrow{\mathbf{v}}}_u>$$<\mathbf{\vec v}_i,\mathbf{\vec v}_u>$ 。此外，FM 模型还包含了所有上下文变量的所有 pair 对的交互。这表明 FM 自动包含了矩阵分解模型。

7. FM 模型可以用于求解分类问题（预测各评级的概率），也可以用于求解回归问题（预测各评分大小）。

   • 对于回归问题，其损失函数为MSE 均方误差：

     $$\mathcal{L}=\sum _{(\overrightarrow{\mathbf{x}},y)\in \mathbb{S}}{(\hat{y}(\overrightarrow{\mathbf{x}})-y)}^2+\sum _{\theta \in \mathbf{\Theta }}{\lambda }_{\theta }\times {\theta }^2$$

   • 对于二分类问题，其损失函数为交叉熵：

     $$\begin{array}{c}\varphi (\overrightarrow{\mathbf{x}})=w_0+\sum _{i=1}^K{w}_i\times x_i+\frac{1}{2}\sum _{l=1}^d({(\sum _{i=1}^K{v}_{i,l}\times x_i)}^2-\sum _{i=1}^K{v}_{i,l}^2\times x_i^2)\\ p(\hat{y}=y\mid \overrightarrow{\mathbf{x}})=\frac{1}{1+\exp (-y\varphi (\overrightarrow{\mathbf{x}}))}\\ \mathcal{L}=(-\sum _{(\overrightarrow{\mathbf{x}},y)\in \mathbb{S}}\log p(\hat{y}=y\mid \overrightarrow{\mathbf{x}}))+\sum _{\theta \in \mathbf{\Theta }}{\lambda }_{\theta }\times {\theta }^2\end{array}$$

     其中：

     • 评级集合为 $y\in \{-1,1\}$$y\in \{-1,1 \}$ 一共两个等级。

     • $p(\hat{y}=y\mid \overrightarrow{\mathbf{x}})$$p(\hat y=y\mid \mathbf{\vec x})$ 为样本 $\overrightarrow{\mathbf{x}}$$\mathbf{\vec x}$ 预测为评级 $y$$y$ 的概率，满足：

   $$\begin{array}{c}p(\hat{y}=1\mid \overrightarrow{\mathbf{x}})=\frac{1}{1+\exp (-\varphi (\overrightarrow{\mathbf{x}}))}\\ p(\hat{y}=-1\mid \overrightarrow{\mathbf{x}})=\frac{1}{1+\exp (\varphi (\overrightarrow{\mathbf{x}}))}\end{array}$$

   损失函数最后一项是正则化项，为了防止过拟合，$\mathbf{\Theta }=\{w_0,\overrightarrow{\mathbf{w}},\mathbf{V}\}$$\mathbf \Theta = \{w_0,\mathbf{\vec w}, \mathbf V\}$ 。其中 ${\lambda }_{\theta }$$\lambda_\theta$ 为参数 $\theta$$\theta$ 的正则化系数，它是模型的超参数。

   可以针对每个参数配置一个正则化系数，但是选择合适的值需要进行大量的超参数选择。论文推荐进行统一配置：

   • 对于 $w_0$$w_0$，正则化系数为 ${\lambda }_{w_0}=0$$\lambda_{w_0} = 0$ ，这表示不需要对全局偏差进行正则化。

   • 对于 $w_i$$w_i$，统一配置正则化系数为 ${\lambda }_w$$\lambda_w$ 。

   • 对于 $v_{i,l}$$v_{i,l}$，统一配置正则化系数为 ${\lambda }_v$$\lambda_v$ 。

8. FM 模型可以处理不同类型的特征：

   • 离散型特征 （categorical）：FM 对离散型特征执行 one-hot 编码。

     如，性别特征：“男” 编码为 (0,1)，“女” 编码为 (1,0) 。

   • 离散集合特征（ categorical set）：FM 对离散集合特征执行类似 one-hot 的形式，但是执行样本级别的归一化。

     如，看过的历史电影。假设电影集合为：“速度激情9，战狼，泰囧，流浪地球”。如果一个人看过 “战狼，泰囧，流浪地球”， 则编码为 (0,0.33333,0.33333,0.33333) 。

   • 数值型特征（real valued）：FM直接使用数值型特征，不做任何编码转换。

9. FM 的优势：

   • 给定特征 representation 向量的维度时，预测期间计算复杂度是线性的。

   • 在交互特征高度稀疏的情况下，参数仍然能够估计。

     因为交互特征的参数不仅仅依赖于这个交互特征，还依赖于所有相关的交互特征。这相当于增强了有效的学习数据。

   • 能够泛化到未被观察到的交互特征。

     设交互特征 “看过电影 A且 年龄等于20” 从未在训练集中出现，但出现了 “看过电影 A” 相关的交互特征、以及 “年龄等于20” 相关的交互特征。

     于是可以从这些交互特征中分别学习 “看过电影 A” 的 representation 、 “年龄等于20”的 representation，最终泛化到这个未被观察到的交互特征。

1.2.2 ALS 优化算法

a. 最优化解

1. FM 的目标函数最优化可以直接采用随机梯度下降 SGD 算法求解，但是采用 SGD 有个严重的问题：需要选择一个合适的学习率。

   • 学习率必须足够大，从而使得 SGD 能够尽快的收敛。学习率太小则收敛速度太慢。

   • 学习率必须足够小，从而使得梯度下降的方向尽可能朝着极小值的方向。

     由于 SGD 计算的梯度是真实梯度的估计值，引入了噪音。较大的学习率会放大噪音的影响，使得前进的方向不再是极小值的方向。

   我们提出了一种新的交替最小二乘（ alternating least square:ALS ）算法来求解 FM 目标函数的最优化问题。与 SGD 相比ALS 优点在于无需设定学习率，因此调参过程更简单。

2. 根据定义：

   $$\hat{y}(\overrightarrow{\mathbf{x}};\mathbf{\Theta })=w_0+\sum _{i=1}^K{w}_i\times x_i+\frac{1}{2}\sum _{l=1}^d({(\sum _{i=1}^K{v}_{i,l}\times x_i)}^2-\sum _{i=1}^K{v}_{i,l}^2\times x_i^2)$$

   对每个 $\theta \in \mathbf{\Theta }=\{w_0,\overrightarrow{\mathbf{w}},\mathbf{V}\}$$\theta \in \mathbf \Theta = \{w_0,\mathbf{\vec w}, \mathbf V\}$ ，可以将 $\hat{y}$$\hat y$ 分解为 $\theta$$\theta$ 的线性部分和偏置部分：

   $$\hat{y}(\overrightarrow{\mathbf{x}};\mathbf{\Theta })=h_{\theta }(\overrightarrow{\mathbf{x}})\times \theta +g_{\theta }(\overrightarrow{\mathbf{x}})$$

   其中 $g_{\theta }(\overrightarrow{\mathbf{x}}),h_{\theta }(\overrightarrow{\mathbf{x}})$$g_\theta(\mathbf{\vec x}), h_\theta(\mathbf{\vec x})$ 与 $\theta$$\theta$ 无关。如：

   • 对于 $w_0$$w_0$ 有：

     $$\begin{array}{c}{h}_{w_0}=1\\ g_{w_0}=\sum _{i=1}^K{w}_i\times x_i+\frac{1}{2}\sum _{l=1}^d({(\sum _{i=1}^K{v}_{i,l}\times x_i)}^2-\sum _{i=1}^K{v}_{i,l}^2\times x_i^2)\end{array}$$

   • 对于 $w_i,i=1,2\cdots ,K$$w_i,i=1,2\cdots,K$ 有：

     $$\begin{array}{c}{h}_{w_i}=x_i\\ g_{w_i}=w_0+\sum _{j=1,j\ne i}^K{w}_j\times x_j+\frac{1}{2}\sum _{l=1}^d({(\sum _{j=1}^K{v}_{j,l}\times x_j)}^2-\sum _{j=1}^K{v}_{j,l}^2\times x_j^2)\end{array}$$

   • 对于 $v_{i,l},i=1,2,\cdots ,K,l=1,2,\cdots ,d$$v_{i,l}, i=1,2,\cdots,K,l=1,2,\cdots,d$ 有：

     $$\begin{array}{c}{h}_{v_{i,l}}=\sum _{j=1,j\ne i}^K{v}_{j,l}\times x_j\times x_i\\ g_{v_{i,l}}=w_0+\sum _{j=1}^K{w}_j\times x_j+\sum _{i^{\prime }=1}^K\sum _{j^{\prime }=i^{\prime }+1}^K\sum _{\begin{array}{c}{l}^{\prime }=1,\\ l^{\prime }\ne l\mathrm{\&}{i}^{\prime }\ne i\mathrm{\&}{j}^{\prime }\ne i\end{array}}^d{v}_{i^{\prime },l^{\prime }}\times v_{j^{\prime },l^{\prime }}\times x_{i^{\prime }}\times x_{j^{\prime }}\end{array}$$

   因此有：

   $$\frac{\partial \hat{y}(\overrightarrow{\mathbf{x}};\mathbf{\Theta })}{\partial \theta }=h_{\theta }(\overrightarrow{\mathbf{x}})$$

   考虑均方误差损失函数：

   $$\mathcal{L}=\sum _{(\overrightarrow{\mathbf{x}},y)\in \mathbb{S}}{(\hat{y}(\overrightarrow{\mathbf{x}};\mathbf{\Theta })-y)}^2+\sum _{\theta \in \mathbf{\Theta }}{\lambda }_{\theta }\times {\theta }^2$$

   最小值点的偏导数为 0 ，有：

   $$\frac{\partial L}{\partial \theta }=2\sum _{(\overrightarrow{\mathbf{x}},y)\in \mathbb{S}}(\hat{y}(\overrightarrow{\mathbf{x}};\mathbf{\Theta })-y)\times \frac{\partial \hat{y}(\overrightarrow{\mathbf{x}};\mathbf{\Theta })}{\partial \theta }+2\times {\lambda }_{\theta }\times \theta =0$$

   则有：

   $$\theta =-\frac{\sum _{(\overrightarrow{\mathbf{x}},y)\in \mathbb{S}}(g_{\theta }(\overrightarrow{\mathbf{x}})-y)\times h_{\theta }(\overrightarrow{\mathbf{x}})}{(\sum _{(\overrightarrow{\mathbf{x}},y)\in \mathbb{S}}{h}_{\theta }^2(\overrightarrow{\mathbf{x}}))+{\lambda }_{\theta }}$$

3. ALS 通过多轮次、轮流迭代求解 $\theta \in \mathbf{\Theta }=\{w_0,\overrightarrow{\mathbf{w}},\mathbf{V}\}$$\theta \in \mathbf \Theta = \{w_0,\mathbf{\vec w}, \mathbf V\}$ 即可得到模型的最优解。

   • 在迭代之前初始化参数，其中： $w_0,\overrightarrow{\mathbf{w}}$$w_0,\mathbf{\vec w}$ 通过零初始化， $\mathbf{V}$$\mathbf V$ 的每个元素通过均值为0、方差为 $\sigma$$\sigma$ 的正太分布随机初始化。

   • 每一轮迭代时：

     • 首先求解 $w_0,\overrightarrow{\mathbf{w}}$$w_0,\mathbf{\vec w}$ ，因为相对于二阶交互的高阶特征，低阶特征有更多的数据来估计其参数，因此参数估计更可靠。

     • 然后求解 $\mathbf{V}$$\mathbf V$。这里按照维度优先的准确来估计：先估计所有 representation 向量的第 1 维度，然后是第 2 维，... 最后是第 d 维。

       这是为了计算优化的考量。

b. 计算优化

1. 直接求解 ALS 的解时复杂度较高：在每个迭代步中计算每个训练样本的 $g_{\theta }(\overrightarrow{\mathbf{x}})$$g_\theta(\mathbf{\vec x})$ 和 $h_{\theta }(\overrightarrow{\mathbf{x}})$$h_\theta(\mathbf{\vec x})$ 。

   对于每个样本，求解 $g_{\theta }(\overrightarrow{\mathbf{x}})$$g_\theta(\mathbf{\vec x})$ 和 $h_{\theta }(\overrightarrow{\mathbf{x}})$$h_\theta(\mathbf{\vec x})$ 的计算复杂度为：

   • 计算 $h_{w_0}(\overrightarrow{\mathbf{x}})$$h_{w_0}(\mathbf{\vec x})$ 的复杂度为 $O(1)$$O(1)$ ，计算 $g_{w_0}(\overrightarrow{\mathbf{x}})$$g_{w_0}(\mathbf{\vec x})$ 的复杂度为 $O(Kd)$$O(Kd)$ 。

   • 计算 $h_{w_i}(\overrightarrow{\mathbf{x}})$$h_{w_i}(\mathbf{\vec x})$ 的复杂度为 $O(1)$$O(1)$ ，计算 $g_{w_i}(\overrightarrow{\mathbf{x}})$$g_{w_i}(\mathbf{\vec x})$ 的复杂度为 $O(Kd)$$O(Kd)$ 。

   • 计算 $h_{v_{i,l}}(\overrightarrow{\mathbf{x}})$$h_{v_{i,l}}(\mathbf{\vec x})$ 的复杂度为 $O(K)$$O(K)$ ，计算 $g_{v_{i,l}}(\overrightarrow{\mathbf{x}})$$g_{v_{i,l}}(\mathbf{\vec x})$ 的复杂度为 $O(K^{2}d)$$O(K^2d)$ 。

   因此求解 $\theta$$\theta$ 的计算复杂度为 $O(|\mathbb{S}|\times K^2\times d)$$O(|\mathbb S|\times K^2\times d)$ 。

2. 有三种策略来降低求解 $\theta$$\theta$ 的计算复杂度，从 $O(|\mathbb{S}|\times K^2\times d)$$O(|\mathbb S|\times K^2\times d)$ 降低到 $O(|\mathbb{S}|\times \overline{K}\times d)$$O(|\mathbb S|\times \bar K\times d)$ ，其中 $\overline{K}$$\bar K$ 表示平均非零特征的数量：

   • 利用预计算的误差项 $e$$e$ 降低 $(g_{\theta }(\overrightarrow{\mathbf{x}})-y)$$(g_\theta(\mathbf{\vec x})-y)$ 的计算代价 。

   • 利用预计算的 $q$$q$ 项降低交互特征的 $h_{\theta }$$h_\theta$ 的计算代价。

   • 利用数据集 $\mathbb{S}$$\mathbb S$ 的稀疏性降低整体计算代价。

3. 预计算误差项 $e$$e$ ：

   定义误差项：

   $$e(\overrightarrow{\mathbf{x}},y;\mathbf{\Theta }):=\hat{y}(\overrightarrow{\mathbf{x}};\mathbf{\Theta })-y$$

   考虑到 $\hat{y}(\overrightarrow{\mathbf{x}};\mathbf{\Theta })=h_{\theta }(\overrightarrow{\mathbf{x}})\times \theta +g_{\theta }(\overrightarrow{\mathbf{x}})$$\hat y(\mathbf{\vec x};\mathbf \Theta) = h_{\theta}(\mathbf{\vec x}) \times \theta +g_\theta(\mathbf{\vec x})$ ，则有：

   $$g_{\theta }(\overrightarrow{\mathbf{x}})-y=e(\overrightarrow{\mathbf{x}},y;\mathbf{\Theta })-\theta \times h_{\theta }(\overrightarrow{\mathbf{x}})$$

   因此如果计算 $e(\overrightarrow{\mathbf{x}},y;\mathbf{\Theta })$$e(\mathbf{\vec x},y;\mathbf \Theta)$ 的计算代价较低，则计算 $(g_{\theta }(\overrightarrow{\mathbf{x}})-y)$$(g_\theta(\mathbf{\vec x})-y)$ 的计算复杂度也会降低。

   • 首先对每个样本，计算其初始误差：

     $$\overrightarrow{\mathbf{e}}={(e({\overrightarrow{\mathbf{x}}}_1,y_1;\mathbf{\Theta }),\cdots ,e({\overrightarrow{\mathbf{x}}}_{|\mathbb{S}|},y_{|\mathbb{S}|};\mathbf{\Theta }))}^T\in {\mathbb{R}}^{|\mathbb{S}|}$$

     考虑到 $\hat{y}$$\hat y$ 的计算复杂度为 $O(K\times d)$$O(K\times d)$ ，因此 $\overrightarrow{\mathbf{e}}$$\mathbf{\vec e}$ 的计算复杂度为 $O(|\mathbb{S}|\times K\times d)$$O(|\mathbb S|\times K\times d)$ 。

   • 当参数 $\theta$$\theta$ 更新到 ${\theta }^{\ast }$$\theta^*$ 时，重新计算误差：

     $$\begin{array}{c}e(\overrightarrow{\mathbf{x}},y;{\mathbf{\Theta }}^{\ast })=\hat{y}(\overrightarrow{\mathbf{x}};{\mathbf{\Theta }}^{\ast })-y=h_{\theta }(\overrightarrow{\mathbf{x}})\times {\theta }^{\ast }+g_{\theta }(\overrightarrow{\mathbf{x}})-y\\ =h_{\theta }(\overrightarrow{\mathbf{x}})\times \theta +g_{\theta }(\overrightarrow{\mathbf{x}})-y+h_{\theta }(\overrightarrow{\mathbf{x}})({\theta }^{\ast }-\theta )\\ =e(\overrightarrow{\mathbf{x}},y;\mathbf{\Theta })+h_{\theta }(\overrightarrow{\mathbf{x}})({\theta }^{\ast }-\theta )\end{array}$$

     计算代价由 $h_{\theta }(\overrightarrow{\mathbf{x}})$$h_\theta(\mathbf{\vec x})$ 决定 （根据下面的讨论，其计算复杂度为 $O(1)$$O(1)$ ）。

4. 预计算 $q$$q$ 值：

   如果能够降低计算 $h_{\theta }(\overrightarrow{\mathbf{x}})$$h_\theta(\mathbf{\vec x})$ 的代价，则整体计算复杂度可以进一步降低。由于 $h_{w_0}(\overrightarrow{\mathbf{x}}),h_{w_i}(\overrightarrow{\mathbf{x}})$$h_{w_0}(\mathbf{\vec x}),h_{w_i}(\mathbf{\vec x})$ 的复杂度为 $O(1)$$O(1)$ ，因此重点考虑 $h_{v_{i,l}}(\overrightarrow{\mathbf{x}})$$h_{v_{i,l}}(\mathbf{\vec x})$ 的计算复杂度。

   重写 $h_{v_{i,l}}(\overrightarrow{\mathbf{x}})$$h_{v_{i,l}} (\mathbf{\vec x})$ ，有：

   $$h_{v_{i,l}}(\overrightarrow{\mathbf{x}})=\sum _{j=1,j\ne i}^K{v}_{j,l}\times x_j\times x_i=x_i\times [\sum _{j=1}^K{v}_{j,l}\times x_j]-v_{i,l}\times x_i^2$$

   定义：

   $$q(\overrightarrow{\mathbf{x}},l;\mathbf{\Theta }):=\sum _{j=1}^K{v}_{j,l}\times x_j$$

   因此如果计算 $q(\overrightarrow{\mathbf{x}},l;\mathbf{\Theta })$$q(\mathbf{\vec x},l;\mathbf\Theta)$ 的计算代价较低，则 $h_{v_{i,l}}(\overrightarrow{\mathbf{x}})$$h_{v_{i,l}}(\mathbf{\vec x})$ 的计算复杂度也会降低。

   • 对每个样本、每个representation 向量维度计算初始 $q$$q$ 值：

     $$\begin{array}{c}\mathbf{Q}=\left[\begin{array}{cccc}q({\overrightarrow{\mathbf{x}}}_1,1;\mathbf{\Theta })& q({\overrightarrow{\mathbf{x}}}_1,2;\mathbf{\Theta })& \cdots & q({\overrightarrow{\mathbf{x}}}_1,d;\mathbf{\Theta })\\ q({\overrightarrow{\mathbf{x}}}_2,1;\mathbf{\Theta })& q({\overrightarrow{\mathbf{x}}}_2,2;\mathbf{\Theta })& \cdots & q({\overrightarrow{\mathbf{x}}}_2,d;\mathbf{\Theta })\\ ⋮& ⋮& \ddots & ⋮\\ q({\overrightarrow{\mathbf{x}}}_{|\mathbb{S}|},1;\mathbf{\Theta })& q({\overrightarrow{\mathbf{x}}}_{|\mathbb{S}|},2;\mathbf{\Theta })& \cdots & q({\overrightarrow{\mathbf{x}}}_{|\mathbb{S}|},d;\mathbf{\Theta })\end{array}\right]\in {\mathbb{R}}^{|\mathbb{S}|\times d}\end{array}$$

     计算复杂度为 $O(|\mathbb{S}|\times K\times d)$$O(|\mathbb S|\times K\times d)$。

   • 当参数 $v_{j,l}$$v_{j,l}$ 更新到 $v_{j,l}^{\ast }$$v_{j,l}^*$ 时，重新 $q$$q$ 值：

     $$q(\overrightarrow{\mathbf{x}},l;{\mathbf{\Theta }}^{\ast })=q(\overrightarrow{\mathbf{x}},l;\mathbf{\Theta })+(v_{j,l}^{\ast }-v_{j,l})\times x_l$$

     计算代价为 $O(1)$$O(1)$ 。

   • 一旦得到 $q(\overrightarrow{\mathbf{x}},l;\mathbf{\Theta })$$q(\mathbf{\vec x},l;\mathbf\Theta)$ ，则有：

     $$h_{v_{i,l}}(\overrightarrow{\mathbf{x}})=q(\overrightarrow{\mathbf{x}},l;\mathbf{\Theta })-v_{i,l}\times x_i^2$$

     计算代价为 $O(1)$$O(1)$ 。

5. 数据集 $\mathbb{S}$$\mathbb S$ 的稀疏性：

   根据：

   $$\theta =-\frac{\sum _{(\overrightarrow{\mathbf{x}},y)\in \mathbb{S}}(g_{\theta }(\overrightarrow{\mathbf{x}})-y)\times h_{\theta }(\overrightarrow{\mathbf{x}})}{(\sum _{(\overrightarrow{\mathbf{x}},y)\in \mathbb{S}}{h}_{\theta }^2(\overrightarrow{\mathbf{x}}))+{\lambda }_{\theta }}$$

   • 对于 $w_0$$w_0$ ，其计算复杂度为 $O(|\mathbb{S}|\times K)$$O(|\mathbb S|\times K)$

     $$w_0\leftarrow \frac{\sum _{(\overrightarrow{\mathbf{x}},y)\in \mathbb{S}}[e(\overrightarrow{\mathbf{x}},y;\mathbf{\Theta })-w_0]}{|\mathbb{S}|+{\lambda }_{w_0}}$$

   • 对于 $w_i,v_{i,l}$$w_i,v_{i,l}$， 我们只需要迭代 $\mathbb{S}$$\mathbb S$ 中 $h_{\theta }(\overrightarrow{\mathbf{x}})\ne 0$$h_\theta(\mathbf{\vec x}) \ne 0$ 的样本，即 $x_i\ne 0$$x_i \ne 0$ 的样本。

     因此每次更新只需要使用部分样本。总体而言，整体复杂度为 $O(|\mathbb{S}|\times \overline{K}\times d)$$O(|\mathbb S|\times \bar K\times d)$ ，其中 $\overline{K}$$\bar K$ 表示平均非零特征的数量。

6. ALS 优化算法：

   • 输入：

     • 训练样本 $\mathbb{S}$$\mathbb S$

     • $\mathbf{V}$$\mathbf V$ 随机初始化的方差 $\sigma$$\sigma$

   • 输出：模型参数 $w_0,\overrightarrow{\mathbf{w}},\mathbf{V}$$w_0,\mathbf{\vec w},\mathbf V$

   • 算法步骤：

     • 参数初始化：

       $$\begin{array}{c}{w}_0\leftarrow 0\\ w_i\leftarrow 0,i=1,2,\cdots ,K\\ v_{i,l}\leftarrow \mathcal{N}(0,\sigma ),i=1,\cdots ,K;l=1,\cdots ,d\end{array}$$

     • 初始化 $\overrightarrow{\mathbf{e}},\mathbf{Q}$$\mathbf{\vec e},\mathbf Q$ ：

       $$\begin{array}{c}e(\overrightarrow{\mathbf{x}},y;\mathbf{\Theta })\leftarrow \hat{y}(\overrightarrow{\mathbf{x}},y)-y,(\overrightarrow{\mathbf{x}},y)\in \mathbb{S}\\ q(\overrightarrow{\mathbf{x}},l;\mathbf{\Theta })\leftarrow \sum _{i=1}^K{v}_{i,l}\times x_i,(\overrightarrow{\mathbf{x}},y)\in \mathbb{S},l=1,2,\cdots ,d\end{array}$$

     • 迭代直至目标函数收敛或者达到指定步数，每一轮迭代过程为：

       • 更新 $w_0$$w_0$：

         $$\begin{array}{c}{w}_0^{\ast }\leftarrow -\frac{\sum _{(\overrightarrow{\mathbf{x}},y)\in \mathbb{S}}[e(\overrightarrow{\mathbf{x}},y;\mathbf{\Theta })-w_0]}{|\mathbb{S}|+{\lambda }_{w_0}}\\ e(\overrightarrow{\mathbf{x}},y;{\mathbf{\Theta }}^{\ast })\leftarrow e(\overrightarrow{\mathbf{x}},y;\mathbf{\Theta })+(w_0^{\ast }-w_0)\\ w_0\leftarrow w_0^{\ast }\end{array}$$

       • 更新 $w_i,i=1,2\cdots ,K$$w_i,i=1,2\cdots,K$ ：

         $$\begin{array}{c}{w}_i^{\ast }=-\frac{\sum _{(\overrightarrow{\mathbf{x}},y)\in \mathbb{S}}(e(\overrightarrow{\mathbf{x}},y;\mathbf{\Theta })-w_i\times x_i)\times x_i}{\left(\sum _{(\overrightarrow{\mathbf{x}},y)\in \mathbb{S}}{x}_i^2\right)+{\lambda }_{w_i}}\\ e(\overrightarrow{\mathbf{x}},y;{\mathbf{\Theta }}^{\ast })\leftarrow e(\overrightarrow{\mathbf{x}},y;\mathbf{\Theta })+(w_i^{\ast }-w_i)\times x_i\\ w_i\leftarrow w_i^{\ast }\end{array}$$

       • 更新 $v_{i,l},i=1,\cdots ,K;l=1,\cdots ,d$$v_{i,l},i=1,\cdots,K;l=1,\cdots,d$：

         外层循环为 $l$$l$ ，内层循环为 $i$$i$ 。这是为了充分利用 $q(\overrightarrow{\mathbf{x}},l;\mathbf{\Theta })$$q(\mathbf{\vec x},l;\mathbf \Theta)$ 。

         $$\begin{array}{c}{h}_{v_{i,l}}(\overrightarrow{\mathbf{x}})=q(\overrightarrow{\mathbf{x}},l;\mathbf{\Theta })-v_{i,l}\times x_i^2\\ v_{i,l}^{\ast }=-\frac{\sum _{(\overrightarrow{\mathbf{x}},y)\in \mathbb{S}}[e(\overrightarrow{\mathbf{x}},y;\mathbf{\Theta })-v_{i,l}\times h_{v_{i,l}}(\overrightarrow{\mathbf{x}})]\times h_{v_{i,l}}(\overrightarrow{\mathbf{x}})}{(\sum _{(\overrightarrow{\mathbf{x}},y)\in \mathbb{S}}{h}_{v_{i,l}}^2(\overrightarrow{\mathbf{x}}))+{\lambda }_{v_{i,l}}}\\ e(\overrightarrow{\mathbf{x}},y;{\mathbf{\Theta }}^{\ast })\leftarrow e(\overrightarrow{\mathbf{x}},y;\mathbf{\Theta })+(v_{i,l}^{\ast }-v_{i,l})\times x_i\\ q(\overrightarrow{\mathbf{x}},l;{\mathbf{\Theta }}^{\ast })\leftarrow q(\overrightarrow{\mathbf{x}},l;\mathbf{\Theta })+(v_{i,l}^{\ast }-v_{i,l})\times x_i\\ v_{i,l}\leftarrow v_{i,l}^{\ast }\end{array}$$

   .

1.3 实验

1. 在本节中，我们根据实验研究了和 SOTA 的上下文感知方法 Multiverse Recommendation 的对比。此外，我们检查了 SGD 对学习率选择的敏感性，以及我们的 ALS 优化是否可以在没有学习率这个超参数的情况下成功工作。

2. 数据集：

   • Food 数据集：包含 212 个用户对 20 个菜单 item 的 6360 个评分（从 1 分到 5 分），其中包含两个上下文变量：第一个上下文变量捕获用户评分的场景是虚拟的（ virtual） 还是真实的 （real）（即用户想象自己饿了、还是用户真的饿了）；第二个上下文变量刻画用户的饥饿程度。

   • Adom 数据集：包含 1524 个电影评分（从 1 分到 15 分），其中包含五个上下文变量，这些上下文变量关于同伴、工作日、以及其它时间信息。

   • Yahoo! Webscope 数据集：包含 221367 个评分。我们遵循 《Multiverse recommendation: n-dimensional tensor factorization for context-aware collaborative filtering》 并应用他们的方法来处理数据集。我们生成 $\alpha =\beta \in \{0.1,\cdots ,0.9\}$$\alpha=\beta\in \{0.1,\cdots,0.9\}$ 一共九个数据集。

3. baseline 方法：我们将 context-aware FM 和 Multiverse Recommendation 进行比较。注意：Multiverse Recommendation 已经在上述三个数据集上超越了其它上下文感知推荐算法。

   我们使用 FM no-context作为上下文无感（context-unaware）的 baseline，其中仅使用用户变量和 item 变量生成特征向量，这相当于具有 bias 项的矩阵分解。这是最强的上下文无关推荐算法之一。

   FM 使用我们提出的 ALS 算法进行优化，Multiverse Recommendation 使用原始论文中提出的 SGD 算法来学习。

4. 评估方式：我们从每个数据集中删除了 5% 的样本，用作调优超参数以获得最佳 MAE 的验证集。在超参数搜索之后，我们对剩下的 95% 数据集进行 5-fold 交叉验证，即不再使用验证集。我们报告了 5 次实验的平均 RMSE 和 MAE。

   所有方法都是 C++ 实现的，并在相同的硬件上运行。我们使用 ALS 优化的 FM 实现、Multiverse Recommendation 实现和数据集生成脚本可以从我们的网站上下载。

5. ALS vs SGD：我们在 Webscope 数据集上将 SGD 实现的测试误差和我们的 ASL 方法进行了比较，实验结果如下图所示。左图绘制了三种学习率选择的测试误差曲线，右侧的两个图分别显示了在 10 次和100次迭代后不同学习率得到的测试误差曲线（由于 ALS 没有学习率超参数，因此表现为一条水平直线）。可以看到：

   • SGD 的优化效果很大程度上取决于学习率和迭代次数。当精心挑选合适的学习率、足够大的迭代次数（根据验证集执行早停策略从而防止过拟合），SGD 可以达到 ALS 的效果。

   • ALS 不需要精心的、耗时的搜索合适的学习率，就可以达到很好的效果。

   该实验表明：SGD 需要仔细且耗时地搜索学习率，而ALS 不需要这样的搜索因为它没有这个超参数。在预测质量方面SGD 的性能与 ALS 一样好，但是前提是选择了正确的学习率。这使得 ALS 在应用中明显有利。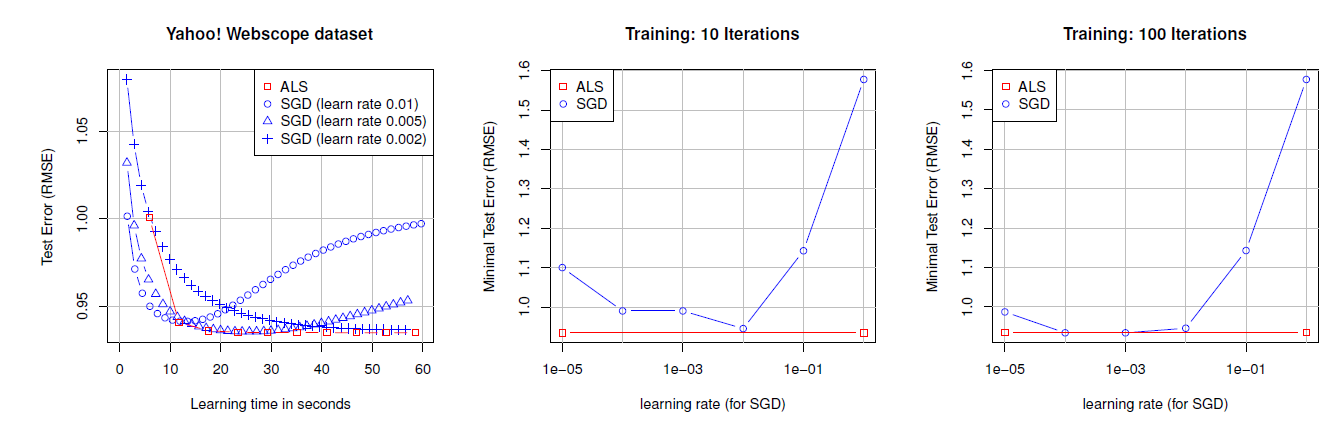

   

6. 运行时间：Multiverse Recommendation 在实际使用中的主要缺点之一是模型的计算复杂度为 $O(d^K)$$O(d^K)$ ，这对于学习和预测都是一个问题。这意味着即使对于标准的非上下文感知推荐系统，运行时间对于分解维度 $d$$d$ 上也是二次的，对于上下文感知问题至少是三次的。这使得很难应用于较大的因子维度 $d$$d$ 和较多的变量数量 $K$$K$ 。相反，FM 的计算复杂度对于 $d$$d$ 和 $K$$K$ 都是线性的，即 $O(dK)$$O(dK)$ 。

   在本实验中，我们考察所有训练样本的一次完整迭代的运行时间。我们使用 webscope 数据集，$K=4$$K=4$ ， $d\in \{1,2,4,8,16,32,64,128\}$$d\in \{1,2,4,8,16,32,64,128\}$ 。对于 Multiverse Recommendation，我们选择的最大 $d=32$$d=32$ 。实验结果如下图所示（单位为妙），其中左图为对数尺度。可以看到，实验结果和理论复杂度分析相匹配：

   • FM 的运行时间是线性的，例如可以在大约 11s 内完成所有训练样本的完整迭代（对于 $d=128$$d=128$ ）。

   • Multiverse Recommendation 的复杂度随着 $d^4$$d^4$ 的增加而增加，使得 $d=16$$d=16$ 的运行时间已经是 30 分钟，而 $d=32$$d=32$ 的运行时间大约是 8 小时。

   

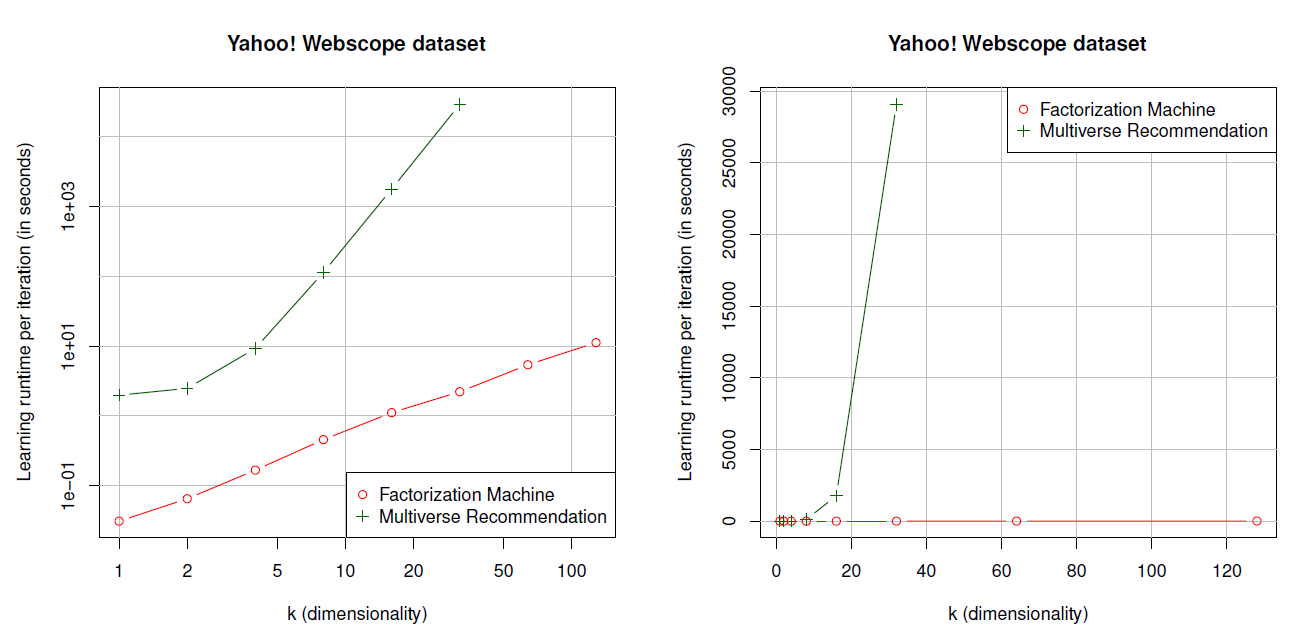
7. 预测质量：最后我们想知道，上下文感知 FM 的灵活性和快速运行时间是否会以较差的预测质量为代价。为此我们比较了 Food、Adom、Webscope 数据集上的预测质量，如下图所示。可以看到：

   • 上下文感知 FM 和 Multiverse Recommendation 对 Food 和 Adom 数据集的预测质量相当。

   • 上下文感知 FM 和 Multiverse Recommendation 都优于上下文无感方法（相当于矩阵分解模型）。

   

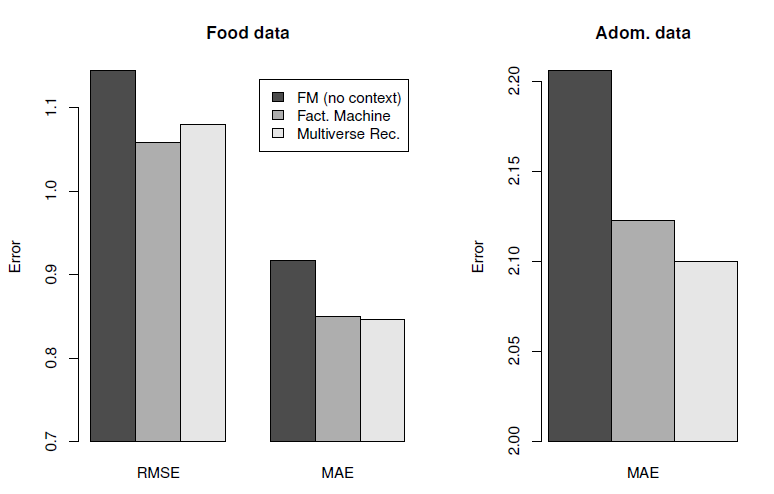
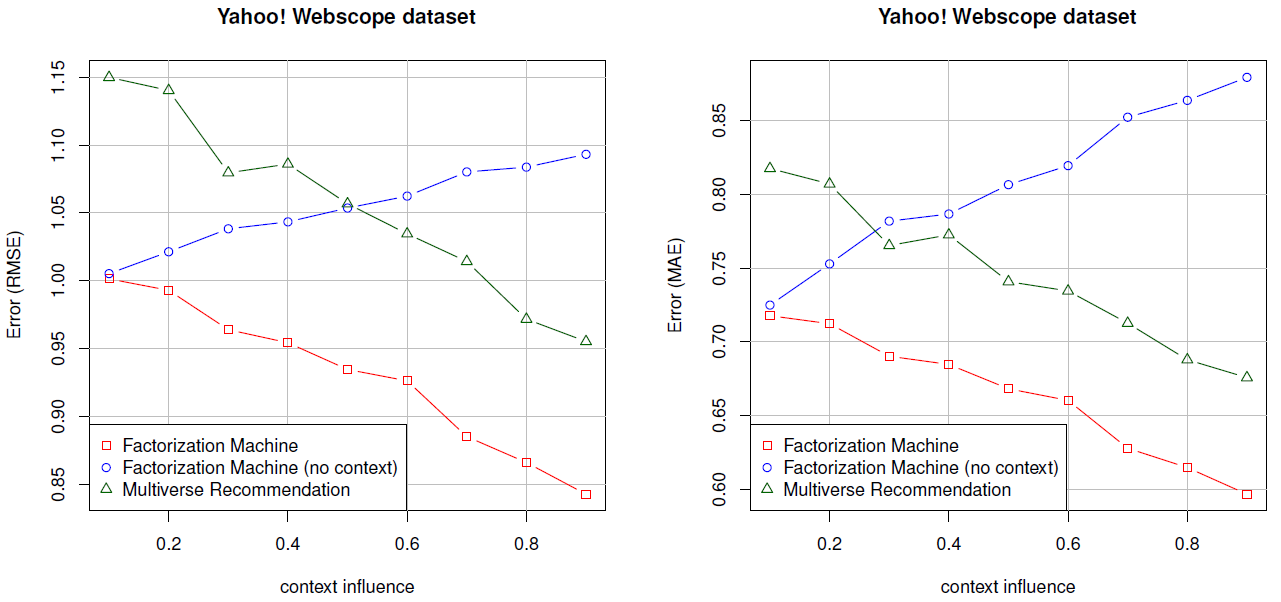
   在第三个实验中，我们考察了人工特征丰富的 Webscope 数据集，其中上下文变量（由 context influence 刻画）对于评分的影响越来越大。结果如下图所示，可以看到：

   • 上下文感知的 FM 和 Multiverse Recommendation 都受益于对上下文有更强依赖性的评分。

   • 当评分更依赖于上下文时，上下文无关 FM 的预测质量会变差，因为对于上下文无关 FM，上下文是未观测到的，因此它们无法解释这种依赖性。

   • 将两种上下文感知方法相互比较，可以看到 FM 始终生成比 Multiverse Recommendation 更好的预测。例如，RMSE 下降 0.10 ~ 0.15 ，而 MAE 下降 0.08 ~ 0.10 。

   

8. 结论：实验结果表明：

   • 上下文感知 FM 能够考虑上下文信息来增强预测。

   • 在运行时间方面 FM 是线性的，这使得它们可以应用于大维度的因子、更多上下文变量。相比之下，Multiverse Recommendation 无法处理大维度的因子、也无法处理很多上下文变量。

   • FM 在运行时间方面的优势并没有以预测质量为代价，相反：

     • 在稠密数据集（Food 和 Adom）上，上下文感知 FM 和 Multiverse Recommendation 的预测质量相当。

     • 而在稀疏数据集上，上下文感知 FM 的性能优于 Multiverse Recommendation 。

   • 最后，ALS 优化的 FM 很容易应用，因为它不像 SGD 那样对学习率进行昂贵的搜索。