一、DCN [2017]

《Deep & Cross Network for Ad Click Predictions》

1. 点击率（CTR）预估是一个大规模问题，对价值数十亿美金的在线广告行业至关重要。在广告行业中，广告主向媒体平台付费从而在媒体的网站上展示他们的广告。一种流行的付费方式是按点击付费（cost-per-click: CPC），其中仅发生点击的时候平台才向广告主收费。因此，平台的收入很大程度上依赖于准确预估点击率的能力。

   特征工程一直是许多预测模型成功的关键。识别常见的、预测性（predictive）的特征，并同时探索未见的（unseen）或罕见的交叉特征（cross feature）是做出良好预测的关键。然而，这个过程并不简单，而且通常需要手动特征工程或详尽的搜索（exhaustive searching）。web-scale 推荐系统的数据大多数是不连续（discrete）的、离散（categorical）的，导致特征空间庞大而稀疏，这对特征探索带来了挑战。因此大多数大型系统限制为线性模型，如逻辑回归（logistic regression）。

   线性模型简单（simple）、可解释（interpretable）、且易于扩展（scale），然而它们的表达能力有限。另一方面，交叉特征（cross features）已被证明在提高模型的表达能力方面具有重要意义。不幸的是，交叉特征通常需要手动特征工程或详尽的搜索（exhaustive search）来识别 。此外，泛化到未见过的特征交互（unseen feature interactions） 是困难的。

   DNN 模型能够自动学习特征交互（feature interactions），然而它们隐式地生成所有交互，并且在学习某些类型的交叉特征（cross features）时不一定有效。

   在论文 《Deep & Cross Network for Ad Click Predictions》 中，通过引入一种新颖的神经网络结构，交叉网络（cross network），以自动方式显式应用特征交叉（feature crossing ），从而避免特定于任务的特征工程。交叉网络由多个交叉层组成，其中交互的最高阶（highest-degree）由层的深度决定。每一层在现有阶次交互的基础上产生更高阶的交互，并保留来自前一层的交互。

   交叉网络和深度神经网络 DNN 联合训练。DNN 虽然可以捕获跨特征（across features）的非常复杂的交互，但是和交叉网络相比，DNN 需要几乎高一个数量级的参数、无法显式地形成交叉特征（cross features）、并且可能无法有效地学习某些类型的特征交互。通过联合训练交叉网络和 DNN 网络，模型可以有效地捕获预测性的特征交互，并且在 Criteo CTR 数据集上提供了 SOTA 的性能。

2. 相关工作：由于数据集的大小和维度的急剧增加，已经提出了许多方法来避免大量的任务特定（task-specific）的特征工程，这些方法大多数基于 embedding 技术和神经网络。

   • 因子分解机（Factorization machine: FM）将稀疏特征投影到低维稠密向量上，并从向量内积中学习特征交互。

     field 感知因子分解机（field-aware factorization machine: FFM）进一步允许每个特征学习多个向量，其中每个向量与一个 field 相关联。

     遗憾的是，FM 和 FFM 的浅层结构限制了它们的表达能力（representative power）。已经有工作将 FM 扩展到更高阶，但是一个缺点在于它们的大量参数会产生高昂的计算成本。

   • 由于 embedding 向量和非线性激活函数，深度神经网络 DNN 能够学习重要的高阶（high-degree）特征交互。

     残差网络最近的成功使得训练非常深的网络成为可能。Deep Crossing 扩展了残差网络，并通过 stacking 所有类型的输入来实现自动特征学习 feature learning 。

   深度学习的显著成功引发了对其表达能力的理论分析。有研究表明，在给定足够多的隐单元或隐层的情况下，DNN 能够在某些平滑性假设（smoothness assumption）下以任意准确性逼近任意函数。此外在实践中，已经发现 DNN 在参数数量适中的情况下运行良好。一个关键的原因是：大多数具有实际兴趣（practical interest）的特征都不是任意的。

   然而，剩下的一个问题是：在代表这种实际兴趣的特征方面，DNN 是否确实是最有效的。在 Kaggle 竞赛中，很多获胜解决方案中的手工制作特征都是低阶（low-degree）的，以显式的格式（explicit format）并且有效。另一方面，DNN 学习的特征是隐式的，且高度非线性。这为设计一个能够比通用 DNN 更有效、更显式地学习有界阶次特征交互的模型提供了启发。Wide & Deep 模型就是这种精神的典范，它将交叉特征（cross features）作为线性模型的输入，并与 DNN 模型联合训练线性模型。然而，Wide & Deep 的成功取决于交叉特征的正确选择，这是一个指数问题，目前还没有明确有效的方法。

3. 论文 《Deep & Cross Network for Ad Click Predictions》 提出了深度交叉网络（Deep & Cross Network: DCN）模型，该模型支持具有稀疏和稠密输入的 web-scale 自动特征学习。DCN 有效地捕获有界阶次的特征交互，学习高度非线性交互，不需要手动特征工程或详尽的搜索，并且计算成本低。

   论文的主要贡献包括：

   • 提出了一种新颖的交叉网络，它在每一层显式地应用特征交叉，有效地学习有界阶次的、预测性的交叉特征，并且无需手动特征工程或详尽的搜索。

   • 交叉网络简单而有效。根据设计，多项式最高阶次在每一层都增加，并且由层的深度来决定。网络由最低阶到最高阶的所有阶次的、系数不同的交叉项（cross terms）来组成。

   • 交叉网络内存高效，易于实现。

   • 实验结果表明，采用交叉网络的DCN 的 logloss 比 DNN 更低，而且 DCN 的参数数量相比 DNN 要少了接近一个量级。

1.1 模型

1. 我们将描述 DCN 模型的架构，如下图所示。DCN 模型从 embedding and stacking 层开始，然后是并行的交叉网络和深度网络，然后是一个组合层（combination layer）从而拼接了来自两个网络的输出。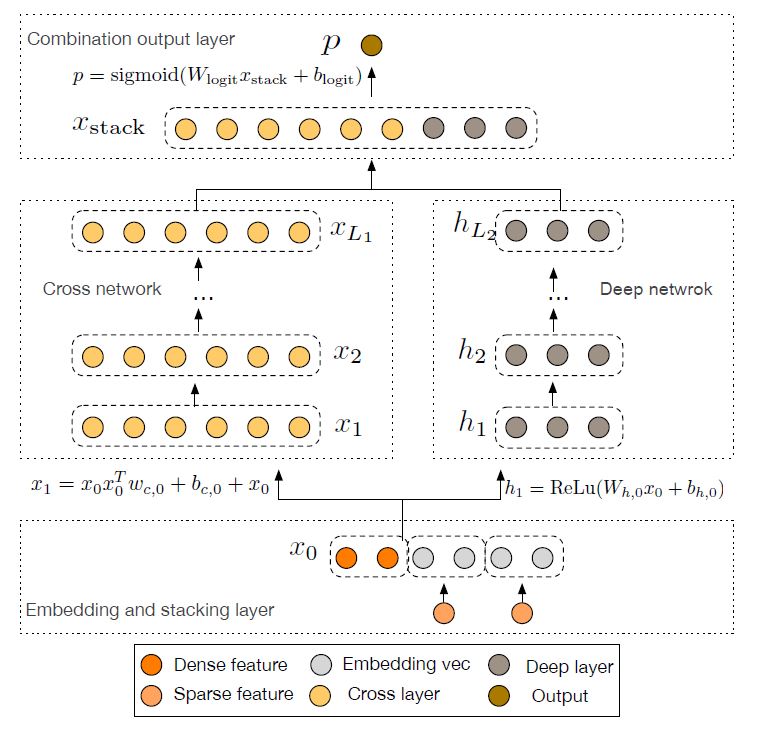

   

2. Embedding and Stacking Layer：我们考虑具有稀疏和稠密特征的输入数据。在 CTR 预估等 web-scale 推荐系统中，输入主要是离散特征，如 country=usa 。这些特征通常被编码为 one-hot 向量，如 [0, 1, 0] 。然而，这通常会导致大型词表vocabulary 的高维特征空间。

   为了降低维度，我们采用 embedding 技术将这些二元特征转换为实值的稠密向量（通常称作 embedding 向量）：

   $${\overrightarrow{\mathbf{f}}}_{\text{embed}}^{(i)}={\mathbf{W}}_{\text{embed}}^{(i)}{\overrightarrow{\mathbf{f}}}^{(i)}$$

   其中：

   • ${\overrightarrow{\mathbf{f}}}_i$$\mathbf{\vec f}_i$ 为第 $i$$i$ 个 field 的 one-hot 向量。

   • ${\overrightarrow{\mathbf{f}}}_{\text{embed}}^{(i)}$$\mathbf{\vec f}_\text{embed}^{(i)}$ 为第 $i$$i$ 个 field 的 embedding 向量。

   • ${\mathbf{W}}_{\text{embed}}^{(i)}\in {\mathbb{R}}^{n_e^{(i)}\times n_v^{(i)}}$$\mathbf W_\text{embed}^{(i)}\in \mathbb R^{n^{(i)}_e\times n_v^{(i)}}$ 为待优化的、对应的 embedding 矩阵，$n_e^{(i)}$$n_e^{(i)}$ 为 embedding size，$n_v^{(i)}$$n_v^{(i)}$ 为第 $i$$i$ 个 field 的词表大小。

   最后我们将 embedding 向量以及归一化的稠密特征 ${\overrightarrow{\mathbf{f}}}_{\text{dense}}\in {\mathbb{R}}^{n_d}$$\mathbf{\vec f}_\text{dense}\in \mathbb R^{n_d}$ stack（即拼接）到单个向量中：

   $${\overrightarrow{\mathbf{x}}}_0=[{\overrightarrow{\mathbf{f}}}_{\text{embed}}^{(1)}||\cdots ||{\overrightarrow{\mathbf{f}}}_{\text{embed}}^{(K)}||{\overrightarrow{\mathbf{f}}}_{\text{dense}}]\in {\mathbb{R}}^{n_e^{(1)}+\cdots +n_e^{(K)}+n_d}$$

   其中：$K$$K$ 为输入的field 的数量，$n_d$$n_d$ 为稠密特征维度，$||$$||$ 表示向量拼接操作。

3. Cross Network：我们新颖的交叉网络的核心思想是：以有效的方式应用显式的特征交叉。

   交叉网络由交叉层（cross layers ）来组成，每层可以公式化为：

   $${\overrightarrow{\mathbf{x}}}_{l+1}=f({\overrightarrow{\mathbf{x}}}_l,{\overrightarrow{\mathbf{w}}}_l,{\overrightarrow{\mathbf{b}}}_l)+{\overrightarrow{\mathbf{x}}}_l={\overrightarrow{\mathbf{x}}}_0{\overrightarrow{\mathbf{x}}}_l^{\mathrm{\top }}{\overrightarrow{\mathbf{w}}}_l+{\overrightarrow{\mathbf{b}}}_l+{\overrightarrow{\mathbf{x}}}_l$$

   其中：

   • ${\overrightarrow{\mathbf{x}}}_l\in {\mathbb{R}}^d$$\mathbf{\vec x}_l\in \mathbb R^d$ 为第 $l$$l$ 层交叉层的输出。

   • ${\overrightarrow{\mathbf{w}}}_l,{\overrightarrow{\mathbf{b}}}_l\in {\mathbb{R}}^d$$\mathbf{\vec w}_l,\mathbf{\vec b}_l \in \mathbb R^d$ 为第 $l$$l$ 层交叉层的参数， $d=n_e^{(1)}+\cdots +n_e^{(K)}+n_d$$d=n_e^{(1)}+\cdots+n_e^{(K)} + n_d$ 。

   注意：这里没有非线性激活函数，因此每一层的输出都是 ${\overrightarrow{\mathbf{x}}}_0$$\mathbf{\vec x}_0$ 的线性函数。

   每个交叉层在特征交叉函数 $f(\cdot )$$f(\cdot)$ 之后加上它的输入，这使得交叉函数 $f:{\mathbb{R}}^d\to {\mathbb{R}}^d$$f:\mathbb R^d\rightarrow \mathbb R^d$ 拟合残差 ${\overrightarrow{\mathbf{x}}}_{l+1}-{\overrightarrow{\mathbf{x}}}_l$$\mathbf{\vec x}_{l+1} - \mathbf{\vec x}_l$ 。

   单个交叉层的可视化如下图所示。

   

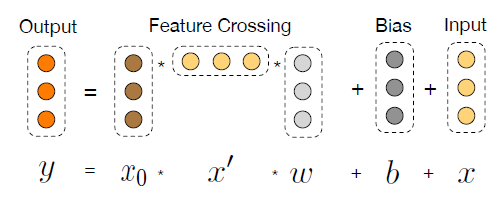
   • 高阶特征交互：交叉网络的特殊结构导致交叉特征的阶次随着层的深度而增加。 $L$$L$ 层交叉网络的最高多项式阶次（就输入 ${\overrightarrow{\mathbf{x}}}_0$$\mathbf{\vec x}_0$ 而言）是 $L+1$$L+1$ 。

     事实上，交叉网络包含输入 ${\overrightarrow{\mathbf{x}}}_0$$\mathbf{\vec x}_0$ 中所有阶次从 $1$$1$ 到 $L+1$$L+1$ 的交叉项（cross term） $x_{0,1}^{{\alpha }_1}{x}_{0,2}^{{\alpha }_2}\cdots x_{0,d}^{{\alpha }_d}$$x_{0,1}^{\alpha_1}x_{0,2}^{\alpha_2}\cdots x_{0,d}^{\alpha_d}$ 。详细参考后面的分析。

   • 复杂度分析：假设交叉层的数量为 $L_c$$L_c$ ，交叉层输入特征维度为 $d$$d$ ，那么交叉网络的参数数量为 $d\times L_c\times 2$$d\times L_c\times 2$ 。

     交叉网络的时间和空间复杂度在输入维度 $d$$d$ 上是线性的。因此，和deep 组件（DCN 的 deep 部分）相比，交叉网络引入的复杂度可以忽略不计，使得 DCN 的整体复杂度保持在和传统 DNN 相同的水平。这种效率得益于矩阵 ${\overrightarrow{\mathbf{x}}}_0{\overrightarrow{\mathbf{x}}}_l^{\mathrm{\top }}$$\mathbf{\vec x}_0\mathbf{\vec x}_l^{\top}$ 的 rank-one 属性（即这个矩阵的秩为 1 ），这使得我们能够生成所有交叉项，而无需计算或存储整个矩阵。

   交叉网络的参数太少从而限制了模型的容量。为了捕获高度非线性交互，我们引入了一个并行的深度网络（Deep Network）。

4. Deep Network：深度网络是一个全连接的前馈神经网络，每一个 deep layer 可以公式化为：

   $${\overrightarrow{\mathbf{h}}}_{l+1}=\sigma ({\mathbf{W}}_l{\overrightarrow{\mathbf{h}}}_l+{\overrightarrow{\mathbf{b}}}_l^{\prime })$$

   其中： $\sigma (\cdot )$$\sigma(\cdot)$ 为激活函数，${\mathbf{W}}_l\in {\mathbb{R}}^{d_{l+1}\times d_l},{\overrightarrow{\mathbf{b}}}_l^{\prime }\in {\mathbb{R}}^{d_{l+1}}$$\mathbf W_l\in \mathbb R^{d_{l+1}\times d_l},\mathbf{\vec b}_l^\prime\in \mathbb R^{d_{l+1}}$，$d_l$$d_l$ 为 ${\overrightarrow{\mathbf{h}}}_l$$\mathbf{\vec h}_l$ 的向量长度。

   • 复杂度分析：假设所有隐层的维度都是 $d_1=d_2=\cdots =d_{L_d}=m$$d_1=d_2=\cdots=d_{L_d}=m$ ，一共 $L_d$$L_d$ 层，则deep network 的参数数量为：

     $$d\times m+m+(m^2+m)\times (L_d-1)$$

     其中：

     • 输入为 ${\overrightarrow{\mathbf{x}}}_0\in {\mathbb{R}}^d$$\mathbf{\vec x}_0\in \mathbb R^d$ ，所以第一层的参数数量为 $d\times m+m$$d\times m + m$。

     • 后续的 $L_d-1$$L_d-1$ 层，每一层的参数数量为 $m\times m+m$$m\times m + m$ 。

5. Combination Layer：组合层将来自两个网络的输出拼接起来，并将拼接后的向量馈入标准的 logits 层。

   对于二类分类问题，这可以公式化为：

   $$p=\text{sigmoid}({\overrightarrow{\mathbf{w}}}_{\text{logits}}\cdot [{\overrightarrow{\mathbf{x}}}_{L_c}||{\overrightarrow{\mathbf{x}}}_{L_d}]+b_{\text{logits}})$$

   其中：

   • ${\overrightarrow{\mathbf{x}}}_{L_c}\in {\mathbb{R}}^d$$\mathbf{\vec x}_{L_c}\in \mathbb R^d$ 为交叉网络的输出，${\overrightarrow{\mathbf{x}}}_{L_d}\in {\mathbb{R}}^m$$\mathbf{\vec x}_{L_d}\in \mathbb R^m$ 为深度网络的输出，|| 表示向量拼接。

   • ${\overrightarrow{\mathbf{w}}}_{\text{logits}}\in {\mathbb{R}}^{d+m}$$\mathbf{\vec w}_\text{logits}\in \mathbb R^{d+m}$ 为 logits 层的权重向量，$b_{\text{logits}}\in \mathbb{R}$$b_\text{logits}\in \mathbb R$ 为 logits 层的bias，sigmoid(.) 为 sigmoid 激活函数。

6. 模型的损失函数为带正则化的对数似然函数：

   $$\mathcal{L}=-\frac{1}{N}\left(\sum _{i=1}^N[y_i\log p_i+(1-y_i)\log (1-p_i)]\right)+\lambda (\sum ||\mathbf{W}|{|}_2^2+\sum ||\overrightarrow{\mathbf{w}}|{|}_2^2)$$

   其中： $N$$N$ 为样本数量，$y_i$$y_i$ 为样本的真实 label ，$\lambda$$\lambda$ 为 L2 正则化系数。

   我们联合训练交叉网络和深度网络，因为这允许每个 individual 网络在训练期间了解其它网络。

1.2 理论分析

1. 这里我们从理论上分析 DCN 的交叉网络，从而了解它的有效性。交叉网络 可以理解为：多项式逼近（ polynomial approximation）、FM 泛化（generalization to FM）、或者有效投影（efficient projection）。

2. 在这里为了讨论方便，我们假设所有的 bias 项都是零。记 ${\overrightarrow{\mathbf{w}}}_l$$\mathbf{\vec w}_l$ 的第 $i$$i$ 个元素为 $w_{l,i}$$w_{l,i}$。令 $\overrightarrow{\mathbf{x}}=(x_1,\cdots ,x_d{)}^{\mathrm{\top }}\in {\mathbb{R}}^d$$\mathbf{\vec x} = (x_{ 1},\cdots,x_{ d})^\top \in \mathbb R^d$，交叉项为 $x_1^{{\alpha }_1}\times x_2^{{\alpha }_2}\times \cdots \times x_d^{{\alpha }_d}$$x_{ 1}^{\alpha_1}\times x_{ 2}^{\alpha_2}\times\cdots \times x_{ d}^{\alpha_d}$ ，其中 $\overrightarrow{\alpha }=({\alpha }_1,\cdots ,{\alpha }_d{)}^{\mathrm{\top }}\in {\mathbb{N}}^d$$\vec\alpha=(\alpha_1,\cdots,\alpha_d)^\top\in \mathbb N^d$ 为每一项的度（degree），并且 ${\alpha }_i$$\alpha_i$ 为非负整数。则该交叉项的度为：

   $$|\overrightarrow{\alpha }|=\sum _{i=1}^d{\alpha }_i,{\alpha }_i\in \mathbb{N}$$

   如果多项式中有多个交叉项，则多项式的degree（也称作阶次）为所有交叉项中 degree 的最大值。

3. 多项式逼近（polynomial approximation）：根据 Weierstrass 逼近定理，任何在一定平滑性假设（smoothness assumption）下的函数都可以通过多项式以任意准确性逼近。因此我们从多项式逼近的角度来分析交叉网络。特别是，交叉网络以一种有效的、表达能力强的、以及更好地泛化到真实世界数据集的方式来逼近相同阶次的多项式。

   定义多项式：

   $$P_n(\overrightarrow{\mathbf{x}})=\{\sum _{\overrightarrow{\alpha }}{w}_{\overrightarrow{\alpha }}{x}_1^{{\alpha }_1}\cdots x_d^{{\alpha }_d}|0\le |\overrightarrow{\alpha }|\le n,\overrightarrow{\alpha }\in {\mathbb{N}}^d\}$$

   该多项式的项一共有 $O(d^n)$$O(d^n)$ 个，即参数数量有 $O(d^n)$$O(d^n)$ 个。

   我们表明，在只有 $O(d)$$O(d)$ 个参数的情况下，交叉网络可以包含相同阶次多项式中出现的所有交叉项，每个交叉项的系数彼此不同。

   定理：考虑一个 $L$$L$ 层的交叉网络，第 $l+1$$l+1$ 层定义为 ${\overrightarrow{\mathbf{x}}}_{l+1}={\overrightarrow{\mathbf{x}}}_0{\overrightarrow{\mathbf{x}}}_l^{\mathrm{\top }}{\overrightarrow{\mathbf{w}}}_l+{\overrightarrow{\mathbf{x}}}_l$$\mathbf{\vec x}_{l+1} = \mathbf{\vec x}_0\mathbf{\vec x}_l^\top \mathbf{\vec w}_l + \mathbf{\vec x}_l$ 。定义交叉网络的输入 ${\overrightarrow{\mathbf{x}}}_0=(x_1,x_2,\cdots ,x_d{)}^{\mathrm{\top }}$$\mathbf{\vec x}_0=(x_1,x_2,\cdots,x_d)^\top$，交叉网络输出为 $g_L\left({\overrightarrow{\mathbf{x}}}_0\right)={\overrightarrow{\mathbf{x}}}_L\cdot {\overrightarrow{\mathbf{w}}}_L$$g_L\left(\mathbf{\vec x}_0\right)= \mathbf{\vec x}_L\cdot \mathbf{\vec w}_L$，其中 ${\overrightarrow{\mathbf{w}}}_l\in {\mathbb{R}}^d$$\mathbf{\vec w}_l\in \mathbb R^d$ 为参数。则多元多项式 $g_L\left({\overrightarrow{\mathbf{x}}}_0\right)$$g_L\left(\mathbf{\vec x}_0\right)$ 复现（reproduces）了以下的多项式：

   $$\begin{array}{c}\{\sum _{\overrightarrow{\alpha }}{c}_{\overrightarrow{\alpha }}({\overrightarrow{\mathbf{w}}}_0,\cdots ,{\overrightarrow{\mathbf{w}}}_L)x_1^{{\alpha }_1}\cdots x_d^{{\alpha }_d}|0\le |\overrightarrow{\alpha }|\le L+1,\overrightarrow{\alpha }\in {\mathbb{N}}^d\}\\ c_{\overrightarrow{\alpha }}({\overrightarrow{\mathbf{w}}}_0,\cdots ,{\overrightarrow{\mathbf{w}}}_L)=M_{\overrightarrow{\alpha }}\sum _{\overrightarrow{\mathbf{i}}\in B_{\overrightarrow{\alpha }}}\sum _{\overrightarrow{\mathbf{j}}\in P_{\overrightarrow{\alpha }}}\prod _{k=1}^{|\overrightarrow{\alpha }|}{w}_{i_k,j_k}\end{array}$$

   其中：

   • $M_{\overrightarrow{\alpha }}$$M_\vec\alpha$ 为 ${\overrightarrow{\mathbf{w}}}_i$$\mathbf{\vec w}_i$ 无关的常量。

   • $\overrightarrow{\mathbf{i}}=(i_1,\cdots ,i_{|\overrightarrow{\alpha }|}{)}^{\mathrm{\top }}$$\mathbf{\vec i} = (i_1,\cdots,i_{|\vec\alpha|})^\top$为索引向量 ，$B_{\overrightarrow{\alpha }}=\{\overrightarrow{\mathbf{y}}\in \{0,1,\cdots ,L{\}}^{|\overrightarrow{\alpha }|}|y_i<y_j\text{ for }i<j\text{ and }{y}_{\overrightarrow{\alpha }}=L\}$$B_\vec\alpha = \left\{\mathbf{\vec y}\in \{0,1,\cdots,L\}^{|\vec\alpha|}\bigg |y_i \lt y_j \text{ for } i\lt j \text{ and } y_{\vec\alpha} = L\right\}$ 。

   • $\overrightarrow{\mathbf{j}}=(j_1,\cdots ,j_{|\overrightarrow{\alpha }|}{)}^{\mathrm{\top }}$$\mathbf{\vec j} = (j_1,\cdots,j_{|\vec\alpha|})^\top$ 为索引向量，$P_{\overrightarrow{\alpha }}$$P_\vec\alpha$ 为索引 $(\underset{{\alpha }_1}{\underbrace{1,\cdots ,1}},\cdots ,\underset{{\alpha }_d}{\underbrace{d,\cdots ,d}})$$(\underbrace{1,\cdots,1}_{\alpha_1 },\cdots,\underbrace{d,\cdots,d}_{\alpha_d} )$ 的所有排列组合构成的集合。

   证明见原始论文。

4. FM 泛化（generalization to FM）：交叉网络和 FM 模型一样具有参数共享（parameter sharing）的精神，并进一步将其扩展到更深的结构。

   • 相同点：在 FM 模型中，特征 $x_i$$x_i$ 关联一个权重向量 ${\overrightarrow{\mathbf{v}}}_i$$\mathbf{\vec v}_i$ ，交叉项 $x_i{x}_j$$x_ix_j$ 的权重计算为 ${\overrightarrow{\mathbf{v}}}_i\cdot {\overrightarrow{\mathbf{v}}}_j$$\mathbf{\vec v}_i\cdot \mathbf{\vec v}_j$ 。在 DCN 中，特征 $x_i$$x_i$ 关联一组标量 ${\left\{w_{l,i}\right\}}_{l=1}^L$$\left\{w_{l,i}\right\}_{l=1}^L$ ，交叉项 $x_i{x}_j$$x_ix_j$ 的权重是来自集合 ${\left\{w_{l,i}\right\}}_{l=0}^L$$\left\{w_{l,i}\right\}_{l=0}^L$ 和 ${\left\{w_{l,j}\right\}}_{l=0}^L$$\left\{w_{l,j}\right\}_{l=0}^L$ 的参数的乘积。两种模型中，每个特征都学习了一些独立于其它特征的参数，交叉项的权重是相应参数的某种组合。

     参数共享不仅使模型更加高效，而且使模型能够泛化到未见（unseen）的特征交互，并对噪声具有更强的鲁棒性。例如，以具有稀疏特征的数据集为例。如果两个二元特征 $x_i$$x_i$ 和 $x_j$$x_j$ 在训练数据中很少同时出现或者从未同时出现，那么针对交叉项 $x_i{x}_j$$x_ix_j$ 学习的权重将没有任何有意义的预测信息。

   • 不同点：FM 是一种浅层结构，仅限于表达二阶交叉项。相反，DCN 能够表达 $L$$L$ 阶交叉特征，其中 $L$$L$ 为交叉网络的深度。因此，交叉网络将参数共享的思想从单层扩展到多层以及高阶交叉项。注意，和高阶 FM 不同，交叉网络中的参数数量仅随输入维度 $d$$d$ 线性增长。

5. 有效投影 efficient projection ：交叉网络的每一层都是在 ${\overrightarrow{\mathbf{x}}}_0$$\mathbf{\vec x}_0$ 和 ${\overrightarrow{\mathbf{x}}}_l$$\mathbf{\vec x}_l$ 之间计算成对交互（pariwise interaction），然后投影到 $d$$d$ 维。

   $$\begin{array}{c}{\overrightarrow{\mathbf{x}}}_{l+1}={\overrightarrow{\mathbf{x}}}_0{\overrightarrow{\mathbf{x}}}_l^T{\overrightarrow{\mathbf{w}}}_l=[x_{0,1}{x}_{l,1},x_{0,1}{x}_{l,2},\cdots ,x_{0,d}{x}_{l,d}]\left[\begin{array}{cccc}{\mathbf{w}}_l& 0& \cdots & 0\\ 0& {\mathbf{w}}_l& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & {\mathbf{w}}_l\end{array}\right]\end{array}$$

   其中：

   • 行向量包含了 $d^2$$d^2$ 个元素，它代表 pariwise interaction $x_{0,i}{x}_{l,j},1\le i,j\le d$$x_{0,i}x_{l,j},\; 1\le i,j\le d$ 。

   • 投影矩阵是一个分块对角矩阵，由 ${\mathbf{w}}_l\in {\mathbb{R}}^d$$\mathbf w_{l} \in \mathbb R^{d}$ 作为列向量来构成。

1.3 实验

1. 这里我们在一些热门的分类数据集上评估 DCN 的性能。

2. 数据集为 Criteo Display Ads 数据集，用于预测广告点击率。数据集包含 13 个整数特征和 26 个离散特征（categorical features），这些离散特征的基数（cardinality）都很高。

   数据集包含 7 天的 11GB 用户日志，大约 4100 万条记录。我们使用前 6 天的数据进行训练，第 7 天的数据随机分成大小相等的验证集和测试集。

   对于该数据集，logloss 的 0.001 的改进都被认为具有实际意义。当考虑到庞大的用户规模，预测准确性的小幅提升可能会导致公司收入的大幅增加。

3. 实现：DCN 是用 TensorFlow 实现的，我们简要讨论使用 DCN 进行训练的一些实现细节。

   • 数据处理和 embedding：

     • 通过应用对数变换（log transform）来对实值特征进行归一化。

     • 对于离散特征，我们将特征嵌入到维度为 $6\times {\text{(category cardinality)}}^{1/4}$$6\times \text{(category cardinality)}^{1/4}$ 维的 embedding 向量。然后拼接所有 embedding 从而得到一个维度为 1026 的向量。

   • 优化（optimization）：我们使用 Adam 优化器应用了 mini-batch 随机优化，batch size 设置为 512 。我们在深度网络部分采用了 batch normalization，并将梯度裁剪设为 100 。

   • 正则化（regularization）：我们使用了早停策略（early stopping），因为我们发现 L2 正则化或 dropout 没有效果。

   • 超参数：我们根据隐层数量、隐层维度、初始学习率、交叉层的数量执行 grid search ，然后在实验中报告最佳超参数的结果。

     • 对于所有模型（包括 baseline ），隐层数量从 2 ~ 5、隐层维度从 32 ~ 1024，初始学习率从 1e-4 ~ 1e-3，增量为 1e-4 。

     • 对于 DCN模型，交叉层数量从 1 ~ 6 。

     所有实验都在训练step = 150000 处早停，超过该时刻开始发生过拟合。

4. baseline 方法：我们将 DCN 和五种模型进行比较：没有交叉网络的 DCN 模型（DNN）、逻辑回归 （LR）、因子分解机（FM）、Wide & Deep （W&D）、Deep Crossing（DC）。

   • DNN：embedding 层、输出层、超参数调优过程和 DCN 完全相同，它和 DCN 模型的唯一区别在于 DNN 没有交叉层。

   • LR：我们使用了 Sibyl，一种用于分布式逻辑回归的大规模机器学习系统。整数特征在对数尺度下离散化。交叉特征是由复杂的特征选择工具来选择的。所有的 single 特征都被使用。

   • FM：我们使用一个带有专属细节（proprietary details）的 FM-based 模型。

   • W&D：和 DCN 不同的是，W&D 的 wide 组件将原始稀疏特征作为输入，并依赖于详尽的搜索（exhaustive searching）和领域知识（domain knowledge）来选择预测性的交叉特征。

     我们跳过了和 W&D 的比较，因为没有什么好的方法来选择交叉特征。

   • DC：和 DCN 相比，DC 没有形成显式的交叉特征。DC 主要依靠 stacking（即 embedding 向量拼接） 和残差单元来构建隐式交叉特征。

     我们应用了和 DCN 相同的 embedding 层（即 stacking），然后是另一个 ReLU 层作为一系列残差单元的输入。残差单元的层数从 1 ~ 5 来调优，隐层维度从 100 到 1026 来调优。

1.3.1 性能比较

1. 这里我们首先比较不同模型的 logloss 性能，然后我们详细比较了 DCN 和 DNN，即进一步研究了交叉网络带来的影响。

2. 不同模型的最佳测试 logloss 参考下表。最佳超参数为：

   • DCN 模型：使用2 层 deep layer，每层维度 1024；使用 6 层 cross layer 。cross layer 的维度不需要调优，因为该层的维度就等于 ${\overrightarrow{\mathbf{x}}}_0$$\mathbf{\vec x}_0$ 的维度 $d$$d$ 。

   • DNN 模型：使用 5 层 deep layer，每层维度 1024。

   • DC 模型：使用 5 层残差单元，残差单元的输入维度为 424、残差单元隐层维度为 537。

   • LR 模型：使用 42 个交叉特征。

   可以看到：

   • 最佳的性能是在最深的交叉架构中发现的，这表明交叉网络的高阶特征交互是有价值的。

   • DCN 大大优于所有其他模型。特别是，它优于 SOTA 的 DNN 模型，但是仅使用了 DNN 中消耗的 40% 的内存。

   

   对于每个模型的最佳超参数设置，我们还报告了 10 次独立运行的测试集logloss 的均值和标准差：：DCN $0.4422\pm 9\times {10}^{-5}$$0.4422 \pm 9\times 10^{-5}$ 、DNN $0.4430\pm 3.7\times {10}^{-4}$$0.4430\pm 3.7\times 10^{-4}$ 、DC $0.4430\pm 4.3\times {10}^{-4}$$0.4430\pm 4.3\times 10^{-4}$ 。可以看到，DCN 始终大幅优于其它模型。

3. 考虑到交叉网络仅引入了 $O(d)$$O(d)$ 个额外的参数，我们将 DCN 与其 deep network ，一个传统的 DNN，进行比较，并在改变内存预算和 loss 阈值的同时展示了实验结果。

   给定一定数量参数， loss 被报告为在所有学习率和模型结构中最好的验证损失。我们的计算中省略了 embedding 层中的参数数量，因为它在两个模型中都相同。

   • 下表报告了实现目标 logloss 阈值所需的最少参数数量（比如 $7.9\times {10}^5$$7.9\times 10^{5}$ 表示 7.9 万个参数）。可以看到，DCN 的内存效率比 single DNN 高出近一个量级。这要归功于更有效地学习有界阶次特征交互的交叉网络。

     

   • 下表比较了受固定内存预算影响的神经网络模型的性能，指标为验证集 logloss。可以看到，DCN 始终优于 DNN。

     • 在小型参数（small-parameter）的情况下，cross network 中的参数数量和deep network 中的参数数量相当，显著的改进表明 cross network 在学习有效特征交互方面更有效。

     • 在大型参数（large-parameter）的情况下，DNN 弥补了一些差距，但是 DCN 仍然在很大程度上优于 DNN。这表明 DCN 可以有效地学习某些类型的有意义的特征交互，这些特征交互即使是巨大的 DNN 模型也无法学习。

     

4. 我们通过展示将交叉网络引入给定 DNN 模型的效果来更详细地分析 DCN。我们给出在相同的层数和层维度的情况下比较 DNN 和 DCN 的最佳性能，然后对于每个设置，我们展示了验证集 logloss 如何随着添加更多 cross layer 而变化。

   下表给出了 DCN 和 DNN 模型在 logloss 上的绝对差异（需要乘以 ${10}^{-2}$$10^{-2}$），负值表示 DCN 超越了 DNN。Nodes 表示 deep network 隐层维度，layers 表示 cross network 深度。 DNN 模型相当于将 DCN 模型的 cross layer 层数设为 0 。

   可以看到：在相同的实验设置下，来自 DCN 模型的最佳 logloss 始终优于来自相同结构的 single DNN 模型。所有超参数的改进都是一致的，这缓解了初始化和随机优化带来的随机性的影响。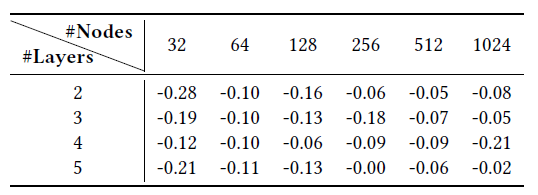

   

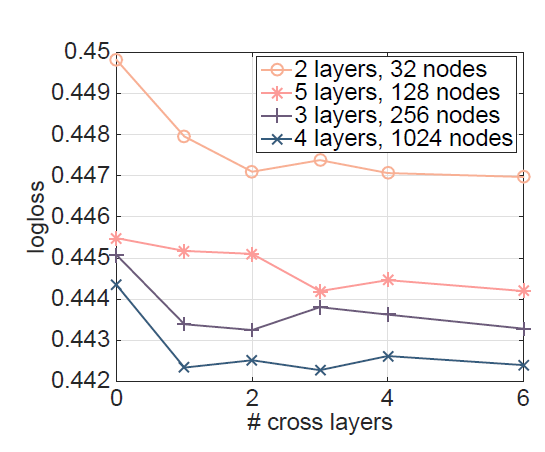
5. 下图显示了我们在随机选择的设置上增加 cross layer 层数对验证 logloss 的改进。cross layer 层数为 0 表示 single DNN 模型。 layers 表示deep layer 层数，nodes 为 deep layer 隐层维度。不同的符号表示deep network不同的超参数。

   可以看到：

   • 当向DNN 模型中添加 1个 cross layer 时，会有明显的改进。

   • 随着更多 cross layer 的引入，对于某些设置的 logloss 继续下降，表明引入的交叉项在预测中是有效的；对于其他设置的 logloss 开始波动，甚至略有增加，这表明引入的更高阶次的特征交互没有帮助。

   

1.3.2 Non-CTR 数据集

1. 我们表明DCN 在 Non-CTR 预测问题上表现良好。我们使用了来自 UCI repository 的 forest covertype 数据集（包含 581012 个样本和 54 个特征）、以及 Higgs 数据集（包含 1100 万个样本和 28 个特征） 。数据集被随机拆分为训练集（90%）、测试集（10%）。

   我们对超参数进行grid search，其中：

   • deep layer 层数从 1 ~ 10、层的维度从 500 ~ 300 。

   • cross layer 的层数从 4 ~ 10。对于 DCN，输入向量直接馈送到 cross network 因此不需要探索 cross layer 的维度。

   • 残差单元的层数从 1~5，其中隐层维度从 50 ~ 300 。

   对于 forest covertype 数据集，DCN 以最少的内存消耗实现了 最佳的准确率 0.9740。DNN 和 DC 均达到 0.9737。此时最佳超参数设置为：

   • DCN：8 层维度为 54 的 cross layer， 6 层维度为 292 的 deep layer 。

   • DNN：7 层维度为 292 的 deep layer 。

   • DC：4 层残差单元，残差单元的输入维度为 271、残差单元隐层维度为 287 。

   对于 Higgs 数据集，DCN 达到了最好的测试 logloss 0.4494，而 DNN 达到了 0.4506。DCN 在使用DNN一半的内存并且超越了 DNN。此时最佳超参数设置为：

   • DCN：4 层维度为 28 的 cross layer、4 层维度为 209 的 deep layer。

   • DNN：10 层维度为 196 的 deep layer。