一、DCN V2 [2020]
《DCN V2: Improved Deep & Cross Network and Practical Lessons forWeb-scale Learning to Rank Systems》
有效的特征交叉(
feature cross)对于许多learning to rank: LTR模型的成功至关重要。特征交叉提供了单个特征之外的额外交互信息。例如,"国家" 和 "语言" 的组合比其中单个特征更有信息量。在线性模型时代,机器学习从业者依靠手动识别这种特征交叉来增加模型的表达能力。不幸的是,这涉及到一个组合搜索空间,在数据大多是categorical的web-scale的应用中,这个搜索空间很大而且很稀疏。在这种情况下的搜索是耗时耗力的,往往需要领域的专业知识,并使模型更难以泛化。后来,
embedding技术被广泛采用,将特征从高维稀疏向量投影到更低维的稠密向量。Factorization Machine: FM利用embedding技术,通过两个latent vector的内积来建模pairwise特征交互。与那些传统的线性模型中的特征交叉相比,FM带来了更多的泛化能力。在过去的十年中,随着更大的算力和巨大的数据规模,工业界的
LTR模型已经逐渐从线性模型和FM-based的模型迁移到深度神经网络(DNN)。这使得搜索和推荐系统的模型性能得到了全面的提升。人们普遍认为DNN是通用的函数近似器,可以潜在地学习各种特征交互。然而,最近的研究(《Latent cross: Making use of context in recurrent recommender systems》、《Deep & Cross Network for Ad Click Predictions》)发现:DNN甚至对二阶特征交叉或三阶特征交叉进行近似建模都是低效的。为了更准确地捕捉有效的特征交叉,常见的补救措施是通过更宽或更深的网络进一步提高模型容量。这自然是一把双刃剑:
我们在提高模型性能的同时也使模型的服务速度大大降低。在许多生产环境中,这些模型正在处理极高的
QPS,因此对实时推理有非常严格的延迟要求。可能,serving系统已经被推到了一个极限,无法承受更大的模型。此外,更深的模型往往引入可训练性问题,使模型更难训练。
这已经揭示了设计一个能够有效地学习
predictive特征交互的模型的关键需求,特别是在一个处理数十亿用户的实时流量的资源限制环境中。 最近的许多工作试图解决这一挑战。共同的思想是:利用那些从DNN学到的隐式高阶交叉、以及显式的和有界的特征交叉(在线性模型中已经发现,显式的和有界的特征交叉是有效的)。隐式交叉是指通过端到端的函数来学习交互,而没有任何明确的公式来建模这种交叉。另一方面,显式交叉是通过一个具有可控交互阶次的显式公式来建模的。在所有这些方法中,
Deep & Cross Network: DCN是有效和优雅的。然而,在大规模工业系统中部署DCN面临许多挑战。DCN的cross network是有局限性的:cross network代表的多项式仅由random cross patterns的灵活性。此外,
cross network和DNN之间的分配容量是不平衡的。当将DCN应用于大规模生产数据时,这种差距明显增加。绝大部分的参数将被用于学习DNN中的隐式交叉。
在论文
《DCN V2: Improved Deep & Cross Network and Practical Lessons forWeb-scale Learning to Rank Systems》中,作者提出了一个新的模型DCN-V2,改进了原来的DCN模型。作者已经在整个谷歌的相当多的learning to rank system中成功部署了DCN-V2,在离线模型准确性和在线业务指标方面都有显著的提高。DCN-V2首先通过cross layer学习输入(通常是embedding layer)的显式特征交互,然后与深度网络相结合从而学习互补的隐式交互。DCN-V2的核心是cross layer,它继承了DCN中cross network的简单结构,然而在学习显式的和有界的交叉特征方面的表达能力显著增强。论文研究了以点击为正标签的数据集,然而DCN-V2与标签无关,可以应用于任何learning to rank system。论文贡献:
论文提出了一个新的模型
DCN-V2来学习有效的显式特征交叉和隐式特征交叉。与现有的方法相比,DCN-V2更具有表达能力,但仍然是高效和简单的。观察到
DCN-V2中所学到的矩阵的低秩性质,论文提出利用低秩技术从而在子空间中近似feature cross,以获得更好的性能和延迟的trade-off。此外,论文提出了一种基于
Mixture-of-Expert架构的技术,以进一步将矩阵分解为多个较小的子空间。然后,这些子空间通过一个门控机制被聚合起来。论文利用人工合成数据集进行并提供了广泛的研究,证明了传统的基于
ReLU的神经网络学习高阶特征交叉的低效率。通过全面的实验分析,论文证明了的
DCN-V2模型在Criteo和MovieLen-1M基准数据集上的表现明显优于SOTA算法。论文提供了一个案例研究,并分享了在一个大规模工业
ranking系统中部署DCN-V2的经验,这带来了显著的离线收益和在线收益。
相关工作:最近
feature interaction learning工作的核心思想是利用显式的和隐式的特征交叉。为了建模显式交叉,最近的工作引入了乘法运算(pairwise interaction。我们根据他们如何结合显式部分和隐式部分来组织相关工作。并行结构:一个工作方向是联合训练两个并行网络,其灵感来自于
wide and deep模型,其中wide组件将原始特征的交叉作为输入,而deep组件是一个DNN模型。然而,为wide组件选择交叉特征又回到了线性模型的特征工程问题。尽管如此,wide and deep模型已经激发了许多工作从而采用这种并行的架构并改进wide部分。DeepFM通过在wide组件采用FM模型从而自动进行feature interaction learning。xDeepFM通过生成多个feature map增加了DCN的表达能力,每个feature map都编码了当前level和输入level的特征之间的pairwise交互。此外,它还将每个feature embeddingunit,而不是将每个元素unit。不幸的是,它的计算成本很高(#params的10倍),使得它在工业规模的应用中不实用。此外,
DeepFM和xDeepFM都要求所有的feature embedding具有相同的大小,这在应用于工业数据时又是一个限制,因为工业数据的词表大小(categorical features的大小)从AFM通过一个注意力网络为每个特征交互分配重要性。AutoInt利用带残差连接的multi-head self-attention机制。InterHAt进一步采用了分层注意力。
堆叠结构:另一个工作方向是在
embedding layer和DNN模型之间引入一个interaction layer,该interaction layer创建了显式的特征交叉。这个interaction layer在早期阶段捕捉到了特征交互,并促进了后续隐层的学习。product-based neural network: PNN引入了inner product layer(IPNN)和outer product layer(OPNN)作为pairwise interaction layer。OPNN的一个缺点在于其高计算成本。Neural FM: NFM通过用Hadamard积代替内积来扩展FM。DLRM遵从FM,通过内积来计算特征交叉。
这些模型只能创建到二阶显式交叉。
AFN将特征转化为对数空间,并自适应地学习任意阶的特征交互。
与
DeepFM和xDeepFM类似,这些方法只接受大小相等的embedding size。
尽管这些年经过了许多发展,我们的综合实验表明,
DCN仍然是一个强大的基线。我们将此归因于其简单的结构,它促进了optimization。然而,正如所讨论的,其有限的表达能力使其无法在web-scale的系统中学习更有效的特征交叉。在下文中,我们提出了一个新的架构,它继承了DCN的简单结构,同时提高了它的表达能力。
1.1 模型
这里描述了一个新颖的模型架构
DCN-V2来学习显式特征交互和隐式特征交互。DCN-V2从一个embedding layer开始,然后是一个包含多个cross layer的cross network(用于建模显式特征交互),然后结合一个深度神经网络(用于建模隐式特征交互)。DCN-V2中的改进对于将DCN用于高度优化的生产系统至关重要。DCN-V2极大地提高了DCN在web-scale的生产数据中在建模复杂的显式的交叉项的表达能力,同时保持其优雅的公式,便于部署。DCN-V2所建模的函数族是DCN所建模的函数族的严格超集。模型整体架构如下图所示,有两种方式将
cross network与deep network结合起来:堆叠式、并行式。此外,考虑到cross layer的低秩性质,我们建议利用low-rank cross layer的混合来实现模型性能和效率之间更健康的trade-off。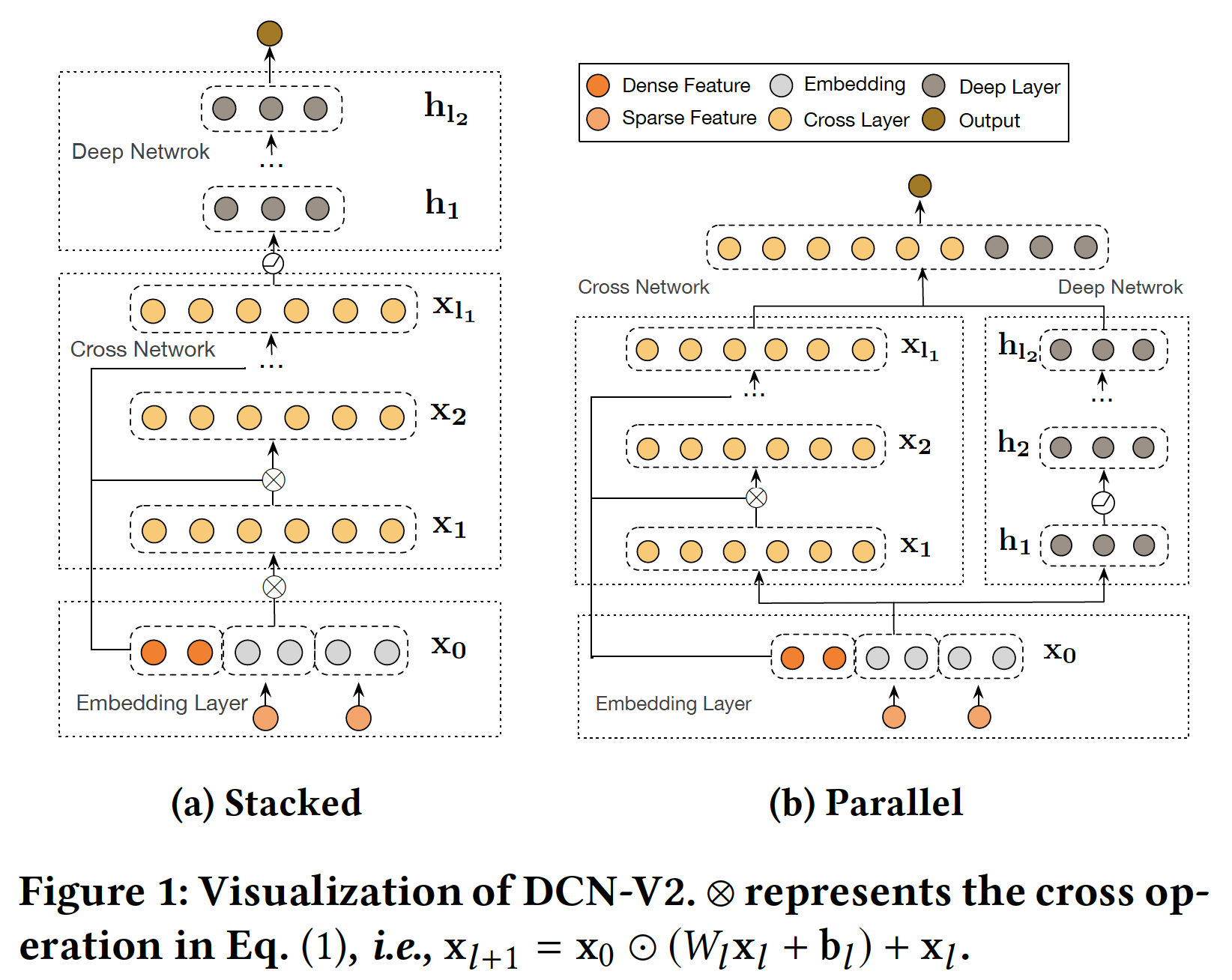
Embedding Layer:embedding layer将categorical (sparse)特征和dense特征的组合作为输入,并输出DCN类似的setting。与DeepFM, NFM, xDeepFM, DLRM, IPNN, FM不同的是,DCN-V2接受任意的embedding size。这对于词表规模从Cross Network:DCN-V2和核心在于cross layer,它创建了显式的特征交叉。其中第cross layer如下所示:其中:
base layer,它包含原始的一阶特征,通常被设置为embedding layer。bias向量。
下图展示了一个单独的
cross layer。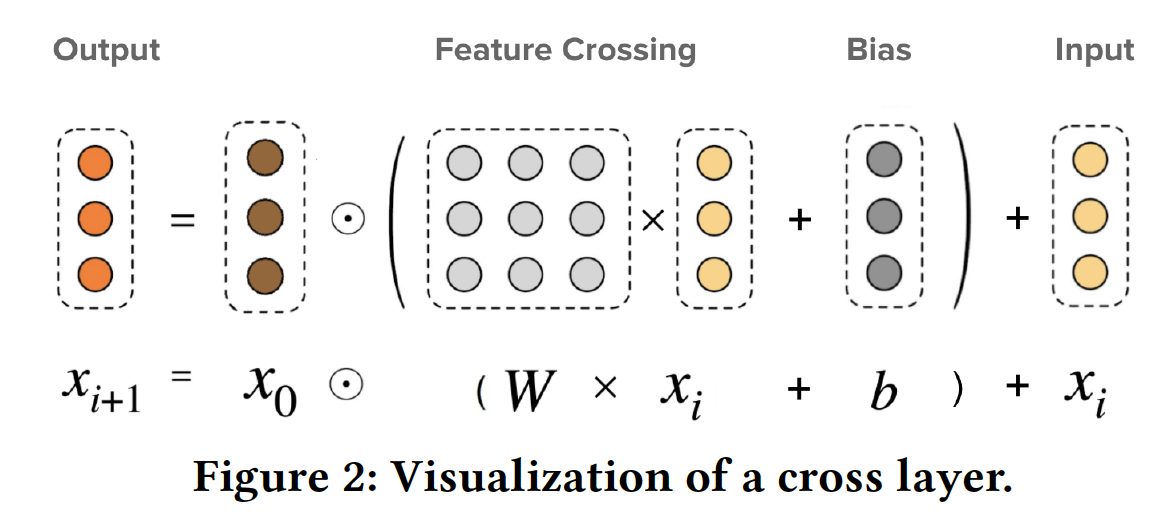
对于一个
cross network,最高的多项式阶数是DCN-V2退化到DCN。cross layer仅能建模有界的多项式类,而其他任何复杂的函数空间只能被近似。因此,我们接下来引入了一个deep network来补充数据中固有分布的建模。DCN V1的公式为:DCN V2的公式为:bias项即:
DCN V1中,DCN V2中,DCN V2的模型容量更高。DCN V2的核心:用Deep Network:第deep layer的公式为:其中:
deep layer的的输入和输出。bias向量。ReLU。
Deep and Cross Combination:我们提出了两种结构:Stacked Structure(如Figure 1a):输入cross network,然后是deep network,最后是输出层输出Parallel Structure(如Figure 1b):输入cross network和deep network,然后这两个网络的输出拼接起来作为最终输出
prediction为:其中:
sigmoid函数。对于损失函数,我们使用
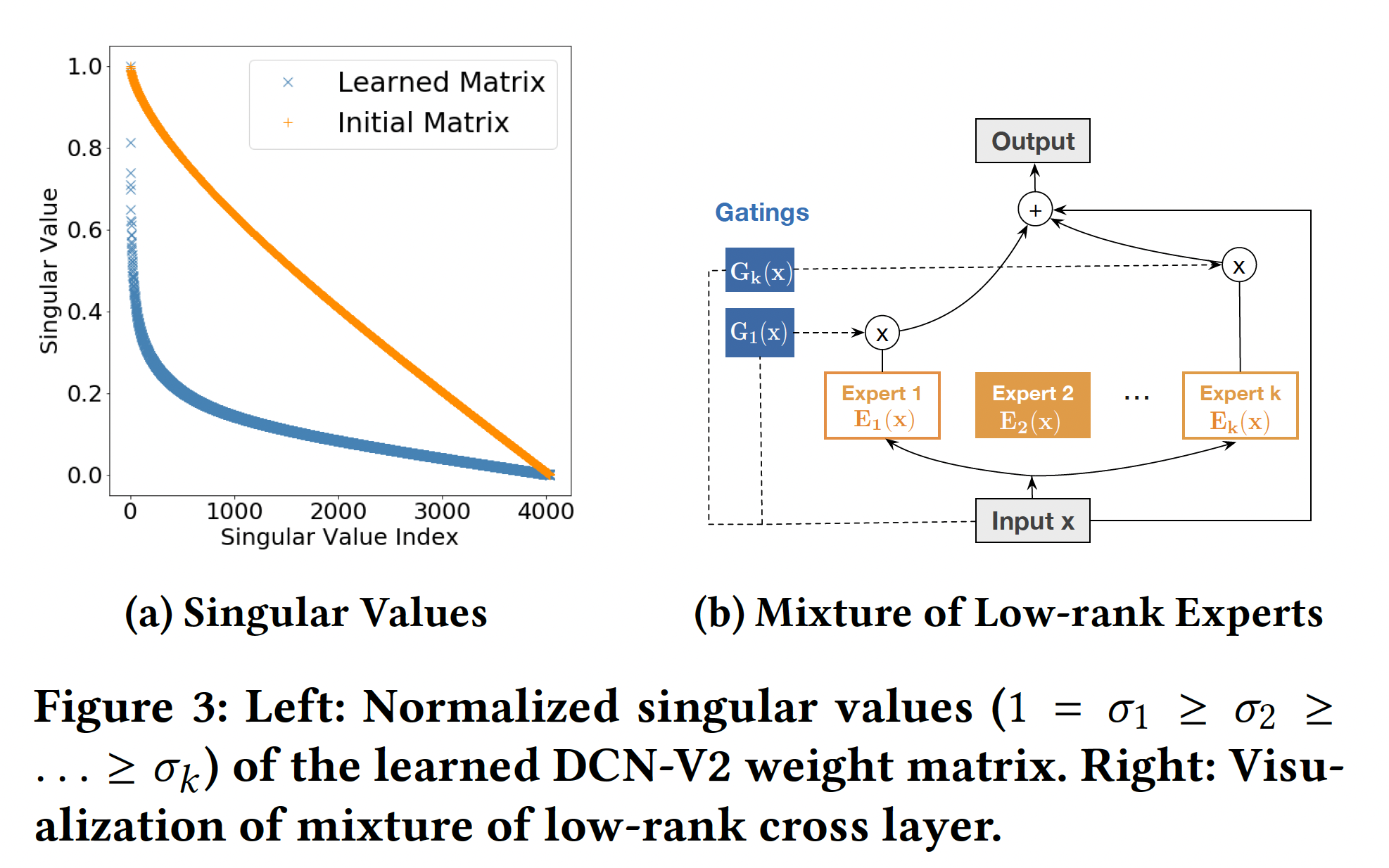
logloss(带正则化项)。注意,DCN-V2本身是对prediction-task和损失函数无关的。Cost-Effective Mixture of Low-Rank DCN:对于那些生产模型来说,模型容量往往受到有限的serving资源、严格的latency要求的限制。因此,我们寻求使DCN-v2更具cost-efficient的方法。DCN-V2结构简单,计算瓶颈在于matrix-vector乘法,这使得我们可以利用矩阵近似技术来降低成本:通过两个低秩矩阵gap或快速的谱衰减时,该方法是最有效的。在许多情况下,我们确实观察到所学的矩阵下图
(a)显示了DCN-V2中来自生产模型的学到的矩阵因此,我们定义第
cross layer的低秩版本为:其中:
这个新的公式有两种解释:
我们在一个子空间中学习特征交叉。
这个解释启发我们采用
Mixture-of-Experts: MoE的思想。MoE-based模型由两部分组成:experts(通常是一个小网络)和gating(输入的一个函数)。在我们的案例中,我们不是依靠一个单一的专家来学习特征交叉,而是利用多个这样的专家,每个专家在不同的子空间学习特征交互,并使用门控机制(取决于输入mixture的公式如下(如下图(b)所示):其中:
sigmoid或softmax函数。
我们将输入
这个解释激励我们利用投影空间的低维性质。我们不是立即从
refine the representation:其中:
我们旨在有效利用固定的内存/时间预算来学习有意义的特征交叉。以下公式从上到下都代表一个严格意义上的、逐渐增大的函数族:
这一组模型有比较大的工程参考意义,它描述了从简单模型到复杂模型的升级路径,同时也具有一定的物理意义。
算法复杂度:令
embedding size,cross layers数量,DCN专家的数量。此外,我们假设每个专家具有相同的小维度cross network的时间复杂度和空间复杂度为mixDCN(低秩DCN) 的时间复杂度和空间复杂度为从
bit-wise和feature-wise的角度来看,对于cross network,cross network能够创造出直到与
DCN相比,DCN-V2用更多的参数来刻画相同的多项式类,表达能力更强。此外,DCN-V2中的特征交互具有更强的表达能力,可以从bit-wise和feature-wise两方面来看;而在DCN中,它只是从bit-wise的角度来看。
1.2 实验
"CrossNet"或"CN"代表cross network,"Mix"代表低秩混合版本。
1.2.1 人工合成数据集
大多数工作只研究了具有未知交叉模式和噪音的数据的公共数据集。很少有工作在一个干净的环境中用已知的
ground-truth模型进行研究。因此,重要的是要了解:在哪些情况下,传统的神经网络会变得没有效率。
在我们提出的模型
DCN-V2中每个组件的作用。
我们用
DCN模型中的cross network来表示那些特征交叉方法,并与工业推荐系统中常用的ReLU进行比较。为了简化实验和便于理解,我们假设每个特征难度增加时的性能:仅考虑二阶特征交叉,令
ground-truth model为稀疏性 (
交叉模式的相似性(
因此,我们创建了难度不断增加的人工合成数据集:
其中:
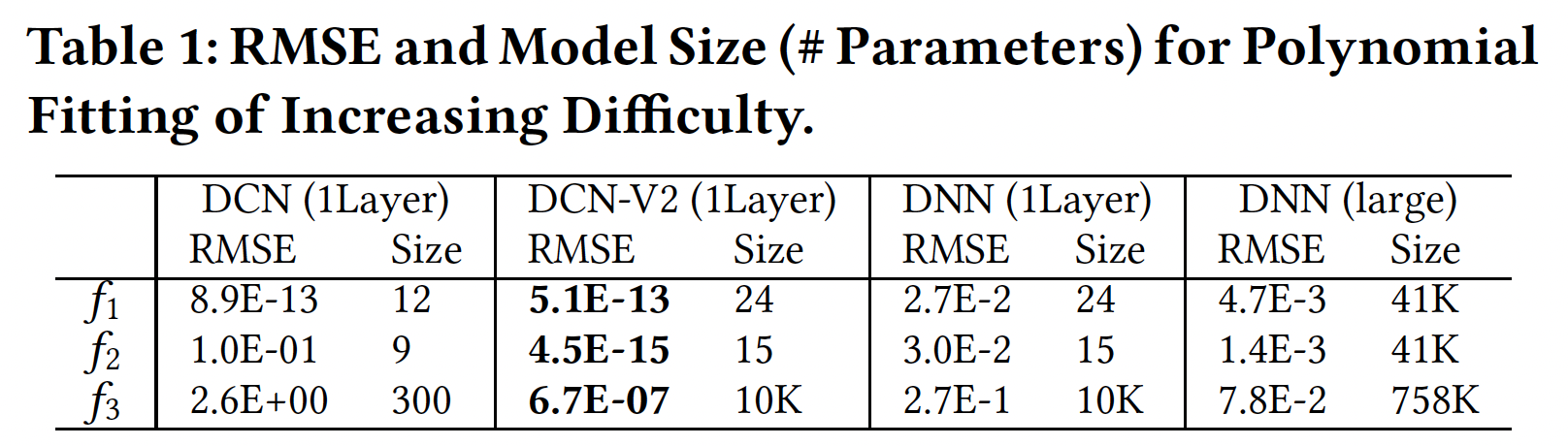
[-1, 1]之间均匀采样的。下表报告了
5次运行和model size的平均RMSE。可以看到:当交叉模式很简单时(即,
DCN-V2和DCN都很有效。当模式变得更加复杂时(即,
DCN-V2仍然准确,而DCN则准确性下降了。即使采用更宽更深的结构,
DNN的性能仍然很差。这表明DNN在建模单项式模式时效率不高。
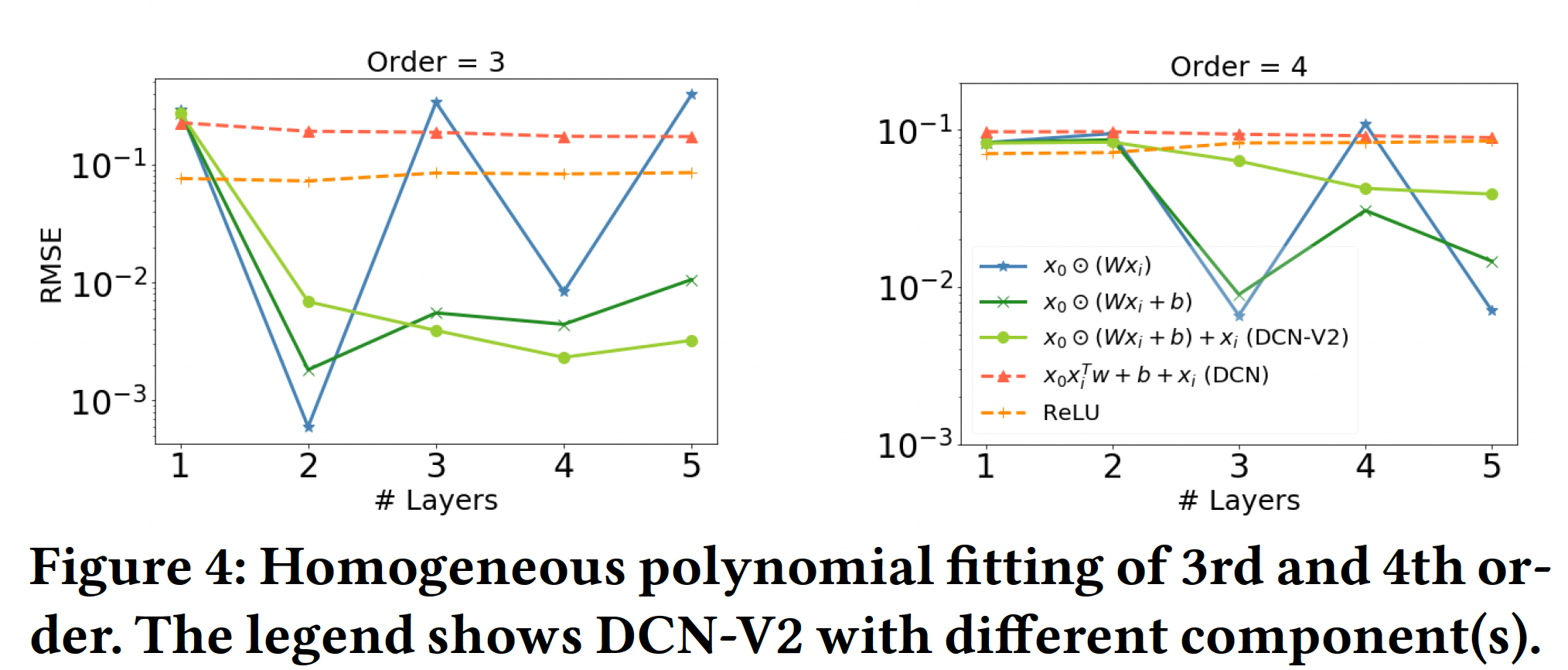
每个组件的作用:我们还分别对
3阶和4阶的同质多项式进行了消融研究。对于3阶和4阶,我们从20个交叉项。下图展示了层深度对于平均RMSE的影响。显然,
2层对3阶多项式取得的最佳性能得到验证(4阶多项式也是类似的)。在其他层,性能明显下降。DCN(红色虚线)在复杂的交叉模式建模方面的有限表达能力。
总而言之,
ReLU(即,ReLU激活函数的DNN)在捕获显式的特征交叉(乘法关系)方面效率不高,即使有更深更大的网络。DCN准确地捕捉到了简单的交叉模式,但在更复杂的模式中却失败了。DCN-V2对于复杂的交叉模式仍然是准确和有效的。
1.2.2 真实数据集
数据集:
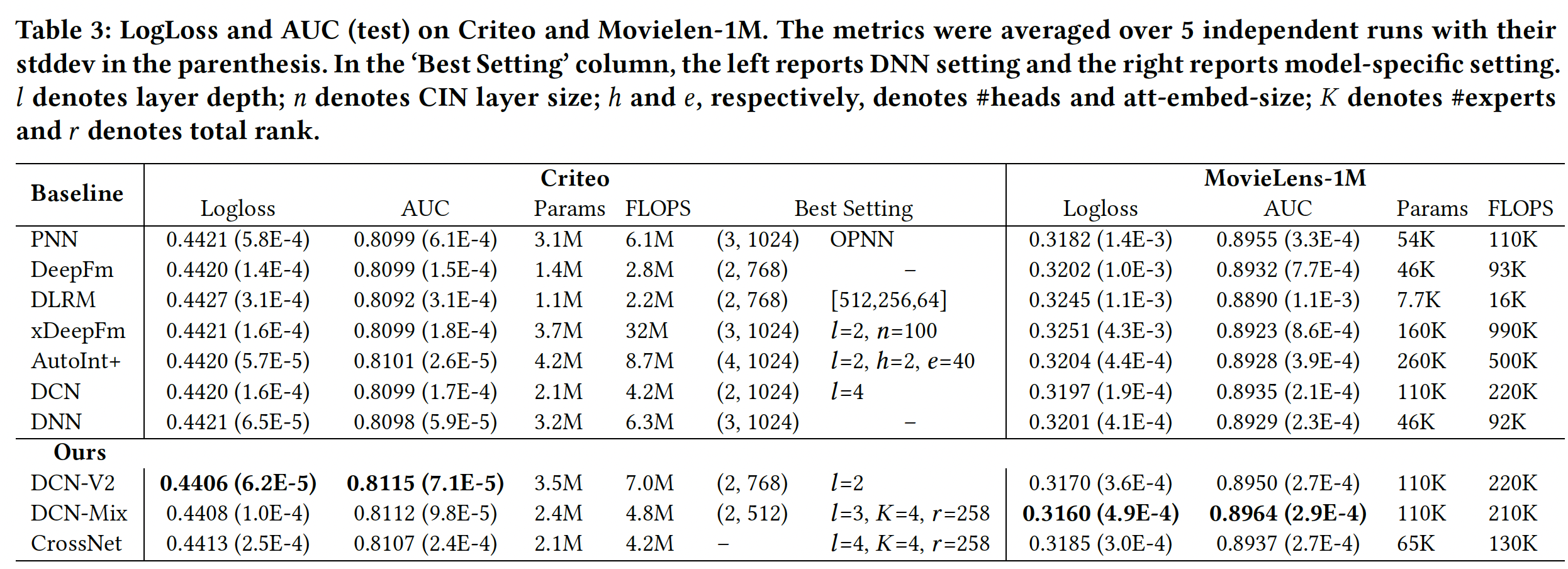
Criteo:包含7天内的用户日志,包含45M个样本和39个特征。我们使用前6天的数据进行训练,并将最后一天的数据随机平均分成验证集和测试集。我们对13个dense特征执行log归一化(feature-2为26个categorical feature。MovieLen-1M:包含740k个样本和7个特征。每个训练样本包括一个<user-features, movie-features, rating>三元组。我们将任务形式化为一个回归问题:所有一分和两分的评分都被归一化为0、四分和五分被归一化为1、三分被删除。使用和嵌入6个non-multivalent categorical feature。数据被随机分成80%用于训练、10%用于验证、10%用于测试。
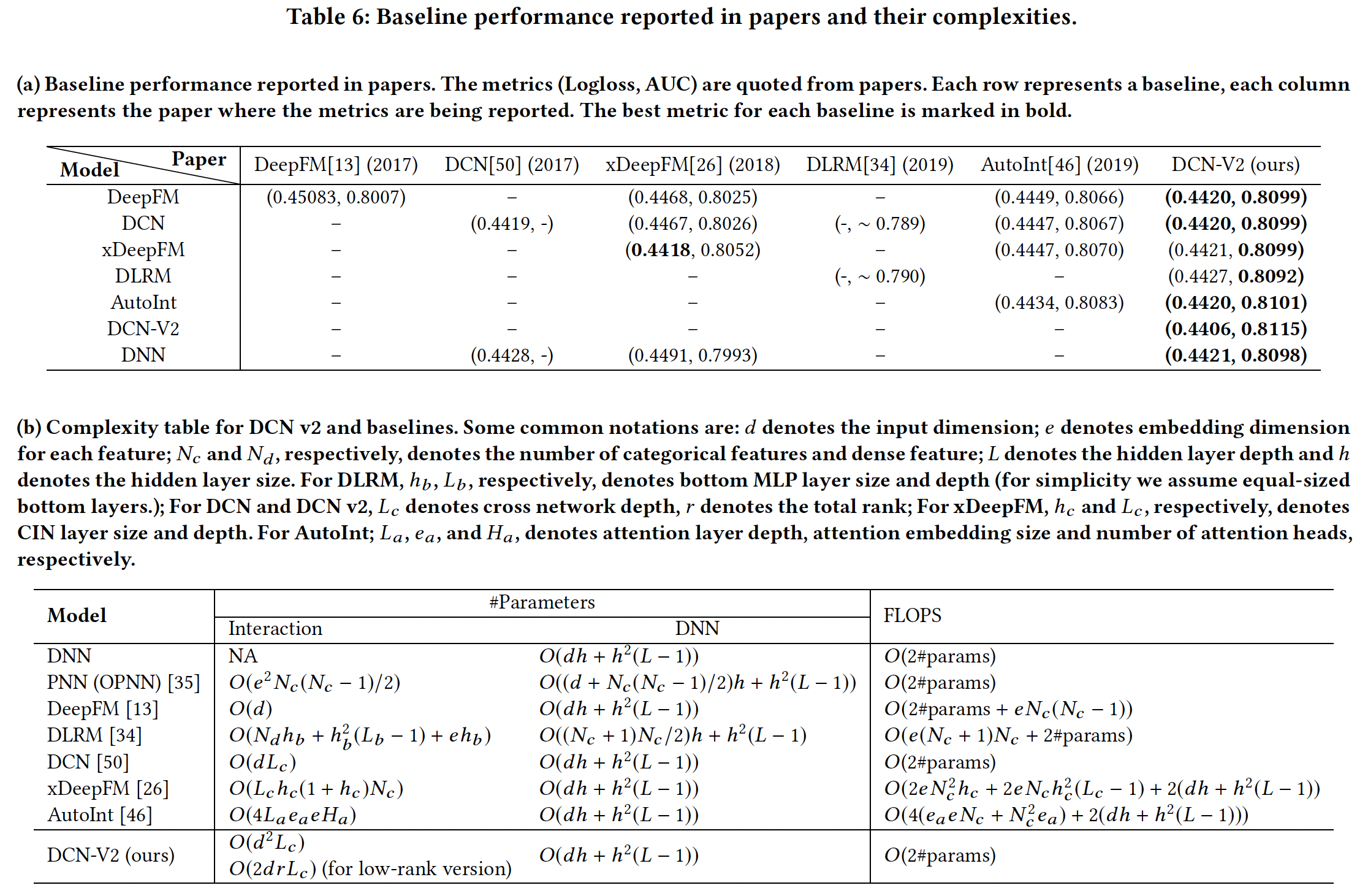
baseline方法:SOTA的feature interaction learning算法,如下表所示。
实现细节:所有
baseline和我们的方法都在TensorFlow v1中实现。为了公平比较,除了特征交互组件,所有模型的实现都是相同的。embedding:除了DNN和DCN模型,所有的baseline都要求每个特征的embedding size是相同的。因此,我们将所有的模型固定为Criteo为39、Movielen-1M为30)。optimization:Adam优化器,batch size = 512(MovieLen batch size = 128)。权重以He Normal来初始化,bias被初始化为零,梯度被截断为范数10。对参数采用decay = 0.9999的指数移动平均。超参数调优:对于所有的
baseline,我们对超参数进行了粗粒度(大范围)的网格搜索,然后再进行细粒度(小范围)的搜索。为了确保可重复性和减少模型方差,对于每个方法和数据集,我们报告了最佳配置的5次独立运行的均值和标准差。我们在下面描述了Criteo的详细设置。对于MovieLens,我们也遵循类似的过程。对于
Criteo的所有baseline:学习率调优范围:对数尺度上从
训练步数调优范围:
{150k, 160k, 200k, 250k, 300k}隐层深度调优范围:
{1, 2, 3, 4}。隐层维度调优范围:
{562, 768, 1024}。正则化参数调优范围:
每个模型自己的超参数:
DCN:交叉层的数量调优范围{1, 2, 3, 4}。AutoInt:注意力层的数量调优范围{2, 3, 4};attention embedding size调优范围{20, 32, 40};attention head数量调优范围{2, 3};残差连接调优范围{enable, disable}。xDeepFM:CIN layer size调优范围{100, 200},CIN layer depth调优范围{2, 3, 4},激活函数为恒等映射,计算为direct或indirect。DLRM:bottom MLP layer size和数量的调优范围{(512,256,64), (256,64)}。PNN:我们运行了IPNN、OPNN和PNN*,对于后两者,kernel type调优范围{full matrix, vector, number}。
对于所有的模型,参数总数上限为
DCN-V2和baseline比较结果:每个模型的最佳setting是超参数空间中搜索出来的。如果两个setting的性能相当,我们就报告成本较低的那个。可以看到:我们看到,
DCN-V2的表现一直优于baseline(包括DNN),并实现了健康的quality/cost trade-off。注意,在我们为
baseline模型的最佳setting而进行的彻底的超参数搜索中,我们确实探索了更宽、更深的模型。然而,更大的模型也不能产生更多的质量收益,清楚地表明许多bseline的瓶颈是质量而不是效率。Best Setting:对于
DCN-V2模型,"stacked"和"parallel"结构都优于所有baseline,而"stacked"在Criteo上效果更好、"parallel"在Movielen-1M上效果更好。在实践中,我们发现:
"stacked"结构更能提高质量,而"parallel"结构有助于减少模型方差。
与
baseline的比较:对于二阶方法,
DLRM的表现不如DeepFM,尽管它们都来自FM。这可能是由于DLRM在点积层之后省略了一阶稀疏特征。对于高阶方法,
xDeepFM、AutoInt和DCN在Criteo上的表现相似;而在MovieLens上,xDeepFM在Logloss上表现出很高的方差。DCN-V2在Criteo上取得了最好的性能,它显式地建模三阶特征交互。DCN-Mix有效地利用了内存,并在保持准确性的同时减少了30%的成本。单独的CrossNet在两个数据集上的表现都优于DNN。
与
DNN的比较:我们调优了DNN模型,并使用了更大的layer size。令我们惊讶的是,DNN的表现与大多数baseline相差无几,甚至超越了某些模型。我们的假设是:那些来自
baseline的显式特征交叉的模型并不是以一种富有表达能力、以及易于优化的方式建立的。前者使其性能容易被具有大容量的DNN所匹配,后者则容易导致可训练性问题从而使模型不稳定。因此,当与DNN组合时,整体性能被DNN组件所支配。在表达能力方面,考虑二阶方法。
PNN的模型比DeepFM和DLRM更具有表达能力,这导致它在MovieLen-1M上的表现更出色。这也解释了DCN与DCN-V2相比性能较差的原因。在可训练性方面,某些模型可能天生就比较难训练,导致性能不尽如人意。
在
Criteo上,PNN的平均性能与DNN相当。这是由PNN的不稳定性造成的。虽然它的最好成绩比DNN好,但它在多次试验中的高标准差推高了平均损失。
模型效率:
对于大多数模型,
FLOPS大约是参数数量的2倍。然而,对于xDeepFM,FLOPS要高出参数数量一个量级,这使得它在工业规模的应用中难以部署。在所有的方法中,
DCN-V2提供了最好的性能,同时保持了相对的效率。DCN-Mix进一步降低了成本,在模型效率和质量之间取得了更好的trade-off。
超参数研究:
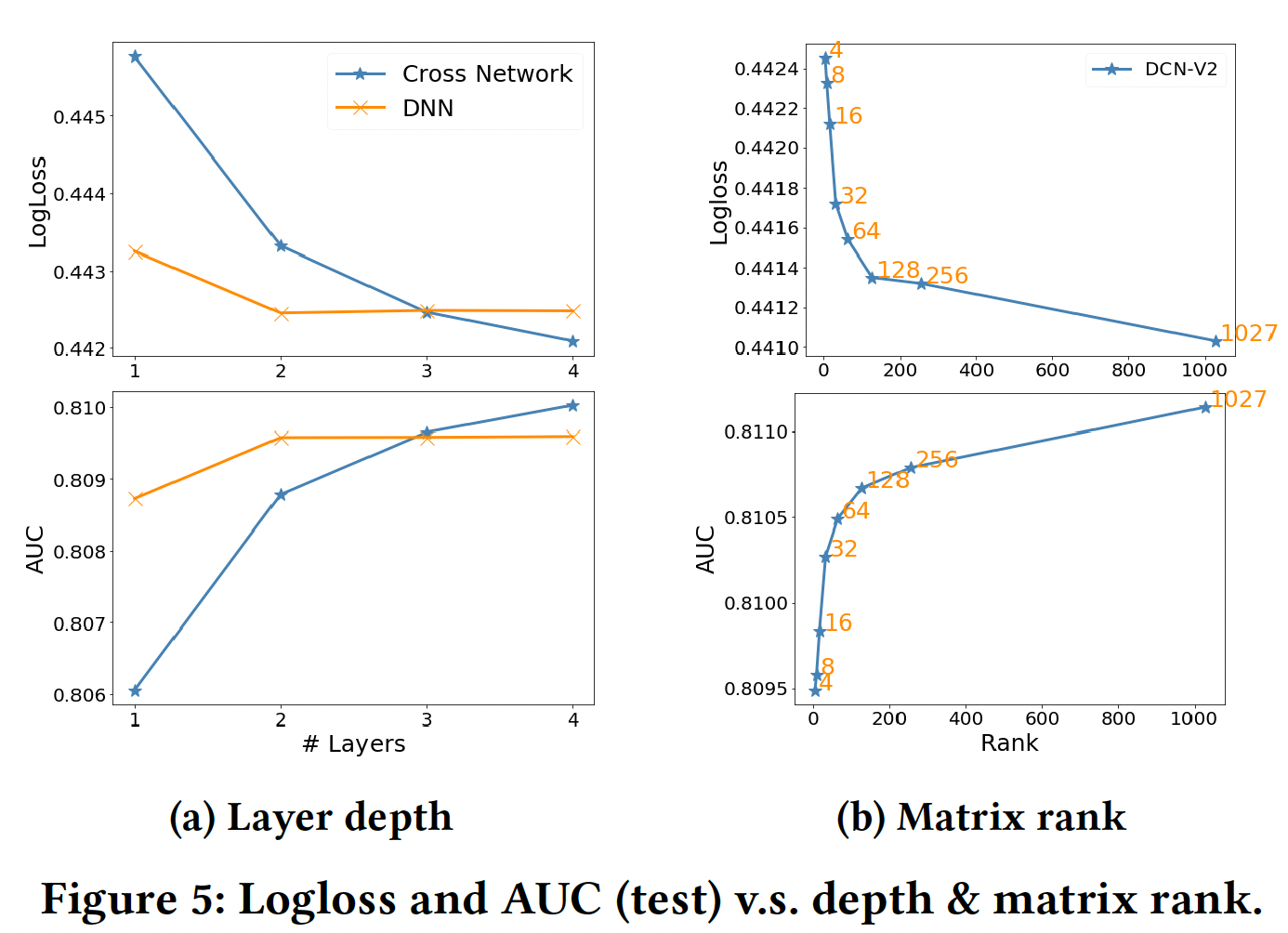
Depth of Cross Layer:根据设计,cross network捕获的最高阶特征交叉随着层深的增加而增加。如图Figure 5 (a)所示:随着
cross network的加深,质量有了稳定的提高,表明它能够捕捉到更多有意义的交叉。然而,当使用更多的层时,改善的速度放缓了。这表明高阶交叉的贡献比低阶交叉的贡献要小。
我们还用一个同样大小的
DNN作为参考。当有≤2层时,DNN的表现优于交叉网络;当有更多层时,cross network开始缩小性能差距,甚至优于DNN的表现。矩阵的秩:模型是
3个交叉层,然后是3个512-size ReLU层。如图Figure 5 (b)所示:当
4时,性能与其他baseline持平。当
4增加到64时,LogLoss几乎随当
64进一步增加到满时,LogLoss的改善速度减慢了。
我们把
64称为rank阈值。从64开始的明显放缓表明:刻画特征交叉的重要信号可以在前64个奇异值中捕获。专家数量:我们观察到:
表现最好的
setting(专家数量、gate类型、激活函数类型)受到数据集和模型架构的影响。每种
setting的最佳表现模型产生了相似的结果。更多的lower-rank experts并没有比单个higher-rank expert表现更好,这可能是朴素的gating函数、以及采取的optimizations所导致。我们相信更复杂的gating和optimization会在mixture of experts架构下产生更好的结果。
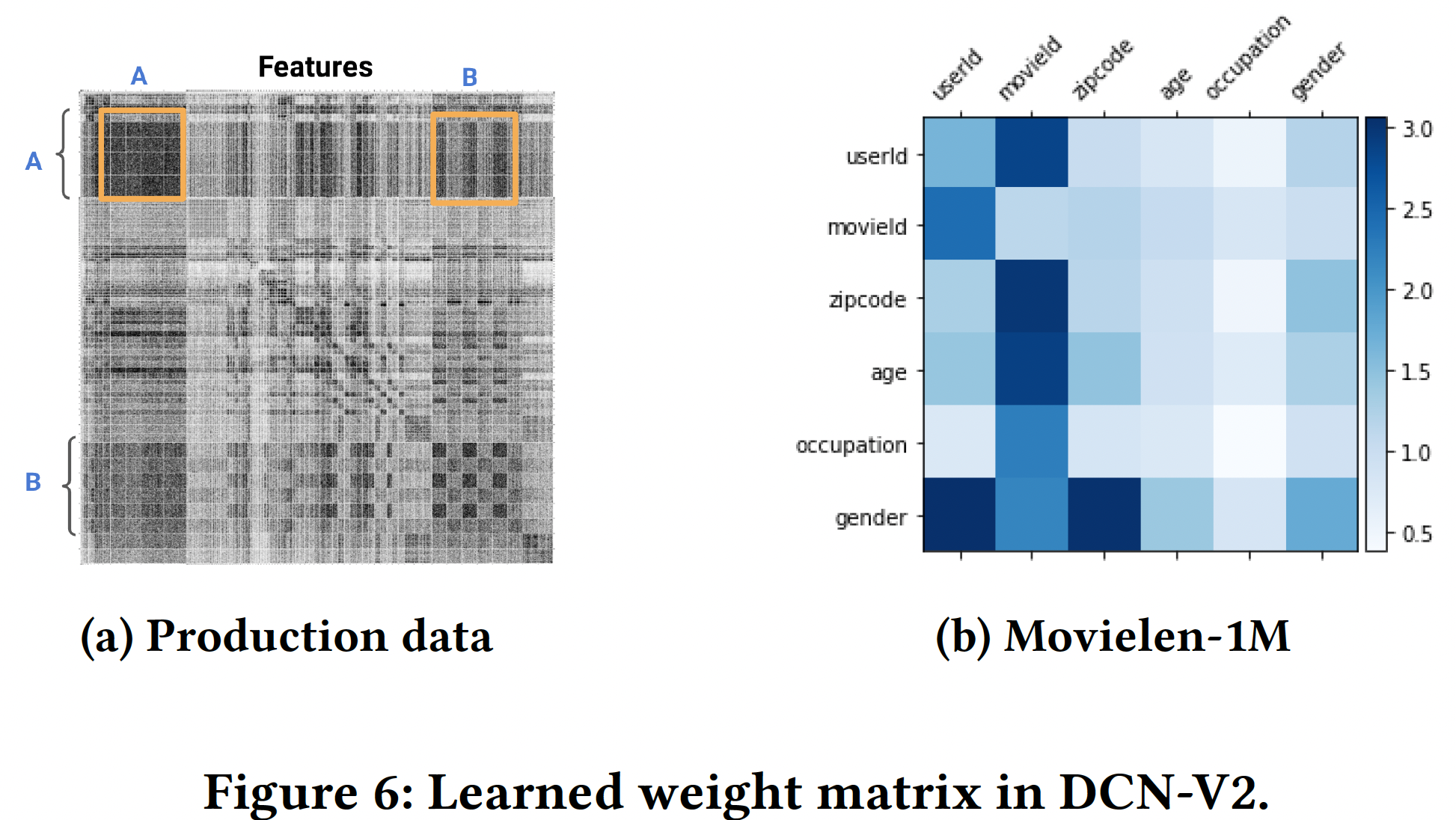
模型可视化:
DCN-V2中的权重矩阵block-wise视图(由下图展示了第一个交叉层中学到的权重矩阵
(a)中,由于版权的原因,特征名称被省略了;深色的像素代表较大的权重。在图(b)中,每个block代表它的Frobenius范数。图
(a)展示了整个矩阵,橙色方框突出了一些值得注意的特征交叉。非对角线的block对应于重要的交叉,这表明DCN-V2的有效性。对角线的block对应于self-interaction(即,图
(b)表现学到的一些强交互,如Gender × UserId、MovieId × UserId。图
(a)包含的特征更多,因此方块更小;图(b)包含很少的特征,因此方块显得很大。
DCN-V2在谷歌中的产品化:我们通过DCN-V2同时在离线模型的准确性、以及在线关键业务指标方面都取得了显著的收益。与公共数据集相比,收益也更加明显,这可能是由于生产数据集的数据量明显更大,数据分布更复杂。生产数据和模型:生产数据是由数以千亿计的训练样本组成的抽样用户日志。稀疏特征的词表规模从
2到数百万不等。baseline模型是一个全连接的多层感知机,采用ReLU激活函数。与生产模型的比较:与生产模型相比,
DCN-V2产生了0.6%的AUCLoss(即,1.0 - AUC)改进。我们还观察到显著的在线关键业务指标收益。baseline为多层感知机,所以DCN-V2表现好是符合预期的。为什么不和DeepFM进行比较?
我们分享一些我们通过产品化
DCN-V2学到的实际经验:最好在
DNN的输入层和隐层之间插入交叉层。我们看到,通过堆叠或拼接
1-2个交叉层,准确性得到了一致的提高。超过2个交叉层,收益开始趋于平稳。我们观察到,堆叠交叉层和拼接交叉层的效果都不错。堆叠层(
stacking layers)可以学到高阶的特征交互,而拼接层(concatenating layers)(类似于多头机制)可以捕获到互补的交互。我们观察到,使用
rank = (input size)/4的low-rank DCN始终保持了full-rank DCN-V2的准确性。