Numpy学习笔记 （基于Numpy 1.11.0）

1. Python的列表中保存的是对象的指针。因此为了保存一个简单的列表，如[1,2,3]，则需要三个指针和三个整数对象。

2. numpy提供了两种基本的对象：

   • ndarray：它是存储单一数据类型的多维数组，简称数组
   • ufunc：它是一种能够对数组进行处理的特殊函数

一、 ndarray

1. ndarray 对象的内存结构

1. ndarray对象在内存中的结构如下：

   • ndarray.dtype：存储了数组保存的元素的类型。float32
   • ndarray.ndim：它是一个整数，保存了数组的维度，即多少个轴
   • ndarray.shape：它是一个整数的元组，每个元素一一对应地保存了数组某个维度的大小（即某个轴的长度）。
   • ndarray.strides：它是一个整数的元组，每个元素保存着每个轴上相邻两个元素的地址差。即当某个轴的下标增加1 时，数据存储区中的指针增加的字节数
   • ndarray.data：它指向数组的数据的存储区

   可以看到：该数组中元素类型为float32；该数组有2 个轴。每个轴的长度都是 3 个元素。第 0 轴增加1时，下标增加 12字节（也就是 3个元素，即一行的距离）； 第 1 轴增加 1时，下标增加 4字节（也就是一个元素的距离）。

2. 元素在数据存储区中的排列格式有两种：C语言格式和Fortran语言格式。

   • C语言中，多维数组的第 0 轴是最外层的。即 0 轴的下标增加 1时，元素的地址增加的字节数最多
   • Fortran语言中，多维数组的第 0 轴是最内层的。即 0 轴的下标增加 1时，元素的地址增加的字节数最少

   numpy中默认是以 C语言格式存储数据。如果希望改为Fortran格式，则只需要在创建数组时，设置order参数为"F"

3. 数组的flags属性描述了数据存储区域的一些属性。你可以直接查看flags属性，也可以单独获取其中某个标志值。

   • C_CONTIGUOUS:数据存储区域是否是C语言格式的连续区域
   • F_CONTIGUOUS:数据存储区域是否是F语言格式的连续区域
   • OWNDATA:数组是否拥有此数据存储区域。当一个数组是其他数组的视图时，它并不拥有数据存储区域，通过视图数组的base属性可以获取保存数据存储区域的那个原始数组。

4. 数组的转置可以通过其T属性获取。转置数组可以简单的将其数据存储区域看作是Fortran语言格式的连续区域，并且它不拥有数据存储区域。

5. 修改数组的内容时，会直接修改数据存储区域。所有使用该数据存储区域的数组都将被同时修改！

1.1 dtype

1. numpy 有自己的浮点数类型： float16/float32/float64/float128等等。

   • 在需要指定dtype参数时，你可以使用numpy.float16，也可以传递一个表示数值类型的字符串。numpy中的每个数值类型都有几种字符串表示。字符串和类型之间的对应关系都存储在numpy.typeDict字典中。
   • dtype是一种对象，它不同于数值类型。只有dtype.type才能获取对应的数值类型
   • 你可以通过np的数值类型np.float32来创建数值对象。但要注意：numpy的数值对象的运算速度比python内置类型的运算速度要慢很多。所以应当尽量避免使用numpy的数值对象

2. 使用ndarray.astype()方法可以对数组元素类型进行转换。

1.2 shape

1. 你可以使用ndarray.reshape()方法调整数组的维度。

   • 你可以在某个维度设置其长度为 -1，此时该维度的长度会被自动计算

2. 你可以直接修改ndarry的shape属性，此时直接修改原始数组。

   • 你可以在某个维度设置其长度为 -1，此时该维度的长度会被自动计算

1.3 view

1. 我们可以通过ndarray.view()方法，从同一块数据区创建不同的dtype数组。即使用不同的数值类型查看同一段内存中的二进制数据。它们使用的是同一块内存。
2. 如果我们直接修改原始数组的dtype，则同样达到这样的效果，此时直接修改原始数组。

1.4 strides

1. 我们可以直接修改ndarray对象的strides属性。此时修改的是原始数组。
2. 你可以使用np.lib.stride_tricks.as_stride()函数创建一个不同strides的视图。 注意：使用as_stride时并不会执行内存越界检查，因此shape和stride设置不当可能会发生意想不到的错误。

1.5 拷贝和视图

1. 当处理ndarray时，它的数据存储区有时被拷贝，但有时并不被拷贝。有三种情况。

   • 完全不拷贝：简单的赋值操作并不拷贝ndarray的任何数据，这种情况下是新的变量引用ndarray对象（类似于列表的简单赋值）

   • 视图和浅拷贝：不同的ndarray可能共享相同的数据存储区。如ndarray.view()方法创建一个新的ndarray但是与旧ndarray共享相同的数据存储区。新创建的那个数组称作视图数组。

     • 对于视图数组，ndarray.base返回的是拥有数据存储区的那个底层ndarray。而非视图数组的ndarray.base返回None
     • ndarray.flags.owndata返回数组是否拥有基础数据
     • 对于数组的分片操作返回的是一个ndarray的视图。对数组的索引返回的不是视图，而是含有基础数据。

   • 深拷贝：ndarray.copy()操作会返回一个完全的拷贝，不仅拷贝ndarray也拷贝数据存储区。

2. 数组的创建

1. 这里有几个共同的参数：

   • a：一个array-like类型的实例，它不一定是数组，可以为list、tuple、list of tuple、list of list、tuple of list、tuple of tuple等等。

   • dtype：数组的值类型，默认为float。你可以指定Python的标准数值类型，也可以使用numpy的数值类型如：numpy.int32或者numpy.float64等等。

   • order：指定存储多维数据的方式。

     • 可以为'C'，表示按行优先存储（C风格）；
     • 可以为'F'，表示按列优先存储（Fortran风格）。
     • 对于**_like()函数，order可以为：'C'，'F'，'A'（表示结果的order与a相同），'K'（表示结果的order与a尽可能相似）

   • subok：bool值。如果为True则：如果a为ndarray的子类（如matrix类），则结果类型与a类型相同。如果为False则：结果类型始终为ndarray。默认为True。

2.1 创建全1或者全0

1. np.empty(shape[,dtype,order])：返回一个新的ndarray，指定了shape和dtype，但是没有初始化元素。因此其内容是随机的。

   • np.empty_like(a[,dtype,order,subok])：返回一个新的ndarray，shape与a相同，但是没有初始化元素。因此其内容是随机的。

   

2. np.eye(N[, M, k, dtype])：返回一个二维数组，对角线元素为1，其余元素为0。M默认等于N。k默认为0表示对角线元素为1，如为正数则表示对角线上方一格的元素为1，如为负数表示对角线下方一格的元素为1.

   • np.identity(n[, dtype]) ：返回一个单位矩阵

   

3. np.ones(shape[, dtype, order])：返回一个新的ndarray，指定了shape和type，每个元素初始化为1.
   

   • np.ones_like(a[, dtype, order, subok]) ：返回一个新的ndarray，shape与a相同，每个元素初始化为1。

   

4. np.zeros(shape[, dtype, order]) ：返回一个新的ndarray，指定了shape和type，每个元素初始化为0.

   • np.zeros_like(a[, dtype, order, subok])：返回一个新的ndarray，shape与a（另一个数组）相同，每个元素初始化为0。

   

5. np.full(shape, fill_value[, dtype, order])：返回一个新的ndarray，指定了shape和type，每个元素初始化为fill_value。

   • np.full_like(a, fill_value[, dtype, order, subok])：返回一个新的ndarray，shape与a相同，每个元素初始化为fill_value。

   

2.2 从现有数据创建

1. np.array(object[, dtype, copy, order, subok, ndmin]):从object创建。

   • object可以是一个ndarray，也可以是一个array_like的对象，也可以是一个含有返回一个序列或者ndarray的__array__方法的对象，或者一个序列。
   • copy：默认为True，表示拷贝对象
   • order可以为'C'、'F'、'A'。默认为'A'。
   • subok默认为False
   • ndmin：指定结果ndarray最少有多少个维度。

2. np.asarray(a[, dtype, order])：将a转换成一个ndarray。其中a是array_like的对象， 可以是list、list of tuple、tuple、tuple of list、ndarray类型。order默认为C。

3. np.asanyarray(a[, dtype, order])：将a转换成ndarray。

4. np.ascontiguousarray(a[, dtype]) ：返回C风格的连续ndarray

5. np.asmatrix(data[, dtype])：返回matrix

6. np.copy(a[, order])：返回ndarray的一份深拷贝

7. np.frombuffer(buffer[, dtype, count, offset])：从输入数据中返回一维ndarray。count指定读取的数量，-1表示全部读取；offset指定从哪里开始读取，默认为0。创建的数组与buffer共享内存。buffer是一个提供了buffer接口的对象（内置的bytes/bytearray/array.array类型提供了该接口）。

8. np.fromfile(file[, dtype, count, sep]) ：从二进制文件或者文本文件中读取数据返回ndarray。sep：当从文本文件中读取时，数值之间的分隔字符串，如果sep是空字符串则表示文件应该作为二进制文件读取；如果sep为" "表示可以匹配0个或者多个空白字符。

9. np.fromfunction(function, shape, **kwargs)：返回一个ndarray。从函数中获取每一个坐标点的数据。假设shape的维度为N，那么function带有N个参数，fn(x1,x2,...x_N)，其返回值就是该坐标点的值。

10. np.fromiter(iterable, dtype[, count])：从可迭代对象中迭代获取数据创建一维ndarray。

11. np.fromstring(string[, dtype, count, sep])：从字符串或者raw binary中创建一维ndarray。如果sep为空字符串则string将按照二进制数据解释（即每个字符作为ASCII码值对待）。创建的数组有自己的数据存储区。

12. np.loadtxt(fname[, dtype, comments, delimiter, ...]):从文本文件中加载数据创建ndarray，要求文本文件每一行都有相同数量的数值。comments：指示注释行的起始字符，可以为单个字符或者字符列表（默认为#）。delimiter:指定数值之间的分隔字符串，默认为空白符。converters：将指定列号(0,1,2...)的列数据执行转换，是一个map，如{0:func1}表示对第一列数据执行func1(val_0)。skiprows：指定跳过开头的多少行。usecols：指定读取那些列（0表示第一列）。

2.3 从数值区间创建

1. np.arange([start,] stop[, step,][, dtype]):返回均匀间隔的值组成的一维ndarray。区间是半闭半开的[start,stop)，其采样行为类似Python的range函数。start为开始点，stop为终止点，step为步长，默认为1。这几个数可以为整数可以为浮点数。注意如果step为浮点数，则结果可能有误差，因为浮点数相等比较不准确。
   

2. np.linspace(start, stop[, num, endpoint, ...]) ：返回num个均匀采样的数值组成的一维ndarray（默认为50）。区间是闭区间[start,stop]。endpoint为布尔值，如果为真则表示stop是最后采样的值（默认为True），否则结果不包含stop。retstep如果为True则返回结果包含采样步长step，默认为True。

3. np.logspace(start, stop[, num, endpoint, base, ...])：返回对数级别上均匀采样的数值组成的一维ndarray。采样点开始于base^start，结束于base^stop。base为对数的基，默认为 10。

   • 它逻辑上相当于先执行arange获取数组array，然后再执行base^array[i]获取采样点
   • 它没有retstep 关键字参数

   

3. 数组的索引

3.1 一维数组的索引

1. 一维数组的索引和列表相同。假设a1 是一维数组

   • 可以指定一个整数i作为索引下标，如a1[i]

   • 可以指定一个切片作为索引下标，如a1[i:j]。通过切片获得的新的数组是原始数组的一个视图，它与原始数组共享相同的一块数据存储空间。

   • 可以指定一个整数列表对数组进行存取，如a1[[i1,i2,i3]]。此时会将列表中的每个整数作为下标(i1/i2/i3)，使用列表作为下标得到的数组(为 np.array([a1[i1],a1[i2],a1[i3]]))不和原始数组共享数据。

   • 可以指定一个整数数组作为数组下标，如a1[a2]此时会得到一个形状和下标数组a2相同的新数组。新数组的每个元素都是下标数组中对应位置的值作为下标从原始数组中获得的值。新数组不和原始数组共享数据。

     • 当下标数组是一维数组时，其结果和用列表作为下标的结果相同
     • 当下标是多维数组时，结果也是多维数组

   • 可以指定一个布尔数组作为数组下标，如a1[b]。此时将获得数组a1中与数组b中的True对应的元素。新数组不和原始数组共享数据。

     • 布尔数组的形状与数组a1 完全相同，它就是一个mask

xxxxxxxxxx
- 如果是布尔列表，情况也相同
- 如果布尔数组的长度不够，则不够的部分作为`False`（该特性是`deprecating`，建议不要使用）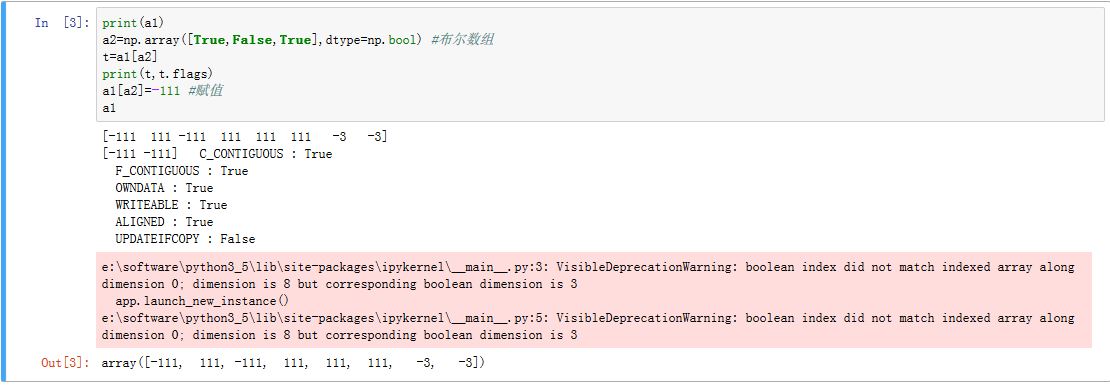
  ![index_bool](../imgs/ndarray/index_bool.JPG)

2. 上述介绍的一维数组的索引，既可以用于数组元素的选取，也可以用于数组元素的赋值

   • 你可以赋一个值，此时该值会填充被选取出来的每一个位置

   • 你可以赋值一个数组或者列表，此时数组或者列表的形状要跟你选取出来的位置的形状完全匹配（否则报出警告）

     • 数组不同于列表。对于列表，你无法对列表切片赋一个值，而是要赋一个形状相同的值

   

3.2 多维数组的索引

1. 多维数组使用元组作为数组的下标，如a[1,2]，当然你也可以添加圆括号为a[(1,2)]。

   • 元组中每个元素和数组的每个轴对应。下标元组的第 0 个元素与数组的第 0 轴对应，如第 1 个元素与数组的第 1 轴对应...

2. 多维数组的下标必须是一个长度和数组的维度ndim相等的元组。

   • 如果下标元组的长度大于数组的维度ndim，则报错
   • 如果下标元组的长度小于数组的维度ndim，则在元组的后面补 :，使得下标元组的长度等于数组维度ndim。
   • 如果下标对象不是元组，则Numpy会首先将其转换为元组。

   下面的讨论都是基于下标元组的长度等于数组维度ndim的条件。

3. 单独生成切片时，需要使用slice(begin,end,step) 来创建。其参数分别为：开始值，结束值，间隔步长。如果某些参数需要省略，则使用None。因此， a[2:,2]等价于a[slice(2,None,None),2]

   • 使用python内置的slice()创建下标比较麻烦(首先构造切片，再构造下标元组)，numpy提供了一个numpy.s_对象来帮助我们创建数组下标。s_对象实际上是IndexExpression类的一个对象

4. 多维数组的下标元组的元素可能为下列类型之一：整数、切片、整数数组、布尔数组。如果不是这些类型，如列表或者元组，则将其转换成整数数组。

   • 多维数组的下标全部是整数或者切片：索引得到的是元素数组的一个视图。

   • 多维数组的下标全部是整数数组：假设多维数组为 $X$ 。假设这些下标整数数组依次为 $A_1,A_2,\cdots,A_n$。这 $n$ 个数组必须满足广播条件。假设它们进行广播之后的维度为 $M$ ，形状为 $(d_0,d_1,\cdots,d_{M-1})$ 即：广播之后有 $M$ 个轴：第 0 轴长度为 $d_0$ ，...，第 $M-1$ 轴长度为 $d_{M-1}$ 。假设 $A_1,A_2,\cdots,A_n$ 经过广播之后分别为数组 $A^{\prime}_1,A^{\prime}_2,\cdots,A^{\prime}_n$

     则：索引的结果也是一个数组 $R$ ，结果数组 $R$ 的维度为 $M$ ，形状为 $(d_0,d_1,\cdots,d_{M-1})$ 。其中

     $$R[i_0,i_1,\cdots,i_{M-1}]=\\ X[A^{\prime}_1[i_0,i_1,\cdots,i_{M-1}],A^{\prime}_2[i_0,i_1,\cdots,i_{M-1}],\cdots,A^{\prime}_n[i_0,i_1,\cdots,i_{M-1}]]$$

     结果数组的下标并不来源于 $X$，而是来源于下标数组的广播之后的数组。相反，如果多维数组的下标为整数或者切片，则结果数组的下标来源于 $X$

   

   • 多维数组的下标包含整数数组、切片：则切片/整数下标与整数数组下标分别处理。

   • 多维数组的下标是布尔数组或者下标元组中包含了布尔数组，则相当于将布尔数组通过nonzero 将布尔数组转换成一个整数数组的元组，然后使用整数数组进行下标运行。

     • nonzero(a)返回数组a中，值非零的元素的下标。它返回值是一个长度为a.ndim的元组，元组的每个元素都是一个一维的整数数组，其值为非零元素的下标在对应轴上的值。如：第 0 个元素为a中的非零值元素在0轴的下标、第 1 个元素为a中的非零值元素在1轴的下标，...

5. 当下标使用整数或者切片时，所取得的数据在数据存储区域中是等间隔分布的。因为只需要修改数组的ndim/shape/strides等属性以及指向数据存储区域的data指针就能够实现整数和切片下标的索引。所以新数组和原始数组能够共享数据存储区域。

   当使用整数数组（整数元组，整数列表页转换成整数数组），布尔数组时，不能保证所取得的数据在数据存储区中是等间隔的，因此无法和原始数组共享数据，只能对数据进行复制。

6. 索引的下标元组中：

   • 如果下标元组都是切片，则索引结果的数组与原始数组的维度相同（轴的数量相等）
   • 每多一个整数下标，则索引结果的数组就少一个维度（少一个轴）
   • 如果所有的下标都是整数，则索引结果的维度为 0
   • 如果下标元组中存在数组，则还需要考虑该下标数组广播后的维度
     

7. 通过索引获取的数组元素的类型为数组的dtype类型 。如果你想获取标准python类型，可以使用数组的item()方法。

   

3.3 索引的维度变换

1. 对于数组，如果我们不考虑下标数组的情况，也就是：其下标仅仅为整数、或者切片，则有：

   • 每次下标中出现一个整数下标，则索引结果的维度降 1。该维度被吸收掉
   • 每次下标中出现一个切片下标，则该维度保持不变

2. 前面提到：多维数组的下标必须是一个长度和数组的维度 ndim 相等的元组。但是如果下标中包含None，则可以突破这一限制。每多一个None，则索引结构维度升 1 。

   • 当数组的下标元组的长度小于等于数组的维度ndim时，元组中出现的None等价于切片:
   • 当数组的下标元组的长度大于数组的维度ndim时，元组中哪里出现None，索引结果就在哪里创建一个新轴，该轴长度为 1。如c=a[0,:,None]，索引结果的维度为 (3,1)；而d=a[0,None,:]的索引结果维度为(1,3)

   

4. 操作多维数组

1. numpy.concatenate((a1, a2, ...), axis=0)：连接多个数组。其中(a1,a2,...)为数组的序列，给出了待连接的数组，它们沿着axis指定的轴连接。

   • 所有的这些数组的形状，除了axis轴之外都相同

2. • numpy.vstack(tup):等价于numpy.concatenate((a1, a2, ...), axis=0)。沿着 0 轴拼接数组

     • 沿0轴拼接（垂直拼接），增加行

   • numpy.hstack(tup):等价于numpy.concatenate((a1, a2, ...), axis=1)。沿着 1 轴拼接数组

     • 沿1轴拼接（水平拼接），增加列

   • numpy.column_stack(tup)：类似于hstack，但是如果被拼接的数组是一维的，则将其形状修改为二维的(N,1)。

     • 沿列方向拼接，增加列

   • numpy.c_对象的[]方法也可以用于按列连接数组。但是如果被拼接的数组是一维的，则将其形状修改为二维的(N,1)。

     • 沿列方向拼接，增加列

   

   

3. numpy.split(ary, indices_or_sections, axis=0)用于沿着指定的轴拆分数组ary。indices_or_sections指定了拆分点：

   • 如果为整数N，则表示平均拆分成N份。如果不能平均拆分，则报错
   • 如果为序列，则该序列指定了划分区间（无需指定最开始的0起点和终点）。如[1,3]指定了区间：[0,1],[1,3],[3:]

   而numpy.array_split(ary, indices_or_sections, axis=0)的作用也是类似。唯一的区别在于：当indices_or_sections为整数，且无法平均拆分时，并不报错，而是尽可能的维持平均拆分。

4. numpy.transpose(a, axes=None)：重置轴序。如果axes=None，则默认重置为逆序的轴序（如原来的shape=(1,2,3)，逆序之后为(3,2,1)）。如果axes!=None，则要给出重置后的轴序。它获得的是原数组的视图。

   numpy.swapaxes(a, axis1, axis2)：交换指定的两个轴axis1/axis2。它获得是原数组的视图。

   

5.打印数组

1. 当打印ndarray时，numpy按照Python的嵌套list的格式打印输出，但是按照以下顺序打印：

   • 最底层的axis按照从左到右的顺序输出
   • 次底层的axis按照从上到下的顺序输出
   • 其他层的axis也是按照从上到下的顺序输出，但是每个slice中间间隔一条空行

   如： 一维的ndarray按行打印；二维的ndarray按照矩阵打印；三维的ndarray按照矩阵的list打印

   如果ndarray太大，那么numpy默认跳过中间部分的数据而只是输出四个角落的数据。

2. 要想任何时候都打印全部数据，可以在print(array)之前设置选项numpy.set_printoptions(threshold='nan')。这样后续的打印ndarray就不会省略中间数据。

6. Nan 和无穷大

1. 在numpy中，有几个特殊的数：

   • numpy.nan表示NaN（Not a Number），它并不等价于numpy.inf（无穷大）。
   • numpy.inf：正无穷
   • numpy.PINF：正无穷（它就引用的是numpy.inf）
   • numpy.NINF：负无穷

2. 有下列函数用于判断这几个特殊的数：

   • numpy.isnan(x[,out])：返回x是否是个NaN，其中x可以是标量，可以是数组

   • numpy.isfinite(x[, out])：返回x是否是个有限大小的数，其中x可以是标量，可以是数组

     • numpy.isfinite(np.nan)返回False，因为NaN首先就不是一个数

   • numpy.isposinf(x[, out])：返回x是否是个正无穷大的数，其中x可以是标量，可以是数组

     • numpy.isposinf(np.nan)返回False，因为NaN首先就不是一个数
       

   • numpy.isneginf(x[, out])：返回x是否是个负无穷大的数，其中x可以是标量，可以是数组

     • numpy.isneginf(np.nan)返回False，因为NaN首先就不是一个数

   • numpy.isinf(x[, out])：返回x是否是个无穷大的数，其中x可以是标量，可以是数组

     • numpy.isinf(np.nan)返回False，因为NaN首先就不是一个数

3. 下列函数用于对这几个特殊的数进行转换：

   • numpy.nan_to_num(x)：将数组x中的下列数字替换掉，返回替换掉之后的新数组：

     • NaN：替换为0
     • 正无穷：替换为一个非常大的数字
     • 负无穷：替换为一个非常小的数字

二、 ufunc 函数

1. ufunc 函数是对数组的每个元素进行运算的函数。numpy很多内置的ufunc函数使用C语言实现的，计算速度非常快。

2. 基本上所有的ufunc函数可以指定一个out参数来保存计算结果数组，并返回out数组。同时如果未指定out参数，则创建新的数组来保存计算结果。

   • 如果你指定了out参数，则要求out数组与计算结果兼容。即：数组的尺寸要严格匹配，并且数组的dtype要匹配。

3. numpy的某些ufunc函数，如numpy.sin()，支持计算单个数值。但是在单个数值的计算速度上，python的math.sin()要快得多。两个原因：

   • numpy.sin()为了同时支持数组和单个数值运算，其C语言的内部实现要比math.sin()复杂
   • 单个数值的计算上：numpy.sin()返回的是numpy.float64类型，而math.sin()返回的是python的标准float类型

1. 广播

1. 当使用ufunc函数对两个数组进行计算时，ufunc函数会对这两个数组的对应元素进行计算。这就要求这两个数组的形状相同。如果这两个数组的形状不同，就通过广播broadcasting进行处理：

   • 首先让所有输入数组都向其中维度最高的数组看齐。看齐方式为：在shape属性的左侧插入数字1
   • 然后输出数组的shape属性是输入数组的shape属性的各轴上的最大值
   • 如果输入数组的某个轴的长度为 1，或者与输出数组的各对应轴的长度相同，该数组能正确广播。否则计算出错
   • 当输入数组的某个轴的长度为 1时，沿着此轴运算时都用此轴上的第一组值。

   

2. 可以通过numpy.broadcast_arrays() 查看广播之后的数组

3. 你可以通过ndarray.repeat()方法来手动重复某个轴上的值.其用法为ndarray.repeat(repeats, axis=None)，其中：

   • repeats为重复次数
   • axis指定被重复的轴，即沿着哪一轴重复。如果未指定，则将数组展平然后重复。返回的也是一个展平的数组

   被重复的是该轴的每一组值。

   

4. numpy提供了ogrid对象，用于创建广播运算用的数组。ogrid对象像多维数组一样，使用切片元组作为下标，返回的是一组可以用于广播计算的数组。其切片有两种形式：

   • 开始值：结束值：步长。它指定返回数组的开始值和结束值（不包括）。默认的开始值为 0；默认的步长为 1。与np.arange类似
   • 开始值：结束值：长度 j。当第三个参数为虚数时，表示返回的数组的长度。与np.linspace类似。
   • 有多少个下标，则结果就是多少维的，同时也返回相应数量的数组。每个返回的数组只有某一维度长度大于1，其他维度的长度全部为 1。假设下标元组长度为3，则结果元组中：第一个数组的shape=(3,1,1)，第二个数组的shape=(1,3,1)，第三个数组的shape=(1,1,3)。

5. numpy还提供了mgrid对象，它类似于ogrid对象。但是它返回的是广播之后的数组，而不是广播之前的数组：

   ​ !mgrid

6. numpy提供了meshgrid()函数，其用法为：numpy.meshgrid(x1,x2,...xn)。其中xi是都是一维数组。返回一个元组 (X1,X2,...Xn)，是广播之后的数组。假设xi的长度为 li，则返回元组的每个数组的形状都是 (l1,l2,...ln)。

   

7. numpy.ix_()函数可以将N个一维数组转换成可广播的N维数组。其用法为numpy.ix_(x1,x2,x3)，返回一个元组。元组元素分别为对应的可广播的N维数组。

   • 返回的是广播前的数组，而不是广播后的数组

   • 每个转换前的一维数组，对应了一个转换后的 N 维数组

     ​

2. 四则运算

1. numpy提供的四则运算如下，这些四则运算同时提供了函数形式以及表达式形式：

   • 加法：表达式形式y=x1+x2，使用ufunc函数的形式：numpy.add(x1,x2[,out=y])

   • 减法：表达式形式y=x1-x2，使用ufunc函数的形式：numpy.subtract(x1,x2[,out=y])

   • 乘法：表达式形式y=x1*x2，使用ufunc函数的形式：numpy.multiply(x1,x2[,out=y])

   • 真除法：表达式形式y=x1/x2，使用ufunc函数的形式：numpy.true_divide(x1,x2[,out=y])

     • python3 中，numpy.divide(x1,x2[,out=y])也是真除法

   • 取整除法：表达式形式y=x1//x2，使用ufunc函数的形式：numpy.floor_divide(x1,x2[,out=y])

   • 取反：表达式形式y=-x，使用ufunc函数的形式：numpy.negative(x[,out=y])

   • 乘方：表达式形式y=x1**x2，使用ufunc函数的形式：numpy.power(x1,x2[,out=y])

   • 取余数：表达式形式y=x1%x2，使用ufunc函数的形式：numpy.remainder(x1,x2[,out=y])

   

2. 对于 np.add(a,b,a) 这种可以使用a+=b来表示。这些四则运算都可以采用这种方式。

3. 当表达式很复杂时，如果同时数组很大，则会因为产生大量的中间结果而降低程序的运算速度。如： x=a*b+c等价于：

   xxxxxxxxxx
     t=a*b
     x=t+c
     del t
   

   我们可以使用：

   xxxxxxxxxx
     x=a*b
     x+=c
   

   从而减少了一次内存分配。

3. 比较运算

1. numpy提供的比较运算如下，这些比较运算同时提供了函数形式以及表达式形式，并且产生的结果是布尔类型的数组：

   • 等于： 表达式形式y=x1==x2，使用ufunc函数的形式：numpy.equal(x1,x2[,out=y])
   • 不等于： 表达式形式y=x1!=x2，使用ufunc函数的形式：numpy.not_equal(x1,x2[,out=y])
   • 小于： 表达式形式y=x1<x2，使用ufunc函数的形式：numpy.less(x1,x2[,out=y])
   • 小于等于： 表达式形式y=x1<=x2，使用ufunc函数的形式：numpy.less_equal(x1,x2[,out=y])
   • 大于： 表达式形式y=x1>x2，使用ufunc函数的形式：numpy.greater(x1,x2[,out=y])
   • 大于等于： 表达式形式y=x1>=x2，使用ufunc函数的形式：numpy.greater_equal(x1,x2[,out=y])

   

4. 逻辑运算

1. 由于python中的布尔运算使用and/or/not关键字，因此它们无法被重载。numpy提供的数组布尔运算只能通过ufunc函数进行，这些函数以logical_开头。进行逻辑运算时，对于数值零视作False；对数值非零视作True。运算结果也是一个布尔类型的数组：

   • 与：ufunc函数的形式：numpy.logical_and(x1,x2[,out=y])
   • 或：ufunc函数的形式：numpy.logical_or(x1,x2[,out=y])
   • 否定：ufunc函数的形式：numpy.logical_not(x[,out=y])
   • 异或：ufunc函数的形式：numpy.logical_xor(x1,x2[,out=y])

   

2. 对于数组x，numpy定义了下面的操作：

   • numpy.any(x)：只要数组中有一个元素值为True（如果数值类型，则为非零），则结果就返回True；否则返回False
   • numpy.all(x)：只有数组中所有元素都为True（如果数值类型，则为非零），则结果才返回True；否则返回False

5. 位运算

1. numpy提供的位运算如下，这些位运算同时提供了函数形式（这些函数以bitwise_开头）以及表达式形式。其中输入数组必须是整数或者布尔类型（如果是浮点数则报错）：

   • 按位与：表达式形式y=x1&x2，使用ufunc函数的形式：numpy.bitwise_and(x1,x2[,out=y])
   • 按位或：表达式形式y=x1|x2，使用ufunc函数的形式：numpy.bitwise_or(x1,x2[,out=y])
   • 按位取反：表达式形式y=~x，使用ufunc函数的形式：numpy.bitwise_not(x[,out=y])
   • 按位异或：表达式形式y=x1^x2，使用ufunc函数的形式：numpy.bitwise_xor(x1,x2[,out=y])

   

2. 有几点注意：

   • 位运算符的优先级要比比较运算符高
   • 整数数组的位运算和C语言的位运算符相同，注意正负号

6. 自定义 ufunc 函数

1. 可以通过frompyfunc()将计算单个元素的函数转换成ufunc函数。调用格式为：my_ufunc=frompyfunc(func,nin,nout)。其中：

   • func：计算单个元素的函数
   • nin：func的输入参数的个数
   • nout：func返回值的个数

   调用时，使用my_ufunc(...)即可。

2. 也可以通过vectorize()函数来实现frompyfunc()的功能。其原型为： np.vectorize(func, otypes='', doc=None, excluded=None)。其中：

   • func：计算单个元素的函数
   • otypes：可以是一个表示结果数组元素类型的字符串，也可以是一个类型列表。如果使用类型列表，可以描述多个返回数组的元素类型
   • doc：函数的描述字符串。若未给定，则使用func.__doc__
   • excluded：指定func中哪些参数未被向量化。你可以指定一个字符串和整数的集合，其中字符串代表关键字参数，整数代表位置参数。

   

7. ufunc 对象的方法

1. ufunc函数对象本身还有一些方法。

   • 这些方法只对于两个输入、一个输出的ufunc函数函数有效。对于其他的ufunc函数对象调用这些方法时，会抛出ValueError异常。

2. ufunc.reduce方法：类似于Python的reduce函数，它沿着axis参数指定的轴，对数组进行操作。

   • 相当于将<op>运算符插入到沿着axis轴的所有元素之间：<op>.reduce(array,axis=0,dtype=None)
   • 经过一次reduce，结果数组的维度降低一维

   

3. ufunc.accumulate方法：它类似于reduce()的计算过程，但是它会保存所有的中间计算结果，从而使得返回数组的形状和输入数组的形状相同：

4. ufunc.outer方法：相当于将<op>运算符对输入数组A和输入数组B的每一对元素对(a,b)起作用：<op>.reduce(A,B)。结果数组维度为A.dim+B.dim。设A的shape=(4,5)，B的shape为(4,)，则结果数组的shape=(4,5,4)

   • 一维数组和一维数组的outer操作为二维数组
   • 多维数组的outer拆分成各自的一维操作

8. 数学函数

1. 下面是一元的数学函数：

   • abs/fabs：计算整数、浮点数或者复数的绝对值。对于非复数值，可以使用更快的fabs
   • sqrt ：计算平方根，相当于a**0.5
   • square：计算平方，相当于a**2
   • exp：计算指数 $e^{x}$
   • log/log10/log2/log1p：分别为 $\log_e(a),\log_{10}(a),\log_2(a),\log_e(1+x)$
   • sign：计算 $sign(a)$
   • ceil：计算各元素的ceiling值：大于等于该值的最小整数
   • floor：计算个元素的floor值：小于等于该值的最大整数
   • rint：将各元素四舍五入到最接近的整数，保留dtype
   • modf：将数组的小数和整数部分以两个独立数组的形式返回
   • isnan：返回一个布尔数组，该数组指示那些是NaN
   • isfinite/isinf：返回一个布尔数组，该数组指示哪些是有限的/无限数
   • cos/cosh/sin/sinh/tan/tanh：普通和双曲型三角函数
   • arccos/arcsosh/arcsin/arcsinh/arctan/arctanh:反三角函数

三、 函数库

1. 随机数库

1. numpy中的随机和分布函数模块有两种用法：函数式以及类式

1.1 函数式

1. 随机数

   • numpy.random.rand(d0, d1, ..., dn):指定形状(d0, d1, ..., dn)创建一个随机的ndarray。每个元素值来自于半闭半开区间[0,1)并且服从均匀分布。

     • 要求d0, d1, ..., dn为整数
     • 如果未提供参数，则返回一个随机的浮点数而不是ndarray，浮点数值来自于半闭半开区间[0,1)并且服从均匀分布。

   • numpy.random.randn(d0, d1, ..., dn)：指定形状(d0, d1, ..., dn)创建一个随机的ndarray。每个元素值服从正态分布，其中正态分布的期望为0，方差为1

     • 要求d0, d1, ..., dn为整数或者可以转换为整数
     • 如果di为浮点数，则截断成整数
     • 如果未提供参数，则返回一个随机的浮点数而不是ndarray，浮点数值服从正态分布，其中正态分布的期望为0，方差为1

   • numpy.random.randint(low[, high, size])：返回一个随机的整数ndarray或者一个随机的整数值。

     • 如果high为None，则表示整数值都取自[0,low)且服从discrete uniform分布
     • 如果high给出了值，则表示整数值都取自[low,high)且服从discrete uniform分布
     • size是一个整数的元组，指定了输出的ndarray的形状。如果为None则表示输出为单个整数值

   • numpy.random.random_integers(low[, high, size])：返回一个随机的整数ndarray或者一个随机的整数值。

     • 如果high为None，则表示整数值都取自[1,low]且服从discrete uniform分布
     • 如果high给出了值，则表示整数值都取自[low,high]且服从discrete uniform分布
     • size是一个整数的元组，指定了输出的ndarray的形状。如果为None则表示输出为单个整数值
       

     它与randint区别在于randint是半闭半开区间，而random_integers是全闭区间

   • numpy.random.random_sample([size])：返回一个随机的浮点ndarray或者一个随机的浮点值，浮点值是[0.0,1.0)之间均匀分布的随机数

     • size为整数元组或者整数，指定结果ndarray的形状。如果为None则只输出单个浮点数
     • 如果想生成[a,b)之间均匀分布的浮点数，那么你可以用(b-a)*random_sample()+a

     如果size有效，它的效果等于numpy.random.rand(*size)； 如果size无效，它的效果等于numpy.random.rand()

     

   • numpy.random.random([size])：等价于numpy.random.random_sample([size])

   • numpy.random.ranf([size])：等价于numpy.random.random_sample([size])

   • numpy.random.sample([size])：等价于numpy.random.random_sample([size])

     

   • numpy.random.choice(a[, size, replace, p]):从一维数组中采样产生一组随机数或者一个随机数

     • a为一位数组或者int，如果是int则采样数据由numpy.arange(n)提供，否则采用数据由a提供
       

     • size为整数元组或者整数，指定结果ndarray的形状。如果为None则只输单个值

     • replace：如果为True则可以重复采样（有放回的采样）；如果为False，则采用不放回的采样

     • p：为一维数组，用于指定采样数组中每个元素值的采样概率。如果为None则均匀采样。

     • 如果参数有问题则抛出异常：比如a为整数但是小于0，比如p不满足概率和为1，等等。。

       

   • numpy.random.bytes(length)：返回length长度的随机字节串。length指定字节长度。

     

2. 排列组合

   • numpy.random.shuffle(x):原地随机混洗x的内容，返回None。x为array-like对象，原地修改它

   • numpy.random.permutation(x)：随机重排x，返回重排后的ndarray。x为array-like对象，不会修改它

     • 如果x是个整数，则重排numpy.arange(x)

     • 如果x是个数组，则拷贝它然后对拷贝进行混洗

       • 如果x是个多维数则只是混洗它的第0维

     

3. 概率分布函数：下面是共同参数：size若非None，则它指定输出ndarray的形状。如果为None，则输出单个值。

   • numpy.random.beta(a, b[, size])：Beta分布。其中a,b都是Beta分布的参数，要求非负浮点数。

     • 贝塔分布为：

       $$f(x;\alpha,\beta)=\frac {1}{B(\alpha,\beta)} x^{\alpha-1}(1-x)^{\beta-1}$$

       其中：

       $$B(\alpha,\beta)=\int_0^{1} t^{\alpha-1}(1-t)^{\beta-1}\,dt$$

       ​

   • numpy.random.binomial(n, p[, size]):二项分布。其中n,p都是二项分布的参数，要求n为大于等于0的浮点数，如果它为浮点数则截断为整数；p为[0,1]之间的浮点数。

     • 二项分布为：

       $$P(N)=\binom{n}{N}p^{N}(1-p)^{n-N}$$

   • numpy.random.chisquare(df[, size]):卡方分布。其中df为整数，是卡方分布的自由度（若小于等于0则抛出异常）。

     • 卡方分布为：

       $$p(x)=\frac{(1/2)^{k/2}}{\Gamma(k/2)} x^{k/2-1}e^{-x/2}$$

       其中

       $$\Gamma(x)=\int^{\infty}_0 t^{x-1}e^{-t}\,dt$$

   • numpy.random.dirichlet(alpha[, size]):狄利克雷分布。其中alpha是个数组，为狄利克雷分布的参数。

   • numpy.random.exponential([scale, size]):指数分布。scale为浮点数，是参数 $\beta$

     • 指数分布的概率密度函数为:

       $$f(x;\frac {1}{\beta})=\frac{1}{\beta}\exp(-\frac{x}{\beta})$$

   • numpy.random.f(dfnum, dfden[, size]):F分布。dfnum为浮点数，应该大于0，是分子的自由度； dfden是浮点数，应该大于0，是分母的自由度。

   • numpy.random.gamma(shape[, scale, size]):伽玛分布。其中shape是个大于0的标量，表示分布的形状；scale是个大于0的标量，表示伽玛分布的scale（默认为1）。

     • 伽玛分布的概率密度函数为:

       $$p(x)=x^{k-1} \frac {e^{-x/\theta}}{\theta^{k}\Gamma(k)}$$

       ，其中k为形状， $\theta$ 为scale

   • numpy.random.geometric(p[, size]):几何分布。其中p是单次试验成功的概率。

     • 几何分布为：

       $$f(k)=(1-p)^{k-1}p$$

   • numpy.random.gumbel([loc, scale, size]):甘贝尔分布。其中loc为浮点数，是分布的location of mode，scale是浮点数，为scale。

     • 甘贝尔分布:

     • xxxxxxxxxx

        

       p(x)=\frac {e^{-(x-\mu)/\beta}}{\beta}  e^{-e-(x-\mu)/\beta}

       Preview OK

       $$p(x)=\frac {e^{-(x-\mu)/\beta}}{\beta} e^{-e-(x-\mu)/\beta}$$

       $$p(x)=\frac {e^{-(x-\mu)/\beta}}{\beta} e^{-e-(x-\mu)/\beta}$$

       ，其中 $\mu$ 为location of mode， $\beta$ 为scale

   • numpy.random.hypergeometric(ngood, nbad, nsample[, size]): 超几何分布。其中ngood为整数或者array_like，必须非负数，为好的选择；nbad为整数或者array_like，必须非负数，表示坏的选择。

     • 超级几何分布：

       $$P(x)= \frac {\binom{m}{n} \binom{N-m}{n-x}} {\binom{N}{n}}, 0 \le x \le m \ \text{and} \ n+m-N \le x \le n$$

       ，其中n=ngood，m=nbad，N为样本数量。P(x)为x成功的概率

   • numpy.random.laplace([loc, scale, size]):拉普拉斯分布。loc为浮点数，scale为浮点数

     • 拉普拉斯分布：

       $$f(x;\mu,\lambda)=\frac {1}{2\lambda} \exp(- \frac{\|x-\mu\|}{\lambda})$$

       ，其中 loc=$\mu$ ， scale=$\lambda$

   • numpy.random.logistic([loc, scale, size]):逻辑斯谛分布。其中loc为浮点数，scale为大于0的浮点数

     • 逻辑斯谛分布：

       $$P(x)= \frac {e^{-(x-\mu)/s}}{s(1+e^{-(x-\mu)/s})^{2}}$$

       ， 其中 loc=$\mu$, scale= $s$

   • numpy.random.lognormal([mean, sigma, size]):对数正态分布。其中mean为浮点数，sigma为大于0的浮点数。

     • 对数正态分布：

       $$p(x)=\frac {1}{\sigma x \sqrt{2\pi}} e^{-(\ln(x)-\mu)^{2}/(2\sigma^{2})}$$

       ，其中mean=$\mu$ ， sigma= $\sigma$

   • numpy.random.logseries(p[, size]):对数分布，其中p为[0.0--1.0]之间的浮点数。

     • 对数分布：

       $$P(k)=\frac {-p^{k}}{k\ln(1-p)}$$

   • numpy.random.multinomial(n, pvals[, size]):多项式分布。n为执行二项分布的试验次数，pvals为浮点序列，要求这些序列的和为1，其长度为n。

   • numpy.random.multivariate_normal(mean, cov[, size]):多元正态分布。mean为一维数组，长度为N；cov为二维数组，形状为(N,N)

   • numpy.random.negative_binomial(n, p[, size]):负二项分布。n为整数，大于0；p为[0.0--1.0]之间的浮点数。

     • 负二项分布：

       $$P(N;n,p)=\binom{N+n-1}{n-1}p^{n}(1-p)^{N}$$

   • numpy.random.noncentral_chisquare(df, nonc[, size]):非中心卡方分布。df为整数，必须大于0;noc为大于0的浮点数。

     • 非中心卡方分布：

       $$P(x;k,\lambda)= \sum_{i=0}^{\infty } f_Y(x) \frac {e^{-\lambda/2}(-\lambda/2)^{i}}{i!}$$

       其中 $Y=Y_{k+2i}$为卡方分布， df为k，nonc为 $\lambda$

   • numpy.random.noncentral_f(dfnum, dfden, nonc[, size]):非中心F分布。其中dfnum为大于1的整数，dfden为大于1的整数，nonc为大于等于0的浮点数。

   • numpy.random.normal([loc, scale, size]):正态分布。其中loc为浮点数，scale为浮点数。

     • 正态分布：

       $$p(x)=\frac {1}{\sqrt{2\pi\sigma^{2}}}e^{-(x-\mu)^{2}/(2\sigma^{2})}$$

       ，其中loc=$\mu$， scale=$\sigma$

   • numpy.random.pareto(a[, size]):帕累托分布。其中a为浮点数。

     • 帕累托分布：

       $$p(x)= \frac {\alpha m ^{\alpha}}{x^{\alpha+1}}$$

       ，其中a=$\alpha$, m为scale

   • numpy.random.poisson([lam, size]):泊松分布。其中lam为浮点数或者一个浮点序列（浮点数大于等于0）。

     • 泊松分布：

       $$f(k;\lambda)=\frac {\lambda^{k}e^{-\lambda}}{k!}$$

       ，其中lam=$\lambda$

   • numpy.random.power(a[, size]):幂级数分布。其中a为大于0的浮点数。

     • 幂级数分布：

       $$P(x;a)=ax^{a-1},0\le x \le 1,a \gt 0$$

   • numpy.random.rayleigh([scale, size]): 瑞利分布。其中scale为大于0的浮点数。

     • 瑞利分布：

       $$P(x;\sigma)=\frac{x}{\sigma^{2}}e^{-x^{2}/(2\sigma^{2})}$$

       ，其中scale=$\sigma$

   • numpy.random.standard_cauchy([size]):标准柯西分布。

     • 柯西分布：

       $$P(x;x_0,\gamma)=\frac{1}{\pi\gamma[1+((x-x_0)/\gamma)^{2}]}$$

       ，其中标准柯西分布中， $x_0=1,\gamma=1$

   • numpy.random.standard_exponential([size]):标准指数分布。其中scale等于1

   • numpy.random.standard_gamma(shape[, size]):标准伽玛分布，其中scale等于1

   • numpy.random.standard_normal([size]):标准正态分布，其中mean=0，stdev等于1

   • numpy.random.standard_t(df[, size]):学生分布。其中df是大于0的整数。

     • 学生分布:

       $$f(t;\nu)=\frac{\Gamma((\nu+1)/2)}{\sqrt{\nu\pi}\Gamma(\nu/2)}(1+t^{2}/\nu)^{-(\nu+1)/2}$$

       ， 其中 df= $\nu$

   • numpy.random.triangular(left, mode, right[, size]): 三角分布。其中left为标量，mode为标量，right为标量

     • 三角分布（其中left=l，mode=m，right=r）：
     $$P(x;l,m,r)= \left\{ \begin{matrix} \frac{2(x-l)}{(r-l)(m-l)}, & \text{for $l \le x \le m$} \\ \frac{2(r-x)}{(r-l)(r-m)}, & \text{for $m \le x \le r$} \\ 0, & \text{otherwise} \end{matrix} \right.$$

   • numpy.random.uniform([low, high, size]):均匀分布。其中low为浮点数；high为浮点数。

     • 均匀分布：

       $$p(x)=\frac {1}{b-a}$$

       ，其中low=a, high=b

   • numpy.random.vonmises(mu, kappa[, size]):Mises分布。其中mu为浮点数，kappa为大于等于0的浮点数。

     • Mises分布：

       $$p(x)= \frac{e^{\kappa \cos(x-\mu)}}{2\pi I_0(\kappa)}$$

       ，其中mu=$\mu$， kappa=$\kappa$， $I_0(\kappa)$是 modified Bessel function of order 0

   • numpy.random.wald(mean, scale[, size]):Wald分布。其中mean为大于0的标量，scale为大于等于0的标量

     • Wald分布：

       $$P(x;\mu,\lambda)=\sqrt{\frac {\lambda}{2\pi x^{3}}} \exp \{\frac{-\lambda(x-\mu)^{2}}{2\mu^{2}x}\}$$

       ，其中mean=$\mu$， scale=$\lambda$

   • numpy.random.weibull(a[, size])： Weibull分布。其中a是个浮点数。

     • Weibull分布:

       $$p(x)= \frac {a}{\lambda} (\frac {x}{\lambda})^{a-1} e^{-(x/\lambda)^{a}}$$

       ，其中a=$a$，$lambda$ 为scale

   • numpy.random.zipf(a[, size]):齐夫分布。其中a为大于1的浮点数。

     • 齐夫分布：

       $$p(x)=\frac {x^{-a}}{\zeta(a)}$$

       ，其中 a=$a$， $\zeta$ 为 Riemann Zeta函数。

4. numpy.random.seed(seed=None)：用于设置随机数生成器的种子。int是个整数或者数组，要求能转化成32位无符号整数。

1.2 RandomState类

1. 类式用法主要使用numpy.random.RandomState类，它是一个Mersenne Twister伪随机数生成器的容器。它提供了一些方法来生成各种各样概率分布的随机数。

   构造函数:RandomState(seed)。其中seed可以为None, int, array_like。这个seed是初始化伪随机数生成器。如果seed为None，则RandomState会尝试读取/dev/urandom或者Windows analogure来读取数据，或用者clock来做种子。

   Python的stdlib模块random也提供了一个Mersenne Twister伪随机数生成器。但是RandomState提供了更多的概率分布函数。

   RandomState保证了通过使用同一个seed以及同样参数的方法序列调用会产生同样的随机数序列（除了浮点数精度上的区别）。

   RandomState提供了一些方法来产生各种分布的随机数。这些方法都有一个共同的参数size。

   • 如果size为None，则只产生一个随机数
   • 如果size为一个整数，则产生一个一维的随机数数组。
   • 如果size为一个元组，则生成一个多维的随机数数组。其中数组的形状由元组指定。

2. 生成随机数的方法

   • .bytes(length)：等效于numpy.random.bytes(...)函数
   • .choice(a[, size, replace, p])：等效于numpy.random.choice(...)函数
   • .rand(d0, d1, ..., dn)：等效于numpy.random.rand(...)函数
   • .randint(low[, high, size])：等效于numpy.random.randint(...)函数
   • .randn(d0, d1, ..., dn) ：等效于numpy.random.randn(...)函数
   • .random_integers(low[, high, size])：等效于numpy.random_integers.bytes(...)函数
   • .random_sample([size])：等效于numpy.random.random_sample(...)函数
   • .tomaxint([size])：等效于numpy.random.tomaxint(...)函数

3. 排列组合的方法

   • .shuffle(x)：等效于numpy.random.shuffle(...)函数
   • .permutation(x) ：等效于numpy.random.permutation(...)函数

4. 指定概率分布函数的方法

   • .beta(a, b[, size])：等效于numpy.random.beta(...)函数
   • .binomial(n, p[, size])：等效于numpy.random.binomial(...)函数
   • .chisquare(df[, size])：等效于numpy.random.chisquare(...)函数
   • .dirichlet(alpha[, size])：等效于numpy.random.dirichlet(...)函数
   • .exponential([scale, size])：等效于numpy.random.exponential(...)函数
   • .f(dfnum, dfden[, size])：等效于numpy.random.f(...)函数
   • .gamma(shape[, scale, size])：等效于numpy.random.gamma(...)函数
   • .geometric(p[, size])：等效于numpy.random.geometric(...)函数
   • .gumbel([loc, scale, size])：等效于numpy.random.gumbel(...)函数
   • .hypergeometric(ngood, nbad, nsample[, size])：等效于numpy.random.hypergeometric(...)函数
   • .laplace([loc, scale, size])：等效于numpy.random.laplace(...)函数
   • .logistic([loc, scale, size])：等效于numpy.random.logistic(...)函数
   • .lognormal([mean, sigma, size])：等效于numpy.random.lognormal(...)函数
   • .logseries(p[, size])：等效于numpy.random.logseries(...)函数
   • .multinomial(n, pvals[, size])：等效于numpy.random.multinomial(...)函数
   • .multivariate_normal(mean, cov[, size])：等效于numpy.random.multivariate_normal(...)函数
   • .negative_binomial(n, p[, size])：等效于numpy.random.negative_binomial(...)函数
   • .noncentral_chisquare(df, nonc[, size])：等效于numpy.random.noncentral_chisquare(...)函数
   • .noncentral_f(dfnum, dfden, nonc[, size])：等效于numpy.random.noncentral_f(...)函数
   • .normal([loc, scale, size])：等效于numpy.random.normal(...)函数
   • .pareto(a[, size])：等效于numpy.random.pareto(...)函数 -. poisson([lam, size])：等效于numpy.random.poisson(...)函数
   • .power(a[, size])：等效于numpy.random.power(...)函数
   • .rayleigh([scale, size])：等效于numpy.random.rayleigh(...)函数
   • .standard_cauchy([size])：等效于numpy.random.standard_cauchy(...)函数
   • .standard_exponential([size])：等效于numpy.random.standard_exponential(...)函数
   • .standard_gamma(shape[, size])：等效于numpy.random.standard_gamma(...)函数
   • .standard_normal([size])：等效于numpy.random.standard_normal(...)函数
   • .standard_t(df[, size])：等效于numpy.random.standard_t(...)函数
   • .triangular(left, mode, right[, size])：等效于numpy.random.triangular(...)函数
   • .uniform([low, high, size])：等效于numpy.random.uniform(...)函数
   • .vonmises(mu, kappa[, size])：等效于numpy.random.vonmises(...)函数
   • .wald(mean, scale[, size])：等效于numpy.random.wald(...)函数
   • .weibull(a[, size])：等效于numpy.random.weibull(...)函数
   • .zipf(a[, size])：等效于numpy.random.zipf(...)函数

5. 类式的其他函数

   • seed(seed=None)：该方法在RandomState被初始化时自动调用，你也可以反复调用它从而重新设置伪随机数生成器的种子。

   • get_state()：该方法返回伪随机数生成器的内部状态。其结果是一个元组(str, ndarray of 624 uints, int, int, float)，依次为：

     • 字符串'MT19937'
     • 一维数组，其中是624个无符号整数key
     • 一个整数pos
     • 一个整数has_gauss
     • 一个浮点数cached_gaussian

   • set_state(state)：该方法设置伪随机数生成器的内部状态,如果执行成功则返回None。参数是个元组(str, ndarray of 624 uints, int, int, float)，依次为：

     • 字符串'MT19937'
     • 一维数组，其中是624个无符号整数key
     • 一个整数pos
     • 一个整数has_gauss
     • 一个浮点数cached_gaussian

2. 统计量

1. 这里是共同的参数：

   • a：一个array_like对象

   • axis：可以为为int或者tuple或者None：

     • None：将a展平，在整个数组上操作
     • int：在a的指定轴线上操作。如果为-1，表示沿着最后一个轴（0轴为第一个轴）。
     • tuple of ints：在a的一组指定轴线上操作

   • out：可选的输出位置。必须与期望的结果形状相同

   • keepdims：如果为True，则结果数组的维度与原数组相同，从而可以与原数组进行广播运算。

2. 顺序统计：

   • numpy.minimum(x1, x2[, out])：返回两个数组x1和x2对应位置的最小值。要求x1和x2形状相同或者广播之后形状相同。
   • numpy.maximum(x1, x2[, out])：返回两个数组x1和x2对应位置的最大值。要求x1和x2形状相同或者广播之后形状相同。
   • numpy.amin(a[, axis, out, keepdims]) ：返回a中指定轴线上的最小值（数组）、或者返回a上的最小值（标量）。
   • numpy.amax(a[, axis, out, keepdims]) ：返回a中指定轴线上的最大值（数组）、或者返回a上的最小值（标量）。
   • numpy.nanmin(a[, axis, out, keepdims]): 返回a中指定轴线上的最小值（数组）、或者返回a上的最小值（标量），忽略NaN。
   • numpy.nanmax(a[, axis, out, keepdims]) :返回a中指定轴线上的最大值（数组）、或者返回a上的最小值（标量）忽略NaN。
   • numpy.ptp(a[, axis, out]) ：返回a中指定轴线上的最大值减去最小值（数组），即peak to peak
   • numpy.argmin(a, axis=None, out=None)：返回a中指定轴线上最小值的下标
   • numpy.argmax(a, axis=None, out=None)：返回a中指定轴线上最大值的下标
   • numpy.percentile(a, q[, axis, out, ...]) ：返回a中指定轴线上qth 百分比数据。q=50表示 50% 分位。你可以用列表或者数组的形式一次指定多个 q。
   • numpy.nanpercentile(a, q[, axis, out, ...])：返回a中指定轴线上qth 百分比数据。q=50表示 50% 分位。
   • numpy.partition(a, kth, axis=-1, kind='introselect', order=None)：它将数组执行划分操作：第 $k$ 位左侧的数都小于第 $k$；第 $k$位右侧的数都大于等于第 $k$。它返回划分之后的数组
   • numpy.argpartition(a, kth, axis=-1, kind='introselect', order=None)：返回执行划分之后的下标（对应于数组划分之前的位置）。

3. 排序：

   • numpy.sort(a, axis=-1, kind='quicksort', order=None)：返回a在指定轴上排序后的结果（并不修改原数组）。

     • kind：字符串指定排序算法。可以为'quicksort'(快速排序)，'mergesort'(归并排序)，'heapsort'(堆排序)
     • order：在结构化数组中排序中，用于设置排序的字段（一个字符串）

   • numpy.argsort(a, axis=-1, kind='quicksort', order=None)：返回a在指定轴上排序之后的下标（对应于数组划分之前的位置）。

   • numpy.lexsort(keys, axis=-1)：

     • 如果keys为数组，则根据数组的最后一个轴的最后一排数值排列，并返回这些轴的排列顺序。如数组a的shape=(4,5)，则根据a最后一行（对应于最后一个轴的最后一排）的5列元素排列。这里axis指定排序的轴 。对于argsort，会在最后一个轴的每一排进行排列并返回一个与a形状相同的数组。
     • 如果keys为一维数组的元组，则将这些一维数组当作行向量拼接成二维数组并按照数组来操作。

   • numpy.searchsorted(a, v, side='left', sorter=None)：要求a是个已排序好的一维数组。本函数将v插入到 a中，从而使得数组a维持一个排序好的数组。函数返回的是v应该插入的位置。side指定若发现数值相等时，插入左侧left还是右侧right

     • 如果你想一次插入多个数值，可以将v设置为列表或者数组。
     • 如果sorter=None，则要求a已排序好。如果a未排序，则要求传入一个一维数组或者列表。这个一维数组或者列表给出了 a的升序排列的下标。（通常他就是argsort的结果）
     • 它并不执行插入操作，只是返回待插入的位置

   

4. 均值和方差：

   • numpy.sum(a, axis=None, dtype=None, out=None, keepdims=False)：计算a在指定轴上的和

   • numpy.prod(a, axis=None, dtype=None, out=None, keepdims=False)：计算a在指定轴上的乘积

   • numpy.median(a[, axis, out, overwrite_input, keepdims]):计算a在指定轴上的中位数（如果有两个，则取这两个的平均值）

   • numpy.average(a[, axis, weights, returned]):计算a在指定轴上的加权平均数

   • numpy.mean(a[, axis, dtype, out, keepdims]) :计算a在指定轴上的算术均值

   • numpy.std(a[, axis, dtype, out, ddof, keepdims]):计算a在指定轴上的标准差

   • numpy.var(a[, axis, dtype, out, ddof, keepdims]) :计算a在指定轴上的方差。方差有两种定义：

     • 偏样本方差biased sample variance。计算公式为 （$\bar x$ 为均值）：

       $$var=\frac 1N\sum_{i=1}^{N}(x_i-\bar x)^{2}$$

     • 无偏样本方差unbiased sample variance。计算公式为 （$\bar x$ 为均值）：

       $$var=\frac 1{N-1}\sum_{i=1}^{N}(x_i-\bar x)^{2}$$

       当ddof=0时，计算偏样本方差；当ddof=1时，计算无偏样本方差。默认值为 0。当ddof为其他整数时，分母就是N-ddof。

   • numpy.nanmedian(a[, axis, out, overwrite_input, ...]) :计算a在指定轴上的中位数，忽略NaN

   • numpy.nanmean(a[, axis, dtype, out, keepdims]) :计算a在指定轴上的算术均值，忽略NaN

   • numpy.nanstd(a[, axis, dtype, out, ddof, keepdims]):计算a在指定轴上的标准差，忽略NaN

   • numpy.nanvar(a[, axis, dtype, out, ddof, keepdims]) :计算a在指定轴上的方差，忽略NaN

   

5. 相关系数：

   • numpy.corrcoef(x[, y, rowvar, bias, ddof]) : 返回皮尔逊积差相关
   • numpy.correlate(a, v[, mode]) ：返回两个一维数组的互相关系数
   • numpy.cov(m[, y, rowvar, bias, ddof, fweights, ...])：返回协方差矩阵

6. 直方图：

   • numpy.unique(ar, return_index=False, return_inverse=False, return_counts=False)：返回ar中所有不同的值组成的一维数组。如果ar不是一维的，则展平为一维。

     • return_index：如果为True，则同时返回这些独一无二的数值在原始数组中的下标
     • return_inverse：如果为True，则返回元素数组的值在新返回数组中的下标（从而可以重建元素数组）
     • return_counts：如果为True，则返回每个独一无二的值在原始数组中出现的次数

   • numpy.histogram(a, bins=10, range=None, normed=False, weights=None, density=None):计算一组数据的直方图。如果a不是一维的，则展平为一维。bins指定了统计的区间个数（即统计范围的等分数）。range是个长度为2的元组，表示统计范围的最小值和最大值（默认时，表示范围为数据的最小值和最大值）。当density为False时，返回a中数据在每个区间的个数；否则返回a中数据在每个区间的频率。weights设置了a中每个元素的权重，如果设置了该参数，则计数时考虑权重。它返回的是一个元组，第一个元素给出了每个直方图的计数值，第二个元素给出了直方图的统计区间的从左到右的各个闭合点 （比计数值的数量多一个）。

     • normed：作用与density相同。该参数将被废弃
     • bins也可以为下列字符串，此时统计区间的个数将通过计算自动得出。可选的字符串有：'auto'、'fd'、'doane'、'scott'、'rice'、'sturges'、'sqrt'

   • numpy.histogram2d(x, y, bins=10, range=None, normed=False, weights=None) ：计算两组数据的二维直方图

   • numpy.histogramdd(sample, bins=10, range=None, normed=False, weights=None) ：计算多维数据的直方图

   • numpy.bincount(x[, weights, minlength])：计算每个数出现的次数。它要求数组中所有元素都是非负的。其返回数组中第i个元素表示：整数i在x中出现的次数。要求x必须一维数组，否则报错。weights设置了x中每个元素的权重，如果设置了该参数，则计数时考虑权重。minlength指定结果的一维数组最少多长（如果未指定，则由x中最大的数决定）。

   • numpy.digitize(x, bins, right=False) ：离散化。如果x不是一维的，则展平为一维。它返回一个数组，该数组中元素值给出了x中的每个元素将对应于统计区间的哪个区间。区间由bins这个一维数组指定，它依次给出了统计区间的从左到右的各个闭合点。right为True，则表示统计区间为左开右闭合(]；为False，则表示统计区间为左闭合右开[)

   注意：matplotlib.pyplot也有一个建立直方图的函数（hist(...)），区别在于matplotlib.pyplot.hist(...)函数会自动绘直方图，而numpy.histogram仅仅产生数据

   

   

3. 分段函数

1. numpy.where(condition[, x, y])：它类似于python的 x if condition else y。condition/x/y都是数组，要求形状相同或者通过广播之后形状相同。产生结果的方式为： 如果condition某个元素为True或者非零，则对应的结果元素从x中获取；否则对应的结果元素从y中获取

2. 如果分段数量增加，则需要嵌套多层的where()。此时可以使用select()：numpy.select(condlist, choicelist, default=0)。

   • 其中condlist为长度为 N的列表，列表元素为数组，给出了条件数组

   • choicelist为长度为N的列表，列表元素为数组，给出了结果被选中的候选值。

   • 所有数组的长度都形状相同，如果形状不同，则执行广播。结果数组的形状为广播之后的形状。

   • 结果筛选规则如下：

     • 从condlist左到右扫描，若发现第 i 个元素（是个数组）对应位置为True或者非零，则输出元素来自choicelist 的第 i 个元素（是个数组）。因此若有多个condlist的元素满足，则只会使用第一个遇到的。
     • 如果扫描结果是都不满足，则使用default

3. 采用where/select时，所有的参数需要在调用它们之前完成。在计算时还会产生许多保存中间结果的数组。因此如果输入数组很大，则将会发生大量内存分配和释放。 为此numpy提供了piecewise函数： numpy.piecewise(x, condlist, funclist, *args, **kw)。
   

   • x：为分段函数的自变量取值数组

   • condlist：为一个列表，列表元素为布尔数组，数组形状和x相同。

   • funclist：为一个列表，列表元素为函数对象。其长度与condlist相同或者比它长1。

     • 当condlist[i]对应位置为 True时，则该位置处的输出值由 funclist[i]来计算。如果funclist长度比condlist长1，则当所有的condlist都是False时，则使用 funclist[len(condlist)]来计算。如果有多个符合条件，则使用最后一个遇到的（而不是第一个遇到的）
     • 列表元素可以为数值，表示一个返回为常数值（就是该数值）的函数。

   • args/kw：用于传递给函数对象funclist[i]的额外参数。

4. 多项式

1. 一元多项式类的构造：（注意系数按照次数从高次到低次排列）

   xxxxxxxxxx
   class numpy.poly1d(c_or_r, r=0, variable=None)
   

   • c_or_r：一个数组或者序列。其意义取决于r
   • r：布尔值。如果为True，则c_or_r指定的是多项式的根；如果为False，则c_or_r指定的是多项式的系数
   • variable：一个字符串，指定了打印多项式时，用什么字符代表自变量。默认为x

   多项式的属性有：

   • .coeffs属性：多项式的系数
   • .order属性：多项式最高次的次数
   • .variable属性：自变量的代表字符

   多项式的方法有：

   • .deriv(m=1)方法：计算多项式的微分。可以通过参数m指定微分次数
   • .integ(m=1,k=0)方法：计算多项式的积分。可以通过参数m指定积分次数和k积分常量

   

2. 操作一元多项式类的函数：

   • 多项式对象可以像函数一样，返回多项式的值
   • 多项式对象进行加减乘除，相当于对应的多项式进行计算。也可以使用对应的numpy.polyadd/polysub/polymul/polydiv/函数。
   • numpy.polyder/numpy.polyint：进行微分/积分操作
   • numpy.roots函数：求多项式的根（也可以通过p.r方法）

   

3. 使用np.polyfit(x, y, deg, rcond=None, full=False, w=None, cov=False)函数可以对一组数据使用多项式函数进行拟合（最小均方误差）。其参数为：

   • x：数据点的x坐标序列
   • y：数据点的y坐标序列。如果某个x坐标由两个点，你可以传入一个二维数组。
   • deg：拟合多项式的次数
   • rcond：指定了求解过程中的条件：当某个特征值/最大特征值<rcond时，该特征值被抛弃
   • full：如果为False，则仅仅返回拟合多项式的系数；如果为True，则更多的结果被返回
   • w：权重序列。它对y序列的每个位置赋予一个权重
   • cov：如果为True，则返回相关矩阵。如果full为True，则不返回。

   默认情况下，返回两个数组：一个是拟合多项式的系数；另一个是数据的相关矩阵

   

4. numpy提供了更丰富的多项式函数类。注意其中的多项式的系数按照次数从小到大排列。

   • numpy.polynomial.Polynomial：一元多次多项式
   • numpy.polynomial.Chebyshev：切比雪夫多项式
   • numpy.polynomial.Laguerre：拉盖尔多项式
   • numpy.polynomial.Legendre：勒让德多项式
   • numpy.polynomial.Hermite：哈米特多项式
   • numpy.polynomial.HermiteE：HermiteE多项式

   所有的这些多项式的构造函数为： XXX(coef, domain=None, window=None)。其中XXX为多项式类名。domain为自变量取值范围，默认为[-1,1]。window指定了将domain映射到的范围，默认为[-1,1]。

   如切比雪夫多项式在[-1,1]上为正交多项式。因此只有在该区间上才能正确插值拟合多项式。为了使得对任何区域的目标函数进行插值拟合，所以在domain指定拟合的目标区间。

   所有的这些多项式可以使用的方法为：

   • 四则运行
   • .basis(deg[, domain, window])：获取转换后的一元多项式
   • .convert(domain=None, kind=None, window=None)：转换为另一个格式的多项式。kind为目标格式的多项式的类
   • .degree()：返回次数
   • .fit(x, y, deg[, domain, rcond, full, w, window])：拟合数据，返回拟合后的多项式
   • .fromroots(roots[, domain, window])：从根创建多项式
   • .has_samecoef(other)、.has_samedomain(other)、.has_sametype(other) 、.has_samewindow(other)：判断是否有相同的系数/domain/类型/window
   • .roots()：返回多项式的根
   • .trim([tol])：将系数小于 tol的项截掉
   • 函数调用的方式

   

5. 切比雪夫多项式可以降低龙格现象。所谓龙格现象：等距离差值多项式在两个端点处有非常大的震荡，n越大，震荡越大。
   

5. 内积、外积、张量积

1. • numpy.dot(a, b, out=None)：计算矩阵的乘积。对于一维数组，他计算的是内积；对于二维数组，他计算的是线性代数中的矩阵乘法。

   • numpy.vdot(a, b)：返回一维向量之间的点积。如果a和b是多维数组，则展平成一维再点积。

     

   • numpy.inner(a, b)：计算矩阵的内积。对于一维数组，它计算的是向量点积；对于多维数组，则它计算的是：每个数组最后轴作为向量，由此产生的内积。

   • numpy.outer(a, b, out=None)：计算矩阵的外积。它始终接收一维数组。如果是多维数组，则展平成一维数组。

   

2. numpy.tensordot(a, b, axes=2)：计算张量乘积。

   • axes如果是个二元序列，则第一个元素表示a中的轴；第二个元素表示b中的轴。将这两个轴上元素相乘之后求和。其他轴不变
   • axes如果是个整数，则表示把a中的后axes个轴和b中的前axes个轴进行乘积之后求和。其他轴不变

3. 叉乘：numpy.cross(a, b, axisa=-1, axisb=-1, axisc=-1, axis=None):计算两个向量之间的叉乘。叉积用于判断两个三维空间的向量是否垂直。要求a和b都是二维向量或者三维向量，否则抛出异常。（当然他们也可以是二维向量的数组，或者三维向量的数组，此时一一叉乘）

   

6. 线性代数

1. 逆矩阵：numpy.linalg.inv(a)：获取a的逆矩阵（一个array-like对象）。

   • 如果传入的是多个矩阵，则依次计算这些矩阵的逆矩阵。

   • 如果a不是方阵，或者a不可逆则抛出异常

     

2. 单位矩阵:numpy.eye(N[, M, k, dtype])：返回一个二维单位矩阵行为N，列为M，对角线元素为1，其余元素为0。M默认等于N。k默认为0表示对角线元素为1（单位矩阵），如为正数则表示对角线上方一格的元素为1（上单位矩阵），如为负数表示对角线下方一格的元素为1（下单位矩阵）

3. 对角线和：numpy.trace(a, offset=0, axis1=0, axis2=1, dtype=None, out=None)：返回对角线的和。

   • 如果a是二维的，则直接选取对角线的元素之和（offsert=0），或者对角线右侧偏移offset的元素之和（即选取a[i,i+offset]之和）

• 如果a不止二维，则由axis1和axis2指定的轴选取了取对角线的矩阵。

• 如果a少于二维，则抛出异常

  

4. 计算线性方程的解 $Ax=b$ ：numpy.linalg.solve(a,b)：计算线性方程的解ax=b，其中a为矩阵，要求为秩不为0的方阵，b为列向量（长度等于方阵大小）；或者a为标量，b也为标量。

   • 如果a不是方阵或者a是方阵但是行列式为0，则抛出异常

   

5. 特征值：numpy.linalg.eig(a)：计算矩阵的特征值和右特征向量。如果不是方阵则抛出异常，如果行列式为0则抛出异常。

   

6. 奇异值分解：numpy.linalg.svd(a, full_matrices=1, compute_uv=1)：对矩阵a进行奇异值分解，将它分解成u*np.diag(s)*v的形式，其中u和v是酉矩阵，s是a的奇异值组成的一维数组。 其中：

   • full_matrics:如果为True，则u形状为(M,M)，v形状为(N,N)；否则u形状为(M,K)，v形状为(K,N)，K=min(M,N)
   • compute_uv：如果为True则表示要计算u和v。默认为True。
   • 返回u、s、v的元组
   • 如果不可分解则抛出异常

   

四、数组的存储和加载

1. 二进制

1. numpy.save(file, arr, allow_pickle=True, fix_imports=True)：将数组以二进制的形式存储到文件中。

   • file：文件名或者文件对象。如果是个文件名，则会自动添加后缀.npy如果没有该后缀的话
   • arr：被存储的数组
   • allow_pickle：一个布尔值，如果为True，则使用Python pickle。有时候为了安全性和可移植性而不使用pickle
   • fix_imports：用于python3的数组import到python2的情形

2. numpy.savez(file, *args, **kwds)：将多个数组以二进制的形式存储到文件中。

   • file：文件名或者文件对象。如果是个文件名，则会自动添加后缀.npz如果没有该后缀的话

   • args：被存储的数组。这些数组的名字将被自动命名为arr_0/arr_1/...

     如果没有名字，则完全无法知晓这些数组的区别

   • kwds：将被存储的数组，这些关键字参数就是键的名字

3. numpy.load(file, mmap_mode=None, allow_pickle=True, fix_imports=True, encoding='ASCII')：将二进制文件中读取数组。

   • file：一个文件名或者文件对象。它存放着数组
   • mmap_mode：如果不是None，则memory-map该文件。此时对数组的修改会同步到文件上。当读取大文件的一小部分时很有用，因为它不必一次读取整个文件。可选值为None/'r+'/'r'/'w+'/'c'
   • allow_pickle：一个布尔值，如果为True，则使用Python pickle。有时候为了安全性和可移植性而不使用pickle
   • fix_imports：用于python3的数组import到python2的情形
   • encoding：只用于python2，读取python2字符串。

   该函数返回一个数组，元组，或者字典（当二进制文件时savez生成时）

2. 文本文件

1. numpy.genfromtxt(fname, dtype=<type 'float'>, comments='#', delimiter=None, skip_header=0, skip_footer=0, converters=None, missing_values=None, filling_values=None, usecols=None, names=None, excludelist=None, deletechars=None, replace_space='_', autostrip=False, case_sensitive=True, defaultfmt='f%i', unpack=None, usemask=False, loose=True, invalid_raise=True, max_rows=None) ：从文本文件中加载数组，通用性很强，可以处理缺失数据的情况。

   loadtxt()函数只能处理数据无缺失的情况。

   • fname：指定的数据源。可以为：

     • 文件名字符串。如果后缀为gz或者bz2，则首先自动解压缩
     • 文件对象/字符串列表/其他可迭代对象：这些可迭代对象必须返回字符串（该字符串被视为一行）

   • dtype：数组的元素类型，可以提供一个序列，指定每列的数据类型

   • comments：一个字符串，其中每个字符都指定了注释行的第一个字符。注释行整体被放弃

   • delimiter：指定了分隔符。可以为：

     • 字符串：指定分隔符。默认情况下，所有连续的空白符被认为是分隔符
     • 一个整数：指定了每个字段的宽度
     • 一个整数序列：依次给出了各个字段的宽度

   • skiprows：被废弃，推荐使用skip_header

   • skip_header：一个整数，指定跳过文件头部多少行

   • skip_footer：一个整数，指定跳过文件尾部多少行

   • converters：用于列数据的格式转换。你可以指定一个字典，字典的键就是列号：

     xxxxxxxxxx
     converters={0: lambda s: float(s or 0),
     1: lambda s: int(s or 199),...
     }
     

   • missing：被废弃，推荐使用missing_values

   • missing_values:指定缺失数据。你可以自定一个字典，字典的键就是缺失位置的字符串，值就是缺失值。比如你可以指定NNNN为缺失数据，此时遇到NNNN时，numpy解析为np.nan

   • filling_values：指定缺失值的填充值。即解析到np.nan时，用什么值代替它

   • usecols：一个序列，指定了要读取那些列（列从0 计数）

   • names：

     • 如果为True，则在skip_header行之后第一行被视作标题行，将从该行读取每个字段的name。
     • 如果为序列或者一个以冒号分隔的字符串，则使用它作为各个字段的name
     • 如果为None,则每个dtype字段的名字被使用

   • excludelist：一个序列，给出了需要排除的字段的name。

   • deletechars：A string combining invalid characters that must be deleted from the names

   • defaultfmt：A format used to define default field names, such as “f%i” or “f_%02i”.

   • autostrip：一个布尔值。如果为True，则自动移除数据中的空白符

   • replace_space：一个字符。如果变量名中有空白符，如user name，则使用该字符来替代空白符。默认为_，即变量名转换为user_name

   • case_sensitive：一个布尔值或者字符串。如果为True，则字段名是大小写敏感的。如果为False或者'upper'，则字段名转换为大写字符。如果为'lower'则转换为小写字符。

   • unpack:If True, the returned array is transposed

   • usemask:If True, return a masked array

   • loose:If True, do not raise errors for invalid values

   • invalid_raise:If True, an exception is raised if an inconsistency is detected in the number of columns. If False, a warning is emitted and the offending lines are skipped

   • max_rows:一个整数，指定读取的最大行数。

2. numpy.loadtxt(fname, dtype=<type 'float'>, comments='#', delimiter=None, converters=None, skiprows=0, usecols=None, unpack=False, ndmin=0)：它作用与genfromtxt相同，但是它只能用于规则比较简单的文件，并且它的解析速度更快。

   • ndim：一个整数。指定结果数组必须拥有不少于ndim维度。
   • 其他参数参考genfromtxt

3. numpy.fromstring(string, dtype=float, count=-1, sep='')：从raw binary或者字符串中创建一维数组。

   • string：一个字符串，给出数据源
   • dtype：指定数据类型
   • count：一个整数。从数据源（一个字符串）中读取指定数量的数值类型的数值。如果为负数，则为数据长度加上这个负值
   • sep：如果未提供或者为空字符串，则string被认为是二进制数据。如果提供了一个非空字符串，则给出了分隔符。

4. numpy.savetxt(fname, X, fmt='%.18e', delimiter=' ', newline='\n', header='', footer='', comments='# ')：存储到文本文件

   • fname：给出了文件名或者file对象。如果为.gz后缀，则自动压缩

   • X：被存储的数组

   • fmt：一个字符串或者一个字符串序列，指定存储格式。一个字符串可以指定所有的格式化方式；一个字符串序列可以对每列指定一个格式化方式。如果是虚数，你可以通过%.4e%+.4j的方式指定实部和虚部。

   • delimiter：一个字符串，用于分隔符，分隔每个列

   • newline：一个字符串，指定换行符

   • header：一个字符串。它会写到文件的首行

   • footer：一个字符串。它会写到文件的末尾

   • comments：一个字符串。它会写到文件的中间，并且用注释符作为行首，如#

     ​

   注：fmt分隔字符串的格式为%[flag]width[.precision]specifier。其中：

   • flags：可以为'-'（左对齐）、'+'（右对齐）、'0'（左侧填充0）

   • width：最小的位宽。

   • precision：

     • 对于specifier=d/i/o/x，指定最少的数字个数
     • 对于specifier=e/E/f，指定小数点后多少位
     • 对于specifier=g/G，指定最大的significant digits
     • 对于specifier=s，指定最大的字符数量

   • specifier：指定格式化类型。c（字符）、d/i（带符号整数）、e/E（科学计数法）、f（浮点数）、g/G（使用shorter e/E/f）、o（带符号八进制）、s（字符串）、u（无符号整数）、x/X（无符号十六进制）

5. ndarray.tofile(fid, sep="", format="%s")：保存到文件中。

   • fid：一个file对象或者文件名
   • sep：一个字符串，指定分隔符。如果为空或者空字符串，则按照二进制的方式写入，等价于file.write(a.tobytes())
   • format：一个字符串，指定了数值的格式化方式