线性代数
一、基本知识
本书中所有的向量都是列向量的形式:
本书中所有的矩阵 都表示为:
简写为: 或者 。
矩阵的
F范数:设矩阵 ,则其F范数为: 。它是向量的 范数的推广。
矩阵的迹:设矩阵 ,则的迹为: 。
迹的性质有:
- 的
F范数等于 的迹的平方根: 。 - 的迹等于 的迹: 。
- 交换律:假设 ,则有: 。
- 结合律: 。
- 的
二、向量操作
一组向量 是线性相关的:指存在一组不全为零的实数 ,使得: 。
一组向量 是线性无关的,当且仅当 时,才有: 。
一个向量空间所包含的最大线性无关向量的数目,称作该向量空间的维数。
三维向量的点积: 。
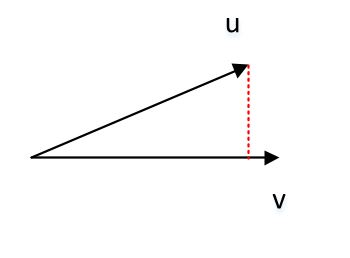
三维向量的叉积:
其中 分别为 轴的单位向量。
- 和 的叉积垂直于 构成的平面,其方向符合右手规则。
- 叉积的模等于 构成的平行四边形的面积
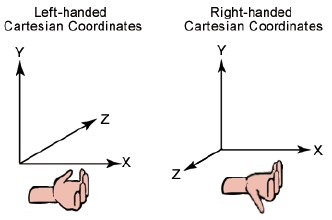
三维向量的混合积:
其物理意义为:以 为三个棱边所围成的平行六面体的体积。 当 构成右手系时,该平行六面体的体积为正号。
两个向量的并矢:给定两个向量 ,则向量的并矢记作:
也记作 或者 。
三、矩阵运算
给定两个矩阵 ,定义:
阿达马积
Hadamard product(又称作逐元素积):克罗内积
Kronnecker product:
设 为 阶向量, 为 阶方阵,则有:
如果 是一元函数,则:
其逐元向量函数为: 。
其逐矩阵函数为:
其逐元导数分别为:
各种类型的偏导数:
标量对标量的偏导数: 。
标量对向量( 维向量)的偏导数 : 。
标量对矩阵( 阶矩阵)的偏导数:
向量( 维向量)对标量的偏导数: 。
向量( 维向量)对向量 ( 维向量) 的偏导数(雅可比矩阵,行优先)
如果为列优先,则为上面矩阵的转置。
矩阵( 阶矩阵)对标量的偏导数
对于矩阵的迹,有下列偏导数成立:
假设 是关于 的矩阵值函数(),且 是关于 的实值函数(),则下面链式法则成立:
四、特殊函数
- 这里给出机器学习中用到的一些特殊函数。
4.1 sigmoid 函数
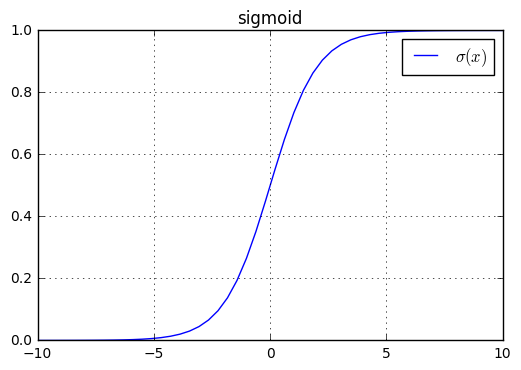
sigmoid函数:- 该函数可以用于生成二项分布的 参数。
- 当 很大或者很小时,该函数处于饱和状态。此时函数的曲线非常平坦,并且自变量的一个较大的变化只能带来函数值的一个微小的变化,即:导数很小。
4.2 softplus 函数
softplus函数: 。- 该函数可以生成正态分布的 参数。
- 它之所以称作
softplus,因为它是下面函数的一个光滑逼近: 。
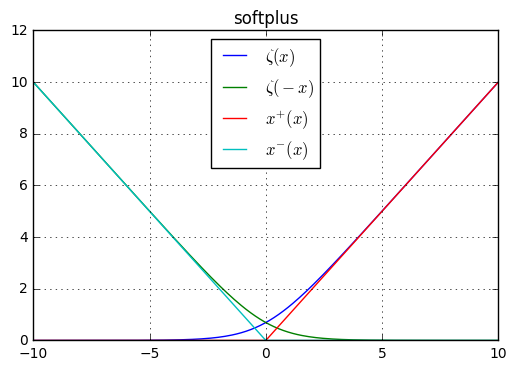
如果定义两个函数:
则它们分布获取了 的正部分和负部分。
根据定义有: 。而 逼近的是 , 逼近的是 ,于是有:
sigmoid和softplus函数的性质:其中 为反函数。
也称作
logit函数。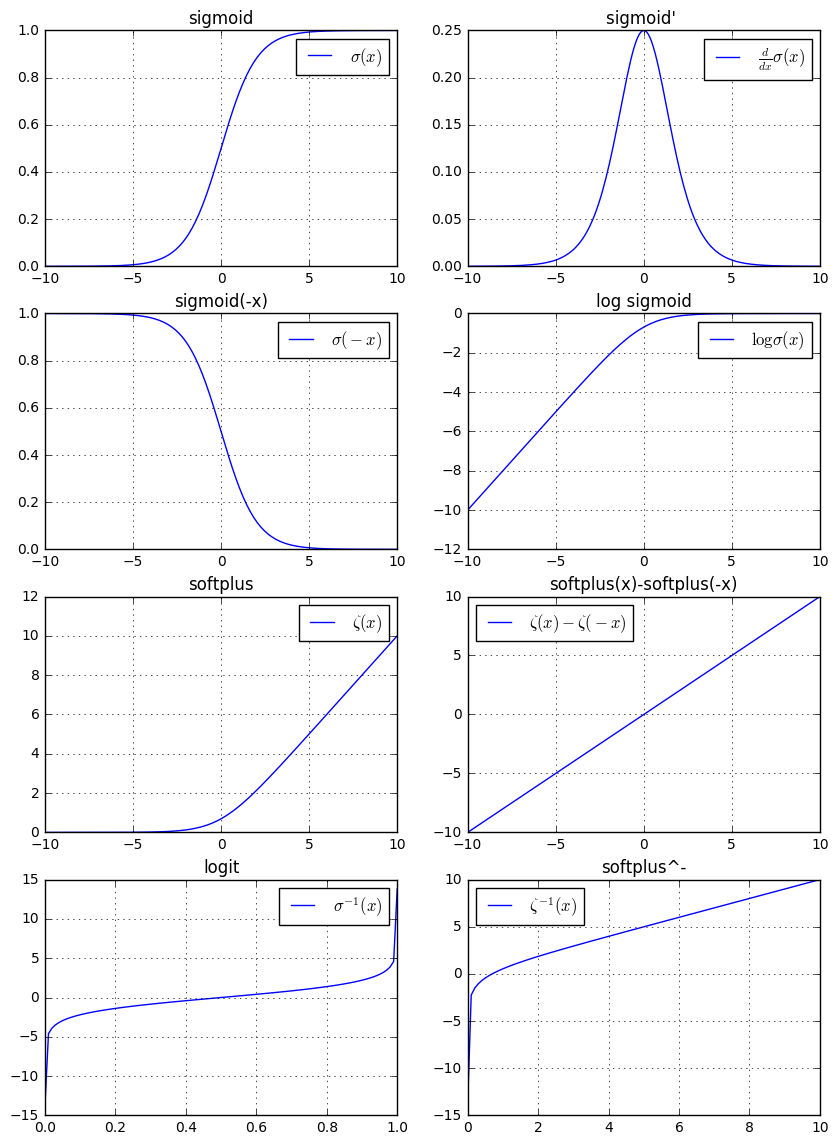
4.3 伽马函数
伽马函数定义为:
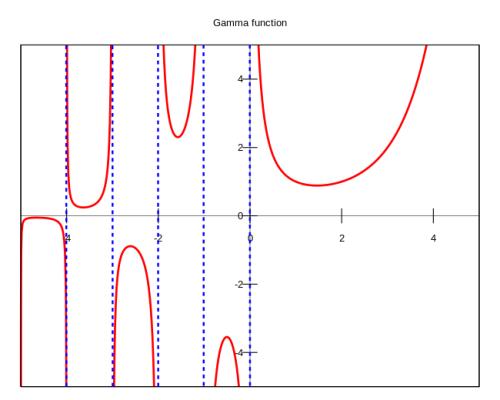
性质为:
对于正整数 有: 。
,因此伽马函数是阶乘在实数域上的扩展。
与贝塔函数的关系:
对于 有:
则可以推导出重要公式: 。
对于 ,伽马函数是严格凹函数。
当 足够大时,可以用
Stirling公式来计算Gamma函数值: 。
4.4 贝塔函数
对于任意实数 ,定义贝塔函数:
其它形式的定义:
性质:
连续性:贝塔函数在定义域 内连续。
对称性: 。
递个公式:
当 较大时,有近似公式:
与伽马函数关系:
对于任意正实数 ,有:
。