Graph Embedding 综述
一、A Comprehensive Survey of Graph Embedding[2017]
图自然存在于现实世界的各种场景中,例如社交媒体网络中的社交图/扩散图、研究领域的引文图、电商领域的用户兴趣图、知识图等。有效的图分析可以使很多应用受益,如节点分类、节点聚类、节点检索/推荐、链接预测等。尽管图分析
graph analytics是实用的和必要的,但大多数现有的图分析方法都存在昂贵的计算成本和空间成本的问题。然而,图嵌入graph embedding提供了一种有效而高效的方法来解决图分析问题。具体来说,graph embedding将图转换为一个低维空间,其中的图信息被保留下来。通过将图表示为一个(或一组)低维向量,然后可以有效地计算图算法。graph embedding的问题与两个传统的研究问题有关,即图分析和representation learning:- 一方面,图分析的目的是从图数据中挖掘有用的信息。
- 另一方面,
representation learning的目的是获得更好的data representation从而用于构建分类器或其他预测器。
graph embedding位于这两个问题的重叠部分,侧重于学习低维representation。这里区分了graph rerpesentation learning和graph embedding。注意,graph rerpesentation learning并不要求学到的representation是低维的。将图嵌入到低维空间并不是一件简单的事情。
graph embedding的挑战取决于问题的设置,它由嵌embedding input和embedding output组成。论文《A Comprehensive Survey of Graph Embedding: Problems, Techniques and Applications》将input graph分为四类,包括同质图homogeneous graph、异质图heterogeneous graph、带有辅助信息的图、和由非关系型数据non-relational data构建的图。不同类型的
embedding input带有不同的信息要在emebdding空间中保留,因此对图的嵌入问题提出了不同的挑战。例如,当嵌入一个只有结构信息的图时,节点之间的连接是需要保留的目标。然而,对于带有节点标签或属性信息的图来说,辅助信息(即节点标签、属性信息)从其他角度提供了图的属性,因此在嵌入过程中也需要被考虑。与
embedding input是给定的、固定的不同,embedding output是任务驱动的。例如,最常见的embedding output类型是node embedding,它将临近的节点表示为相似的向量。node embedding可以有利于节点相关的任务,如节点分类、节点聚类等。然而,在某些情况下,目标任务可能与图的更高粒度有关,例如,
node pair、子图、整个图。因此,在embedding output方面的第一个挑战是为目标任务找到一个合适的embedding output类型。论文《A Comprehensive Survey of Graph Embedding: Problems, Techniques and Applications》将graph embedding output分为四种类型,包括node embedding、edge embedding、hybrid embedding和whole-graph embedding。不同的输出粒度对
good embedding有不同的标准,并面临不同的挑战。例如,一个好的node embedding保留了与嵌入空间中的邻近节点的相似性。相比之下,一个好的whole-graph embedding将整个图表示为一个矢量,这样就可以保留graph-level的相似性。
根据对不同问题设置中所面临的挑战的观察,作者提出了两个
graph embedding工作的分类法,即根据问题设置和嵌入技术对graph embedding文献进行分类。具体而言:- 作者首先介绍了
graph embedding问题的不同设置,以及在每个设置中面临的挑战。 - 然后,作者描述现有研究如何在他们的工作中解决这些挑战,包括他们的见解和他们的技术解决方案。
需要注意的是,尽管已经有一些尝试来综述
graph embedding,但它们有以下两个局限性:- 首先,他们通常仅根据
graph embedding技术来进行分类。他们都没有从问题设置的角度分析graph embedding工作,也没有总结每个问题设置中的挑战。 - 其次,在现有的
graph embedding综述中,仅涉及了有限的相关工作。例如,《Graph embedding techniques, applications, and performance: A survey》主要介绍了12种有代表性的graph embedding算法,《Knowledge graph embedding: A survey of approaches and applications》只关注知识图的嵌入。此外,没有对每种graph embedding技术背后的洞察力进行分析。
论文贡献:
- 论文提出了一个基于问题设置的
graph embedding分类法,并总结了每个设置中面临的挑战。作者是第一个根据问题设置对graph embedding工作进行分类的人,这为理解现有工作带来了新的视角。 - 论文对
graph embedding技术进行了详细的分析。与现有的graph embedding综述相比,论文不仅综述了一套更全面的graph embedding工作,而且还提出了每个技术背后的见解总结。与简单地罗列过去如何解决graph embedding的问题相比,总结的见解回答了问题:为什么能(以某种方式)解决graph embedding问题。 - 论文对
graph embedding的应用进行了系统的分类,并将这些应用划分为节点相关、边相关、图相关。对于每个类别,论文提出了详细的应用场景作为参考。 - 在计算效率、问题设置、解决技术和应用方面,论文在
graph embedding领域提出了四个有希望的未来研究方向。对于每个方向,论文对其在当前工作中的缺点(不足)进行了全面分析,并提出了未来的研究方向。
1.1 定义
给定图
- 每个节点
- 每条边
定义:
- 同质图
- 异质图
- 知识图谱
knowledge graphentity,边为subject-property-object三元组。每条边由(head entity, relation, tail entity)的形式组成,记作
- 每个节点
定义节点
first-order proximity为节点定义
定义节点
second-order proximity为节点如果我们用
cos函数作为邻域相似性的度量,则二阶邻近性为:节点
higher-order proximity也可以类似地定义。例如,节点可以采用递归定义:
注意:也可以使用其它的一些指标来定义高阶邻近度,如
Katz Index, Rooted PageRank, Adamic Adar等等。定义
grap embedding为:给定一个图embedding维度graph embedding需要将图- 可以将整张图表示为一个
- 也可以将单张图表示为一组
embedding(如节点、边、子结构)。
如下图所示,单张图以不同粒度嵌入到一个二维空间,其中
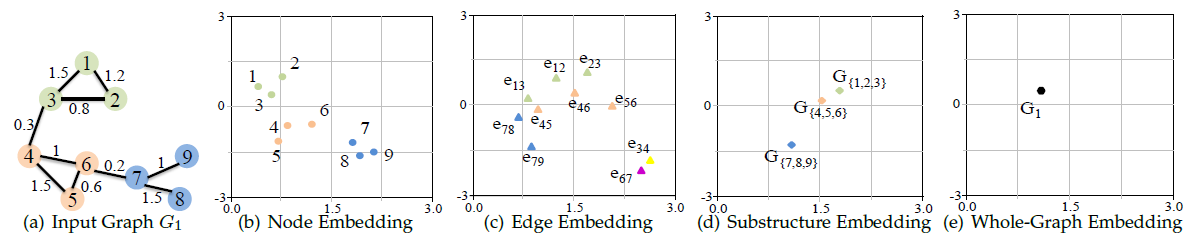
- 可以将整张图表示为一个
1.2 问题
1.2.1 Graph Embedding Input
graph embedding的输入是图,这里我们将输入图划分为四类:同质图homogeneous graph、异质图heterogeneous graph、带辅助信息的图、从非关系数据人工构造的图。每种类型的图都会给graph emebdding带来不同的挑战。同质图:图的节点和边分别只有一种类型。同质图可以进一步划分为加权图、无权图,以及有向图,无向图。
挑战:如何捕获图中观察到的各种各样的连接模式?由于同质图中仅有结构信息可用,因此同质图
graph embedding的挑战在于如何在embedding中保持输入图中观察到的这些连接模式。异质图:异质图包含三种场景:
- 基于社区的问答网站
Community-based Question Answering:cQA:cQA是基于互联网的众包服务,用户可以在网站上发布问题,然后由其它用户回答。直观来看,cQA图中有不同类型的节点,如问题question、答案answer、用户user。 - 多媒体网络:包含多种类型媒体数据(如图像、文本)的网络。
- 知识图谱:在知识图谱中,实体(节点)和关系(边)通常都具有不同的类型。
除了以上三种类型的异质图之外,还有其它类型的异质图。
挑战:
- 如何探索不同类型对象之间的全局一致性?在异质图
embedding中,不同类型的节点(或者不同类型的边)被嵌入到同一个公共空间中。如何确保embedding的全局一致性是一个问题。 - 如何处理不同类型对象之间的不平衡?在异质图中,不同类型的对象数量差异很大,因此学习嵌入时需要考虑数据倾斜问题。
- 基于社区的问答网站
带辅助信息的图:除了包含节点结构之外,带辅助信息的图还包含节点/边/全图的辅助信息。有五种类型的辅助信息:
label:节点带标签信息(离散值)。带相同标签的节点的embedding应该彼此靠近、不同标签的节点的embedding应该彼此远离。attribute:节点带属性信息。和标签不同,属性值可以是连续的也可以是离散的。属性值差异较小的节点的embedding应该彼此靠近、属性值差异较大的节点的embedding应该彼此远离。node feature:节点带特征信息。和属性值不同,特征可能包含文本、向量、图像等多种类型的内容。节点特征通过提供丰富的结构化信息来提升graph emebdding性能。另外,这也使得inductive graph embedding成为可能。information progapation:消息传播。一个典型例子是Twitter中的转发。knowledge base:知识库。流行的知识库包括Wikipedia, Freebase, YAGO, DBPedia等。以Wikipedia为例,concept是用户提出的实体entity,文本是该实体相关的文章。
其它类型的辅助信息包括用户
check-in数据(用户位置信息)、用户item偏好排名信息等等。注意,辅助信息不仅局限于一种类型,也可以考虑多种类型如label & node feature。挑战:如何融合丰富的非结构化信息,使得学到的
embedding同时编码了图的拓扑结构和辅助信息?除了图结构信息之外,辅助信息还有助于定义节点相似性。因此如何融合图拓扑结构和辅助信息这两个信息源,这是一个问题。人工构造图:此时没有图数据,需要通过不同的方法从非关系数据中人工构建图。大多数情况下,输入为特征矩阵
通常使用样本
一种直接的计算方法是将
为解决该问题,一个方法是从
kNN graph,并基于kNN图估计一个邻接矩阵Isomap将测地线距离融合到kNN图,然后找到两个节点之间的最短距离作为它们的测地线距离。另一种构造图的方法是基于节点的共现,从而在节点之间建立边。如在图像领域,研究人员将像素视为节点,像素之间的空间关系视为边。
除了上述基于成对节点相似性以及节点共现的方法之外,还针对不同目的设计了其它的图构造方法。
挑战:
- 如何构造一个图从而对样本之间的成对关系进行编码?即如何计算非关系数据的样本之间的关系,并构造这样的图。
- 如何将节点邻近度矩阵保留在
embedding空间中?即如何在embedding空间中保留构造图的节点邻近性。
1.2.2 Graph Embedding Output
graph emebdding的输出是图(或者图的一部分)的一个(或者一组)低维向量。根据输出粒度,可以将graph embedding输出分为node embedding、edge embedding、hybrid embedding、whole-graph embedding。与固定的且给定的输入不同,
graph embedding的输出是任务驱动的。例如,node embedding可用于各种与节点相关的图分析任务,而某些任务可能需要全图whole-graph embedding。因此,embedding输出的第一个挑战是如何找到满足特定任务需求的、合适的graph embedding。node embedding:将每个节点表示为低维空间中的向量,图中临近的节点在embedding空间中有相似的向量表示。各种
graph embedding方法之间的差异在于如何定义两个节点之间的相近程度closeness,其中一阶邻近度和二阶邻近度是计算两个节点相近程度的常用度量,某些工作中也使用高阶邻近度。挑战:如何在各种类型的输入图中定义成对节点的邻近性,以及如何在
embedding中对这种相近程度进行编码?edge embedding:将每条边表示为低维空间中的向量。edge embedding在以下两种情况下很有用:- 知识图谱
embedding需要学习node embedding和edge embedding。每条边都是三元组edge embedding需要在embedding空间中保留 - 一些工作将节点
pair对嵌入为一个向量,从而预测这对节点之间是否存在链接。
总之,
edge embedding有利于与边相关的图分析,如链接预测、知识图谱的实体/关系预测。挑战:
- 如何定义
edge-level相似度?边的相似度不同于节点相似度,因为边通常包含一对节点。 - 对于有向边,如何建模边的非对称属性?和节点不同,边可以是有向的。因此
edge embedding需要编码这种不对称属性。
- 知识图谱
hybrid embedding:嵌入图的不同类型的组件,如node + edge(子结构substructure)、node + community。已有大量工作研究了子结构嵌入
substructure embedding,而社区嵌入community embedding目前关注较少。substructure embedding或者community embedding也可以通过聚合结构中的node embedding和edge embedding来得到,但是这种间接的方式并未针对结构的表示进行优化。而且,node embedding和edge embedding可以彼此强化:通过融合社区感知community-aware的高阶邻近度,可以学到更好的node embedding;而当学到更好的node embedding时,就可以检测到更好的社区。挑战:
- 如何生成目标子结构?和其它类型的
embedding输出相反,hybrid embedding并未提供需要嵌入的目标(如子图,社区)。因此第一个挑战是如何生成这种目标结构。 - 如何在一个公共空间中嵌入不同类型的图组件?不同类型的目标(如社区、节点)可以同时嵌入到一个公共空间中。如何解决
embedding目标类型的异质性是一个问题。
- 如何生成目标子结构?和其它类型的
whole-graph embedding:将整个图输出为一个embedding向量,这通常用于蛋白质、分子等较小的图。这种情况下,一个图表示为一个向量,相似的图被嵌入到相近的embedding空间。whole-graph embedding提供了图相似度计算的一种简单有效解决方案,使得图分类任务受益。挑战:
- 如何捕获整个图的属性?
whole-graph embedding需要捕获整个图的属性,而不是单个节点或者边的属性。 - 如何在表达性
expressiveness和效率efficiency之间平衡? 由于需要捕获全图属性,因此和其它类型的embedding相比,whole-graph embedding耗时更多。whole-graph embedding的关键挑战是如何在学到的embedding的表达能力和embedding算法的效率之间平衡。
- 如何捕获整个图的属性?
1.3 技术
- 通常
graph embedding目标是在低维embedding空间中表达一个图,其中该embedding空间保留尽可能多的图属性信息。不同graph embedding算法之间的差异主要在于如何定义需要保留的图属性。不同的算法对于节点相似性、边相似性、子结构相似性、全图相似性有不同的定义,以及对于如何将这种相似性保留在embedding空间有各自不同的见解insight。
1.3.1 矩阵分解
基于矩阵分解
Matrix Factorization的graph emebdding方法以矩阵形式表示图属性,如节点成对相似性node pairwise similarity,然后分解该矩阵从而得到node embedding。基于矩阵分解的
graph embedding方法也是graph embedding的早期研究方式。大多数情况下,输入是非关系型的non-relational、高维的数据通过人工构造而来的图,输出是一组node embedding。因此可以将graph embedding视为保留结构信息的降维问题,该问题假设输入数据位于低维流形中。有两种类型的基于矩阵分解的
graph embedding方法:分解图拉普拉斯特征图Laplacian Eigenmaps、分解节点邻近度矩阵proximity matrix。总结:矩阵分解主要用于两种场景:嵌入由非关系数据构成的图的
node embedding(这是拉普拉斯特征图的典型应用场景)、嵌入同质图。
a. Graph Laplacian Eigenmaps
图拉普拉斯特征图分解的思想是:保留的图属性为成对节点相似性,因此如果两个相距较远的节点(通过
embedding距离衡量)的相似度较大,则给予较大的惩罚。为方便讨论,假设
embedding的维度为一维,即将每个节点insight,则最优化embedding为:假设
embedding维度为embedding。其中:
embedding,embedding组成的embedding向量。
但是,上述最优化方程没有唯一解。假设
则最优解
eigenproblemeigenvalue对应的特征向量eigenvector。上述
graph embedding的问题是该方法是transductive的,它仅能嵌入已有的节点。实际应用中还需要嵌入未见过的、新的节点。一种解决方案是设计线性函数
feature vector。这样只要提供节点的特征向量,我们就可以求得其embedding。因此inductive graph embedding问题的核心在于求解合适的同样地我们认为如果相距较远的两个节点(通过
embedding距离衡量)的相似度较大,则给与较大的惩罚。则最优化embedding为:其中
类似地,为了移除缩放因子的效果,我们通常增加约束条件
则最优解
eigenproblemeigenvalue对应的特征向量eigenvector。上述讨论都是假设
embedding为一维的。事实上如果希望embedding是多维的,如top d特征值对应的特征向量。现有方法的差异主要在于如何计算节点
eigenmaps-based graph embedding方法,并给出了它们如何计算节点相似度矩阵其中:
Eq.2表示目标函数Eq.4表示目标函数SVM分类器的目标函数。最初的研究
MDS直接采用两个特征向量MDS不考虑节点的相邻关系,也就是说,任何一对训练样本都被认为是相连的。后续研究(如
Isomap、LE、LPP、LLE)通过首先从数据特征中构建一个k nearest neighbour graph来克服这个问题。每个节点只与它的top-k相似邻居相连。之后,利用不同的方法来计算相似性度矩阵最近设计了一些更先进的模型。例如:
AgLPP入了一个anchor graph,以显著提高LPP的效率。LGRM学习了一个local regression model来掌握图的结构,以及一个全局回归global regression项来进行out-of-sample的数据推断。- 最后,与之前保留
local geometry的工作不同,LSE使用local spline regression来保留global geometry。
当辅助信息(如
label、属性)可用时,目标函数被调整以保留更丰富的信息:- 例如,
SR构建了一个邻接图adjacent graphlabelled graphLPP数据集的局部几何结构local geometric structure,另一部分试图在标记的训练数据上获得最佳类别可分的embedding。 - 同样,
ARE也构建了两个图:一个是编码局部几何结构的邻接图pairwise relation的feedback relational graph RF-Semi-NMF-PCA的目标函数由三个部分组成,从而同时考虑聚类、降维和graph embedding:PCA、k-means和graph Laplacian regularization。
- 例如,
其他一些工作认为,不能通过简单地枚举成对的节点关系来构建
semidefinite programming: SDP来学习SDP旨在找到一个内积矩阵,使图中不相连的任何两个输入之间的成对距离最大化,同时保留最近的邻居距离。MVU构建了这样的矩阵,然后将MDS应用于学到的内积矩阵。《Unsupervised large graph embedding》证明:如果PSD的、以及秩为LPP等价于正则化的SR。

b. Node Proximity Matrix
除了上述求解广义特征值方法之外,另一个方向是试图直接分解节点邻近度矩阵。可以基于矩阵分解技术在低维空间中近似节点邻近度,使得节点邻近度的近似损失最小化。
给定节点邻近度矩阵
其中:
embedding矩阵。content embedding矩阵。
该目标函数是寻找邻近度矩阵
SVD分解:其中:
则我们得到最优
embedding为:根据是否保留不对称性,节点
embedding可以为我们在下表中总结了更多的矩阵分解方案,例如正则化的高斯矩阵分解、正则化的低秩矩阵分解、带更多正则化约束的矩阵分解等。
其中:
Eq.5表示目标函数
1.3.2 深度学习
- 基于深度学习的
graph embedding在图上应用深度学习模型,这些模型的输入可以是从图采样得到的路径,也可以是整个图本身。因此基于是否采用随机游走从图中采样路径,我们将基于深度学习的graph embedding分为两类:带随机游走的deep learning、不带随机游走的deep learning。 - 总结:由于深度学习的鲁棒性和有效性,深度学习已被广泛应用于
graph emebdding中。除了人工构造的图之外,所有类型的图输入以及所有类型的embedding输出都可以应用基于深度学习的graph embedding方法。
a. Deep Learning based Graph Embedding with Random Walk
基于带随机游走的
deep learning的graph embedding的思想是:对于给定的节点,通过给定该节点的embedding的条件下最大化该节点邻域的条件概率,则可以在embedding空间中保留图的二阶邻近度。在基于带随机游走的
deep learning的grap emebdding中,图表示为从图中采样的一组随机游走序列。然后深度学习模型被应用于这些随机游走序列从而执行grap embedding。在嵌入过程中,embedding保留了这些随机游走序列携带的图属性。基于以上的洞察,
DeepWalk采用神经语言模型(SkipGram) 执行grap embedding,其中SkipGram旨在最大化窗口内单词之间的共现概率。DeepWalk首先应用截断的随机游走从输入图采样一组随机序列,然后将SkipGram应用于采样到的随机序列,从而最大化给定节点条件下节点邻域出现的概率。通过这种方式,相似邻域(具有较大的二阶邻近度)的节点共享相似的embedding。DeepWalk的目标函数为:其中:
embedding;SkipGram不考虑窗口内节点的属性,因此有:这里假设给定节点
其中
embedding时,节点softmax函数:上述概率难以计算,因为分母需要计算
embedding的内积,算法复杂度为Hierarchical Softmax:我们构造二叉树来高效计算假设根节点到叶节点
sigmoid函数;embedding。现在
Hierarchical Softmax函数将SkipGram的时间复杂度从负采样:负采样的核心思想是将目标节点和噪声区分开来。即对于节点
其中:
通常
最终负采样将
SkipGram的时间复杂度从
DeepWalk的成功引起了很多后续的研究,这些研究在graph embedding的采样路径上应用了各种深度学习模型(如SkipGram或LSTM),我们在下表中总结了这些方法。其中:Eq.11表示Eq.12表示
如下表所示,大多数研究都遵循了
DeepWalk思想,但是改变了随机游走采样方法或者要保留的邻近度。注意:SkipGram仅能嵌入单个节点,如果需要嵌入一个节点序列到固定维度的向量(如将一个句子嵌入为一个向量),则需要使用LSTM。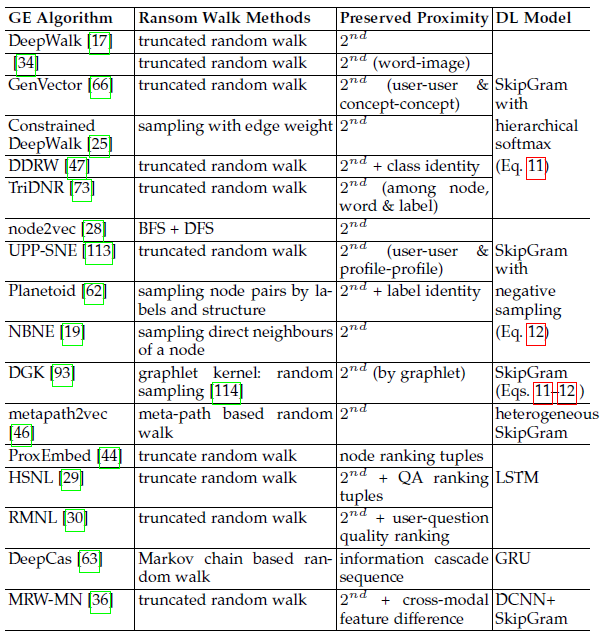
b. Deep Learning based Graph Embedding without Random Walk
不基于带随机游走的
deep learning的graph embedding的思想是:深度神经网络体系结构是将图编码到低维空间的强大、有效的解决方案。这一类
deep learning方法直接将深度神经网络应用于整个图(或者图的邻接矩阵)。以下是一些用于graph embedding的流行深度学习模型:自编码器
autoencoder:自编码器旨在通过其编码器encoder和解码器decoder,使得自编码器的输出和输入的重构误差最小。编码器和解码器都包含多个非线性函数,其中编码器将输入数据映射到representation space、解码器将representation space映射到重构空间。就邻域保持而言,采用自编码器的
grap embedding思想类似于节点邻近度矩阵分解。具体而言,由于邻接矩阵包含了节点的邻域信息,因此如果将邻接矩阵作为自编码器的输入,则重构过程将使得具有相似邻域的节点具有相似的embedding。Deep Neural Network:卷积神经网络及其变种已被广泛用于graph embedding。- 一些工作直接使用原始
CNN模型,并对input graph进行重构从而适应CNN。 - 另一些工作尝试将深度神经网络推广到非欧几何邻域(如,图结构)。这些方法之间的差异在于它们在图上采取了不同的、类似于卷积的运算方式。例如,模仿卷积定理来定义谱域中的卷积、以及将卷积视为空间域中的邻域匹配。
- 一些工作直接使用原始
还有一些其他类型的基于深度学习的
graph embedding方法,如:DUIF使用hierarchical softmax作为前向传播来最大化modularity。HNE利用深度学习技术来捕捉异质组件之间的交互,如CNN组件用于图片、FC层用于文本。
我们在下表中总结了所有不带随机游走的基于深度学习的 graph embedding 方法,并比较了它们使用的模型以及每个模型的输入。
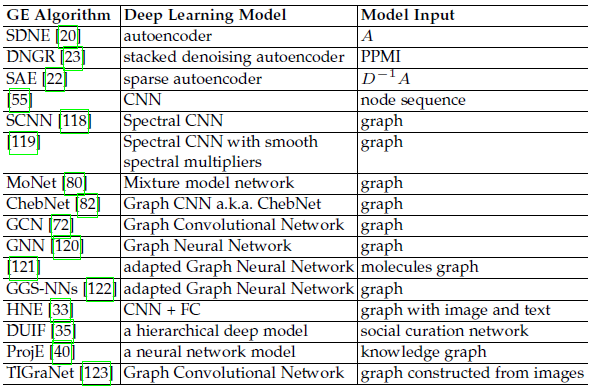
1.3.3 边重构
基于边重建
edge reconstruction的node embedding基本思想是:通过node embedding重建的边应该和输入图中的边尽可能一致。因此,基于边重建的
node embedding方法通过最大化边的重建概率edge reconstruction probability或最小化边的重建损失edge reconstruction loss,从而优化边重建的目标函数。其中重建损失又分为distance-based损失和margin-based ranking损失。总结:基于边重构的方法适用于大多数
grap embedding场景。根据我们的观察发现,只有非关系数据中构建的人工图embedding、whole-graph embedding还未应用这种方式。原因是:- 人工构造的图中,所谓的 “边” 是我们人工构造的,并没有真实的物理含义。而且不同的构造方式得到的 “边” 不同。
- 边仅代表两个节点之间的关系,因此基于边重建的方法聚焦于局部的连接性,因此它不适合
whole-graph embedding。
a. 最大化边的重建概率
最大化边的重建概率的基本思想是:好的
node embedding应该能够最大程度地重建图中的边。因此,该方法最大化所有观察到的边的生成概率。给定节点
embedding它表示节点
为学习
node embedding,我们最大化图中所有边的生成概率,因此目标函数为:类似地,节点
则最大化二阶邻近性的目标函数为:
其中
{start_node, end_node}组成的集合,即从每条随机游走序列上随机截取的两个点。这使得节点之间的二阶邻近度转换为从起点到终点的随机游走概率。
b. 最小化基于距离的重建损失
最小化边的重建
distance-based损失的基本思想:通过node embedding计算的节点邻近度,应该尽可能和图中通过边计算的节点邻近度一致,从而最小化邻近度之间的差异,最终保留图的邻近度属性。通过
node embedding计算的一阶邻近度为:而通过图中边计算的经验一阶邻近度为:
其中
KL散度为距离函数来计算类似地,通过
node embedding计算的二阶邻近度为:而通过图中边计算的经验二阶邻近度为:
其中
out-degree(或者在无向图中就是节点的degree)。同样地,由于计算KL散度为距离函数来计算
c. 最小化 Margin-based 排序损失
最小化边的重建
margin-based排序损失的基本思想:边暗示了一对节点之间的相关性relevance。因此,对于一个节点A,假设它和节点B存在边、和节点C不存在边,则在节点B和C之间,节点A的embedding和节点B的embedding更相似。定义
margin-based ranking loss为:其中
margin超参数。最小化该损失函数鼓励
margin,因此鼓励下表中我们总结了现有的利用
graph embedding的边重建技术,给出了它们的目标函数和保留的节点邻近度。通常大多数方法使用上述目标函数之一。注意:当在graph embedding期间同时优化另一个任务时,该task-specific目标函数将融合到总的目标函数中。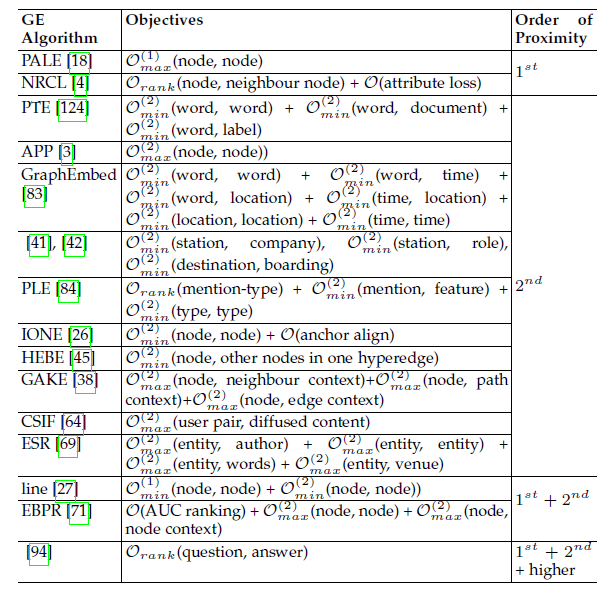
大多数现有的知识图谱
embedding方法都选择优化margin-based ranking损失函数。知识图谱head entitytail entityembedding可以解释为保留图的排名ranking属性,使得真实的三元组具体而言,在知识图谱
embedding中,我们设计了能量函数embedding之间的相似性得分。embedding的距离得分。
embedding空间的转换。可选的最终,知识图谱的
graph embedding目标函数为:其中
现有知识图谱
embedding方法主要优化上述
1.3.4 Graph Kernel
Graph Kernel的原理是:整个图结构可以表示为一个向量,其中向量每个分量表示被分解的基本子结构的计数。Graph Kernel是R卷积的一个实例,它是一种在离散的复合对象discrete compound object上定义kernel的一种通用方法。这种方法通过将结构化对象递归地分解为 “原子” 的子结构,并两两进行比较。Graph Kernel将每个图表示为一个向量,并使用两个向量的内积来比较两个图的相似性。在Graph Kernel中通常定义三种类型的 “原子” 子结构:Graphlet、Subtree Pattern、Random Walk。Graphlet:一个Graphlet是一个size-k的、诱导的induced、非同构的non-isomorphic子图。假设将图
graphletgraphletSubtree Pattern:在这种kernel中,图被分解为subtree pattern。一个例子是
Weisfeiler-Lehman子树。对于带标记的图(即具有离散型的节点标签)执行relabeling迭代过程。每次迭代过程中如下图所示:- 根据节点的标签及其邻居标签为节点得到
multiset label,multiset label中对邻居标签进行升序排列。 - 将
multiset label映射称为新的label。这里使用字符串到ID的映射,也可以采用其它映射函数如哈希函数。 - 使用新
label执行relabel过程。
假设在图
relabelling过程,则embeddingblock,第block的第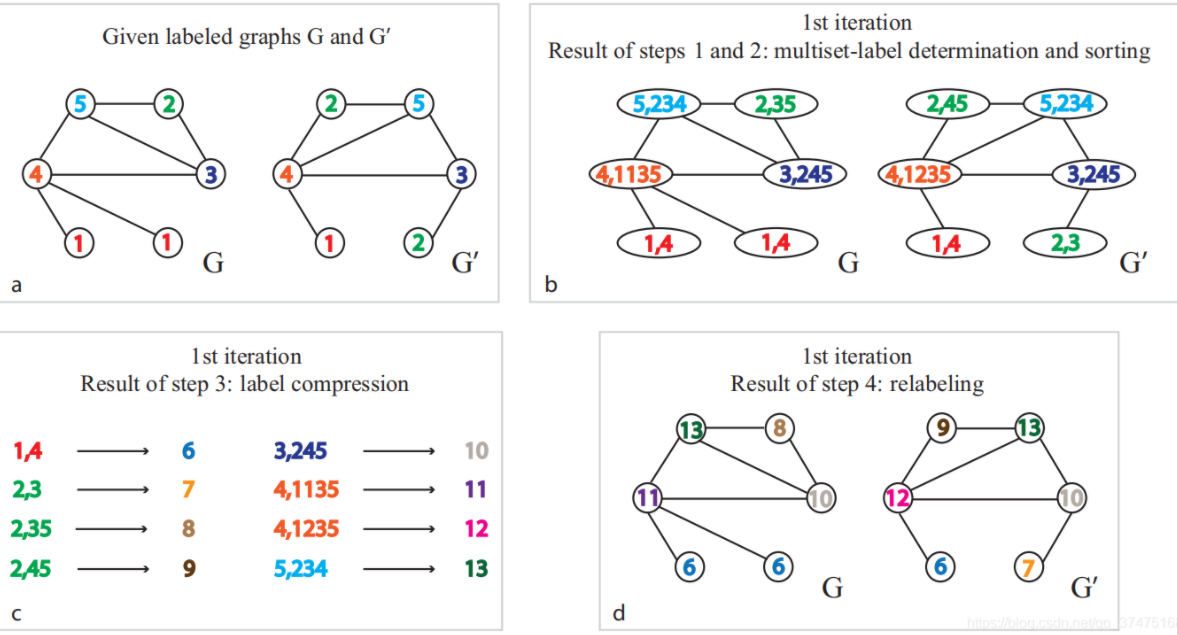
- 根据节点的标签及其邻居标签为节点得到
Random Walk:在这种kernel中,图被分解为随机游走序列或路径(注意,这里的路径是固定的不是随机的),而kernel表示随机游走序列或路径出现的频次。以路径为例,假设图
总结:
Graph Kernel用于捕获整个图的全局属性,因此仅用于whole-graph emebdding。输入图的类型通常是同质图,或者带有辅助信息的图。
1.3.5 生成式模型
可以指定输入特征和类别标签的联合分布来定义生成式模型
generative model。一个典型的例子是潜在迪利克雷分配Latent Dirichlet Allocation: LDA,其中文档被解释为主题的分布,主题是单词的分布。有两种生成式模型用于
graph embedding:Embed Graph Into The Latent Semantic Space:原理是节点被嵌入到潜在语义空间中,其中节点之间的距离解释了观察到的图结构。该方法直接将图嵌入到潜在空间,每个节点都表示为潜在空间中的一个向量。换句话讲,它将观察到的图视为从生成模型生成而来。例如在
LDA中,文档被嵌入到topic空间中,单词相似的文档具有相似的topic向量。Incorporate Latent Semantics for Graph Embedding:原理是图中距离较近、且具有相似语义的节点应该紧密嵌在一起。其中节点语义可以通过生成式模型从节点描述信息中获取。该方法使用潜在语义作为节点辅助信息从而进行
graph embedding。最终embedding不仅取决于图结构信息,还取决于节点的潜在语义信息。
这两种方法的不同之处在于:第一种方法中
emebdding空间就是潜在空间latent space;第二种方法中,潜在空间用于融合节点的不同来源的信息,并帮助将一个图嵌入到另一个空间。总结:生成式模型可以用于
node embedding、edge embedding。由于该方法考虑了节点语义,因此输入图通常是异质图,或者带有辅助信息的图。
1.3.6 混合技术和其它
有时在一项工作中结合了多种技术:
《Cross view link predictionby learning noise-resilient representation consensus》通过最小化margin-based ranking loss学习edge-based embedding,并通过矩阵分解学习attribute-based embedding。《Semantically smooth knowledge graph embedding》优化了margin-based ranking loss,并将基于矩阵分解的损失作为正则化项。《Community-based question answering via asymmetric multifaceted ranking network learning》使用LSTM来学习嵌入cQA中的句子,并使用margin-based ranking loss来融合好友关系。《Context-dependent knowledge graph embedding 》采用CBOW/SkipGram进行知识图谱实体嵌入,然后通过最小化margin-based ranking loss对embedding进行微调。《Text-enhanced representation learning for knowledge graph》使用word2vec来嵌入文本上下文,使用TransH来嵌入实体/关系,从而在知识图谱嵌入中利用了丰富的上下文信息。《Collaborative knowledge base embedding for recommender systems》利用知识库中的异质性信息来提高推荐性能。它使用TransR进行network embedding,并使用自编码器进行textual embedding和visual embedding。- 最后,人们提出了生成式模型,从而将协同过滤与
items semantic representation相结合。
除了所介绍的五类技术外,还有其他方法:
《Hierarchical graph embedding in vector space by graph pyramid》提出了通过图与prototype graph的距离来嵌入图的方法。《On the embeddability of random walk distances 》首先使用pairwise最短路径距离来嵌入一些landmark节点。然后嵌入其他节点,使其与landmark节点的距离尽可能地接近真实的最短路径。《Cross view link predictionby learning noise-resilient representation consensus》联合优化了基于边的损失(最大化观察一个节点的邻居的可能性)和基于属性的损失(学习link-based representation的线性投影)。KR-EAR(《Knowledge representation learning with entities, attributes and relations》) 将知识图谱中的关系区分为attribute-based和relation-based。它构建了一个relational triple encoder(TransE、TransR)来嵌入实体和关系之间的关联,以及一个attributional triple encoder来嵌入实体和属性之间的关联。Struct2vec通过hierarchical metric考虑了节点的结构身份structral identify,从而用于node embedding。《Fast network embedding enhancement via high order proximity approximation》通过近似高阶邻近性矩阵提供了一种快速嵌入方法。
1.3.7 总结
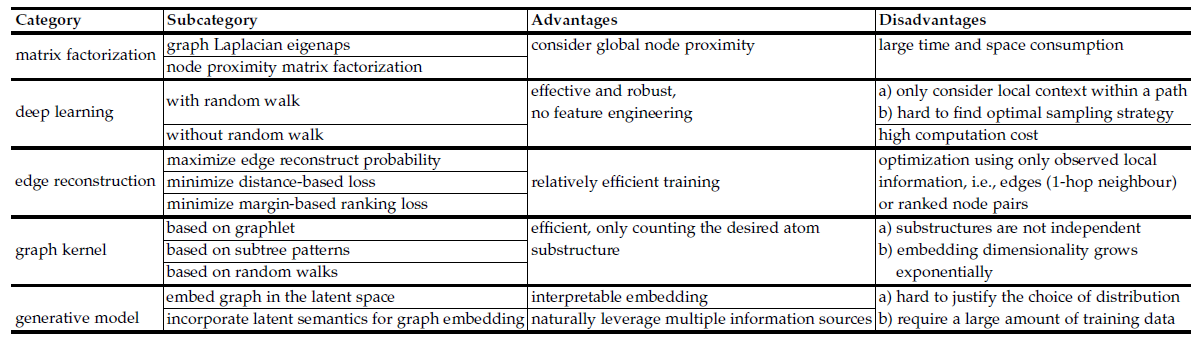
我们在下表给出所有五种
graph embedding的优缺点。基于矩阵分解的
graph embedding使用global pairwise相似度的统计信息来学习embedding。由于某些任务依赖于独立的局部上下文窗口,因此它可以超越基于深度学习的
graph embedding方法。但是,无论是邻接矩阵的构造还是矩阵的特征值分解,其时间代价、空间代价都很高。这使得矩阵分解的效率较低,并且无法扩展到大规模的图。基于深度学习的
grap emebdding效果突出。我们认为深度学习适用于graph embedding,因为它具有从复杂图结构中自动识别出有用representation的能力。例如:- 带随机游走的深度学习方法可以通过图上的采样路径自动探索邻域结构。
- 不带随机游走的深度学习方法可在同质图中建模可变大小的子图结构,或者在异质图中建模各种类型节点之间丰富的交互。
另一方面,基于深度学习的方法也有局限性:
对于带随机游走的深度学习方法,它仅考虑路径内的局部邻域,因此忽略了全局结构信息。
另外,由于无法在统一的框架中同时优化
embedding和路径采样,因此很难找到最佳的采样策略。对于不带随机游走的深度学习方法,计算代价通常很高。
最后,传统的深度学习架构假设输入数据是
grid结构从而充分利用GPU,但是图数据不具备grid结构,因此需要不同的解决方案来提高计算效率。基于边重建的
graph embedding方法可以基于观察到的边或者有序三元组从而优化目标函数。和前两类graph embedding相比,它的训练效率更高。但是这一系列方法是使用直接观测到的局部信息进行训练的,因此获得的
embedding缺乏对全局图结构的了解。基于
graph kernel的graph embedding将整个图转换为一个向量,从而促进graph-level的图分析任务,例如图分类。它比其它类型的技术更加高效,因此它只需要枚举图中出现的“原子”的子结构。但是,这种类似于
bag-of-word的方法有两个局限:- 首先,子结构之间不是相互独立的。例如
size为k+1的graphlet可以通过size为k的graphlet通过添加一些新的节点和一些新的边得到。这意味着通过graphlet的graph representation存在冗余信息。 - 其次,随着子结构
size的增加,graph embedding维度通常呈指数型增长,从而导致embedding的稀疏性问题。
- 首先,子结构之间不是相互独立的。例如
基于生成式模型的
graph embedding可以自然地利用统一模型中不同来源的信息(如,图结构、节点属性)。直接将图嵌入到潜在的语义空间中,得到的emebdding可以用语义来解释。但是,假设观测数据满足某种分布通常很难证明。并且生成式方法需要大量的训练数据来估计模型。因此对于较小的图或者少量的图,它无法很好地工作。
1.4 应用
节点相关应用:
节点分类:通常先将每个节点嵌入为一个低维向量,然后通过在标记节点的
embedding向量上应用分类器进行训练。另外,和上面的两阶段节点分类相比,一些工作设计了一个统一的框架来共同优化
node embedding和节点分类,从而学到每个节点的classification-specific representation。节点聚类:通常先将每个节点嵌入为一个低维向量,然后将传统的聚类算法应用于
node embedding。作为无监督算法,当节点标签不可用时可以使用聚类算法。现有大多数方法都使用
k-means作为聚类算法。也有一些方法在一个目标中共同优化了聚类和node embedding,从而学到每个节点的clustering-specific representation。节点推荐/检索/排序:节点推荐任务是基于某些标准(如相似性),将
top-K相似节点推荐给目标节点。在
knowledge graph embedding中被广泛讨论的一个具体应用是entity ranking:在三元组
边相关的应用:
链接预测:
graph embedding旨在用低维的向量来表示图,但有趣的是,得到的embedding向量也可以反过来帮助推断图结构。实际上输入的图通常是残缺的。例如,在社交网络中实际上彼此认识的两个用户可能因为种种原因并没有添加为好友。在
graph embedding中,低维embedding向量预期会保留不同阶次、不同尺度的邻近度,因此这些embedding向量编码了有关网络结构的丰富信息,并可以用于预测图中的缺失链接。基于
graph embedding的链接预测大多数应用于同质图,也有少量工作涉及异质图的链接预测。三元组分类
Triple Classification:三元组分类是知识图谱的特定应用,其目标是对未见过的三元组
图相关应用:
- 图分类:图分类是将类别标签分配给整个图。这不同于节点分类,节点分类是将类别标签分配给每个节点。当图作为基本的单元时,这一点很重要。如,在化合物分类任务中,每个图都是一个化合物。
- 可视化:图可视化是在低维空间中生成图的可视化。通常,出于可视化的目的,所有节点都使用二维向量
embedding,然后在二维空间中使用不同的颜色绘制从而表示节点类别。图可视化生动地展示了属于同一个类别节点的embedding是否彼此靠近。
其它应用:上面讨论的是一些通用的应用,这里是一些具体的应用:
- 知识图谱相关:包括从大规模纯文本中提取
relational fact、从文本中提取医学实体、将自然语言文本与知识图谱中的实体联系起来,等等。 - 多媒体网络相关:包括嵌入了
geo-tagged的社交媒体的记录<time, location, message>从而在给定其中两个元素的情况下恢复缺失的第三个元素;使用graph embedding来数据维度从而用于人脸识别;将图像映射到一个语义流形中从而促进content-based的图像检索。 - 信息传播相关:包括通过嵌入
social interaction graph来预测propagation user并识别领域专家。 - 社交网络对齐:包括预测两个不同社交网络中的两个用户账户是否为同一用户所有。
- 图像相关:一些工作嵌入了由图像构建的
graph,然后将emebdding用于图像分类、图像聚类、图像分割、模式识别,等等。
- 知识图谱相关:包括从大规模纯文本中提取
1.5 未来方向
这里我们总结了
graph embedding四个未来方向,包括计算效率、问题设置、技术、应用场景。计算效率
computation efficiency:传统的深度学习模型(专为欧式结构的数据来设计)利用现代GPU来优化计算效率,通常假设输入数据为一维或二维网格形状。但是图不具备这种网格结构,因此需要针对graph embedding设计深度架构来提高模型效率。问题设置
problem setting:动态图是graph embedding的一种有前景的方向。图并不总是静态的,可以是动态演进的。一方面,图的结构可能随时间发生变化,如出现一些新节点、新的边,而有一些旧节点、旧的边消失;另一方面,图中节点的属性可能随时间发生变化。与静态图的嵌入不同,动态图的技术需要可扩展的(最好是增量的),以便有效地处理动态变化。这使得大多数现有的
graph embedding方法都存在效率低的问题,不再适用。如何针对动态图设计有效的graph embedding方法,仍然是悬而未决的问题。技术
techniques:结构感知structure-aware对基于边重建的graph embedding非常重要。目前基于边重建的graph embedding方法仅依赖于一阶邻域,图的全局结构(如路径、树、子图模式)被忽略。从直觉上讲,一个子结构包含的信息要比单条边更丰富。因此,需要有一种有效的结构感知
graph embedding优化框架以及子结构采样策略。应用:
graph embedding已应用于许多不同的应用中。它可以将不同数据源、不同平台、不同视角的数据映射到公共的空间,从而便于直接比较。如content-based图像检索、keyword-based图像/视频检索等。使用
graph embedding进行表示学习的优势在于:训练数据的graph的流形被保留在embedding中,并可以进一步使得后续的应用受益。因此,graph embedding可以使那些假定输入数据实例与某些关系(即通过某些link来连接)相关的任务受益。探索从graph embedding中受益的应用场景是非常重要的,因为它从不同的角度为传统问题提供了有效的解决方案。
二、Graph Embedding Techniques, Applications, and Performance[2017]
近年来,由于网络在现实世界中无处不在,图分析
graph analysis已经引起了越来越多的关注。图分析任务可以大致抽象为以下四类:节点分类、链接预测、节点聚类、以及可视化:- 节点分类的目的是根据其他标记的节点和网络的拓扑结构来确定节点的标签。
- 链接预测指的是预测缺失的链接或未来可能出现的链接。
- 节点聚类是用来寻找类似节点的子集,并将它们分组。
- 可视化有助于提供对网络结构的洞察力。
在过去的几十年里,人们为上述任务提出了许多方法:
- 对于节点分类,大致有两类方法:使用随机游走来传播标签的方,以及从节点中提取特征并对其应用分类器的方法。
- 链接预测的方法包括:基于相似性的方法、最大似然模型、以及概率模型。
- 聚类方法包括:基于属性的模型、以及直接最大化(或最小化)簇间(或簇内)距离的方法。
论文
《Graph Embedding Techniques, Applications, and Performance: A Survey》提供了一种分类方法,来分析现有的方法以及应用领域。通常图任务的模型要么在原始图的邻接矩阵上执行,要么在一个派生的向量空间上执行。近年来,基于向量空间的
graph representation方法能够保持图的属性,因此被广泛应用。获得这样的embedding对于图分析任务非常有用。可以将node embedding作为模型的特征输入,这可以避免使用一个非常复杂的模型直接应用到图数据上。获得每个节点的
embedding向量非常困难,并存在一些挑战:属性选择:节点的良好的
embedding向量应该保持图结构信息。第一个挑战是:embedding应该保留图的哪个属性?由于在图上存在多种距离度量和属性(如一阶邻近度、二阶邻近度),因此这种选择可能很困难,并且依赖于具体的任务。
可扩展性:大多数真实网络都很大,并且包含数百万节点和边。
embedding算法应该是可扩展的,并能够处理大图。embedding维度:选择最佳的embedding维度可能很困难。例如,更高的维度可以提高边重建的准确性,但是具有更高的时间复杂度和空间复杂度。根据方法的不同,具体的最佳embedding维度也是task-specific的。如,在链接预测任务中,如果使用的模型仅捕获节点之间的局部连接,则较小的embedding维度可能导致更好的链接预测准确性。
论文贡献:
- 论文提出了一个
graph embedding方法的分类法,并解释了它们的差异。作者定义了四个不同的任务,也就是graph embedding技术的应用领域。作者说明了graph embedding的演变、所面临的挑战、以及未来可能的研究方向。 - 论文对各种
graph embedding模型进行了详细而系统的分析,并讨论了它们在各种任务上的表现。对于每一种方法,作者通过对一些常见的数据集和应用场景的综合比较评估,分析其保留的属性及其准确性。此外,作者对所评估的方法进行了超参数敏感性分析以测试它们的鲁棒性,并提供对最佳超参数的理解。 - 为了促进
graph embedding的进一步研究,论文最后介绍了GEM,这是作者开发的开源Python库,在一个统一的接口下提供了本综述中讨论的所有graph embedding方法的实现。就作者所知,这是第一篇综述graph embedding技术及其应用的论文。
2.1 算法
给定图
邻接矩阵
定义节点
first-order proximity为节点我们认为:如果两个节点之间具有较大权重的连接,则它们更为相似。由于边
定义
定义节点
second-order proximity为节点cos函数作为邻域相似性的度量,则二阶邻近性为:节点
higher-order proximity也可以类似地定义。例如,节点和
《A Comprehensive Survey of Graph Embedding[2017]》类似,也可以采用递归定义:也可以使用其它的一些指标来定义高阶邻近度,如
Katz Index, Rooted PageRank, Common Neighbors, Adamic Adar等等。给定一个图
graph embedding是一个映射因此,
embedding将每个节点映射到低维特征向量,并尝试保留节点之间的连接信息。graph embedding技术的历史演进:在
21世纪初,研究人员开发了graph embedding算法,作为降维技术的一部分。他们会根据邻居关系为similarity graph,然后将图的节点嵌入到一个embedding的思想是:让相连的节点在向量空间中相互靠近。Laplacian Eigenmaps和Locally Linear Embedding: LLE是基于这个原理的算法的例子。然而,可扩展性是这种方法的一个主要问题,其时间复杂度为自
2010年以来,关于graph embedding的研究已经转向获得可扩展的graph embedding技术,这些技术利用了现实世界网络的稀疏性。例如:Graph Factorization使用邻接矩阵的近似分解化作为embedding。LINE扩展了这种方法,并试图保留一阶邻近性和二阶邻近性。HOPE扩展了LINE,试图通过使用广义的奇异值分解Singular Value Decomposition: SVD来分解相似性矩阵而不是邻接矩阵,从而保留高阶接近性。SDNE使用自编码器来嵌入图的节点并捕获高度非线性的依赖关系。
新的可扩展方法的时间复杂度为
我们将近年来提出的
graph embedding技术分为三类:- 基于矩阵分解的方法
factorization-based。 - 基于随机游走的方法
random walk-based。 - 基于深度学习的方法
deep learning-based。
这些类别代表性的方法以及简要介绍如下表所示。
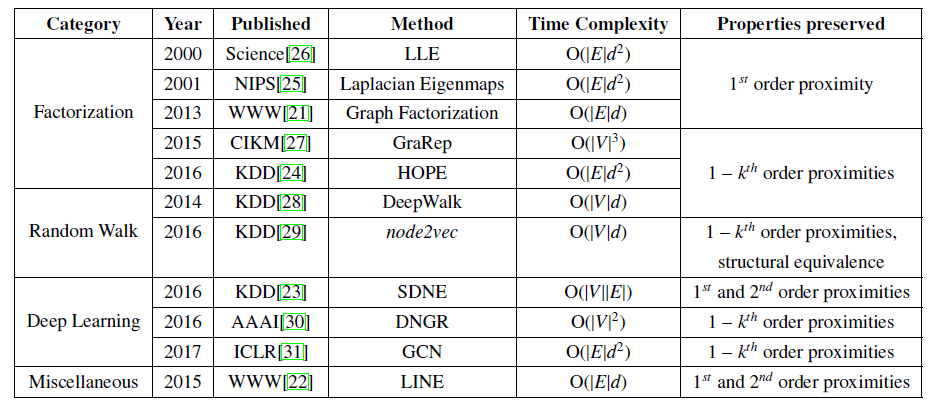
- 基于矩阵分解的方法
2.1.1 基于分解的方法
基于分解的方法以矩阵形式表示节点之间的连接,然后将该矩阵分解从而获得
node embedding。用于表示连接的矩阵可以为节点邻接矩阵、图拉普拉斯矩阵、节点转移概率矩阵、Katz相似度矩阵。Katz Index:KI用于区分不同邻居节点的不同影响力,它给邻居节点赋予不同的权重:对于短路径赋予较大权重、对于长路径赋予较小的权重。给定节点
其中
令
KI矩阵为由于存在矩阵求逆运算,因此总的算法复杂度为
矩阵分解的方法因矩阵属性而异。如果获得的矩阵是半正定的(例如,图拉普拉斯矩阵),则可以使用特征值分解
eigenvalue decomposition。对于非结构化矩阵unstructured matrices,可以使用梯度下降法在线性时间内获得embedding。LLE:局部线性嵌入Locally Linear Embedding:LLE假设每个节点的embedding都是其邻居节点的embedding的线性组合。假设图
embeddingnode embedding的线性组合近似为:我们通过最小化近似误差来得到目标函数:
其中
embedding矩阵。可以看到当
进一步地,为消除平移不变性,因为如果
embedding以零点为中心:因此得到最优化方程:
可以将上述最优化问题简化为一个特征值问题
eigenvalue problem,最终的解为稀疏矩阵eigenvalue对应的特征向量eigenvector,并剔除最小特征值对应的特征向量。Laplacian Eigenmaps:拉普拉斯特征图Laplacian Eigenmaps旨在当embedding距离较近。具体而言,其目标函数为:其中
tr(.)为矩阵的迹trace,可以看到当
上述最优化问题的解为归一化的图拉普拉斯矩阵
eigenvalue对应的特征向量eigenvector。Cauchy Graph Embedding:对于任意节点则我们称该
embedding保留了局部拓扑结构local topology。即:对于任意一对节点在拉普拉斯特征图中,由于
embedding距离使用二次函数,因此:对于embedding距离较大的不相似的节点,其距离的平方较大;对于embedding距离较小的相似节点,其距离平方较小。因此该目标函数更侧重于找到 ”不相似性性“,而不是”相似性“ 。即:- 如果将不相似节点映射到相似的
embedding,则惩罚较小。 - 如果将相似节点映射到不相似的
embedding,则惩罚较大。
因此拉普拉斯特征图倾向于将节点都映射到相似的
embedding,这使得emebdding无法保留图的局部拓扑结构。Cauchy Graph Embedding通过将注意这里为
max而不是min。这一变化得核心在于:对于较大的
但是对于较小的
- 如果将不相似节点映射到相似的
SPE:结构保持嵌入Structure Preserving Embedding:SPE是扩展拉普拉斯特征图的另一种方式。SPE目标是准确地重建输入图。embedding存储为一个半正定的核矩阵connectivity algorithm我们求解最优化方程:
从而试图重建
rank-1的谱嵌入spectral embedding。连通算法
此时求解的
kernel为了处理图中的噪音,可以添加一个松弛变量
其中
slackness。Graph Factorization:图分解Graph Factorization:GF算法是第一个可以在graph embedding的算法。为了获得embedding,GF通过最小化以下目标函数来分解邻接矩阵:其中
注意:求和是在所有观测到的边上,而不是所有的节点
pair对上。GF是一种可扩展的、近似的求解方案。由于邻接矩阵通常不是半正定的,因此即使embedding的维度选择为GraRep:GrapRep定义节点的转移概率矩阵为其中
最终执行矩阵分解:
其中
embedding,embedding。最终拼接节点所有阶的
embedding得到node embedding。GrapRep的缺陷在于其可扩展性,因为HOPE:HOPE通过最小化node embedding矩阵,coordinate矩阵,如果将
embedding空间中的一组基向量,则embedding空间的坐标,作者尝试了不同的相似性度量,包括
Katz Index, Rooted Page Rank, Common Neighbors, Adamic-Adar。例如当选择Katz Index时,高阶邻近度矩阵为:其中
HOPE可以使用广义奇异值分解可以有效获得node embedding。其它方法:为了对高维数据降维,这里其它一些方法能够执行
graph embedding,包括:主成分分析Principal Component Analysis:PCA、线性判别分析Linear Discrimant Analysis:LDA、IsoMap、多尺度缩放Multidimesional Scaling:MDS、局部特性保持Locality Preserving Properties:LPP、核特征图Kernel Eigenmaps。《Non-negative graph embedding》提出了一个通用框架用于为这些算法产生非负的graph embedding。最近的一些技术聚焦在联合学习网络结构和节点属性信息上:
Augmented Relation Embedding: ARE用基于内容的图像特征来增强网络,并修改graph-Laplacian矩阵来捕获这些信息。Text-associated DeepWalk: TADW对节点的相似度矩阵执行分解,同时用到了文本特征矩阵。Heterogeneous Network Embedding: HNE学习网络每个模态的表示,然后使用线性变换将它们映射到同一个公共空间中。
2.1.2 基于随机游走的方法
随机游走已被用于近似求解图中的很多属性,包括节点中心性
centrality、节点相似性similarity。当只能观察到图的一部分,或者图太大而无法整体计算时,随机游走的方法特别有用。人们已经提出一些使用随机游走的方法来获得
node representation。DeepWalk:DeepWalk通过最大化随机游走过程中节点此外,可以通过基于内积的解码器来从
node embedding中重建边。node2vec:类似于Deepwalk,node2vec通过最大化给定节点在随机游走序列中后续节点出现的概率,从而保留节点之间的高阶邻近度。和
Deepwalk区别在于:node2vec采用了有偏的随机游走,可以在广度优先搜索BFS和深度优先搜索DFS之间平衡。因此,node2vec可以产生比DeepWalk更高质量的embedding。选择正确的balance能够保留社区结构community structure、或者保留节点的结构等价性structural equivalence。Hierarchical Representation Learning for Network: HARP:Deepwalk和node2vec随机初始化node embedding来训练模型,由于它们的目标函数是非凸的,因此这种随机初始化可能卡在局部最优点。Hierarchical Representation Learning for Networks:HARP引入了一种策略,可以通过更好的权重初始化策略来改进方法并避免局部最优。为此,
HARP构建了一种层次结构hierarchy,每一层都是通过将前一层的节点聚合从而对图进行粗化coarsening。然后,HARP生成最粗粒度的图的embedding,并将该embedding初始化更细粒度的图的embedding。就这样一层一层地训练和初始化来传播这些不同层的
embedding,直到获得初始图的embedding。因此,HARP可以和基于随机游走的方法结合使用,从而获得更好的embedding。Walklets:DeepWalk和node2vec通过随机游走来隐式地保留节点之间的高阶邻近度。由于随机性,节点之间的距离在不同随机游走序列中可能不同。而基于分解的方法通过目标函数从而显式保留节点之间的距离。Walklets将显式建模的思想和随机游走思想相结合,该模型通过跳过随机游走序列的DeepWalk中的随机游走策略。其它方法:也有上述方法的几种变体。
GenVector, Discriminative Deep Random Walk:DDRW, Tri-party Deep Network Representation:TriDNR通过联合学习网络结构和节点属性来扩展了随机游走方法。
2.1.3 基于深度学习的方法
越来越多的深度学习方法应用于图分析。由于深度自编码器能够对数据中的非线性结构进行建模,因此被广泛应用于降维。最近
SDNE, DNGR利用深度自编码器这种能力来生成embedding从而捕获图的非线性。Structural Deep Network Embedding: SDNE:SDNE提出使用深度自编码器来保留网络的一阶邻近度和二阶邻近度,它通过共同优化两个邻近度来实现这一目标。SDNE使用高度非线性的函数来获取embedding,模型分为两个部分:- 无监督部分:该部分由一个自编码器组成,目标是为节点找到重构误差最小的
embedding。 - 监督部分:该部分基于拉普拉斯特征图,利用一阶邻近度(即链接信息)作为监督信息来约束节点的
embedding,使得相似的节点在embedding空间中更紧密。
- 无监督部分:该部分由一个自编码器组成,目标是为节点找到重构误差最小的
Deep Neural Networks for Learning Graph Representations:DNGR:DNGR结合了随机游走和深度自编码器。该模型由三部分组成:随机游走、positive pointwise mutual information :PPMI矩阵、堆叠式的降噪自编码器。- 输入图通过随机游走模型生成概率共现矩阵,类似于
HOPE中的相似矩阵。 - 然后将概率共现矩阵转换为
PPMI矩阵。 - 最后将
PPMI矩阵输入到堆叠的降噪自编码器中获得embedding。
输入的
PPMI矩阵可以确保自编码器模型可以捕获更高阶的邻近度。此外,使用堆叠式的降噪自编码器有助于在图中存在噪声的情况下增强模型的鲁棒性,并有助于捕获具体任务所需的底层结构,这些任务包括链接预测、节点分类等。- 输入图通过随机游走模型生成概率共现矩阵,类似于
Graph Convolutional Networks:GCN:上述讨论的基于深度神经网络的方法(SDNE,DNGR等)将每个节点的全局邻域(DNGR中PPMI的一行、SDNE中邻接矩阵的一行)作为输入。对于大型稀疏图,这可能计算代价太大。图卷积神经网络GCN通过在图上定义卷积算子来解决该问题。GCN迭代式地聚合节点邻域embedding,并使用邻域聚合后的emebdding和节点前一轮embedding来更新节点这一轮的embedding。由于GCN仅聚合节点的局部邻域,因此可扩展性更强。经过多次迭代之后,节点学到的embedding能够刻画全局邻域。可以将卷积滤波器大致分为空间滤波器
spatial filter、谱域滤波器spectral filter。空间滤波器直接作用于原始图和邻接矩阵,谱域滤波器作用于图的拉普拉斯矩阵的谱域。Variational Graph Auto-Encoders:VGAE:图的变分自编码器使用GCN作为编码器、使用向量内积作为解码器。输入为图的邻接矩阵,并依赖GCN来学习节点之间的高阶邻近度。实验表明,和非概率non-probabilistic的自编码器相比,使用变分自编码器可以提升性能。
2.1.4 其它方法
LINE:LINE显式地定义了两个目标函数,分别用于保持一阶邻近度和二阶邻近度。一阶邻近度目标函数类似于因子分解
Graph Factorization:GF,因为它们都旨在保持邻接矩阵和成对embedding内积产生的矩阵的之间差异足够小。区别在于GF通过直接最小化二者之间的差异来实现,而LINE通过最小化理论联合概率分布和经验联合概率分布的KL距离来实现。LINE为每对节点定义了两个联合概率分布,其中理论联合概率分布采用embedding定义为:经验联合概率分布使用邻接矩阵定义为:
因此一阶邻近度目标函数为:
类似地,
LINE定义了二阶邻近度目标函数:
.
2.1.5 讨论
我们可以将
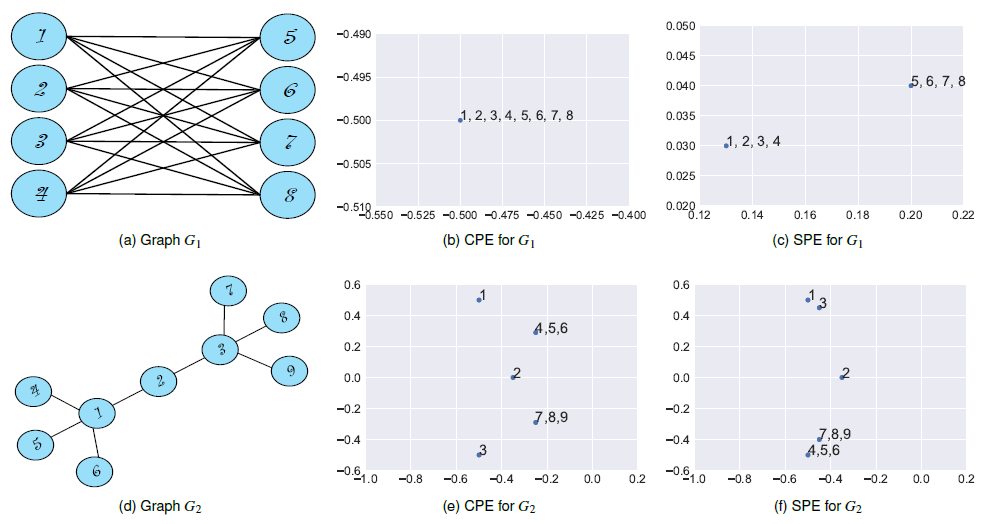
embeddign解释为描述图数据的representation,因此它可以深入了解图的属性。我们以下图为例,考虑一个全连接的二部图
- 试图保持相连节点的
embedding距离紧凑的embedding算法(Community Preserving Embedding:CPE)无法捕获图结构,如下图(b)所示。 - 试图嵌入结构相等的
structurally-equivalent节点的embedding距离紧凑的embedding算法(Structural-equivalence Preserving Embedding:SPE)效果很好,如下图(c)所示。
类似地,考虑将两个星形结构通过一个
hub节点相连的图1,3是结构等价的,因此在下图(f)中它们的embedding相距很近、在下图(e)中它们相距很远。因此,可以根据
embedding算法解释图属性的能力将这些算法分类:- 基于因子分解的方法无法学到任何可解释性,如解释网络的连接性
connectivity。另外,除非显式地在目标函数中包含结构对等性structural equivalence,否则基于因子分解的方法也无法学习结构对等性。 - 基于随机游走的方法中,可以通过修改随机游走参数在一定程度上控制
embedding方法学到的连接性和结构性的mixture。 - 在基于深度学习的方法中,提供足够的参数则它们可以学到连接性和结构性的
mixture。例如,下图(c)中给出了SDNE学到的针对完全二部图complete bipartite graph的node embedding。
- 试图保持相连节点的
2.2 应用
作为图的
representation,embedding可以应用于各种下游任务,包括:网络压缩network compression、可视化visualization、聚类clustering、链接预测link prediction、节点分类node classification。网络压缩:给定图
aggregation based的方法来压缩图。这方面工作的主要思路是利用图的链接结构link structure来分组节点和边。《Graph summarization with bounded error》利用信息论中的Minimum Description Length: MDL将图summarize为一个graph summary和edge correction。类似于这些
representation,graph embedding也可以解释为图的summarization。《Structural deep network embedding》和《Asymmetric transitivity preserving graph embedding》通过从embedding中重建原始图并评估重建误差来明确地测试这一假设。他们表明,每个节点的低维representation(在100的数量级)有助于图的重建。可视化:由于
embedding是图在向量空间的表示,因此可以使用降维技术,如主成分分析PCA、t-SNE等技术来对图进行可视化。如DeepWalk, LINE, SDNE的原始论文中都展示了node embedding的可视化。聚类:聚类分为两类,即基于结构的聚类、基于属性的聚类。
基于结构的聚类:它又分为两类,即基于社区
community-based的聚类、基于结构等效structurally equivalent based的聚类。- 基于社区的聚类旨在找到稠密的子图,其中子图内部具有大量的簇内边
intra-cluster edge、子图之间具有少量的簇间边inter-cluster edge。 - 基于结构等效的聚类相反,其目标是识别具有相似角色的节点(如
hub节点、异常点)。
- 基于社区的聚类旨在找到稠密的子图,其中子图内部具有大量的簇内边
基于属性的聚类:基于属性的聚类除了观测到的链接之外,还利用节点属性来聚类。
《A spectral clustering approach to finding communities in graphs》在embedding上使用k-means对节点进行聚类,并将在Wordnet和NCAA数据集上获得的聚类可视化,验证了所获得的聚类有直观的解释。链接预测:网络是根据观测到的实体之间的交互而构建的,这些交互可能是不完整
incomplete的或者不准确inaccurate的。链接预测的目标是识别虚假的交互并预测缺失的交互。人们综述了链接预测领域的最新进展,并将算法分为:基于相似性(局部相似性和全局相似性)的方法、基于最大似然的方法、概率性的方法。embedding可以显式或隐式地捕获网络的固有动态inherent dynamics,从而可以执行链接预测。实验表明:通过使用embedding执行链接预测要比基于传统相似度的链接预测方法更准确。节点分类:通常由于各种原因,在网络中只有部分节点被标记,大部分节点的标记都是未知的。节点分类任务是通过网络结构和已标记节点来预测这些缺失的标记。
节点分类方法大概分为两类,即基于特征提取的方法和基于随机游走的方法:
- 基于特征提取的方法根据节点邻域和局部网络统计信息生成节点的特征,然后使用逻辑回归或朴素贝叶斯等分类器来预测标签。
- 基于随机游走的方法通过随机游走来传播标签。
embedding可以解释为基于网络结构自动抽取的特征,因此属于第一类。实验表明:通过使用embedding的节点分类可以更准确地预测缺失的标签。
2.3 实验
实验配置:
32 core 2.6 GHz的CPU、128 GB RAM、Nvidia Tesla K40C的单机,Ubuntu 14.04.4 LTS操作系统。数据集:我们使用一个人工合成的数据集
SYN-SBM以及6个真实数据集,这些数据集的统计信息见下表(No. of labels表示标签类别数) 。SYB-SNM:使用Stochastic Block Model方法人工创建的图,其中包括1024个节点、3个社区。我们设置in-block概率为0.1以及cross-block概率为0.01。由于我们知道这个图中的社区结构community structure,我们用它来可视化通过各种方法学到的emebdding。KARATE:Zachary的karate network是一个著名的大学空手道俱乐部的社交网络。它在社交网络分析中被广泛研究。BLOGCATALOG:这是一个由BlogCatalog网站上博主的社交关系组成的网络。标签代表了博主的兴趣,这是通过博主提供的meta data推断出的。YOUTUBE:这是一个Youtube用户的社交网络。标签代表了喜欢的视频类型。HEP-TH:原始数据集包含1993年1月至2003年4月期间的High Energy Physics Theory的论文摘要。我们为这一时期发表的论文建立了一个合作网络collaboration network。ASTRO-PH:这是一个由1993年1月至2003年4月期间提交到arXiv的论文的作者组成的合作网络。PPI:这是一个人类蛋白质之间的生物交互网络biological interaction network。

评估指标:
对于图重构和链接预测任务,我们使用
Precision at K:Pr@K、Mean Average Precision:MAP为评估指标。Pr@K表示对于节点top K节点中和节点AP@K给出节点Pr@k均值,即:MAP@K进一步评估了所有节点的Pr@k值。
对于节点分类任务,我们使用
micro-F1和macro-F1指标。
2.3.1 Graph Reconstruction
我们使用
graph embedding重建节点的邻近度,然后根据节点邻近度对节点进行排序,并计算top K个预测中实际链接的占比作为重构精度reconstruction precision。由于对所有节点pair对计算的代价很大 (复杂度为1024个节点进行评估。为缓解采样随机性对评估结果的影响,我们随机采样并评估五次,并上报评估结果的均值和方差。为获得每种
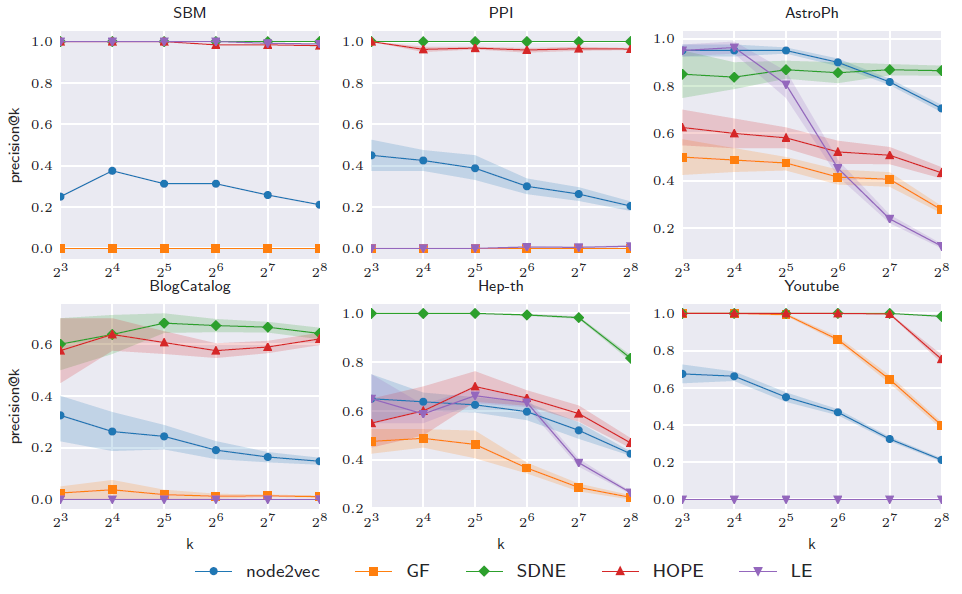
embedding方法的最佳超参数,我们进行超参数搜索并评估每种超参数的平均MAP(评估时采样五次)。最后我们使用最佳超参数来重新训练模型并报告5次采样的平均结果。下图给出了不同方法
128维embedding获得的重构精度。结论:虽然
embedding性能与数据集有关,但是总体而言保留高阶邻近度的embedding方法要更好。拉普拉斯特征图
LE在SBM上的出色表现归因于数据集中缺乏高阶结构。SDNE在所有数据集上均表现良好,这归因于它从网络中学习复杂结构的能力。虽然
SDNE效果好,但是其计算复杂度为node2vec学到的embedding具有较低的重构精度,这可能是由于高度非线性的降维导致了非线性的流形。理论上
node2vec的高度非线性会导致更好的表达能力,这里node2vec结果交叉表明出现了严重的过拟合。HOPE学习线性的embedding但是保留了高阶邻近度,它可以很好地重建图,无需任何额外参数。
进一步地,我们考察
embedding维度对于重建误差的影响。结论:- 除了少数几个例外,随着
embedding维度的增加,MAP值也增加。这是很直观地,因为更高的embedding维度能存储更多信息。 SDNE可以将图以很高的精度嵌入到16维向量空间中,尽管需要解码器及其参数来获得这种精度。
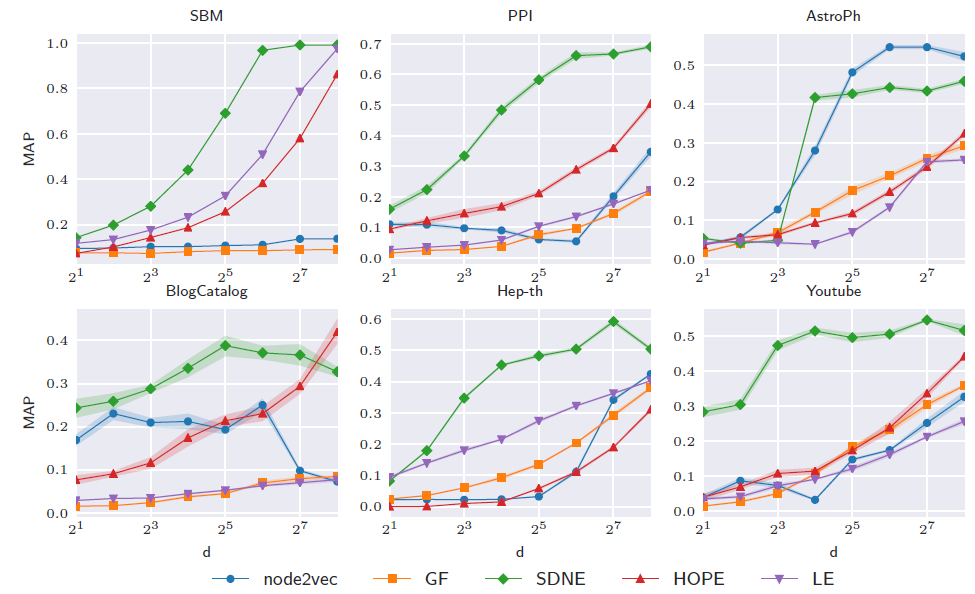
- 除了少数几个例外,随着
2.3.2 Visualization
由于
embedding是图中节点的低维向量表示,因此我们可以利用embedding来可视化节点从而了解网络拓扑结构。由于不同embedding方法保留了网络中的不同结构,因此它们的能力以及对节点可视化的解释也有所不同。例如,设置广度优先
BFS超参数的node2vec学到的embedding倾向于将结构等效的节点聚集在一起;直接保留节点之间k-hop距离的方法(GF,LE,LLE的HOPE,SDNE的我们对
SBM, Karate数据集使用不同方法生成128维的节点embedding,并通过t-SNE将这些embedding可视化到2D空间。SBM数据集的可视化结果如下图所示。由于我们已知底层社区结构,因此我们使用社区标签为节点着色,不同颜色代表不同社区。结论:尽管数据集结构良好,所有
embedding都一定程度上捕获了社区结构,但是由于HOPE,SDNE保留了高阶邻近性,因此相比于LE,GF,LLE,HOPE,SDNE可视化的不同社区的间隔更清晰。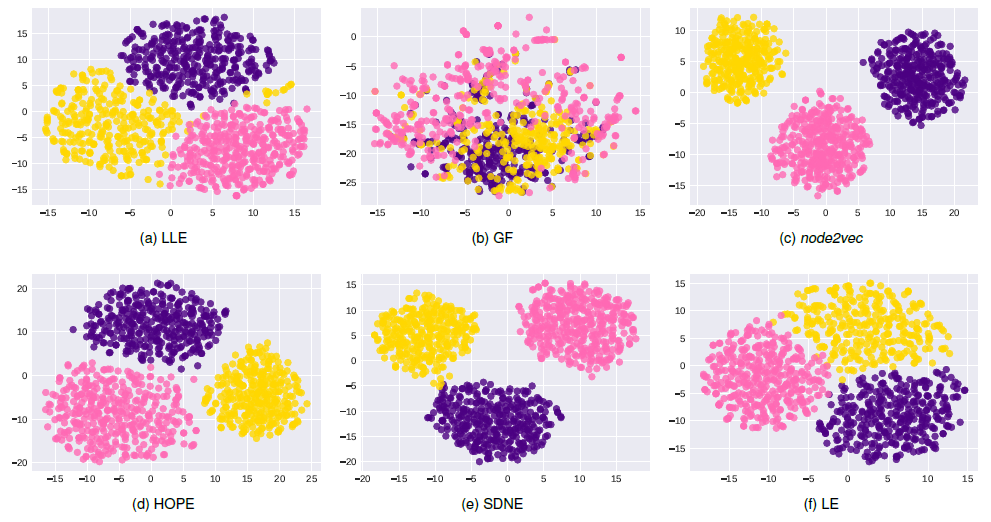
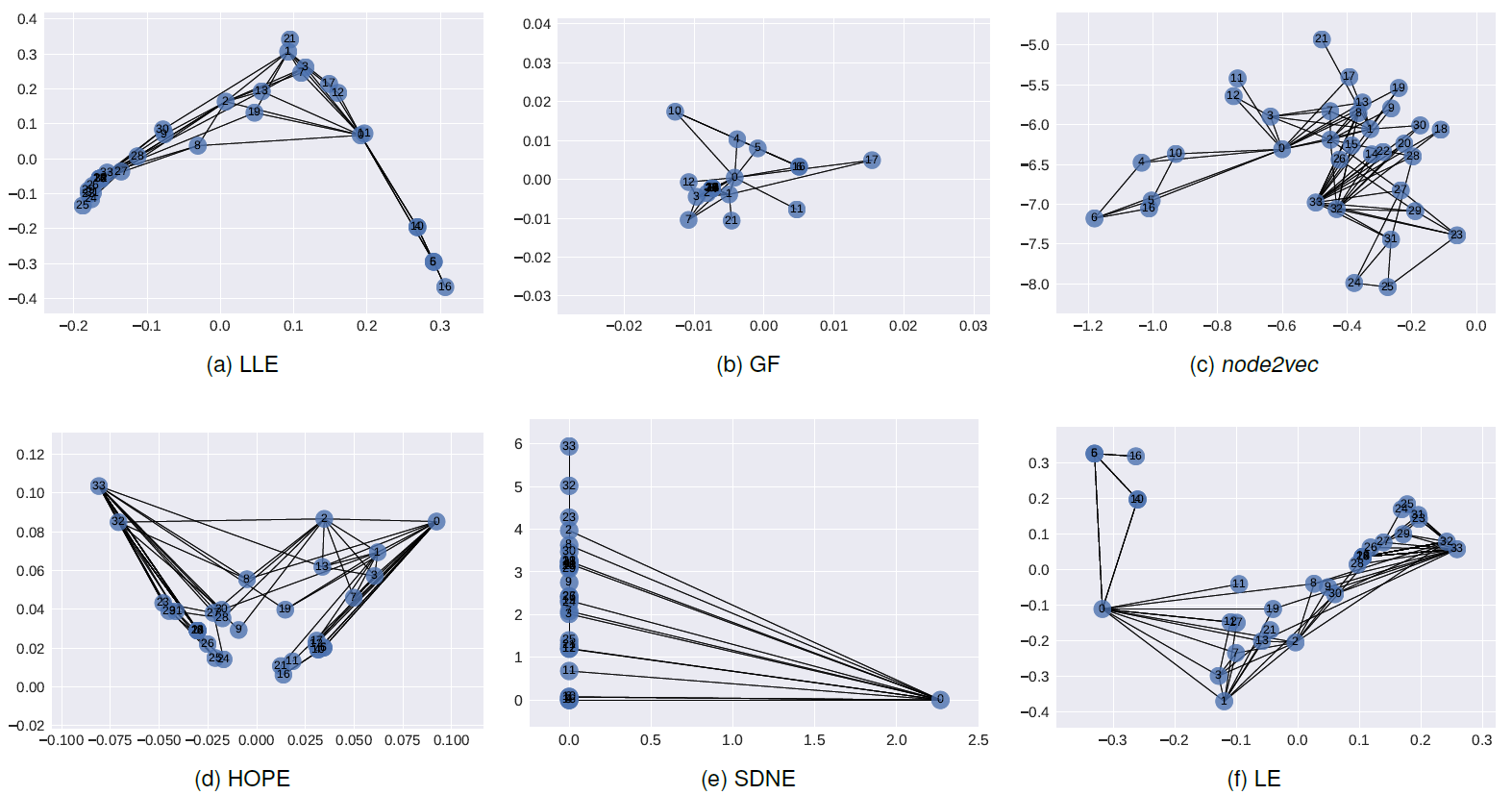
Karate可视化结果如下图所示。结论:LLE,LE试图保留图的社区结构,并将较高intra-cluster边的节点聚类在一起。GF将社区结构紧密地嵌在一起,并使社区内节点远离其它节点。在
HOPE中,我们观察到编号为16,21的节点,它们在原始图的Katz相似度非常低(0.0006),并在embedding空间中相距最远。node2vec,SDNE同时保留了节点社区结构和节点结构角色。- 节点
32,33是degree很高的hub节点,并且是它们各自社区的中心节点。它们被嵌入在一起,并远离其它低degree的节点,并且更靠近各自社区的节点。 - 节点
0充当社区之间的bridge,因此SDNE将节点0嵌入到远离其它节点。注意,与其它方法不同,这并不意味着节点0和其它节点断开连接,而是SDNE将节点0标识为独有的节点类型。
虽然尚未研究过深度自编码器识别网络中重要节点的能力,但是鉴于这一发现我们认为这一方向是有希望的。
- 节点
2.3.3 Link Prediction
graph embedding另一个重要应用是预测图中未观测的连接。一个好的network representation应该能够很好地捕获图的固有结构,从而预测可能的、但是未观测的链接。为测试链接预测任务中不同
embedding方法的性能,对于每个数据集我们随机隐藏20%的边,并利用剩余80%边来学习embedding。然后根据学到的embedding来预测训练数据中未观测到的、最有可能的边。和图重构任务一样,我们随机采样
1024个节点的随机子图,并针对子图中的隐藏边来预测边是否存在。为缓解采样随机性对评估结果的影响,我们随机采样并评估五次,并上报评估结果的均值和方差。直接在原始的图上进行评估需要评估
node pair,这对于大一点的图而言计算量太大。我们对每个
emebdding方法执行超参数搜索,并使用最佳超参数重新在80%:20%拆分得到的训练集上重新训练模型。下图给出了不同方法的
128维embedding的效果。结论:- 不同方法的性能和数据集高度相关。
node2vec在BlogCatalog数据集上表现良好,但是在其它数据集上表现不佳(垫底)。HOPE在所有数据集上均表现良好,这意味着保留高阶邻近性有利于预测未观测到的链接。SDNE优于所有其它方法,但是在PPI数据集上除外。在PPI数据集上,随着embedding尺寸增加到8以上,SDNE性能急剧下降。
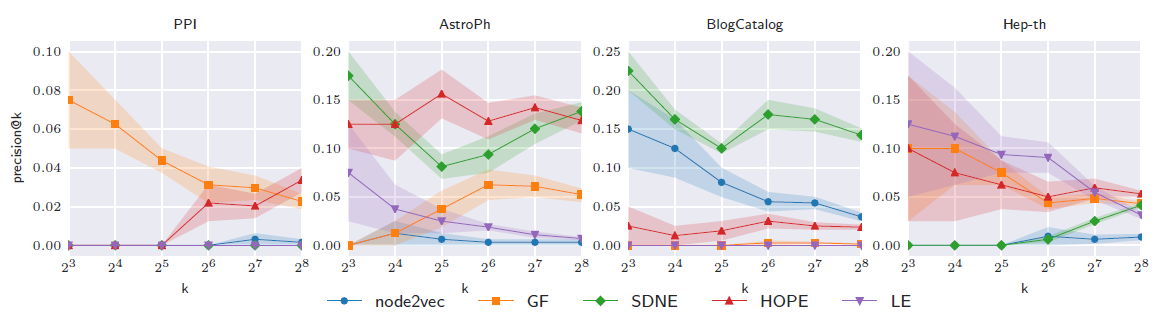
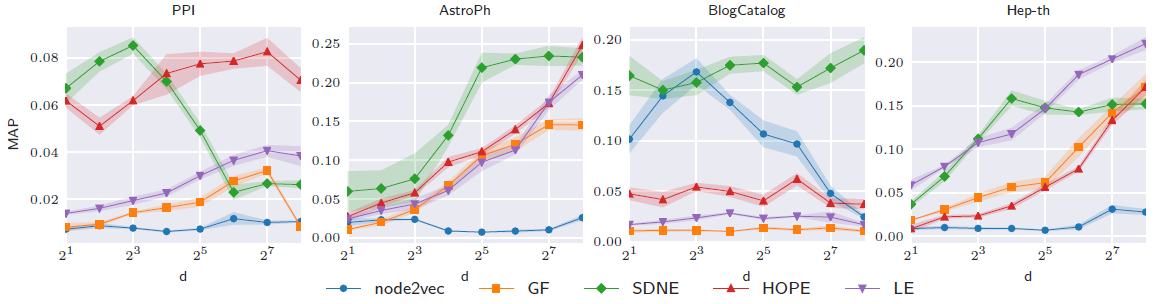
进一步地,我们考察
embedding维度对于链接预测性能的影响。结论:在
PPI数据集上,随着embedding尺寸增加到8以上,SDNE性能急剧下降。在
PPI, BlogCatalog数据集中,与图重构任务不同,随着embedding维度的增加链接预测性能不会得到改善。这可能是因为具有更多参数的模型在观测到的链接上过拟合,并且无法预测到未观测的链接。即使在相同数据集上,方法性能也取决于
embedding维度。例如:- 在
PPI数据集上,HOPE在高维度embedding上的效果超越了其它方法。 - 在所有数据集上,
SNDE在低维度embedding上的效果超越了其它方法。
我们最终要评估的是在各模型的最佳
embedding上,每个模型的效果。- 在
2.3.4 Node Classification
良好的
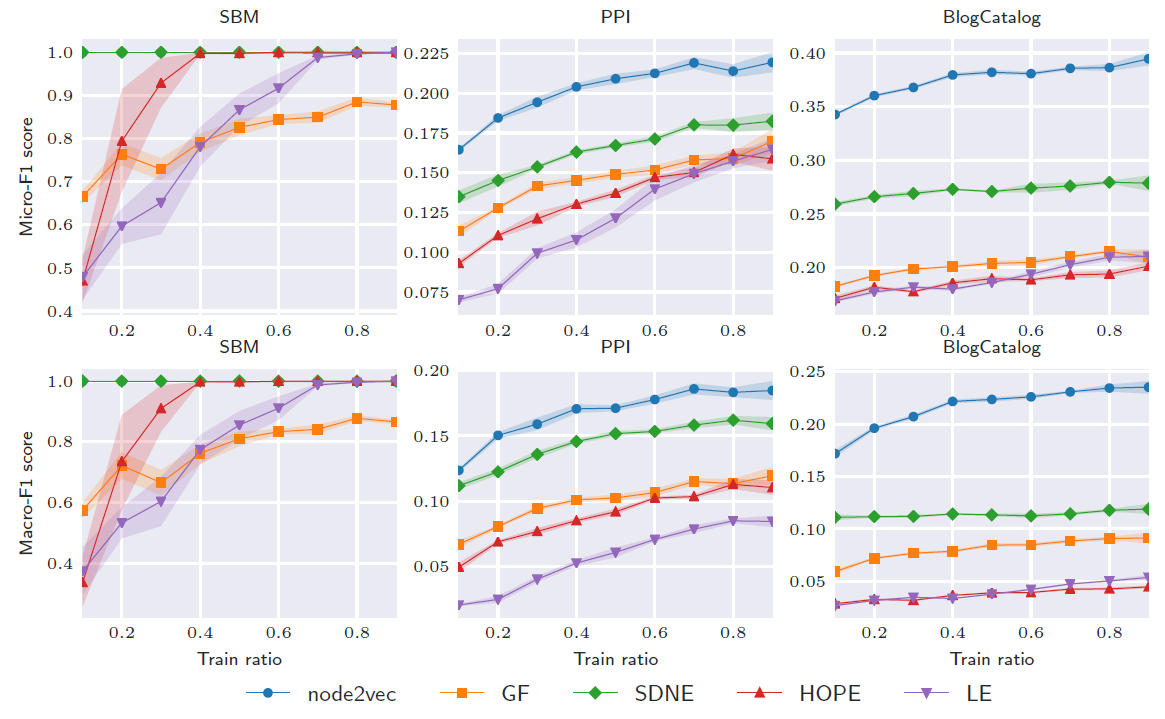
graph embedding可以捕获网络结构,这对于节点分类很有用。通过使用生成的embedding作为特征对节点进行分类,我们比较了不同embedding方法的有效性。其中分类算法为LIBLINEAR库提供的one-vs-one逻辑回归模型。对于每个数据集,在分类期间我们随机抽取
10% ~ 90%的标记节点作为训练集,剩余标记节点作为测试集。我们随机执行5次拆分并报告测试集上评估结果的均值。下图给出了节点分类实验的结果。结论:
node2vec在大多数节点分类任务上超越了其它方法。如前所述,node2vec保留了节点之间的同质性homophily,以及结构对等性structural equivalence。这表明这在节点分类中可能很有用。例如在
BlogCatalog中,用户之间可能具有相似的兴趣,但是网络是通过社交关系而不是兴趣关系而建立的。在
SBM数据集中,其它方法性能超越了node2vec。这是因为SBM数据集的标签反映了社区,而节点之间没有结构上的对等性。
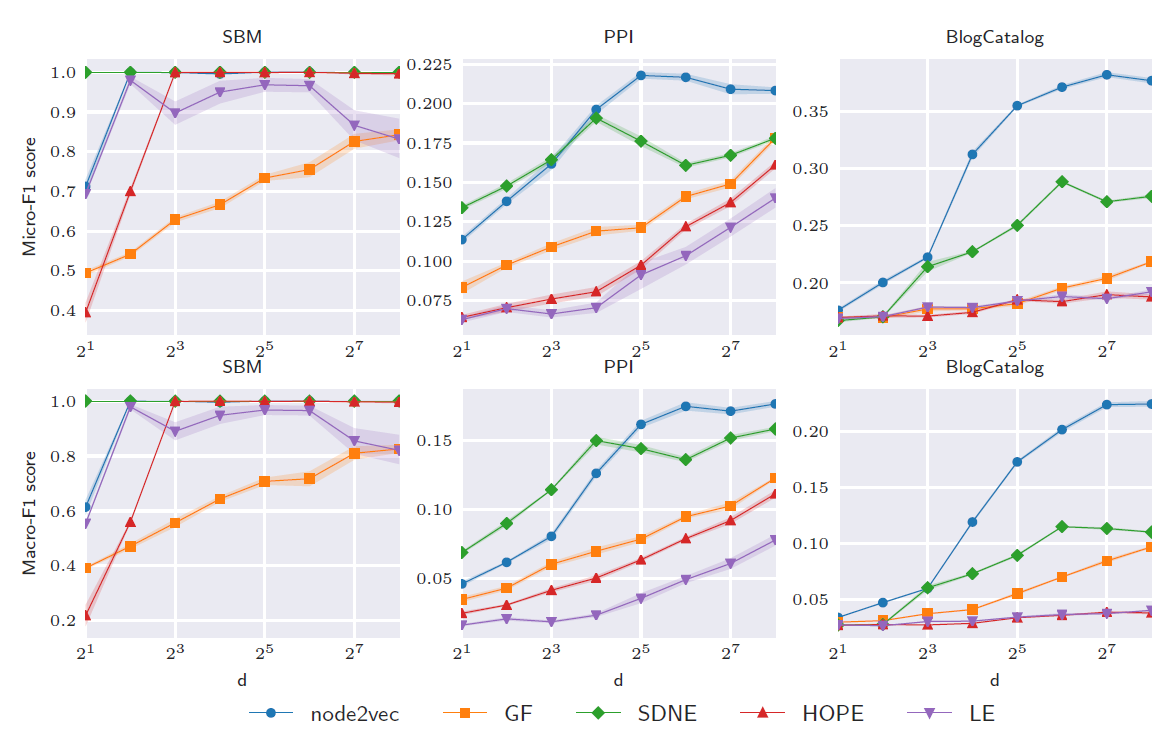
进一步地,我们考察
embedding维度对于节点分类性能的影响。其中训练集、测试集拆分比例为50%:50%。结论:- 和链接预测任务一样,节点分类任务性能在某些大小的维度之后达到饱和或者下降。这可能是模型对于训练数据过拟合。
- 由于
SBM是非常结构化的社区,因此即使是8维的embedding也可以达到很好的效果。 - 在
PPI,BlogCatalog数据集,node2vec需要128维的embedding才能达到最佳性能。
2.3.5 参数敏感性
这里我们要解决三个问题:
embedding方法对于超参数鲁棒性如何?- 最佳超参数是否取决于
embedding被使用的下游任务? - 超参数的性能差异对数据集提供了什么洞察?
我们通过分析每个
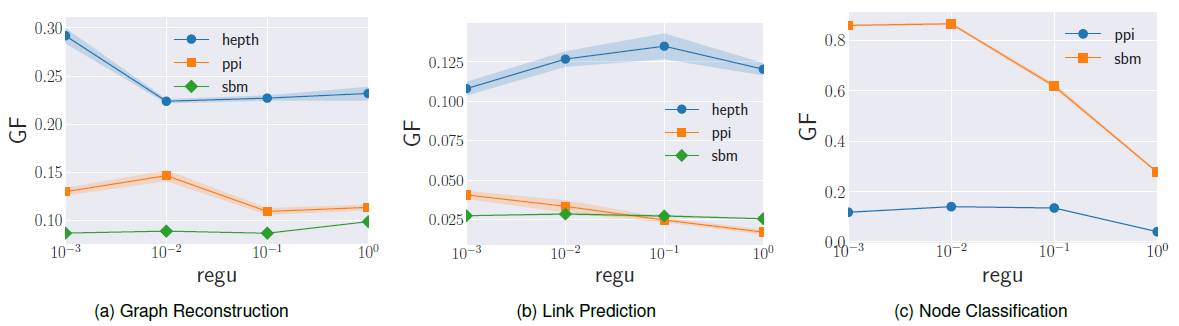
embedding方法上不同超参数的性能来回答这些问题。我们评估了SBM, PPI, Hep-th数据集。由于图拉普拉斯没有超参数,因此不在我们分析范围之内。Graph Factorization:GF:GF模型的目标函数包含了权重正则化项,该项带有一个超参数:正则化系数。正则化系数可以控制embedding的泛化能力:- 较低的正则化系数有助于更好地重建图,但是可能会对观察到的图过拟合,从而导致较差的预测性能。
- 较高的正则化系数可能对数据欠拟合,因此在所有任务上效果都较差。
我们在下图的实验结果中观察到这种效果。可以看到:
- 随着正则化系数的提高,预测任务(链接预测、节点分类)的性能先达到峰值,然后开始恶化。
- 随着正则化系数的提高,图重建任务的性能恶化。
- 不同数据集上性能变化很大,因此需要为不同数据集仔细调整正则化系数。
HOPE:HOPE将节点相似度矩阵分解从而得到node embedding,因此超参数取决于获得相似度矩阵的方法。由于我们在实验中使用Katz指数来计算相似度,因此我们评估了衰减因子- 对于具有紧密联系的、社区结构良好的图,较高的
embedding空间中相近的位置。 - 对于弱社区结构
weak community的图,重要的是捕获高阶距离,因此较高的embedding。
下图的实验结果验证了我们的假设。结论:
- 由于人工合成数据集
SBM由紧密的社区组成,因此增加 - 在
PPI, HEP-th数据集中,随着PPI, Hep-th数据集包含高阶的链接。 - 在所有数据集中,最佳最佳
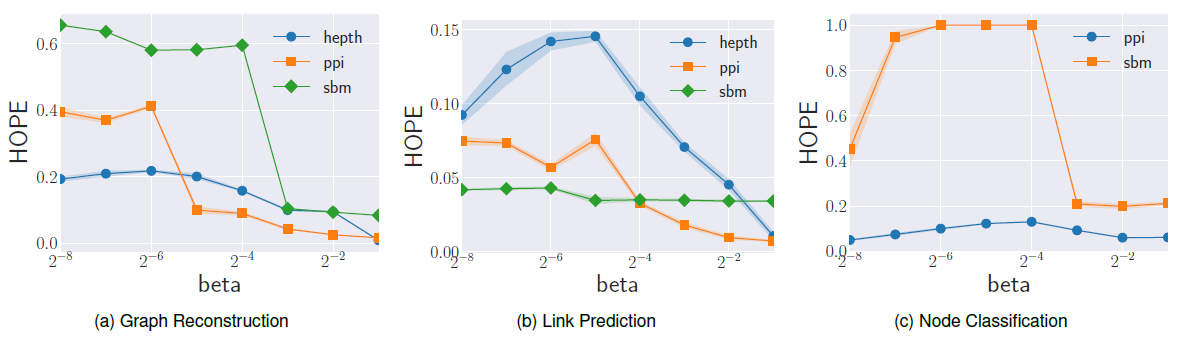
- 对于具有紧密联系的、社区结构良好的图,较高的
SDNE:SDNE使用耦合的深度自编码器来嵌入图,它利用超参数下图给出了不同参数值的实验结果。结论:
- 链接预测性能随
Hep-th数据集,最佳MAP提升超过3倍;对于PPI数据集,最佳MAP提升大约2倍。 - 节点分类性能受
- 总体而言,最佳性能在
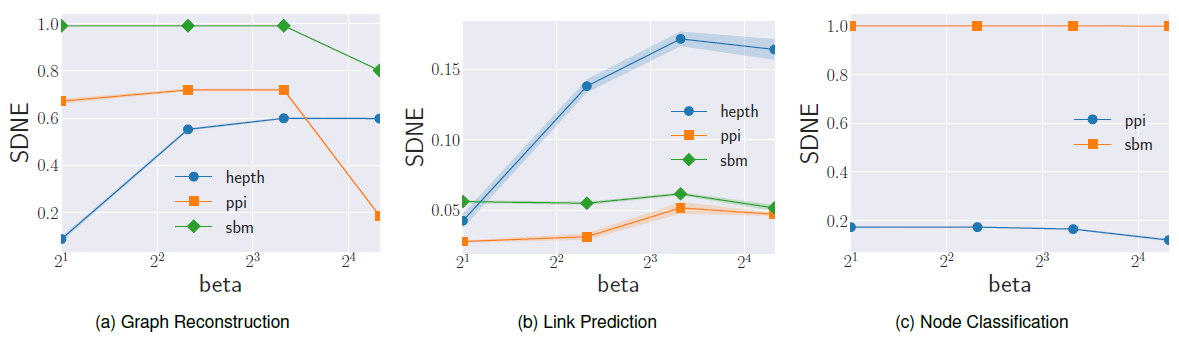
- 链接预测性能随
node2vec在图上执行有偏得随机游走,并将共现的节点嵌入到embedding空间中靠近得位置。在该方法得各个超参数中,我们分析超参数10,随机游走序列长度为80)。超参数
BFS和DFS之间插值,从而反应结点的不同类型的相似性。返回参数
Return Parameter一个较大的值
这种策略鼓励适当的进行探索新结点,并避免采样过程中的冗余
2-hop(即:经过两步转移又回到了结点本身)。一个较小的值
这种策略使得随机游走序列尽可能地留在源点
内外参数
In-out parameter- 如果
BFS的行为。 - 如果
DFS的行为。
但是这种策略和
BFS、DFS本质上是不同的:我们的策略采样的结点与源点的距离并不是严格相等的(BFS)、也不是严格递增的 (DFS)。另外我们的策略易于预处理,且采样效率很高。- 如果

我们实验不同
PPI, Hep-th数据集得效果如下图所示。结论:- 较低值
- 较高的
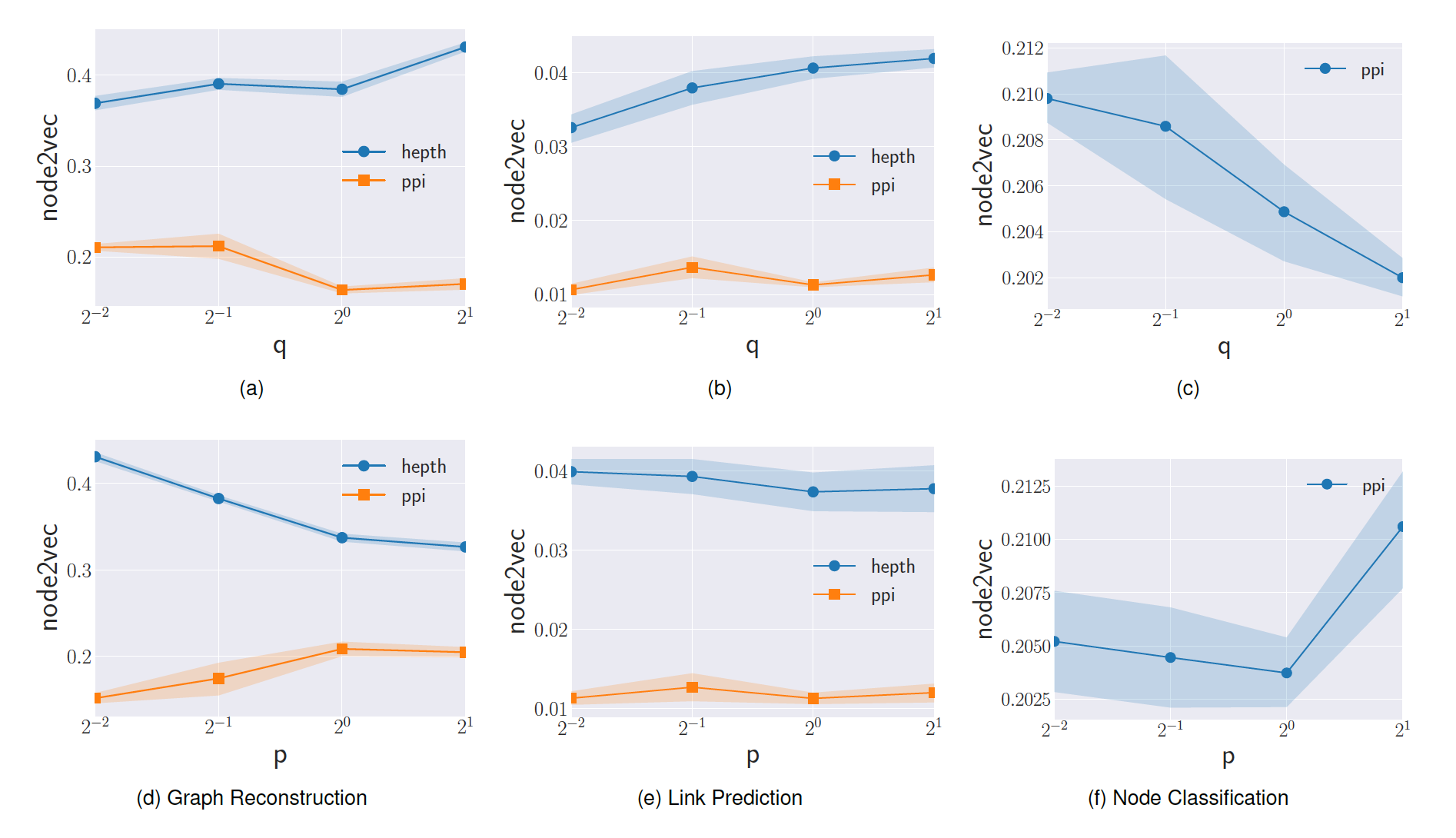
我们实验不同
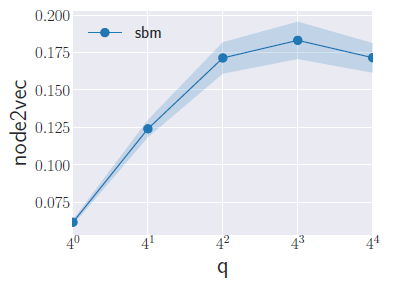
SBM的效果。结论:- 随着
MAP性能得到提升,直到最佳性能。 - 由于
SBM具有紧密联系的、结构良好的社区,因此最优
2.4 GEM
我们发布了一个开源的
Python库:Graph Embedding Methods: GEM(https://github.com/palash1992/GEM),它为这里介绍的所有方法的实现及其评估指标提供了一个统一的接口。该库同时支持加权图和无权图。GEM的hierarchical design和模块化实现有助于用户在新的数据集上测试所实现的方法,并作为一个platform来轻松开发新的方法。GEM提供了Locally Linear Embedding、Laplacian Eigenmaps、Graph Factorization、HOPE、SDNE、以及node2vec的实现。对于node2vec,我们使用作者提供的C++实现并提供一个Python接口。此外,
GEM提供了一个接口来在上述四个任务上评估学到的embedding。该接口很灵活,支持多种边重建指标,包括余弦相似度、欧氏距离、以及decoder based指标。对于多标签的节点分类,该库使用one-vs-rest逻辑回归分类器,并支持使用其他临时ad hoc的分类器。
2.5 未来方向
我们认为在图嵌入领域有三个有前途的研究方向:
探索非线性模型:如综述所示,通用的非线性模型(如,基于深度学习的模型)在捕获图的固有动态
inherent dynamics方面显示出巨大的前景。这些非线性模型有能力近似任意函数,但是缺点是可解释性有限。进一步研究这些模型所学到的
embedding的可解释性,可能是非常有用的。研究网络的演变
evolution:利用embedding来研究图的演变是一个新的研究领域,需要进一步探索。生成具有真实世界特征的人工合成网络:生成人工合成网络一直是一个流行的研究领域,主要是为了便于模拟。真实
graph的低维向量representation可以帮助理解图结构,因此对生成具有真实世界特征的人工合成图很有帮助。
三、Representation Learning on Graphs[2017]
图机器学习的核心问题是:找到一种将图结构信息结合到机器学习模型中的方法。例如:
- 在社交网络的链接预测任务中,可能需要对节点之间的成对属性进行编码,如关系强度
relationship strength或者共同好友数量。 - 在节点分类任务中,可能需要包含节点在图中全局位置相关的信息,或者节点局部邻域结构相关的信息。
从机器学习角度来看,面临的挑战是:没有直接的方法可以将有关图结构的高维非欧信息编码为特征向量。为了从图上提取图结构信息,传统的机器学习方法通常依赖于图的统计信息(如
degree等)、核函数、或者精心设计的用于衡量图局部邻域结构的特征。但是,这些方法都有局限性:- 这些人工设计的特征不灵活,无法在学习过程中自适应地调整。
- 人工设计特征可能是一个耗时耗力的过程。
最近涌现出很多方法来寻求学习图的有效
representation从而能够编码有关图结构信息,这些方法背后的思想是:学习一个映射,该映射将节点或者子图或者整个图映射到低维向量空间emebdding空间中的几何关系能够反映原始图结构。一旦得到这样的映射,就可以将学到的embedding用作下游机器学习任务的特征输入。表示学习
representation learning方法和之前工作的主要区别在于如何处理图结构表示的问题。- 之前工作将该问题视为预处理步骤,通过人工设计的统计信息来提取图结构信息。
representation learning将该问题视为机器学习任务本身,使用数据驱动的方法来学习对图结构进行编码的emebdding。
- 在社交网络的链接预测任务中,可能需要对节点之间的成对属性进行编码,如关系强度
假设
representation learning的输入为无向图representation learning的目标是利用大多数方法仅使用
论文
《Representation Learning on Graphs: Methods and Applications》以综述的形式总结了这些representation learning方法。
3.1 节点 embedding
我们首先讨论节点
embedding,其目的是将节点编码为低维向量,从而包含节点在图中的位置信息以及节点的局部邻域结构。这些低维embedding可以看作是将节点投影到低维潜在空间中,其中潜在空间中节点之间的几何关系对应于原始空间中节点之间的交互(如是否存在边)。下图给出了著名的
Zachary Karate Club社交网络的节点embedding,这些二维的节点embedding捕获了社交网络中隐式的社区结构community structure。下图中,如果两个用户是好友关系,则他们之间存在边。节点根据不同社区community进行着色。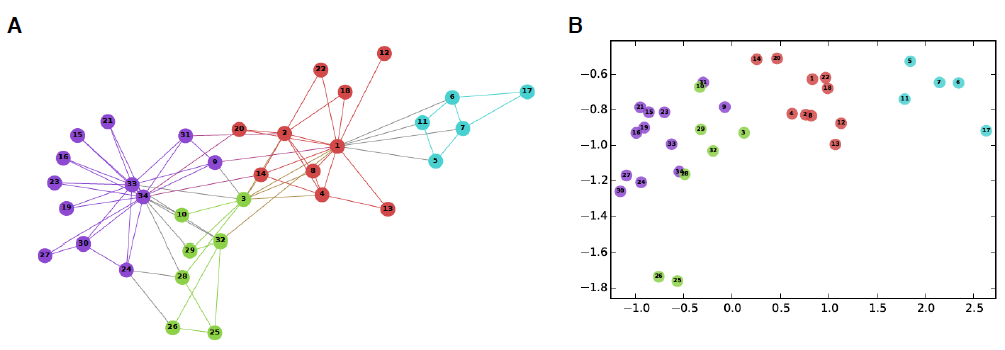
3.1.1 Encoder-Decoder 视角
在讨论各种节点
embedding技术之前,我们首先提出一个统一的encoder-decoder框架,在该框架中统一了各种各样的节点embedding方法。在
encoder-decoder框架中,我们围绕两个关键的映射函数来组织各种方法:- 一个编码器
encoder:它将每个节点映射到一个低维向量。 - 一个解码器
decoder:它从学到的embedding中解码有关图结构的信息。
encoder-decoder思想背后的直觉如下:如果我们可以从encoder的低维的embedding中解码高维的图信息(如,节点在图中的全局位置或节点的局部邻域结构),则原则上这些embedding包含了下游机器学习任务所需的所有信息。encoder是一个函数:embedding向量embedding向量维度。decoder也是一个函数,它接收一组节点embedding,并从这些embedding中解码人工指定的图统计信息。如,decoder可能会根据给定节点的embedding预测节点之间的边,或者预测节点所属的社区。原则上
decoder可以有很多选择,但是绝大多数方法都是采用基础的pairwise decoder:它将一对节点的
embedding映射到一个实数值的节点相似度,从而刻画原始图中两个节点的相似性。
- 一个编码器
encoder-decoder框架整体架构如下图所示。- 首先
encoder根据节点在图中的位置、节点局部邻域结构信息、节点属性信息,从而将节点 - 然后
decoder从低维向量
通过联合优化
encoder和decoder,系统学会了将图结构有关的信息压缩到低维embedding空间中。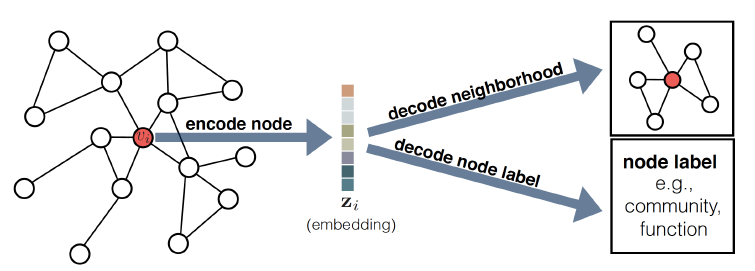
- 首先
我们将
pairwide decodr应用到一对embeddingencoder, decoder,从而最大程度地减少重构误差,使得:即,我们要优化
encoder-decoder模型,以便可以从节点的低维embedding其中
- 可以定义
- 也可以根据图
在实践中,大多数方法通过最小化经验损失
其中:
pair对组成。
- 可以定义
一旦我们优化了
encoder-decoder,就可以使用训练好的encdoer为节点生成embedding,然后将其作为下游机器学习任务的特征输入。例如,可以将学到的embedding作为逻辑回归分类器的输入,从而预测节点所属的社区。通过这种
encoder-decoder视角,我们沿着以下四个部分对各种节点embedding方法进行讨论:- 成对节点相似性函数
pairwise similarity function encoder函数ENC:用于生成节点embedding。该函数包含大量可训练的参数,这些参数在训练期间进行优化。decoder函数DEC:用于从生成的节点embedding中重建pairwise节点相似性。该函数通常不包含可训练的参数。- 损失函数
正如我们即将讨论的,各种节点
embedding方法之间的主要区别在于如何定义这四个部分。- 成对节点相似性函数
我们讨论的所有方法都涉及通过最小化损失函数来优化
encoder的参数。大多数情况下我们使用随机梯度下降算法来优化,尽管某些算法确实允许通过矩阵分解来获得闭式解。注意,这里我们关注的重点并不是优化算法,而是不同
embedding方法之间的更高层次的差异,而与底层优化方法的细节无关。
3.1.2 浅层 embedding
大多数节点
embedding方法都依赖于我们所说的浅层嵌入shallow embedding。对于这些浅层embedding方法,将节点映射到embedding向量的encoder函数仅仅是一个embedding lookup:其中:
embedding向量的embedding矩阵,第embedding向量。one-hot向量。
浅层
embedding方法的可训练参数仅仅是embedding矩阵浅层
embedding方法在很大程度上受到降维dimensionality reduction和多维缩放multi-dimensional scaling中的经典矩阵分解技术的启发。但是,我们在encoder-decoder框架中重新解释了它们。下表总结了
encoder-decoder框架中的一些著名的浅层embedding方法,我们根据几个方面来区分它们:decoder函数、图相似性度量、损失函数。总体而言它们分为基于矩阵分解的方法
Matrix Factorization、基于随机游走的方法Random Walk。注意,在基于随机游走的方法中,decoder和similarity函数都是非对称的,其中相似度函数注意,相似度函数

a. Matrix Factorization
早期的节点
embedding方法主要集中于矩阵分解上,这直接受到经典的降维技术的启发。拉普拉斯特征图
Laplacian Eigenmaps:最早的、最著名的基于矩阵分解的方法是拉普拉斯特征图Laplacian Eigenmaps:LE方法。我们可以将拉普拉斯特征图视为一种encoder-decoder框架内的浅层embedding方法,其中decoder定义为:损失函数根据节点
pair对的相似性进行加权:内积方法
Inner-product method:在拉普拉斯特征图之后,有大量基于pairwise的、内积式decoder的embedding方法,其中decoder定义为:即两个节点之间关系的强度
strength和它们embedding的内积成正比。图因子分解
Graph Factorization:GF、GraRep、HOPE都完全属于此类。这三种方法都使用内积式decoder,都采用均方误差mean squared error:MSE损失函数:它们之间的主要区别在于采用的节点相似性函数不同,即如何定义
GF算法直接基于邻接矩阵来定义节点相似度,即GraRep算法考虑邻接矩阵的各种幂次从而捕获高阶节点相似性,如HOPE算法支持通用的相似性度量,如基于Jaccard指标的邻域交集。
这些不同的相似性函数在建模一阶邻近性(如
本节中我们将这些方法统称为基于矩阵分解的方法,因为大致上它们优化了以下形式的损失函数:
其中:
embedding矩阵。
直观上讲,这些方法的目标是为每个节点学习
embedding,使得学到的embedding向量之间的内积近似于某个给定的节点相似性度量。
b. Random Walk
最近一些比较成功的浅层
embedding方法都是基于随机游走统计信息来学习节点embedding。它们的关键创新在于:优化节点embedding,使得随机游走序列上共现的节点具有相似的embedding,如下图所示。因此,这些随机游走方法并没有像基于矩阵分解方法那样使用确定性的节点相似性度量,而是采用一种灵活的、随机的节点相似性度量,从而在很多场景下都具有出色的性能。
基于随机游走的方法从每个节点
embedding向量,使得两个embedding向量
DeepWalk & node2vec:与上述矩阵分解方法一样,DeepWalk和node2vec依赖浅层embedding并使用内积式decoder。但是,这些方法不是对确定性的节点相似性度量进行解码,而是优化embedding从而对随机游走的统计信息进行编码。这些方法背后的基本思想是学习
embedding,使得:其中:
注意:不像基于矩阵分解方法那样使用确定性的、对称的节点相似性度量(如边的强度
进一步地,
DeepWalk和node2vec最小化以下交叉熵损失函数:其中训练集
由于计算
DeepWalk和node2vec使用不同的优化和近似来计算Softmax和负采样技术。node2vec和DeepWalk之间的关键区别在于:node2vec允许定义灵活的随机游走策略,而DeepWalk只能使用简单的无偏随机游走。具体而言,node2vec引入两个随机游走超参数bias。假设随机游走当前节点为返回参数
Return Parameter一个较大的值
这种策略鼓励适当的进行探索新结点,并避免采样过程中的冗余
2-hop(即:经过两步转移又回到了结点本身)。一个较小的值
这种策略使得随机游走序列尽可能地留在源点
内外参数
In-out parameter- 如果
BFS的行为。 - 如果
DFS的行为。

- 如果
通过引入这些超参数,
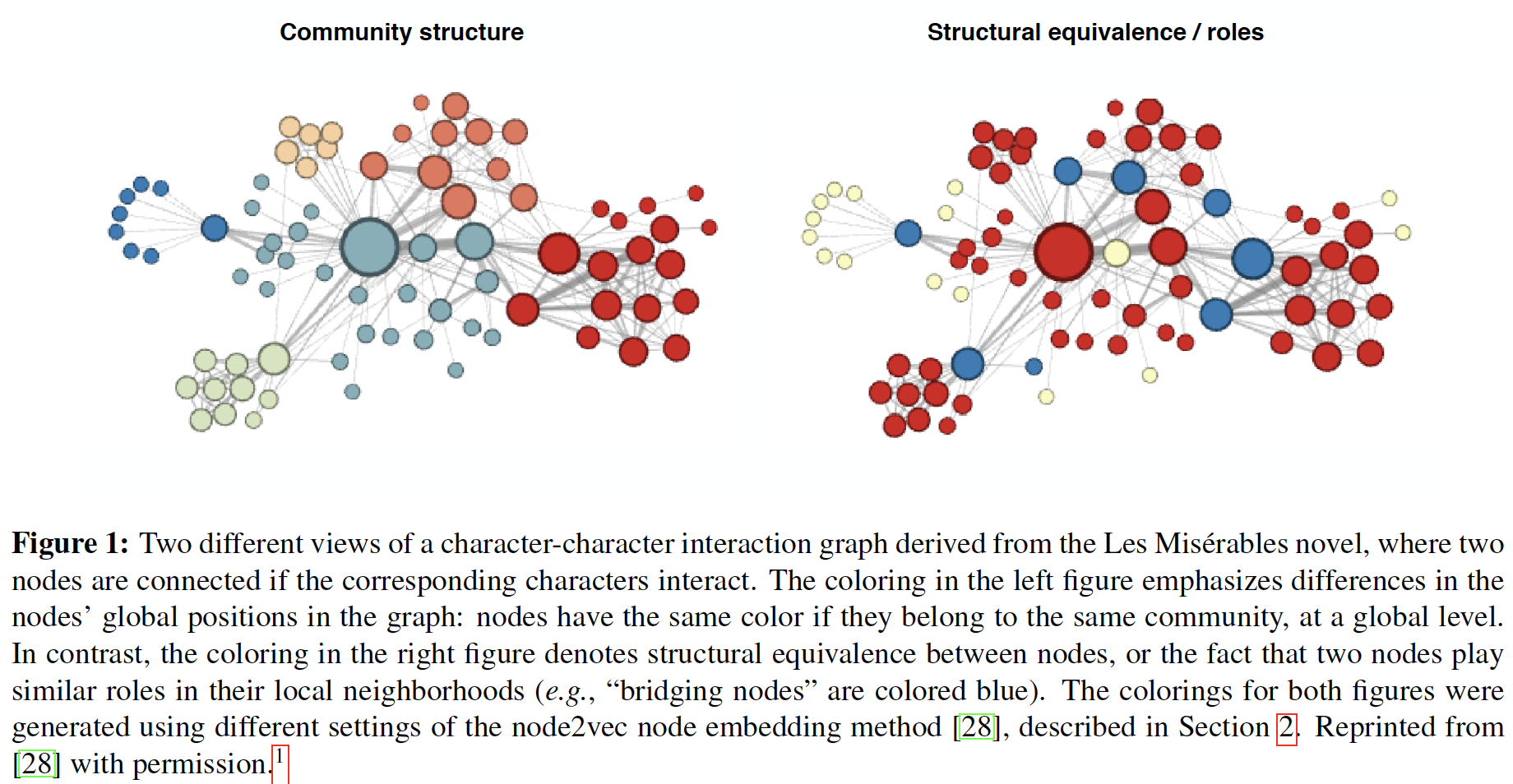
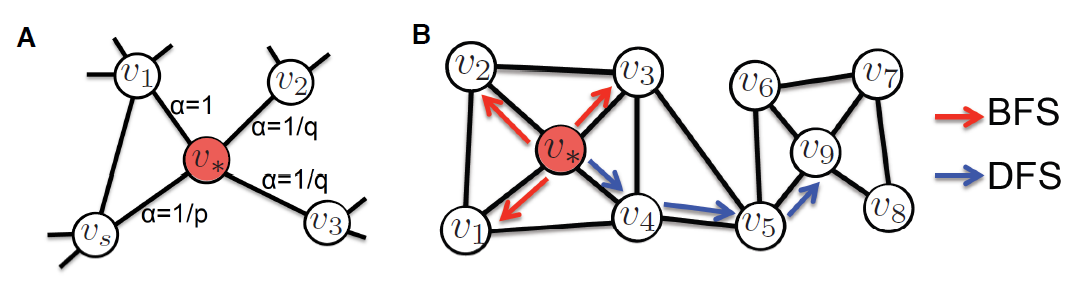
node2vec可以在广度优先搜索和深度优先搜索之间折衷。实验发现:调整这些超参数可以使得模型在学习社区结构community structure和局部结构角色local structrual role之间折衷,如下图所示。下图表示从《悲惨世界》小说中得到的人物与人物互动图的两个不同的视角,如果相应的人物有互动则两个节点就会连接起来。- 左图:不同的颜色代表节点在图中全局位置的不同:如果节点在全局层面上属于同一个社区,那么它们的颜色就相同。
- 右图:不同的颜色代表节点之间的结构等价性
structural equivalence,或者说两个节点在其局部邻域中扮演类似的角色(例如,bridging node为蓝色)。
下图说明了
node2vec如何通过图
A:假设随机游走刚从节点图
B:广度优先搜索BFS和深度优先搜索DFS的随机游走之间的差异。- 类似
BFS的随机游走主要探索节点的1-hop邻域,因此在捕获局部结构角色方面更为有效。 - 类似
DFS的随机游走主要探索得更远,对于捕获社区结构方面更为有效。
- 类似
LINE:LINE是另一种非常成功的浅层embedding方法,它不是基于随机游走,而基于共现。LINE经常与DeepWalk和node2vec进行比较,它结合了两个encoder-decoder目标,分别优化了一阶节点相似性和二阶节点相似性。一阶节点相似性为
decoder为:二阶节点相似性为
decoder为:
一阶目标和二阶目标都是基于
KL距离的损失函数。因此,LINE在概念上和node2vec, DeepWalk有关,因为LINE使用了概率性的decoder和损失函数。但是,LINE明确地分解了一阶相似度和二阶相似度,而不是采用固定长度的随机游走序列。HARP:HARP(《Harp: Hierarchical representation learning for networks》)是一种元数据策略,通过图预处理步骤来改善各种随机游走方法。HARP使用图粗化coarsening过程将DeepWalk, node2vec, LINE等。在得到embedding之后,每个超级节点学到的emebdding将作为超级节点中每个组成节点的初始embedding,然后执行更细粒度的embedding学习。这种方式在不同粒度上以层次方式反复执行,每次都能得到更细粒度的
emebdding。实践表明HARP可以持续改善DeepWalk, node2vec, LINE等方法的性能。
3.1.3 通用 encoder-decoder
目前为止我们研究过的所有节点
embedding方法都是浅层embedding方法,其中encoder只是一个简单的embedding lookup。这种方式有很多缺点:浅层
embedding的encoder中节点之间没有共享任何参数,即encoder只是基于节点ID的embedding lookup。- 由于参数共享可以充当一种强大的正则化,因此浅层
embedding方法的泛化能力较差。 - 浅层
embedding方法中参数数量为
- 由于参数共享可以充当一种强大的正则化,因此浅层
浅层
embedding的encoder无法利用节点属性。在很多大型图中,节点有丰富的属性信息(如社交网络的用户画像),这些属性信息对于节点在图中的位置和角色具有很高的信息价值。浅层
embedding方法本质是transductive的,它们只能为训练阶段存在的节点生成embeddign,无法为从未见过的节点生成embedding。因此无法应用到不断演变的图、需要泛化到新的图等场景。
最近已经提出很多方法来解决这些问题。这些方法仍然使用
encoder-decoder框架,但是和浅层embedding不同之处在于:它们使用更复杂的encoder(通常基于深度神经网络),并且更依赖于图的结构和节点属性。
a. 邻域自编码器
Deep Neural Graph Representations: DNGR和Structural Deep Network Embeddings: SDNE解决了上面的第一个问题。和浅层embedding方法不同,它们使用深度神经网络将图结构直接融合到encoder算法中。它们背后的基本思想是:使用自编码器来压缩有关邻域的信息(如下图所示)。另外,不同于之前的方法,
DNGR, SDNE的decoder只有一个节点而不是一对节点。在这两个方法中,令
DNGR和SDNE自编码器的目标是基于邻域向量embedding向量中重建因此这些方法的损失函数为:
和
pairwise decoder一样,我们选择embeddingDNGR,SDNE将节点的邻域信息压缩为低维向量。对于
SDNE,DNGR,encoder和decoder函数均由多个堆叠的神经网络层组成,encoder的每一层都降低了其输入的维度,decoder的每一层都增加了其输入的维度。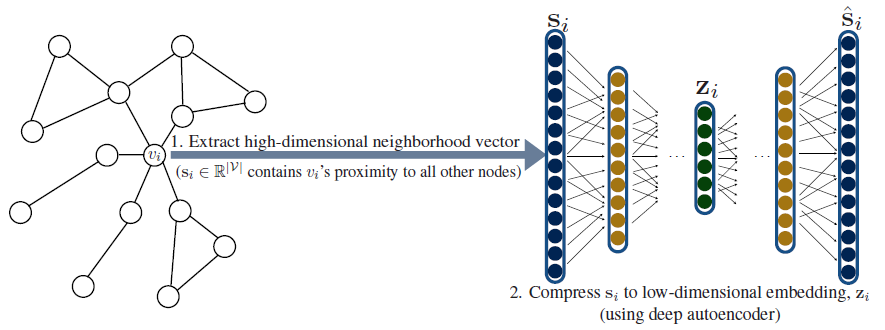
SDNE和DNGR在相似度函数(用于构造邻域向量DNGR根据随机游走序列中两个节点共现的pointwise mutual information:PMI来定义DeepWalk和node2vec。SDNE简单地定义SDNE还结合了自编码器的损失函数和拉普拉斯特征图的损失函数:
注意:公式
SDNE, DNGR可以将有关节点全局邻域的结构信息以正则化的形式直接合并到encoder中。这对于浅层
embedding方法是不可能的,因为浅层embedding方法的encoder取决于节点ID,而不是节点全局邻域结构。尽管
SDNE, DNGR在encoder中编码了有关节点全局邻域的结构信息,但是它们仍然存在一些严重的局限性。- 最突出的局限性是:自编码器的输入维度固定为
- 另外,自编码器的结构和大小也是固定的,因此
SDNE,DNGR也是transductive的,无法处理不断演变的图,也无法跨图进行泛化。
- 最突出的局限性是:自编码器的输入维度固定为
b. 邻域聚合卷积 encoder
最近许多节点
embedding方法旨在通过设计依赖于局部邻域(而不是全局邻域)的encoder来解决浅层embedding方法和自编码器方法的缺陷。这些方法背后的直觉是:通过聚合来自局部邻域的信息来为节点生成embedding,如下图所示。为了生成节点
A的embedding,模型聚合了来自A的局部邻域(节点B,C,D)的消息。然后,这些邻域节点又基于它们各自邻域来聚合消息,依次类推。下图给出了一个迭代深度为2的版本,它聚合了节点A的2-hop邻域消息,原则上可以为任意深度。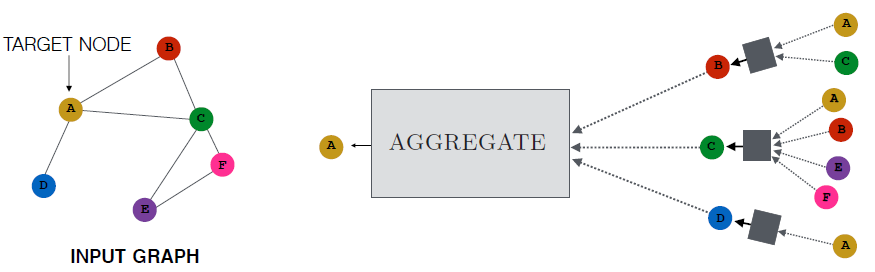
和之前讨论的方法不同,这些邻域聚合算法依赖于节点属性
embedding。在没有属性信息的情况下,也可以使用简单的图统计信息(如节点degree)作为节点属性;或者也可以为每个节点分配一个one-hot indicator作为属性。这些邻域聚合方法通常称作卷积,因为它们将节点
embedding表示为周围邻域的函数,这和计算机视觉中的卷积算子很类似。在编码阶段,邻域聚合方法以迭代或递归的方式构建节点的
embedding。- 首先,节点
embedding初始化为节点属性向量。 - 然后,在
encoder算法的每次迭代过程中,节点使用一种聚合算法来聚合邻域的embedding。 - 接着,在聚合之后每个节点被分配一个新的
embedding,它结合了邻域聚合embedding以及该节点上一轮迭代的embedding。 - 最后,这个新的
embedding被馈入一个dense层从而得到本轮迭代的embedding。
以上过程不断重复进行,使得节点
embedding聚合了图中距离该节点越来越远的信息。但是embedding维度仍然保持不变并限制在低维,迫使encoder不断将越来越大范围的邻域的信息压缩到低维向量。经过
emebdding向量作为节点的输出representation。整体算法如下所示:
邻域聚合
encoder算法:输入:
- 图
- 节点特征向量集合
- 深度
- 每层的权重矩阵
- 非线性激活函数
- 每层可微的聚合函数
- 邻域函数
- 图
输出:节点的
representation算法步骤:
初始化:
迭代,
对于每个节点
执行归一化:
返回
- 首先,节点
有很多遵循上述算法的最新方法,包括
GCN、Column Network、GraphSAGE等。这些算法中的可训练参数包括一组权重矩阵embedding方法不同,这些参数在所有节点之间共享。对每个节点都相同的聚合函数和权重矩阵为所有节点生成
embedding,在这个过程中仅输入节点属性和邻域结构在不同节点之间发生变化。这种参数共享提高了效率(即参数规模和图的大小无关),也提供了正则化,还允许为训练期间从未见过的节点生成embedding(即inductive learning)。GraphSAGE, Column Network以及各种GCN方法都遵循以上算法,但是区别在于执行聚合(Agg函数)、向量组合(COMBINE函数)的方式不同。GraphSAGE使用向量拼接作为COMBINE函数,并允许使用通用聚合函数作为Agg函数,如均值池化、最大池化、LSTM。他们发现更复杂的聚合器,尤其是最大池化,获得了明显的收益。GCN和Column Network使用加权和的方式作为COMBINE函数,并使用均值聚合(加权或者不加权)作为Agg函数。Column Network使用一个额外的插值项,即在Normalize之前:其中
这个插值项允许模型在迭代过程中保留局部信息。由于随着
原则上可以将
GraphSAGE, Column Network, GCN的encoder和前面讨论的任何一种decoder以及损失函数一起使用,并使用SGD来优化。在节点分类、链接预测的
benchmark上,实验发现这些方法相对浅层embedding的encoder提供了一致的增益。从
high level上讲,这些方法解决了浅层embedding的四个主要限制:- 它们将图结构合并到
encoder中。 - 它们利用了节点属性信息。
- 它们的参数规模可以为
sub-linear,即低于 - 它们可以为训练期间未见过的节点生成
embedding,即inductive learning。
- 它们将图结构合并到
3.1.4 task-specific 监督信息
目前为止
encoder-decoder架构默认都是无监督的。即,模型在一组节点上进行优化,优化目标是重构依赖于图但是,很多
embedding算法(尤其是邻域聚合方法)也可以包含task-specific监督信息,尤其是通常会结合节点分类任务中的监督信息来学习节点embedding。为简单起见,我们讨论节点具有二元类别标签的情形,但是我们的讨论很容易扩展到更复杂的多类分类问题。
假设每个节点
sigmoid函数,函数的输入为节点embedding:其中
然后我们计算预测标签和真实标签之间的交叉熵作为损失函数:
最后我们通过
SGD来优化模型的参数。这种
task-specific监督信息可以完全替代掉decoder中的重建损失,也可以和decoder重建损失一起使用(即同时包含监督损失和无监督损失)。
3.1.5 多模态
前面讨论的都是简单的无向图,而现实世界中很多图具有复杂的多模态
multi-modal、多层级(如异质节点、异质边) 的结构。已有很多工作引入了不同的方法来处理这种异质性。很多图包含不同类型的节点和边。如,推荐系统中包含两种类型的节点:用户节点、
item节点。解决该问题的通用策略是:对不同类型的节点使用不同的
encoder。使用
type-specific参数扩展pairwise decoder。例如,在具有不同类型边的图中,可以将标准的内积式edge decoder(即bilinear形式:其中
最近人们提出了一种从异质图中采样随机游走序列的策略,其中随机游走仅限于特定类型节点之间。这种方法允许我们将基于随机游走的浅层
embedding方法应用于异质图。
某些场景下图有很多层,其中不同层包含相同的节点,即多层图
multi-layer graph。注意,这里不是神经网络的层数,而是图数据的层数。此时跨层的信息共享是有益的,因为节点在其中一层的embedding可以接收节点在其他层的embedding信息。OhmNet结合了带正则化项的node2vec从而跨层绑定embedding。具体而言,假设节点其中:
embedding。
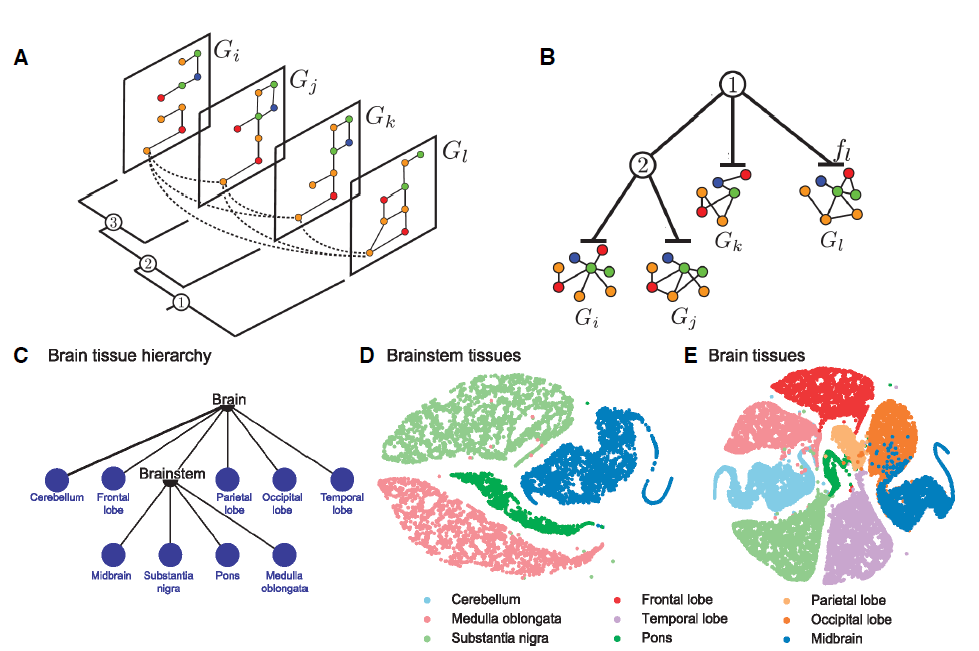
OhmNt通过使用hierarchy来扩展这个思想,从而可以学习不同graph layer上的embedding,而正则化项可以在graph layer的parent-child关系之间依次使用。如下图所示:
A:一个包含四层的图,其中相同节点出现在不同的层。这种多层结构可以通过正则化来学习,使得相同节点在不同层之间的emebdding彼此相似。B:通过层次结构来展示多层图,其中non-root层包含所有子层的所有节点和所有边。这种结构可以学习不同层级结构的
embedding,并在parent-child层级关系之间应用正则化,使得相同节点在parent和child层级之间的embedding相似。C-E:大脑组织中不同的 “蛋白质-蛋白质”作用图protein-protein interaction graph对应的multi-layer graph embedding。embedding是通过OhmNet方法得到并通过t-SNE可视化。C:不同组织区域中的层级结构。D:脑干brainstem层得到的蛋白质embedding的可视化。E:全脑whole-brain层得到的蛋白质embedding的可视化。
3.1.6 结构角色
目前为止我们研究的所有方法都优化节点
embedding,使得图中距离相近的节点具有相似的embedding。但是在很多任务中,更重要的是学习和节点结构角色structural roles相对应的表示形式,而与它们在图中的全局位置无关。node2vec为这个问题提供了一种解决方案,它采用有偏的随机游走从而更好地捕获结构角色。- 近期
struc2vec和graphwave提出了专门用于捕获结构角色的节点embedding方法。
struc2vec涉及一系列从原始图k-hop邻居之间的结构相似性。具体而言,令
k-hop的节点集合,degree的有序序列。在辅助图其中:
degree序列dynamic time wariping:DTW来计算这两个序列之间的距离。通过
在计算得到这些加权辅助图之后,
struc2vec对它们执行有偏的随机游走,并将这些随机游走作为node2vec优化算法的输入。graphwave采用另一种非常不同的方法来捕获结构角色,它依赖于谱图小波spectral graph wavelet以及heat kernel技术。简而言之,令
degree矩阵,eigenvector组成的矩阵eigenvector matrix,对应的特征值eigenvalues为定义
heat kernel为scale超参数。对于每个节点
graphwave使用其中:
one-hot indicator向量,表示
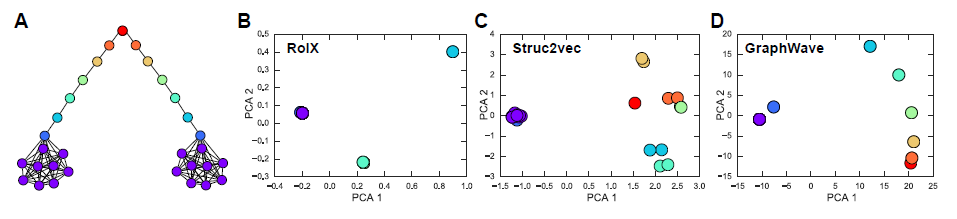
graphwave表明这些degree。选择一个合适的scalegraphwave能够有效地捕获有关图中节点角色的结构信息。graphwave的一个典型示例如下图所示:A:一个人工合成的杠铃图,其中节点根据其结构角色着色。B-D:杠铃图上不同结构角色检测算法输出的节点emedding,通过PCA降维来可视化。B:RoIX算法,它采用人工设计的特征,是baseline方法。C:struc2vec算法。D:graphwave算法。
所有方法都可以正确区分杠铃末端和杠铃其它部分,只有
graphwave方法能够正确区分所有结构角色。另外,
D的节点看起来比A中原始图节点少得多,因为graphwave将颜色相同(即结构角色相同)的节点映射到embedding空间中几乎相同的位置。
3.1.7 应用
节点
embedding最常见的应用是可视化visualization、聚类clustering、节点分类node classification、链接预测link prediction。可视化和模式挖掘:节点
embedding为可视化提供了强大的新的范式paradigm。因为节点被映射到实值向量,因此研究人员可以轻松地利用现有的通用技术对高维数据集进行可视化。例如,可以将节点
embedding和t-SNE, PCA之类的通用技术结合,从而得到图的二维可视化。这对于发现社区以及其它隐藏结构非常有用。聚类和社区检测:和可视化类似,节点
embedding也是对相关节点进行聚类的强大工具。同样地,由于每个节点都和实值向量相关联,因此可以将通用聚类算法应用到节点embedding上,如k-means, DB-scan等。这为传统的社区检测技术提供了开放的、更强大的替代方案,并且还开辟了新的天地,因为节点
embedding不仅可以捕获社区结构,还可以捕获不同节点扮演的结构角色。节点分类和半监督学习:节点分类可能是评估节点
embedding的最常见baseline任务。大多数情况下,节点分类任务是半监督学习的一种形式,其中仅一小部分节点的标签可用,目标是仅基于这一小部分标记节点来标记整个图。链接预测:节点
embedding作为链接预测的特征也非常有用,其目标是预测缺失的边或将来可能形成的边。链接预测是推荐系统的核心,其中节点
embedding反映了节点之间的深度交互。典型的场景包括预测社交网络中缺失的好友链接,电影推荐中预测用户和电影之间的亲和力affinity。
3.2 子图 embedding
现在我们考虑子图或者全图的
embedding,其目标是将子图或者整个图编码为低维embedding。正式地讲,我们需要学习一个诱导子图
induced subgraphembedding。然后子图的
representation learning和graph kernel密切相关。graph kernel定义了子图之间的距离度量,但是这里我们不会对graph kernel进行仔细讨论,因为这是一个庞大、丰富的研究领域。我们讨论的方法和传统的graph kernel不同,我们寻求从数据中学习有用的representation,而不是通过graph kernel函数得到预先指定的feature representation。有很多方法都是基于前面介绍的单个节点
embedding的技术。但是,和节点embedding不同,大多数子图emebdding方法都是基于完全监督的fully-supervised。因此,这里我们假设子图embedding都是采用交叉熵损失函数。
3.2.1 sets of node embedding
有几种子图
emebdding技术可以看作是基于卷积的节点embedding算法的直接扩展。这些方法背后的基本直觉是:它们将子图等价于节点embedding的集合。它们使用卷积的邻域聚合思想为节点生成embedding,然后使用额外的模块来聚合子图对应的节点embedding集合。这里不同方法之间的主要区别在于:如何聚合子图对应的节点
embedding集合。sum-based方法:《convolutional molecular fingerprints》通过对子图中所有节点embedding进行求和,从而得到子图的embedding:其中
encoder算法的变体来生成的。《Discriminative embeddings of latent variable models for structured data》采用类似于sum-based方法,但是概念上它和mean-field inference相关:如果图中的节点视为潜在变量,则邻域聚合卷积encoder算法可以视为一种mean-field inference的形式,其中消息传递操作被可微的神经网络替代。因此,该论文提出了基于Loopy Belief Propagation的encoder,基本思想是为每条边embedding然后根据这些临时
embedding聚合得到节点embedding:一旦得到节点
embedding,论文使用子图中所有节点embedding的简单求和从而得到子图的embedding。
graph-coarsening方法:《Spectral networks and locally connected networks on graphs》也采用了卷积方法,但是它并未对子图的节点embedding求和,而是堆叠了卷积层以及图粗化graph coarsening层(类似于HARP方法)。在图粗化层中,节点被聚类在一起(可以使用任何图聚类算法),并且聚类之后使用一个簇节点来代表簇内所有节点。这个簇节点的
embedding为簇内所有节点embedding的最大池化。然后,新的、更粗粒度的图再次通过卷积encoder,并不断重复该过程。
3.2.2 GNN 方法
从概念上讲,
GNN和邻域聚合卷积encoder算法密切相关。但是GNN的直觉是:将图视为节点之间消息传递的框架,而不是从邻域那里收集信息。在原始
GNN框架中,每个节点以一个随机的embeddingGNN算法每轮迭代过程中,节点根据其邻域消息更新embedding为:其中:
embedding向量维度。上述公式以递归的方式重复迭代直到
embedding收敛为止,其中必须确保一旦经过
embedding为《Gated Graph Sequence Neural Networks》使用GRU扩展和修改了GNN框架,它使用节点属性来初始化其中
《Neural Message Passing for Quantum Chemistry》考虑GNN的另一种迭代方式:其中:
这个称为消息传递神经网络
Message Passing Neural Networks:MPNNs,它可以概括很多图神经网络方法。所有这些图神经网络方法原则上可以用于
node-level的embedding,尽管它们更经常用于subgraph-level的embedding。为了计算子图
embedding,可以采用任何聚合过程。也可以引入一个“虚拟”的超级节点来完成聚合,该超级节点连接到目标子图中的所有节点。
3.2.3 应用
- 子图
embedding主要用于子图分类。例如对不同分子对应的图的属性进行分类,包括分子药物的治疗效果、分子材料的功能等。也可以将子图embedding用于图像分类(将图像转换为graph之后)、预测计算机程序是否满足某种形式的属性、以及执行逻辑推理任务。
3.3 未来方向
目前
graph representation领域还有很多悬而未决的问题:可扩展性
scalability:尽管大多数方法理论上都有很高的可扩展性(时间复杂度embedding,并且假设用于训练和测试的所有节点的属性、embedding、以及edge list都可以放在内存中,这在现实中与实际情况不符。解码高阶主题
motifs:近年来很多工作都致力于改善生成节点embedding的encoder,但是decoder还是最基础的pairwise decoder。这种decoder可以预测节点之间的成对关系,并忽略涉及两个以上节点的高阶图结构。众所周知,高阶结构主题对于复杂网络的结构和功能是必不可少的,设计能够解码复杂主题的
decoder算法是未来工作的重要方向。动态图:很多领域都涉及高度动态的图,但是目前我们缺乏建模动态图
embedding的方法。大量候选子图的
inference:当前子图embedding方法的主要技术限制在于它们要求在学习过程之前预先指定目标子图。我们需要改善子图embedding方法,使得该方法能够有效地自动推断大量的候选子图,无需人工指定。可解释性:
representation learning缓解了人工设计特征的负担,但是代价是可解释性较差。除了可视化和benchmark评估之外,还必须开发新技术以提高学到的embedding的可解释性。我们需要确保这些embedding方法真正学到图相关的信息,而不仅仅是利用benchmark的一些统计趋势。