GNN(续)
十四、GCMC[2017]
随着电商平台和社交媒体平台的爆炸式增长,推荐算法已经成为很多企业不可或缺的工具。通常而言,推荐算法有两个主流方向:基于内容的推荐系统、基于协同过滤的推荐系统。
- 基于内容的推荐系统使用
user和item的内容信息来进行推荐,如用户的职业、item的类型。 - 基于协同过滤的推荐使用
user-item交互数据(如购买、评分等)来进行推荐。
论文
《Graph Convolutional Matrix Completion》将矩阵补全问题视为一个图的链接预测问题:协同过滤中的交互数据可以由用户节点和item节点之间的二部图来表示,观察到的评分/购买由链接来表示。内容信息自然地以节点特征的形式包含在这个框架中。评分预测问题变为预测user-item二部图中的labeled link。论文提出了图卷积矩阵补全
graph convolutional matrix completion: GCMC:一种graph-based的自编码器框架用于矩阵补全,它建立在图上深度学习的最新进展的基础上。自编码器auto-encoder通过在二部图上消息传递的形式来产生user latent feature和item latent feature。这些潜在user representation和item representation用于通过双线性解码器重建评分链接rating link。当有额外的辅助信息
side information可用时,将矩阵补全问题视为二部图上的链接预测问题带来的好处尤为明显。将辅助信息和交互数据结合在一起可以有效缓解冷启动问题。论文证明了所提出的图自编码器模型有效地结合了交互数据和辅助信息。- 基于内容的推荐系统使用
相关工作:
自编码器
auto-encoder:user-based或item-based自编码器是最近一类state-of-the-art协同过滤模型,可以视为我们的图自编码器模型的一个特例,其中仅考虑了user embedding或仅考虑了item embedding。《Autorec: Auto-encoders meet collaborative filtering》是第一个这样的模型,其中user(或item)部分观察到的评分向量rating vector通过编码器层encoder layer投影到潜在空间,并使用具有均方重构误差损失mean squared reconstruction error loss的解码器层decoder layer进行重构。《A neural autoregressive approach to collaborative filtering》提出的CF-NADE算法可以被认为是上述自编码器架构的一个特例。在user-based的设置中,消息仅从item传递给user;而在item-based的设置中,消息仅从user传递给item。我们的图自编码器同时考虑了
item传递给user,以及user传递给item。注意,与我们的模型相比,
CF-NADE给未评分的item在编码器中被分配了默认评分3,从而创建了一个全连接的交互图interaction graph。CF-NADE对节点进行随机排序,并通过随机切割random cut将传入消息划分为两组,并仅保留其中一组。因此,该模型可以看做是一个降噪自编码器,其中在每次迭代中随机丢弃输入空间的一部分。我们的模型仅考虑观测的评分,因此不是全连接的。
分解模型:很多流行的协同过滤算法都是基于矩阵分解
matrix factorization: MF模型,这种方式假设评分矩阵可以很好滴近似为低秩矩阵:其中:
embedding矩阵,每一行代表一个用户的user embedding向量,即user latent feature representation。item embedding矩阵,每一行代表一个item embedding向量,即item latent feature representation。embedding向量的维度,并且满足user集合,item集合。
在这些矩阵分解模型中:
《Probabilistic matrix factorization》提出的概率矩阵分解probabilistic matrix factorization: PMF假设《Matrix factorization techniques for recommender systems》提出的BiasedMF通过融合user-specifc bias, item-specific bias, global-bias来改进PMF。《Neural network matrix factorization》提出的Neural network matrix factorization: NNMF通过将latent user feature和latent item feature传递给前馈神经网络来扩展MF方法。《Local low-rank matrix approximation》提出的局部低秩矩阵近似介绍了使用不同低秩近似的组合来重建评分矩阵的思想。
带辅助信息的矩阵补全
matrix completion with side information:在矩阵补全问题中,目标是使用低秩矩阵来逼近rank的最小化是一个棘手的问题。《Exact matrix completion via convex optimization》使用最小化核范数nuclear norm(矩阵的奇异值之和)来代替秩的最小化,从而将目标函数变成了可处理的凸函数。Inductive matrix completion: IMC将user和item的内容信息融入到特征向量中,并预估useritem其中
itemuser embedding矩阵和item embedding矩阵。《Matrix completion on graphs》提出的geometric matrix completion: GCM模型通过以user graph和item graph的形式添加辅助信息,从而对矩阵补全模型进行正则化。在
《Collaborative filtering with graph information: Consistency and scalable methods》提出的GRALS将一种更有效的交替最小二乘优化方法引入了图正则化矩阵补全问题。最近,
《Geometric matrix completion with recurrent multi-graph neural networks》提出,通过在图上使用卷积神经网络将graph-based辅助信息融合到矩阵补全中,并结合递归神经网络来建模动态评分生成过程。和他们不同,
GCMC直接使用图卷积编码器/解码器对评分的二部图进行建模,通过一个non-iterative步骤即可预测unseen的评分。相比之下,
sRGCNN需要用迭代式的多个step才能预测评分。
14.1 模型
给定用户集合
item集合item我们将矩阵补全问题转化为链接预测问题。考虑二部图
item如下图所示:
- 左图为评分矩阵
user-item之间的评分(评分在1~5分之间),或者未观测(评分记作0)。 - 第二幅图表示
user-item评分的二部图,边对应于评分行为,边上的数字对应于评分数值。 - 最后两幅图表示矩阵补全问题可以转换为二部图上的链接预测问题,并使用端到端的可训练的图自编码器进行建模。
矩阵补全问题转化为链接预测问题的核心是:链接如何对应到评分?
GCMC的做法是:每个等级的评分对应一条边,因此有- 每种类型的边都有一个编码器,所有编码器的结果聚合得到
node embedding。 - 每种类型的边都有一个解码器,所有解码器的结果求期望得到预估的评分。
但是,这里没有考虑评分之间的大小关系:评分为
1要小于评分为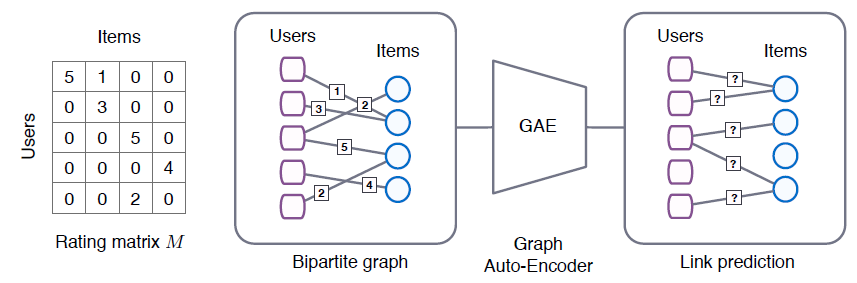
- 左图为评分矩阵
之前的
graph-based推荐算法通常采用multi-stage pipeline,其中包括图的特征抽取模型(如graph embedding模型)以及图的链接预测模型。这些模型都是独立分开训练。但是最近的研究结果表明:通过端到端的技术来建模图结构化数据可以显著提升效果。在这些端到端技术中,应用于无监督学习和链接预测的图自编码
graph auto-encoder技术尤为突出。因此我们提出一种图自编码器的变种来应用于推荐任务。
14.1.1 图自编码器
图自编码器由一个编码器和一个解码器组成,其中:
编码器模型:
embedding矩阵,每一行代表一个节点的embedding向量,node embedding向量维度。
解码器模型:
embedding
对于二部图
其中:
user embedding矩阵,item embedding矩阵。{0,1}内取值,item因此,
这里对每种类型的边定义了一个邻接矩阵,不同的邻接矩阵代表了不同的模型,因此类似于
《Convolutional Networks on Graphs for Learning Molecular Fingerprints》提出的neural graph fingerprint模型。
类似地,我们重新定义解码器为:
解码器输入一对
user-item的embedding向量,并返回useritem我们通过最小化预测评分矩阵
RMSE(将评分预测视为回归问题)或者交叉熵(将评分预测视为分类问题)。最后,我们注意到可以将最近提出的几个矩阵补全
state-of- the-art模型纳入我们的框架中,并将它们视为我们模型的特例。
14.1.2 图卷积编码器
这里我们选择了一种特定的编码器模型,它可以有效地利用图中
location之间的权重共享,并为每种边类型我们选择局部图卷积
local graph covolution作为编码器模型。这类局部图卷积可以视为消息传递的一种方式,其中消息在图的链接之间传递和转换。在我们
case中,我们为每个评分等级分配一个level-specific变换,使得从item其中:
left normalization) 或者根据论文的描述,这里应该是
level-specific权重矩阵。
同理,用户
item这里也可以选择使用不同的
level-specific权重矩阵user -> item和item -> user传递消息时,权重矩阵不同)。在消息传递之后:
- 首先通过求和来聚合类型为
representation向量。 - 然后将所有邻域类型的
representation向量聚合,从而得到节点的单个聚合向量。 - 最后对聚合向量进行变换,最终得到节点的
embedding向量。
以下公式为用户节点
embedding计算公式,item节点embedding也是类似的。其中第一行公式称作卷积层,第二行公式称作
dense层。注意:
当没有辅助信息可用时,
dense层对于user和item都采用相同的参数矩阵当存在辅助信息可用时,
dense层对于user和item都采用单独的参数矩阵这里卷积层只有一层。虽然可以堆叠更多的卷积层来构建更深的模型,但是在最初的实验中我们发现堆叠更多卷积层并不能提高性能。
同理,堆叠更多的
dense层也不能提高性能。因此,最终我们选择单层卷积层 + 单层dense层的组合作为图编码器。这里给出的模型仅仅是一种可能性。虽然编码器的选择相对简单,但是也可以选择不同的变种。例如:
- 可以使用神经网络来计算消息传递(
- 可以使用
attention机制从模型中学习每个消息的权重,从而替代消息的归一化常数
- 可以使用神经网络来计算消息传递(
14.1.3 双线性解码器
我们使用双线性解码器
bilinear decoder来重建二部图的链接。令用户item其中每个评分等级
embedding向量的维度。每个评分登记
模型最终预估的评分为所有评分等级预估结果的期望值:
14.1.4 模型训练
损失函数:模型训练期间我们将
GCMC模型的损失函数定义为:最小化预估评分其中:
mask矩阵:对于观测值对应的项,
因此,上述目标函数仅在所有观测的评分上优化。
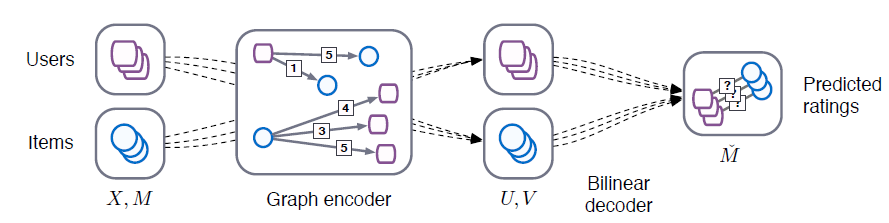
GCMC模型的整体框架如下所示。模型由图卷积编码器- 编码器从
user-> item或者item -> user传递并变换消息。 - 解码器根据
user embedding和item embedding的pair对来预估评分。
- 编码器从
node dropout:为使得模型能够很好地泛化到未观测的评分,我们以概率node dropout。注意:和常规dropout一样,在消息丢弃之后需要rescale。这种
node-level的dropout和常规的dropout不同。常规的dropout是在message-level进行dropout,称作message dropout。- 在
message dropout中,每条消息随机独立地丢弃,使得最终embedding对于边的扰动更为鲁棒。 - 而在
node dropout中,每个节点随机独立地丢弃,使得最终embedding对于特定用户和特定item的影响更为鲁棒。这会缓解一些热门用户或热门item的影响。
最后,我们还对卷积自编码器的
dense层的隐单元使用了常规的dropout。- 在
mini-batch训练:为了训练较大的数据集(如MovieLens-10M数据集),我们需要对观测数据进行采样,从而进行mini-batch训练。这是将MovieLens-10M的完整模型加载到GPU内存所必须的。我们从每个等级的观测评分中采样固定比例的评分,然后仅考虑该
mini-batch的损失。这样我们在训练过程中仅需要考虑当前mini-batch中出现的user和item。这既是正则化的有效手段,又可以降低训练模型需要的内存。通过在
Movielens-1M数据集上使用mini-batch训练和full-batch训练的实验对比(对比时针对二者分别调优了各自的正则化参数),我们发现二者产生了可比的结果。最后,对于
MovieLens-10M以外的其它数据集,我们选择full-batch训练,因为full-batch训练相比mini-batch训练的收敛速度更快。
14.1.5 向量化实现
在
GCMC的实现中,我们可以使用高效的稀疏矩阵乘法来实现图自编码器模型,其算法复杂度和边的数量呈线性关系,即假设聚合函数
accum为累加,则图卷积编码器为(采用左归一化):其中:
degree matrix,这里是否要替换为
另外,采用对称归一化的图卷积编码器以及双线性解码器的向量化
vectorization也以类似的方式进行。
14.1.6 辅助信息
理论上可以将包含每个节点的信息(如内容信息)的特征直接作为节点的输入特征(即特征矩阵
item)及其兴趣时,将内容信息直接馈入图卷积层会导致严重的信息流瓶颈bottleneck of information flow。此时,可以通过单独的处理通道
channel,从而将用户特征向量或item特征向量以辅助信息的形式纳入全连接层中。由于内容信息灌入到模型的最后一层,因此上述的信息流瓶颈不会出现,因为瓶颈只会出现在中间层。那么这么做对不对?理论依据是什么?
我们选择输入特征矩阵
one-hot表示。令用户节点embedding为:其中:
bias向量。user节点的参数为item节点的参数为user,item类型的节点使用两套不同的参数。因为
user节点和item节点具有不同的输入特征空间。本文实验中使用的数据集中,用户内容以及
item内容的信息大小有限,因此我们使用这种辅助信息的方式。
注意:辅助信息不一定要以节点特征向量的形式出现,也可以是图结构(如社交网络)、自然语言或者图像数据。此时可以将上式中的
dense层替换为适当的可微模块,如RNN、CNN或者其它图卷积网络。
14.1.7 权重共享
编码器权重共享:在辅助信息的方式中,我们使用节点的
one-hot向量作为输入。此时矩阵user节点(如果节点item节点)或者item节点(如果节点user节点)。但是,并非所有用户拥有评分等级为
item拥有评分等级为遵从
《A neural autoregressive approach to collaborative filtering》我们实现了以下权重共享策略:由于更高的评分等级包含的权重矩阵数量更多,因此我们称这种权重共享为有序权重共享
ordinal weight sharing。为什么更高评分包含的权重矩阵数量更多?完全没有道理。
解码器权重共享:对于成对双线性解码器,我们采用一组基权重矩阵
basis weight matrix其中:
这种解码器的权重共享是一种有效的正则化手段。
14.2 实验
数据集:我们在多个常见的协同过滤
benchmark数据集上评估我们的模型。MovieLens(100K,1M, 10M)数据集:包含多个用户对多部电影的评级数据,也包括电影元数据信息(如电影题材)和用户属性信息(如用户年龄、性别、职业)。该数据集有多个版本,对应于不同的数据量。Flixster数据集:来自于社交电影网站Flixster的电影评分数据集,数据集包含了用户之间的好友关系。Douban数据集:来自豆瓣的电影评分数据集,数据集包含用户之间的好友关系。YahooMusic数据集:来自Yahoo! Music社区的用户对音乐家的评分数据集。
对于
Flixster,Douban, YahooMusic数据集,我们使用《Geometric matrix completion with recurrent multi-graph neural networks》论文提供的预处理的子集。预处理后,每个数据集包含3000个用户节点以及3000个item节点,以及对应的user-user或item-item交互图。下图给出了数据集的统计信息,其中
Features表示是否包含用户特征或者item特征,Ratings表示数据集的评分数量,Density表示评分矩阵中已观测评分的占比,Rating level表示评分等级范围。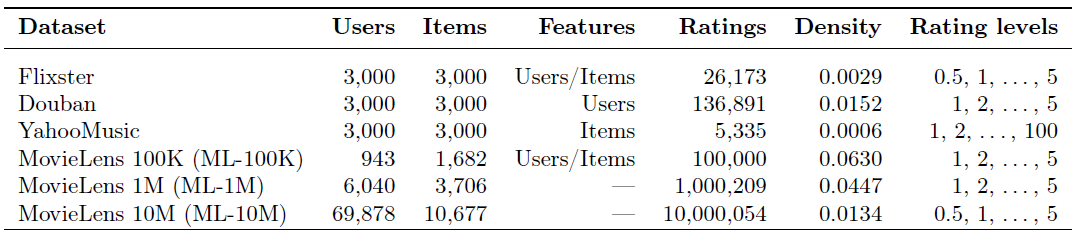
baseline模型:- 矩阵补全模型,包括
MC, IMC, GMC, GRALS, sRGCNN。具体细节参考前文所述。 - 矩阵分解模型,包括
PMF, I-RBM, BiasMF, NNMF。 具体细节参考前文所述。 - 协同过滤模型,包括
LLORMA-Local, I-AUTOREC, CF-NADE。 具体细节参考前文所述。
另外我们还对比了我们不带额外信息的
GCMC模型,以及带辅助信息的GCMC+Feat模型。- 矩阵补全模型,包括
参数配置:
所有
baseline方法直接采用原始论文中的实验结论数据(因此也不需要实现和运行这些baseline方法)。对于
GCMC模型,我们通过验证集从以下超参数范围选择最佳的超参数:- 聚合函数
accumulation:stack vs sum。 - 是否在编码器中使用有序权重共享:是
vs否。 - 编码器中
vs对称归一化。 node dropout比例:
另外,除非另有说明,否则我们使用以下超参数配置:
- 使用学习率为
0.01的Adam优化器。 - 解码器基权重矩阵数量
- 编码器采用:维度
500的单层卷积层(使用ReLU激活函数) + 维度50的单层dense层(无激活函数)。
最后,我们使用学习模型参数的指数移动平均(衰减因子
0.995)在保留的测试集上评估模型。- 聚合函数
Movielens-100k数据集(特征向量形式的辅助信息实验):我们直接使用数据集原始的u1.base/u1.test的训练集/测试集拆分结果。对于该数据集,我们使用辅助信息来参与所有模型的训练。在该数据集我们对比了矩阵补全baseline方法和我们的GCMC方法,其中:GMC, GRALS, sRGCNN通过user/item特征。- 其它方法直接使用原始特征向量。
对于
GCMC的超参数,我们将原始训练集按照80:20进行训练集/验证集的拆分,然后通过验证集来调优超参数:在图卷积中使用stack作为累积函数,选择对于
GCMC模型,我们不带任何辅助信息。对于GCMC + Feat我们使用辅助信息,并且辅助信息的side information layer使用维度大小为10的dense层(采用ReLU激活函数)。我们使用
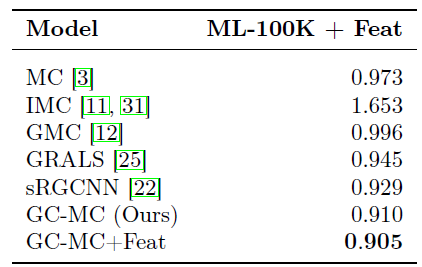
1000个full-batch epoch来训练GCMC和GCMC + Feat。我们随机重复执行5次并报告测试集上的平均RMSE结果。整体评估结果如下(baseline数据直接来自于《Geometric matrix completion with recurrent multi-graph neural networks》)。结论:
我们的
GCMC方法明显优于baseline方法,即使在没有辅助信息的情况下也是如此。和我们方法最接近的是
sRGCNN方法,它在用户和item的近邻图上使用图卷积,并使用RNN以迭代的方式学习表示。实验结果表明,使用简单的解码器(而不是复杂的
RNN)直接从学到的user embedding/ item embedding中直接评估评分矩阵可以更有效,同时计算效率更高。
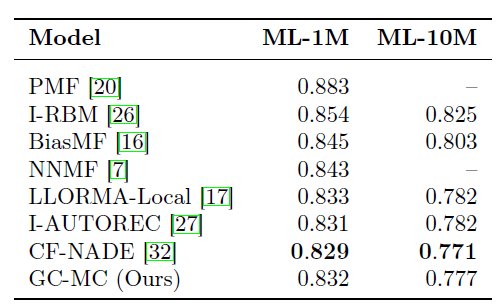
MovieLens-1M, MovieLens-10M数据集(无辅助信息的实验):在该数据集上我们和当前的state-of-the-art协同过滤算法(如AutoRec, LLorma, CF-NADE)进行比较。我们采取和
《A neural autoregressive approach to collaborative filtering》相同的训练集/测试集拆分方式,拆分比例90:10。另外,baseline方法的结果直接使用该论文的数值。该数据集不带任何辅助信息,因此我们没有比较
GCMC + Feat。我们对原始训练集按照95:5随机拆分为训练集/验证集,然后通过验证集来调优超参数:对于
MovieLens-1M数据集,我们使用sum作为累计函数,选择对于
MovieLens-10M,我们使用stack作为累计函数,选择另外考虑到该数据集的评分等级数量翻倍,我们选择解码器的基参数矩阵数量
一旦选择好超参数之后,我们就在整个原始训练集上重新训练模型,并利用训练好的模型来评估测试集。
对于
MovieLens-1M我们训练3500个full-batch epoch,对于MovieLens-10M我们训练18000个mini-batch step(对应于batch size =10000, epoch = 20)。我们按照
90:10随机拆分原始训练集/测试集,并重复执行5轮,报告模型在测试集上的平均RMSE。所有baseline评分来自于论文《A neural autoregressive approach to collaborative filtering》中的数据。对于CF-NADE我们报告了最佳性能的变体。结论:
GCMC方法可以扩展到大规模数据集,其性能可以达到user-based或者item-based协同过滤的state-of-the-art方法。CF-NADE引入的几种技术,如:layer-specific学习率、特殊的ordinal损失函数、评分的自回归建模,这些都和我们的方法正交,因此这些技术也可以和我们的GCMC框架结合使用。
Flixster, Douban, YahooMusic(图形式的辅助信息实验):这些数据集包含了一些图结构的辅助信息。我们通过使用这些图的邻接向量(根据degree进行归一化)作为相应的user/item的特征向量,从而引入辅助信息。注意:辅助信息的图是社交网络等
user-user图,或者item-item图。它们不同于user-item二部图。我们根据论文
《Geometric matrix completion with recurrent multi-graph neural networks》的训练集/测试集拆分。所有baseline方法的结果都取自于该论文的数值。我们从训练集中按照
80:20随机拆分为训练集/验证集,然后通过验证集来调优超参数:在图卷积中使用stack作为累积函数,选择对于
GCMC模型,我们使用辅助信息,并且辅助信息的side information layer使用维度大小为64的dense层(采用ReLU激活函数)。我们使用
full-batch训练200个epoch。最终我们重复执行
5轮,并报告模型在测试集上的平均RMSE。其中Flixster有两组结果:左侧结果表示同时引入了user辅助信息和item辅助信息;右侧结果表示仅考虑item辅助信息。结论:
GCMC在所有baseline中取得了state-of-the-art效果。注意:
GCMC在所有三个数据集上都采用相同的超参数配置,如果针对各自数据集调优,效果会进一步提升。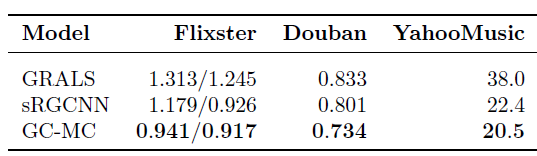
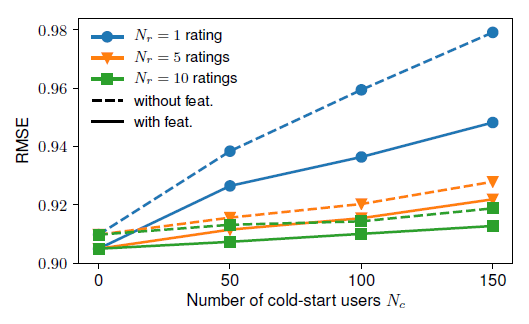
冷启动实验:为深入了解
GCMC模型如何通过辅助信息来提升冷启动性能,我们选择MovieLens-100K数据集,随机选择固定数量的冷启动用户MovieLens=100K原始数据仅包含具有至少20个评分的用户。我们考察当
GCMC的性能(可以看到:对于冷启动用户,使用辅助信息能够带来显著的提升,在只有一个评分的用户上表现尤为突出。
十五、JK-Net[2018]
图是一种普遍存在的结构,广泛出现在数据分析问题中。现实世界的图(如社交网络、金融网络、生物网络和引文网络)代表了重要的丰富的信息,这些信息无法仅仅从单个实体中看到(如一个人所在的社区、一个分子的功能角色、以及企业资产对外部冲击的敏感性)。因此,图中节点的
representation learning旨在从节点及其邻域中抽取高级特征,并已被证明对许多application非常有用,如节点分类、节点聚类、以及链接预测。最近的工作集中在
node representation的深度学习方法上。其中大多数深度学习方法遵循邻域聚合(也称作消息传递message passing)方案。这些模型迭代式地聚合每个节点的hidden feature及其周围邻域节点的hidden feature,从而作为该节点的新的hidden feature。其中每一次迭代都由一层神经网络来表示。理论上讲,执行hidden feature的聚合过程,利用了以节点Weisfeiler-Lehman图同构测试graph isomorphism test的推广,并且能够同时学习图的拓扑结构以及邻域节点特征的分布。但是,这种聚合方式可能会产生出人意料的结果。例如,已经观察到
GCN的深度为2时达到最佳性能;当采用更深网络时,虽然理论上每个节点能够访问更大范围的信息,但是GCN的效果反而更差。在计算机视觉领域中,这种现象称作学习退化degradation,该问题可以通过残差连接来解决,这极大地帮助了深度模型的训练。但是在GCN中,在很多数据集(如,引文网络)上即使采用了残差连接,多层GCN的效果仍然比不过2层GCN。基于上述观察,论文
《Representation Learning on Graphs with Jumping Knowledge Networks》解决了两个问题:- 首先,论文研究了邻域聚合方案的特点及其局限性。
- 其次,基于这种分析,论文提出了
jumping knowledge network: JK-Net框架。该框架和现有的模型不同,JK-Net为每个节点灵活地利用不同的邻域范围,从而实现自适应的结构感知表示structure-aware representation。
通过大量实验,论文证明了
JK-Net达到了state-of-the-art性能。另外,将JK-Net框架和GCN/GraphSage/GAT等模型结合,可以持续改善这些模型的性能。模型分析:为评估不同邻域聚合方案的行为,论文分析了节点
representation依赖的邻域范围。论文通过节点的影响力分布the influence distribution(即不同邻域节点对于representation的贡献的分布)来刻画这个邻域范围。邻域范围隐式的编码了nearest neighbors的先验假设。具体而言,我们将看到这个邻域范围严重受到图结构的影响。因此引发了一个疑问:是否所有的节点
tree-like子图、expander-like子图)。进一步地,论文形式化地分析将
eigenvalue的函数。改变的局部性
changing locality:为了说明图结构的影响和重要性,请回想一下许多现实世界的图具有强烈局部变化的结构locally strongly varying structure。在生物网络和引文网络中,大多数节点几乎没有连接,而一些节点 (hub)连接到许多其它节点。社交网络和web网络通常由expander-like部分组成,它们分别代表well-connected实体和小社区small community。除了节点特征之外,这种子图结构对于邻域聚合结果也有非常大的影响。邻域范围扩张的速度(或者叫影响半径的增长)通过随机游走的
mixing time来刻画(即:从节点例如考虑如下
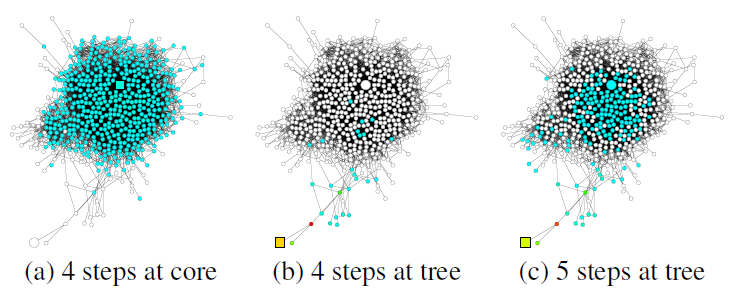
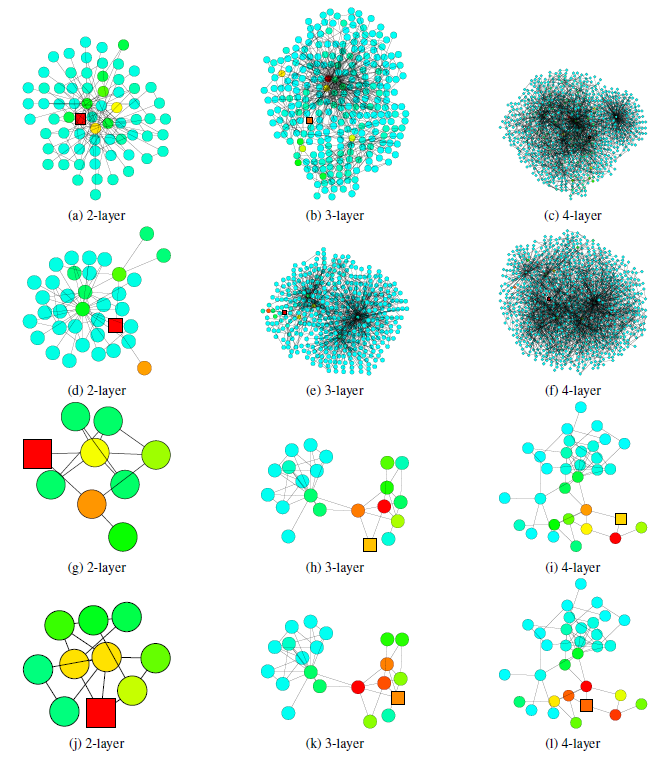
GooglePlus的社交网络,该图说明了从正方形节点开始的随机游走的扩散(随机游走的扩散也代表了影响力分布的扩散)。可以看到:不同结构的子图带来不同的邻域范围。- 图
a中,来自核心区域内节点的随机游走很快就覆盖了几乎整个图(随机游走覆盖的节点以绿色表示)。 - 图
b中,来自tree形区域节点的随机游走经过相同的step之后,仅覆盖图的一小部分(随机游走覆盖的节点以绿色表示)。 - 图
c中,来自tree形区域节点使用更长的step之后达到了核心区域,并且影响力突然快速扩散。
在
graph representation模型中,这种随机游走的扩散转换为影响力分布。这表明:在同一个图中,相同数量的随机游走step可以导致非常不同的效果。因此我们需要根据具体的图,同时结合较大的邻域范围和较小的邻域范围:- 太大的邻域范围可能会导致过度平滑,从而丢失局部信息。
- 太小的邻域范围可能信息不足,从而不足以支撑准确的预测。
- 图
JK network:上述观察提出一个问题:能否有可能对不同的图和不同的节点自适应地调整邻域范围。为此论文《Representation Learning on Graphs with Jumping Knowledge Networks》提出了JK-Net框架,该框架在网络最后一层选择性地组合不同邻域范围,从而自适应地学习不同邻域的局部性locality。如,将不同邻域范围jump到最后一层,因此这个网络被称作Jumping Knowledge Networks: JK-Nets。相关工作:谱图卷积神经网络
spectral graph convolutional neural network使用图拉普拉斯特征向量作为傅里叶基,从而在图上应用卷积。与诸如邻域聚合之类的空间方法spatial approach相比,谱方法spectral method的一个主要缺点是:需要提前知道图拉普拉斯矩阵(是transductive的)。因此,谱方法无法推广到unseen的图。
15.1 模型
定义图
定义图
假设基于消息传递的模型有
hidden feature为hidden feature的维度。为讨论方便,我们选择所有层的hidden feature维度都相等。另外,我们记定义节点
则典型的消息传递模型可以描述为:对于第
hidden feature更新方程为:其中:
AGG为聚合函数,不同的模型采用不同的聚合函数。
GCN图卷积神经网络(《Semi-supervised classification with graph convolutional networks》)hidden feature更新方程为:其中
degree。《Inductive representation learning on large graphs》推导出一个在inductive learing中的GCN变体(即,GraphSAGE),其hidden feature更新方程为:其中
degree。Neighborhood Aggregation with Skip Connections:最近的一些模型并没有同时聚合节点及其邻域,而是先聚合邻域,然后将得到的neighborhood representation和节点的上一层representation相结合。其hidden feature更新方程为:其中
在这种范式中,
COMBINE函数是关键,可以将其视为跨层的跳跃连接skip connection。 对于COMBINE的选择,GraphSAGE在特征转换之后直接进行拼接,Column Network对二者进行插值,Gated GCN使用GRU单元。但是,该跳跃连接是
input-specific的,而不是output-specific的。考虑某个节点skip。则后续更高层skip。我们无法做出这样的选择:对于第skip、对于第skip。即跳跃连接是由输入决定,而不是由输出决定。因此,跳跃连接无法自适应地独立调整final-layer representation的邻域大小。Neighborhood Aggregation with Directional Biases:最近有些模型没有平等地看到邻域节点,而是对“重要”的邻居给与更大的权重。可以将这类方法视为directional bias的邻域聚合,因为节点受到某些方向的影响要大于其它方向。例如:
GAT和VAIN通过attention机制选择重要的邻居,GraphSAGE的max-pooling隐式地选择重要的邻居。这个研究方向和我们的研究方向正交。因为它调整的是邻域扩张的方向,而我们研究的是调整邻域扩张的范围。我们的方法可以和这些模型相结合,从而增加模型的表达能力。
在下文中,我们证明了
JK-Net框架不仅适用于简单的邻域聚合模型(GCN),还适用于跳跃连接 (GraphSAGE)和directional bias(GAT)。
15.1.1 影响力分布
我们首先利用
《Understanding black-box predictions via influence functions》中的敏感性分析sensitivity analysis以及影响力函数的思想,它们衡量了单个训练样本对于参数的影响。给定节点representation。从这个影响范围,我们可以了解到节点我们通过衡量节点
final representation的影响程度,从而测量节点影响力得分和分布的定义:给定一个图
hidden feature,final representation。定义雅可比矩阵:
定义节点
influence score为:雅可比矩阵其中:
定义节点
influence distribution为:所有节点对于节点对于任何节点
representation的影响。考虑在
其物理意义为:随机游走第
类似的定义适用于具有非均匀转移概率的随机游走。
随机游走分布的一个重要属性是:如果图是非二部图
non-bipartite,则它随着spread,并收敛到极限分布。收敛速度取决于以节点spectral gap(或者conductance) 的限制bounded。
15.1.2 模型分析
不同聚合模型和节点的影响力分布可以深入了解各个
representation所捕获的信息。以下结果表明:常见的聚合方法的影响力分布和随机游走分布密切相关。这些观察暗示了我们接下来要讨论的优缺点。假设
relu在零点的导数也是零(实际上relu函数在零点不可导),则我们得到GCN和随机游走之间的关系:定理:给定一个
GCN变体,假设以相同的成功率证明:令
则有:
这里我们简化了
这里
假设存在
其中
则根据链式法则,我们有:
对于每条路径
现在我们考虑偏导数
其中
relu激活函数在假设
因此有:
另外,我们知道从节点
假设每一层的权重相同:
这里的证明缺少了很多假设条件的说明,因此仅做参考。
很容易修改上述定理的证明,从而得到
GCN版本的近似结果。唯一区别在于,对于随机游走路径其中
degree接近时。类似地,我们也可以证明具有
directional bias的邻域聚合方案类似于有偏的随机游走分布。这可以通过替换掉上述定理中相应的概率得到证明。从经验上看,我们观察到即使假设有所简化,但是我们的理论分析仍然接近于实际情况。
我们可视化了训练好的
GCN的节点(正方形标记)的影响力分布的热力图,并与从同一节点开始的随机游走分布的热力图进行比较。较深的颜色对应于较高的影响力得分(或者较高的随机游走概率)。我们观察到GCN的影响力分布对应于随机游走分布。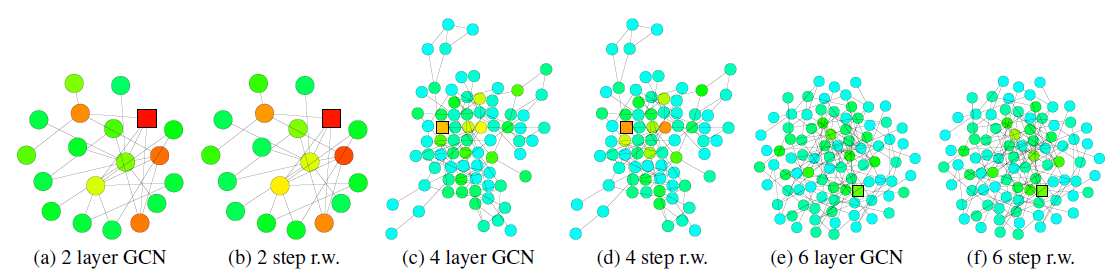
为显示跳跃连接的效果,下图可视化了一个带跳跃连接的
GCN的节点的影响力分布热力图。同样地,我们发现带跳跃连接的GCN的节点影响力分布大致对应于lazy随机游走分布(lazy表示每步随机游走都有较高的概率停留在当前节点,这里lazy因子为0.4)。由于每次迭代过程中,所有节点的局部信息都以相似的概率进行保留,因此这无法适应不同高层节点的各种各样的需求。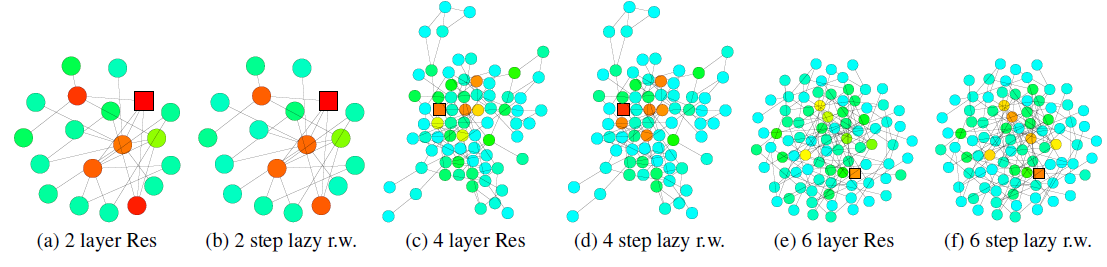
为进一步理解上述定理,以及相应邻域聚合算法的局限性,我们重新审视了下图中社交网络的学习场景。
- 对于
expander(左图)内部开始的随机游走以step快速收敛到几乎均匀分布。根据前述的定理,在经过representation几乎受到expander中所有任何其它节点的影响。因此,每个节点的representation将代表global graph,以至于过度平滑并带有节点自身的非常少的信息。 - 对于
tree-like(右图)开始的随机游走,其收敛速度较慢。这使得经过消息传递模型的聚合之后,每个节点的representation保留了更多的局部信息。
如果消息传递模型的层数
representation。
- 对于
最后我们描述了热力图的相关细节,并提供了更多的可视化结果。
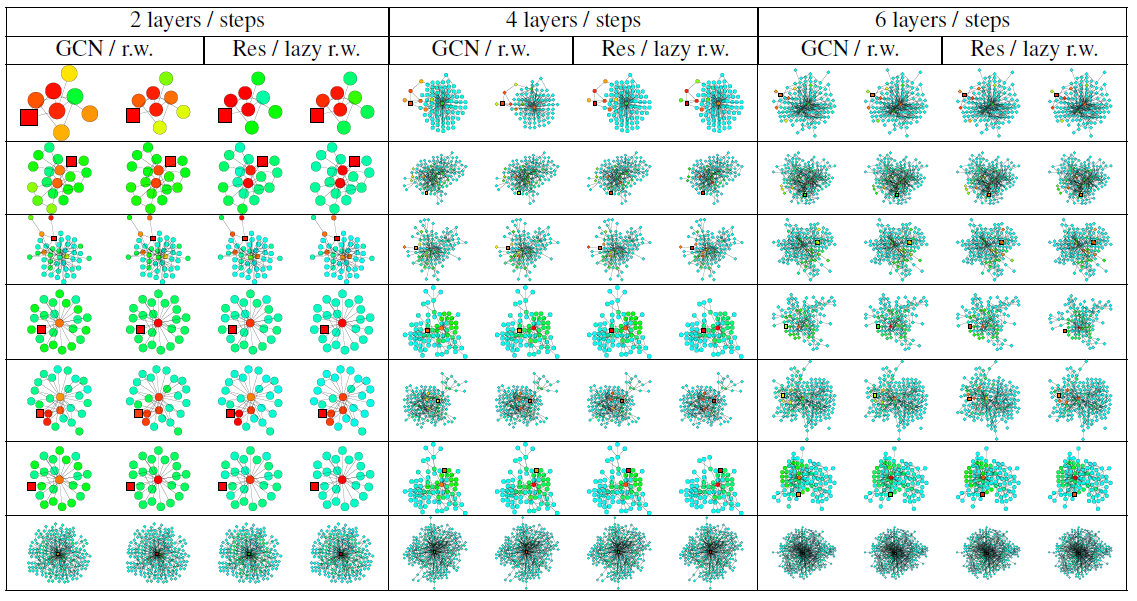
热力图中的节点颜色对应于影响力分布得分或者随机游走分布的概率。颜色越浅则得分越低、颜色越深则得分越高。我们使用相同的颜色来表示得分(或者概率)超过
0.2的情形,因为很少有节点的影响力得分(或概率)超过0.2。对于得分(或概率)低于0.001的节点,我们没有在热力图中展示。首先我们比较
GCN的影响力分布vs随机游走概率分布,以及带跳跃连接的GCN的影响力分布vs惰性随机游走概率分布。目标节点(被影响的节点或者随机游走的起始节点)标记为方块。
数据集为
Cora citation网络,模型分别为2/4/6层训练好的GCN(或者带跳跃连接的GCN Res)。我们使用《Semi-supervised classification with graph convolutional networks》描述的超参数来训练模型。影响力分布、随机游走分布根据前述的公式进行计算。
lazy随机游走使用lazy factor = 0.4的随机游走,即每个节点在每次转移时有0.4的概率留在当前节点。注意:对于
degree特别大的节点,GCN影响力和随机游走概率的颜色有所不同。这是因为我们这里的GCN是基于公式这使得在
GCN影响力模型中,degree更大的节点,其权重越低。
然后我们考察了不同子结构,这些可视化结果进一步支持了前述的定理。
下图中,使用
2层的GCN模型分类错误,但是使用3层或4层GCN模型分类结果正确。当局部子图结构是
tree-like时,如果仅仅使用2层GCN(即查看2-hop邻域),则抽取的信息不足以支撑其预测正确。因此,如果能够从3-hop邻域或4-hop邻域中抽取信息,则可以学到节点的局部邻域的更好表示。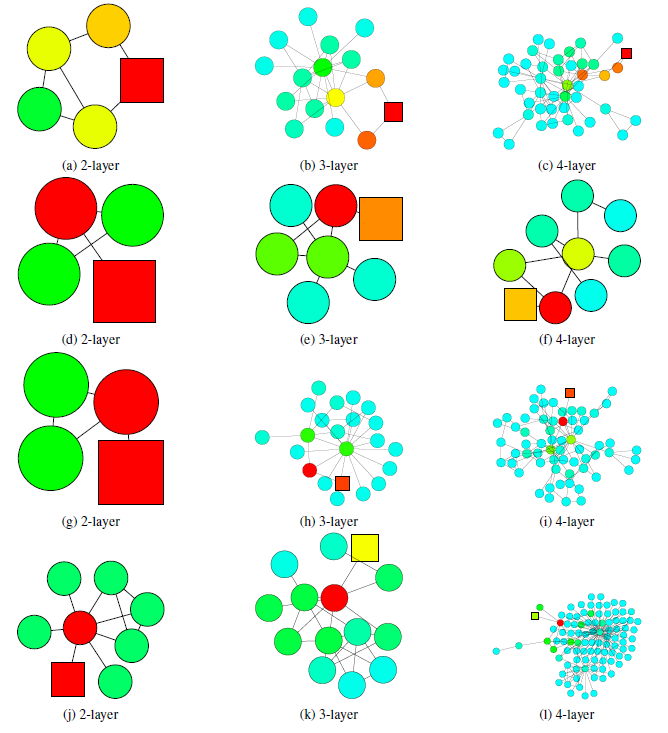
下图中,使用
3或4层的GCN模型分类错误,但是使用2层GCN模型分类结果正确。这意味着从3-hop或4-hop邻域中抽取了太多无关的信息,从而使得节点无法学到正确的、有助于预测的representation。- 在
expander子结构中,随机游走覆盖的节点爆炸增长,3-hop或者4-hop几乎覆盖了所有的节点。因此这种全局信息的representation对于每个节点的预测不是很理想。 - 在
bridge-like子结构中,抽取更远的节点的信息可能意味着从一个完全不同的community中获取信息,这可能意味着噪音并影响最终预测。
- 在
15.1.3 JK-Net
前述观察提出了一个问题,即:在通用聚合方案中使用固定的、但是结构依赖的影响力半径大小是否能够实现所有任务中节点的
best representation。- 如果选择的影响力半径过大,则可能导致过度平滑
oversmoothing。 - 如果选择的影响力半径国小,则可能导致聚合的信息量不足。
为此,我们提出了两个简单有效的体系结构调整:跳跃连接 + 自适应选择的聚合机制。
如下图所示为
JK-Net的主要思想。- 和常见的邻域聚合网络一样,每一层都是通过聚合来自上一层的邻域来扩大影响力分布的范围。
- 但是在最后一层,对于每个节点我们都从所有的这些
itermediate representation中仔细挑选(jump到最后一层),从而作为最终的节点representation。
由于这是针对每个节点独立完成的,因此模型可以根据需要为每个节点调整有效邻域范围,从而达到自适应的效果。
可以理解为常规的
GCN模型之上再添加一个聚合层。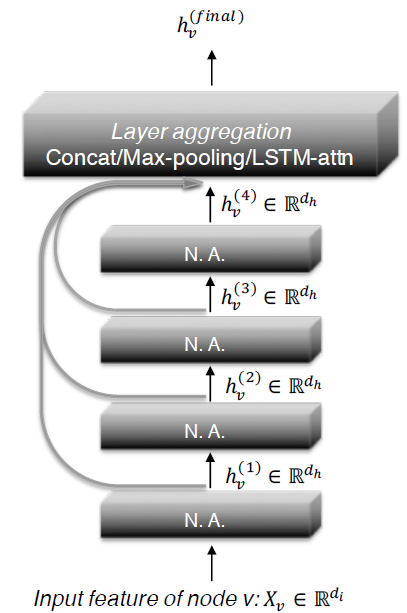
- 如果选择的影响力半径过大,则可能导致过度平滑
JK-Net也使用通用的层聚合机制,但是最终的节点representation使用自适应选择的聚合机制。这里我们探索三种主要的聚合方法,其它方法也可以在这里使用。令
representation(每个中间层代表了不同的影响力范围),并将它们jump到最后一层。concatenation聚合:直接拼接- 如果这个线性变换的权重
node-adaptive的。 - 如果这个线性变换的权重
node-adaptive的。
- 如果这个线性变换的权重
max-pooling聚合:对feature coordinate选择信息最丰富的layer。这种方式是自适应的,并且不会引入任何其它额外的学习参数。LSTM-attention聚合:注意力机制通过对每个节点representation对于节点representation为所有中间层的representation的加权平均:对于
LSTM-attention:- 先将
LSTM的输入,并对每层LSTM hidden featureLSTM hidden feature - 然后通过对层
hidden feature - 然后通过一个
softmax layer应用到attention得分。 - 最后,将
attention得分的加权和,作为节点final representation。
LSTM-attention是node-adaptive的,因为不同节点的attention score是不同的。实验表明,这种方法适用于大型复杂的图。由于其相对较高的复杂度,会导致在小型图上过拟合。另外,也可以将
LSTM和最大池化相结合,即LSTM max-pooling。这种
LSTM聚合的方式太复杂,可以简单地基于- 先将
JK-Net的实现比较简单,大量的篇幅都在形容理论。但是,这里的理论仅仅是解释问题,并没有解决问题。这里的layer aggregation方式既没有理论解释,也没有解决问题(针对不同的节点自适应地选择不同的邻域大小):- 为什么如此聚合?论文未给出原因。
- 不同的聚合方式代表了什么样的领域大小?这里也没有对应的物理解释。
层聚合
layer aggregation函数设计的关键思想是:在查看了所有中间层学到的representation之后,确定不同影响力范围内子图representation的重要性,而不是对所有节点设置固定的、相同的影响力范围。假设
relu在零点的导数也是零(实际上relu函数在零点不可导),则layer-wise max-pooling隐式地自适应地学习了不同节点的局部影响力。layer-wise attention也是类似的。推论:假设计算图中相同长度的路径具有相同的激活概率
layer-wise max-pooling的JK-Net中,对于任意证明:假设经过层聚合之后节点
representation为其中
根据前述的定理,我们有:
其中:
下图给出了采用
max-pooling的6层JK-Net如何学习从而自适应引文网络上不同的子结构。在
tree-like结构中,影响力仍然停留在节点所属的small community中。相反,在
6层GCN模型中,影响力可能会深入到与当前节点不想关的其它community中;而如果使用更浅层的GCN模型,则影响力可能无法覆盖当前节点所在的community。对于
affiliate to hub(即bridge-like)节点,它连接着不同的community,JK-Net学会了对节点自身施加最大的影响,从而防止将其影响力扩散到不想关的community。GCN模型不会捕捉到这种结构中节点自身的重要性,因为在几个随机游走step之后,停留在bridge-like节点自身的概率很低。对于
hub节点(即expander),JK-Net会在一个合理范围内将影响力扩散到相邻节点上。这是可以理解的,因为这些相邻节点和hub节点一样,都具有信息性。

JK-Net的结构有些类似于DenseNet,但是一个疑问是:是否可以像DenseNet一样在所有层之间都使用跳跃连接,而不仅仅是中间层和最后一层之间使用跳跃连接。如果在所有层之间都使用跨层的跳跃连接,并使用layer-wise concatenation聚合,则网络结构非常类似于DenseNet。从
graph theory角度审视DenseNet,图像对应于规则的graph,因此不会面临具有变化的子图结构的挑战。确实,正如我们在实验中看到的,使用concatenation聚合的模型在更规则的图(如图像、结构良好的社区)上表现良好。作为更通用的框架,
JK-Net接受更通用的layer-wise聚合模型,并在具有更复杂结构的图上实现更好的structure-aware representation。
15.2 实验
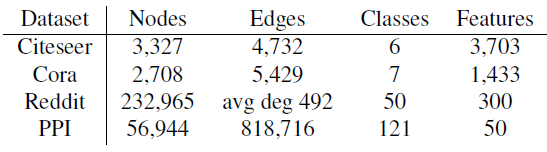
数据集:
引文网络数据集 (
Citeseer, Cora) :数据集中每个节点代表一篇论文,特征为论文摘要的bag-of-word,边代表论文之间的引用链接。节点类别为论文的主题。Reddit数据集:数据集中每个节点代表一个帖子,特征为帖子所有单词的word vector。如果某个用户同时在两个帖子上发表评论,则这两个帖子之间存在链接。节点类别为帖子所属的community。PPI数据集:数据集包含24个图,每个图对应于一个人体组织的蛋白质结构图。图中每个节点都有positional gene sets, motif gene sets, immunological signatures作为特征,gene ontology sets作为标签。我们使用
20个图进行训练、2个图进行验证、剩余的2个图作为测试。
数据集的统计信息如下表所示:
baseline模型:GCN、GraphSage、GAT。实验配置:
在
transductive实验中,我们只允许访问单个图中的节点子集作为训练数据,剩余节点作为验证集/测试集。在
Citeseer, Cora, Reddit数据集上的实验是transductive的。在
inductive实验中,我们使用多个完整的图作为训练数据,并使用训练时未见过的、剩余的图作为验证集/测试集。在
PPI数据集上的实验是inductive的。
对于
Citeseer和Cora数据集,我们选择GCN作为base模型,因为在我们的数据集实验中它超越了GAT。我们分别选择
MaxPooling(JK-MaxPool)、Concatenation(JK-Concat)、LSTM-attention(JK-LSTM)作为最终聚合层来构建JK-Net。在进行最终聚合时,被聚合的representation除了图卷积中间层的representation之外,我们还考虑了第一个线性变换的representation(可以理解为第零层的representation)。最终预测是通过final聚合层的representation之上的全连接层来完成。我们将每个图的节点根据
60%:20%:20%的比例随机拆分为训练集、验证集、测试集。对于每个模型,我们将层数从1到6,针对验证集选择性能最佳的模型(及其对应的卷积层深度)。JK-Net配置:- 学习率为
0.005的Adam优化器。 - 比例为
0.5的dropout。 - 从
hidden feature维度(Citeseer为16,Cora为32)。 - 在模型参数上添加
0.0005的
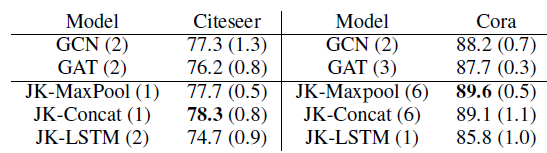
每组实验随机执行
3次并报告准确率accuracy的均值和标准差(标准差在括号中给出),实验结果如下表所示。可以看到:就预测准确率而言,
JK-Net优于GAT和GCN这两个baseline。尽管
JK-Net总体表现良好,但是没有始终如一的赢家,并且各个数据集上的性能略有不同。模型名字后面括号中的数字(
1~6之间)表示表现最佳的层数。仔细研究Cora的结果发现:GCN和GAT都在模型为2层或3层时才能达到最佳准确率。这表明局部信息比全局信息更有助于分类。层数越浅,则表明邻域范围越小,则表明是局部信息。
JK-Net在模型为6层上获得最佳性能,这表明全局信息和局部信息事实上都有助于提高性能。这就是JK-Net这类模型发挥价值的所在。
LSTM-attention可能由于复杂性太高,从而不适用于此类小模型。因此JK-LSTM在这两个数据集中表现最差。
- 学习率为
对于
Reddit数据集,由于它太大使得无法由GCN或GAT很好地处理。因此我们使用可扩展性更高的GraphSAGE作为JK-Net的base模型。在
GraphSAGE中存在不同的节点聚合方式,我们分别使用MeanPool和MaxPool来执行节点聚合,然后跟一个线性变换。考虑到JK-Net最后一层的三种聚合模式MaxPooling、Concatenation、LSTM-attention,两两组合得到6种JK-Net变体。我们采用和原始论文完全相同的
GraphSAGE配置,其中模型由两层卷积层组成,hidden layer维度为128维。我们使用学习率维0.01的Adam优化器,无权重衰减。实验结果如下表所示,评估指标维
Micro-F1得分。结论:当采用
MaxPool作为节点聚合器、Concat作为层聚合器时,JK-Net获得了最佳的Micro-F1得分。注意:原始的
GraphSAGE在Reddit数据集上的表现已经足够好(Micro-F1 = 0.950),JK-Net继续将错误率下降了30%。Reddit数据集中的社区是从表现良好的中等规模大小的社区中挑选而来,这是为了避免太大的社区中包含大量噪音、太小的社区是tree-like的。结果,该图比原始Reddit数据集更加规则,因此不会出现子图结构多样性的问题。在这种情况下,
node-specific自适应邻域选择所增加的灵活性可能不是那么重要,而concatenation的稳定特点开始发挥作用。这也是为什么JK-Concat效果较好的原因。
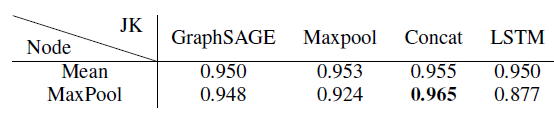
对于
PPI数据集,我们用它来证明自适应JK-Net的强大能力,该数据集的子图结构比Reddit数据集的子图结构更多样和复杂。我们将
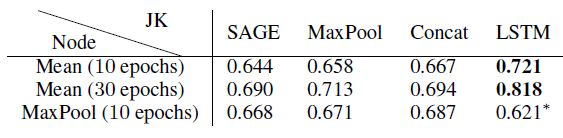
GraphSAGE和GAT都作为JK-Net的base model。GraphSAGE和GAT有很大的区别:GraphSAGE基于采样,其中对每个节点的邻域采样固定的邻居数量;GAT基于attention,它考虑每个节点的所有邻居。这种差异在可扩展性和性能方面导致巨大的差距。鉴于GraphSAGE可以扩展到更大的图,因此评估JK-Net在GraphSAGE上的提升显得更有价值。但是我们的实验在二者上都进行。我们的评估指标为Micro-F1得分。对于
GraphSAGE,我们遵循Reddit实验中的配置,只是在可能的情况下使用3层网络,并训练10到30个epoch。带有*的模型采用2层(由于GPU内存限制),其它模型采用3层。作为对比,采用两层的GraphSAGE性能为0.6(未在表中给出)。实验结果见下表。
对于
GAT及其JK-Net变体,我们使用两层或三层网络,其中有4个attention head,每个head有256维(共1024维)。最后一个预测层有6个attention head,每个head有121维。我们将这6个head执行均值池化,并灌入到sigmoid激活函数。我们在中间attention层之间引入跳跃链接。所有这些模型都使用学习率为
0.005的Adam优化器,并使用batch size = 2的mini-batch训练。我们的
baseline为GAT和MLP模型,网络层数从2,3之间选择。由于GPU内存限制,JK-Dense-Concat和JK-Dense-LSTM的层数为2。实验结果见下表。
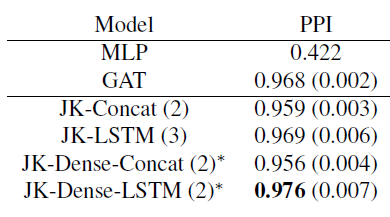
结论:
- 带有
LSTM-attention聚合器的JK-Net超越了具有concatenation聚合器的非自适应性JK-Net模型,以及GraphSAGE/GAT/MLP等baseline模型。 - 在训练
30个epoch之后,JK-LSTM在Micro-F1得分上比GraphSAGE高出0.128(绝对提升)。 - 结构感知的节点自适应模型在
PPI这类具有不同结构的复杂图上特别有效。
- 带有
十六、PPNP[2018]
目前有很多流行的图神经网络算法。
graph embedding算法使用随机游走或矩阵分解来直接训练每个节点的embedding,这类算法通常以无监督的方式学习并且不需要节点的特征信息。- 另外一些方法以有监督方式学习,并且同时利用了图结构和节点特征信息,其中包括谱图卷积神经网络
spectral graph convolutional neural network、消息传递message passing方法(或者也称作邻域聚合neighbor aggregation方法)以及基于RNN的邻域聚合方法。
所有这些方法中,消息传递方法由于其灵活性和良好的性能最近引起了特别的关注。已有一些工作通过使用
attention机制、随机游走、edge feature来改善基础的邻域聚合方式,并使得邻域聚合可以扩展到大图。但是,所有这些方法对于每个节点仅支持非常有限的邻域规模。事实上,如果能够使用更大的邻域,则可以为模型提供更多的有效信息。尤其是对于图的外围节点或者标签稀疏的节点。增加这些算法的邻域大小并不简单,因为这些方法中的邻域聚合本质上是拉普拉斯平滑的一种,如果层数太多将导致过度平滑
over-smoothing。在JK-Net的论文中,作者强调了这个挑战,并建立了随机游走和消息传递机制之间的关联。通过这个关联我们发现:随着层数的增加,GCN会收敛到随机游走的极限分布。这个极限分布是整个图的属性,和随机游走的起始节点无关。因此这个分布无法描述随机游走起始节点的邻域(因为过度平滑)。因此GCN的性能必然会随着卷积层数量(具体而言是随着aggregation层的数量)的增加而下降。为解决这个问题,论文
《 PREDICT THEN PROPAGATE: GRAPH NEURAL NETWORKS MEET PERSONALIZED PAGERANK》首先分析了这个极限分布和PageRank之间的内在联系,然后提出了personalized propagation of neural predictions: PPNP算法,该算法利用Personalized PageRank衍生而来的消息传递方案。PPNP算法增加了消息回传根节点的机会,从而确保PageRank Score编码了每个根节点的局部邻域。这个回传概率teleport probability使得我们能够平衡以下两方面的需求:保留节点的局部性(即,避免过度平衡)vs利用来自大型邻域的信息。作者表明,这种消息传递方案允许使用更多的层(理论上无限多),而不会导致过度平滑。另外,
PPNP的训练时间相比以前的模型相同或者更快,参数数量相比以前的模型相同或者更少,计算复杂度和边的数量呈线性关系。此外,PPNP利用一个大的、可调整的邻域来分类,并且可以轻松地和任何神经网络相结合。实验表明,PPNP超越了最近提出的几种GCN-like的半监督分类模型。在传统的消息传递方法中,
propagation和classification固有地耦合在一起,即classification依赖于propagation。但是在PPNP中,作者将propagation和classification解耦,使得二者相互独立。这使得我们能够在不改变神经网络的情况下实现更大的邻域。而在消息传递方法中,如果想多传递一个step就需要多加一个layer。PPNP的基本思想是:首先预测节点的标签(classification步骤),然后利用标签传播算法重新修正得到最终的标签(propagation步骤)。这种方法有效的前提是:相邻节点具有相似的label。PPNP还允许传播算法、以及根据节点特征执行预测的神经网络独立开发。这意味着我们可以将任何state-of-the-art预测方法和PPNP的传播算法相结合。作者甚至发现:在训练期间没有使用到任何图结构信息的模型,仅在inference阶段使用PPNP的传播算法可以显著提升模型预测的准确性。相关工作:
有些工作试图在每个节点添加跳跃连接,从而改善消息传递算法的训练,以及增加每个节点上可用的邻域大小。如,
JK-Net将跳跃连接和邻域聚合方案相结合。但是这些方法的邻域范围仍然有限,当消息传递的layer数量很少的情况下非常明显。虽然可以在我们的
PPNP中使用的神经网络中添加跳跃连接,但是这不会影响我们的传播方案。因此,我们解决邻域范围的方法和这些模型无关。《Deeper Insights Into Graph Convolutional Networks for Semi-Supervised Learning》通过将消息传递和co-training & self-training相结合来促进训练,通过这种组合实现的改善与其它半监督分类模型报告的结果相似。注意,大多数算法,包括我们的算法,都可以用
co-training & self-training进行改进。但是,这些方法使用的每个additional setp都对应一个完整的训练周期,因此会大大增加训练时间。在最近的工作中,人们通过将跳跃连接和
batch normalization相结合,提出了避免过度平滑问题的Deep GNN(《Mean-field theory of graph neural networks in graph partitioning》、《Supervised Community Detection with Line Graph Neural Networks》)。但是,我们的模型通过解耦预测和传播,从而简化了体系结构并解决该问题。并且我们的方法不依赖于任何临时性
ad-hoc技术,这些临时性的技术进一步复杂化模型并引入额外的超参数。此外,我们的
PPNP在不引入额外层的情况下增加了邻域范围,因此和Deep GNN相比,训练速度会更快更容易。
16.1 模型
定义图
假设每个节点
假设每个节点
one-hot向量假设图的邻接矩阵为
self-loops的邻接矩阵。
16.1.1 GCN 及其限制
卷积神经网络
GCN是一种用于半监督分类的简单且应用广泛的消息传递算法。假设有两层消息传递,则预测结果为:其中:
label分布。
对于两层
GCN,它仅考虑2-hop邻域中的邻居节点。基本上有两个原因使得消息传递算法(如GCN)无法自然地扩展到使用更大的邻域:- 首先,如果使用太多的层,则基于均值的聚合会导致过度平滑
over-smoothing。因此,模型失去了局部邻域的信息。 - 其次,最常用的邻域聚合方案在每一层使用可学习的权重矩阵,因此使用更大的邻域必然会增加神经网络的深度和参数数量。虽然参数数量可以通过权重共享来避免,但这不是通用的做法。
理论上,邻域大小和神经网络的深度是不相关的、完全正交的两个因素。它们应该互不影响才对。实际上在
GCN中它们是相互捆绑的(给定神经网络深度就意味着给定了邻域大小),并导致了严重的性能问题。我们首先关注第一个问题。在
JK-Net中已经证明:对于一个GCN,任意节点如果选择极限
irreducible且非周期性的,则这个随机游走概率分布显然,极限分布取决于整个图,并且独立于随机游走的起始节点
16.1.2 PPNP
我们可以考察极限分布和
PageRank之间的联系来解决这个局部邻域失去焦点lost focus问题。极限分布和
PageRank的区别仅在于前者在邻接矩阵中增加了自循环,并对分布进行了归一化。原始的PageRank的分布为:其中
建立这种联系之后,我们现在可以考虑使用结合了根节点的
PageRank变体 --Personalized PageRank。我们定义回传向量
teleport vectorone-hot向量,只有节点1、其它元素为0。对于节点
Personalized PageRank的分布为:其中
teleport probability(也叫做重启概率)。通过求解该等式,我们得到:
可以看到:通过使用回传向量
因为在该模型中,节点
考虑所有节点的回传向量,则我们得到了完整的
Personalized PageRank矩阵其中
注意到由于对称性
事实上这里需要考虑矩阵
证明:要想证明矩阵
由于
通过
Gershgorin circle theorem可以证明1,因此为了将上述影响力得分用于半监督分类,我们首先根据每个节点的自身特征来生成预测
prediction,然后通过我们的Personalized PageRank机制来传播prediction从而生成最终的预测结果。这就是personalized propagation of neural predictions: PPNP的基础。PPNP模型为:其中:
注意:由于
PPNP每个节点预测的label分布。
事实上,还可以用任何传播矩阵来代替
可以看到,
PPNP将神经网络预测和图的传播相互分离。这种分离还解决了上述提到的第二个问题:神经网络的深度现在完全独立于传播算法。正如我们将在GCN和PageRank联系时所看到的,Personalized PageRank能够有效地使用无限多个卷积层,这在传统的消息传递框架中显然是不可能的。此外,分离还使得我们可以灵活地运用任何方法来生成预测。这个就是标签传播
label propagation: LP的思想,将MLP和LP相结合。该方法有效的前提是:相邻节点具有相似的label。PPNP传播的是prediction,而传统GCN传播的是representation。虽然在
inference阶段,生成单个节点的预测和传播这个预测是连续进行的(看起来是多阶段的),实际上模型的训练是端到端的。即,在反向传播期间梯度流经传播框架(相当于隐式地考虑了无限多个邻域聚合层)。因此,采用传播框架之后大大提高了模型的准确性。
16.1.3 APPNP
直接计算完整的
Personalized PageRank矩阵为解决这个问题,重新考虑等式:
除了将
Personalized PageRank矩阵prediction矩阵Topic-sensitive PageRank的变体,其中每个类别对应于一个主题。在这个角度下,teleport set。因此,我们可以通过采用Topic-sensitive PageRank来近似计算PPNP,我们称其为approximate personalized propagation of neural predictions: APPNP。APPNP通过Topic-sensitive PageRank的幂次迭代power iteration来达到线性复杂度。Topic-sensitive PageRank的幂次迭代和带重启的随机游走相关,它的每个幂次迭代步定义为:其中:
prediction矩阵starting vector和teleport set的作用;注意:这个方法保持了图的稀疏性,并且从未构建一个
但是,
可以证明:当
APPNP收敛到PPNP。证明:
APPNP的迭代公式:在经过
当取极限
这就是
PPNP。PPNP/APPNP的传播框架propagation scheme不需要训练任何其它额外的参数。与GCN这样的模型不同,GCN通常需要为每个propagation layer(GCN中的传播层就是聚合层)提供更多的参数。因此,PPNP/APPNP中可以使用很少的参数传播得更远。实验结果表明:这种传播能力确实非常有益。将
PPNP视为不动点fixed-point迭代,这和最原始的图神经网络GNN模型存在关联。图神经网络中也是需要通过迭代来求解不动点,但是PPNP和GNN存在以下几点不同:PPNP的不同点迭代实际上通过Personalized PageRank已经求解到,因此直接使用Personalized PageRank矩阵PPNP在传播之前应用学到的特征变换,而GNN中在传播过程中应用学到的特征变换。
PPNP/APPNP中,影响每个节点的邻域大小可以通过回传概率最后,我们给出
PPNP模型的示意图。- 首先利用神经网络
- 然后使用
Personalized PageRank来传播预测
注意该模型是端到端训练的,而不是
pipeline训练的。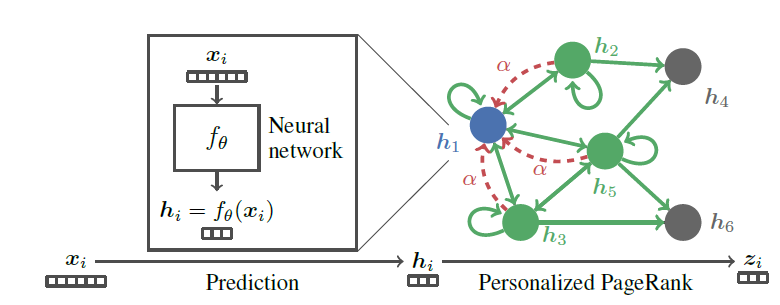
- 首先利用神经网络
16.2 实验
数据集:我们使用四个文本分类数据集。
CITESEER:引文网络,每个节点代表一篇论文,边代表它们之间的引用。CORA-ML:引文网络,每个节点代表一篇论文,边代表它们之间的引用。PUBMED:引文网络,每个节点代表一篇论文,边代表它们之间的引用。MICROSOFT ACADEMIC数据集:引文网络,每个节点代表一篇论文,边代表co-authorship。
对于每个图,我们使用其最大连通分量。所有数据集都使用论文摘要的
bag-of-word作为特征。下图给出了这些数据集的统计信息,其中SP表示平均最短路径长度。注意:更大的图不一定具有较大的直径(以
SP来衡量)。总体而言,这些图的平均直径为5~10,因此常规的两层GCN网络无法覆盖整个图。
因为使用了不同的训练配置和过拟合,很多实验评估都遭受了肤浅的统计评估
superficial statistical evaluation和实验偏差experimental bias。实验偏差的原因是:对于训练集/验证集/测试集的单次拆分没有明显区分验证集和测试集,或者对于每个数据集甚至是数据集的每次拆分都微调超参数。正如我们评估结果中显示的,消息传递算法对于数据集的拆分以及权重初始化非常敏感,因此精心设计的评估方法非常重要。
我们的工作旨在建立一个全面彻底的评估方法:
首先,我们对每个实验执行
100次,其中每次都是随机拆分训练集并随机初始化权重。我们采用Glorot权重初始化方法。其次,我们将数据集拆分为可见集和测试集,这种拆分固定不变。其中测试集仅用于报告最终性能,并不会进行训练和超参数择优。
- 对于引文网络,可见集采样了
1500个节点,剩余节点为测试集。 - 对于
MICROSOFT ACADEMIC网络,可见集采样了5000个节点,剩余节点为测试集。
可见集被随机拆分为训练集、验证集、以及早停集。训练集中每种类别包含
20个节点,早停集包含500个节点,剩余节点作为验证集。我们选择
20个不同的随机数种子并固定下来,接下来选择其中的一部分用于随机拆分可见集--测试集、另一部分用于随机拆分训练集--验证集。 另外,每种数据拆分都进行5次随机初始化,因此实验一共进行100次。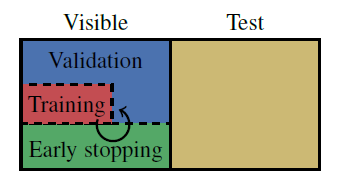
- 对于引文网络,可见集采样了
为进一步防止过拟合,考虑到所有实验的数据集都使用
bag-of-word特征,因此我们对所有数据集都采用相同数量的层数、相同的hiddel layer维度、相同的dropout比例、相同的为防止实验偏差,我们使用
CITESEER和CORA-ML上的网格搜索来分别优化所有模型的超参数,并在模型之间使用相同的早停准则:patience = 100的阈值,以及最多epoch(实际上永远无法达到这么多epoch)。只要在早停数据集的准确率提升或者损失函数降低,则重设
patience。我们选择在早停数据集上准确率最高的patience。该准则受到GAT的启发。最后,为了确保我们实验配置的统计鲁棒性,我们通过
bootstrapping计算出置信区间,并报告主要结论的t-test的p-value。
据我们所知,这是迄今为止对
GCN模型的最严格的研究。Baseline方法:GCN:图卷积神经网络。N-GCN:结合了无监督的随机游走和半监督学习两方面优势的N-GCN模型。GAT:图注意力神经网络。bootstrapped feature propagation: FP:将经典的线性的图扩散结合self-training框架,从而得到的FP网络。jumping knowledge networks with concatenation: JK:JK-Net网络。- 对于
GCN我们还给出了未经过超参数优化的普通版本V.GCN来说明早停和超参数优化的强大影响。
模型配置:
V.GCN:使用原始论文的配置,其中包括两层的卷积层、隐层维度dropout、200个step,以及早停的patience = 10。择优的
GCN:使用两层卷积层、隐层维度dropout rate = 0.5的dropout、N-GCN:每个随机游走长度使用4个head以及隐层维度1 step到4 step。使用attention机制来合并所有head的预测。GAT:使用优化好的原始论文的超参数,除了0.01。和原始论文相反,对于PUBMED数据集我们并未使用不同的超参数。FP:使用10个传播step、10个self-training step,每个step增加我们在预测中添加交叉熵最小的训练节点。每个类别添加的节点数基于预测的类别的比例。注意,该模型在初始化时不包含任何随机性,因此我们在每个
train/early stopping/test集合拆分时仅拆分一次。JK-Net:我们使用concatenation层聚合方案,采用三层卷积神经网络,每层的隐层维度dropout rate = 0.5的dropout。但是正则化和dropout并不作用在邻接矩阵上。PPNP:为确保公平的模型比较,我们为PPNP的预测模型使用了神经网络,该网络在结构上和GCN非常相似,并具有相同的参数数量。我们使用两层网络,每层的隐层维度为我们在第一层的权重矩阵上应用
dropout rate = 0.5的dropout。对于
APPNP,我们在每个幂次迭代步之后,都会对邻接矩阵的dropout重新采样。对于传播过程,我们使用
对于
MICROSOFT ACADEMIC数据集,我们使用
注意:
PPNP使用浅层的神经网络和较大的APPNP不同深度的网络对于验证集的准确率。可以看到:更深的预测网络无法提高准确率,这可能是因为简单的Bag-of-word特征以及训练集太小导致的。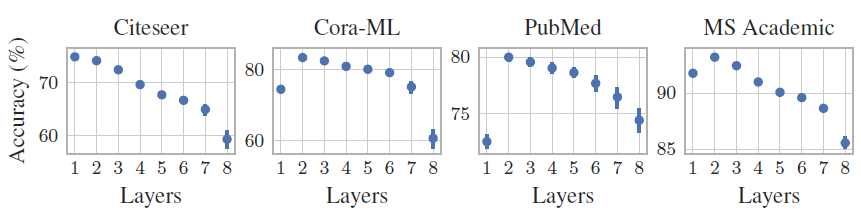
另外,我们使用
Adam优化器并且所有模型的学习率都为0.01。我们使用交叉熵损失函数,并且将特征矩阵按行进行不同模型在测试集上的指标如下表所示,其中第一张表为
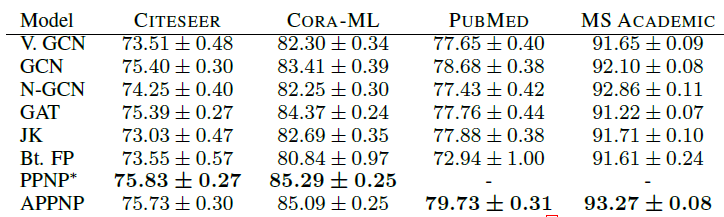
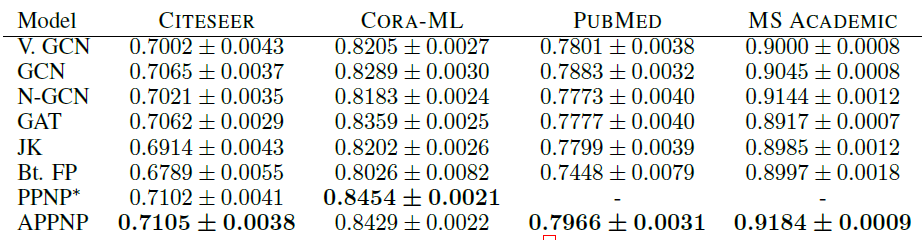
Micro-F1 Score,第二张表为Macro-F1 Score,最后两张表为t检验结果。*表示模型在PUBMED, MS ACADEMIC上Out Of Memory。结论:
我们的
PPNP/APPNP在所有数据集上均明显优于SOA baseline方法。我们的严格的比较方式可能会低估
PPNP/APPNP的优势。通过t检验表明,该比较结果具有统计学意义这种严格的比较方式还表明:当考虑更多的数据集拆分、适当地超参数优化、合理地模型训练时,最近的一些工作(如
N-GCN, GAT, JK-Net, FP等)的优势实际上消失了。在我们的配置中,一个简单的、经过超参数优化的
GCN就超越了最近提出的这几种模型。

我们给出不同模型在不同数据集上,由于不同的随机初始化以及不同的数据集拆分带来的测试准确率的变化。这表明严格的评估方式对于模型比较的结论至关重要。
此外,这还展示了不同方法的鲁棒性。如
PPNP, APPNP, GAT通常具有较低的方差。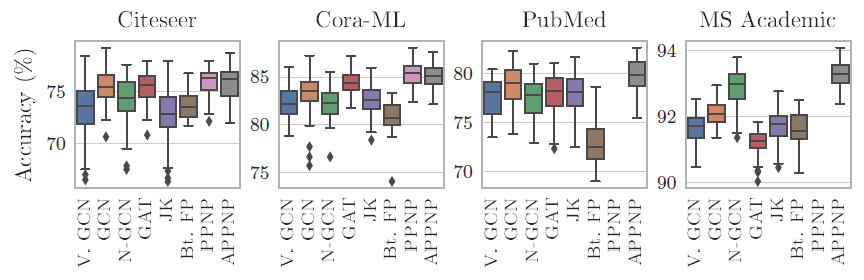
我们考虑不同模型的训练时间。这里考虑每个
epoch的平均训练时间(而不是整个训练过程的时间)。我们并未考虑收敛速度(需要多少个epoch收敛),因为不同模型的超参数都各自调优,并且不同模型使用的early stopping准则不同(调优之后各自的patience不一样)。*表示无法实现,因为无法训练;**表示在PUBMED, MS ACADEMIC上Out Of Memory。结论:
PPNP只能应用于中等规模的图,APPNP可以扩展到大图。平均而言,
APPNP比GCN慢25%,因为APPNP的矩阵乘法的数量更多。但是APPNP的可扩展性和GCN相似。APPNP比GCN慢一些但是效果好一点点,所以这是一个速度和效果的trade-off。此外,如果GCN总的训练时间与APPNP相同(即,GCN多25%的epoch),是否二者效果一致?这样的话,APPNP就没有什么优势了。APPNP比其它更复杂的模型(如GAT)快得多。

由于现实世界数据集的
label比例通常很小,因此研究小样本模型的性能非常重要。下图依次给出CORA_ML, CITESEER, PUBMED数据集上,每个类别训练节点数量结论:训练的
label节点越稀疏,PPNP/APPNP的优势越大。这可以归因于PPNP/APPNP较高的传播范围,从而将label节点传播到更远的地方。为支持这种归因,我们找到了更多的证据:我们比较了
APPNP和GCN的准确率的提升幅度 ,发现准确率提升幅度依赖于测试节点和训练集的距离(以最短路径衡量)。如下面最后一幅图所示,横坐标为最短路径(单位为hop),纵坐标为提升幅度,APPNP相对于GCN的性能提升,随着测试节点到训练集的距离的增加而增加。这表明距训练集较远的节点从APPNP的传播范围的增加中收益更多。
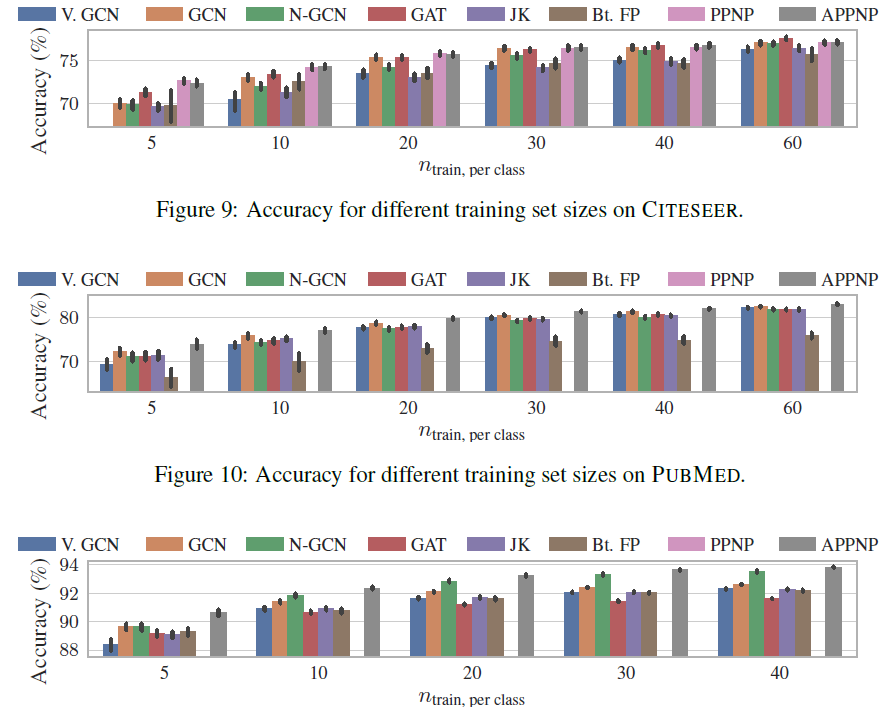
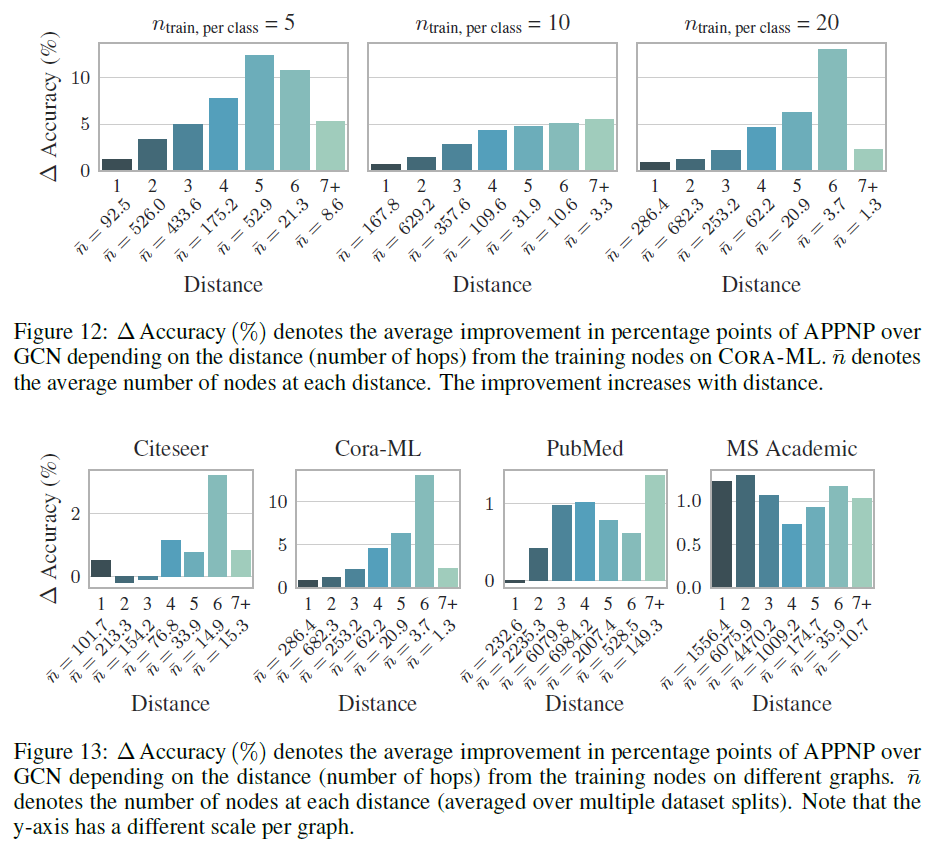
我们评估了幂次迭代
power iteration数量K来表示)对于模型准确性的影响。结论:
对于
GCN-like(对应于PageRank方法),其性能随着对于
APPNP(对应于Personalized PageRank),其性能随着当
APPNP收敛到PPNP。但是我们发现,当APPNP已经足以有效地逼近PPNP。有趣的是,我们发现这个数字和数据集的半径相符。
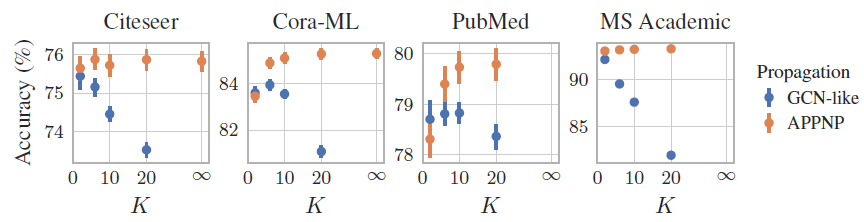
我们评估了超参数
结论:
- 尽管每个数据集的最优
- 应该对不同的数据集采用不同的
注意:较高的
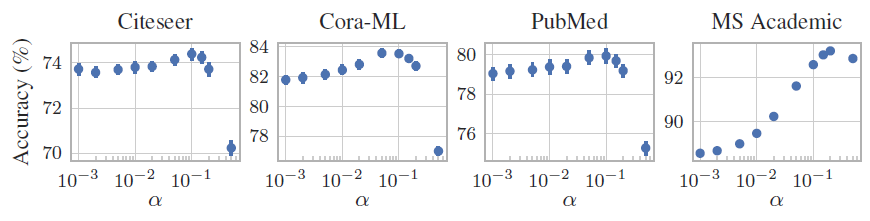
- 尽管每个数据集的最优
PPNP和APPNP虽然分为预测网络Never:表示从来不使用传播。这表示我们仅使用节点特征来训练和使用一个标准的多层感知机MLPTraining:表示我们使用APPNP来训练模型(采用了传播),但是在inference时仅使用Inference:表示我们仅使用特征来训练多层感知机inference时结合传播来预测。Inf & Training:表示常规的APPNP模型,即在训练和inference时总是使用传播。
结论:
Inf & Training总是可以获得最佳结果,这验证了我们的方法。在大多数数据集上,仅在
inference中使用传播时,准确率下降得很少。训练期间跳过传播可以大大减少大型数据集的训练时间,因为所有节点都可以独立地处理。
这也表明我们的模型可以与不包含任何图结构信息的预训练神经网络相结合,并可以显著提高其准确性。
Training相对于Never也有较大的改善。这表明仅在训练期间进行传播也是有价值的。因此我们的模型也可以应用于online/inductive learning,其中只有特征信息(而不是观察到的邻域信息)可用。

十七、VRGCN[2017]
图卷积网络
graph convolution network: GCN将卷积神经网络CNN推广到图结构化数据。图卷积graph convolution操作对节点的所有邻居应用相同的线性变换,然后是均值池化和非线性激活函数。通过堆叠多个图卷积层,GCN可以利用来自遥远邻居的信息来学习node representation。GCN及其变体已被应用于半监督节点分类、inductive node embedding、链接预测、 以及知识图谱,超越了不使用图结构的多层感知机MLP以及不使用节点特征的graph embedding方法。然而,图卷积操作使得
GCN难以高效地训练。考虑一个GCN,节点的第hidden feature需要递归地通过其邻域内所有节点的第hidden feature来计算。因此,如下图(a)所示,单个节点的感受野receptive field的大小随网络层数呈指数型增长。- 为解决感受野太大的问题,
《Semi-supervised classification with graph convolutional networks》提出通过batch算法来训练GCN,该方法同时计算batch内所有节点的representation。但是,由于batch算法收敛速度慢,以及需要将整个数据集放入到GPU中,因此无法处理大规模数据集。 《Inductive representation learning on large graphs》尝试邻域采样neighbor sampling: NS的方法为GCN提出随机训练算法。在NS算法中,他们并未考虑节点的所有邻居,而是为每个节点在第(b)所示。这可以将感受野的大小减小到GCN网络,选择GCN相当的性能。
理论上当
MLP。虽然Hamilton的方法复杂度降低,但是仍然比MLP要大另外,使用基于邻域采样的随机训练算法能否确保模型收敛,尚无理论上的保证。
在论文
《Stochastic Training of Graph Convolutional Networks with Variance Reduction》中,作者为GCN设计了新颖的基于控制变量的control variate-based随机逼近算法,即GCN with Variance Reduction: VRGCN。VRGCN利用节点的历史激活值(即历史hidden feature)作为控制变量control variate。作者表明:通过邻域采样NS策略得到的hidden feature的方差取决于hidden feature的幅度magnitude(因为hidden feature是一个向量),而VRGCN得到的hidden feature的方差取决于hidden feature和它历史均值之间的差异difference。另外,
VRGCN还带来了理论上的收敛性保证。VRGCN可以给出无偏的(相比较于原始的GCN)、零方差的预测。并且训练算法可以收敛到GCN损失函数的局部最优值,而与采样大小VRGCN可以通过仅对节点采样两个邻居节点来显著降低模型的时间复杂度,同时保持模型的质量。作者在六个
graph数据集上对VRGCN进行了实验测试,并表明VRGCN显著降低了具有相同感受野大小的NS的梯度的偏差bias和方差variance。尽管仅采样VRGCN在所有数据集上的可比数量的epoch中实现了与精确算法相同的预测性能,即,VRGCN降低了时间复杂度同时几乎没有损失收敛速度,这是我们可以预期的最好结果。在最大的Reddit数据集上,VRGCN算法的训练时间相比精确算法(《Semi-supervised classification with graph convolutional networks》)、邻域采样算法(《Inductive representation learning on large graphs》)、重要性采样算法(《Fastgcn: Fast learning with graph convolutional networks via importance sampling》)要少7倍。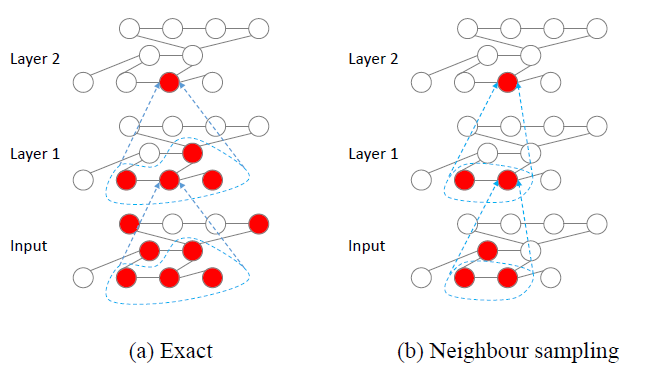
- 为解决感受野太大的问题,
17.1 模型
17.1.1 GCN
我们以半监督节点分类任务的
GCN作为说明,当然我们的算法不局限于任务类型,也不局限于模型类型。我们的算法适用于任何涉及到计算邻居平均激活值的其它模型,以及其它任务。给定图
每个节点
labellabel,这部分节点的集合记作label。定义邻接矩阵
定义传播矩阵
propagation matrix其中
self-loop的邻接矩阵。因此一个图卷积层可以定义为(假设当前为第
其中:
hidden feature矩阵,也称作激活矩阵activataion matrix。第
hidden feature向量,也称作激活值activation。
假设
GCN模型有GCN模型的训练损失函数为:其中:
final representation。
卷积层通过
hidden feature向量为:它就是
hidden feature的加权和。定义节点
receptive field为:为计算- 对于一个
GCN,节点L-hop邻域集合。 - 当
GCN退化为一个多层感知机MLP,其中不涉及任何图结构信息。对于多层感知机,节点
- 对于一个
GCN训练损失函数的batch梯度为:由于每次迭代都涉及整个标记节点集合
batch梯度代价太大。一个可行的方案是采用随机梯度作为
batch梯度的近似值:其中
mini-batch。但是,由于感受野太大,
mini-batch梯度的计算代价仍然很高。例如,NELL数据集的2-hop邻域平均包含1597个节点,这意味着在一个2层GCN中,为计算单个节点的梯度需要涉及1597/65755 = 2.4%的全部节点。
17.1.2 GraphSAGE
为降低感受野大小,
GraphSAGE提出了邻域采样neighbor sampling: NS策略。 在第NS策略随机采样hidden feature其中
因此
NS策略降低了感受野大小,从L-hop邻域大小降低到采样后的邻域大小我们将
NS估计量,而exact。上述邻域采样策略以矩阵的形式可以重写为:
其中传播矩阵
在
GraphSAGE的随机梯度下降过程中,存在两个随机性来源:- 选择
mini-batch - 选择大小为
尽管
NS策略中节点的final representaion矩阵NS策略中随机梯度下降SGD的收敛性得不到保障,除非采样大小- 选择
在
GraphSAGE中,由于梯度是有偏的,因此NS策略中的采样大小exact策略相近的预测性能。在
GraphSAGE中Hamilton选择MLP的感受野(大小为1),因此训练仍然代价较高。
17.1.3 FastGCN
FastGCN是另一种类似于NS的基于采样的算法。FastGCN并没有为每个节点采样邻域,而是直接采样每一层的、所有节点共享的感受野。对于第
FastGCN首先采样hidden feature其中重要性分布:
我们将这种邻域均值
hidden feature的估计称作重要性采样importance sampling: IS。- 注意,
IS采样策略和NS采样策略的区别在于:前者为第 - 当
IS可以视为NS,因为每个节点NS可以看作是IS的一种。
- 注意,
尽管
IS策略的感受野大小为NS策略的感受野大小IS仍然仅在采样大小从实验来看,我们发现
IS策略的效果要比NS更差,这是因为:在IS策略中我们为所有节点采样了共同的一组节点集合,对于部分节点我们采样到了它们的很多个邻居,对于另一些节点我们没有采样到任何邻居。对于后者,这些节点的邻域均值hidden featurehidden feature
17.1.4 控制变量
我们提出一种新的基于控制变量
control variate: CV的算法,该算法基于历史hidden feature来降低估计量的方差。当计算邻域均值
hidden featureaffordable的近似值。每次计算令
定义:
其中
这里的核心思想是:主要的
因为主要部分是精确值,次要部分是近似值,因此这会大幅度降低近似计算带来的影响。
则有:
hidden featureCV估计量。写作矩阵的形式为:其中
这里我们仅对
由于我们预期
即估计量的偏差和方差都为零。
我们定义控制变量
control variate为:我们将控制变量
NS的现在
采用
CV估计量来训练GCN的方法和NS估计量都相同。具体而言,在GCN的每轮迭代中都执行以下算法。VRGCN迭代算法:随机选择一个
mini-batch的节点构建一个计算图,其中包含当前
mini-batch每个节点的hidden feature计算时需要的其它节点的hidden feature根据下面的前向传播公式进行传播:
这里控制变量
通过反向传播计算梯度,并更新参数。
更新
hidden feature历史均值
其中,第二步的计算图是通过每层的感受野
hidden featuremini-batch。我们自顶向下构建
令
对于第
注意:我们假设
VRGCN的感受野如下图(c)所示,其中红色节点为感受野,其hidden featuremini-batch。蓝色节点的历史hidden feature均值mini-batch。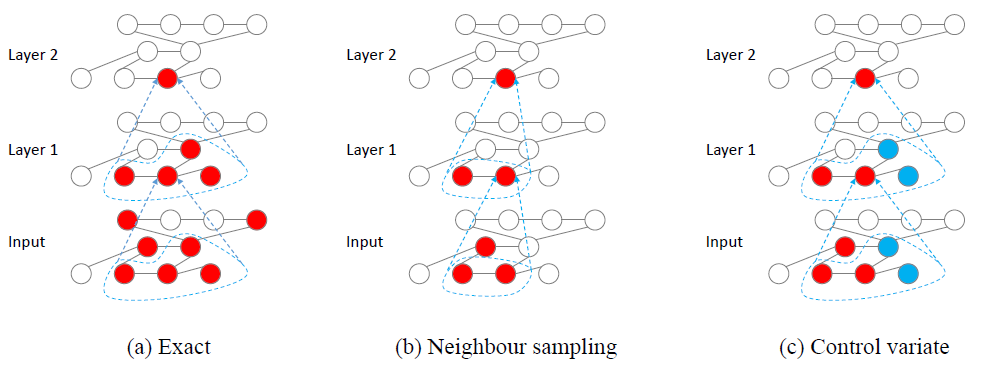
17.1.5 理论分析
为便于理论分析估计量的方差,这里我们假设所有的特征都是一维的。通过分别处理每个维度,我们的分析结论可以推广到多维。
假设
其中
根据以上结论,对于
NS估计量我们有:即邻域内所有邻居
pair对的加权hidden feature之间的距离之和。如果邻域内所有节点的同样地,对于
CV估计量我们有:相比较于
NS估计量,这里仅需要将CV估计量通常都比NS估计量的方差更小。进一步地,正如我们在下文中分析到的,由于训练期间 间
除了较小的方差,
CV估计量比NS估计量还具有更强的理论收敛性保证。这里我们提出两个定理:- 如果模型参数固定,则在
inference期间,CV会在epoch之后产生exact预测。 - 无论邻域采样大小如何,模型都会朝着局部最优解收敛。
- 如果模型参数固定,则在
假设算法执行多个
epoch,在每个epoch中我们将节点集合mini-batch:mini-batchhidden feature均值。注意:在每个
epoch中我们扫描所有节点,而不仅仅是标记的训练节点,从而确保每个epoch中对每个节点的历史hidden feature均值至少进行了一次更新。记第
SGD随时间更新,在测试期间记第
exact hidden feature为CV估计量的hidden feature为在第
mini-batch对于
exact算法,其损失函数和梯度分别为:对于
exact算法,如果constant序列,则可以忽略下标对于
CV算法,其损失函数和梯度分别为:梯度
- 选择
mini-batch - 选择大小为
因此我们考虑
- 选择
以下定理解释了
CV的近似预测和exact预测之间的关系:对于一个
constant sequenceepoch之后),通过CV估计量计算的hidden feature和exact计算的相等。即:其证明见原始论文附录。
该定理表明:在
inference期间,我们可以使用CV估计量进行前向传播epoch(通常GCN网络中exact预测。这优于NS估计量,因为除非邻域大小无穷大,否则NS估计量无法恢复exact预测。和直接进行
exact预测的batch算法相比,CV估计量可扩展性更强,因为它不需要将整个图加载到内存中。以下定理表明,无论邻域采样大小
SGD训练仍然收敛于局部最优。因此我们可以选择任意小的定理:假设:
激活函数
损失函数的梯度
对于任意的采样
损失函数
其中
则存在
SGD迭代时,有:其中:
[1, N]之间均匀随机分布的变量。每次迭代都使用
CV的近似梯度其中步长
从定理中我们看到:
简而言之,我们证明了近似梯度
SGD收敛到局部最优解。
17.1.6 dropout
这里我们引入第三种随机性来源:对输入特征的随机
dropout。令
dropout算子,其中iid的伯努利随机变量,记
dropout的期望。引入
dropout之后,即使在GCN中采用exact算法,hidden featuredropout。此时节点的邻域均值
hidden feature在
dropout场景下,dropout控制变量control variate for dropout: CVD。我们的方法基于权重缩放
weight scaling技术来近似计算均值dropout模型中,我们可以运行没有dropout的模型的copy,从而获得均值(d)所示。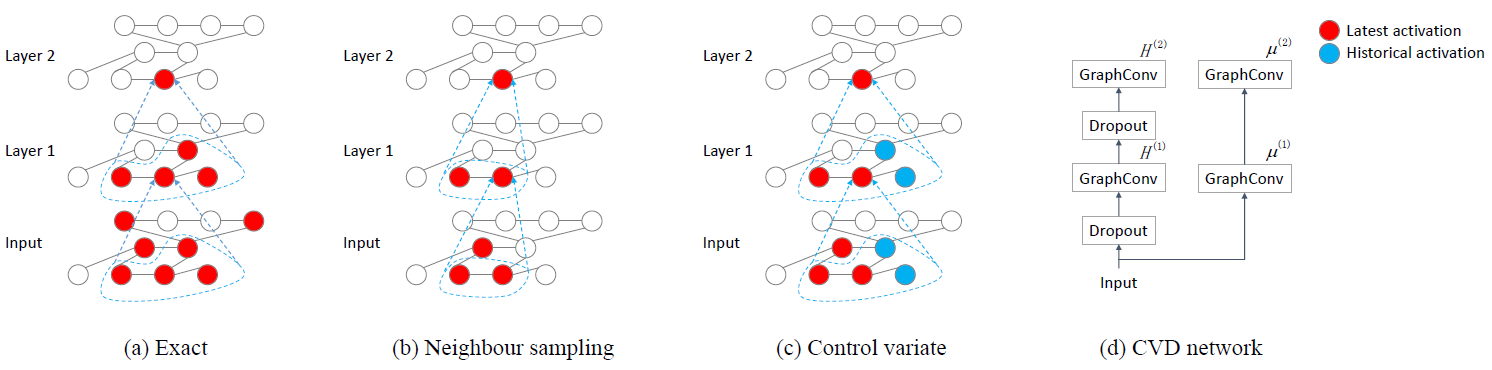
我们通过
CVD估计量。我们将
其中:
CV估计量中的dropout)和dropout)之间的差距。
因此定义:
则有:
第一项考虑
dropout current value和no-dropout current value之间的gap,使用no-dropout current value和no-dropout avg value之间的gap。第三项就是no-dropout avg value本身。考虑第一项对于
dropout具有零均值,即第一个等式成立是因为当移除
dropout时,CVD估计量就退化为CV估计量。因此,
CVD估计量是无偏的。下面我们即将看到,如果CVD估计量具有良好的方差。假设节点的
hidden feature之间不相关,即假设
则有:
令
这些结论的证明参考原始论文的附录。
通过上述结论,我们有:
我们将第一项视为从
dropout中引入的方差variance from dropout: VD,第二项视为从邻域采样中引入的方差variance from neighbor sampling: VNS。理想情况下,VD应该等于VNS应该等于零。和前述相同的分析,我们可以通过将
VNS。令 :根据这里的第一个结论,
CVD的VD部分为:exact估计量的VD部分。我们总结出所有这些估计量及其方差,推导过程参考原始论文。
exact:VNS部分为零,VD部分为NS估计量:VNS部分为VD部分为CV估计量:VNS部分VD部分CVD估计量:VNS部分VD部分为
CV/CVD的VNS取决于NS的VNS取决于非零的
17.1.7 预处理
有两种可能的
dropout方式:区别在于:第一种方式是在邻域聚合之前应用
dropout、第二种方式在邻域聚合之后应用dropout。《Semi-supervised classification with graph convolutional networks》采用前者,而我们采用后者。实验效果上,我们发现这两种方式的效果都相差无几,因此不同的方式不影响模型的效果。采用第二种方式的优势是提升训练速度:我们可以对输入进行预处理,并定义
由于大多数
GCN仅有两层卷积层,因此这种方式可以显著减少感受野大小,并加快训练速度。我们称该优化为预处理策略preprocessing strategy。
17.2 实验
我们在六个数据集上通过实验验证了
VRGCN算法的方差和收敛性,其中包括来自GCN的Citeseer, Cora, PubMed, NeLL四个数据集以及来自GraphSAGE的PPI, Reddit两个数据集。对于这些数据集的统计见下表所示。最后两列给出了节点的
1-hop邻域平均大小、2-hop邻域平均大小。由于是无向图,因此每条边被计算两次,但是self-loop仅被计算一次。- 对于每个数据集,所有模型在该数据集上采用相同的训练集/验证集/测试集拆分 (而不是每个模型单独的一个拆分)。
- 对于
PPI数据集(多标签分类数据集)我们报告测试集的Micro-F1指标,对于其它多分类数据集我们报告准确率accuracy。 - 对于
Citeseer, Cora, PubMed, NELL数据集,baseline模型为GCN;对于PPI, Reddit数据集,baseline模型为GraphSAGE。 - 对于收敛性实验,我们在
Citeseer, Cora, PubMed, NELL数据集上重复执行10次,在Reddit, PPI数据集上重复执行5次。 - 所有实验都在
Titan X GPU上完成。
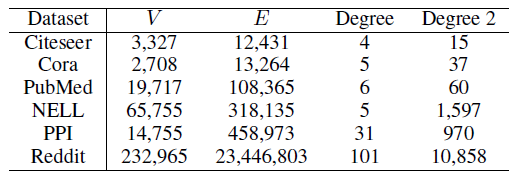
首先我们评估预处理
PreProcessing: PP的影响。我们比较了三种配置:M0:dropout在前、计算邻域均值在后,且计算邻域的exact均值(未对邻域进行任何采样)M1:计算邻域均值在前、dropout在后,且计算邻域的exact均值(未对邻域进行任何采样)M1 + PP:计算邻域均值在前、dropout在后,且使用较大的邻域大小exact的。
实验结果如下所示。我们固定了训练的
epoch,然后给出不同配置的GCN在不同数据集上的测试accuracy。我们的实现不支持NELL上的M0配置,因此未报告其结果。可以看到:三种配置都具有相近的性能,即更换
dropout的位置不会影响模型的预处性能。因此后续的收敛性实验中,我们以最快的M1 + PP配置作为exact baseline。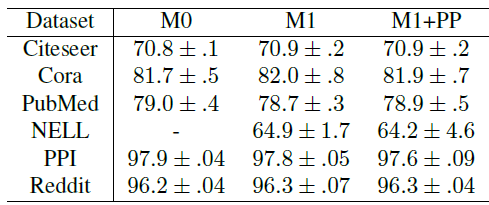
然后我们评估
VRGCN的收敛性。我们将M1 + PP配置作为exact baseline,然后对比MLP。我们对四种近似策略进行比较,其中NS:没有使用预处理的NS估计量(邻域采样)。NS + PP:采用了预处理的NS估计量。IS + PP:采用了预处理的IS估计量(重要性采样)。CV + PP:采用了预处理的CV估计量。CVD + PP:采用了预处理的CVD估计量。
当
epoch都具有很低的、相近的时间复杂度,相比之下baseline M1 + PP的baseline相比,它们的收敛速度。首先我们不考虑
dropout(dropout rate = 0),然后绘制不同方法每个epoch的损失函数值,如下图所示。在前
4个数据集中,CV + PP的损失曲线和exact损失曲线相重叠;部分数据集上未给出NS损失曲线和IS + PP损失曲线,因为损失太大;我们并未绘制CVD + PP,因为当dropout rate = 0时,它等价于CV + PP。结论:
CV + PP总是可以达到和M1 + PP相同的训练损失。NS, NS + PP, IS + PP由于它们的梯度是有偏的,因此其训练损失更高。
这些结果和前述定理相符。定理指数:
CV估计量的训练能够收敛到exact的局部最优,和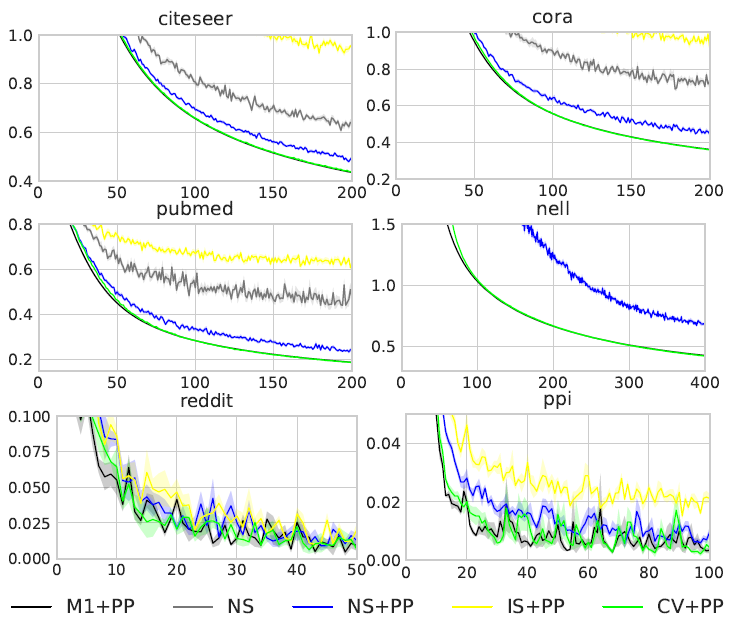
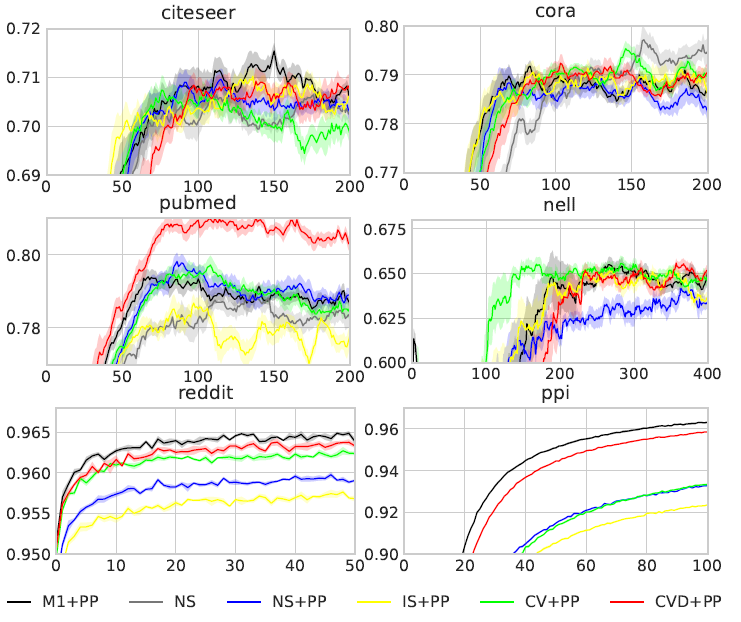
然后我们考虑使用
dropout,然后比较每个epoch使用不同方式训练的模型验证accuracy。其中不管训练算法采取何种方式,inference都采用exact算法来预测。结果如下图所示。注意:NS在Reddit数据集上收敛到0.94、在PPI数据集上收敛到0.6,由于太低所以未在图中给出。结论:
当存在
dropout时,CVD + PP是唯一可以在所有数据集上达到和exact算法相近的验证准确率的算法。当存在
dropout时,CVD + PP的收敛速度(以epoch数量衡量)和M1 + PP相当。这意味着尽管CVD + PP的收敛速度几乎没有损失。这已经是我们期待的最佳结果:具有和
MLP可比的计算复杂度,但是具有和GCN相近的模型质量。在
PubMed数据集上,CVD + PP性能比M1 + PP好得多,我们怀疑它找到了更加的局部最优值。对
PPI以外的所有其它数据集,简单的CV + PP的准确率就可以和M1 + PP相媲美。在
Reddit,PPI数据集上,IS + PP性能比NS + PP更差。这可能是部分节点没有采样到任何邻居,正如我们前文所述。我们对
IS + PP的准确率结果和FastGCN的报告结果相符,而他们的GraphSAGE baseline并未实现预处理技术。
下面给出了在最大的
Reddit数据集上达到给定的96%验证准确率所需要的平均训练epoch和训练时间。可以看到:CVD + PP比exact快7倍左右。这是因为CVD + PP的感受野大小显著降低。另外,
NS, IS + PP无法收敛到给定的准确率(即无法收敛到96%验证准确率)。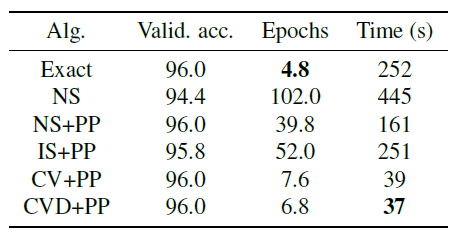
我们使用相同的、由
M1 + PP训练的模型,然后采用不同的算法进行预测,并给出预测质量。如前所述,
CV可以达到和exact算法相同的测试准确率,而NS, NS + PP的性能要差得多。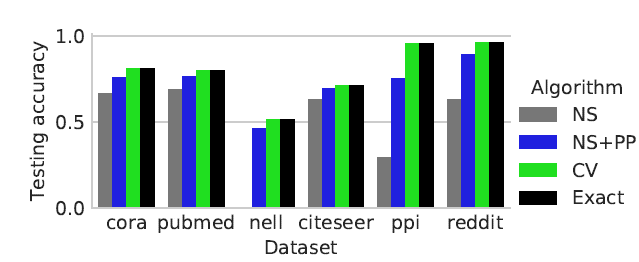
最后,我们比较了训练期间第一层权重每一维梯度的平均
bias和方差(对权重自身进行了归一化)。结论:
- 对于没有
dropout的模型,CV + PP的梯度几乎所无偏的。 - 对于存在
dropout的模型,CV + PPheCVD + PP梯度的bias和方差通常小于NS和NS + PP。

- 对于没有
十八、ClusterGCN[2019]
图卷积网络
graph convolutional network: GCN在解决许多graph-based的应用程序中变得越来越流行,包括半监督节点分类、链接预测、推荐系统。给定一个图,GCN使用图卷积操作逐层获得node embedding:在每一层,节点的embedding是通过收集其邻居的embedding来获得的,然后是一层或几层的线性变换和非线性激活。然后将最后一层的embedding用于一些终端任务。由于
GCN中的图卷积运算需要利用图中节点之间的交互来传播embedding,因此GCN的训练非常困难。和其它神经网络不同,GCN的损失函数中每个节点对应的损失不是相互独立的,而是依赖于大量其它节点,尤其是当GCN的深度很深时。相比之下,其它神经网络的损失函数中,每个样本的损失是相互独立的。由于节点的依赖性,GCN的训练非常缓慢并且需要大量的内存,因为反向传播阶段需要将图中所有的embeding存储到GPU内存中。为了说明研究可扩展的
GCN训练算法的必要性,我们从以下三个因素来讨论现有算法的优缺点:内存需求、epoch训练速度(每个epoch的训练时间)、epoch收敛速度(每个epoch损失函数下降的值)。这三个因素对于评估训练算法至关重要。注意:内存需求直接限制了算法的可扩展性,epoch训练速度和epoch收敛速度一起决定了整个训练时间。令
embedding维度、GCN的深度。full-batch梯度下降:GCN原始论文使用full-batch梯度下降来训练。为计算整个训练集损失的梯度,它需要存储所有中间embedding(intermediate embedding),从而导致另外,尽管每个
epoch训练时间高效(单个epoch训练时间很短),但是单个epoch的收敛速度很慢,因为每个epoch仅更新一次参数。整体而言,
full-batch梯度下降内存需求差、epoch训练速度快、epoch收敛速度慢。mini-batch随机梯度下降:GraphSAGE使用了基于mini-batch的随机梯度下降来训练。由于每次迭代仅基于mini-batch梯度,因此它可以减少内存需求,并在每个epoch进行多次更新从而加快epoch收敛速度。但是,由于邻域扩展问题,
mini-batch随机梯度下降会引入大量的计算开销:为计算第embedding,而这又需要邻域节点的邻域节点在第embedding,并向底层不断递归。这导致计算的时间复杂度和GCN的深度GraphSAGE提出使用固定数量的邻域样本,而FastGCN提出了重要性采样。但是这些方法的开销仍然很大,并且当GCN层数更深时情况更糟。整体而言,
mini-batch随机梯度下降内存需求好、epoch训练速度慢、epoch收敛速度快。VR-GCN:VR-GCN提出方差缩减variance reduction技术来减少邻域采样规模。尽管这种方法成功地降低了邻域采样的数量(在Cluster-GCN的实验中,VR-GCN对每个节点仅采样2个邻居的效果很好),但是它仍然需要将所有节点的中间embedding存储在内存中,从而导致VR-GCN的内存需求可能太高导致无法放入到GPU中。整体而言,
VR-GCN内存需求差、epoch训练速度快、epoch收敛速度快。
论文
《Cluster-GCN: An Efficient Algorithm for Training Deep and Large Graph Convolutional Networks》提出了一种新的GCN训练算法,该算法利用图聚类结构graph clustering structure来加速GCN的训练。作者发现:
mini-batch算法的效率可以通过embedding利用率embedding utilization的概念来刻画。embedding利用率和单个batch内的边的数量成正比。这一发现促使作者利用图聚类算法来设计batch,目标是构造分区partition使得同一个分区内的边的数量比跨区之间的边的数量更多。基于图聚类
graph clustering的思想,作者提出了Cluster-GCN:一种基于图聚类算法(如METIS)来设计batch的算法。进一步地,作者提出一个随机多聚类框架stochastic multi-clustering framework来改善Cluster-GCN的收敛性。核心思想是:尽可能地将内存和计算控制在
batch内。这要求仔细安排batch内节点。但是,这么做破坏了
mini-batch的随机性要求,因为mini-batch要求随机选取batch-size),而Cluster-GCN中的采样方法不再随机。这使得mini-batch梯度不再是full-batch梯度的无偏估计。作者的解决办法是:随机将多个簇合并为一个大簇,然后将这个大簇作为
mini-batch,使得batch内的节点分布尽可能和full-batch一致。Cluster-GCN带来了巨大的内存优势和计算优势:- 在内存需求方面,
Cluster-GCN仅需要将当前batch中的节点embedding存储在内存中,内存复杂度为batch-size。这比VR-GCN、full-batch梯度下降、以及其它mini-batch随机梯度下降等方法要小得多。 - 在计算复杂度方面,
Cluster-GCN在每个epoch都具有相同的时间代价,并且比邻域搜索方法快得多。 - 在收敛速度方面,
Cluster-GCN相比其它SGD-based方法具有可比的竞争力。 - 最后,
Cluster-GCN算法易于实现,因为它只需要计算矩阵乘法,而无需任何邻域采样策略。
整体而言,
Cluster-GCN内存需求好、epoch训练速度快、epoch收敛速度快。通过对几个大型图数据集进行全面实验,证明了
Cluster-GCN的效果:Cluster-GCN在大型图数据集(尤其是深层GCN)上实现了最佳的内存使用效率。例如在Amazon2M数据集上的3层GCN模型中,Cluster-GCN使用的内存比VR-GCN少5倍。对于浅层网络(例如
2层),Cluster-GCN达到了和VR-GCN相似的训练速度;但是当网络更深(如4层)时,Cluster-GCN可以比VR-GCN更快。这是因为Cluster-GCN的复杂度和层数VR-GCN的复杂度是Cluster-GCN能够训练具有很大embedding size并且非常深的网络。尽管之前的一些工作表明:深层
GCN无法提供更好的性能,但是作者发现通过适当的优化,深层GCN可以帮助提高模型准确性。例如使用5层GCN,Cluster-GCN在PPI数据集上的accuracy为99.36,而之前的最佳效果为98.71。
18.1 模型
给定图
- 节点
- 节点
labellabel的节点集合为
定义一个包含
GCN,其中第其中:
representation矩阵,representation向量的维度。representation向量。为简化讨论,我们假设
其中
self-loop的邻接矩阵。ReLU。
GCN模型的损失函数为:其中:
final representation。
我们首先讨论之前方法的一些不足,从而启发我们提出
Cluster-GCN。原始
GCN:原始GCN中,作者通过full-batch梯度下降来训练GCN,其计算代价和内存需求都很高。- 在内存需求方面,通过反向传播来计算损失函数的梯度需要
embedding矩阵 - 在收敛速度方面,由于模型每个
epoch仅更新一次参数,因此模型需要训练很多个epoch才能收敛。
- 在内存需求方面,通过反向传播来计算损失函数的梯度需要
GraphSAGE:GraphSAGE通过mini-batch SGD来改善GCN的训练速度和内存需求。SGD不需要计算完整的梯度,而是仅在每轮更新中基于一个mini-batch来计算梯度。记
mini-batch节点集合为SGD迭代中,梯度的估计量为:尽管
mini-batch SGD在收敛速度方面更快,但是它在GCN训练过程中引入了另一种计算开销,这使得它与full batch梯度下降相比,每个epoch的训练速度慢得多。原因如下:考虑计算单个节点embeddingrepresentation,而这又依赖于这些邻域节点的邻域节点在第representation,... 。假设
GCN具有degree为hop-k(representation向量需要如果一个
batch中有很多节点,则时间复杂度就不是那么直接,因为不同节点具有重叠的top-k邻域,那么依赖的节点数量可以小于最差的
为反应
mini-batch SGD的计算效率,我们定义embedding利用率embedding utilization的概念,从而刻画计算效率。在算法过程中,如果节点
embedding计算之后,被第embedding计算过程使用了embedding利用率为- 对于具有随机采样的
mini-batch SGD,由于图通常比较大且稀疏,因此hop-k邻域之间几乎没有重叠),则mini-batch SGD在每个batch需要计算embedding,这导致每个mini-batch的训练时间为epoch的训练时间为 - 相反,对于
full-batch梯度下降,每个embedding将在更上一层中重复利用degree),因此具有最大的embedding利用率。结果full-batch SGD在每个epoch需要计算embedding,训练时间为embedding就可以得到一个节点的梯度,相比之下mini-batch SGD需要计算embedding。
如下图所示给出了传统的
GCN中指数级邻域扩展(左图)。红色节点是扩展的起始节点,不同颜色代表不同的hop。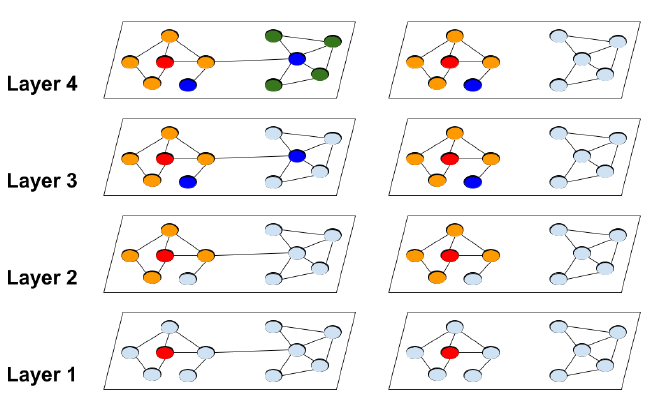
- 对于具有随机采样的
为了使得
mini-batch SGD顺利工作,已有的一些算法试图限制邻域扩展的大小,但是这无法提升embedding利用率。GraphSAGE均匀采样一个固定大小的邻域,而不是完整的邻域集合。我们将这个固定大小记作embedding,并且也使得梯度估计的准确性降低。FastGCN提出了一种重要性采样策略来改善梯度估计。VR-GCN提出了一种策略,通过存储所有embedding的历史均值,从而应用于未采样邻居节点的embedding计算。尽管存储所有
embedding的内存需求很高,但我们发现该策略非常有效,并且在实践中即使对于非常小的
18.1.1 Cluster-GCN
Cluster-GCN技术受到以下问题的启发:在mini-batch SGD更新过程中,能否设计mini-batch以及对应的计算子图,使得最大程度地提高embedding利用率?解决该问题的关键在于将embedding利用率和聚类相结合。考虑我们计算
batch1层到第embedding。定义embedding利用率是这个batch内链接的数量因此,为了最大化
embedding利用率,我们应该设计一个batchbatch内链接的数量,这使得我们可以将SGD更新的效率和图聚类算法联系起来。现在我们正式地介绍
Cluster-GCN。对于图subgraph:其中
经过节点的重新排列之后,图
其中:
- 每个对角块
同样地,我们可以根据
label为label组成。现在我们用块对角矩阵
cluster(每个cluster对应一个batch)。令
embedding矩阵变为:其中
因此损失函数可以分解为:
在每一步我们随机采样一个簇
SGD更新。在这个更新过程中,仅依赖于当前batch的子图label可以看到,
Cluster-GCN仅需要进行矩阵乘法和前向/反向传播,而之前的SGD-based方法中需要对邻域进行搜索,因此我们的方法更容易实现。- 每个对角块
Cluster-GCN使用图聚类算法对图进行分组。图聚类算法(如Metis和Graclus)旨在对图的节点进行划分,使得簇内的链接比簇间的链接更多,从而更好地捕获图的聚类和社区结构。这正是我们需要的结果,因为:- 如前所述,
embedding利用率等于每个batch的batch内链接数量。 - 由于我们用块对角矩阵
- 如前所述,
下图给出了在完整图
hop。可以看到:
Cluster-GCN可以避免繁重的邻域搜索,从而将精力集中在每个簇内的邻居上。
我们比较了两种不同的节点划分策略:随即划分
random partition、聚类划分clustering partition。我们分别通过随即划分、
METIS聚类划分将图划分为10个分组,然后每个分组作为一个batch来执行SGD更新。数据集为三个GCN公共数据集,评估指标为测试集F-1 score。可以看到:在相同epoch下,使用聚类划分可以获得更高的准确性。这表明使用图聚类很重要,并且不应该使用随机划分。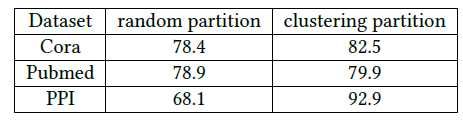
算法复杂度:由于仅考虑
batch的复杂度仅有矩阵乘法batch的时间复杂度为epoch的时间复杂度为平均而言,每个
batch只需要计算embedding,它是线性的而不是batch的空间复杂度为另外,我们的算法仅需要将子图加载到
GPU内存中,无需加载整个图(虽然整个图的存储通常不是瓶颈)。我们在下表中总结了时间复杂度和空间复杂度。显然,所有
SGD-based算法在层数方面都是指数复杂度。对于VR-GCN,即使GPU的内存容量。接下来我们介绍我们的
Cluster-GCN算法,它兼顾了full-batch梯度下降下每个epoch的时间复杂度、以及在普通SGD梯度下降下的空间复杂度。其中:
embedding维度(为方便起见,所有层的embedding以及输入特征的维度都是node degree,mibi-batch size,注意:
由于采用了方差缩减技术,
VR-GCN的GraphSAGE和FastGCN。对于空间复杂度,
embedding。为简单起见,我们忽略了存储
Graph以及子图的需求,因为它们通常都是固定的,且通常不是主要瓶颈。Cluster-GCN具有最好的计算复杂度和最好的空间复杂度。从实验部分得知,
Cluster-GCN的最大优势是内存需求更小从而可以扩展到更大的图。训练速度和训练准确率方面,Cluster-GCN和VR-GCN各有优势(在不同的层数方面)。
18.1.2 随机多重聚类 SMC
尽管前述的
Cluster-GCN实现了良好的计算复杂度和空间复杂度,但是仍然有两个潜在的问题:- 对图进行划分之后,某些链接被删除了(即
- 图聚类算法倾向于将相似的节点聚合在一起,因此每个
batch的节点分布和原始数据集不一致,从而导致在SGD更新时,batch的梯度是完整梯度的一个有偏的估计。
我们以
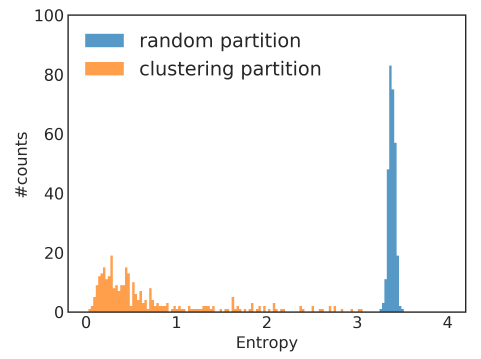
Reddit数据集为例,考察随机划分来选择mini-batch、通过Metis聚类算法选择mini-batch的数据分布的差异,划分数量为300个分区。数据分布以batch内节点标签分布的熵来衡量。我们给出不同batch的标签熵label entropy的分布直方图如下所示,可以看到:- 大多数聚类
batch具有较低的标签熵,这表明聚类的batch倾向于某些特定的label,从而与整体的数据分布不一致。这可能会影响SGD算法的收敛性。 - 随机
batch具有较高的标签熵,这表明随机batch的数据分布和整体数据分布更为一致。
- 对图进行划分之后,某些链接被删除了(即
为解决这些问题,我们提出了一个随机多重聚类框架
stochastic multiple clustering: SMC,该框架通过随机合并多个簇,从而减少batch之间的数据分布差异。我们首先将节点划分到
batchbatch通过这种方式,所有簇间链接将被重新合并到模型中,并且簇的随机组合可以使得
batch之间的数据分布的差异更小。这种随机多重聚类框架如下图所示,每个
batch包含2个簇,相同的batch的簇具有相同的颜色。不同的epoch中选择不同的簇组合。这种方法只能缓解问题,但是无法解决问题。因为即使是随机组合多个簇,新的
batch内节点分布与整体分布仍然是有差异的。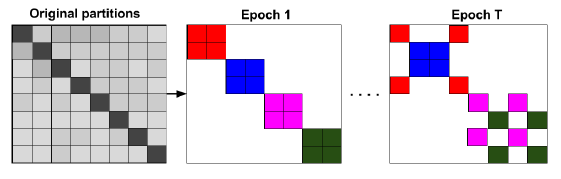
我们在
Reddit数据集上进行实验,对比了SMC和普通Cluster-GCN的效果。在Cluster-GCN中我们选择划分为300个分区,在SMC中我们选择划分为1500个分区并随机选择5个簇来构成一个batch。实验结果如下图所示,其中
x轴为epoch,y轴为F1-score。可以看到随机多重聚类可以显著改善Cluster-GCN的收敛性。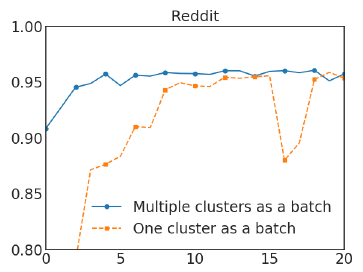
Cluster-GCN算法:输入:
- 图
- 输入特征矩阵
- 节点标签矩阵
one-hot或者multi-hot向量) - 最大迭代 步
max-iter - 划分簇的数量
- 每个
batch的簇的数量
- 图
输出:模型的参数
embedding矩阵算法步骤:
通过
METIS聚类算法划分迭代:
- 随机无放回选择
- 以节点集合
- 根据子图的损失函数来计算梯度
- 基于
Adam优化算法使用梯度
- 随机无放回选择
输出模型的参数
embedding矩阵
METIS是Karypis Lab开发的一个功能强大的图切分软件包,支持多种切分方式。优势:METIS具有高质量的划分结果,据称比常规的谱聚类要准确10% ~ 50%。METIS执行效率非常高,比常见的划分算法块1~2个数量级。百万规模节点的图通常几秒钟之内就可以切分为256个簇。METIS具有很低的空间复杂度和时间复杂度,从而降低了存储负载和计算量。
18.1.3 深层 GCN
GCN原始论文表明:对GCN使用更深的层没有任何效果。但是,实验中的这些数据集太小,可能没有说服力。例如,实验中只有数百个节点的图,太深的GCN可能会导致严重过拟合。另外,我们观察到更深的
GCN模型的优化变得更困难,因为更深的模型可能会阻碍前几层的消息传递。在原始GCN中,他们采用类似于残差连接的技术,使得模型能够将信息从前一层传递到后一层。具体而言,第这里我们提出另一种简单的技术来改善深层
GCN的训练。在原始GCN中,每个节点都聚合了来自前一层邻域的representation。但是在深层GCN的背景下,该策略可能不太合适,因为它没有考虑深度。凭直觉,附近的邻居应该比远处的节点贡献更大。因此我们提出了一种更好的解决该问题的技术:放大邻接矩阵
GCN层的聚合把更大的权重放到前一层的representation上。即:这种方式看起来似乎合理,但是这对所有节点都使用相同的权重,无论其邻居数量是多少,这现得有些不合适。此外,当使用更深的层时,某些数值可能出现指数型增长,可能会导致数值不稳定。因此我们提出修改版,从而更好地维护邻域信息和数值范围。
我们首先将一个单位矩阵添加到原始的
然后对消息进行传播:
其中
实验表明这种对角线增强
diagonal enhancement技术可以帮助构建更深的GCN并达到state-of-the-art性能。这就是人工构造的
attention:对self施加相对更大的重要性(这意味着对邻居施加更小的重要性)。可以通过GAT来自适应地学习self和邻居的重要性。根据论文的实验,当层数很深时,模型效果退化并且训练时间大幅上涨,因此没有任何意义。所以这一小节的内容没有价值。
18.2 实验
我们在两种任务上评估了
Cluster-GCN的效果:在四个公共数据集上的multi-label分类任务和multi-class分类任务。这些数据集的统计信息如下表所示。注意:
Reddit数据集是迄今为止我们所看到的最大的GCN公共数据集。- 而
Amazon2M数据集是我们自己收集的,比Reddit数据集更大。
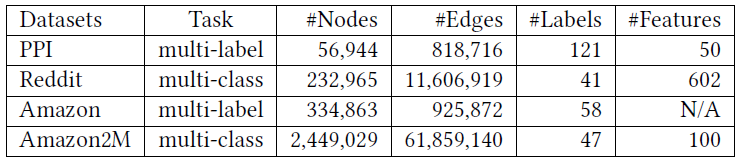
这些数据集的
training/validation/test拆分如下表所示: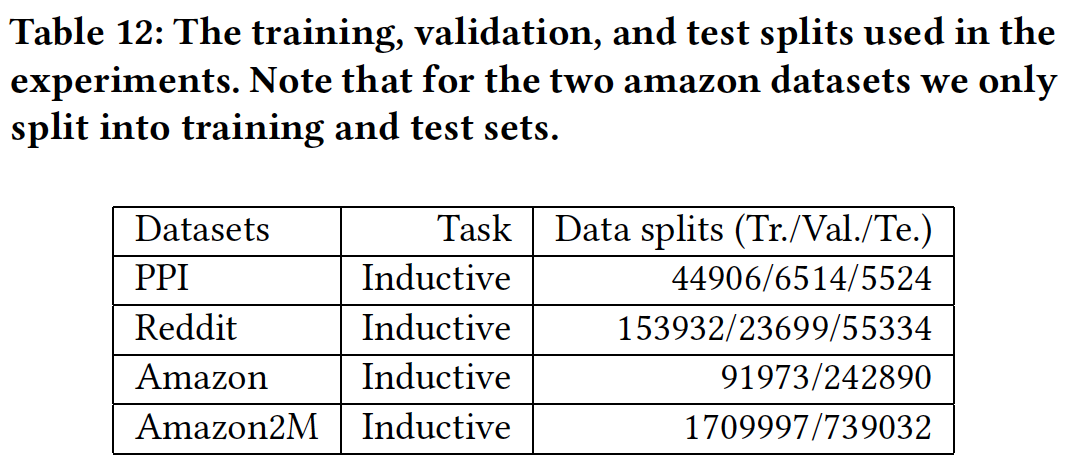
baseline方法:我们比较了以下state-of-the-art的GCN训练算法以及Cluster-GCN方法:VRGCN:保留图中所有节点的历史embedding均值,并仅采样少数几个邻居来加快训练速度。我们采用原始论文中的建议,将采用邻居数量设为2。GraphSAGE:对每个节点采样固定数量的邻居。我们使用原始论文中默认的邻居数量 :双层GCN第一层、第二层采样数量分别为
由于原始
GCN很难扩展到大图,因此我们不比较原始GCN。根据VRGCN论文所述,VRGCN比FastGCN更快,因此我们也不比较FastGCN。实验配置:我们使用
PyTorch实现了Cluster-GCN。对于其它baseline,我们使用原始论文提供的代码。所有方法都采用
Adam优化器,学习率为0.01,dropout比例为20%,权重衰减weight decay为零。所有方法都采用均值聚合,并且隐层维度都相同。
所有方法都使用相同的
GCN结构。在比较过程种我们暂时不考虑
diagonal enhancement之类的技术。对于
VRGCN和GraphSAGE,我们遵循原始论文种提供的配置,并将batch-size设为512。对于
Cluster-GCN,下表给出了每个数据集的分区数量,以及每个batch的簇的数量。
所有实验均在
20核的Intel Xeon CPU(2.20 GHz)+192 GB内存 +NVIDIA Tesla V100 GPU(16GB RAM)上执行。
注意:在
Cluster-GCN种,聚类算法被视为预处理步骤,并且未被计入训练时间。聚类只需要执行一次,并且聚类时间很短。此外,我们遵从
FastGCN和VR-GCN的工作,对GCN的第一层执行pre-compute,这使得我们节省了第一层昂贵的邻域搜索过程。为了用于
inductive setting,其中测试节点在训练期间不可见,我们构建了两个邻接矩阵:一个邻接矩阵仅包含训练节点,另一个邻接矩阵包含所有节点。图划分仅作用在第一个邻接矩阵上。为了计算内存用量,对于
TensorFlow我们使用tf.contrib.memory_stats.BytesInUse(),对于PyTorch我们使用torch.cuda.memory_allocated()。
18.2.1 中等规模数据集
我们首先在训练速度和训练准确性方面评估
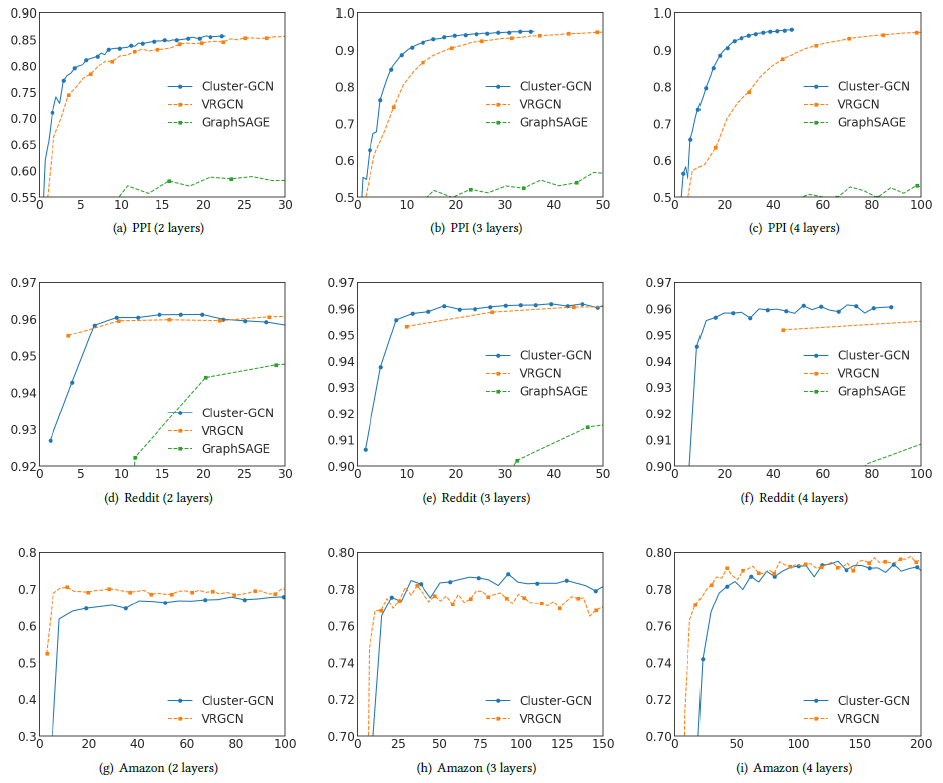
Cluster-GCN。我们给出两层GCN、三层GCN、四层GCN在三个中等规模数据集PPI、Reddit、Amazon上的训练时间和预测准确性,如下图所示。其中x轴为训练时间(单位秒),y轴为验证集准确性(单位F1-Score)。由于
GraphSAGE比VRGCN、Cluster-GCN更慢,因此GraphSAGE的曲线仅出现在PPI、Reddit数据集上。对于
Amazon数据集,由于没有节点特征,因此我们用一个单位矩阵334863 x 128。因此,计算主要由稀疏矩阵运算决定(如结论:
- 在
PPI和Reddit数据集中,Cluster-GCN的训练速度最快,同时预测准确性也最好。 - 在
Amazon数据集中,Cluster-GCN训练速度比VRGCN更慢,预测准确性除了三层GCN最高以外都差于VRGCN。
- 在
Cluster-GCN比VRGCN更慢的原因可能是:不同框架的稀疏矩阵的运算速度不同。VRGCN在Tensorflow中实现,而Cluster-GCN在PyTorch中实现。PyTorch中的稀疏张量支持目前处于早期阶段。下表中我们显示了
Tensorflow和PyTorch对于Amazon数据集执行前向、反向操作的时间,并使用一个简单的、两层线性网络对这两个框架进行基准测试,括号中的数字表示隐层的维度。我们可以清楚地看到Tensorflow比PyTorch更快。当隐层维度更高时,差异会更大。这解释了为什么Cluster-GCN在Amazon数据集中训练时间比VRGCN更长。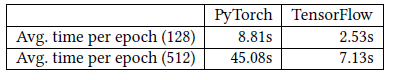
对于
GCN而言,除了训练速度以外,内存需求通常更重要,因为这将直接限制了算法的可扩展性。- 内存需求包括训练多个
epoch所需的内存。为加快训练速度,VRGCN需要在训练过程中保持历史embedding,因此和Cluster-GCN相比VRGCN需要更多的内存。 - 由于指数级邻域扩展的问题,
GraphSAGE也比Cluster-GCN需要更多的内存。
下表中,我们给出了不同方法在不同数据集上训练两层
GCN、三层GCN、四层GCN所需要的内存。括号中的数字表示隐层的维度。可以看到:- 当网络更深时,
Cluster-GCN的内存使用并不会增加很多。因为每当新增一层,引入的额外变量是权重矩阵 - 尽管
VRGCN只需要保持每一层的历史embedding均值,但是这些embedding通常都是稠密向量。因此随着层的加深,它们很快统治了内存需求。 Cluster-GCN比VRGCN有更高的内存利用率。如在Reddit数据集上训练隐层维度为512的四层GCN时,VRGCN需要2064MB内存,而Cluster-GCN仅需要308MB内存。

- 内存需求包括训练多个
18.2.2 大规模数据集
迄今为止评估
GCN的最大的公共数据集是Reddit数据集,其统计数据如前所述。Reddit数据集大约包含200K个节点,可以在几百秒之内训练GCN。为测试
GCN训练算法的可扩展性,我们基于Amazon co-purchasing网络构建了一个更大的图,图中包含200万节点、6100万边。原始的co-purchase数据来自于Amazon-3M。图中每个节点都是一个商品,图中的连接表示是否同时购买了两个商品。每个节点特征都是从商品描述文本中抽取的
bag-of-word,然后通过PCA降维到100维。此外,我们使用top-level的类别作为节点的label。下表给出了数据集中频次最高的类别: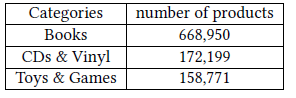
我们在这个大型数据集上比较了
Cluster-GCN和VRGCN的训练时间、内存使用、测试准确性(F1-Score来衡量)。可以看到:
- 训练速度:对于两层
GCN,VRGCN训练速度更快;但是对于更深的GCN,Cluster-GCN训练速度更快。 - 内存使用:
VRGCN比Cluster-GCN需要多得多的内存,对于三层GCN时VRGCN所需内存是Cluster-GCN的五倍。当训练四层GCN时VRGCN因为内存耗尽而无法训练。 - 测试准确性:
Cluster-GCN在四层GCN时可以达到该数据集上的最佳准确性。

- 训练速度:对于两层
18.2.3 深层 GCN
这里我们考虑更深层的
GCN。我们首先给出Cluster-GCN和VRGCN在PPI数据集上不同深度的训练时间的比较,其中每种方法都训练200个epoch。可以看到:
VRGCN的训练时间因为其代价较高的邻域发现而呈现指数型增长,而Cluster-GCN的训练时间仅线性增长。
然后我们研究更深的
GCN是否可以得到更好的准确性(衡量指标为验证集的F1-score)。我们在PPI数据集上进行实验并训练200个epoch,并选择dropout rate = 0.1。其中:Cluster-GCN with (1)表示:原始的Cluster-GCN。Cluser-GCN with (10)表示:考虑如下的Cluster-GCN:Cluster-GCN with (10) + (9)表示:考虑如下的Cluster-GCN:Cluster-GCN with (10) + (11)表示:考虑如下的Cluster-GCN:其中
可以看到:
对于
2层到5层,所有方法的准确性都随着层深度的增加而提升,这表明更深的GCN可能是有效的。当使用
7层或8层时,前三种方法无法在200个epoch内收敛,并会大大降低准确性。可能的原因是针对更深GCN的优化变得更加困难。其中红色的数字表示收敛性很差。即使是第四种方法,它在层数很深时虽然收敛,但是模型效果下降、训练时间暴涨(根据前面的实验),因此没有任何意义。
此外,原始
Cluster-GCN在五层时达到最好的效果,所以对角增强技术失去了价值。

为考察更深层
GCN的详细收敛性,我们给出了采用对角增强技术(即GCN在不同epoch上的验证准确性(F1-Score)。可以看到:我们提出的对角增强技术可以显著改善模型的收敛性,并得到较好的准确性。
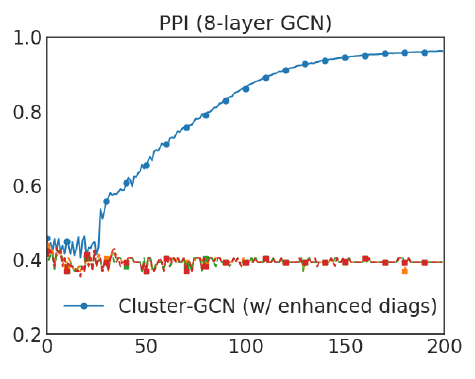
采用了对角增强技术的
Cluster-GCN能够训练更深的GCN从而达到更好的准确性(F1-Score)。我们在下表中给出不同模型在不同数据集上的测试F1-Score。可以看到:
- 在
PPI数据集上,Cluter-GCN通过训练一个具有2048维的隐层的5层GCN来取得state-of-the-art效果。 - 在
Reddit数据集上,Cluster-GCN通过训练一个具有128维隐层的4层GCN取得state-of-the-art效果。
这个优势并不是对角增强技术带来的,而是因为
Cluster-GCN的内存需求更少从而允许训练更深的模型,而更深的模型通常效果更好。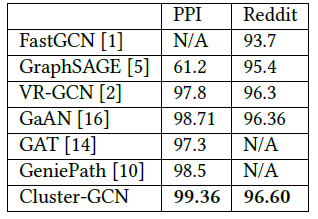
- 在
前面的实验都未考虑
ClusterGCN的预处理时间(如,数据集加载,graph clustering等等)。这里我们给出Cluster-GCN在四个数据集上的预处理时间的细节。对于graph clustering,我们使用Metis。结果如下表所示。可以看到:graph clustering算法仅占用预处理时间的很小比例。graph clustering可以扩展到大型的数据集。
此外,
graph clustering仅需要执行一次,并且之后被后续的训练过程重复使用。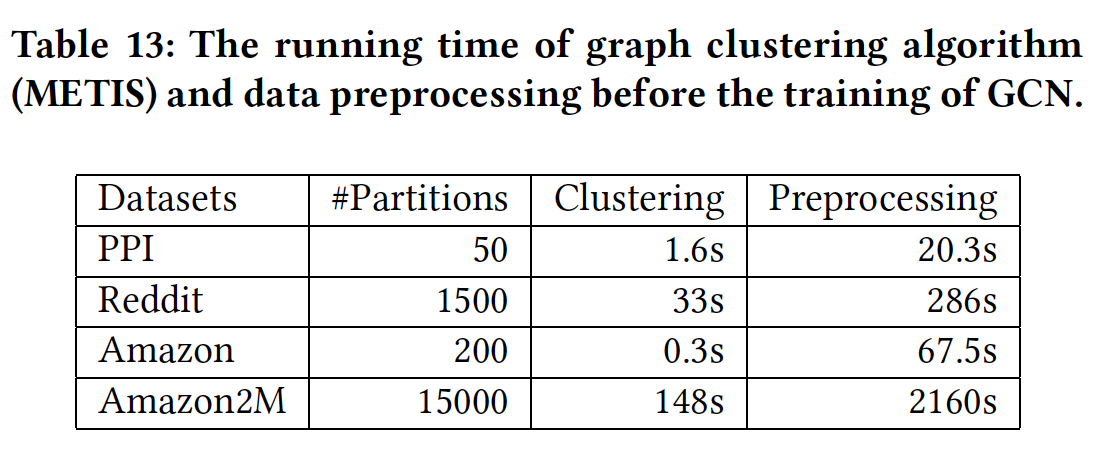
十九、LDS-GNN[2019]
关系学习
relational learning同时利用了样本自身的属性以及样本之间的关系。例如:患者诊断不仅需要考虑患者本身的信息,还需要考虑患者亲属的信息。因此,关系学习不会假设数据点之间的独立性,而是显式建模它们之间的依赖关系。图是表示关系信息relational information的自然的方式,并且已经有很多利用图结构的方法,如图神经网络GNN。虽然图结构在某些领域可用(如社交网络),但是在另一些领域中我们必须构造图结构。
一种常用的人工构造图结构的方法是:基于样本之间的某种相似性来构建
kNN图。这种方法被很多算法采用(如LLE,IsoMap),但是它存在不足:模型效果取决于另外在这种方法中,图的构建和
GNN参数的学习是相互独立的,图的构建需要启发式方法并反复实验。另一种方法是简单地使用核矩阵
kernel matrix来隐式建模样本之间的相似性,但是得到了稠密的相似性矩阵(对应于全连接图)维代价。
论文
《Learning Discrete Structures for Graph Neural Networks》提出了不同的方法同时学习了图的构建和GNN参数,即LDS-GNN。简单而言,论文提出了学习图生成概率模型,其中节点来自于训练集和测试集,边被建模为随机变量,其参数视为bilevel学习框架中的超参数。论文在最小化内层目标函数(GCN训练误差)的同时对图结构进行迭代式采样,并通过最小化外层目标函数(GCN验证误差)来优化边的分布参数。两层优化:内层在训练集上优化训练损失,外层在验证集上优化验证损失。该方法仅用于小型图,计算量很大并且不能保证收敛性。
据作者所知,这是针对半监督分类问题中,同时学习图结构和
GNN参数的第一种方法。此外,论文使用基于梯度的超参数优化来处理不连续的超参数(边是否存在)。通过一系列实验,结果证明了论文的方法比现有方法的优势,同时验证了图生成模型具有有意义的边概率(即:边是否存在的概率)。相关工作:
半监督学习
Semi-supervised Learning:基于图的半监督学习的早期工作使用图拉普拉斯正则化graph Laplacian regularization,包括标签传播label propagation: LP、流形正则化manifold regularization: ManiReg、半监督嵌入semi-supervised embedding: SemiEmb。这些方法假设给定一个图,其中边代表节点之间的某种相似性。- 后来,
《Revisiting semi-supervised learning with graph embeddings》提出了一种方法,该方法不使用图进行正则化,而是通过联合classification和graph context prediction这两个任务来学习embedding。 《Semi-supervised classification with graph convolutional networks》提出了第一个用于半监督学习的GCN。
现在有许多
GCN变体,所有这些变体都假设给定了图结构。与所有现有的graph-based半监督学习相反,LDS即使在图不完整或图缺失的情况下也能工作。- 后来,
图合成和生成
graph synthesis and generation:LDS学习图的概率生成模型。- 最早的图概率生成模型是
《On the evolution of random graphs》提出的随机图模型,其中边概率被建模为独立同分布的伯努利随机变量。 - 人们已经提出了几种网络模型来建模特定的图属性,如
degree分布(《Graphs overtime: densification laws, shrinking diameters and possible explanations》)、网络直径(《Collective dynamics of small-world networks》)。 《Kronecker graphs: An approach to modeling networks》提出了一种基于Kronecker乘积的生成模型,该模型将真实图作为输入并生成具有相似属性的图。- 最近,人们已经提出了基于深度学习的图生成方法。
然而,这些方法的目标是学习一个复杂的生成模型
generative model,该模型反映了训练图的属性。另一方面,LDS学习图生成模型,并将其作为分类问题的一种良好的手段,并且LDS的输入不是图的集合。最近的工作提出了一种无监督模型,该模型学习推断实体之间的交互,同时学习物理系统(如弹簧系统)的动力学(
《Neural relational inference for interacting systems》)。与LDS不同,该方法特定于动态交互系统,是无监督的,并且使用变分自编码器。最后,我们注意到
《Learning graphical state transitions》提出了一个完全可微的神经模型,能够在input/representation/output level处理和生成图结构。然而,训练模型需要根据ground truth graph进行监督。- 最早的图概率生成模型是
链接预测:链接预测是一个几十年前的问题。有几篇综述论文涵盖了从社交网络到知识图谱中的链接预测的大量工作。虽然大多数方法都是基于
node pair之间的某种相似性度量,但是也有许多基于神经网络的方法(《Link prediction based on graph neural networks》)。我们在本文中研究的问题与链接预测有关,因为我们也想学习
learn或扩张extend一个图。然而,现有的链接预测方法不会同时学习一个GNN node classifier。统计关系学习statistical relational learning: SRL模型通常通过二元或一元谓词的存在来执行链接预测和节点分类。然而,SRL模型本质上是难以处理的,并且网络结构和模型参数学习步骤是独立的。离散随机变量的梯度估计:由于两个
bilevel objective的难以处理的特性,LDS需要通过随机计算图stochastic computational graph来估计超梯度hypergradient。使用得分函数估计器(也称作REINFORCE)会将外层目标视为黑盒函数,并且不会利用inner optimization dynamics是可微的。相反,路径估计器path-wise estimator并不容易使用,因为随机变量是离散的。LDS借鉴了之前提出的解决方案(《Estimating or propagating gradients through stochastic neurons for conditional computation》),但是代价是估计有偏。
19.1 模型
19.1.1 背景知识
给定图
邻接矩阵
图拉普拉斯矩阵为
每个节点
所有节点的输入特征向量拼接为特征矩阵
每个节点
labelone-hot向量为所有节点的
label向量拼接为label矩阵
定义所有的邻接矩阵的取值空间为
label矩阵的取值空间为则图神经网络的目标是学习函数:
其中
为学习目标函数,我们在训练集上最小化经验损失:
其中:
point-wise损失函数。
在
GCN中,一个典型的其中:
- 网络为两层网络,参数
Bilevel program是一种优化问题,其中目标函数中出现的一组变量被约束为另一个优化问题的最优解。Bilevel program出现在很多常见下,比如超参数调优、多任务学习、meta-learning学习等。给定外层目标函数
outer objectiveinner objectiveouter variableinner variablebilevel program定义为:直接求解上式非常困难,因为内层问题
inner problem通常没有闭式解。一种标准的求解方式是:利用迭代式的动态优化过程令
假设
我们称其为超梯度
hypergradient。其中这种技术允许我们同时调优多个超参数,其调优数量比经典的超参数优化技术大几个量级。
但是这种方法需要执行更多的
19.1.2 LDS
在现实世界中,经常会出现带噪音的图(
noisy graph)、结构残缺的图(incomplete graph)、甚至完全没有图结构(missing graph) 。为解决这些问题,我们必须在训练GCN网络参数的同时,还需要学习图结构。我们将这个问题构造为一个
Bilevel program问题,其中外层变量为图生成概率模型的参数,内层变量为GCN模型的参数。我们的方法同时优化了GCN模型参数以及图生成概率模型的参数。下图给出了我们方法的示意图:
假设真实邻接矩阵
nosisy, incomplete, missing),我们的目标是寻找最小泛化误差的模型。给定验证集其中
因此:
我们将
GCN的最佳参数。我们将
注意,
即使是很小的图,
bilevel问题也难以直接求解。另外,上述模型包含连续变量(GCN参数)和离散变量(网络结构),这使得我们无法直接求解梯度(离散型变量无法求导)。一种可能的解决方案是对离散型变量构造连续性松弛
continuous relaxation;另一种方案是对离散型变量使用概率分布。这里我们采用第二种方案。我们利用二元伯努利随机变量对图的每条边进行建模,并假设每条边是否存在是相互独立的,则我们可以采样一个图
这种边的独立性假设可能并不成立。假设
我们基于图结构的生成模型来重写
bilevel问题为:利用期望,现在内层目标函数和外层目标函数都是伯努利分布的参数的连续函数。
上式给出的
bilevel问题仍然难以有效求解,这是因为内层目标函数对于GCN而言没有闭式解(目标函数非凸)。因此有效的算法仅能找到近似的解。在给出近似解之前,我们先关注于
GCN模型的输出。对于具有GCN的期望输出为:不幸的是,即使对于很小的图,计算这个期望值也非常困难。于是我们可以计算期望输出的经验估计:
其中
注意:
bilevel中学到的GCN- 由于
给定具有伯努利随机变量的图生成模型(边的概率分布
如果将伯努利参数直接作为
GCN的邻接矩阵,则这相当于一个全连接图,图中每条边的权重就是边存在的概率。此时计算GCN输出的计算复杂度为如果采样
GCN的平均输出,由于每个采样的图都是稀疏图,则总的计算复杂度为另外,使用图生成模型的另一个优势是:我们能够在概率上解释它。而学习稠密的邻接矩阵则无法做到。
对于具有百万级别以上的大型图,
现在我们考虑
bilevel问题的近似解。我们基于图结构的生成模型来重写
bilevel问题为:其中图生成模型的参数
GCN模型参数对于内层问题,我们考虑期望
0或1)。因此即使对于很小的图,其计算复杂度也非常高。但是,换个角度来看,我们可以利用迭代式的动态优化过程其中
在合适的假设下,当
SGD收敛到权重向量这种方法就是标准的随机梯度下降,其中邻接矩阵
step发生改变。但是,这种方式是否保证能够收敛到最小值?论文并未证明。直觉上看,难以保证收敛,因为在梯度下降过程中GCN所应用的图在不断变化。对于外层问题,令
根据:
我们有:
我们使用所谓的
straight-through估计,并令
最后,我们对上式采用单个样本的蒙特卡洛估计来更新参数
0到1之间)。在计算外层问题的超梯度时,需要对
这在时间和空间上都代价太大。
此外,我们依赖于梯度的有偏估计,因此并不期望从完整的计算中获得太多收益。因此我们建议截断计算,并在每
short-horizon优化过程,其中带有对warm restart。LDS算法:输入:
- 特征矩阵
- 标签矩阵
- 可能有(也可能没有)邻接矩阵
- 学习率
- 超梯度截断步长
- 可能有(也可能没有)用于计算
kNN的
- 特征矩阵
输出:最佳的权重
算法步骤:
如果没有邻接矩阵
kNN来初始化邻接矩阵通过
外层迭代,当停止条件未满足时(基于验证集):
内层迭代,当内层目标函数还在下降时(基于训练集):
采样一个新的图:
优化内层目标函数:
如果
采样一个新的图:
计算
迭代
- 采样一个结构:
- 计算
- 计算
- 采样一个结构:
优化外层目标函数:
返回最佳的权重
LDS算法包含外层停止条件和内层停止条件。对于内层停止条件,我们发现以内层目标函数的下降作为内层停止条件非常有效。
我们持续优化
patience窗口为对于外层停止条件,我们发现使用早停策略非常有效。
我们选择一部分验证集
但是当需要优化的参数数量太多、验证集规模太小时,可能会存在验证集的过拟合。
每次外层迭代中,对超梯度的估计都存在偏差。偏差即来自于
straig-through估计,也来自于超梯度的截断。尽管如此,我们从实验中发现该算法能够取得良好的效果,并能够在边的分布空间中找到适合于当前任务的参数。LDS借鉴了之前提出的启发式方案,但是代价是超梯度估计是有偏的。给定一个函数
straight-through估计量为:则有:
通常
LDS算法有两个缺陷:- 计算复杂度太高,导致无法扩展到大图。
- 仅限于
transductive learning,无法扩展到未见过的节点。对于新的、未见过的节点,需要从头开始重新训练模型。
19.2 实验
我们针对三个目标进行了一系列实验:
首先,我们在节点分类问题上评估
LDS,其中图结构虽然可用但是缺失了一定比例的边。这里我们将LDS和包括普通GCN在内的基于图的学习算法进行比较。其次,我们想验证我们的假设,即
LDS可以在没有图的半监督分类问题上取得有竞争力的结果。这里我们将LDS和许多现有的半监督分类算法进行比较。此外,我们对比了一些图算法,图是通过在数据集上创建的
kNN近邻图。最后,我们分析了学到的图生成模型,从而了解
LDS如何学到有意义的边的概率分布。
数据集:
图数据集:
Cora, Citeseer是图的两个基准数据集,输入特征是bag of word,任务是节点分类。我们遵循之前的工作,执行相同的数据集拆分和实验配置。为评估残缺图上
LDS的鲁棒性,我们通过随机采样25%, 50%, 75%的边来构造残缺图。非图数据集:我们使用
scikit-learn中的基准数据集,如Wine, Breast Cancer(Cancer), Digits, 20 NewsGroup(20News)等数据集,这些数据集都不是图结构。我们用这些非图数据集来评估LDS。对于
20 NewsGroup数据集,我们从中挑选出10个类别,然后使用词频超过5%的单词的TF-IDF作为特征。FMA数据集:该数据集从7994个音乐曲目中提取了140个音频特征,任务是音乐风格分类。
所有这些数据集的统计信息如下:
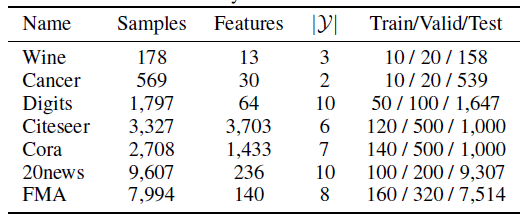
baseline方法:对于图算法,我们对比了以下方法:普通
GCN、GCN-RND、标签传播算法label propagation: LP、流形正则化算法manifold regularization: ManiReg、半监督embedding算法semi-supervised embedding: SemiEmb。其中ManiReg, SemiEmb将一个kNN图作为拉普拉斯正则化的输入。GCN-RND是在普通GCN的每个优化step中添加随机采样的边。通过这种方法,我们打算证明:仅将随机边添加到GCN中不足以提高模型的泛化能力。对于非图算法,我们对比了以下方法:
GC、 逻辑回归logistic regression: LogReg、支持向量机support vector machines: Linear and RBF SVM、随机森林random forests: RF、前馈神经网络feed-forward neural networks:FFNN。当没有图结构时,
GCN退化为前馈神经网络,此时我们通过下列的手段来构造图结构:- 随机创建一个稀疏的图结构,记作
Sparse-GCN。 - 以相等的边概率构建一个稠密图,记作
Dense-GCN。 - 基于输入特征构建一个
RBF核的稠密图,记作RBF-GCN。 - 基于输入特征构建一个
kNN近邻图的稀疏图,记作kNN-GCN。
对于
LDS,我们使用KNN近邻图作为初始的边概率,即kNN-LDS。另外,我们进一步比较了LDS的稠密版本,此时我们学习一个稠密的相似度矩阵,记作kNN-LDS(dense)。- 随机创建一个稀疏的图结构,记作
当需要用到
kNN时,需要考虑两个超参数:k值的选择、度量函数的选择。我们从cosine距离 ,然后通过验证集的准确性来调优这两个超参数。对于
kNN-LDS,GCN和LDS配置:对于所有用到
GCN的网络,我们使用两层GCN网络,隐层维度为16,采用ReLU激活函数。我们使用
0.5的dropout rate来执行dropout,从而执行额外的正则化。我们使用
Adam优化器,学习率从SemiEmb核FFNN使用相同数量的隐层维度、相同的激活函数。我们使用带正则化的交叉熵损失函数:
其中
one-hot向量,对于
LDS,除了已知的边或者kNN构造的边我们设置为我们将验证集平均划分为验证集
(A)和早停集(B)。对于外层目标,我们使用(A)上的不带正则化的交叉熵损失,并通过随机梯度下降对其进行优化。我们通过超参数调优来优化外层循环的步长
最后我们采样
对于
LDS和GCN,我们以20步的窗口大小来应用早停。
其它方法的实现来自于
skicit-learn或者原始论文。所有方法的超参数都是通过验证集的accuracy来调优。
19.2.1 图数据集
我们比较了在图数据集(
Cora左图、Citeseer中间图)的残缺图上的结果。我们给出边的每个保留比例,以及对应的验证集准确率(虚线,用于早停)和测试集准确率(实线),阴影表示标准差。所有结果都随机执行5次并取均值。可以看到:
LDS在所有情况下都具有竞争性优势,准确率提升了7%。最终Cora和Citeseer的准确率分别为84.1%和75.0%,超越了所有的state-of-the-art模型。- 当保留所有的边(
100%)时,LDS还可以通过学习其它额外的、有用的边来提高GCN模型的泛化准确率。 - 从
GCN和GCN-RND对比中可以看到,随机添加边并不能减少泛化误差,这对于模型没有任何帮助。
右图给出超梯度截断的更新次数
LDS的影响。20并不会带来明显提升,同时会增加计算成本
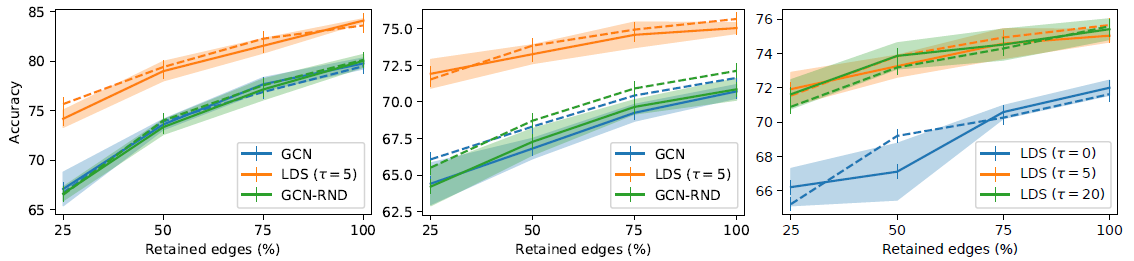
上述实验更详细的结果如下表所示,其中(
+-表示标准差)。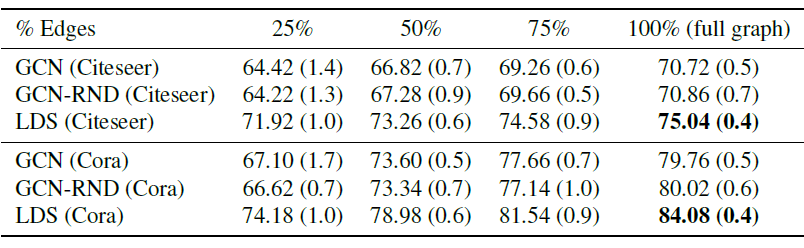
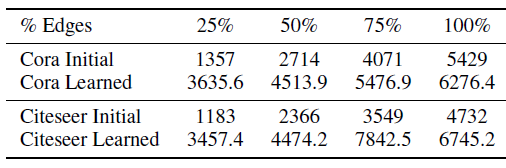
我们考虑
LDS在Cora,Citeseer数据集上期望的边的数量,从而分析学到的图生成器采样的图的属性。LDS期望的边的数量高于原始图的边的数量,这是可以预期的,因为LDS具有比普通GCN更高的准确率。- 尽管如此,
LDS学到的图仍然是非常稀疏的,如,对于Cora而言平均只有不到0.2%的边。这有助于LDS的内层循环中有效学习GCN。
19.2.2 半监督学习
我们考察
LDS在所有数据集上的半监督学习效果。每个实验随机执行5次并报告平均的测试准确率和标准差(以+-表示)。有竞争力的结果以粗体展示。结论:
- 非图算法在某些数据集上效果很好(如
Wine,Cancer,FMA),但是在Digits,Citeseer,Cora,20news等其它数据集上效果较差。 LP, ManiReg, SemiEmb只能改善Digits,20news数据集的效果。- 和非图算法相比,
kNN-GCN效果很好,并提供了具有竞争力的结果。 kNN-LDS是所有数据集中最具竞争力的方法之一,并且在图数据集上获得最高的收益。kNN-LDS的性能略优于其dense模型,并且其稀疏图可以扩展到更大的数据集。
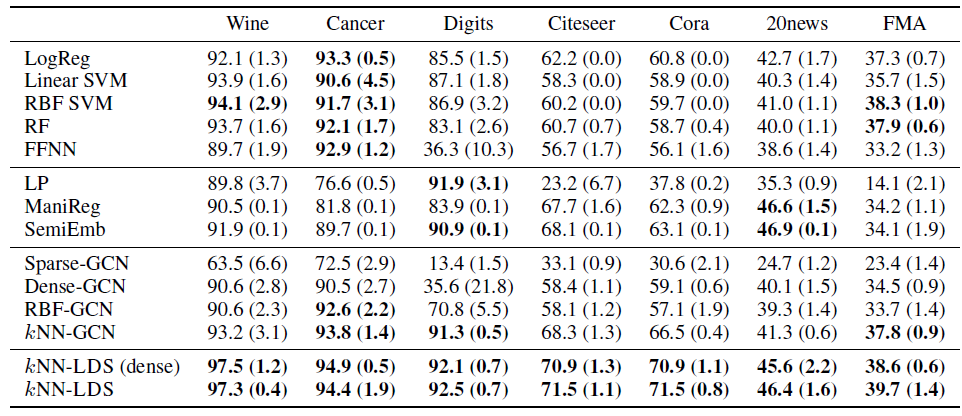
- 非图算法在某些数据集上效果很好(如
19.2.3 图生成模型
我们给出
LDS(Cora数据集(保留25%的边)学习过程中,三种类型的节点(训练集、验证集、测试集,对应于下图的从左到右)的平均的边概率的演变,每种类型一个节点。对于每个样本节点,所有其它节点被划分为四个分组:底层真实图中相邻的节点(True link)、相同类别的节点(Same class)、不同类别的节点(Different classes)、未知类别的节点(Unknown classes) 。图中灰色竖线指示内层优化何时重启。纵坐标以log 10来表示。- 平均而言,
LDS将相同类别标签样本之间存在边的概率提高了10到100倍。 LDS能够为真实相邻的边赋予一个较高的概率。
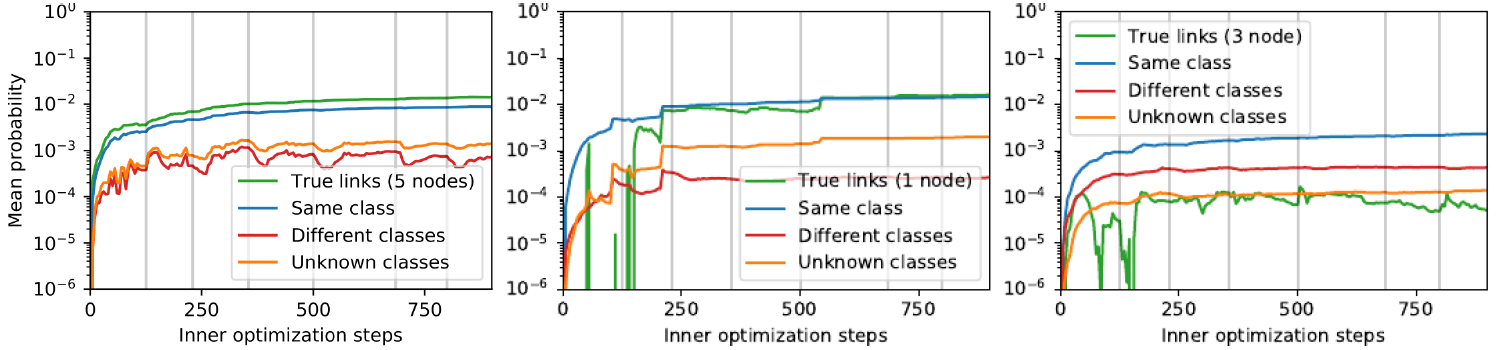
- 平均而言,
我们给出
LDS(Cora数据集(保留25%的边)学习完成之后,三种类型的节点(训练集、验证集、测试集,对应于下图的从左到右)的边的概率的归一化直方图,每种类型一个节点。对于每个样本节点,所有其它节点被划分为两个分组:相同类别的节点(Same class)、不同类别或未知类别的节点(Different/Unknown classes) 。直方图统计按照log 10分为六个桶。可以看到:
LDS学到边的高度非均匀的概率分布能够反应节点的类别。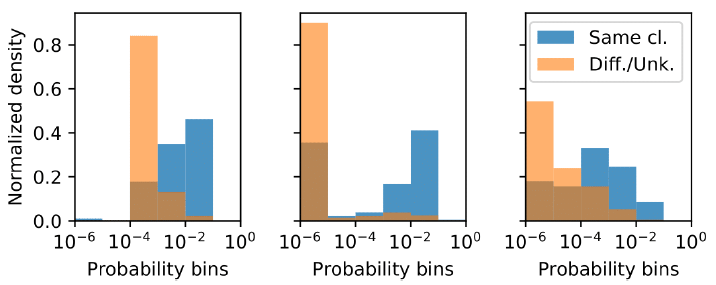
我们给出
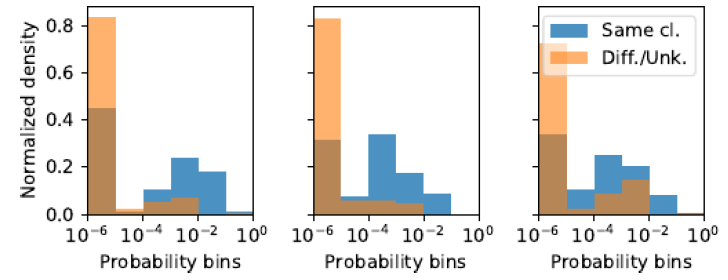
LDS(Citeseer数据集(保留25%的边)学习完成之后,被kNN-GCN误分类但是被kNN-LDS正确分类的测试集的三个节点的边的概率的归一化直方图。。对于每个样本节点,所有其它节点被划分为两个分组:相同类别的节点(Same class)、不同类别或未知类别的节点(Different/Unknown classes) 。直方图统计按照log 10分为六个桶。可以看到:
LDS学到边的高度非均匀的概率分布能够反应节点的类别,这和前面的结论相同。- 可能更重要的是捕获有效的边的分布(即相同类别之间存在边的概率更高),而不是选择正确的连接。
我们用
t-SNE进一步可视化了GCN和LDS学到的embedding。下图给出了Citeseer数据集上使用Dense-GCN(左)、kNN-GCN(中)、kNN-LDS(右)学到的embedding的的t-SNE可视化。该embedding是最后一层卷积层的输出。可以看到:
kNN-LDS学到的embedding在所有不同类别之间提供了最佳分隔。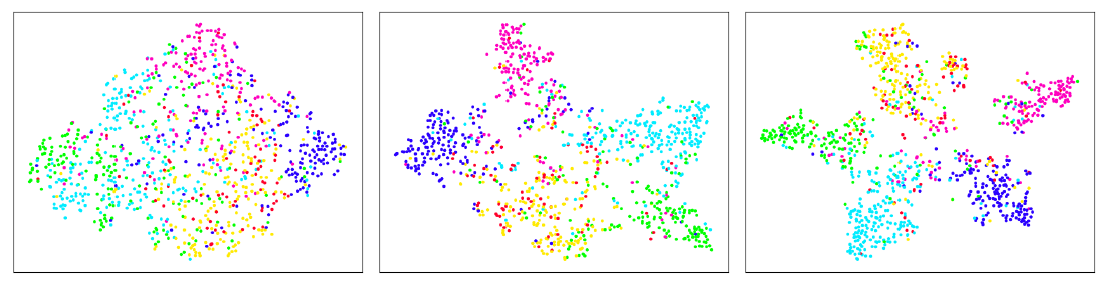
二十、DIAL-GNN[2019]
近年来图神经网络
GNN被广泛使用,不幸的是只有图结构的数据才能使用GNN。很多真实世界中的数据(如社交网络)天然就是图结构数据,但是对于下游任务而言,这些天然的图结构是否对于当前任务是最优的则不一定。更重要的是,很多场景下可能没有图结构数据,因此需要从原始数据中构造图结构数据。- 在图信号处理领域,研究人员探索了从数据中学习图结构的各种方法,但是他们并未考虑下游任务。
- 另外,越来越多的工作研究交互系统的动态建模从而利用隐式的交互模型,但是这些方法无法在很多噪音甚至没有图结构的情况下直接联合学习图结构和
graph representation。 - 最近,研究人员探索了对非图结构数据自动构建图结构并应用
GNN,但是这些方法仅优化了针对下游任务的图结构,并未利用已被证明在图信号处理中非常有用的技术。 - 最近,论文
《Learning Discrete Structures for Graph Neural Networks》提出了一种新的方法(即,LDS-GNN),该方法通过近似求解一个bilevel program从而共同学习图结构和GCN参数。但是,该方法存在严重的可扩展性问题,因为它需要学习transductive learning,这意味着该方法在测试期间无法应用于新的、未见过的节点。
为解决这些限制,论文
《Deep Iterative and Adaptive Learning for Graph Neural Networks》提出了一种用于GNN的深度迭代和自适应学习框架Deep Iterative and Adaptive Learning for Graph Neural Networks: DIAL-GNN,该框架共同学习针对具体任务的最优图结构和GNN网络参数。DIAL-GNN将构建图的图学习graph learning问题转换为数据驱动的相似性度量学习问题similarity metric learning。然后作者利用自适应图正则化来控制生成的图结构的平滑性
smoothness、连接性connectivity以及稀疏性sparsity。更重要的是,作者提出了一种新颖的迭代方法来搜索隐藏的图结构hidden graph structure,该隐藏的图结构将初始图结构优化到监督学习(或半监督学习)任务的最优图结构。另外,论文的方法可以同时处理transductive learning和inductive learning。最后,通过广泛的实验表明,在下游任务性能以及计算时间方面,论文提出的
DIAL-GNN模型可以始终超越或者接近state-of-the-art基准模型。
20.1 模型
给定
图结构学习任务的目标是自动学习图结构
GNN-based模型来应用于下游的预测任务。大多数现有方法通过预处理过程来基于人工规则或特征来构造图,如
kNN近邻图。和这些方法不同,我们提出的DIAL-GNN框架将问题描述为一个迭代式学习问题,该问题以端到端的方式联合学习图结构和GNN参数。DIAL-GNN整体架构如下图所示,其中最左侧图中的虚线表示原始的图结构kNN近邻图构建的图结构。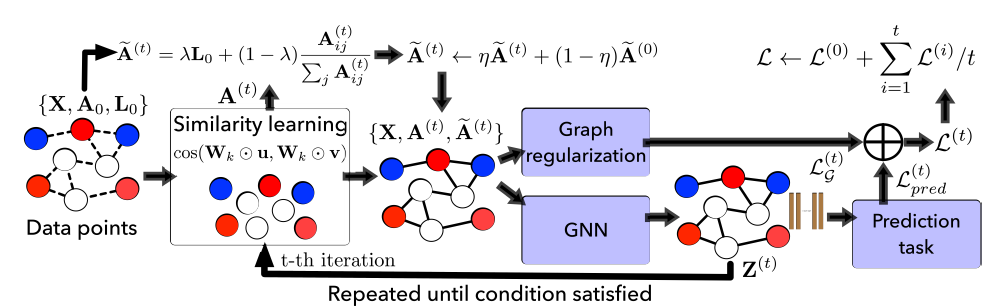
20.1.1 相似度量学习
构建图的一个常用策略是:首先基于某种度量来计算节点
pair对之间的相似度,然后在下游任务中使用人工构建的图。和这些方法不同,我们为图结构学习设计了一个可学习的度量函数,它将与下游任务的模型一起训练。Similarity Metric Learning:类似于multi-head attention机制,我们设计了multi-head余弦相似度:其中:
head的数量。head的权重向量,它在所有节点之间共享,并代表一个视图perspective。每个视图捕获了节点之间的部分相似语义。
我们用
这里采用权重向量的逐元素乘积,而不是基于矩阵乘法的投影(即,
vs权重向量这里多个视图的相似性取平均,也可以考虑取最大值或者中位数?
Graph Sparsification:邻接矩阵应该是非负的(度量metric也应该是非负的),而[-1,1]。此外,很多真实的图结构都是稀疏的。进一步地,一个稠密图不仅计算代价较高,而且对于大多数场景意义不大。因此我们仅考虑每个节点的
.
20.1.2 图正则化
在图信号处理
graph signal processing中,对图信号广泛采用的假设是:value在相邻节点之间平滑变化。给定一个加权无向图
smoothness通常由迪利克雷能量Dirichlet energy来衡量:其中:
trace。
可以看到:最小化
上述平滑损失
smoothness loss最小化存在一个平凡解trivial solution:sparsity。考虑《How to learn a graph from smooth signals》的做法,我们对学习的图结构施加了额外的约束:其中:
F范数。第一项通过对数的
barrier来惩罚不连续图的形成,即连通性connectivity。当存在孤立节点
第二项惩罚第一项造成的较大
degree,从而控制稀疏性。在构造邻接矩阵
图的总体正则化损失为上述损失之和,从而控制学习的图结构的平滑性、连通性、稀疏性:
其中
20.1.3 迭代式图学习
a. Joint Graph Structure and Representation Learning
我们期望图结构能起到两个作用:它应该遵循节点之间的语义关系;它应该适合下游预测任务的需求。
因此,我们通过结合任务预测损失和图正则化损失来联合学习图结构和
graph representation,即:注意:我们的图学习框架与各种
GNN无关,也和预测任务无关。为方便讨论,我们采用两层GCN,其中第一层将节点特征映射到embedding空间,第二层将embedding映射到输出空间:其中:
sigmoid或softmax)。label矩阵,
对于节点分类任务,
softmax函数,现在我们讨论如何获得归一化的邻接矩阵
initial graph structure可用,则完全丢失初始图结构是有害的。之前的一些工作通过执行
masked attention从而将初始图结构注入到图结构学习中,但是这会限制图结构学习的能力。因为这种方法无法学到初始图结构中不存在、但是实际上有用的那些边。我们假设最优图结构和初始图结构的差异很小,因此我们认为最优图结构和初始图结构、度量学习学到的图结构满足以下关系:其中:
- 超参数
上式等价于:
如果初始图结构 kNN 近邻图从而作为初始图结构。
“最优图结构和初始图结构的差异很小” 这是一个非常强的假设。当
时模型就回退到使用初始图结构的版本。
b. Iterative Method for Graph Learning:
以前的一些工作仅依靠原始节点特征并基于某些注意力机制来学习图结构。我们认为这有一些局限性,因为原始节点特征可能不包含足够的信息来学习号的图结构。我们的初步实验表明:简单地在这些原始节点特征上应用一些注意力函数无助于学习有意义的图。
为解决上述限制,我们提出了一种用于图神经网络的深度迭代和自适应学习框架,即
Deep Iterative and Adaptive Learning framework for Graph Neural Network: DIAL-GNN。具体而言,除了基于原始特征计算节点相似度之外,我们还引入了另一个可学习的、基于节点embedding计算到的相似度度量函数。这么做的目的是在node embedding空间上定义的度量函数能够学习拓扑信息,从而补充仅基于原始节点特征学到的拓扑信息。为了结合原始节点特征和节点embedding双方的优势,我们将最终学到的图结构作为它们的线性组合:其中:
DIAL-GNN算法:输入:
- 特征矩阵
label矩阵 - 初始的邻接矩阵(如果有的话)
- 超参数
- 特征矩阵
输出:最优图结构
label矩阵算法步骤:
随机初始化
GCN模型参数如果初始邻接矩阵
kNN来给出初始邻接矩阵:根据
其中,
计算节点
embedding:计算预测损失:
计算图正则化损失:
计算联合损失:
迭代,停止条件为:
基于
基于
multi-head余弦相似度来计算。根据度量学习矩阵
计算
计算节点
embedding:计算预测损失:
计算图正则化损失:
计算联合损失:
总的损失为:
如果为训练截断,则反向传播
从上述算法可以看到:
算法使用更新后的节点
embeddingembedding这个迭代过程动态停止,直到学到的邻接矩阵以指定的阈值收敛,或者最大迭代步
采用动态的阈值收敛相比固定的迭代步,在
mini-batch训练时优势更为明显:我们可以使得mini-batch中每个样本图exaple graph动态停止(每个样本表示一个图)。在所有迭代之后,总的损失将通过所有之前的迭代进行反向传播,从而更新模型参数。
20.1.4 理论分析
收敛性分析:理论上证明迭代式学习过程的收敛性是一个挑战,因为所涉及的学习模的任意复杂性,这里我们从概念上理解它为何在实践中有效。下图给出了迭代式学习过程中,学到的邻接矩阵
embedding可以看到:在第
进一步地,我们用
- 如果我们假设有
node embedding矩阵(即更小的 - 同样地,如果我们假设有
根据这一推理链条,我们可以轻松地扩展到后续的迭代。
现在讨论为什么在实践过程中
我们将在实验部分经验性地检验迭代式学习过程的收敛性。
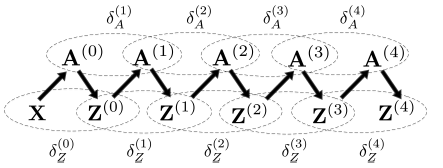
- 如果我们假设有
模型复杂度:
- 学习一个邻接矩阵的算法复杂度为
embedding维度。 - 计算节点
embedding矩阵的算法复杂度为 - 计算输出的算法复杂度为
- 计算总的损失函数的代价为
假设迭代式图学习的迭代次数为
- 学习一个邻接矩阵的算法复杂度为
20.2 实验
这里我们进行一系列实验,从而验证
DIAL-GNN框架的有效性,并评估不同部分的影响。数据集:
- 图数据集:
Cora和Citeseer是评估图学习算法的两个常用的基准数据集,输入的特征是bag-of-word,任务是节点分类。在这两个数据集中,图结构可用。 - 非图数据集:
Wine, Breast Cancel, Digits是三个非图数据集,任务是节点分类。在这些数据集中没有图结构。 inductive learning数据集:为了证明IDAL-GNN在inductive learning任务上的有效性,我们分别对20Newsgroups数据集(20News)、movie review数据集(MRD)进行文档分类和回归任务。我们将每个文档视为一个图,其中文档中的每个单词作为图的节点。
对于
Cora,Citeseer,我们遵循之前工作的实验配置(GCN, GAT, LDS-GNN)。对于Wine, Cancer, Digits,我们遵循LDS-GNN的实验配置;对于20News,我们从训练数据中随机选择30%样本作为验证集;对于MRD,我们使用60%:20%:20%的比例将数据集拆分为训练集、验证集、测试集。所有实验都是采用不同的随机数种子执行
5次的均值。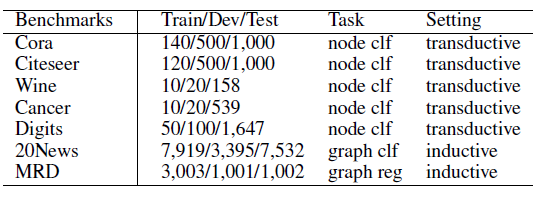
- 图数据集:
baseline方法:在
transductive learning中的baseline为LDS-GNN。与我们的工作类似,LDS-GNN也是共同学习图结构和GNN参数,但是LDS-GNN无法应用于inductive-learning。因为它旨在直接优化底层图的边上的离散概率分布,这使得它无法在测试阶段处理unseen的节点或图。LDS-GNN论文给出了几种半监督baseline的实验结果,这里我们直接复制结果到这里,而并没有花时间重跑这些baseline。对于
Cora,Cteseer数据集,我们还将GCN, GAT作为baseline。为评估
DIAL-GNN在带噪音的图上的鲁棒性,我们还将DIAL-GNN, GCN在添加额外噪声的边、或删除已有的边的图上进行比较。对于非图数据集,我们给出了一个
kNN-GCN作为baseline,其中先在数据集上构建kNN近邻图,然后对这个图应用GCN。对于
inductive learning,我们将DIAL-GNN和BiLSTM, kNN-GCN进行比较。
实验配置:
在我们所有实验中(拷贝的实验除外),除了输出层之外,我们在
GCN最后一层卷积层之后、输出层之前应用dropout rate = 0.5的dropout。在迭代式学习过程中,除了
Citeseer(无dropout)、Digits(dropout rate = 0.3),我们也在GCN中间的卷积层应用dropout rate = 0.5的dropout。对于文本数据集,我们选择数据集中词频超过
10次的单词,并训练了一个300维的GloVe向量。对于长文本,为提高效率我们将文本长度限制为最大
1000个单词。在
word embedding层和BiLSTM层之后,我们使用dropout rate = 0.5的dropout。我们使用
Adam优化器,batch size = 16。对于
20News,隐层维度为128;对于MRD,隐层维度为64。对于其它benchmark,隐层维度为16。对于
text benchmark,我们将学习率设为0.001;所有其它benchmark,学习率为0.01,并应用0.0005的权重衰减。
下图给出了
benchmark上DIAL-GNN相关的超参数。所有超参数都在验证集上进行了优化:
在
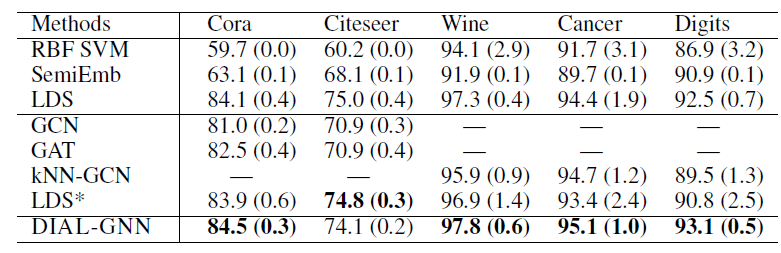
transductive learning和inductive learning上的实验结果如下所示。其中上图为transductive learning,评估指标为测试准确率accuracy(+-标准差);下图为inductive learning,评估指标分别为测试准确率(分类问题)和测试R2 score(回归问题) ,括号内为+-标准差。结论:
DIAL-GNN在7个benchmark中有6个优于所有的baseline方法,这证明了DIAL-GNN的有效性。- 即使图结构可用,
DIAL-GNN也可以极大地帮助完成节点分类任务。 - 当图结构不可用时,和
kNN-GCN相比,DIAL-GNN在所有数据集上始终获得更好的结果。这表明联合学习图结构和GNN的强大能力。 - 和
LDS相比,DIAL-GNN在5个benchmark上的4个获得了更好的性能。 20News和MRD上的良好表现证明了DIAL-GNN在inductive learning中的能力。
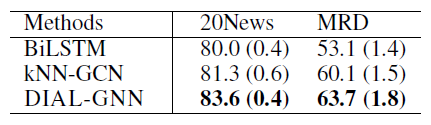
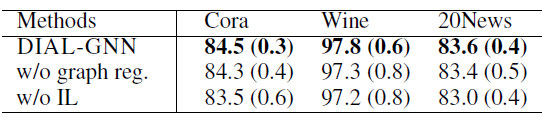
我们进行消融实验从而评估
DIAL-GNN框架不同部分的影响,评估指标为测试集accuracy(+-标准差)。其中w/o表示without。结论:
- 关闭迭代式学习(
w/o IL),所有数据集的性能持续下降。这证明了迭代式学习对于图结构学习问题的有效性。 - 关闭图正则化(
w/o graph reg.),所有数据集的性能也在持续下降。这证明了结合图正则化损失共同训练模型的好处。
- 关闭迭代式学习(
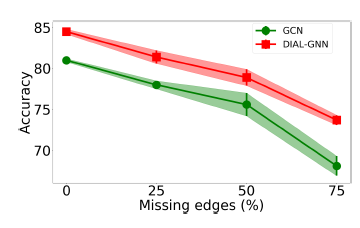
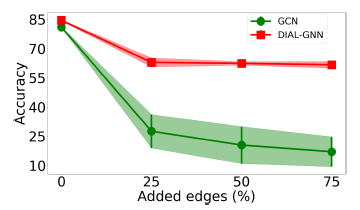
为评估
DIAL-GNN在噪音图上的鲁棒性,我们对于Cora数据集构建了随机添加边、随机删除边的图。具体而言,我们随机删除原始图中25%, 50%, 75%的边(上图),或者随机添加原始图中25%, 50%, 75%的边(下图)。评估指标为测试集accuracy(+-标准差)。结论:
- 在所有的情况下,
DIAL-GNN都比GCN获得更好的结果,并且对带噪音的图更鲁棒。 GCN在添加噪音边的场景下完全失败,但是DIAL-GNN仍然能够合理地执行。我们猜测是因为等式
- 在所有的情况下,
我们通过测试阶段的迭代式学习过程中的迭代,展示了迭代式学习学到的邻接矩阵的演变,以及模型测试
accuracy的演变。我们将迭代式学习过程中相邻矩阵之间的差定义为:
其典型取值范围是
0~1。结论:邻接矩阵和
accuracy都通过迭代快速收敛,这从经验上验证了我们对迭代式学习过程的收敛性做出的分析。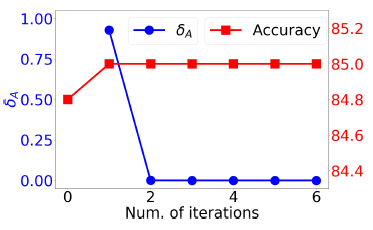
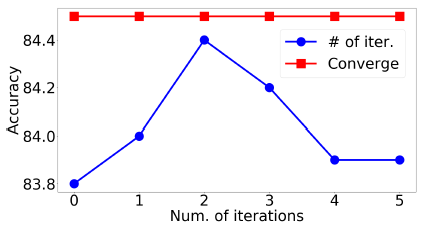
DIAL-GNN迭代式学习方法的停止策略有两种:迭代固定数量的迭代步之后停止、应用某些停止条件从而动态停止。下图我们比较了两种策略的有效性,其中蓝线表示使用固定数量的迭代次数,红线表示使用动态停止条件。评估指标为Cora数据集的测试集上的平均accuracy。结论:使用停止条件从而动态停止的效果更好。
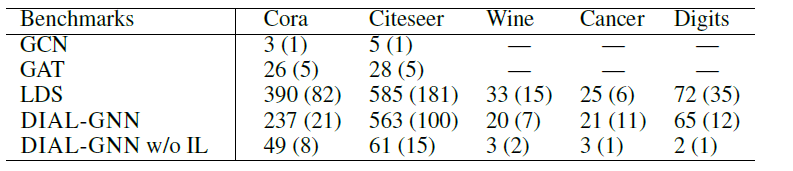
最后,我们在各种
benchmark中比较了DIAL-GNN, LDS以及其它经典GNN(如GCN, GAT)的训练效率。所有实验均在
Intel i7-2700K CPU, NVIDIA Titan XP GPU和16GB RAM的同一台机器上运行,并使用不同随机数种子重复执行5次。结果见下表(单位秒)。结论:
DIAL-GNN和LDS都要比GCN,GAT更慢。这是可以预期的,因为GCN和GAT不需要同时学习图结构。DIAL-GNN始终比LDS更快,但总体而言它们是差不多的水平。- 通过移除迭代式学习(
DIAL-GNN w/o IL) 可以发现,迭代式学习的部分是DIAL-GNN中最耗时的。
二十一、HAN[2019]
现实世界中的数据很多包含图结构,如社交网络、引文网络、万维网。图神经网络
GNN作为一种强大的图结构数据的深度representation learning方法,在图数据分析中表现出卓越的性能,并引起广泛的研究。例如,一些工作(《A new model for learning in graph domains》、《Gated graph sequence neural networks》、《The graph neural network model》)利用神经网络来学习基于节点特征和图结构的node representation。一些工作(《Convolutional neural networks on graphs with fast localized spectral filtering》、GraphSAGE、GCN)通过将卷积推广到图来提出图卷积网络。深度学习的最新研究趋势是注意力机制,该机制可以处理可变大小的数据,并鼓励模型更关注于数据中最重要的部分。注意力机制已被证明在深度神经网络框架中的有效性,并广泛应用于各个领域,如文本分析、知识图谱、图像处理。
Graph Attention Network: GAT是一种新颖的卷积式图神经网络,它利用注意力机制来处理仅包含一种类型的节点或边的同质图。尽管注意力机制在深度学习中取得成功,但是目前的异质图神经网络架构尚未考虑注意力机制。事实上,现实世界中的图通常带有多种类型的节点和边,这通常被称作异质信息网络
heterogeneous information network: HIN或异质图heterogeneous graph。异质图包含更全面的信息和更丰富的语义,因此被广泛应用于许多数据挖掘任务中。由于异质图的复杂性,传统的GNN模型无法直接应用于异质图。metapath表示了不同类型对象之间的关系,它是一种广泛用于捕获语义的结构。以电影数据集IMDB为例,它包含三种类型的节点:电影Movie、演员Actor、导演Director。metapath“电影-演员-电影”MAM表示两部电影之间的共同演员关系。metapath“电影-导演-电影”MDM表示两部电影之间的共同导演关系。
可以看到:采用不同的
metapath,异质图中节点之间的关系可以具有不同的语义。由于异质图的复杂性,传统的图神经网络无法直接应用于异质图。
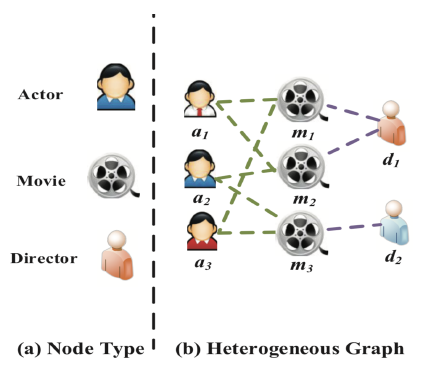
基于以上分析,在为异质图设计具有注意力机制的神经网络体系结构时,需要满足以下需求:
图的异质性:异质性
heterogeneity是异质图的固有属性,即图中包含各种类型的节点和边。例如,不同类型的节点具有不同的特征,它们的特征可能位于不同的特征空间。如何同时处理如此复杂的异质图结构信息,同时保持多样化的特征信息是需要解决的问题。semantic-level注意力:异质图涉及不同的有意义和复杂的语义信息,这些语义信息通常以metapath来刻画。因此,异质图中不同的metapath可以抽取不同的语义信息。如何选择最有意义的metapath,并为task-specific融合语义信息是需要解决的问题。semantic-level注意力旨在了解每个metapath的重要性,并为其分配适当的权重。如,电影 “《终结者》” 可以通过Movie-Actor-Movie连接到 “《终结者2》” (都是由施瓦辛格主演),也可以通过Movie-Year-Movie连接到 “《Birdy》” (都是在1984年拍摄)。但是在影片分类任务中,MAM通常要比MYM更重要。因此,均匀对待所有
metapath是不切实际的,这会削弱某些有用的metapath提供的语义信息。node-level注意力:在异质图中,节点可以通过各种类型的关系来连接。给定一个metapath,每个节点多有很多基于该metapath的邻居。我们需要知道如何区分邻居之间的重要性,并选择一些信息丰富的邻居。对于每个节点,node-level注意力旨在了解metapath-based邻居的重要性,并为他们分配不同的注意力值。
为解决这些问题,论文
《Heterogeneous Graph Attention Network》提出了一个新的异质图注意力网络Heterogeneous graph Attention Network,简称HAN。HAN同时考虑了 同时考虑了node-level注意力和semantic-level注意力。具体而言,给定节点特征作为输入:- 首先,
HAN使用type-specific转换矩阵将不同类型节点的特征投影到相同的特征空间。 - 然后,
HAN使用node-level注意力机制来获得节点及其metapath-based邻居之间的注意力得分。 - 然后,
HAN使用semantic-level注意力机制来获得各metapath针对具体任务的注意力得分。
基于这两个级别学到的注意力得分,
HAN可以通过分层hierarchical的方式获得邻居和多个metapath的最佳组合,使得学到的node embedding可以更好地捕获异质图中复杂的结构信息和丰富的语义信息。之后,可以通过端到端的反向传播来优化整个模型。论文的主要贡献:
- 据作者所知,这是研究基于注意力机制的异质图神经网络的首次尝试。论文的工作使图神经网络能够直接应用于异质图,并进一步促进了基于异质图的应用。
- 论文提出了一种新颖的异质图注意力网络
heterogeneous graph attention network: HAN,它同时包含node-level attention和semantic-level attention。受益于这种分层的注意力机制,所提出的HAN可以同时考虑节点重要性和metapath重要性。此外,HAN模型效率高效,其复杂度是metapath-based节点pair对的数量的线性复杂度,因此可以应用于大规模异质图。 - 论文进行了广泛的实验来评估所提出模型的性能。通过与
state-of-the-art模型进行比较,结果表明了HAN的优越性。更重要的是,通过分析分层注意力机制,HAN展示了它对于异质图分析的潜在的量向好可解释性。
相关工作:
GNN:《new model for learning in graph domains》和《The graph neural network model》中介绍了旨在扩展深度神经网络以处理任意图结构数据的图神经网络GNN。《Gated graph sequence neural networks》提出了一种传播模型,该模型可以融合gated recurrent unit: GRU从而在所有节点上传播信息。
最近很多工作在图结构数据上推广卷积运算。图卷积神经网络的工作一般分为两类,即谱域
spectral domain卷积和非谱域non-spectral domain卷积。一方面,谱域卷积利用图的
spectral representation来工作。《Spectral networks and locally connected networks on graphs》通过找到图的傅里叶基Fourier basis从而将卷积推广到一般的图。《Convolutional neural networks on graphs with fast localized spectral filtering》利用approximate平滑的滤波器。《Semi-Supervised Classification with Graph Convolutional Networks》提出了一种谱方法,称作图卷积网络Graph Convolutional Network: GCN。该方法通过普卷积的局部一阶近似来设计图卷积网络。
另一方面,非谱域卷积直接在图上定义卷积。
《Inductive Representation Learning on Large Graphs》提出了GraphSAGE,它在固定大小的节点邻域上执行基于神经网络的聚合器。它可以通过聚合来自节点局部邻域的特征来学习一个函数,该函数用于生成node embedding。
注意力机制(如
self-attention和soft-attention)已经成为深度学习中最有影响力的机制之一。先前的一些工作提出了用于图的注意力机制,如《Aspect-Level Deep Collaborative Filtering via Heterogeneous Information Network》、《Leveraging Meta-path based Context for Top-N Recommendation with A Neural Co-AttentionModel》。受到注意力机制的启发,人们提出Graph Attention Network: GAT来学习节点与其邻居之间的重要性,并融合fuse邻居进行节点分类。但是,上述图神经网络无法处理多种类型的节点和边,它们仅能处理同质图。
Network Embedding:network embedding,即network representation learning: NRL,用于将网络嵌入到低维空间中并同时保留网络结构和属性,以便将学到的embedding应用于下游网络任务。如,基于随机游走的方法(node2vec, Deepwalk)、基于深度神经网络的方法(《Structural deep network embedding》)、基于矩阵分解的方法(《Asymmetric transitivity preserving graph embedding》,《Community Preserving Network Embedding》)、以及其它方法(LINE)。然而,所有这些算法都是针对同质图提出的。异质图嵌入主要聚焦于保留
metapath-based的结构信息。ESim接受用户定义的metapath作为指导,在用户偏好user-preferred的embedding空间中学习node embedding从而进行相似性搜索。即使ESim可以利用多个metapath,它也无法了解metapath的重要性。为了达到最佳性能,ESim需要进行网格搜索从而找到所有的metapath的最佳权重。metapath2vec设计了一种metapath-based随机游走,并利用skip-gram来执行异质图嵌入。但是,metapath2vec只能使用一个metapath,可能会忽略一些有用的信息。- 与
metapath2vec类似,HERec提出了一种类型约束策略type constraint strategy来过滤节点序列并捕获异质图中反应的复杂语义。 HIN2Vec执行多个预测的训练任务,同时学习节点和metapath的潜在向量。《PME: Projected Metric Embedding on Heterogeneous Networksfor Link Prediction》提出了一个叫做PME的投影度量嵌入模型projected metric embedding model,该模型可以通过欧式距离来保持节点邻近性。PME将不同类型的节点投影到同一个关系空间relation space中,进行异质链接的预测。- 为了研究如何全面地描述异质图,
《Easing Embedding Learning by Comprehensive Transcription of Heterogeneous InformationNetworks》提出了hEER,它可以通过edge representation来嵌入异质图。 《Gotcha-sly malware!: Scorpion a metagraph2vec based malware detection system》提出了一个嵌入模型metapath2vec,其中网络结构和语义都被最大限度地保留从而用于恶意软件检测。《Joint embedding of meta-path and meta-graph for heterogeneous information networks》提出了metapath-based的network embedding模型,该模型同时考虑了meta-graph的所有meta信息的隐藏关系hidden relation。
综上所述,上述所有算法都没有考虑异质图
representation learning中的注意力机制。
21.1 模型
异质图是一种特殊类型的信息网络,包含多种类型的节点或多种类型的边。
定义异质网络
- 节点有多种类型,节点类型集合为
- 边有多种类型,边类型集合为
对于异质网络,有
- 节点有多种类型,节点类型集合为
定义
metapathmetapath定义了composition。metapath表示不同对象之间的语义路径semantic path。定义
metapath-based邻居:给定一个metapathmetapath-based邻居metapath如下图所示,我们构建了
IMDB的一个异质图,它包含多种类型的节点(演员Actor:A,电影Movie:M,导演Director:D),以及多种类型的关系。- 两个电影可以通过多种
metapath连接,如MAM, MDM。 - 不同的
metapath通常表示不同的语义,如:MAM表示两部电影是同一个演员参演的;MDM表示两部电影是同一个导演主导的。 - 图
d中,给定metapath MAM的情况下,metapath-based邻居包含metapath MDM的情况下,metapath-based邻居包含
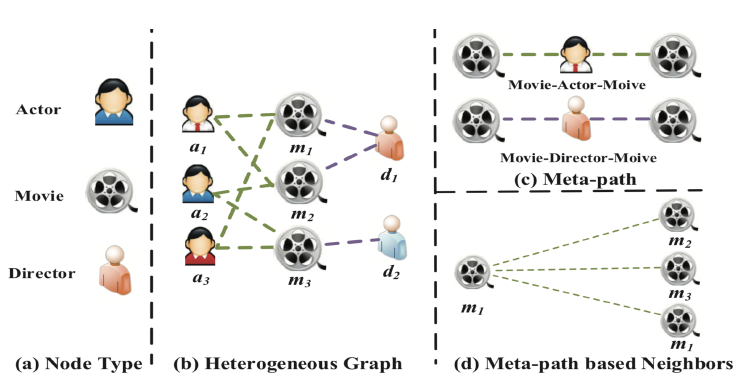
- 两个电影可以通过多种
现有的图神经网络可以处理任意图结构数据,但是它们都是针对同质网络来设计。由于
metapath和metapath-based邻居是异质图的两个基本结构,因此我们为异质图设计一种新的半监督图神经网络HAN。HAN采用hierarchical attention结构:node-level注意力机制、semantic-level注意力机制。下图给出了HAN的整体框架:- 首先我们提出
node-level注意力,从而获取metapath-based邻居的权重,并在特定语义下(每个metapath对应一个语义)聚合这些邻居从而得到节点的embedding。 - 然后我们提出
semantic-level注意力,从而区分metapath的权重。从而最终结合了node-level注意力和semantic-level注意力来获取node embedding的最佳加权组合。

- 首先我们提出
21.1.1 node-level attention
每个节点的
metapath-based邻居扮演了不同的角色,并且在task-specific node embedding学习中表现出不同的重要性。因此,我们考虑node-level注意力,它能够学习异质图中每个节点的metapath-based邻居的重要性,并聚合这些重要的邻居embedding从而生成node embedding。由于节点的异质性,不同类型节点具有不同的特征空间。因此,对于类型为
type-specific转换矩阵节点特征的投影过程为:
其中:
通过
type-specific特征投影过程,node-level注意力可以处理任意类型的节点。然后,我们利用
self-attention机制来学习metapath-based邻居之间的重要性。给定一对节点
metapathnode-level注意力基于
metapath的节点pair对其中:
node-level注意力的深度神经网络。给定
metapathmetapath-based节点pair对之间共享,这是因为在metapathmetapath节点重要性是非对称的,即node-level注意力可以保留异质图的不对称性,而这种不对称性是异质图的关键特性。即使
给定
metapathmetapath-based节点pair对
通常我们选择
其中:
metapathnode-level注意力向量attention vector,它是metapath-specific的。
然后,我们通过
masked attention将结构信息注入到模型,这意味着我们计算metapath-based邻居(包括其自身)。在获得
metapath-based节点pair对的重要性之后,我们通过softmax函数对其进行归一化,从而获得权重系数可以看到:
- 权重系数
- 权重系数
- 由于权重系数
metapath生成的,因此它是semantic-specific的,并且能够捕获一种语义信息。
- 权重系数
最后,节点
metapath-based embedding可以通过邻居的投影后的特征和相应的权重系数进行聚合:其中
metapathembedding。为更好地理解
node-level聚合过程,我们以下图(a)为例进行简要说明。每个节点的embedding均由其metapath-based邻居的特征聚合而来。由于注意力权重metapath而生成的,因此它是semantic-specific并且能够捕获一种语义信息。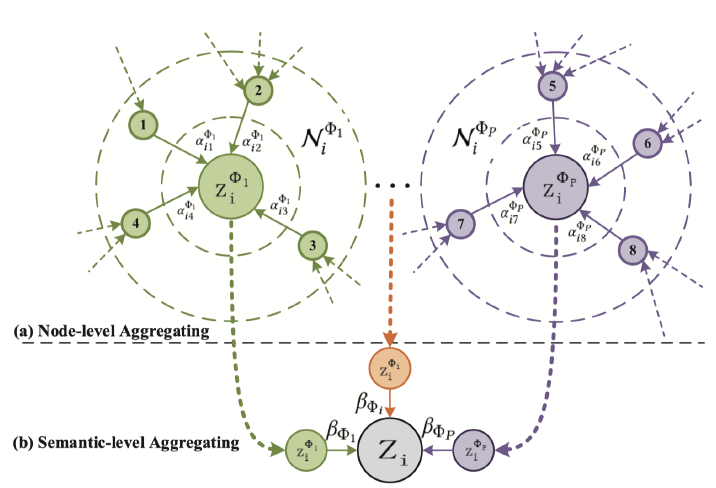
由于异质图的数据规模可大可小,其规模的方差很大。为使得
HAN能够应用到各种规模的异质图,我们将node-level注意力扩展为multi-head注意力,从而使得训练过程更为稳定。具体而言,我们重复
node-level注意力embedding拼接,从而作为最终的semantic-specific embedding:其中
head学到的权重系数。给定
metapath集合node-level注意力机制之后,我们可以获得semantic-specific node embedding,记作semantic-specific node embedding包含了图中所有的节点。如何确定这个
metapath集合,论文并未给出任何答案或方向。
21.1.2 semantic-level attention
通常异质图中每个节点都包含多种类型的语义信息,并且
smantic-specific node embedding仅能反映节点某个方面的语义。为学到更全面的节点embedding,我们需要融合各种类型语义。为解决多种类型语义融合的挑战,我们提出一种新的
semantic-level attention机制,可以自动学习task-specific下不同metapath的重要性,从而融合多种类型的语义。考虑
node-level注意力下学到的semantic-specific node embeddingmetapath的重要性为其中
semantic-level注意力的深度神经网络。为学习
metapath的重要性:- 我们首先通过非线性变换(如单层
MLP)来转换semantic-specifc node embedding。 - 然后,我们将转后的
embedding和一个semantic-level注意力向量attention vector - 最后我们聚合所有
semantic-specific node embedding的重要性,从而得到每个metapath的重要性。
记
metapath其中:
semantic-level的注意力向量。
注意:为进行有意义的比较,所有的
metapath和semantic-specific node embedding都共享相同的上式重写为:
metapathmetapath-level的embedding这里对不同
metapath共享相同的投影矩阵在得到每个
metapath重要性之后,我们通过softmax函数对其进行归一化。metapathmetapathmetapathmetapath使用学到的权重作为系数,我们可以融合这些
semantic-specifc node embedding,从而得到最终的embedding为:- 我们首先通过非线性变换(如单层
为更好地理解
sementic-level聚合过程,我们在下图的(b)中进行简要说明。最终的embedding由所有semantic-specific node embedding进行聚合。
对于不同的任务,我们可以设计不同的损失函数。对于半监督节点分类任务,我们可以使用交叉熵损失函数:
其中:
label的one-hot向量。embedding向量。
在标记数据的指导下,我们可以通过反向传播优化
HAN模型,并学习node embedding。HAN算法:输入:
- 异质图
- 所有节点的特征
metapath集合multi-head数量
- 异质图
输出:
- 最终的
node embedding矩阵 node-level每个head的注意力权重semantic-level的注意力权重
- 最终的
算法步骤:
迭代
metapath:迭代多头
进行
type-specific转换:遍历所有节点
找到
metapath-based邻域集合对于
计算
semantic-specific节点embedding:
拼接多头学到的
semantic-specific节点embedding:
计算
metapath融合
semantic-specific node embedding:计算交叉熵损失:
反向传播并更新参数
返回
21.1.3 分析
HAN可以处理异质图中各种类型的节点和各种类型的关系,并融合了丰富的语义信息。信息可以通过多种关系从一种类型的节点传播到另一种类型的节点。得益于这种异质的图注意力网络,不同类型节点的embedding能够不断相互促进提升。HAN是高效的,可以轻松并行化。每个节点的注意力可以独立地并行化,每条metapath的注意力也可以独立地计算。给定一个
metapathnode-level注意力的时间复杂度为metapathmetapathpair对的数量。multi-head的数量。
总体复杂度和
metapath中节点数量成线性,和metapath中节点pair对的数量成线性。分层注意力的参数在整个异质图上共享,这意味着
HAN的参数规模不依赖于异质图的大小,并且HAN可以应用于inductive learning。HAN对于学到的node embedding具有潜在的良好解释性,这对于异质图的分析是一个很大的优势。有了节点重要性和
metapath重要性,HAN可以在具体任务下更关注于一些有意义的节点或metapath,并给异质图一个更全面的描述。根据注意力值,我们可以检查哪些节点或
metapath为任务做出了更多(或更少)的贡献,这有助于分析和解释我们预测的结果。
21.2 实验
数据集:
DBLP:我们提取了DBLP的子集,其中包含14328篇论文(paper:P)、4057位作者(author:A)、20个会议(conference:C)、8789个术语 (term:T) 。作者分为四个领域:数据库database、数据挖掘data mining、机器学习machine learning、信息检索information retrieval。我们根据作者提交的会议来标记每个作者的研究领域。作者的特征是他们发表文档的关键词的
bag-of-word。这里我们使用metapath集合ACM:我们提取在KDD, SIGMOD, SIGCOMM, MobiCOMM, VLDB中发表的论文,并将论文分为三个类别:数据库database、无线通信wireless commmunication、数据挖掘data mining。然后我们构建一个包含3025篇论文(paper:P)、5835名作者(auther:A)、56个主题(subject:S)的异质图,论文标签为它被发表的会议。论文的特征为关键词的
bag-of-word。这里我们使用metapath集合IMDB:我们提取IMDB的子集,其中包含4780部电影(movie:M)、5841名演员(actor:A)、2269位导演(director:D)。电影根据类型分为三个类别:动作片Action、喜剧Comedy、戏剧Drama。电影的特征为电影情节的
bag-of-word。这里我们使用metapath集合
数据集的统计结果如下所示:

baseline方法:我们和一些最新的baseline方法比较,其中包括:同质网络embedding、异质网络embedding、基于图神经网络的方法。为分别验证node-level注意力和semantic-level注意力,我们还测试了HAN的两个变体。DeepWalk:一种基于随机游走的网络embedding方法,仅用于同质图。这里我们忽略节点的异质性,并在整个异质图上执行DeepWalk。ESim:一种异质图的embedding方法,可以从多个metapath捕获语义信息。由于难以搜索一组
metapath的权重,因此我们将HAN学到的metapath权重分配给ESim。metapath2vec:一种异质图embedding方法,该方法执行metapath-based随机游走,并利用skip-gram嵌入异质图。这里我们测试
metapath2vec的所有metapath并报告最佳性能。HERec:一种异质图embedding方法,该方法设计了一种类型约束策略来过滤节点序列,并利用skip-gram来嵌入异质图。这里我们测试了
HERec的所有metapath并报告了最佳性能。GCN:用于同质图的半监督图神经网络。这里我们测试了
GCN的所有metapath,并报告了最佳性能。GAT:用于同质图的半监督神经网络,它考虑了图上的注意力机制。这里我们测试了
GAT的所有metapath,并报告了最佳性能。HAN的一个变体,它移除了node-level注意力机制,并给节点的每个邻域赋予相同的权重。HAN的一个变体,它移除了semantic-level注意力机制,并给每个metapath赋予相同的权重。HAN:我们提出的半监督图神经网络,它同时采用了node-level注意力和semantic-level注意力。
这里有些
baseline是无监督的、有些是半监督的。将半监督方法和无监督方法进行比较是不公平的,因为半监督方法可以获得部分的label信息,因此半监督方法通常都会比无监督方法更好。实验配置:
HAN:- 随机初始化参数并使用
Adam优化器,学习率为0.005,正则化参数为0.001。 semantic-level注意力向量128,multi-head数量attention dropout比例为dropout rate = 0.6- 执行早停策略,早停的
patience = 100。即:如果100个连续的epoch中,验证集损失没有降低则停止训练。
- 随机初始化参数并使用
对于
GCN,GAT,我们使用验证集来调优其超参数。对于
GCN,GAT,HAN等半监督图神经网络,我们使用完全相同的训练集、验证集、测试集,从而确保公平性。对于
DeepWalk, ESim, metapath2vec, HERec等基于随机游走的方法,我们将每个节点开始的随机游走数量设为40,每个随机游走序列长度为100,上下文窗口大小为5,负样本的采样数量为5。为公平起见,我们将上述所有方法的
embedding维度设为64。
21.2.1 分类任务
我们使用
KNN分类器对节点进行分类,分类器的输入为模型学到的node embedding。由于图结构数据的方差可能很大,因此我们重复该过程10次,并报告平均的Macro-F1和Micro-F1。HAN在所有数据集中超越了其它baseline。- 对于传统的异质图
embedding方法,能够利用多个metapath的ESim比metapath2vec表现更好。 - 通常结合了图结构信息性和节点特征信息的图神经网络(如
GCN,GAT)要优于异质图embedding方法。 - 相较于
GCN和GAT和HAN可以对邻居进行适当地加权,从而提高了学到的embedding的性能。 - 和
GAT相比,为异质图设计的HAN能够成功地捕获丰富的语义信息并展示其优越性。 - 在没有
node-level注意力 (semantic-level注意力 (HAN更差。这表明node-level注意力建模和semantic-level注意力建模的重要性。 - 相比
DBLP,HAN在ACM,IMDB数据集的效果提升更明显,这是因为在DBLP中,metapath APCPA比其它的metapath重要得多,因此仅针对该metapath的HERec/GCN/GAT已经能够取得很好的效果。。我们在下文通过分析semantic-level注意力来解释该现象。
因此,结论证明了在异质图中捕获
node-level和semantic-level的重要性非常重要。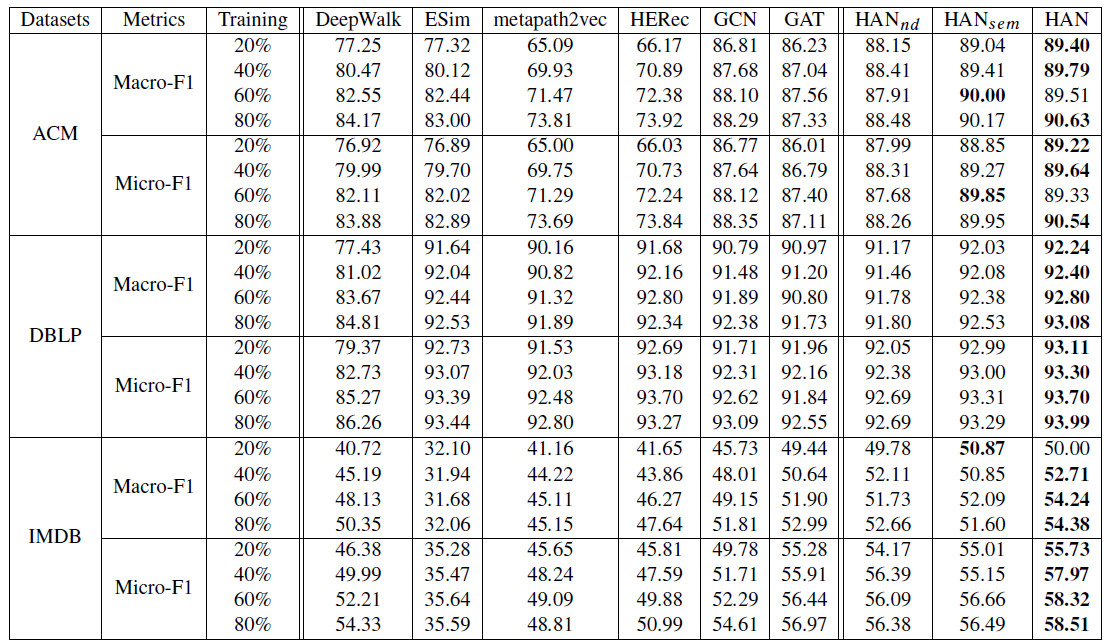
21.2.2 聚类
我们还对学到的
node embedding执行聚类,从而评估embedding的聚类效果。这里我们使用KMeans聚类算法,聚类数量设为节点的类别数量。我们使用节点的真实类别为真实的聚类类别,并使用NMI和ARI来评估聚类结果的质量。归一化互信息
NMI:其中:
ADjusted Rand index:ARI:其中:
RI指标的最大值;RI指标的期望。这是为了使得随机聚类的情况下该指标为零。
由于
KMeans的性能受到初始质心的影响,因此我们将该过程随机重复执行10次,并报告平均结果。结论:
HAN在所有数据集上始终优于其它baseline。- 基于图神经网络的算法通常可以获得更好的性能。
- 由于不区分节点和
metapath的重要性,因此metapath2vec和GCN的聚类效果较差。 - 在多个
metapath的指导下,HAN的性能明显优于GCN/GAT。 - 如果没有
node-level注意力 (semantic-level注意力 (HAN的性能会退化。这表明node-level注意力建模和semantic-level注意力建模的重要性。
基于上述分析,我们发现
HAN可以对异质图进行全面描述,并取得显著改善。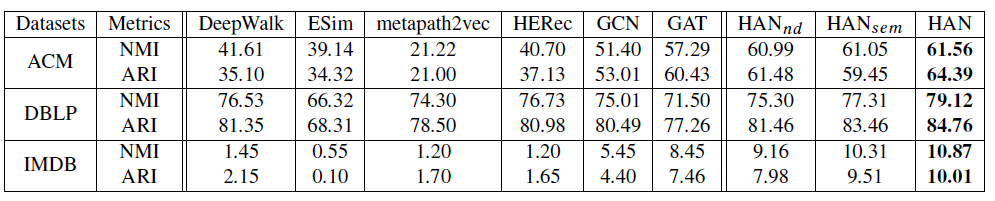
21.2.3 分层 attention
HAN的一个显著特性是结合了分层attention机制,从而在学习embedding时同时考虑了节点邻居的重要性和metapath的重要性。为了更好地理解邻居重要性和metapath重要性,我们对分层注意力机制进行详细的分析。node-level注意力:如前所述,HAN可以学到metapath中节点及其邻居之间的注意力值。对于具体的任务,重要的邻居往往具有更大的注意力值。这里我们以
ACM数据集中的论文P831为例。给定一个描述不同论文的author关系的metapath Paper-Author-Paper,我们枚举了论文P831的metapath-based邻居,其注意力值如下图所示。不同颜色表示不同的类别,如绿色表示数据挖掘、蓝色表示数据库、橙色表示无线通信。从图
a中可以看到:P831链接到P699和P133,它们都属于数据挖掘。P831链接到P2384和P2328,它们都属于数据集。P831和P1973相连,它们都属于无线通信。
从图
b中可以看到:P831从node-level注意力中获得最大的注意力值,这意味着P831自身在学习其embedding中起着最重要的作用。这是合理的,因为通常节点类别主要由其本身的特性决定,而邻居信息仅作为一种补充。
P699和P133在node-level注意力种获得第二、第三大的注意力值。这是因为P699和P133也属于数据挖掘,它们为识别P831的类别做出重大贡献。其余邻居的注意力较小,无法为识别
P831的类别做出重要贡献。
根据以上分析,我们可以看到
node-level注意力可以区分邻居之间的差别,并为某些有意义的邻居分配更大的权重。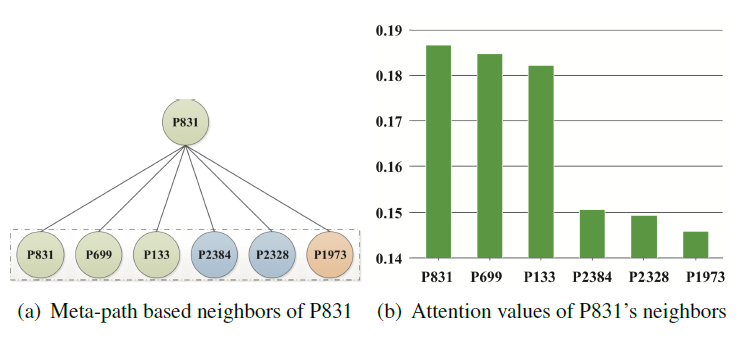
semantic-level注意力:如前所述,HAN可以学到metapath对特定任务的重要性。为验证semantic-level注意力的能力,我们以DBLP和ACM为例,给出了单个metapath聚类结果(NMI),以及对应注意力值。显然,单个
metapath的性能和它的注意力权重之间存在正相关。对于
DBLP,HAN赋予APCPA更大的权重,这意味着HAN认为APCPA是确定作者研究领域的最关键的metapath。这是有道理的,因为作者的研究领域和他们提交的会议是高度相关的。如,一些NLP研究人员主要将其论文提交给ACL或EMNLP;另一些数据挖掘研究人员可能将其论文提交给KDD或WWW。另外,
APA很难准确地确定作者的研究领域。因此,如果我们平等地对待这些metapath(如根据每个
metapath的注意力值,我们发现metapath APCPA比APA, APTPA有用的多。因此,即使HAN将这些metapath聚合在一起,APCPA在确定作者研究领域方面仍然起着主导作用。这也是为什么在
DBLP中,HAN性能可能不如ACM和IMDB中提升得那么多。对于
ACM,我们也得出类似得结论。对于ACM,PAP的权重更高。由于
PAP的性能略好于PSP,因此
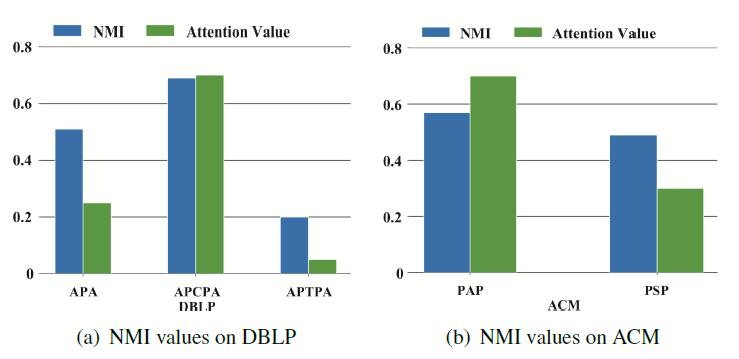
21.2.4 可视化
为直观地进行比较,我们执行可视化任务,从而在低维空间中可视化异质图。具体而言,我们基于模型学习节点
embedding,并将学到的embedding映射到二维空间。这里,我们使用t-SNE来可视化DBLP的author节点,并根据节点类别来进行染色。结论:
为同质图设计的
GCN和GAT效果不佳,属于不同研究领域的作者彼此混杂。metapath2vec的性能比上述同质图的神经网络效果好得多,它表明适当的metapath(如APCPA) 对异质图分析做出重要贡献。但是,由于
metapath2vec仅考虑一条metapath,因此不同类别节点之间的边界仍然模糊。HAN的可视化效果最好。在多种metapath指导下,HAN学到的embedding具有高度的簇内相似性,并将具有不同研究领域学者的边界的区分开来。
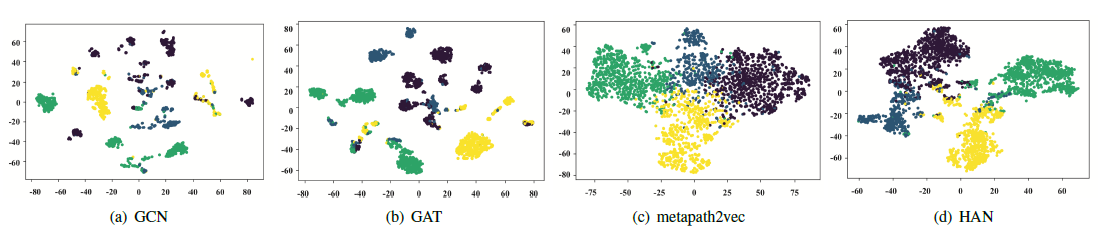
21.2.5 参数敏感性
这里我们研究参数敏感性,并报告了不同参数下,
ACM数据集上的聚类NMI结果。最终
embeddingembedding维度的增加,HAN性能先提高后下降。原因是:
HAN需要一个合适的维度来编码语义信息,但是维度过大之后可能会引入额外的冗余(即,过拟合)。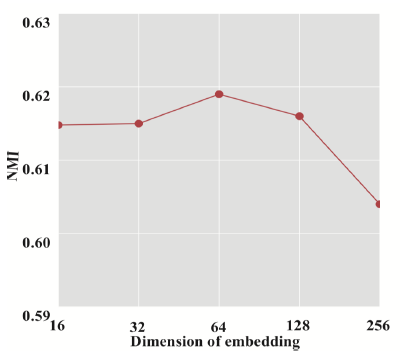
semantic-level注意力向量维度:可以看到,HAN的性能首先随着semantic-level注意力向量128时达到最佳性能;然后随着维度的增加而下降,这可能是因为过拟合导致。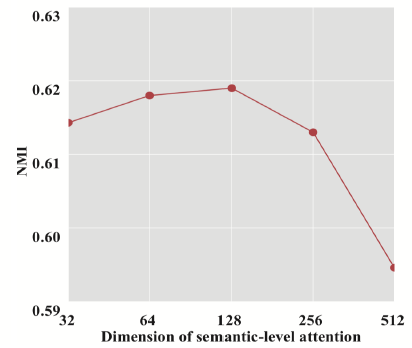
multi-head数量HAN性能越好。但是随着HAN的性能略有改善(改善幅度不大)。同时,我们还发现multi-head attention可以使得训练过程更为稳定。注意:当
multi-head退化为单头。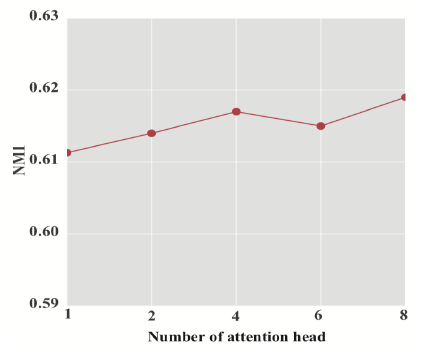
二十二、HetGNN[2019]
异质图
heterogeneous graph: HetG包含多种类型的节点,以及节点之间的多种关系。如下图的学术网络包含了author节点、paper节点以及venue节点,并包含了author和paper之间的write关系、paper和paper之间的cite关系、paper和venue之间的publish关系。此外,节点还具有属性(author id)以及文本(论文摘要)等特征。异质图的这种普遍性导致大量的研究开始涌入相应的图挖掘方法和算法,例如关系推理relation inference、个性化推荐、节点分类等等。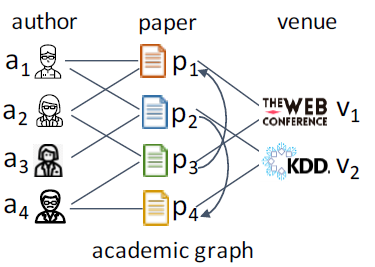
传统的异质图任务中,很多方法都依赖于从手工特征中得到特征向量。这种方式需要分析和计算有关异质图的不同统计特性和属性,从而作为下游机器学习任务的特征向量。但是这种方式仅局限于当前任务,无法推广到其它任务。近期出现的
representation learning方法使得特征工程自动化,从而促进下游的机器学习任务。从同质图开始,graph representation learning已经扩展到异质图、属性图、以及特定的图。例如:shallow model(如DeepWalk)最初是为了将图上的短随机游走的集合提供给SkipGram模型,从而近似approximate这些游走中的节点共现概率node co-occurrence probability并获得node embedding。- 随后,人们提出了语义感知
semantic-aware方法(如metapath2vec),从而解决异质图中的节点异质性node heterogeneity和关系异质性relation heterogeneity。 - 此外,内容感知方法(如
ASNE)利用latent feature和属性来学习图中的node embedding。
这些方法直接学习节点的潜在
embedding,但是在捕获丰富的邻域信息方面受到限制。图神经网络GNN采用深度神经网络来聚合邻域节点的特征信息,这使得aggregated embedding更加强大。此外,GNN可以自然地应用于inductive任务,该任务涉及到训练期间unseen的节点。例如,GCN, GraphSAGE, GAT分别采用卷积操作、LSTM架构、以及注意力机制来聚合邻域节点的特征信息。GNN的进步和应用主要集中在同质图上。但是,当前state-of-the-art的GNN无法解决异质图学习的以下问题:问题
C1:异质图中很多节点连接到多种类型的邻居,连接的邻居节点的种类和数量可能各不相同。例如,下图中节点a有5个直接邻居而节点c只有2个直接邻居。现有的大多数
GNN仅聚合直接邻域的特征信息,而特征传播过程可能会削弱更远邻域的影响。此外,hub节点的embedding生成受到弱相关的邻居(即,噪声邻居)的影响,并且“冷启动”节点的embedding无法充分地被表达(由于邻域信息有限所导致)。第一个问题是:如何对每个节点采样和它
embedding最相关的异质邻居?如下图中的C1阶段所示。问题
C2:异质图中的节点可能具有非结构化的异质内容,如属性、文本、图像等。另外,不同类型节点关联的内容可能有所不同。如下图中:type-1的节点(如b,c)关联的内容为属性、文本。type-2的节点(如f,g)关联的内容为属性、图像。type-k的节点(如d,e)关联的内容为文本、图像。
当前
GNN的直接拼接操作或者线性变换操作无法对节点异质内容之间的深层交互deep interaction进行建模。而且,由于不同类型节点的内容多种多样,因此针对所有类型节点使用相同的特征变换函数是不合适的。第二个问题是:如何设计节点内容encoder,从而编码异质图中不同节点的内容异质性?如下图中的C2阶段所示。问题
C3:不同类型的邻居对异质图中node embedding的贡献不同。如学术网络中,author和paper类型的邻居对author节点的embedding产生更大的影响,因为venue类型的节点包含多样化的主题因此具有更general的embedding。当前大多数GNN仅关于同质图,并未考虑节点类型的影响。第三个问题是:如何考虑不同类型节点的影响,从而聚合异质邻居的特征信息。如下图中的C3阶段所示。
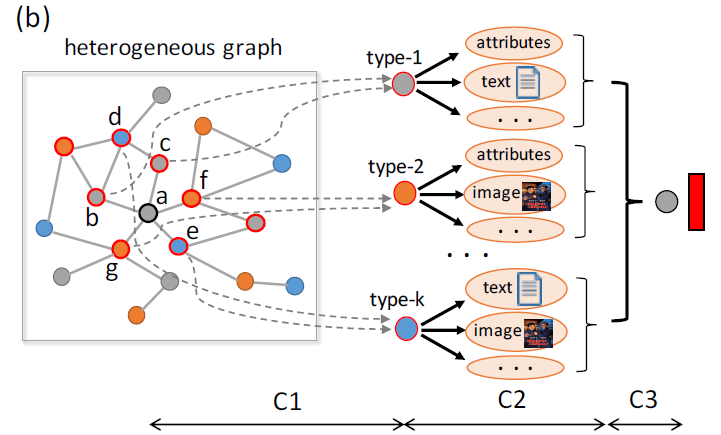
为解决这些问题,论文
《Heterogeneous Graph Neural Network》提出了heterogeneous graph neural network: HetGNN。HetGNN是一种用于异质图的representation learning图神经网络模型。首先,作者设计了一种基于重启的随机游走策略,从而对异质图中每个节点采样固定大小的、强相关的异质邻域,并根据节点类型对其进行分组。
然后,作者设计了一个具有两个模块的异质图神经网络体系结构,从而聚合上一步中采样到的邻居的特征信息。
第一个模块采用
RNN对异质内容的deep interaction进行编码,从而获得每个节点的内容embedding。因为单个节点可能具有多个内容(既有文本又有图像),因此需要通过一个模块来融合多种不同的内容从而得到内容
embedding。第二个模块采用另一个
RNN来聚合不同分组邻居的内容embedding,然后通过注意力机制将其进一步组合,从而区分不同异质节点类型的影响,并获得最终embedding。
最后,论文利用图上下文损失
graph context loss和mini-batch随机梯度下降来训练模型。
总而言之,论文的主要贡献:
论文形式化了异质图
representation learning的问题,该问题涉及到图结构异质性和节点内容异质性。论文提出了一种创新的异质图神经网络模型
heterogeneous graph neural network model: HetGNN,用于异质图上的representation learning。HetGNN能够捕获结构异质性和内容异质性,并对transductive task和inductive task都很有用。下表总结了HetGNN与最近的一些模型(包括同质图模型、异质图模型、属性图模型、以及图神经网络模型)相比的主要优势。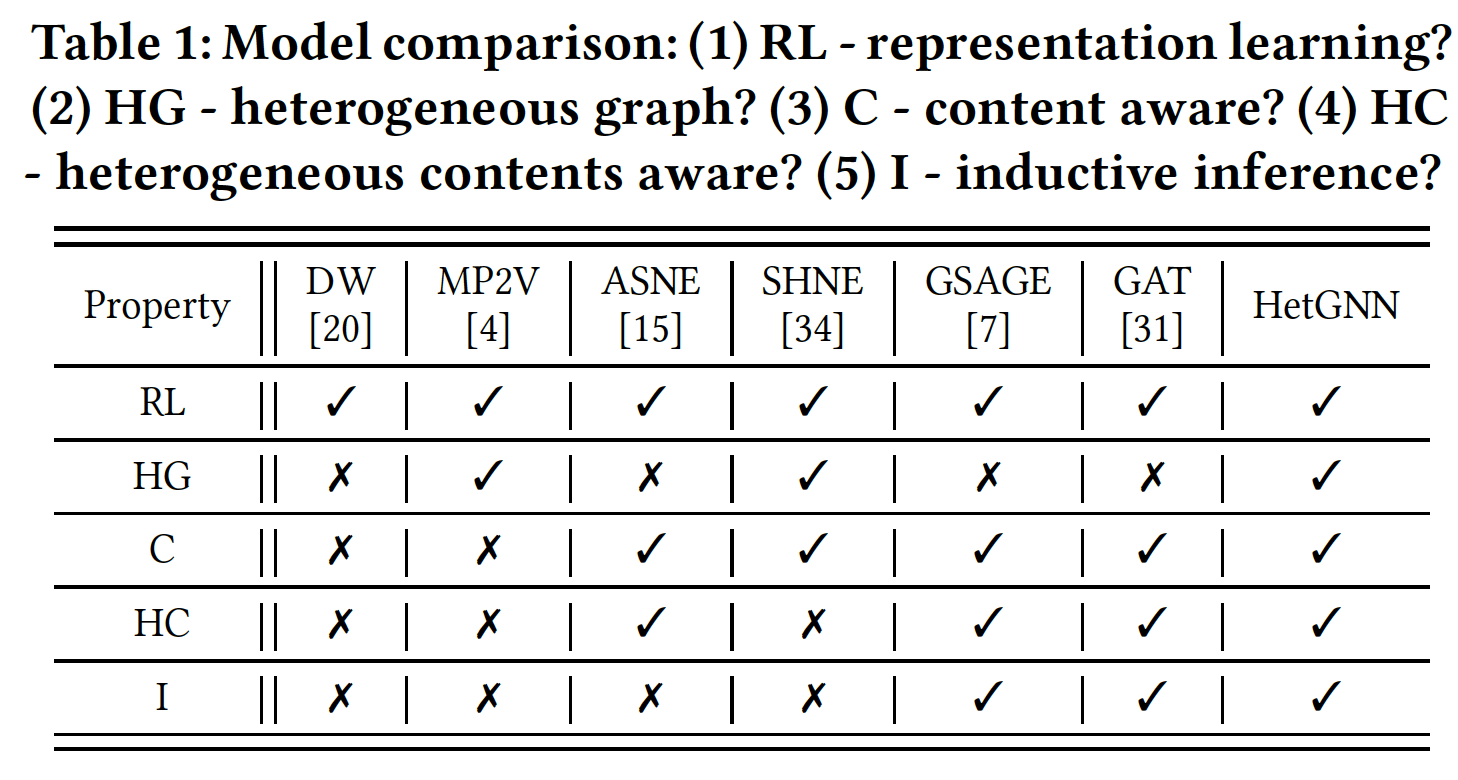
论文在几个公共数据集上进行了广泛的实验,结果表明:
HetGNN在各种图数据挖掘任务(链接预测、推荐、节点分类、聚类)中可以超越state-of-the-art的baseline方法。
相关工作:
异质图挖掘
heterogeneous graph mining:在过去的十年中,许多工作致力于挖掘异质图从而用于不同的application,如关系推断、个性化推荐、节点分类等等。《When will it happen?: relationship prediction in heterogeneous information networks》利用metapath-based方法来抽取拓扑特征并预测学术图academic graph中的引用关系。《Task-Guided and Path-Augmented Heterogeneous Network Embedding for Author Identification》设计了一个基于异质图的ranking model来识别匿名论文的作者。《Deep Collective Classification in Heterogeneous Information Networks》提出了一种深度卷积分类模型,用于异质图中的collective classification。
图表示学习
graph representation learning:graph epresentation learning已经成为过去几年最流行的数据挖掘主题之一。人们提出了基于图结构的模型来学习向量化的node embedding从而进一步用于下游各种图挖掘任务。- 受到
word2vec的启发,《Deepwalk: Online learning of social representations》创新性地提出了DeepWalk,它在图中引入了node-context的概念(类比于word-context),并将图上的随机游走的集合(类比于sentence集合)提供给SkipGram从而获得node embedding。 - 后来,为了解决图结构的异质性,
《metapath2vec: Scalable Representation Learning for Heterogeneous Networks》引入了metapath-guided随机游走,并提出metapath2vec模型来用于异质图中的representation learning。 - 此外,人们已经提出了属性图嵌入模型(
《Attributed network embedding for learning in a dynamic environment》、《Attributed social network embedding》、《SHNE: Representation Learning for Semantic-Associated Heterogeneous Networks》)来利用图结构和节点属性来学习node embedding。 - 除了这些方法之外,人们还提出了许多其它方法(
《Heterogeneous network embedding via deep architectures》、《Hierarchical Taxonomy Aware Network Embedding》、《Network embedding as matrix factorization: Unifying deepwalk, line, pte, and node2vec》、《Pte: Predictive text embedding through large-scale heterogeneous text networks》、《Learning Deep Network Representations with Adversarially Regularized Autoencoders》)。
- 受到
图神经网络
graph neural networks:最近,随着深度学习的出现,图神经网络获得了很多关注。与之前的graph embedding模型不同,GNN背后的关键思想是:通过神经网络从节点的局部邻域中聚合特征信息。Graph-SAGE使用神经网络(如LSTM)来聚合邻域的特征信息。GAT使用自注意力机制来衡量不同邻居的影响力,并结合它们的影响力来获得node embedding。- 此外,人们已经提出了一些
task dependent的方法从而为特定任务获得更好的node embedding,例如用于恶意账户检测的GEM(《Heterogeneous Graph Neural Networks for Malicious Account Detection》)。
22.1 模型
定义一个带内容的异质图
content associated heterogeneous graph:C-HetG为attribute、文本text、图像image。给定一个
C-HetGHeterogenous Graph Representation Learning的目标是设计一个模型embedding,从而能够同时编码异质结构信息和异质内容信息,其中学到的
node embedding可以应用于下游各种图挖掘任务,如链接预测、推荐、多标签分类、节点聚类等。我们首先给出
HetGNN的整体框架如下图所示,其中包含四个部分:对异质邻居节点进行采样、编码节点的异质内容、聚合节点的异质邻居、定义目标函数并给出训练过程。下图中:
图
(a)为整体框架:- 首先为每个节点(以节点
a为例)采样固定数量的异质邻居节点。 - 然后通过
NN-1神经网络编码每个节点的异质内容。 - 然后通过
NN-2神经网络和NN-3神经网络来聚合采样到的异质邻居节点的内容embedding。 - 最后通过图上下文损失函数来优化模型。
- 首先为每个节点(以节点
图
(b)为NN-1神经网络,它是节点异质内容编码器。图
(c)为NN-2神经网络,它是type-based邻域聚合器。图
(d)为NN-3神经网络,它是异质类型组合器。
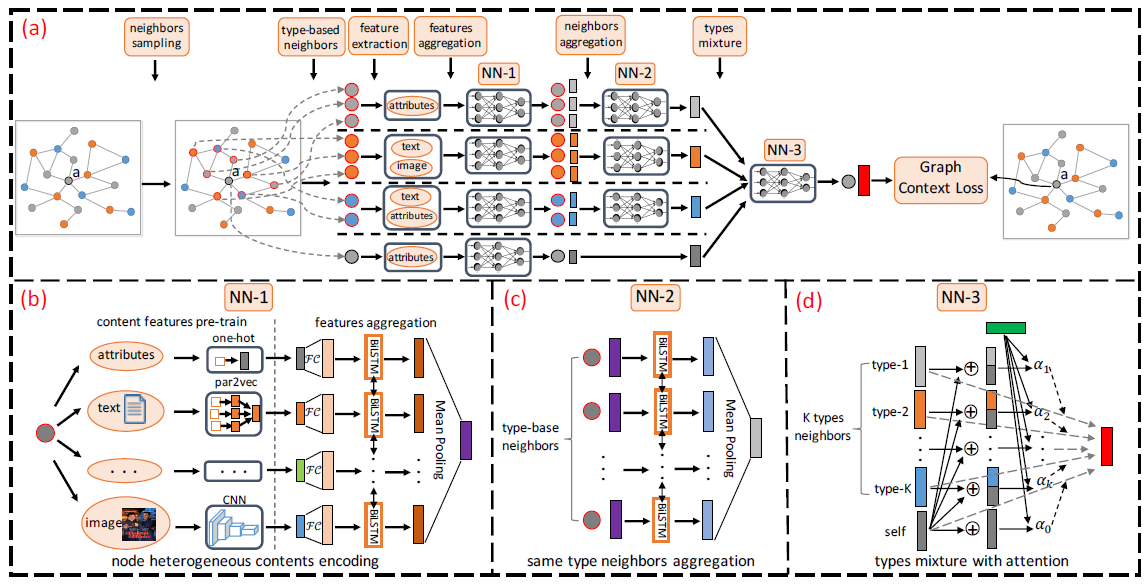
22.1.1 异质邻居采样
大多数神经网络
GNN的关键思想是聚合来自节点的直接邻居(一阶邻居)的特征信息,如GraphSAGE或GAT。但是,直接将这些方法应用到异质图可能会引起一些问题:- 它们无法从不同类型的异质邻居的直接链接中捕获充分的信息。如,在学术网络中,
author并未和其它author或venue直接相连,但是可能存在间接连接。如果仅考虑直接连接的邻居,则可能导致学到的representation表达能力不足。 embedding可能受到不同邻居规模的影响。如在推荐常见中,某些item和很多用户交互,另一些item可能只有很少的用户交互。因此:某些热门节点的embedding可能会被某些弱相关的邻居而损害,而一些冷门节点的embedding可能未能充分学习。- 无法直接聚合具有不同内容特征的异质邻居。异质邻居的内容可能需要不同的特征变换,从而处理不同的特征类型和特征维度。
针对这些问题并解决问题
C1,我们设计了一种基于重启的随机游走策略random walk with restart: RWR来对异质邻居进行采样。RWR包含两个连续的步骤:step1:基于RWR采样固定数量的邻居。我们从节点我们始终执行
RWR直到收集到固定数量的节点,收集到的节点集合记作注意:
step2:对采样的邻居节点集合根据节点类型进行分组。对于节点类型top
由于下列原因,
RWR策略能够避免上述问题:RWR能够为每个节点收集到所有类型的邻居。- 每个节点采样的邻居规模是固定的,并且访问最频繁的邻居节点(即最相关的)被挑选出来。
- 根据节点类型对邻居进行分组(每个分组具有相同的内容格式),以便可以设计基于类型的聚合。
- 它们无法从不同类型的异质邻居的直接链接中捕获充分的信息。如,在学术网络中,
22.1.2 异质内容编码
我们设计了一个具有两个模块的异质图神经网络体系结构,从而聚合每个节点的采样后异质邻居的特征信息。
为解决问题
C2,我们设计了一个模块,从节点embedding。具体而言,我们将
Par2Vec来预训练文本内容,可以利用CNN来预训练图像内容。之前的一些方法直接拼接不同的内容特征,或者将不同的内容特征经过线性映射到相同的特征空间。和这些方法不同,我们基于
Bi-LSTM设计了一种新的架构来捕获deep feature interaction,并获得更强的表达能力。因此,节点
embedding为:其中:
embedding,embedding维度。feature transformer,它可以是恒等映射(没有任何变换)、也可以是一个全连接神经网络(参数为LSTM之前,首先进行特征变换。
具体而言,上述架构首先使用不同的
FC层来转换不同的内容特征,然后使用Bi-LSTM来捕获deep feature interaction,并聚合所有内容特征的表达能力。最后取所有隐状态的均值来获得节点embedding。通过内容拼接然后馈入全连接层也可以捕获
deep feature interaction。这里用Bi-LSTM个人觉得不太合理,因为Bi-LSTM强调有序的输入,而这里的输入是无序的。虽然通过随机排列内容集合Bi-LSTM中,但是这仅仅是一种变通方案,而没有很好地捕获到内容信息之间的关联(如互补关系、overlap关系)。注意:
Bi-LSTM应用在无序的内容集合GraphSAGE在聚合无序邻居的启发。- 我们使用不同的
Bi-LSTM来聚合不同类型节点的内容特征,因为它们的内容类型互不相同。
上述内容
embedding体系结构有三个主要优点:- 具有较低复杂度的间接架构(参数较少),使得模型的实现和调整都相对容易。
- 能够融合异质内容信息,具有很强的表达能力。
- 增加额外的特征很灵活,使得模型扩展很方便。
22.1.3 异质邻居聚合
为聚合每个节点的异质邻居的内容
embedding(问题C3),我们设计了另一个type-based神经网络模块,它包含两个步骤:同一类型的邻居聚合、类型组合。同一类型的邻居聚合:我们使用基于
RWR的策略为每个节点采样固定数量的、包含不同类型的邻居集合,并针对类型topembedding:其中:
embedding向量,embedding维度。CNN网络、或者是RNN网络。这里我们选中
Bi-LSTM,因为实践中它的效果最好。因此:我们使用
Bi-LSTM聚合所有类型为embedding。注意:
- 我们使用
Bi-LSTM来区分不同节点类型的邻域聚合。 Bi-LSTM应用在无序邻居上,这是受到GraphSAGE在聚合无序邻居的启发。
- 我们使用
类型组合
type combination:前面为每个节点embeddingtype-based邻域聚合embedding以及节点的内容embedding,我们采用了注意力机制。我们认为:不同类型的邻域对final embedding做出的贡献不同。因此,节点embedding为:其中:
final embedding。embedding的重要性。embedding,embedding。
定义节点
embedding集合为其中:
LeakyReLU。embedding向量。attention vector,是待学习的参数。
在整个框架中,为了使得
embedding维度一致并且模型易于调整,我们使用相同的维度embedding、节点邻域聚合embedding、节点final embedding。
22.1.4 模型训练
为学习异质图的
node embedding,我们定义目标函数为:其中:
条件概率
softmax函数:final embedding。
我们利用负采样技术来调整目标函数,此时
其中:
noise distributioin。即:对于节点
最终我们的损失函数为:
其中
注意,
类似于
DeepWalk,我们设计了一个随机游走过程来生成- 首先,我们在异质图中统一生成一组随机游走序列的集合
- 然后,对于随机游走序列集合
- 最后,对于每个上下文节点
degree,也等于它在
- 首先,我们在异质图中统一生成一组随机游走序列的集合
在训练的每轮迭代中,我们对
mini-batch的三元组,然后通过Adam优化器来更新模型参数。我们反复迭代直到模型收敛为止。
22.2 实验
这里我们进行广泛的实验:
HetGNN在各种图挖掘任务中和state-of-the-art baseline方法的比较,如链接预测、个性化推荐、节点分类&聚类任务。HetGNN在inductive learning任务中和state-of-the-art baseline方法的比较,如inductive节点分类&聚类任务。HetGNN中不同组件(如异质节点内容编码器,异质邻域聚合器)对模型性能的影响。HetGNN中各种超参数(如embedding维度、异质邻居采样大小)对模型性能的影响。
数据集:我们采用两种异质图数据集:学术图
academic graph、评论图review graph。学术图:我们从
AMiner数据集中抽取两个数据集:A-I包含1996 ~ 2005年之间计算机科学会议的论文。A-II包含2006 ~ 2015年之间若干个人工智能和数据科学相关的顶会的论文,因为考虑到大多数研究人员关注于顶会的论文。
每篇论文都有各种内容信息,包括:标题、摘要、作者、参考文献、年份、所属会议。
评论图:我们从公开的
Amazon数据集抽取了两个数据集,即R-I(电影类别的评论)、R-II(CD类别的评论)。数据集包含1996-05 ~ 2014-07之间用户的评论信息、商品元数据信息。每个商品都有各种内容信息,包括:标题、描述文本、类型、价格、图片。
下表给出了这四个数据集的主要统计信息:
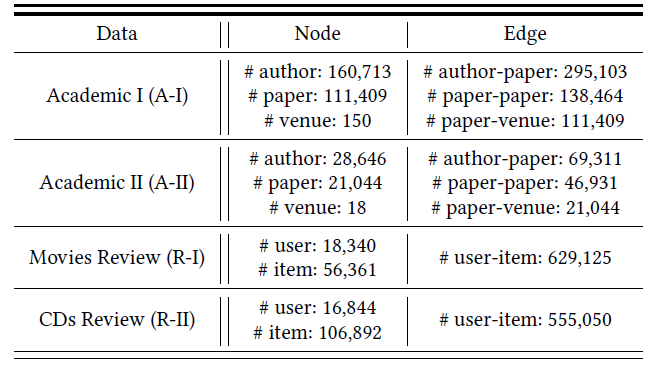
内容特征编码:
在学术网络中,我们使用
ParVec预训练论文的标题和摘要。此外,我们还使用DeepWalk来预训练异质图中所有节点的embedding(将异质图视为同质图来训练)。- 每个作者节点关联一个预训练的
author embedding(通过DeepWalk得到)、作者的所有论文(经过采样之后)的论文摘要embedding均值(通过ParVec得到)、作者的所有论文(经过采样之后)的论文标题embedding均值。因此,作者的内容编码器的Bi-LSTM的长度为3。 - 每篇论文关联一个预训练的
paper embedding(通过DeepWalk得到)、论文的摘要embedding(通过ParVec得到)、论文的标题embedding(通过ParVec得到)、论文作者预训练embedding的均值(通过DeepWalk得到,一篇论文可能有多个作者)、论文会议的预训练embedding(通过DeepWalk得到)。因此,论文的内容编码器的Bi-LSTM的长度为5。 - 每个会议节点关联一个预训练的会议
embedding(通过DeepWalk得到)、会议中随机抽取的论文的摘要的平均embedding(通过ParVec得到)、会议中随机抽取的论文的标题的平均embedding(通过ParVec得到)。因此,会议的内容编码器的Bi-LSTM的长度为3。
- 每个作者节点关联一个预训练的
在评论网络中,我们使用
ParVec预训练商品标题和描述内容,用CNN预训练商品图片。此外,我们还使用DeepWalk来预训练异质图中所有节点的embedding(将异质图视为同质图来训练)。- 每个用户关联一个预训练的用户
embedding(通过DeepWalk得到)、所有用户评论过的(经过采样之后)商品的描述文本embedding均值(通过ParVec得到)、所有用户评论过的(经过采样之后)商品的图片embedding均值(通过CNN得到)。因此,用户的内容编码器的Bi-LSTM长度为3。 - 每个商品关联一个预训练的
item embedding(通过DeepWalk得到)、商品描述文本的embedding(通过ParVec得到)、商品图片的embedding(通过CNN得到)。因此,商品的内容编码器的Bi-LSTM长度为3。
- 每个用户关联一个预训练的用户
baseline方法:我们使用5个baseline,包括异质图embedding模型、属性网络模型、图神经网络模型。metapath2vec: MP2V:一个异质图embedding模型,它基于metapath指导的随机游走来生成随机游走序列,并通过SkipGram模型来学习node embedding。ASNE:一种属性网络embedding方法,它使用节点的潜在特征和属性来学习node embedding。SHNE:一种属性网络embedding方法,它通过联合优化图结构邻近性和文本语义相似性,从而学习文本相关的异质图的node embedding。GraphSAGE:一个图神经网络模型,它聚合了邻居的特征信息。GAT:一个图注意力网络模型,它通过self-attention机制来聚合邻居的特征信息。
HetGNN的参数配置:embedding维度为128。邻域采样规模:
- 对于学术网络,邻域采样大小为
23,其中作者节点选择top-10、论文节点选择top-10、会议节点选择top-3。 - 对于评论网络,邻域采样大小为
20,其中用户节点选择top-10、商品节点选择top-10。
- 对于学术网络,邻域采样大小为
对于
RWR,我们选择返回概率RWR序列长度为100(即在获取三元组集合
10,每条随机游走序列长度为30,上下文窗口大小为5。我们使用
Pytorch来实现HetGNN,并在GPU上进行实验。
baseline参数配置:为公平起见,所有
baseline的维度设为128。对于
metapath2vec,对于学术网络我们使用三个metapath:APA(author-paper-author)、APVPA(author-paper-venue-paper-author)、APPA(author-paper-paper-author);对于评论网络我们使用一个metapath:UIU(user-item-user)。每个节点开始的随机游走序列数量为
10,每条随机游走序列的长度为30,这和HetGNN保持一致。对于
ASNE,除了latent特征之外,我们使用HetGNN相同的内容特征,然后将它们拼接为一个通用的属性特征。对于
SHNE,对于两个数据集我们分别利用论文摘要和商品描述(文本序列= 100)作为deep semantic编码器(如LSTM)的输入。此外,随机游走序列的配置和metapath2vec相同。对于
GraphSAGE和GAT,我们使用HetGNN相同的内容特征作为输入特征(拼接为一个通用的属性特征),并将每个节点的采样邻居数量设为和HetGNN相同。
22.2.1 链接预测
之前的做法是:随机采样一部分链接进行训练,然后使用剩余链接用于预测。我们认为应该根据时间顺序来拆分训练集和测试集,而不是随机拆分。
对于学术图,我们令
对于
A-I数据集,我们考虑两种拆分情况:A-II数据集,我们也考虑两种拆分情况:另外,对于学术图我们仅考虑两种类型的边:作者之间的共同撰写关系(
type-1)、作者和论文之间的引用关系(type-2)。对于评论图,我们按顺序拆分。对于
R-I数据集,根据边的数量拆分比例为7:3,对于R-II数据集,根据边的数量拆分比例为5:5。
对于测试集:
- 删除测试集中重复的边。
- 随机采样相等数量的“负边”(即不存在的噪音边)加入测试集。
我们使用所有节点 + 训练集的边来学习
node embedding,然后使用训练集的链接来训练逻辑回归分类器。逻辑回归分类器的输入为边的embedding,每条边的embedding是两端node embedding的逐元素乘积。最后,我们使用训练好的分类器来评估测试集,评估指标为
AUC和F1-Score。链接预测结果见下表所示,其中最佳结果以粗体突出显示。
结论:
- 大多数情况下,最好的
baseline是属性图embedding方法或图神经网络方法,这表明融合节点属性或使用深度神经网络能产生更好的node embedding,从而有利于链接预测。 - 在所有情况下,尤其是评论图中,
HetGNN均优于所有baseline方法。这证明了HetGNN是有效的,它产生了针对链接预测任务更有效的node embedding。
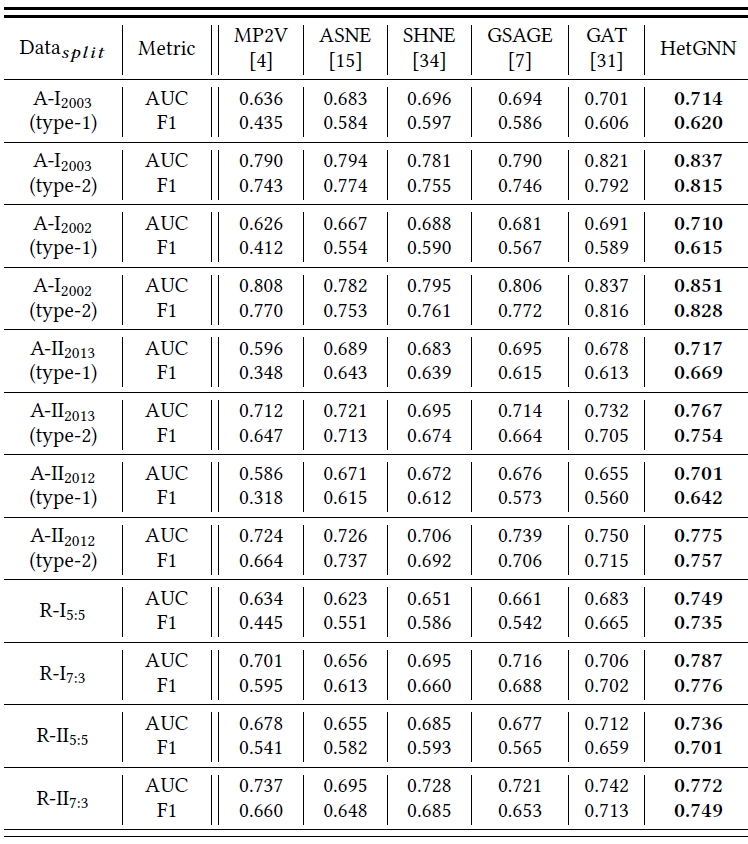
- 大多数情况下,最好的
22.2.2 个性化推荐
我们在学术图中评估顶会推荐 (
author-venue链接) 的表现。具体而言,训练数据用于学习node embedding。推荐的ground-truth为:给定测试集中的顶会,作者在测试数据集中出现(发表过论文)。和链接预测任务相同,对于
A-I数据集,我们考虑两种拆分情况:A-II数据集,我们也考虑两种拆分情况:我们采用两个节点的
embedding内积作为推荐分,并挑选top-k推荐分的作者作为推荐列表。对于A-I数据集,k=5;对于A-II数据集,k=3。推荐的评估指标为
top-k推荐列表的Recall(Rec), Precision(Pre), F1-Score,最终我们给出所有作者的均值作为报告得分。此外,重复的author-venue pair将从评估中删除。个性化推荐结果见下表所示,其中最佳结果以粗体突出显示。
结论:
- 大多数情况下,最好的
baseline是属性图embedding方法或图神经网络方法,这表明融合节点属性或使用深度神经网络能产生更好的node embedding,从而有利于个性化推荐。 - 在所有情况下,尤其是评论图中,
HetGNN均优于所有baseline方法。这证明了HetGNN是有效的,它产生了针对个性化推荐任务更有效的node embedding。
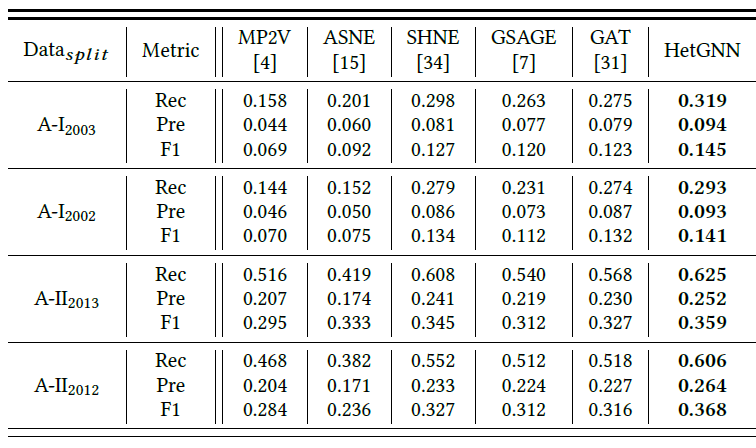
- 大多数情况下,最好的
22.2.3 节点分类&聚类
类似
metapath2vec,我们将A-II数据集中的作者分类到四个选定的研究领域:数据挖掘data mining:DM、计算机视觉computer vision:CV、自然语言处理natural language processing:NLP、数据库databse:DB。具体而言,我们为每个领域选择三个热门会议,每个作者标记为他/她大部分论文所属的领域。如果在这些会议中未发表论文的作者将被剔除评估。如果作者在这些会议的多个领域发表过论文,则作者为多个标签。因此这是一个多标签节点分类问题。
我们从完整数据集中学习
node embedding,然后将学到的node embedding来作为逻辑回归分类器的输入。我们将带标记的节点随机拆分,训练集的大小从10%~30%,剩余节点作为测试集。评估指标为测试集的Micro-F1和Macro-F1。对于节点聚类任务,我们将学到的
node embedding作为聚类模型的输入。这里我们采用Kmeans算法作为聚类算法,然后采用NMI和ARI作为评估指标。下表给出了所有方法的评估结果,最佳结果以粗体突出显示。
结论:
- 大多数模型在多标签分类任务中表现良好,并得到较高的
Macro-F1和Micro-F1指标。这是因为这四个选定领域的作者彼此完全不同,分类相对容易。 - 尽管如此,
HetGNN在多标签分类和节点聚类方面仍然达到了最佳性能或者可比的性能。这证明了HetGNN是有效的,它产生了针对节点分类和聚类任务更有效的node embedding。
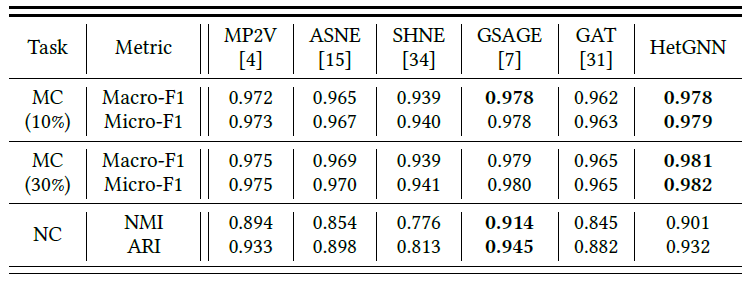
- 大多数模型在多标签分类任务中表现良好,并得到较高的
此外,我们还通过
tensorflow embedding projector来可视化四个领域作者的embedding。我们随机采样了100位作者,如下图所示分别位2D可视化和3D可视化。可以看到:同类别作者的
embedding紧密地聚集在一起,从而证明了学到的node embedding的有效性。
22.2.4 inductive 节点分类&聚类
该任务的配置和之前的节点分类&聚类任务类似,不同之处在于:我们对
A-II数据集进行按年份拆分,拆分年份为2013,然后将2013年以及之前的数据作为训练集、之后的数据作为测试集。我们用训练集中的数据来训练模型并得到训练集中节点的
embedding,然后用训练好的模型来推断测试集中新节点的embedding。最后我们使用推断的新node embedding来作为分类和聚类模型的输入。注:逻辑回归分类器使用训练集中的节点来训练。
下表给出了
inductive节点分类和聚类任务的结果,其中最佳结果以粗体显示。结论:
大多数模型在
inductive多标签分类任务中表现良好,并得到较高的Macro-F1和Micro-F1指标。这是因为这四个选定领域的作者彼此完全不同,分类相对容易。尽管如此,
HetGNN在inductive多标签分类任务中仍然达到了最佳性能或者可比的性能HetGNN在inductive节点聚类任务中优于所有其它方法。
结果表明
HetGNN模型可以有效地推断新节点的embedding。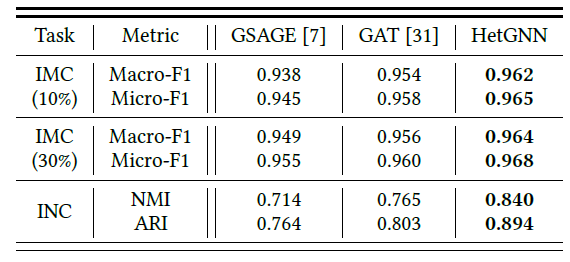
22.2.5 消融研究
我们考察了
HetGNN模型的几种变体:No-Neigh:直接使用异质内容编码来表示每个节点的embedding,不考虑邻居信息。即:Content-FC:使用全连接层来作为异质内容编码器,从而代替Bi-LSTM。Type-FC:使用全连接层来融合不同邻居类型的embedding,而不是BiLSTM + attention。
下图报告了
A-II数据集(训练集--测试集拆分年份2013)上链接预测和节点推荐的结果。结论:
- 大多数情况下,
HetGNN性能优于No-Neigh,这表明聚合邻域信息对于生成更好的node embedding是有效的。 HetGNN优于Content-FC,这表明基于Bi-LSTM的内容编码要比浅层编码器(如全连接层)要更好,Bi-LSTM可以捕获深度的内容特征交互。HetGNN优于Type-FC,这表明在捕获节点类型的影响方面,基于attention机制要优于全连接层。
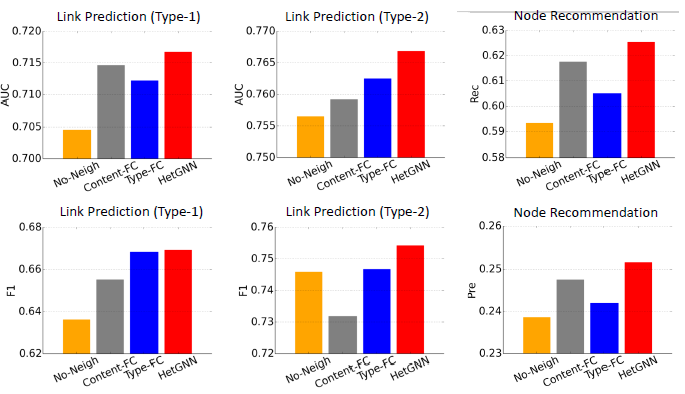
22.2.6 参数敏感性
我们考察
HetGNN链接预测和推荐的性能随embedding维度A-II训练集上评估,训练集--测试集拆分年份位2013。当固定采样邻居规模(设为23),我们选择不同的结论:当
8增加到256时,所有指标都会增加,因为学到了更好的embedding。但是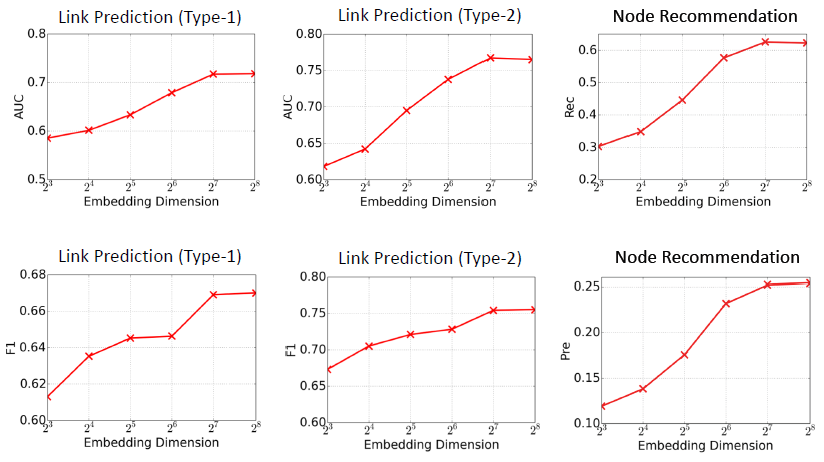
我们考察
HetGNN链接预测和推荐的性能随样本邻域大小的影响。我们在A-II训练集上评估,训练集--测试集拆分年份为2013。当固定embedding维度topxxxxxxxxxx6 = 2 (author) + 2 (paper) + 2 (venue)12= 5 (author) + 5 (paper) + 2 (venue)17 = 7 (author) + 7 (paper) + 3(venue)23 = 10 (author) + 10 (paper) + 3 (venue)28 = 12 (author) + 12 (paper) + 4 (venue)34 = 15 (author) + 15 (paper) + 4 (venue)结论:当邻域大小从
6增加到34时,所有指标都会增加,这是因为考虑了更多的邻域信息。但是当邻域规模超过某个值时,性能可能会缓缓降低,这可能是因为涉及到不相关的(噪音)邻居导致。最佳邻域大小为20 ~ 30。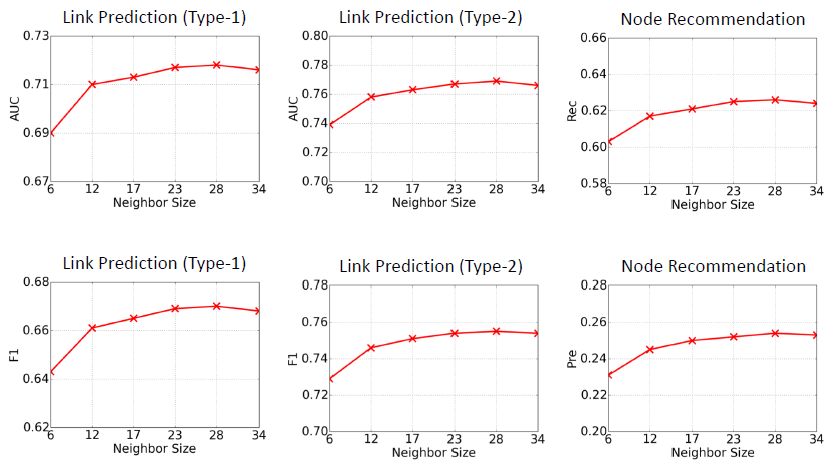
二十三、HGT[2020]
异质图通常用于对复杂系统进行抽象和建模,图中包含不同类型的对象、不同类型的链接。如,
Open Academic Graph:OAG数据中包含五种类型的节点:论文Paper、作者Author、机构Institution、会议Venue、领域Field,以及它们之间各种不同类型的关系,如下图所示。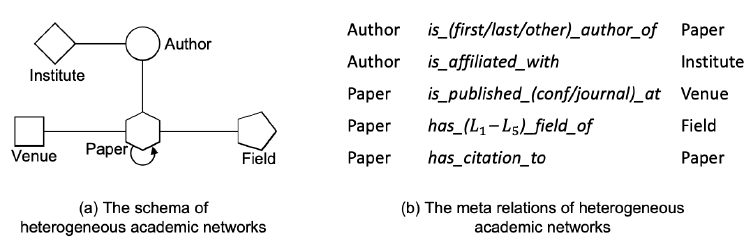
关于异质图挖掘已有大量的研究。一种经典的范式
paradigm是定义和使用metapath元路径来建模异质图,例如PathSim和metapath2vec。最近,鉴于图神经网络GNN的成功,有几种方法尝试采用GNN来学习异质图。然而,这类工作面临以下几个问题:- 首先,大多数针对异质图的
metapath设计需要特定的领域知识。 - 其次,它们要么简单地假设不同类型的节点/边共享相同的特征和
representation space,要么假设不同类型的节点/边都有各自的特征和representation space。这两种极端使得它们都不足以捕获异质图的属性。 - 再次,大多数现有方法忽略了异质图的动态特性。
- 最后,它们固有的设计和实现使其无法建模
web-scale异质图。
以
OAG为例:- 首先,
OAG中的节点和边可能有不同的特征分布,例如paper节点有文本特征,而institution节点可能有附属学者的特征,作者之间的co-authorship关系明显不同于论文之间的citation关系。 - 其次,
OAG一直在不断演变,例如,出版物的数量每隔12年翻一番,KDD会议在1990年更多地与数据库相关而近年来更多地与机器学习相关。 - 最后,
OAG包含数亿个节点和数十亿个关系,这使得现有的异质GNN无法扩展以处理它。
为了解决上述问题,论文
《Heterogeneous Graph Transformer》提出了建模web-scale异质图的Heterogeneous Graph Transformer:HGT架构,目标是:维护node-type dependent representation和edge-type dependent representation、捕获网络动态、避免自定义metapath、以及能够扩展到web-scale的图。为了处理图的异质性,
HGT引入了节点类型依赖的attention机制node-type dependent attention、边类型依赖的attention机制edge-type dependent attention。HGT并未参数化每种类型的边,而是通过每条边HGT的异质互注意力heterogeneous mutual attention。这个关系三元组为<node type of s, edge type of e between s&t , node type of t >。HGT使用这些元关系来对权重矩阵进行参数化,从而计算每条边上的注意力。这样允许不同类型的节点、边保持其特有的representation space,同时不同类型的、相连的节点仍然可以交互、传递、聚合消息,不受它们类型不同的影响。由于
HGT架构的性质,HGT可以通过跨层信息传递来聚合来自不同类型高阶邻居的信息,这些信息可以被视为soft metapath。换句话讲,HGT仅使用其one-hop边作为输入,无需手动设计metapath,最终提出的注意力机制也可以自动隐式地学习和提取针对不同下游任务很重要的metapath。为解决动态图的问题,
HGT提出了相对时间编码relative temporal encoding:RTE策略来增强HGT。HGT建议不要把输入图划分为不同的时间戳,而是建议将在不同时间发生的所有边作为一个整体来维护,并设计RTE策略来建模任意时间区间(甚至是未知的和未来的)的时间依赖性temporal dependency。通过端到端的训练,RTE使HGT能够自动学习异质图的时间依赖和演变。为处理
web-scale规模的图数据,HGT设计了用于mini-batch图训练的首个异质子图采样算法HGSampling。其主要思想是对异质子图进行采样,在采样到的子图中不同类型的节点具有相似的比例。因为如果直接使用现有的同质图采样算法,如GraphSage/FastGCN/LADIES,会导致采样子图的节点类型、边类型高度不平衡。此外,HGSampling还被设计为使得采样子图保持稠密,从而最大程度地减少信息丢失。通过
HGSampling,所有的GNN模型包括论文提出的HGT,都可以在任意大小的异质图上进行训练和推断。
论文在
web-scale的OAG数据集上实验了HGT的有效性和效率,该数据集由1.79亿个节点、20亿条边组成,时间跨度1900 ~ 2019年,是迄今为止规模最大、时间跨度最长的异质图数据集。实验结果表明:和
state-of-the-art的GNN以及异质图模型相比,HGT可以显著改善各种下游任务,效果提高9% ~ 21%。进一步研究表明,HGT确实能够自动捕获隐式metapath针对不同任务的重要性。- 首先,大多数针对异质图的
23.1 基础知识和相关工作
23.1.1 异质图挖掘
异质图定义:定义异质图
元关系
meta relation定义:对于每条边meta relation为三元组inverse relation。经典的metapath范式被定义为这种元关系的序列。注意:为更好地建模真实世界的异质网络,我们假设不同类型的节点之间可能存在多种类型的关系。如
OAG中,通过考虑作者顺序(如“第一作者”、“第二作者”等),作者类型节点和论文类型节点之间存在不同类型的关系。动态异质图:为建模真实世界异质图的动态特性,我们为每条边
- 我们假设边的时间戳是不变的,表示边的创建时间。例如当一篇论文在时刻
- 我们假设节点可以有多个时间戳。例如,会议节点
WWW可以分配任何时间戳。WWW@1994意味着我们正在考虑第一版WWW,它更多地关注互联网协议和web基础设施;而WWW@2020意味着即将到来的WWW,其研究主题将扩展到社交分析、普适计算ubiquitous computing、搜索和信息检索、隐私等等。
在挖掘异质图方面已经有了重要的研究方向,例如节点分类、节点聚类、节点排序、以及
node representation learning,然而异质图的动态视角尚未得到广泛的探索和研究。- 我们假设边的时间戳是不变的,表示边的创建时间。例如当一篇论文在时刻
23.1.2 GNN
GNN可以视为基于输入图结构的消息传递,它通过聚合局部邻域信息来获得节点的representation。假设节点
GNN第representation为GNN的node representation更新方程为:其中:
GNN有两个基本的算子:Extract(.)算子:邻域信息抽取器extractor。它使用target节点representationquery,并从source节点representationAgg(.)算子:邻域信息聚合器aggregator。它用于聚合target节点mean, sum, max等函数作为聚合函数,也可以设计更复杂的聚合函数。
此外,还有很多将注意力机制集成到
GNN的方法。通常,基于注意力的模型通过估计每个source节点的重要性来实现Extract(.)算子,并在此基础上应用加权聚合。在上述
GNN通用框架之后,人们已经提出了各种GNN架构(同质的):《Semi-Supervised Classification with Graph Convolutional Networks》提出了图卷积网络graph convolutional network: GCN,它对图中每个节点的一阶邻域进行均值池化,然后进行线性投影和非线性激活操作。《Inductive Representation Learning on Large Graphs》提出了GraphSAGE,将GCN的聚合操作从均值池化推广到sum池化、最大池化、以及RNN。《Graph Attention Networks》通过将注意力机制引入GNN从而提出了graph attention network: GAT。这种注意力机制允许GAT为同一个邻域内的不同节点分配不同的重要性。
23.1.3 异质 GNN
最近,一些工作试图扩展
GNN从而建模异质图。《Modeling Relational Data with Graph Convolutional Networks》提出了relational graph convolutional network: RGCN来建模知识图谱。RGCN为每种类型的边保留不同的线性投影权重。《Heterogeneous Graph Neural Network》提出了heterogeneous graph neural network: HetGNN,它针对不同的节点类型采用不同的RNN来融合多模态特征。《Heterogeneous Graph Attention Network》基于注意力机制为不同的metapath-based边保留不同的权重,同时对不同的metapath也保留不同的权重。
尽管实验上看这些方法都比普通的
GCN或GAT要好,但是它们对不同类型的节点或不同类型的边采用不同的权重矩阵,从而没有充分利用异质图的特性。因为不同类型的节点/边的数量可能差异很大,对于出现次数不多的边,很难准确地学到合适的relation-specific权重。为解决这个问题,我们提出了参数共享从而实现更好的泛化,这类似于推荐系统中的
FM思想。具体而言,给定一条边meta relation为例如,在 “第一作者”关系 和 “第二作者”关系中,它们的源节点类型都是作者、目标节点类型都是论文。换句话讲,从一种关系中学到的有关作者和论文的知识可以迅速地迁移并适应于另一种关系。因此,我们将该思想和功能强大的、类似于
Transformer注意力体系结构相结合,这就是Heterogeneous Graph Transformer: HGT。综上所述,
HGT和现有异质图建模方法的主要区别在于:- 我们并没有试图对单独的节点类型或单独的边类型建模,而是使用元关系
HGT使用相同的甚至更少的参数来同时捕获不同模型之间的通用模式common pattern以及特定模式specific pattern。 - 与大多数现有的
metapath-based方法不同,我们依赖于神经网络体系结构本身来融合高阶异质邻域信息,从而自动学习隐式的metapath的重要性。 - 以前的大多数工作都未考虑图(异质的)的动态特性,而我们提出了相对时间编码
RTE技术,从而在有限的计算资源内融合了时间信息。 - 现有的异质
GNN都不是为了web-scale图数据而设计的,也没有在web-scale图上进行实验。我们提出了为web-scale的图训练设计的mini-batch异质子图采样算法,可以在十亿规模的Open Academic Graph上进行实验。
- 我们并没有试图对单独的节点类型或单独的边类型建模,而是使用元关系
23.2 模型
HGT的核心思想是:使用元关系来参数化权重矩阵,从而实现异质互注意力heterogeneous mutual attention、消息传递message passing、传播propagation。另外,为进一步融合网络的动态性,我们在模型中引入相对时间编码机制。下图给出了
HGT的总体架构。给定一个采样的异质子图sampled heterogeneous sub-graph,HGT提取所有相连的节点pair对,其中目标节点HGT的目标是聚合来自于源节点的信息,从而获得目标节点contextualized representation。这样的过程可以分解为三个部分:元关系感知的异质互注意力meta relation-aware heterogeneous mutual attention、从源节点发出的异质消息传递heterogeneous message passing from source nodes、特定于目标的异质消息聚合target-specific heterogeneous message aggregation。我们将第
HGT层的输出记作HGT层的输入。通过堆叠representation为下图中,
HGT使用边HGT遵循GAT的attention机制,但是HGT在计算query, key, value时考虑了节点和边的异质性。此外,在计算节点的representation时考虑了相对时间编码(类似于相对位置编码)。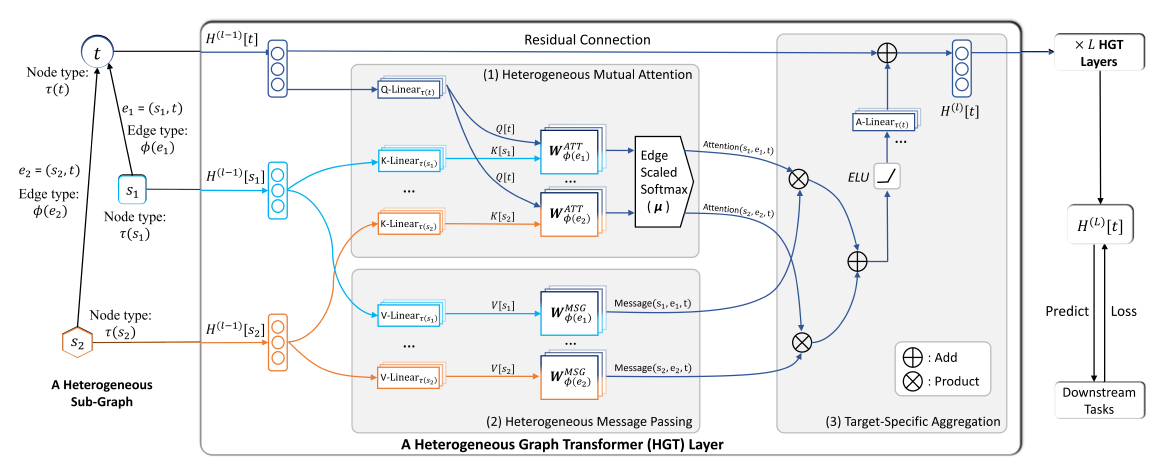
23.2.1 Heterogeneous Mutual Attention
HGT的第一步是计算源节点GNN为:其中有三个基础算子:
Attention算子:评估每个源节点Message算子:抽取源节点Agg算子:利用注意力权重来聚合邻域的消息。
例如,
GAT采用一种加性机制additive mechanism来作为Attention算子,采用共享的权重矩阵来计算每个节点的消息,采用简单的均值然后接一个非线性激活函数来作为Agg算子。即:其中:
attention vector。
尽管
GAT可以有效地给更重要的节点以更高的注意力,但是它假设节点有鉴于此,我们设计了异质互注意力机制。给定一个目标节点
受到
Transformer体系结构设计的启发,我们将目标节点Query向量,将源节点Key向量,然后计算它们内积作为attention。但是和Transformer的区别在于:常规的Transformer对所有单词都使用同一组映射矩阵,但是在HGT中每种元关系都有它们自己的一组映射矩阵。为最大程度地共享参数,同时保持不同关系的各自特性,我们将元关系的权重矩阵参数化为源节点投影矩阵、边投影矩阵、目标节点投影矩阵。具体而言,对于
attention为:其中:
attention head中的query向量,它是类型为attention head中的key向量,它是类型为attention head中,query向量key向量异质图的一个特点是:在一对节点之间可能存在多种不同类型的边。因此,和常规的
Transformer将query向量和key向量直接内积不同,HGT考虑对每种边类型edge-based矩阵此外,由于并非所有关系均对目标节点做出相同的共享,因此我们采用了一个先验张量
prior tensor最后,我们将
attention head拼接起来,从而获得每对节点pair对的attention向量。然后对于每个目标节点softmax,使其满足:即:对于目标节点
head邻域内的注意力之后为1:
23.2.2 Heterogeneous Message Passing
和注意力计算过程类似,我们希望将边的元关系融合到消息传递过程中,从而缓解不同类型节点和不同类型边的分布差异。
对于边
multi-head消息为:其中:
message head,它先将类型为这里的
然后,我们拼接所有的
message head从而为每条边得到
计算
multi-head注意力过程和计算multi-head消息过程,二者之间可以并行进行。
23.2.3 Target-Specific Aggregation
在计算出异质
multi-head注意力、异质multi-head消息之后,我们需要将它们从源节点聚合到目标节点。我们可以简单地使用每个
head的注意力向量作为权重,从而加权平均对应head每个源节点的消息。因此聚合过程为:这将信息从不同类型的所有邻居(源节点)的信息聚合到目标节点
最后一步是将目标节点
representation向量映射回其特定类型。为此,我们采用一个线性投影这样我们就获得了目标节点
因为前面将邻域节点信息 映射到公共空间,那么现在需要将公共空间映射回目标节点的特定类型空间。
由于真实世界的图具有
small-world属性,因此堆叠HGT层(HGT为每个节点生成高度上下文相关的表示在
HGT的整个体系结构中,我们高度依赖使用元关系和常规的
Transformer相比,我们的模型区分了不同的节点类型和不同的关系类型,因此能够处理异质图中的分布差异。和为每种元关系保留独立的权重矩阵的现有方法相比,
HGT的三元组参数化可以更好地利用异质图的schema来实现参数共享。- 一方面,几乎从未出现过的关系仍然可以从这种参数共享中受益,从而可以实现快速适应和泛化。
- 另一方面,不同类型的节点和关系仍然可以使用更少的参数集合来维持其独有的特点。
23.2.4 Relative Temporal Encoding
这里我们介绍用于
HGT的相对时间编码RTE技术来处理动态图。传统的融合时间信息的方法是为每个时间片
time slot构建一个独立的图,但是这种方式可能丢失跨不同时间片的结构相关性。同时,节点在时刻representation可能依赖于其它时刻发生的连接。因此,对动态图进行建模的一种正确方式是:维持在不同时刻发生的所有边,并允许具有不同时间戳的节点和边彼此交互。有鉴于此,
HGT提出了相对时间编码RTE机制来建模异质图中的动态依赖性dynamic dependency。RTE的灵感来自于Tansformer中的位置编码方法,该方法已成功地捕获了长文本中单词的顺序依赖性sequential dependency。具体而言,给定源节点
注意:训练数据集可能没有覆盖所有可能的时间间隔,因此
RTE应该能够泛化到未看到的时间和时间间隔。因此我们使用一组固定的正弦函数作为basis,并使用一个可训练的线性映射RTE:最终,针对目标节点
representation中:该过程发生在每个
step的信息聚合之前。通过这种方式,融合时间的
representationRTE的详细过程如下图所示: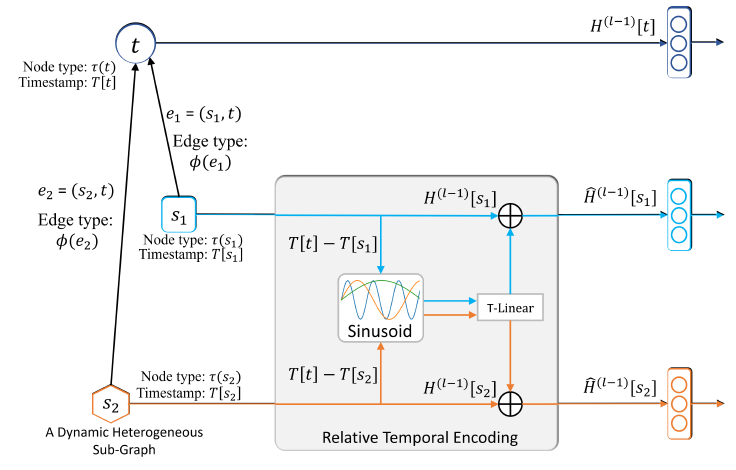
目前为止我们为每个节点
plain节点。如:论文数据集中,WWW会议在1974年和2019年都举行,但是这两年的研究主题截然不同。因此我们需要决定将哪个时间戳添加到WWW节点。与
plain节点相反,异质图中存在一些event节点,它存在唯一的、固定的时间戳。如:论文数据集中,论文节点和该论文发表时间明确相关。为此,我们提出了一种
inductive时间戳分配算法,它对plain节点基于该plain节点相连的event节点来分配时间戳。基本思想是:plain节点从event节点中继承时间戳。我们检查节点是否为event节点:如果节点是
event节点,如特定年份发表的论文节点,则我们保留该event节点的时间戳从而捕获时间依赖性temporal dependency。如果节点不是
event节点,则可以像作者节点一样关联多个时间戳,我们将相连节点的时间戳分配给这个plain节点。如果有多个时间戳,那么怎么计算
这样我们可以在子图采样过程中自适应地分配时间戳。
23.2.5 HGSampling
full-batch的GNN训练要求计算每层所有节点的representation,这使得它无法扩展到web-scale图。为解决这些问题,已有各种基于采样的方法在一个节点子集上训练GNN。但是这些方法无法直接应用到异质图,因为在异质图中每种类型节点的degree分布和节点总数可能差异非常大,所以这些采样方法直接应用到异质图中可能得到节点类型极为不平衡的子图。为解决该问题,我们提出了一种有效的异质图
mini-batch采样算法HGSampling,使得HGT和传统GNN都能够处理web-scale异质图。其核心是为每种节点类型importance sampling strategy来降低方差。HGSampling优势:- 为每种类型保留相似数量的节点和边。
- 采样到的子图保持稠密,从而最大程度地减少信息损失并降低采样方差。
HGSampling算法:输入:
- 包含所有元关系的邻接矩阵
- 每种类型的节点的采样数量
- 采样深度
mini-batch节点集合
- 包含所有元关系的邻接矩阵
输出:最终输出节点集合
算法步骤:
初始化采样节点集合
初始化一个空的预算
degree。对
degree。迭代
对
对
其中分子为节点
degree的平方,分母为degree的平方和。从
对于每个采样到的节点
- 添加节点
- 添加节点
- 从
- 添加节点
基于输出节点集合
返回
Add-In-Budget算法:输入:
- 集合
degree - 被添加的节点
- 包含所有元关系的邻接矩阵
- 采样节点集合
- 集合
输出:更新后的集合
算法步骤:
对于每种可能的源节点类型
根据
degree:其中
这里计算的是目标节点
degree,而不是degree。对于每个源节点
- 如果
s.time = t.time。 - 将节点
degree:
- 如果
返回更新后的
算法解释:假设节点
Add-In-Budget算法将其所有一阶邻居添加到对应的degree添加到这些邻居上,然后将其应用于计算采样概率。这样的归一化等效于累积每个采样节点到其邻域的随机游走概率,从而避免采样被高阶节点统治。直观地看,该值越高,则候选节点和当前节点之间的相关性越大,因此应该赋予其更高的采样概率。HGSampling算法的前几行计算采样概率,通过计算degree的平方来计算重要性采样的概率。通过这种采样概率,我们可以降低采样方差。然后,我们使用计算到的概率对类型为
重复这样的过程
通过使用上述算法,被采样的子图对每个类型包含相似的节点数量,并且足够稠密,且通过归一化的
degree和重要性采样来降低方差。因此这种方式适用于web-scale图上训练GNN。整个采样过程如下图所示:不同颜色表示不同的节点类型。
(0):选择初始节点(1):选择degree和时间戳(根据inductive时间戳分配)。(2):对每种类型采样(3):对于新采样的节点degree值进行累加。(4):对每种类型采样(5):采样结束。
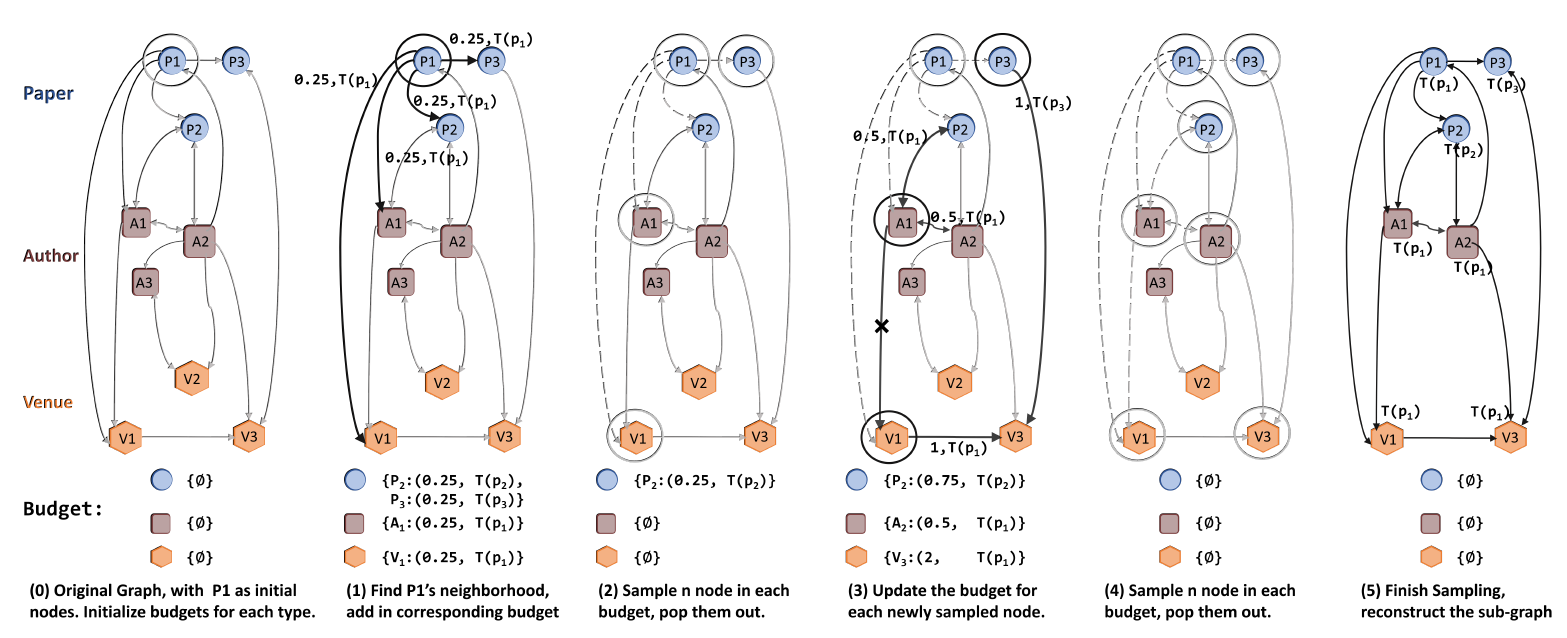
23.3 实验
我们在三个异质学术图数据集上评估
HGT,并分别执行Paper-Field预测、Paper-Venue预测、Author Disambiguation任务。数据集:我们使用
Open Academic Graph:OAG数据集,它包含超过1.78亿节点和22.36亿条边,这是最大的公开可用的异质学术数据集。此外,OAG中所有论文关联一个发表日期,该日期从1900到2019年。数据集包含五种类型的节点
Paper、Author、Field、Venue、Institute,其中OAG的领域Field字段一共包含L0到L5共六个层级,这些层级通过层级树hierarchical tree来组织。因此,我们根据领域层级来区分Paper-Field边。此外,我们还区分了不同的作者顺序(第一作者、最末作者、其它作者)和会议类型(期刊jornal、会议conference、预印本preprint)。最后,self类型对应于自环连接,这是GNN架构中广泛添加的。除了self关系是对称的之外,其余所有关系都是不对称的,每种关系reverse relation为测试
HGT的泛化能力,我们还从OAG构造了两个特定领域的子图:计算机科学CS学术图、医学Med学术图。CS和Med图都包含数千万个节点和数亿条边。所使用的三个数据集比以前
GNN研究中广泛使用的小型引文网络(Cora,Citeseer,Pubmed)大得多,后者仅包含数千个节点。下表给出了数据集的统计信息,其中
P-A表示“论文 -- 作者”、P-F表示 “论文 -- 研究领域”、P-V表示 “论文 -- 会议”、A-I表示 “作者 -- 研究机构”、P-P表示论文引用。
我们通过四个不同的下游任务来评估
HGT:Paper -- Field(L1)预测、Paper -- Field(L2)预测、Paper -- Venue预测、Author Disambiguation。前三个任务是节点分类任务,目标是分别预测每篇论文的一级领域、二级领域、发表会议。
我们使用不同的
GNN获取论文的上下文节点representation,并使用softmax输出层来获取其分类标签。对于
Author Disambiguation任务,我们选择所有同名的作者及其相关的论文,任务目标是在这些论文和候选作者之间进行链接预测。从
GNN获得论文节点和作者节点的representation之后,我们使用Neural Tensor Network来获得每个author -- paper节点对之间存在链接的概率。
对于所有任务,我们使用
2015年之前发布的论文作为训练集,使用2015 ~ 2016年之间的论文作为验证集,使用2016 ~ 2019年之间的论文作为测试集。我们使用
NDCG和MRR这两个广泛应用的ranking指标作为评估指标。我们对所有模型进行5次训练,并报告测试集性能的均值和标准差。baseline方法:我们比较了两类state-of-the-art图神经网络,所有baseline以及我们的HGT都通过PyTorch Geometric(PyG) package来实现。同质图
GNN baseline:GCN:简单地对邻域embedding取平均,然后跟一个线性映射。我们使用PyG提供的实现。GAT:对邻域节点采用multi-head additive attention。我们使用PyG提供的实现。
异质图
GNN baseline:RGCN:对每种元关系(三元组)保持不同的权重。我们使用PyG提供的实现。HetGNN:对不同的节点类型采用不同的Bi-LSTM来聚合邻域信息。我们根据作者提供的官方代码使用PyG重新实现。HAN:通过不同的metapath使用分层注意力来聚合邻域信息。我们根据作者提供的官方代码使用PyG重新实现。
此外,为了系统地分析
HGT的两个主要部分的有效性,即异质权重参数化Heterogeneous Weight Parameterization:Heter、相对时间编码Relative Temporal Encoding:RTE,我们进行了消融研究。我们比较了移除这些部分的HGT模型性能。具体而言,我们用-Heter表示对所有元关系使用相同的权重集合,使用-RTE表示没有相对时间编码。考虑所有的排列,我们得到以下模型:我们使用
HGSampling采样算法应用到所有baseline GNN,从而处理大规模的OAG数据集。为了避免数据泄露,我们从子图中删除我们目标预测的链接。输入特征:我们对不同的节点类型采用不同的特征:
- 论文节点:使用预训练的
XLNet来获取标题中每个单词的representation。然后,我们根据每个单词的注意力对它们进行加权平均,从而得到每篇论文的标题representation。 - 作者节点:使用该作者发表的所有论文的标题的
representation取平均。 - 领域节点、会议节点、机构节点:使用
metapath2vec来训练其node embedding,从而反映异质网络结构。
另外,同质
GNN假设所有节点都是相同类型的特征。因此,为了进行公平的比较,我们在输入特征和同质GNN之间添加一个适配层,该层用于对不同类型的节点进行不同的线性映射。可以认为该过程能够将异质特征映射到相同的特征空间。- 论文节点:使用预训练的
实现方式:
- 对于所有的
baseline,我们在整个神经网络网络中使用隐层维度为256。 - 对于所有基于
multi-head attention方法,我们将head数量设为8。 - 所有
GNN均为三层(不包括适配层),使得每个网络的感受野完全相同。 - 所有
baseline方法均通过Cosine Annealing Learning Rate Scheduler的AdamW优化器优化。 - 每个模型我们训练
200个epoch,然后选择验证损失最小的那个作为评估模型。 - 我们选择使用
GNN文献中默认使用的超参数,并未进行超参数调优。
- 对于所有的
所有模型在所有数据集上的表现如下表所示,其中评估指标为
NGCD, MRR。结论:HGT在所有数据集的所有任务上均显著优于所有baseline。总体而言,在所有三个大规模数据集上的四个任务中,HGT平均优于GCN, GAT, RGCN, HetGNN, HAN大约20%。此外,
HGT具有更少的参数、差不多的batch时间。这表明HGT根据元关系schema建模异质边,从而以更少的资源实现更好的泛化和完整模型
- 删除异质权重参数化的模型,即
4%的性能。 - 删除相对时间编码的模型,即
2%的性能。
这表明了权重参数化、相对时间编码的重要性。
- 删除异质权重参数化的模型,即
最后我们还尝试了一个
baseline,它为每个关系类型保留不同的参数矩阵。但是,这样的baseline包含太多参数,因此我们的实验设置没有足够的GPU内层对其进行优化。这也表明:使用元关系对权重矩阵进行分解可以在较少的资源条件下获得有竞争力的优势。
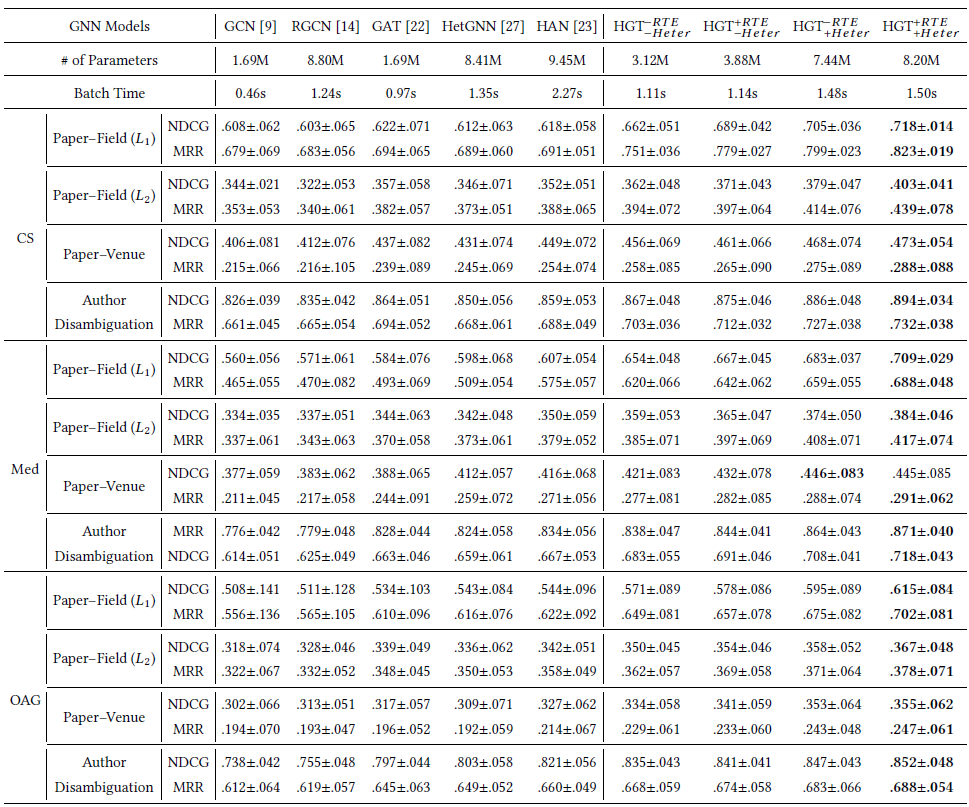
为进一步评估相对时间编码
RTE如何帮助HGT捕获图的动态性,我们进行一个案例研究来展示会议主题的演变。我们选择被引用次数最多的100个计算机科学会议,为它们分配了三个不同的时间戳2000、2010、2020,并构造了由它们初始化的子图。我们使用训练好的HGT来获取这些会议的representation,然后计算这些会议之间的欧式距离。我们以
WWW、KDD、NeuraIPS为例,对于每个会议我们选择其top 5最相似的会议,从而显示会议主题随时间的变化。结果如下表所示。结论:2000年的WWW和某些数据库会议(SIGMOD和VLDB) 以及一些网络会议(NSDI和GLOBECOM) 更相关。但是,除了SIGMOD, GLOBECOM之外,2020年的WWW和某些数据挖掘和信息检索会议(KDD, SIGIR, WSDM) 更相关。2000年的KDD和传统的数据库和数据挖掘会议更相关,而2020年的KDD倾向于和多种主题相关,如机器学习(NeurIPS)、数据库 (SIGMOD)、Web(WWW)、AI(AAAI)、NLP(EMNLP)。- 除此之外,
HGT还能捕获新会议带来的差异。例如2020年的NeurIPS和ICLR(这是一个新的深度学习会议) 相关。
该案例研究表明:相对时间编码可以帮助捕获异质学术图的时间演变。
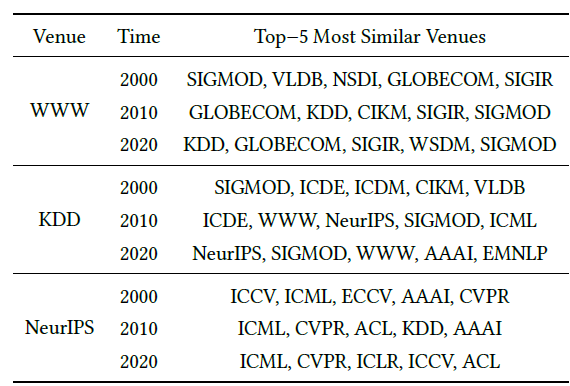
为说明融合的元关系模型如何使得异质消息传递过程受益,我们选择在前两层
HGT层中具有最高注意力的模式,并在图中绘制元关系注意力层次树。例如,为计算论文的
representation,最重要的三个元关系序列为:这可以分别视为
metapath: PVP, PFP, IAP。注意:无需手动设计既可以自动从数据中学到这些
metapath及其重要性。右图给出了计算作者
representation的另一个case。这些可视化结果表明,HGT能够隐式地学到为特定下游任务构造的重要的metapath,无需手动构建。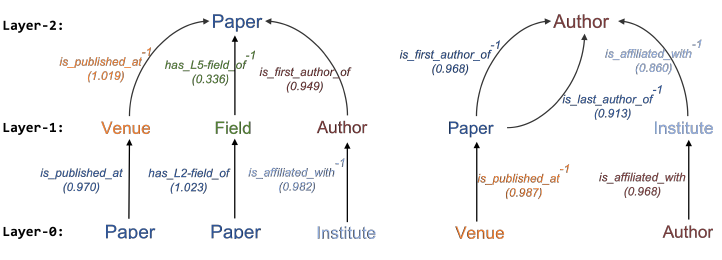
二十四、GPT-GNN[2020]
图神经网络
GNN的突破彻底改变了图数据挖掘的过程,从图的结构特征工程structural feature engineering到图的表示学习representation learning。最近的GNN发展已被证明有利于各种graph application和网络任务,例如半监督节点分类、推荐系统、知识图谱推断knowledge graph inference。通常,
GNN将带有属性的图作为输入,并应用卷积滤波器来逐层生成node-level representation。通常,对于输入图上的一个任务,GNN模型以端到端的方式使用监督信息进行训练。即:对于给定图上的任务,需要足够多的标记样本来训练GNN模型。通常对于这些任务,尤其是大型图,获取足够多的标记数据的代价很高,有时甚至是不可行的。以学术图academic graph中的作者消歧任务为例,迄今为止,该任务仍然面临着缺少ground-truth的挑战。在
NLP中也遇到类似的问题。NLP的最新进展通过训练大量的未标记数据,并将学到的模型迁移transfer到带少量标记的下游任务来解决该问题,即预训练pre-training的思想。如,预训练的BERT语言模型通过重构输入文本(next sentence predict和masked language predict)来学习单词的representation,因此可以显著提高各种下游任务的性能。此外,计算机视觉也证明了类似的观察结果,即:未标记的数据本身包含丰富的语义知识,捕获数据分布的模型可以迁移到各种下游任务。受到预训练的启发,论文
《GPT-GNN: Generative Pre-Training of Graph Neural Networks》提出对图神经网络进行预训练从而进行图数据挖掘。预训练的目的是使得GNN能够捕获输入图的结构属性structural property和语义属性semantic property,以便进行微调fine-tuning就可以迁移到同一个领域domain内的其它的图任务。为实现该目标,GPT-GNN提出通过学习重建reconstruct输入的属性图attributed graph来对图分布graph distribution建模。一种图重建方式是直接采用神经图生成
neural graph generation技术,但是它不适合预训练GNN:- 首先,大多数神经图生成技术仅关注于生成不带属性的图结构,这无法捕获节点属性和图结构之间的底层模式
underlying pattern。 - 其次,这些神经图生成技术被设计于处理小图,从而限制了它们在大规模图上进行预训练的潜力。
贡献:在
GPT-GNN中,作者设计了一种用于GNN预训练的自监督属性图生成任务self-supervised attributed graph generation task,通过该任务对图结构和节点属性进行建模。基于该任务,作者提出了用于GNN的生成式预训练generative pretraining of graph neural network: GPT-GNN框架 (如下图所示)。然后可以将输入图上的预训练GNN用作同一类型的图上不同下游任务的GNN模型的初始化。具体而言,论文的贡献如下:- 首先,作者设计了一个属性图生成任务
attributed graph generation task来建模节点属性和图结构。作者将图生成目标分解为两个部分:属性生成attribute generation,边生成edge generation,它们的联合优化相当于最大化整个属性图的概率似然。通过这种做法,模型可以在生成过程中捕获节点属性和图结构之间的固有依赖性inherent dependency。 - 其次,作者提出了一个有效的框架
GPT-GNN来对上述任务进行生成式的预训练generative pre-training。GPT-GNN可以同时计算每个节点的属性生成损失和边生成损失,因此只需要为图运行一次GNN。此外,GPT-GNN可以通过子图采样处理大型图,并通过自适应embedding queue来缓解负采样带来的inaccurate loss。 - 最后,作者在两个大型图上预训练了
GNN:1.79亿节点和20亿边的Open Academic Graph: OAG、1.13亿节点的Amazon推荐数据。大量实验表明:GPT-GNN预训练框架可以显著地有利于各种下游任务。例如,通过在OAG上应用预训练模型,节点分类和链接预测任务的性能比没有预训练的state-of-the-art GNN平均可达9.1%。此外,作者表明:GPT-GNN可以在各种setting下持续提高不同的base GNN的性能。
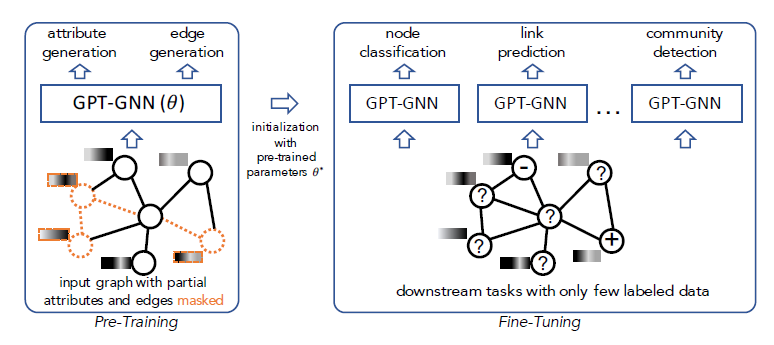
- 首先,大多数神经图生成技术仅关注于生成不带属性的图结构,这无法捕获节点属性和图结构之间的底层模式
24.1 基础知识和相关工作
- 预训练的目的是允许模型(通常是神经网络)使用预训练的权重来初始化模型参数,这样模型可以充分利用预训练和下游任务之间的共性
commonality。最近,预训练在提高计算机视觉和自然语言处理中许多下游application的性能方面显示出优势。
24.1.1 GNN 的基础知识
GNN可以视为基于输入图结构的消息传递,它通过聚合局部邻域信息来获得节点的representation。假设节点
GNN第representation为GNN的节点representation更新方程为:其中:
GNN有两个基本的算子:Extract(.)算子:邻域信息抽取器extractor。它使用target节点representationquery,并从source节点representationAgg(.)算子:邻域信息聚合器aggregator。它用于聚合target节点mean, sum, max等函数作为聚合函数,也可以设计更复杂的聚合函数。
在这个框架下,人们已经提出了各种
GNN架构:《Semi-Supervised Classification with Graph Convolutional Networks》提出了图卷积网络graph convolutional network: GCN,它对图中每个节点的一阶邻域进行均值池化,然后进行线性投影和非线性激活操作。《Inductive Representation Learning on Large Graphs》提出了GraphSAGE,将GCN的聚合操作从均值池化推广到sum池化、最大池化、以及RNN。
此外,还有很多将注意力机制集成到
GNN的方法。通常,基于注意力的模型通过估计每个source节点的重要性来实现Extract(.)算子,并在此基础上应用加权聚合。例如:《Graph Attention Networks》提出了GAT,它采用加性的注意力机制additive mechanism来计算注意力。《Heterogeneous Graph Transformer》提出了heterogeneous graph transformer: HGT,它利用针对不同关系类型的multi-head attention来获得type-dependent注意力。
我们提出的预训练框架
GPT-GNN可以适用于所有这些GNN模型(包括GCN, GraphSAGE, GAT, HGT)。
24.1.2 用于图的预训练
已有一些研究提出利用预训练来学习节点的
representation,其中主要分为两类:第一类通常称作
graph embedding,它直接参数化node embedding向量,并通过保持某些相似性度量来优化embedding向量,如网络邻近性network proximity(《Line: Large-scale information network embedding》)或者随机游走得到的统计数据(metapath2vec, node2vec, 《Network embedding as matrix factorization: Unifying deepwalk, line, pte, and node2vec》)。但是,这种方式学到的
embedding无法用于初始化其它模型从而微调其它任务(因为embedding模型是transductive的)。相反,我们需要考虑一种迁移学习方式,其目标是预训练一个适用于各种下游任务的通用的GNN。第二类通过直接在未标注数据上预训练
GNN。例如:《Variational Graph Auto-Encoders》提出变分图自编码器来重建图结构。《Inductive Representation Learning on Large Graphs》提出GraphSAGE从而使用基于随机游走的相似性度量来优化无监督损失。《Deep Graph Infomax》引入Graph Infomax,它最大化从GNN获得的node representation和一个池化的graph representation之间的互信息。
尽管这些方法显示了对纯监督学习
purely-supervised learning的增强enhancement,但是这些方法迫使相近的节点具有相似的embedding,从而忽略了图中丰富的语义和高阶结构higher-order structure。我们的方法通过提出排列式的生成式目标permutated generative objective来预训练GNN,这是一项更难的图任务,因此可以指导模型学到输入图的更复杂的语义和结构信息。另外,还有一些工作尝试预训练
GNN来抽取graph-level representation。《InfoGraph:Unsupervised and Semi-supervised Graph-Level Representation Learning via Mutual Information Maximization》提出了InfoGraph,它最大化了从GNN获得的graph-level representation与子结构representation之间的互信息。《Strategies for Pre-training Graph Neural Networks》引入了在node-level和graph-level预训练GNN的不同策略,并表明将它们组合在一起可以提高图分类任务的性能。
我们的工作与他们不同,因为我们的目标是在单个大型图上预训练
GNN并进行node-level迁移学习 。
24.1.3 用于计算机视觉和自然语言处理的预训练
预训练已广泛用于计算机视觉和自然语言处理。
在计算机视觉中,早期的预训练技术(
《Decaf: A deep convolutional activation feature for generic visual recognition》、《Rich feature hierarchies for accurate object detection and semantic segmentation》、《Context Encoders: Feature Learning by Inpainting》)大多遵循首先在大型监督数据集(如ImageNet)上预训练模型,然后在下游任务上微调预训练的模型,或者直接利用预训练的模型抽取样本的representation作为特征。最近,一些自监督任务(
《A Simple Framework for Contrastive Learning of Visual Representations》、《Momentum contrast for unsupervised visual representation learning》、《Representation Learning with Contrastive Predictive Coding》)也被用于预训练视觉模型。在自然语言处理中,早期的工作一直聚焦于利用文本语料库的共现来学习
word embedding(《Distributed representations of words and phrases and their compositionality》、《Glove:Global vectors for word representation》)。最近,人们在
contextualized word embedding方面取得了重大进展,如BERT, XLNET, GPT。以BERT为例,它通过两个自监督任务来预训练一个文本编码器,以便更好地对word和context进行编码。这些预训练方法已被证明可以在广泛的自然语言处理任务中产生state-of-the-art性能,因此被用作许多NLP系统的基础组件。
24.2 模型
给定属性图
GNN模型在特定下游任务(如节点分类)的监督下学习输出node representation。有时候在单个图上存在多个任务,并且对于每个任务,大多数GNN需要提供足够多的标记数据。然而,获得足够多的标记数据通常具有挑战性,特别是对于大型图,这阻碍了GNN的训练。因此,需要一个预训练的GNN模型,该模型可以通过很少的标签来进行泛化。从概念上讲,该预训练的模型应该:捕获图背后的固有结构intrinsic structure和属性模式attribute pattern,从而使得该图上的各种下有任务受益。GNN预训练的目标是学到一个通用的GNN模型GNN模型?
24.2.1 Generative Pre-Training Framework
NLP和CV自监督学习的最新进展表明,未标记数据本身包含丰富的语义知识,因此可以捕获数据分布的模型能够迁移到各种下游任务。受此启发,我们提出了GPT-GNN,它通过重建/生成input graph的结构和属性来预训练GNN。形式上,给定属性图
GNN模型GNN模型likelihood建模为GPT-GNN目标是最大化图的似然来预训练GNN模型,即:第一个问题是:如何建模图的似然
auto-regressive manner来分解概率目标,即:图中的节点按照顺序依次访问,并通过将每个新的节点连接到现有节点来生成边。类似地,我们使用排列向量
permutation vector其中:
为简单起见,我们假设任何节点顺序
给定一个排列顺序,我们可以自回归地分解对数似然:
其中:
因此,这个对数似然给出了属性图的自回归生成过程
autoregressive generative process。该模型是一个节点一个节点地生成,因此是生成式模型。
本质上,上述公式描述了属性图的自回归生成过程
autoregressive generative process。现在的问题是如何建模条件概率
24.2.2 Factorizing Attributed Graph Generation
一种朴素的想法是假设
这种分解完全忽略了节点的属性和它的边之间的依赖关系。但是,这种依赖关系恰好是属性图的核心特性,也是
GNN中卷积聚合的基础。因此,这种朴素的分解无法应用于预训练GNN。为解决该问题,我们为属性图生成过程提出依赖感知
dependency-aware的因子分解机制。具体而言:- 在预估新节点的属性时,我们采用节点的结构信息。
- 在预估新节点的连接时,我们采用节点的属性信息。
在这个过程中,一部分边已经被观察到,然后属性图生成过程分解为两个耦合的部分:
- 给定观测到的边,生成节点属性。
- 给定观测到的边和生成的节点属性,生成剩余的边。
这样,模型可以捕获到每个节点的属性和图结构之间的依赖关系。
我们定义变量
mask的边的索引组成的向量,因此这种分解设计能够建模节点
第一项
第二项
注意这里是
我们以一个学术图为例来阐述上述分解的工作原理。假设我们希望生成一个论文节点,节点属性为论文标题,节点的边为论文及其作者、论文及其发表会议、论文及其引用论文。
- 基于论文和它的某些作者之间观测到的边,我们的生成过程首先生成论文标题。
- 然后基于观测到的边和论文标题再预测剩余的边(“论文--作者”、“论文--发表会议”、“论文--引用论文”)。
通过这种方式,该生成过程可以对论文的属性(论文标题)和结构(观测到的边和剩余边)之间的相互作用进行建模。
能不能先进行边的生成然后再进行节点属性的生成?可以通过实验来说明。
目前为止,我们将属性图的生成过程分解为节点属性生成
node attribute generation和边生成edge generation两步。一个新的问题是:如何通过同时优化属性生成和边生成来有效预训练GNN?
22.2.3 Efficient Attribute and Edge Generation
为提高效率,我们希望通过仅对输入图运行一次
GNN来计算属性生成损失和边生成损失。另外,我们希望同时进行属性生成和边生成。但是,由于边生成过程需要将节点属性作为输入,这可能会泄露信息给属性生成过程。为避免信息泄露,我们将每个节点同时加入到两个类别:属性生成节点
Attribute Generation Nodes:对于该集合中的节点,我们使用dummy token来代替它们的节点属性,从而掩盖节点属性,并学习一个共享的输入向量dummy token。这等价于在masked language model中使用[Mask] token技巧。边生成节点
Edge Generation Nodes:对于该集合中的节点,我们保留其属性并将节点属性作为输入。
我们修改输入图,将每个节点分裂为两个节点:一个为属性生成节点,另一个为边生成节点(它们之间不存在边)。
我们将修改后的图输入到
GNN模型中并得到节点的embedding,我们分别用embedding。由于属性生成节点的属性被遮盖,因此GNN消息传递时,我们仅使用边生成节点的来向外传递消息。GNN模型计算得到(运行一次GNN前向传播)。有两个细节需要注意:- 根据
- 如何在
GNN中运行一次而为每个节点生成两个embedding?论文未给出细节。理论上讲,GNN的前向传播仅能得到每个节点的单个embedding。
还有一个问题:如果使用
可以看到:节点
然后,我们使用这两组节点的
embedding通过不同的解码器来生成属性和边。属性生成:对于属性生成,我们将解码器记作
解码器类型依赖于属性的类型:
- 如果节点的属性为文本,则可以使用文本生成模型(如
LSTM)来生成属性文本。 - 如果节点的属性为标准的向量,则可以使用多层感知机来生成属性向量。
然后我们将距离函数定义为生成的属性和真实属性之间的度量,如文本属性的度量为困惑度
perplexity、属性向量的度量为向量的L2距离。因此,我们定义属性生成损失为:最小化生成的属性和被遮盖的属性之间的距离,等价于最大化每个观测节点的属性的似然,即
- 如果节点的属性为文本,则可以使用文本生成模型(如
边生成:对于边生成,我们假设每条边的生成相互独立,则有:
其中
然后在得到边生成节点的
embedding我们采用负对比估计
negative contrastive estimation来计算节点contrastive loss为:最小化
下图给出了属性图的生成过程。具体而言:
图
(a):确定输入图的节点排序图
(b):随机选择目标节点的一部分边作为观测边图
(c) - (e):- 从输入图中删除被遮盖的边。
- 将每个节点分裂为属性生成节点和边生成节点,从而避免信息泄露。
- 在上述预处理之后,使用修改的邻接矩阵来计算节点
3,4,5的embedding,包括它们的属性生成embedding和边生成embedding。注意:仅使用边生成节点的来向外传递消息。
最后,如图
(c) - (e)所示,我们通过并行的属性预测和遮盖边预测任务来训练GNN模型。
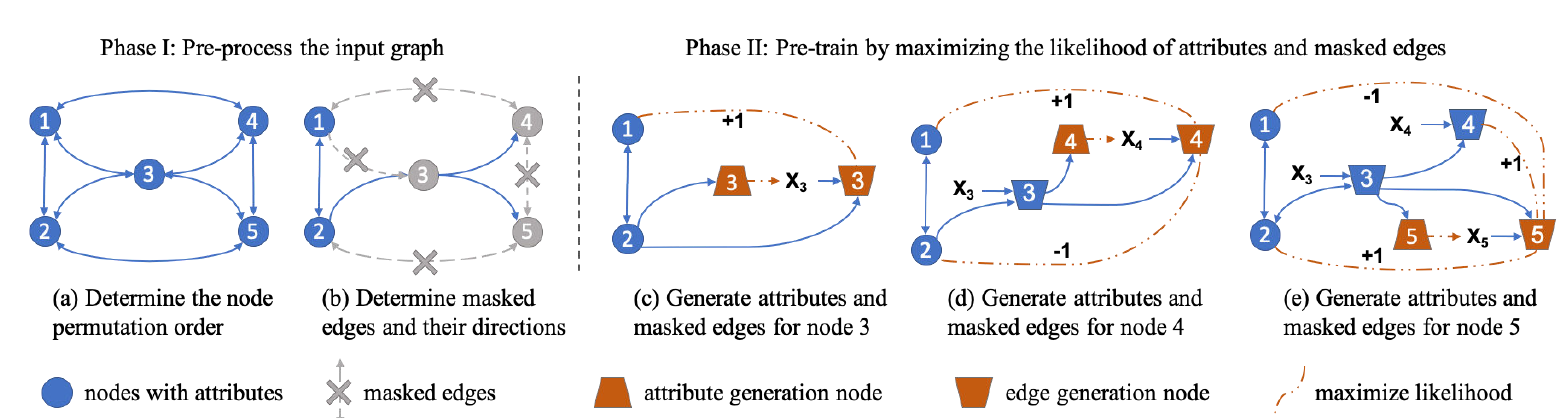
22.2.4 用于异质图和大型图的 GPT-GNN
异质图:
GPT-GNN框架可以直接应用于预训练异质GNN。此时,每种类型的节点和边都可能有自己的解码器,该解码器由异质GNN确定而不是预训练框架指定。其它部分和同质GNN预训练完全相同。大型图:为了在非常大的图上预训练
GNN,我们采样LADIES算法及其异质版本HGSampling从同质图或异质图采样一个稠密的子图。理论上讲,这两种方法都保证了采样节点之间的高度互连,并最大程度地保留了结构信息。为了估算对比损失
Adaptive Queue,它存储了之前曾经采样的子图中的node embedding。我们将自适应队列中的节点作为负节点加入到embedding并删除最早的node embedding,从而逐步更新自适应队列。由于不会严格更新模型参数,因此队列中存储的负样本是一致且准确的consistent and accurate。自适应队列使得我们能够使用更大的负样本集合
22.2.5 GPT-GNN 算法
GPT-GNN预训练算法:输入:
- 属性图
- 子图采样器
Sampler(.) GNN模型
- 属性图
输出:预训练模型的参数
算法步骤:
初始化
GNN模型初始化共享属性向量
node embedding队列对每个采样到的子图
对每个节点,采样一组观测到的边的索引
将所有节点分别同时分裂为属性生成节点、边生成节点。将属性生成节点集合的节点输入替换为
GNNnode embedding对每个节点
计算属性生成损失
通过拼接子图中未连接的节点和自适应队列
计算边生成损失:
通过最小化
添加
edge embedding。
返回预训练的模型参数
上述算法给出了总体流程。给定一个属性图
第一步是确定节点排列顺序
embedding,以便我们可以同时计算每个节点的损失,而不是递归地计算每个节点。因此,我们根据embedding,从而直接应用于生成式预训练。注意:这一步未在上述算法中体现。理论上在采样子图的外层还有一个循环:采样排列顺序的循环。
然后,我们需要确定要遮盖的边。对于每个节点,我们选择其所有出边
out edge并随机选择遮盖一部分边。然后,我们执行节点分裂,并获得节点的
embedding,这将用于计算生成式损失。我们通过拼接该子图内未连接节点和存储在自适应队列
gap。最后我们更新自适应队列。
一旦得到预训练模型,我们就可以使用预训练模型作为初始化,从而微调其它下游任务。
24.3 实验
数据集:
异质图:
Open Academic Graph:OAG:包含超过1.78亿节点、22.36亿条边,是迄今为止最大的公开可用的异质学术数据集。每篇论文都包含一组研究领域的标签,发表日期为1900 ~2019。数据集包含五种类型的节点:论文
Paper、作者Author、领域Field、会议Venue、机构Institute,以及这些节点之间的14种类型的边,这些边的关系如下图所示。例如:领域包含L0 ~ L5六个级别,这些级别通过层级树hierarchical tree来表示;领域之间的层级关系通过is_organized_in关系表示;我们区分了不同的作者位置,即第一作者、最后作者、其它作者。另外,数据集还包含自连接,这是GNN框架中广泛添加的。对于论文和作者节点,节点编号非常大。因此传统的
node embedding算法不适合为其抽取属性。因此我们借助论文标题来抽取属性。对于每篇论文,我们获取其论文标题,然后使用预训练的XLNet获取标题中每个单词的embedding,然后我们根据每个单词的注意力对它们进行加权平均,从而获得每篇论文的标题embedding,作为论文节点属性。作者节点的属性是作者已发表论文的embedding的均值。对于领域、会议、机构等节点,由于节点数量很少,因此我们使用
metapath2vec模型来训练它们的node embedding,从而作为节点属性。我们考虑对
Paper-Field, Paper-Venue, Author Name Disambiguation(Author ND)预测作为三个下游任务来评估预训练模型的效果。性能指标为MRR进行评估。- 对于前两个任务,我们希望模型能够预测论文所属的正确领域或正确会议。我们将这两个任务建模为节点分类问题,其中使用
GNN来获得论文的node embedding,然后使用一个softmax输出层来获得分类结果。 - 对于最后一个任务,我们选择所有同名的作者,以及链接到其中任何一位作者的论文。任务是在论文和候选同名作者之间进行链接预测。我们使用
GNN获得论文和节点的embedding,然后使用Neural Tensor Network来获取每对author-paper存在链接的概率。
mean reciprocal rank: MRR:多个query的排名倒数的均值。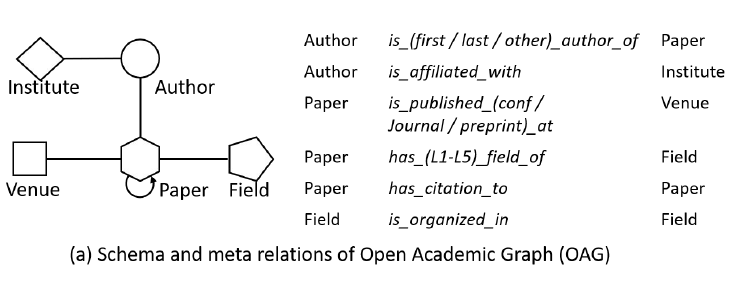
- 对于前两个任务,我们希望模型能够预测论文所属的正确领域或正确会议。我们将这两个任务建模为节点分类问题,其中使用
Amazon Review Recommendation:包含8280万条评论、2090万用户、930万商品。评论发布于1996~ 2018年,每条评论都包含一个从1~5的离散评分,以及一个特定领域(包括书籍Book、时装Fashion等)。数据集包含三种类型的节点:评论(评分和评论文本)、用户 、商品。另外还有商品的其它一些元数据,包括颜色、尺寸、样式和数量。和一般的
user-item二部图相比,该数据集存在评论数据。为简单起见,我们将评论的连接视为categorize_in类型,因此图中共有三种类型的关系。我们通过预训练的
XLNet获取每个评论的embedding作为评论节点的属性。用户节点、商品节点的属性都是和它们关联的评论的embedding取均值。我们将评分预测作为下游任务,该任务是一个
node-level的五类分类任务。我们使用micro-F1得分作为评估指标。我们使用GNN获取评论的上下文表示,然后使用softmax输出层来获得分类预测。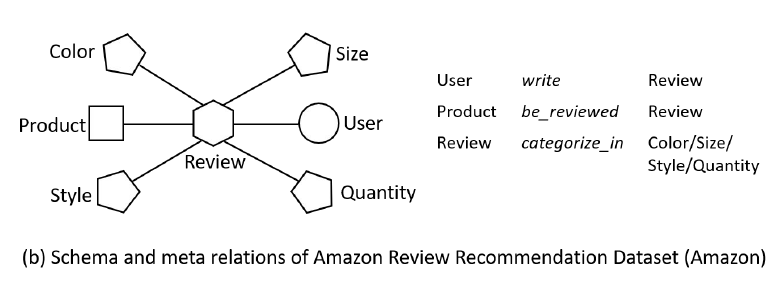
同质图:
Reddit数据集、从OAG提取的引文网络。
Base model:在OAG和Amazon数据集上,我们使用最新的异质GNN模型Heterogeneous Graph Transformer: HGT作为base model来预训练GPT-GNN。另外我们也对比了其它异质GNN作为base model的效果。baseline方法(均用于预训练):GAE:图自编码器,聚焦于传统的链接预测任务。它随机遮盖固定比例的边,然后要求模型重建这些遮盖的边。GraphSAGE(无监督):强迫相连的节点具有相似的embedding。它和GAE的主要区别在于:GraphSAGE在预训练过程中不会遮盖边。Graph InfoMax:尝试使用全局的图summary embedding来最大化局部node embedding。对于每个采样的子图,我们混洗子图来构造负样本。- 此外,我们还单独使用
GPT-GNN的两个预训练任务来进行对比,即属性生成GPT-GNN(Attr)、边生成GPT-GNN(Edge)。
GPT-GNN模型配置:- 所有的
base model,其隐层维度为400,head数量为8,GNN层数为3。 - 所有
GPT-GNN都采用PyTorch Geometric(PyG) package实现。 - 使用
AdamW优化器,使用Cosine Annealing Learning Rate Scheduler训练500个epoch,并选择验证损失最低的模型作为预训练模型。 - 自适应队列大小为
256。 - 在下游评估阶段,我们使用相同的优化配置来微调模型,微调期间训练
200个epoch。 - 我们对下游任务重复训练
5次,并报告测试结果的均值和标准差。
- 所有的
迁移学习配置:我们首先预训练
GNN,然后使用预训练的模型权重来初始化下游任务的模型。然后我们使用下游任务的训练集来微调模型,并评估测试集性能。大体而言,有两种不同的配置:
- 第一种是在完全相同的图上进行预训练和微调。
- 第二种是在一张图上进行预训练,但是在另一张图(和预训练的图具有相同类型)上进行微调。
其中第二种更为实用,我们选择第二种进行测试。
如果是跨图的微调,如何处理训练期间
unseen节点的embedding?- 如果是
transductinve的,那么只能要求两个图中的节点尽可能重合。 - 如果是
inductive的,那么两个图可以不同,因为我们只需要预训练模型权重矩阵(如GAT中的投影矩阵)即可。
具体而言,我们选择以下三种图迁移学习:
时间迁移
Time Transfer:使用来自不同时间段的数据进行预训练和微调。对于OAG和Amazon,我们使用2014年之前的数据进行预训练,使用2014年之后的数据进行微调。领域迁移
Field Transfer:使用来自不同领域的数据进行预训练和微调。- 在
OAG中,我们选择计算机科学领域CS的论文用于微调,其它领域的论文用于预训练。 - 在
Amazon中,我们选择艺术Art、手工艺品Craft、缝纫品Sewing进行预训练,并对时尚、美容、奢侈品进行微调。
- 在
组合迁移
Time + Field Transfer:使用2014年之前特定领域的数据来预训练,使用2014年之后另一些领域的数据来微调。这比单独的时间迁移或领域迁移更具挑战。
在微调期间,对于这两个数据集我们选择
2014~2016年的节点进行训练,2017年的节点作为验证,2018年的节点作为测试。为满足缺乏训练数据的假设,默认情况下我们仅提供
10%的标记数据用于微调训练。在预训练期间,我们随机选择部分数据(
2014年以前)作为验证集。在
OAG和Amazon数据集上的不同预训练方法的下游任务性能如下表所示。结论:
总体而言,
GPT-GNN框架显著提高了所有数据集上所有下游任务的性能。- 平均而言,
GPT-GNN相比于没有预训练的base model,在OAG和Amazon上获得了13.3%和5.7%的相对提升。 GPT-GNN也超越了其它的预训练模型,如Graph Informax。
- 平均而言,
预训练在领域迁移学习中的提升要超过时间迁移学习,而组合迁移学习的提升比例最低。这体现了组合迁移学习的挑战性。
但是,即使是在最具有挑战的组合迁移学习中,
GPT-GNN仍然分别在两个数据集上实现了11.7%和4.6%的性能提升。这表明:GPT-GNN使得GNN能够捕获输入图的通用结构和语义知识,从而可用于微调图数据的未见过的部分。通过对比
GPT-GNN的两个预训练任务(属性生成任务和边生成任务)的有效性,我们可以评估哪个对GPT-GNN以及下游任务更有效。- 在
OAG上,GPT-GNN(Attr)和GPT-GNN(Edge)平均性能分别提升7.4%和10.3%,表明边生成任务更有效。 - 但是在
Amazon上,结论相反,二者分别为5.2%和4.1%。
这表明
GPT-GNN从属性生成任务和边生成任务带来的收益因不同的数据集而不同。但是,将两个预训练任务结合起来可以获得最大收益。- 在
将边生成任务和其它基于边的预训练方法(如
GAE, GraphSAGE)相比。在OAG上,GPT-GNN(Edge), GAE, GraphSAGE相对于没有预训练分别提升10.3%, 7.4%, 4.0%。在Amazon上,提升比例分别为5.2%, 3.1%, 1.3%。- 首先,在这两个数据集上,
GAE和GPT-GNN(Edge)都要比GraphSAGE提供更好的结果,这表明在边上进行遮盖是用于自监督的图表示学习的有效方式。 - 其次,
GPT-GNN(Edge)始终超越了GAE。GPT-GNN(Edge)的优势在于它会自动生成缺失的边,从而捕获被遮盖边之间的依赖关系,这些依赖关系已被GAE丢弃。
总之,结果表明:
GPT-GNN可以为GNN预训练提供有效的自监督。- 首先,在这两个数据集上,
节点分裂旨在缓解属性生成任务的信息泄露问题,如果没有该部分,则属性将会出现在输入中。此时属性生成任务只需要简单的把输入预测为输出即可,即它无法学到输入图的任何知识,因此对结果有负面影响。
从
w/o node seperation可以看到,移除节点分裂使得预训练模型效果很多情况下甚至比没有预训练的更差。这证明了节点分裂在避免属性信息泄露方面的重要性。自适应队列旨在缓解采样子图和完整图之间的
gap。从GPT-GNN(Edge)和w/o adaptive queue之间的对比可以看到:移除自适应队列使得模型性能下降。这表明通过使用自适应队列来添加更多负样本,确实有助于预训练框架的效果提升。
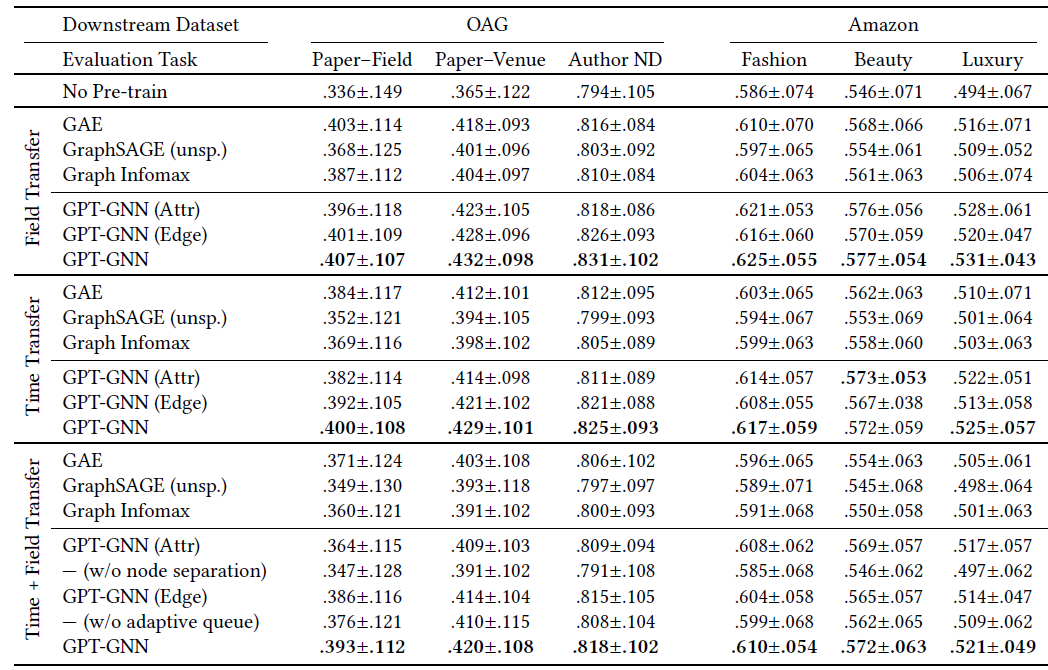
我们考察其它
GNN框架能否从GPT-GNN框架中受益。因此,除了HGT之外,我们还考察了GCN, GAT, R-GCN, HAN作为base model。我们在
OAG上对它们进行预训练,然后在组合迁移配置下使用paper-field预测任务,并使用10%的微调训练数据来微调。模型无关的超参数(如隐层维度、优化器)保持不变。结果如下所示,可以看到:HGT在所有非预训练模型中效果最好。- 采用
HGT的GPT-GNN在所有模型中效果最好。 GPT-GNN预训练框架可以增强所有GNN模型的下游性能。
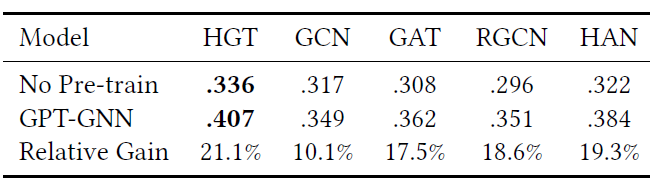
我们考察微调期间不同训练数据规模的效果。可以看到:
GPT-GNN和其它预训练框架通过更多的标签数据可以不断提高下游任务的效果。GPT-GNN在所有预训练框架中表现最好。GPT-GNN仅需要10% ~ 20%的数据来微调,就可以达到监督学习100%训练数据的效果。这证明了GPT-GNN的优越性。
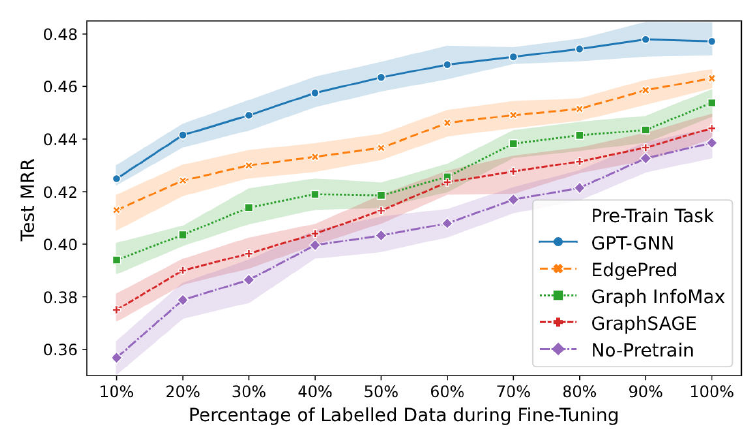
除了异质图之外,我们还评估了
GPT-GNN预训练框架是否可以应用于同质图的迁移学习。我们在两个同质图上进行预训练和微调:OAG的计算机科学领域的论文引文网络,对每个论文的主题进行预测。Reddit帖子组成的Reddit网络,对每个帖子的社区进行推断。
我们将
HGT忽略其异质部分从而用于base model。下表给出了10%标记数据的训练结果。可以看到:- 两个同质图的下游任务都可以从所有预训练框架中受益。
GPT-GNN可以提供最大的性能提升。
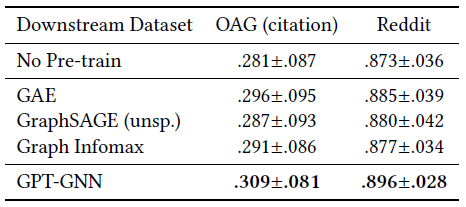
我们给出
OAG上预训练和微调的收敛曲线。下图给出了预训练期间每个
epoch的验证误差曲线。结果表明:模型的验证损失不断下降,而不是很快地找到一个平凡解。这在某种程度上表明:生成式预训练任务足够艰巨,因此可以指导模型真正捕获数据的内在结构。整个GPT-GNN预训练收敛大约需要12个小时。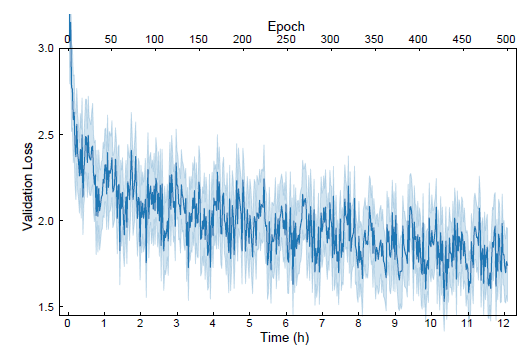
下图给出了微调期间的验证
MRR曲线(同时对比了没有预训练的验证MRR曲线)。可以看到,GPT-GNN总是可以获得更泛化的模型,并且由于预训练的良好初始化,微调期间对于过拟合更鲁棒。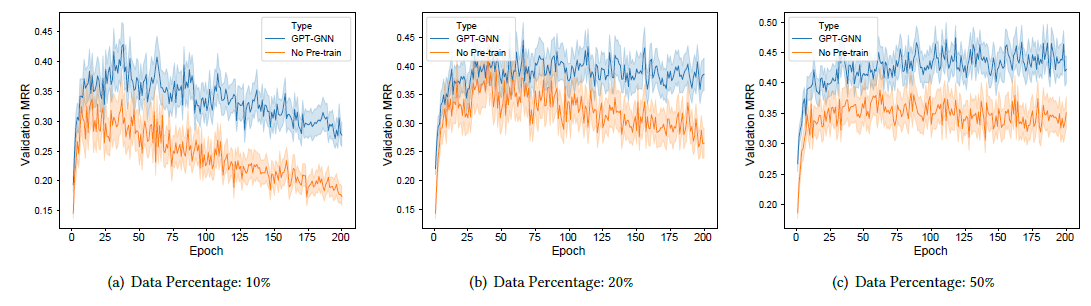
对于
OAG数据集,我们的属性生成任务是生成论文标题,所以我们希望了解GPT-GNN如何学习生成标题,结果见下表。可以看到:模型仅通过查看部分邻域即可捕获需要预测的论文的主要含义。例如,对于第一句话,我们的模型成功地预测了本文的关键词,包括
person recognition, probabilistic等。这表明图本身包含了丰富的语义信息,也解释了为什么预训练模型可以很好地泛化到下游任务。
二十五、Geom-GCN[2020]
消息传递神经网络
Message-Passing Neural Networks:MPNN(如GNN, ChebNet, GG-NN, GCN)已经成功地应用于各种实际应用中的图表示学习graph representation learning。在MPNN的每一层网络中,每个节点向邻域内的其它节点发送该节点的representation作为消息message,然后通过聚合从邻域内收到的所有消息来更新它的representation。其中,邻域通常定义为图中相邻节点的集合。通过采用排列不变permutation-invariant的聚合函数(如sum, max, mean聚合函数),MPNN能够学到同构图isomorphic graph(即,拓扑结构相同的图)的不变的representation。虽然现有的
MPNN已经成功应用于各种场景,但是MPNN聚合器aggregator的两个基本缺陷限制了它们表示图结构数据的能力:首先,聚合器丢失了邻域的结构信息。
排列不变性
permutation invariance是任何图学习方法的基本要求。为满足这一要求现有的MPNN采用了排列不变的聚合函数,这些聚合函数将来自邻域的所有消息视为一个集合。例如,GCN只是对所有一阶邻居的归一化消息求和。这种聚合会丢失邻域节点的结构信息,因为它无法区分不同节点的消息。因此,在聚合之后,我们也就无法知晓哪个节点对最终的聚合输出做出了贡献。如果不对邻域结构进行建模,现有的
MPNN将无法区分某些非同构图non-isomorphic graph。在这些非同构图中,MPNN可能将不同的邻域结构映射为相同的feature representation,这显然不适合graph representation learning。与MPNN不同,经典的CNN通过特殊的聚合器(即,滤波器)来避免这个问题从而能够区分每个input unit,其中这些聚合器具有结构化的感受野receiving filed并定义在网格grid上。正如论文
《GEOM-GCN: GEOMETRIC GRAPH CONVOLUTIONAL NETWORKS》的实验所示,这些邻域结构信息通常包含图中拓扑模式topology pattern的线索,因此应该提取并被应用于学习图的更有区分度的rerepenstation。其次,聚合器缺乏捕获异配图
disassortative graph(指的是相似的节点没有聚合在一起的图)中长程依赖long-range dependency的能力。在
MPNN中,邻域被定义为MPNN倾向于对图中相近的节点学到相似的representation。这意味这些MPNN可能是同配图assortative graph(如引文网络、社区网络)representation learning的理想方法。在这些同配图中,节点的同质性homophily成立,即相似的节点更可能在图中相近,图中相近的节点更可能相似。而对于节点同质性不成立的异配图,此时有些高度相似的节点在图中距离较远。这种情况下
MPNN的表示能力可能会受到严重限制,因为它们无法从距离遥远、但是包含丰富信息的相似节点中捕获重要特征。解决这个限制的简单策略是使用多层架构,以便从远程节点接收消息。例如,虽然经典
CNN中的卷积滤波器只能捕获局部数据,其单层卷积层的表示能力受限,但是通过堆叠多层卷积层,CNN可以学到复杂的全局表示。和
CNN不同,多层MPNN很难学到异配图的良好representation,这里有两个原因:- 一方面,在多层
MPNN中,来自远程节点的相关信息和来自近端节点的大量无关信息无差别地混合在一起,意味着相关信息被冲洗掉washed out,无法有效地提取。 - 另一方面,在多层
MPNN中,不同节点的representation将变得非常相似,因为每个节点的representation实际上承载了关于整个图的信息,即over-smooth。
- 一方面,在多层
在论文
《GEOM-GCN: GEOMETRIC GRAPH CONVOLUTIONAL NETWORKS》中,作者从两个基本观察出发,克服了图神经网络的上述缺陷:由于连续空间
continuous space的平稳性stationarity、局部性locality、组合性compositionality,经典的神经网络有效地解决了类似的局限。网络几何
network geometry有效地弥补了连续空间和和图空间之间的gap。网络几何的目的是通过揭示潜在的连续空间来理解网络,它假设节点是从潜在的连续空间中离散地采样,并根据节点之间的距离来构建边。在潜在空间中,图中复杂的拓扑模式(如子图、社区、层次结构)可以保留下来,并以直观的几何方式呈现。
受这两个观察结果的启发,作者对图神经网络中的聚合方案提出了一个启发性问题:图上的聚合方案能否受益于连续的潜在空间?例如使用连续的潜在空间中的几何结构来构建邻域,从而捕获图中的长程依赖?
为回答上述问题,作者提出了一种新的图神经网络聚合
scheme,称作几何聚合方案geometric aggregation scheme。在该方案中,作者通过node embedding将一个图映射到一个连续的潜在空间,然后利用潜在空间中定义的几何关系来构建邻域从而进行聚合。同时,作者还设计了一个基于结构邻域的bi-level聚合器来更新节点的representation,保证了图结构数据的排列不变性。和现有的MPNN相比,该方法提取了更多的图结构信息,并通过连续空间中定义的邻域来聚合远程节点的feature representation。然后,作者提出了几何聚合方案在图卷积网络上的实现,称作
Geom-GCN,从而在图上执行transductive learning、node classification。作者设计了特定的几何关系来分别从欧式空间和hyperbolic embedding空间中构建结构邻域structural neighborhood。作者选择不同的embedding方法将图映射到适合不同application的潜在空间,在该潜在空间中保留了适当的图拓扑模式。最后,作者在大量公开的图数据集上对
Geom-GCN进行了实验,证明了Geom-GCN达到了state-of-the-art效果。总之,论文的主要贡献如下:
- 作者提出了一种新的几何聚合方案用于图神经网络,它同时在图空间和潜在空间中运行,从而克服上述两个局限性。
- 作者提出了该方案的一个实现,即
Geom-GCN,用于图中的transductive learning。 - 作者通过在几个具有挑战性的
benchmark上与state-of-the-art方法进行广泛的比较来验证和分析Geom-GCN。
相关工作:
25.1 几何聚合方案
- 这里首先介绍几何聚合方案,然后概述它和现有工作相比的优点和缺点。
25.1.1 基础模块
如下图所示,几何聚合方案由三个模块组成:
node embedding(A1和A2)、结构邻域(B1和B2)、bi-level聚合(C)。图中:A1-A2:原始图(A1)被映射到一个潜在的连续空间(A2)。B1-B2:结构邻域(B2)。为可视化,我们放大了中心节点(红色)周围的邻域。关系算子3x3网格表示,每个单元格代表了和红色目标节点的几何关系(即几何位置是左上、左下、右上、右下等等)。C:在结构邻域上的bi-level聚合。虚线和实线箭头分别表示low-level聚合和high-level聚合。蓝色箭头和绿色箭头分别表示图上的聚合以及潜在空间上的聚合。
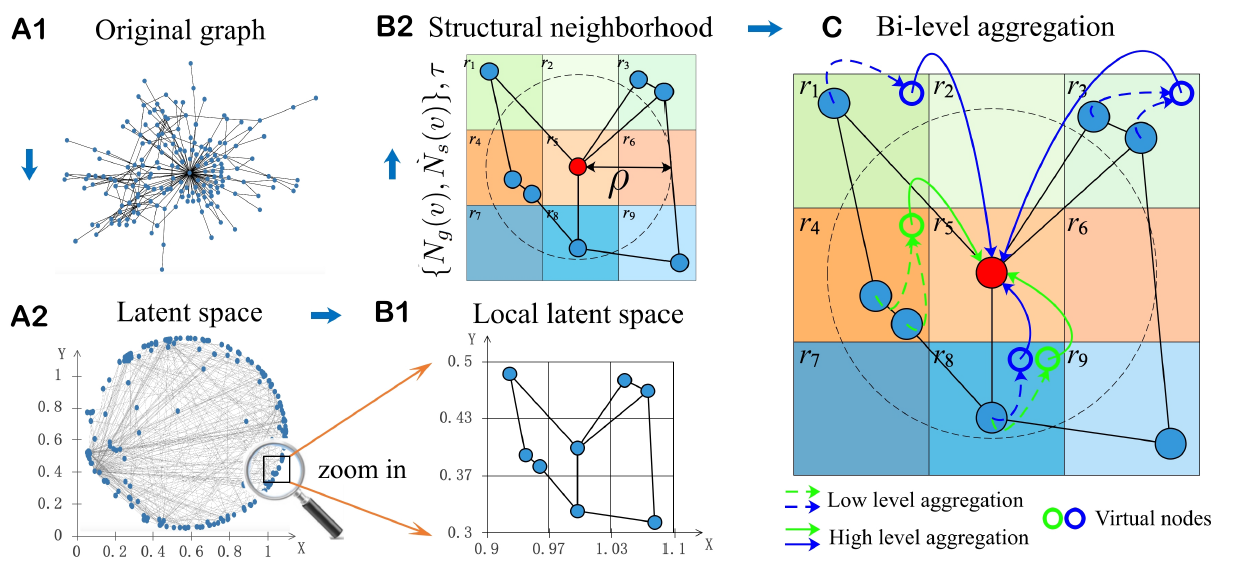
node embedding:这是一个基础组件,它将图中的节点映射到潜在的连续空间latent continuous space。令图
令
representation向量representation向量的维度。这可以理解为将节点geometry。这里可以使用各种embedding方法来得到不同的潜在连续空间(《A comprehensive survey of graph embedding: Problems, techniques, and applications》、《A united approach to learning sparse attributed network embedding》)。结构邻域
structural neighborhood:基于离散的图空间和连续的潜在空间,我们构建一个结构邻域和
关系算子
representation pair对geometric relationship:其中
B2中,{左上、中上、右上、左中、相同、右中、左下、中下、右下 }。根据不同的潜在空间和不同的应用,
representation pair对,它们的关系应该是唯一的。
bi-level聚合:借助结构邻域bi-level聚合方案来更新节点的hidden feature。bi-level聚合方案由两个聚合函数组成,它可以有效地提取邻域节点的结构信息,并保持图的排列不变性。令
hidden feature,其中hidden feature注意:节点
representation:node embedding用于构建结构邻域(通常具有较小的维度)、node representation用于具体的任务(图,节点分类)。low-level聚合:在
low-level聚合,处于相同类型的邻域hidden feature通过聚合函数- 这个虚拟节点的特征是
average pooling, enerage pooling, max pooling。
low-level聚合如上图C1的虚线箭头所示。- 这个虚拟节点的特征是
high-level聚合:在
high-level,虚拟节点由函数这里聚合了图空间邻域和潜在空间邻域,共两种类型的邻域。也可以构建
非线性映射:
high-level聚合的输出是向量hidden featureReLU。
25.1.2 排列不变性
排列不变性
permutation invariance是图神经网络中聚合器的基本要求,随后我们将证明我们提出的bi-level聚合公式能够保证邻域节点的任何排列都不变。图的排列不变映射的定义:给定一个双射函数
引理:对于组合函数
证明:令
isomorphic graph,如果定理:给定图
bi-level聚合是排列不变的映射。证明:
bi-level聚合是一个组合函数,其中low-level聚合是high-level聚合的输入。因此,如果能够证明low-level聚合是排列不变的,则bi-level聚合是排列不变的。现在我们来证明
low-level聚合是排列不变的。low-level聚合由- 首先,每个子聚合的输入都是排列不变的,因为
- 其次,子聚合采用了排列不变的聚合函数
low-level聚合是排列不变的。
- 首先,每个子聚合的输入都是排列不变的,因为
25.1.3 与相关工作的比较
这里讨论我们提出的几何聚合方案如何克服之前提到的两个缺点,即:如何有效地对邻域结构进行建模、如何捕获长程依赖。
为了克服
MPNN的第一个缺点,即丢失邻域中节点的结构信息,几何聚合方案利用潜在空间中节点之间的几何关系,然后使用bi-level聚合有效地提取信息,从而对结构信息进行显式建模。相反,现有的一些方法试图学习一些隐式的、类似于结构的信息,从而在聚合时区分不同的邻居。如
GAT(《Graph attention networks》)、LGCL(《Large-scale learnable graph convolutional networks》)、GG-NN(《Gated graph sequence neural networks》)等通过使用注意力机制以及节点/边的属性来学习来自不同邻居消息的权重。CCN利用协方差架构来学习structure-aware representation(《Covariant compositional networks for learning graphs》)。这些工作和我们之间的主要区别在于:我们利用潜在空间的几何信息提供了一种显式的、可解释的方式来建模节点邻域的结构信息。另外,我们的方法和现有的这些方法是正交的,因此可以容易地和现有方法融合从而进一步改善性能。具体而言,我们从图拓扑的角度利用几何关系,而其它方法更关注
feature representation,这两个方面是互补的。为了克服
MPNN的第二个缺点,即缺乏捕获远程依赖的能力,几何聚合方案以两种不同的方式对异配图中的远程关系进行建模:- 首先,可以将图中相似但是相距很远的节点映射到目标节点在潜在空间的邻域中,然后聚合这些邻域节点的
representation。这种方式取决于保留节点相似性的适当的embedding方法。 - 其次,结构信息使得该方法能够区分图中邻域中的不同节点。
informative node和目标节点可能具有某些特殊的几何关系(如特定的角度、特定的距离)。因此相比uninformative node,informative node的相关的特征将以更高的权重传递给目标节点。
最终通过整个消息传递过程间接捕获了长程依赖关系。
此外,
《Representation learning on graphs with jumping knowledge networks》中提出了一种方法JK-Nets通过在特征聚合期间skip connection来捕获长程依赖关系。- 首先,可以将图中相似但是相距很远的节点映射到目标节点在潜在空间的邻域中,然后聚合这些邻域节点的
有些文献构造了一些非同构
non-isomorphic图(《Covariantcompositional networks for learning graphs》、《How powerful are graph neural networks? 》),它们无法被现有的MPNN聚合器(如均值、最大值)很好地区分。这里我们给出两个示例,它们来自于《How powerful are graph neural networks?》。如下左图所示,每个节点都具有相同的特征
graph中,节点final representation都是相同的。即,均值聚合器和最大值聚合器无法区分这两个不同的图。相反,如果在聚合过程中应用结构邻域,则这两个图可以很容易地区分。应用结构邻域之后,其它节点和
- 对于
- 然后,两个图中的聚合器具有不同的输入,左边的输入为
- 最终在两个图中,聚合器(平均值或最大值)对节点
- 对于
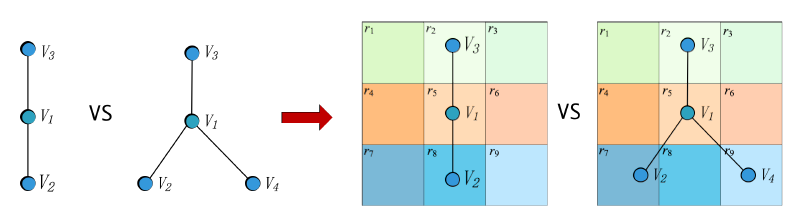
25.2 Geom-GCN
这里我们介绍
Geom-GCN,它是几何聚合方案在GCN上的具体实现,主要用于图的transductive learning。为实现几何聚合方案,需要给出其中的三个模块:
node embedding、结构邻域、bi-level聚合。node embedding:如我们实验所示,仅保留图中的边以及距离模式的常见embedding方法已经可以使几何聚合方案受益。对于特定的应用,可以指定特定的
embedding方法来建立合适的、保留特定拓扑结构(如层次结构)的潜在空间。我们使用了三种embedding方法,即:Isomap、Poincare Embedding、Struc2vec,这导致了三种Geom-GCN变体:Geom-GCN-I、Geom-GCN-P、Geom-GCN-S。Isomap是一种广泛应用的isometry embedding方法,在该方法中,距离模式(最短路径的长度)被显式地保留在潜在空间中。Poincare Embedding和Struc2vec能够创建特定的潜在空间,分别保留图中的层次结构和局部结构。
为了便于说明,我们的
embedding空间维度为2(即结构邻域:节点
图空间邻域
另外对于不同的潜在空间我们使用不同的距离:在欧式空间中我们使用欧式距离;在双曲空间
hyperbolic space中,我们通过两个节点在局部切平面上的欧式距离来近似测地线距离。我们简单地将几何算子
因为
embedding size = 2,所以划分为四种关系。也可以设计更复杂的几何算子
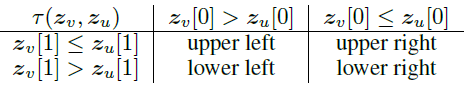
bi-level聚合:我们采用和GCN相同的归一化hidden feature聚合作为low-level聚合函数其中
degree。聚合时仅考虑和节点对于最后一层我们使用均值聚合作为
high-level聚合函数其中:
ReLU。
25.3 实验
这里我们比较了
Geom-GCN和GCN, GAT的性能,从而验证Geom-GCN的效果。数据集:我们使用
9个图数据集:引文网络:
Cora, Citeseer, Pubmed是标准的引文网络benchmark数据集。在这些网络中,节点表示论文,边表示论文被另一篇论文引用,节点特征是论文的
bag-of-word表示,节点标签是论文的学术主题。WebkB数据集:WebKB由卡内基梅隆大学从各大学的计算机科学系收集的网页数据集,我们使用它的三个子集:Cornell, Texas, Wisconsin。在这些网络中,节点代表网页,边代表网页之间的超链接,节点的特征是网页的
bag-of-word表示。网页被人工分为五个类别:student, project, course, staff, faculty。Actor co-occurrence数据集:该数据集是film-directoractor-writer网络导出的仅包含演员的子图。在该网络中,节点代表演员,边表示同一个维基百科上两个演员的共现,节点特征为该演员的维基百科页面上的关键词。根据演员的维基百科的词汇,我们将节点分为五类。
这些数据集的统计信息如下表所示:

实验配置:我们使用三种
embedding方法,即Isomap、Poincare embedding、struc2vec,从而构建三种Geom-GCN变体,即Geom-GCN-I、Geom-GCN-P、Geom-GCN-S。所有
Geom-GCN的embedding空间维度为2,并使用前面介绍的关系算子low-level聚合函数high-level聚合函数即
所有模型的网络层数固定为
2,采用Adam优化器。对于Geom-GCN我们采用ReLU作为激活函数,对于GAT我们采用GAT作为激活函数。我们使用验证集来搜索超参数,这些超参数包括:隐层维度、初始学习率、权重
decay、dropout。为确保公平,每个模型的超参数搜索空间都是相同的。最终得到的超参数配置为:dropout rate = 0.5、初始化学习率0.05、早停的patience为100个epoch。对于
WebKB数据集,weight decay为weight decay为对于
GCN模型,隐层维度为:Cora数据集16、Citeseer数据集16、Pubmed数据集64、WebKB数据集32、Wikipedia数据集48、Actor数据集32。对于
Geom-GCN模型,隐层维度是GCN的8倍,因为Geom-GCN有8个虚拟节点。即
对于
GAT模型的每个attention head,隐层维度为Citation网络为8、WebKB数据集为32、Wikipedia数据集为48、Actor数据集为32。对于
GAT模型,第一层具有8个head;Pubmed数据集的第二层具有8个head,其它数据集的第二层只有1个head。
对于所有数据集,我们将每个类别的节点随机拆分为
60%, 20%, 20%来分别作为训练集、验证集、测试集。我们随机拆分
10次并报告模型在测试集上的平均性能。
所有模型在所有数据集上的评估结果如下表所示,其中评估指标为平均分类准确率(以百分比表示)。最佳结果突出显式。
结论:
Geom-GCN可以实现state-of-the-art性能。- 仅保留图中边和距离模式的
Isomap Embedding (Geom-GCN-I)已经可以使得几何聚合方案受益。 - 可以指定一种
embedding方法从而为特定应用构建合适的潜在空间,从而显著提升性能(如Geom-GCN-P)。
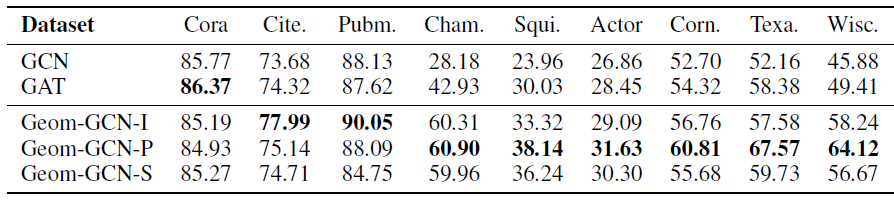
Geom-GCN聚合了来自两个邻域的消息,这两个邻域分别在图空间和潜在空间中定义。这里我们通过构建仅有一个邻域的Geom-GCN变体来进行消融研究,从而评估每种邻域的贡献。- 对于仅具有图空间邻域的变体,我们用
g后缀来区分(如Geom-GCN-Ig)。 - 对于仅具有潜在空间邻域的变体,我们用
s后缀来区分(如Geom-GCN-Is)。
我们将
GCN设为baseline,从而评估这些变体相对GCN的性能提升。比较结果见下表所示,其中正向提升用向上箭头表示,负向衰减用向下箭头表示。评估指标为测试集的平均准确率。我们定义了指标
homophily:同质性以节点标签来衡量,其中相似的节点倾向于相互连接。较大的
assortative graph(如引文网络)具有比异配图disassortative graph(如WebKB网络)大得多的结论:
大多数情况下,图空间邻域和潜在空间邻域都有利于聚合。
潜在空间邻域在异配图(更小的
问题是:图空间邻域在异配图(更小的
因此这里的结论不成立。
令人惊讶的是,只有一个邻域的几种变体(下表)要比具有两个邻域的变体(上表)具有更好的性能。我们认为,原因是两个邻域的
Geom-GCN相比单个邻域的Geom-GCN聚合了更多无关的消息,并且这些无关消息对于性能产生了不利的影响。我们认为注意力机制可以有效缓解这个问题,并留待以后工作进行研究。
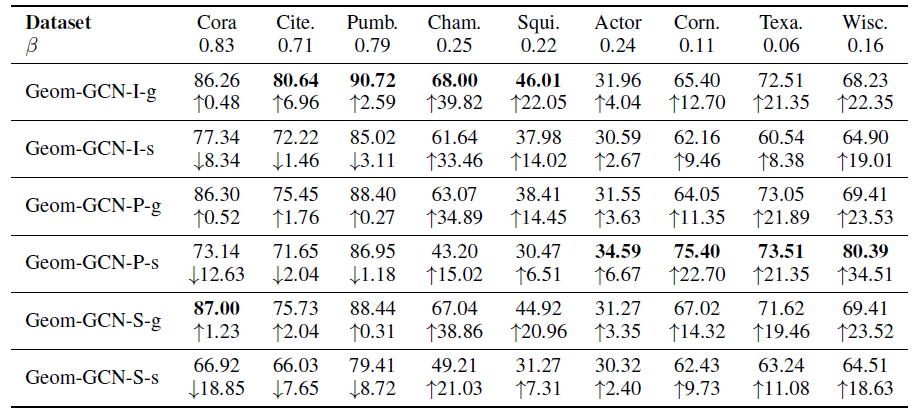
- 对于仅具有图空间邻域的变体,我们用
Geom-GCN的结构邻域非常灵活,可以组合任意的embedding空间。为了研究哪种embedding空间是理想的,我们通过采用由不同embedding空间构建的结构邻域来创建新的Geom-GCN变体。对于采用Isomap构建图空间邻域、采用Poincare Embedding构建潜在空间邻域的变体,我们用Geom-GCN-IP来表示。其它组合的命名规则依此类推。这里构建了两种潜在空间,从而得到
3种类型的结构邻域(一个来自图控件,两个来自潜在空间)。下表给出了所有变体的性能,评估指标为测试集的平均准确率。
结论:有一些组合的性能要优于标准的
Geom-GCN,有一些组合的性能更差。因此,如何设计自动选择合适的embedding空间的端到端框架是未来的重要方向。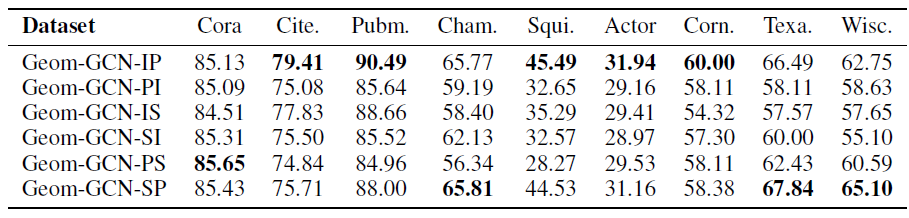
这里我们首先介绍
Geom-GCN的理论时间复杂度,然后比较GCN, GAT, Geom-GCN的实际运行时间。Geom-GCN更新一个节点的representation的时间复杂度为GCN更新一个节点representation的时间复杂度为我们给出所有数据集上
GCN, GAT, Geom-GCN的实际运行时间(500个epoch)进行比较,结果如下图所示。结论:
GCN训练速度最快,GAT和Geom-GCN处于同一水平。未来的一个重要方向是开发Geom-GCN的加速技术,从而解决Geom-GCN的可扩展性。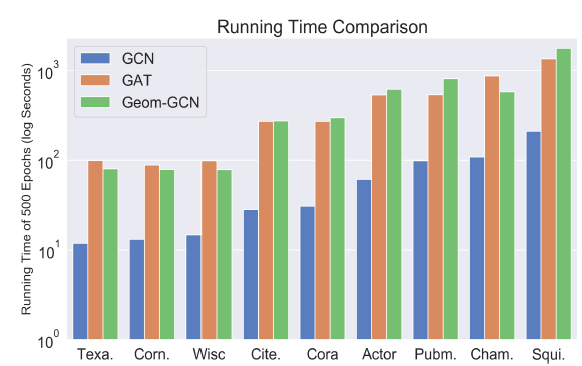
为研究
Geom-GCN在节点feature representation中学到的模式,我们可视化了Cora数据集在Geom-GCN-P模型最后一层得到的feature representation。我们通过t-SNE将该特征表示映射到二维空间中,如下图所示。节点的不同颜色代表不同的类别。可以看到:
- 具有相同类别的节点表现出空间聚类
spatial clustering,这可以显示Geom-GCN的判别能力。 - 图中所有节点均呈现放射状分布,这表明通过
Poincare Embedding提出的Geom-GCN学到了图的层次结构。
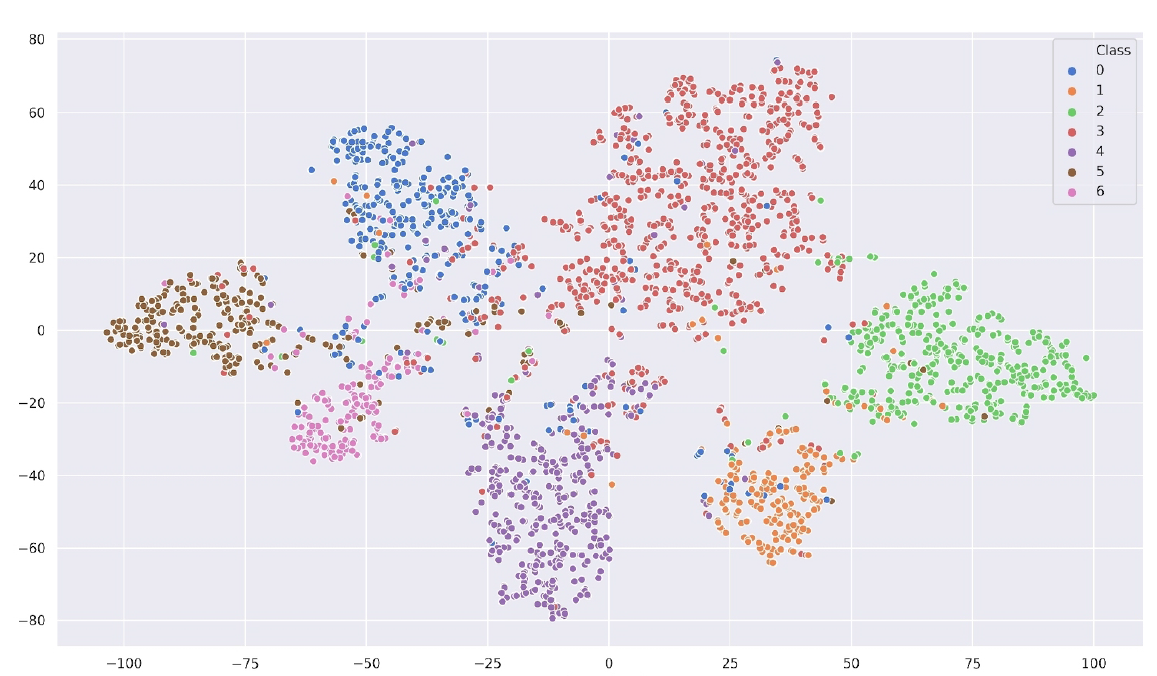
- 具有相同类别的节点表现出空间聚类