GNN(续)
二十六、Graph Network[2018]
摘要:人工智能
Artificial intelligence: AI最近经历了一场复兴,并在视觉、语言、控制、决策等关键领域取得了重大进展。取得这些进展的部分原因是由于廉价的数据、廉价的计算资源,这符合深度学习的天然优势。然而,在不同压力下发展起来的人类智力,其许多决定性特点对于目前的人工智能方法而言仍然是触不可及的。具体而言,超越经验的泛化能力--人类智力从幼年开始发展的标志--仍然是现代人工智能面临的巨大挑战。论文
《Relational inductive biases, deep learning, and graph networks》认为:组合泛化combinatorial generalization是AI实现人类相似能力的首要任务,而结构化表示和计算structured representations and computations是实现该目标的关键。正如生物学把先天nature和后天nurture相结合,论文摒弃手动设计特征hand-engineering、端到端学习end-to-end learning之间进行二选一选择的错误做法,而是提倡一种利用它们进行优势互补的做法。论文探索深度学习框架中使用关系归纳偏置
relational inductive biases如何促进对实体entity、关系relation、以及构成它们的规则rule的了解。论文为AI toolkit提供了一个新的、具有强大关系归纳偏置的构建块building block:Graph Network。Graph Network概括和扩展了图上运行的各种神经网络方法,并为操作结构化知识manipulating structured knowledge和产生结构化行为producing structured behaviors提供了直接接口。论文讨论
Graph Network如何支持关系推理relational reasoning、组合泛化combinatorial generalization。这为更复杂、更可解释、更可扩展的推理模式reasoning pattern奠定了基础。作为论文的补充,作者还发布了一个用于构建
Graph Network的开源软件库,并演示了如何在实际工作中应用它们。引言:人类智能的一个重要标志是 “无限使用有限方法” (
infinite use of finite means) 的能力,其中一小部分的、有限的原始(如单词word)可以无限地组合(如构成无限多的句子sentence)。这反映了组合泛化combinatorial generalization的原理,即从已知的构建块building block来创建新的推论inference、预测prediction、行为behavior。这里我们探索如何通过将偏置学习biasing learning用于结构化的表示和计算structured representations and computations从而提高现代AI的组合泛化能力,尤其是对图graph进行操作的系统。人类的组合泛化能力很大程度上取决于我们表达结构
representing structure和推理关系reasoning about relations的认知机制。- 我们将复杂系统表示为实体
entity及其相互作用interaction的组合。 - 我们使用层次结构来抽象细粒度
fine-grained的差异,并捕获representations和behaviors之间的更一般的共性,比如:同一个物体的一部分、同一个场景的物体、同一个城镇的社区。 - 我们通过组合熟悉的技能
skills和惯例routines来解决新的问题。 - 我们通过将两个领域之间的关系结构对齐,并根据其中一个领域的相应知识得出另一个领域的推论来进行类比。
Kenneth Craik的The Nature of Explanation将世界的组成结构compositional structure of the world和我们内在的心理模型internal mental model的组织方式联系起来,即:世界是组合的compositional,或者至少我们是从组合的角度来理解它的。当我们学习的时候,我们要么将新知识放入现有的结构化表示structured representations中、要么调整结构本身从而更好地适应(和使用)新旧知识。自
AI诞生以来,如何构建具有组合泛化的人工智能系统一直就是AI的核心问题,它是很多结构化方法structured approach的核心,包括:逻辑logic、语法grammar、经典规划classic planning、图模型graphical model、因果推理causal reasoning、贝叶斯非参数化Bayesian nonparametric以及概率规划probabilistic programming。所有子领域都集中于显式的以实体
entity和关系relation为中心的学习上,例如关系强化学习relational reinforcement learning、统计关系学习statistical relational learning。结构化方法对于之前的机器学习如此重要的一个关键原因,部分是因为数据和计算资源的昂贵,而结构化方法强大的归纳偏置inductive biases所带来的样本复杂度sample complexity的改善是非常有价值的。与过去的人工智能方法相比,现代深度学习经常遵循 “端到端”(
end-to-end) 的设计理念,强调最小限度的先验表征的、计算的假设minimal a priori representational and computational assumptions,并力求避免使用显式的结构explicit structure和特征工程hand-engineering。这种强调emphasis和当前的大量廉价数据和廉价计算资源非常契合,也得到了充分的验证。这使得牺牲样本效率sample efficiency从而更灵活地学习成为一种理性的选择。从图像分类到自然语言处理,深度学习在很多具有挑战性的领域中取得了令人瞩目的快速发展,这证明了这种极简主义原则minimalist principle的成功。一个突出的例子是语言翻译,事实证明sequence-to-sequence方法非常有效,无需使用显式的解析树parse tree或者语言实体linguistic entity之间的复杂关系。尽管深度学习取得了巨大成功,但是也有一些严厉的批评:深度学习在复杂的语言和场景理解
complex language and scene understanding、结构化数据的推理reasoning about structured data、训练条件之外的迁移学习transferring learning beyond the training condition以及少量经验中学习learning from small amounts of experience时面临重大挑战。这些挑战需要组合泛化,因此摒弃组合性compositionality以及显式结构explicit structure的方法难以满足这些挑战,这并不奇怪。当深度学习的前辈连接主义
connectionist面临诸如结构性的structured、符号性的symbolic立场position等类似批评时,有些工作直接地、细致地做出了建设性的努力来解决这些挑战。在诸如模拟制造analogy-making、语言分析linguistic analysis、符号操作symbol manipulation以及其它形式的关系推理之类的领域中,符号主义开发了用于表示和推理结构化对象的各种创新的亚符号sub-symbolic方法,以及有关大脑如何工作的更多综合理论integrative theory。这些工作还有助于培养更多的深度学习进展advances,这些进展使用分布式向量表示来捕获文本text、图graph、代数表达式algebraic expression、逻辑表达式logical expression、以及程序programs中的丰富语义内容。我们认为,现代
AI的关键途径是致力于将组合泛化作为首要任务,并且我们主张采用综合方法integrative approache来实现这一目标。正如生物学没有在先天nature和后天nurture之间进行选择一样(生物学同时利用先天和后天,这种整体效果强于每个部分之和),我们也拒绝这样的观念(即,结构struture和灵活性flexibility在某种程度上是矛盾的或不相容的),并且我们同时拥抱结构和灵活性从而获得它们的互补优势。根据大量最新的一些混合了structure-based方法、deep learning方法的案例,我们发现:将当今最好的方法(即deeplearning方法)和早期算力昂贵时必不可少的方法(即结构化方法)相结合的综合技术具有广阔的前景。近年来,在深度学习和结构化方法的交集中出现了一类模型,这些模型聚焦于推理有关显式结构化数据(特别是图
graph)的方法。这些方法的共同点是可以对离散实体entity以及实体之间的关系relation进行计算。这些方法和经典方法不同之处在于:如何学习实体和关系的representation以及structure,以及相应的计算,从而缓解了事先需要指定它们的负担。即,这些知识是通过学习而来,而不是预先指定的。至关重要的是,这些方法以特定的体系架构假设的形式引入强烈的关系归纳偏置relational inductive biases,这些偏置指导这些方法学习实体和关系。我们和很多其他人一起认为,这是类似人类智力的基本组成部分。在文章的剩余部分,我们通过关系归纳偏置的角度考察了各种深度学习方法,表明现有方法通常带有关系假设
relational assumptions,这些假设并不总是很明显或者显而易见。然后我们提出了一个基于实体和关系推理的通用框架,我们称之为Graph Network:GN。GN统一和扩展了图上运行的现有方法,并描述了使用Graph Network作为构建块building block来构建强大架构的关键设计原理。我们还发布了一个用于构建Graph Network的开源库。- 我们将复杂系统表示为实体
26.1 关系归纳偏置
26.1.1 Relational Reasoning
定义结构
structure为通过一组已知构建块building block组成的产品product。结构化表示Structured representations捕获了这种组成composition,如元素element的排列arrangement。结构化计算structured computations以一个整体的方式对所有这些元素及其组合进行操作。关系推理Relational Reasoning涉及利用实体entity和关系relation的组成规则composed rule,从而操作实体和关系的结构化表示。我们用以下数据来描述认知科学、理论计算机科学、人工智能的相关概念:实体
entity:具有属性的元素,如具有大小、质量的物理对象。关系
relation:实体之间的属性。如两个对象之间的关系可能包括:相同大小same size as、比.. 更重heavier than、距离distance from。- 关系也可以具有属性。比如
more than X times heavier than带有一个属性X,它决定了这个关系取值为true/false的阈值。 - 关系也可能对全局上下文敏感。比如对于石头和羽毛,关系
falls with greater accelaration than取决于环境是在空气中还是真空中。
这里我们关注实体之间的成对关系
pairwise relations。- 关系也可以具有属性。比如
规则
rule:将实体和关系映射到其它实体和关系的函数,就像一个非二元的逻辑谓词non-binary logical predicate。例如is entity X large?、is entity X heavier than entity y?这样的尺度比较scale comparison。这里我们仅考虑带有一个参数或两个参数、并返回一个属性的规则。
我们以图模型
graphical model来作为机器学习中关系推理的示例性说明。图模型可以通过在随机变量之间指定显式的条件独立性来建模复杂的联合分布。这样的模型非常成功,因为它捕获了稀疏结构
sparse structure,而稀疏结构是很多现实世界生成过程generative processes的基础,并且它们支持有效的学习和推理算法。例如,隐马尔可夫模型可以显式指定条件独立性:
- 当前状态仅依赖于前一个状态,与其它历史状态无关。
- 当前观测值仅依赖于当前状态,和其它历史状态、其它观测值无关。
这和很多现实世界因果过程
causal process的关系结构非常契合。明确表达变量之间的稀疏依赖关系提供了各种高效的推断
inference和推理reasoning算法。例如,消息传递算法在图模型内的各个位置之间采用通用的消息传播过程,从而导致一个可组合的composable、部分并行化的partially parallelizable推理过程reasoning procedure,这适用于不同大小和形状的图模型。
26.1.2 Inductive Biases
学习是通过观察世界并与世界互动来理解有用知识的过程,它涉及搜索解空间
space of solutions以期找到可以更好地解释数据、或获得更高回报的解决方案solution。但是在很多情况下,有多种解决方案同样出色。归纳偏置inductive bias允许学习算法独立于观测到的数据,从而将一种解决方案(或者解释)优先于另一种解决方案(或解释)。在贝叶斯模型中,归纳偏置通常以先验分布的选择
choice、参数化parameterization来表示。而在其它模型中,归纳偏置可能是为避免过拟合而添加的正则化项,也可能被编码到算法本身的体系结构中。归纳偏置通常以灵活性
flexibility为代价从而换取改善的样本复杂性sample complexity,并且可以从偏差-方差平衡bias-variance tradeoff的角度来理解。理想情况下,归纳偏置既可以在不显著降低性能的情况下改善对于解空间的搜索,又可以帮助找到理想泛化的解决方案。但是,不匹配mismatched的归纳偏置也会引入过强的约束从而导致欠拟合。归纳偏置可以表达关于数据生成过程
data-generating process或解空间的假设。例如,当使用一维函数拟合数据时,线性最小二乘法遵循近似函数为线性模型的约束,并且在additive Gaussian noise破坏的线性过程line process。类似地,
ill-posed problem可以得到唯一的解决方案和全局结果。这可以解释为关于学习过程的一种假设:当解决方案之间的分歧较少时,寻找好的解决方案更加容易。注意,这些假设不需要明确地解释模型或算法如何与世界交互。
26.1.3 Relational Inductive Biases
机器学习和
AI中很多具有关系推理能力的方法使用关系归纳偏置relational inductive bias。虽然不是精确的正式定义,但是我们通常使用该术语来指归纳偏置inductive bias,它对于学习过程中实体之间的关系和交互施加了约束。近年来新型的机器学习体系架构迅速增加,从业人员经常遵循通过组合基本构建块
elementary building block来形成更复杂、更深计算的层次hierarchies和计算图。例如:
- 全连接层
full connected layer被堆叠到多层感知机multilayer perceptrons: MLPs中。 - 卷积层
convolutional layers被堆叠到卷积神经网络convolutional neural networks: CNNs中。 - 图像处理网络的标准配置是由各种
CNN变体 +MLP的组合。
这种
layer的组合提供了一种特殊类型的关系归纳偏置:层次处理hierarchical processing的关系归纳偏置。其中计算分阶段in stages进行,这会导致输入信号中的信息之间产生越来越长距离的交互long range interaction。正如我们在下面探讨的那样,构建块本身也带有各种关系归纳偏置(如下表所述)。尽管超出了本文的范围,但是在深度学习中也使用各种非关系归纳偏置
non-relational inductive biases,例如:激活值的非线性non-linearity、权重衰减、dropout、batch normalization/layer normalization、data augmentation、训练方式、优化算法都对学习的轨迹和结果施加了约束。
- 全连接层
要探索各种深度学习方法中表达的关系归纳偏置,我们必须确定几个关键因素:实体是什么、关系是什么、组成实体和关系的规则是什么、计算实体和关系的规则是什么。在深度学习中,实体和关系通常表示为分布式表示
distributed representation,规则通常表示为神经网络函数逼近器approximator。然后,实体、关系、规则的精确形式在不同体系架构之间有所不同。为了理解架构之间的这些差异,我们通过以下探索进一步理解每种架构如何支持关系推理:- 规则函数
rule function的自变量argument,例如:哪些实体和关系作为输入。 - 规则函数如何在计算图上重用或共享,例如:跨不同实体和关系、跨不同时间或
step。 - 架构如何定义
representation之间的交互interaction与隔离isolation。例如:通过在相关的实体上应用规则来得出结论,而不是对每个实体独立处理。
- 规则函数
26.1.4 标准 deep learning 构建块
Fully Connected Layers全连接层:也许最常见的构建块是全连接层。通常全连接层被实现为输入向量的非线性函数:
其中
因此实体是网络中的单元,关系是
all-to-all:- 所有输入单元都连接到所有输出单元,规则由权重矩阵和偏置向量指定。
- 规则的自变量是完整的输入信号,没有参数共享,也没有信息隔离。
因此,在全连接层中的隐式关系归纳偏置非常弱
week:所有输入单元之间可以交互从而决定任何输出单元的值,并且所有输出单元之间相互独立。Convolutional Layers卷积层:另一个常见的构建块是卷积层。卷积层通常被实现为输入向量或张量的卷积:
其中
这里的实体仍然是单个单元(或者网格元素,如像素),但是实体之间的关系更为稀疏。全连接层和卷积层之间的差异在于卷积层增加了一些重要的关系归纳偏置:局部性
locality和平移不变性translation invariance。- 局部性反映了关系规则
relational rule的自变量是那些在输入信号的坐标空间中紧密相邻的实体、并且和远处实体隔离。 - 平移不变性反映了在输入中跨区域重复使用相同的规则。
这些偏置对于处理天然的图像数据非常有效,因为图像数据局部邻域内存在较高的协方差,且随着距离增加,协方差会减小。并且统计量在整个图上大多是平稳的
stationary。- 局部性反映了关系规则
Recurrent Layers递归层:第三种常用的构建块是递归层,它是通过一系列step来实现的。这里我们将每个step的输入和hidden state视为实体,将马尔可夫过程视为关系:当前hidden state依赖于前一个hidden state和当前input。实体组合的规则将当前step的输入、前一个hidden state作为规则的自变量,然后更新当前hidden state。这个规则在每个
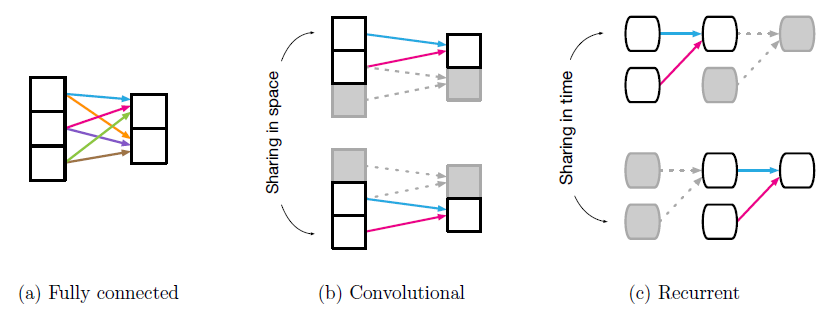
step被复用,这反映了时间不变性(类似于CNN在空间上的平移不变性)的关系归纳偏置。例如,某些物理事件序列的结果不应该取决于一天中的某个时刻。RNN也通过其马尔可夫结构对序列带来局部性locality的bias。下图给出了常见的深度学习构建块中的复用和共享,共享的权重由具有相同颜色的箭头表示。
(a):全连接层,其中所有权重都是独立的,并且没有共享。(b):卷积层,其中局部核函数在输入中多次重复使用。(c):循环层,其中相同的函数可以在不同的step中复用(水平方向代表了时间线)。
26.1.5 sets 和 graphs 上的计算
虽然标准的深度学习工具包所包含的方法具有各种形式的关系归纳偏置,但是没有默认的深度学习组件可以在任意关系结构上运行。我们需要模型具有显式的实体表示和关系表示,并需要学习算法,该算法用于找到计算实体和关系交互的规则、以及将规则置于数据中的方式。
重要的是,世界上的实体(如对象、
agent)没有自然顺序。相反,可以通过关系的性质来定义顺序。如:可以根据对象之间的大小、质量、年龄、毒性、价格之间的关系来对它们进行排序。顺序不变性invariance to ordering(除了处理关系时)是一种理想的属性,这种不变性应该由用于关系推理的深度学习组件来反映。集合
sets是描述包含一组无序实体的系统的自然表达形式。具体而言,集合的关系归纳偏置并不是来自于something的存在,而是来自于something的缺失。为了说明,考虑由
但是,如果要使用
MLP来预测该任务,即使已经知道了特定顺序输入MLP可能会认为每种顺序从根本上看是不同的,因此需要指数级的输入/输出训练样本来学习近似函数。处理类似组合爆炸的自然方法是允许预测依赖于输入的对称函数。这可能意味着首先计算
per-object参数共享的特征Deep Sets以及相关模型的本质。我们在后文进一步讨论。当然,在很多问题中排列不变性
permutation invariance并不是底层结构的唯一重要形式。例如,一个集合中的每个对象都可能受到集合中其它对象的pairwise interaction的影响。在我们的行星case中,考虑在时间间隔取而代之的是,我们可以将每个对象的状态计算为
我们在各处都使用相同的
global permutation invariance。但是,它也支持不同的关系结构,因为上述太阳系的例子说明了两种关系结构
relation structure:一种完全没有关系,一种包含所有的pairwise关系。很多现实世界的系统(如下图所示)的关系结构在这两种极端case之间:某些实体pair对之间存在关系、另一些实体pair对之间缺乏关系。在我们的太阳系例子中,如果该系统改为由行星及其卫星组成,则可能会试图通过忽略不同行星的卫星之间的相互作用来近似。实际上,这意味着仅计算某些对象之间的交互,即:
其中
graph,因为第注意:节点
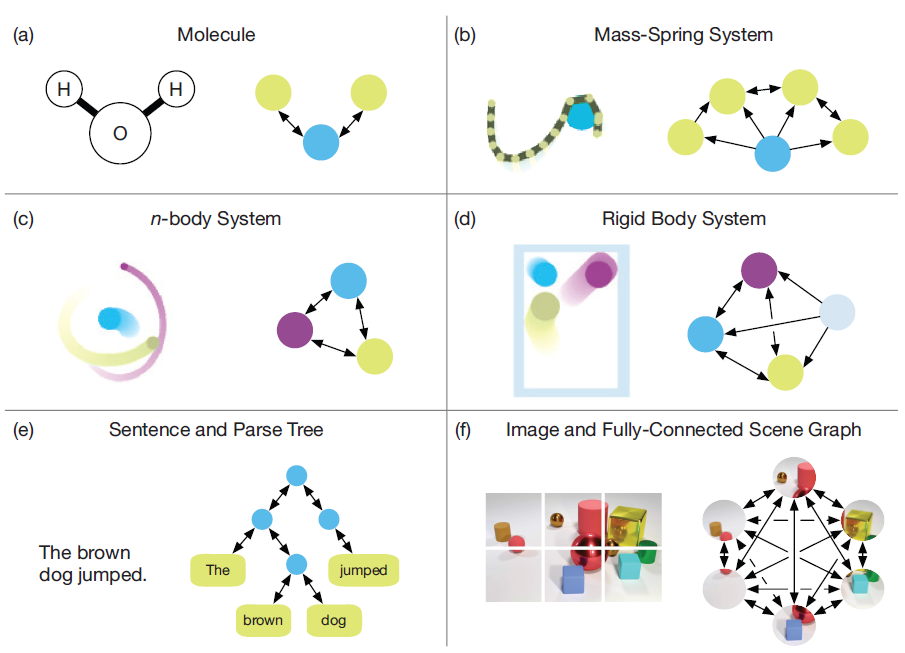
下图为现实世界的不同系统,以及对应的
graph的表达:(a):一个分子图,其中每个原子表示为一个节点,边对应于化学键。(b):一个质点弹簧系统,其中绳索由一个质点序列定义,这些质点在图中表示为节点。(c):一个n body系统,其中每个body为节点,节点之间全连接。(d):一个刚体系统,其中球和墙壁都为节点,底层的graph定义了球之间、球和墙壁之间的相互作用。(e):一个句子,其中单词对应于解析树上的叶结点,其它节点和边可以由解析器提供。或者也可以使用一个全连接的图。(f):一张图片,可以将其分解为图像块patch,每个块代表一个节点,并且节点之间全连接。
通常,图
graph是支持任意pairwise关系结构的表示形式,并且图上的计算提供了超越卷积层、递归层的强大的关系归纳偏置。
26.2 Graph Network
图神经网络已经在监督学习、半监督学习、无监督学习、强化学习领域被应用。
- 图神经网络被认为在具有丰富的关系结构的任务上很有效,例如视觉场景理解
visual scene understanding任务、few-shot learning任务等。 - 图神经网络也被用于物理系统
physical system和多智体系统multi-agent system,从而推理知识图谱、预测分子化学性质、预测道路交通流量、分类和分割图像/视频/3D网格/点云、分类图像中的区域、执行半监督文本分类及机器翻译。 - 图神经网络已经在
model-free和model-based连续控制中都被使用,用于model-free的强化学习,以及更经典的规划问题。 - 图神经网络还探索了很多涉及离散实体和结构推理的传统计算机科学问题,例如组合优化、布尔满足性
satisfiability、程序表示和验证、元胞自动机及图灵机建模,以及图模型上的inference。最近的工作还关注于图的生成模型、graph embedding的无监督学习。
- 图神经网络被认为在具有丰富的关系结构的任务上很有效,例如视觉场景理解
这里介绍我们的图网络框架
Graph Networks:GN,该框架定义了一族函数用于图结构表示graph-structured representations的关系推理relational reasoning。我们的GN框架概括并扩展了各种图神经网络、MPNN、以及NLNN方法,并支持从简单的构建块构建复杂的体系架构。注意,我们避免在
Graph Network中使用术语neural来反映GN可以使用除神经网络以外的函数来实现,尽管这里我们的重点是神经网络的实现。GN框架中的主要计算单元是GN块GN block。GN块是一个graph-to-graph的模块,它将图作为输入,对结构进行计算,然后将图作为输出返回。图的节点表示实体,图的边表示关系,图的全局属性表示system-level属性。GN框架的block组织强调可定制性customizability,以及综合了新的架构,这个新架构能够表达预期的关系归纳偏置。GN框架的主要设计原则是:灵活的表示形式flexible representations、可配置的块内结构configurable within-block structure、可组合的多块体系架构composable multi-block architectures。
我们引入一个例子来更具体的说明
GN。可以在任意重力场中预测一组橡胶球的运动,这些橡胶球不会彼此弹跳,而是每个橡胶球都有一个或多个弹簧,这些弹簧将它们和其它橡胶球相连。我们将在下文中参考这个例子,从而启发motivate图的表示以及图上进行的计算。
26.2.1 图的定义
这里我们使用图来表示带全局属性的、有向的、带属性的多图
multi-graph。- 带全局属性:每个图具有一个
graph-level属性 - 有向的:每条边
sender节点receiver节点 - 带属性的:每个节点
- 属性:节点、边、图的属性可以编码为向量、集合、甚至另一个图。
- 多图
multi-graph:节点之间可能存在多条边,包括自连接self-edge。
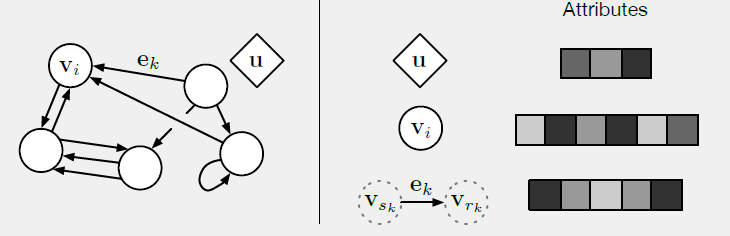
- 带全局属性:每个图具有一个
在我们的
GN框架内,图被定义为三元组receiver节点,sender节点。例如:
26.2.2 GN block
一个
GN块包含三个更新函数其中:
其物理意义为:
sender节点属性receiver节点属性receiver为当前节点的所有边的属性(更新后的边属性)聚合后的- 每个
permutation invariant,并且应该采用可变数量的自变量。一些典型的例子包括:逐元素求和、均值池化、最大值池化等。
GN块的计算步骤:通过执行
- 更新后,边的集合为
- 更新后,节点
receiver。
- 更新后,边的集合为
执行
通过执行
更新后,所有节点的属性集合为
通过执行
通过执行
通过执行
尽管这里我们给出了计算步骤的顺序,但是并不是严格地根据这个顺序来执行。例如,可以先更新全局属性、再更新节点属性、最后更新边属性。
GN block更新函数GraphNETWORK():输入:图
输出:更新后的图
计算步骤:
迭代更新边的属性:
迭代更新节点的属性:
- 令
receiver为当前节点 - 聚合
- 更新节点属性
- 令
令
令
根据全局属性、聚合后的节点属性、聚合后的边属性来更新全局属性
返回更新后的图
给定一个图
GN块的输入时,计算过程从边、节点、global-level。下图给出了这些计算中,每一个计算都涉及哪些图元素。蓝色表示待更新的元素,黑色表示更新中涉及的其它元素(注意,蓝色元素更新之前的值也用于它的本次更新)。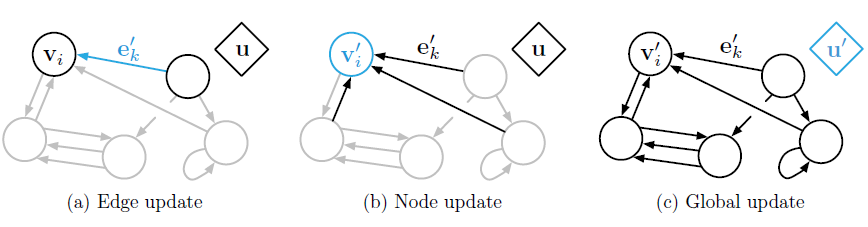
下图给出了具有更新函数、聚合函数的完整
GN块。它根据输入的节点属性、边属性、全局属性来预测输出的节点属性、边属性、全局属性。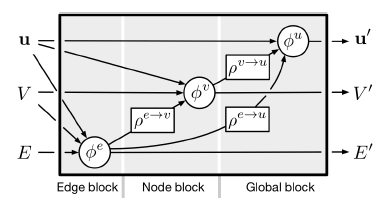
26.2.3 关系归纳偏置
当用于
learning process的组成部分时,我们的GN框架会强制添加几个很强的关系归纳偏置:首先,图可以表达实体之间的任意关系。这意味着
GN的输入决定了representation是如何交互interact和隔离isolated的,而不是由固定fixed的体系架构来决定的。即实体的交互和隔离是由数据决定,而不是由模型决定。
例如:
- 如果两个实体对应的节点之间存在边,则认为这两个实体之间有关联,即有交互。
- 如果两个实体对应的节点之间不存在边,则认为这两个实体之间没有关联,即隔离的。
其次,图将实体及其关系表示为集合,这是排列不变的
permutation invariant。这意味着GN对于这些元素的顺序是不敏感的,这通常是我们所需要的。最后,
GN的per-edge函数、per-node函数分别在所有边、所有节点之间重用。这意味着GN自动支持某种形式的组合泛化:由于图由边、节点、以及全局属性组成,因此单个GN可以在不同大小(以边和节点数量刻画)、不同形状(不同的连通性)的图上进行操作。
26.3 GN 设计原则
根据前述列出的设计原则,
GN框架可用于实现各种各样的体系架构。通常,GN框架和特定的属性表示attribute representation和函数形式functional form无关。但是这里我们重点关注深度学习架构,该架构允许GN充当可学习的graph-to-graph的函数逼近器function approximator。这里再回顾一下
GN设计原则:灵活的表示flexible representations、可配置的块内结构con gurable within-block structure、可组合的多块体系架构composable multi-block architectures。这三个设计原则再我们的
GN框架中结合在一起,非常灵活,适用于从感知、语言、到符号推理的广泛领域。并且,如前所述,GN具有的强大的关系归纳偏置支持组合泛化,因此使得GN在实际和理论上都成为强大的工具。
26.3.1 Flexible Representations
灵活的表示有两层含义:
- 属性形式:
GN块的全局属性、节点属性、边属性可以为任意表示形式arbitrary representational formats。 - 图结构形式:输入数据可以包含关系结构,或者不包含关系结构,即输入数据的图结构形式可以任意。
- 属性形式:
属性形式:
GN块的全局属性、节点属性、边属性可以使用任意表示形式。在深度学习实现中,通常使用实值向量或张量。但是,也可以使用其它数据结构,如序列sequence、集合set、甚至是图graph。通常我们需要决定:对某个问题采用何种表示形式来描述属性。例如:
- 当输入数据是图像时,节点属性可以为图像
patches的张量。 - 当输入数据为文档时,节点属性可以为句子对应的单词序列。
- 当输入数据是图像时,节点属性可以为图像
对于更广泛的体系架构中的每个
GN块,每个边/节点的输出通常对应于一个张量/向量,而全局输出对应于单个张量/向量。这使得GN块的输出可以传递到其它深度学习构建块building block中,如MLP,CNN,RNN。GN块的输出也可以根据任务需求进行定制化。具体而言:edge-focused GN可以仅仅将边作为输出。例如,做出有关实体之间相互作用的决策。node-focused GN可以仅仅将节点作为输出。例如,用于推理物理系统。graph-focused GN可以仅仅将全局属性作为输出。例如,预测物理系统的势能、分子性质、关于某个视觉场景问题的答案。
节点属性、边属性、全局属性的输出也可以根据任务混合使用。
图结构形式:在定义如何将输入数据表示为图结构时,有两种情形:
首先,输入数据明确指定了关系结构。例如:知识图谱、社交网络、化学分子图、交通网络、以及具有已知交互作用的物理系统。
其次,需要从输入数据中推断或假设关系结构,即关系结构没有明确指定。例如视觉场景、文本文档等。
这里可以将数据表示为一组没有关系的实体,甚至仅表示为向量或张量(如:图像)。
如果未明确指定实体,则可以通过将诸如句子中的每个单词、或者
CNN输出feature map中的feature vector视为节点来指定实体。或者,也可以使用单独的学习机制从非结构化信号中推断实体,如通过解析树算法从文本中得到解析树。
如果关系不可用,则最简单的方法是在实体之间添加所有可能的有向边。如在图像的
patches之间两两添加有向边。但是,这对于拥有大量实体的图而言是不可行的,因为边的数量会随着节点数量的增加而平方规模的增加。因此,研发更复杂的方法来从非结构化数据中推断稀疏的图结构是未来的重要方向。
26.3.2 Configurable Within-block Structure
GN块中的结构和函数可以通过不同的方式进行配置,从而可以灵活地确定哪些信息可以用作函数的输入,以及如何更新边属性、节点属性、全局属性。具体而言,GN块中的每个argument signature决定了它需要哪些信息作为输入。通过选择不同的函数
GN框架可以表达其它各种架构,如下图所示。接下来讨论如何使用不同的方式配置GN的块内结构。下图中,每个
incoming箭头表示是否将(a):full GN(即完整的、原始的GN块)根据传入的节点属性、边属性、全局属性来输出节点属性、边属性、全局属性。(b):独立的循环块使用input和hidden state来进行更新,其中RNN。(c):MPNN根据传入的节点属性、边属性来输出节点属性、边属性、全局属性。注意,全局预测中不包含聚合的边,输入中不包含全局属性。(d):NLNN仅输出节点属性。(e):Relation Network仅使用预测的边属性来输出全局属性。(f):Deep Set没有采用边更新从而输出全局属性。
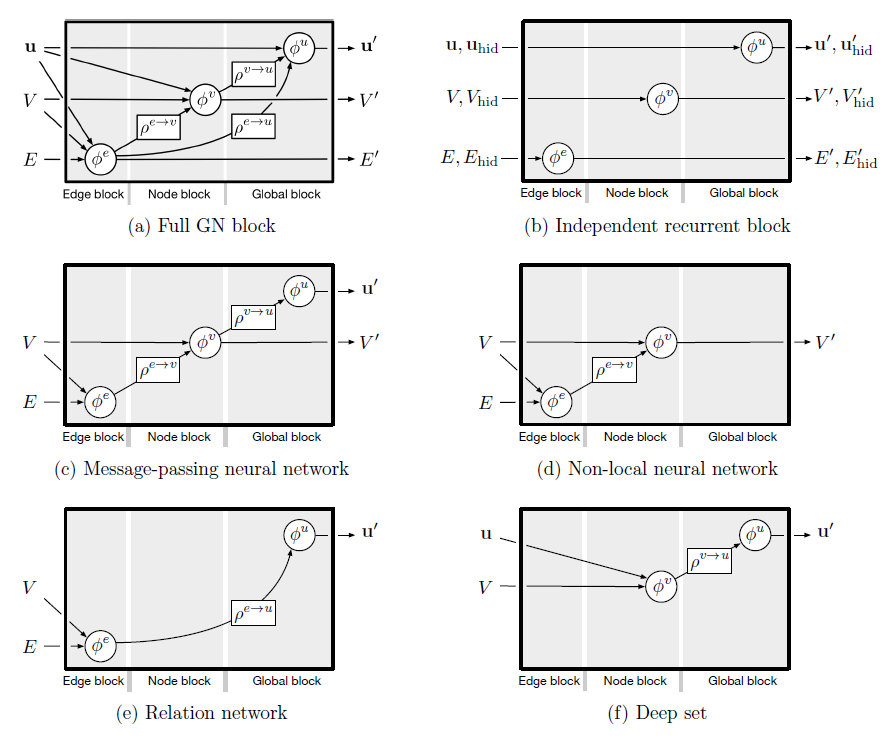
Full GN block:《Relational inductive bias for physical construction in humans and machines》和《Graph networks as learnable physics engines for inference and control》使用完整的GN块,如上图的(a)所示。- 他们使用神经网络来实现
- 他们的
更新方程为:
其中:
- 对于向量属性,通常采用
MLP作为feature map),通常采用CNN作为
- 他们使用神经网络来实现
RNN,这需要额外的hidden state作为输入和输出。上图(b)展示了一个非常简单的GN块,其中RNN作为block可用于对某些dynamic graph state进行递归平滑recurrent smoothing。当然,
RNN作为full GN block中使用。Message-passing neural network: MPNN概括了很多之前的体系架构,并且可以很自然地转换为GN的格式:- 消息函数
GN中的 GN的- 更新函数
GN中的 readout函数GN中的GN的GN中的GN的
上图
(c)展示了如何根据GN块来构建MPNN。- 消息函数
Non-local Neural Networks:NLNN统一了各种intra/self/vertex/graph attention方法,它也可以转换为GN的格式。attention指的是节点的更新方式:每个节点更新均基于其邻域节点属性(或者它的某些函数)的加权和,其中一个节点和它某个邻居之间的权重由属性之间的scale pairwise函数(然后整个邻域归一化)给出。已发表的
NLNN公式并未显式包含边,而是计算所有节点之间的pairwise注意力权重。但是,各种NLNN-compliant模型,例如节点注意力交互网络vertex attention interaction network、图注意力网络graph attention network都可以通过有效地将没有边的节点之间的权重设为零来显式处理边。在
NLNN中,pairwise-interaction函数,该函数返回:- 未归一化的
attention系数,记作 - 一个
non-pairwise的向量值,记作
在
receiver的所有边上归一化,然后在
NLNN论文中,set(而不是图graph)、并且这个图是根据集合中所有实体之间添加所有可能的边来构建的。Transformer体系架构中的single-headed self-attention,即SA, 实现为公式为:其中
《Attention is all you need》的multi-head self-attention机制增加了一个有趣的特性:Gated Graph Sequence Neural Networks。具体而言,
multi-head self-attention计算Vertex Attention Interaction Networks和SA很相似,但是它将欧几里得距离用于attention相似性度量,并在attention输入的embedding中共享参数,且在节点更新函数中使用节点的输入特征:Graph Attention Networks和multi-head self-attention相似,但是它使用神经网络作为attention相似性度量,并在attention输入的embedding中共享参数:《Self-attention with relative position representations》提出相对位置编码relative position encodings来扩展multi-head self-attention。relative是指对序列中节点之间的空间距离进行编码、或度量空间中其它信号进行编码。这可以在GN中表示为边的属性multi-head self-attention中的
下图展示了如何在
GN框架下通过NLNN。 通常NLNN假设图像(或句子中的单词)对应于全连接图中的节点,并假设注意力机制在聚合步骤中定义节点上的加权和。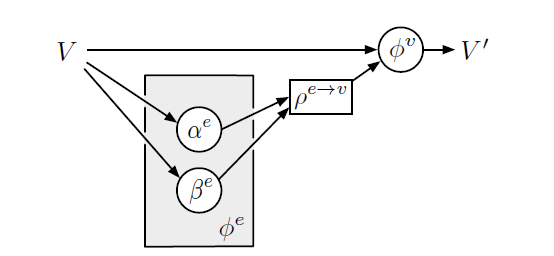
- 未归一化的
完整的
GN block公式可以预测完整的图同样的思路可以适用于其它
GN变体,这些变体不使用完整的mappingreductionInteraction Networks和Neural Physics Engine使用full GN,但是没有使用全局属性来更新边属性。该工作还包括对上述公式的扩展:输出全局的、而不是
per-node的预测:这里没有使用全局属性来更新边属性,也没有用边属性来更新全局属性。
Relation Networks完全绕开了节点更新,并直接从池化的边信息中预测全局属性输出:Deep Sets完全绕开了边更新,并直接根据池化的节点信息中预测全局属性输出:PointNet使用类似的更新规则,但是对于Gated Graph Sequence Neural Networks: GGS-NN使用稍微泛化的公式,其中每条边关联一个类别这里
GRU,上述更新递归进行,然后接一个全局解码器,该解码器计算所有节点的最终
embedding的加权和。CommNet的更新公式为:structure2vec也可以适配我们的算法,只需要进行少量的修改:其中
边的属性现在在
receiver和sender之间具有message的含义。注意,对于边和节点更新,现在只有一组参数需要学习。
注意:对于
CommNet、structure2vec、Graph Sequence Neural Networks使用一种非对称的pairwise interaction,而是忽略receiver node而仅考虑sender节点,并且某种程度上是在边属性上进行。这种做法可以通过具有以下签名signature的.
26.3.3 Composable Multi-block Architectures
GN的主要设计原理是通过组合GN block来构建复杂的体系架构。我们将GN block定义为包含边属性、节点属性、全局属性的图作为输入,并返回新的边属性、节点属性、全局属性的图作为输出。如果某些元素不需要更新,则只需要直接对应的输入传递到输出即可。这种
graph-to-graph的input/output接口可以确保GN block的输出可以传递给另一个GN block作为输入。这两个GN block内部可以使用完全不同的配置,这类似于深度学习toolkit的tensor-to-tensor接口。这种接口最基本的形式是:给定两个
GN blockGN1和GN2,可以通过将GN1的输出作为GN2的输入,从而将它们组合在一起:可以组合任意数量的
GN block,如下图所示。图中M个重复的内部处理子步骤repeated internal processing sub-steps,可能包含共享或者不共享的GN block。- 这些
block可以不共享(采用不同的函数或参数,类似于CNN的不同的layer),即 - 这些
block也可以共享(采用相同的函数或参数,类似于展开的RNN),即
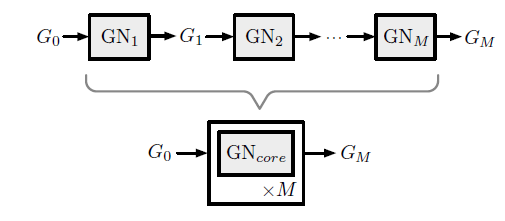
- 这些
配置共享(采用相同的函数或参数)类似于消息传递,其中反复应用相同的局部更新过程从而在整个结构中传播消息,如下图所示。如果不考虑全局属性
step之后,可访问的信息由最多m-hop的节点和边的集合确定。这可以解释为将复杂的计算分解为较小的基础步
elementary step。这些step也可以用于捕获时间上的顺序。在我们的橡胶球示例中,如果每个
step预测持续时间为step的总的模拟时间为下图中,每一行突出显式了从特定节点开始、然后扩展到整个图的信息。
- 第一行中,初始节点在右上方;第二行中,初始节点在右下方。
- 阴影节点表示距初始节点经过
step能够传播的范围。 - 粗边表示消息传播的边。
注意:在完整的消息传递过程中,这种消息传播同时发生在图中所有节点和所有边上,而不仅仅是这里的两个初始节点。
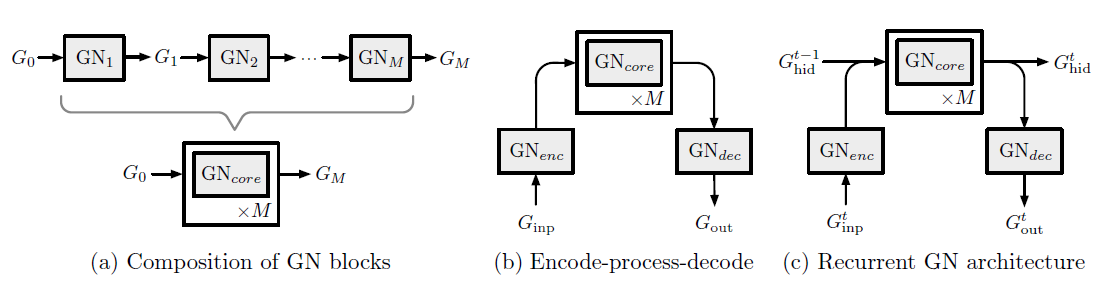
可以通过
GN block构建两种常见的体系架构:一种体系架构我们称之为
encode-process-decode配置,如下图(b)所示。其中:- 一个输入图
- 一个共享的
core block - 通过解码器
例如在我们的橡胶球例子种,编码器可能会计算球之间的初始力和相互作用势能,
core可能会应用基本动力学更新,解码器可能从更新后的图状态读取最终位置。- 一个输入图
类似
encode-process-decode设计,另一种体系架构我们称之为recurrent GN-based配置,如下图(c)所示。其中在step每个
step维护一个hidden graph一个输入图
其中
(c)的箭头合并),然后传递给一个共享的
core blockunrolled(一共展开GRU或者LSTM。(c)的箭头拆分),其中一路输出由通过解码器
这种设计以两种方式重用
GN block:step- 在每个
step内,sub-step内共享。
这种类型的体系架构常用于预测
graph序列,例如预测一段时间内动力系统的轨迹。
其它一些技术对于设计
GN体系架构可能也有用。例如:Graph Skip Connection可以将GN block的输入Recurrent GN架构中合并输入图和hidden图的信息可以使用LSTM或GRU风格的gating scheme,而不是简单地拼接。或者在其它
GN block之前和/或之间组合不同的递归GN块,从而提高多个传播step中representation的稳定性。
26.3.4 实现
类似于可天然并行的
CNN(在GPU上),GN具有天然并行结构:- 由于
- 通过将多个图视为较大图的非连通分量
disjoint component,可以自然地将几张图打包一起。因此可以将几个独立图上进行的计算打包在一起。
- 由于
重用
GN的样本效率。类似于卷积核,GN中用于优化我们已经发布了用于构建
GN的开源软件库,在github.com/deepmind/graph_nets。我们也给出了一些demo包括:在最短路径搜索任务、排序任务、物理系统预测等任务上,如何创建、操作、训练GN来推理图结构数据。每个demo使用相同的GN体系架构,这凸显了该方法的灵活性。
26.4 讨论
GN的结构天然支持组合泛化,因为它们并不严格地在系统级别执行计算,而且还跨实体、跨关系执行共享计算。这样可以推理未曾见过的系统,因为它们都是由熟悉的组件构成的,从而体现了infinite use of finite means的方式。GN和MPNN的消息传递学习方式的局限性之一是无法解决某些类型的问题,如区分某些非同构图non-isomorphic graph。更一般而言,尽管图是表示结构信息的有效方式,但是它们也有局限性。诸如递归、控制流、条件迭代之类的概念并不容易用图来表示。就这些概念而言,
program和更多的computer-like处理过程可以提供更好的表示性。关于使用
Graph Network还存在很多悬而未决的问题:一个紧迫的问题是:运行
GN的图如何构建?深度学习的标志之一是它能够对原始的感官数据
sensory data(如图像、文本)执行复杂的计算,但是尚不清楚如何将感官数据转换为更结构化的表示形式(如graph)。一种方法(我们已经讨论过)假设空间或语言实体之间是全连接的图结构,例如在
self-attention的文献采用这种方法。但是,这样的representation可能不完全对应于真实的实体,如卷积feature map并不直接对应于真实场景中的对象。此外,很多底层图结构比全连接的图稀疏的多,如何引入这种稀疏性也是一个悬而未决的问题。
有一些研究正在探索这些问题,但是目前为止并没有一种方法能够可靠地从感官数据中提取离散实体。开发这种方法是一个令人兴奋的挑战,一旦解决就可以推开更强大、更灵活的推理算法的大门。
一个相关的问题是如何在计算过程中自适应地修改图结构。例如,如果一个对象分解为多个片段,则代表该对象的节点也应该拆分为多个节点。同样,仅保留交互对象之间的边可能很有用,因此需要根据上下文添加、删除边的能力。
人类的认知提出了一个强有力的假设,即世界是由对象和关系组成的。并且,由于
GN做出了类似的假设,因此它的行为往往更具有解释性。GN所处理的实体和关系通常对应于人类理解的实物(如物理对象),因此支持更可解释的分析和可视化。未来一个有趣的方向是进一步探索网络行为的可解释性。
尽管我们的重点是图,但是本文的重点不是图本身,而更多是将强大的深度学习方法和结构化表示相结合的方法。
二十七、GIN[2019]
对图结构数据的学习需要有效地对图结构进行表示。最近,对图表示学习
graph representation learning的图神经网络Graph Neural Network: GNN引起了人们的广泛兴趣。GNN遵循递归邻域聚合方案,其中每个节点聚合其邻居的representation向量从而计算节点的新的representation。已经有很多
GNN的变体,它们采用不同的邻域聚合方法、graph-level池化方法。从实验上看,这些GNN变体在很多任务(如节点分类、链接预测、图分类)中都达到了state-of-the-art性能。但是,新的GNN的设计主要基于经验直觉empirical intuition、启发式heuristics、以及实验性experimental的反复试验。人们对
GNN的性质和局限性的理论了解很少,对GNN的表达容量representational capacity的理论分析也很有限。论文《How powerful are graph neural networks?》提出了一个用于分析GNN表达能力representational power的理论框架。作者正式刻画了不同GNN变体在学习表达represent和区分distinguish不同图结构上的表达能力expressive。论文的灵感主要来自于
GNN和Weisfeiler-Lehman:WL图同构检验graph isomorphism test之间的紧密联系。WL-test是一种强大的、用于区分同构图的检验。类似于GNN,WL-test通过聚合其网络邻域的特征向量来迭代更新给定节点的特征向量。WL-test如此强大的原因在于它的单射聚合更新injective aggregation update,这可以将不同的节点邻域映射到不同的特征向量。单射函数:假设
论文的主要洞察是:如果
GNN的聚合方案具有很高的表达能力expressive并且建模单射函数injective function,那么GNN可以具有与WL-test一样强大的判别力discriminative power。为了从数学上形式化该洞察,论文的框架首先将给定节点的邻居的特征向量集合表示为
multiset,即可能包含重复元素的集合。可以将GNN中的邻域聚合视为multiset上的聚合函数aggregation function over the multiset。因此,为了具有强大的表征能力 ,GNN必须能够将不同的multiset聚合为不同的representation。论文严格研究了multiset函数的几种变体,并从理论上刻画了它们的判别能力,即不同的聚合函数如何区分不同的multiset。multiset函数的判别力越强,则底层GNN的表征能力就越强。然后论文设计出一种简单的架构Graph Isomorphism Network:GIN,该架构被证明是GNN中最具表达能力的,并且和WL-test一样强大。论文在图分类数据集上进行实验来验证该理论,其中
GNN的表达能力对于捕获图结构至关重要。具体而言,作者比较了使用各种聚合函数的GNN的性能。实验结果证明了最强大的GNN(即作者提出的GIN)在实验中也具有很高的表征能力,因为它几乎完美拟合训练数据。而能力更弱的GNN变体通常对于训练数据严重欠拟合underfit。此外,GIN在测试集上的准确率也超过了其它GNN变体,并在图分类benchmark上达到了state-of-the-art性能。论文的主要贡献:
- 证明
GNN在区分图结构方面最多和WL-test一样强大。 - 给出邻域聚合函数和图
readout函数在什么条件下所得的GNN和WL-test一样强大。 - 识别那些无法被主流的
GNN变体(如GCN,GraphSAGE)判别的图结构,然后刻画这些GNN-based模型能够捕获的图结构。 - 设计了一个简单的神经网络架构,即
Graph Isomorphism Network: GIN,并证明了其判别能力/表征能力等于WL-test。
- 证明
相关工作:尽管
GNN在经验上取得成功,但是在数学上研究GNN特性的工作很少。《Computational capabilities of graph neural networks》表明:早期的GNN模型在概率上逼近测度函数。《Deriving neural architectures fromsequence and graph kernels》表明:该论文提出的架构位于graph kernel的PKHS中,但没有明确研究该架构可以区分哪些图。
这些工作中的每一个都专注于特定的体系结构,并且不容易推广到多种体系结构。相反,我们的研究为分析和刻画一系列
GNN模型的表征能力提供了一个通用框架。另外,近期提出了一些基于
GNN的体系结构大多数没有理论推导。与此相比,我们的GIN是有理论推导的,而且简单、强大。
27.1 GNN 模型
我们首先总结一些常见的
GNN模型。令图
- 每个节点
通常我们关心图上的两类任务:
- 节点分类任务:每个节点
representation向量 - 图分类任务:给定一组图
representation向量
GNN利用图结构和节点特征representation向量representation向量现代
GNN使用邻域聚合策略,在该策略中我们通过聚合邻域的representation来迭代更新节点的representation。在经过representation将捕获其k-hop邻域内的结构信息。以数学公式来讲,
GNN的第其中:
representation。另外
在
GraphSAGE的最大池化变体中,聚合函数为:其中:
relu非线性激活函数。
而
GraphSAGE中的拼接函数为简单的向量拼接:其中
[,]表示向量拼接,在
Graph Convolutional Networks: GCN中,聚合函数采用逐元素的均值池化。此时聚合函数、拼接函数整合在一起:其中
MEAN(.)为逐元素的均值池化,
对于节点分类任务,节点
representationrepresentation。对于图分类任务,
READOUT函数聚合所有节点最后一层的representation从而得到整个图的representationREADOUT函数可以是简单的排列不变函数permutation invariant function,例如求和函数;也可以是更复杂的graph-level池化函数。
27.2 WL-test
图同构问题
graph isomorphism problem是判断两个图在拓扑结构上是否相同。这是一个具有挑战性的问题,尚不知道多项式时间polynomial-time的算法。除了某些极端情况之外,图同构的
Weisfeiler-Lehman(WL) test是一种有效且计算效率高的算法,可用于各种类型的图。它的一维形式是naïve vertex refinement,它类似于GNN中的邻域聚合。在
WL-test过程中,每个节点都分配一个label。注意:这里的label和分类任务中的label不同,这里的label更多的表示“属性”, 而不是“监督信息”。WL-test对节点邻域进行反复迭代,最终根据两个图之间的节点label是否完全相同,从而判断两个图是否同构的。WL-test迭代过程如下:- 聚合节点及其邻域的
label。 - 将聚合后的
label经过哈希函数得到不同的、新的label,即relabel。
如下图所示:
首先将图中每个节点初始化为
label = 1。然后经过三轮迭代,最终:
- 图
1具有1个label = 8、2个label = 7、2个label = 9。 - 图
2具有1个label = 8、2个label = 7、2个label = 9。
因此我们不排除图
1和图2同构的可能性。- 图
下图的哈希函数为:
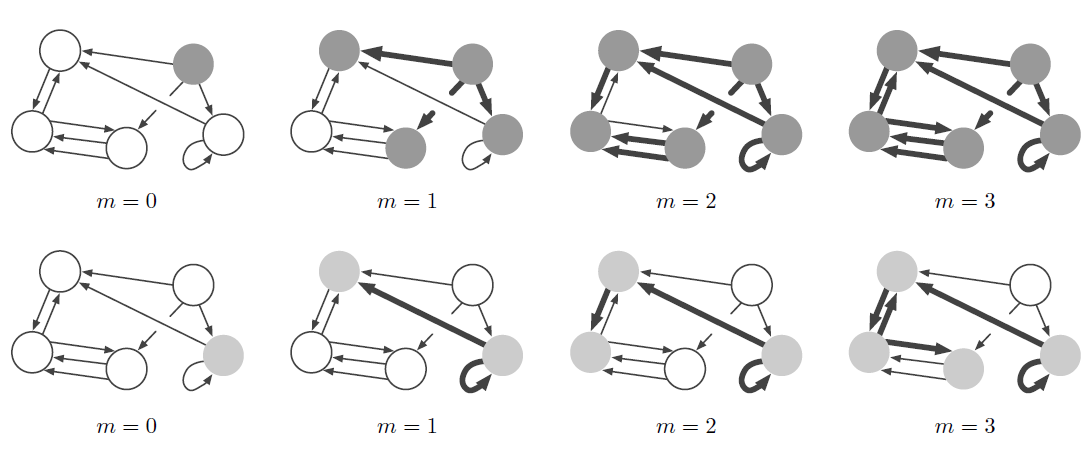
{1,1} --> 2{1,1,1} --> 3{2,3} --> 4{3,3} --> 5{2,2,3} --> 6{4,6} --> 7{6,6} --> 8{4,5,6} --> 9注意:这里的
label集合需要根据label大小排序,并且每次哈希之后都需要分配一个新的label。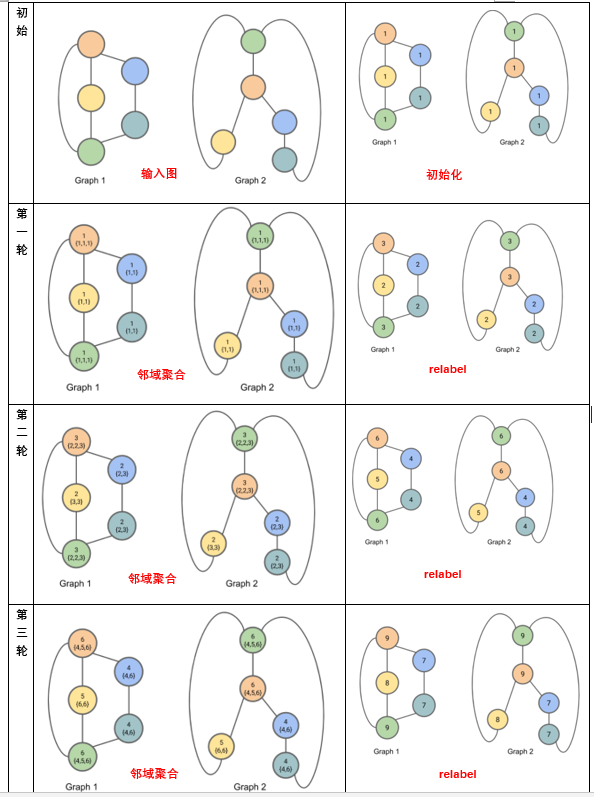
- 聚合节点及其邻域的
《Weisfeiler-lehman graph kernels》根据WL-test提出了WL subtree kernel来衡量两个图的相似性。核函数利用WL tet的不同迭代中使用的节点label数作为图的特征向量。直观地讲,
WL test第label代表了以该节点为根的、高度为WL subtree kernel考虑的图特征本质上是不同根子树的计数。如下图所示为一棵高度
WL subtree。 这里label = 8的节点代表一棵高度为1的subtree模式,其中subtree根节点的label为2、包含label=3和label=5的邻居节点。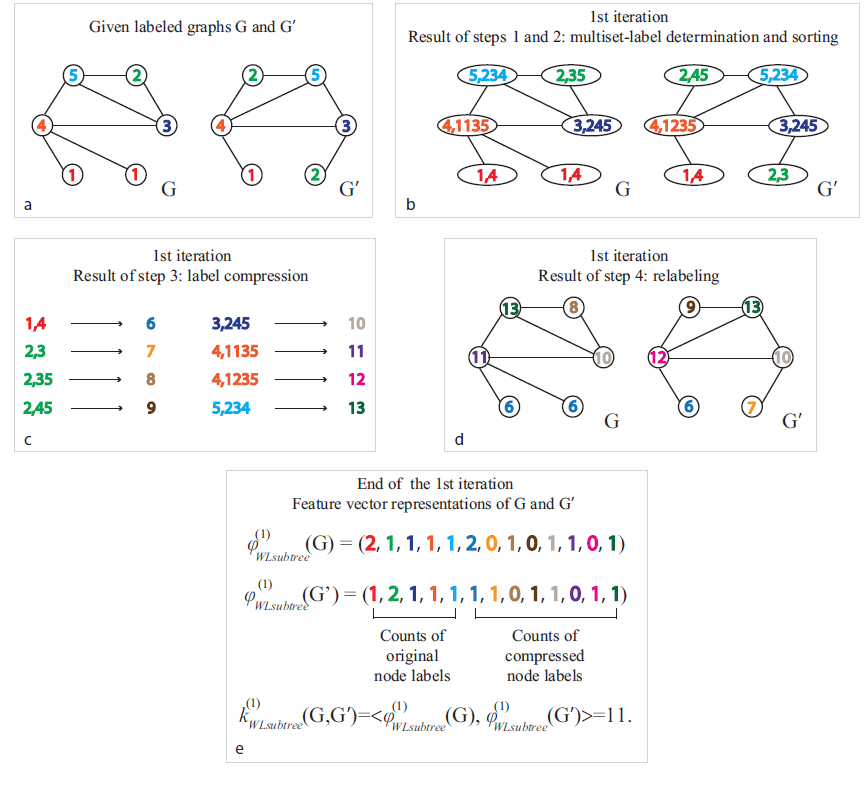
27.3 模型
我们首先概述我们的框架,下图说明了我们的思想:
GNN递归更新每个节点的representation向量,从而捕获网络结构和邻域节点的representation,即它的rooted subtree结构。在整篇论文中,我们假设:
- 节点输入特征来自于可数的范围
countable universe。 - 模型的任何
layer的representation也是来自可数的范围。
通常浮点数是不可数的,而整数是可数的。我们可以将浮点数离散化为整数,从而使得数值可数。
为便于说明,我们为每个
representation vector(输入特征向量是第0层的representation vector)分配唯一的label,label范围在label然后节点的邻域节点
representation vector就构成一个multiset:由于不同的节点可以具有相同的representation向量,因此同一个label可以在multiset中出现多次。下图中:
- 左图:一个图结构的数据。
- 中图:
rooted subtree结构,用于在WL test中区分不同的图。 - 右图:如果
GNN聚合函数捕获节点邻域的full multiset,则GNN能够以递归的方式捕获rooted subtree结构,从而和WL test一样强大。
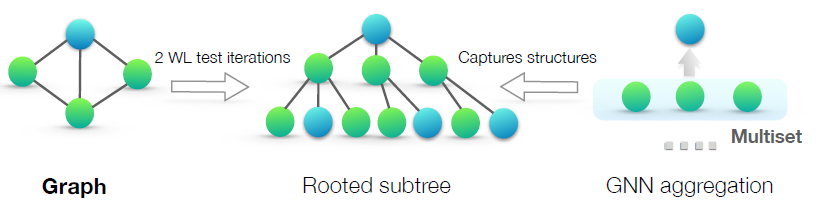
- 节点输入特征来自于可数的范围
multiset定义:multiset是set概念的推广,它允许包含相同的多个元素。正式地讲,,multiset是一个2-tupleset,它包含唯一distinct的元素。multiplicity。
为研究
GNN的表征能力,我们分析GNN何时将两个节点映射到embedding空间中的相同位置。直观地看,能力强大的
GNN仅在两个节点具有相同subtree结构、且subtree上相应节点具有相同特征的情况下才将两个节点映射到相同的位置。由于
subtree结构是通过节点邻域递归定义的,因此我们可以将分析简化为:GNN是否将两个邻域(即两个multiset)映射到相同的embedding或representation。能力强大的
GNN绝对不会将两个不同的邻域(即representation向量的multiset)映射到相同的representation。这意味着聚合函数必须是单射函数。因此我们将GNN的聚合函数抽象为神经网络可以表示的、multiset上的函数,并分析它们能否表示multiset上的单射函数。接下来我们使用这种思路来设计能力最强的
GIN。最后我们研究了主流的GNN变体,发现它们的聚合函数本质上不是单射的因此能力较弱,但是它们能够捕获图的其它有趣的特性。
27.3.1 定理
我们首先刻画
GNN-based通用模型的最大表征能力。理想情况下,能力最强大的
GNN可以通过将不同的图结构映射到embedding空间中不同的representation来区分它们。这种将任意两个不同的图映射到不同embedding的能力意味着解决具有挑战性的图同构问题。即,我们希望将同构图映射到相同的representation,将非同构图映射到不同的representation。在我们的分析中,我们通过一个稍弱的准则来刻画
GNN的表征能力:一种强大powerful的、启发式heuristic的、称作Weisfeiler-Lehman(WL)的图同构测试graph isomorphism test。WL-test通常工作良好,但是也有一些例外,如正规图regular graph。正规图是图中每个节点的degree都相同。如:立方体包含四个节点,每个节点的degree为3,记作4k3。
引理
2:令non-isomorphic graph。如果一个图神经网络embedding,则WL-test也会判定证明:这里采用反证法。
假设经过
WL-test无法区分WL-test中从迭代0到迭代label collection都相同。具体而言,
label multisetlabel集合WL-test第label。否则WL-test在第label collection从而区分出现在我们证明:如果
当
WL-test和GNN都使用节点的特征向量来初始化。如前所述,对于任意label假设对于第
考虑第
根据第
由于两个图
AGGREGATE函数和COMBINE函数。因此相同的输入(如邻域特征)产生相同的输出。因此有:因此第
因此如果
WL-test节点label满足representation集合graph-level readout函数对于节点representation集合是排列不变的permutation invariant,因此有根据引理
2,任何基于聚合的GNN在区分不同图结构方面最多和WL-test一样强大。一个自然的问题是:是否存在和
WL-test一样强大的GNN?在定理3中,我们将证明:如果邻域聚合函数和graph-level readout函数是单射的,则得到的GNN和WL-test一样强大。定理
3:令GNN。在具有足够数量GNN层的条件下,如果满足以下条件,则WL-test判定为非同构的两个图embedding:representation:其中
multiset上。graph-level readout函数是单射函数。其中readout函数作用在节点embedding multiset
证明:令
WL-test在我们假设
representation为:其中
假设
WL-test应用一个预定义的单射函数label:其中
接下来我们通过数学归纳法证明:对于任意迭代轮次
当
WL-test和GNN都使用节点的特征向量来初始化。如前所述,对于任意label假设对于
现在考虑第
由于单射函数的复合函数也是单射函数,因此存在某个单射函数
则有:
因此复合函数
因此对于任意迭代轮次
经过
WL-test判定label multisetinjectivity,embedding集合对于可数集,单射性
injectiveness很好地描述了一个函数是否保持输入的唯一性distinctness。节点输入特征是连续的不可数集则需要进一步考虑。此外,刻画学到的
representation在embedding空间中的邻近程度(如果两个embedding不相等的话)也很有意义。我们将这些问题留待以后的工作,本文重点放在输入节点特征来自可数集的情况,并仅考虑输出representation相等/不等的情况。引理
4:假设输入特征空间GNN第size有界的multisetrepresentation证明:证明之前我们先给出一个众所周知的结论,然后将其简化:对于任意
现在回到我们的的引理证明。如果我们可以证明在可数集上的、
size有限的multiset上定义的任何函数range也是可数的,则对于任意现在我们的目标是证明
首先,因为
layer定义良好well-defined的函数,因此很明显multiset由于两个可数集的并集也是可数的,因此
dummy元素且不在正如
multiset的集合映射到由于
我们对于
由于
multisetsize有界,则存在其中最后
dummy element
显然
size有界的multiset这里还值得讨论
GNN在图结构判别能力上的一个重要优点,即:捕获图结构的相似性。WL-test中的节点特征向量本质上是one-hot编码,因此无法捕获subtree之间的相似性。相反,满足定理
3条件的GNN将subtree嵌入到低维空间来推广WL-test。这使得GNN不仅可以区分不同的结构,还可以学习将相似的图结构映射到相似的embedding从而捕获不同图结构之间的依赖关系。捕获
node label的结构相似性有助于泛化generalization,尤其是当subtree的共现co-occurrence很稀疏时、或者存在边噪音和/或节点特征噪音时。
27.3.2 GIN
在研究出能力最强的
GNN的条件之后,我们接下来将设计一种简单的架构,即图同构网络Graph Isomorphism Network:GIN。可以证明GIN满足定理3中的条件。GIN将WL-test推广从而实现了GNN的最大判别力。为建模用于邻居聚合的
multiset单射函数,我们研究了一种deep multiset理论,即:使用神经网络对multiset函数进行参数化。我们的下一个引理指出:
sum聚合实际上可以表示为multiset上的通用单射函数。引理
5:假设输入特征空间size的multisetunique。进一步地,任何multiset函数证明:我们首先证明存在一个映射
size的multiset由于
multisetcardinality是有界的,则存在自然数one-hot向量或N-digit数字的压缩表示。因此multiset的单射函数。permutation invariant,因此它是定义良好的well-defined的multiset函数。对于任意multiset函数引理
5将《Deep sets》中的结论从set扩展到multiset。deep multiset和deep set之间的重要区别是:某些流行的set单射函数 (如均值聚合)不再是multiset单射函数。通过将引理
5中的通用multiset函数建模机制作为构建块building block,我们可以设想一个聚合方案,该方案可以表示单个节点及其邻域的multiset上的通用函数,因此满足定理3中的第一个条件。我们的下一个推论是在所有这些聚合方案中选择一个简单而具体的形式。
推论
6:假设pair对unique,其中size的multisetpair上的函数证明:接着推论
5的证明过程,我们考虑5。令
我们用反证法证明。
对于任意
此时
根据推论
5该等式不成立,因为我们重写
因为
对于定义在
注意:这样的
well-defined,因为由于通用逼近定理
universal approximation theorem,我们可以使用多层感知机multi-layer perceptrons:MLPs来建模和学习推论6中的函数实际上我们使用一个
MLP来建模MLPs可以表示组合函数。在第一轮迭代中,如果输入特征是
one-hot编码,则在求和之前不需要MLP,因为它们的求和本身就是单射的。即:
我们将
GIN的节点representation更新方程为:
通常而言,可能存在很多其它强大的
GNN。GIN是这些能力强大的GNN中的一个简单的例子。GIN学到的节点embedding可以直接用于诸如节点分类、链接预测之类的任务。对于图分类任务,我们提出以下readout函数,该函数可以在给定每个节点embedding的情况下生成整个图的embedding。关于
graph-level readout函数的一个重要方面是:对应于subtree结构的node embedding随着迭代次数的增加而越来越精细化refine和全局化global。足够数量的迭代是获得良好判别力的关键,但是早期迭代的representation可能会泛化能力更好。为了考虑所有结构信息,我们使用来自模型所有深度的信息。我们通过类似于
Jumping Knowledge Networks的架构来实现这一点。在该架构体系中,我们将GIN所有层的representation拼接在一起:通过定理
3和推论6,如果GIN使用求和函数(求和针对相同迭代轮次中所有节点的representation进行)替代了上式中的READOUT(因为求和本身就是单射函数,因此在求和之前不必添加额外的MLP),它就可证明地provably推广了WL-test和WL subtree kernel。
27.4 Less Powerfull GNN
现在我们研究不满足定理
3中条件的GNN,包括GCN、GraphSAGE。另外,我们对GIN的聚合器的两个方面进行消融研究:- 单层感知机代替多层感知机
MLP。 - 均值池化或最大池化代替求和。
我们将看到:这些
GNN变体无法区分很简单的图,并且比WL-test能力更差。尽管如此,具有均值聚合的模型(如GCN)在节点分类任务中仍然表现良好。为了更好地理解这一点,我们精确地刻画了哪些GNN变体可以捕获或无法捕获图结构,并讨论了图学习的意义。- 单层感知机代替多层感知机
27.4.1 单层感知机
引理
5中的函数multiset映射到唯一的embedding。MLP可以通过通用逼近定理对GNN改为使用单层感知机relu)。这种单层映射是广义线性模型Generalized Linear Models的示例。因此,我们有兴趣了解单层感知机是否足以进行图学习。引理
7表明:确实存在使用单层感知机的图模型永远无法区分的网络邻域(multiset)。引理
7:存在有限size的multiset证明:考虑示例
multiset,但是它们的sum结果相同。我们将使用ReLU的同质性homogeneity。令
- 如果
- 如果
- 如果
因此得到:
- 如果
引理
7的证明的主要思想是:单层感知机的行为和线性映射非常相似。因此GNN层退化为简单地对邻域特征进行求和。我们的证明基于以下事实:线性映射中缺少偏置项。使用偏置项和足够大的输出维度,单层感知机可能区分不同的multiset。尽管如此,和使用
MLP的模型不同,单层感知机(即使带有偏置项)也不是multiset函数的通用逼近器。因此,即使具有单层感知机的GNN可以在不同程度上将不同的图嵌入到不同的位置,此类embedding也可能无法充分捕获结构相似性,并且可能难以拟合简单的分类器(如线性分类器)。在实验中,我们观察到带单层感知机的
GNN应用于图分类时,有时对于训练数据严重欠拟合underfit。并且在测试集准确率方面要比带MLP的GNN更差。
27.4.2 均值池化和最大池化
如果我们把
GCN、GraphSAGE中的那样,结果会如何?均值池化和最大池化仍然是
multiset上定义良好的函数,因为它们是排列不变的permutation invariant。但是,它们不是单射函数。下图按照表征能力对这三种聚合器(
sum/mean/max聚合器)进行排名rank。左图给出了输入的multiset,即待聚合的网络邻域。后面的三幅图说明了给定的聚合器能够捕获multiset的哪个方面:sum捕获了完整的multiset。mean捕获了给定类型的元素的比例/分布。max忽略了多重性multiplicity,将multiset简化为简单的set。
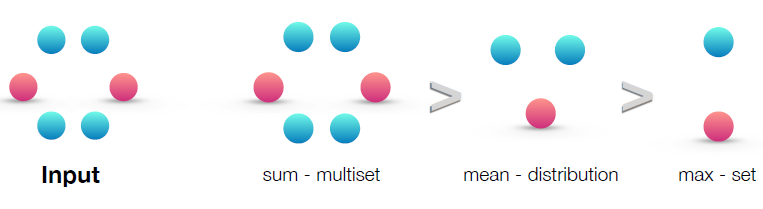
下图说明了
mean池化和max池化无法区分的一对图结构。这里节点颜色表示不同的节点特征,我们假设GNN首先将邻域聚合在一起,然后再将它们与标记为combine在一起。在两个图之间,节点
embedding,即使它们的图结构是不同的。如前所述:sum捕获了完整的multiset;mean捕获了给定类型的元素的比例/分布;max忽略了多重性multiplicity,将multiset简化为简单的set。图
(a)给出均值池化和最大池化都无法区分的图。这表明:均值池化和最大池化无法区分所有节点特征都相同的图。图
(b)给出最大池化无法区分的图。令r表示红色、g表示绿色) 为max池化:collapse到相同的representation(即使对应的图结构不同)。因此最大池化也无法区分它们。相反,均值池化是有效的,因为
图
(c)给出均值池化和最大池化都无法区分的图。这表明:均值池化和最大池化无法区分节点特征分布相同的图。因为: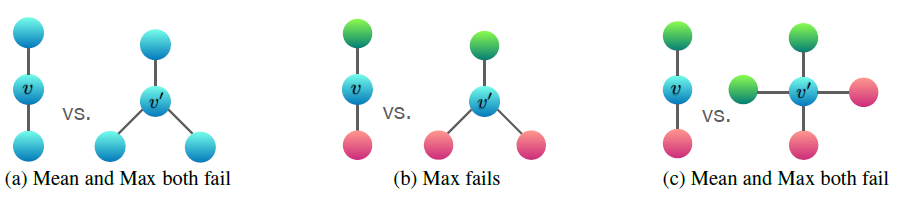
a. 均值池化
为了刻画均值聚合器能够区分的
multiset类型,考虑两个multiset:distinct元素,但是embedding,因为均值聚合器只是对各元素特征取均值。因此,均值聚合器捕获的是
multiset中元素的分布(比例),而不是捕获确切的multiset本身。推论
8:假设1的整数。证明:假设
multiset1的正整数。即set,并且multiplicity为因此有:
现在我们证明存在一个函数
distributionally equivalent的unique的。由于multisetcardinality是有界的,因此存在一个数如果某个任务中,图的统计信息和分布信息比确切结构更重要,则对于该任务使用均值聚合器可能会表现良好。
此外,当节点特征多种多样
diverse,且很少重复时,均值聚合器的能力几乎和sum聚合器一样强大。这可以解释为什么尽管存在限制(只能捕获multiset中元素的分布、而不是捕获确切的multiset本身),但是具有均值聚合器的GNN对于节点特征丰富的节点分类任务(如文章主题分类和社区检测)有效,因为邻域特征分布足以为任务提供强有力的信号。
b. 最大池化
最大池化将多个具有相同特征的节点视为仅一个节点(即,将
multiset视为一个简单的set)。最大池化无法捕获确切的结构或分布。但是,它可能适合于需要识别代表性元素或者骨架
skeleton,而不适合需要区分确切结构或分布的任务。实验表明:最大池化聚合器学会了识别
3D点云的骨架,并对噪声和离群点具有鲁棒性。为了完整起见,下一个推论表明最大池化聚合器捕获了multiset底层的set。推论
9:假设set有证明:假设
multisetset现在我们证明存在一个映射
set的unique的。由于其中
multiset映射到它的one-hot embedding。
27.4.3 其它聚合器
- 我们还没有覆盖到其它非标准的邻域聚合方案,如通过
attention加权平均的聚合器、LSTM池化聚合器。我们强调,我们的理论框架足以通用从而刻画任何基于聚合的GNN的表征能力。未来我们会研究应用我们的框架来分析和理解其它聚合方案。
27.5 实验
我们评估和对比了
GIN以及能力较弱的GNN变体的训练和测试性能。- 训练集上的性能比较让我们能够对比不同
GNN模型的表征能力。 - 测试集上的性能比较让我们能够对比不同
GNN模型的泛化能力。
- 训练集上的性能比较让我们能够对比不同
数据集:我们使用
9种图分类benchmark数据集,包括4个生物信息学数据集(MUTAG, PTC, NCI1, PROTEINS)、5个社交网络数据集(COLLAB, IMDB-BINARY, IMDB-MULTI, REDDITBINARY and REDDIT-MULTI5K) 。社交网络数据集:
IMDB-BINARY和IMDB-MULTI是电影协作collaboration数据集。每个图对应于演员的协作图,节点代表演员。如果两个演员出现在同一部电影中,则节点之间存在边。
每个图都来自于预先指定的电影流派
genre,任务的目标是对图的流派进行分类。REDDIT-BINARY和REDDIT-MULTI5K是平衡的数据集。每个图对应于一个在线讨论话题
thread,节点对应于用户。如果一个用户评论了另一个用户的帖子,则两个节点之间存在一条边。任务的目标是将每个图分类到对应的社区。
COLLAB是一个科学协作collaboration数据集,它来自3个公共协作数据集,即High Energy Physics, Condensed Matter Physics, Astro Physics。每个图对应于来自每个领域的不同研究人员的协作网络。任务的目标是将每个图分类到所属的领域。
生物学数据集:
MUTAG是包含188个诱变mutagenic的芳香族aromatic和异芳香族heteroaromatic硝基化合物nitro compound的数据集,具有7个类别。PROTEINS数据集中,节点是二级结构元素secondary structure elements:SSEs,如果两个节点在氨基酸序列或3D空间中是邻居,则两个节点之间存在边。它具有3个类别,分别代表螺旋helix、片sheet、弯turn。PTC是包含344种化合物的数据集,给出了针对雄性和雌性老鼠的致癌性,具有19个类别。NCL1是美国国家癌症研究所公开的数据集,是化学化合物平衡数据集的子集balanced datasets of chemical compounds。这些化合物经过筛选具有抑制一组人类癌细胞系生长的能力,具有37个类别。
重要的是,我们的目标不是让模型依赖于节点的特征,而是主要从网络结构中学习。因此:在生物信息图中,节点具有离散
categorical的输入特征;而在社交网络中,节点没有特征。对于社交网络,我们按照如下方式创建节点特征:- 对于
REDDIT数据集,我们将所有节点特征向量设置为相同。因此这里特征向量不带任何有效信息。 - 对于其它社交网络,我们使用节点
degree的one-hot编码作为节点特征向量。因此这里的特征向量仅包含结构信息。
下表给出了数据集的统计信息。

baseline方法:WL sbuntree kernel,其中使用C-SVM来作为分类器。SVM的超参数C以及WL迭代次数通过超参数调优得到,其中迭代次数从{1,2,3,4,5,6}之中选择。state-of-the-art深度学习架构,如Diffusionconvolutional neural networks: DCNN、PATCHY-SAN、Deep Graph CNN: DGCNN。Anonymous Walk Embeddings:AWL。
对于深度学习方法和
AWL,我们报告其原始论文中的准确率。实验配置:我们评估
GIN和能力较弱的GNN变体。在
GIN框架下,我们考虑两种变体:一种是通过梯度下降来学习
另一种是固定
GIN-0。GIN的邻域聚合就是sum池化(不包含当前节点自身)。
正如我们将看到的,
GIN-0将表现出强大的实验性能:GIN-0不仅与对于能力较弱的
GNN变体,我们考虑使用均值池化或最大池化替代GIN-0中的sum聚合,或者使用单层感知机来代替GIN-0中的多层感知机。这些变体根据使用的聚合器、感知器来命名。如
mean-1-layer对应于GCN、max-1-layer对应于GraphSAGE,尽管有一些小的体系架构修改。
对于
GIN和所有的GNN变体,我们使用相同的graph-level readout函数。具体而言,由于更好的测试性能,生物信息学数据集的readout采用sum函数,而社交网络数据集的readout采用mean函数。我们使用
LIB-SVM执行10-fold交叉验证,并报告10-fold交叉验证中验证集准确率的均值和标准差。对于所有配置
configurations:- 我们使用
5层GNN layer(包含输入层),并且MLP都有2层(它不算在5层GNN内)。 - 我们对于每个
hidden layer应用batch normalization。 - 我们使用初始学习率为
0.01的Adam学习器,并且每50个epoch进行学习率衰减0.5。
超参数是针对每个数据集进行调优的:
- 对于生物学数据集,隐层维度为
16或32;对于社交网络数据集,隐层维度为64。 batch size为32或128。dropout在dense层后,dropout比例为0或0.5。epoch数量通过10-fold交叉验证来确定。
注意:由于数据集规模较小,因此使用验证集进行超参数选择极其不稳定。例如对于
MUTAG,验证集仅包含18个数据点。因此上述有很多超参数是我们人工调优的。我们也报告了不同
GNN的训练准确率。其中所有的超参数在所有数据集上都是固定的(调优之后):5层GNN layer(包括输入层)、hidden维度为64、batch size = 128、dropout比例为0.5。为进行比较,我们也报告了
WL subtree kernel的准确率,其中迭代数量为4。这和5 GNN layer相当。
27.5.1 训练准确率
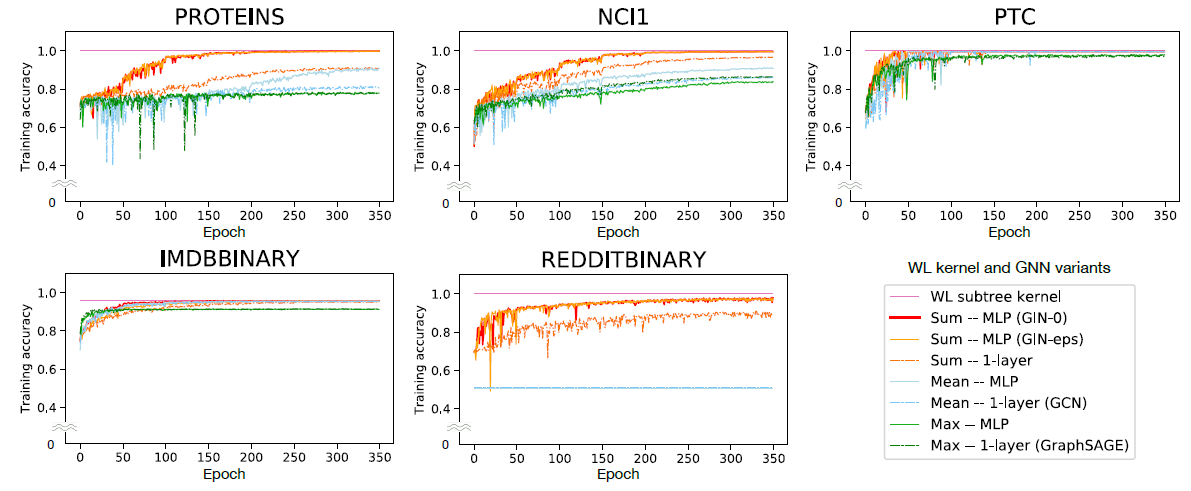
通过比较
GNN的训练准确率,我们验证了我们关于表征能力的理论分析。具有较高表达能力的模型应该具有较高的训练准确率。下图给出了具有相同超参数设置的GIN和能力较弱的GNN变体的训练曲线。首先,
GNN,它们都可以几乎完美地拟合训练集。在我们的实验中,在拟合训练数据集这个方面 ,显式学习
0的相比之下,使用均值/最大值池化聚合、或者单层感知机的
GNN变体在很多数据集中严重欠拟合。具体而言,训练准确率模式和我们通过模型表征能力的排名相符:
- 采用
MLP的GNN变体要比采用单层感知机的GNN变体拟合训练集效果更好。 - 采用
sum聚合器的GNN变体要比采用均值/最大值池化聚合的GNN变体拟合训练集效果更好。
- 采用
在我们的数据集上,
GNN训练准确率永远不会超过WL subtree kernel。这是可以预期的,因为
GNN的判别力通常比WL-test更低。例如在IMDB-BINARY数据集上,没有一个模型能够完美拟合训练集,而GNN最多可达到与WL kernel相同的训练准确率。这种模式和我们的结果一致,即
WL-test为基于聚合的GNN的表征能力提供了上限。但是,WL kernel无法学习如何组合节点特征,这对于给定的预测任务非常有用。我们接下来会看到。
27.5.2 测试准确率
接下来我们比较测试准确率。尽管我们的理论分析并未直接提及
GIN的泛化能力,但是可以合理地预期具有强大表达能力的GNN可以准确地捕获感兴趣的图结构,从而更好地泛化。下表给出了
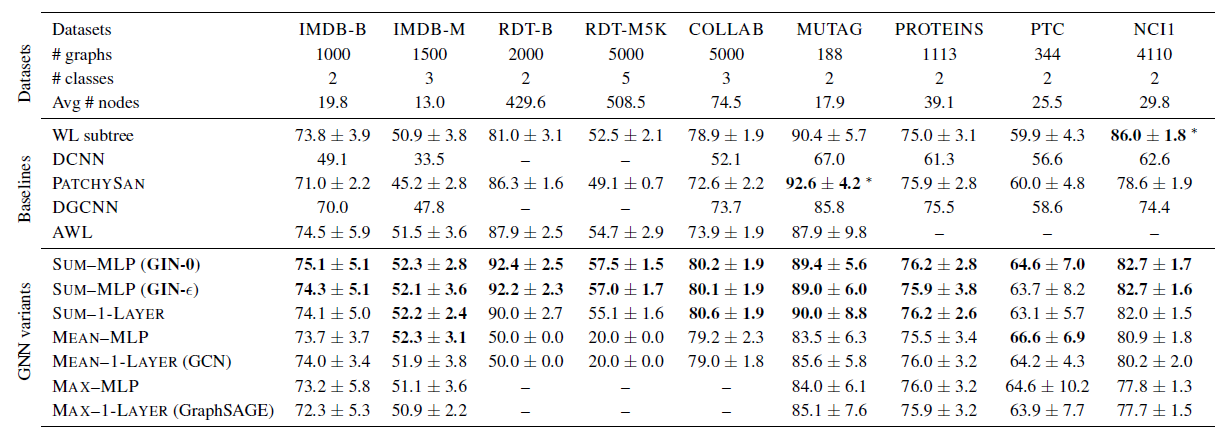
GIN(Sum-MLP) 、其它GNN变体、以及state-of-the-art baseline的测试准确率。表现最好的GNN以黑色突出显示。在有些数据集上GIN的准确率在所有GNN变体之间并非最高,但是和最佳GNN相比GIN仍然具有可比的性能,因此GIN也已黑色突出显示。如果baseline的性能明显高于所有GNN,则我们用黑体和星号同时突出显示。结论:
首先,
GIN,尤其是GIN-0,在所有9个数据集上均超越了(或者达到可比的)能力较弱的GNN变体,达到了state-of-the-art性能。其次,在包含大量训练数据的社交网络数据集中,
GIN效果非常好。对于
Reddit数据集,所有节点都使用相同的特征,因此模型仅能捕获图结构信息。GIN以及sum聚合的GNN准确地捕获到图结构,并且显著优于其它模型。- 均值聚合
GNN无法捕获图的任何结构,并且其测试准确率和随机猜测差不多。
对于其它社交网络数据集,虽然提供了节点
degree作为输入特征,但是基于均值聚合的GNN也要比基于sum聚合的GNN差得多。对于
GIN-0和GIN-0稍微、但是一致地超越了GIN-0相比
二十八、MPNN[2017]
机器学习预测分子和材料的性质仍处于起步阶段。迄今为止,将机器学习应用于化学任务的大多数研究都围绕着特征工程展开,神经网络在化学领域并未广泛采用。这使人联想到卷积神经网络被广泛采用之前的图像模型
image model的状态,部分原因是缺乏经验证据表明:具有适当归纳偏置inductive bias的神经网络体系结构可以在该领域获得成功。最近,大规模的量子化学计算
quantum chemistry calculation和分子动力学模拟molecular dynamics simulation,加上高通量high throughput实验的进展,开始以前所未有的速度产生数据。大多数经典的技术不能有效地利用现在的大量数据。假设我们能找到具有适当归纳偏置的模型,将更强大和更灵活的机器学习方法应用于这些问题的时机已经成熟。原子系统的对称性表明,在图结构数据上操作并对图同构graph isomorphism不变的神经网络可能也适合于分子。足够成功的模型有朝一日可以帮助实现药物发现或材料科学中具有挑战性的化学搜索问题的自动化。在论文
《Neural Message Passing for Quantum Chemistry》中,作者的目标是为化学预测问题展示有效的机器学习模型,这些模型能够直接从分子图molecular graph中学习特征,并且对图同构不变invariant。为此,论文描述了一个在图上进行监督学习的一般框架,称为信息传递神经网络(Message Passing Neural Network: MPNN)。MPNN简单地抽象了现有的几个最有前景的图神经模型之间的共性,以便更容易理解它们之间的关系,并提出新的变体。鉴于许多研究人员已经发表了适合MPNN框架的模型,作者认为社区应该在重要的图问题上尽可能地推动这种通用方法,并且只提出由application所启发的新变体,例如论文中考虑的应用:预测小有机分子的量子力学特性(如下图所示)。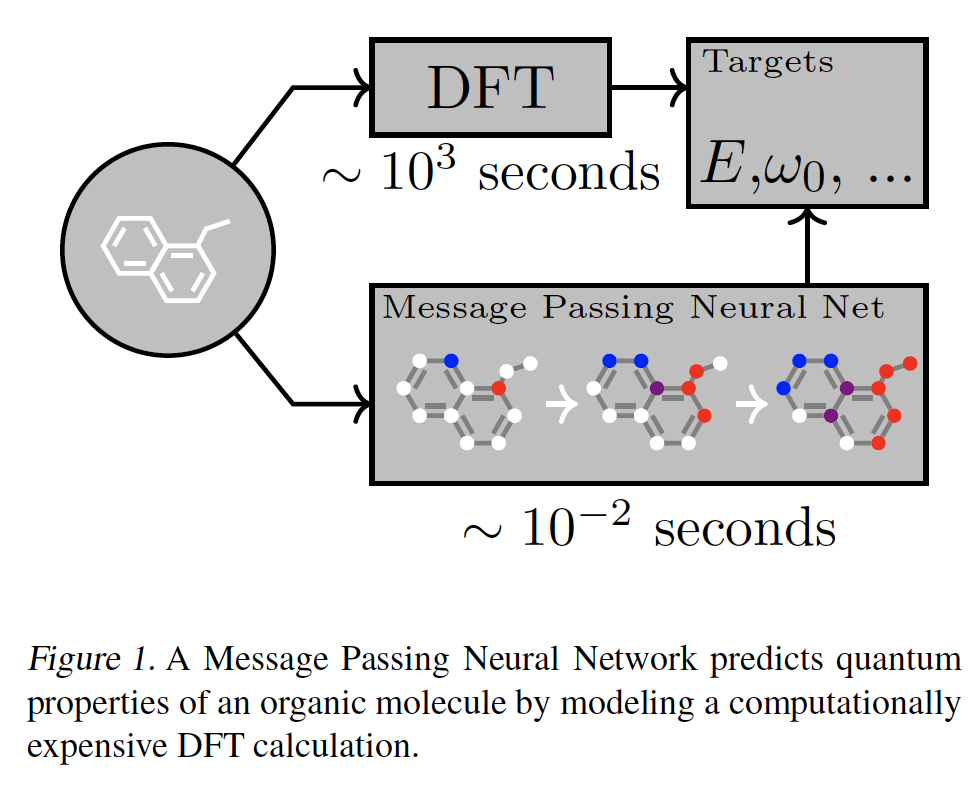
最后,
MPNN在分子属性预测benchmark上取得了state-of-the-art的结果。论文贡献:
- 论文开发了一个
MPNN框架 ,它在所有13个目标target上都取得了SOTA的结果,并在13个目标中的11个目标上预测到DFT的化学准确性。 - 论文开发了几种不同的
MPNN,在13个目标中的5个目标上预测到DFT的化学准确性,同时仅对分子的拓扑结构进行操作(没有空间信息作为输入)。 - 论文开发了一种通用的方法来训练具有更大
node representation的MPNN,而不需要相应地增加计算时间或内存,与以前的MPNN相比,在高维node representation方面产生了巨大的节省。
作者相信论文的工作是朝着使设计良好的
MPNN成为中等大小分子上的监督学习的默认方法迈出的重要一步。为了实现这一点,研究人员需要进行仔细的实证研究,以找到使用这些类型的模型的正确方法,并对其进行必要的改进。- 论文开发了一个
相关工作:尽管原则上量子力学可以让我们计算分子的特性,但物理定律导致的方程太难精确解决。因此,科学家们开发了一系列的量子力学近似方法,对速度和准确率进行了不同的权衡,如带有各种函数的密度功能理论(
Density Functional Theory: DFT)以及量子蒙特卡洛Quantum Monte-Carlo。尽管被广泛使用,DFT仍然太慢,无法应用于大型系统(时间复杂度为DFT表现出系统误差和随机误差。《Combined first-principles calculation and neural-network correction approach for heat of formation 》使用神经网络来近似DFT中一个特别麻烦的项,即交换相关势能exchange correlation potential,以提高DFT的准确性。然而,他们的方法未能提高DFT的效率,而是依赖于一大套临时的原子描述符atomic descriptor。另一个方向试图直接对量子力学的解进行近似,而不求助于DFT。这两个方向都使用了有固有局限性的手工设计的特征。
28.1 MPNN
为简单起见我们考虑无向图。给定无向图
- 每个节点
- 每条边
将无向图推广到有向的多图
multigraph(即多条边)也很容易。- 每个节点
GNN的前向传播具有两个阶段:消息传递阶段、readout阶段:消息传递阶段执行
step,它通过消息函数message functionupdate function在消息传递阶段,节点
其中
readout阶段根据所有节点在embedding向量其中
readout函数readout function。permutation invariant从而使得MPNN对图的同构不变性graph isomorphism invariant。
注意:你也可以在
MPNN中通过引入边的状态向量消息函数
readout函数《Convolutional Networks for Learning Molecular Fingerprints》:消息函数
节点更新函数
degree,并且不同的degree使用不同的映射矩阵。sigmoid函数。
Readout函数skip connection连接所有节点的所有历史状态其中
这种消息传递方案可能是有问题的,因为得到的消息向量
Gated Graph Neural Networks:GG-NN:消息函数
edge labellabel是离散的。节点更新函数
GRU为Gated Recurrent Unit。该工作使用了权重绑定
weight tying,因此在每个时间步都使用相同的更新函数。即,它将每个节点的
Readout函数sigmoid函数。
Interaction Networks:该工作既考虑了node-level目标,也考虑了graph-level目标。也考虑了在节点上施加的外部效应。- 消息函数
- 节点更新函数
- 当进行
graph-level输出时,Readout函数1。
- 消息函数
Molecular Graph Convolutions:该工作和MPNN稍有不同,因为它在消息传递阶段更新了边的表示消息函数
节点更新函数
relu为ReLU非线性激活函数,边更新函数:
其中
Deep Tensor Neural Networks:- 消息函数
bias向量。 - 节点更新函数
Readout函数
- 消息函数
Laplacian Based Methods,例如GCN:消息函数
其中
deg(v)为节点degree。节点更新函数
将这些方法抽象为通用的
MPNN的好处是:我们可以确定关键的实现细节,并可能达到这些模型的极限,从而指导我们进行未来的模型改进。所有这些方法的缺点之一是计算时间。最近的工作通过在每个
time step仅在图的子集上传递消息,已经将GG-NN架构应用到更大的图。这里我们也提出了一种可以改善计算成本的MPNN修改。
28.2 MPNN 变体
我们基于
GG-NN模型探索MPNN,我们认为GG-NN是一个很强的baseline。我们聚焦于探索不同的消息函数、输出函数,从而找到适当的输入representation以及正确调优的超参数。消息函数探索:
矩阵乘法作为消息函数:首先考察
GG-NN中使用的消息函数,它定义为其中
edge labellabel是离散的。Edge Network:为了支持向量值的edge特征,我们使用以下消息函数:其中
edge特征Pair Message:前面两种消息函数仅依赖于隐状态其中
当我们将上述消息函数应用于有向图时,将使用两个独立的函数
虚拟节点 & 虚拟边:我们探索了两种方式来在图中添加虚拟元素,从而修改了消息传递的方式(使得消息传播得更广):
虚拟边:在未连接节点
pair对之间添加虚拟边,这个边的类型是特殊类型。这可以实现为数据预处理步骤,并允许消息在传播阶段传播很长一段距离。虚拟节点:虚拟一个
master节点,该节点以特殊的边类型来连接到图中的每个输入节点。此时
master节点充当全局暂存空间,每个节点都在消息传递的每个step中从master读取信息、向master写入信息。这允许信息在传播阶段传播很长的距离。我们允许
master节点具有单独的节点维度master节点在内部状态更新函数中使用单独的权重矩阵。由于加入了
master节点,理论上模型复杂度有所增加,并提升了模型型容量。
Readout函数:我们尝试了两种Readout函数。一种是在
GG-NN中使用的Readout函数:另一种是
Set2Set模型,该模型专门为Set输入而设计的,并且比简单地累加final node state具有更强的表达能力。该模型首先将线性投影应用于每个元组
set的元组投影作为输入。然后,在经过step之后,Set2Set模型将产生graph-level embeddingembedding对于set的顺序具有不变性。我们将这个embedding
Multiple Towers:MPNN的一个问题是可扩展性,特别是对于稠密图。消息传递阶段的每个step需要我们将
embeddingembeddingembedding。然后我们在每个隐空间
embedding最后这
embedding结果通过以下方式混合:其中:
这种混合方式保留了节点的排列不变性
permutation invariant,同时允许图的不同embedding在传播阶段相互交流。这种方法是有利的,因为对于相同数量的参数数量,它能产生更大的假设空间,表达能力更强。并且时间复杂度更低。当消息函数是矩阵乘法时,某种
embedding的传播step花费embedding,因此总的时间复杂度为Multiple Towers就是multi-head的思想。
28.3 实验
数据集:
QM-9分子数据集,包含130462个分子。我们随机选择10000个样本作为验证集、10000个样本用于测试集、其它作为训练集。特征(如下表所示)和label的含义参考原始论文。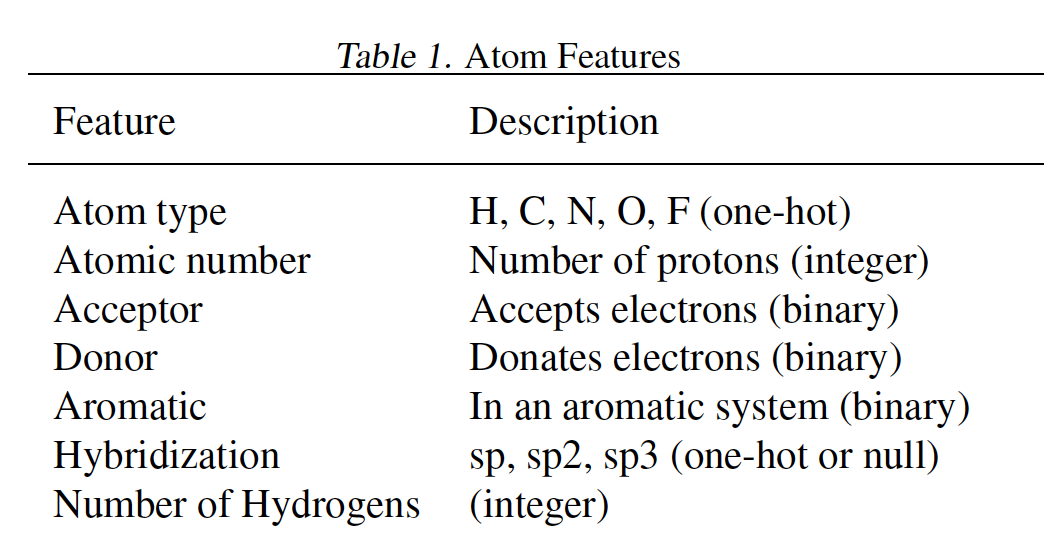
我们使用验证集进行早停和模型选择,并在测试集上报告
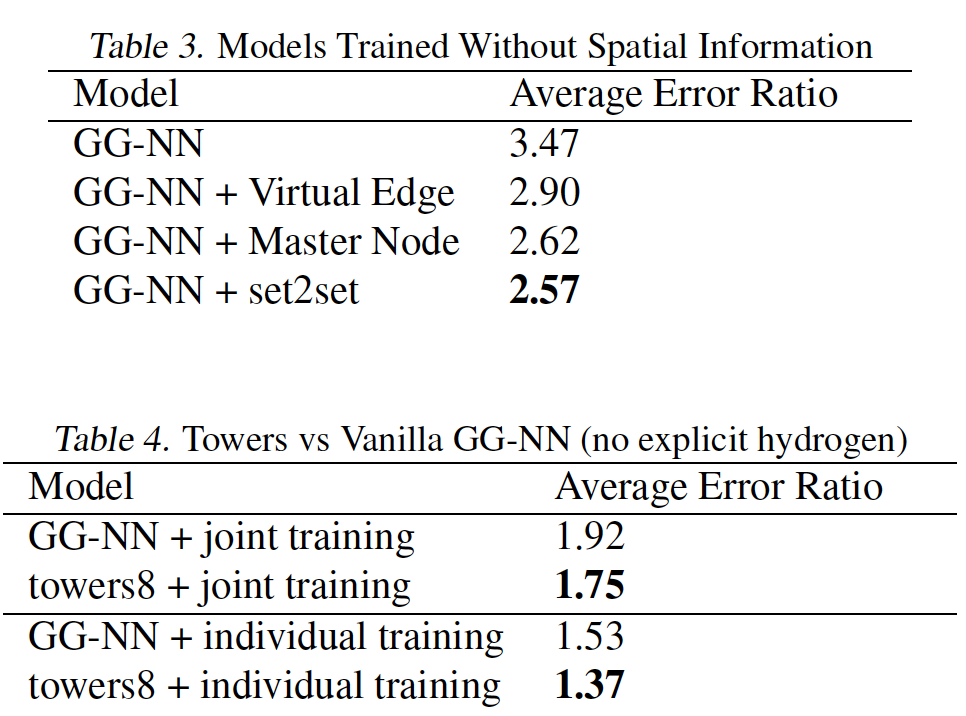
mean absolute error:MAE。结论:
- 针对每个目标训练一个模型始终优于对所有
13个目标进行联合训练。 - 最优的
MPNN变体使用edge network消息函数。 - 添加虚拟边、添加
master节点、将graph-level输出修改为Set2Set输出对于13个目标都有帮助。 Multiple Towers不仅可以缩短训练时间,还可以提高泛化性能。
具体实验细节参考原始论文。
下图中,
enn-s2s表示最好的MPNN变体(使用edge network消息函数、set2set输出、以及在具有显式氢原子的图上操作),enn-s2s-ens5表示对应的ensemble。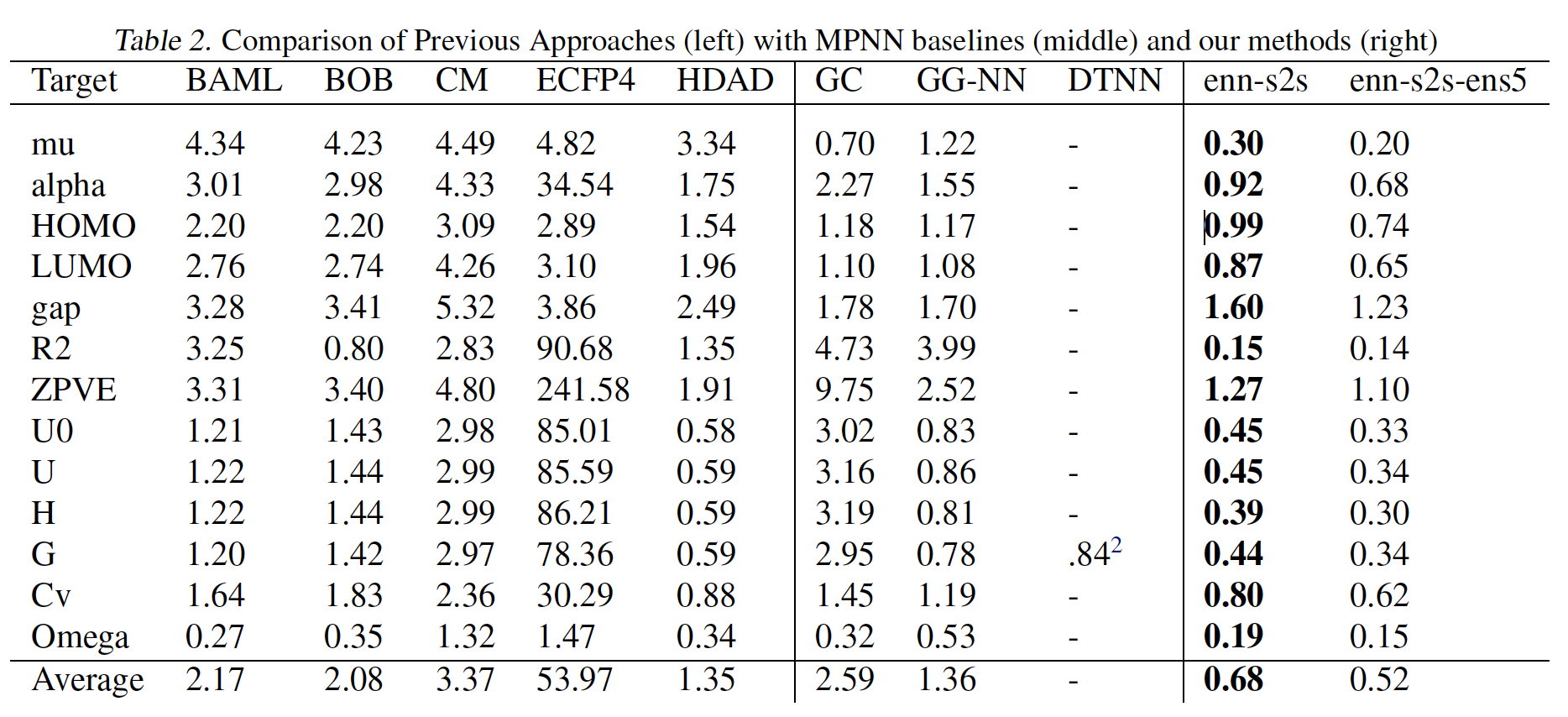
- 针对每个目标训练一个模型始终优于对所有
二十九、UniMP[2020]
在半监督节点分类任务中,我们需要学习带标签的样本,然后对未标记样本进行预测。为更好地对节点进行分类,基于拉普拉斯平滑性假设
Laplacian smoothing assumption,人们提出了消息传递模型来聚合节点邻域的信息从而获得足够的事实fact来对未标记节点产生更可靠的预测。通常有两种实现消息传递模型的实用方法:
- 图神经网络
Graph Neural Network:GNN:通过神经网络执行特征传播feature propagation以进行预测。 - 标签传播算法
Label Propagation Algorithm:LPA:跨graph adjacency matrix的标签传播label propagation来进行预测。
由于
GNN和LPA基于相同的假设:通过消息传播进行半监督分类。因此有一种直觉认为:将它们一起使用可以提高半监督分类的性能。已有一些优秀的研究提出了基于该想法的图模型。例如,APPNP和TPN通过将GNN和LPA拼接在一起,GCN-LPA使用LPA来正则化GCN模型。但是,如下表所示,上述方法仍然无法将GNN和LPA共同融入消息传递模型,从而在训练和预测过程中同时传播特征和标签。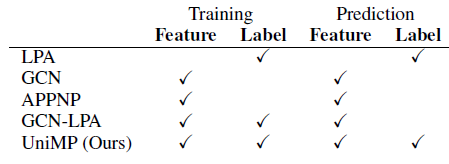
为了统一特征传播和标签传播,主要有两个问题需要解决:
聚合特征信息和标签信息:由于节点特征是由
embedding表达的,而节点标签是一个one-hot向量。它们不在同一个向量空间中。此外,它们的信息传递方式也不同:
GNN可以通过不同的神经网络架构来传播信息,如GraphSAGE、GCN和GAT;但是LPA只能通过图邻接矩阵来传递标签信息。监督训练:用特征传播和标签传播进行监督训练的模型不可避免地会在
self-loop标签信息中出现过拟合,这使得在训练时出现标签泄漏label leakage,导致预测的性能不佳。
受
NLP发展的启发,论文《Masked label prediction: unified message passing model for semi-supervised classification》提出了一个新的统一消息传递模型Unified Message Passing:UniMP,并且使用带masked label prediction的UniMP来解决上述问题。UniMP模型可以通过一个共享的消息传递网络将特征传播和标签传播xx,从而在半监督分类中提供更好的性能。UniMP是一个多层的Graph Transformer,它使用label embedding来将节点标签转换为和节点特征相同的向量空间。一方面,
UniMP像之前的attention-based GNN一样传播节点特征;另一方面,UniMP将multi-head attention视为转移矩阵从而用于传播label vector。因此,每个节点都可以聚合邻域的特征信息和标签信息。即,
label vector的转移矩阵来自于attention,而不是来自于图的邻接矩阵。为了监督训练
UniMP模型而又不过拟合于self-loop标签信息,论文从BERT中的masked word prediction中吸取经验,并提出了一种masked label prediction策略。该策略随机mask某些训练样本的标签信息,然后对其进行预测。这种训练方法完美地模拟了图中标签信息从有标签的样本到无标签的样本的转移过程。
论文在
Open Graph Benchmark:OGB数据集上对三个半监督分类数据集进行实验,从而证明了UniMP获得了state-of-the-art半监督分类结果。论文还对具有不同输入的模型进行了消融研究,以证明UniMP方法的有效性。此外,论文还对标签传播如何提高UniMP模型的性能进行了最彻底的分析。- 图神经网络
29.1 模型
定义图
每个节点
每条边
每个节点
one-hot表示为one-hot构成标签矩阵实际上在半监督节点分类任务中,大部分节点的标签是未知的。因此我们定义初始标签矩阵
one-hot标签向量或者全零向量组成:对于标记节点,它就是标签的one-hot向量;对于未标记节点,它就是全零的向量。图的邻接矩阵定义为
degree。归一化的邻接矩阵定义为
特征传播
Feature Propagation模型:在半监督节点分类中,基于拉普拉斯平滑假设,GNN将节点特征GNN的特征传播范式为:在第其中:
representation矩阵,final embedding矩阵
标签传播
Label Propagation模型:LPA假定相连节点之间的标签是平滑的,并在整个图上迭代传播标签。LPA的特征传播范式为:在第其中
在
LPA中,标签信息通过归一化的邻接矩阵
29.1.1 UniMP 模型
UniMP整体架构如下图所示。我们采用了Graph Transformer并结合使用label embedding来构建UniMP模型,从而将上述特征传播和标签传播结合在一起。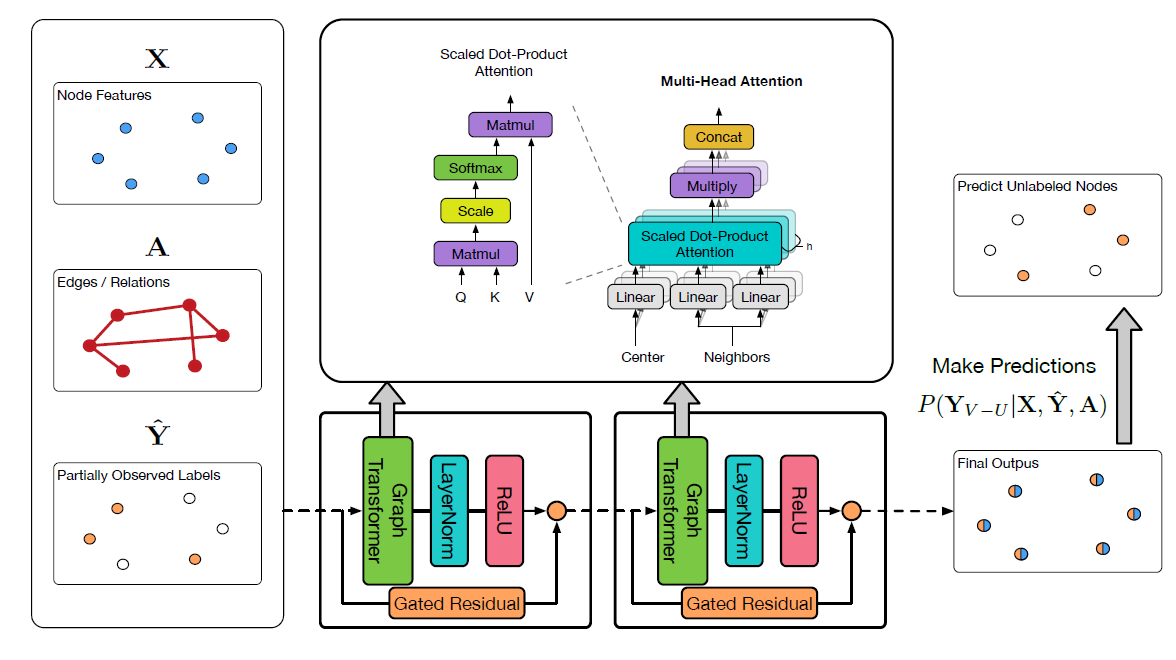
Graph Transformer:由于Transformer已经在NLP中被证明功能强大,因此我们将常规的multi-head attention应用到graph learning中。给定节点
representation集合multi-head attention:其中:
head的隐层大小。head attention。
我们首先将
source featurequery向量distant featurekey向量edge featurekey向量作为额外的信息。编码过程中使用了可训练的参数edge feature跨层共享。在计算注意力系数时,edge feature作为key的附加信息。当得到
graph multi-head attention,我们聚合节点注:这里的公式和上面的架构图不匹配。根据公式中的描述,残差应该连接在
Graph Transformer层之后。即:残差连接 ->LayerNorm->ReLU。其中:
节点
embeddingvalue向量考虑了
和特征传播相比,
multi-head attention矩阵代替了原始的归一化邻接矩阵作为消息传递的转移矩阵(类似于GAT)。另外,我们提出一个层间的门控残差连接gated residual connection来防止过度平滑oversmoothing。门控机制由
类似于
GAT,如果我们在输出层应用Graph Transformer,则我们对multi-head output应用均值池化(并且没有LayerNorm和relu):Label Embedding and Propagation:我们提出将部分观测到的标签信息embed到节点特征相同的空间中:label embedding向量和未标记节点的零向量。然后,我们通过简单地将节点特征和标签特征相加得到传播特征
propagation feature:我们可以证明,通过将部分标记的
证明:令
Graph Transformer中的attention矩阵(即edge feature,并且bias向量。那么我们有:其中
APPNP中预定义的超参数。为简单起见,我们取
其中
因此我们发现
UniMP模型可以近似分解为特征传播
29.1.2 Masked Label Prediction
已有的
GNN相关工作很少考虑在训练和推断阶段都使用部分观测的标签。大多数工作仅将这些标签信息作为ground truth target,从而监督训练模型参数其中
但是,我们的
UniMP模型会传播节点特征和标签信息从而进行预测:inference性能很差。我们向
BERT学习,它可以mask输入的word并预测被masked的word从而预训练BERT模型。有鉴于此,我们提出了一种masked label prediction策略来训练我们的模型。训练过程中,在每个iteration,我们随机屏蔽部分节点标签为零并保留剩余节点标签,从而将label_rate所控制(label_rate表示保留的标签比例)。假设被
masked之后的标签矩阵为其中:
masked标签的节点数量,masked标签。每个
batch内的target节点的label都是被屏蔽掉的。否则的话,对target节点预测标签会发生标签泄漏。通过这种方式,我们可以训练我们的模型从而不会泄露
self-loop标签信息。这篇论文就是一篇水文,其思想就是把
node label作为一个节点特征拼接到原始节点特征上去(当然,目标节点拼接全零信息而不是node label从而防止信息泄露),然后在所有输入的特征上执行随机mask。在推断过程中,我们可以将所有
29.2 实验
数据集:和实际工程应用的图相比,大多数论文常用的图数据集规模很小。
GNN在这些论文数据集上的性能通常不稳定,因为数据集太小、不可忽略的重复率或泄露率、不切实际的数据切分等。最近发布的
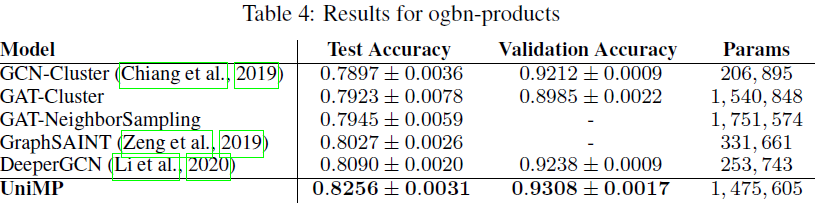
OGB数据集克服了常用数据集的主要缺点,它规模更大、更有挑战性。OGB数据集涵盖了各种现实应用,并覆盖了多个重要领域,从社交网络、信息网络到生物网络、分子图、知识图谱。它还覆盖了各种预测任务,包括node-level预测、graph-level预测、edge-level预测。因此我们在该数据集上进行实验,并将
UniMP和SOTA模型进行比较。如下表所示,我们对三个OGBN数据集进行实验,它们是具有不同大小的不同任务。其中包括:ogbn-products:关于47种产品类别的分类(多分类问题),其中每个产品给出了100维的节点特征。ogbn-proteins:关于112种蛋白质功能的分类(多标签二分类问题),其中每条边并给出了8维的边特征。ogbn-arxiv:关于40种文章主题的分类(多分类问题),其中每篇文章给出了128维的节点特征。

实现细节:
这些数据集大小或任务各不相同,因此我们使用不同的抽样方法对模型进行评估。
- 在
ogbn-products数据集中,我们在训练期间每一层使用size=10的NeighborSampling来采样子图,并在推断期间使用full-batch。 - 在
ogbn-proteins数据集中,我们使用随机分区Random Partition将稠密图拆分为子图,从而训练和测试我们的模型。训练数据的分区数为9、测试数据的分区数为5。 - 在小型的
ogbn-arxiv数据集中,我们对训练数据和测试数据进行full batch处理。
- 在
我们为每个数据集设置了模型的超参数,如下表所示。
label rate表示我们在应用masked label prediction策略期间保留的标签比例。我们使用
lr=0.001的Adam优化器来训练模型。此外,我们在小型ogbn-arxiv数据集中将模型的权重衰减设置为0.0005来缓解过拟合。所有的模型都通过
PGL以及PaddlePaddle来实现,并且所有实验均在单个NVIDIA V100 32 GB上实现。

实验结果:
baseline方法和其它SOTA方法均由OGB排行榜给出。其中一些结果是原始作者根据原始论文官方提供,其它结果由社区重新实现的。并且所有这些结果都保证可以用开源代码复现。按照
OGB的要求,我们对每个数据集运行10次实验结果,并报告均值和标准差。如下表所示,我们的UniMP模型在三个OGBN数据集上都超过所有其它模型。由于大多数模型仅考虑基于特征传播来优化模型,因此结果表明:将标签传播纳入GNN模型可以带来重大改进。具体而言:
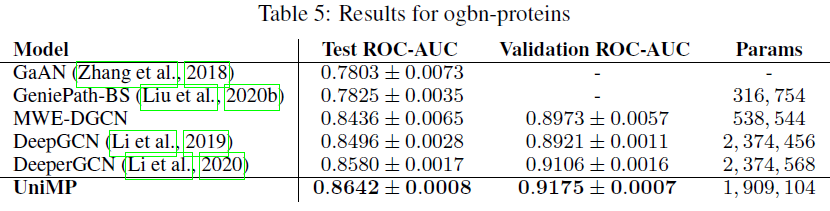
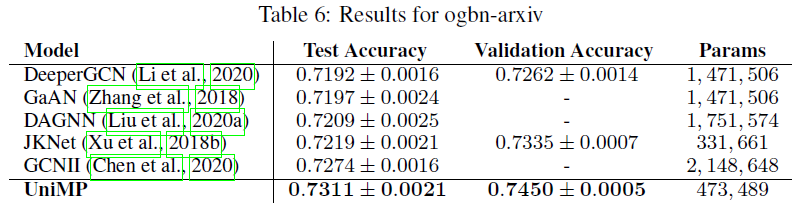
UniMP在gbn-products中获得了82.56%的测试准确率,相比SOTA取得了1.6%的绝对提升。UniMP在gbn-proteins中获得了86.42%的测试ROC-AUC,相比SOTA取得了0.6%的绝对提升。UniMP在gbn-arxiv中获得了73.11%的测试准确率,相比SOTA实现了0.37%的绝对提升。
作者没有消融研究:
- 不同
label_rate对于模型性能的变化(当label_rate = 0时表示移除标签传播)。 - 除了
Graph Transformer之外,UniMap采用其它base model的效果是否也很好。
三十、Correct and Smooth [2020]
摘要:
GNN是在图上学习的主要技术。然而,人们对GNN在实践中取得成功的原因、以及它们是否是良好性能所必需的了解相对较少。在这里,论文表明:对于许多标准的transductive node classification benchmark,可以结合忽略图结构的浅层模型、以及利用标签结构中相关性的两个简单后处理步骤,从而超过或匹配SOTA的GNN的性能。这些后处理步骤利用了标签结构label structure中的相关性:- 误差相关性
error correlation:它将训练数据中的残差residual error扩散,从而纠正测试数据中的误差。 - 预测相关性
prediction correlation:平滑了测试数据上的预测结果。
论文的这个
pipeline称作 “矫正和平滑”Correct and Smooth:C&S。论文的方法在各种transductive节点分类benchmark上都超过或接近了SOTA GNN的性能,而参数规模小得多,运行速度也快了几个量级,并可以轻松scale到大型图。例如在OGB-Products数据集上,论文的方法相比于著名的GNN模型减少了137倍参数、提高了100倍的训练时间,并且效果还更好。还可以将论文的技术整合到大型GNN模型中,从而获得适度的收益。- 误差相关性
引言:
Graph Neural Network: GNN目前在图数据领域取得巨大成功,并且经常排在Open Graph Benchmark等排行榜的榜首。通常GNN的方法论都围绕着创建比基本变体(如GCN,GraphSAGE)更具有表达力的体系架构,如GAT、GIN以及其它各种深度模型。然而,随着这些模型变得越来越复杂,理解它们的性能为什么提升是一个重大挑战,而且将它们扩展到大型数据集也很困难。相反,论文
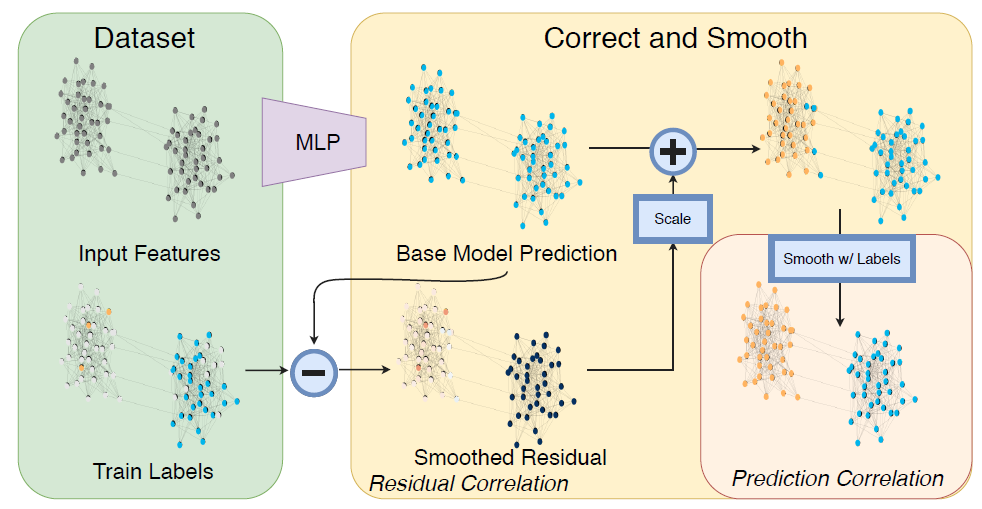
《Combining label propagation and simple models out-performs graph neural networks》研究了结合更简单的模型来获得收益。为此,论文提出了一个简单的pipeline,它包含三个主要部分(如下图所示):base prediction:使用忽略图结构(如MLP或线性模型)的节点特征进行基础预测base prediction。correction step:将训练数据中的误差传播到整个图,从而校正基础预测。smoothing:最后,对图上的预测进行平滑。
这里第二步和第三步只是后处理
post-processing,并且使用经典的标签传播label propagation: LP技术进行基于图的半监督学习。在该框架中,图结构不是用来学习参数的,而是作为一种后处理机制。这种简单性导致模型的参数数量减少,训练时间也减少了几个数量级,并且可以很容易地扩展到大型图。还可以将论文的思想与SOTA的GNN结合起来,从而得到适度的性能提升。论文性能提升的一个主要来源是:直接使用标签进行预测。这个思想并不新鲜,早期的
diffusion-based的图半监督学习算法(如spectral graph transducer、Gaussian random field model和label spreading)都使用了这个思想。然而,这些方法的动机是对点云数据进行半监督学习,所以特征被用来构建图。然后,这些技术被用于仅从标签(即没有特征)来在关系数据上学习,而这种学习方式在GNN中基本上被忽略了。即,作者发现:即使是简单的标签传播(忽略了特征)在一些benchmark上也有令人惊讶的表现。这启发了作者结合结合两个正交的预测能力:一个预测能力来自节点特征(忽略图形结构),一个预测能力来自在预测中直接使用已知标签。最近的研究将
GNN与标签传播label propagation以及马尔科夫随机场Markov Random field联系起来,一些技术在特征中使用标签信息的临时融合 (如UniMP)。然而,这些方法的训练成本仍然很高,而论文以两种可以理解的低成本方式使用标签传播:论文从一个无视图结构的模型开始进行廉价的 "基础预测";之后,论文使用标签传播进行纠错,然后对最终预测进行平滑处理。这些后处理步骤是基于
error和label在相连节点上是正相关的这一事实。假设相连节点之间的相似性是许多网络分析的中心,并对应于同质性homophily或同源混合assortative mixing。在半监督学习文献中,类似的假设是平滑性smoothness或聚类假设cluster assumption。论文在各种数据集上看到的标签传播的良好表现表明:这些相关性在普通benchmark上是成立的。总的来说,论文的方法表明:结合几个简单的思想,可以在模型大小(即参数数量)和训练时间方面,以很小的成本产生出色的
transductive节点分类性能。例如,在OGB-Product benchmark上,论文的表现超过了目前最著名的GNN,参数数量少了两个数量级,训练时间少了两个数量级。然而,论文的目标并不是说目前的graph learning方法很差或不合适。相反,论文的目标是强调提高graph learning预测性能的更容易的方法,并更好地理解性能提高的来源。论文的主要发现是:将标签更直接地纳入学习算法中是关键。而通过将论文的思想与现有的GNN相结合,也可以看到改进,尽管这些改进是微小的。作者希望论文的方法能够激发新的思想,帮助其他的graph learning任务,如inductive节点分类、链接预测和图预测。下图为
C&S方法的概览。左图表示数据集中有两个类别:橙色和蓝色。- 首先使用
MLP进行基础预测,从而忽略了图结构。这里假设所有节点都给出了相同的预测。 - 然后从训练数据中传播误差来校正基础预测。
- 最后校正后的预测通过标签传播得以平滑。
相关工作:
Approximate Personalized Propagation of Neural Predictions:APPNP框架是和我们工作最相关的,因为它们也是平滑了基础预测。但是,他们专注于将这个平滑处理集成到训练过程中,以便可以端到端地训练他们的模型。这种方式不仅显著增加计算成本,而且还使APPNP无法在推断时纳入标签信息。和
APPNP相比,我们的框架可以产生更准确的预测、训练速度更快,并且更容易scale到大规模图数据。我们的框架还补充了
Simplified Graph Convolution,以及旨在提高可扩展性的算法。然而,我们的方法的主要重点是直接使用标签,而可扩展性是一个副产品。之前也有将
GCN和标签传播联系起来的工作:《Unifying graph convolutional neural networks and label propagation》将标签传播作为预处理步骤从而用于GNN的edge加权,而我们将标签传播作为后处理步骤并避免使用GNN。《Residual correlation in graph neural network regression》将具备标签传播的GNN用于回归任务,我们的error correction步骤将他们的一些思想适配为分类的情况。
最后,最近有几种方法将非线性纳入标签传播从而与
GNN竞争并实现可扩展性,但这些方法专注于low label rate setting,并且没有纳入feature learning。
30.1 模型
给定无向图
每个节点
令
degree度矩阵,节点集合
one-hot向量one-hot向量记作全零
所有节点标签的
one-hot向量组成标签矩阵进一步地,我们将标记节点集合
我们任务的目标是:给定
C&S方法从基于节点特征的、简单的base predictor开始,这个predictor不依赖于对图的任何学习。然后执行两种类型的标签传播:- 一种是通过对误差相关性进行建模来校正
base prediction,即误差平滑性。 - 另一种是平滑最终预测,即标签平滑性。
标签传播只是后处理步骤
post-processing step,因此我们的pipeline没有端到端的训练。- 一种是通过对误差相关性进行建模来校正
在
C&S方法中,图数据仅在这些后处理步骤和预处理步骤pre-processing step中使用(比如构建节点特征),和标准的GNN模型相比,这使得训练更快且可扩展性更好。图数据在预处理步骤中用于生成节点
embedding,从而增强特征此外,
C&S方法同时使用了标签传播和节点特征,这些互补的信号会产生更出色的预测结果。标签传播本身往往在没有特征的情况下也表现得很出色。
30.1.1 Base Predictor
首先我们使用不依赖于图结构的、简单的
base predictor。具体而言,我们首先训练模型其中:
one-hot向量。
所有损失在标记的训练集
本文选择
multilayer perceptron: MLP后接一个softmax输出层。这种base predictor忽略图结构,因此可以避免GNN的可扩展问题。不过我们可以使用任何base predictor,甚至包括GNN的base predictor。但是,为了使得我们的
pipeline简单且可扩展,我们仅使用线性模型或者MLP作为base predictor。
30.1.2 误差校正
接下来我们通过融合标签信息来提高
base prediction的准确率。核心思想是:我们预期基础预测的误差在图上正相关。换句话讲:节点我们在图上传播
spread这种误差相似性。我们的方法在某种程度上受到残差传播的启发。在残差传播中,类似的概念用于节点回归任务。为此,我们定义一个误差矩阵
其中:
base predictor做出完美预测时,误差矩阵才为零。
现在我们已知误差矩阵
应该是在训练集上和误差矩阵
因此我们使用标签扩散技术来平滑误差,优化目标:
其中:
第一项鼓励误差估计在图上的平滑性。这等价于:
第二项使得最终的解接近已知的真实误差
这个目标函数可以通过迭代来求解:
其中:
该迭代方程快速收敛到
一旦得到平滑误差
我们强调这是一种后处理技术,没有和
base predictor相结合的训练过程。在回归问题中,基于高斯假设,这种方式的误差传播被证明是正确的方法。但是对于分类问题,平滑误差
考虑到:
其中
因此,传播没有足够多的总质量
total mass,所以传播无法完全纠正图中所有节点上的误差。并且,实验发现调整残差的比例实际上可以提供帮助。有鉴于此,我们提出了两种缩放残差的方法:
autoscale:直观地,我们希望将由于我们仅知道训练节点上的真实误差,所以我们用训练节点上的平均误差来计算这个缩放比例。
形式上,令
其中
然后我们将未标记节点
其中
FDiff-scale:另一种方法,我们可以选择一种扩散方法,该方法在标记节点上(包括训练集和验证集)保持真实误差具体而言,我们在未标记节点上迭代平滑误差为:
迭代过程中固定
直观地看,这将在标记节点
另外,我们仍然发现学习缩放的超参数
30.1.3 平滑预测
现在我们得到每个节点
score vectorbase predictor为了做出最终预测,我们进一步对校正后的预测进行平滑处理。这样做的动机是:图中相邻的节点可能具有相似的标签,这在网络同质性
homophily或者分类混合assortative mixing的属性下是可以预期的。因此,我们通过另一个标签传播来鼓励图上标签分布的平滑性。
首先我们定义标签矩阵的最优猜测
我们也可以在验证节点上使用真实标签,这将在后面的实验中讨论。
然后我们使用迭代公式:
其中
我们迭代上式直到收敛,从而得到最终预测
最终测试节点
和误差校正一样,这里的预测平滑是一个后处理步骤。这里的预测平滑在本质上类似于
APPNP,我们稍后将其进行比较。但是,APPNP是端到端训练的,在最后一层representation上进行传播而不是softmax,不使用标签,并且动机不同。
30.1.4 总结
回顾我们的
pipeline:首先,我们从低成本的基础预测
然后,我们通过在训练数据上传播已知真实误差来估计平滑误差
将训练节点的真实误差传播到所有节点。注意,我们仅关心测试节点的误差,因为测试误差需要用于纠正测试节点的预测标签。而训练节点的标签是已知的,直接使用
ground-truth。最后,我们通过另外一个标记传播步骤将校正预测与已知标签相结合,从而生成平滑的最终预测。
标签传播时,训练节点传播的是真实标签,测试节点传播的是预测标签。
我们将这个通用的
pipeline称作Correct and Smooth:C&S。其核心就是两个平滑:误差平滑、输出平滑。
在显示该
pipeline在transductive节点分类上实现SOTA性能之前,我们简要介绍了另一种提高性能的简单方法:特征增强。深度学习的标志是:我们可以自动学习特征而不是手动的特征工程,但是
GNN仍然依靠输入的特征来执行预测。有很多方法可以从图拓扑中获取有用的特征来扩展原始节点的特征。在我们的
pipeline中,我们使用来自矩阵eigenvector作为规范化的谱域嵌入regularized spectral embedding,从而增强特征。这里:degree。degree。
虽然底层的矩阵是稠密的,但是我们可以应用矩阵向量乘法,并使用迭代的特征向量求解器
eigensolver来在embedding。在论文的实验部分,作者在进行训练速度的比较时没有考虑计算
spectral embedding的预处理时间,因此是不公平的比较。此外,计算spectral embedding对于大图而言是不可行的。
30.2 实验
数据集:为证明我们方法的效果,我们使用了九个数据集,其中包括:
Open Graph Benchmark:OGB中的Arxiv数据集和Products数据集:标签为论文类别或商品类别,特征从文本内容派生而来。- 三个经典引文网络
benchmark数据集Cora,Citeseer,Pubmed:标签为论文类别,特征从文本内容派生而来。 - 一个
web graph数据集wikiCS::标签为网页类别,特征从文本内容派生而来。 Rice University的Facebook社交网络数据集:类别为宿舍dorm residence,特征为画像诸如性别、专业、班级等属性。US County数据:类别为2016年选举结果,特征为人口统计特征。- 欧洲研究所的
email数据集:类别为成员的部门,没有特征。
数据集的统计信息如下所示。另外我们还给出了我们方法相比较于
SOTA GNN:参数数量降低的比例、准确率的提升(绝对值)、以及我们方法的训练时间(秒)。结果表明:通过避免使用昂贵的GNN,我们的方法需要较少的参数、更快的训练速度,并且通常得到更准确的结果。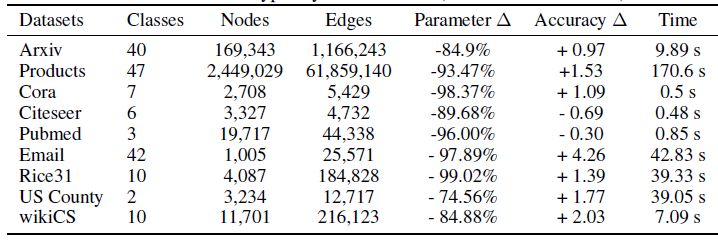
数据集拆分:
- 在
Arxiv数据集和Products数据集中,训练集、验证集、测试集的拆分由benchmark本身来提供。 - 对于
wikiCS数据集的拆分,我们和《A wikipedia-based benchmark for graph neural networks》的拆分一致。 - 对于
Rice, US County, Email数据集,我们随机拆分为40%/10%/50%。 - 对于更小的引文网络数据集,我们使用
60%/20%/20%的随机拆分。
我们并没有采用很低的
label rate,这是为了改善数据集对于超参数的敏感性。在我们的所有实验中,不同拆分的预估准确率标准差在
1%以内,并且通常不会改变我们的定性比较。- 在
base predictor和baseline:base predictor:- 我们使用线性模型
Linear和MLP模型作为简单的base predictor,其中输入特征是原始节点特征和spectral embedding。 - 我们还使用了仅使用原始特征的普通线性模型
Plain Linear作为base predictor进行比较。
- 我们使用线性模型
变种:我们对比了仅使用
base predictor的方法、使用autoscale和FDiff-scale的方法。baseline:我们对标签传播
Label Propagation模型进行比较。我们选择
GCN, SGC, APPNP作为对比的GNN模型。对于GCN模型,我们将输入到每一层、以及从每一层到输出层都添加了额外的残差链接residual connection,从而产生了更好的效果。GCN的层数、隐层维度和MLP相同。注意:这里的
GCN一种GCN风格的模型,而不是原始的、Kipf&Welling提出的模型。
最后,我们还包含了几个
state-of-the-art的baseline:- 对于
Arxiv和Product数据集,我们使用UniMP模型。该模型在2020-10-01位于OGB排行榜的榜首。 - 对于
Cora,Citeseer,Pubmed数据集,我们复用《 Simple and deep graph convolutional networks》论文给出的最好的结果。 - 对于
Email和US County数据集,我们使用GCNII模型。 - 对于
Rice31,我们使用带spectral embedding的GCN、以及带node2vec embedding的GCN。这是我们发现的、效果最好的GNN-based模型。 - 对于
WikiCS,我们使用APPNP。
- 对于
对于所有模型,我们通过验证集来选择一组固定的超参数。
30.2.1 仅训练标签
在平滑预测阶段,我们仅在训练节点上使用真实标签,即:
下表给出了实验结果,其中
Base Prediction表示仅使用基础预测而没有任何后处理;Autoscale和FDiff-scale表示使用不同的平滑预测缩放方式。我们重点介绍一些重要发现:
首先,在我们模型中
C&S后处理带来可观的收益。例如在Product数据集上,应用了后处理之后MLP base prediction的测试准确率从63%提升到84%。其次,在很多
case中:- 具有
C&S的Plain Linear模型也足以战胜常规的GCN模型。 - 标签传播
LP(一种没有可训练参数的方法)通常与GCN具有相当的竞争力。
鉴于
GCN的主要动机是解决连接的节点可能没有相似的标签的事实,这一点令人惊讶。我们的结果表明:通过简单地使用特征从而将相关性融合到图中,这通常是一个更好的主意。- 具有
第三,我们模型的变体在
Product,Cora,Email,Rice31, US County上的表现优于SOTA。在其它数据集上,我们表现最好的模型和SOTA之间没有太大差异。
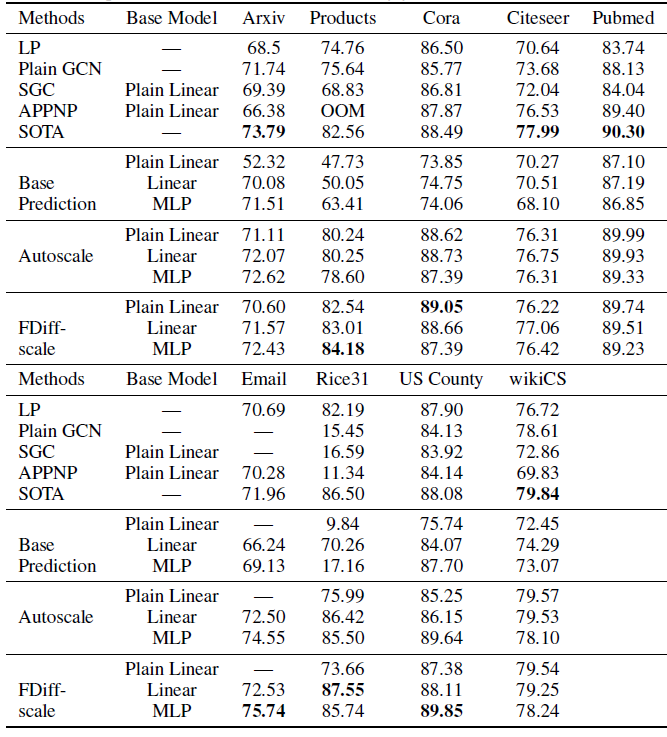
为了了解直接使用
ground truth标签有多大帮助,我们还尝试了没有标签的C&S版本,其中不执行C&S步骤,而是使用《Learning with local and global consistency》中的方法来平滑base predictor的输出,我们称这个版本为Basic Model。即:- 标签信息仅用于
base predictor的训练。 - 图结构信息仅用于
base predictor预测结果的平滑。
这里面缺少了误差的平滑,仅保留预测结果的平滑。
结果如下表所示。我们看到:
Linear和MLP的base predictor通常可以超过GCN的性能。这些结果再次表明输出平滑非常重要,而GCN的原始动机具有误导性。相反,我们假设GCN可以通过平滑图上的输出来获得性能提升。这与《Simplifying graph convolutional networks》的观察类似。- 另外,我们也看到下图中这个
Basic Model和上图中使用C&S的方法之间仍然存在性能差异。
Plain Linear缺少了节点的spectral embedding特征。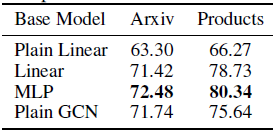
- 标签信息仅用于
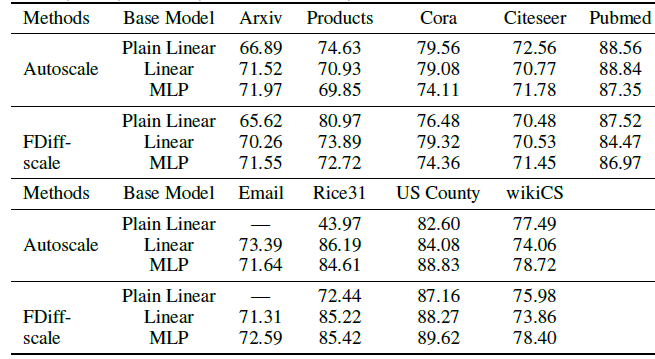
下表给出了仅使用误差校正,但是未使用平滑预测的实验结果。
实验结果表明:误差校正、平滑预测这两个标签传播步骤对于最终效果提升都是至关重要的。
30.2.2 更多标签
可以使用验证标签是我们方法的优势,这甚至可以进一步提升我们框架的性能。
在平滑预测阶段,我们在训练节点和验证节点上使用真实标签,即:
注意:我们不使用验证标签来训练
base predictor模型,而是用于选择base predictor的超参数。通过引入验证集标签,更多的节点被指定了
ground-truth,因此网络中传播的信息量更大。下表给出了实验结果(另外,数据集统计信息表给出了相对于
SOTA的收益)。应用了验证标签之后,我们的最佳模型在9个数据集中的7个中超越了SOTA,并且具有可观的收益。可以看到:
- 融合验证标签的能力是我们方法的优势。而
GNN并没有这种优势,因为它们通常依靠早停来防止过拟合,可能并不总是从更多数据中受益(比如,在标签分布偏移shift的情况下),并且不直接使用标签。 - 对于很多数据集上的
transductive节点分类,要获得良好的性能,实际上并不需要大型的而且昂贵的GNN模型。 - 将经典的标签传播思想和简单的
base predictor相结合,在这些任务上的性能超越了GNN模型。
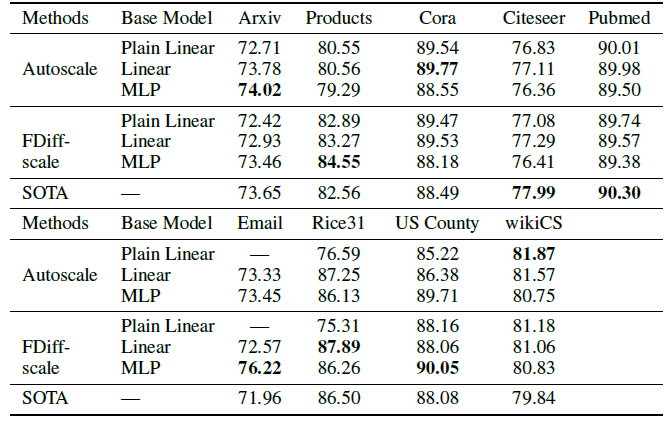
- 融合验证标签的能力是我们方法的优势。而
30.2.3 改善 GNN
和
GNN以及其它SOTA解决方案相比,我们的C&S框架通常需要更少的参数。例如我们在下图绘制了Product数据中,不同模型的参数和性能的关系。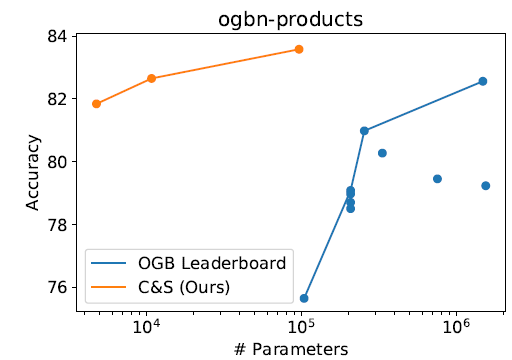
我们的方法不仅使用更少的参数,但真正的收益在于训练时间更快。和具有可比准确率的模型相比,我们的模型的训练时间要快几个量级。因为我们的
base prediction不需要使用图结构。例如:- 在
Arxiv数据集上,我们的MLP+C&S模型和GCN + label的模型具有相似的参数数量。但是我们的模型训练中,每个epoch的训练速度要快7倍,并且收敛速度更快。 - 在
Products数据集上,和SOTA相比,我们的linear base predictor +C&S模型具有更高的准确率,训练速度提高了100倍、参数数量减少了137倍。 - 我们还在更大的数据集
papers 100M上评估了我们的方法。这里我们以Linear + C&S模型,可以达到65.33%的准确率,比SOTA的63.29%更高。
这种比较是不公平的比较,因此
C&S方法需要节点的spectral embedding作为输入,这通常是非常昂贵的且通常无法扩展到大型图。一种解决办法是用DeepWalk来得到node emebdding,但是这种预处理也非常耗时。如果没有
spectral embedding(即,Plain Linear),则C&S的效果出现巨大的下降。而且这种依赖于人工特征工程(虽然是通过graph embedding自动计算得到)的方式不太鼓励,因为强烈依赖于经验。- 在
一般而言,我们的
pipeline还可以用于改善GNN的性能。我们将误差校正、平滑预测应用到了更复杂的base predictor上,诸如GCNII和GAT。实验结果如下表所示。这提升了我们在某些数据集上的结果,包括在
Arxiv上击败了SOTA。但是,有时性能提升只是很小的,这表明大型模型可能正在捕获与我们简单的C&S框架相同的信号。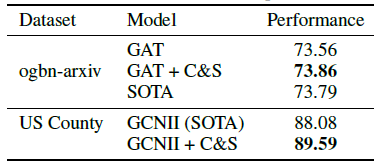
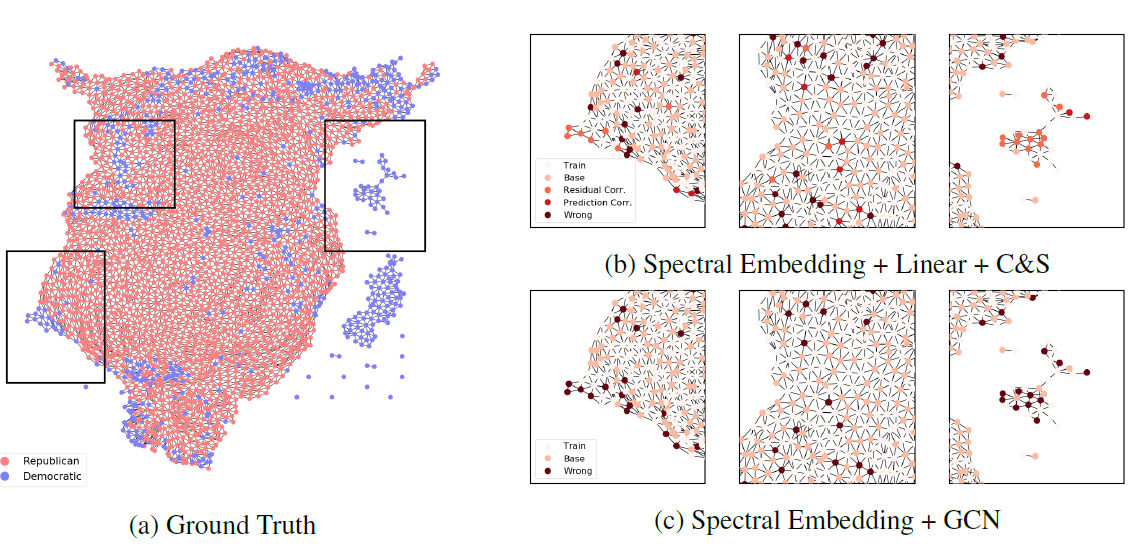
30.2.4 可视化
为了帮助理解
C&S框架的性能,我们在US County数据集上的预测可视化。(a):US County可视化,其中embedding由GraphViz提供,颜色对应于类别标签。总体而言是经纬度坐标的压缩旋转版本。(b):和(a)部分对应的pannel,显示C&S在哪个阶段做出了正确的预测。(c):显示了相同pannel上GNN做出的预测。
如预期的那样,残差相关性倾向于校正节点,其中临县为这些节点提供了相关信息。例如:
- 我们看到
base prediction中的很多误差已被残差相关性校正(图3b的左图和右图)。在这些情况下,对应于德克萨斯州和夏威夷州的部分地区,县的人口统计特征和全国其它地区相比是异常的,这误导了Linear模型和GCN模型。而来自相邻县的残差相关性能够校正预测。 - 我们还看到最终的预测相关性使得预测变得平滑,如图
3b的中间部分所示,这使得可以基于邻居的正确分类来校正误差。
三十一、LGCN[2018]
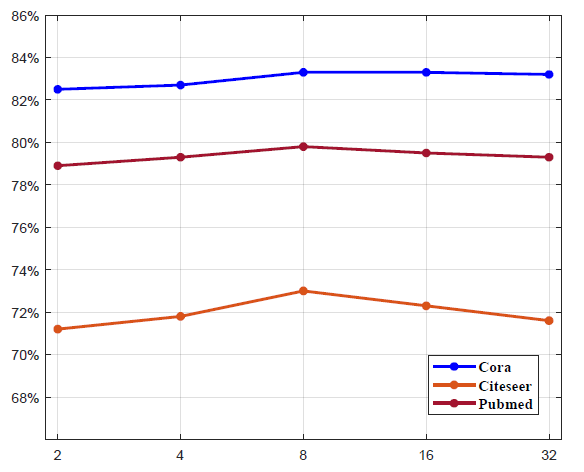
CNN在很多领域已经获得巨大成功,如图像领域、NLP领域。这些领域背后的一个共同点是数据可以由网格结构表示,这使得可以在输入的每个位置上应用卷积算子。但是在很多实际应用中数据是图结构,如社交网络、引文网络、生物网络。网格结构是图结构的特殊情况,因此将图像领域的深度学习模型(尤其是CNN)推广到图结构数据很有吸引力。但是,在图结构数据上应用常规卷积算子面临两个主要挑战。这些挑战来自于这样一个事实:常规卷积算子要求每个节点的邻域节点数量不变,并且这些邻域节点是有序的。论文
《Large-Scale Learnable Graph Convolutional Networks》为解决这些挑战提出了优雅的解决方案。两个挑战:图数据中,不同节点的邻域节点数量不同,并且邻域节点没有排序信息。
最近的一些研究试图将卷积算子推广到通用图结构:
GCN提出使用类似卷积的运算来聚合每个节点的所有邻域节点的特征,然后进行线性变换来生成给定节点的新的representation。可以将其视为类似于卷积的运算,但是它在两个方面和常规的卷积算子有本质的不同:首先,它不使用相同的局部滤波器来扫描每个节点。即,邻域数量不同的节点具有不同尺寸
size和权重的滤波器。其次,对于感受野
receptive field中所有的邻域节点,滤波器中的权重均相同,权重为相比之下,
CNN滤波器的权重是可训练的。
GAT采用注意力机制,通过衡量邻域节点的特征向量和中心节点的特征向量之间的相关性,从而获得邻域节点的不同、且可训练的权重。但是,
graph attention操作仍然不同于常规卷积,后者直接学习局部滤波器的权重。此外,注意力机制需要根据成对的特征向量进行额外的计算,从而在实践中导致过多的内存和计算资源需求。
和这些方法不同,论文
《Large-Scale Learnable Graph Convolutional Networks》为在通用图结构数据上应用CNN做出了两个主要贡献:首先,论文提出可学习的图卷积层
learnable graph convolutional layer: LGCL,以便能够在图上使用常规的卷积运算。注意:之前的研究修改了原始卷积运算来适配图数据。相比之下,
LGCL修改了图数据来适配卷积运算。LGCL为每个特征维度根据取值的排名自动选择固定数量的邻域节点,以便将graph数据转换为1-D格式的网格结构,从而可以在通用的graph上应用卷积运算。实验结果表明,基于
LGCL的模型在transductive learning和inductive learning的节点分类任务上均表现出更好的性能。其次,论文观察到现有方法的另一个局限性,即:现有的训练过程将整个图的邻接矩阵作为输入。当图包含大量节点时,这需要过多的内存和计算资源。
为克服这一局限性,论文提出了一种子图训练方法
sub-graph training method。该方法是一种简单而有效的方法,可以对大规模图数据进行训练。子图训练方法可以显著减少所需的内存和计算资源,而在模型性能方面的损失可以忽略不计。
31.1 模型
31.1.1 背景和相关工作
给定图
- 每个节点
- 令
degree度矩阵。degree矩阵。
- 每个节点
GCN模型中,每一层的操作可以表示为:其中:
embedding矩阵,ReLU函数。
可以看到该操作类似于卷积运算:每个节点的感受野由其本身和邻域节点组成,然后在感受野上应用一个局部滤波器。但是这种运算和
CNN中的常规卷积运算有两点区别:- 通常图数据中不同节点具有不同数量的邻域节点,这使得不同节点的感受野大小有所不同,从而导致不同的局部滤波器。这是和常规卷积运算的主要区别,在常规卷积运算中,网格数据的每个输入位置都使用相同的滤波器。
- 此外,即使对图数据使用大小不同的局部滤波器似乎是合理的,但是值得注意的是
因此,
GCN中这种不可训练的聚合操作限制了CNN在通用图数据上的能力。两点区别:
GCN中每个节点采用不同的滤波器(滤波器不会跨节点共享,且滤波器的尺寸不固定),且滤波器是不可训练的。GAT试图通过注意力机制来聚合邻域特征向量,从而使得学习聚合权重成为可能。像
GCN一样,GAT中每个节点仍然具有局部滤波器,其感受野包含节点本身及其邻域。当执行特征向量的加权和时,每个邻居节点都通过衡量它与中心节点之间的相关性来接收不同的权重。正式地,在第
其中:
attention向量。attention权重。
尽管通过这种方式
GAT向不同的邻域节点提供了不同、且可训练的权重,但学习权重的过程和常规CNN的学习过程不同。在常规CNN中,直接学习局部滤波器的权重。另外,注意力机制需要在中心节点和所有邻域节点之间进行额外的计算,这在实践中会引起内存和计算资源的问题。
和现有的这些修改常规卷积运算使得其适合通用的图数据不同,我们提出将图转换为类似网格的数据来直接应用
CNN。这个想法以前在《Learning convolutional neural networks for graphs》中有所探讨,但是该论文中的变换是在预处理过程中实现的。而我们的方法在模型中包含转换。此外,我们的工作还提出了一种子图训练方法,这是一种允许大规模图的训练的简单而有效的方法。
31.1.2 LGCL
这里我们介绍通用图数据的可学习图卷积层
learnable graph convolutional layer:LGCL。LGCL的传播规则为:其中:
embedding矩阵,k-largest节点并将通用图结构转换为网格数据的操作。1-D CNN来聚合邻域信息并为每个节点输出新的representation向量。
下面我们分别讨论
k-largest node selectionk-largest node selection的新颖方法,从而实现从图数据到网格数据的转换,其中LGCL的超参数。执行该操作后,每个节点将聚合来自邻域的信息,并表示为具有
1D-CNN来更新representation向量。假设
representation。representation的维度。给定邻接矩阵
representation向量拼接为矩阵:不失一般性假设
k-largest节点选择是在k-largest个节点。注意,这里是对每一列单独进行排序,而不是根据维度取值来对节点进行排序。此外,这里不仅仅是选择了最大的
CNN卷积的要求。这里的核心的两个操作是:如何
select、如何sort。除了论文里提到的这种维度独立的选择和排序,还可以选择样本独立的选择和排序:从第一个维度到最后一个维度,依次选择最后,我们将
k-largest node selection过程:中心节点具有6个邻居;对于每个特征,根据特征取值从邻域中选择四个最大的值;最后将中心节点自己的特征拼接起来得到通过在每个节点上应用这一过程,
1D网格数据,其中batch size、k-largest node selection函数k-largest node selection操作利用了实数之间的自然排名信息,并强制每个节点具有固定数量的有序邻居。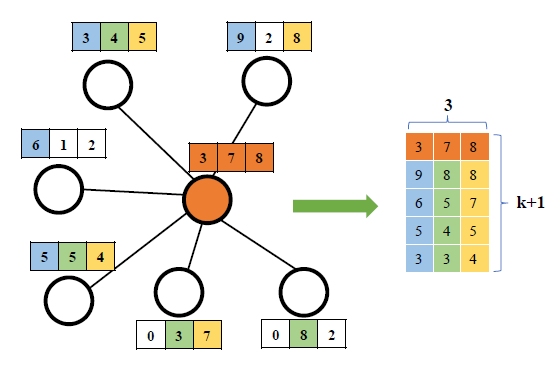
1D-CNN1D网格数据,因此我们采用1-D CNN模型LGCL的基本功能是聚合邻域信息并更新每个节点的representation,因此1-D CNN1。batch size,它和考虑节点
k-largest node selection转换的输出为由于任何常规卷积算子(滤波器尺寸大于
1并且没有填充)都会减小空间尺寸,因此最简单的同时,也可以使用任何多层
CNN,只要其最终输出的尺寸为同样地,对所有
总之,我们的
LGCL使用k-largest node selection方法将通用的图数据转换为网格数据,并应用标准的1-D CNN进行特征聚合从而为每个节点更新representation。下图为
LGCL的一个例子。考虑具有6个邻域节点的中心节点(橙色表示),每个节点具有3维特征(特征由三个分量的特征向量来表示)。LGCL选择邻近的1-D CNN来更新中心节点的representation。- 左侧描述了从邻域中为每个特征选择
k-largest节点的过程。 - 右侧给出了通过
1-D CNN作用于生成的网格数据并得到中心节点的representation。输出为5维特征(输出通道数为5)。
这里
1-D CNN的输入通道数和输出通道数都不相同,并且1-D CNN可以为任何CNN模型。这里采用了两层的
1-D卷积:第一层输入通道数为3、输出通道数为4;第二层输入通道数为4、输出通道数为5。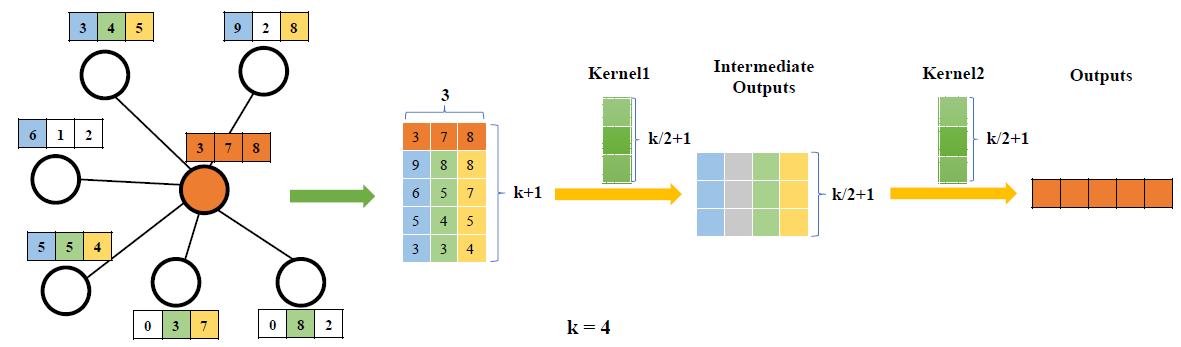
- 左侧描述了从邻域中为每个特征选择
31.1.3 LGCN
众所周知更深的网络通常会产生更好的性能,但是之前
GCN之类的图模型通常只有两层,因为它们层数加深时会受到性能损失。但是在我们的LGCL中可以采用更深的层,从而为图节点分类提供可学习的图卷积网络learnable graph convolutional networks: LGCNs。我们基于
densely connected convolutional networks:DCNNs体系架构来构建LGCN,因为DCNNs在ImageNet分类挑战中获得了state-of-the-art性能。在
LGCN中,我们首先应用一个graph embedding layer来生成节点的低维representation。因为某些图数据集中,原始输入通常是很高维度的特征向量。第一层中的
graph embedding layer实际上是一个线性变换,即:其中:
也可以使用一个
GCN layer作为graph embedding layer。在
graph embedding layer之后,根据图数据的复杂性,我们堆叠了多个LGCL。由于每个LGCL仅聚合来自于一阶邻域的信息,因此多个LGCL可以收集到更大感受野中的信息。为了提高模型性能并简化训练过程,我们应用了
skip-connection来连接LGCL的输入和输出。最后,我们在
softmax输出层之前采用一个全连接层。
遵循
LGCNs的设计原理,LGCL堆叠层数是最重要的超参数。- 图中节点的平均
degree可以作为选择 LGCL层的数量取决于任务的复杂性,如类别数量、图中节点数量等。通常更复杂的任务需要更深度的模型。
- 图中节点的平均
LGCN的一个例子如下图所示。在这个例子中,输入的节点具有两维特征。首先,我们使用
graph embedding layer将输入特征向量转换为低维representation。然后,我们使用两个
LGCL层,每个LGCL层和skip-connection堆叠在一起。注意:
LGCL层和skip-connection输出是拼接起来,而不是相加。最后,使用一个全连接层和
softmax输出层用于节点分类。这里有三个不同的类别。

31.1.4 子图训练
通常而言,在训练期间,图模型的输入是所有节点的特征向量及整个图的邻接矩阵。这些模型可以在小规模图上正常工作。但是对于大规模图,这些方法通常会导致过多的内存和计算资源需求,从而限制了这些模型的实际应用。
对于其它类型的数据(如网格数据)的深度神经网络,也会遇到类似的问题。如,在处理大尺寸图像时,模型通常使用随机裁剪的
patch。受到该策略的启发,我们打算随机 “裁剪”graph从而获得较小的graph来进行训练。但是,图像的矩形
patch自然地保持了像素之间的相邻信息,而如何处理图中的节点之间的不规则连接仍然具有挑战性。这里我们提出了一种子图选择算法来解决大规模图数据上的内存和计算资源问题。具体而言,给定一个图:
- 我们首先对一些初始节点进行采样。
- 从这些节点开始,我们使用广度优先搜索
BFS算法将相邻节点迭代地扩展到子图中。 - 通过多次迭代,我们得到了初始节点和它们的高阶邻域节点。
Sub-Graph Selection Algorithm:输入:
- 邻接矩阵
- 所有节点数量
- 子图大小
- 初始的节点数量
- 每轮迭代扩展的最大节点数量
- 邻接矩阵
输出:子图的节点集合
算法步骤:
初始化
从
更新
记
当
候选节点集合为
更新
- 如果
- 如果
- 如果
更新
注:为简单期间这里我们使用单个参数
下图是一个子图选择过程的示例。我们从
- 在第一次迭代中,我们使用
BFS查找3个初始节点(橙色)中的所有一阶相邻节点(不包括它们自己)。在这些节点中,我们随机选择 - 在下一次迭代中,我们从蓝色节点的邻居中选择
经过两次迭代,我们选择了
3+5+7=15个节点并获得了所需的子图。这些节点以及相应的邻接矩阵将在训练迭代期间作为LGCN的输入。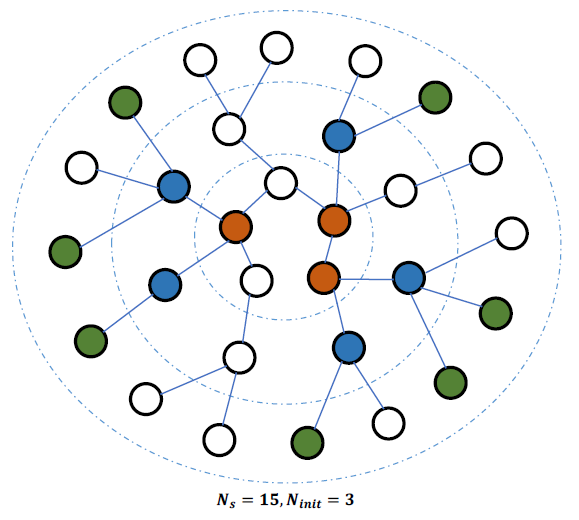
- 在第一次迭代中,我们使用
有了这样的随机 “裁剪” 子图,我们就能够在大规模图上训练深度模型。
此外,我们可以利用
mini-batch训练策略来加速学习过程。在每次训练迭代中,我们可以使用提出的子图选择算法来采样若干个子图,然后将这些子图放到mini-batch中。相应的特征向量和邻接矩阵构成了网络的输入。子图采样也可以作为
GNN的通用策略从而帮助GNN的mini-batch训练。
31.1.5 未来方向
我们的方法主要解决节点分类问题,实践中有些任务需要对图进行分类,即图分类问题。
但是目前的图卷积方法(包括我们的方法)无法对图进行降采样(类似于图像数据的池化操作),我们需要一个
layer来有效地减少节点数,这是图分类所必须的。另外,我们的方法主要应用于通用图数据,如引文网络。对于其它数据,如文本,我们的方法也可能会有所帮助,因为我们可以将文本数据视为图。
31.2 实验
我们评估在
transductive learning和inductive learning环境下LGCN在大规模图的节点分类任务上的表现。另外,除了和
state-of-the-art模型进行比较之外,我们还进行了一些性能研究,从而研究如何选择超参数。最终实验结果表明,
LGCN可以提高性能,并且子图训练比全图训练更有效。数据集:
transduction Learning:在transductive learning环境下,未标记的测试节点可以在训练期间访问到,包括测试节点的特征和连接。这意味着训练期间知道包含测试节点的图结构。我们使用三个标准的
benchmark数据集:Cora, Citeseer, Pubmed。这三个数据集是引文网络数据集,节点代表文档、边代表引用关系。每个节点的特征向量是文档的bag-of-word表示。对于这三个数据集,我们采用和GCN中相同的实验设置:对于每个类别,我们选择20个节点进行训练、500个节点进行验证、1000个节点用于测试。inductive Learning:在inductive learning环境下,未标记的测试节点可以在训练期间不可用。这意味着训练期间不知道测试图的结构。在
inductive learning环境下,我们通常具有不同的训练图、验证图、测试图。在训练期间模型仅使用训练图、而无法访问验证图和测试图。我们使用
protein-protein interaction: PPI数据集,其中包含20个训练图、2个验证图、2个测试图。由于验证图和测试图是独立的,因此训练过程中不会使用它们。平均每个图包含2372个节点,每个节点包含50个特征。每个节点都有来自121个类别的多个标签。
下表给出这些数据集的统计量。
degree属性是每个数据集的平均节点degree,这有助于选择LGCL中的超参数
实验配置:
transduction Learning:由于
transductive learning数据集使用高维的bag-of-word作为特征向量,因此输入经过graph embedding layer来减小维度。这里我们使用
GCN layer来作为graph embedding layer,embedding的输出维度为32。然后我们使用
LGCL,每个LGCL使用8的特征向量。对于Cora/Citesser/Pubmed,我们分别堆叠了2/1/1个LGCL。另外,我们在
skip-connection中使用拼接操作。最后,将全连接层用作分类器以进行预测。在全连接层之前,我们执行一个简单的
sum操作来聚合邻域节点的特征向量。在每一层的输入特征向量和邻接矩阵上都应用
dropout,dropout比例分别为0.16和0.999。所有
LGCN模型都使用子图训练策略,子图大小设置为2000。
inductive Learning:除了某些超参数之外,使用和transductive learning相同的配置。- 对于
graph embedding layer,输出特征向量维度为128。 - 我们堆叠两层
LGCL, - 我们还使用子图训练策略,子图初始节点大小等于
500和200。 - 在每一层应用
dropout,dropout比例为0.9。
- 对于
对于
transductive learning和inductive learning,LGCN模型共享以下配置:- 对于所有层仅使用线性激活函数,这意味着网络中不涉及非线性。
- 为了避免过拟合,使用
L2正则化。 - 训练期间,使用学习率为
0.1的Adam优化器。 LGCN中的权重使用Glorot方法初始化。- 我们根据验证集准确率来执行早停策略,最多训练
1000个epoch。
实验结果:
Transduction Learning实验结果:我们报告了不同模型在节点分类任务上的准确率。根据结果,LGCN模型在Cora, Citeseer, Pubmed数据集上的性能比state-of-the-art的GCN分别提高了1.8%, 2.7%, 0.5%(绝对提升)。其中LGCN模型。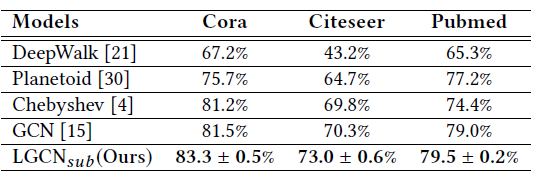
Inductive Learning实验结果:我们报告了不同模型的micro-averaged F1得分。根据结果,LGCN模型的性能比GraphSAGE-LSTM提高了16%。这表明在训练期间看不到测试图的情况下,LGCN模型仍然取得很好的泛化能力。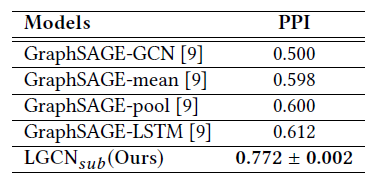
上述实验结果表明:
- 在通用的图数据上提出的
LGCN模型在不同节点分类数据集上一致性地达到state-of-the-art性能。 - 这些结果证明了在变换后的图数据上应用常规卷积运算的有效性。
- 另外,通过
k-largest node selection实现的转换方法被证明是有效的。
LGCL vs GCL Layer:有人认为LGCN性能的提高仅仅是因为LGCN模型采用的网络体系结构比GCN更深。但是,已有论文提出:通过堆叠更多的层来加深GCN会导致性能更差。因此,这里我们进行另一项实验:将
LGCN模型中所有LGCL替换为GCN Layer,称之为下表给出了
LGCL比GCN Layer更为有效。
子图训练
vs全图训练:上述实验中我们使用子图训练策略来训练LGCN模型,旨在节省内存和训练时间。但是,由于子图选择算法从整个图中抽取一些节点作为子图,这意味着以这种方式训练的模型在训练过程中不了解整个图的结构。同时,在transductive learning环境下,测试节点的信息可能会被忽略,从而增加了性能下降的风险。为解决这个问题,我们在
transductive learning环境下进行实验,从而比较子图训练策略subgraph training strategy和全图训练策略whole-graph training strategy。通过实验,我们证明了子图训练策略的优势,同时在模型性能方面的损失可以忽略不计。对于子图选择过程,在
transductive learning环境下我们仅从带有训练标签的节点中采样初始节点,以确保训练可以进行。具体而言,对于Cora/Citeseer/Pubmed数据集,我们分别随机采样140/120/60个初始节点。在迭代过程中,我们并没有设置2000。对于我们的GPU而言这是可行的大小。为进行比较,我们使用相同的
LGCN模型进行实验,但使用和GCN相同的全图训练策略来训练它们。这意味着输入是整个图的表示。和使用子图训练策略的下表给出了这两种模型和
GCN的比较结果:报告的节点数表示一次迭代训练使用了多少个节点;报告的时间是使用单个TITAN Xp GPU运行100个epoch的训练时间;报告的准确率是测试准确率。可以看到:
Cora/Citeseer/Pubmed数据集的子图训练中,子图的实际节点数量分别为644/442/354,远小于最大的子图大小2000。这表明这三个数据集中的节点是稀疏连接的。具体而言,从带有训练标记的几个初始节点开始,通过扩展相邻节点以形成连接的子图,只会选择一小部分节点。尽管通常将这些数据集视为一个大图,但是整个图实际上只是由彼此独立的几个单独的子图组成。子图训练策略利用了这一事实,并有效利用了带训练标签的节点。
由于只有初始节点具有训练标签,并且所有这些初始节点的连接性信息都包含在所选子图中,因此子图训练中的信息丢失量降到最低,从而导致性能损失几乎可以忽略不计。
通过对比
Cora数据集上有0.5%的微小性能损失,而在Citeseer和Pubmed数据集上却具有相同的性能。在调查了性能损失的风险之后,我们看到子图训练策略在训练速度方面的巨大优势。通过使用子图训练策略,和全图训练策略相比,
从结果可以看到,这种训练效率的提升是显著的。尽管
GCN的计算更简单,它在Pubmed之类的大规模图数据集上的运行时间比LGCN模型要长的多。通常在大规模图数据上应用强大的深度学习模型,这使得子图训练策略在实践中很有用。子图训练策略可以使用更复杂的层,如
LGCL,而无需担心训练时间。结果,带有子图训练策略的大型LGCN不仅效果好而且效率高。
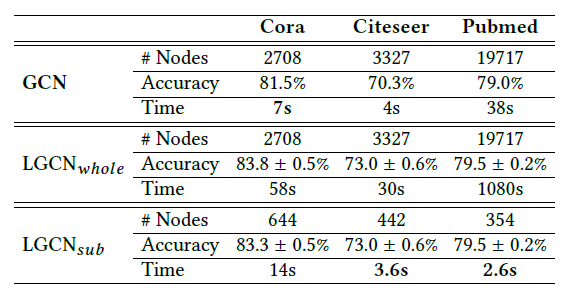
超参数
LGCN中选择超参数degree会有所帮助。这里我们进行实验来展示不同的LGCN模型的性能。我们在
Cora,Citeseer,Pubmed数据集上调整[2,4,8,16,32],这覆盖了合理范围内的整数值。下图给出了不同
LGCN模型的性能变化。可以看到:LGCN模型上的所有三个数据集在Cora, Citeseer, Pubmed数据集中,平均节点degree分别为4/5/6。这表明最佳的degree稍大一点。- 当
LGCN模型的性能会降低。可能的解释是:如果degree大得多,那么在k-largest node selection过程中使用了太多的零填充,这会不利于接下来的1-D CNN模型的性能。 - 对于
PPI数据集上的inductive learning任务,我们也探索了不同的degree为31。这和我们上面讨论的结果一致。
三十二、DGCNN[2018]
摘要:直接读取
graph并对graph进行分类,有两个挑战:- 如何编码
graph中丰富的信息从而用于分类。为此论文《An End-to-End Deep Learning Architecture for Graph Classification》设计了一个局部图卷积模型localized graph convolution model,并展示了它与两个graph kernel的联系。 - 如何以一个有意义
meaningful且一致的consistent顺序来读取一个graph。为此论文《An End-to-End Deep Learning Architecture for Graph Classification》设计了一个新颖的SortPooling层,该层以一致的顺序对图的节点进行排序,以便可以在图上训练传统的神经网络。
在
benchmark图分类数据集上的实验表明,所提出的架构与最先进的graph kernel和其他图神经网络方法相比,取得了极具竞争力的性能。此外,该架构允许使用原始图进行端到端的梯度训练,而不需要首先将图转化为向量。整个架构称之为Deep Graph Convolutional Neural Network:DGCNN。- 如何编码
引言:过去几年中,神经网络在图像分类、自然语言处理、强化学习、以及时间序列分析等应用领域日益盛行。层与层之间的连接结构使神经网络适合处理张量形式的信号,其中张量元素以有意义的顺序排列。这种固定的输入顺序是神经网络提取高层次特征的基石。例如,如果我们随机混洗下图所示图像的像素,那么
SOTA的卷积神经网络就无法将其识别为一只鹰。
虽然图像和许多其他类型的数据都是有自然的顺序,但还有另一大类结构化数据,即
graph,它们通常缺乏具有固定顺序的张量表示tensor representation。graph的例子包括分子结构、知识图谱、生物网络、社会网络、以及有依赖关系的文本文档。有序张量表示的缺乏,限制了神经网络在图上的适用性。最近,人们对将神经网络推广到图上的兴趣越来越大:
《Spectral networks and locally connected networks on graphs》将卷积网络推广到谱域中的graph,其中滤波器应用于图的频率模式frequency mode。这个频率模式由图傅里叶变换计算得到。- 图傅里叶变换涉及到与图拉普拉斯矩阵的特征向量的昂贵乘法。为了减少计算负担,
《Convolutional neural networks on graphs with fast localized spectral filtering》将谱域滤波器参数化为特征值的Chebyshev多项式,并实现了高效的和局部化的滤波器。
上述谱域公式的一个局限性是:它们依赖于图拉普拉斯矩阵的固定频谱,因此只适合于具有固定单一结构的图。相反,空域公式不限于固定的图结构。为了提取局部特征,有几项工作独立提出在相邻节点之间传播特征。
《Convolutional networks on graphs for learning molecular fingerprints》提出了可微分的神经图指纹Neural Graph Fingerprint,它在1-hop邻居之间传播特征,以模拟传统的圆形指纹circular fingerprint。《Diffusion-convolutional neural networks》提出了Diffusion-CNN,它使用不同的权重将不同hop的邻居传播到中心节点。- 后来,
《Semi-supervised classification with graph convolutional networks》开发了针对《Convolutional neural networks on graphs with fast localized spectral filtering》提出的谱域卷积的一阶近似,这也导致了相邻节点之间的传播。 《Learning convolutional neural networks for graphs》提出了另一种空域图卷积的方式,从节点的邻域中提取固定大小的local patch,并用graph labeling方法和graph canonization工具对这些patch进行线性化处理。由此产生的算法被称为PATCHY-SAN。
由于空域方法不需要单一的图结构,它们可以被应用于节点分类和图分类任务。虽然取得了
SOTA的节点分类结果,但以前的大多数工作在图分类任务上的表现相对较差。其中一个原因是,在提取局部节点特征后,这些特征被直接sum从而用于图分类的图graph-level特征。在论文《An End-to-End Deep Learning Architecture for Graph Classification》中,作者提出了一个新的架构,可以保留更多的节点信息并从全局图的拓扑结构中进行学习。一个关键的创新是一个新的SortPooling层,它从空域图卷积中获取图的无序节点特征作为输入。SortPooling不是将这些节点特征相加,而是将它们按照一致的顺序排列,并输出一个固定大小的sorted graph representation,这样传统的卷积神经网络就可以按照一致的顺序读取节点并在这个representation上进行训练。作为图卷积层和传统神经网络层之间的桥梁,SortPooling层可以通过它来反向传播损失的梯度,将graph representation和graph learning融合为一个端到端的架构。论文贡献如下:
- 论文提出了一个新颖的端到端深度学习架构,用于图分类。它直接接受图作为输入,不需要任何预处理。
- 论文提出了一个新颖的空域图卷积层来提取多尺度
multi-scale的节点特征,并与流行的graph kernel进行类比,从而解释为什么它能发挥作用。 - 论文开发了一个新颖的
SortPooling层来对节点特征进行排序,而不是将它们相加,这样可以保留更多的信息,并允许我们从全局范围内学习。
相关工作:
Graph Kernel:Graph Kernel通过计算一些半正定的graph similarity度量,使SVM等kernel machine在图分类中变得可行,在许多图数据集上取得了SOTA的分类结果。- 一个开创性的工作是在
《Convolution kernels on discrete structures》中引入了convolution kernel,它将图分解成小的子结构substructure,并通过增加这些子结构之间的成对相似度来计算核函数kernel function。常见的子结构类型包括walk、subgraph、path、以及subtree。 《Graph invariant kernels》以一种通用的方式重新表述了许多著名的基于子结构的核,称为图不变核graph invariant kernel。《Deep graph kernels》提出了deep graph kernel,它学习子结构的潜在representation从而利用其依赖信息。
convolution kernel根据两个图的所有子结构对进行比较。另一方面,assignment kernel倾向于找到两个图的子结构之间的对应关系。《An aligned subtree kernel for weighted graphs》提出了包含显式子树对应关系的aligned subtree kernel。《On valid optimal assignment kernels and applications to graph classification》为一种类型的hierarchy-induced kernel提出了最佳分配。
大多数现有的
graph kernel侧重于对比小的局部模式。最近的研究表明,对比图的全局模式可以提高性能。《Discriminative embeddings of latent variable models for structured data》使用latent variable model表示每个图,然后以类似于graphical model inference的方式显式地将它们嵌入到特征空间。结果在准确性和效率方面与标准graph kernel相比都很好。DGCNN与一类基于structure propagation的graph kernel密切相关,具体而言是Weisfeiler-Lehman(WL) subtree kernel和propagation kernel (PK)。为了编码图的结构信息,WL和PK基于中心节点的邻居的特征迭代更新中心节点的特征。WL对hard节点标签进行操作,而PK对soft标签分布进行操作。由于这种操作可以有效地实现为随机行走,这些graph kernel在大型图上是有效的。与WL和PK相比,DGCNN有额外的参数graph kernel的两阶段框架。- 一个开创性的工作是在
用于图的神经网络:
将神经网络推广到图的研究有两条线:给定一个单一的图结构,推断单个节点的标签或者单个图的标签;给定一组具有不同结构和大小的图,预测未见过的图的类标签(图分类问题)。
在本文中,我们专注于第二个问题,这个问题更加困难,因为:图的结构不是固定的,每个图内的节点数量也不是固定的。此外,在第一个问题中来自不同图的节点具有固定的索引或对应的索引,但是在第二个问题中节点排序往往是不可用的。
我们的工作与一项使用
CNN进行图分类的开创性工作有关,称为PATCHY-SAN。为了模仿CNN在图像上的行为,PATCHY-SAN首先从节点的邻域中提取固定大小的局部patch作为卷积滤波器的感受野。然后,为了在这些patch上应用CNN,PATCHY-SAN使用外部软件(如图规范化工具NAUTY)在预处理步骤中为整个图定义一个全局节点顺序,以及为每个patch定义一个局部顺序。之后,graph被转换为有序的tensor representation,并在这些张量上训练CNN。虽然取得了与
graph kernel有竞争力的结果,但这种方法的缺点包括繁重的数据预处理、以及对外部软件的依赖。我们的DGCNN继承了其为图节点施加顺序的思想,但将这一步骤集成到网络结构中,即SortPooling层。在如何提取节点特征方面,
DGCNN也与GNN、Diffusion-CNN、以及Neural Graph Fingerprint相关。然而,为了进行graph-level分类,GNN监督单个节点(是一个虚拟的超级节点,它节点与所有其它真实节点相连),而Diffusion-CNN和Neural Graph Fingerprint使用sum的节点特征。相比之下,DGCNN以某种顺序对节点进行排序,并将传统的CNN应用于有序的representation上,这样可以保留更多的信息,并能从全局图拓扑结构中学习。
32.1 模型
给定图
0/1矩阵。并且图中没有自环self-loop。- 每个节点
DGCNN包含三个连续的阶段:- 图卷积层
graph convolution layer抽取节点的局部子结构特征,并定义一致的节点顺序。 SortPooling层按照前面定义的顺序对节点特征进行排序,并统一输入尺寸size。- 传统的卷积层和
dense层读取排序的graph representation并进行预测。
DGCNN整体架构如下图所示:图数据首先通过多个图卷积层,其中节点信息在邻域之间传播;然后对节点特征排序并通过SortPooling层池化;然后传递给传统的CNN结构以学习模型。节点特征以颜色来可视化。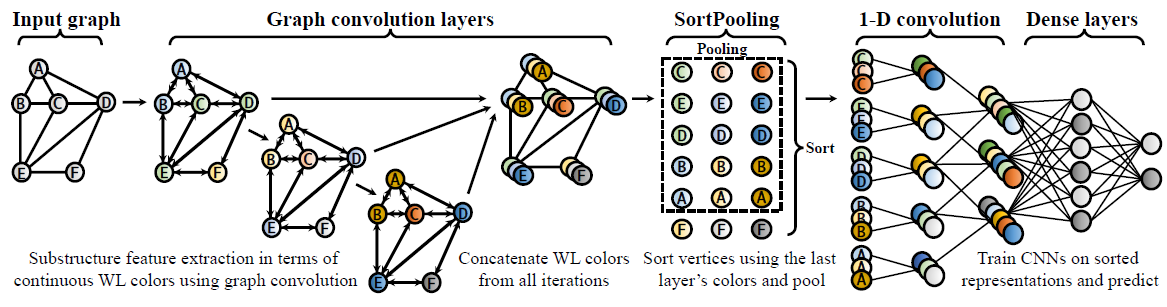
- 图卷积层
32.1.1 图卷积层
我们的图卷积层的形式为:
其中:
self-loop的邻接矩阵。
图卷积层聚合局部邻域的节点信息从而抽取局部子结构。为了抽取多尺度
multi-scale的子结构特征,我们堆叠多个图卷积层。第其中:
representation,representation。
假设一共有
拼接的结果
feature descriptor,它编码了节点的多尺度局部子结构信息multi-scale local substructure information。我们的图卷积层和
GCN层很相似,区别在于它们使用不同的传播矩阵。GCN layer采用可以证明,我们的图卷积层有效地模仿了两个流行的
graph kernel(Weisfeiler-Lehman subtree kernel、propagation kernel)的行为,这有助于解释其graph-level分类行为。WL-test对节点邻域进行反复迭代,最终根据两个图之间的节点label是否完全相同,从而判断两个图是否同构的。注:这里的label更多地是节点的离散特征,而不是节点的监督信息。WL-test迭代过程如下:聚合节点及其邻域的label;将聚合后的label经过哈希函数得到不同的、新的label,即relabel。《Weisfeiler-lehman graph kernels》根据WL-test提出了WL subtree kernel来衡量两个图的相似性。核函数利用WL tet的不同迭代中使用的节点label数作为图的特征向量。直观地讲,WL test第label代表了以该节点为根的、高度为WL subtree kernel考虑的图特征本质上是不同根子树的计数。如果我们记
我们可以视
continuous color。因此我们的图卷积公式可以视为WL-test算法的一个soft版本。soft版本有两个好处:- 首先,卷积参数
WL subtree kernel具有更好的表达能力。 - 其次,使用稀疏矩阵乘法更容易实现
soft WL-test,避免了读取和排序可能非常长的WL signature字符串。
- 首先,卷积参数
propagation kernel:PK比较了两个图的label分布,它基于扩散更新的方案diffusion update scheme:其中:
label distribution向量。其初始值就是每个节点label的one-hot。
最终将所有迭代过程中的
label distribution向量通过locality-sensitive hashing:LSH映射到离散的分桶,从而计算label distribution向量之间的相似性。PK具有和WL kernel类似的graph分类性能,甚至具有更高的效率。而我们的图卷积公式和PK非常相似。
WL kernel在hard vertex label上进行,而PK在soft label distribution上进行。这些操作都可以有效地实现为随机游走,因此这些核函数在大规模图上非常有效。和WL kernel和PK相比,DGCNN在传播之间具有其它参数,这些参数是通过端到端优化进行训练的。这允许从标签信息中进行有监督的特征学习,使其不同于graph kernel的两阶段框架。WL kernel的基本思想是将节点的颜色和其1-hop邻域的颜色拼接起来作为节点的WL-signature,然后按照字典顺序对signature字符串进行排序从而分配新的颜色。具有相同signature的节点将分配相同的新颜色。这种 “聚合--分配” 动作和我们的图卷积层是类似的,因此我们称
WL color。
32.1.2 SortPooling 层
SortPooling层的主要功能是将特征描述符输入传统的1-D卷积层和dense层之前,以一致的顺序对特征描述符进行排序,其中每个特征描述符对应于一个节点。问题是:以什么样的顺序对节点进行排序?在图像分类中,像素天然地以某种空间顺序排序。在
NLP任务中,可以使用字典顺序对单词进行排序。在图中,我们可以根据节点在图中的结构角色structural role对节点进行排序。一些工作使用
graph labeling方法(如WL kernel)来在预处理阶段对节点进行排序,因为最终的WL color定义了基于图拓扑的排序。WL施加的这种节点顺序在各个图之间是一致的,这意味着如果两个不同图中的节点在各自图中具有相似的结构角色,那么它们会被分配以相似的相对位置。结果,神经网络可以按顺序读取图节点并学习有意义的模型。在
DGCNN中,我们也使用WL color来对节点进行排序。幸运的是,我们已经看到图卷积层的输出正好是连续的WL colorSortPooling层。对于SortPooling层:- 输入是一个
feature channel。 - 输出是一个
在
SortPooling层中,首先根据WL color,并根据这个final color对所有节点进行排序。通过这种方式,我们对图节点施加了一致的排序,从而可以在排序的
graph representation上训练传统的神经网络。理想情况下,我们需要图卷积层足够深(意味着- 输入是一个
基于
node representation的最后一维)。- 如果两个节点在
- 如果两个节点在
- 如果两个节点在
除了一致性的顺序对节点特征进行排序外,
SortPooling还有一个能力是统一输出张量的尺寸size。排序后,我们将输出张量的尺寸从
graph size,使得不同数量节点的图将其大小同一为- 如果
- 如果
这和
LGCN的k-largest节点选择方法很类似。只是LGCN独立地选择并排序最大的k个特征,而SortPooling根据final color选择最大的k个节点。除此之外,LGCN和DGCNN还有一个最大的区别:LGCN中,卷积层用于根据邻域节点的k-largest representation来更新中心节点的representation,因此最终用于节点分类。DGCNN中,卷积层根据所有节点的GCN representation来获得graph representation,因此最终用于图分类。
- 如果
作为图卷积层和传统层之间的桥梁,
SortPooling还有另一个好处,就是通过它可以记住输入的排序顺序从而将损失梯度传递给前一层,从而可以训练前一层的参数。相比之下,一些工作在预处理阶段对节点进行排序,因此无法在排序之前进行参数训练。
32.1.3 其它层
在
SortPooling层之后,我们得到一个大小为- 为了在
CNN,我们添加若干个1-D卷积层和最大池化层,从而学习节点序列上的局部模式。 - 最后我们添加一个全连接层和一个
softmax输出层。
- 为了在
32.1.4 讨论
GNN设计的一个重要标准是:网络应该将同构图isomorphic graph映射到相同的representation,并且输出相同的预测。否则邻接矩阵中的任何排列permutation都可能对同一个图产生不同的预测。对于基于求和的方法这不是问题,因为求和对于节点排列是不变的。但是对于排序的方法
DGCNN, PATCHY-SAN需要额外注意。为了确保将同构图预处理为相同的张量,
PATCHY-SAN首先使用WL kernel算法,然后使用图规范化工具NAUTY。尽管NAUTY对于小图足够有效,但是理论上讲,图规范化graph canonization问题至少在计算上和图同构检验一样困难。相比之下,我们表明
DGCNN可以避免这种图规范化步骤。DGCNN使用最后一个图卷积层的输出对节点进行排序,我们表明:这可以视为是soft WL输出的连续颜色。因此DCNN能够将节点排序视为图卷积的副产品,从而避免像PATCHY-SAN这样显式运行运行WL kernel算法。并且,由于SortPooling中的排序方案,DGCNN不再需要图规范化。因此DGCNN不需要显式运行WL kernel或NAUTY,这使我们摆脱了数据预处理和外部软件的束缚。我们还指出,尽管
DGCNN在训练过程中会动态地对节点进行排序,但是随着时间的增加,节点顺序会逐渐变得稳定。这是因为参数continuous WL color。此外,训练过程中定理:在
DGCNN中,如果两个图SortPooling之后它们的图representation是相同的。证明:注意,第一阶段的图卷积对于节点索引是不变的。因此,如果
multiset。由于
SortPooling对于节点排序的方式是:当且仅当两个节点具有完全相同的特征描述符时,两个节点才有联系have a tie,因此排序的representation对于两个节点的排名具有不变性。因此,在SortPooling之后,representation。
32.2 实验
32.2.1 Graph Kernel 比较
数据集:五个
benchmark生物信息学数据集,包括MUTAG、PTC、NCI1、PROTEINS、D&D。所有节点都有label信息。baseline方法:四种graph kernel,包括graphlet kernel: GK、random walk kernel: RW、propagation kernel: PK、Weisfeiler-Lehman subtree kernel: WL。实验配置:使用
LIBSVM进行10-fold交叉验证,训练集为9 fold、测试集为1 fold,并使用训练集中的1 fold进行超参数搜索。每个实验重复
10次(因此每个数据集训练了100次),报告了平均的准确率和标准差。实验结果如下表所示,可以看到:
DGCNN相比graph kernel具有很强的竞争力。- 另外
DGCNN通过SGD进行训练,避免了graph kernel所需的DGCNN优势更大。
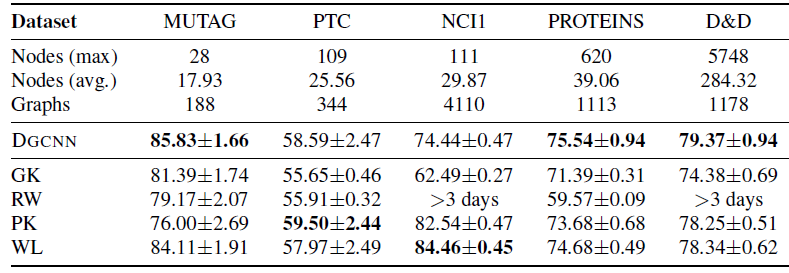
32.2.2 GNN 比较
数据集:六个数据集,其中包括三个生物信息学数据集
NCI1, PROTEINS, D&D、三个社交网络数据集COLLAB, IMDB-B, IMDB-M。这些社交网络数据集中的图没有节点label,因此是纯结构。baseline:四种深度学习方法,包括PATCHY-SAN: PSCN, DiffusionCNN: DCNN, ECC, Deep Graphlet Kernel: DGK。实验配置:对于
PSCN, ECC, DGK,我们报告原始论文中的最佳结果,因为他们实验配置和我们这里相同。对于DCNN,我们使用我们的实验配置重新实验。PSCN, ECC能够额外地利用边特征,但是由于这里很多数据集没有边特征,以及其它一些方法无法使用边特征,因此这里都没有利用边特征来评估效果。实验结果如下表所示,可以看到:
DGCNN在PROTEINS, D&D, COLLAB, IMDB-M数据集上表现出最高的分类准确率。和
PATCHY-SAN相比,DGCNN的改进可以解释如下:- 通过使梯度信息通过
SortPooling向后传播,DGCNN甚至可以在排序开始之前就启用参数训练,从而实现更好的表达能力。 - 通过动态排序节点,
DGCNN不太可能过拟合特定的节点排序。相比之下,PATCHY-SAN遵从预定义的节点顺序。
- 通过使梯度信息通过
DGCNN的另一个巨大优势是:它提供了一种统一方法,将预处理集成到神经网络结构中。和使用
sum节点特征来分类的DCNN相比,DGCNN表现出显著的提升。为了证明
SortPooling优于求和的优势,我们进一步列出了DGCNN(sum)的结果,该结果采用sum layer替换DGCNN的SortPooling和后面的1-D卷积层。可以看到,大多数情况下性能下降很多。
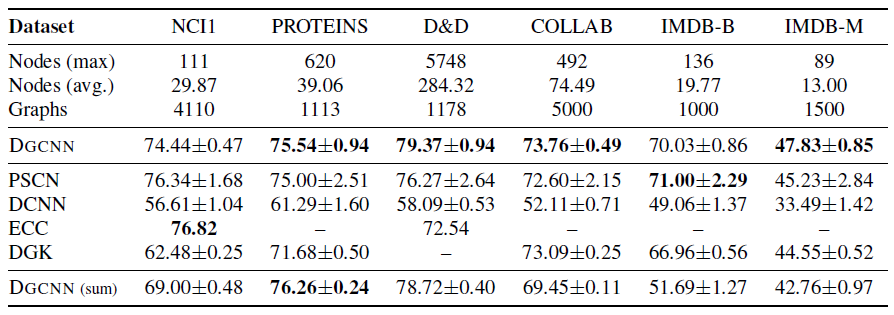
三十三、AS-GCN
当前图神经网络
GNN的一个明显挑战是可扩展性。在GCN中计算图卷积需要跨层递归扩张邻域,这在计算上是不现实的,并且需要占用大量内存。即使对于单个节点,当图是稠密的或者满足幂律powerlaw分布时,由于邻域的逐层扩张,这将迅速覆盖图的很大一部分。传统的mini-batch训练无法加快图卷积的计算速度,因为每个batch都将涉及大量节点,即使mini-batch本身很小。为缓解过度扩张
over-expansion的问题,一些工作通过控制采样邻域的大小来加速GCN的训练。有几种基于采样的方法用于图上进行快速的representation learning:GraphSAGE通过对每个节点的邻域进行采样(node-wise采样),然后执行特定的聚合器以进行信息融合来计算节点的representation。FastGCN模型将图卷积解释为embedding函数的积分变换,并独立采样每一层中的节点(layer-wise采样)。VRGCN是control-variate-based方法 ,这种采样方法也是node-wise,并且需要节点的历史激活值。
论文
《Adaptive Sampling Towards Fast Graph Representation Learning》提出了一种新的layer-wise采样方法:按照自上而下的方式逐层构建网络,其中下层的节点是根据上层的节点有条件采样而来。这种层级采样layer-wise sampling在两个技术方面是有效的:- 首先,由于较低层中的节点是可见的
visible,并且由于它们在较高层中的不同父节点之间共享,因此我们可以复用采样邻域的信息(即低层节点)。 - 其次,很容易固定
fix每一层的大小,从而避免邻域的过度扩张,因为较低层的节点是整体采样的。
和基于节点采样的
GraphSAGE相比,论文的方法基于层级采样,因为所有邻域都被一起采样,因此可以实现邻域共享;和独立构造每一层的FastGCN相比,论文的方法可以捕获跨层连接。因为较低的层根据上层的条件进行采样。论文方法的核心是为
layer-wise采样定义合适的采样器。通常,设计采样器的目标是使得结果的方差最小化。不幸的是,由于在论文的网络中自上而下的采样和自下而上的传播的不一致,使得方差最小化的最佳采样器是无法计算的uncomputable。为解决这个问题,作者通过使用自依赖函数代替不可计算的部分,然后将方差添加到损失函数,从而逼近最佳采样器。结果,通过共同训练模型参数和采样器 ,方差得到显著降低,这反过来又促进了模型的训练。此外,论文还探索了如何使得有效的消息跨远程节点
distant node来传递。有些方法通过随机游走以生成各个step的邻域,然后对multi-hop邻域进行整合。相反,本文通过在第skip-connection从而提出了一种新的机制。这种跳跃连接将第2-hop邻域,因此它自然地保持了二阶邻近性,而无需进行额外的计算。总之本文做出了以下贡献:
- 开发了一种新的
layer-wise采样方法来加速GCN模型,该模型共享层间信息,并可控制采样节点的规模。 - 用于
layer-wise采样的采样器是自适应的,并通过训练阶段显式降低方差来确定。 - 提出了一种简单而有效的方法,即通过在两层之间指定
skip-connection来保留二阶邻近性。
最后,论文在节点分类的四个流行
benchmark上评估了新方法的性能,包括Cora, Citeseer, Pubmed, Reddit。大量实验证明了新方法在分类准确率和收敛速度方面的有效性。相关工作:
如何设计高效的图卷积网络已成为一个热门研究课题。图卷积方法通常被分为谱域卷积和空域卷积两类:
谱域卷积方法首先由
《Spectral networks and locally connected networks on graphs》提出,并在傅里叶域定义卷积操作。后来,
《Deep convolutional networks on graph-structured data》通过应用高效的频滤波器实现了局部滤波。《Convolutional neural networks on graphs with fast localized spectral filtering》采用图拉普拉斯矩阵的Chebyshev多项式来避免特征分解eigen-decomposition。最近,
《Semi-supervised classification with graph convolutional networks》提出了GCN,它用一阶近似和重参数化技巧re-parameterization trick简化了以前的方法。空域卷积方法通过直接使用空间连接来定义图的卷积。例如:
《Convolutional networks on graphs for learning molecular fingerprints》为每个node degree学习一个权重矩阵。《Diffusion-convolutional neural networks》通过使用转移矩阵transition matrix的一系列幂次来定义multiple-hop邻域。《Learning convolutional neural networks for graphs》提取了包含固定数量节点的规范化的邻域。
最近的一个研究方向是通过利用
patch操作和自注意力来泛化卷积。与GCN相比,这些方法隐含地为邻域中的节点分配不同的重要性,从而实现了模型容量的飞跃。具体而言:《Geometric deep learning on graphs and manifolds using mixture model cnns》提出了mixture model CNN,使用patch操作在图上建立CNN架构。《Graph attention networks》通过attend中心节点的每个邻居,按照自注意力策略计算中心节点的hidden representation。
最近有两种基于采样的方法(即,
GraphSAGE和FastGCN被开发出来),用于图上的fast representation learning。具体而言:GraphSAGE通过对每个节点的邻域进行采样,然后执行特定的信息融合聚合器来计算节点的representation(node-wise采样)。FastGCN模型将图的卷积解释为embedding函数的积分变换,并对每一层的节点独立采样(layer-wise采样)。
虽然我们的方法与这些方法密切相关,但我们在本文中开发了一个不同的采样策略:
- 与
GraphSAGE以节点为单位的方法相比,我们的方法是基于layer-wise采样的,因为所有的邻域都是整体采样的,因此可以允许邻域共享。 - 与独立构建每一层的
FastGCN相比,我们的模型能够捕捉到层与层之间的联系,因为下层是以上层为条件进行采样的。
另一项相关工作是
《Fastgcn: Fast learning with graph convolutional networks via importance sampling》的基于控制变量的方法。然而,这种方法的采样过程是node-wise的,需要节点的历史激活historical activation。
33.1 模型
给定图
- 邻接矩阵
degree矩阵,它是一个对角矩阵, - 归一化的邻接矩阵定义为
- 每个节点
- 邻接矩阵
GCN是用于图representation learning的最成功的卷积网络之一。为区分不同层的节点,我们将第GCN的前向传播公式为:其中:
representation,representation。representation的维度。
GCN的前向传播公式表明:GCN要求邻域的完整扩张full expansion才能对每个节点进行前向计算。这使得在包含数十万个节点的大规模图上的学习变得计算量大而且消耗内存。为解决这个问题,本文通过自适应采样
adaptive sampling来加快前向传播。我们提出的采样器是自适应的,并且可以减少方差。- 我们首先将
GCN公式重写为期望的形式,并相应地引入node-wise采样。然后我们将node-wise采样推广为一个更有效的框架,称为layer-wise采样。 - 为了使得采样方差最小化,我们进一步提出通过显式执行方差缩减
variance reduction来学习layer-wise采样器。
最后,我们介绍了
skip-connection的概念,通过应用skip-connection来实现前向传播的二阶邻近性second-order proximity。- 我们首先将
33.1.1 自适应采样
node-wise采样:我们首先观察到GCN前向传播公式可以重写为期望的形式,即:其中:
degree:
加快上式的一个自然想法是通过蒙特卡洛采样
Monte-Carlo sampling来近似期望的计算。具体而言,我们通过其中
使用蒙特卡洛采样之后,
GCN前向传播公式的计算复杂度从然后我们以自顶向下的方式构造网络结构:递归地对当前层中每个节点的邻居进行采样,如下图所示。这里实线表示采样到的节点,虚线表示为未采样到的节点,红色节点表示至少有两个父节点的节点。
虽然
node-wise采样能够降低单层的计算复杂度,但是对于深度网络而言,这样的node-wise采样在计算上仍然昂贵,因为要采样的节点数量随着层数呈指数增长。假设网络有通常
graph是稀疏的,因此节点邻域的规模远远小于degree。layer-wise采样:通过应用重要性采样,我们进一步地将GCN前向传播公式重写为以下形式:其中
类似地,我们通过蒙特卡洛
Monte-Carlo方法来估计这个期望值从而加速计算:我们这种方法称作
layer-wise采样策略。layer-wise采样和node-wise采样方法不同:在
node-wise采样方法中,每个父节点并且每个父节点的邻域(子节点集合)对于其它父节点是不可见的。
另外采样节点数量随着网络深度指数增长。
在
layer-wise采样方法中,所有父节点并且采样到的子节点集合
更重要的是,每层的大小固定为
33.1.2 显式方差缩减
layer-wise采样剩下的问题是如何定义采样器为简单起见,我们将分布
《Monte Carlo theory, methods and examples》中重要性抽样的推导,我们得出结论:命题:
estimator最小化上式中方差
不幸的是,这里得到的最优采样器是不可行的。根据定义,采样器
hidden feature为缓解这个 “鸡和蛋” 的困境,我们学习了每个节点的自依赖函数
self-dependent function,从而确定每个节点对于采样的重要性。令
hidden feature,则得到:在本文中,我们定义
其中
hidden feature的维度。现在我们得到了
node-wise采样器,并且对于不同的layer-wise采样,我们汇总了所有节点这里定义的采样器是高效的,因为
注意,通过
假设有一个
mini-batch的数据pair对ground-truth label。- 通过
layer-wise采样,给定 - 然后执行自下而上的传播以计算
hidden feature并获得节点 - 然后将某些非线性函数和
softmax函数进一步添加到
考虑分类损失和采样方差,我们将混合损失定义为:
其中:
trade-off超参数,在我们的实验中固定为0.5。
注意:这里的方差实际上是节点
embedding向量的各维度方差的和(方差是跨多个采样之间来计算)。另外这里只考虑最后一层embedding的方差,并未考虑中间层embedding的方差。为了计算最后一项(方差项),需要对每个
batch执行多次采样,从而对同一个父节点的多个估计激活值计算方差。在损失函数中我们仅对最后一层的
embedding的方差进行惩罚以进行有效的计算,并发现它足以在我们的实验中提供有效的性能。- 通过
为了使得混合损失最小化,我们需要对混合损失进行梯度计算。
- 对于网络参数,如
Tensorflow)轻松得到。 - 对于采样器参数,如
幸运的是,我们证明了分类损失相对于采样器的梯度为零。我们还推导出有关采样器方差项相对于采样器的梯度。详细内容在原始论文的补充材料给出。
- 对于网络参数,如
33.1.3 Skip Connection
GCN的更新方程仅聚合来自1-hop邻域的消息。为了使网络更好地利用远处节点上的信息,我们可以用类似于随机游走的方式来采样multi-hop邻域,从而用于GCN更新。然而,随机游走需要额外的采样来获得远处的节点,这对于稠密图而言计算代价太高。本文中我们提出通过
skip connection来传播远处节点的信息。skip connection的关键思想是重用第2-hop邻域。如果我们进一步从skip connection,则聚合将涉及1-hop邻域和2-hop邻域。具体而言,
skip connection的更新方程为:其中:
由于
虽然论文实验表明显式计算
skip connection能提高模型效果,但是这里的近似计算带来的噪音使得最终没有效果提升。我们并未学习一个额外的参数
其中
skip connection的输出可以加到GCN layer,在非线性层之前。考虑到
skip connection的更新方程为:通过
skip connection,无需额外的2-hop采样即可保持二阶邻近性。此外,skip connection允许信息在两个远距离的层之间传递,从而实现了更有效的反向传播和模型训练。尽管设计相似,但是我们使用
skip-connection的动机和ResNet中的残差函数不同:- 在
ResNet中,使用skip connection的目的是通过增加网络深度来获得更好的准确率。 - 在我们这里,使用
skip connection用于保留二阶邻近性second-order proximity。
另外和
ResNet中使用恒等映射相反,我们模型中沿着skip connection的计算更加复杂,如- 在
如下图所示,使用不同采样方法来构建网络:
(a)表示node-wise采样方法;(b)表示layer-wise方法;(c)表示考虑skip-connection的采样方法。实线表示采样节点,虚线表示未采样节点,红色圆圈表示该节点在上层至少有两个父节点。
- 在
node-wise采样中,每个父节点的邻域都不会被其它父节点看到,因此父节点邻域和其它父节点之间的连接未被复用。 - 相反,在
layer-wise采样中,所有邻域被上层所有父节点所共享,因此利用了所有的层间连接。
- 在
33.1.4 讨论
和其它采样方法的联系:我们的方法和
GraphSAGE、FastGCN等方法的区别如下:我们提出的
layer-wise采样方法是新颖的。GrphSAGE对每个节点随机采样固定大小的邻域,是node-wise采样的。FastGCN虽然是layer-wise采样的,但是采样的分布对于每一层都是相同的。- 我们的
layer-wise方法,较低层的节点是在较高层节点的条件下进行采样的,这能够捕获层之间的相关性。
我们的框架是更通用的。
GraphSAGE和FastGCN都可以归类为我们框架的特定变体,具体而言:- 如果将
GraphSAGE被视为一个node-wise采样器。 - 如果将
FastGCN可以视为一个特殊的layer-wise方法。
- 如果将
我们的采样器是参数化的,并且可以训练来显式减少方差。
GraphSAGE和FastGCN的采样器不包含任何参数,并且没有自适应来最小化方差。- 相反,我们的采样器通过自依赖函数来调整最优重要性采样分布
optimal importance sampling distribution。通过对网络和采样器进行微调,可以显著减少结果的方差。
考虑
attention机制:GAT将self-attention机制应用于图representation learning。简而言之,它使用特定的attention值来取代GCN中的归一化邻接矩阵,即:其中
hiden feature之间的attention value。它通常计算为:其中
直接在我们的框架中应用类似于
GAT的注意力机制是不可行的,因为概率attention值hidden feature来决定。如前所述,除非在采样后已经建立了网络,否则就不可能计算出较低层的hidden feature。为解决这个问题,我们通过应用类似于自依赖函数开发了一种新的注意力机制:
其中:
33.2 实验
数据集:
- 引文网络数据集
Cora,Citeseer,Pubmed:目标是对学术论文进行分类。 Reddit数据集:目标是预测不同的帖子属于哪个社区community。
这些图的规模从小到大都有所不同。具体而言:
Cora,Citeseer的节点数量为Pubmed数据集包含超过Reddit数据集包含超过下表给出了这些数据集的统计量。

- 引文网络数据集
实验配置:
- 根据
FastGCN中的监督学习场景,我们使用训练样本的所有标签进行训练。 - 我们的采样框架是
inductive learning的。和提供了所有节点的transductive learning不同,我们的方法聚合来自每个节点的邻域信息,从而学到可以泛化到未见过节点的结构属性。 - 为了进行测试,可以使用全部邻域来计算新节点的
embedding,也可以像模型训练中那样通过采样进行近似。这里我们使用完整的邻域,因为它更直接、更容易实现。 - 对于所有数据集,我们使用具有两个隐层的网络。对于引文网络数据集,隐层维度为
16;对于Reddit数据集,隐层维度为256。 - 对于
Reddit数据集,我们固定底层的权重,并且预计算 - 对于所有数据集,顶层的
layer-wise采样数量为256,非顶层的layer-wise采样数量为:Cora, Citeseer数据集128、Pubmed数据集256、Reddit数据集512。 - 使用
Adam优化器,初始学习率为:对于Cora,Citeseer,Pubmed设置为0.001、对于Reddit为0.01。 - 所有数据集的权重衰减设置为
0.0004。 - 所有数据集采用
ReLU激活函数,并且没有dropout。 - 训练期间使用窗口为
30的早停来训练所有模型,并选择最佳验证准确率的模型用于测试。 - 所有实验是在单个
Tesla P40 GPU上进行。
- 根据
baseline方法:由于GraphSAGE和FastGCN它们作者提供的代码不一致,这里我们根据我们的框架重新实现它们,从而进行更公平的比较。- 我们通过对
node-wise采样,从而实现GraphSAGE方法。其中每个节点的邻域采样大小为5。这种重新实现命名为Node-Wise。 - 我们使用
《Fast learning with graph convolutional networks via importance sampling》中提出的独立同分布采样器来实现IID。 - 我们还将
Full GCN体系架构作为强大的baseline。
所有比较的方法共享相同的网络结构和训练设置,以进行公平的比较。
我们还对所有方法进行了前述介绍的注意力机制。
- 我们通过对
不同采样方法的比较:这里我们固定随机数种子,并且不进行任何早停实验。下图报告了
Cora,Citeseer, Reddit训练期间所有采样方法的收敛行为。曲线代表测试数据上的准确率曲线accuracy curve。这里一个training epoch意味着对所有训练样本进行一次完整的遍历。另外,为证明方差缩减的重要性,我们通过设置
Adapt(no vr)。其中自依赖函数的参数被随机初始化,并且不进行训练。可以看到:
我们的方法(称作
Adapt) 在所有三个数据集上的收敛速度都比其它采样方法更快。有趣的是,我们的方法甚至优于
Cora,Reddit上的Full模型。和我们的方法类似,
IID采样也是layer-wise的,但是它独立地构造了每一层。和IID采样相比,由于有条件采样,我们的方法获得了更稳定的收敛曲线。事实证明,考虑层间信息有助于提高模型训练的稳定性
stability和准确性accuracy。移除方差缩减的损失项确实会降低我们的方法在
Cora和Reddit上的准确率。对于Citeseer而言,移除方差缩减的损失项的效果不是很明显。我们推测这是因为Citeseer的平均degree(1.4)小于Cora(2.0)和Reddit(492),并且由于邻域的多样性有限,因此对方差的惩罚并没有那么重要。
此外我们还给出了
Pubmed和Reddit数据集的训练时间,单位:second/epoch。可以看到:所有方法的训练速度都比完整模型更快。
和
node-wise方法相比,我们的方法具有更紧凑的体系结构,因此具有更快的训练速度。为了说明这一点,假设顶层的节点数量为
node-wise方法的输入层、隐层、顶层的大小分别为5)。而我们模型中所有层的节点数量为node-wise方法。
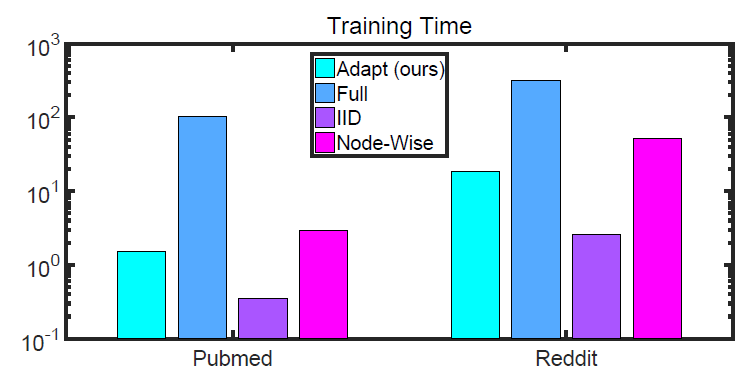
和其它
state-of-the-art方法的比较:我们使用graph kernel方法KLED和Diffusion Convolutional Network:DCN对比了我们方法的性能。- 我们使用
Cora和Pubmed在《Diffusion-convolutional neural networks》中报道的KLED和DCN的结果。 - 我们还通过其原始实现总结了
GraphSAGE和FastGCN的结果。对于GraphSAGE,我们报告了具有默认参数的均值聚合结果。对于FastGCN,我们直接使用《Diffusion-convolutional neural networks》提供的结果。
对于
baseline和我们的方法,我们使用随机数种子进行20多个随机实验,并记录了测试集的平均准确率和标准差。所有结果如下表所示,可以看到:- 我们的方法在所有数据集中都实现了最佳性能。
- 移除方差缩减将降低我们方法的性能,尤其是在
Cora和Reddit上。
另外,仅对顶层进行方差缩减就能够提升性能。事实上,在我们的方法中对所有层进行方差缩减也是方便的,例如将它们都添加到损失函数中。为说明这一点,我们通过最小化第一层和顶层隐层的方差来对
Cora进行实验,其中实验配置和下表相同。结果为0.8780 +- 0.0014,这比下表中的0.8744 +- 0.0034要更好。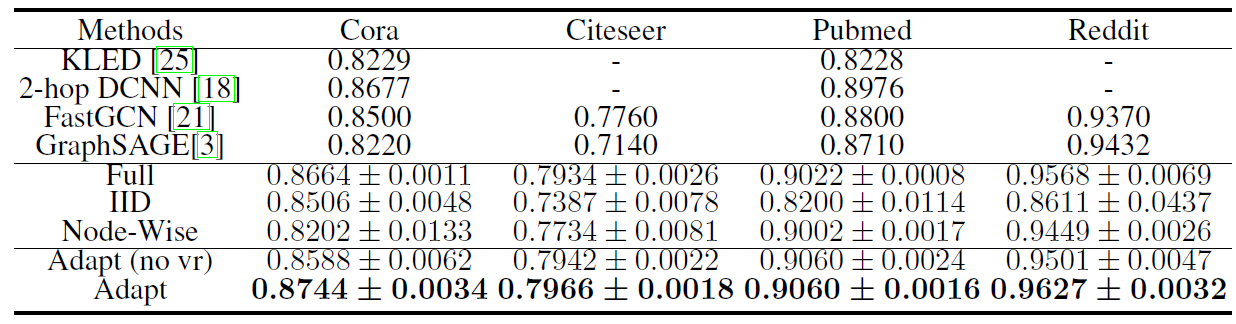
- 我们使用
我们使用公开的代码重新运行了
FastGCN实验。四个数据集的FastGCN的平均准确率为0.840 +- 0.005、0.774 +- 0.004、0.881 +- 0.002、0.920 +- 0.005。显然,我们的方法仍然超越了FastGCN。这里重新运行的
FastGCN和上表给出的结果(来自于各自的原始论文)不一致。我们观察到
GraphSAGE和FastGCN的官方实现之间的不一致之处,包括邻接矩阵的构造、隐层维度、mini-batch size、最大训练epoch数量、以及其它在论文中未提及的工程技巧。
我们评估在
Cora数据集上skip-connection的有效性。我们进一步在输入层和顶层之间添加了skip-connection。下图显式了原始Adapt方法以及带skip-connection变体的收敛曲线。其中随机种子是共享的,并且没有使用早停。可以看到:尽管就最终准确率而言,我们的
skip-connection带来的提升并不大,但是确实可以显著增加收敛速度。添加skip-connection可以将收敛epoch数量从150降低到100。
我们在
20个实验中使用不同的随机数种子进行实验,并在下表报告了使用早停获得的平均结果。可以看到,使用skip-connection可以稍微改善性能。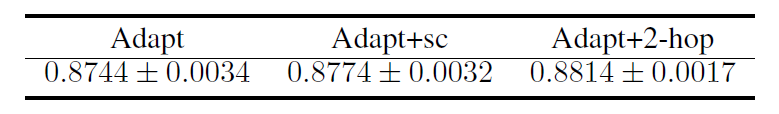
另外,通过将归一化的邻接矩阵
2-hop邻域采样包含在我们的方法中(直接计算归一化矩阵的二次幂)。如上表所示,显式2-hop邻域采样进一步提高了分类准确率。尽管skip-connection要比显式2-hop采样略差一点,但是它避免了最后,我们评估了
Citeseer,Pubmed数据集上skip-connection的有效性。- 对于
Citeseer数据集,skip-connection有助于更快地收敛。 - 对于
Pubmed数据集,添加skip-connection仅在训练的早期才有效果。
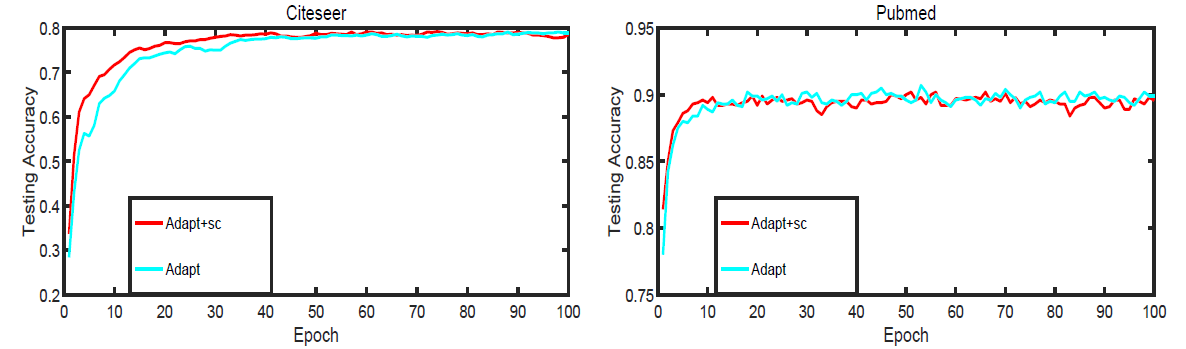
- 对于
三十四、DGI[2018]
目前将神经网络推广到图结构数据上已经取得了长足的进步,但是大多数成功的方法都是使用监督学习,而现实很多场景中图数据是缺乏标签信息的。此外,通常希望从大型的图中挖掘新颖或有趣的结构。因此,无监督的图学习对于很多任务至关重要。
目前图的无监督学习的主要算法依赖于随机游走的目标
random walk-based objective,有时会进一步简化为重建邻域信息。背后的直觉是:训练编码器网络,使得在输入图中邻近的节点在embedding空间中也是邻近的。尽管随机游走的方法的能力强大,但是仍然存在一些已知的限制:
- 首先,众所周知,随机游走目标会过分强调邻近信息
aproximity information,从而忽略图的结构信息structural information,并且性能高度依赖于超参数的选择。 - 此外,随着基于图卷积的更强大的编码器模型的引入,还不清楚随机游走目标是否实际上提供了任何有用的信号,因为这些图卷积编码器已经施加了
inductive bias,即相邻的节点具有相似的representation。
在论文
《Deep graph infomax》中,作者提出了一个基于互信息mutual information而不是随机游走的无监督的图学习的目标。作者提出了Deep Graph Infomax:DGI,这是一种以无监督方式学习图结构化数据的节点representation的通用方法。DGI依赖于最大化图的patch representation(即节点embedding)和相应的high-level summary之间的互信息mutual information,二者均使用已构建的图卷积网络体系结构得到。学到的path representation总结了目标节点为中心的子图,因此可复用于下游的node-wise学习任务。和大多数以前的使用
GCN进行无监督学习的方法相比,DGI不依赖于随机游走目标,并且很容易应用于transductive learning和inductive learning。该方法在各种节点分类benchmark上表现出有竞争力的性能,有时甚至超越了监督学习的性能。- 首先,众所周知,随机游走目标会过分强调邻近信息
最近
Mutual Information Neural Estimation:MINE使得互信息的可扩展估计scalable estimation可行又实用。MINE认为,利用神经网络的梯度下降法可以实现高维连续随机变量之间互信息的估计。具体而言,给定随机变量其中:
根据定义有
KL散度。MINE利用了KL散度的对偶表示,并依赖于训练一个统计网络作为样本的分类器,而样本来自于两个随机变量的联合分布(类别一)及其边际概率的乘积(类别二)。继
MINE之后,Deep InfoMax: DIM训练编码器模型,从而最大化high-level全局representation和局部的部分输入(如图像的patch)的局部representation之间的互信息。这鼓励编码器携带在所有位置location都存在的信息类型(因此是全局相关的),例如图像类别标签。DIM在图像数据场景中严重依赖于卷积神经网络结构。据我们所知,目前还没有工作将互信息最大化应用于图结构数据。这里我们将DIM的思想应用到图数据,因而提出了称之为Deep Graph Infomax:DGI的方法。相关工作:
对比方法
contrastive method:无监督学习representation的一种重要方法是训练编码器,使得编码器在捕获感兴趣的representation和不感兴趣的representation之间形成对比。例如,可以使得编码器对于real输入增加评分、对于fake输入降低评分。评分函数有很多种,但是在图数据相关论文中,常见的是分类的得分。DGI也使用了对比学习,因为我们的目标是基于真实local-global pair对、以及负采样的local-global pair对进行分类。采样策略:对比学习的关键是如何采样正样本和负样本。
- 关于无监督的
graph representation learning的先前工作依赖于局部对比损失,即强制相邻的节点具有相似的representation。正样本通常对应于图的short random walk中共现的pair对。从语言模型的观点来看,这是将随机游走视为句子、将节点视为word。 - 最近的工作采用
node-anchored采样方法,该方法的负样本主要基于随机采样。例如:有一些curriculum-based负采样方法,它逐渐采样更靠近closer的负样本。或者,引入对抗方法来选择负样本。
- 关于无监督的
预测编码
predictive coding:对比预测编码contrastive predictive coding: CPC是另一种基于互信息最大化的深度学习表示方法。和我们方法不同,CPC和上述的图方法都是预测性的predictive:对比目标有效地在输入的结构之间训练了一个predictor,如相邻节点pair对或者节点和它的邻域。而我们的方法同时对比了图的global部分和local部分,其中global变量是根据所有local变量计算而来。
34.1 模型
给定图
每个节点
这里我们假设图是无权重的,即
我们的目标是学习一个编码器
encoderrepresentation矩阵,它的第representation向量,representation向量的维度。一旦学到
representation向量就可以用于下游的任务,如节点分类任务。这里我们重点介绍图卷积编码器,它是一种灵活的
node embedding架构,并且通过在局部邻域上反复聚合从而生成节点representation。一个关键结果是:生成的节点
embeddingsummarize了节点patch的信息,而不仅仅是节点patch representation来强调这一点。我们学习编码器的方法依赖于最大化局部互信息
local mutual information,即:我们寻求节点的representation(局部的),它捕获了整个图的全局信息内容(通过一个summary vector为了获得
graph-level的summary vectorreadout函数patch representation总结为graph-level representation:作为最大化局部互信息的代理
proxy,我们使用了一个判别器discriminatorpatch-summary的pair对之间的概率得分。如果summary包含这个patch,则会返回一个更高的得分。判别器的正样本来自于
patch representation和summary vector的pair对注意,正样本来自于联合分布
判别器的负样本来自于另一个图
patch representation和图summary vector的pair对在多图的环境下,可以将
注意,负样本来自于边际分布乘积
负样本的选择将决定特定类型的结构信息,这些结构信息是作为这种互信息最大化的副产品而希望捕获的。
我们遵循
Deep InfoMax:DIM的直觉,使用对比噪音类型的目标函数noise-contrastive type objective:在联合分布(正样本)和边际概率乘积(负样本)之间应用标准的二元交叉熵binary cross-entropy:BCE损失。遵从DIM的工作,我们使用以下目标函数:基于联合分布与边际概率乘积之间的
JS散度,该方法有效地最大化
由于迫使所有得到的
patch representation都保持全局graph summary的互信息,这使得可以保留patch-level的相似性。例如,具有相似结构角色structural role的距离遥远的节点(众所周知,这些节点是很多节点分类任务的强力的predictor)。假设在单图环境下,
DGI的过程如下图所示:使用随机扰动函数
扰动函数的选择非常重要,可以仅扰动
通过编码器获取输入图
patch representation:通过编码器获取负样本
patch representation:通过
readout函数获取输入图summary vector:通过对损失函数
34.2 定理
现在我们提供一些直觉,将判别器
graph representation上的互信息最大化联系起来。令
node representation(每一组代表一个图,一共readout函数,summary vector,边际概率分布为当
证明见原始论文。
可以证明:
其中:
- 第一个不等式可以通过
Jensen不等式来证明。 - 第二个不等式当
readout函数是一个常量时成立,此时没有任何分类器表现得比随机分类更好。
- 第一个不等式可以通过
推论:从现在开始,假设所使用的
readout函数summary vector数量)满足summary证明见原始论文。
定理一:记
MI为互信息,则有证明见原始论文。
该定理表明:对于有限的输入集和合适的确定性函数,可以通过最小化判别器中的分类误差来最大化输入和输出之间的互信息。
定理二:令
high-level特征为:假设有
证明见原始论文。
这激发了我们在联合分布和边际概率乘积的样本之间使用分类器,并且在神经网络优化的上下文下,使用
binary cross-entropy:BCE损失来优化该分类器。
34.3 实验
我们评估了
DGI编码器在各种节点分类任务(transductive learning和inductive learning)上学到的representation的优势。在每种情况下,都是用
DGI以完全无监督方式学到了patch representation,然后用简单的线性(逻辑回归)分类器来进行node-level分类。分类器的输入就是节点的representation。数据集:
引文网络
Cora, Citeseer, Pubmed:它们是transductive learning数据集。在这些数据集中,节点表示论文,边表示论文之间的引用关系,节点特征对应于论文的bag-of-word。每个节点都有一个类别标签。我们对每个类别仅允许使用
20个节点进行训练。但是,为了遵循transductive learning,无监督学习算法可以访问所有节点的特征向量。我们在
1000个测试节点上评估了学到representation的预测能力。Reddit数据集:它是大图上的inductive learning数据集。我们使用2014年9月期间创建的Reddit帖子作为数据集,每个帖子代表节点,如果同一个用户对两个帖子都发表了评论则这两个帖子之间存在边。数据集包含
231443个节点、11606919条边。节点特征是帖子内容和评论的GloVe embedding向量、以及帖子的评分或者评论数量等指标。我们的目标是预测帖子所属的社区。我们将前
20天发布的帖子用于训练、剩余帖子用于验证或测试。并且训练期间,验证集和测试集是不可见的。PPI数据集:它是多图的inductive learning数据集。该数据集由不同人体组织对应的graph组成,其中包含20个图用于训练、2个图用于验证、2个图用于测试。注意,在训练过程中,测试图完全未被观察到。每个节点具有
50个特征,这些特征由positional gene sets, motif gene sets, immunological signatures等组成。一个节点可能具有多个标签,这些标签是从分子本体数据库收集的基因本体标签,共有121个。
所有数据集的统计信息如下表。
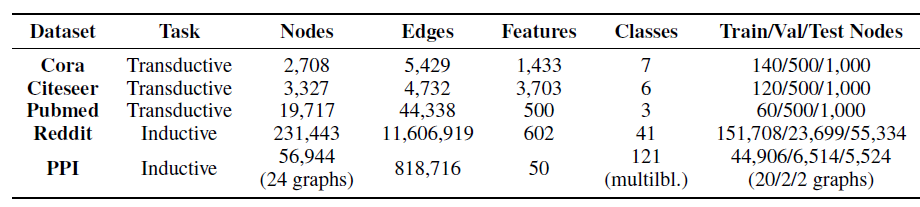
34.3.1 配置
我们对于
transductive learning、单图inductive learning、多图inductive learning使用不同的编码器和扰动函数。transductive learning:我们使用单层GCN作为编码器,即:其中:
ReLU(即parametric ReLU: PReLU)。Pubmed数据集,由于内存限制我们选择
这里使用的扰动函数旨在鼓励
representation正确编码图中不同节点的结构相似性,因此patch representation。论文证明了
DGI对于其它扰动函数是稳定的(参考原始论文),但是我们发现:保留图结构的那些扰动函数效果最好。单图
inductive learning:这里我们不再使用单层GCN作为编码器,因为这种编码器依赖于固定且已知的邻接矩阵。相反,我们使用GraphSAGE-GCN,并选择均值池化:这里通过度矩阵
GAT模型来编码。我们的编码器采用三层
GraphSAGE-GCN,并使用skip connection:其中
- 这里我们选择
PReLU激活函数。 - 考虑到
Reddit数据集规模较大,无法完全放入GPU内存。这里我们采用GraphSAGE中的采样方法:分别在第一层、第二层、第三层对邻域采样10/10/25个邻居节点。因此每个中心节点将采样1+10+100+2500=2611个3-hop邻域节点(称作一个patch)。 - 在整个训练过程中,我们使用了
batch-size=256的mini-batch随机梯度下降。 - 我们使用和
transductive learning中类似的扰动函数,但是将每个采样的patch视为要扰动的子图。注意,这可能导致中心节点的特征被替换为采样邻居的特征,从而进一步促进了负样本的多样性。然后将中心节点的patch representation馈入到判别器。
- 这里我们选择
多图
inductive learning:我们的编码器是一个三层的GraphSAGE均值池化模型,并且带skip connection:其中
inductive learning区别在于:这里的skip connection是sum融合,而前述的skip connection是concate融合。- 这里我们选择
PReLU激活函数。 - 在多图环境下,我们选择使用随机采样的训练
graph来作为负样本。即我们的扰动函数只是从训练集中采样了不同的图。考虑到该数据集中40%以上的节点包含全零的特征,因此这种方法最为稳定。 - 为进一步扩大负样本的范围,我们还对采样的
graph的输入特征应用dropout。 - 我们还发现将学到的
embedding馈入到逻辑回归模型之前,对包括训练集上的embedding进行标准化是有益的。
- 这里我们选择
在所有的配置下,我们使用统一的
readout函数、判别器架构:我们使用简单的均值函数来作为
readout函数:其中
sigmoid非线性函数。尽管我们发现该
readout函数在所有实验中表现最佳,但是我们假设其能力会随着graph size的增加而降低。此时,可能需要使用更复杂的readout架构,如set2vec或者DiffPool。判别器通过应用简单的双线性评分函数对
summary-patch进行评分:其中
sigmoid非线性激活函数。
所有模型都使用
Glorot初始化,并使用Adam SGD优化器进行训练,初始学习率为0.001(对于Reddit为在
transductive数据集上,我们在training loss上应用早停策略,patience epoch = 20。在inductive数据集上,我们训练固定数量的epoch,对于Reddit为150、对于PPI为20。
34.3.2 结果
baseline方法:transductive learning:我们进行了50次实验并报告测试集上的平均准确率和标准差。然后将我们的结果和DeepWalk, GCN, Label Propagation:LP, Planetoid等方法进行比较。另外我们还提供了对原始特征进行逻辑回归分类、将原始特征和
DeepWalk特征拼接进行逻辑回归分类的结果。inductive learning:我们进行了50次实验并报告了测试集上的micro-F1得分的均值。我们直接复用GraphSAGE论文中的结果进行比较。由于我们的方法是无监督的,因此我们对比了无监督的
GraphSAGE方法。我们还提供了两种监督学习的方法比较:
FastGCN和Avg. pooling。
实验结果如下表所示,其中第一列中我们给出每种方法在训练过程中可用的数据类型:
X为特征信息,A为邻接矩阵,Y为标签信息。GCN对应于以监督方式训练的两层DGI编码器。结论:
DGI在所有五个数据集上均实现了出色的性能。尤为注意的是,DGI方法和监督学习的GCN模型相比具有竞争力,并且在Cora数据集和Citeseer数据集上甚至超越了监督学习的GCN。我们认为这些优势源自事实:
DGI方法间接地允许每个节点都可以访问整个图的属性,而监督学习的GCN仅限于两层邻域(由于训练信号的极其稀疏,因此可能会遭受过拟合的风险)。应当指明的是,尽管我们能够超越同等编码器架构的监督学习,但是我们我们的性能仍然无法超越
state-of-the-art的transductive架构。DGI方法在Reddit和PPI数据集上成功超越了所有竞争的无监督GraphSAGE方法,从而验证了inductive learning节点分类任务中,基于局部互信息最大化方法的潜力。DGI在Reddit上的结果和监督学习的state-of-the-art相比具有竞争力,而在PPI上差距仍然很大。我们认为这可以归因于节点可用特征的极度稀疏:在PPI数据集上超过40%的节点具有全零特征。而我们的DGI方法中的编码器非常依赖于节点特征。我们注意到,随机初始化的图卷积网络(不需要经过训练)可能已经提取了非常有用的特征,并代表了强大的
baseline。这是众所周知的事实,因为它和WL test图同构测试有关。这已被GCN和GraphSAGE等论文所研究过。为此,我们提供了
Random-Init这个baseline,它是从随机初始化的编码器(不需要训练)获取节点embedding,然后馈入逻辑回归分类器。DGI可以在这个强大的baseline上进一步提升。- 在
inductive数据集上的结果表明:以前基于随机游走的负采样方法可能对于学习分类任务是无效的。
这个编码器其实就是
GCN/GraphSAGE等常用架构。最后,应该注意的是,更深的编码器减少了我们正负样本之间的有效变异性。我们认为这就是为什么浅层架构在某些数据集上表现更好的原因。虽然我们不能说这个趋势普遍存在,但是通过
DGI损失函数我们发现,通常采用更wider的模型而不是更deeper的模型可以带来收益。
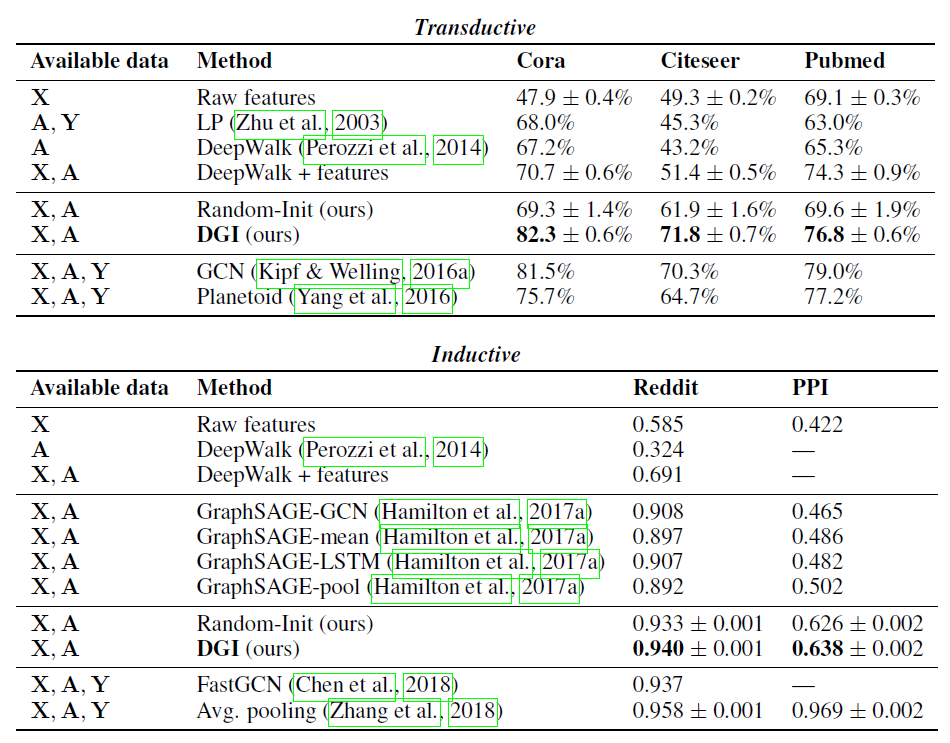
定性分析:我们给出
Cora数据集的embedding经过t-SNE可视化结果(因为该数据集节点数最少)。左图为原始特征的可视化,中间为Random-Init得到embedding的可视化,右图为训练好的DGI得到embedding的可视化。可以看到:
DGI得到的embedding的投影表现出明显的聚类。
在
t-SNE可视化之后,我们关注Cora数据集上判别器的得分。我们对于正样本和负样本(随机采样的)可视化了每个节点的判别器得分:左图为正样本(真实的图)、右图为负样本(负采样的图)。可以看到:
在正样本学到的
embedding的簇上,只有少数hot节点得到较高的判别器得分。这表明用于判别和分类的embedding各维度之间可能存在明显的差异。正如预期的那样,模型无法在负样本中找到任何强大的结构。
一些负样本种的节点获得了较高的判别器得分,这是由于
Cora中的一些low-degree节点引起的。正样本的平均分高于负样本的平均分。
我们将判别器打分
top-score的正样本和负样本的embedding进行可视化。如下图所示:上半部分为highest-scored正样本,下半部分为lowerst-scored负样本。可以看到:在某些维度上,正样本和负样本都存在着严重的
bias。我们假设:在随机
shufflebias需要将负样本的判别器得分拉下来。对于正样本,可以使用其它维度来抵消这些维度上的bias,同时编码patch相似度。
为证明这一假设,我们根据正样本和负样本之间的可区分性对
512个维度进行排序。我们从embedding中根据该顺序依次删除这些维度(要么从最有区分度的维度开始,记作可以看到,观察到的趋势在很大程度上支持了我们的假设:如果我们首先删除
biased维度(embedding维度,同时仍保持对监督GCN的竞争优势)。正样本仍然能够保持正确的判别,直到移除了一半以上的维度为止。注意:
biased维度指的是正样本和负样本都存在着严重的bias的维度,因此无法区分正样本和负样本。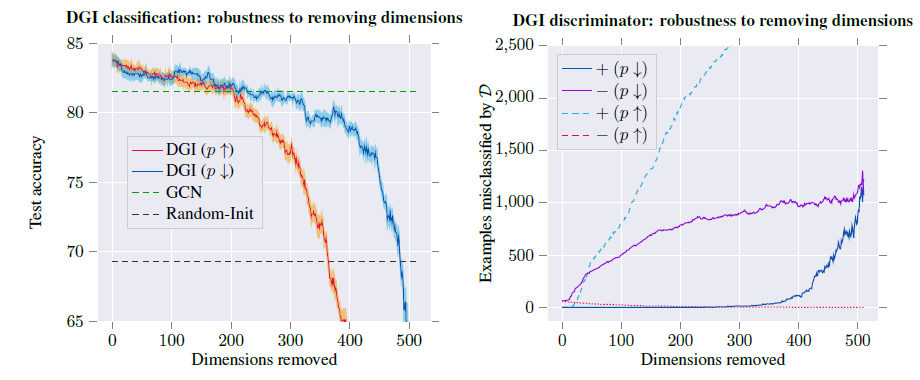
三十五、DIFFPOLL[2018]
当前
GNN架构的主要局限性在于它们本质上是平的flat,因为它们仅仅跨图的边来传播信息,并且无法以层次hierarchical的方式推断和聚合信息。这种缺乏层次结构的情况对于graph分类任务尤其成为问题。当GNN应用到图分类时,标准方法是为图中的所有节点生成embedding,然后将所有这些节点embedding执行全局池化。这种全局池化忽略了图中可能存在的任何层次结构,并阻碍了人们为graph-level预测任务建立有效的GNN模型。论文
《Hierarchical Graph Representation Learning with Differentiable Pooling》提出了DIFFPOOL,这是一种可微分的graph pooling模块,可以通过层次的、端到端的方式适应各种GNN架构,如下图所示。DIFFPOOL允许开发更深的 、可以学习操作图的层次表示hierarchical representation的GNN模型。下图中,在每个层次的
layer上运行一个GNN模型来获取节点embedding。然后,DIFFPOOL使用这些学到的embedding将节点聚类到一起,并在这个粗化的图上运行另一个GNN layer。重复representation来对图进行分类。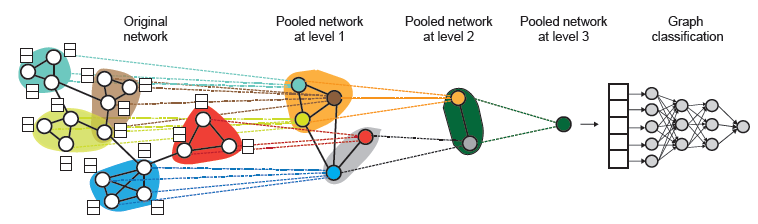
DIFFPOOL类似于CNN的空间池化。和标准的CNN相比,GNN面临的挑战是:- 首先,
graph不包含自然的空间局部性概念,即不能简单的在graph上对一个patch上的所有节点进行池化,因为图的复杂拓扑结构使得无法定义patch。 - 其次,和图像数据不同,图数据集通常包含数量变化的节点和边的图,这使得定义图池化运算更具挑战性。
为解决上述挑战,我们需要一个模型,该模型学习如何将节点聚类在一起从而在底层图之上搭建一个层次的
multi-layer结构。DIFFPOOL方法在GNN的每一层上学习可微的soft assignment,并根据其学到的embedding将节点映射到簇。在DIFFPOOL框架中,我们通过以层次的方式堆叠GNN layer,从而生成deep GNN:第DIFFPOOL的每一层都将输入图越来越粗化,并且DIFFPOOL能够在训练后生成任何输入图的hierarchical representation。实验表明:
DIFFPOOL可以和各种GNN方法结合使用,从而使得平均准确率提高7%,并且在五个benchmark中的四个达到了state-of-the-art性能。最后,论文证明
DIFFPOOL可以学习和输入图中定义明确的社区相对应的、可解释的层次聚类。- 首先,
相关工作:
通用的图神经网络:近年来提出了各种各样的图神经网络模型。这些方法大多符合
《Neural message passing for quantum chemistry》提出的 "neural message passing"的框架。在消息传递框架中,GNN被看作是一种消息传递算法,其中node representation是使用可微聚合函数从其邻居节点的特征中反复计算出来的。《Representation learning on graphs: Methods and applications》对该领域的最新进展进行了回顾,《Geometric deep learning:Going beyond euclidean data》概述了图神经网络与谱图卷积spectral graph convolution的联系。基于图神经网络的图分类:图神经网络已经被应用于各种任务,包括节点分类、链接预测、图分类、和化学信息学。在图分类的背景下应用
GNN的一个主要挑战是如何从node embedding到整个图的representation。解决这个问题的常见方法包括:- 在网络最后一层简单地求和或平均所有的
node embedding。 - 引入一个与图中所有节点相连的 "
virtual node"。 - 使用一个能够操作集合的深度学习架构来聚合
node embedding。
然而,所有这些方法都有一个局限性,即它们不学习
hierarchical representation(即所有的node embedding都在单个layer中被全局地池化),因此无法捕捉到许多现实世界中图的自然结构。最近的一些方法也提出了将CNN架构应用于所有node embedding的拼接,但这需要指定(或学习)节点的典型排序(一般来说这非常困难,相当于解决图的同构性graph isomorphism)。- 在网络最后一层简单地求和或平均所有的
35.1 模型
DIFFPOOL的关键思想是:通过提供可微的模块来层次地池化图节点,从而构建深度的multi-layer GNN模型。给定图
每个节点
为方便讨论,我们将所有维度(包括输入特征维度和
embedding向量维度)都设为这里我们假设图是无权重的,即
注意:这里我们未考虑边特征。
给定一组带标签的图
graph到label的映射函数和标准的监督学习任务相比,这里的挑战是:我们需要一种从这些输入图中抽取有用的特征向量的方法。即,我们需要一个过程来将每个图转换为一个有限维的向量。
本文我们以
GNN为基础,以端到端的方式学习图分类的有用representation。具体而言,我们考虑采用以下的message-passing架构的GNN:其中:
embedding,其中embedding
我们提出的可微池化模块可以应用于任何
GNN模型,并且对于如何实现消息传递函数
GCN中采用一个线性映射和一个ReLU非线性激活函数来实现:其中:
完整的
GNN模块可能包含embedding为2~6层。为简化讨论,在后续内容中,我们将忽略
GNN的内部结构,并使用GNN模块,它根据邻接矩阵上述
GNN的本质上是flat的,因为它们仅在图的边之间传播信息。我们的目标是定义一种通用的、端到端的可微策略,该策略允许人们以层次化的方式堆叠多个GNN模块。形式上,给定一个邻接矩阵
GNN模块的输出embedding然后,而可以将这个新的粗化图用作另一个
GNN layer的输入,并且可以将整个过程重复GNN layer的模型,该模型对输入图的一系列越来越粗的版本进行操作。因此,我们的目标是学习如何使用GNN的输出将节点聚类在一起,以便我们可以将这个粗化图用作另一个GNN layer的输入。和常规的图粗化任务相比,为
GNN设计这样的池化层尤其具有挑战性的原因是:我们的目标不是简单地将一个图中的节点聚类,而是提供一个通用的方法对输入图的一组广泛的节点进行层次池化hierarchically pool。即,我们需要模型来学习一种池化策略,该策略将在具有不同节点、边的图之间进行泛化,并且在推断过程中可以适配各种图结构。
35.1.1 DIFFPOOL 方法
DIFFPOOL方法通过使用GNN模型的输出来学习节点上的cluster assignment矩阵来解决上述挑战。关键的直觉是:我们堆叠了GNN模块,其中基于第GNN生成的embedding并以端到端的方式学习如何将节点分配给第因此,我们不仅使用
GNN来抽取对graph分类有用的节点embedding,也使用GNN来抽取对层次池化有用的节点embedding。通过这种方式,DIFFPOOL中的GNN学会编码一种通用的池化策略。我们首先描述
DIFFPOOL模块如何在给定assignment矩阵的情况下在每一层上池化节点,接下来我们讨论如何使用GNN架构生成assignment矩阵。给定
assignment矩阵的池化:我们将第cluster assignment矩阵定义为soft assignment给下一个粗化的、第假设
assignment矩阵。我们假设第embedding矩阵为DIFFPOOL层将粗化coarsen输入图,生成一个新的粗化的邻接矩阵embedding矩阵其中:
DIFFPOOL根据cluster assignment矩阵embeddingembedding。物理意义:第
embedding等于它包含的子节点的embedding的加权和,权重为子节点属于这个簇的可能性(由assignment矩阵给出)。DIFFPOOL根据cluster assignment矩阵cluser pair对之间的连接强度。物理意义:第
assignment矩阵给出)。
这样,
DIFFPOOL粗化了图:下一层邻接矩阵cluster node的粗化图,其中每个簇点cluster node对应于第注意:
embedding。粗化的邻接矩阵
embeddingGNN layer的输入。我们接下来详述。学习
assignment矩阵:现在我们描述DIFFPOOL如何生成assignment矩阵embedding矩阵GNN来生成这两个矩阵,这两个GNN都作用到簇点cluster node特征第
embedding GNN是标准的GNN模块:即,我们采用第
GNN来获取簇点的新的embedding矩阵第
pooling GNN使用簇点的邻接矩阵和特征矩阵来生成assignment矩阵:其中
softmax是逐行进行。
注意:
这两个
GNN采用相同的输入数据,但是具有不同的参数化parameterization并发挥不同的作用:embedding GNN为第embedding;pooling GNN为第当
在倒数第二层
assignment矩阵1的向量,即:将最后一层final embedding向量。然后可以将这个
final embedding向量用于可微分类器(如softmax层)的特征输入,并使用随机梯度下降来端到端地训练整个系统。
排列不变性
permutation invariance:注意,为了对图分类有用,池化层应该是节点排列不变的。对于DIFFPOOL,我们得到以下正面的结论,这表明:只要GNN的组件component是排列不变的,那么任何基于DIFFPOOL的deep GNN模型都是排列不变的。推论:令
permutation matrix,则只要满足证明:假设
GNN模块是排列不变的,则
35.1.2 辅助链接预测和熵正则化
在实践中,仅使用来自图分类任务的梯度信号来训练
pooling GNN可能会很困难。直观地讲,我们有一个非凸优化问题,在训练初期很难将pooling GNN推离局部极小值。为缓解该问题,我们使用辅助的链接预测目标
auxiliary link prediction objective训练pooling GNN,该目标编码了先验知识:应该将相邻的节点映射到相同的簇。具体而言,在每一层其中
Frobenius范数。pooling GNN将相连的节点分配到相同的簇、将不相连的节点分配到不同的簇。注意:邻接矩阵
assignment矩阵的函数,并且在训练期间会不断改变。pooling GNN的另一个重要特点是:每个节点的输出cluster assignment通常应该接近一个one-hot向量,从而清楚地定义节点属于哪个cluster。因此,我们通过最小化以下目标来对cluster assignment的熵进行正则化:其中:
assignment矩阵在训练期间,来自每一层的
cluster assignment。
35.2 实验
我们针对多个
state-of-the-art图分类方法评估了DIFFPOOL的优势,目的是回答以下问题:Q1:DIFFPOOL对比其它GNN中的池化方法(如sort pooling或者Set2Set方法)相比如何?Q2:结合了DIFFPOOL的GNN对比图分类任务中的state-of-the-art方法(包括GNN方法和kernel-based方法)相比如何?Q3:DIFFPOOL是否在输入的图上计算得到有意义且可解释的聚类?
数据集:蛋白质数据集,包括
ENZYMES, PROTEINS, D&D;社交网络数据集REDDIT-MULTI-12K;科学协作数据集COLLAB。对这些数据集,我们执行
10-fold交叉验证来评估模型性能,并报告10个fold的平均分类准确率。模型配置:在我们的实验中,用于
DIFFPOOL的GNN模型是建立在GraphSAGE架构之上的,因为我们发现GraphSAGE比标准的GCN效果更好。我们使用
GraphSAGE的mean变体,并在我们的体系架构中每隔两个GraphSAGE layer之后应用一个DIFFPOOL layer。在每个DIFFPOOL层之后、下一个DIFFPOOL层(或者readout层)之前,我们添加3层图卷积层。这里感觉前后矛盾,就是是
3层图卷积层还是2层图卷积层?要看代码。数据集一共使用
2个DIFFPOOL层。对于小型数据集(如ENZYMES, COLLAB),1个DIFFPOOL层就可以实现相似的性能。embedding矩阵和assignment矩阵分别由两个单独的GraphSAGE模型计算。在
2个DIFFPOOL层的体系架构中,cluster数量设置为DIFFPOOL之前节点数量的25%;在1个DIFFPOOL层的体系架构中,cluster数量设置为DIFFPOOL之前节点数量的10%。在
GraphSAGE的每一层之后都应用了batch normalization。我们还发现,在每一层的节点
embedding中添加所有模型都训练最多
3000个epoch,并基于验证损失来执行早停策略。我们还评估了
DIFFPOOL的两个简化版本:DIFFPOOL-DET:是一个DIFFPOOL的变体,其中使用确定性的图聚类算法来生成assignment矩阵。DIFFPOOL-NOLP:是一个DIFFPOOL的变体,其中移除链接预测的辅助目标。
另外,我们还将在
Structure2Vec架构上测试了DIFFPOOL的类似变体,从而演示如何将DIFFPOOL应用于其它GNN模型。baseline方法:这里我们考虑使用不同了池化的GNN方法,以及state-of-the-art的kernel-based方法。GNN-based方法:- 带全局均值池化的
GraphSAGE。其它GNN变体被忽略,因为根据经验,GraphSAGE在任务中获得更高性能。 Structure2Vec:S2V是一种state-of-the-art的graph representation learning方法,它将一个潜在变量模型latent variable model和GNN相结合,并使用全局均值池化。ECC将边信息融合到GCN模型中,并使用一个图粗化算法来执行池化。PATCHYSAN对每个节点定义一个感受野,并使用规范化的节点顺序,从而对节点embedding的序列应用卷积。SET2SET使用Set2Set方法来代替传统GNN架构中的全局均值池化。这里我们使用GraphSAGE作为base GNN model。SORTPOOL应用GNN架构,然后执行单层soft pooling层,然后对排序的节点embedding执行一维卷积。
对于所有
GNN baseline,我们尽可能使用原始作者报告的10-fold交叉验证的结果。如果作者没有公开结果,则我们从原始作者获取代码运行模型,并根据原始作者的准则执行超参数搜索。对于
GraphSAGE和SET2SET,我们像DIFFPOOL方法一样使用基本的实现和超参数择优。- 带全局均值池化的
kernel-based算法:我们使用GRAPHLET、SHORTEST-PATH 、WEISFEILERLEHMAN kernel:WL、 WEISFEILER-LEHMAN OPTIMAL ASSIGNMENT KERNEL:WLOA等方法。对于每个
kernel,我们计算归一化的gram矩阵。我们使用10-fold交叉验证,并使用LISVM计算分类准确率。超参数C的搜索范围WL和WL-OA的迭代范围从0到5。
下表给出了实验结果,这为
Q1和Q2给出了正面的回答。最右侧的Gain列给出了相对于GraphSAGE方法在所有数据集上的平均性能提升。可以看到:
DIFFPOOL方法在GNN的所有池化方法中获得了最好的性能,在GraphSAGE体系结构上平均提升6.27%,并且在5个benchmark上的4个达到了state-of-the-art。- 有趣的是,我们的简化模型变体
DIFFPOOLDET在COLLAB数据集上达到了state-of-the-art性能。这是因为COLLAB的很多协作图仅显示了单层社区结构,这些结构可以通过预先计算的图聚类算法很好地捕获。

有一个现象是:尽管性能有了显著提升,但是
DIFFPOOL可能无法稳定训练。并且即使采用相同的超参数设置,不同运行之间的准确率也存在着差异。可以看到添加链接预测目标可以使得训练更加稳定,并减少不同运行之间准确率的标准差。除了
GraphSAGE之外,DIFFPOOL也可以应用于其它GNN架构,从而捕获图数据中的层次结构。为此我们在Structure2Vec:S2V上应用了DIFFPOOL。我们使用三层的
S2V架构:- 在第一个变体中,在
S2V的第一层之后应用一个DIFFPOOL层,并在DIFFPOOL的输出的顶部堆叠另外两个S2V层。 - 在第二个变体中,在
S2V的第一层、第二层之后分别应用一个DIFFPOOL层。
在这两个变体中,
S2V模型用于计算embedding矩阵,而GraphSAGE模型用于计算assignment矩阵。实验结果如下所示。可以看到:
DIFFPOOL显著改善了ENZYMES和D&D数据集上S2V的性能。在其它数据集上也观察到类似的趋势。结果表明:
DIFFPOOL是一个可以提升不同GNN架构的通用池化策略。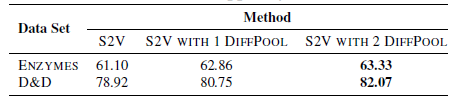
- 在第一个变体中,在
尽管
DIFFPOOL需要对asignment矩阵进行额外的计算,但我们观察到DIFFPOOL实际上并不会带来大量的额外运行时间。这是因为每个DIFFPOOL层都通过粗化来减小了图的大小,从而加快了下一层中图的卷积操作。具体而言,我们发现带有
DIFFPOOL的GraphSage模型要比带有SET2SET池化的GraphSage模型快12倍,并且仍能实现明显更高的准确率。为回答问题
Q3, 我们通过可视化不同层中的cluster assignment来调研DIFFPOOL是否学习有意义的节点聚类。下图给出COLLAB数据集中,第一层和第二层的节点分配的可视化,其中:- 节点颜色表示
cluster成员关系。节点的cluster成员关系是通过对cluster assignment的概率取argmax来确定的。 - 虚线表示簇关系。
- 下图是三个样本的聚类(每个样本代表一个
graph),图(a)给出两层的层次聚类,图(b),(c)给出一层的层次聚类。 - 注意,尽管我们将簇的数量设置为前一层节点的
25%,但是assignment GNN可以自动学习适当数量的、且有意义的簇,从而分配给这些不同的图。(即大量的簇没有分配到任何节点)。
可以看到:
即使仅基于图分类目标,
DIFFPOOL仍可以捕获层次的社区结构。我们还通过链接预测辅助目标观察到cluster assignment质量的显著提升。稠密的子图结构
vs稀疏的子图结构:我们观察到DIFFPOOL学会了以非均匀方式将所有节点折叠collapse为soft cluster,并且倾向于将稠密的子图折叠为簇。- 由于
GNN可以有效地对稠密的、clique-like的子图执行消息传递(由于较小的直径),因此在这种稠密的子图中将节点池化在一起不太可能导致结构信息的丢失。这直观地解释了为什么折叠稠密子图是DIFFPOOL的有效池化策略。 - 相反,稀疏子图可能包含许多有趣的结构,包括路径、循环、树状结构,并且由于稀疏性导致的大直径,
GNN消息传递可能无法捕获这些结构。因此,通过分别池化稀疏子图的不同部分,DIFFPOOL可以学习捕获稀疏子图中存在的有意义的结构。
- 由于
相似
representation节点的分配:由于assignment network基于输入节点及其邻域特征来计算soft cluster assignment,因此具有相似的输入特征和邻域结构的节点将具有相似的cluster assignment。实际上,可以构造一个人工
case:其中两个节点尽管相距很远,但是它们具有相同的节点特征和邻域特征。这种情况下,pooling GNN迫使它们分配到同一个cluster中。这和其它体系结构中的池化概念完全不同。在某些情况下,我们确实观察到不相连的节点被池化到一起。另外,我们观察到辅助链接预测目标有助于阻止很远的节点池化到一起。并且,可以使用更复杂的
GNN聚合函数(诸如高阶矩)来区分结构相似和特征相似的节点,总体的框架保持不变。预定义聚类数的敏感性:我们发现
assignment根据网络深度和pooling GNN可以对更复杂的层次结构进行建模,但是会导致更大的噪声和更低的训练效率。尽管
pooling GNN通过端到端训练来学习使用适当数量的cluster。具体而言,assignment矩阵可能不会用到某些簇。对于未被使用的cluster对应的矩阵列,它在所有节点上都具有较低的值。例如图2(c)中,节点主要分配到3个簇上。
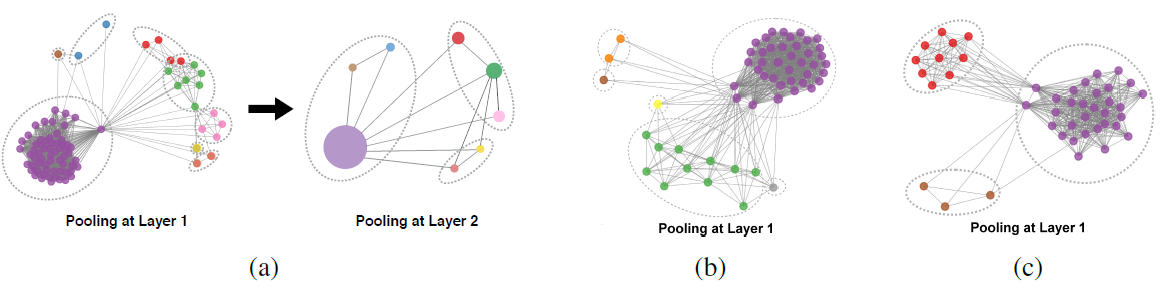
- 节点颜色表示
三十六、DCNN[2016]
与结构化数据打交道是一种挑战。一方面,找到正确的方式来表达和利用数据中的结构可以改善预测性能;另一方面,找到这样的
representation可能是困难的,而且在模型中添加结构会大大增加预测的复杂性。论文
《Diffusion-Convolutional Neural Networks》的目标是为通用的结构化数据设计一个灵活的模型,在提高预测性能的同时避免复杂性的增加。为了实现这一目标,作者引入 "diffusion-convolution"操作,将卷积神经网络扩展到通用的图结构数据。简而言之,diffusion-convolution操作不是像标准卷积操作那样在网格结构的输入中扫描一个 "正方形",而是通过在图结构的输入中扫描每个节点的diffusion process来建立一个latent representation。这个模型的动机是这样的:封装了
graph diffusion的representation可以为预测提供一个比graph本身更好的basis。graph diffusion可以表示为一系列的矩阵幂次从而包含上下文信息,并且可以在多项式时间内计算,以及可以在GPU上有效实现。在论文
《Diffusion-Convolutional Neural Networks》中,作者提出了diffusion-convolutional neural network: DCNN,并探讨了它们在图数据的各种分类任务中的表现。许多技术在分类任务中包括结构信息,如概率关系模型probabilistic relational model和核方法kernel method。DCNN提供了一种补充方法,在节点分类任务的预测性能上有了明显的改善。DCNN的主要优势:- 准确性:在实验中,
DCNN在节点分类任务中的表现明显优于其他方法,在图分类任务中的表现与baseline方法相当。 - 灵活性。
DCNN提供了一种灵活的图数据表示方法,可以编码节点特征、边特征、以及单纯的结构信息,只需进行少量的预处理。DCNN可用于图数据的各种分类任务,包括节点分类和图分类。 - 速度快。
DCNN的预测可以表示为一系列的多项式时间的张量运算,并且该模型可以使用现有的库在GPU上有效地实现。
- 准确性:在实验中,
相关工作:
其它
graph-based神经网络方法:其他研究者已经研究了如何将CNN从网格结构扩展到更普遍的图结构数据。《Spectral networks and locally connected networks on graphs》提出了一种与层次聚类hierarchical clustering相联系的空间方法,其中网络的层是通过节点集合的hierarchical partitioning来定义的。在同一篇论文中,作者提出了一种谱方法,将卷积的概念扩展到graph spectra。- 后来,
《Deep Convolutional Networks on Graph-Structured Data》将这些技术应用于这样的数据:图并不是立即出现但是必须被推断。
属于空间类别的
DCNN与这项工作不同,因为DCNN的参数化parameterization使模型可以迁移:在一个图上学习的DCNN可以应用于另一个图。概率关系模型:
DCNN也与概率关系模型probabilistic relational model: PRM有着密切的联系。概率关系模型是一族graphical model,能够代表关系数据的分布(《Probabilistic Graphical Models: Principles and Techniques》)。与概率关系模型相比,DCNN是确定性的,这使得DCNN能够避免指数爆炸(指数爆炸阻碍了概率关系模型的学习和推断)。我们的研究结果表明:
DCNN的表现优于部分观察的条件随机场conditional random field: CRF,即半监督学习的SOTA概率关系模型。此外,DCNN以相当低的计算成本提供这种性能。学习DCNN和部分观测的CRF的参数需要数值上最小化一个非凸目标:对于DCNN来说是反向传播误差,对于CRF来说是负的边际对数似然。- 在实践中,部分观测的
CRF的边际对数似然是使用对比分区函数contrast-of-partition-function方法来计算的,这需要运行两次循环的信念传播belief propagation:一次是在整个图上,一次是在固定观测标签的情况下。这种算法,以及数值优化中的每个step,具有指数级的时间复杂度maximal clique的大小。 - 相比之下,
DCNN的学习程序只需要对训练数据中的每个实例进行一次前向传播和反向传播。复杂度由graph definition matrixgraph design matrix
其中,
- 在实践中,部分观测的
核方法:核方法
kernel method定义了节点之间(即kernel on graph)或图之间(即graph kernel)的相似性度量,这些相似性可以作为通过核技巧kernel trick进行预测的基础。graph kernel的性能可以通过将图分解为子结构,将这些子结构视为句子中的一个词,并拟合一个word-embedding模型来获得矢量化来提高。DCNN与kernel on graph的exponential diffusion族有联系。exponential diffusion graph kerneldiffusion-convolution activation也是由幂级数构造的。然而,它和- 首先,
kernel representation不是从数据中学习的。 - 其次,
diffusion-convolution representation是由节点特征和图结构来建立的,而exponential diffusion kernel则仅由图结构来建立。 - 最后,这两种
representation有不同的维度:kernel matrix,而kernel的定义。其中K-hop邻域。
- 首先,
36.1 模型
DCNN模型建立在扩散核diffusion kernel的思想上:基于两个节点之间的所有路径来衡量两个节点的邻近关系,其中路径越短权重越高。术语 “扩散卷积” 表明网络的三个思想:特征学习
feature learning、参数共享、不变性。DCNN的核心是抽取图结构数据的特征。DCNN也用到参数共享,其中共享是发生在扩散搜索深度上diffusion search depth,而不是CNN的网格位置上。DCNN关于节点索引不变,即两个同构输入图的扩散卷积的representation将是相同的。
和
CNN不同,DCNN没有池化操作。考虑我们有
degree矩阵,其中- 节点
- 对于节点分类任务,每个节点
定义
令
定义扩散卷积为:
其中:
k-hop;因此节点
representation是对图- 节点之间的转移概率
- 指定维度、指定路径长度的权重
以张量形式表示为:
其中:
representation张量。
可以看到,模型只有
DCNN可以应用到另一个图。这里的核心是
- 节点之间的转移概率
DCNN可以用于节点分类或者图分类。节点分类:一旦得到
dense层和softmax输出层来进行节点分类。图分类:如果将图
graph-level的representation:其中:
1的行向量;representation张量。一旦得到
dense层和softmax输出层来进行图分类。
注意:
hop的representation,在接入dense层之前可以把这representation拼接或者相加从而得到final representation。对于没有节点特征的图,可以人工构造节点特征:
- 可以为每个节点构造一个取值为
1.0的bias feature。 - 可以使用节点的结构统计信息,如
pagerank值、节点degree等。
- 可以为每个节点构造一个取值为
DCNN局限性:可扩展性
scalability:DCNN被实现为对稠密张量的一系列运算。存储out-of-memory:OOM错误。可以通过随机游走来近似
局部性
locality:DCNN旨在捕获图结构数据中的局部行为。我们是从每个节点开始的、最高K阶的扩散过程来构建representation,因此可能无法对长程依赖或者其它非局部行为进行编码。
DCNN的训练:通过mini-batch随机梯度下降来学习。可以证明:如果两个图
diffusion-convolutional representation是相同的;如果两个图diffusion-convolutional representation是不同的。证明见原始论文。
36.2 实验
实验配置:
使用
AdaGrad算法进行梯度提升,学习率为0.05。从均值为
0、方差为0.01的正态分布随机采样来初始化所有权重。选择双曲正切
tanh函数作为非线性激活函数选择多分类
hinge loss作为损失函数。假设一共其中
36.2.1 节点分类
数据集:
Cora,Pubmed论文引用数据集,每个节点代表一篇论文,边代表论文之间的引用关系,标签为论文的主题subject。这里我们将引文网络视为无向图。Cora数据集包含2708篇论文、5429条边。每篇论文都分配一个标签,标签来自7个可能的机器学习主题。每篇论文都由一个向量表示,向量的每一位对应于是否存在从词典中抽取的1433个术语是否存在。Pubmed数据集包含关于糖尿病的19717篇论文、44338条边。论文被分配到三个类别之一。每篇论文都由一个TFIDF向量来表示,其中词典大小为500(即论文的特征向量维度为500)。
这里集合
我们报告了测试集分类准确率以及
micro-F1和macro-F1,每个指标为多次实验计算得到的均值。我们还提供了
CORA和Pubmed数据集的learning curve,其中验证集和测试集分别包含10%的节点,训练集包含剩余节点的10% ~ 100%。baseline方法:l1logistic和l2logistic:分别代表L1正则化的逻辑回归、L2正则化的逻辑回归。逻辑回归模型的输入仅仅是节点的特征(并未使用图结构),并使用验证集对正则化参数进行调优。KED和KLED:分别代表图上的exponential diffusion kernel和Laplacian exponential diffusion kernel。这些kernel model将图结构作为输入(并未使用节点特征)。CRF-LBP:表示使用循环信念传播loopy belief propagation:LBP进行推断的、部分观测partially-observed的条件随机场conditional random field:CRF。该模型的结果来自前人论文的实验结果。
下表给出了实验结果,可以看到:
DCNN(K=2)提供了最佳性能。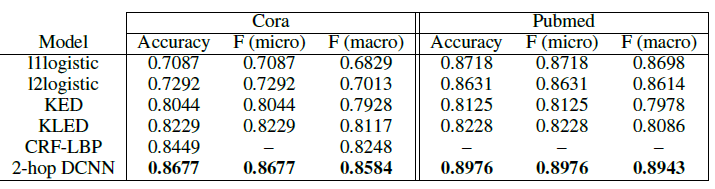
下图的
(a),(b)给出了learning curve,可以看到:在Cora数据集上,无论可用的训练数据量如何,DCNN通常都优于baseline方法。图
(c)给出hop数量的影响。可以看到:随着hop数从0-hop逐渐增加的过程中,性能先增加然后稳定,在3-hop达到收敛。
36.2.2 图分类
数据集:我们采用
NCI1、NCI109、MUTAG、PTC、ENZYMES等标准的图分类数据集。NCI1、NCI109数据集由代表化合物的4100和4127个图组成,每个图都标有它是否具有抑制一组人类肿瘤细胞系生长的能力。图中每个节点分类有37个(对于NCI1)或38个(对于NCI109) 可能的标记之一。MUTAG数据集包含188个硝基化合物,被标记为芳族或非芳族化合物。节点包含7个特征。PTC包含344个化合物,被标记为是否对于大鼠致癌。节点包含19个特征。ENZYMES包含600个蛋白质的图,每个节点包含3个特征。
输入的图集合随机拆分为训练集、验证集、测试集,每个集合包含数量相等的图,我们报告测试集的准确率、
micro-F1和macro-F1。每个指标为多次实验计算得到的均值。baseline方法:l1logistic和l2logistic:分别代表L1正则化的逻辑回归、L2正则化的逻辑回归,它们仅利用节点特征。deepwl:表示Weisfeiler-Lehman (WL) subtree deep graph kernel,它仅利用图结构。
下表给出了实验结果,可以看到:和节点分类实验相反,没有明确的最佳模型在所有数据集、所有指标上最优。
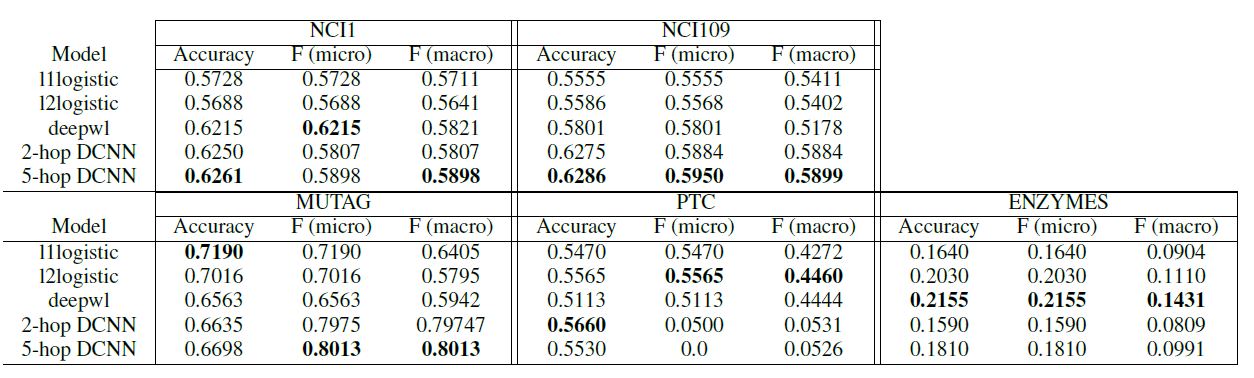
我们还提供了
MUTAG(图(a))和ENZYMES(图(b)) 数据集的learning curve,其中验证集和测试集都分别包含10%的图、训练集包含剩余图的10% ~ 100%。从下图(c)可以看到:扩大hop数量并没有明显的好处。
这些结果表明:尽管扩散卷积可以得到节点的有效表示,但是它们在
summarize整个图的representation方面做得很差。可以寻找一种方法来更有效地聚合节点来改善graph-level的representation,这留待以后工作。
三十七、IN[2016]
关于对象
object、关系relation、物理physic的推理reasoning是人类智能的核心,也是人工智能的主要目标。论文《Interaction Networks for Learning about Objects, Relations and Physics》提出了交互网络interaction network:IN模型,该模型可以推理复杂系统中的对象如何交互、支持动态预测dynamical prediction、以及推断系统的摘要属性abstract property(即系统的整体属性,如物理系统的势能)。IN结合了三种强大的方法:结构化模型structured model、仿真simulation、深度学习deep learning。- 结构化模型可以利用对象之间关系的丰富的、显式的知识,这种知识与对象本身无关,从而支持跨各种上下文的通用推理。
- 仿真是近似
approximating动态系统,预测复杂系统中的元素如何受到彼此的交互影响、以及系统动态影响的有效方法。 - 深度学习将通用架构和高效的优化算法结合在一起,可以在具有挑战性的现实环境中提供高可扩展的学习和推断能力。
IN明确地将对关系的推理与对对象的推理分开,每个任务分配不同的模型,即:以对象为中心的推理object-centric reasoning、以关系为中心的推理relation-centric reasoning。这使得IN可以自动地将学习泛化到任意数量的、任意顺序的对象和关系,并且还可以通过新颖的、组合的方式重新组合IN学到的、关于对象和关系的知识。IN模型将关系作为显式的输入,使得模型可以针对不同的输入数据有选择地处理不同的潜在交互,而不必被迫考虑每种可能的交互,也不必由固定的架构fixed architecture施加特定的交互。论文评估了
IN在推理几个物理领域的能力:n体问题n-body problem、刚体碰撞问题rigid-body collision、非刚体动力学问题non-rigid dynamics。实验结果表明:可以训练IN模型从而精确模拟数千个time step上数十个对象的物理轨迹。IN是第一个通用的、可学习的物理引擎,并且是强大的通用框架,可用于在各种复杂的现实世界领域中进行对象和关系的推理。
37.1 模型
为描述我们的模型,我们以物理系统的推理为例(如下图所示),并从简单的模型构建完整的
interaction network:IN。为了预测单个对象的动力学
dynamics,可以使用对象为中心的函数object-centric function如果两个或者多个对象由相同的动力学方程控制,那么
但是,如果对象之间彼此交互,那么
senderreceiver如下图所示,一个固定的物体、一个自由移动的质点通过弹簧连接,则固定物体(
sender)通过弹簧影响自由质点(receiver)的动力学。可以通过以关系为中心的函数
relation-centric functioneffect

上面的公式仅考虑两个对象以及它们之间关系的简单系统。通过将对象和关系表示为图
我们假设一个带属性的、有向的多图
multigraphrigid interaction、磁性作用magnetic interaction。- 每个对象
- 每个对象
external effect sender对象receiver对象
basic IN模型定义为:其中:
marshalling function,它将对象及其它们之间的关系重排为三元组向量:其中
||表示向量拼接。所有三元组构成关系矩阵
relational model,它通过在每条边interaction effect所有关系的交互效应组成交互效应矩阵
聚合函数
receiver对象receiver的交互效应所有对象模型的输入为对象模型输入矩阵
object model,它通过在每个对象所有对象模型的输出为预测结果矩阵
这个基础的
IN可以预测动态系统中状态的演变。对于物理仿真,还可以使用其它组件来扩展
IN,从而对系统进行摘要推断abstract inference。例如,不是将IN预测系统的整体势能从而探索这种变体。IN分别对每个commutative和关联的associative。使用sum操作可以满足这个要求,但是除法操作不行。IN模型的通用定义和函数、算法的选择无关,这里我们描述了一种易于学习的实现,该实现能够对具有非线性关系和动态的复杂系统进行推理。定义
receiver对象的one-hot索引;定义sender对象的one-hot索引。定义根据定义有:
即,每个关系的三元组由
receiver状态、sender状态、关系属性而组成。对
MLP)从而构成了交互效应矩阵receiver对象receiver的交互效应对
MLP)从而得到输出矩阵为了推断系统的摘要属性,我们首先在
然后将
MLP)的输入,然后返回一个向量abstract的、全局的属性。
训练
IN需要在由于
CNN,由于CNN的参数共享使得CNN非常高效。CNN将局部邻域的像素视为相关的交互实体,每个像素实际上是receiver对象、相邻像素是sender对象。卷积算子类似于skip connection大体上类似于IN将
37.2 实验
我们探索了两种类型的物理推理任务:预测系统的未来状态、估计系统的
abstract属性(尤其是势能)。我们在三个复杂的物理领域中进行实验:
n体系统n-body system:所有- 在整个模型过程中,对象的质量各不相同,而所有其它固定属性均保持常量。
- 训练是在包含
6个body的训练集上进行的,但是测试时我们分别测试了3-body、6-body、12-body。
弹跳球
bouncing ball:固定盒子中的球,其中移动的球可能会相互碰撞,也可能和固定的墙壁碰撞。墙被表示为对象,其形状属性为一个矩形,inverse-mass为零(质量无穷大)。一共有- 碰撞比万有引力更难模拟,并且数据分布更具有挑战性:每个球只有在不到
1%的时间发生碰撞,其它所有时间都遵循直线运动。因此,该模型必须了解:尽管两个对象之间存在刚性关系,但是仅在它们接触时才存在有意义的、碰撞的相互作用。 - 对象的属性之间也各不相同,包括形状
shape、质量等,以及恢复系数restitution coefficiency(关系的一种属性)。 - 训练是在装有
6个球的盒子的训练集上进行的,其中盒子有四种不同尺寸。但是测试时我们分别测试了3个球、6个球、9个球。
- 碰撞比万有引力更难模拟,并且数据分布更具有挑战性:每个球只有在不到
线条
string:由带质量的线条(通过弹簧连接的、带重量的质点)和位于线条下方静态的、刚性的圆组成。线条上的- 重力加速度是外部输入。
- 训练是在
15个质点的线条上进行的。但是测试时我们分别测试了5个质点的线条、15个质点的线条、30个质点的线条。 - 在训练时,随机选择线条一端的质点始终保持静止,就好像固定在墙上一行,而其它质点可以自由移动。但是测试时,我们还测试了两端都固定的线条、两端都未固定的线条,从而评估泛化能力。
我们使用物理引擎模拟了这些系统对象的
2D轨迹,并记录它们的状态序列- 预测实验
prediction experiment的目标是输出对象在随后time step的速度。 - 势能估计实验
energy estimation experiment的目标是当前time step的势能。
我们还为
prediction experiment生成了包含未来多个时间步的rollout版本,从而评估模型在创建视觉的真实的仿真visually realistic simulation模拟时的有效性。此时,时刻panel,分别代表三个视频帧,每帧代表1000个rollout step。前两列表示
n体系统的真实情况和模型预测、中间两列表示弹跳球的真实情况和模拟预测、最后两列表示线条的真实情况和模拟预测。上方的
pannel表示对系统进行训练的结果、中间和底部的pannel表示模型对于不同大小、结构的系统的泛化:- 对于
n体系统,训练针对6-body、泛化针对3-body,12-body。 - 对于弹跳球,训练针对
6-ball、泛化针对3-ball,12-ball。 - 对于线条,训练针对
15个质点且固定线条的一端、泛化针对20个质点且固定线条的0个末端或2个末端。
- 对于

训练集:每个训练、验证、测试数据集都是通过在
1000个time step上仿真2000个场景,并随机采样100万、200k、200k个单步的(输入, 目标)的pair对组成。我们报告模型在测试集的性能。模型训练
2000个epoch,在每个epoch对数据进行随机混洗。我们使用
mini-batch随机梯度下降,batch size = 100,并且数据分布保持平衡使得对象之间有相似的目标统计分布。我们尝试在训练的初始阶段,将少量高斯噪声添加到
20%数据的输入位置、速度,然后在epoch的50~250期间降低到0%。噪音的标准差是验证集每个对象相应位置、速度标准差的0.05倍。它使得模型能够体验物理上不可能由物理引擎生成的状态,并学会将其投影回附近的可能的状态。
我们报告的误差结果并没有看出有噪音、无噪音结果的明显差异,但是经过噪音训练的模型的
rollout在视觉上更逼真,并且静态对象在很多step上的漂移drift也较小。
模型架构:
MLP,我们通过对隐层维度、层数进行网格搜索从而选择最佳的模型结构。- 所有训练目标和评估结果都采用预测值和真实直之间的均方误差
MSE。
baseline:很少有文献可以和我们的模型进行比较。我们考虑几种baseline:- 常量速度的
baseline:输出速度和输入速度相同。 MLP的baseline:具有两层的300维隐层,将所有输入数据展平为向量从而作为输入。- 移除了
IN的变体:将交互效应
- 常量速度的
实验结果:
prediction experiment:实验结果表明,IN可以在训练后非常准确地预测下一步动态,其测试误差要比baseline低几个量级。每个物理领域的动力学主要取决于对象之间的交互,因此IN能够学习利用这些关系进行预测。- 没有交互的
IN变体,其执行方式和效果与恒定速度的baseline相似。 - 全连接的基准
MLP理论上可以学习对象之间的交互,但是它不会受益于关系和对象之间的共享学习,而是被迫为每个对象并行地学习交互。
- 没有交互的
energy estimation experiment:实验结果表明,IN的准确性要高得多。IN总体上学习了重力势能和弹簧势能函数,并将它们应用于各自物理领域的关系中。