GNN (其它)
一、Deeper Insights into GCN[2018]
众所周知训练深度神经网络通常需要大量的标记数据。由于获得标记样本的成本较高,因此在很多情况下无法大量标记数据的需求无法满足。为了降低模型训练所需的标记数据量,最近很多研究集中在
fewshot learning上:学习一个分类模型,其中每个类别只有很少的标记数据。和fewshot learning密切相关的是半监督学习,其中大量未标记数据来辅助训练少量的标记数据。很多研究表明:如果使用得当,在训练中使用未标记数据可以显著提升模型的预测能力。关键问题是如何最大程度地有效利用未标记数据的结构信息和特征信息。目前已有一些基于神经网络的半监督学习模型取得成功,包括
ladder network, semi-supervised embedding, planetoid, graph convolutional network。最近的图卷积神经网络
graph convolutional neural networks: GCNN成功地推广了CNN来处理图结构数据。《Semisupervised classification with graph convolutional networks》提出了一种简化的GCNN模型,称作图卷积网络GCN,并将其应用于半监督分类中。GCN模型很自然地融合了图结构信息和节点特征信息,并在某些benchmark上明显优于许多state-of-the-art的方法。但是,
GCN模型面临很多其它神经网络模型类似的问题:- 用于半监督学习的
GCN模型的工作机制尚不清楚。 - 虽然
GCN只需要少量的标记数据用于训练,但是GCN仍然需要大量标记数据作为验证集从而用于超参数调优和模型选择。这违背了半监督学习的目的。
论文
《Deeper Insights into Graph Convolutional Networks for Semi-Supervised Learning》深入洞察GCN模型,并提出:GCN模型的图卷积只是拉普拉斯平滑的一种特殊形式,这种平滑混合了节点及其周围邻域的特征。平滑操作使得同一个簇cluster中节点的特征相似,从而大大简化了分类任务,这是GCN表现出色的关键原因。但是,这也会带来过度平滑
over-smoothing的潜在风险。如果GCN有很多层的卷积层,则最终输出的特征可能过于平滑,使得来自不同cluster之间的节点变得难以区分。如下图所示为karate club数据集分别使用1、2、3、4、5层GCN训练的节点embedding可视化的结果,不同颜色表示不同的类别。可以看到,随着卷积层数量的增加,过度平滑很快发生。除此之外,使用很多层的卷积层也使得训练变得更加困难。
但是卷积层数量太少也会有问题。在半监督学习中标记数据太少,这使得浅层
GCN无法将标签信息有效地传播到整个图。这就是卷积滤波器局部性带来的困扰。如下图所示(Cora数据集),随着训练的标签数据的减少,GCN性能迅速下降。即使采用了额外的500个标记样本作为验证集(图中的GCN with validation曲线),GCN的性能也是迅速下降。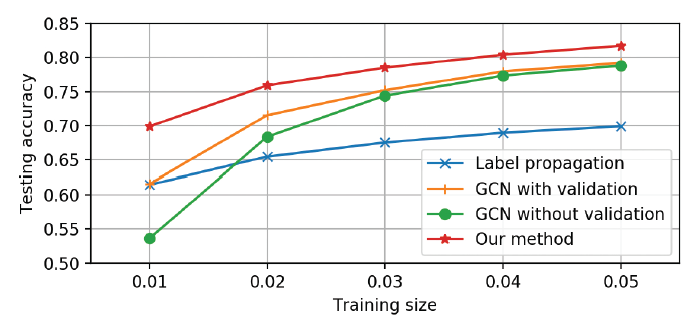
为了克服
GCN模型的缺陷并实现模型的全部潜力,论文提出了一种共同训练Co-Training方法和一种自训练Self-Training方法来训练GCN。- 通过将
GCN和随机游走模型共同训练,从而利用随机游走模型补充GCN在探索全局图拓扑结构方面的不足。 - 通过自训练,从而利用
GCN的特征抽取能力来克服卷积滤波器的局部性。
通过将
Co-Training和Self-Training相结合,可以大大改善带少量标记数据的半监督学习的GCN模型,并使得它不需要额外的标记数据进行验证。如上图所示,论文提出的方法(红色曲线)在很大程度上超越了GCN的表现。论文贡献:
- 对半监督
GCN模型提供了新的洞察和分析。 - 提出了改进半监督
GCN模型的解决方案。
- 用于半监督学习的
1.1 基本原理和相关工作
给定图
定义非负的邻接矩阵
这里我们只考虑图上的半监督分类问题。假设标记节点集合为
1.1.1 基于图的半监督学习
基于图的半监督学习利用数据的拓扑结构从而可以通过很少的标签进行学习。很多基于图的半监督学习方法都采用聚类假设
cluster assumption:假设图上距离相近的节点倾向于共享相同的标签。采用这种假设的方法包括:最小割min-cuts、随机最小割randomized min-cuts、spectral graph transducer、标签传播label propagation及其变体、modified adsorption、iterative classification algorithm。但是图仅仅代表拓扑结构信息,在很多应用场景中,数据还带有属性信息。如引文网络中,文档可以表示为描述其内容的
bag-of-words向量。许多半监督学习方法试图联合建模图结构和特征属性。一个常见的想法是用一些正则器对supervised learner进行正则化。例如:LapSVM使用流形正则化manifold regularization从而通过拉普拉斯正则化器来正则化支持向量机。deep semi-supervised embedding用基于embedding的正则器对深度神经网络进行正则化。Planetoid也通过联合预测一个节点的类别标签和上下文来正则化神经网络。
1.1.2 GCN
Graph convolutional neural networks: GCNN将传统的卷积神经网络推广到图数据。GCNN主要有两种类型:空间GCNN、谱域GCNN。空间
GCNN将卷积视为patch operator,它基于节点邻域信息为每个节点构建一个新的representation向量。谱域
GCNN通过谱域分解图信号spectral component上应用谱域滤波器其中:图信号
eigenvector组成的矩阵。
谱域
GCNN需要显式计算图的拉普拉斯特征向量eigenvector,这对于很多实际的大图来讲是难以实现的。解决该问题的一种方法是对谱域滤波器进其中:
《Semisupervised classification with graph convolutional networks》通过限定其中:
hidden representation,这个简化的模型被称作
GCN。
1.1.3 采用 GCN 的半监督分类
在
《Semisupervised classification with graph convolutional networks》论文中,GCN模型用于半监督分类。模型采用两层卷积层,并使用softmax分类器:其中:
ReLU(.)为ReLU激活函数。损失函数为在所有标记数据上的交叉熵损失:
其中:
one-hot向量。
GCN模型很自然地在卷积中结合了图拓扑结构和节点属性,其中未标记节点的属性和附近的标记节点的属性混合,并通过多层GCN传播到图上。实验表明,在某些benchmark上(如引文网络),GCN性能明显优于很多state-of-the-art方法。这里的半监督学习仅考虑监督损失,而并未考虑无监督损失。还有一些工作会同时考虑监督损失和无监督损失。
1.2 分析
- 尽管
GCN效果很好,但是我们还不清楚它的机制。这里我们仔细研究GCN模型,分析其原理并指出其局限性。
1.2.1 为什么 GCN 有效
为分析
GCN工作良好的原因,我们将其与最简单的全连接网络fully-connected networks:FCN进行比较,其中layer-wise传播规则为:可以看到
GCN和FCN的区别在于:GCN在FCN的左边乘以一个图卷积矩阵graph convolution matrix为分析图卷积矩阵的影响,我们在
Cora引文网络上对比了GCN和FCN在半监督分类上的性能,其中每个类别有20个标记数据。对比结果如下表所示,可以看到:即使只有一层,GCN也要比FCN效果好得多。
首先我们考虑单层的
GCN网络,它包含两步:通过对节点特征矩阵
representation矩阵然后将新的
representation矩阵
显然,图卷积是
GCN相对于FCN获得巨大性能提升的关键。拉普拉斯平滑:假设我们向图中每个节点添加一个自连接
self-connection,则新的邻接矩阵为在输入特征每个维度上的拉普拉斯平滑
Laplacian Smoothing定义为:其中:
degree。
我们以矩阵的形式重写拉普拉斯平滑:
其中
令
这刚好就是图卷积公式。因此,我们将图卷积视为拉普拉斯平滑的一种特殊形式,称作对称拉普拉斯平滑
Symmetric Laplacian Smoothing。注意:虽然拉普拉斯平滑将节点的
representation计算为自身以及邻域特征的加权平均。由于同一个cluster中的节点倾向于紧密连接densely connected,因此平滑处理使得它们的representation彼此相似,这有助于后续的分类过程。从下图(Cora引文网络)可以看到,仅使用一次拉普拉斯平滑操作就能够带来巨大的性能提升。
多层架构:从上图中我们也看到,虽然两层
FCN相对于一层FCN有少许提升,但是两层GCN比一层GCN提升很大。这是因为在第一层representation上再次应用平滑会使得同一个cluster中节点的输出representation更为相似,进一步提升分类性能。
1.2.2 为什么失败
我们已经表明:图卷积本质上是一种拉普拉斯平滑。一个自然的问题是,
GCN中应该包含多少卷积层?显然层数不是越多越好。一方面,深层GCN非常难以训练;另一方面,反复应用拉普拉斯平滑可能会混合来自不同cluster的节点的信息,使得它们无法区分。我们用
karate club数据集为例。该数据集包含34个节点、78条边、两种节点类型。我们将隐层维度设为16,输出层维度为2。每个节点的特征向量为节点的one-hot向量。可以观察到拉普拉斯平滑对该数据集的影响。- 在进行一次平滑之后,不同类型节点之间的区分不明显。
- 在进行两次平滑之后,不同类型节点之间的区分相当明显。
- 在进行更多次平滑之后,不同类型节点被混合
mixing。
由于这是一个很小的数据集,而且两种类别节点之间存在很多连接,因此混合很快发生。

我们即将证明:通过多次重复应用拉普拉斯平滑,图的每个连通分量
connected component内的节点representation将收敛到相同的值。对于对称拉普拉斯平滑,它们将收敛到与节点的degree的平方根成正比。连通分量:任意两点之间都存在路径来访问。
假设图
因此
1的项对应于属于第定理:如果一个图没有
bipartite components,则对于任意信号其中
证明:
eigenvalues,但是有不同的特征向量eigenvectors。如果图没有bipartite components,则所有特征值都位于[0,2)之间。 则0的特征空间eigenspaces分别由对于
(-1,1]。因此特征值1对应的特征空间分别由由于
1,所以经过多次反复相乘之后,它们的结果收敛到特征值1对应的特征向量的线性组合,即注意,由于每个节点都添加了额外的自连接,因此图中没有
bipartite component。根据上述结论,过度平滑over-smoothing将使得节点之间特征难以区分从而有损于分类性能。上述分析总结了堆叠多层卷积层导致
GCN过度平滑的问题,此外深层的GCN也难以训练。因此《Semisupervised classification with graph convolutional networks》使用的GCN采用两层卷积层。但是,由于图卷积是局部滤波器,即邻域节点的特征向量的线性组合,因此浅层
GCN无法将标签信息充分传播到整个图上。如下图所示(Cora数据集),随机训练标记数据的减少,GCN算法的性能迅速下降。可以看到GCN准确率随着标记数据规模减少而下降的速度,要比label propagation下降速度快得多。由于标签传播label propagation算法仅使用图结构,而GCN同时使用图结构和节点特征,因此这反应了GCN模型无法探索全局图结构。
GCN的另一个问题是,它需要额外的验证集来实现早停,这本质上是需要额外的标记数据作为验证集来执行模型选择。如果我们不使用验证集来训练GCN,则其性能会大大降低。如上图所示,不带验证集的GCN性能(GCN without validation)要比带验证集的GCN性能(GCN with validation)差得多。《Semisupervised classification with graph convolutional networks》使用了额外500个标记数据作为验证集,这远多于训练标记数据。这是不可取的,因为这违反了半监督学习的目的。此外,这也使得GCN和其它方法的比较不公平,因为其它方法(如标签传播)可能根本不需要验证集。
1.3 解决方案
我们总结了
GCN模型的优缺点:优点:
- 图卷积(拉普拉斯平滑)有助于分类问题。
- 多层神经网络是功能强大的特征抽取器。
缺点:
- 图卷积是一个局部滤波器,在标记数据很少的情况下效果不理想。
- 神经网络需要大量的标记数据作为验证集,从而进行模型选择。
注:读者认为还有一个缺点是容易过度平滑。
我们希望在克服缺点的同时充分利用
GCN模型的优点。因此我们提出了Co-Training、Self-Training等思想。
1.3.1 Co-Training
我们提出将
GCN和随机游走模型一起共同训练,因为后者可以探索全局图结构,从而解决卷积局部性的问题。具体而言,我们首先使用随机游走模型找到最置信
confidence的节点(即,每个标记节点的最近邻居),然后将它们添加到标记数据集合从而训练GCN。和
《Semisupervised classification with graph convolutional networks》不同,我们直接在训练集上优化GCN,无需任何其它标记数据来作为验证集。我们使用
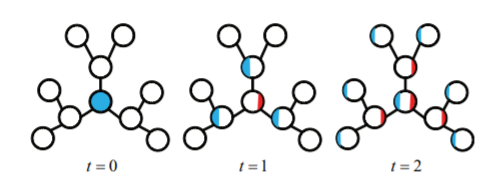
partially absorbing random walks:ParWalks算法作为我们的随机游走模型。ParWalks是一个二阶马尔科夫链,它在每个状态下都有部分吸收partial absorption。考虑下图的简单扩散过程:
首先将单位能量(蓝色)注入到指定的节点。
第一步,某些能量(红色)“存储” 在当前节点,剩余能量(蓝色)传播到邻居中。
每当能量通过节点时,一部分能量就会保留在当前节点、剩余能量继续传播。
随着该过程的持续,每个节点中存储的能量将累积,并且图中流动的能量越来越少。经过一定数量的
step后,几乎没有剩余能量流动,并且存储的能量总和几乎为1。
正式地,考虑一个离散时间的随机过程
即:如果前一个状态和当前状态是相同的,则下一个状态也永远保持不变;否则下一个状态和前一个状态无关、仅和当前状态有关(类似于普通的随机游走)。
对于图
ParWalks转移概率为:其中:
absorbing state;当transient state。degree。
定义
regularizer matrix。我们关心的是从节点
我们可以求解
ParWalks算法:输入:
- 图拉普拉斯矩阵
- 正则化器矩阵
- 图拉普拉斯矩阵
输出:新的标记节点集合
算法步骤:
计算吸收概率矩阵
对于每个类别
即计算每个节点
confidence vector。然后从
top - t个节点,并将这些节点添加到标签用随机游走来描述就是:观察哪些节点开始的随机游走序列最容易被类别为
1.3.2 Self-Training
让
GCN“看到” 更多标记数据的另一个方法是对GCN进行self-train。具体而言,我们首先通过给定的标记数据来训练GCN,然后通过比较softmax得分为每个类别选择最置信的未标记数据,然后将这些未标记数据添加到对应的类别的标记数据集合中。然后,我们使用扩展的标记数据集合来训练GCN,并使用预先训练好的GCN来作为初始化。GCN发现的最置信的样本应该和标记数据共享相似(但不相同)的representation,将它们添加到标记数据集合有助于训练更强大和准确的分类器。此外,它还在以下场景补充了Co-Training方法:当图具有很多孤立的、小的连通分量时,此时无法通过随机游走来传播标签。Co-Training和Self-Training本质都是寻找最置信的未标记数据,从而将它们加入到标记数据中来扩充标记数据集。Co-Training是通过图结构来寻找最置信的节点,方法是基于随机游走寻找最近邻节点,无需模型参与。Self-Training是通过图结构和节点特征来寻找最置信的节点,方法是基于GCN模型寻找最相似节点。
Self-Training算法:输入:训练好的
GCN模型、图输出:新的标记节点集合
算法步骤:
- 计算所有节点的预测输出:
- 对每个类别
top - t个节点,并将这些节点添加到标签
- 计算所有节点的预测输出:
为提升标签多样性
diversity并训练更鲁棒的分类器,我们提出联合Co-Training和Self-Training。具体而言:- 使用
Co-Training、Self-Training分别挖掘出各自最置信的未标记节点。 - 使用二者未标记节点的并集来扩充标记数据集合,并继续训练
GCN,这称为Union。其中使用预先训练好的GCN来作为二次训练的初始化。 - 使用二者未标记节点的交集来扩充标记数据集合,并继续训练
GCN,这称为Intersection。其中使用预先训练好的GCN来作为二次训练的初始化。
注意:我们在扩展的标记数据上训练
GCN,无需任何额外其它验证数据。只要扩展的标记数据包含足够多的正确的标记数据,则我们的方法就有希望训练出良好的GCN分类器。- 使用
但是,训练一个
GCN分类器需要多少标记数据?假设GCN层数为degree为GCN需要多少标记数据可以传播到整个图。
1.4 实验
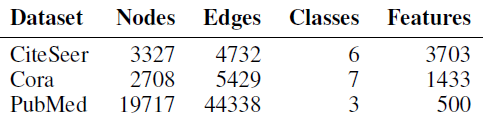
数据集:我们在三种常用的引文网络上进行实验:
CiteSeer, Cora, PubMed。每个数据集上,文档采用bag-of-word特征向量,文档之间的引文链接通过0/1值的邻接矩阵来描述。这些数据集的统计信息如下表所示。
baseline方法:我们和几种
state-of-the-art方法比较,包括:带验证集的GCN:GCN+V、不带验证集的GCN:GCN-V、使用切比雪夫滤波器的GCN(Cheby)、使用ParWalks的标记传播算法label propagation:LP、Planetoid算法、DeepWalk算法、流形正则化manifold regularization:ManiReg、半监督嵌入semi-supervised embedding:SemiEmb、iterative classification algorithm:ICA。我们对比了我们提出的
Co-Training、Self-Training、Union、Intersection等方法。参数设置:
对于
ParWalks,我们设置对于
GCN,我们使用和《Semisupervised classification with graph convolutional networks》相同的超参数,这些超参数是模型在Cora数据集上验证好的:学习率0.01、最多200轮epoch、2层卷积层、隐层维度16。对于
GCN(Cheby),我们选择多项式的阶数为每次执行时,我们随机拆分标记数据,随机选择其中一小部分标记数据作为训练集,然后随机选择
1000个标记数据作为测试集。对于
GCN +V,我们还选择额外的500个标记数据作为验证集。对于
GCN -V,我们仅简单地优化GCN的训练accuracy。对于所有方法,我们分别评估不同规模的训练标记数据的效果:
- 在
Cora,CiteSeer数据集上,训练标记数据规模分别为0.5%, 1%, 2%, 3%, 4%, 5%。 - 在
PubMed数据集上,训练标记数据规模为0.03%, 0.05%, 0.1%, 0.3%。
我们选择这些比例是为了方便和
《Semisupervised classification with graph convolutional networks》的实验结果进行比较。- 在
对于
Cora,CiteSeer数据集,每种方法执行50轮并报告平均的accuracy;对于PubMed数据集,每种方法执行10轮并报告平均的accuracy。
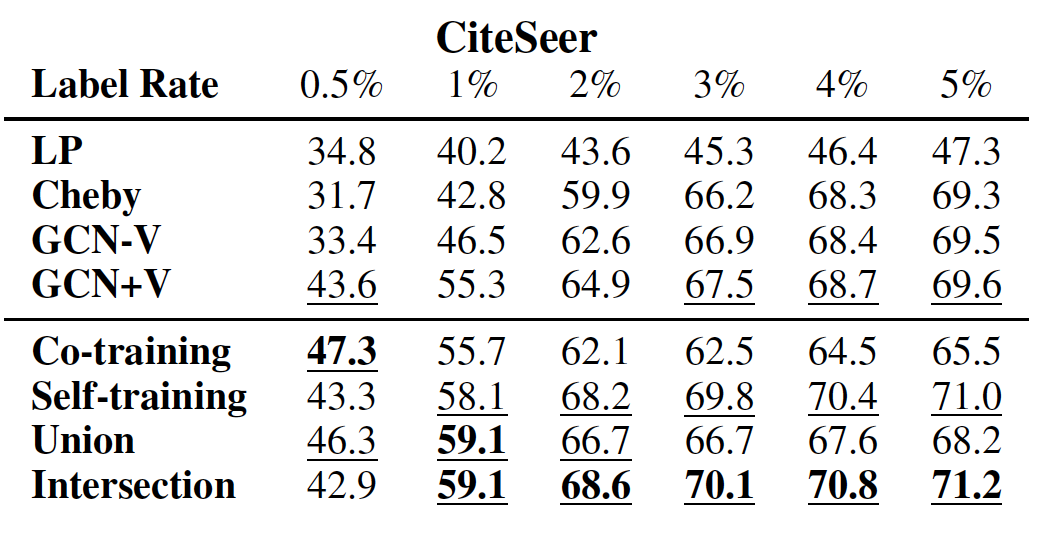
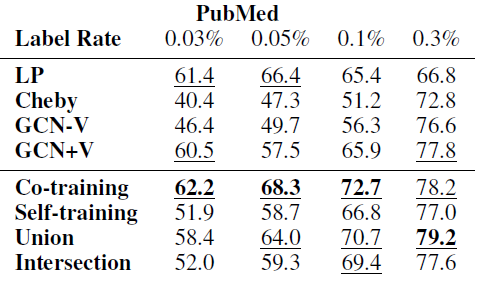
不同方法在各数据集上的效果如下表所示,其中每列测试准确率最高的方法以粗体突出显示,
top 3方法以下划线显示。结论:
在每个数据集上,我们的方法大多数情况下都要比其它方法好得多。
如果数据具有很强的流形结构(如
PubMed),则Co-Training效果更好;否则Self-Training效果更好。Self-Training在PubMed上表现较差,因为它未能充分利用图结构。当训练标记数据规模较大时,
Intersection效果更好,因为它会过滤很多扩展的、但是无效的标记数据;大多数情况下,Union表现最佳,因为它为训练集添加了更多种多样的标签数据。当训练标记数据规模较小时,我们所有的方法都远远超越
GCN-V、并在大多数情况下超越了GCN +V。这验证了我们的分析,即
GCN模型无法在标记数据较少时有效地将标签信息传播到整个图。随着训练标记数据规模的增加,大多数情况下我们的方法仍然优于
GCN +V,这表明我们方法的有效性。当训练标记数据规模足够大时,我们方法和
GCN表现差不多,这表明当标记数据充足时已经可以训练一个良好的GCN分类器。Cheby在大多数情况下表现不佳,这可能是由于过拟合造成的。
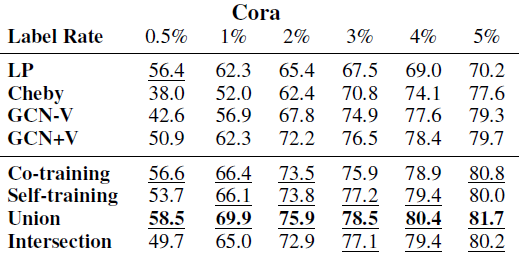
我们将我们的方法和其它
state-of-the-art方法比较,比较结果如下表所示。实验配置和前面的相同,除了对于每个数据集我们对每个类别采样20个训练标记数据,这对应于CiteSeer训练集大小3.6%、Cora的5.1%、PubMed的0.3%。其它
baseline直接拷贝自《Semisupervised classification with graph convolutional networks》。结论:我们方法的效果和
GCN类似,并明显优于其它baseline方法。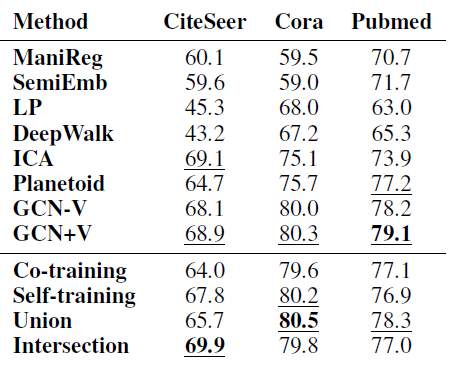
我们方法一个常用的超参数是新添加标记数据的数量:添加太多标记数据会引入噪声,添加太少标记数据则无法训练出良好的
GCN分类器。如前文所述,我们估计训练
GCN所需要的总的标记数据量我们在实验中选择
我们遵循
《Semisupervised classification with graph convolutional networks》将卷积层数量设为2。我们观察到2层GCN表现最好。当卷积层数量增加时,分类准确率急剧下降,这可能是因为过度平滑。计算代价:
对于
Co-Training,额外的计算开销是随机游走模型,这需要求解Cora/CiteSeer只有数千个节点,因此计算时间几乎可以忽略不记;而PubMed在Matlab R2015b上花的时间也不到0.38秒。我们可以使用基于节点的
graph engine进一步加速计算速度,因此我们方法的可扩展性不是问题。对于
Self-Training,我们只需要训练GCN几个额外的epoch,它建立在预先训练好的GCN之上,因此收敛速度很快。因此Self-Training训练时间和GCN相当。
二、GNNEXPLAINER[2019]
图是强大的数据表示形式,而图神经网络
Graph Neural Network: GNN是处理图的最新技术。GNN能够递归地聚合图中邻域节点的信息,从而自然地捕获图结构和节点特征。尽管
GNN效果很好,但是其可解释性较差。由于以下几个原因,GNN的可解释性非常重要:- 可以提高对
GNN模型的信任程度。 - 在越来越多有关公平
fairness、隐私privacy、以及其它安全挑战safety challenge的关键决策应用application中,提高模型的透明度transparency。 - 允许从业人员理解模型特点,从而在实际环境中部署之前就能识别并纠正模型的错误。
尽管目前尚无用于解释
GNN的方法。但是在更高层次,我们可以将包括GNN和Non-GNN的可解释性方法分为两个主要系列:使用简单的代理模型
surrogate model局部逼近locally approximate完整模型full model,然后探索这个代理模型以进行解释。这可能是以模型无关
model-agnostic的方式来完成的,通常是通过线性模型linear model或者规则集合set of rules来学习预测的局部近似,可以充分代表预测结果。仔细检查模型的相关特征
relevant feature,并找到high-level特征的良好定性解释good qualitative interpretation,或者识别有影响力的输入样本influential input instance。如通过特征梯度
feature gradients、神经元反向传播中输入特征的贡献、反事实推理counterfactual reasoning等。
上述两类方法专注于研究模型的固有解释,而后验
post-hoc的可解性方法将模型视为黑盒,然后对其进行探索从而获得相关信息。但是所有这些方法无法融合关系信息,即图的结构信息。由于关系信息对于图上机器学习任务的成功至关重要,因此对
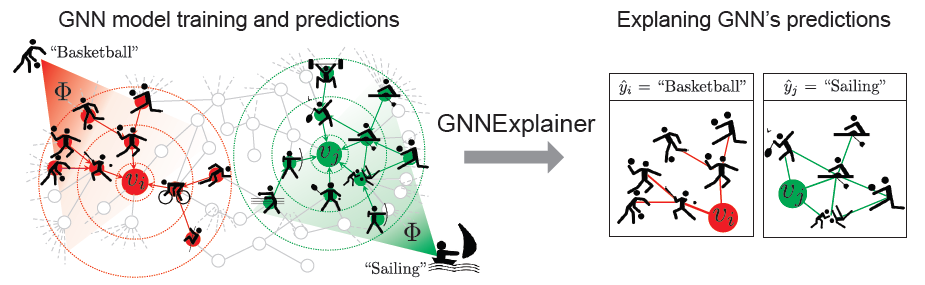
GNN预测的任何解释都应该利用图提供的丰富关系信息、以及节点特征。论文《GNNExplainer: Generating Explanations for Graph Neural Networks》提出了 一种解释GNN预测的方法,称作GNNEXPLAINER。GNNEXPLAINER接受训练好的GNN及其预测,返回对于预测最有影响力的、输入图的一个小的子图small subgraph,以及节点特征的一个小的子集small subset。如下图所示,这里展示了一个节点分类任务,其中在社交网络上训练了
GNN模型GNNGNNEXPLAINER通过识别对预测explanation,如右图所示。- 通过检查
explanation,我们发现GNN预测 - 同样地,通过检查
explanation我们发现GNN预测
GNNEXPLAINER方法和GNN模型无关,可以解释任何GNN在图的任何机器学习任务上的预测,包括节点分类、链接预测、图分类任务。它可以解释单个实例的预测single-instance explanation,也可以解释一组实例的预测multi-instance explanation。- 在单个实例预测的情况下,
GNNEXPLAINER解释了GNN对于特定样本的预测。 - 在多个实例预测的情况下,
GNNEXPLAINER提供了对于一组样本(如类别为“篮球”的所有节点)的预测的一致性解释(即这些预测的共同的解释)。
GNNEXPLAINER将解释指定为训练GNN的整个输入图的某个子图,其中子图基于GNN的预测最大化互信息mutual information。这是通过平均场变分近似mean field variational approximation,以及学习一个实值graph mask来实现的。这个graph mask选择了GNN输入图的最重要子图。同时,GNNEXPLAINER还学习了一个feature mask,它可以掩盖不重要的节点特征。论文在人工合成图、以及真实的图上评估
GNNEXPLAINER的效果。实验表明:GNNEXPLAINER为GNN的预测提供了一致而简洁的解释。- 可以提高对
虽然解释
GNN问题没有得到很好的研究,但相关的可解释性interpretability和神经调试neural debugging的问题在机器学习中得到了大量的关注。在high-level上,我们可以将那些non-graph neural network的可解释性方法分为两个主要方向:- 第一个方向的方法制定了完整神经网络
full neural network的简单代理模型。这可以通过模型无关model-agnostic的方式完成,通常是通过学习prediction周围的局部良好近似(例如通过线性模型或规则集合),代表预测的充分条件sufficient condition。 - 第二个方向方法确定了计算的重要方面,例如,特征梯度
feature gradient、神经元的反向传播对输入特征的贡献、以及反事实推理。然而,这些方法产生的显著性映射saliency map已被证明在某些情况下具有误导性,并且容易出现梯度饱和等问题。这些问题在离散输入(如图邻接矩阵)上更加严重,因为梯度值可能非常大而且位于一个非常小的区域interval。正因为如此,这种方法不适合用来解释神经网络在图上的预测。
事后可解释性
post-hoc interpretability方法不是创建新的、固有可解释的模型,而是将模型视为黑箱,然后探测模型的相关信息。然而,还没有利用关系型结构(如graph)方面的工作。解释图结构数据预测的方法的缺乏是有问题的,因为在很多情况下,图上的预测是由节点和它们之间的边的路径的复杂组合引起的。例如,在一些任务中,只有当图中存在另一条替代路径形成一个循环时,一条边才是重要的,而这两个特征,只有在一起考虑时,才能准确预测节点标签。因此,它们的联合贡献不能被建模为单个贡献的简单线性组合。最后,最近的
GNN模型通过注意力机制增强了可解释性。然而,尽管学到的edge attention值可以表明重要的图结构,但这些值对所有节点的预测都是一样的。因此,这与许多应用相矛盾,在这些应用中,一条边对于预测一个节点的标签是至关重要的,但对于另一个节点的标签则不是。此外,这些方法要么仅限于特定的GNN架构,要么不能通过共同考虑图结构和节点特征信息来解释预测结果。- 第一个方向的方法制定了完整神经网络
GNNEXPLAINER提供了各种好处 ,包括可视化语义相关结构以进行解释的能力、以及提供洞察GNN的错误的能力。
2.1 方法
定义图
- 每个节点
不失一般性,我们考虑节点分类问题的可解释性。定义
GNN模型label。我们假设
GNN模型GNN模型首先,模型计算每对节点
pair对之间传递的消息。节点pair对其中:
MSG(.)为消息函数;representation;然后,对于每个节点
GNN聚合来自其邻域的所有消息:其中:
AGG(.)为一个邻域聚合函数;最后,对于每个节点
GNN根据representation:其中
UPDATE(.)为节点状态更新函数。
最终节点
embedding为representation:对于采用
MSG,AGG,UPDATE计算组成的任何GNN,我们的GNNEXPLAINER可以提供解释。我们的洞察
insight是观察到:节点computation graph是由GNN的neighborhood-based聚合来定义,如下图所示。这个计算图完全决定了用于生成节点GNN如何生成节点embedding定义节点
computation graph为binary邻接矩阵0或1; 也关联一个特征矩阵GNN模型一旦
GNN模型学到这样的分布之后,对于节点GNN的类别预测结果为A所示。正式地讲,
GNNEXPLAINER为预测explanation,记作small subgraph,如图A所示。small subset。F表示通过mask F来遮盖,即:B所示。假设原始的节点特征集合为
mask F遮盖之后的特征集合为:它是原始特征集合的一个小的特征子集,且有:
下图中:
图
A给出了一个GNN在节点GNN都会具有所有消息(包括不重要的消息)从而进行预测,这可能会稀释重要的消息。GNNEXPLAINER的目标是识别少量对于预测至关重要的重要特征和路径(绿色)。图
B表示GNNEXPLAINER通过学习节点特征mask来确定
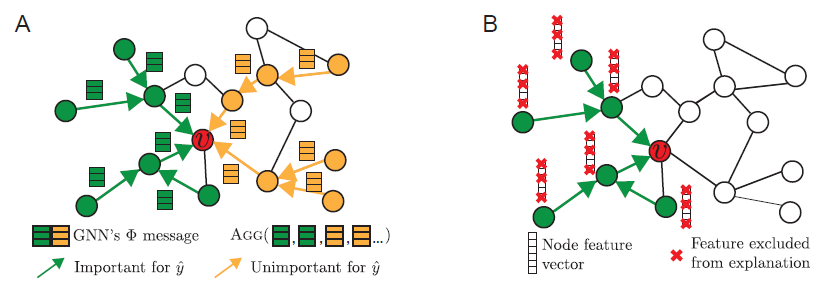
接下来我们详细描述
GNNEXPLAINER。给定训练好的GNN模型prediction(即单实例解释single-instance explanation)、或者一组预测(即多实例解释multi-instance explanation),GNNEXPLAINER将通过识别对模型在多实例解释中,
GNNEXPLAINER将每个实例的解释聚合在一起并自动抽取为一个原型proto。这个原型代表每个实例解释的公共部分,即proto可以对所有这些实例进行解释。
2.1.1 单实例解释
给定一个节点
GNN预测mask,这留待下一步讨论。我们使用互信息
mutual information:MI来刻画子图的重要性,并将GNNEXPLAINER形式化为以下最优化问题:其中:
GNN对于节点GNN预测节点注意:这里没有任何关于节点
GNN预测得准不准,而是仅关心哪些因素和GNN预测结果相关。GNN预测结果不确定性程度。
MI刻画了当节点- 考虑
- 类似地,考虑
GNN,节点因此,对于预测
GNN被限制在uncertainty。在效果上,理论上当
GNNEXPLAINER旨在通过采取对预测提供最高互信息的直接优化
GNNEXPLAINER的目标函数很困难,因为fractional adjacency matrix,即0~1.0之间。此外我们施加约束这种连续性松弛
continuous relaxation可以解释为variational approximation。具体而言,我们将random graph variable,则目标函数变为:我们假设目标函数是凸函数,则
Jensen不等式给出以下的上界:实际上由于神经网络的复杂性,凸性假设不成立。但是通过实验我们发现:优化带正则化的上述目标函数通常求得一个局部极小值,该局部极小值具有高质量的解释性。
为精确地估计
mean-field variational approximation,并将multivariate Bernoulli distribution:这允许我们估计对于平均场近似的期望从而获得
我们从实验观察到:尽管
GNN是非凸的,但是这种近似approximation结合一个可以提升离散型discreteness的正则化器一起,结果可以收敛到良好的局部极小值。可以通过使用邻接矩阵的计算图的掩码
其中:
mask矩阵。sigmoid函数,它将mask映射到0.0~1.0之间。
GNNExplainer的核心在于:用0.0 ~ 1.0之间的mask矩阵(待学习)来调整邻接矩阵,从而最小化预测的熵。但是,这种方法只关心哪个子图对预测结果最重要,并不关心哪个子图对ground-truth最有帮助。可以通过标签类别和模型预测之间的交叉熵来修改上式中的条件熵,从而得到哪个子图对
ground-truth最有帮助。在某些应用
application中,我们不关心模型预测结果的尽管有不同的动机和目标,在
Neural Relational Inference中也发现了masking方法。最后,我们计算
2.1.2 图结构 & 节点特征
为确定哪些节点特征对于预测
GNNEXPLAINER针对GNNEXPLAINER考虑我们通过一个
mask来定义特征选择器:其中
0或1,当它为1时表示保留对应特征,否则遮盖对应特征。因此mask out的节点特征。我们定义特征
mask矩阵为:则有:
现在我们在互信息目标函数中考虑节点特征,从而得到解释
explanation该目标函数同时考虑了对预测
从直觉上看:
- 如果某个节点特征不重要,则
GNN权重矩阵中的相应权重应该接近于零。mask这类特征对于预测结果没有影响。 - 如果某个节点特征很重要,则
GNN权重矩阵中相应权重应该较大。mask这类特征会降低预测为
但是在某些情况下,这种方法会忽略对于预测很重要、但是特征取值接近于零的特征。为解决该问题,我们对所有特征子集边际化
marginalize,并在训练过程中使用蒙特卡洛估计从此外,我们使用
reparametrization技巧将目标函的梯度反向传播到mask矩阵具体而言,为了通过
reparametrize其中:
上式等价于:
这种特征可解释方法可以用于普通的神经网络模型。
- 如果某个节点特征不重要,则
为了在解释
explanation中加入更多属性,可以使用正则化项扩展GNNEXPLAINER的目标函数。可以包含很多正则化项从而产生具有所需属性的解释。- 例如,我们使用逐元素的熵来鼓励结构
mask和节点特征mask是离散的。 - 例如,我们可以将
mask参数的所有元素之和作为正则化项,从而惩罚规模太大的mask。 - 此外,
GNNEXPLAINER可以通过诸如拉格朗日乘子Lagrange multiplier约束、或者额外的正则化项等技术来编码domain-specific约束。
- 例如,我们使用逐元素的熵来鼓励结构
最后需要重点注意的是:每个解释
explanation必须是一个有效的计算图。具体而言,GNN的消息流向节点GNN做出预测重要的是,
GNNEXPLAINER的解释一定是有效的计算图,因为它在整个计算图上优化结构mask。即使一条断开的边对于消息传递很重要,GNNEXPLAINER也不会选择它作为解释,因为它不会影响GNN的预测结果。实际上,这意味着small connected subgraph。这是因为
GNNExplainer会运行GNN,如果计算图无效则运行GNN的结果失败或者预测效果很差,因此也就不会作为可解释结果。
2.1.3 多实例解释
有时候我们需要回答诸如 “为什么
GNN对于一组给定的节点预测都是类别c” 之类的问题。因此我们需要获得对于类别c的全局解释。这里我们提出一个基于
GNNEXPLAINER的解决方案,从而在类别c中的一组不同节点的各自单实例解释中,找到针对类别c的通用的解释。这个问题与寻找每个解释图中最大公共子图密切相关,这是一个NP-hard问题。这里我们采用了解决该问题的神经网络方案,案称作基于对齐alignment-based的multi-instance GNNEXPLAINER。对于给定的类
c,我们首先选择一个参考节点reference nodeprototypical node。- 可以通过计算类别
c中所有节点的embedding均值,然后选择类别c中节点embedding和这个均值最近的节点作为参考节点。 - 也可以使用有关先验知识,选择和先验知识最匹配的节点作为类别
c的参考节点。
给定类别
c的参考节点reference解释图利用微分池化
differentiable pooling的思想,我们使用一个松弛relaxed的对齐矩阵alignment matrix来找到解释图reference解释图relaxed alignment matrix其中:
1.0。
上式第一项表示:经过对齐之后,
实际上对于两个大图
- 可以通过计算类别
一旦得到类别
c中所有节点对齐后的邻接矩阵,我们就可以使用中位数来生成一个原型prototype。之所以使用中位数,是因为中位数可以有效对抗异常值。即:其中
c中第explanation的对齐后的邻接矩阵(即原型
explanation和类别原型进行比较,从而研究该特定节点。在多个解释图的邻接矩阵对齐过程中,也可以使用现在的图库
graph library来寻找这些解释图的最大公共子图,从而替换掉神经网络部分。在多实例解释中,解释器
explainer不仅必须突出与单个预测的局部相关信息,还需要强调不同实例之间更高level的相关性。这些实例之间可以通过任意方式产生关联,但是最常见的还是类成员
class-membership关联。假设类的不同样本之间存在共同特征,那么解释器需要捕获这种共同的特征。例如,通常发现诱变化合物mutagenic compounds具有某些特定属性的功能团,如NO2。如下图所示,经验丰富的专家可能已经注意到这些功能团的存在。当
GNNEXPLAINER生成原型prototype时,可以进一步加强这方面的证据。下图来自于MUTAG数据集的诱变化合物。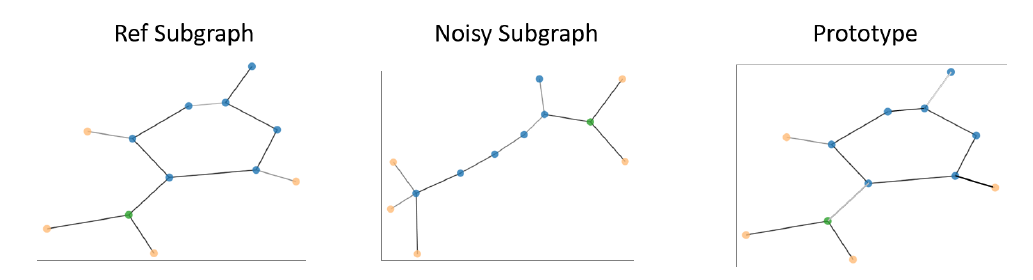
2.1.4 扩展
机器学习任务的扩展:除了解释节点分类之外,
GNNEXPLAINER还可以解释链接预测和图分类,无需更改其优化算法。- 在预测链接
GNNEXPLAINER为链接的两个端点学习两个mask - 在图分类时,目标函数中的邻接矩阵是图中所有节点邻接矩阵的并集
union。
注意:图分类任务和节点分类任务不同。由于图分类任务存在节点
embedding的聚合,因此解释- 在预测链接
模型扩展:
GNNEXPLAINER能够处理所有基于消息传递的GNN,包括:Graph Convolutional Networks:GCN、Gated Graph Sequence Neural Networks:GGS-NNs、Jumping Knowledge Networks:JK-Net、Attention Networks-GAT、Graph Networks:GN、具有各种聚合方案的GNN、Line-Graph NNs、position-aware GNN、以及很多其它GNN架构。GNNEXPLAINER优化中的参数规模取决于节点GNNEXPLAINER学习的。但是,由于单个节点的计算图通常较小,因此即使完整的输入图很大
GNNEXPLAINER仍然可以有效地生成解释。
2.2 实验
数据集:
人工合成数据集:我们人工构建了四种节点分类数据集,如下表所示。
BA-SHAPES数据集:我们从300个节点的Barabasi-Albert:BA基础图、以及一组80个五节点的房屋house结构的主题motif开始,这些motif被随机添加到基础图的随机选择的节点上。进一步地我们添加根据节点的结构角色,节点为以下四种类型之一:
house顶部节点、house中间节点、house底部节点、非house节点。BA-COMMUNITY数据集:是两个BA-SHAPES图的并集。节点具有正态分布的特征向量,并且根据其结构角色、社区成员(两种社区)分配为8种类别之一。TREE-CYCLES:从8-level平衡二叉树为基础图、一组80个 六节点的环状motif开始,这些motif随机添加到基础图的随机选择的节点上。TREE-GRID:和TREE-CYCLES相同,除了使用3x3的网格motif代替六节点的环motif之外。
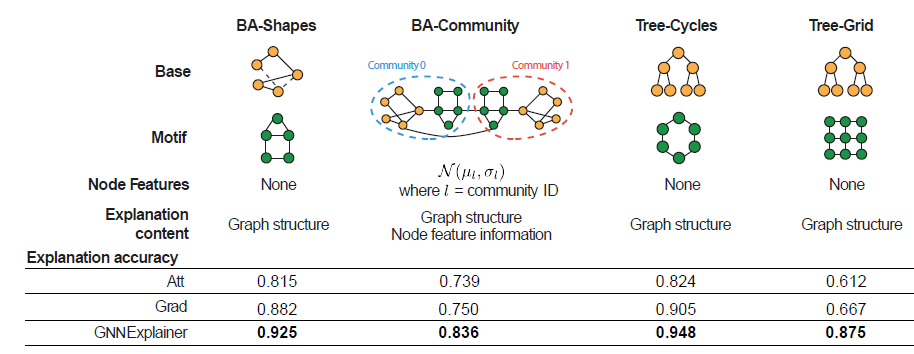
真实数据集:我们考虑两个图分类数据集。
MUTAG:包含4337个分子图的数据集,根据分子对于革兰氏阴性菌伤寒沙门氏菌Gram-negative bacterium S.typhimurium的诱变作用mutagenic effect进行标记。REDDIT-BINARY:包含2000个图的数据集,每个图代表Reddit上讨论的话题thread。在每个图中,节点代表话题下参与讨论的用户,边代表一个用户对另一个用户的评论进行了回复。图根据话题中用户交互类型进行标记:
r/IAmA, r/AskReddit包含Question-Answer交互,r/TrollXChromosomes and r/atheism包含Online-Discussion交互。
Baseline方法:很多可解释性方法无法直接应用于图,尽管如此我们考虑了以下baseline方法,这些方法可以为GNN的预测提供解释。GRAD:基于梯度的方法。我们计算损失函数对于邻接矩阵的梯度、损失函数对于节点特征的梯度,这类似于显著性映射方法saliency map approach。ATT:基于graph attention GNN:GAT的方法。它学习计算图中边的注意力权重,并将其视为边的重要性。尽管
ATT考虑了图结构,但是它并未考虑节点特征的解释,而且仅能解释GAT模型。此外,由于环
cycle的存在(如下图所示),节点的1hop邻居也是它的2-hop邻居。因此使用哪个注意力权重(1hop vs 2hop)也不是很清楚。通常我们将这些hop的注意力权重取均值。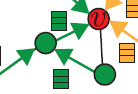
实验配置:对于每个数据集,我们首先为这个数据集训练一个
GNN,然后使用GARD和GNNEXPLAINER来对GNN的预测做出解释。注意,
ATT baseline需要使用GAT之类的图注意力架构,因此我们在同一个数据集上单独训练了一个GAT模型,并使用学到的边注意力权重进行解释。我们对所有的节点分类任务、图分类任务中调整权重正则化参数。这些超参数在所有实验中使用。
- 子图大小正则化超参数为
0.005,该正则化倾向于得到尽可能小的子图。 - 拉普拉斯正则化参数为
0.5。 - 特征数量正则化参数为
0.1,该正则化倾向于得到尽可能少的unmasked特征。
- 子图大小正则化超参数为
我们使用
Adam优化器训练GNN和 解释方法explaination methods。所有
GNN模型都训练1000个epoch,学习率为0.001, 从而对节点分类数据集达到至少85%的准确率、对于图分类数据集达到至少95%的准确率。对于所有数据集,
train/valid/test拆分比例为80%:10%:10%。GNNEXPLAINER使用相同的优化器和学习率,并训练100 ~300个epoch。因为
GNNEXPLAINER仅需要在少于100个节点的局部计算图上进行训练,因此训练epoch要更少一些。
为了抽取解释子图
GRAD的梯度、ATT的注意力权重、GNNEXPLAINER的masked邻接矩阵)。然后我们使用一个阈值来删除权重较低的边,从而得到对于所有方法,我们执行线性搜索从而找到临界阈值,使得
所有数据集的
ground truth explanation是连接的子图。对于节点分类,我们将不同方法得到的
GNNEXPLAINER方法来讲,对于图分类,我们抽取
超参数
- 对于人工合成数据集,我们将
ground truth的大小。 - 对于真实世界数据集,我们设置
- 对于人工合成数据集,我们将
定量分析:对于人工合成数据集,我们已有
ground-truth解释,然后使用这些ground-truth来评估所有方法解释的准确性。具体而言,我们将解释问题形式化为二元分类任务,其中真实解释中的边视为label,而将可解释性方法给出的重要性权重视为预测得分。一种更好的可解释性方法对于真实解释的边的预测得分较高,从而获得更好的解释准确率。下表给出了人工合成数据集节点分类评估结果。实验结果表明:
GNNEXPLAINER的平均效果相比其它方法高出17.1%。
定性分析:
在没有节点特征的
topology-based预测任务中(如BA-SHAPES、TREE-CYCLES),GNNEXPLAINER正确地识别解释节点标签的motif。如下图所示,
A-B给出了四个人工合成数据集上节点分类任务的单实例解释子图,每种方法都为红色节点的预测提供解释(绿色表示重要的节点,橙色表示不重要的节点)。可以看到GNNEXPLAINER能识别到house, cycle, trid等motif,而baseline方法无法识别。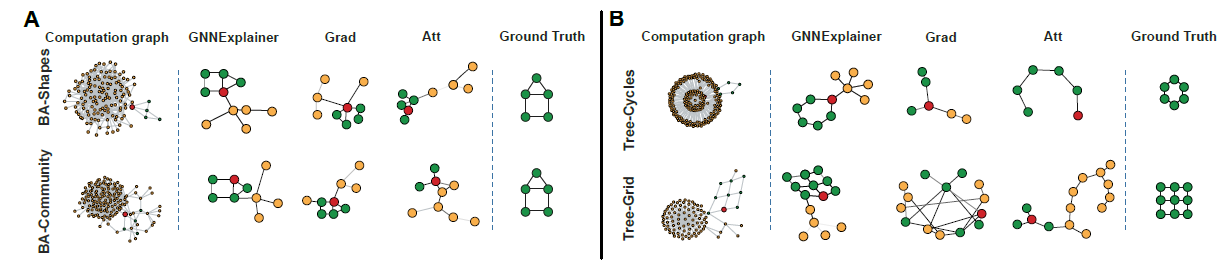
我们研究图分类任务的解释。
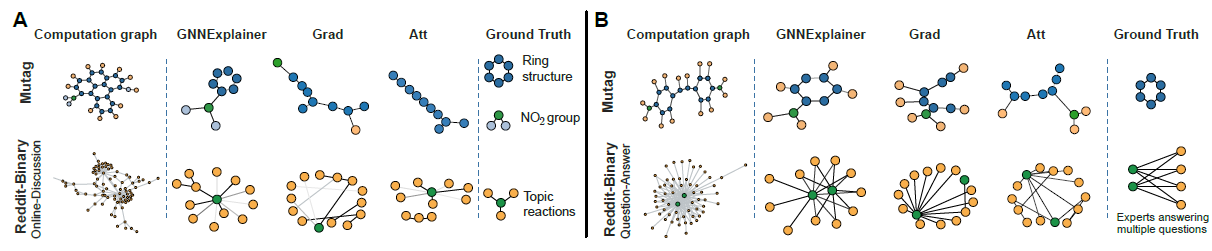
在
MUTAG实例中,颜色表示节点特征,这代表原子类型(氢H、碳C等)。GNNEXPLAINER可以正确的识别对于图类别比较重要的碳环、以及化学基团NH2和NO2,它们确实已知是诱变的mutagenic官能团。在
REDDIT-BINARY示例中,我们看到Question-Answe图(B的第二行)具有2~3个同时连接到很多低degree节点的高degree节点。这是讲得通的,因为在Reddit的问答模式的话题中,通常具有2~3位专家都回答了许多不同的问题。相反,在
REDDIT-BINARY的讨论模式discussion pattern图(A的第二行),通常表现出树状模式。GRAD,ATT方法给出了错误的或者不完整的解释。例如两种baseline都错过了MUTAG数据集中的碳环。此外,尽管
ATT可以将边注意力权重视为消息传递的重要性得分,但是权重在输入图中的所有节点之间共享,因此ATT无法提供高质量的单实例解释。
解释
explanations的基本要求是它们必须是可解释的interpretable,即,提供对输入节点和预测之间关系的定性理解。下图显式了一个实验结果,其中给出不同方法预测的解释的特征。特征重要性通过热力度可视化。可以看到:
GNNEXPLAINER确实识别出了重要的特征;而gradient-based无法识别,它为无关特征提供了较高的重要性得分。ground-truth特征从何而来?作者并未讲清楚。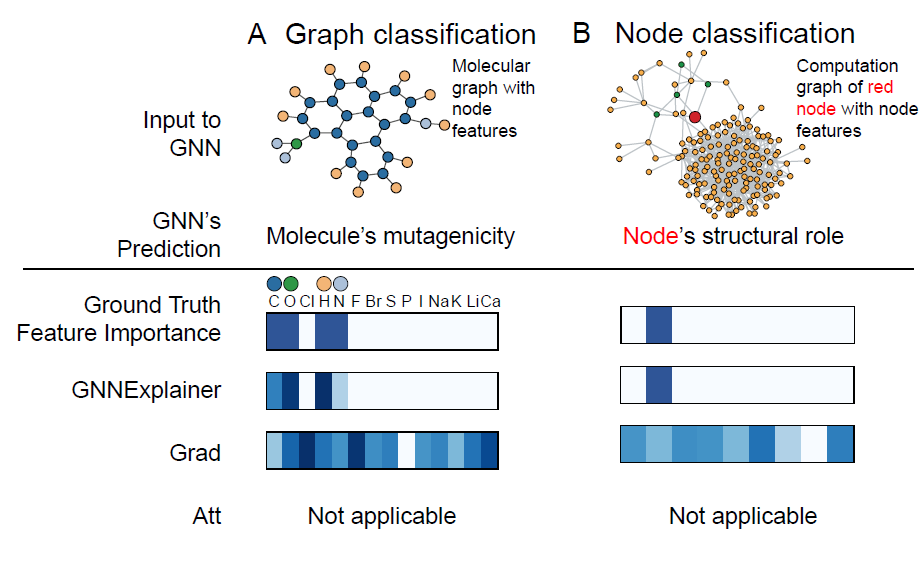
三、GCN 自监督学习[2020]
图卷积神经网络
GCN将卷积神经网络CNN推广到了图结构数据,从而利用图的属性。在很多graph-based任务(诸如节点分类、链接分类、链接预测、图分类任务)中,GCN的性能优于传统方法,其中很多是半监督学习任务。这里我们主要讨论transductive半监督节点分类任务,其中图包含大量未标记节点、少量的标记节点,任务目标是预测剩余未标记节点的label。与此同时,自监督
self-supervision在计算机视觉领域引起了人们的广泛关注。自监督利用了丰富的未标记数据,旨在通过预训练pretraining(随后紧跟着微调finetuning)、多任务学习multi-task learning等前置任务pretext task帮助模型从未标记的数据中学习更可迁移的transferable、更泛化generalized的representation。前置任务必须经过精心设计使得网络可以学习下游任务相关的语义特征。目前已经为
CNN提出了很多前置任务,包括:旋转rotation、exemplar、jigsaw、relative patch location等等的prediction。最近,
《Using self-supervised learning can improve model robustness and uncertainty》表示自监督学习可以作为辅助正则化auxiliary regularization来提高鲁棒性robustness和不确定性估计uncertainty estimation;《Adversarial robustness: From selfsupervised pre-training to fine-tuning》将对抗训练引入自监督,从而提供了第一个通用的鲁棒性预训练。简而言之,
GCN任务通常遇到具有大量未标记节点的transductive半监督setting,同时自监督在利用CNN中未标记数据方面扮演越来越重要的角色。因此我们自然地探讨以下有趣的问题:自监督学习能否在GCN中发挥类似的作用,从而提高其泛化性generalizability和鲁棒性robustness?论文
《When Does Self-Supervision Help Graph Convolutional Networks?》是第一个系统性地研究如何将自监督纳入GCN的文章。该论文研究了三个具体问题:GCN能否在分类任务中受益于自监督学习?如果答案是yes,那么如何将自监督融合到GCN中从而最大化收益?- 前置任务的设计重要吗?
GCN有哪些有效的自监督前置任务? - 自监督还会影响
GCN的对抗鲁棒性adversarial robustness吗?如果是,如何设计前置任务?
针对这三个问题,论文给出了三个回答:
论文通过多任务学习
multi-task learning的方式将自监督纳入GCN从而展示了自监督的有效性,即作为GCN训练中的正则化项。相对于预训练pretraining、自训练self-training等自监督方式,多任务学习效果更好。论文基于图属性调研了三种自监督任务。除了之前工作提及的节点聚类
node clustering任务之外,论文还提出了两种新类型的任务:图划分graph partitioning、图补全graph completion。作者进一步说明,不同的模型和数据集似乎倾向于不同的自监督任务。
论文将上述发现进一步推广到对抗训练
setting中。论文提供的结果表明:自监督还可以提高GCN在各种攻击下的鲁棒性,无需使用更大的模型或更多的数据。
相关工作:
graph-based半监督学习:基于图的半监督学习的关键假设是,较大权重的边连接的节点更可能具有相同的标签。基于图的半监督学习方法有大量的工作,例如
mincuts、Boltzmann machine、和graph random walk。最近,图卷积网络GCN及其变体通过将假设从人工设计的方式扩展到数据驱动的方式,从而得到大家的青睐。自监督学习:自监督
self-supervision是神经网络在计算机视觉领域学习更可迁移的、更通用的、和更鲁棒的特征的一个有前途的方向。到目前为止,CNN中自监督的使用主要分为两类:预训练和微调pretraining & finetuning,以及多任务学习multi-task learning。- 在预训练和微调中,
CNN首先用自我监督的前置任务进行预训练,然后用带标签的监督的目标任务进行微调。 - 在多任务学习中,网络是以目标监督任务和自监督任务的联合目标同时训练的。
据我们所知,最近只有一项在
GCN中追求自监督的工作(《Multi-stage self-supervised learning for graph convolutional networks》),其中采用了通过self-training的节点聚类任务。然而,self-training存在局限性,包括性能 "饱和saturation" 和退化。此外,它还限制了自监督任务的类型。- 在预训练和微调中,
图上的对抗性攻击和防御:与
CNN类似,GCN的广泛适用性和脆弱性提出了提高其鲁棒性的迫切要求。人们提出了几种算法来对图进行攻击和防御。《Adversarial attack on graph structured data》通过dropping edge,基于梯度下降、遗传算法和强化学习开发了攻击方法。《Adversarial attacks on neural networks for graph data》提出了一种基于FSGM的方法来攻击edge和特征。
最近,出现了更多样化的防御方法。
《Adversarial attack on graph structured data》通过直接在扰动的图上进行训练来防御对抗性攻击。《Adversarial examples on graph data: Deep insights into attack and defense》通过从连续函数中学习graph来获得鲁棒性。《Adversarial defense framework for graph neural network》使用graph refining和adversarial contrasting learning来提升模型的鲁棒性。《Graphdefense: Towards robust graph convolutional networks》提出使用未标记数据的伪标签,增强了对大图的可扩展性。
3.1 自监督方式
给定图
每个节点
定义图邻接矩阵
且
典型的采用两层的半监督分类
GCN模型定义为:其中:
这里我们没有对输出应用
softmax函数,而是将其视为以下所述损失的一部分。我们将
GCN特征抽取器GCN变体中对应网络架构的其它参数。因此,GCN分解为特征抽取feature extraction和线性映射linear transformation两个部分:其中参数集
考虑
transductive半监督任务。给定标记样本集合label矩阵label维度,对于节点分类任务我们通过最小化输出和节点真实标记之间的损失来学习
GCN模型的参数。即:其中:
label向量。
受到
CNN中相关讨论的启发(《Scaling and benchmarking self-supervised visual representation learning》、《Revisiting self-supervised visual representation learning》、《Using self-supervised learning can improve model robustness and uncertainty》),我们调研了三种可能自监督任务(ss)来融合到GCN中。其中:自监督任务的节点集合为Pretraining&Finetuning、自训练Self-Training、多任务学习Multi-Task Leraning。
a. 预训练和微调
在预训练过程中,模型通过自监督任务来训练特征抽取器:
其中:
target任务的线性映射参数target任务共享。
然后在微调任务中,特征抽取器
预训练和微调可以说是有利于
GCN的自监督方法的最直接的选择。但是我们发现:在大型数据集Pubmed上,该方法几乎没有提高性能(见下表)。我们猜测是因为:预训练期间的目标函数
gap。在微调过程中,由于从一个目标函数(即
transductive半监督学习使用浅层的GCN,而这个浅层GCN的很容易被overwrite。至于为什么不用深层
GCN,是因为更深的GCN会导致过度平滑。
下表为
PubMed数据集上的预训练&微调P&F、多任务学习MTL的性能比较,其中自监督任务为图划分。数字表示分类准确率。
b. 自训练
《self-supervised learning for graph convolutional networks》是GCN中唯一进行自监督的工作,它是通过自训练来实现的。对于同时包含标记样本、未标记样本的数据集,典型的自训练
pipeline:- 首先对标记样本训练一个模型。
- 然后对置信度很高的未标记样本分配伪标记
pseudo-label。 - 接着将这些伪标记样本、标记样本视作新的标记样本进行下一轮训练。
该过程可以重复几轮,并且每轮中都会对未标记样本分配伪标记。
这篇论文的作者提出了
multi-stage self-supervised: M3S训练算法,其中采用了自监督来对齐和完善未标记节点的伪标签。尽管在few-shot实验中该方法的性能有所提高,但是随着标记率(标记样本的占比)提升,M3S的性能增益趋于饱和。
c. 多任务学习
多任务学习同时考虑
GCN的目标任务target task和自监督任务,训练过程的目标函数为:其中:
因此目标任务和自监督任务共享相同的特征抽取器
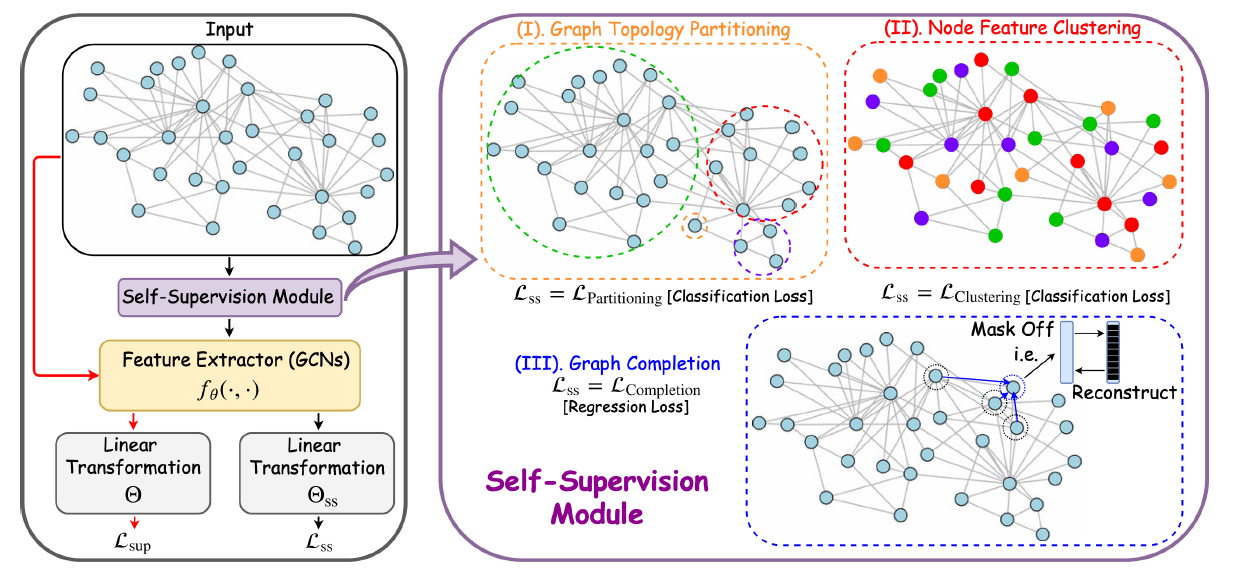
在多任务学习中,我们将自监督任务视为整个模型训练中的一个正则化项。
正则化项在传统上广泛应用于图信号处理,著名的是图拉普拉斯正则化器
graph Laplacian regularizer: GLR,它惩罚了相邻节点之间的不相干(即不平滑)的信号。尽管GLR的有效性已经在图信号处理中得到了证明,但正则化器是根据平滑先验smoothness prior人工设置的,没有数据的参与。而自监督任务扮演了一个正则化器的角色,它从未标记数据中学到,弱化了人工的先验指导。因此,一个合适的自监督任务将引入数据驱动的先验知识,从而提高模型的泛化能力。
总而言之,多任务学习是三者中最通用的框架,并在训练过程中充当数据驱动的正则化器。它不对自监督任务类型做任何假设。经实验验证,它是所有三个方法中最有效的。
3.2 自监督任务
前面讲到我们可以通过自监督任务来训练
GCN,这里我们给出:针对GCN都有哪些自监督任务。我们表明:通过利用图中丰富的节点信息、边信息,可以定义各种
GCN-specific自监督任务(如下表所示),这些自监督任务可以帮助下游任务。
节点聚类
node clustering:参考M3S的做法,一种构造自监督任务的直接方法是节点聚类。给定节点集合
我们将每个节点分配它所属的类簇编号:
通过聚类算法来获得自监督任务的
node label。采用何种聚类算法?论文这里没有讲述。图划分
graph partitioning:节点聚类相关的算法基于节点特征,其原理是对具有相似属性的节点进行分组。对节点进行分组的另一个思路是:基于图的拓扑结构。具体而言,如果两个节点之间存在强链接(即链接权重很大),则这两个节点很可能属于同一标签类别。因此我们提出使用图分区的基于拓扑结构topology-based的自监督任务。图分区是将图的节点划分为大致相等的子集,并使得跨子集的链接最小化。给定节点集合
这类似于节点聚类。
另外,对图划分施加平衡约束
balance constraint:其中
图分区的目标是最小化
edgecut:我们将分区
index作为自监督任务的label:与基于节点特征的节点聚类不同,图划分提供了基于图拓扑结构的先验正则化,这类似于图拉普拉斯正则化器
GLR(它也采用了connection-prompting similarity的思想 )。但是,GLR已经注入inject到GCN架构中,它会对所有节点局部平滑它们的邻居节点。相反,图划分利用所有连接,对具有较高连接密度的节点群进行分组来考虑全局平滑性global smoothness。图补全
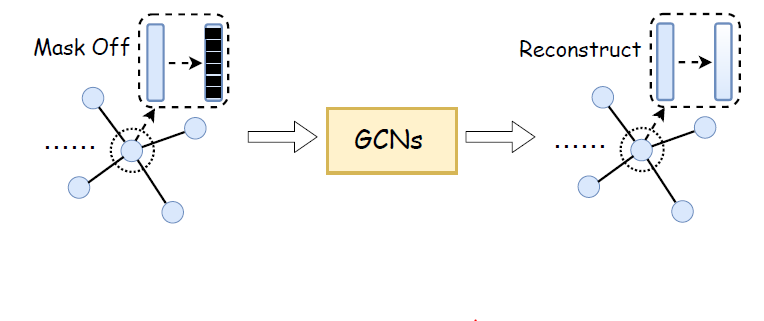
graph completion:受计算机视觉领域中的图像修复和补全的启发(它旨在补全图像的缺失像素),我们提出了一种的新的回归任务作为自监督任务:图补全。如下图所述,和图像补全
image completion任务类似,我们的图补全任务:- 首先,删除目标节点的特征来遮盖
mask目标节点。 - 然后,向
GCN输入未遮盖的节点特征来恢复被遮盖的节点特征。
我们设计这种自监督任务的原因如下:
- 可以自由地获取
completion label,即节点特征本身。 - 我们认为图补全任务可以帮助网络更好地表示特征,从而教会网络从上下文
context中抽取特征。
还有一种自监督任务:链接预测。链接预测也同时利用了节点特征和图结构。
- 首先,删除目标节点的特征来遮盖
3.3 图对抗防御
通过为
GCN引入三个自监督任务,可以使得GCN在图半监督学习上获得更好的泛化能力。我们继续研究自监督任务在针对各种图对抗攻击的鲁棒性方面的表现。这里我们仅关注于单个节点的直接规避攻击
direct evasion attack:基于目标节点node-specific攻击(攻击满足某些约束条件),而训练好的模型(模型参数为攻击者
其中
label、以及模型参数作为输入。攻击可以发生在链接
link上、节点特征上、或者二者同时攻击。对抗防御
adversarial defense:一种有效的对抗防御方法(尤其是在图像领域)是采用对抗训练adversarial training。在对抗训练中通过对抗样本adversarial examples来增强训练集。 但是,由于在transductive半监督setting中的标记率较低,因此很难在图领域中生成对抗样本。《Graphdefense: Towards robust graph convolutional networks》提出利用未标记节点来生成对抗样本。具体而言,他们训练了原始GCN,将伪标签对图数据的对抗训练可以形式化为同时对标记节点的监督学习、以及对未标记节点(
pseudo label的recovering:其中
带自监督的对抗防御:引入自监督学习以及对抗训练的
GCN为:其中自监督损失函数也参与训练过程,它将扰动图作为输入(自监督的标签矩阵
从
CNN中观察到:自监督可以提高鲁棒性和不确定性估计uncertainty estimation,无需更大的模型或额外的数据。因此我们通过实验探索了这一点是否也适用于GCN。这里需要提前训练一个仅包含监督任务的
GCN模型从而获得伪标签。
3.4 实验
数据集如下所示,
N表示特征维度: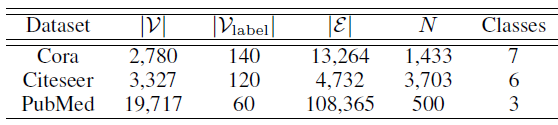
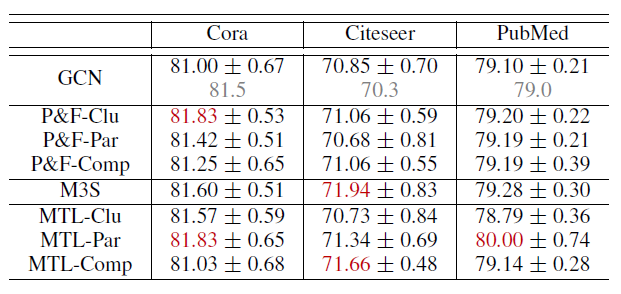
三种自监督方式、三种自监督任务的对比。其中
M3S的超参数设置为原始论文的默认值。表中:每个结果都采用不同的随机数种子随机执行
50次,并报告平均的准确率和标准差。Clu: Node Clustering、Par: Graph Partition、Comp: Graph Completion表示三种自监督任务;P&T:pretraining&finetuning、M3S、MTL:multi-task learning表示三种自监督方式。P&T-Clu表示自监督方式和自监督任务的组合。红色数字表示在该数据中,超过
GCN至少0.8的、表现最佳的两项。在
GCN一栏,灰色数字表示公开发表的结果。
结论:
三种自监督方式中,预训练&微调为小型数据集
Cora提供了一些改善,但对于大型数据集Citeseer和PubMed却几乎没有改善。即使是采用不同的自监督任务,结论也是如此。这证明了我们之前的猜测:尽管在预训练阶段通过自监督任务
在
GCN中特别观察到这种信息丢失的可能原因是:在微调过程中,从一个目标函数切换到另一个目标函数时,在transductive半监督学习setting中使用的浅层GCN很容易被overwritten。剩下的两种自监督方式相比于原始
GCN,在节点分类上得到更大的提升。和预训练&微调相比,自学习、多任务学习的自监督方式都通过一个优化问题(即,一个联合损失函数)从而将自监督融合到
GCN中,二者本质上都会给GCN中的原始公式带来额外的自监督损失。它们的区别在于:使用了哪些伪标签以及如何为未标记的节点生成伪标签。在自训练的情况下,伪标签和目标任务标签类型相同,并且这些伪标签根据未标记节点
embedding和标记节点embedding之间的邻近性来分配。在多任务学习的情况下,伪标签不再局限于目标任务标签类型,而是可以通过探索未标记数据的图结构和节点特征来构造伪标签。并且多任务学习中的目标监督学习和自监督学习仍然通过
grap embedding来耦合。因此和自训练相比,多任务学习可以更通用(在伪标签方面),并且可以更多地利用图数据(通过正则化)。
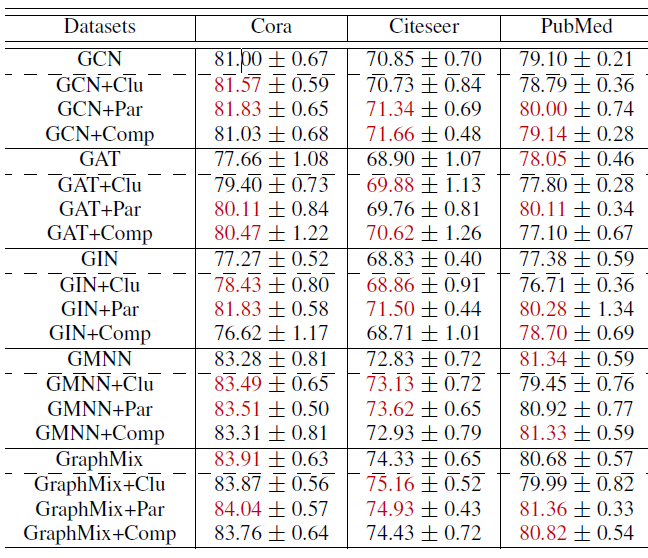
我们通过一组实验来回答三个问题:
多任务自监督学习对于
SOTA GCN是否有帮助?下表显示:不同的自监督任务可以在不同程度上对不同数据集上的不同网络体系结构有帮助。表中红色数字表示每个
SOTA方法最佳的两个性能(包括没有自监督学习的版本)。多任务自监督何时、并且为什么能帮助
SOTA GCN?我们注意到:图分区任务通常对所有三个数据集上的所有三个
SOTA都有利,而节点聚类任务对PubMed上的SOTA没有好处。如前所述,多任务学习将自监督任务引入到
GCN中,从而作为数据驱动的正则化。不同的自监督任务代表不同的先验条件:基于特征的节点聚类假设特征相似性,从而意味着
target-label相似性,并且可以将具有相似特征的遥远节点分组在一起。当数据集很大,且特征维度相对较低时(如
PubMed),基于特征的聚类可能难以提供有效的伪标签。基于拓扑的图分区假设拓扑结构的连接性,从而意味着
target-label相似性。这对于所有三个引文网络数据集都是安全的。另外,图分区作为一个分类任务并不会过于强调该假设。因此,由于图分区代表的先验是通用且有效的,因此可以使得
GCN任务受益(至少对于实验中的数据集以及对应的目标任务而言)。同时考虑拓扑结构和节点特征的图补全任务假设特征相似性、以及图的小范围邻域内的平滑性。它可以极大地提高目标任务性能,尤其是当邻域规模较小时(如在所有三个数据集中平均
degree最小的Citeseer)。但是,面对具有更大邻域的稠密图、更困难的补全任务时(如
PubMed数据集,它有更大、更稠密的图,且待补全的特征是连续的),回归任务面临很大挑战。话虽如此,图补全的潜在先验信息可以极大地有利于其它任务。
GNN架构会影响多任务自监督吗?对于每个
GNN架构,所有三个自监督的任务都能提高某些数据集的性能(PubMed上的GMNN除外)。对于
GCN,GAT,GIN而言,改善更为明显。我们推测:通过各种先验的数据正则化可以使这三种架构(尤其是GCN)受益。相反,带图补全自监督学习的
GMNN没有什么改善。GMNN将统计关系学习statistical relational learning:SRL引入到体系架构中,从而对节点及其邻居之间的依赖关系进行建模。考虑到图补全有助于
content-based representation,并且起着和SRL相似的作用,因此自监督先验和体系结构的先验可能相似,因此它们的组合可能没有效果。同样,
GraphMix在架构中引入了一种数据增强方法Mixup,从而优化特征embedding。这也和图补全任务的目标重叠从而降低了图补全任务的效果。
多任务自监督学习除了给
GCN带来graph embedding泛化能力的提升之外,还有哪些额外的好处?我们还对
GCN进行了针对Nettack的多任务自监督的对抗实验,从而检验它在鲁棒性方面的潜在优势。我们首先以相同的扰动强度
robust generalization。对于每个自监督任务,将超参数设置和前面实验一样。每个实验重复5次并报告平均的实验结果,因为对测试节点的攻击过程非常耗时。实验结果如下表所示。结论:节点聚类更有效地抵抗特征攻击。在对抗训练中,节点聚类为
GCN提供了扰动特征先验perturbed feature prior从而增强了GCN抵抗特征攻击的能力。图分区更有效地抵抗链接攻击。在对抗训练中,图分区为
GCN提供了扰动链接先验perturbed link prior,从而增强了GCN抵抗链接攻击的能力。令人惊讶的是,在
Cora数据集上,图补全可以针对链接攻击将对抗准确率提升4.5%(相对于AdvT)、针对链接且特征的攻击将对抗准确率提升8.0%(相对于AdvT)。图补全也是针对
Citeseer的链接攻击、链接且特征攻击的最佳自监督任务之一,尽管提升幅度较小(1%) 。这和我们在前文的推测一致:同时考虑基于拓扑和基于特征的图补全构建了链接和特征上的扰动先验
perturbation prior,这有利于GCN抵抗链接攻击或链接且特征攻击。
注:下表为在
Cora数据集上的对抗训练(AdvT),带或者不带自监督学习。攻击发生在链接Links、节点特征Feats、链接且节点特征Links&Feats。红色表示在每种攻击场景中最佳的两个表现。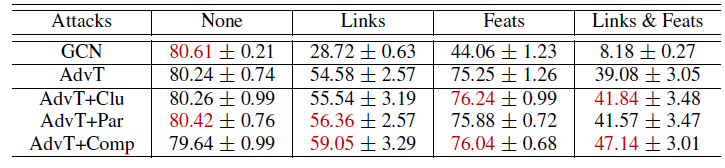
注:下表为在
Citeseer数据集上的对抗训练(AdvT),带或者不带自监督学习。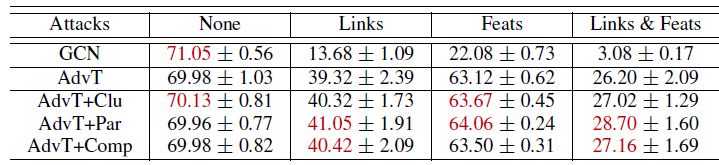
此外,我们产生具有不同扰动强度的攻击(
GCN仍然可以提高其鲁棒性,从而应对各种强度的各种攻击。结论:我们简单总结如下:
首先,在将自监督纳入
GCN的三种方案中:- 多任务学习可以作为正则化器,并通过适当的自监督任务使得
GCN的效果得到一致地提升。 - 预训练&微调将目标函数从自监督损失转换为目标监督损失,这很容易
overwrite浅层GCN,并获得有限的性能提升。 - 自训练受限于分配了哪些伪标签,以及使用哪些数据来生成伪标签。它的性能提升在
few-shot learning中更明显,并随着标记率的提升而逐渐减少。
- 多任务学习可以作为正则化器,并通过适当的自监督任务使得
其次,通过多任务学习,自监督任务提供了有益的先验来提升
GCN的性能。- 节点聚类提供节点特征的先验。
- 图分区提供图结构的先验。
- 图补全同时提供节点特征、图结构的先验,从而帮助
GCN进行得到context-based representation。
另外,自监督任务是否有助于
SOTA GCN取决于数据集是否生成针对目标任务的高质量的伪标签,以及自监督的先验是否补充了现有体系结构的先验。链接预测作为自监督任务,也同时提供节点特征、图结构的先验。
最后,对抗训练中多任务自监督提高了
GCN抵御各种图攻击的鲁棒性。- 节点聚类提供节点特征的先验,因此可以更好地抵御节点特征攻击。
- 图分区提供图结构的先验,因此可以更好地抵御链接攻击。
- 图补全同时提供节点特征、图结构的先验,因此能同时抵御节点特征攻击、链接攻击,一致地提高了鲁棒性。
四、GNN 公平比较[2019]
多年以来研究人员对于学术界的一些缺陷提出了担忧,如机器学习、科学领域的实验的可重复性
reproducibility和可复制性replicability。最近,图神经网络已经成为图上的机器学习的标准工具,但是这些模型的实验在很多情况下是模棱两可
ambiguous或者不可复现的。一些常见的可复现问题包括: 超参数的选择、数据集的拆分。而且,一些论文的模型评估代码缺失或不完整的。另外,不同论文在节点特征、边的特征选取上也未标准化。实际上对模型的评估包括两个不同的阶段:
- 模型选择:在验证集上通过超参数调优来选择最优超参数,这对应着模型选择。
- 模型评估:在测试集上对选择出来的模型进行效果评估。
显然,如果没有把这两个阶段很好地区分,则可能会导致对模型真实性能的过于乐观和有偏的估计。这使得模型评估的结果不置信。这也使得其它竞争者也很难在严格的评估程序下超越这种不置信的结果。
有鉴于此,论文
《A FAIR COMPARISON OF GRAPH NEURAL NETWORKS FOR GRAPH CLASSIFICATION》提出了使用标准化、且可复现的实验环境来为GNN框架提供公平的性能比较。具体而言,作者在严格的模型选择、模型评估框架内进行了大量的实验,其中所有模型均使用相同的特征、相同的数据集拆分来进行比较。其次,论文研究了当前
GNN模型是否、以及何种程度上可以有效地利用图结构。为此,作者添加了两个领域特定的domain-specific、结构无感知的structure-agnostic基准方法baseline(这些方法没有利用结构信息),其目的是从节点特征中区分出结构信息的贡献。令人惊讶的是,作者发现这些baseline甚至在某些数据集上的性能甚至优于GNN。最后,作者研究了节点
degree在社交数据集中作为特征的影响。作者证明:提供degree可以提高性能,并且对达到良好结果所需要的GNN层数也有影响。作者表明:这项工作并非旨在确定性能最佳(或最差)的
GNN,也并未否认大家在开发这些模型上的努力。作者只是试图为GNN建立标准、统一的评估框架,以便模型之间可以进行公平、客观地比较。相关工作:
GNN:GNN的核心是为图中的每个节点计算一个状态,这个状态根据相邻节点的状态迭代更新。GNN最近得到了普及,因为它可以有效地从图中自动提取相关的特征。在过去,处理复杂图结构的最流行的方法是使用核函数
kernel function来计算与任务相关的特征。然而,这种核函数是非适应性non-adaptive的,而且通常计算成本很高,这使得GNN更有吸引力。尽管在这项工作中,我们特别关注为图分类而设计的架构,但所有的
GNN都共享节点邻域上的 "卷积 " 的概念。例如:GraphSAGE首先对邻域执行sum池化、均值池化、或最大池化的聚合,然后它在卷积之上应用线性投影更新node representation。它还依靠邻域采样方案来保持计算复杂度不变。- 相反,
Graph Isomorphism Network: GIN建立在GraphSAGE的局限性之上,用multi-set上的任意聚合函数来扩展GraphSAGE。GIN模型被证明在理论上与Weisfeiler-Lehman的图同构测试graph isomorphism test一样强大。 - 最近,
《On the limitations of representing functions on sets》给出了在set和multi-set上学习排列不变函数permutation-invariant function所需的隐单元数量的上限。 - 与上述方法不同,
Edge-Conditioned Convolution: ECC为每个edge label学习一个不同的parameter。因此,邻域聚合是根据特定的edge parameter进行加权的。 - 最后,
Deep Graph Convolutional Neural Network: DGCNN提出了与GCN的表述类似的卷积层。
一些模型还利用了池化方案,在卷积层之后应用,以减少图的大小。例如:
ECC的池化方案通过一个可以预先计算的可微分的pooling map来粗化图形。- 同样,
DiffPool提出了一种自适应的池化机制,根据监督准则来对节点进行折叠。在实践中,DiffPool将可微分的图编码器与其池化策略相结合,因此该架构是可以端到端的训练。 - 最后,
DGCNN与其他工作的不同之处在于,节点是通过一种名为SortPool的特定算法进行排序和对齐的。
模型评估:
《Pitfalls of graph neural network evaluation》的工作与我们的贡献有类似的目的。具体而言,作者在节点分类任务上比较了不同的GNN,表明结果高度依赖于所选择的特定train/validation/test split,以至于改变split会导致巨大的不同性能排名。因此,他们建议在多个test split上评估GNN,以实现公平的比较。尽管我们在一个不同的
setting中操作(图分类而不是节点分类),但我们遵循作者的建议,在一个受控和严格的评估框架下评估模型。最后,
《Are we really making much progress? A worrying analysis of recent neural recommendation approaches》的工作批评了大量的神经推荐系统,其中大多数都是不可复制的,表明其中只有一个真正比简单的baseline有所提高。
4.1 风险评估&模型选择
这里对风险评估
risk assessment(也称作模型评估model evaluation)和模型选择model selection过程进行概述,从而明确本文遵循的实验过程。我们首先给出总体评估框架,如下图所示。使用外层
使用内层的
hold-out或者如果采用了
模型评估期间也需要重新训练模型(利用寻找到的最优超参数在训练集+验证集上)。
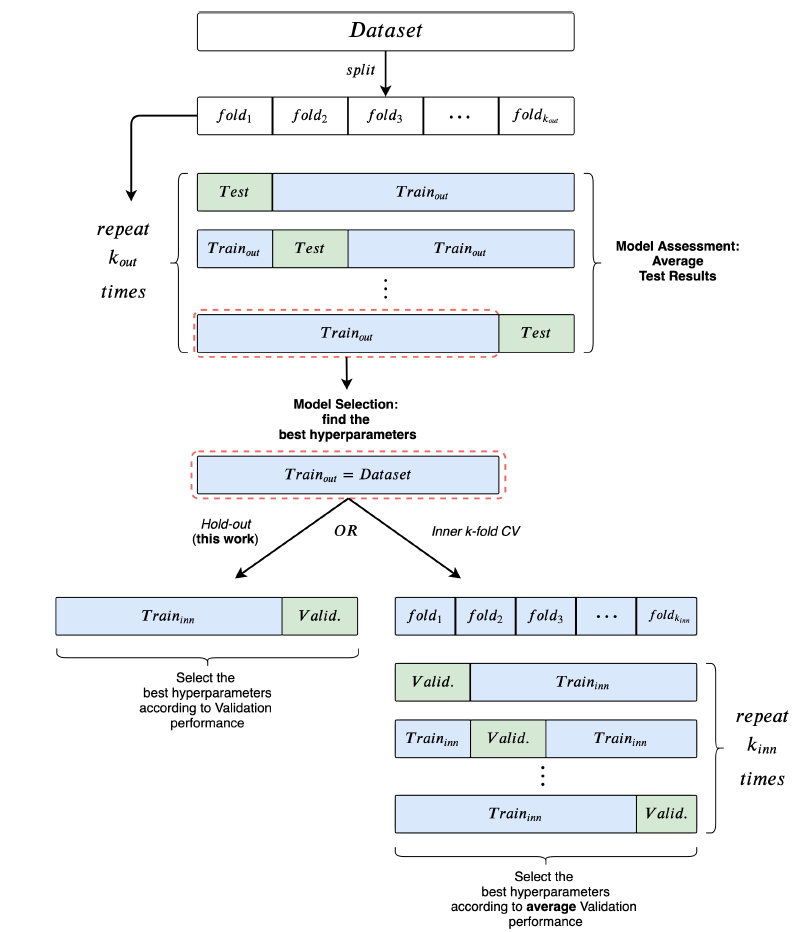
风险评估(也称作模型评估):风险评估的目的是对一类模型的性能进行估计。
如果未明确给出测试集,则常用的方式是采用
k-fold交叉验证Cross Validation:CV。k-fold CV使用train/test拆分来评估模型的泛化性能。对于每一个拆分,我们进行模型选择过程仅仅使用训练集来选择超参数。此时测试集不会参与模型选择。
由于模型选择是针对每个
train/test拆分单独执行的,因此我们就获得了不同的“最优” 超参数配置。这就是为什么我们指的是一类模型的性能。然后我们将所有拆分中的测试集性能取均值,则得到这一类模型的性能估计。
模型选择(也称作超参数调优):模型选择的目的是在一组候选超参数配置中选择特定验证集上最优的配置。
如果未明确提供验证集,则可以使用留出法
hold-out进行train/validation拆分,或者一个内层的k-fold交叉验证。模型选择的一个关键点是:验证集的性能是真实泛化能力的有偏估计。因此,模型选择的评估结果(即验证集性能)往往过于乐观。这个问题已经在论文
《On over-fitting in model selection and subsequent selection bias in performance evaluation》中进行了详细记录。这也是为什么我们的主要贡献是将模型选择、模型评估清晰地分开。这也是很多文献缺少的、或含糊不清的地方。
模型选择算法
Select:输入:
- 训练集
- 超参数选择集合
- 训练集
输出:最佳超参数
算法步骤:
将训练集
train和valid两个集合初始化验证集评估指标
对每组超参数
- 训练模型
- 评估验证集
- 训练模型
将验证集表现最好的模型挑选出来,并返回对应的超参数:
如果是
模型评估算法
Assessment:输入:
- 数据集
- 超参数选择集合
- 数据集
输出:模型的性能
算法步骤:
将
fold:循环执行
选择
根据模型选择算法选择最优的超参数:
通过最佳的超参数重复训练
然后将
最终将
fold的结果取均值:
4.2 可重复性
我们首先简要回顾了五种不同的最新
GNN模型,重点介绍了原始论文中的实验配置问题以及实验结果的可重复性。我们的观察仅基于原始论文的内容和可用的代码。我们挑选
GNN模型的原则:论文的实验使用10-fold CV评估性能、同行评审过、很强的架构差异、热门的模型。具体而言我们选择了GGCNN, DiffPool, ECC, GIN, GraphSAGE等五个模型。每个模型的详细说明请参考各自的论文。我们考察
evaluation质量和可重复性的标准是:- 是否提供了数据预处理、模型选择、模型评估的代码。
- 是否提供了数据集拆分。
- 是否进行了分层
stratification拆分,即拆分前后每个集合中的类别比例保持不变。 - 是否报告了
10-fold CV的均值和标准差,且是否在测试集上进行(即模型评估)、而不是在验证集上进行(相当于模型选择)。
我们总结了这五个模型的可重复性,如下表所示。其中:
(Y)表示满足条件;(N)表示不满足条件;(A)表示模棱两可ambiguity,即不清楚是否满足条件;(-)表示信息不足,即没有关于该条件的任何信息。注意,这里不包括
GraphSAGE,因为原始论文没有直接将其应用于图分类任务。DGCNN:作者使用10-fold CV来评估模型。所有数据集的模型结构都是固定的(比如网络层数、隐层维度),然后仅使用一个随机的CV fold来调优learning rate和epoch数量,然后将这两个超参数应用到其它fold。尽管这种做法仍然可以接受,但是可能会导致性能欠佳。而且,作者没有提供模型选择的复现代码。此外,作者对
10个fold进行评估,并报告了10个最终得分的均值,这使得标准差偏小。此外,其它对比模型并没有使用相同的过程。最后,
CV数据集拆分可以正确地分层拆分并可以公开获得,使得可以评估过程可以复现。DiffPool:尚不清楚是否在测试集而不是验证集上获得了报告的结果。尽管作者声称使用了10-fold CV,但是未报告DiffPool及其竞争对手的标准差。此外,作者确认对验证集应用了早停来防止过拟合。不幸的是,模型选择代码和验证集拆分都不可用。
此外,根据代码,数据被随机拆分(未分层拆分)并且没有设置随机种子,因此每次执行代码时,拆分都是不同的(因此无法复现)。
ECC:论文报告说ECC是10-fold评估的,但结果不包含标准差。和DGCNN相似,超参数是预先固定的,因此尚不清楚是否以及如何进行模型选择。重要的是,在代码中没有对数据预处理、数据分层拆分stratification、数据拆分、模型选择的任何参考。GIN:作者正确地列出了所有已调优的超参数。但是,正如论文和公开的评论里明确指出的,他们报告了10-fold CV的验证准确率。换句话讲,报告的结果涉及模型选择,而不是模型评估。模型选择的代码并未提供。GraphSAGE:原始论文没有在图分类数据集上测试该模型,但是GraphSAGE在其它论文中经常作为Baseline。因此,图分类的GraphSAGE结果应该附有代码以复现实验。尽管如此,报告GraphSAGE结果的两个工作(DiffPool, GIN) 都没有这样做。
结论:我们的分析表明,就评估质量和结果可复现而言,
GNN的工作很少遵循良好的机器学习规范。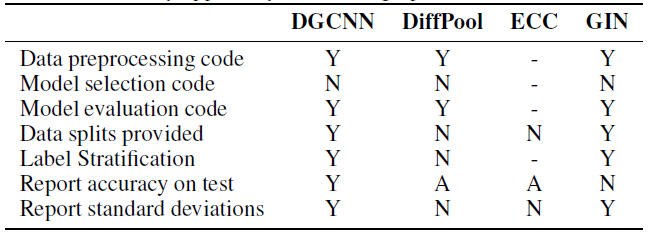
4.3 实验
我们采用严格实践来使用模型选择和模型评估框架,从而对
9个数据集(4个化学数据集,5个社交数据集)来重新评估上述5个模型。此外,我们还是实现了两个baseline,其目的是了解GNN是否能够利用结构信息。- 所有模型均已通过
Pytorch Geometrics库来实现,这个库提供了图的预处理程序,并使得图卷积的定义更容易实现。有时我们发现论文和相关代码之间存在差异,此时我们遵从论文中的规范。 - 由于
GraphSAGE在原始工作中并未应用于图分类,因此我们选择了最大池化全局聚合函数对图进行分类。此外,我们未使用GraphSAGE等人定义的采样邻域聚合方案,而是直接使用整个邻域。
- 所有模型均已通过
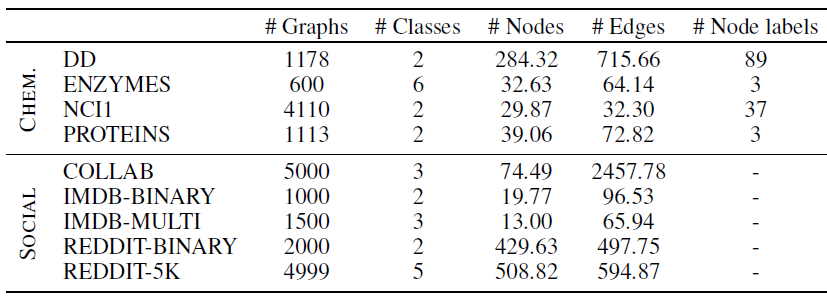
数据集:所有图数据集都是公开可用的,代表了文献中最常用于比较
GNN的那些数据集。D&D, PROTEINS, NCI1, ENZYMES为化合物数据集,IMDB-BINARY, IMDB-MULTI, REDDIT-BINARY, REDDIT-5K, COLLAB为社交网络数据集。数据集的统计信息如下所示。- 当节点特征(即
node label列)不可用时,我们要么为所有节点赋予特征1,要么为所有节点赋予节点的degree。另外,遵从文献的做法,对于ENZYMES数据集使用18个附加的节点属性。
特征:在
GNN文献中,常见的做法是将节点结构属性作为节点特征。如:DiffPool将degree和聚类系数coefficient作为节点的特征。GIN使用节点degree的one-hot向量作为节点的特征向量。GIN之所以如此选择是平衡了性能的提升(sum函数的单射性质) 和模型的泛化能力(无法将模型推广到任意degree的图)。
一般而言,良好的实验做法建议所有模型应该使用相同的输入形式来进行一致性
consistently的比较。这就是为什么我们使用相同的节点特征重新评估所有模型的原因。具体而言,对于化学领域,我们使用一种通用配置;对于社交领域,我们使用两种可选配置。对于化学领域,节点特征为原子类型的
one-hot编码。但是在ENZYMES上,我们遵循文献并使用了18种附加特征。在社交领域,节点没有特征。我们对所有节点使用无差别的特征(即所有节点特征均为
1)、或者使用节点degree作为特征。因此,我们能够了解模型所施加的结构归纳偏置structural inductive bias是否有效。即,模型是否能够隐式地学到图的结构特征。已经有论文(
《Leveraging label-independent features for classification in sparsely labeled networks: An empirical study》)研究了向图的通用机器学习模型种添加结构特征的效果,因此这里我们重点关注节点degree特征。
baseline方法:我们对化学数据集、社交数据集使用两种截然不同的baseline。对于除
ENZYMES以外的所有化学数据集,我们采用分子指纹技术Molecular Fingerprint technique。- 首先应用全局
sum池化,即通过将图中所有节点的特征加在一起来统计图中每个类型原子出现的次数。 - 然后应用带
ReLU激活函数的单层MLP。
- 首先应用全局
在社交数据集和
ENZYMES(由于存在附加特征):- 我们首先在节点特征上应用单层
MLP。 - 然后是全局
sum池化。 - 最后是一个用于分类的单层
MLP。
- 我们首先在节点特征上应用单层
注意:这两个
baseline都没有使用图的拓扑结构,即结构无感知的。因此这两个baseline作为一个参考标准,可以评估特定数据集上GNN的有效性。实际上,如果
GNN的性能接近结构无感知的baseline,则可以得出两个结论:- 该任务不需要拓扑结构信息就可以有效地解决。这个结论可以通过
domain-specific的专家的专业知识进行验证。 GNN没有充分利用图结构信息。这个结论很难验证,因为多种因素会起作用,如:训练数据集的规模、体系结构所施加的结构归纳偏置、用于模型选择的超参数等。
但是,
GNN性能相对于这些结构无感知baseline的显著提升,是图拓扑结构有效利用的证据。因此,结构无感知baseline对于了解是否、以及如何改进模型至关重要。实验配置:我们使用
10-fold CV进行模型评估,并使用内层holdout技术(90%:10%的training/validation拆分)来进行模型选择。每次选择模型之后,我们在整个训练
fold上训练三次模型,并随机保留数据的10%来进行早停。我们需要采用这三个独立的训练来平滑不利的随机权重初始化的影响。最终的测试
fold得分是这三个训练模型的测试得分均值。我们采用
patience参数为n个epoch而验证集的性能没有任何改善,则训练将停止。高的
n值对于验证集得分的波动不敏感从而更有利于模型选择,但是也会有更多的计算量作为代价。数据集拆分是预先计算好的,所以模型选择、模型评估都是在相同的数据集拆分上进行的。
所有数据都是分层拆分的,这使得每个集合中各类别的比例和原始数据集是保持不变的。
超参数:我们通过网格搜索来执行超参数调优。我们总是包含其它论文中用到的超参数。其中包括:
- 对所有模型都通用的超参数:卷积层数、
embedding空间维度、学习率、早停标准(基于验证集准确率或者验证集损失)。 model-specific的超参数:正则化项、dropout、以及模型特有的其它超参数。
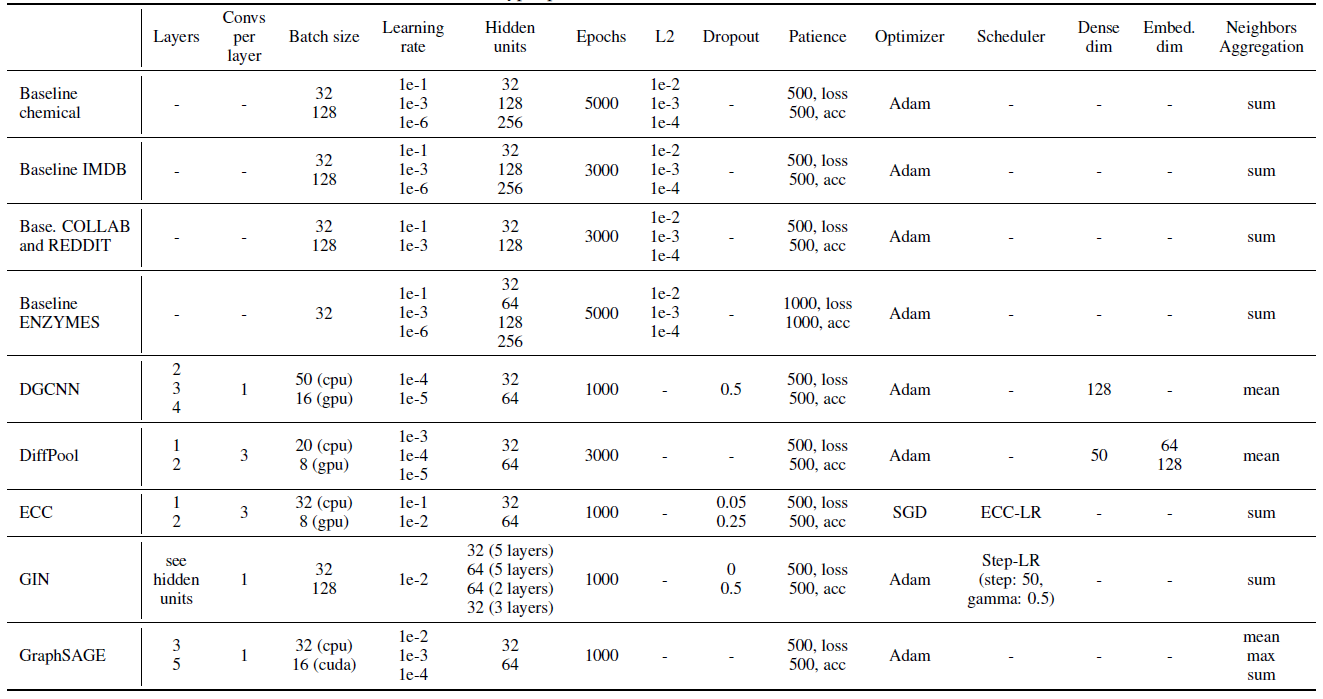
所有超参数搜索空间如下表所示。
- 对所有模型都通用的超参数:卷积层数、
我们的实验涉及大量训练。对所有模型,超参数搜索规模从
32到72种可能的配置(具体取决于超参数数量)。完成一次模型评估过程需要超过47000次(以单次训练次数为单位)。如此大量的工作需要同时利用CPU和GPU的并行性,从而在合理的时间内完成实验。我们重点强调某些情况下(如社交网络数据集中的
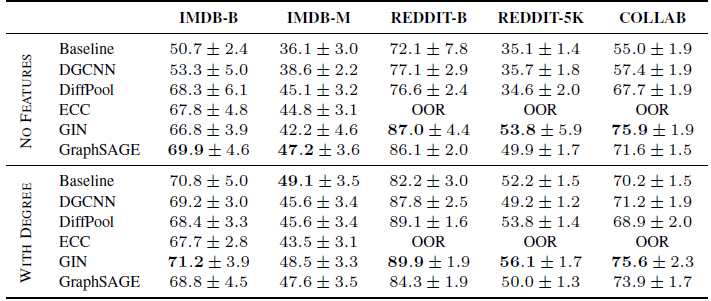
ECC),当单个超参数配置的训练需要超过72个小时,这使得对单个网格的搜索需要持续一个月。因此,由于需要大量的实验和大量的计算资源,我们将完成一次训练的时间限制为72个小时。下表给出了我们的实验结果,包括平均准确率和标准差。上表为化学数据集的结果、下表为社交网络数据集的结果,最佳结果以粗体突出显示。
OOR表示超出资源限制(Out of Resources) ,要么是时间超出(单次训练时间超过72小时)、要么是GPU内存超出。总体而言:
GIN似乎在社交网络数据集上非常有效。D&D, PROTEINS, ENZYMES数据集上,没有一个GNN能够超越baseline方法。相反,在
NCI1上,GNN明显超越了baseline。这表明:GNN确实利用到了NCI1的图的拓扑结构信息。在
NCI1上,即使是非常多参数的baseline也无法完全拟合训练集。我们考虑具有10000个隐单元、没有正则化的baseline,它仅达到67%的训练准确率。相反,
GNN很容易地对训练集过拟合(训练准确率接近100%)。这表明结构信息极大地影响了拟合训练集的能力。在社交网络数据集上,将节点
degree作为特征是有利的。
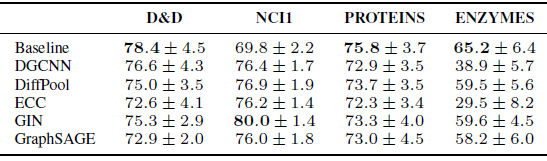
baseline的重要性:我们的研究结果还表明:结构无感知的baseline是了解GNN有效性、并提取有用的洞察insight的重要工具。例如,在
D&D, PROTEINS, ENZYMES数据集上,没有一个GNN能够超越baseline。我们认为:这些SOTA的GNN模型还不能完全利用这些数据集上的结构。实际上在化学领域,众所周知:结构特征和分子特性是存在相关性的。而这些
GNN模型并没有成功地利用到拓扑结构信息。因此,我们推荐
GNN的从业者在未来工作中包括baseline比较,从而更好地刻画他们的贡献程度。结论:结构无感知的
baselien很重要,它可以评估GNN模型是否捕获了图结构信息。节点
degree效果:我们的研究结果还表明:使用节点degree作为输入特征几乎总是有益于社交网络数据集上的模型性能,某些时候甚至提高得非常多。degree信息平均使得baseline模型的效果提升大约15%,因此在很多数据集上都有竞争力。具体而言,baseline在IMDB-BINARY上达到了最佳性能。相反,添加
degree特征对于大多数GNN而言并不重要,因为它们可以从结构中自动推断出这类信息。DGCNN是一个值得注意的例外,它明确地需要节点degree信息从而在所有数据集上表现良好。
此外,我们观察到:在添加节点
degree作为特征之后,模型的排名发生翻天覆地的变化。这就带来一个问题:对节点采用结构特征(如节点degree、聚类系数clustering coefficient)之后,对模型性能的影响。这留待以后的工作。最后,我们还想知道:采用节点
degree特征之后,是否会影响解决任务所需的模型层数。因此,我们通过计算10个不同fold中超参数调优得到的最优层数的中位数来研究这个问题。我们观察到一个总体趋势(其中GraphSAGE是唯一的例外):degree的使用使得所需的网络层数减小了大约1层,如下表所示(1表示所有节点的特征都是相同的,即无信息的特征)。这可能是由于大多数架构在第一层就发现计算degree很有用的事实。结论:节点特征很重要,像
degree之类的节点统计特征的引入可以改变GNN模型、baseline模型的效果和排名。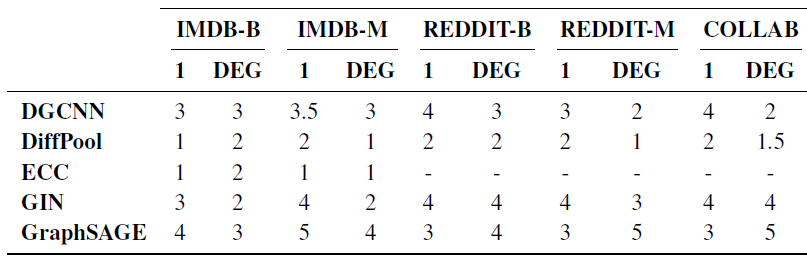
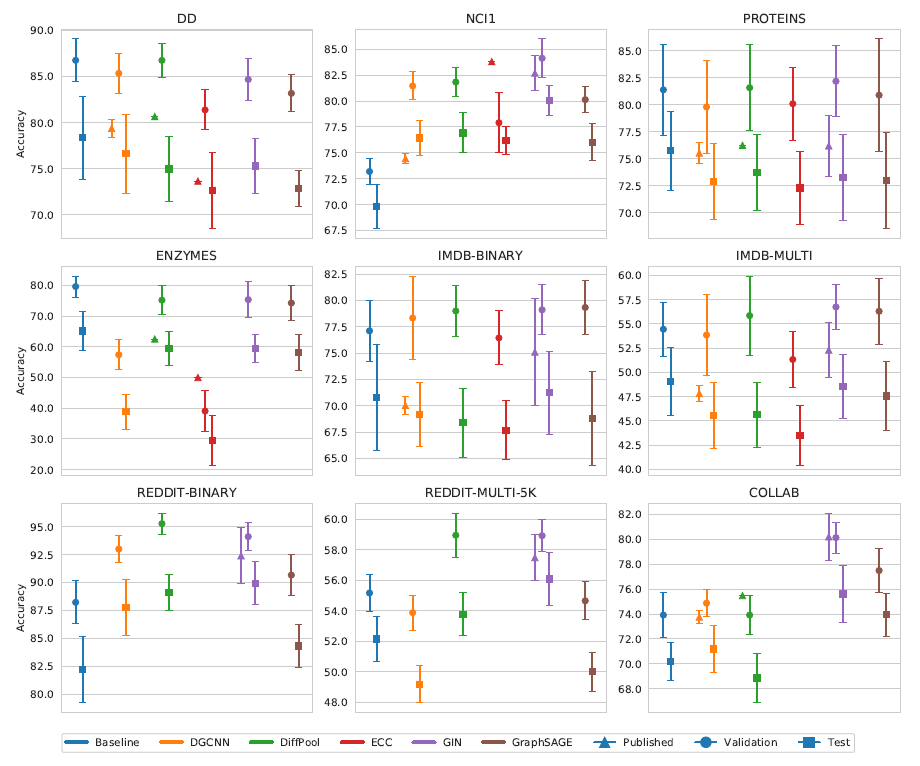
最后我们将测试结果的均值和文献报告的结果相比较。此外,我们还汇总了
10个不同模型选择中(因为是10-fold CV),验证集的均值,即平均验证准确率。- 我们的测试准确率在大多数情况下和文献中报告的有所不同,并且这两个结果之间的差距通常都是一致的(文献报告的普遍高估)。
- 平均验证准确率始终高于或等于测试准确率。这是预料之中的。
最后,我们再次强调我们的结果是:在严格的模型选择和评估协议的框架内获得的;公平地为所有模型使用相同的数据集拆分、数据特征;可复现。
结论:必须评估测试集,验证集的指标往往会高估模型的能力。
但是从下图中发现:验证集的排名与测试集的排名相一致。这个现象没有理论上保证,仅仅是从实验数据中观察到。
五、GNN 评估陷阱[2018]
图的半监督节点分类是图挖掘中的一个经典问题,最近提出的图神经网络
graph neural network:GNN在这个任务上取得了瞩目的成就。尽管取得了巨大的成功,但是由于实验评估程序的某些问题,我们无法准确判断模型所取得的进展:首先,很多提出的模型仅仅是在
《Revisiting semi-supervised learning with graph embeddings》给出的三个数据集(CORA,CiteSeer,PubMed) 上、且使用该论文相同的train/validation/test数据集拆分上评估的。这种实验配置倾向于寻找最过拟合
overfit the most的模型,并且违反了train/validation/test拆分的目的:寻找泛化能力最佳best generalization的模型。其次,在评估新模型的性能时,新模型和
baseline通常采用不同的训练程序。例如,有的采用了早停策略,有的没有采用早停策略。这使得很难确定新模型性能的提升是来自于新模型的优秀架构,还是来自于训练过程或者超参数配置。这使得对新模型产生不公平的好处unfairly benefit。
有鉴于此,论文
《Pitfalls of Graph Neural Network Evaluation》表明现有的GNN模型评估策略存在严重缺陷。为解决这些问题,论文在
transductive半监督节点分类任务上对四种著名的GNN架构进行了全面的实验评估。论文在同一个框架内实现了四个模型:GCN, MoNet, GraphSage, GAT。在评估过程中,论文专注于两个方面:
对所有模型都使用标准化的训练和超参数选择过程。在这种情况下,性能的差异可以高度确定地
high certainty归因于模型架构的差异,而不是其它因素。对四个著名的引文网络数据集进行实验,并为节点分类问题引入四个新的数据集。
对于每个数据集使用
100次随机train/validation/test拆分,对于每次拆分分别执行20次模型的随机初始化。这种配置使得我们能够更准确地评估不同模型的泛化性能,而不仅仅是评估模型在一个固定测试集的上的性能。
论文声明:作者不认为在
benchmark数据集上的准确性是机器学习算法的唯一重要特性。发展和推广现有方法的理论,建立与其他领域的联系(和适应来自其他领域的思想)是推动该领域发展的重要研究方向。然而,彻底的实证评估对于理解不同模型的优势和局限性至关重要。实验结果表明:
- 考虑数据集的不同拆分会导致模型排名的显著不同。
- 如果对所有模型都合理地调整超参数和训练过程,那么简单的
GNN架构就可以超越复杂的GNN架构。
5.1 模型和数据集
考虑图上的
transductive半监督节点分类问题。本文中我们比较了以下四种流行的图神经网络架构:Graph Convolutional Network: GCN:是早期的模型,它对谱域卷积执行线性近似。Mixture Model Network: MoNet:推广了GCN架构从而允许学习自适应的卷积滤波器。Graph Attention Network: GAT:采用一种注意力机制从而允许在聚合步骤中以不同的权重加权邻域中的节点。GraphSAGE:侧重于inductive节点分类,但是也可用于transductive配置中。我们考虑原始论文中的三个变体:GS-mean, GS-meanpool, GS-maxpool。
所有上述模型的原始论文和参考实现均使用不同的训练程序,包括:不同的早停策略、不同的学习率衰减
decay、不同的full-batch /mini-batch训练。如下图所示:
不同的实验配置使得很难凭实验确定模型性能提升的背后原因。因此在我们的实验中,我们对所有模型都使用标准化的训练和超参数调优程序,从而进行更公平的比较。
此外,我们考虑了四个
baseline模型,包括:逻辑回归Logistic Regression: LogReg、多层感知机Multilayer Perceptron: MLP、标签传播Label Propagation: LabelProp、归一化的拉普拉斯标签传播Normalized Laplacian Label Propagation: LabelProp NL。其中:LogReg,MLP是基于属性的模型,它们不考虑图结构;LabelProp, LabelProp NL仅考虑图结构而忽略节点属性。数据集:
我们考虑四个著名的引文网络数据集:
PubMed, CiteSeer, CORA, CORA-Full。其中CORA-Full是CORA的扩展版本。我们还为节点分类任务引入了四个新的数据集:
Coauthor CS、Coauthor Physics、Amazon Computers、Amazon Photo。Amazon Computers和Amazon Photo是Amazon co-purchase图的一部分。其中:节点代表商品、边代表两个商品经常被一起购买,节点特征为商品评论的bag-of-word,类别标签label为产品类目category。Coauthor CS和Coauthor Physics是基于Microsoft Academic Graph的co-authorship图。其中:节点代表作者、边代表两名作者共同撰写过论文,节点特征为每位作者论文的论文关键词,类别标签为作者最活跃的研究领域。
我们对数据集进行了标准化,其中对
CORA_full添加了self-loop,并删除CORA_full样本太少的类别。 我们删除了CORA_full中样本数量少于50个节点的3个类别,因为我们对这些类别无法执行很好的数据集拆分(在后续数据集拆分中,每个类别至少要有20个标记节点作为训练集、30个标记节点作为验证集)。对于所有数据集,我们将图视为无向图,并且仅考虑最大连通分量。
数据集的统计量如下表所示。其中:
Label rate为数据集的标记率,它表示训练集的标记节点的占比。因为我们对每个类别选择20个标记节点作为训练集,因此:Edge density为图的链接占所有可能链接的比例,它等于: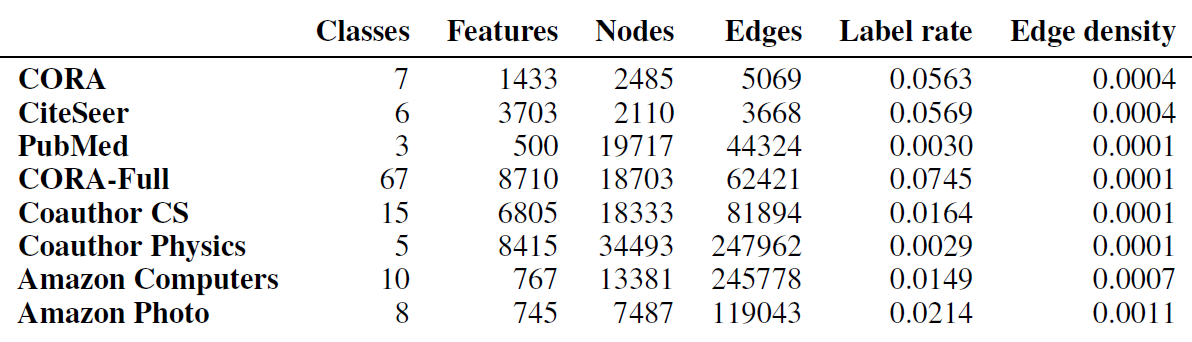
5.2 实验配置
模型架构:我们保持原始论文/参考实现中相同的模型架构,其中包括:层
layer的类型和顺序、激活函数的选择、dropout的位置、我们还将
GAT的attention head数量固定为8、MoNet高斯核的数量固定为2。所有模型都有
2层:input features --> hidden layer --> output layer。训练过程:为了更公平的比较,我们对所有模型都使用相同的训练过程。对于所有的模型:
- 相同的优化器,即:带默认参数的
Adam优化器。 - 相同的初始化,即:根据
Glorot初始化权重,而bias初始化为零。 - 都没有学习率衰减。
- 相同的最大训练
epoch数量。 - 相同的早停准则、相同的
patience、相同的验证频率validation frequency。 - 都使用
full-batch训练,即:每个epoch都使用训练集中的所有节点。 - 同时优化所有的模型参数,包括:
GAT的attention weights、MoNet的kernel parameters、所有模型的权重矩阵。 - 所有情况下,我们选择每个类别
20个带标签的节点作为训练集、每个类别30个带标签的节点作为验证集、剩余节点作为测试集。
我们最多训练
100k个epoch,但是由于我们使用了严格的早停策略,因此实际训练时间大大缩短了。具体而言,如果总的验证损失(数据损失 +正则化损失)在50个epoch都没有改善,则提前停止训练。一旦训练停止,则我们将权重的状态重置为验证损失最小的step。- 相同的优化器,即:带默认参数的
超参数选择:我们对每个模型使用完全相同的策略进行超参数选择。具体而言,我们对学习率、
hidden layer维度、dropout rate执行网格搜索。搜索空间:- 隐层维度:
[8, 16, 32, 64]。 - 学习率:
[0.001, 0.003, 0.005, 0.008, 0.01]。 dropout rate:[0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8]。attention系数的dropout rate(仅用于GAT):[0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8]。[1e-4, 5e-4, 1e-3, 5e-3, 1e-2, 5e-2, 1e-1]。
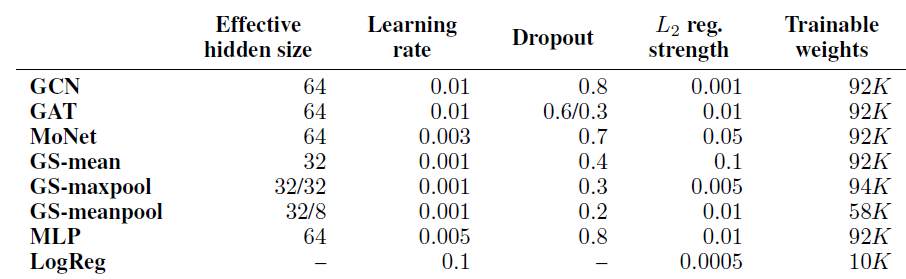
对于每个模型,我们选择使得
Cora数据集和CiteSeer数据集上平均准确率最高的超参数配置。这是对每个数据集执行100次随机train/validation/test拆分、对于每次拆分分别执行20次模型的随机初始化从而取得的。所选择的最佳超参数配置如下表所示,这些配置用于后续实验。这里应该针对不同数据集进行超参数调优,而不是所有数据集都采用相同的超参数(即,在
Cora数据集和CiteSeer数据集上平均准确率最高的超参数配置)。注意:
GAT有两个dropout rate:节点特征上的dropout、注意力系数上的dropout。- 所有
GraphSAGE模型都有额外的权重用于skip connection,这使得实际的hidden size翻倍。因此这里GS-mean的Effective hiden size = 32。 GS-meanpool/GS-maxpool具有两个hidden size:隐层的size、中间特征转换的size。GAT使用8个head的multi-head架构,而MoNet使用2个head。
- 隐层维度:
5.3 实验结果
所有
8个数据集的所有模型的平均准确率(以及标准差)如下表所示。结果是在100次随机train/validation/test拆分、对于每次拆分我们分别执行20次模型的随机初始化上取得的。对每个数据集,准确率最高的得分用粗体标记。
N/A表示由于GPU RAM的限制而无法由full-batch版本的GS-maxpool处理的数据集。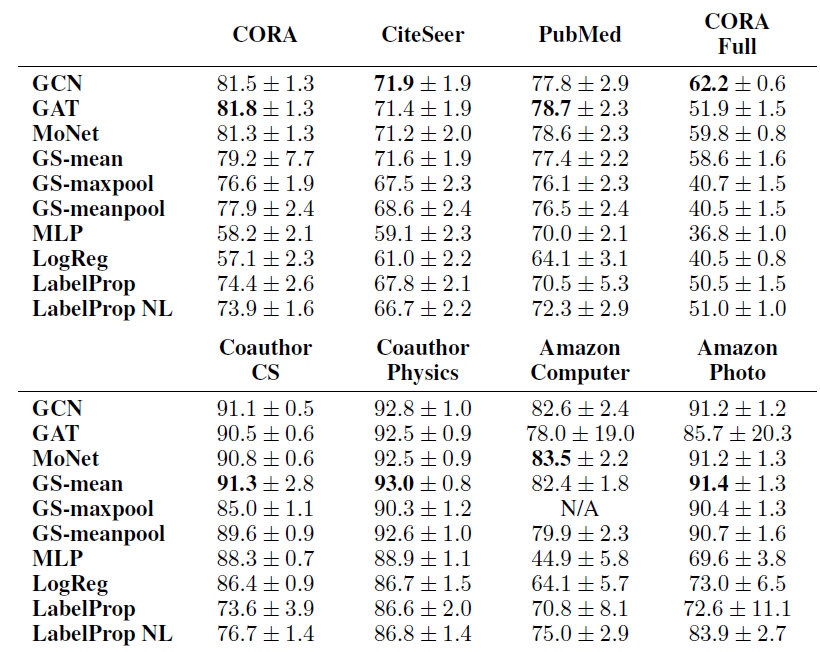
结论:
首先,在所有数据集中,基于
GNN的方法(GCN, MoNet, GAT, GraphSAGE) 显著优于baseline方法(MLP, LogReg, LabelProp, LabelProp NL) 。这符合我们的直觉,并证明了与仅考虑属性或仅考虑结构的方法相比,同时考虑了结构和属性信息的、基于
GNN的方法的优越性。其次,
GNN方法中没有明显的winner能够在所有数据集中占据主导地位。实际上,在
8个数据集中的5个数据集,排名第二、第三的方法得分和排名最高的方法得分,平均相差不到1%。如果我们有兴趣对模型之间进行比较,则可以进行
pairwise t-test。这里我们考虑模型之间的相对准确率作为pairwise t-test的替代。具体而言:- 首先对每个数据集进行随机拆分。
- 然后在这个拆分中,训练并得到每个模型的准确率(已经对
20次随机初始化取平均)。 - 对于这个拆分中,准确率最高模型的准确率为最优准确率。我们将每个模型的准确率除以最优准确率,则得到相对准确率。
- 然后我们对模型根据相对准确率排名,
1表示最佳、10表示最差。
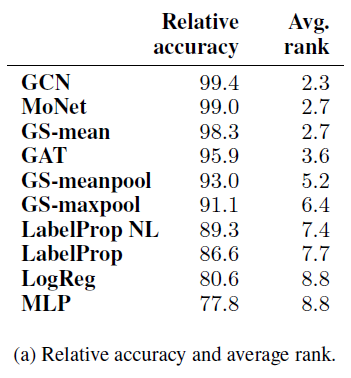
对于每个模型,考虑所有拆分的排名、以及平均相对准确率,如下表所示。我们观察到:
GCN在所有模型中实现最佳性能。尽管这个结论令人惊讶,但是在其它领域都有类似报道。如果对所有方法均谨慎地执行超参数调优,则简单的模型通常会超越复杂的模型。
最后,令人惊讶的是
GAT针对Amazon Computers和Amazon Photo数据集获得的结果得分相对较低,且方差很大。为研究这个现象,我们可视化了
Amazon Photo数据集上不同模型的准确率得分。尽管所有GNN模型的中位数median得分都很接近,但是由于某些权重初始化,GAT模型的得分非常低(低于40%)。尽管这些异常值较少出现(2000次结果中有138次发生),但是这显著降低了GAT的平均得分。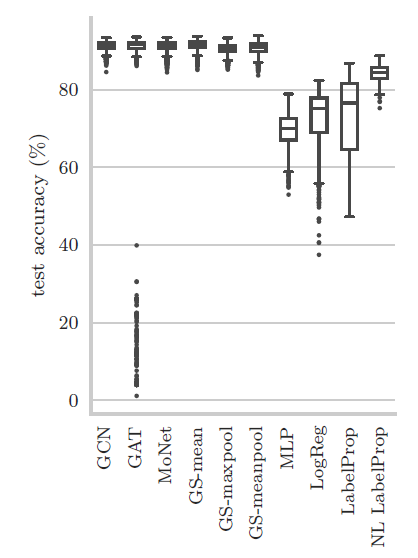
我们评估
train/validation/test拆分的效果。为此,我们执行以下简单实验:将数据集按照《Revisiting semi-supervised learning with graph embeddings》中的随机拆分(仅拆分一次),然后运行四个模型并评估模型的相对准确率。可以看到:如果执行另外一次随机拆分(拆分比例都相同),则模型的相对准确率排名完全不同。
这证明了单次拆分中的评估结果的脆弱和误导性。考虑到小扰动的情况下,
GNN的预测可能发生很大变化,这进一步明确了基于多次拆分的评估策略的必要性。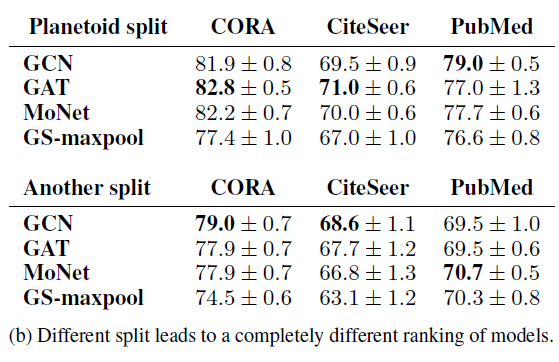
六、AGL [2020]
为了利用图机器学习技术来解决工业级的图分析任务,我们需要构建一个可扩展的
scalable、容错性的fault-tolerance、同时包含训练和推理的学习系统。但是由于图的数据依赖性,图机器学习任务的计算图和传统机器学习任务完全不同。在传统机器学习任务中,我们假设样本之间的计算图相互独立。这也是现有的、经典的参数服务器
parameter server框架假设的数据并行性。但是在图机器学习任务中,每个节点的计算图依赖于该节点
k-hop邻居。这种数据依赖性使得我们不再能够将训练或推理样本存储在磁盘中、然后通过
piepeline来访问。相反,我们必须将图数据存储在内存中以便快速访问数据。这使得我们无法基于现有的参数服务器框架简单地构建用于图学习任务的学习和推理系统。
多家公司致力于为各种图机器学习技术设计新颖的系统架构:
Facebook展示了一种大规模graph embedding系统PyTorch-BigGraph: PBG,该系统旨在从multi-relation数据中生成无监督的节点embedding。但是PBG不适合处理丰富属性的图(节点属性或边属性)。已有
Deep Graph Library: DGL、PyTorch Geometric: PyG、AliGraph用于大规模、带属性的图上训练GNN。DGL、PyG被设计为单机系统,它通过在巨型机(如具有2TB内存的AWS x 1.32 x large)来处理工业级的图数据。AliGraph是一个分布式系统,它实现了分布式的、内存的图存储引擎graph store engine,该引擎需要在训练GNN模型之前独立部署。
但是,实际的工业级图数据可能非常庞大。
Facebook中的社交网络包括超过20亿节点和超过1万亿条边,蚂蚁金服Ant Financial的异质金融网络、阿里巴巴Alibaba电商网络包含数十亿节点和数千亿条以及丰富的属性信息。下表总结了几个最新的SOTA图机器学习系统报告的图数据的规模。考虑到节点、边关联的特征,这种规模的图数据可能会产生高达100TB的数据。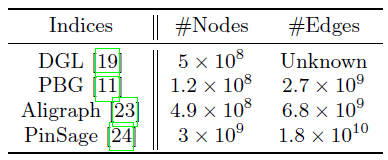
这些数据不可能存储在像
DGL这样的单机中。此外,保存图数据的图存储引擎和worker之间的通信将非常庞大。例如,假设包含节点的子图包含1000个节点、10000条边,我们有一个batch的子图,这可能会导致1MB的bulk在图存储引擎和worker之间通信,这是我们无法容忍的。另外,这需要结构良好的、足够大带宽的网络。总之:
- 首先,现有的工业级的学习系统要求图数据要么在单台机器的内存中(这使得工业级数据无法存储)、要么要求图数据在自定义的图存储引擎中(这导致图存储引擎和
worker之间的庞大通信开销)。这使得学习系统无法扩展到更大规模的图数据。 - 其次,它们需要额外的开发来支持
graph store,无法很好地利用已有的基础设施(例如MapReduce或者参数服务器)来实现容错的目的。 - 最后,大多数学习系统都侧重于图模型的训练,但是忽略了系统的完整性。例如,忽略了部署图模型时优化
inference任务。
考虑所有这些问题,论文
《AGL: A Scalable System for Industrial-purpose Graph Machine Learning》提出了Ant Graph machine Learning system: AGL,这是用于工业级图学习的集成系统。AGL系统设计的关键洞察是基于图神经网络计算图背后的消息传递方案。在
GNN的训练阶段,我们提出构造k-hop邻域。该邻域提供节点的完备信息的子图,从而用于计算基于消息传递机制的、每个节点的k-hop embedding。将原始图分解为小的子图片段
pieces(即k-hop邻域)的好处是每个节点的计算图独立于其它节点。这意味着我们仍然可以享受经典的参数服务器框架所具有的容错性、灵活的模型一致性等优势,而无需付出额外的精力来维护图存储引擎。在
GNN的推断阶段,我们提出将训练好的K层GNN模型划分为K个分片slice、以及一个和模型预测相关的分片。通过分片,在第
in-edge邻居的embedding,然后将自己的embedding传播到各自的出边out-edge邻居。1开始到K。我们将训练和推断阶段的消息传递机制抽象化,然后简单地使用
MapReduce来实现它们。由于
MapReduce和参数服务器已经成为工业界常用的基础设置,因此即使在价格低廉且广泛使用的商用机器上,我们的图机器学习系统仍然可以受益于诸如容错性、可扩展性之类的属性。此外,和基于
DGL,AliGraph等架构的推断相比,我们的推断的实现最大程度地利用了每个的embedding,从而显著加速了推断工作。此外,我们提出了几种技术从而加速训练过程中的、从
model-level到operator-level的浮点数计算。
结果,和
DGL/PyG相比,我们在单台机器上成功地加速了GNN的训练,并在实际应用场景中使用商用机器的CPU集群实现了近线性near-linear的加速。实验结果表明:在具有AGL使用100个worker可以在14个小时内训练完一个2-layer GAT模型,其中包括target nodes,训练7个epoch模型就达到收敛。另外,模型只需要
1.2小时即可完成对整个图的推断。据我们所知,这是
graph embedding的最大规模的应用,并证明了我们的系统在实际工业场景的高可扩展性和效率。
6.1 消息传递机制
这里我们重点介绍
GNN中的消息传递机制。然后我们介绍了K-hop邻域的概念,从而帮助实现图学习任务中的数据独立性。消息传递机制、K-hop邻域在我们的系统设计中都起着重要的作用。定义有向图
这里我们认为无向图是特殊的有向图。对于无向图的每条边
定义
in-edge邻居集合,out-edge邻居集合:节点
节点
AGL主要关注基于消息传递机制的GNN。在GNN的每一层都通过聚合目标节点的in-edge邻居的信息从而生成intermediate embedding。在堆叠几层GNN layer之后,我们得到了final embedding,它集成integrate了目标节点的整个感受野。具体而言,第
GNN layer的计算范式paradigm为:其中:
intermediate embedding,并且- 函数
embedding、节点
可以在消息传递机制中表达
GNN的上述计算。即:收集
keys(如node id)以及对应的values(如embedding)。对于每个节点:
- 首先
merge入边邻居的所有values,从而使得目标节点具有新的value。 - 然后通过出边来将新的
value传播propagate到其它节点。
- 首先
经过
GNN的计算。后续讨论中我们将这种机制推广到GNN的训练和推断过程中。定义节点
k-hop邻域为
定理:节点
k-hop邻域为sufficient和necessary的信息来使得一个k层GNN模型生成节点embedding。该定理可以通过数学归纳法来证明。这个定理显示了
GNN的计算和k-hop邻域之间的关系。可以看到:在一个k层GNN模型中,节点embedding仅取决于其k-hop邻域,而不是整个图。
6.2 系统
- 这里我们首先概述我们的
AGL系统,然后我们详细说明了三个核心模块(即GraphFlat、GraphTrainer、GraphInfer),最后我们给出了一个demo来说明如何使用AGL系统实现简单的GCN模型。
6.2.1 系统总览
我们构建
AGL的主要动机是:工业界渴望一个支持图数据训练和推断的集成系统,并且具有可扩展性
scalability,同时具有基于成熟的工业基础设施(如MapReduce、参数服务器等)的容错性。即,工业界不需要具有巨大内存和高带宽网络的单个巨型机或自定义的图存储引擎,因为这对于互联网公司升级其基础设施而言代价太大。
我们试图提供一种基于成熟和经典基础设施的解决方案,该方案易于部署,且同时享受容错性等各种优点。
其次,我们需要基于成熟的基础设施扩展到工业级规模图数据的解决方案。
最后,除了优化训练之外,我们的目标是在图上加速推断任务。因为在实践过程中,与未标记数据(通常需要推断数十亿节点)相比,标记数据通常非常有限(例如只有千万级别)。
设计
AGL的原则是基于GNN背后的消息传递机制。即,对于每个节点我们首先合并其入边in-edge邻居的信息,然后向该节点的出边out-edge邻居传播消息。我们将这种规则反复应用于训练和推断过程,并设计了
GraphFlat、GraphTrainer和GraphInfer。GraphFlat在训练过程中生成独立的K-hop邻域。GraphTrainer训练节点的embedding。GraphInfer通过训练好的GNN模型来推断节点的embedding。
根据动机和设计原则,
AGL利用MapReduce和Parameter Server等几种强大的并行体系架构,通过精心设计的分布式实现来构建每个组件。结果,即使将AGL部署在具有相对较低的算力和有限内存的计算机的集群上,AGL和几种先进的系统相比,仍然具有相当的效果effectiveness和更高的效率efficiency。而且,AGL具有对数十亿节点、数千亿边的工业级规模的图执行完整的图机器学习的能力。下图描述了
AGL的系统架构,它由三个模块组成:GraphFlat:是基于消息传递的、高效的efficient、分布式的distributed生成器,用于生成包含每个目标节点完整信息子图的K-hop邻域。这些小的K-hop邻域被展平flatten为protobuf字符串,并存储在分布式文件系统上。由于
K-hop邻域包含每个目标节点的足够的和必要的信息,因此我们可以将其中的一个或者batch加载到内存中,而不是加载整个图,并且可以像其他任何传统学习方法一样进行训练。此外,我们提出了一种重索引
re-indexing技术以及一个采样sampling框架,从而处理真实应用场景中的hub节点(具有非常多的邻居)。我们的设计基于以下观察:标记节点的数量是有限的,我们可以将标记节点关联的那些
K-hop邻域存储在磁盘中,而不会花费太多代价。GraphTrainer:基于GraphFlat保证的数据独立性,GraphTrainer利用许多技术(如pipeline、剪枝pruning、边分区edge-partition)来降低I/O开销,并在训练GNN模型期间优化浮点数计算。结果,即使在基于商用机器的通用
CPU集群上,GraphTrainer在实际工业场景中也能获得很高的近线性near-linear加速。GraphInfer:这是一个分布式推断模块,可以将K层GNN模型分成K个分片slice,并基于MapReduce应用K次消息传递。GraphInfer最大限度地利用了每个节点的embedding,因为第k层的所有intermediate embedding都将传播到下一轮的消息传递。这显著提高了推断速度。
可以看到,
AGL仅适用于基于消息传递的半监督GNN模型。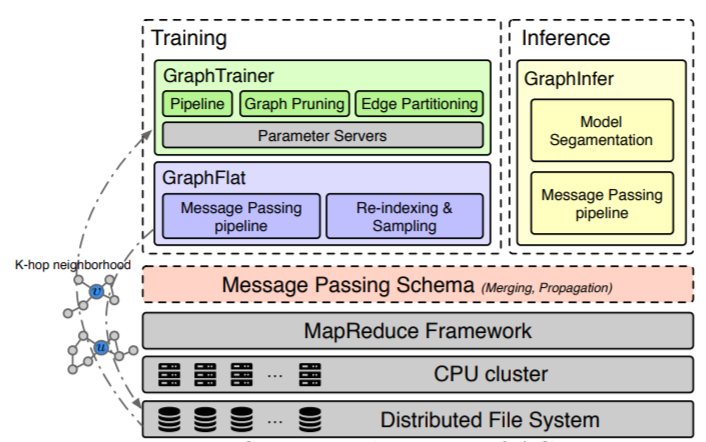
6.2.2 GraphFlat
训练
GNN的主要问题是图数据之间固有的数据依赖性。要对每个节点进行前向传播,则我们必须读取节点关联的邻居、以及邻居的邻居,依此类推。这使得我们无法在现有的参数服务器上部署这类模型,因为参数服务器假设数据并行。此外,对于大多数工业公司而言,开发额外的图存储引擎来查询每个节点的子图代价太大。
并且这种做法也无法利用现有成熟、且容错性好的常规基础设施。
但是,目标节点的
k-hop邻域提供了足够的、必要的信息来生成第k层节点embedding。因此,我们可以根据目标节点,将工业级规模的图划分为大量的、微小的k-hop邻域,然后在训练阶段将其中的一个或一批(而不是整个图)加载到内存中。沿着这个思路,我们开发了
GraphFlat,一个高效的k-hop邻域的分布式生成器。此外,我们还进一步引入了重索引re-indexing策略,并设计了一个采样框架来处理hub节点并确保GraphFlat的负载均衡。分布式的
k-hop邻域生成器:我们基于消息传递的机制设计一个分布式pipeline来生成k-hop邻域,并使用MapReduce基础设施来实现它。下图说明了这个pipeline的工作流。背后的关键洞察是:对于每个节点
k-hop邻域。假设我们将
node table和edge table作为输入。假设node table由节点ID、节点特征组成,edge table由源节点ID、目标节点ID、边特征组成。生成K-hop邻域的piepline的总体流程如下:Map阶段:Map阶段仅在pipeline的开始执行一次。对于某个节点,Map阶段生成三种信息:自身信息(即节点特征)、入边信息(入边的特征和入边的邻居节点)、出边信息(出边的特征和出边的邻居节点)。注意:我们将节点
ID设为shuffle key,并将各种信息作为value,从而用于下游的Reduce阶段。Reduce阶段:Reduce阶段运行K次从而生成K-hop邻域。在第
reducer首先收集相同shuffle key(即相同的节点id)的所有的values(即三种类型的信息),然后将自己的信息self information和入边信息作为新的self information。注意:新的self information是节点的k-hop邻域。然后,新的
self information传播到出边的节点。注意:在下一个
reduce阶段之前,所有出边的信息保存不变。最后,
reducer向磁盘输出新的数据记录,其中每个节点id作为shuffle key,而更新后的信息作为新的value。
Storing阶段:在经过K轮Reduce阶段之后,最终的self information就是节点的K-hop邻域。我们将所有目标节点的
self information转换为protobuf字符串,并存储到分布式文件系统中。
在整个
MapReduce pipeline中,关键操作是合并merging和传播propagation。 在每轮迭代中,给定节点self information和上一轮的入边信息合并,然后合并后的结果作为节点self information。然后,我们将新的self information通过出边传播到出边节点。在pipeline的最后,每个目标节点的k-hop邻域将展平flatten为protobuf字符串。这就是为什么我们将这个pipeline称作GraphFlat。注意,由于节点的
k-hop邻域将这个节点和其它节点区分开,因此我们也将其称作GraphFeature。在整个迭代过程中,
update和propagate的都是节点的self information,边的信息保持不变(边的方向、特征、权重)。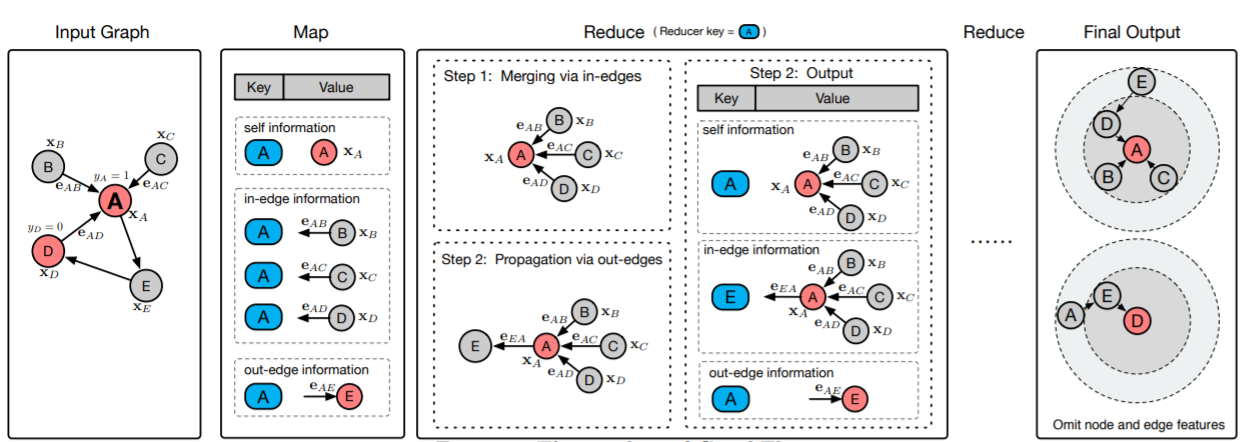
采样和重索引:前面介绍的分布式
pipeline在大多数情况下都能很好地工作。但是由于存在hub节点,因此图的degree可能会发生倾斜,尤其是在工业场景中。这使得某些节点的k-hop邻域可能覆盖几乎整个图。- 一方面,在
GrapFlat的Reduce阶段,处理此类hub节点的reducer可能会比其它reducer慢得多,因此会不利于GraphFlat的负载均衡。 - 另一方面,这些
hub节点的巨大的k-hop邻域可能使得GraphFlat和下游模型训练产生Out Of Memory:OOM问题。 - 此外,倾斜的数据也可能导致训练到的
GNN模型的准确率较差。
因此,我们采用了重索引
re-indexing策略,并为GraphFlat中的reducer设计了一个采样框架。下图说明了GraphFlat中带重索引和采样策略的reducer。在执行重索引、采样策略时引入了三个关键组件:- 重索引
Re-indexing:当某个shuffle key(即节点ID)的入度超过预定阈值(如10k)时,我们将通过添加随机后缀来更新shuffle key。这个随机后缀用于将原始shuffle key的数据记录随机划分到更小的块piece。 - 采样框架
Sampling framework:我们建立了分布式采样框架,并实现了一套采样策略(如:均匀采样、加权采样),从而降低k-hop邻域的规模,尤其是对于那些hub节点。 - 倒排索引
Inverted indexing:该组件负责用原始的shuffle key来替换重索引的shuffle key。之后,数据记录将输出到磁盘,等待用于下游任务。
在采样之前,重索引组件将同一个
hub节点关联的数据记录均匀地映射到一组reducer。这有助于缓解那些hub节点可能引起的负载均衡问题。然后,采样框架针对shuffle key随机采样其一小部分数据记录。此后,合并、传播操作就像原始Reducer一样执行。接下来,倒排索引组件将重索引的shuffle key恢复为原始的shuffle key(即节点ID)从而应用于下游任务。通过重索引,我们将
hub节点的处理过程划分为一组reducer,从而很好地保持了负载均衡。通过采样,我们将k-hop邻域的规模降低到可接受的大小。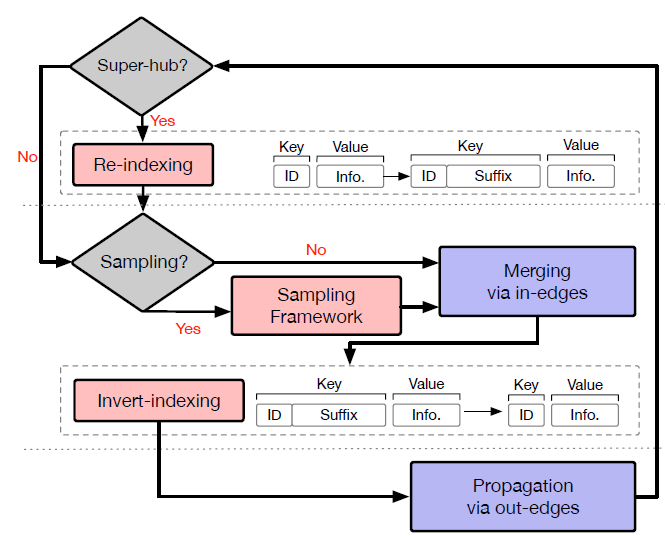
- 一方面,在
6.2.3 GraphTrainer
为了对
GraphFlat生成的k-hop邻域进行有效的训练,我们实现了分布式的图训练框架:GraphTrainer。如下图所示。GraphTrainer的总体架构遵循参数服务器的设计,参数服务器由两部分组成:worker:worker在模型训练期间执行大量计算。server:server在模型训练期间维持图模型参数的最新版本。
由于
k-hop邻域包含足够的、必要的信息来训练GNN模型,因此GraphTrainer的训练worker变得相互独立。它们只需要处理自己的数据分区partition即可,不需要与其它worker进行额外的交流。因此,GNN模型的训练变得类似于传统机器学习模型的训练(在传统的机器学习模型中,每个worker的训练数据都是独立的)。此外,由于大多数
k-hop邻域都是很小的子图,占用的内存很少,因此GraphTrainer中的训练worker仅需要部署在计算资源(即CPU、内存、网络带宽)有限的商用机器上。考虑到
k-hop邻域的性质以及GNN训练计算的特点,我们提出了几种优化策略,包括训练training pipeline、图剪枝graph pruning、边划分edge partition,从而提高训练效率。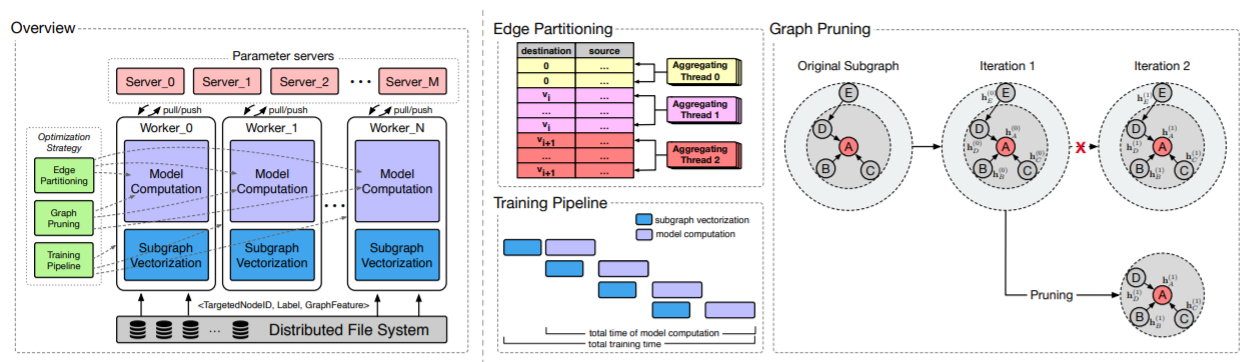
训练工作流
workflow:训练工作流主要包含两个阶段,即子图向量化subgraph vectorization、模型计算。我们以节点分类任务为例来说明这两个阶段。在节点分类任务中,可以将一个
batch的训练样本形式化为三元组的集合:和直接执行模型计算的常规机器学习模型的训练过程不同,
GNN的训练过程必须将GraphFeature描述的子图合并在一起,然后将合并的子图向量化为以下三个矩阵:- 邻接矩阵
destination节点排序(因为是有向图)。 - 节点特征矩阵
- 边特征矩阵
注意:这三个矩阵包含有关
target节点的k-hop邻域的所有信息。它们将与节点ID和label一起馈入模型计算阶段。基于这三个矩阵以及目标节点的ID和label,模型计算阶段负责执行前向传播计算和反向传播计算。- 邻接矩阵
优化策略:这里我们详细阐述三种不同级别的、
graph-specific的优化策略,从而提高训练效率。即:training pipeline(batch-level)、图剪枝graph pruning(graph-level)、边分区edge partition(edge-level)。training pipeline:在GNN模型训练期间,每个worker首先从磁盘读取一个batch的训练数据,然后执行子图向量化和模型计算。按顺序依次执行这些步骤非常耗时。为解决这个问题,我们构建了一个包含两阶段的
pipeline:预处理阶段(包括数据读取和子图向量化)、模型计算阶段。这两个阶段以并行的方式执行。由于预处理阶段所花费的时间相对于模型计算阶段更短,因此经过几轮训练之后,总的训练时间几乎等于仅执行模型计算所花的时间。
graph training:给定batch其中:
k-hop邻域中节点的第intermediate embedding构成的矩阵。
假设一共有
k-hop邻域中所有节点最终的embedding为unnecessary的计算。- 一方面,只有
embedding需要提供给模型的剩余部分(比如损失函数计算的部分)。这意味着embedding对于模型的剩余部分来讲是不必要的。 - 另一方面,三个矩阵
embedding可能无法正确生成。
为解决这些问题,我们提出了一种图剪枝策略,从而减少上述不必要的计算。给定目标节点
给定一个
batch的目标节点在深入研究
GNN模型的计算范式之后,我们有以下观察:给定第embedding之后,第embedding的感受野变为1-hop邻域。这种观察促使我们从具体而言,在第
因此,上式重写为:
注意:如果将邻接矩阵视为稀疏张量,则模型计算中仅涉及非零值。本质上,图裁剪策略是减少每层邻接矩阵中的非零值的数量。因此,它确实有助于减少大多数
GNN算法中的不必要的计算。此外,每个training pipeline策略,几乎不需要额外的时间来执行图剪枝。上图的右侧给出了一个示例,从而说明针对一个目标节点(即节点
A)的图剪枝策略。读者注:随着
embedding。Edge partitioning:如上式所示,聚合器aggregation operator,这使得聚合的优化对于图机器学习系统而言变得非常重要。但是,传统的深度学习框架(例如
TensorFlow,PyTorch)很少解决该问题,因为它们不是专门为图机器学习系统设计的。为解决该问题,我们提出了一种边分区策略来并行地执行图聚合。关键的洞察是:节点仅沿着指向它的边(入边)来聚合信息。如果具有相同目标节点的所有边都可以使用同一个线程来处理,那么多线程聚合将非常有效。因为任何两个线程之间都不会发生冲突。为实现该目标,我们将稀疏邻接矩阵划分为
destination节点的边落在相同的分区partition。边分区策略在上图的中间部分的顶部区域来说明。
在边分区之后,每个分区将由一个线程独立地执行聚合操作。
- 一方面,一个
batch的训练样本中,节点的数量通常远大于线程数。 - 另一方面,在
GraphFlat中应用采样之后,每个节点的邻居数量(即邻接矩阵中每行的非零项的数量)不会太大。
因此,多线程聚合可以实现负载均衡
load balancing,从而在训练GNN模型时获得显著加速。- 一方面,一个
6.2.4 GraphInfer
在工业级规模的图上执行
GNN模型推断可能是一个棘手的问题。- 一方面,推断任务的数据规模和使用频率可能比工业场景中训练任务的数据规模和使用频率高得多。这需要一个设计良好的推断框架来提高推断任务的效率。
- 另一方面,由于
GraphFeatures描述的不同k-hop邻域可能会相互重叠,因此直接在GraphFeatures上进行推断可能会导致大量重复embedding推断,因此变得非常耗时。
因此,我们通过遵循消息传递机制设计了
GraphInfer,它是一种用于大型图上进行GNN模型推断的分布式框架。我们首先执行层次的模型分割
hierarchical model segmentation,从而将训练好的K层GNN模型拆分为K+1个分片slices。然后,基于消息传递机制,我们开发了
MapReduce pipeline,从而从底层到高层的顺序推断不同的分片slice。具体而言,第
Reduce阶段加载第slice,合并入边in-edge邻居上一层embedding来生成第intermediate embedding。然后通过出边out-edge传播这些intermediate embedding到destination node从而用于第Reduce阶段。
下图描述了
GraphInfer的整体架构。这就是模型并行。因为推断期间只需要前向传播,不需要反向传播,因此不需要维持
GNN的节点状态,因此可以通过map-reduce来计算。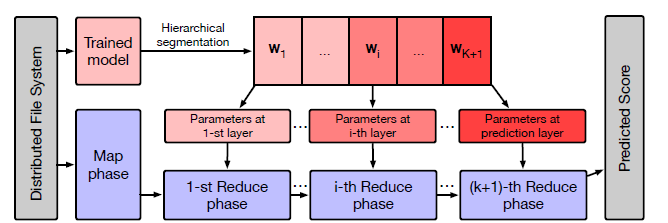
GraphInfer总结如下:层次的模型分割
Hierarchical model segmentation:一个K层的GNN模型以模型层次方面拆分为slice。具体而言,第slice由第GNN layer的所有参数组成,而第slice由最终prediction layer的所有参数组成。Map阶段:类似于GraphFlat,这里的Map阶段仅仅在pipeline的开始运行依次。对于每个节点,Map阶段也生成三种信息,即:自信息self information、入边信息in-edge information、出边信息out-edge information。然后,节点
ID设置为shuffle key、各种信息设置为value,从而用于下游的Reduce阶段。Reduce阶段:Reduce阶段运行embedding,最后一轮将执行最终预测。对于前
reducer的作用类似于GraphFlat。但是在合并阶段,reducer这里不会生成k-hop邻域,而是加载其模型分片slice从而根据self-information、in-edge information从而推断节点embedding,并将结果设置为新的self-information。注意,在第
reducer推断出第embedding,只需要将其输出给最后一个Reduce阶段,而不是将所有三种信息都输出给最后一个Reduce阶段。最后的
Reduce阶段负责推断最终的预测得分,并将其作为推断结果输出。
上述
pipeline中没有重复的推断,这在很大程度上减少了时间成本。此外,在对整个图的一部分执行推断任务的情况下,类似于GraphTrainer中的剪枝策略也可以在pipeline中使用。值得注意的是,我们还在GraphInfer中实现了前面介绍的采样和索引策略,从而保持与GraphFlat中数据处理的一致性,这可以为基于GraphFlat和GraphTrainer训练的模型提供无偏推断。
6.2.5 示例
下面的代码展示了
AGL的用法:通过GraphFlat执行数据生成、通过GraphTrainer进行模型训练、通过GraphInfer执行模型推断。此外,我们还给出了有关如何实现简单GCN模型的示例。########### GraphFlat ###########GraphFlat -n node_table -e edge_table -h hops -s sampling_strategy ;########### GraphTrainer ###########GraphTrainer -m model_name -i input -t train_strategy -c dist_configs ;########### GraphInfer ###########GraphInfer -m model -i input -c infer_configs ;########### Model File ###########class GCNModel :def __init__ (self , targetID , GraphFeatue , label , ...)# get adj , node_feature and edge_feature from GraphFeatueadj , node_feature , edge_feature = subgraph_vectorize (GraphFeatue )....# pruning edges for different layersadj_list = pruning ( adj )def call ( adj_list , node_feature , ...) :# initial node_embedding with raw node_feature , like :# node_embedding = node_feature....# multi - layersfor k in range ( multi_layers ):node_embedding = GCNlayer ( adj_list [k], node_embedding )# other process like dropout...target_node_embedding = look_up ( node_embedding , targetID )return target_node_embedding...class GCNLayer :def __init__ (...)# configuration and init weights...def call (self , adj , node_embedding ):# some preprocess...# aggregator with edge_partitionnode_embedding = aggregator (adj , node_embedding )return node_embeddin对于前面描述的每个模块,我们分别提供了一个封装良好的接口。
GraphFlat将原始输入转换为k-hop邻域。用户只需要选择一种采样策略,并准备一个node table和一个edge table,即可为目标节点生成k-hop邻域。这些k-hop邻域是GraphTrainer的输入,并被形式化为三元组的集合- 然后,通过为
GraphTrainer提供一组配置,如模型名称、输入、分布式训练配置(worker数量、参数服务器数量) 等等,将在集群上分布式训练GNN模型。 - 之后,
GraphInfer将加载训练好的模型以及推断数据,从而执行推断过程。
这样,开发人员只需要关心
GNN模型的实现即可。这里我们以
GCN为例,说明如何在AGL中开发GNN模型。首先,我们应该使用子图向量化函数
subgraph vectorize function将GraphFeature解析为邻接矩阵、节点特征矩阵、边特征矩阵(如果需要)。然后,通过调用剪枝函数
pruning function启用剪枝策略,则会生成一个邻接矩阵的列表adj_list。然后,
adj_list中的第intermediate embedding将被馈入第注意,在每个
GCNLayer中,通过调用聚合函数aggregator function,信息将从入边的邻居聚合到目标节点。
通过这些接口,可以快速实现
GNN模型,并且与单台机器的代码没有什么区别。
6.3 实验
数据集:我们使用三个数据集,包括两个流行的数据集
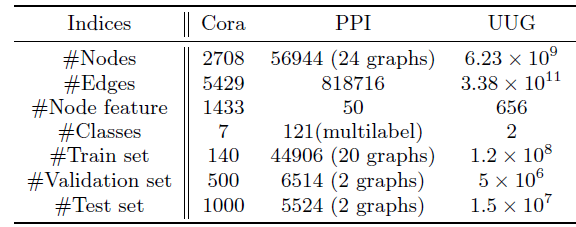
Cora,PPI,以及一个工业级的社交网络User-User Graph: UUG(由支付宝Alipay提供)。Cora:引文网络数据集,包含2708个节点、5429条边。每个节点关联一个1433维的特征,节点属于七种类别中的一个。PPI:蛋白质相互作用数据集,由24个独立的图组成。这些图一共包含56944个节点、818716条边。每个节点关联一个50维的特征,节点属于121种类别种的几个。UUG:包含从支付宝的各种场景中收集的大量社交关系,其中节点代表用户、边代表用户之间的各种关系。它包含高达656维特征,节点属于两个类别中的一种。据我们所知,这是所有文献中图机器学习任务的最大规模的属性图
attributed graph。
根据之前论文的配置,我们将
Cora,PPI数据集分别拆分为三部分:training/validation/test。对于UUG数据集,我们一共有所有这些数据集的统计信息见下表所示。
评估的配置:我们将
AGL和两个著名的开源图机器学习系统进行比较,从而证明我们系统的有效性effectiveness、效率effciency、和可扩展性scalability:Deep Graph Library:DGL:一个Python package,可以基于现有的面向张量的框架(如PyTorch/MXNet)为图结构数据提供接口。PyTorch Geometric:PyG:一个基于PyTorch的深度学习库,用于对不规则结构的数据(如Graph图、点云point cloud、流形manifold)进行深度学习。
对于每个系统,我们分别在两个公共数据集(
Cora,PPI)上评估了三种广泛使用的GNN:GCN、GAT、GraphSAGE。另外,我们将这三个模型对应的原始论文报告的那些GNN的性能作为baseline。为了公平地进行比较,我们仔细地调优了这些
GNN的超参数(如学习率、dropout ratio等)。对于Cora,PPI的实验,embedding size分别设置为16和64。所有的GNN模型使用Adam优化器优化,最多训练200个epoch。对于
UUG数据集,embedding size仅为8。为了减小方差,我们为每个实验记录了
10次运行后的平均结果。注意,在评估公共数据集的训练效率时,所有系统都在独立容器(机器)上以相同的
CPU(Intel Xeon E5-2682 v4@2.50GHz)运行。对于
UUG实验,我们将系统部署在蚂蚁金服的集群上,从而验证我们的AGL在工业场景中的真实性能。注意,这里集群并不是只有我们这个任务,还有其它任务此时都在这个集群上运行,这在工业环境中很常见。我们通过改变worker数量来分析收敛曲线和加速比,从而验证AGL的可扩展性。但是,
DGL和PyG都无法在UUG数据集上运行,因为这两个系统无法支持分布式模式,并且以单机模式运行会导致OOM问题。因此我们不包括DGL和PyG在UUG数据集上的结果。评估指标:我们从几个方面来评估
AGL。- 首先,我们报告
Cora,PPI的准确率和micro-F1得分,从而证明不同系统训练的GNN模型的有效性。 - 其次,我们报告训练阶段每个
epoch的平均时间成本,从而证明不同系统的训练效率。 - 此外,我们使用
UUG数据集训练节点分类模型,并对整个User-User Graph进行推断。通过报告训练阶段和推断阶段的时间成本,我们证明了AGL在工业场景的优越性。 - 最后,我们报告了工业级的
UUG数据集的收敛曲线和训练的加速比,从而证明了AGL的可扩展性。
- 首先,我们报告
6.3.1 公开数据集
这里我们报告了两个公共数据集(
Cora,PPI)上AGL和DGL,PyG的对比,从而评估不同系统的效果和效率。效果
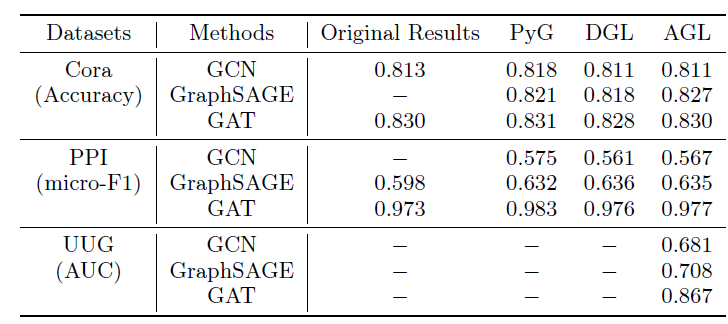
Effectiveness:下表给出了不同的图机器学习系统实现的三个GNN模型(GCN,GAT,GraphSAGE)在两个公共数据集、一个工业数据集上的效果。评估指标为:对于
Cora数据集为准确率、对于PPI数据集为micro-F1、对于UUG数据集为AUC。同时我们还报告了这些GNN模型在原始论文中提供的结果作为baseline。结论:
在这两个公共数据集上,
AGL实现和训练的所有这三个GNN模型的性能都可以和PyG/DGL中的模型相媲美。大多数情况下,
GNN模型的性能偏差都小于0.01。但是,对于PPI上的GraphSAGE,这三个系统的性能均高于baseline,这是由于传播阶段的差异所致。具体而言,在聚合邻域信息时,这三个系统采用add算子,而原始论文使用concat算子。此外,
AGL的这三个GNN模型都可以很好地在UUG上工作并取得合理的结果。其中GAT的效果最佳,这是可以预期的,因为它为不同邻居学习了不同的权重。
效率
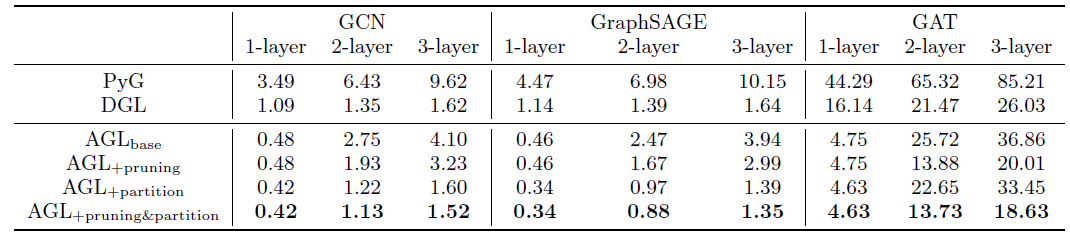
Efficiency:基于PPI数据集,我们比较了三个图机器学习系统上训练的不同深度(1层、2层、3层)的不同GNN模型(GCN, GraphSAGE, GAT)的训练效率。下表报告了所有训练任务每个
epoch的平均时间成本。同时我们还给出了不同优化策略的结果(即图剪枝、边分区)。具体而言:- 下标为
Base表示不采用任何优化策略的原始pipeline方法。 - 下标为
+pruning表示采用图剪枝优化策略的方法。 - 下标为
+partition表示采用边分区优化策略的方法。 - 下标为
+pruning&partition表示同时采用图剪枝和边分区优化策略的方法。
注意,我们的系统是专为工业级规模的图而设计的。在训练阶段,数据将从磁盘而不是内存加载(
PyG和DGL就是从内存加载)。因此我们将AGLBase视为公平的baseline。尽管我们的系统是为工业级规模的图上分布式训练GNN模型而设计的,它也证明了在单机模式standalone mode下CPU的出色的训练速度。下表为单机模式下,PPI数据集训练阶段每个epoch的时间成本(单位秒)。通常在训练阶段,
AGL与PyG相比实现了5 ~ 13倍的加速、与DGL相比实现了1.2 ~ 3.5倍的加速。对于所有不同深度的三个GNN模型上,AGL在不同程度上都优于其它两个图机器学习系统。此外,我们还进一步验证了所提出的优化策略(即图剪枝、边分区)的优越性。
首先,图剪枝策略或边分区策略在不同
GNN模型上都能很好地工作。这可以通过比较AGL + pruning vs AGL_base、以及AGL + edge partitioning vs AGL_base得以证明。并且,当采用
AGL + pruning + partition时,这两种优化策略可以实现更大的提升。其次,这两种策略在不同情况下的加速比有所不同。
- 边分区策略在
GCN, GraphSAGE中的加速比要比GAT更高。 - 图剪枝策略在训练
1层GNN模型时不起作用,但是在训练更深层GNN时效果很好。
这种观察是由于两种策略背后的不同见解
insight引起的。图剪枝策略旨在减少不必要的计算(通过裁剪不会用于传播信息给目标节点的边来进行)。边划分策略以一种有效的、并行的方式实现了邻居之间的信息聚合。一方面,这两种策略优化了训练
GNN模型的一些关键step,因此它们能够使得GNN模型的训练受益。另一方面,也存在一些限制。
- 例如,如果我们训练一个
1层的GNN模型,则图剪枝策略不起作用是合理的。因为每条边在将信息传播到目标节点中都扮演着角色,并且没有不必要的计算。 - 此外,如果模型包含比沿着边聚合信息更稠密的计算(如计算注意力),则这些策略的效果将会被降低,因为稠密的计算将占据总时间成本中的大部分。
- 例如,如果我们训练一个
- 边分区策略在
- 下标为
6.3.2 工业数据集
我们使用
MapReduce和参数服务器来实现AGL,并将其部署在由一千多台计算机组成的CPU集群中,每台计算机由具有64G内存、200G HDD的32-core CPU组成。然后我们对工业数据集(即UUG数据集)进行实验,从而证明AGL在工业场景中的可扩展性和效率。工业级的训练:可扩展性
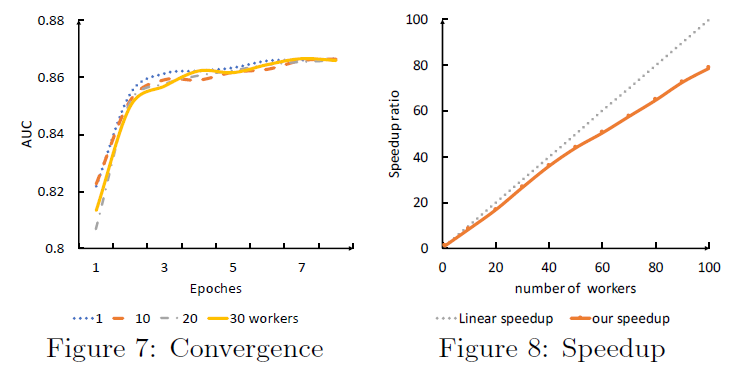
scalability是工业级图机器学习系统最重要的标准之一。这里我们集中在两个方面评估AGL的训练可扩展性,即收敛convergence和加速比speedup。为此,我们使用不同数量的worker来在工业级的UUG数据集上训练GAT模型,并且在下图中分别报告了收敛性和加速比的结果。收敛性:左图给出了
AGL在收敛性方面的训练可扩展性。其中y轴表示GNN模型的AUC、x轴表示训练的epoch数量。一般而言,无论训练
worker的数量如何,AGL最终都可以收敛到相同水平的AUC。如左图所示,尽管分布式模式下需要更多的训练epoch数量,但是收敛曲线最终达到单机训练的AUC相同的水平。因此,在分布式训练下可以保证模型的有效性,这证明了AGL无需考虑收敛性就可以扩展到工业级规模的图。这里是训练
AUC还是验证AUC?论文并未讲清楚。此外可以看到:在相同
epoch情况下,分布式训练的效果通常略差于单机。这似乎是一个普遍现象。加速比:我们还展示了加速比方面的训练可扩展性。如右图所示,
AGL实现了近线性near-linear的加速,斜率约为0.8。这意味着如果将训练worker的数量增加一倍,则训练速度将提高到1.8倍。注意:
- 在实验中,我们将训练
worker的数量从1扩展到100,间隔为10。结果,AGL实现了持续的高的加速比,并且斜率几乎不降低。例如,当训练worker的数量达到100个时,我们的速度加快78倍,仅略低于预期的80。
- 所有这些实验都是在实际生产环境中的集群上进行的。可能在同一台物理机上运行了不同的任务。随着训练
worker的增加,网络通信的开销可能会略有增加,从而导致加速比曲线的斜率扰动。这再次证明了AGL系统在工业级场景中的鲁棒性。
- 在实验中,我们将训练
值得注意的是,在
UUG上训练2层GAT模型只需要大约14个小时,直到收敛为止。具体而言:GraphFlat使用大约1000个worker需要3.7个小时来生成GraphFeature。GraphTrainer只需要100个worker大约10个小时来训练GAT模型。
整个
pipeline可以在14个小时内完成,这对于工业级应用而言非常出色。如果只有
100个worker,那么需要37个小时来生成GraphFeature,此时总的pipeline耗时为47个小时。可以看到:最大的时间消耗在GraphFeature生成上面。此外,在训练阶段,训练任务的每个
worker只需要5.5 GB的内存(总计550GB),这远远少于存储整个图的内存成本(35.5 TB) 。总之,由于
AGL巧妙的体系结构的设计,AGL满足了在工业级图上训练GNN模型的工业可扩展性的要求。工业级的推断:我们在整个
UUG数据集上评估了GraphInfer的效率,数据集包含由于没有图机器学习系统能够处理如此大的图,因此我们将
GraphInfer和基于GraphFeature的原始推断模块进行了比较。注意,所有这些实验的并发度concurrency都相同,即1000个worker。可以看到:
GraphInfer在时间成本和资源成本上始终优于原始推断模块。对于两层的GAT模型(模型生成的embedding维度为8维),GraphInfer需要大约1.2小时来推断62.3亿个节点的预估得分,这大约是原始推断模块所花费时间的1/4。此外,GraphInfer还分别节省了50%的CPU成本、76%的内存成本。与基于
GraphFeature的原始推断模块相比,GraphInfer通过采用消息传递方案避免了重复计算,这就是它优于原始推断模块的原因。
七、AliGraph [2019]
传统的图分析任务经常受到计算复杂度、空间复杂度的困扰,而一种新的、称之为
graph embedding:GE的范式为解决这类问题提供了一条有效途径。具体而言,GE将图数据转换为低维空间,从而可以最大程度地保留图的拓扑结构和内容信息。之后,生成的embedding将作为特征输入到下游机器学习任务中。此外,通过结合深度学习技术,人们提出了 图神经网络
Graph Neural Network:GNN。CNN使用共享权重以及多层架构来提升模型的学习能力。图是典型的局部链接结构,共享权重可以显著降低计算代价,而多层架构是捕获各种尺寸特征的同时处理层次模式hierarchical pattern的关键。因此,GNN是CNN在图上的推广。目前已有很多
GE和GNN算法,但是它们主要集中在简单的图数据上。现实世界商业场景相关的绝大多数图数据具有四个属性:大规模large-scale、异质性heterogeneous、带属性attributed、动态性dynamic。例如,当今的电商网络通常包含数十亿个具有各种类型和丰富属性的节点、边,并且随着时间的推移而迅速演变。这些特性带来了巨大挑战:
- 如何提高大规模图上
GNN的时间和空间效率? - 如何优雅地将异质信息整合为统一的
embedding结果? - 如何统一定义要保留的拓扑结构信息和属性信息(它们位于不同的空间)?
- 如何在动态图上设计有效的增量
GNN方法?
为应对上述挑战,已有大量的工作来设计效率高、效果好的
GNN方法。下表给出了流行的GE和GNN模型的分类,其中包括阿里巴巴内部开发的模型(黄色阴影表示)。如图所示,大多数现有方法同时集中于一个或者两个特点。但是现实世界中的商业数据通常面临更多挑战。为了缓解这种情况,阿里巴巴的一篇论文《AliGraph: A Comprehensive Graph Neural Network Platform》提出了一种针对GNN的全面而系统的解决方案。论文设计并实现了一个叫做AliGraph的平台,该平台提供了系统和算法来解决实际的问题(即前面提出的四个问题)从而很好地支持了各种GNN方法和应用。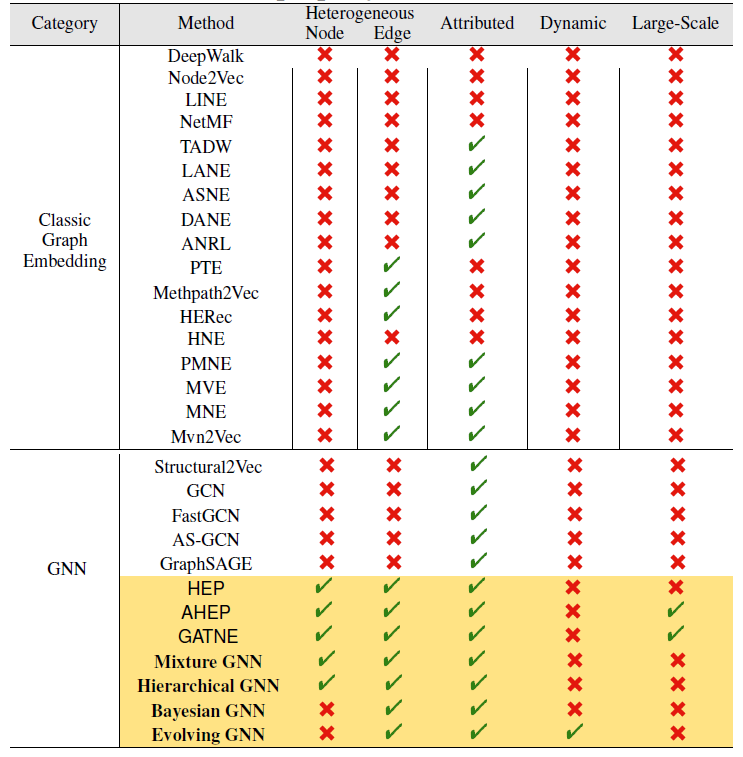
- 如何提高大规模图上
AliGraph的主要贡献:系统:在
AliGraph的基础组件中,我们构建了一个支持GNN算法和应用application的系统。该系统架构是从通用GNN方法抽象而来的,由存储层storage layer、采样层sampling layer、算子层operator layer组成。具体而言:
- 存储层应用了三种新的技术来存储大规模的原始数据,从而满足
high-level操作和算法对数据的快速访问要求。这三种技术为:结构化structural和属性特定attributed specific的存储、图分区、缓存某些重要节点的邻居。 - 采样层优化了
GNN方法中的关键采样操作。我们将采样方法分为遍历TRAVERSE、邻居NEIGHBORHOOD、负采样NEGATIVE三种采样,并提出了无锁方法在分布式环境中执行采样操作。 - 算子层在
GNN算法中提供了两个常用的算子的优化实现,即AGGREGATE、COMBINE。
我们使用一种缓存策略来存储一些中间结果以加快计算过程。这些组件经过共同设计和共同优化,从而使得整个系统有效且可扩展。
- 存储层应用了三种新的技术来存储大规模的原始数据,从而满足
算法:该系统提供了灵活的接口来设计
GNN算法。我们表明:所有现有的GNN方法都可以在我们的系统上轻松实现。此外,我们还针对实际需求内部开发了几种新的
GNN,并在这里详细介绍了其中的六种(上表中的黄色阴影表示的),每种方法在处理实际问题时都更加灵活实用。评估:我们的
AliGraph平台实际上已经部署在阿里巴巴公司中,从而支持各种业务场景,包括阿里巴巴电商平台的商品推荐、个性化搜索。通过对具有
4.92亿节点、68.2亿条边以及丰富属性的真实世界数据集进行广泛的实验,AliGraph在图构建方面的执行速度提高了一个量级(5分钟vsSOTA的PowerGraph平台的数小时)。在训练方面,
AliGraph使用新颖的缓存策略可以将运行速度提高40%~50%,并通过改进的runtime达到大约12倍的加速比。我们在
AliGraph平台上内部开发的GNN模型将归一化的评估指标提升了4.12% ~ 17.19%(如下图所示)。这些数据是从阿里巴巴电商平台淘宝收集而言,我们将数据集贡献给社区从而促进社区进一步的发展。因此实验结果从系统和算法两个层面都验证了
AliGraph的效率和效果。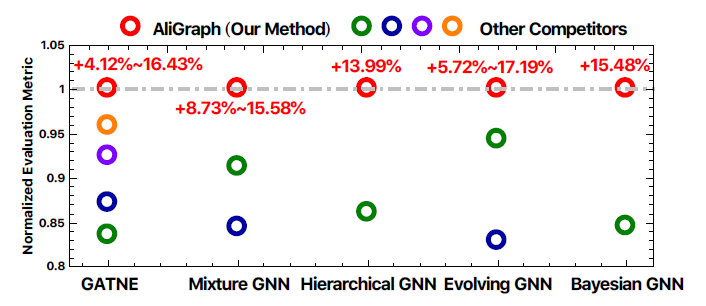
相关工作:
同质图
homogeneous graph:DeepWalk首先通过随机行走在图上生成一个语料库,然后在语料库上训练一个skip-gram模型。LINE通过同时保留一阶邻近性和二阶接近性来学习node presentation。NetMF是一个统一的矩阵分解框架unified matrix factorization framework,用于从理论上理解和改进DeepWalk和LINE。Node2Vec增加了两个超参数来控制随机游走过程。SDNE提出了一种结构保留的emebdding方法。GCN使用卷积运算来融合了邻居的feature representation。GraphSAGE提供了一种归纳式方法inductive approach,将结构信息与节点特征相结合。
异质图
heterogeneous graph:- 对于具有多种类型节点和/或边的图,
PMNE提出了三种方法将multiplex network投影到连续向量空间。 MVE使用注意力机制将具有多个视图的网络嵌入到一个collaborated embedding中。MNE为每个节点使用一个common embedding和几个附加embedding(每个边类型对应一个附加的emebdding),这些embedding是由一个统一的network embedding模型共同学习的。Mvn2Vec通过同时建模preservation和collaboration来探索embedding result。HNE联合考虑内容和拓扑结构是unified vector representation。PTE从标签信息中构建大规模异质文本网络,然后将其嵌入到低维空间。Metapath2Vec和HERec形式化了meta-path based的随机行走从而构建节点的异质邻域,然后利用skip-gram模型来进行node embedding。
- 对于具有多种类型节点和/或边的图,
属性图
attributed graph:attributed network embedding的目的是寻求低维vector representation从而同时保留拓扑和属性信息。TADW通过矩阵分解将节点的文本特征纳入network representation learning。LANE顺利地将标签信息纳入attributed network embedding,同时保留了它们的相关性。AANE使联合学习过程以分布式方式完成,以加速attributed network embedding。SNE提出了一个通用框架,通过捕获结构邻近性和属性邻近性来嵌入社交网络。DANE可以捕获高非线性,并同时保留拓扑结构和节点属性的各种邻近性。ANRL使用邻域增强自编码器对节点属性信息进行建模,并使用skip-gram模型来捕获网络结构。
动态图
dynamic graph:- 实际上,一些静态方法也可以基于
static embedding来更新new node从而处理动态网络。 - 考虑到新节点对原始网络的影响,
《Dynamic network embedding: An extended approach for skip-gram based network embedding》扩展了skip-gram方法来更新原始节点的embedding。 《Dynamic network embedding by modeling triadic closure process》专注于捕获triadic structure property从而用于学习network embedding。- 同时考虑到网络结构和节点属性,
《Attributed network embedding for learning in a dynamic environment》侧重于更新streaming network的top特征向量eigen-vector和特征值eigen-value。
- 实际上,一些静态方法也可以基于
7.1 基本概念
给定图
对于每个节点
in-edge邻居集合记作out-edge邻居集合记作令
为全面描述现实世界中的商业数据,实际的图中通常包含丰富的内容信息,例如多种类型的节点、多种类型的边、节点属性、边属性等。因此我们定义了属性异质图
Attributed Heterogeneous Graph:AHG为了确保异质性,我们要求
对于节点
一个典型的属性异质图如下图所示,其中包含两种类型的节点(
user节点和item节点)、四种类型的边。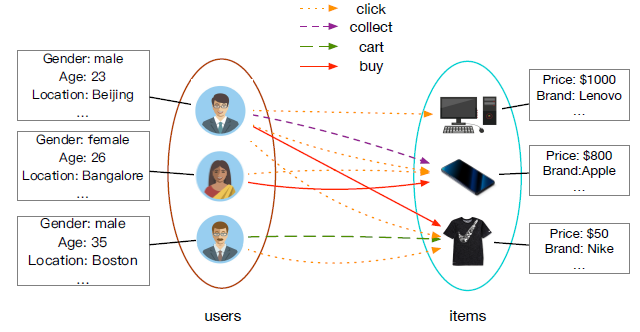
现实世界的图通常随时间动态演化。给定一个时间区间
[1, T],动态图Dynamic Graph是一个图序列为了便于说明,我们采用上标
给定输入图
embedding问题是将图GNN是一种特殊的graph embedding方法,它通过在图上应用神经网络来学习embedding结果。注意,本文中我们专注于
node-level的embedding。即对于每个节点embedding向量emebdding、子图的embedding、甚至整个图的embedding。
7.2 系统
在我们的
AliGraph平台中,我们设计并实现了一个底层系统(蓝色实线的方框标记)从而很好地支持高级GNN算法和应用程序。接下来我们详细介绍该系统。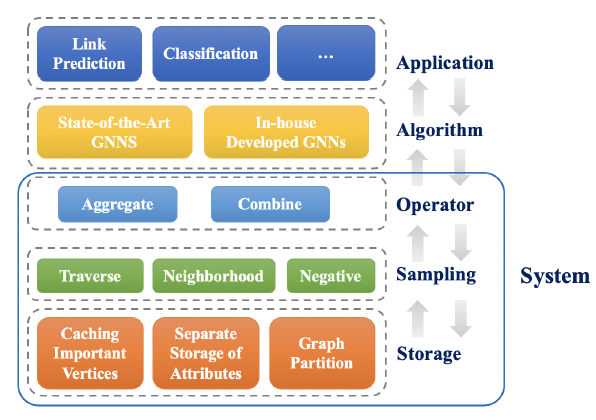
7.2.1 GNN 算法框架
这里我们为
GNN算法抽象出一个通用的框架。一系列经典的GNN算法,如Structure2Vec, GCN, FastGCN, AS-GCN, GraphSAGE可以通过对这个框架的算子进行实例化来实现。GNN框架算法:输入:图
embedding维度hop邻域输出:每个节点
embedding向量算法步骤:
对每个节点
迭代
对每个节点
- 对节点
- 聚合节点
- 生成节点
embedding:
- 对节点
归一化所有节点
embedding向量
对所有节点
final embedding。
GNN框架的输入包括图embedding维度hop邻域GNN框架的输出为每个节点embedding向量embedding馈入到下游机器学习任务,如节点分类、链接预测任务等。GNN框架首先将节点embeddingembedding来更新自己的embedding。具体而言:
- 首先使用
SAMPLE函数来对节点 - 然后通过
AGGREGATE函数来聚合embedding来获得邻域embedding - 然后使用
COMBINE函数来拼接 - 处理完所有节点之后,将
embedding向量归一化normalized。 - 最后,经过
final embedding
- 首先使用
基于上述
GNN算法框架,我们自然地构建了AliGraph平台的系统架构。该平台整体上由五层组成,其中底部三层用于支撑顶部的算法层algorithm layer和应用层application layer。- 存储层
storage layer可以组织和存储各种原始数据,从而满足high-level操作和算法对快速访问数据的要求。 - 在此基础上,结合
GNN算法框架,我们发现SAMPLE, AGGREGATE, COMBINE这三个主要的算子operator在各种GNN算法中起着重要作用。其中SAMPLE算子为AGGREGATE, COMBINE奠定基础,因为它直接控制了后者需要处理的信息的范围。因此我们设计了sampling layer来访问存储,从而快速、正确地生成训练样本。 - 在采样层的上方,
operator layer专门优化了AGGREGATE和COMBINE函数。 - 在系统顶部,可以在
algorithm layer构建GNN算法,并在application layer服务于实际任务。
- 存储层
7.2.2 存储层
这里我们讨论如何存储和组织原始数据。注意,存储真实世界的图的空间成本非常大。常见的电商网络可能包含数百亿节点和数千亿边,其存储成本很容易超过
10TB。大规模的图为有效的图访问带来了巨大的挑战,尤其是在集群的分布式环境中。为了很好地支持
high-level算子和算法,我们在AliGraph的存储层应用了以下三种策略:图分区graph partition、属性的分离存储separate storage of attributes、重要节点的邻居缓存caching neighbors of important vertices。
a. 图分区
AliGraph平台建立在分布式环境上,因此整个图被划分并分别存储在不同的worker中。图分区的目标是最小化交叉边crossing edge的数量。其中交叉边指的是:一条边的两个节点位于不同的worker上。已有一些文献提出了一系列算法。这里我们实现了四种内置的图分区算法,这四种算法适用于不同的情况。
MEIS算法:适用于稀疏图。- 节点
cut和边cut分区算法:适用于稠密图。 2-D分区算法:适用于worker数量固定的场景。- 流式
streaming-style分区策略:适用于边频繁更新的场景。
用户可以根据自己的需求选择最佳的分区策略。此外,用户还可以将其它的图分区算法实现为系统中的插件。
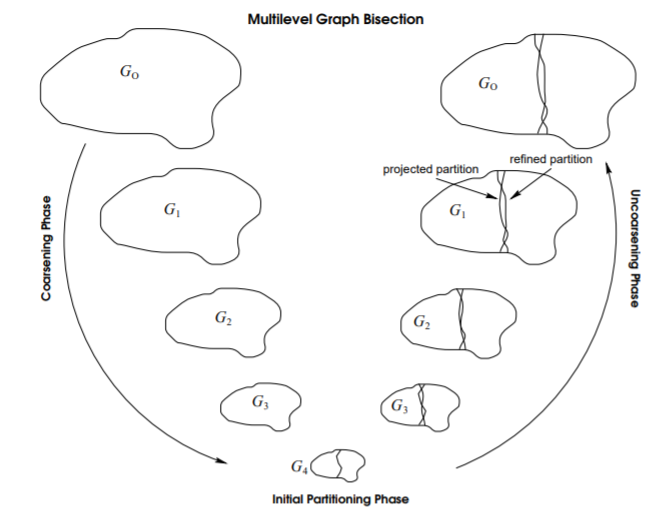
MEIS算法背后的基本思想非常简单:- 粗化阶段
coarsening phase:将图coarsen为一个很小的子图。在这个阶段,图的规模不断缩减。 - 初始划分阶段
initial partitioning phase:对这个子图一分为二bisection。 - 逆粗化阶段
uncoarsening phase:把这个子图的划分不断映射回原始的大图,映射过程中不断微调refine划分边界。
这个过程如下图所示。
- 粗化阶段
节点
cut和边cut分区算法:edge-cuts:已有一些方法的目标是将节点均匀分配给worker从而使得cut edges(跨机器的边)数量最小化。但是这种方式对于幂律分布的图low graph效果非常差。因此edge-cuts使用随机的节点划分。定理:如果节点被随机分配到
进一步地,如果节点
degree分布服从指数为其中:
degree;vertex-cut:我们既可以按照节点来划分graph,也可以按照边来划分graph。节点的degree的分布是高度倾斜的,但是每条边相邻的节点数量的分布是恒定的(如每条边仅与两个节点相连)。因此vertex-cut具有更好的潜力。在
vertex-cut中,每条边都分配给单个机器,并且在所有机器之间cut节点。如果相邻的两条边位于不同的机器,则相邻边的共同节点在这两台机器之间拷贝。如下图所示分别为
edge-cut(按节点划分并切割边)、vertex-cut(按边划分并切割节点)。虚线节点表示被拷贝的ghost节点,1,2,3表示三台机器。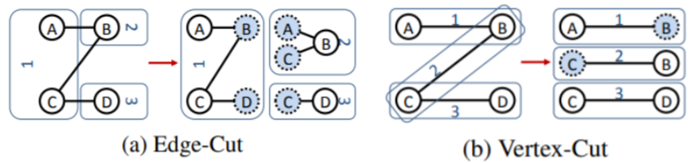
定理:如果边被随机分配到
其中
degree。进一步地,如果节点
degree分布服从指数为其中
随机的
vertex-cut实现了很好的预期的性能,在机器之间获得了几乎完美的平衡。replication factor),但是随机的vertex-cut也获得了更好的收益。2D划分算法:从原理上将,2D划分算法将图的邻接矩阵划分为如下图所示为
2D划分到6台机器上的情况,每种颜色代表一台机器。对角线的block包含大量的非零元素,非对角线的block包含少量的非零元素。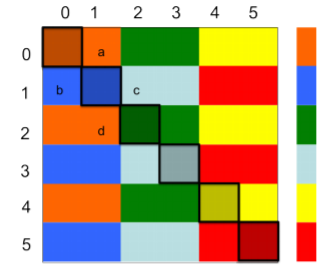
流式分区:在流式分区中,我们将以
edge stream的形式将节点分发到各个worker。当节点到达时,一个partitioner决定将节点放置在哪个worker上。节点一旦放置则永不移动。edge stream的顺序可以是随机的、广度优先搜索、深度优先搜索。- 边可以是有向的或者无向的。如果是无向图,则每条边在流中出现两次。
- 我们运行分区算法访问已经落地的节点定义的整个子图,或者仅仅是有关这个子图的局部信息(直接邻域)。
流式分区理论上可以处理非常大的图(只要集群资源足够),并且只需要加载一次图,并且只需要很少的通信成本。
Partition and Caching算法:输入:图
cache深度输出:
算法步骤:
初始化
graph server分区:对于每条边
ASSIGN(.)为图分区函数,它根据边- 将边
partition。
缓存:对每个节点
- 计算
- 如果
hop 1到hop k的出边邻居。
- 计算
b. 属性的分离存储
对于异质图,我们需要在每个
worker进行中存储分区图的结构和属性。图的结构信息可以通过邻接表简单地存储。即,对于每个节点
对于节点和边上的属性,不宜将它们一起存储在邻接表中。有两个原因:
- 属性通常占用更多的空间。例如存储节点
ID的空间成本最多为8个字节,但是存储节点上的属性的空间成本可能从0.1KB到1KB。 - 不同节点或边之间的属性有很大的重叠。例如,很多节点可能具有表示性别的标签
man。
因此,单独存储属性更为合理。
- 属性通常占用更多的空间。例如存储节点
在
AliGraph中,我们通过构建两个索引集合unique属性。unique属性。
如下图所示,在邻接表中:
- 对于每个节点
- 对于每条边
令
distinct属性的数量。显然,我们的属性分离存储策略将空间成本从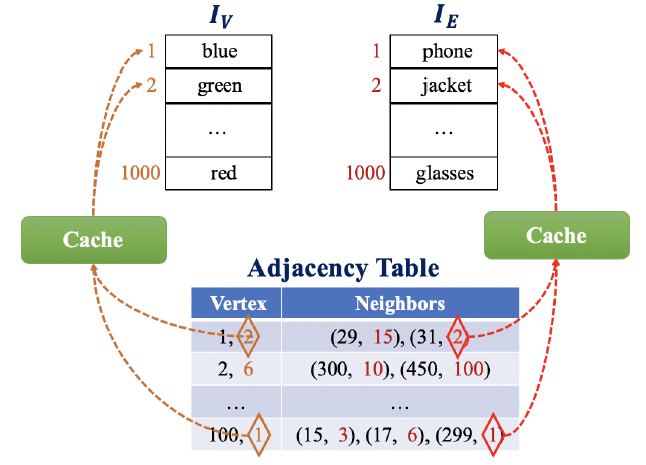
毫无疑问,属性的分离存储将增加检索属性的访问时间。平均而言,每个节点需要访问索引
为缓解这个问题,我们添加了两个缓存组件
cache components,分别将cache中。我们对每个cache采用least recently used:LRU策略来更新cache内容。
c. 重要节点的邻居缓存
在每个
worker中,我们进一步提出了一种在局部cache某些重要节点的邻居的方法从而降低通信成本。直观的想法是:如果节点
out-neighbors存储在它出现的每个分区中。这样就可以大大降低访问但是,如果
trade-off,我们定义了一个指标来评估每个节点的重要性,这个指标决定了是否值得缓存一个节点。定义
k-hop入边邻居in-neighbors,它衡量了缓存节点因为
定义
k-hop出边邻居out-neighbors。它衡量了缓存节点因为邻居节点也需要以该邻居节点为
key来缓存当前节点(作为该邻居的邻居),因此
因此,定义节点
k-th重要性为:仅当节点
注意:这里考虑的是有向图。对于无向图,入边邻居等于出边邻居,则
Partition and Caching算法给出了缓存重要节点的出边邻居的过程。k-hop邻居的阈值。如果1...k-hop出边邻居。- 注意,将
2)就足以支持一系列实际中的GNN算法。 - 实际上我们发现
0.2左右的较小的值可以在缓存成本和收益之间取得最佳平衡。
- 注意,将
有趣的是,我们发现要缓存的节点只是整个图的很小一部分。现实世界中节点的、直接相连的
in-degreeout-degreepower-law distribution。即,图中的极少数节点具有较大的in-degree和out-degree。有鉴于此,我们得出两个定理:
定理一:如果
in-degree和out-degree服从幂律分布,则对于任意k-hop的in-degree和out-degree也服从幂律分布。该定理可以通过数学归纳法证明,具体过程参考原始论文。
定理二:如果图的
in-degree和out-degree服从幂律分布,则图中节点的importance取值也服从幂律分布。该定理可以直接证明,具体过程参考原始论文。
定理二表明:图中的极少数节点具有较大的
importance。这意味着我们只需要缓存少量的、重要的节点即可显著降低图遍历的成本。虽然要缓存的节点比较少,但是这些节点覆盖的邻居节点集合比较大,整体空间占用也比较高。
7.2.3 采样层
GNN算法需要聚合邻域信息来生成每个节点的embedding。但是,现实世界的degree分布通常会倾斜,这使得卷积运算难以执行。为解决这个问题,现有的GNN通常采用各种采样策略来采样邻域的子集。由于采样的重要性,在我们的系统中我们抽象出了一个采样层来优化采样策略。正式地,采样函数接受一个节点集合
GNN模型,我们抽象出三种不同的采样器,即:TRAVERSE:用于从整个分区的子图中采样一个batch的节点或者边。NEIGHBORHOOD:用于从节点的邻域中采样节点作为上下文。邻域可以是直接邻域或者k-hop邻域。NEGATIVE:用于生成负样本从而加快训练过程的收敛速度。
在之前的工作中,采样方法在提高
GNN算法的效率和准确性方面起着重要作用。在我们的系统中,我们将所有采样器都视为插件,它们每个都可以独立地实现。上述三种类型的采样器可以实现如下:TRAVERSE:可以从局部子图获取数据。NEIGHBORHOOD:可以从局部存储获取1-hop邻域,也可以从局部cache获取k-hop邻域。如果节点的邻居没有被缓存,则需要调用远程的graph server。当获取一个
batch节点的邻域时,我们首先将这些节点划分为多个sub-batch,然后每个sub-batch节点的邻域从相应的graph server返回,然后将返回结果组合在一起。NEGATIVE:通常从局部graph server获得负采样。对于某些特殊情况,可能需要从其它graph server进行负采样。负采样在算法上很灵活,我们不需要在一个
batch中调用所有的graph server。
总之,下述代码给出了一个典型的采样阶段:
xxxxxxxxxx# Define a TRAVERSE sampler as s1# Define a NEIGHBORHOOD sampler as s2# Define a NEGATIVE sampler as s3# ...def sampling(s1, s2, s3, batch_size):vertex = s1.sample(edge_type, batch_size)# hop_nums contains neighbor count at each hopcontext = s2.sample(edge_type, vertex, hop_nums)neg = s3.sample(edge_type, vertex, neg_num)return vertex, context, neg通过使用带动态权重的几种有效的采样策略,我们可以加快训练速度。我们在采样器的反向传播阶段实现了权重更新操作,类似于算子的梯度反向传播。因此,当需要权重更新时,我们应该做的是为采样器注册一个梯度函数。权重更新的模式(同步的或者异步的)取决于模型训练算法。
目前为止,读取和更新都将在内存中的
graph storage上进行,这可能会导致性能下降。根据邻域要求,图将按照源节点进行划分。基于此,我们将graph server上的节点分为几组。每一组都与一个request-flow bucket相关联。在这个request-flow bucket中,包括读取、更新在内的所有操作都将与该组中的节点相关。bucket是无锁的队列。如下图所示,我们将每个
bucket绑定到一个CPU core,然后bucket中的每个操作都将被顺序处理而不会加锁。这将进一步提高系统效率。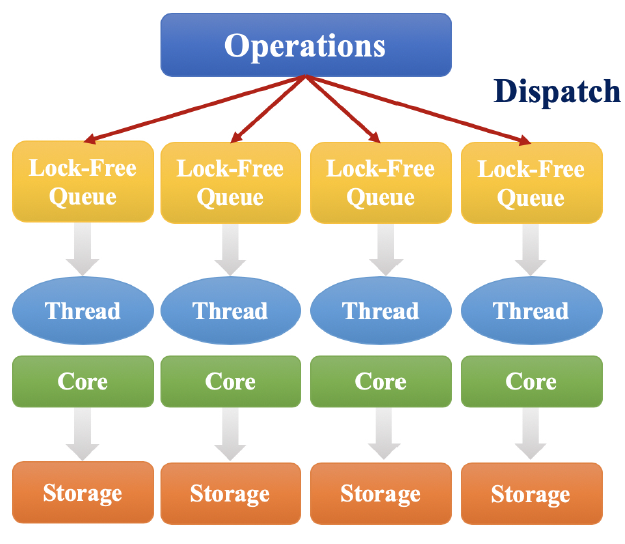
7.2.4 算子层
经过采样之后,得到的输出将被对齐
aligned,然后我们可以轻松地对采样后的集合进行处理。我们需要一些
GNN-like算子来处理这些采样后的结果。在我们的系统中,我们抽象了两种算子,即AGGREGATE和COMBINE:AGGREGATE:收集每个节点的邻域信息从而产生单个结果。例如,AGGREGATE将一系列向量AGGREGATE函数充当卷积算子的作用,因为它从周围邻域收集信息。在不同的GNN方法中采用了不同的聚合函数,如均值池化、最大池化、LSTM等。COMBINE:它给出如何使用邻域信息来更新节点的embedding。例如,COMBINE函数将两个向量COMBINE函数可以将前一层的信息以及邻域信息整合到一个统一的空间中。通常在现有的GNN方法中,将
典型的算子由前向计算和反向计算组成。采样器和
GNN-like算子不仅执行前向计算,而且在需要时会反向计算从而更新参数。这样我们可以将整个模型作为一个网络从而进行端到端的训练。和
SAMPLE类似,AGGREGATE, COMBINE也是AliGraph的插件,可以独立地实现。基于算子,用户可以快速搭建GNN模型。考虑到图数据的特点,可以使用大量优化从而获得更好的性能。
为了进一步加速这两个算子的计算,我们通过具体化
materializationmini-batch,我们可以为mini-batch中的所有节点共享一组采样的邻居。同样地,我们可以为同一个mini-batch中的所有节点之间共享向量- 我们对
mini-batch中的所有节点存储 - 然后在
AGGREGATE函数中,我们通过 - 最后,我们在
COMBINE函数中通过
通过这种策略,可以大大降低算子上的计算成本。这本质上是空间换时间的策略。
这种方式避免了针对
mini-batch中的每个子图来进行独立地计算,因为独立地计算每个子图可能会导致重复计算。- 我们对
7.3 GNN 方法
这里我们讨论
GNN算法的设计。我们表明:现有的GNN可以轻松地在AliGraph上构建。此外,我们还提出了一系列新的GNN算法,从而解决前面概述的、在embedding真实世界图数据的四个挑战。所有这些都是AliGraph平台的算法层的插件。由于我们的
AliGraph平台时从通用GNN算法中抽象出来的,因此可以在该平台上轻松实现所有的GNN。这里以GraphSAGE为例,其它GNN可以用类似的方式实现,由于篇幅所限我们这里省略。- 注意到,
GraphSAGE采用了简单的node-wise采样,从而在每个节点的邻域集合中采样一个小的子集。显然,使用我们的SAMPLING算子可以轻松实现其采样策略。 - 然后,我们需要实现
AGGREGATE和COMBINE函数。GraphSAGE可以通过加权平均的方式实现AGGREGATE函数。也可以使用更复杂的函数,如最大池化、LSTM等。
对于其它的
GNN方法(如GCN, FastGCN, AS-GCN)中,我们可以对SAMPLING, AGGREGATE, COMBINE采用不同的策略。- 注意到,
除了已有的
GNN算法之外,我们还开发了一些内部的GNN。我们内部开发的GNN专注于各个不同方面,如采样(AHEP)、多重性(GATNE)、多模态(Mixture GNN)、层次性(Hierarchical GNN)、动态性(Evolving GNN)、多源信息(Bayesian GNN)。
7.3.1 AHEP
HEP: Heterogeneous Embedding Propagation尝试通过聚合每种类型的邻居来重构节点embedding。对于每个节点
embedding为:其中
其中:
bias参数,它在相同类型的边上共享。
注意:
然后我们将所有类型的邻域的
embedding向量进行拼接,从而得到总的邻域embedding向量:最后我们根据总的邻域
embedding向量来重构节点embedding其中:
bias向量,它在相同的节点类型上共享。
我们的重构损失为
hinge loss:其中:
物理意义为:节点
embedding和节点embedding之间的距离,要小于节点embedding和随机选择的节点embedding之间的距离。除了重构损失之外,如果有监督信息则
HEP还会考虑监督损失。则总的损失为:其中:
trade-off系数。
AHEP算法(HEP with adaptive sampling)旨在缓解异质图上传统的embedding传播embedding propagation:EP算法(HEP)沉重的计算和存储成本。在
AHEP中,我们对重要邻居进行采样,而不是考虑整个邻域。在这个过程中:我们通过节点的结构信息和特征信息设计了一个指标,从而评估了邻居的重要性。
然后,不同类别邻居根据各自的概率分布独立地进行采样。
我们精心设计了概率分布,从而最大程度地减少采样方差。
实验分析表明:
AHEP运行速度要比HEP快得多,同时具有相当的准确率。
7.3.2 GATNE
General Attributed Multiplex HeTerogeneous Network Embedding:GATNE旨在处理节点、边上具有异质信息和属性信息的图。在GATNE中,每个节点的最终embedding由三部分组成:通用
embedding:每个节点base embeddingspecific emebdding(即子视图的embedding):边类型为embedding的迭代方程为:其中:
agg(.)为聚合函数,它可以为均值聚合,也可以为池化聚合。
则节点
emebdding为edge embedding维度。所有子视图
embedding通过self-attention机制来加权聚合。假设边的类型取值为embedding得到节点embedding矩阵:我们使用
self-attention机制来计算每个子视图的加权系数edge embedding:属性
embedding:每个节点
final embedding由通用embedding、specific embedding、属性embedding组成。它们分别刻画了结构信息、异质信息、属性信息。节点类型为final embedding为:其中
trade-off系数,这里三种类型的
embedding在final时候才进行交互。实际上如果在一开始的时候就交互,可能会得到更好的embedding。这就是特征交互的pre-fuse和post-fuse之间的重要区别。
7.3.3 Mixture GNN
Mixture GNN用于处理具有多模态的异质图。在该模型中,我们扩展了同质图上的skip-gram模型来适配异质图上的多义性场景polysemous situation在传统的
skip-gram模型中,我们尝试通过最大化似然来找到参数为graph embedding:其中
softmax函数。在我们的异质图中,每个节点属于多个意义
sense。为区分它们,令注意:这个分布
此时,很难结合负采样方法来直接优化上述公式。一种可选的方法是推导出上式的一个新的下界
EM算法的思想。结果,可以通过稍微修改现有的工作(如
Deepwalk, node2vec)中的采样过程,可以轻松实现训练过程。
7.3.4 Hierarchical GNN
当前
GNN方法本质上是平的flat,并且无法学习图的hierarchical representation。这种限制在显式研究各种类型的用户行为的相似性时尤为突出。Hierarchical GNN结合了层次结构以增强GNN的表达能力。令
GNN经过embedding矩阵,GNN迭代式地通过结合在我们的
Hierarchical GNN中,我们以layer-to-layer的方式来学习节点embedding。具体而言:令
embedding矩阵GNN以及输入我们对图的节点聚类,从而得到邻接矩阵
assignment matrix。pooling GNN以及输入softmax函数来获得。当有了
如实验所验证的,多层
Hierarchical GNN比单层的传统GNN效果更好。这就是
DiffPool的核心思想。
7.3.5 Evolving GNN
Evolving GNN用于对动态网络的节点进行embedding,即学习图序列embedding。为了捕获动态图的演变性质
evolving nature,我们将演变的链接划分为两种类型:- 代表大多数边的合理变化的正常演变
normal evolution。 - 代表罕见的、异常的演变边
evolving edge的突然burst连接。
基于这两种类型的边,动态图中所有节点的
embedding以交错的方式interleave manner学习。具体而言,在时间戳- 图
burst链接通过GraphSAGE集成在一起,从而得到embedding - 然后,我们通过使用变分自编码器
Variational Autoencoder:VAE以及RNN模型来预测normal链接和burst链接。
该过程以迭代方式进行,从而在每个时间戳
embedding结果。- 代表大多数边的合理变化的正常演变
7.3.6 Bayessian GNN
Bayessian GNN模型通过贝叶斯框架集成了两种信息源:知识图embedding(如symbolic)、行为图embedding(如relation)。具体而言,它模仿了认知科学中的人类理解过程。在该过程中,每种认知都是通过调整特定任务下的先验知识来驱动的。给定知识图
basic embedding然后,根据
task-specific embedding其中
注意,学到精确的
对于每个实体
然后,对于每对实体
pair对其中
令
embedding,task-specific的矫正的embedding。
7.4 实验
7.4.1 平台能力评估
这里我们将从
storage(图构建和邻居缓存)、sampling、operator等角度评估AliGraph平台中底层系统的性能。所有实验都在下表中描述的Taobao-small和Taobao-large上进行,后者的存储规模是前者的六倍。它们都是从淘宝电商平台获取的、代表用户和item的子图。
图构建:图构建的性能在图计算平台中起着核心作用。
AliGraph支持来自不同文件系统的各种原始数据。下图给出了两个数据集上图构建的时间成本和worker数量的关系。可以看到:
- 随着
worker数量的增加,图构建的时间明显降低。 AliGraph可以在几分钟内构建大图,如Taobao-large五分钟构建完成。
这比大多数
SOTA的实现要快很多(例如PowerGraph需要几个小时)。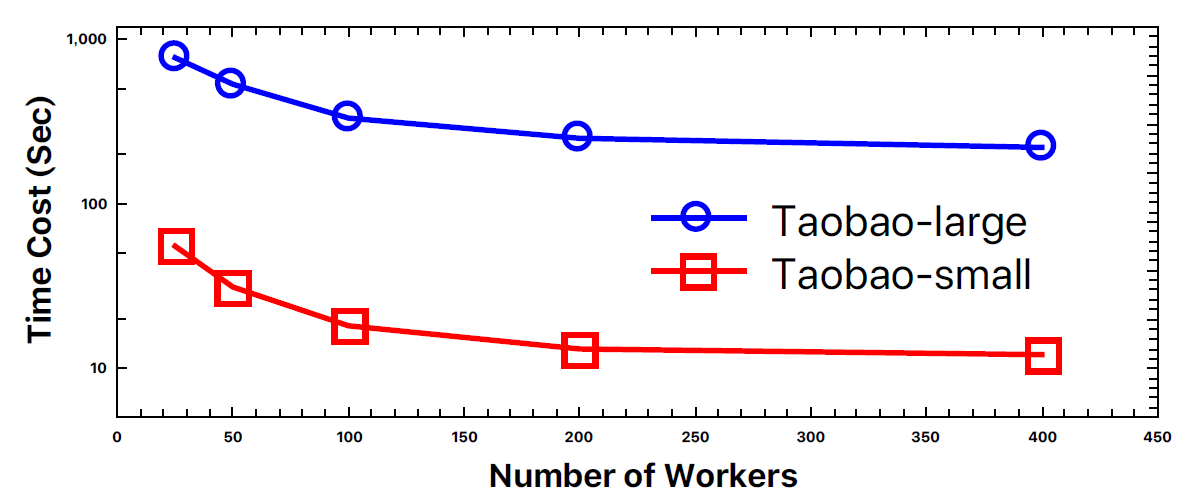
- 随着
缓存邻居的效果:我们研究了缓存重要节点的
k-hop邻居的影响。在我们的缓存算法中,我们需要通过分析在实验中,我们在本地缓存所有节点的
1-hop邻居(直接邻居),并且调整阈值从而控制2-hop邻域的缓存。我们将阈值逐渐从0.05增加到0.45从而测试其敏感性sensitivity和有效性effectiveness。下图给出了被缓存的节点数量的百分比和阈值之间的关系。我们注意到:随着阈值的增加,被缓存的节点数量百分比在下降。当阈值小于
0.2时,百分比下降速度较快;当阈值大于等于0.2时,百分比相对稳定。这是因为如定理中所证明的那样,节点的importance服从幂律分布。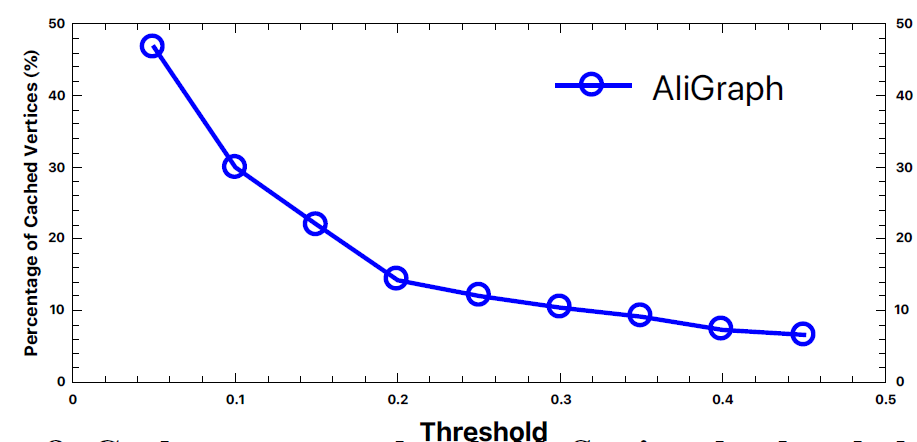
为了在缓存成本和收益之间取得平衡,我们将阈值设置为
0.2,此时只需要缓存大约20%的额外节点。我们还比较了基于
importance的缓存策略以及另外两种策略:随机策略(它随机选择一部分比例节点,然后缓存这些节点的邻域)、LRU策略。下图说明了时间成本和缓存节点比例之间的关系。我们发现我们的方法相对于随机策略节省了大约
40%~50%的时间、相对于LRU策略节省了大约50%~60%的时间。原因很简单:- 随机选择的节点不太可能被访问。
- 由于
LRU策略经常替换缓存的节点,因此会产生额外的成本。 - 基于重要性的缓存节点更可能被其它节点访问到。
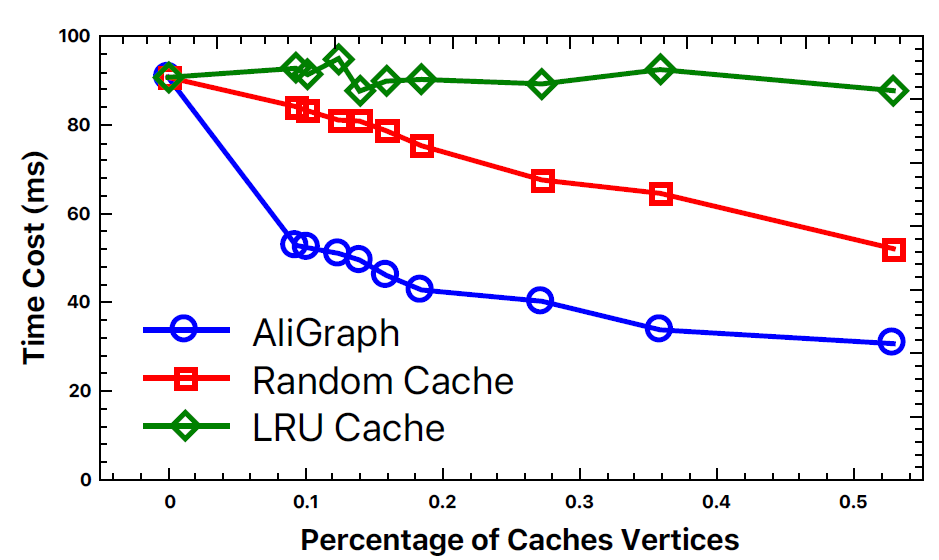
采样的效果:我们以
512的batch size和20%的cache rate来测试采样策略的影响。下表给出了三种采样策略的时间成本。我们发现:- 采样方法非常有效,它们可以在几毫秒到不超过
60毫秒内完成。 - 采样时间随着图的大小缓慢增长。尽管
Taobao-large是Taobao-small的六倍,但是这两个数据集的采样时间却非常接近。
这些观察结果证明了我们对采样方法的实现是有效且可扩展的。

- 采样方法非常有效,它们可以在几毫秒到不超过
Operators的效果:我们进一步检查了我们的AGGREGATE和COMBINE算子的影响。下表给出了这两个算子的时间成本,以及我们提出的实现方案可以加速一个量级。这仅仅是因为我们通过缓存策略来消除中间
embedding向量的冗余计算。这再次证明了我们AliGraph平台的优越性。W/O Our Implementation表示不采用我们方法的实现方式。
7.4.2 算法效果评估
数据集:我们使用两个数据集,包括来自
Amazon的公开数据集,以及Taobao-small数据集。我们没有考虑Taobao-large是因为考虑到一些baseline模型的可扩展性问题。下表给出了数据集的统计信息。这些数据集都是属性异质图。
- 亚马逊公共数据集包含亚马逊公司电子产品类目下的产品元数据。在图中,每个节点代表了带属性的商品,并且每条边代表同一个用户的共同查看
co-view或者共同购买co-buy行为。 Taobao-small具有两种类型的节点,即用户和商品,以及用户和商品之间的四种类型的边:点击click、添加收藏add-to-preference、添加购物车add-to-cart、购买buy。

- 亚马逊公共数据集包含亚马逊公司电子产品类目下的产品元数据。在图中,每个节点代表了带属性的商品,并且每条边代表同一个用户的共同查看
baseline方法:同质的
graph embedding方法:DeepWalk, LINE, Node2Vec。这些方法仅用于同质图,并且仅使用结构信息。带属性的
graph embedding方法:ANRL。它可以通过同时捕获结构信息和属性信息来生成embedding。异质的
graph embedding方法:Metapath2Vec, PMNE, MVE, MNE。Metapath2Vec只能处理具有多种节点类型的图,而其它三种方法只能处理具有多种类型边的图。PMNE涉及三种不同的方法来扩展Node2Vec方法,分别表示为PMNE-n, PMNE-r, PMNE-c。GNN-based方法:Structure2Vec, GCN, Fast-GCN, AS-GCN, GraphSAGE, HEP。
为公平起见,所有算法都是通过在系统上应用优化的算子来实现的。如果模型无法处理属性以及多种类型的节点,则在
embedding中我们忽略这些信息。对于同质的、基于GNN的模型,我们为具有相同边类型的每个子图生成embedding,然后将它们拼接在一起成为最终结果。注意,在我们的实验中,我们并未针对所有
baseline来比较我们提出的每一种GNN算法。这是因为每种算法的设计重点不同。评估指标:我们评估了所提出方法的效率和效果。
- 可以通过算法的执行时间简单地评估效率。
- 为了评估效果,我们将算法应用于链接预测任务。我们随机抽取一部分数据作为训练集,将剩余部分作为测试集。为了衡量效果,我们使用了四个常用指标,即
ROC-AUC、PR-AUC、F1-score、hit recall rate:HR Rate。
值得注意的是:每个指标是在不同类型的边之间取平均的。
这里的评估结果仅供参考,因为不同实验中的指标未能统一,此外也没有进行科学的超参数调优、
n-fold交叉验证。超参数:对于所有算法,我们选择
embedding向量的维度为200。AHEP算法:AHEP算法的目标是在不牺牲太多准确率的情况下快速获得embedding结果。在下表中,我们给出了在
Taobao-small数据集上AHEP和它的竞争对手的比较结果。N.A.表示算法无法合理的时间内结束;O.O.M.表示算法由于内存溢出而终止。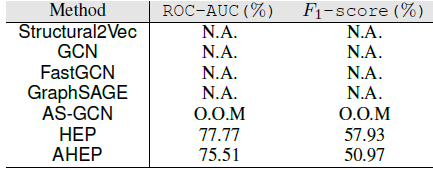
在下图中,我们说明了不同算法的时间和空间成本。
x表示算法无法合理的时间内结束。显然,我们观察到:在
Taobao-small数据集上,HEP和AHEP是仅有的两种可以在合理时间和空间限制下产生结果的算法。但是,AHEP比HEP要快2~3倍,并且比HEP使用更少的内存。从下图指标来看,
AHEP的时间与HEP相差无几?就结果质量而言,
AHEP的ROC-AUC和F1-score和HEP可比。
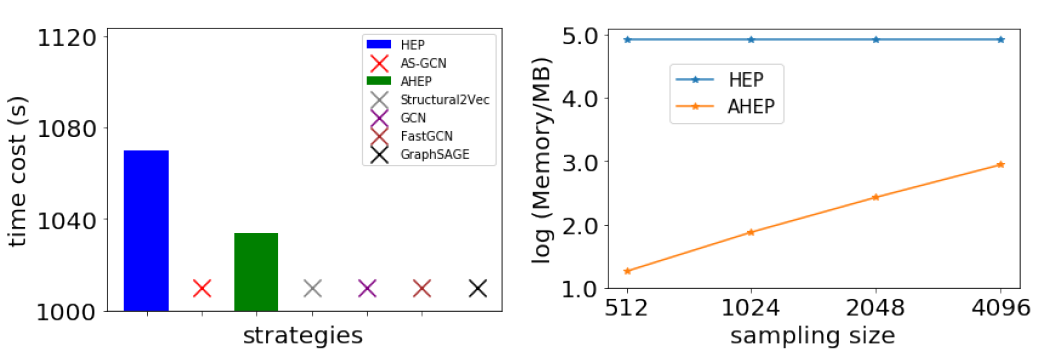
这些实验结果说明
AHEP可以使用更少的时间和空间来产生可比于HEP的结果。GATNE算法:GATNE的目标旨在处理节点和边上都有异质信息和属性信息的图。我们在下表给出了GATNE和它的竞争对手的结果。显然,我们发现GATNE在所有指标上都优于所有现有方法。例如,在
Taobao-small数据集上,GATNE的ROC-AUC提升4.6%、PR-AUC提升1.84%、F1-score提升5.08%。这仅仅是因为GATNE同时捕获了节点和边的异质信息和属性信息。同时,我们发现GATNE的训练时间随着worker数量增加而几乎线性减少。GATNE模型在150个worker下,不到2个小时就可以收敛。这验证了GATNE方法的高效性和可扩展性。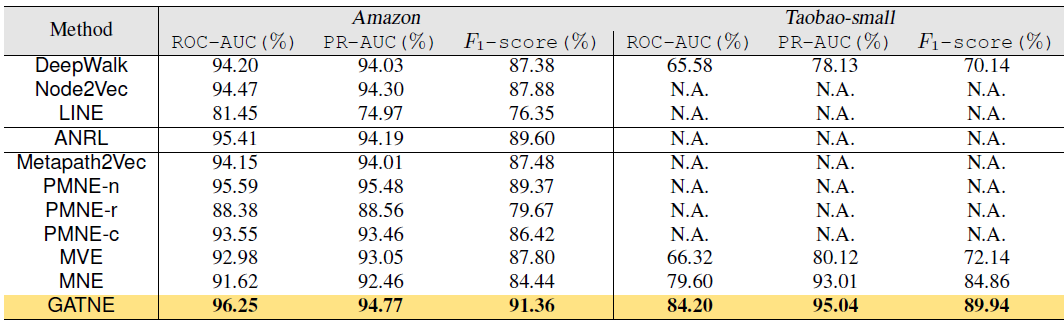
Mixture GNN:我们将Mixture GNN方法和DAE、Taobao-small数据集上进行对比。下表给出了将embedding结果应用于推荐任务的点击召回率hit recall rate。可以看到Mixture GNN的hit recall rate提升大约2%。
Hierarchical GNN:我们将Hierarchical GNN方法和GraphSAGE在Taobao-small数据集上进行比较。结果见下表所示。可以看到F1-score提升大约7.5%。这表明Hierarchical GNN可以产生效果更好的embedding。
Evolving GNN:我们将Evolving GNN方法和其它方法在multi-class链接预测任务上进行比较。对比的方法包括:DeepWalk,DANE,DNE,TNE,GraphSAGE等。这些竞争对手无法处理动态图,因此我们在动态图的每个快照上运行算法,并报告所有时间戳的平均性能。下表给出了
Taobao-small数据集的比较结果。我们很容易发现在所有指标上,Evolving GNN优于所有其它方法。
Bayesian GNN:该模型的目标是将贝叶斯方法和传统GNN模型相结合。我们对比了GraphSAGE模型。下表给出了在Taobao-small数据集上推荐结果的hit recall rate。注意,我们同时考虑了商品品牌粒度以及类目粒度。显然,使用Bayesian GNN时,hit recall rate分别提高了1%到3%。