推荐系统-传统算法
一、Tapestry[1992]
在
1992年的论文《Using Collaborative Filtering to Weave An Information Tapestry》中,论文提出了一个基于协同过滤collaborative filtering的电子邮件过滤系统。Tapestry是Xerox Palo Alto研究中心开发的实验邮件系统,其动机来自于电子邮件的日益使用,导致用户被大量的邮件所淹没。处理大量电邮的一种方法是提供邮件列表,这使得每个用户只能订阅他们感兴趣的那些列表。但是,特定用户感兴趣的文档集合很少能够完整的映射到现有的列表。
更好的解决方式是为每个用户指定一个
filter过滤器,该过滤器将扫描所有的列表,然后在所有列表中选择用户感兴趣的文档。目前已经有一些邮件系统支持基于文档内容的过滤。
Tapestry系统可以在基于内容的过滤之外,通过引入人们的行为来执行更有效的过滤,这种过滤被称作协同过滤collaborative filtering。协同过滤通过记录人们对于他/她所阅读文档的反应
reaction来协同从而帮助彼此进行过滤,这种反应可能是文档特别有趣(或者特别无趣)。这些反应(通常也被称作注解annotation)可以由其它过滤器访问。下图给出了
Tapestry的整体架构:Indexer:从电子邮件、Netnews等外部来源读取文档,并将其添加到Document Store中。Indexer负责将文档解析为一组索引字段从而方便在query中使用。Document store:为所有Tapestry文档提供长期存储,该存储仅支持追加。它还在存储的文档上维护索引,以便可以有效地执行对文档数据库的query。Annotation store:为文档关联的注解提供长期存储,该存储也只支持追加。Filterer:重复对文档集合运行用户指定的一组query,那些与query匹配的文档将被返回。Little box:将特定用户感兴趣的文档排队。每个用户都有一个little box,它里面的文件由过滤器填充,并由用户的文件阅读器消费。Remailer:通过电子邮件定期的将little box的内容发送给用户。Appraiser:对用户的文档进行个性化分类(如用户的little box中的文档)。该功能可以自动地对文档进行优先级排序和分类。Reader~Browser:提供用于访问Tapestry服务的用户界面,如添加/删除/编辑过滤器、检索新文档、显示文档等。
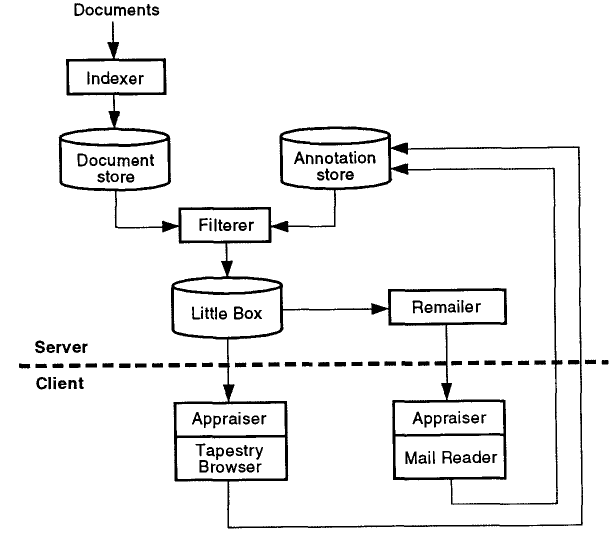
在
Tapestry系统中,用户需要显式指定协同的用户以及该用户的行为构建协同过滤器。在后续的演变过程中,协同过滤已经改进了这种方式,无需用户手动指定即可实现协同过滤。
二、GroupLens[1994]
在
1994年的论文《GroupLens: An Open Architecture for Collaborative Filtering of Netnews》进一步的发扬了这种UserBased协同过滤的思想。GroupLens是一个采用协同过滤的网络新闻过滤系统,它设计了一种机制来帮助用户筛选他/她感兴趣的新闻。GroupLens基于一个朴素的思想:用户在过去的兴趣会延续到将来。GroupLens利用了用户对文章的评分:- 首先计算不同用户的评分序列之间的相关性,从而得到用户兴趣之间的相似性。
- 然后根据相似用户的评分来预测当前用户对于新文章的评分。
给定评分矩阵:
其中 表示用户 对于文章 的评分,该评分可能是已知的,也可能是未知的(因为用户尚未阅读该文章)。当用户评分未知时,我们将其填充为
GroupLens首先计算用户兴趣之间的相似性。给定用户 和 ,定义他们共同评分的文章集合为:然后计算用户 在这些共同评分文章上的均值、方差、以及协方差:
则用户 和 的兴趣相似性由二者评分集合的相关系数
correlation coefficient定义为:当预测用户 在未阅读文章 上的评分时,我们首先找出在 上存在评分的用户集合 :
然后我们基于用户 和集合 中用户的相似性来预测:
评分 不仅受到用户 对文章 的偏好的影响,还受到用户 整体打分的影响。如,有的用户倾向于都打高分,有的用户倾向于都打低分。因此这里通过 来剔除整体性偏好的影响,得到文章 的偏好。
三、ItemBased CF[2001]
世界上信息量的增长速度远远超过我们处理信息的能力。我们都有体会:被每年出版的海量的新书、期刊文章和会议纪要所淹没的感觉。技术大大降低了发布
publishing和分发distributing信息的障碍。现在是时候创造新的技术,从而可以帮助我们从所有可用信息中找到最有价值的信息。此类最有前途的技术之一是协同过滤
collaborative filtering。协同过滤的工作原理是建立用户对item的偏好数据库。对于一个新用户,假设叫做Neo,我们从数据库中匹配邻居,这些邻居是历史上与Neo有相似品味taste的其它用户。然后我们将邻居喜欢的item推荐给Neo,因为Neo可能也会喜欢这些item。协同过滤在研究和实践中都非常成功,在信息过滤应用和电商应用中都非常成功。然而,协同过滤推荐系统有两个基本挑战仍然未能克服:可扩展性
scalability:这些算法能够实时搜索数以万计的潜在邻居,但是现代系统需要搜索数千万个潜在邻居。由于整体计算复杂度为 ,其中 为用户数量、 为平均每个用户评分的item数量,因此随着用户规模的增加其计算复杂度难以忍受。此外,现有算法对于拥有大量历史行为的单个用户
individual user也存在性能问题。例如,某些用户可能在成千上万个item上有过行为,那么这批用户会拖慢每秒可以搜索的相似用户的数量(因为计算用户之间的相似度的计算复杂度为 , 为用户评分的item数量),从而进一步降低了可扩展性。推荐质量
quality:用户需要他们可以信任的推荐,从而帮助他们找到感兴趣的item。对于质量较差的推荐,用户一般都是“用脚投票”,直接拒绝使用该推荐系统。
某种程度上这两个挑战是相互冲突的:算法花在搜索邻居上的时间越少,它的可扩展性就越强、推荐质量也就越差。出于这个原因,同时处理这两个挑战很重要,这样的解决方案既有效又实用。 论文
《Item-Based Collaborative Filtering Recommendation Algorithms》提出了Item-Based CF来同时解决这两个挑战。传统的协同过滤算法的瓶颈是在大量用户中搜索邻居,而
Item-Based算法通过首先探索item之间的关系、而不是用户之间的关系来避免这个瓶颈。通过查找用户喜欢item相似的其它item来获取对用户的推荐。 由于item之间的关系是相对静态static的,Item-Based算法可以减少在线计算的数量,同时保持与User-Based算法相同的推荐质量。论文主要贡献:
- 分析
Item-Based的预测算法,并识别identification实现其子任务的不同方法。 - 形式化
item相似度的预计算模型pre-computed model,从而提高Item-Based推荐的在线可扩展性。 - 几种不同的
Item-Based算法与经典的User-Based算法(最近邻)的实验效果比较。
相关工作:这里我们简要介绍一些与协同过滤、推荐系统、数据挖掘、以及个性化相关的研究文献。
Tapestry是基于协同过滤的推荐系统的最早实现之一。该系统依赖于来自紧密社区close-knit community(如办公室工作组)的人们的显式意见explicit opinion,其中每个用户都了解其它用户。但是大型社区的推荐系统不能依赖于每个用户都了解其它用户。后来,人们开发了几个基于评级
ratings-based的自动推荐系统。GroupLens研究系统为Usenet新闻和电影提供了匿名协同过滤解决方案。Ringo和Video Recommender是分别生成音乐推荐和电影推荐的email-based系统和web-based系统。
ACM的通讯特刊《Recommender Systems》介绍了许多不同的推荐系统。其他技术也已经应用于推荐系统,包括贝叶斯网络、聚类
clustering、以及Horting。贝叶斯网络创建一个基于训练集的模型,每个节点都有一个决策树,边代表用户信息。该模型可以在几个小时或者几天内离线构建。生成的模型非常小,速度非常快,并且基本上与最近邻方法一样准确。
贝叶斯网络被证明可能适用于用户偏好缓慢变化(相对于构建模型所需的时间)的环境,但是不适用于必须快速或频繁更新用户偏好模型的环境。
聚类技术通过识别似乎具有相似偏好的用户组
user group来工作。一旦创建了簇cluster,就可以通过对该簇中其它用户的意见进行平均来对单个用户进行预测。某些聚类技术将每个用户划分到多个
cluster,然后预测时按照跨cluster取加权平均值,权重是参与这个cluster的程度。聚类技术通常比其它方法产生较少个性化的推荐,并且在某些情况下聚类的准确性比最近邻算法更差。然而,一旦聚类完成,性能就会非常好,因为必须分析的组的数量要小得多。
聚类技术也可以作为
first step来应用,用于在最近邻算法中缩小候选集、或者在多个推荐引擎之间分配最近邻计算。虽然将用户划分为clusters可能会损害cluster边缘附近用户的准确性或推荐,但是pre-clustering可能是准确性和吞吐量之间的一个值得的trade-off。Horting是一种graph-based技术,其中节点是用户、节点之间的边表示两个用户之间的相似程度。预测是通过游走到附近节点,然后结合附近用户的意见来产生的。Horting和最近邻不同,因为它探索了graph上的高阶关系而最近邻仅探索graph上的一阶关系(直接关系),从而探索最近邻算法中没有考虑的信息传递。在一项使用人工合成数据的研究中,Horting产生了比最近邻更好的预测算法。
《Recommender Systems in E-Commerce》展示了电商中使用的推荐系统的详细分类和示例,以及它们如何提供一对一的个性化,同时可以捕获客户忠诚度loyalty。
尽管这些系统在过去取得了成功,但是它们的广泛使用暴露了它们的一些局限性,例如数据集的稀疏性问题、与高维相关的问题等。
推荐系统中的稀疏性问题已经在
《Using Filtering Agents to Improve Prediction Quality in the GroupLens Research Collaborative Filtering System》和《Combining Collaborative Filtering With Personal Agents for Better Recommendations》中得到解决。推荐系统中与高维相关的问题已经在
《Learning Collaborative Information Filters》中讨论过,在《Application of Dimensionality Reduction in Recommender System -- A Case Study》中已经研究了应用降维技术解决这些问题。
我们的工作探索了
Item-Based推荐算法(一类新的推荐算法)能够在多大程度上解决这些问题。
3.1 模型
3.1.1 CF-Based 推荐系统
推荐系统主要解决以下问题:通过为给定用户生成预测的可能性得分、或者
top-N的推荐item列表,从而帮助用户找到他们想在电商网站上购买的item。可以使用不同的方法进行
item推荐,例如基于用户的人口统计demographics、热门item、或者用户历史购买习惯。协同过滤Collaborative Filtering: CF是迄今为止最成功的推荐技术。基于CF的算法的基本思想是:根据其他志趣相投用户的意见提供item推荐或预测。用户的意见可以显式explicitly地从用户那里获取,也可以通过一些隐式implicit的手段获取。协同过滤处理
Overview:协同过滤算法的目标是根据用户历史偏好、或者其他志趣相投用户的意见,为目标用户推荐新item或者预测某个item的效用utility。在典型的
CF场景中,有一个 个用户的列表 、以及一个包含 个item的列表 。每个用户 都有一个item列表 ,对该列表中的每个item,用户 已经表达了他/她的意见opinion。 意见可以由用户显式给出(如位于某个数字区间的评级分数rating score),也可以通过分析日志从购买记录中隐式地获取。注意,,并且 可能是空集。给定目标用户 ,协同过滤算法的任务是为 找到一个
item偏好item likeliness。这种偏好有两种形式:- 预测:预测用户 对于
item的评分 。 - 推荐:为用户 推荐他/她可能最喜欢的由 个
item组成的列表 。注意,推荐列表必须位于目标用户尚未购买的item上,即 。这被称作Top-N推荐。
下图给出了协同过滤任务的示意图。
CF算法将整个 个user-item数据表示为一个评分矩阵 ,矩阵中的每一个元素 表示第 个user在第 个item上的评分。每个评分在一定范围之内(如1~5),也可以为0,表示用户尚未对该item评分。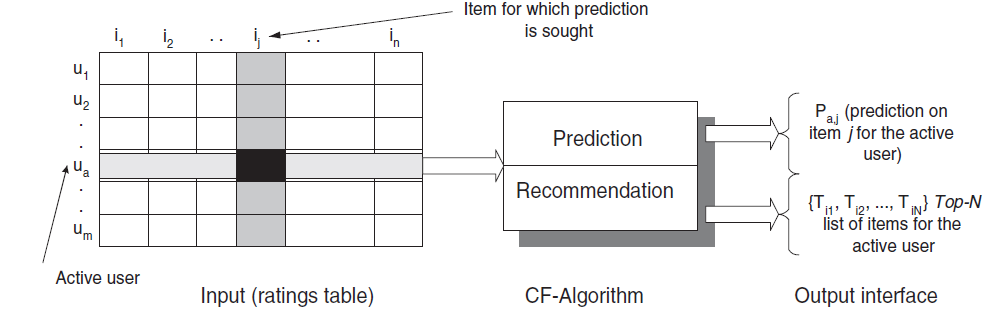
协同过滤算法可以分为两类:
memory-based基于内存的(也称作user-based)协同过滤:利用整个评分矩阵来生成预测。该算法采用统计技术来找出与目标用户最相似的一组用户(称作邻居),然后使用不同的组合方式来组合这些邻居的偏好,从而为目标用户生成推荐或
Top-N推荐。因此该技术也被称为最近邻nearest-neighbor或者UserBased CF技术。model-based基于模型的(也称作item-based)协同过滤:通过建立用户打分模型来提供item推荐。这些方法首采用概率性的方法
probabilistic approach,然后根据给定用户在其它item评分的条件下来预测未打分item上的评分。模型构建过程由不同的机器学习算法执行,例如贝叶斯网络、聚类、以及基于规则rule-based的方法。- 贝叶斯网络模型为协同过滤问题形式化了概率模型。
- 聚类模型将协同过滤视为分类问题,并通过将相同类别的相似用户聚类,并估计给定用户属于特定类别 的概率来工作,并由此计算评分的条件概率。
- 基于规则的方法应用关联规则挖掘
association rule discovery算法来发现共同购买co-purchase的item之间的关联,然后根据item之间的关联强度生成item推荐。
- 预测:预测用户 对于
User-Based CF的挑战:User-Based协同过滤系统在过去非常成功,但是它们的广泛使用暴露了一些潜在的挑战,例如:稀疏性
Sparsity:在实践中,许多商业推荐系统用于评估大型item集合(如Amazon.com推荐书籍、CDnow.com推荐音乐专辑)。在这些系统中,即使是活跃用户购买的item也可能占比远低于1%(200万本书的1%是2万本书)。因此,基于最近邻算法的推荐系统,其推荐的准确性可能很差。注意:因为
user的行为太稀疏,导致user-to-user的相似度不可置信。可扩展性
Scalability:最近邻算法的计算复杂度随着用户数量和item数量的增长而增长。对于数以百万的用户和item,运行现有算法的、典型的web-based推荐系统将面临严重的可扩展性问题。
最近邻算法在大型稀疏数据集上的弱点促使我们探索替代的推荐系统算法。
我们的第一种方法试图将半智能过滤代理
semi-intelligent filtering agent结合到推荐系统中来,从而弥合稀疏性。这些代理使用文法特征syntactic feature对每个item进行评估和打分。通过提供稠密的评分集合,它们有助于缓解覆盖度coverage并提高推荐质量quality。然而,过滤代理解决方案并没有解决志趣相同、但是评分稀疏的用户之间关系不佳的根本问题。为了探索这一点,我们采用了一种算法方法,并使用潜在语义索引Latent Semantic Indexing: LSI来捕获降维空间中用户和item之间的相似度。在本文中我们研究了另一种技术,即
model-based方法,来应对这些挑战,尤其是可扩展性挑战。这里的主要思想是分析user-item表示矩阵representation matrix来识别不同item之间的关系,然后利用这些关系来计算目标user-item pair的预测分。这种方法背后的直觉是:用户有兴趣购买历史喜欢item类似的item,并倾向于厌恶历史不喜欢item类似的item。这些技术不需要在请求推荐时识别用户的相似用户,因此它们往往会更快地给出推荐。已经有很多不同的方案来计算
item之间的关联,从概率性方法到更传统的item-item相关性。接下来我们将详细分析我们的方法。
3.1.2 Item-Based CF
这里我们研究了一类
Item-Based的推荐算法,用于对用户进行推荐预测。与前面讨论的User-Based CF算法不同,Item-Based的方法查看目标用户历史评分item集合并计算它们与目标item的相似度,然后选择top-k最相似的item。同时,top-k对应的相似度 也被计算。一旦得到最相似的
item及其相似度,我们可以通过目标用户对这些相似item已有评分的加权均值来执行预测。我们这里详细描述了这两个方面,即相似度计算和预测生成。Item相似度计算:Item-Based CF最关键的步骤之一是如何计算item之间的相似度。计算item之间相似度的基本思想是:首先挑选既对 打分、又对 打分的用户 ,然后基于这些用户的打分来计算相似度 。下图给出了这一过程,其中矩阵的行代表user、列代表item。
其中有多种方法可以计算
item之间的相似度,我们这里介绍三种方法,即基于余弦cosine-based的相似度、基于相关系数correlation-based的相似度、基于修正余弦adjusted-cosine based的相似度。基于余弦的相似度
cosine-based similarity:两个item被认为是 维用户空间中的两个向量。它们之间的相似度是通过计算这两个向量之间夹角的余弦来衡量的。其中 为用户 在
item上的评分。我们只考虑 。基于相关系数的相似度
correlation-based similarity:两个item之间的相似度是通过计算Pearson-r相关系数 来衡量的。其中 为
item在 上的打分均值。如果令 ,则上式等价于: 。
基于修正余弦的相似度
adjusted-cosine similarity:基于余弦的相似度有个缺陷:未考虑不同用户之间的打分差异。修正的余弦相似度通过从每个用户的打分中减去该用户的打分均值来修复这个问题:其中 是用户 在他/她所有打分
item上的打分均值。如果令 ,则上式等价于: 。它和基于相关系数的相似度区别在于:后者仅考虑
item和item的评分,而前者考虑了整个评分矩阵的评分。
预测:协同过滤系统中最重要的一步是生成预测。一旦我们根据相似性得到了目标
item最相似的一组item,则下一步是为用户执行打分预测。这里我们考虑两种技术:加权和
weighted sum:该方法通过计算用户 对item相似item给出的评分的加权和,从而计算用户 对item的预测。加权的权重为item和 之间的相似度 。使用下图中的概念,我们可以将预测 表示为:
这种方式捕获了目标用户 对相似
item的评分。加权的权重进行了归一化,从而确保预测打分在预定范围内。下图中,使用了
5个相似的item来进行预测。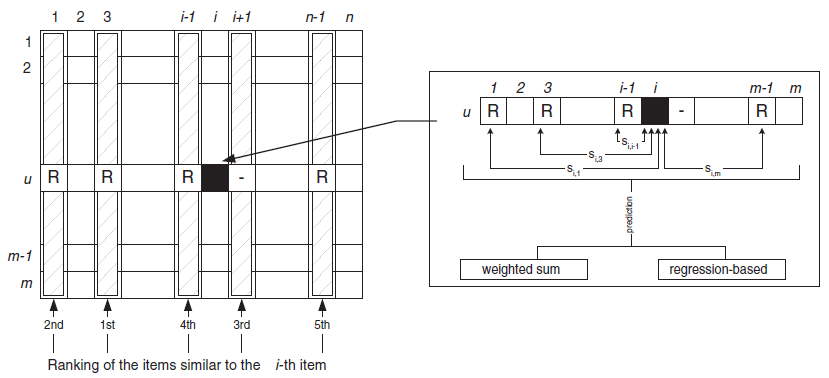
回归
regression:这种方式类似于加权和,但是不是直接使用相似item的打分,而是基于回归模型来拟合的修正打分。实践中使用余弦相似度或者相关系数相似度可能导致两个向量相似度很高,但是实际上差距很远(夹角相同,长度差异较大)。这种情况下使用原始评分来计算,可能会导致预测不佳。
回归方法的思想是:采用加权和相同的公式,但是不使用原始打分 ,而是使用基于线性回归的近似值 。假设目标
item的打分向量为 ,相似item的修正打分为:然后根据 最小化来求解参数 。最终有:
性能分析:
User-Based CF中,邻域的生成过程,尤其时user-user相似度计算步骤被证明是性能瓶颈,从而使得整个过程不适合实时推荐。在本文中,我们提出了一种model-based方法来预计算item-item相似度得分。相似度计算方案仍然是基于相关性的(如基于相关系数或者基于余弦),但是计算是在item空间上执行的。在典型的电子商务场景中,与经常变化的用户数量相比,item数量相比之下更为静态static。item的静态属性使得我们想到了预计算item相似性的想法。预计算
item相似度的一种可能方法是计算所有item之间的相似度,然后执行快速查表从而检索到所需的相似度。这种方法虽然节省时间,但是对于 个item需要 的空间。事实上对于任何一个目标item,我们只需要一小部分最相似的item来预测,这使得我们找到了一种替代的mode-based方案。因此对于每个item,我们仅计算 个最相似的item,其中 。我们称 为模型大小。基于这个模型构建步骤,为目标用户 生成对目标
item的预测的工作原理如下。邻域生成过程:首先检索与目标
item对应的、预计算的 个最相似的item。这里的 表示预测时使用的相似
item数量,它不同于模型大小 (表示预计算相似度的item数量)。预测生成过程:查看用户 购买了这 个
item中的多少个,基于此交集使用Item-Based CF预测算法。
这里有质量和性能的权衡
quality-performance trade-off:为了确保高质量,我们必须有较大的模型大小 ,而这会导致推荐的可扩展性问题。在极端情况下我们可以将模型大小设置为 ,这将确保与原始Item-Based CF完全相同的质量,但是具有很高的空间复杂度。然而,我们的替代方案确保我们保留最相似的item,在生成预测时这些item对预测结果的贡献最大。因此,我们假设这种替代方案即使在 很小时也能够提供相当好的预测质量,从而提供良好的可扩展性。我们后续实验验证了我们的假设。具体而言,我们通过改变 值来验证模型大小对整个系统的质量和性能的影响。
读者注:理论上也可以将
User-Based CF拆分为两阶段:邻域生成 + 预测生成。考虑到用户行为非常稀疏,因此用户的任何新的行为对user-user相似度影响较大。因此user-user相似度必须根据最近的用户行为在线实时计算。相对来说,用户的任何新的行为对
item-item相似度影响较小,因此item-item相似度相对静态,可以离线计算。如:假设
user-item矩阵规模为1000万用户、100万item。假设平均每个用户对5个item进行打分,则平均每个item包含50个用户。假设某个用户 刚刚对一个新的item进行打分,则它会影响所有涉及到u的user-user相似度,相似度波动范围大致为20%;它也会影响所有涉及到 的item-item相似度,但是相似度波动范围大致为2%。因此相对而言,item-item相似度要稳定得多。其本质是
user-item矩阵的行比列更为稀疏。
3.2 实验
数据集:我们使用
MovieLens数据集来评估Item-Based CF的效果。MovieLens是一个web-based的研究research推荐系统,于1997年秋季首次亮相。每周都有数百名用户访问MovieLens来评估和接受电影推荐。该网站现在拥有超过43000名用户,他们对3500多部电影进行评分。我们随机选择打分超过20部电影的用户及其对应的电影评分,得到十万个打分,其中包括943个用户、1682部电影。即我们的user-item矩阵 。我们将数据集随机拆分为训练集和测试集,拆分比例为 。如, 表示
80%的训练集和20%的测试集。实验中我们还考虑了数据集的稀疏水平sparsity level。给定一个矩阵,我们定义它的稀疏水平为:其中 表示矩阵非零元素的总数, 表示矩阵所有元素的总数。我们数据集的稀疏水平为 。
评估指标:推荐系统用来评估推荐质量的指标主要可以分为两类:
统计准确性指标
statistical accuracy metrics:通过测试集上user-item的真实打分和预测打分的对比,从而评估推荐的准确性。平均绝对误差
MAE是其中应用广泛的指标。对每个真实打分和预测打分pair对 ,平均绝对误差为 。考虑所有的 组测试数据,则有:MAE越低则推荐质量越好。另外,均方误差
RMSE、相关系数Correlation也是类似的统计意义上的准确率指标。决策支持准确性指标
decision support accuracy metrics:评估推荐系统帮助用户筛选高质量item的有效性。事实上给用户推荐
item之后,用户会在被推荐item上给出反馈:推荐有效(用户感兴趣)还是推荐无效(用户不感兴趣)。因此这是一个典型的二元分类:有效推荐则为1、无效推荐则为0。我们认为用户打分在4.0分及以上的item是有效推荐(5分制),从而根据预测的二元标签和真实的二元标签得到precision、recall、auc等指标。这种做法基于我们的观察:对于一个无效推荐的item,算法预测它是1.5分还是2.5分没有任何意义。
实验中我们使用 MAE 来报告实验结果,因为它最常用并且最容易直观的解释。另外我们每次随机选择不同的训练集和测试集,重复进行10-fold 交叉验证并报告MAE 的均值。
baseline模型:一个User-Based CF模型(基于Pearson最近邻算法 ),该模型召回全量的user-user相似度而不考虑计算代价。我们调优了该算法的超参数,从而得到最好的Pearson最近邻算法。实验配置:我们首先将数据集划分为训练集和测试集 。在开始对不同算法进行全面的实验评估之前,我们确定了不同算法对不同超参数的敏感性,并从敏感性实验中确定了这些超参数的最佳值,并且将这些最佳超参数用于剩余的实验。
为了确定超参数敏感性,我们仅使用训练集,并将其进一步细分为 “训练--训练集” 和 “训练--验证集”,并对其进行实验。
所有的实验都是使用
C语言实现,在基于linux的PC上运行实验。PC配置为600M HZ的Intel Pentium III处理器以及2GM内存。实验结果主要分为推荐质量结果和推荐性能结果两部分。为了得到较高的推荐质量,我们首先确定了一些超参数敏感性,包括:邻域大小 、训练集拆分比例 、不同的相似度度量。
超参数敏感性:为了确定各种超参数的敏感性,我们仅关注训练集,并将原始的训练集进一步拆分为 “训练--训练集” 和 “训练--验证集”。
相似度算法的影响:我们实现了三种不同的相似度算法,包括基础的余弦相似度、修正的余弦相似度、相关性相似度,并在我们的数据集上测试它们。对于每种相似度算法,我们基于加权和算法来生成预测。实验结果如下图所示,我们给出了验证集的
MAE。可以看到:修正的余弦相似度效果最好,因为它的MAE明显更低。因此,在接下来的实验中我们选择修正的余弦相似度。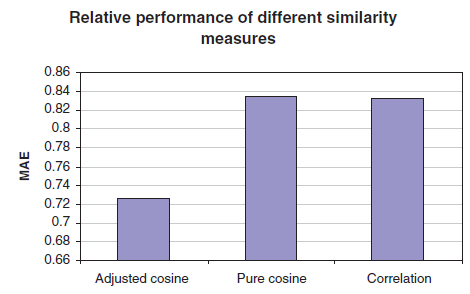
训练集测试集拆分比例的影响:为了确定数据集密度的敏感性,我们以
0.1的增量将 的值从0.2增加到0.9。我们分别使用两种预测生成技术:最简单的加权和,以及基于回归的加权和。实验结果如下图所示。可以看到:预测质量随着 的增加而得到提高。对于较小的 ,基于回归加权和的方法更好;随着 的增加,基于简单加权和的方法反而更好。
我们从曲线图中选择 作为后续实验的参数。
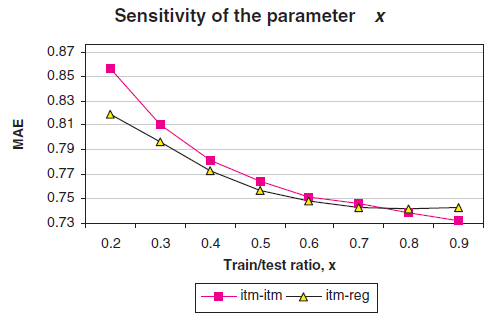
邻域大小 :邻域大小 对预测质量有着显著的影响。 为了确定该参数的敏感性,我们针对不同 值得到了验证
MAE。我们分别使用两种预测生成技术:最简单的加权和,以及基于回归的加权和。实验结果如下图所示。可以看到:邻域大小 确实会影响预测的质量。但是这两种预测生成技术表现出不同的敏感性:当邻域大小从
10增加到30时:简单加权和的方法的推荐质量一直得到改善,但是改善的速度逐渐降低,
MAE曲线趋于平缓。- 基于回归的加权和的方法推荐质量反而逐渐下降。
我们选择 作为最佳邻域大小。
注意:这里离线预计算
item-item相似度时,保留全量的相似度(即模型大小 )。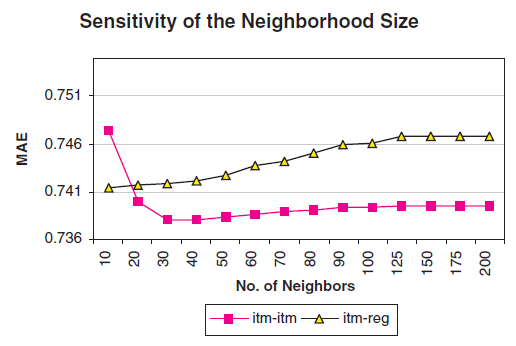
推荐质量:一旦获得了最佳超参数,我们将
User-Based CF和Ite-Based CF进行比较,我们也比较了非个性化算法non-personalized(如推最热门的),结果如下所示。可以看到:
- 简单加权和的
Item-Based CF在所有 (邻域大小为30)、以及所有邻域尺寸( )上的表现都最好。例如在 (邻域大小为30)时,User-Based CF的测试MAE = 0.755,而简单加权和Item-Based CF的测试MAE = 0.749;而在邻域大小为60() 时,User-Based CF的测试MAE = 0.732,而简单加权和Item-Based CF的测试MAE = 0.726。 - 回归加权和的
Item-Based CF的表现比较有趣:它在非常小的 和非常小的邻域大小上战胜了其它两个算法。但是随着 的增加或者邻域尺寸的扩大,它的表现反而更差,甚至比User-Based CF效果都要差。 - 我们还将我们的算法与朴素的非个性化算法进行了比较。
我们从这些结果中得出两个结论:
- 首先,简单加权和的
Item-Based CF算法在所有稀疏级别上都比User-Based CF算法提供更好的推荐质量。 - 其次,回归加权和的
Item-Based CF算法在非常稀疏的数据集上表现更好,但是随着我们添加更多数据,推荐质量会下降。我们认为这是由于模型过拟合。
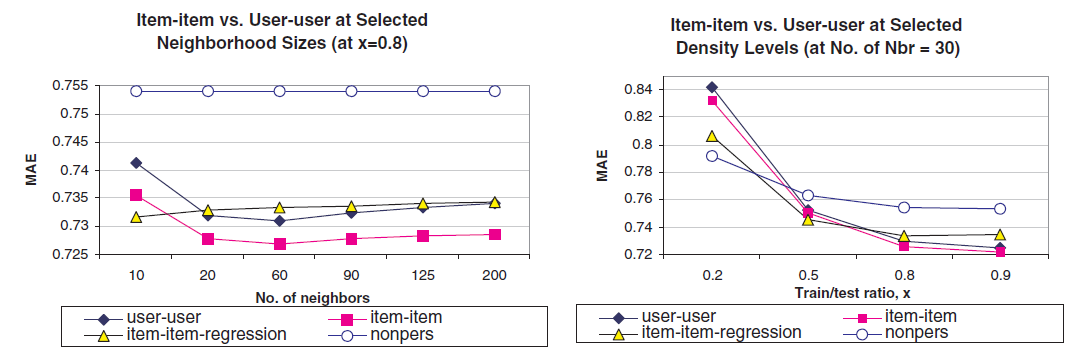
- 简单加权和的
推荐性能:在表明
Item-Based CF算法比User-Based CF算法提供更好的预测质量之后,我们将重点放在可扩展性问题上。如前所述,Item-Based的相似度更加静态,并允许我们预计算item邻居。模型的这种预计算具有一定的性能优势。为了提高系统的可扩展性,我们研究了模型大小 的敏感性,然后研究了模型大小对响应时间和吞吐量的影响。推荐质量对模型大小 的敏感性:我们将相似度计算的
item数量 从25增加到200,增量为25。模型大小 意味着我们仅考虑 个最相似的item来构建模型,然后使用其中的 个用于预测生成过程,其中 。我们前面讨论的 等于全量的item。下图给出了不同 值在不同模型大小上的验证MAE。另外我们还给出全量 的测试MAE(虚线之后的最后一个点)。可以看到:
随着 的增加,
MAE的值会改善,但是改善的效果逐渐降低。仅仅使用一小部分
item即可实现高准确性。在 时,我们保留1.5%的模型大小( 时,验证MAE=0.754)即可得到全尺寸模型( 时,MAE=0.726)96%的准确性;保留3%的模型大小( 时,验证MAE=0.738)即可得到全尺寸模型98.3%的准确率。这种模型大小敏感性具有重要的性能影响,这表明仅使用一小部分
item来预计算item相似度很有效,并且仍然可以获得良好的预测质量。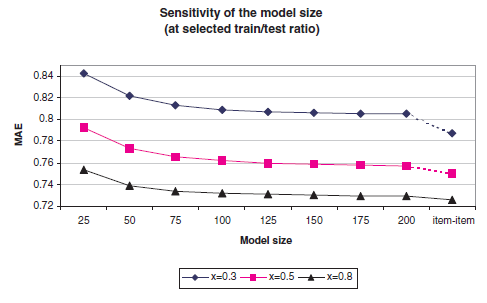
模型大小 对于运行时间和吞吐量的影响:我们记录测试集生成预测结果所需要的时间,注意不同的 拥有不同的测试集大小。
可以看到:小尺寸模型和全尺寸模型的预测结果生成时间存在很大差异。
- 当 (测试集大小
7.5万) 的模型的运行时间为2.002秒,而全尺寸模型为14.11秒。 - 当 (测试集大小
2万) 的模型的运行时间为1.292秒,而全尺寸模型为36.34秒。

由于不同 的测试集大小不同,因此我们根据吞吐量重新绘制了下图。可以看到:
- 当 时, 的模型
1.487秒完成7万个测试样本的打分,即47361个/秒,而全尺寸模型只有4961个/秒。 - 当 时, 的模型吞吐量为
21505个/秒,全尺寸模型只有550个/秒。
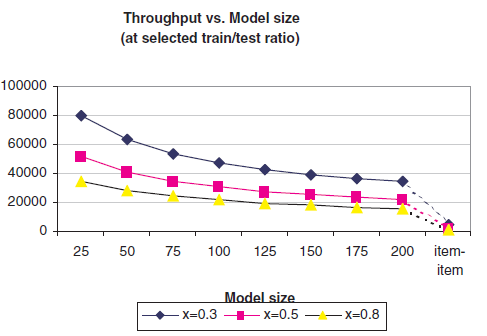
- 当 (测试集大小
讨论:从
Item-Based CF的试验评估中,我们得出了一些重要的观察:- 首先,
Item-Based CF比使用User-Based CF提供更好的预测质量。预测质量的提高在不同邻域大小 和训练集比例 上是一致的,但是改进并不显著。 - 其次,
item邻域是相当静态的,可以预计算,这会导致非常高的在线性能。 - 此外,
model-based方法可以只保留一小部分item并产生相当好的预估质量。我们的实验结果支持这一说法。因此,Item-Based CF能够解决电商推荐系统中的两个最重要的挑战:预测质量和预测性能。
- 首先,
四、Amazon I-2-I CF[2003]
推荐算法以其在电商网站上的使用而闻名,这些算法使用有关用户兴趣的输入来生成推荐
item列表。许多应用程序仅使用用户购买/评分的item来表示他们的兴趣,但是也可以使用其它属性,如浏览过的item、人口统计数据demographic data、主题兴趣、最喜欢的艺术家等。在Amazon.com,我们使用推荐算法为每位用户个性化在线商城online store。商城根据用户兴趣发生了根本性的变化:向软件工程师展示编程书籍、向新妈妈展示婴儿玩具。结果,点击率click-through rate: CTR和转化率conversion rate: CVR(它们是web-based广告和email广告的效果指标) 大大超过了untargeted内容(如banner广告和热门列表)的点击率和转化率。电商推荐算法通常在具有挑战性的环境中运行。如:
- 大型零售商可能有海量数据,如数千万用户、数百万的
item。 - 许多应用程序要求在不超过半秒的时间内实时返回结果集合,同时仍然能够产生高质量的推荐。
- 新用户的信息通常极其有限,仅仅只有极少数的购买/评分记录。
- 老用户的信息通常较大大,可能具有数以千计的购买/评分记录。
- 用户数据易变:每次交互都提供有价值的用户数据,算法必须立即响应新信息。
解决推荐问题的常用方法有三种:传统的协同过滤
traditional collaborative filtering、聚类模型cluster model、search-based方法。在论文《Amazon.com Recommendations: Item-to-Item Collaborative Filtering》中,我们提出了item-to-item collaborative filtering,并与这些方法进行比较。与传统的协同过滤不同,我们的算法的在线计算与用户数量、item数量无关。我们的算法实时生成推荐,可以扩展到海量数据集,并生成高质量的推荐。- 大型零售商可能有海量数据,如数千万用户、数百万的
4.1 三种推荐方法
大多数推荐算法首先找到目标用户历史购买/评分
item有重叠的一组用户(称作相似用户),然后算法聚合来自这些相似用户的历史购买/评分item、剔除目标用户已购买/评分过的item、并将剩余的item推荐给目标用户。这些算法的两个流行版本是协同过滤和聚类模型cluster model。其它的一些方法,包括
search-based方法以及我们的item-to-item协同过滤方法,专注于寻找相似的item而不是相似的用户。对于用户购买/评分过的每个item,这些方法都尝试找到相似的item,然后聚合相似的item并进行推荐。传统
Collaborative Filtering: CF:传统的协同过滤算法将用户表示为一个 维item空间的向量,其中 为item数量。向量的分量对于购买过的或者正面评价的item是正数、对于负面评价的item是负数。为了打压最热门的item,该算法通常将向量分量乘以逆频率inverse frequency(购买/评价该item的用户数量的倒数),从而使得冷门的item更具相关性。对于几乎所有用户来说,这个向量都非常稀疏。该算法根据目标用户最相似的几个用户生成推荐。它可以通过多种方式衡量两个用户 和 的相似度。一种常用的方法是余弦相似度:
一旦找到目标用户的相似用户,该算法使用各种方法从相似用户的
item中选择推荐。一种常见的技术是根据相似用户购买的数量对每个item进行排序。为单个目标用户使用协同过滤生成推荐的计算成本很高。在最坏的情况下它是 ,其中 是用户数量、 是
item数量,因为它需要检查 个用户、每个用户最多 个item。然而,由于平均而言用户向量极其稀疏,因此算法的性能往往更接近 。- 扫描每个用户大约是 而不是 ,因为几乎所有用户向量都包含稀疏的
item(而不是 )。 - 但是有些用户已经购买/评价了很大一部分
item,所以需要 处理时间。
因此,该算法的最终性能约为 。即便如此,对于非常大的数据集,例如
1000万或者更多的用户、100万或者更多的item, 算法会遇到严重的性能和可扩展性问题。这里评估的是单个用户的推荐性能,如果是所有用户那么算法性能为 。
可以通过减少数据规模来解决可扩展性问题。我们可以通过随机采样用户、或者丢弃购买量少的用户从而降低 ,也可以通过丢弃非常热门或者非常冷门的
item从而降低 。还可以通过基于item类别或者主题分类划分item空间,从而减少一定比例的item数量。诸如聚类或者PCA之类的降维技术可以将 或者 减少一个大的因子factor。不幸的是,所有这些降低数据规模的方法也以不同的方式降低了推荐质量。
首先,如果算法仅检查了一小部分用户,那么所选择的相似用户与目标用户的相似度将有所下降(相比在全量用户中选择相似用户)。
因为最相似的用户可能不在我们检查的一小部分用户中。
其次,
item空间的划分使得推荐限制在特定类别或者主题的区域。第三,如果算法丢弃最热门或者最冷门的
item,那么这些item将永远不会被推荐到,只购买这些item的用户也将不会得到推荐。第四,应用于
item空间的降维技术通过消除低频item往往也具有相同的效果(丢弃冷门item)。第五,应用于用户空间的降维技术有效地将相似的用户分组,正如我们前面所描述的(仅检查了一小部分用户),这种聚类也将降低推荐质量。
- 扫描每个用户大约是 而不是 ,因为几乎所有用户向量都包含稀疏的
聚类模型
Cluster Model:为了找到与目标用户相似的用户,聚类模型将用户集合划分为许多部分segment,并将任务视为分类问题。该算法的目标是将用户分配到包含最相似用户的segment。然后,它使用segment中用户的购买/评级来生成推荐。这些
segment通常是使用聚类或其它无监督学习算法创建的,尽管有一些应用程序使用人工确定的segment。使用一种相似性度量,聚类算法将最相似的用户分组在一起从而形成segment。由于对大型数据集进行最佳聚类是不切实际的,因此大多数应用程序使用各种形式的贪心聚类生成。这些算法通常从一组初始segment集合开始,每个segment通常包含一个随机选择的用户。然后,算法反复将用户与现有的segment匹配,通常会根据规则创建新的segment或者合并现有的segment。对于非常大的数据集,尤其是那些高维特征的数据集,采样或降维也是必要的。一旦生成了
segment之后,算法会计算目标用户与每个segment的相似度,然后选择相似度最高的segment并相应地对目标用户进行分类。一些算法将目标用户划分到多个segment,并描述目标用户与每个segment的关系强度。cluster model比协同过滤具有更好的在线可扩展性和性能,因为它们将目标用户与可控数量的segment、而不是整个用户集合相比较。复杂且昂贵的聚类计算是离线运行的。但是这种方法推荐质量较差。
cluster model将众多用户分组到一个segment中,将一个目标用户与一个segment相匹配,然后将segment中所有用户都考虑为目标用户相似的用户,从而进行推荐。因为cluster model找到的相似用户并不是最相似的用户,因此它们产生的推荐不太相关。可以通过使用大量的细粒度segment来提高推荐质量,但是在线的user-segment分类将变得几乎与使用协同过滤查找相似用户一样昂贵。基于搜索
search-based的方法:基于搜索或者基于内容的方法将推荐问题视为对相关item的搜索。给定用户购买/评分的item,该算法构建一个搜索query,从而查找同一作者、艺术家、导演、或者相似关键字或主题的其它热门item。例如,如果用户购买教父DVD合集,那么系统可能会推荐其它犯罪剧、Marlon Brando主演的其它作品、或者Francis Ford Coppola导演的其它电影。如果用户很少购买/评分,基于搜索的推荐算法的可扩展性和表现都很好。然而,对于购买量数以千计的用户而言,基于所有
item进行query是不切实际的。该算法必须使用数据的子集或者summary,从而降低质量。无论是哪种情况(用户购买量太少或者太多),推荐质量都相对较差。这些推荐通常要么太宽泛(例如,最畅销的戏剧
DVD作品)、要么太狭隘(例如,同一作者的所有书籍)。推荐系统应该帮助用户找到和发现新的、相关的、和有趣的item。同一作者或者同一主题中的热门item无法实现该目标。
4.2 Item-to-Item CF
Amazon.com在许多电子邮件营销campaign和大多数网站页面(包括高访问量的Amazon.com主页)中使用推荐作为一个定向营销工具targeted marketing tool。点击Your Recommendations链接会将用户引导至一个区域,在这个区域中用户可以根据item类别、主题类型来过滤推荐,并且对推荐的item进行评分、对用户历史购买的item进行评分,以及了解推荐item的推荐原因。如下图所示。
下图为我们的购物车推荐,它根据用户购物车中的
item为用户提供推荐建议。它该功能类似于超市收银台中的冲动商品impulse item,但是我们的冲动商品针对每个用户个性化定制。
Amazon.com广泛使用推荐算法来根据每个用户的兴趣个性化其网站。由于现有的推荐算法无法扩展到Amazon.com的数千万用户和数百万item,因此我们开发了自己的算法,即item-to-item协同过滤 。我们的算法可以扩展到海量数据并实时生成高质量的推荐。即使现代的深度神经网络模型在预测用户个性化兴趣方面的能力远远超越了传统协同过滤模型,但是传统协同过滤模型在可解释性方面更好,这有助于引导用户接受和信任推荐系统,从而得到更好的转化。
工作原理:
item-to-item协同过滤不是将用户与相似用户进行匹配match,而是将用户购买/评分的每个item与相似item进行匹配,然后将这些相似item组合到推荐列表中。为了确定目标
item的最相似匹配,该算法通过查找用户共同购买的item来构建similar-items table。我们可以通过迭代所有item,并为每对item计算相似度来构建item-to-item矩阵。然而,许多item pair没有共同的用户,因此该方法在计算时间和内存占用方面效率低下。以下迭代算法通过计算单个item与所有相关item之间的相似度,从而提供了更好的方法:xxxxxxxxxx41遍历 item 集合,对集合中的每个 item i1 :2遍历购买/评分 i1 的用户集合,对集合中的每个用户 u:3遍历用户 u 购买/评分的 item 集合,对集合中的每个 item i2 ,记录 pair (i1,i2)4对每个 pair (i1,i2),计算它们之间的相似度可以通过多种方式计算两个
item之间的相似度,但是一种最常用的方法是使用我们之前描述的余弦相似度,其中每个向量对应于一个item而不是一个用户,向量的 维对应于购买/评分了该item的用户。similar-items table的这种离线计算非常耗时,最坏情况为 。然而,在实践中它更接近 ,因为大多数用户的购买量很少。对购买热门item的用户进行采样(热门item列向量的元素进行采样)会进一步降低运行时间,而推荐质量几乎没有降低。给定一个
similar-items table,该算法找到与目标用户的每个购买/评分相似的item,聚合这些item,然后推荐最热门或最相关的item。这种计算非常快,仅取决于用户购买/评分的item数量。可扩展性:
Amazon.com拥有超过2900万用户和数百万个item。几乎所有现有算法都是在小数据集上进行评估的。例如MovieLens数据集包含35000个用户和3000个item,而EachMovie数据集包含4000个用户和1600个item。对于非常大的数据集,可扩展的推荐算法必须离线执行最昂贵的计算。如前所述,现有方法存在不足:- 传统的协同过滤很少或者从不进行离线计算,其在线计算会随着用户数量和
item数量而增加。该算法在大型数据集上是不切实际的,除非它使用降维、采样、或者划分partitioning,而所有这些操作都会降低推荐质量。 cluster model可以离线执行大部分计算,但是推荐质量相对较差。为了改进它,可以增加segment的数量,但是这又会使得user-segment分类变得代价昂贵。search-based model离线构建关键字、类别、作者的索引,但是无法提供有趣的、个性化的item推荐。对于具有大量购买/评分的用户,该方法的可扩展性也很差。
item-to-item协同过滤的可扩展性和性能的关键在于它离线创建昂贵的similar-items table。该算法的在线部分(为用户的购买/评分item查找相似的item)独立于item数量和用户数量,仅取决于用户购买/评分了多少个item。因此,即使对于非常大的数据集,该算法也很快。由于该算法推荐高度相关的相似item,所以推荐质量非常好。与传统的协同过滤不同,该算法在用户数据有限的情况下也表现良好,甚至可以基于少到两三个item来生成高质量的推荐。- 传统的协同过滤很少或者从不进行离线计算,其在线计算会随着用户数量和
五、Slope One Rating-Based CF[2005]
基于评分的协同过滤
RatingBased CF方法是从其它用户的评分中预估目标用户如何对目标商品进行评分的过程。一个理想的RatingBased CF需要满足以下条件:- 易于实现和维度:算法的可解释性强,并且易于实现和维护。
- 即时更新:添加新的评分之后,模型能够立即更新预测。
- 高性能:在线推荐速度应该非常快速,这可能需要以内存为代价。
- 数据需求低:能够为评分数量较少的目标用户提供高质量的推荐。
- 合理的推荐准确性:和效果最好的推荐相比具有可比的推荐质量,其中推荐质量的小幅提升并不值得牺牲简单性
simplicity和可扩展性scalability。
为此,论文
《Slope One Predictors for Online Rating-Based Collaborative Filtering》提出的Slope One算法满足上述五个目标。论文的目标并不是比较各种CF算法的准确性,而是证明Slop One算法可以同时满足这五个目标。相比之下,其它的一些CF方法追求其中的一部分目标而牺牲了另外一些目标。Slope One算法的基本思想是:不同item之间的流行度差异popularity differential。我们以pair对的方式来决定item比item要好多少,从而计算流行度差异。一种简单的计算方式是:用item的评分减去item的评分。反之,如果已知item的评分,以及 和 的流行度差异,那么item的评分就可以计算到。考虑下图中的两个用户 和 以及
item和 。用户 给item评分1分、用户 给item评分2分、用户 给item评分1.5分。我们观察到item比item的评分更高,差异在1.5 - 1 = 0.5分,因此我们预计用户 将给item的评分为2 + 0.5 = 2.5分。我们称 为目标用户,item为目标商品。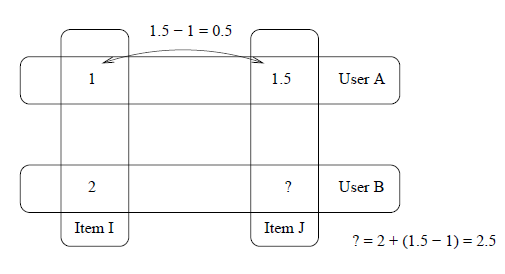
对于每个未知的评分,在训练集中存在大量的这种差异,则我们可以取这些差异的均值。
Slop One算法提供了三种方式来选择差异,并最终得到单个预测结果。Slope One CF的预测形式为 ,其中 为平均的流行度差异。论文的主要贡献是提出了一个
Slope One CF算法,并证明它和memory-based算法相比具有几乎相同的准确性,同时更适合CF任务。相关工作:
MemoryBased CF使用u-2-u相似性来执行预测,其中相似函数的选择决定了推荐的质量。其缺点包括:- 可扩展性
scalability:MemoryBased CF依赖于的u-2-u相似性计算复杂度太高,而这些计算无法通过离线预计算。 - 数据稀疏的敏感性
sensitivity:为满足推荐的高质量,MemoryBased CF要求最低数量的用户(如至少100个用户)、最低数量的评分(如至少20个评分)。
本文中我们将
Slope One CF和众所周知的MemoryBased CF算法Pearson进行对比。- 可扩展性
也有一些
ModelBased CF,如基于线性代数的方法(如SVD、PCA)、基于机器学习的方法(如贝叶斯方法)、基于神经网络的方法、基于聚类的方法。与MemoryBased CF相比,ModelBased CF在线计算的性能很高,但是它们具有昂贵的离线学习阶段或者离线更新阶段。当在线速度至关重要时,ModelBased CF算法相比MemoryBased CF更可取。我们的
Slope One CF的形式为:,其中 为常数、 表示评分变量,因此该方法叫做slope one。对于任何item pair对,我们试图找到从一个item评分中预测另一个item评分的最佳函数 ,不同item pair的函数 可能不同。在
《Item-based collaborative filtering recommender algorithms》中,作者考虑了item pair之间的相关性,然后将用户评分的加权均值作为评分变量,其中权重为相关系数。在该论文的简单版本中,预估形式为 ;在该论文的回归版本中,预估形式为 。
在论文
《A regression-based approach for scaling-up personalized recommender systems in e-commerce》中,作者也使用了 形式的预估。
这两篇论文工作的一个自然扩展是考虑 形式的预估。相反,本文中我们使用形式为 的预估。在
《A regression-based approach for scaling-up personalized recommender systems in e-commerce》中观察到,即使他们使用基于回归的 算法也没有导致相对MemoryBased CF算法的较大改进。因此,证明 形式的预估可以与MemoryBased CF算法竞争,这是本文的一个重要结果。
5.1 模型
给定用户 ,定义他/她的评分
array记作:其中第 个元素 对应于
item的评分。由于存在大量的未评分item,因此这个向量是不全的incomplete。定义用户 评分的所有
item为 ,用户 的平均打分为 :定义训练集的所有评分
array为 : ,其中 为所有用户。定义 为包含
item的用户集合 : 。定义同时包含item的用户集合为: 。定义用户 共同评分的item集合为: 。定义预测 ,其中每个元素代表一个预测结果。
RatingBased CF在线预测时, 首先提供一个评分array(称作query array), 它包含用户的所有评分item;模型返回一个预测array(称作response array),其中包含用户尚未评分的item及其预估的评分。
5.1.1 baseline
最简单的
baseline为PER USER AVERAGE:即:预测用户的所有未评分
item的评分为该用户的评分均值。针对
PER USER AVERAGE的一种改进方式为BIAS FROM MEAN(也被称作NON PERSONNALIZED),其预测结果为:它考虑了用户 的评分均值,以及所有其它用户在该
item上的评分差异(其它用户在该item上的评分减去用户平均均值)。基于
MemoryBased CF的一个经典实现是PEARSON方案:它在
BIAS FROM MEAN的基础上考虑了用户 之间的相似性。其中 为Pearson相关系数,它刻画了用户之间的相似性:其中 为
Case Amplification系数,它降低了数据中的噪音。- 如果相关系数很高,如
corr = 0.9,则经过Case Amplification之后它仍然很高: 。 - 如果相关系数很低,如
corr = 0.1,则经过Case Amplification之后它可以忽略不计: 。
尽管存在更准确的方法,但是
PEARSON相关系数以及Case Amplification一起已经能够提供相当好的推荐质量。- 如果相关系数很高,如
采用
adjusted cosine相似度的ItemBased CF:给定item和 ,定义相似度为:使用基于回归
Regression的预测为:其中 为回归系数,它根据最小化目标来求得:
5.1.2 Slope One
slope one方法同时考虑了来自相同item的其它用户的评分(就像ItemBased CF)、来自相同用户的其它item的评分(就像MemoryBased CF),除此之外slope one方法还依赖于既不是相同item、也不是相同用户的那些评分。因为这些评分数据都有助于我们进行预测。slope one方法的大部分优势都来自于ItemBased CF、MemoryBased CF未考虑的数据。给定用户 ,我们寻找最佳的预测器
predictor来从 的评分中预测 的评分。slope one方法选择的predictor为斜率为1的线性函数 ,这就是名字slope one的由来。 具体而言,我们需要拟合方程:我们通过最小化残差:
通过残差的偏导数为
0,我们得到:因此 是用户 和 的评分差异的均值。
类似地,我们可以通过利用
item的评分来预测item的评分。同样的推导过程,我们有:给定训练集 ,以及任意两个
item,我们定义item到item的平均偏移为:因此在给定 的条件下, 的预测值为:
考虑所有这样的 ,因此用户 在
item上的predictor定义为:其中 ,即:用户 同时评分的、且与 有共同评分用户的
item的集合。当数据足够稠密,即几乎所有
item pair对之间都有评分时,有: 。考虑到:因此有:
可以看到:
slope one方法不依赖于用户对具体item的评分,而依赖于用户的平均评分,以及用户对哪些item进行评分。slop one方法的关键数据是item之间的偏移矩阵:其中 。
偏移矩阵 可以预计算,并且当有新数据进来时实时更新。
ItemBased CF中,我们需要根据相似商品的评分来给出结果。朴素版本的
predictor可以视作 的加权聚合结果:基于回归的
predictor可以视为 的加权聚合结果:
slope one方法采用 的聚合结果,但是没有使用相似性进行加权:事实上可以进一步的扩展到 的形式。
Weighted Slope One:slope one方法的一个缺点是未考虑已经评分的数量。假设给定用户
A对itemJ, K的评分,我们需要预测用户A对itemL的评分。如果有2000个用户同时对itemJ,L评分、有20个用户对itemK,L评分,则商品J相比商品K更适合作为商品L的predictor。因为 比 更为置信。因此定义
Weighted Slope One预测为:.
5.1.3 Bi-Polar Slope One
给定一个
0到10的评分等级表,我们认为评分超过5分表示用户喜欢的item,评分低于5分表示用户不喜欢的item。如果用户的评分是均匀分布的,则阈值设置为5分没有问题。但是通常用户的评分不是均匀分布的,如EachMovie数据集中超过70%的评分都超过5分。考虑到用户评分的分布多种多样,如均匀分布、倾向于乐观的分布(均值超过
5分)、倾向于悲观的分布(均值低于5分)、双峰分布(同时偏向于两个极端)。为了自适应这些分布,我们不再设置固定的阈值,而是使用自适应的阈值:将喜欢/不喜欢阈值设定为用户评分的均值。对于一个用户而言:- 评分低于该用户所有评分均值的
item被视为用户不喜欢的item。 - 评分高于该用户所有评分均值的
item被视为用户喜欢的item。
这种方式可以确保我们能够为每个用户提供合理数量的喜欢/不喜欢
item。- 评分低于该用户所有评分均值的
Weighted Slope One倾向于更加高频的评分模式,Bi-Polar Slope One倾向于某种偏好的评分模式。Bi-Polar Slope One方法将预测拆分为两个部分:- 从用户喜欢的
item中使用Weighted Slope One得出一个预测。 - 从用户不喜欢的
item中使用Weighted Slope One得出另一个预测。
然后合并这两部分的预测,即可得到
Bi-Polar Slope One的预测。- 从用户喜欢的
Bi-Polar Slope One方法从两个角度进行了改进:首先在
item方面,仅考虑用户的两个喜欢item之间的评分偏差,或者两个不喜欢item之间的偏差。即对 进行限制。根据用户不喜欢的
item去预估用户喜欢的item(或者反过来)没有意义。其次在用户方面,在计算
item之间偏差时,我们仅仅考虑同时喜欢、或者同时不喜欢这两个item的用户。即对 进行限制。
我们拆分每个用户的评分
item集合为:然后对于每对
`item pair对 ,拆分它们的共同评分用户集合为:我们计算偏差矩阵为:
最终我们的预测为:
其中 :
- 其中 ,即:用户 同时喜欢的、且与 有共同喜欢用户的
item的集合。 - 其中 ,即:用户 同时不喜欢的、且与 有共同不喜欢用户的
item的集合。
Bi-Polar Slope One将每个用户的item区分为喜欢、不喜欢,这相当于使得用户数量增加一倍。但是由于算法在计算过程中的限制(item方面的限制和用户方面的限制),这使得预测过程的计算量总体上得到降低。另外,由于用户数量翻倍、评分数量不变,这加剧了数据稀疏性。在数据更加稀疏的条件下
Bi-Polar Slope One还能够改善推荐质量,这似乎是违反直觉的。但是如果在预测过程中不去剔除无关的评分,其危害更大。Bi-Polar Slope One无法从 “用户A喜欢商品K、用户B不喜欢商品K” 中预测任何结果,这也是符合直觉的。
5.2 实验
评估指标:测试集上的预测的均方误差
MAE。我们采用All But One MAE。在计算MAE时,我们从测试集每个用户中随机隐藏一个评分,然后预估这个评分。数据集:
EachMovie数据集:Compaq Research提供的EachMovie数据集,评分等级从0.0到1.0, 每0.2一个等级。MovieLens数据集:Minnesota大学Grouplens Research Group提供的Movielens数据集,评分等级从1分到5分,每1分一个等级。
我们选择
5万个用户作为训练集 ,至少10万个用户作为测试集。当预测结果超出范围时,进行修正:EachMovie预测结果超过1.0调整为1.0分,MovieLens预测结果超过5调整为5分。由于
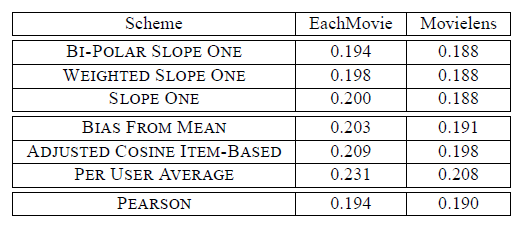
MovieLens分值范围比EachMovie大4倍,因此MovieLens评估的MAE指标除以4从而得到可比的结果。实验结果如下表所示,可以看到:
Slope One方法在所有baseline中表现最好,达到和PEARSON相匹配的准确率。这表明尽管Slope One具有理想的特点,它的准确率仍然可以得到保持。- 针对原始的
Slope One的改进确实能够提高推荐的准确性。Weighted Slope One能够提高大约1%,Bi-Polar Slope One能够提高大约3%。
六、Bipartite Network Projection[2007]
过去几年大量研究致力于理解复杂的网络。一类特殊的网络是二部网络
bipartite network,其中节点被分为两组 ,并且只允许不同组中的节点之间存在连接,如下图(a)所示。许多系统自然地建模为二部网络,例如人类性别网络human sexual network由男性和女性组成、代谢网络metabolic network由化学物质和化学反应组成。有两种二部网络很重要,因为它们在社会、经济、以及信息系统中有特殊意义。一种是所谓的协同网络
collaboration network。这种网络的例子很多,包括共同撰写同一篇科学论文而联系起来的科学家、共同主演同一部电影而联系起来的演员等等。此外,协同网络的概念不一定局限于社会系统。尽管协同网络通常通过对参与者的
one-mode投影来展示,但是它的完整表示是一个二部网络。另一种是所谓的意见网络
opinion network,其中用户集合user-set中的节点和对象集合object set中的节点相连。例如,听众和他们在音乐共享库收集的音乐建立联系、互联网用户和他们在书签网站中收集的web url建立联系、顾客和他们购买的书籍建立联系。
最近,人们对分析和建模二部网络给予了很多关注。但是,为了方便直接表示一组特定节点之间的关系,通常采用
one-mode投影来压缩二部网络。 上的one-mode投影(简称 投影) 是指仅包含 节点的网络,当两个 节点至少存在一个共同的 邻居节点时这两个 节点相连。下图(b)展示了 投影的结果网络、(c)展示了 投影的结果网络。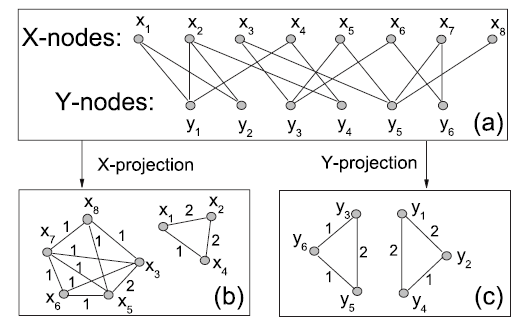
最简单的方法是将二部网络投影到一个未加权的网络上,而不考虑协同
collaboration重复的频次。虽然可以从这个未加权的版本中定性地获得一些拓扑特性,但是信息的损失是显而易见的。例如,如果两位听众各自收集了100首以上的音乐,并且这两位听众仅共享了一首音乐,那么可以得出结论:这两位听众可能具有不同的音乐偏好。相反,如果这两位听众共享了接近100首音乐,那么这两位听众很可能具有非常相似的习惯。然而,在未加权的听众投影中,这两种情况具有完全相同的graph representation。由于
one-mode投影总是比原始二部网络提供的信息更少,为了更好地反映网络的结构,必须使用二部图来量化投影图中的权重。一种直接的方法是直接通过相应partnership重复的次数来对边进行加权。如图(b),(c)所示,这个简单的规则可以获得 投影和 投影的权重。这个加权网络比未加权网络提供更多信息,并且可以通过未加权图的标准技术进行分析,因为它的权重都是整数。然而,这种方法在定量上也是有偏的quantitatively biased。Li等人对科学协同网络进行了实证研究,并指出额外一篇合作论文的影响应该取决于两位作者之间的原始权重。例如,如果两位作者之间之前仅合作一篇论文,那么多一篇合作论文将比两位作者之前合作100篇论文的影响更大。通过将双曲正切函数引入简单的协同次数计数,可以考虑这种饱和效应saturation effect。Newman指出,与许多其他合作者一起出现在同一篇论文的两位作者,他们的平均相互了解程度低于作为论文唯二作者的两位作者。为了考虑这种影响,他引入了因子 来削弱涉及多个参与者的合作的贡献,其中 是参与者的数量。如何对边进行加权是
one-mode投影及其使用的关键问题。然而,我们缺乏对这个问题的系统探索,迄今为止都还没有任何加权方法的坚实理论基础。- 例如,人们可能会问为什么使用双曲正切函数来解决饱和效应而不是其它大量潜在的候选函数的理论依据。
- 此外,为了简单起见,加权邻接矩阵 总是设置为对称的,即 。然而,在科学协同网络中,同一篇合作论文中不同的作者可能会分配不同的权重,可能是发表论文较少的作者给予更高的权重,亦或反之。因此,更自然的加权方法可能是非对称的。
现有方法的另一个缺陷是:在 投影图中,如果 顶点只有一个相连的 顶点,则这个连接关系会在投影过程中丢失。 投影图也有类似的问题,如 仅仅和 关联,这使得在 的投影图中完全丢失了 的信息。即二部网络中
degree为1的边所包含的信息将在one-mode投影中丢失。 这种信息丢失在一些真实的意见网络中可能会很严重。例如在user-web网络delicious中,有相当一部分的web仅被收集一次,而相当一部分user仅收集了一个web。因此,无论是用户投影还是web投影,都将浪费大量信息。与意见网络密切相关的一个核心问题是:如何抽取隐藏信息
hidden information并进行个性化推荐。互联网和World Wide Web的指数级增长使得人们面临信息过载:用户面临太多数据和来源,无法找到与用户最相关的信息。信息过滤的一个里程碑是使用搜索引擎,然而它无法解决这个过载问题,因为它没有考虑个性化,因此对于习惯截然不同的用户返回了相同的结果。因此,如果用户的习惯和主流不同,那么用户很难在无数的搜索结果中找到自己喜欢的东西。迄今为止,有效过滤信息过载的最有潜力的方法是个性化推荐。也就是说,使用用户的个人信息(即该用户活动的历史轨迹)来揭示其习惯并在推荐中加以考虑。例如,Amazon.com使用用户的购买历史来提供个性化推荐。如果你购买了统计物理学教科书,那么亚马逊可能会向你推荐一些其它统计物理学书籍。基于成熟的WEB 2.0技术,推荐系统经常用于web-based的电影共享(音乐共享、书籍共享等)系统、web-based的销售系统、书签网站等。最近,受经济和社会意义的推动,高效推荐算法的设计成为从营销实践到数学分析、从工程科学到物理学界的共同焦点。在论文
《Bipartite network projection and personal recommendation》中,作者提出了一种非对称(即 )、允许自连接(即 )的加权方法。此外,作者提出的方法是沟通二部网络投影、个性化推荐双方的桥梁。数值模拟表明:论文的方法作为个性化推荐算法,其性能显著优于广泛使用的全局排序方法global ranking method: GBM和协同过滤collaborative filtering: CF。
6.1 模型
6.1.1 加权投影图
不失一般性,我们首先确定 加权投影图中边的权重。定义 为:从顶点 的角度看,顶点 的重要性。 我们假设每个 类型的顶点都有一定数量的资源(如推荐强度
power),因此 表示顶点 的资源需要分配给顶点 的比例。通常 。为得到 的解析表达式,我们回归二部图。由于二部图本身是无权的,因此任意 类型顶点的资源应该平均分配给它的 类型的邻居;同理,任意 类型顶点的资源应该平均分配给它的 类型的邻居。如下图所示,我们最初为三个 类型的顶点初始分配了资源 。则资源重新分配过程包含两个步骤:
- 资源先从 类型的顶点流动到 类型的顶点。
- 然后资源从 类型的顶点流回 类型的顶点。
假设最后三个 类型的顶点最终分配到资源 ,则有:
这个
3x3的矩阵是按列归一化的,记作 ,则第 行第 列元素 表示 的初始资源转移到 的比例(占 初始资源的比例)。根据前面的描述,这个矩阵就是我们需要的权重矩阵。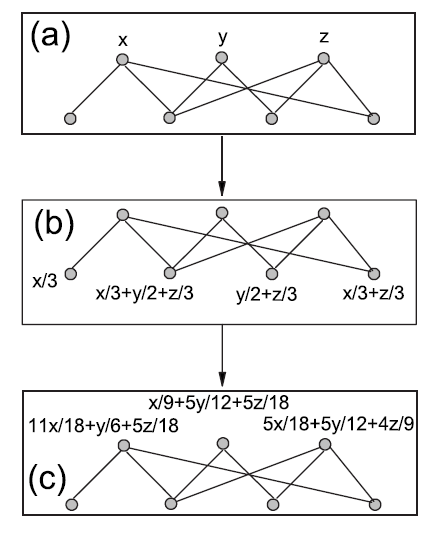
现在考虑更通用的二部图 ,其中 为 类型的顶点, 为 类型的顶点, 为二部图的边。我们定义二部图的邻接矩阵为:
其中 表示 之间的邻接关系:
定义 为顶点 的度
degree: 。定义 为顶点 的度degree: 。假设 类型的顶点 具有初始的资源 。
第一步:所有 的资源流入 中,则 的资源为:
第二步:所有 的资源流入 中,则 的资源为:
如果重写为:
则有:
因此矩阵 就是我们希望得到的 投影图的权重矩阵。因此 的资源重新分配过程可以重写为:
该算法可以看作是
PageRank算法的推广,而这些算法本质上是基于消息传递机制。可以发现权重矩阵 的几个特点:
权重矩阵是非对称的,且满足:
这符合我们的经验,如果某个科学家发表了很多论文,即他的
degree很大,则单篇合作论文的权重相对较小。 代表 资源转移到 的比例,如果 的degree比较大,则它转移到 的比例也会较低。权重矩阵对角线元素非零。这意味着:如果 顶点只有一个相连的 顶点,则这个连接关系会在投影过程中得到保留。假设该顶点为 ,唯一与它相连的顶点为 ,则有:
因此有:
可以看到 的连接关系被保留在 中。
事实上可以证明:权重矩阵对角线元素是每一列的最大元素,即 。当且仅当 的所有 邻居都是 的 邻居的子集时,等式成立。这在论文协作网络上可以发现。如:学生的论文都是和他们的导师共同发表的,因此如果 为学生、 为他/她的导师,则有 。
因此比例系数 可以视为 的研究相对于 的独立性,这个比例越低则独立性越高。最终 的独立性可以刻画为:
注意:度量 仅仅只是一个示例,它用于说明如何使用 中包含的信息,并不能说明独立是好还是不好。
6.1.2 NetworkBased 推荐
一个推荐系统包含用户集合 ,推荐对象
object集合 。假设只存在用户到
object的边,则推荐系统可以描述为一个 的邻接矩阵 。我们假设意见网络是无权重的,即:如果 收藏了 ,则 。 表示用户 对 尚未收藏。我们认为用户收藏了对象表明用户喜欢该对象。
一个更复杂的情况是,用户不仅表示了喜欢的意向,还给出了喜欢的程度(以评分表示)。这两种情况密切相关,但是本文我们重点讨论前一种情况。
定义 为
object的度degree, 为用户 的度degree。Global Ranking Method:GRM:将所有object按照degree降序排列,并推荐degree最高的top对象,即推荐热门对象。尽管
GRM缺乏个性化导致推荐效果不尽人意,但是它简单直接并且节省资源,因此被广泛使用。如 “畅销新书“ 这类推荐都可以视为GRM。MemoryBased CF:基于用户之间相似度的个性化推荐。给定用户 和 ,他们的相似度定义为:
其中 为以
object表示的用户向量,且 (因为是无权图)。则有:用户 在
object上预测的得分为:有两个因素会影响 :
- 如果 的
degree很大,即非零的 越多,则 累加的项越多,结果越大。 - 如果 被更多的、与 相似的用户喜欢,则对应的权重 越大,则 越大。
前者重视全局信息(对象 的度,对每个用户都是无差别的)、后者重视个性化信息(每个用户都不同)。
对于任意用户 ,我们将所有非零 且 ( 表示用户尚未收藏的)的对象根据 降序排列,然后推荐其中的
top K对象。- 如果 的
这里我们基于加权投影图提出了一种推荐算法,该算法是对二部图的加权方法的直接应用。
首先对二部图进行
object映射,得到的加权图定义为 。然后给定用户 ,我们获取用户已经收藏的
object集合为 ,并在该集合的每个object上放置一些资源。为简单起见,我们在 的每个顶点上初始化资源为:
即:如果 喜欢 ,则它初始化资源为单位
1;否则初始化资源为0。注意:对于不同用户, 的初始化配置是不同的,这是个性化的初始化。
最终我们得到 中顶点的资源为:
因此有:
其中 表示 的资源分配到 的比例。
对于每个用户 ,我们将所有非零资源 、且 ( 表示用户尚未收藏)的对象按照资源 降序排列,然后推荐其中的
top K对象。
由于不同用户的初始化配置不同,因此该分配方程需要重复执行 次。写成矩阵的形式为:
其中 第 列为用户 在各
object上的最终分配资源。这种方法我们称作基于网络的推断
NetworkBased Inference: NBI,因为它是基于加权映射网络 的。该方法是标签传播算法的推广,有两个区别:该方法仅传播两次,相比之下标签传播算法不停传播直到收敛;该方法除了邻接矩阵还有权重矩阵,相比之下标签传播算法仅使用邻接矩阵。
NBI方法仅仅考虑用户喜欢的商品,而完全不考虑用户不喜欢的商品,这可能会丢失一些信息。NBI方法的一个重要优点是:它不依赖于任何控制参数,因此不需要调参。另外,这里提出的
NBI推荐算法只是一个粗糙的框架,很多细节尚未详细的探索。例如,顶点的初始配置可以采取更复杂的形式:即它给不同
degree的顶点 分配不同的资源,这可能会比原始的分配产生更好的推荐效果。也可以考虑动态的资源分配过程,这会导致类似于标签传播算法的迭代式推荐算法。虽然这样的算法需要更长的
CPU时间,但是可以提供更准确的预测。定义 为用户的平均
degree, 为object的平均degree,则有:MemoryBased CF的平均计算复杂度为: 。- 第一项来自于用户之间的相似度计算: 对用户、每对用户平均 个
object。 - 第二项来自于预测得分:每个用户平均需要使用 个相似用户(必须在目标
object上有收藏行为)根据相似度(计算复杂度为 )的加权和,一共 个用户。
假设 (它就是二部图中边的数量),则整体计算复杂度为 。
- 第一项来自于用户之间的相似度计算: 对用户、每对用户平均 个
NBI的计算复杂度为: ,其中 为用户degree分布的二阶矩(二阶矩为随机变量平方的期望)。第一项为权重矩阵的计算,第二项为最终资源分布的计算。很明显有 ,因此计算复杂度为 。
在很多推荐系统中,用户数通常比
object数大得多,因此NBI运行速度比MemoryBased CF快得多。另外NBI存储权重矩阵需要 的空间,而MemoryBased CF存储相似度矩阵需要 的空间。因此NBI能够在准确性、时间复杂度、空间复杂度上超越MemoryBased CF。
但是在某些推荐系统中(如书签共享网络),object 数(书签数量)远远大于用户数量,因此 MemoryBased CF 可能更加适用。
6.2 实验
数据集:
Movielens数据集,包含1682部电影和943个用户,通过评分构成了带权二部图。评分从1到5分同五个等级。我们预处理数据集:如果评分大于等于
3分,我们认为用户喜欢该电影。原始数据集包含 个评分,有85.25%的评分大于等于3分,因此我们预处理后的无权二部图包含85250条无权边。注意:这种预处理方式仅保留用户评分较高的边,会丢失大量信息。
我们将所有的边拆分为训练集和测试集,其中训练集包含
90%的边、测试集包含10%的边。注意:训练集和测试集都包含全部的顶点。评估方式:对于任意一个用户 :
我们首先获取他/她尚未收藏的电影集合 ,然后根据
NBI计算到的资源对这些电影降序排列。然后对于测试集中的每条边 ,我们评估 位于有序的、未收藏列表中的位置。
如:假设 有
1500个未收藏的电影,假设测试集存在边 且电影 在 中的排名是第30名(从1开始计数),则我们说 的位置为top 30/1500,记作:由于测试集中的边实际上都是用户收藏的,因此一个好的算法应该产生一个很小的 值。
我们在预处理的
MovieLens数据集上比较了GRM、CF(即MemoryBasedCF)、NBI算法,所有测试样本的 结果的平均值为:
GRM = 0.139, CF =0.120, NBI=0.106。可以看到NBI是其中表现最好的。假设用户 的推荐列表长度为 ,它给出了算法得到的
top L个未收藏的电影。对于测试集中的每条边 ,如果 在该列表中,则我们就说算法命中了。定义命中的测试样本占所有测试样本的比例为命中率。对于给定的 ,命中率越高越好。如果 大于用户所有未收藏的电影数,则推荐列表就是这些全量未收藏的电影。显然,命中率随着 的增加单调增加,上限为
1。下图给出了不同算法的命中率: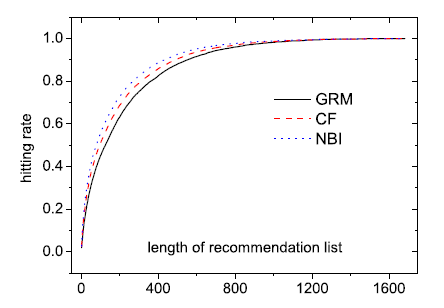
一些典型长度的命中率如下表:
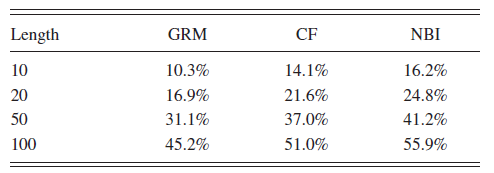
可以看到:命中率表现为
NBI > CF > GRM。因此实验表明NBI的性能显著优于GRM和CF,有力地证明了我们方法的有效性。
七、Implicit Feedback CF[2008]
随着电商越来越受欢迎,一个重要的挑战是帮助用户对提供的各种产品
product进行分类,从而轻松地找到用户喜欢的产品。解决这一挑战的工具之一是推荐系统。最近推荐系统吸引了很多关注。推荐系统为用户提供个性化的产品或服务推荐,希望满足用户独特的品味和需求。这些系统背后的技术基于分析profiling用户和产品,并找到如何将用户和产品进行关联。从广义上讲,推荐系统基于两种不同的策略(或者这两种策略的组合):content-based方法:content-based方法为每个用户或每个产品创建一个画像来刻画其特性nature。例如,电影画像可以包含电影类型、演员、票房排行等属性;用户画像可以包含人口统计信息等。我们可以通过用户画像和
item画像进行匹配从而执行基于内容的推荐。然而,基于内容的策略需要收集一些外部信息(这些外部信息用于构建画像),这些外部信息可能难以获取或者根本无法获取。CF-based方法:协同过滤Collaborative Filtering: CF方法仅依赖于用户历史行为,而无需创建显式的画像。协同过滤这一术语是由第一个推荐系统Tapestry创造的。协同过滤分析用户之间的关系和产品之间的相互依赖性,从而识别新的
user-item关联。例如,一些CF系统识别倾向于评分相似的item pair、或者具有相似评分/相似购买历史的志趣相投的用户,从而推断user-item之间的未知关系。唯一需要的信息是用户历史行为,这可能是用户历史的交易、或者历史评分。CF-based方法的一个主要吸引力在于它是无领域domain free的,但是可以解决数据中通常难以捕获、且很难分析的数据面data aspect。虽然CF-based方法通常比content-based方法更准确,但是它会遇到冷启动问题cold start problem,因为CF-based方法无法解决系统中的新产品(而content-based方法可以处理新产品)。
推荐系统依赖于不同类型的输入。
- 最方便的是高质量的显式反馈
explicit feedback,其中包括用户对产品兴趣的显式输入。例如,Netflix收集电影的星级评分,TiVo用户通过点击thumbs-up/down按钮来表明用户对电视节目的偏好。然而,显式反馈并不总是可用的。 - 数量最多的是隐式反馈
implicit feedback数据,这些隐式反馈数据包括:用户的购买历史、浏览历史、搜索历史、甚至鼠标移动历史等等。推荐器recommender可以从丰富的隐式反馈中推断用户偏好,通过观察用户行为间接地反映用户的意见opinion。例如,购买了同一作者的多本书的用户可能喜欢该作者。
推荐领域的绝大多数文献都专注于处理显式反馈,可能是因为使用这种纯净信息
pure information的便利性。然而,在许多实际情况下,推荐系统更多的需要处理隐式反馈数据,因为可能用户不愿意显式给出评分、或者系统的局限性导致无法收集显式的反馈。在隐式模型中,一旦用户同意系统收集并使用隐式数据,用户就不需要额外的显式反馈(如评分)。论文
《Collaborative Filtering for Implicit Feedback Datasets》对处理隐式反馈的算法进行了探索。这些探索反映了作者构建电视节目推荐引擎时取得的一些主要经验教训和发展。该推荐场景的setup阻止作者主动收集用户的显式反馈,因此该系统完全基于隐式反馈 -- 分析匿名用户的观看习惯。识别隐式反馈的
unique特性至关重要,因为这些特性阻止了直接应用显式反馈算法。下面给出了隐式反馈数据的主要特点:没有负反馈:通过观察用户的行为我们可以推断出用户可能会喜欢的
item,但是难以推断出用户不喜欢的item。例如:没有观看某个节目的用户之所以未观看该节目,可能是因为用户不喜欢这个节目、也可能是用户不知道有这个节目的存在、或者在同一时刻存在用户更喜欢的节目导致用户无法同时观看两个节目。在显式反馈中用户可以直接告诉我们:他们喜欢和不喜欢的item。因此,这种基本的不对称性(即只知喜欢、不知不喜欢)在显式反馈中不存在。这有一些含义。例如,显式推荐器
recommender倾向于关注收集到的信息(观察到的已评分的那些user-item pair),这些信息提供了用户偏好的平衡图balanced picture。因此,剩余的user-item pair关系(这些剩余的pair占比很高)被视为缺失数据missing data,并从分析中省略。这对于隐式反馈是不可能的,因为只关注收集到的隐式反馈会给我们留下正反馈positive feedback,极大地扭曲了完整的用户偏好。因此,在隐式反馈中解决缺失数据也很重要,这是预期会发现大多数负反馈的地方。包含大量噪音:当跟踪用户行为时,我们只能猜测他们的偏好和真实的动机。例如,我们可能会观察用户的购买行为,但这并不一定代表用户对
item的postive评价。该item可能作为礼物来购买,而不是自己使用,因此购买不等于自己喜欢(而是接受礼物的人喜欢);也可能购买的时候用户并不了解产品,使用一段时间后对产品很失望。例如,我们可能会发现用户一直在观看某个节目,但是事实上用户可能在睡觉,只是电视机一直开着而已。这意味着隐式反馈数据中,不仅没有negative数据,postive数据也是不可靠的。显式反馈的数值代表偏好
preference,隐式反馈的数值表示置信度confidence:基于显式反馈的系统可以让用户表达自己的喜好程度,如:评分从1(完全不喜欢)到5(非常喜欢)。而基于隐式反馈的数值描述了行为的频次,如:用户观看某个节目的时长、用户购买某个item的次数。较大的值并不表示较高的偏好。如,用户最喜欢的电影可能就看过一次,但是有些用户喜欢程度一般的电影可能就看了几次(陪朋友一起看)。但是隐式反馈的数值绝对有价值,因为它告诉我们有关某种观察结果的置信度
confidence。单次事件的发生可能是由于和用户偏好无关的偶然因素引起,但是重复事件的发生一定可以反应用户的某种意图。隐式反馈推荐的评估需要采取合适的指标:传统的显式反馈推荐中,我们为每个
user-item预测一个评分,然后通过明确的指标(如均方误差MSE)来衡量预测的准确性。但是在隐式反馈推荐中,我们必须考虑到item是否可用、item之间的竞争、重复反馈等。例如,在电视节目推荐的过程中,如何评估那些看过多次的节目? 如何评估播放时段重叠的两个节目?(因为用户无法在同一时刻观看两个节目)。
给定用户 和
item,我们称 为观测值observation。- 对于显式反馈数据, 代表用户 对
item的偏好评分,其中:评分越高代表越喜欢、评分越低代表越不喜欢。 - 对于隐式反馈数据, 代表用户的行为频次。例如 可以表示用户 购买产品 的次数、或者用户 在网页 上花费的时长。在电视推荐案例中, 表示用户 完整观看节目 的次数。例如, 表示用户观看了
70%的节目,而对于观看了两遍节目的用户则设置 。
对于绝大多数
user-item,显式评分都是未知的,因此基于显式反馈数据的推荐算法使用相对较少的已知评分数据,忽略missing data数据。但是在隐式反馈数据中,所有的user-item的行为次数都是已知的:要么发生了行为,即 ;要么未发生行为,即 ,这表示零购买记录或者零观看时长。- 对于显式反馈数据, 代表用户 对
相关工作:
Neighborhood Model:CF最常见的方法是基于邻域的模型。它的原始形式是User-Based的,根据志趣相投的用户的评分来预估未知评分。后来,Item-Based的方法开始流行,它们使用同一个用户对相似item的评分来预估未知评分。由于Item-Based CF有更好的可扩展性、更高的准确性,因此在大多数情况下更受欢迎。此外,Item-Based CF更适合解释预测背后的原因,这是因为用户熟悉他们以前喜欢的item,但是通常不认识那些据称是志趣相投的用户。大多数
Item-Based CF方法的核心是item之间的相似度,其中 表示item和 的相似度。通常,相似度是基于Pearson相关系数。我们的目标是预测用户 对目标item未观察到的值 。使用相似度,我们识别出 评分过的所有item中与item最相似的 个item。这组 个邻居由 来表示。预估的 为邻居评分的加权均值:但是基于显式反馈数据的
Item-Based CF难以应用到隐式反馈数据中,有两个原因:- 在隐式反馈数据中, 取值范围很广,取值相差很大(最小可为零,最大为万级甚至十万级)。相比之下显式反馈数据中的 取值在固定的几个评分
level,并且相差不大。 - 尚不清楚如何计算隐式反馈数据的相似度。
《Item-based top-N recommendation algorithms》对如何使用具有隐式反馈的Item-Based CF方法进行了很好的讨论。所有
Item-Based CF方法在隐式反馈方面都有一个缺点:它们无法灵活地区分用户偏好、以及我们对这些偏好的信心。- 在隐式反馈数据中, 取值范围很广,取值相差很大(最小可为零,最大为万级甚至十万级)。相比之下显式反馈数据中的 取值在固定的几个评分
潜在因子模型
Latent Factor Model:潜在因子模型是协同过滤的替代方法,它的目标是揭示观测值的潜在特征。这些模型包括:pLSA、神经网络、LDA。这里我们集中讨论观测矩阵的SVD分解:每个用户 对应一个用户因子向量 ,每个item对应一个item因子向量 , 为潜在因子的数量。最终预测结果为两个向量的内积:比较复杂的部分是参数估计。最近应用于显式反馈数据集的很多工作建议仅直接对观察到的评分进行建模,同时通过适当的正则化来避免过拟合,即:
其中:
- 为数据集中存在观测值的部分(剔除
mising data)。 - 为用户因子矩阵,每一行代表一个用户的因子向量; 为
item因子矩阵,每一行代表一个item的因子向量。 - 为正则化系数。
本质上这是将用户和
item同时映射到公共的潜在因子空间common latent factor space。模型参数通常通过随机梯度下降来学习。正如在最大的可用数据集
Netflix数据集上报告的结果一样,上述模型往往优于neighborhood model。在这项工作中,我们将借鉴这种方法来处理隐式反馈数据集,这需要对模型公式和优化技术进行修改。
- 为数据集中存在观测值的部分(剔除
7.1 模型
7.1.1 模型
定义二元变量 来指示用户 是否喜欢
item:即:如果用户 购买了
item( ),则认为用户 喜欢item;如果用户 从未购买item( ),则认为用户 不喜欢item。但是我们的结论和置信度水平confidence level有关。由于隐式数据的特点, 表示非常低的置信度:用户对
item没有任何行为,可能是因为除了用户不喜欢它之外的很多其它原因,如:用户可能压根不知道该item的存在、或者由于价格太高或者已经购买过所以没有购买。另外,用户在
item上的行为()可能是和是否喜欢无关的因素造成的。如:用户观看某个节目,可能仅仅因为他/她停留在之前喜欢看的节目的频道上;用户购买某个商品,可能仅仅作为礼物购买,尽管他/她不需要或者不喜欢这个商品。我们认为:随着 的增长,越能够表明用户确实喜欢该商品。因此我们引入一组变量 用于表明 的置信度水平。 的一个合理选择是:
其中:
超参数 为置信度增长率,通过实验表明 可以得到一个很好的结果。
常数
1是为了对所有的 取值范围都能得到一个非零的置信度。因此 对所有的 都有最小的置信度
1,并且随着观察到更多的证据,则对 的置信度相应增加。
假设每个用户 对应一个用户因子向量 ,每个
item对应一个item因子向量 , 为潜在因子的数量。我们建模用户偏好为两个向量的内积:然后通过最小化代价函数来求解参数:
这类似于显式反馈数据中的矩阵分解技术,但是这里有两个重要区别:
- 需要考虑置信度 。
- 需要考虑所有的
user-item,而不仅仅是观测数据对应的user-item。
7.1.2 优化
注意到代价函数中包含 项,其中 为用户量、 为
item量。对于大型数据集 可以轻松达到数十亿。由于计算规模太大,因此大多数直接优化技术(如随机梯度下降)不适用。这里我们提出了一种替代的高效优化算法。
对于显式反馈数据集,代价函数包含的项为观测值的数量,它远远小于 。
观察到:当用户因子向量或者
item因子向量固定时,代价函数变成二次函数,因此可以轻松计算全局最小值。这就是交替最小二乘alternating-least-square:ALS的优化过程。在
ALS过程中,我们需要交替重新计算用户因子向量、item因子向量,并且保证每一步都可以降低代价函数。ALS可以应用于显式反馈数据,其中计算在观测数据上进行。 但是在隐式反馈数据上,计算在所有user-item上进行,这导致计算规模的急剧增长。我们可以利用代数结构来解决该问题,从而得到一个scalable的优化方法。第一步是重新计算所有的用户因子向量。
在重新计算用户因子向量之前,我们首先计算矩阵 ,其计算复杂度为 。
对于每个用户 ,定义一个对角矩阵 ,它给出了用户 在每个
item的置信度水平;定义向量 ,它给出了用户 在每个item上的偏好。通过对代价函数求偏导,并令偏导为零来最小化代价函数,我们得到新的 为:
一个计算瓶颈是 ,它的计算复杂度为 。考虑所有的 个用户,则计算复杂度高达 。
考虑到 。
- 和 无关,并且已经预计算好了。
- 对于 ,注意到 仅有 个非零元素, 为 的元素个数,通常有 。因此其计算复杂度为 。
由于 仅包含 个非零元素,因此 也仅仅包含 个非零元素。因此重新计算重新计算 的计算复杂度为 。其中:
- 令 ,计算 的计算复杂度为
- 令 ,计算 的计算复杂度为 。虽然存在更高效的矩阵求逆算法,但是对于较小的 值(在几百以内),差距可能不大。
- 计算 的计算复杂度为 。
考虑所有的 个用户,则算法的计算复杂度为 ,其中 为观测到的所有非零 的数量: 。可以看到:计算复杂度为观测值规模 的线性函数。这里 的典型大小在
20~200。
第二步是重新计算所有的
item因子向量。首先计算矩阵 ,其计算复杂度为 。
对于每个
item,定义一个对角矩阵 ,它给出了每个用户在item上的置信度水平;定义向量 ,它给出了每个用户在item上的偏好。通过最小化代价函数,我们得到新的
item因子向量为:采用同样的优化技巧,我们计算
item因子向量的计算复杂度为 。
我们交替优化用户因子向量和
item因子向量,直到模型收敛,典型的交替次数为10次。整个优化过程的计算复杂度是输入数据规模 的线性函数。
在得到用户因子向量、
item因子向量之后,对于用户 我们预估他/她对item的偏好:并选择 最大的 个
item作为推荐结果。
7.1.3 讨论
事实上我们可以修改偏好 和 的关系,如增加阈值 ,使得:
类似地,我们也可以修改置信度 和 的关系:
但是不管它们如何变化,其核心都是解决隐式反馈数据独有的特点:
- 将原始观测 转换为刻画两个不同意义的、独立的变量:偏好 、置信水平 。这可以更好的反应隐式反馈数据的性质,并对提高模型预测效果至关重要。
- 通过利用变量的代数结构,在线性时间内解决所有可能的 个
user-item组合。
一个好的推荐应该有良好的可解释性,即:一段描述文字给出为什么向用户推荐该
item。这有助于提高用户对推荐系统的信任,以及提高用户对推荐结果给出良好的反馈。另外,这也是调试推荐系统、跟踪badcase的宝贵手段。Item-Based CF推荐结果的解释很简单,因为推荐是根据用户历史行为来直接推断出来的。但是潜在因子模型的可解释性比较困难,因此模型使用用户因子向量、item因子向量从而阻断了推荐结果和用户历史行为之间的直接关联。在这里,我们的
ALS优化方法提供了一种新的方法来解释潜在因子模型。考虑到:因此用户 对
item的偏好为:定义 ,它可以认为是与用户 相关的一个权重矩阵。因此以用户 的角度来看,
item和 的相似性为:因此用户 对于
item预估的偏好为:考虑到:
因此有:
因此我们的潜在因子模型简化为一个加权历史行为( )的线性模型,权重为
item-item相似性。在预算 的过程中,每个历史行为都作为一个独立的项,因此我们可以分离每一项的贡献。贡献最大的历史行为可以作为推荐的主要解释。
此外,我们还可以进一步将每个历史行为 的贡献拆分为两个独立的部分:
- 与用户 有关、与 无关的重要性 。
- 与用户 有关、与 也相关的相似性 。注意:
item之间的相似性取决于具体的用户,这反映了一个事实:相同的一对item在不同的用户看来具有不同的相似性。
这和
Item-Based CF模型非常相似,因此可以将我们的模型视为Item-Based CF,其中item相似性根据ALS优化过程计算得到。为了得到可解释性,我们需要求解 从而方便计算 。类似上述讨论,我们预计算 ,最终计算复杂度为 。
7.2 实验
数据集:来自数字电视服务
digital tv service采集的数据,包含大约30万个机顶盒上的数据。数据收集取得了用户协议并遵守隐私政策,数据都是匿名的,未包含任何个人身份信息。我们收集用户的频道切换事件,事件包含机顶盒切换到的频道以及时间戳。训练数据集包含四个星期的数据,其中覆盖大约
17000个不同的电视节目。训练集中给出每个用户 和节目 的 值,它表示用户 观看节目 的次数。我们根据用户观看节目的时长除以节目的时长从而得到观看次数,因此 。如果用户 对节目 发生了多次观看事件,则直接将多次观看事件聚合到一个结果中。最终训练数据集包含约3200万非零 。我们将这四周的下一周数据来构造测试集,测试集的数据通过上标来区分,如 。然后我们使用前四周数据来训练模型,并预测接下来一周用户观看的内容。
之所以选择四周训练是来自于一个实验研究:
周期太短则训练样本不足,模型得不到充分训练从而使得模型效果很差。
由于电视时间表受到季节性变化,因此周期太长会使得我们的训练集和测试集的节目分布不一致,预测没有多少意义。
尽管我们发现我们的模型足够强大,可以避免受到季节性因素的影响。
数据预处理:
看电视的特点是:用户倾向于每周重复观看同样的节目。对于用户来说,推荐从未观看的节目可能更有价值。因此我们从测试数据集中删除用户曾经在训练期间观看过的节目。
为了使得测试结果更为准确,我们令:
我们认为:用户对一个节目观看时间不足
50%并不足以表明用户喜欢该节目。经过这两步预处理,测试集包含大约
200万个非零的 值。用户反复观看相同节目的趋势使得 在很大范围内变化。虽然大量的 位于
0~1之间,但是存在部分 达到数百(如,某些用户每天用DVD记录同一档节目)。因此对于训练集,我们使用对数缩放置信度:其中 。
我们观察到一种特别的现象:用户观看同一个频道连续几个小时。事实上可能只有该频道最初的节目是用户感兴趣的,后面的节目并不感兴趣。只是由于用户做其它事情(或者睡觉),导致电视只是连续播发而已。我们称这一现象为动量效应,因动量效应而观看的节目实际上并不会反应用户的真实偏好。
为克服动量效应的影响,我们在频道切换事件发生之后降低该频道第二个以及后续节目的权重(对原始 打折)。即,对于频道切换事件之后的第 个节目,其权重为:
通过实验发现 的效果较好,并且意义很直观:
- 频道切换之后的第二个节目的 减半。
- 频道切换之后的第五个节目的 降低了
99%。
评估方式:我们为每个用户生成一个有序的推荐列表,列表中的节目按照从预估最喜欢到最不喜欢来排序,然后向用户推荐。
但是要意识到:我们并没有可靠的反馈来表明用户不喜欢那些节目。用户不看节目可能源自多种原因,而不一定是不喜欢。因此基于
precision的指标(它需要知道正样本、负样本)不是很合适,因为它需要知道哪些节目是用户不喜欢的。另一方面,由于用户观看节目表示确实喜欢它,因此召回率recall(它只需要知道正样本)在这里更合适。我们用 来表示为用户 推荐的有序节目列表中,节目 的
percentile rank。- 意味着节目 被预测为用户 最喜欢的,因此位于列表中所有节目之前。
- 意味着节目 被预测为用户 最不喜欢的节目,因此位于列表的末尾。
考虑到每个用户的推荐列表长度不同,因此这里我们使用
percentile rank而不是绝对的排名。这使得不同用户的推荐效果之间可以进行比较。我们的评估指标是测试集的归一化
percentile rank:该指标越低则表明实际观看的节目的
rank更接近推荐列表的头部,因此该指标越低越好。我们对 越大的测试样本给予更大的权重。注意:对于随机预测 接近于
50%,因此 表明算法优于随机预测。Baseline模型:热度模型:根据节目的热度排序,然后推荐其中最热门的。这种方法的效果出人意料的好。
ItemBased CF模型:使用余弦相似度,并将所有item作为邻居(而不是一小部分item)的ItemBased CF模型。我们探索了ItemBased CF的多个变种,并发现这种方式的效果最好。注意:这里使用的
ItemBased CF配置仅适用于隐式反馈数据,对于显式反馈数据我们建议使用不同的配置。
我们考察了不同数量的因子,其中 从
10到200, 在测试集上的结果如下图所示。- 仅根据热门推荐我们就可以达到 ,
Itembased CF可以达到 ,远低于随机预测的 。 - 我们的模型效果最好。另外可以看到,随着 的增加模型效果不断改善,最终当 时 。因此,我们建议在资源限制内使用尽可能大的 。
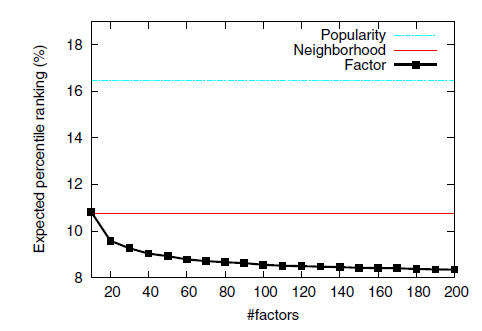
- 仅根据热门推荐我们就可以达到 ,
我们继续考察在测试集上的推荐质量,这里我们固定 。我们考察测试集中观看的节目在我们推荐列表中
percentile rank的分布。对于理想的模型,这些观看的节目应该具有很低的percentile rank。可以看到:
我们推荐的
top 1%节目中,能够召回27%用户真正观看的节目。这远远超过了baseline的表现。如果我们不删除测试集中用户已经在训练期间曾经观看的节目,则结果更好,我们用黑色虚线表示。预测用户是否观看节目,要比预测用户是否首次观看节目容易得多。
尽管向用户推荐一个他/她曾经看过的节目不是那么
exciting,但是它确实有价值。这是在向用户提醒他们不要错过喜欢的节目。事实上仅仅通过检索用户以前观看的节目就可以轻松完成该提醒任务。
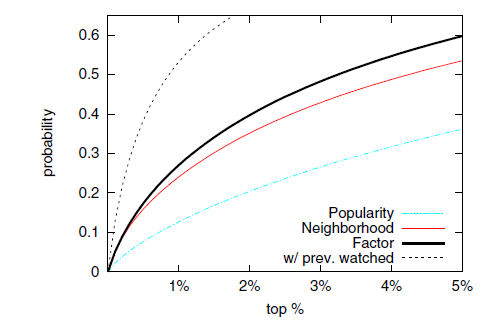
我们研究了是否采用 的模型的效果。
我们首先一个直接使用 的模型,因此我们最小化代价函数:
注意:这是
SVD算法的一个正则化版本,也是协同过滤采用的方法。如果没有正则化( ),则效果非常差,甚至比热门推荐的效果都要差。
当采用正则化时效果得到改善,当 时效果最好。虽然此时效果超过热门推荐,但是还是比
UserBased CF效果更差。此时: 时 ; 时 。
这种较差的推荐质量是可以预期的,正如前面所述,直接将隐式反馈数据中的 作为偏好是不合适的。
然后我们考察仅仅使用 的模型,因此我们最小化代价函数:
其中 。
这个模型的效果要优于上一个模型: 时 ; 时 。其效果略好于
ItemBased CF,但是比完整的模型效果差得多。对于完整模型: 时 ; 时 。这表明我们在二元偏好模型中增加置信水平的重要性。
现在我们考察 的完整模型在不同类型的节目和用户上的表现。
训练数据中不同节目的热度(观看人次)明显不同。有的节目很受人欢迎,而另一些节目则非常冷门。
我们基于递增的热度(从训练集中统计得到)将测试集中的
postive观测结果划分为15个桶,其中第一个桶表示最冷门的节目,第15个桶表示最热门的节目。然后我们评估每个桶中节目在测试集中的性能。可以看到(蓝色曲线),我们的模型效果在不同的桶之间存在巨大的
gap:预测热门节目更为容易,而预测冷门节目更加困难。因此某种意义上,我们的模型倾向于安全地推荐更为热门的节目。另一方面,我们根据用户的观看时长(根据训练集统计)也将用户划分为多个桶。第一个桶表示用户几乎没有观看记录,最后一个桶表示观看时间最长的用户。然后我们评估每个桶中用户在测试集中的性能。
可以看到(红色曲线):除了第一个桶之外,其它所有桶的用户的预测性能都非常相似。这有些出乎我们的意料,因为在显式反馈数据集中我们的经验是:随着我们收集用户相关的信息越多,预测质量会得到显著提高。为什么用户收看的时间越多,效果反而得不到提升?一个可能的解释是:因为这些账户背后对应的不是同一个人,可能家里有多个人使用同一个账户来观看同一台电视,这导致该账号的观看时间会更长。
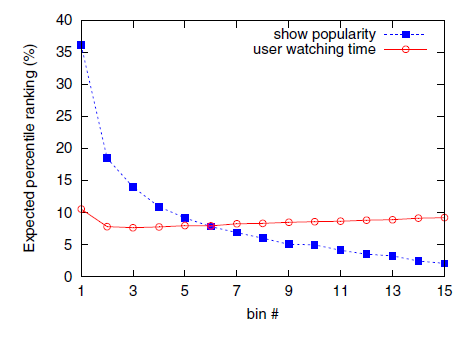
最后我们分析推荐的可解释性。下表给出了我们针对同一个用户的三个推荐(粗体表示),以及每个推荐最相关的
5个用户曾经观看过的节目。第一列都是真人秀、第二列都是漫画、第三列都是医学纪录片。这些符合常识的解释可以帮助用户理解为什么推荐某些节目。另外,我们还报告
top 5相似的、曾经观看过的节目(即 )对该推荐的打分 的贡献。可以看到贡献最大的5个节目占比从35%到40%,这表明用户看过的很多其它节目也有较大的贡献。
总结:在这项工作中,我们研究了隐式反馈数据集的协同过滤,这是一种非常常见的情况。我们的主要发现之一是隐式用户观察值应该转换为两个量:偏好
preference和置信度confidence。这种preference-confidence划分与广泛研究的显式反馈数据集没有相似之处,但是在隐式反馈分析中起到关键作用。我们提供了一种直接解决
preference-confidence范式的潜在因子算法。与显式反馈数据集不同,我们将所有user-item偏好作为输入,包括那些没有任何观察值的输入。这是至关重要的,因为仅仅观察值的输入天生地就偏向于positive preference,因此无法很好地反映用户的个人画像。然而,将所有user-item值作为模型的输入会引发严重的可扩展性问题。我们通过利用模型的代数结构来解决这个问题,这将导致算法与输入规模线性缩放,从而可以解决全量user-item输入而无需求助于任何降采样。该算法的一个有趣特性是:算法允许向用户解释推荐理由,这在潜在因子模型中很少见。这是通过该算法与著名的ItemBased CF产生了一个令人惊讶的、有洞察的链接来实现的。我们的算法作为大规模电视推荐系统被实施和测试。我们的方法力求在隐式反馈数据集的独特属性和计算可扩展性之间找到适当的平衡。我们目前正在探索以增加计算复杂度为代价来提高准确性的改进。例如,模型中我们以统一的置信度水平
confidence level处理所有zero preference的user-item pair。由于绝大多数pair与zero preference相关,因此该决定节省了大量计算资源。但是,可以仔细地分析从而将这些zero preference拆分为不同的置信度水平。在我们的电视推荐案例中,用户没有观看节目这一事实可能意味着用户不知道该节目,或者还有另一个更喜欢的节目同时播放,或者用户根本不感兴趣。对于每一种原因我们可以采取不同的置信度水平。 这将导致我们对模型进行另一种可能的扩展--添加一个动态时间变量来解决用户在特定时间看电视的趋势。同样地,我们想建模某些节目类型在一天中不同时间更受欢迎。这是正在进行的研究的一部分,其中的主要挑战似乎是如何在模型中引入额外的灵活性,同时保持其良好的计算可扩展性。最后,推荐系统的目的是努力将用户指向他们可能没有购买或消费的
item。如果不进行深入的用户研究或调查,则很难评估该指标。在我们的案例中,我们简单的通过在测试集中删除训练集中用户已经观看的节目,从而实现该目标的评估。
八、PMF[2008]
低维因子模型
low-dimensional factor model是最流行的协同过滤方法之一,该模型背后的思想是:用户偏好是由少量未观察到的因子unobserved factor决定的。在线性因子模型
linear factor model中,我们可以通过采用线性加权item因子向量item factor vector来建模用户的偏好,权重为特定于用户的系数user-specific coefficient。例如,对于 个用户、 部电影,则偏好矩阵 由用户系数矩阵 和item因子矩阵 的乘积给出:训练这个模型等价于:在给定损失函数的意义下,寻找 的最佳 秩近似。
通常可以采用奇异值分解
Singular Value Decomposition: SVD寻找到最小平方和损失下的低秩近似。但是, 大多数真实数据集都是非常稀疏的,即 中大量数据是缺失的,此时损失函数仅仅考虑矩阵 的观察值observed entry(即非缺失值)。这种看起来非常微小的修改将导致难以解决的非凸优化问题,从而使得标准的SVD无法解决。《Maximum-margin matrix factorization》方法并非约束矩阵分解的秩,而是对 和 增加范数正则化。但是这会导致需要求解一个稀疏的半正定矩阵,这对于包含数百万个观察值的数据集是不可行的。上面提到的许多协同过滤算法已经应用于
Netflix Prize数据集上建模用户评分。然而,由于以下两个原因,这些方法都不是很成功:- 首先,除了基于矩阵分解的方法之外,上述方法都无法很好地扩展到大型数据集。
- 其次,大多数现有算法都难以为评分很少的用户做出准确的预测。
协同过滤任务的一种常见的数据预处理方法为:删除评分数量低于指定阈值的用户(如评分数量低于
3)。事实上,评分数量很低的用户的推荐难度更大。因此大多数协同过滤算法在MovieLens, EachMovie等标准数据集上效果非常好,因为这些标准数据集剔除了最困难的情况。例如,Netflix数据集非常不平衡,低频用户评分少于5部电影、高频用户评分超过10000部电影。由于Netflix Prize数据集规模之大、不活跃用户之多, 使得它成为协同过滤算法更现实的benchmark数据集。论文
《Probabilistic Matrix Factorization》提出了概率矩阵分解Probabilistic Matrix Factorization:PMF模型,该模型可以轻松的处理非常大的数据,并且也可以处理评分数量稀少的用户。实验表示PMF模型在Netflix数据集上表现良好。PMF模型的计算复杂度和观察次数成线性,因此具有很好的scalability。并且模型在大型、非常稀疏、非常不平衡的数据集(例如Netflix数据集)上表现良好。- 论文进一步扩展了
PMF模型,从而得到能够自动调整超参数的自适应PMF,并展示如何自动控制模型容量。 - 最后,论文引入
PMF模型的约束版本,该变种基于以下假设:对相似item集合评分的用户可能具有相似的偏好。该假设得到的模型对于评分数量很少的用户能产生更好的推荐结果。
当多个
PMF模型的预测与受限玻尔兹曼机模型的预测线性组合时,论文实现了0.8861的RMSE,这比Netflix自己的系统得分好了将近7%。
8.1 模型
8.1.1 PMF
假设有 个用户、 个
item。假设评分为:从整数 , 为用户 对item的评分,其中对于缺失值我们定义 。定义 为用户因子矩阵,第 列 代表用户 的因子向量。定义 为
item因子矩阵,第 列 代表item的因子向量。定义观测值的条件分布为:
其中:
为均值为 、方差为 高斯分布的概率密度函数,其中 为噪音方差。
为示性函数:
进一步的,我们假设用户因子向量和
item因子向量采用零均值的球形高斯先验分布spherical Gaussian:其中 为先验方差。
则后验概率分布的对数为:
其中 为不依赖于任何参数的常数。
当固定 时,最大化后验分布等价于最小化带正则化项的误差平方和:
其中: 为正则化系数; 为
Frobenius范数。我们可以通过对 进行梯度下降从而求解参数 。
PMF模型可以视为SVD模型的概率扩展。当我们能够观察到所有的user-item评分时,在先验方差 无穷大的限制下,PMF模型退化为SVD模型。事实上,上述推导过程存在一个问题:预测结果 容易超出评分范围。因此
PMF使用logistic函数来限定评分范围:在训练过程中我们将评分 使用函数 映射到区间
[0,1];在预测过程中我们使用 将结果映射回评分。可以通过最速下降法优化
PMF的目标函数,其计算复杂度和观察值的规模成线性关系。在
Matlab实现中,当 时我们可以在不到一个小时内训练整个Netflix数据集的1个epoch。训练
PMF模型的高效率来自于:仅找到模型参数和超参数的点估计,而不是推断他们的完整后验分布。如果我们采用完全贝叶斯方法,则计算上更为昂贵,但是初步结果强烈表明:对PMF模型的完全贝叶斯处理将导致预测准确性的显著提高。
8.1.2 自适应 PMF
模型容量对于
PMF模型的泛化至关重要。超参数 可以控制模型容量,当 足够大时
PMF模型能够逼近任何给定的矩阵。因此,控制PMF模型容量的最简单直接的方法是限制 的大小。但是,当数据集不平衡时(即观察值的规模在不同的行或者列之间显著不同),则该方法行不通。因为无论怎么选择 ,总会对于某些因子向量过高、对另外一些因子向量过低。因为某些因子可能需要大容量来包含足够多的信息,而另一些因子只需要很小的容量来包含少量信息。
另一种方式是采用正则化来控制模型容量,如 。
选择合适正则化系数,最简单直接的方法是进行超参数搜索,如
GridSearch, RandomSearch。这种方式的主要缺点是计算量太大:除了训练最终的模型之外,我们必须训练多个模型来确定最佳的正则化系数。
这里我们提出了一个自动确定
PMF正则化系数的变种,称作自适应PMF。这种方式可以自动选择合适的正则化系数,并且不会显著影响模型训练时间。其基本原理是:引入超参数的先验分布,并最大化模型在参数 和超参数 上的对数后验分布:其中:
是和任何参数无关的常数。
分别为针对用户因子向量 、
item因子向量的先验分布的超参数。它们本身也是一个随机变量,分别服从分布 。当先验分布 为球形高斯分布时,这会得到一个常规模型并能够自动选择 和 。假设 和 为均匀分布(其实 就是 , 就是 ), 此时有:
其中 为常数。
根据偏导数为零,则我们得到超参数的闭式解:
当先验分布 为高斯分布时,如果 和 固定,则可以求解最佳超参数的闭式解。因此,我们可以在训练期间通过交替求解超参数、优化参数。
- 在求解超参数时固定参数 ,此时超参数有闭式解。
- 在求解优化参数时固定超参数,此时通过梯度下降法求解。
当先验分布是混合高斯分布时,我们可以通过执行单步
EM算法来更新超参数(参数的更新仍然是通过梯度下降法)。
8.1.3 约束 PMF
上述
PMF模型存在一个问题:对于评分非常少的用户,他们的用户因子向量将趋近于先验均值(或者说用户因子向量的均值),因此这些用户的预测评分将接近所有评分的均值。这里我们提出了一种约束用户因子向量的方法,该方法对于评分稀少的用户具有很强的效果。
定义 为一个潜在的相似约束矩阵
latent similarity constraint matrix,定义用户 的因子向量为:其中 为矩阵 的第 列。
直观的看:
- 矩阵 的第 列捕获了:如果用户对第 个
item评分,则用户因子先验均值受到的影响。因此,看过相同(或者相似)电影的用户,其用户因子向量将具有相似的先验分布。如果两个用户评分的item集合相同,则他们具有相同的用户因子向量。 - 可以视为这种先验分布的一个偏移量。
事实上,这里假设有 和 都作为
item因子向量,但是 用于表达用户、 用于表达item。下图中,左图为无约束
PMF,此时先验均值固定为零,因此 ;右图为约束PMF,此时先验分布非零。(注意下图为原始论文, 的范围与我们这里表述的不一致)。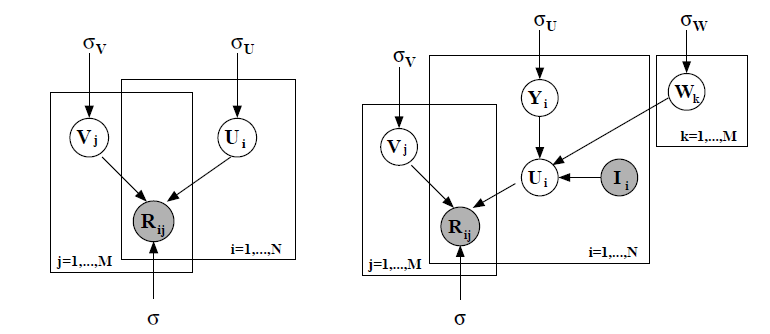
- 矩阵 的第 列捕获了:如果用户对第 个
我们定义观察值的条件分布为:
假设 服从一个零均值的球形高斯分布:
则有:最大化对数后验概率,等价于最小化带正则化项的误差平方和:
其中:
我们可以对 执行梯度下降来求解参数 ,训练时间和观察值的数量成线性比例。
实验表明,这种方式的效果比简单的无约束
PMF模型效果好得多,尤其是针对评分数量稀少的用户。
8.2 实验
数据集:
Netflix数据集。该数据集收集了1998年10月到2005年12月之间Netflix网站上用户的所有评分数据。训练数据集包含来自
480189个 随机选择的匿名用户的100480507个评分,涉及17770个电影标题。作为训练数据的一部分,Netflix还提供了包含1408395个评分的验证数据集。除了训练集和验证集之外,
Netflix还提供了一个包含2817131个user-movie pair的测试集,这些pair是从训练集中部分用户的最新评分中选择的。Netflix给出了测试集中一半数据的评分,另一半数据的评分是未给出的。研究人员需要向官方上传另一半(未知部分)数据的评分结果,并由官方返回该部分的RMSE指标。这种方式是为了防止模型对测试集过拟合。作为Baseline,Netflix给出了他们自己模型在测试集上的RMSE指标为0.9514。为了进一步了解不同算法的性能,我们通过随机选择
50000个用户和1850部电影,从而创建了一个更小、难度更高的数据集。这个小数据集包含1082982个训练数据、10462个验证数据,其中训练数据中超过50%的用户的评分数量少于10。
训练配置:为加快训练速度我们采用随机梯度下降,其中
batch size = 100000。为选择合适的学习率和动量,我们在各种超参数组合上进行实验,最终选择学习率为
0.005、动量为0.9,因为这组配置对所有维度 都工作良好。
8.2.1 自适应 PMF
为评估自适应
PMF模型的性能,我们选择 。选择如此小的维度是为了证明:即使特征维度很低,类似的SVD模型仍然可能过拟合,并且通过自动正则化会有一些性能的提升。模型:
SVD模型:该模型的损失函数为观察值误差的平方和,其中没有采用任何形式的正则化。固定正则化系数的
PMF模型:模型损失函数为观察值误差的平方和,带固定系数的正则化。其中PMF1的正则化系数为 ,PMF2的正则化系数为 。自适应
PMF模型:模型损失函数为观察值误差的平方和,带正则化。其中PMFA1的 和 为球形高斯先验分布;PMFA2的 和 为对角协方差的高斯先验分布。在这种情况下,自适应先验具有可调整的均值。
先验参数和噪音协方差每隔
10到100个 的更新才更新一次。
我们在完整的
Netflix训练集上训练模型,然后评估模型在Netflix验证集上的效果。可以看到:SVD模型的表现几乎和具有适当正则化的PMF模型(PMF2)效果一样好,但是SVD模型在训练结束之前陷入严重过拟合。PMF1模型虽然没有陷入过拟合,但是它仅达到0.9430的RMSE,明显欠拟合。自适应
PMF明显优于其它模型。这里没有给出PMFA2(RMSE为0.9204),因为它的曲线和PMFA1几乎相同(RMSE为0.9197)。这表明:通过自适应先验来自动正则化在实践中效果良好。我们比较了 (左图)和 (右图),结果表明:使用自适应先验而导致性能的差距,可能随着因子维度 的增加而增加。
另外,尽管对角协方差矩阵的使用并未比球形协方差矩阵的版本有明显改善,但是对角协方差可能非常适合自适应
PMF训练的greedy算法,在该算法中模型每次学习一个因子向量。
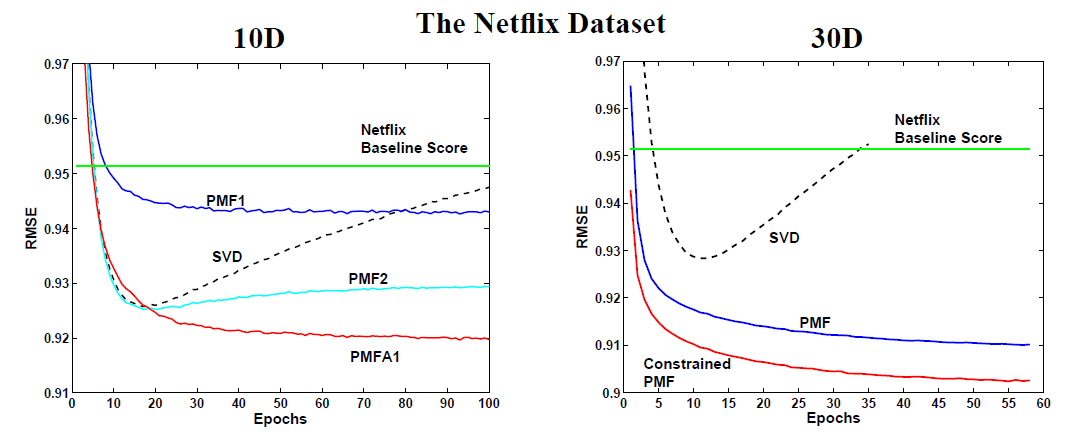
8.2.2 约束PMF
在约束
PMF上我们使用30维特征,因为 可以使得验证集获得最佳效果。对于PMF和约束PMF我们设置正则化参数为 。我们在完整的
Toy训练集(我们构造的小数据集)上训练模型,然后评估模型在Toy验证集上的效果。可以看到:SVD模型明显的陷入了过拟合。约束
PMF模型相比无约束PMF模型具有更好的性能,并且收敛速度更快。右图给出了不同评分数量的用户的评估结果。可以看到:
- 对于训练集中评分数量少于
5个的一组用户,PMF模型性能与均值算法(电影 在所有用户上评分的均值作为用户 对电影 评分的预测结果)的性能相同。 - 约束
PMF模型在评分较少的用户上的性能要好得多。 - 随着评分数量的增加,
PMF和约束PMF的性能相差无几。
- 对于训练集中评分数量少于
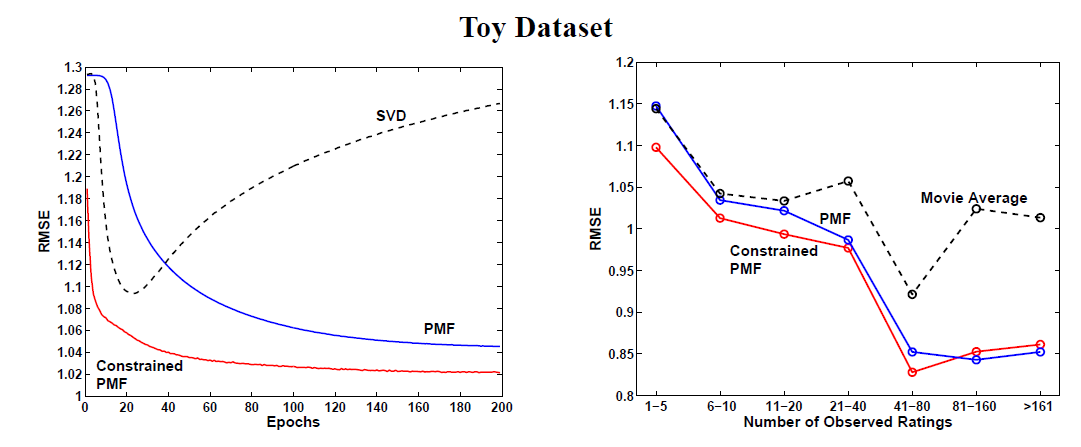
约束
PMF模型的另一个有趣的性质是:即使我们仅知道用户曾经评分的电影,但是不知道评分的值,模型也能够利用该信息从而得到更好的效果。对于用户 如果已知它对电影 产生评分,即使不知道评分大小, 它对于 也是有贡献:对于我们的
toy数据集,我们随机增加了额外的50000个用户来训练,并丢弃这些用户的实际评分。最终约束PMF方法在验证集上的RMSE为1.0510,而简单平均算法的RMSE为1.0726。这表明:仅了解用户评分的电影而不知道具体评分,仍然可以帮助我们更好的建模用户的偏好。
约束
PMF在整个Netflix数据集上的表现与Toy数据集的结果相似。对于PMF和约束PMF我们设置正则化参数为 。结果表明:
SVD模型的RMSE为0.9280,大约10个epoch开始过拟合。约束
PMF模型对于评分数量很少的用户可以有更好的泛化,其中训练集中超过10%的用户其评分不足20个;随着评分数量的增加,PMF和约束PMF性能趋同。考虑到
Netflix数据还有一个额外的信息来源:Netflix会告诉我们测试集中还有哪些user-movie pair,因此我们还知道一个信息:用户已经评分、但是不知道评分大小的电影。约束
PMF可以很容易考虑该信息,如右图所示,这将进一步提高模型的性能。
当我们将
PMF、自适应PMF、约束PMF线性组合在一起时,我们在测试集上达到了0.8970的RMSE,这比Netflix官方Baseline 0.9514提高了将近6%。
九、SVD++[2008]
现代消费者被各种选择所淹没。电商和内容提供商提供种类繁多的产品,有前所未有的机会来满足用户各种特殊的需求和口味。为消费者匹配最合适的产品并非易事,但却是提高用户满意度和忠诚度的关键。这强调了推荐系统的重要性,它提供个性化的产品推荐来满足用户口味。
Amazon、谷歌、Netflix、TiVo、雅虎等互联网领头羊越来越多地采用此类推荐系统。推荐系统通常基于协同过滤
Collaborating Filtering:CF,它仅依赖于用户过去的行为(如,用户历史交易记录或评分记录)而无需创建显式的用户画像或item画像。值得注意的是:一方面,协同过滤不依赖于任何领域知识domain knowledge,也不需要大量的画像数据;另一方面,协同过滤可以发现复杂的或者意料之外的行为模式,这些模型很难基于用户画像或item画像来刻画。 因此,协同过滤在过去十年中引起了广泛的关注,取得了重大进展,并被一些成功的商业系统(如Amazon、TiVo、Netflix)采用。CF系统需要比较本质上不同的两种对象:user和item。主要有两类方法可以执行这种比较,这两种方法构成了CF的两个主要流派discipline:邻域方法
neighborhood approach:邻域方法的核心是计算item之间的相似性或者user之间的相似性。ItemBased CF利用同一个用户的、和item相似的item的评分来评估该用户对item的评分。从某种意义上讲,该方法将user视为一组已评分item的集合,从而将user映射到item空间。这样我们不需要将user和item进行比较,而是直接将item和item进行比较。潜在因子模型
latent factor model:诸如奇异值分解SVD之类的潜在因子模型通过将user和item分别映射到同一个潜在因子空间,从而使得它们可以直接进行比较。潜在因子模型试图根据用户反馈来自动推断出用户因子
user factor、item因子item factor, 从而解释评分。例如,当item是电影时,因子可能是某些显著的维度(如:电影流派、是否适合儿童等等),也可能是不显著的维度(如:演员的气质),甚至也可能是完全无法解释的维度。
自
2006年10月Netflix Prize竞赛开始以来,CF领域一直备受关注。Netflix发布了一个包含1亿个电影评分的数据集,并要求学术界开发能够超越其推荐系统Cinematch准确性的算法。论文《Factorization Meets the Neighborhood: a Multifaceted Collaborative Filtering Model》的作者从这次比赛中学到的一个教训是:邻域方法和潜在因子方法解决了数据中不同层次level的结构,因此它们都不是最优的。- 邻域模型在检测局部关系最为有效,它依赖于少数几个重要的邻域关系,从而忽略了用户的其它绝大多数评分。因此该方法无法捕获用户所有评分中包含的全部弱信号。
- 潜在因子模型通常有效地估计与所有
item有关的整体结构。但是它在检测少数紧密相关的item之间的局部强相关性表现不佳,而这恰恰是邻域模型做得最好的地方。
在论文
《Factorization Meets the Neighborhood: a Multifaceted Collaborative Filtering Model》中,作者提出了一个组合模型,该模型同时利用邻域方法和潜在因子方法的优势来提高预测准确性。据作者所知,这是第一次将这两种方法集成到单个模型中。事实上,过去的一些工作认识到结合这些方法的效用。然而,他们建议对因子分解结果进行后处理,而不是同时地考虑邻域信息和因子信息的统一模型。作者从
Netflix Prize竞赛中吸取的另一个教训是:将不同形式的用户输入集成到模型中的重要性。推荐系统依赖于不同类型的输入。- 最方便的、最高质量的是用户显式反馈,其中包括用户对
item的显式输入。例如,Netflix收集电影的星级评分,TiVo用户通过点击thumbs-up/down按钮来表明他们对电视节目的偏好。 - 但是显式反馈并非始终可以获取,因此推荐系统可以从更丰富的隐式反馈中推断用户的偏好。这些隐式反馈通过观察用户行为来间接反应偏好,反馈类型包括:历史购买记录、历史浏览记录、历史搜索记录甚至历史鼠标移动记录。例如,购买了同一作者的多本书的用户可能喜欢该作者。
论文主要关注提供显式反馈的情况,但是也认识到隐式反馈的重要性:可以解释没有提供足够显式反馈的用户。因此,论文的模型同时集成了显式反馈和隐式反馈。
最终,论文的方法同时利用邻域方法和潜在因子方法、同时利用了用户的显式反馈和隐式反馈。
我们根据
Netflix数据对匿名用户的超过1亿个评分评估了算法。为了保持和其他人发布的结果可比,我们采用Netflix设置的一些标准:采用测试集RMSE来评估模型效果。Netflix提供的测试集包含了140万个近期的评分,另外Netflix还提供了另外的140万个近期评分作为验证集(也称作Probe Set)。注意:
Netflix给出的测试集和验证集包含了很多低频用户,这些用户的评分数量很少。这使得任务难度非常大。在某种程度上,这也代表了CF系统的真实需求:对老用户预测最新的评分,并且公平地对待所有用户,而不仅仅是只考虑高频用户。Netflix数据集是正在进行的Netflix Prize竞赛的一部分,其中benchmark是Netflix专属系统Cinematch,它在测试集上的RMSE为0.9514。大奖将颁发给测试集RMSE低于0.8563(改进10%)的团队。在本文中我们将测试集RMSE降低到0.887左右的水平,这比之前在该数据集上发布的结果要好。
9.1 模型
令 表示用户 在
item上的评分,评分越高表示用户 越喜欢item;令 表示模型预估的用户 对item的评分。定义 为评分已知的
user-item pair对;定义 为所有用户集合, 为所有item集合;定义 为对item评分的用户集合, 为用户 评分的item集合:通常绝大多数评分是未知的,即 占比非常低,其中如,
Netflix数据有99%的评分缺失。为了避免模型对稀疏数据的过拟合,我们通常采用正则化技术。正则化系数由常数 等等来控制,正则化系数越大则正则化越强。
9.1.1 前置知识
a. Baseline Model
最简单的预估模型为: ,其中 为所有
user-item的均值:但是考虑到用户效应或者
item效应:某些用户相对于其它用户始终会给一个较高的评分、某些item相对于其它item始终会收到一个较高的评分,那么我们的Baseline模型为:其中: 为用户 对均值的偏差、 为
item对均值的偏差,它们都是模型的参数。例如:假设所有用户的电影评分为 。假设用户
A的评分比较苛刻,他的评分比平均水平低 分;假设电影I比较热门,它收到的评分比平均水平高0.5。则用户A对电影I的评分预测为: 分。Baseline模型的损失函数为带正则化的平方误差:其中 为所有参数。
第一项为模型预估的平方误差,第二项为正则化项。该最优化问题为简单的凸优化,可以通过最小二乘法求解。
b. 邻域模型
协同过滤方法最常用的模型是邻域模型
neighborhood model。几乎所有早期的协同过滤系统都是
UserBased CF,这种面向用户的方法基于兴趣相同的用户的评分来预估。后来基于
ItemBased CF更为流行,它使用同一个用户在相似item上的评分来预估。ItemBased CF具有更好的可扩展性、准确性,另外它的可解释性也更好:因为用户熟悉他们以前喜欢过的item, 但是用户不认识那些 ”兴趣相投“ 的其它用户。我们这里重点介绍
ItemBased CF,但是也可以通过切换user和item的角色来开发一个UserBased CF版本。
大多数
ItemBased CF方法的核心是计算item之间的相似性。通常采用基于Pearson相关系数 作为相似性的度量,它衡量了所有用户在item和item上评分的相似性。考虑到评分是稀疏的,因此很多
item之间仅共享非常少的几个评分用户,而相关系数的计算仅仅在这些很少的、共同的评分用户上进行。因此,当共享的评分用户越少,计算到的相关系数越不可靠。即:共同评分用户的规模越大,则相关系数越可靠。因此我们调整相关系数为:其中 为
item和item之间共同评分的用户数量, 为平滑系数,典型的值为100。给定
item和用户 ,我们定义用户 已经评分过的、和item最相似的top k个item为 。用户 对
item的预估评分看作是这些相似item的评分的加权均值,同时考虑了user效应和item效应:这里 表示
item权重不仅和item、 的相似度有关,还和用户 有关。因为这种形式的邻域模型直观且易于实现,因此该方法非常流行。但是我们有一些不同的看法:
- 首先,该方法并没有正式的数学模型来证明其有效性。
- 其次,在计算
item和 的相似性时,仅仅考虑这两个item的评分,而完全忽略了所有其它的item。这种方式计算得到的相似性是否合适,该问题还无法证明。 - 最后,上式中的权重 满足 。实际上当用户 的行为非常稀疏时,即使 和 相似度很低时,其权重 仍然可能较大。
因此我们提出了一个更准确的邻域模型:给定邻域集合 ,我们计算插值权重
interpolation weight,从而实现预测:完整的说明参考论文
《Scalable Collaborative Filtering with Jointly Derived Neighborhood Interpolation Weights》。这种插值权重存在一个严重的问题:模型容量空间太大,很容易过拟合。插值权重相当于自动学习
item权重 ,参数规模 ,而数据量仅有 。
c. 潜在因子模型
潜在因子模型是协同过滤的另一种方法,其目标是找出揭示观测评分的潜在因子,典型的模型为
pLSA、神经网络、LDA。我们将集中讨论user-item评分矩阵上的SVD分解相关的模型。近年来,由于
SVD模型具有准确性、可扩展性等优点,因此广受欢迎。对于每个用户 ,SVD模型关联一个用户因子 ; 对于每个item,SVD模型关联一个item因子 。我们通过因子之间的内积来执行预测: 。在信息检索领域已经可以很好地利用
SVD来识别潜在的语义因子,但是在协同过滤领域由于大量的评分缺失,这会给SVD的应用带来困难:- 首先,当矩阵不全时,传统的
SVD是未定义的。 - 其次,如果仅针对稀疏的、已经评分的部分进行拟合,则模型容易陷入过拟合。
可以对已评分部分进行拟合,同时采用正则化技术来缓解过拟合:
其中:
- 其中 为所有参数。
- 第一项为模型预估的平方误差,第二项为正则化项。
然后基于梯度下降来求解该问题。
- 首先,当矩阵不全时,传统的
《Improving Regularized Singular Value Decomposition for Collaborative Filtering》提出了NSVD模型,该模型避免显式地参数化每个用户的参数,而是根据他们已经评分的item来对用户进行建模。因此,每个item关联两个因子向量 和 。用户 的representation为:因此有:
在本文中,我们将扩展该方法。
d. 隐式反馈
如前所述,我们的模型融合了显式反馈和隐式反馈。对于诸如
Netflix之类的数据,最自然的隐式反馈是电影租借的历史记录。这些数据可以间接反馈用户的偏好,但是这类数据我们无法取到。另一种不太明显的隐式数据为:用户是否对电影进行评分。即,可以通过用户是否评分来侧面反应了他们的偏好。这使得评分矩阵退化为
0-1二元矩阵,其中1代表已经评分、0代表尚未评分。这种二元隐式反馈数据并不像其它类型的隐式反馈数据那样独立和数据量大,但是我们发现它确实可以显著提高预测准确性。一个原因是:它可以从测试数据集中获得隐式反馈。我们的模型不限于具体的隐式数据类型。为了保持通用性,每个用户 和两组
item关联:一组item用 表示,它表示显式反馈的item集合;另一组item用 表示,它表示隐式反馈的item集合。
9.1.2 新的邻域模型
前面介绍的邻域模型使用了特定于具体用户的权重 或者插值权重 。为了进行全局优化,我们希望抛弃此类
user-specific权重,转而使用全局权重。定义
item相对于item的权重为 ,模型的初始版本为:其中 为模型参数,它从训练数据中学习得到。
与 相比,我们这里有两个区别:
- 权重 和用户 无关。
- 考虑的
item集合为 ,而不是 。
通常邻域模型中的权重代表了未知评分与已知评分相关的插值系数,但是这里我们采用不同的观点:权重 代表了和
baseline的偏移量,残差 代表了这些偏移量施加的系数。即我们在 对 的评分baseline上增加了 :对于两个相关的item,我们预计 会很高;进一步地,如果 在 上的评分超过预期,即 很大,则我们预计 对 的评分会更高。这一观点带来几个改进:
首先我们可以使用隐式反馈,它提供了另一种方式来了解用户偏好。因此我们修改模型为:
类似于 ,参数 也被视作添加到
baseline预估上的偏移量。对于两个
item,用于 在item上的隐式偏好使得我们可以通过 来影响 。将权重视为全局偏移量,而不是
user-specific的插值系数,可以降低评分缺失的影响,即:用户的偏好不仅取决于他已评分的item,还取决于他未评分的item。可以理解为 是跨用户全局共享的,它是
item之间的固有属性,和具体用户无关(即使用户对item未评分)。在邻域模型中,因为 是通过对 进行插值得到,所以 和 都是兼容的,即它们都采用: 来计算得到。
我们这里不再使用插值的解释,因此可以解耦 和 的定义。一个更通用的做法是:
其中 为其它方法,如潜在因子模型预估的结果。这里我们仍然选择 ,但是我们选择 为常数:它直接根据均值 、用户 在已知评分上的偏移量、
item在已知评分上的偏移量直接计算得到。即:其中 为参数, 为常数。
当且方案的一个特点是:对于显式评分很多(即 很大)、或者隐式反馈很多 (即 很大)的用户,预估评分更大。通常这也是推荐系统预期的:
对于更活跃的用户(显式反馈更多或隐式反馈更多),我们掌握的信息更多,则我们的推荐更激进,我们预估的评分比
baseline有一个很大的偏差。对于不活跃的用户(显式反馈更多或隐式反馈更少),我们掌握的信息非常少,则我们的推荐更保守,这种情况下我们希望保持接近
baseline的安全估计。但是我们的经验表明,模型在某种程度上过分强调了活跃用户和不活跃用户。因此我们通过调整预测模型,从而缓解这个现象:
进一步的,我们可以通过移除不太相似的
item从而减少参数来降低模型复杂度。定义 为和item最相似的 个item(通过相似度 来选取) ,定义 。我们认为:最具影响力的权重与item最相关的item关联,则有:当 时,模型退化到上一个版本。对于一个较小的 值,它可以显著降低参数数量。
新的邻域模型的一个主要设计目标是促进有效的全局优化过程,这是旧模型所欠缺的。我们最小化损失函数:
该问题是一个凸优化问题,可以通过最小二乘求解器来求解。但是,我们发现基于梯度下降的方法来求解时,求解速度更快。
令 为预估的误差 ,对于 中的每个评分 ,我们更新参数为:
其中:
- 超参数 为学习率、 为正则化系数,他们都是通过交叉验证得到的超参数。在
Netflix数据集中我们使用 。 - 超参数 控制邻域大小。经验表明:增加 总是有助于提高测试集结果的准确性。因此, 的选择反应了模型准确性和计算成本之间的折衷。
- 超参数 为学习率、 为正则化系数,他们都是通过交叉验证得到的超参数。在
我们在
Netflix数据集上对新的邻域模型进行评估,评估结果如下图所示。我们将它和前面提到的两个邻域模型进行对比:- 首先是最基础、应用最广泛的邻域模型: ,我们称之为
CorNgbr。在图中用绿色直线表示。 - 然后是基于插值权重的邻域模型: ,我们称之为
WgtNgbr。在图中用青色直线表示。
对这两个模型我们尝试选择最佳的参数和邻域大小,对于
CorNgbr最佳邻域大小为20,对于WgtNgbr最佳邻域大小为50,注意:CorNgbr、WgtNgbr的邻域和这里的 值无关,因为它们是不同的邻域概念,因此二者的曲线都是直线。我们新邻域模型用粉色曲线表示,它给出了不同 值下的效果。黄色曲线为新邻域模型但是不使用隐式反馈数据的情况。结论:
- 随着 的增加,模型准确性会单调增加。注意:
Netflix仅包含17770部电影,因此 等价于 。 - 当没有隐式反馈数据时,模型的准确性会显著下降,并且这种降幅随着 的增加而增加。这证明了隐式反馈数据的价值。
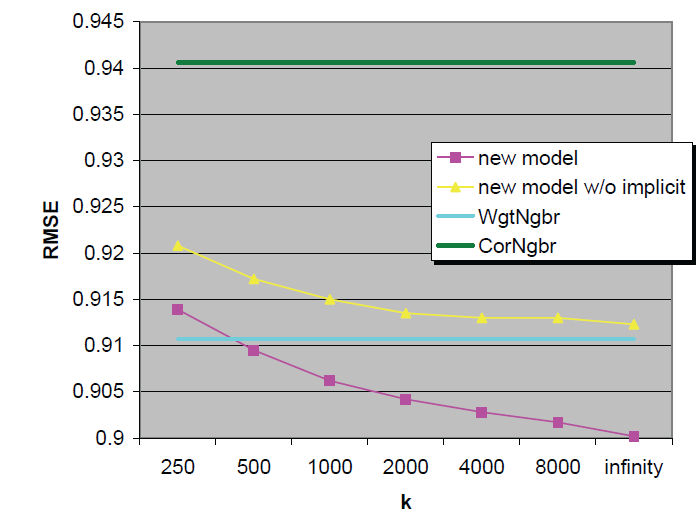
新模型的预处理时间如下所示,可以看到预处理时间随着 的增加而增加。
注意:预处理需要计算常数 、 ,以及每个
item的邻域 。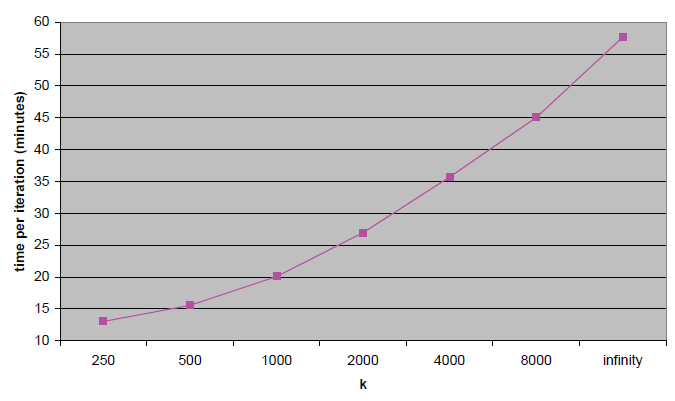
- 首先是最基础、应用最广泛的邻域模型: ,我们称之为
9.1.3 新的潜在因子模型
a. Asymmetric-SVD
基础的
SVD模型为:我们希望通过考虑隐式信息来扩展该模型,我们认为每个
item关联三个因子向量: ,其中用户 的表达通过该用户显式反馈的item因子向量 和隐式反馈的item因子向量 来表示,即:因此模型调整为:
这个新模型我们命名为非对称
SVD(Asymmetric-SVD),它具有以下优点:模型参数更少:通常用户数量远大于
item数量,因此用item参数代替user参数可以显著降低模型复杂度。新用户友好:由于非对称
SVD不存在用户因子向量,因此我们可以在新用户产生行为之后立即处理,无需重新训练模型并得到新用户的因子向量。同样地,我们也可以利用老用户产生的最新行为来即使更新老用户的
representation。注意:我们必须学习新
item的参数。这符合我们的预期:通常系统需要向新用户提供实时的推荐,而对于新item则允许等待一段时间来才被处理。另外,ItemBased CF也表现出同样的、user和item之间的不对称性。可解释性:用户期待推荐系统给出推荐的理由,而不是一个黑箱推荐。这不仅丰富了用户体验,还鼓励用户和系统进行交互,从而获得更多的有效反馈并提高长期预测准确性。
诸如
SVD之类的潜在因子模型在可解释性上面临困难,因为这些模型通过用户因子向量这个中间结果来抽象用户,该中间结果和用户历史行为分离,使得无法得到可解释性。非对称
SVD并没有对用户使用任何抽象,而是直接使用用户过去的行为信息,因此我们可以通过最相关的行为来解释预测结果。这一点和ItemBased CF相同。集成隐式反馈数据:通过集成隐式反馈数据,非对称
SVD可以进一步提高预测准确性。对于隐式反馈数据很多、显式反馈数据很少的用户来讲,隐式反馈数据非常重要。
非对称
SVD的最小化损失函数:其中超参数 为正则化系数。
我们通过随机梯度下降来求解该最优化问题,在
Netflix数据集上我们使用学习率 ,正则化系数 。由于我们使用
item的因子向量来代替用户因子向量,因此会损失一些预测准确性。问题是,非对称SVD带来的好处是否值得我们放弃一些预测准确性? 我们在Netflix数据集上对此进行评估,评估指标为RMSE。可以看到:非对称SVD的效果实际上略好于SVD。一个可能的原因是:非对称SVD考虑了隐式反馈。这意味着我们可以在不牺牲预测准确性的条件下享受非对称SVD提供的好处。如前所述,我们在
Netlifx数据集上实际上并没有太多的独立的隐式反馈数据,因此我们预期在具有更多隐式反馈数据集上,非对称SVD模型能带来进一步的改善。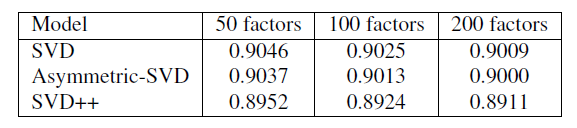
b. SVD++
如果仅仅融合隐式反馈数据,则我们可以得到更准确的结果。我们认为每个
item关联两个因子向量: ,每个用户 关联一个因子向量 。最终用户 通过 来建模。因此SVD模型调整为:我们称这个模型为
SVD++,其中参数可以通过梯度下降来最小化损失函数得到。SVD++没有非对称SVD涉及的诸多好处,这是因为SVD++采用了用户因子向量来抽象每个用户。但是上表可以看到,就预测准确性而言SVD++显然更具有优势。
9.1.4 整合模型
潜在因子模型和邻域模型可以很好的互补,这里我们将邻域模型和
SVD++模型整合在一起,最终得到模型:从某种意义上讲,该公式提供了三层模型:
第一层: 描述了
item和user的一般属性,未涉及任何user-item交互行为。例如:这一层可能认为电影 “《指环王三》” 是高评分的、用户 “张三” 倾向于打低分。
第二层: 提供了用户和
item之间的交互。例如:根据 “张三” 偏好 “西幻” 主题的电影,我们可以预测 “张三” 对 “《指环王三》” 的评分会很高。
第三层:邻域评分有助于进一步的精细化调整。
例如:虽然 ”张三“ 偏好 ”西幻“ 主题的电影, 但是他对 ”《指环王一》、《指环王二》“ 的评分都很低, 那么我们预计他对 ”《指环王三》“ 的评分也会比较低。
我们可以随机梯度下降来最小化损失函数来求解模型的参数。定义 ,对于 我们更新参数为:
其中 为正则化系数、 为学习率。我们对不同的部分采用不同的正则化系数和不同的学习率。
我们在
Netflix数据集上评估整合模型,超参数为:我们使用系数为
0.9的学习率衰减。我们设置邻域 。与单纯的邻域模型不同,这里增加 并没有好处:虽然增加 可以覆盖更多的全局信息,但是这些全局信息已经被
SVD部分充分捕获了。训练过程大约迭代了
30次就收敛,下表给出了不同因子大小对应的模型性能和训练时间。可以看到:通过将邻域模型和潜在因子模型集合,并从隐式反馈中提取信息,模型效果比前面所有方法的效果都要更好。
可以考虑将邻域模型和非对称
SVD模型结合,从而在提升单个模型的准确性的同时仍然得到可解释性等优秀性质,虽然这比邻域模型结合SVD ++的准确性稍低。
9.2 实验
目前为止我们按照常规做法:通过
RMSE指标来评估模型在Netflix数据集上的准确性。事实上,不同模型在Netflix测试集上的RMSE集中在一个很小的区间。即使是最简单的均值预估:这种方式给出的是非个性化的热门电影推荐,最终测试
RMSE为1.053。相比之下,Netflix Cinematch模型可以达到0.9514、我们的模型可以达到0.8870。一个关键问题是:如果
RMSE降低10%,那么用户体验能提升多少?这对于推荐系统准确性指标的合理性至关重要。我们通过研究降低RMSE对推荐结果的影响来阐明该问题。推荐系统的一个常见场景是提供
top K推荐,即系统需要向用户推荐排名top K的item。我们研究降低RMSE对top K推荐质量的影响。在
Netflix数据集中,除了测试集之外还有一个验证集。我们将验证集中的5星评分作为用户感兴趣的电影,我们的目标是找到这些 “用户感兴趣” 电影在我们推荐列表中的排名。对于验证集中的每个用户 评分为5分的电影 ,我们额外随机挑选1000部电影,然后通过模型预估用户 对这1001部电影的评分。我们根据预估评分进行降序排列,然后观察电影 的排名情况。- 由于这里的
1000部电影是随机选取的,因此可能有小部分电影也是用户 真正感兴趣的,但是大部分电影是用户 不感兴趣的。 - 我们采用
percent rank而不是绝对rank来标识电影 的排名,这是为了使得排名和具体的队列长度无关,从而通用性更强。理想情况下电影 的排名为0%(所有随机电影都在它之后),最坏情况下电影 的排名为100%(所有随机电影都在它之前)。
- 由于这里的
Netflix验证集包含384573个 的user-item评分,对其中每个 “用户感兴趣” 电影我们随机抽取1000个电影然后评估 “用户感兴趣” 电影的排名,最终我们得到了384573个percent rank。然后我们评估这384573个排名的分布。我们比较了五种不同的策略:
- 非个性化的均值预估:使用每个电影的评分均值作为预估结果,我们用
MovieAvg表示。其测试RMSE为1.053。 - 基于相关系数的邻域模型:即传统的
ItemBased CF模型,我们用CorNgbr表示。其测试RMSE为0.9406。 - 基于插值权重
interpolation weight的邻域模型:即采用全局插值权重的邻域模型,我们用WgtNgbr表示。其测试RMSE为0.9107。 SVD潜在因子模型:使用因子数量为100的SVD模型,我们用SVD表示。其测试RMSE为0.9025。- 我们的集成模型:使用因子数量为
100的集成模型,我们用integrated表示。其测试RMSE为0.8870。
我们给出了
384573个排名的累积分布(小于等于rank x的样本的比例)。可以看到:所有方法都超越了非个性化的均值预估, 并且我们的集成方法效果最好。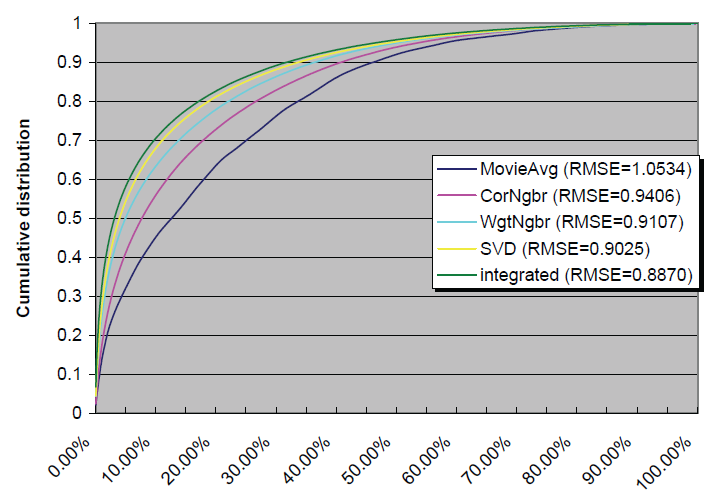
事实上当向用户推荐电影时,我们只会推荐
top K个电影而不是所有的候选电影队列。例如,如果从600部电影中推荐其中的3部,则只有top 0.5%的电影才有机会呈现给用户。从某种意义上说,”用户感兴趣“ 电影排在top 5%、top 20%、top 80%没有任何区别,因为这些位置都没有机会呈现给用户。因此我们重点关注图中 轴的头部,比如top 0%到top 2%,这对应了1000个候选电影中的top 20个电影。如下图所示,这些方法之间存在显著差异:
- 我们的集成方法将”用户感兴趣“ 电影排在第一位(即
top 0%)的概率为0.067,这比MovieAvg高出三倍以上、比CorNgbr高出2.8倍以上,也是WgtNbr和SVD的1.5倍。 - 我们的集成方法将”用户感兴趣“电影排在
top 0.2%的概率为0.157,相比之下其它几种方法的概率要小得多:MovieAvg的概率为0.050、CorNgbr的概率为0.065、WgtNgbr的概率为0.107、SVD的概率为0.115。
实验结果令人振奋和惊讶:
RMSE的微小改进可以带来top K推荐质量的显著提升。另外,我们也从未料到流行的基于相关性邻域模型的性能很差,它并未比非个性化的热门推荐提升很多。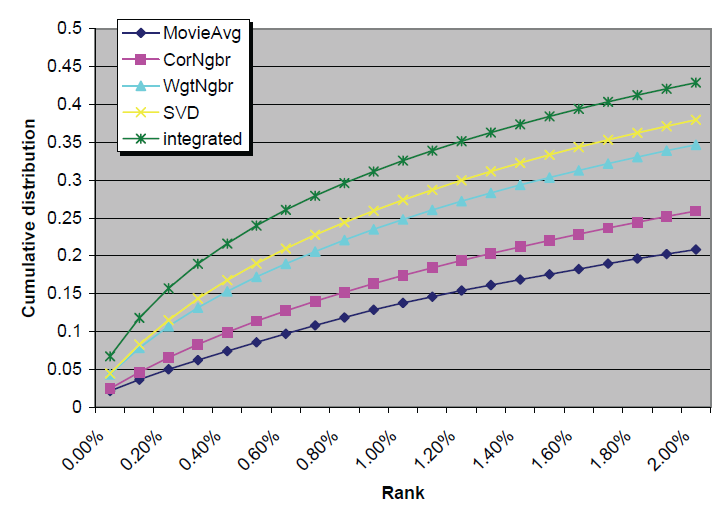
- 非个性化的均值预估:使用每个电影的评分均值作为预估结果,我们用
讨论:在这项工作中,我们提出了对两种最流行的、协同过滤方法的改进:
- 首先,我们提出了一种新的、基于邻域的模型。该模型和以前的邻域方法不同,它基于跨用户全局共享的全局权重。这会在提高预测准确性的同时保持邻域方法的优点,例如:预测的可解释性、无需重新训练即可处理新用户。
- 其次,我们引入了对基于
SVD的潜在因子模型的扩展,通过将隐式反馈集成到模型中来提高准确性。
此外,新的邻域模型使得我们能够首次推导出一个结合了邻域模型和潜在因子模型的集成模型。这有助于提高系统性能,因为邻域模型和潜在因子模型处理不同
level的数据并相互补充。推荐系统的质量有多个维度来刻画,其中包括:准确性、多样性、惊喜度、可解释性、计算效率等。其中一些指标相对容易衡量,如准确性和计算效率,而另一些指标难以量化。我们提出了一种新的方法来衡量
top K推荐的效果,这对于大多数推荐系统来说至关重要。值得注意的是,评估top K推荐显著加剧了模型之间的差异,这种差异超出了传统的准确性指标上的差异。这项工作一个主要见解是:推高推荐质量取决于成功解决数据的不同方面
aspect。一个主要的例子是使用隐式反馈来扩展模型质量。可以集成进来从而提高预测质量的其它数据方面是内容信息,如用户属性或item属性,或者评分相关的日期(这可能有助于解释用户偏好的漂移shift)。
十、MMMF 扩展[2008]
由于在
Amazon、Apple、Netflix等电商网站中的应用,协同过滤在机器学习社区中受到广泛关注。这类网站通常会向用户提供个性化推荐,推荐质量对整体成功overall success至关重要,因为好的推荐会增加用户购买倾向。然而,推荐正确的item是一项非常困难的任务:有很多item可供选择,并且用户只愿意考虑少量推荐(通常在十个左右)。协同过滤通过从当前用户和其它用户的历史评分中学习当前用户的推荐函数来解决这个问题。已知的数据可以认为是稀疏的评分矩阵 ,其中 为用户数量、 为
item数量, 表示用户 对item的评分。通常评分为五星级别,因此 ,0表示用户尚未对item进行评分。从这个意义上讲,0分比较特殊。论文
《Improving maximum margin matrix factorization》提出了针对Maximum Margin Matrix Factorization:MMMF的扩展方法,包括引入偏置项offset term、自适应正则化、user-item二部图的graph kernel。相关工作:协同过滤的一种常见方法是将根据数据来训练一个因子模型
factor model。例如,通过为数据集中每个用户和item抽取一个因子向量,然后基于user因子向量和item因子向量的内积来预测评分。这些方法背后的基本思想是:用户偏好和item属性都可以通过一组因子来建模。矩阵分解方法的基本思想是用低秩矩阵 来近似原始矩阵 。具体而言,矩阵分解方法的目标是找到这样一个近似矩阵 : 中观测值和 中预测值的平方距离之和最小化。一种可行的做法是使用 的奇异值分解,并仅使用分解过程中获得的一部分向量。在信息检索社区中,这种数值运算通常被称作潜在语义索引
Latent Semantic Indexing: LSI。然而,奇异值分解的方法并不能正确判断 的构成方式。 表示我们没有观察到 的
pair,但是它并不表示用户 不喜欢item。论文《Weighted low-rank approximations》提出了一种替代方法,它是本文所述方法的基础。我们的目标是找到两个矩阵 和 ,使得 逼近 中的观察值,而不是同时近似所有的项。一般而言,找到低秩近似的全局最优解是不现实的:特别是
《Weighted low-rank approximations》提出的用于计算加权分解的方法需要半定规划semi-definite programming,这仅支持数百个最多数千个数据。与最小化秩的目标不同,最大边际矩阵分解Maximum Margin Matrix Factorization: MMMF的目标是最小化 和 的Froebenius范数,从而在各自独立的情况下产生一组凸优化问题,因此可以通过当前的优化技术进行处理。《Rank, trace-norm and max-norm》表明:优化Froebenius范数是优化rank的一个很好的代理。在《Probabilistic matrix factorization》中,作者也提出了基于矩阵分解的类似思想。最近,
《Cofi rank—maximum margin matrix factorization for collaborative ranking》提出扩展通用MMMF框架,从而最小化结构化损失(即ranking loss),而不是已知评分的平方误差sum。关键原因是:协同过滤通常是推荐系统的核心,在用户偏好方面只有未评分item的排序才重要。为了有效优化结构化ranking loss,《Bundle methods for machine learning》使用了一种新的优化技术来最小化归一化折扣累计增益Normalized Discounted Cumulative Gain: NDCG损失。本文贡献:基于上述结果,论文
《Improving maximum margin matrix factorization》对这些MMMF模型进行了扩展。- 在多类保序回归
multiclass ordinal regression中计算梯度的有效方法。 - 为处理用户和
item的异质性,提出user bias和item bias。 - 一种自适应正则化方案,可以处理每个用户不同数量的
item、以及每个item不同数量的用户。 - 类似于
《Probabilistic matrix factorization》和《Unifying collaborative and content-based filtering》的精神,论文提出一个graph kernel从而在推荐图中捕获user-item相似性。作者证明这两种方法本质上是等价的,并且等于推荐图上的graph kernel。
对于这些扩展中的每一个,论文展示了如何将它们集成到
MMMF框架中,使得《Cofi rank—maximum margin matrix factorization for collaborative ranking》中提出的结构化估计仍然可行。- 在多类保序回归
10.1 MMMF
令
user-item评分矩阵为 ,其中 为用户数量、 为item数量、 表示用户 为item的评分。假设每个用户 关联一个用户因子向量 ,每个
item关联一个item因子向量 ,则模型预估用户 对item的评分为: 。令所有用户因子向量构成用户因子矩阵 ,其中第 行表示用户 的用户因子向量。令所有
item因子向量构成item因子矩阵 ,其中第 行表示item的item因子向量。则有: 为模型预估的评分矩阵。我们的目标函数为带正则化的损失函数,其中正则化项为 和 的
F范数:其中: 为损失函数, 为正则化系数。
该最优化问题可以通过
semi-definite reformulation精确求解,但是计算复杂度太高。考虑到固定 时目标函数是 的凸函数、固定 时目标函数是 的凸函数,因此可以通过固定变量来交替优化 和 来求解。原始
MMMF中, 为误差的平方和:其中 表示:如果用户 对
item评分则 ,否则 。这种形式的损失函数无法处理用户粒度的损失。事实上对于单个用户 而言,我们希望能够准确预测用户 感兴趣的
item,对于用户 不感兴趣的item我们不太关心。因此对于用户 ,我们需要根据 和 来评估用户粒度的损失。定义 为用户 的观测评分 , 为用户 的预估评分,论文
Weimer et al. 2008提出了一种逐用户的损失:其中 为逐用户的损失。
现在考虑
ranking损失,它也被称作保序回归分ordinal regression score。假设用户 的所有评分 中,真实评分为 的
item有 个,则有 。假设用户 评分的一对
item,如果满足 且 ,则我们认为预估的排序是正确的,否则我们认为产生了一个单位的损失。因此我们定义损失函数为:
其中:
- 为示性函数:当条件为
true时为1,条件为false为0 - 表示对于用户 而言,混淆了
item和 的顺序的损失。
考虑到这里有 项,因此我们需要归一化使得不同用户的损失可以相互比较。另外,为了使得损失函数可导,我们使用一个
soft-margin损失从而得到一个凸的、可微的损失函数:.
- 为示性函数:当条件为
10.2 MMMF 扩展
10.2.1 bias
当考虑用户
bias和item bias时,我们的模型更新为:其中 : 为用户 的
bias、 为item的bias。在实践过程中,可以简单的将 和 扩展为:
.
10.2.2 自适应正则化
为每个
item(或用户)使用单个统一、固定的正则化参数不是一个很好的选择。例如:- 对于评分数量很少的用户,我们需要一个较大的正则化系数从而缓解过拟合。
- 对于评分数量很多的用户,我们需要一个小得多的正则化系数从而期望充分学习。
同样的,对于评分数量差距很大的
item,它们的正则化也需要区别对待。可以考虑使用基于样本规模的自适应正则化
sample-size adaptive regularization。定义对角矩阵:其中: 表示用户 评分的数量, 为
item评分的数量, 为于平滑系数。论文发现当 时效果最好。最终我们的目标函数为:
其中 为矩阵的迹,它满足 。
实验结果证明:该方法效果是负向的!。
10.2.3 Graph Kernel
目前为止我们忽略了一个非常重要的信息:评分本身不是随机的。如:如果某个用户为 《指环王1》 给了一个很高的评分,那么即使不查看评分矩阵 ,我们猜到该用户大概率也会对 《指环王2》感兴趣。因此,我们希望除了评分矩阵 之外,还能够利用这个结构信息
structural information。定义 ,它定义了关于
user-item二部图的邻接矩阵。我们定义用户 和用户 之间的核函数为:其中 为邻接矩阵的第 行。
我们考虑将用户 邻接的
item的线性组合作为用户 的特征,即使用权重矩阵 进行线性变换,则用户的特征矩阵变为: 。考虑到不同用户评分数量不同,则我们也可以对 进行按行归一化,得到:
可以证明该方法等价于在用户和
item之间定义的二部图上应用graph kernel。最终我们的目标函数为:
这相当于将用户 的
representation分解为两部分:第一部分为原始的
user representation。第二部分为item representation的加权,权重为 (即用户 对item的评分,可以考虑归一化)。这里对item引入了另一个representation矩阵 。
10.5 实验
数据集:
EachMovie和MovieLens数据集。EachMovie数据集包含61265个用户、1623部电影、2811717个评分。MovieLens数据集包含983个用户、1682部电影、10万评分。
评估指标:在所有实验中,我们使用
Normalized Discounted Cumulative Gain:NDCG指标。对于用户 的预估值 ,定义 为这些预估结果的一个排序(排序从
1开始):定义 为真实评分的一个排序:
定义累积增益
Cumulative Gain:CG为:每个推荐结果排名相关性得分累加值。即:其中 表示预估排在第 个位置的
item的真实评分。越大表示预估排名
top k的item的真实评分越越高。但是, 未考虑位置因素的影响,折扣累积增益Discounted Cumulative Gain:DCG在CG的基础上考虑了位置因素:可以看到:
- 预估
top k的item的真实评分越高,则 越大。 - 在这
top k的item中,真实评分越高的item越靠前,则 越大。
考虑到不同用户的真实评分数量不同,为了方便在不同用户之间进行比较,我们对
DCG@k进行归一化,得到NDCG@k指标:当
NDCG@k = 1.0时,意味着用户预估的排名和用户真实排名一致。- 预估
我们有三种实验配置:
弱泛化
weak generalization:我们从每个用户看过的电影中随机挑选10/20/50部电影作为训练集,剩余的user-item评分作为测试集,并在测试集上评估模型的NDCG@10指标。强泛化
strong generalization:我们首先丢弃评分数量低于50的电影,然后筛选评分数量最高的100个用户作为测试集,剩余用户的user-item评分作为训练集。在测试的时候,我们从这
100个测试用户中每个用户随机挑选10/20/50部电影来更新模型,更新过程中已训练好的 固定不动,仅更新 。测试这100个用户的剩余user-item评分作为最后的测试集。该配置用于评估模型在训练时不存在的用户上的表现。
反向弱泛化
inverted weak generalization:注意到弱泛化、强泛化中,测试用户的训练item数量是固定的,因此它们无法展示用户bias的有效性。为了评估用户bias的影响,我们交换了弱泛化配置中的训练集和测试集:从每个用户看过的电影中随机挑选10/20/50部电影作为测试集,剩余的user-item评分作为训练集 。
所有实验中的参数配置:
- 正则化参数都是固定的,没有经过调优。
- 和 维度 固定为
10。 我们考察了 的情况,发现 并未产生明显的性能下降。 - 采用最小平方误差损失函数。
- 每组实验均随机进行十轮,并报告评估结果的均值和方差。
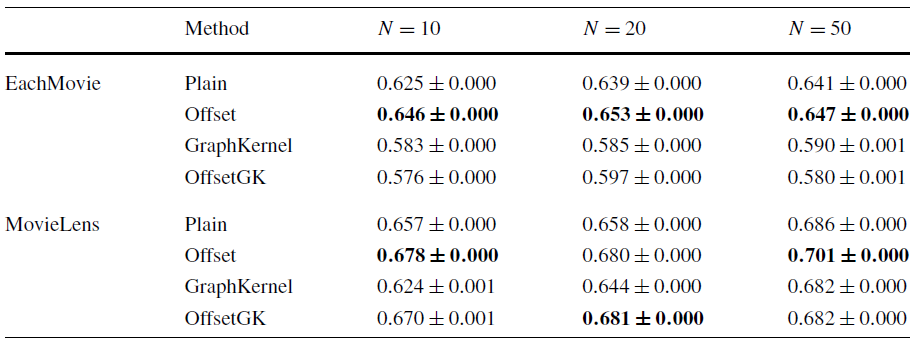
弱泛化的实验结果如下,结论:
- 添加偏移项确实能够提升性能。
- 单独使用
Graph Kernel似乎并未提升性能,可能的原因是并未调整Graph Kernel的超参数。
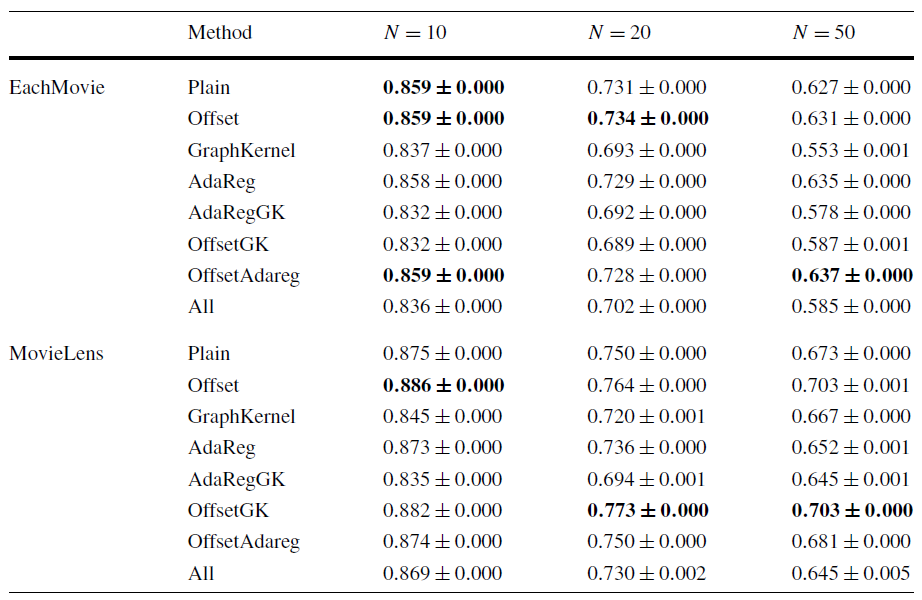
反向弱泛化的实验结果如下,结论:
- 添加偏移项确实能够提升性能。
- 添加偏移项和
Graph Kernel或者自适应正则化配合使用,可以进一步提高性能。
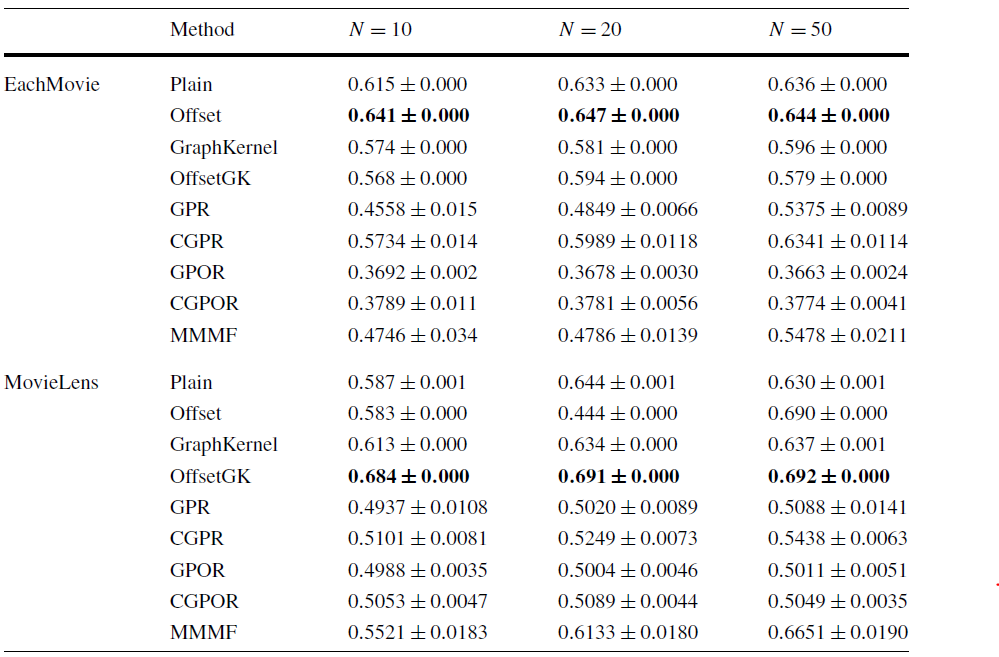
强泛化的实验结果如下。我们将结果与
Gaussian Process Ordinal Regression:GPOR、Gaussian Process Regression:GPR、CPR扩展、CGPOR扩展以及原始的MMMF方法来对比。结论:
对于
Movielens数据集,添加偏移项和Graph Kernel的表现最佳。对于
EachMovie数据集,仅添加偏移项的表现最佳。继续添加Graph Kernel反而效果下降,我们认为这是超参数未调优的原因。在强泛化配置中,我们的方法在这两个数据集上效果都非常好。这是因为:在强泛化阶段,我们的系统为每个新用户解决了一个凸优化问题,从而学习正确的
representation。如果系统在弱泛化阶段为item学到了合理的特征,那么强评估阶段的良好结果是可以预期的。这是我们方法的重要优势:无需重新训练整个模型,就可以为新用户提供快速、准确的模型预估。
每种配置随机运行十次时,评估指标方差都非常低,特别是考虑到我们的目标函数是非凸函数。事实上目标函数的方差也非常低。低方差意味着我们总是到达相同的局部最小值,或者该最小值就是全局最小值。
在所有配置中我们并未优化超参数(如正则化系数),如果模型调优则性能可以进一步提升。另外,当我们采用其它损失函数(如保序回归损失或者
ranking损失),模型性能也能得到提升。但是我们并未在这里评估它们,因为每个损失函数都需要增加960个实验。
十一、OCCF[2008]
个性化服务在
web上变得越来越不可或缺,从提供搜索结果到商品推荐。这类系统的例子包括Amazon.com上的商品推荐、Netflix上的DVD推荐、Google上的新闻推荐等等。这些系统中使用的核心技术是协同过滤collaborative filtering: CF,它旨在根据所有用户历史评分的item预测特定用户的item偏好。在许多的这类系统中,用户可以显式给出以不同分数(例如Netflix中的1 ~ 5分)表示的评分。但是,更多的情况下,也可以通过用户点击或不点击、bookmark或者not-bookmark等用户行为来隐式地表达。这些形式的隐式评分更常见,也更容易获得。虽然隐式评分的优势很明显,但是它的缺点(尤其是在数据稀疏的情况下)是很难识别有代表性的负样本。所有的负样本和缺失的正样本混合在一起,无法区分。我们将仅具有正样本的协同过滤称作
One-Class Collaborative Filtering: OCCF。OCCF发生在不同的场景中,下面给出两个示例:Social Bookmark:Social Bookmark在del.icio.us等Web 2.0服务中非常流行。在这样的系统中,每个用户都为一组网页添加书签,这些网页可以被视为用户兴趣的正样本。但是,用户没有为网页添加书签的行为存在两种可能的解释:- 第一种解释:该网页是用户感兴趣的,但是用户未能看到这个网页。
- 第二种解释:用户看到过这个网页,但是用户不感兴趣。
我们不能假设所有不在用户书签中的网页都是负样本。
Clickthrough History:点击数据被广泛应用于个性化搜索和搜索结果改进。通常三元组 表示用户 提交了query并点击了网页 。通常而言,未被点击的网页不被收集。与书签示例类似,我们无法判断网页未被点击是因为内容与query无关、还是因为用户未看到。
有几种直观的策略可以解决这个问题。
一种方法是标记负样本,从而将数据转换为经典的
CF问题。但是,这需要用户的密切配合来标记数据,代价太大甚至难以进行,因为用户通常不愿意承担这种成本。实际项目中,用户很少能够提供算法所需要的标记数据。而且根据一些用户研究表明:如果要求用户在使用系统之前提供很多正面或负面的反馈,那么用户对该系统就有很不好的印象,甚至可能会拒绝使用该系统。
另一种策略是将所有缺失数据视为负样本,称作
All Missing As Negative:AMAN。经验表明,这种策略的效果很好。但是,由于某些缺失数据可能是正样本,因此推荐的结果是有偏的。还有一种策略是将所有缺失值视为未知的,即忽略所有缺失的样本而仅使用正样本,称作
All Missing As Unkown:AMAU。在使用过程中,我们将这些非缺失值灌入针对非缺失值建模的协同过滤算法。但是该方法存在一个平凡解trivial solution:将所有缺失值预估为正样本。因此,所有缺失值为负AMAN和所有缺失值未知AMAU是OCCF中的两种极端策略。
论文
《One-Class Collaborative Filtering》提出了两种方案来解决OCCF问题。这两种方案考虑了将缺失值视为负样本的程度,导致了整体上性能得到提升:- 第一种方案是基于加权的低秩近似,基本思想是为目标函数中的正样本误差和负样本误差赋予不同的权重。
- 第二种方案是基于负样本的采样,基本思想是利用某些采样策略对一些缺失值进行采样从而得到负样本。
它们都充分利用了缺失值中包含的信息,并纠正了将其视为负样本的
bias。第一种方案可以得到理论上的最优解,第二种方案拥有更好的scalability(计算成本低得多)从而扩展到大型稀疏数据集。论文主要贡献:
首先,论文为
OCCF问题提出了两种可能的框架,并提供了它们的实现。其次,论文使用几个真实世界的数据集实验研究了各种加权、采样方法。论文提出的解决方案在
OCCF问题中明显优于两个极端策略(AMAN和AMAU)。在实验中,论文的方法相比最佳baseline至少提高了8%。此外,实验表明:这两个针对
OCCF提出的解决方案(基于加权、基于负采样)具有几乎相同的性能。
相关工作:
协同过滤:过去,很多学者从不同方面探索了协同过滤
collaborative filtering: CF,从提高算法性能到从异质数据源中整合更多资源。然而,这些关于协同过滤的研究仍然假设我们有正样本(高评分)和负样本(低评分)。在非二元评分的情况下,每个
item被赋予一个评分。大多数先前的工作都集中在这个问题setting上。在所有的CF问题中,有很多样本的评分缺失。在《Spectral analysis of data》和《Collaborative filtering and the missing at random assumption》中,作者讨论了在协同过滤问题中对缺失值分布进行建模的问题。但是,他们都无法处理没有负样本的情况。在二元评分的情况下,每个样本要么是正样本、要么是负样本。
《Google news personalization: scalable online collaborative filtering》研究了新闻推荐,点击新闻为正样本、未点击新闻为负样本。作者在这个大规模二元CF问题上比较了一些实用的方法。KDD Cup 2007举办了Who rated What推荐任务,其训练数据与Netflix prize数据集(带评分)相同。获胜团队(《Who rated what: a combination of SVD, correlation and frequent sequence mining》)提出了一种使用二元训练数据集合SVD和流行度的混合方法。
One-class Classification: OCC:已经针对二分类问题提出了仅从正样本中学习的算法。《Estimating the support of a high-dimensional distribution》提出了one-class SVM解决了只有正样本可用的问题,即单类分类问题。而《Learning with positive and unlabeled examples using weighted logistic regression》不仅使用正样本,也使用未标记的样本。对于
one-class SVM,该模型描述了单类single class,并且仅从正样本中学习。这种方法类似于密度估计。当未标记的数据可用时,解决单类分类问题的一种策略是使用类似于EM算法来迭代预测负样本,并学习分类器。在
《learning from positive statistical queries》中,作者表明,如果每个正样本以恒定概率unlabeled,那么在统计query模型下可学习的函数族也可以从正样本和未标记样本中学习。
我们的研究和这些关于单类数据中学习的研究之间的不同之处在于:他们的目的是学习关于正样本的单个概念
one single concept,而我们探索和学习社交网络中的许多概念。类别不平衡问题
Class Imbalance Problem:我们的工作还和类别不平衡问题有关,该问题通常发生在某些类别的样本远多于其它类别的分类任务中。one-class问题可以视为类别不平衡的一种极端情况。有两种策略来解决类别不平衡问题。- 一种是在数据层面,其思想是使用采样来重新平衡数据。
- 另一种是在算法层面,使用
cost-sensitive算法(即,对稀疏类别的样本对应的损失提高权重)。
两种策略的比较可以在
《Extreme re-balancing for svms: a case study》中找到。
11.1 模型
假设有 个用户和 个
item, 表示user-item评分矩阵。假设用户 对item的评分为 ,当 时表示正样本,当 时表示缺失值。我们的任务是从 的缺失数据中找到潜在的正样本,我们称该任务为单类协同过滤One-Class Collaborative Filtering:OCCF。注意:这里除了评分矩阵 之外,没有任何关于用户和
item的其它信息。
11.1.1 wALS
给定一个评分矩阵 以及对应的非负权重矩阵 ,加权低秩近似
weighted low-rank approximation的目标是:使用一个低秩矩阵 来近似 ,使得加权误差最小:其中: 为平方损失; 为权重:
- 对于正样本 ,由于它是显式给定的,因此置信度为
100%,因此我们设置 。 - 对于缺失值,我们认为其中大多数都是负样本,因此设置缺失值的 。但是缺失值为负样本的置信度并不是
100%,因此我们设置 。
- 对于正样本 ,由于它是显式给定的,因此置信度为
考虑用户的 的
representation向量为 ,item的representation向量为 ,则用户 在item上的预估评分为:令:
则预估的评分矩阵为: 。其中 , 的秩为 。
令 ,则这个低秩矩阵就是我们需要得到的低秩近似。
考虑正则化项之后,我们的目标函数为:
其中 为正则化系数。
上述最优化过程可以通过交替最小二乘法
alternating least squares:ALS方法来有效求解。根据:
则有:
ALS方法首先固定 ,根据 我们可以得到 的解析解;然后固定 ,根据 我们可以得到 的解析解。我们重复交替优化 和 直至算法收敛,这种方法称之为加权交替最小二乘法
Weighted Alternating Least Squares:wALS。权重矩阵 对
wALS方法的效果至关重要。我们的基本思想是:令 包含置信度信息。如:当 时令 ,表示置信度很高。但是对于缺失值,它为负样本的置信度并没有100%,因此我们需要将负样本的权重降低。负样本权重有三种配置:
Uniform配置:假设所有用户或所有item上的缺失值为负样本的概率都是等可能的。即:其中 。
User-Oriented配置:如果用户有更多正样本,则假设用户的缺失值为负样本的概率更高。即如果一个用户对大多数item都给与好评,则用户对缺失的item没有产生行为的原因是不感兴趣的可能性越大。即:
Item-Oriented配置:如果item被大多数用户喜欢,则该item的缺失值为负样本的概率越小。即如果一个item是热门的,则用户对它感兴趣的概率越高。即:
当 时,
wALS方法等价于AMAN(所有缺失值都是负样本)。
11.1.2 sALS-ENS
wALS方法有两个缺点:- 当矩阵 太大时,计算代价太大。
- 负样本数量占绝大多数,因此存在类别不平衡。
为解决这两个问题,我们提出了基于随机采样的方法。
- 第一步,从缺失值中根据假设的概率分布随机采样一组负样本,然后我们根据所有的正样本、采样的负样本得到一个新的评分矩阵 。
- 第二步,根据
wALS算法低秩重构评分矩阵 ,其中近似矩阵为 。 - 最后,对所有的近似矩阵 取均值,得到 的低秩近似矩阵 。其中 为随机采样的总次数。
该方法我们称为
sampling ALS Ensemble:sALS-ENS。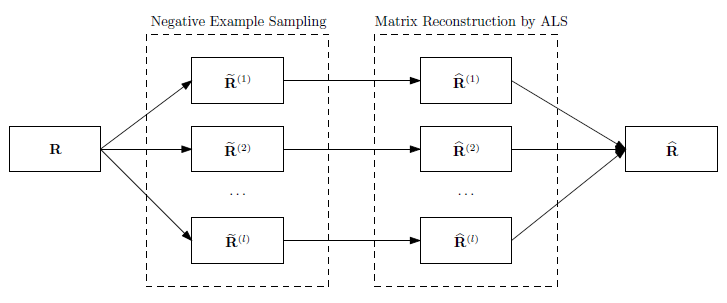
给定原始评分矩阵 、采样概率矩阵 以及负样本大小 ,我们可以使用一种快速的 复杂度的随机采样算法(
《Faster methods for random sampling 》)来生成新的评分矩阵 。我们提出了三种采样概率:
- 均匀随机采样
Uniform: 。即所有缺失值为负样本的概率都是等可能的。 User-Oriented采样: 。即用户对应的正样本越多,则缺失值为负样本的概率越大。Item-Oriented采样: 。即item越热门,则缺失值为负样本的概率越小。
- 均匀随机采样
由于从 中采样的矩阵 是随机的,因此逼近 的矩阵 是有偏的
biased、不稳定的unstable。一种经验的解决方案是利用集成学习
ensemble。这里我们使用bagging的思路:随机采样多次得到 ,然后利用低秩矩阵 来逼近 。最后通过对所有 取平均来得到 的低秩近似 。是观察矩阵, 是从观察矩阵中采样得到的矩阵, 是针对 的重构矩阵。
11.1.3 算法复杂度
假设 :
对于
wALS,每一步更新 或 的时间复杂度为 ,因此wALS的时间复杂度为 ,其中 为迭代的step数。对于
sLAS-ENS,假设NES集成的模型有 个,正样本数量为 ,负样本和正样本比例为 ,则总的时间复杂度为:
实际过程中 都是很小的常数,典型的值为: 从
20到30、、 。并且有 。因此
wALS的算法复杂度为 ,sALS-ENS的算法复杂度为 。因此wLAS-ENS对于大型稀疏数据的scalability更强。
11.2 实验
数据集:
Yahoo新闻数据集:每条记录都是一个user-news的pair对,其中包含用户ID和新闻ID。数据集包含3158个用户和1536条新闻。- 社交书签数据集:来自
http://del.icio.us网站的数据,包含3000个用户和2000个tag标签。
实验配置:数据集以
80%-20%的比例拆分为训练集、测试集,其中训练集包含80%的已知正样本,剩余都是缺失值;测试集包含另外20%的已知正样本,以及剩下的所有缺失值。凭直觉我们认为:一个优秀的算法应该具有更高的概率将已知正样本排序在未知样本之前。因此我们使用
MAP和half-life utility来评估测试集的性能。对于每种配置我们随机重复执行
20次,并报告指标的均值和标准差。另外,所有模型的超参数都是通过交叉验证来确定。
评估指标:
Mean Average Precision:MAP:用于信息检索领域评估一组query召回的doc的排名情况。我们首先计算用户的
AP,其中AP是在所有位置上计算到的precision的均值:其中:
- 为用户 喜欢的
item数量。 - 为排序好的推荐列表的长度。
- 表示推荐列表中第 个
item是否用户喜欢的,如果是喜欢的则为1,否则为0。 - 表示位置 的精度,即推荐列表前 个
item中,用户 真正喜欢的比例。
- 为用户 喜欢的
然后我们计算所有用户的
AP均值:
Half-lie Utility:HLU:假设推荐列表中item的效用utility随着位置的增加而指数下降,则定义用户 的推荐列表的效用为:这里 为参数,实验中设置为
5。测试集所有用户的
HLU定义为:其中 表示用户 的推荐列表中,用户所有喜欢的
item都位于推荐列表的头部,因此也是最大的效用。
对比模型:
AMAN:我们将几种著名的协同过滤算法和AMAN策略结合,包括交替最小二乘ALS-AMAN、奇异值分解SVD、以及基于邻域的方法(包括UserBased CF和ItemBased CF)。AMAU:在AMAU策略下,我们很难使用传统的协同过滤算法得到non-trivial解。此时,根据item的热门程度进行排序,然后推荐热门item是一种简单且广泛使用的方法。另一种方法是将
OCCF问题转换为one-class分类问题。这里我们采用one-class SVM来求解该one-class分类问题。我们为每个item创建一个one-class SVM分类器,该分类器将除了该item以外的其它item评分作为输入特征,然后预测用户对目标item是正向还是负向。
我们首先评估维度 的影响。可以看到:
- 对于
SVD,随着 的增加性能首先提高然后下降。 - 对于
wALS,性能更为稳定并且逐渐提高,最后收敛于大约 。
因此在后续的实验中,我们设置维度 为:
- 对于
wALS,在所有数据集上 。 - 对于
SVD,在雅虎新闻数据集上 ,在社交书签数据集上 。
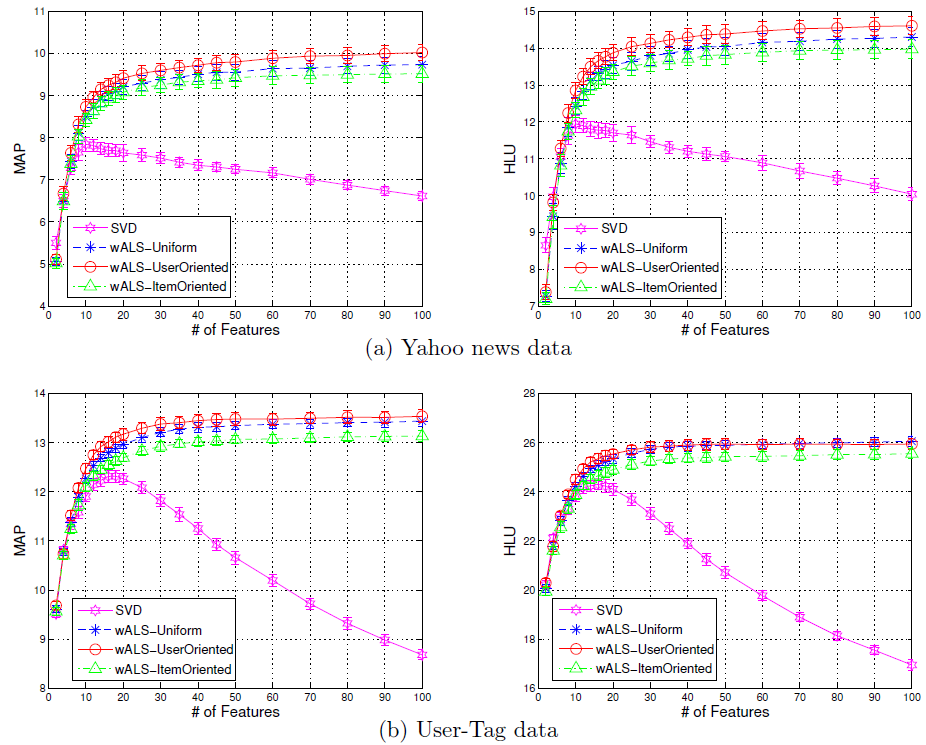
- 对于
我们比较了
wALS、sASL-ENS这两种方法,对于每一种方法我们提出了三种策略:uniform均匀的、user-oriented面向用户的、item-oriented面向item的。下表给出了这些方案的结果。在
wALS方法中,user-oriented效果最好、item-oriented效果最差。这可能是由于用户数量和item数量之间不平衡导致。对于当前数据集,用户数量 远大于item数量 。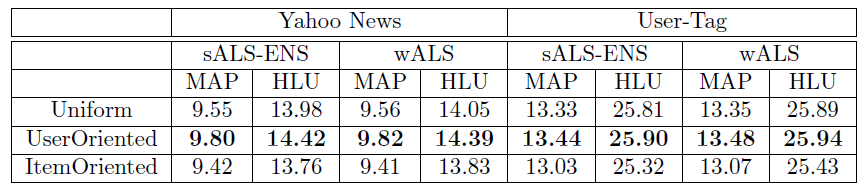
我们比较了
AMAU(基于热门程度的推荐、单类SVM)、AMAN(SVD、ALS-AMAN)以及我们的方法(wALS、sALS-ENS)的效果。其中
x轴为负样本数量和正样本数量的加权比例:控制着负样本的规模。当 时,我们的方法接近
AMAU;当 时我们的方法接近AMAN。为了方便比较,给定 的条件下负采样参数设定为 。由于热门程度策略、
SVD、ALS-AMAN等方法的效果不会随着 改变,因此它们在图中以水平线展示。可以看出:我们的方法要优于
AMAU和AMAN。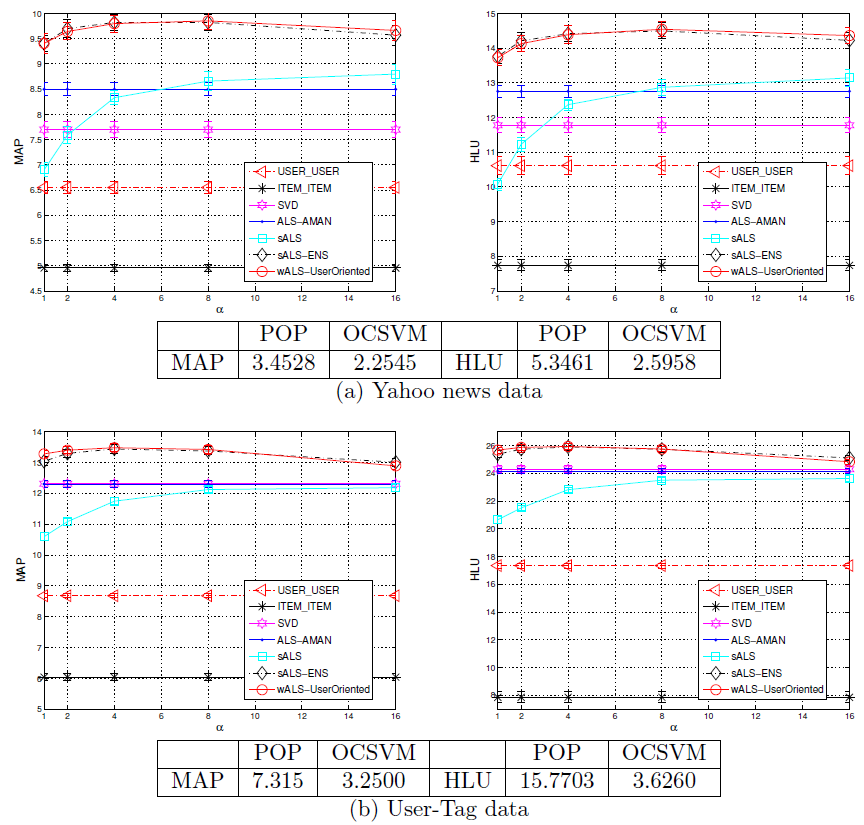
不同方法在雅虎训练集上的训练时间(单位秒)如下所示。可以看到,当 较小时,
sALS的方法训练效率更高。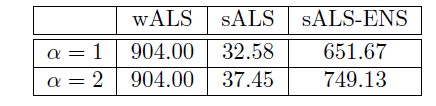
从实验结果可以看到:和
AMAU策略相比,AMAN的效果更好。这是因为:尽管缺失值的标记是未知的,但是我们仍然具有先验知识,即大部分缺失样本都是负样本。这和类别不平衡问题中的结论有所不同。在类别不平衡问题中,假设负样本占据主导地位,那么丢夫部分负样本往往会产生更好的效果。但是在
OCCF问题中,丢弃 “负样本” 反而效果下降。
十二、BPR[2009]
内容推荐是很多信息系统中的一项重要任务,例如像
Amazon这样的在线购物网站为每个客户提供用户可能感兴趣商品的个性化推荐。其它例子像YouTube这样的视频门户网站,为用户推荐电影。个性化对于内容提供商和用户都很有吸引力,前者可以增加销售额或者浏览量,后者可以更容易找到有趣的内容。这里我们专注于item推荐。item推荐任务是为一组item创建user-specific排序。用户对item的偏好是从用户历史行为中获悉的,如用户的购买历史、观看历史等等。推荐系统是一个活跃的研究课题。最近的工作是关于用户提供显式反馈的场景,例如在评分方面。然而,在现实世界的场景中,大多数反馈不是显式而是隐式的。隐式反馈会自动跟踪,例如跟踪点击次数、浏览次数、购买次数等等。隐式反馈的收集要容易的多,因为用户不需要显式表达他的口味。事实上,几乎任何信息系统都已经可以使用隐式反馈,例如
web服务器在日志文件中记录的任何页面浏览行为。在论文
《BPR: Bayesian Personalized Ranking from Implicit Feedback》中,作者提出了一种用于学习个性化排序模型的通用方法。这项工作的主要贡献是:- 论文提出了从最大后验估计导出的、用于最佳个性化排序的通用优化标准
BPR-Opt。论文展示了BPR-Opt与AUC的类比。 - 为了最大化
BPR-Opt,论文提出了通用学习算法LearnBPR,它基于随机梯度下降、以及对训练三元组的bootstrap采样。论文表明作者的算法在优化BPR-Opt方面优于标准的梯度下降方法。 - 论文展示了如何将
LearnBPR应用于两个state-of-the-art的推荐模型族。 - 论文的实验表明,对于个性化排序任务,使用
BPR学习的模型优于其它学习方法。
- 论文提出了从最大后验估计导出的、用于最佳个性化排序的通用优化标准
相关工作:
推荐系统最流行的模型是
k-nearest neighbor: KNN协同过滤。传统上,KNN的相似度矩阵是通过启发式计算的,例如Pearson相关性。但是在最近的工作《Factorization meets the neighborhood: a multifaceted collaborative filtering model》中,相似度矩阵被视为模型参数,并为任务专门学习。最近,矩阵分解
matrix factorization: MF在隐式反馈和显式反馈的推荐系统中变得非常流行。在早期的工作《Incremental singular value decomposition algorithms for highly scalable recommender systems》中,作者已经提出奇异值分解singular value decomposition: SVD来学习特征矩阵。SVD学习的MF模型已经被证明非常容易过拟合,因此人们使用正则化技术。对于item预测,《Collaborative filtering for implicit feedback datasets》和《One-class collaborative fi ltering》提出了一种带有样本权重正则化的最小二乘优化(WR-MF)。样本权重可用于减少负样本的影响。《Latent semantic models for collaborative filtering》提出了一种用于item推荐的概率潜在语义模型。《Compound classifi cation models for recommender systems》将问题转变为多分类问题,并使用一组二分类器解决它。
尽管上面讨论的所有
item预测工作都是在个性化排序数据集上进行评估的,但是这些方法都没有为排序任务直接优化模型参数。相反,他们优化模型参数从而预估用户是否会选择某个item。在我们的工作中,我们导出了一个基于item pair(即特定用户的两个item之间的顺序)的个性化排序优化标准。我们将展示如何根据该标准优化MF或者自适应kNN等state-of-the-art模型,从而提供比常规的学习方法更好的排序质量。我们还详细讨论了
《Collaborative filtering for implicit feedback datasets》和《One-class collaborative fi ltering》的WRMF方法、以及《Improving maximum margin matrix factorization》的maximum margin matrix factorization: MMMF方法与我们方法之间的关系。我们还将讨论我们的优化准则和AUC优化准则的关系。在本文中,我们专注于模型参数的离线学习。在评分预测相关的任务中,
《Online updating regularized kernel matrix factorization models for large-scale recommender systems》已经为MF研究了将学习方法扩展到在线学习的场景(如,添加一个新用户,然后新用户的历史行为记录从0增加到1,2,...)。相同的方法可用于BPR。还有关于学习使用非协同过滤模型进行排序的相关工作(
《Efficient inference for distributions on permutations》,《《Multiobject tracking with representations of the symmetric group》)。一个方向是对排列的分布进行建模。《Learning to rank using gradient descent》针对排序任务,使用梯度下降优化了一个神经网络模型。所有这些方法只学习一个排序,即它们是非个性化的。相反,我们的模型是学习个性化排序的协同过滤模型,即每个用户一个单独的排序。在我们的评估中,我们根据实验表明,在典型的推荐设置中,我们的个性化BPR模型甚至优于非个性化排序的理论上限。个性化排序
personalized ranking任务是为用户提供一个排序的item列表,这也被称作item推荐item recommendation。例如,一家在线商城会向用户推荐用户可能想要购买的商品的个性化排序列表。在本文中,我们研究了从隐式反馈中推断ranking的场景。隐式反馈有意思的地方在于,只有正的观察值是可用的。未观察到的user-item pair(例如,用户尚未购买的商品)的真实反馈是未知的,可能是用户不喜欢(负反馈)、也可能是用户喜欢但是尚未见过。
12.1 BPR 准则
令 为所有用户集合, 为所有
item集合。推荐系统的任务是针对用户 提供个性化排名函数 ,其中 满足以下条件:- 完备性
totality: 。 - 反对称性
antisymmetry: 。 - 传递性
transitivity: 。
- 完备性
常规的
item推荐思路是预测用户 对item的评分 ,从而反映用户对该item的偏好。然后根据预估评分对item进行排序。令隐式反馈数据 。定义缺失样本集合为 ,它为 的补集。定义 。
在隐式反馈系统中,系统只能观察到用户的
postive行为,剩余的数据是缺失值。一种解决缺失值的方法是忽略这些缺失值。但是直接忽略缺失值使得我们没有
negative样本,从而模型无法学习。另一种解决缺失值的方法是将缺失值都是为
negative行为。这意味着模型对 中的样本预估为1、对 中的样本预估为0。考虑到 中的item就是我们候选的、需要向用户推荐的item,因此一个学习能力强的模型会根据这些negative数据学到 中所有得分都为零。 这意味着模型完全无法排序。目前该方法之所以有一定效果的原因是模型采取了一些缓解过拟合的策略,如正则化。
我们采用了不同的思路:使用
item pair来训练模型从而优化item pair的排名,而不是优化单个item的得分。这相比使用negative来代替缺失值更好地刻画了问题。我们从 中构造训练样本。对于用户 :
- 如果
item已被用户购买,即 ,则我们认为:相比于缺失item,用户 更喜欢item。 - 如果
item有 ,则我们无法比较它们之间的任何偏好。 - 如果
item有 ,则我们也无法比较它们之间的任何偏好。
因此我们构建训练集:
其中 为 的补集 : 。
对于任何三元组 意味着用户 在
item之间更喜欢item。由于 的反对称性,在提供正样本的同时也就提供了负样本。这种方式有两个优点:
训练集包含
postive pair、negative pair。 测试集包含所有缺失item pair,这个刚好就是我们希望进行排序的目标item pair。这意味着从pair-wise角度来看,训练集 和测试集是不相交的。训练集包含的是 “(观测样本,未观测样本)” 的
pair,而测试集是 “(未观测样本,未观测样本)” 的pair,因此二者是不相交的。训练数据是为真实的
ranking目标而构建的。
- 如果
在贝叶斯分析框架下,个性化排名的任务是:为每个
item最大化后验概率。即:考虑到 与 无关,因此有:
其中 为用户的偏好, 为模型的参数。
假设用户之间彼此独立,并且假设用户 的
item pair之间的顺序也是相互独立的。因此 可以重写为:其中 为示性函数:
进一步地,根据完备性和反对称性,我们有:
目前为止,我们还无法确保得到个性化排序。为满足完备性、反对称性、传递性,我们定义用户 在
item之间的偏好概率为:其中: 为
sigmoid函数; 为一个模型,它捕获了用户 、item、item之间的关系。即:我们的
BPR通用框架把对 之间的关系建模委托给了诸如矩阵分解、kNN之类的基础模型,由这些模型来预估 。通过这些基础模型以及BPR框架,我们可以对个性化排序 进行建模。我们引入先验概率密度函数 为零均值、协方差矩阵为 的高斯分布概率密度分布函数:
为减少超参数数量,我们选择 。
BPR-OPT:个性化排名通用准则BPR-OPT是最大化后验估计 ,因此有:其中 为模型的正则化参数。
的物理意义是观察到的
item排序在未观察到的item之前的概率。因此 为训练集排序成立的对数似然。
12.2 BPR 学习
和
AUC的联系:我们将BPR和AUC进行类比。用户维度的AUC定义为:即在所有
postive item和missing item组合中,模型预估对postive item和missing item能够正确区分的概率。因此所有用户的平均
AUC为:根据 的定义有:
其中 为归一化常数:
这和
BPR-OPT准则非常类似。BPR-OPT的目标函数为:如果将这个代价函数视为损失函数(第一项)和正则化项(第二项),则
BPR-OPT的损失函数为:这和
AUC有两个区别:AUC使用了归一化常数 。AUC使用不可导的示性函数 ,这等价于Heaviside函数:通常在优化
AUC时我们使用可导的 来替代不可导的Heaviside函数。而
BPR-OPT使用可导的损失函数 。
学习算法:虽然我们已经导出了个性化排名的优化准则,并且该准则是可微的,但是我们无法利用标准的梯度下降算法来求解该最优化问题。为解决该最优化问题,我们提出了基于
bootstrap采样的随机梯度下降算法LearnBPR。BPR-OPT目标函数的梯度为:在
full随机梯度下降算法中,在每个step需要计算所有训练样本的梯度,然后更新参数:这种方法可以确保每次参数更新的方向是正确的,但是缺点是计算复杂度太高: 包含 个三元组,因此在每个
step中计算完整的梯度不可行。另外,使用完整的梯度优化也会存在梯度倾斜问题,这也会拖慢训练的收敛速度:
- 不同的
item为postive的分布不同,因此我们很难选择一个合适的学习率:对于postive较多的item(梯度较大), 我们必须选择一个较小的学习率;对于postive较少的item(梯度较小) ,我们必须选择一个较大的学习率。 - 另外梯度分布差距太大,导致正则化系数的选择非常困难。
- 不同的
在随机梯度下降算法中,我们对单个三元组 执行更新:
这可以解决梯度倾斜问题。但是,随机梯度下降依赖于样本的遍历顺序,需要确保每次都是随机选择 。
LearnBPR学习算法采用每次均匀随机选择三元组 的随机梯度下降算法。通过这种方式,在连续更新step中选择相同user-item组合的机会很小。我们建议使用bootstrap采样方法,这样可以在任何step来停止。在我们的案例中,放弃完整epoch循环的想法特别有用,因为样本数量巨大,并且只需要整个epoch的一小部分模型就能收敛。这就是
batch随机梯度下降,并且batch是随机选择(而不是user-wise或者item-wise选择)。下图给出了典型的
user-wise随机梯度下降,以及LearnBPR随机梯度下降的收敛速度。可以看到learnBPR随机梯度下降的收敛速度更快。
12.3 模型结合 BPR
这里我们展示如何将
BPR和经典的矩阵分解、kNN模型融合。在
BPR-OPT通用框架中,我们需要利用其它模型来预估 。我们将 定义为:现在我们可以使用标准的协同过滤算法来预估 。
- 即使我们使用了和别人一样的模型,我们和它也有本质的不同:我们采用了另一个准则来优化模型,这会导致更好的排序结果。因为我们的准则是直接优化个性化排名。
- 我们的准则并不是尝试通过单个预估值 来拟合某个目标,而是试图拟合两个预估值 之间的差异。
矩阵分解结合
BPR:假设每个用户 关联一个representation向量 , 每个item关联一个representation, 为representation向量维度。用户 对item的预估值为: 。则有:
其中 的各行由所有用户向量 组成 , 的各行由所有
item向量 组成, 远小于用户或item的数量, 为评分矩阵 的估计值。该模型称作矩阵分解
Matrix Factor,模型的参数为 。可以通过奇异值分解
SVD来求解参数 和 ,但是该方法很容易陷入过拟合。为此,一些机器学习方法引入了其它的矩阵分解技术,如:带正则化的矩阵分解、非负矩阵分解non-negative MF、最大裕量矩阵分解maximum margin factorization等等。对于个性化排名任务,更好的方法是采用
BPR-OPT准则进行优化,称作BPR-MF。对于使用了
BPR-OPT准则的矩阵分解模型,LearnBPR优化时使用的梯度为:另外我们还引入三个正则化约束:
- 使用 来约束用户
representation矩阵 。 - 使用 来约束 上的
positive更新 。 - 使用 来约束 上的
negative更新。之所以拆分 和 是因为postive样本和negative样本的规模差异巨大。
- 使用 来约束用户
自适应
kNN结合BPR:kNN可以基于item之间的相似或者user之间的相似来建模,这里我们介绍基于item相似的kNN方法,但是基于user相似性的kNN方法原理类似。基于
item相似的kNN的基本思想是:用户 在item上的预估值依赖于item和 上item的相似性。通常我们仅使用 中和item最相似的top k个item,即kNN。最终基于
item的kNN模型为:其中 为
item之间的相似度矩阵,它也是模型的参数 。注意:这里假设
postive得分为1、negative得分为0。因此最终预估评分就是top k个item的相似度之和。另外,有的方法也对相似度矩阵按行进行归一化。大多数方法使用启发式的相似度函数,如余弦相似度:
一个更好的方法是通过学习相似度矩阵 来自适应:直接将 作为模型参数。如果 规模太大,我们也可以对其进行矩阵分解: 。其中我们只需要学习参数 。
我们考虑通过
BPR-OPT准则和LearnBPR学习方法来利用kNN对个性化排序进行建模,称作kNN-BPR。LearnBPR优化时采用的梯度为:另外我们还引入两个正则化约束:
- 用于更新 。
- 用于更新 。
12.3 BPR VS WR-MF 、MMMF
这里我们讨论
BPR和WR-MF以及MMMF模型之间的联系。Weighted Regularized Matrix Factorization:WR-MF用于从隐式反馈数据中执行矩阵分解(参考Implicit Feedback CF章节),其模型为:其中 为矩阵的
F范数, 为user-item组合的先验权重。例如,对于所有postive样本选择 、对于所有negative样本选择 。这里假设正样本的评分为
1、负样本评分为0,因此 为残差。和
BPT-OPT的 (应该取负号,从而最小化目标函数)相比可以发现:BPT-OPT是对每个用户 优化的是一对item pair,而WR-MF优化的是单个item。BPT-OPT的损失函数为逻辑回归损失,而WR-MF的损失函数为最小平方误差。但是
item预测实际上不是回归任务(定量分析),而是分类任务(定性分析),因此用逻辑回归损失更合适。BPT-OPT对每个损失的权重为1,而WR-MF对每个损失的权重为 。
Maximum Margin Matrix Factorization:MMMF并不适合于隐式反馈数据集。我们可以将缺失值设置为0、将非缺失值设置为1。通过这些修改,MMMF的目标函数为:和
BPT-OPT的 相比可以发现:BPT-OPT的损失函数为逻辑回归损失,而MMMF的损失函数为hinge损失。BPT-OPT准则是通用的,可应用于多种模型;而MMMF方法仅针对矩阵分解。
MMMF:正负样本预估得分之间的差距尽可能大;BPT-OPT:正样本预估得分大于负样本预估得分的概率尽可能大。二者都是排序关系,因此思想上是相近的。如果将Hinge损失替换为逻辑回归损失,则MMMF等价于BPT-OPT。
12.4 实验
数据集:
Rossmann数据集:一个在线商店数据集,包含10000个用户在4000个item上的购买历史,总共有426612条购买记录。我们的任务是为用户推荐该用户下一次可能购买的商品的列表。Netflix数据集:一个DVD出租数据集,包含用户在电影上的显式评分,评分从1~5共五个等级。由于我们需要解决隐式反馈任务,因此我们从数据集中删除了评分分数。现在的任务是预测用户是否可能为电影评分。我们从原始数据集中采样了
10000个用户、5000个item,包含565738个评分。采样时,我们选择至少对10部电影进行评分的用户 , 以及每个item至少有10个用户观看 。
baseline模型:我们选择了矩阵分解MF和kNN这两种流行的模型。- 对于矩阵分解模型,我们采用三种不同的方法来实现:标准矩阵分解
SVD-MF、带权重矩阵分解WR-MF、基于BPR-OPT优化准则的矩阵分解BPR-MF。 - 对于
kNN模型,我们采用两种不同的方法来实现: 基于余弦相似度的kNN方法cosin-kNN、基于BPR-OPT优化准则的自适应kNN方法BPR-kNN。 - 另外我们还比较了基于热门程度的
baseline方法:根据item热门程度排名,然后为每个用户 选择其中的top热门的item。这也是一种非个性化的推荐,即所有用户推荐的item都相同。
- 对于矩阵分解模型,我们采用三种不同的方法来实现:标准矩阵分解
实验配置:我们使用留一法
leave one out来评估。对于每个用户随机删除一条历史记录,并将该历史记录作为测试集。这样我们得到了不相交的训练集 以及测试集 。我们在训练集上训练各个模型,并在测试集上评估模型,评估指标是测试集的平均AUC:其中 为每个用户的评估数据,它由保留的那一条
item,以及所有的缺失item组成:AUC的值越高表明模型效果越好。随机猜测的AUC为0.5, 最好的AUC为1.0。即对每个用户 ,评估其测试集中唯一的正样本和未观测样本之间的排序。
我们还给出了非个性化推荐方法的理论
AUC上界 ,这是通过在测试集 上搜索最佳的排名 函数(不是 ,因为非个性化推荐与用户无关),从而得到理论上的非个性化排名的上界。对于每种实验配置,随机重复执行
10次,在每一次都随机拆分训练、测试集。所有模型的超参数都在第一次执行时采用grid search搜索,并在剩余9次保持不变。在两个数据集上所有模型的效果如下。结论:
BPR-MR和BPR-kNN均优于其它所有方法。这表明我们的BPR-OPT准则以及对应的LearnBPR学习方法在个性化排序任务中的效果。尽管所有的矩阵分解方法
SVD-MF,WR-MF,BPR-MF采用完全相同的模型(即MF),但是它们的效果差别很大。SVD-MF可以对训练数据拟合的更好,但是它会陷入严重的过拟合。这可以从SVD-MF随着维度的增加,测试AUC反而下降来观察到。WR-MF相比之下更为成功。由于正则化的效果,当维度增加时WR-MF的效果并未下降。BPR-WF在所有数据集上都超越了SVD-MF和WR-MF。
即使是
cosin-kNN这样最简单的个性化推荐方法也超越了非个性化的 ,因此也意味着超越了所有的非个性化方法。
十三、MF for RS[2009]
现代消费者被各种选择所淹没。电商和内容提供商提供种类繁多的产品,有前所未有的机会来满足各种特殊需求和口味。为消费者匹配最合适的产品是提高用户满意度和忠诚度的关键。因此,越来越多的电商对推荐系统感兴趣,其中推荐系统分析用户对产品的兴趣模式,从而提供适合用户口味的个性化推荐。由于良好的个性化推荐可以提升用户体验,因此
Amazon.com和Netflix等电商领导者已经将推荐系统作为他们网站的重要组成部分。这样的系统对于诸如电影、音乐、电视节目之类的娱乐产品也特别有用。许多不同的用户将观看同一部电影,而每个用户可能会观看许多不同的电影。事实证明,客户愿意表明他们对特定电影的满意度,因此有大量的、关于哪些电影吸引哪些用户的数据是可用的。公司可以分析这些数据,从而向特定用户推荐电影。
推荐系统策略:广义上讲,推荐系统基本上有两种策略:
基于内容过滤
content filtering的推荐:为每个用户创建用户画像,或为每个商品创建商品画像,然后系统基于用户画像和商品画像进行匹配。如:用户画像包括人口统计信息、调查问卷及其答案;电影画像包括电影类型、演员、票房热度等。然而,基于内容过滤的推荐需要搜集大量的外部信息从而构建画像系统,这些信息可能很难收集或者根本无法收集。
基于内容过滤推荐的一个成功案例是
Music Genome Project项目,该项目用于互联网广播服务Pandora.com。在该项目中,受过训练的音乐分析师会根据数百种不同的音乐特征对每首歌进行打分,从而构建音乐画像。这些特征不仅捕获了歌曲的音乐特性,还捕获了与听众的喜好相关的很多其它特性。基于协同过滤
collaborative filtering的推荐:它根据用户之间的相关性,或者商品之间的相关性进行推荐。这个过程中不需要创建用户画像或商品画像,仅依赖于历史的用户行为,例如历史的交易或者评分。协同过滤的主要优点在于它是
domain free领域无关的,并可以解决内容画像难以描述的一些用户行为模式。协同过滤虽然通常比内容推荐更为准确,但无法解决冷启动问题cold start problem。在冷启动方面,基于内容推荐的表现更好。
协同过滤的两个主要方向是邻域方法
neighborhood method和潜在因子模型latent factor model。邻域方法的重点是计算
item之间的相关性,或用户之间的相关性。ItemBased CF根据同一个用户在相似的item上的评分,来评估该用户对新item的偏好。UserBased CF根据相似用户在同一个item上的评分,来评估新用户对该item的偏好。
潜在因子模型根据所有用户的
item评分模型,从而推断出 个因子来表征用户和item。从某种意义上讲,这些因子包括上述人类创造歌曲基因的、计算机化的替代方案。对于电影,因子可能是某些显著的维度(如:电影流派、是否适合儿童等等),也可能是不显著的维度(如:演员的气质),甚至也可能是完全无法解释的维度。对于用户,这些因子衡量用户对相应因子电影上的喜欢程度。
潜在因子模型的一些最成功的实现是基于矩阵分解
matrix factorization:MF。在矩阵分解的基本形式中,它通过从item评分模式中推断出的因子向量来表征用户和item。然后我们基于用户因子向量和item因子向量的内积来进行推荐。近年来,这些方法因为具有良好的可扩展性、预测准确性从而变得流行。此外,它们为建模各种现实情况提供了很大的灵活性 ,它允许结合额外信息,例如隐式反馈、时间效应、以及置信度水平。论文
《MATRIX FACTORIZATION TECHNIQUES FOR RECOMMENDER SYSTEMS》对协同矩阵分解模型进行了详细的讨论。推荐系统依赖于不同类型的输入数据,这些数据通常放置在一个矩阵中,一个维度代表用户、另一个维度代表感兴趣的
item。显式反馈数据:最方便的数据是高质量的显式反馈,其中包括用户对
item兴趣的显式输入。例如,Netflix收集电影的星级评分,TiVo用户通过thumbs-up和thumbs-down按钮来表明他们对于电视节目的偏好。我们将明确的用户反馈称作评分。通常,显式反馈包含一个稀疏矩阵,因为任何单个用户可能只对所有
item中的一小部分进行了评分。隐式反馈数据:矩阵分解的优势之一是它允许融合附加信息。当显式反馈不可用时,推荐系统可以使用隐式反馈推断用户偏好,通过观察用户行为(包括购买历史、浏览历史、搜索历史、甚至鼠标移动历史)来间接反映用户的意见。隐式反馈通常表示事件的存在或不存在,因此它通常由稠密矩阵来表示。
13.1 基本形式
给定
user-item评分矩阵 ,矩阵分解通过从评分矩阵中推断出用户因子向量和item因子向量。假设用户 关联一个用户因子向量 ,
item关联一个item因子向量 ,其中 为因子数量。则用户 对item评分的预估值为:求解该模型的传统方法是奇异值分解
SVD,由于评分矩阵 通常是缺失的,因此传统的SVD方法是未定义的。- 一种方法是仅拟合数量稀少的非缺失评分,但这会导致模型很容易陷入过拟合。
- 另一种方法是通过插值填补来补全缺失的评分,使得 为一个稠密矩阵。但是,一方面这会显著增加计算量,另一方面不正确的插补会扭曲数据。
因此最近的工作直接对非缺失项进行建模,同时利用正则化来缓解过拟合:
其中:
- 为已知评分的
user-item pair集合, 为所有用户集合, 为所有item集合, 为已知评分。 - 为正则化参数,通常由交叉验证来确定。论文
《Probabilistic Matrix Factorization》为正则化提供了概率论上的理论解释。 - 为用户因子矩阵。
- 为
item因子矩阵。
训练算法:
随机梯度下降:
Simon Frunk提出了该目标函数的随机梯度下降优化算法。算法在迭代过程中遍历训练集的所有user-item评分。对于每个已知评分 ,模型会预估 并计算预测误差:然后算法根据梯度进行参数更新:
其中 为学习率。
这种训练算法易于实现,并且训练时间相对较快。
交替最小二乘法
Alternating Least Squares:ALS:另一种训练算法是交替最小二乘法。由于 和 都是未知的,因此目标函数不是凸函数 。如果固定其中一个变量,则目标函数是另一个变量的凸函数,则可以直接求解最优解。因此,
ALS交替固定 和 ,然后优化另外一个变量。这样不断交替优化直到算法收敛。虽然随机梯度下降比ALS更容易实现、收敛更快,但是至少在两种情况下ALS是有利的:- 首先,
ALS是可以并行化的。当固定 时, 算法可以独立的优化每个 ,这带来算法潜在的大规模并行化能力。 - 其次,对于隐式反馈系统,因为存在大量的隐式反馈数据,因此像随机梯度下降那样遍历每个评分是不现实的。而
ALS可以有效处理这类场景。
- 首先,
13.2 bias 形式
我们观察到很多评分的差异是由用户本身或者
item本身导致的,称作bias偏差。如,某些用户比较吹毛求疵,其评分普遍低于所有用户的平均分;有些电影比较热门,其评分普遍高于所有电影的平均分。因此,系统可以对
bias建模为:其中 为基于
bias的评分预估, 表示所有的评分均值, 表示用户 的评分bias, 表示item的评分bias。如:假设所有用户在所有电影上的平均评分为 分。“张三” 是比较苛刻的用户,其评分普遍比平均水平低
0.3分;电影 “流浪地球” 比较热门,其评分普遍比平均水平高0.5分。则“张三” 对于 “流浪地球” 的评分预估为 分。我们可以用
bias来改进矩阵分解。我们将预估评分分解为四个部分,每个部分分别捕获对应的信号:- 全局均值 :它捕获了所有用户在所有
item上的整体评分情况。 user bias:它捕获了user偏离均值的部分,与item无关。item bias:它捕获了item偏离均值的部分,与user无关。user-item交互部分 :它捕获了user对于特定item的兴趣。
即: 。
基于
bias形式的矩阵分解模型,其目标函数为:其中 为所有
bias参数 组成的向量。- 全局均值 :它捕获了所有用户在所有
13.3 多输入源
推荐系统经常会遇到冷启动问题,即用户提供的评分数据非常稀疏。解决冷启动问题的一种有效方法是:合并有关用户的其它信息来源,如隐式反馈数据。
为方便讨论,考虑使用二元隐式反馈数据。假设 为用户 的隐式偏好的
item集合。对于每个item,系统定义了item隐式反馈因子向量 。则每个用户 可以根据其隐式反馈的item来刻画:考虑到不同用户的隐式数据规模不同,因此这里对其进行归一化:
另一种信息源是已知的用户属性,例如人口统计信息。为简单起见,这里也考虑二元属性。
假设用户 的属性集合为 (即取值为
1的属性的集合) ,该集合可以描述性别(是否女性)、年龄组(是否老年人)、地域(是否一线城市)、收入水平(是否年薪超过百万)等等。对于每个属性 ,系统定义了用户属性因子向量 。则每个用户 可以根据其属性来刻画:
融合了多个数据源之后,矩阵分解模型进化为:
尽管这里给出的是提升用户表达的能力,但是必要的时候也可以对
item进行类似的处理。即可以通过用户隐式反馈因子向量、item属性因子向量来刻画item。事实上这就是
Embedding的基本思想:对历史行为item进行embedding、对用户属性进行embedding,然后对应的取加权均值池化或者sum池化。
13.4 时间效应
目前为止所有的模型都是静态的,实际上随着新的用户、新的产品、新的评分不断加入,产品的认知和热门程度会不断发生变化。同样地,用户的喜好也在不断发生变化,这导致用户的偏好被重新定义。
因此,系统应该考虑
user-item交互的动态的dynamic、随时间漂移time-drifting的时间效应。通过在矩阵分解模型中引入时间效应可以显著提高模型的准确性。我们将评分分解为不同的部分,然后处理每一部分的时间效应。具体而言,下列部分会随着时间变化:
item bias:商品的热门程度可能随着时间的变化而变化。如:电影可能会随着外部事件的发生而开始流行或不再流行。因此,模型将item bias视为时间的函数。user bias:用户可能随着时间的发展而改变其基准评分。如:平均评分为5分的用户(非常乐观)可能因为家庭变故,使得平均评分降低到2分。因此,模型将user bias视为时间的函数。user-item交互:用户可能随着时间的发展而改变其口味。如:可能年轻的时候喜欢啤酒,但是随年龄增长更偏好白酒。和人类不同,商品本质上是静态的,因此系统将
item因子 视为静态的,而用户因子 视为时间的函数。
因此,考虑时间效应的矩阵分解模型为:
.
13.5 置信度水平
并非所有观察到的评分都应该具有相同的权重或者置信度。如:系统可能会遇到某些刷好评的用户,这些好评并不能反应商品的特征。
另外,在隐式反馈系统中,很难准确地量化用户的偏好,因此系统使用粗糙的二元变量来表示 ”喜欢“ 和 ”不喜欢“ 。如:有过购买行为认为是 ”喜欢“ 。但是用户购买
10次和用户购买1次的行为是不同的,前者更能够反应用户的偏好。因此可以考虑对用户的偏好关联一个置信度得分, 该得分可以来自于用户的行为频次, 如购买行为的频次。可以考虑对矩阵分解模型引入置信度,这使得模型对于没有意义的观察到的评分降低权重。令 的置信度为 ,则引入置信度加权的矩阵分解模型为:
.
13.6 效果
Netflix Prize竞赛:在2006年,在线DVD租赁公司Netflix宣布了一项竞赛来改善其推荐系统。为此,该公司发布了一个包含超过1亿个评分的训练集,覆盖了大约50万匿名用户、以及他们对超过1.7万个电影的评分,评分范围是1 ~ 5分。参赛团队需要为测试集提交预测评分,其中测试集规模为300万个user-item pair。Netflix根据持有的、未公开的真实评分来计算各团队测试集的RMSE。第一个能够将Netflix算法的RMSE性能提升10%或者更高的团队将赢得100万美金的奖金。如果没有团队能够达到10%的目标,那么Netflix将在每年的比赛结束后向第一名的团队提供5万美金的进步奖。该比赛在协同过滤领域引起了轰动。在此之前,用于协同过滤研究唯一公开可用的数据集要小几个数量级。
Netflix Prize数据的发布、以及比赛的吸引力激发了协同过滤领域的活力。根据比赛网站,来自182个不同国家的4.8万多个团队下载了数据。我们团队的参赛作品,原名叫
BellKor,在2007年夏天夺得了比赛的第一,并且以当时最好的成绩获得了2007年的进步奖:比Netflix好8.43%。后来,我们与Big Chaos团队联盟,以9.46%的提升赢得了2008年的进步奖。在撰写本文时,我们仍居第一,朝着10%的里程碑前进。我们的获奖作品包含
100多个不同的预测器集合,其中大部分是使用本文描述方法的一些变体的矩阵分解模型。我们与其他顶级团队的讨论,以及公开比赛论坛上的帖子表明:这些是最流行、最成功的预测评分的方法。我们在
Netflix数据集上尝试了多种不同形式的矩阵分解,下图给出了不同模型、不同参数数量的RMSE。结论:- 通过增加因子数量,每个模型的准确性都得到提高。
- 更复杂的因子模型准确性更高。
- 时间效应对于模型尤为重要,因为数据中存在明显的时间效应。

十四、 Netflix BellKor Solution[2009]
Netflix数据集包含从1999-12-31到2005-12-31期间,所有用户在所有电影上的评分。其中用户数量为 ,电影数量为 ,评分数量超过1亿,每个评分关联有评分日期。另外,所有用户都是脱敏的。比赛数据以
training-test的形式给出,其中:大约420万个评分被保留,这些评分包括每个用户最近的9部电影评分。如果用户评论电影的数量少于18个,则保留的电影评分数量会少于9部。剩余的电影评分都作为训练集给出。保留的电影评分被随机划分为三个数据集:
Probe数据集:这部分数据集给出了label,即评分。参赛选手可以自由地在本地利用这部分数据集来作为训练或测试。Quiz数据集:这部分数据集未给出label。参赛选手可以将他们模型在Quiz数据集上的预估结果上传到比赛网站,网站会给出Quiz数据集上的评估的RMSE,并根据该RMSE在公开的排行榜上公布。在比赛结束之前,参赛者可以反复提交他们的在
Quiz数据集上的预估评分,每次都可以看到网站给出的RMSE结果。Test数据集:这部分数据集未给出label。参赛选手可以将他们模型在Test数据集上的预估结果上传到比赛网站,但是只有到比赛结束的那一刻网站才会公布在Test数据集上的评估的RMSE。网站取其中得分最高的结果作为获胜者。
与训练集相比,保留的电影评分数据集包含更多评分稀疏的用户,因此更难预测。从某种意义上看,这代表了对协同过滤系统的实际需求:系统需要从已有的评分中预估新的评分,并且平等地对待所有用户,而不仅仅是活跃用户。
论文
《The BellKor Solution to the Netflix Grand Prize》给出了作者参加Netflix比赛获胜的模型及其思路,论文中所有的结果都是在Quiz数据集上评估的。令用户 对电影 的评分为 ,评分取值为
1~5分;令用户 对电影 的预估评分为 。令评分时间为 ,其粒度为天级。大约
99%的user-item评分是缺失的,因为一个用户通常只会观看很小一部分比例的电影。因此定义观察到的 集合为: 。注意: 也包含了Probe集合。定义所有用户集合为 , 所有电影集合为 ,用户 的评分电影集合为 ,定义电影 收到评分的用户集合为 。
另外,在
Quiz数据集和Test数据集中,我们知道用户对哪些电影评分,但是具体评分不知道。评分这一行为(即使不知道具体数值)已经包含了有效信息,因此我们定义集合 为用户 发生评分行为的电影集合。 是 的扩展,因为它考虑了Quiz数据集和Test数据集。在比赛中,为了防止过拟合我们使用 正则化。
另外,所有超参数都是通过手动搜索的方式来调优:执行多次搜索并在
Netflix的Probe数据集上选择RMSE最佳的参数。这种方式并不是最优的,有两个原因:- 首先一旦设置了超参数的值,我们就不会对其进行修改。但是如果未来引入了新的超参数,则可能还需要回过头来修改它的值,使得整体效果最优。
- 其次我们在相同算法的多个变种之间使用了相同的超参数值,事实上需要对每个变种进行更精细的调整从而使用不同的超参数值。
我们之所以选择这种方便快捷、但是准确性较低的方式是因为我们的经验表明:单个预测器
predictor上准确性的过度调整,并不能在整体组合predictor中起到多大贡献。我们采用的是多个模型混合
blending的方式,而不是采用单个模型。
14.1 Baseline Predictor
协同过滤模型试图建模
user和item之间的交互interaction,这些交互使得用户对不同电影产生了不同的评分。但是,很多观察到的评分是由于用户或item本身导致的,与user-item的交互无关。典型的例子是:系统中某些用户的评分普遍高于其它用户,即user bias;另外系统中某些item收到的评分也普遍高于其它item,即item bias。我们在
baseline predictor中封装了不涉及user-item交互的因素,这使得后续的predictor可以专注于建模user-item交互的部分。令 为所有用户在所有电影上的平均评分,则用户 对电影 的
baseline预估为:其中参数 表述用户 的
bias,参数 为电影 的bias。如:假设所有用户在所有电影上的平均评分为 分。“张三” 是比较苛刻的用户,其评分普遍比平均水平低
0.3分;电影 《流浪地球》 比较热门,其评分普遍比平均水平高0.5分。则“张三” 对于 《流浪地球》 的评分预估为 分。求解参数 的一种简单方法是分别计算 和 :
首先对每个电影 ,根据它收到评分对 的偏离的均值来计算 :
然后对每个用户 ,根据用户评分对 和 的偏离的均值来计算 :
其中分母中的 为正则化参数,这是为了防止除以零。这两个参数通过对
Probe数据集交叉验证得到,这里我们使用 。求解参数 的一种更准确的方法是求解下列目标函数的最优化问题:
这里 代表所有的用户和
item的bias。第一项表示通过 来拟合 ;第二项为正则化项来防止过拟合。该最优化问题可以通过随机梯度下降法来求解。在实际应用中我们也采用这个更准确的求解方法。
14.1.1 时间效应
随着时间的变化,
baseline predictor有两个主要影响:- 电影的热门程度会发生变化。如,电影可能会受到外部事件的发生而热门或爆冷。因此我们将
item bias作为时间的函数。 - 用户的平均评分会发生变化。如,用户可能会因为近期失业或失恋从而对电影的整体评分下降。因此我们将
user bias作为时间的函数。
因此带时间效应的
baseline predictor在时刻 的预估值为:其中 都是时间相关的实值函数。
- 电影的热门程度会发生变化。如,电影可能会受到外部事件的发生而热门或爆冷。因此我们将
长期的时间效应和短期的时间效应是不同的。一方面,我们不希望电影每天的热门程度都在波动,而是在更长周期内变化;另一方面,我们观察到用户的时间效应每天可能变化,这反映出用户行为的天然不一致性
inconsistency。因此与电影的时间效应相比,用户的时间效应更短期,因此捕获用户的时间效应需要更高的分辨率(即时间粒度更细)。
我们首先建模电影的时间效应。我们发现可以将
item bias根据时间分桶,在每个桶内item bias都是固定的。- 分桶数量越大,则时间粒度越细(即,分辨率更高),但是每个桶内的评分数量越少,统计结果越不准确。
- 分桶数量越小,则时间粒度越粗(即,分辨率越低),但是每个桶内的评分数量越多,统计结果越准确。
因此我们需要在分辨率和桶内评分数量之间取得平衡。实际上,很多不同的分桶大小都可以产生相同的模型预估准确率。在我们的实现方式中,我们使得每个分桶对应于连续十周的数据,从而仅用
30个分桶就覆盖了数据集的所有日期。每个时间 关联一个桶编号 ,在我们这里它就是一个从
1到30的整数。每个item bias被拆分为一个稳定的部分、一个时变的部分:通过最近 天的统计量来刻画 。但是两个前提:
item的bias波动缓慢,统计数据规模足够大从而置信。在
item上对item bias分桶的效果很好,但是在user方面这是一个挑战。一方面我们希望为用户提供更高的分辨率,从而捕获短期的时间效应;另一方面我们希望每个分桶内有足够数量的评分从而产生可靠的参数估计。可以考虑为
user bias使用不同的表现形式,一个简单的选择是:使用线性函数来捕获user bias随时间的偏移drift。对用户 , 定义其平均的评分日期为 。假设用户 在日期 有过评分,则在日期 定义:
其中:
- 衡量时刻 到 之间的天数。
- 为符号函数。
- 为超参数,它根据
Probe数据集进行交叉验证得到,这里我们设置为 。
则
user-bias定义为线性函数:其中 为斜率, 为截距,它们都从数据中学习得到。
这里用线性函数来拟合,虽然简单但是实用。当然也可以采用更复杂的函数来拟合。
建模
user bias的线性函数和用户行为中的渐进式漂移gradual drift相吻合。但是我们还观察到用户的突发式漂移sudden drift。如,我们发现用户在某一天给出的多个评分往往几种在单个值。这种效应的跨度通常不到一天,这很可能反映了用户当时的心情。为解决这种超短期效应,我们为每个用户在每一天配置了一个参数 ,从而解决
day-specific效应:考虑了以上这些时间效应之后,
baseline predictor现在为:如果将它作为一个独立的
predictor,则其在Quiz数据集上的RMSE结果为0.9605。除了
item bias和user bias之外,另一个时间效应影响的因素是用户评分范围(即评分的上限和下限)的改变。之前我们考虑
item bias时,认为item bias是和用户无关的。事实上由于用户的评分范围的变化, 也不完全和用户无关。为解决该问题,我们定义一个用户相关的、依赖时间的范围参数 ,则baseline predictor进一步改进为:的实现可以参考 ,即:
其中 是 的时不变的部分, 代表每天变化的部分。
采用了 之后,
baseline predictor在Quiz数据集上的RMSE下降到了0.9555。有意思的是,这个不包含
user-item交互的基准模型得到了和Netflix Cinematch推荐系统几乎相同的效果,后者在Quiz数据集上的RMSE为0.9514。这种思考方式是自顶向下拆解任务的模型:先判断影响任务的背后要素,然后对这些要素分别建模。
14.1.2 频次效应
我们位于另一个参赛小组的同事发现的规律引起了我们的注意:用户在给定日期的评分数量是当天数据变化的重要因素。
令 为用户 在日期 上评分的数量,则它就是当天的评分频次。考虑到不同用户的频次差异非常大,我们采用对数之后四舍五入,即 , 为超参数。
有意思的是:即使 完全由用户 驱动,它也会影响
item bias而不是user bias。其原因在后面解释。因此,对于每个item,我们定义变量 ,它捕获item在对数频次 上的bias。因此baseline predictor进一步改进为:我们注意到:将 乘以 也是有道理的,因为这表示对
bias的范围进行约束。但是我们并未在实际中应用,也没有对此展开实验。将频次项添加到
item bias中的效果非常明显,baseline predictor在Quiz数据集上的RMSE从0.9555下降到了0.9278。这已经优于原始的Netflix Cinematch算法。对于
baseline predictor无论它多么准确,都无法产生个性化的推荐,因为它没有包含任何user-item之间的交互。从某种意义上讲,它捕获了与个性化推荐不太相关的数据部分,这使得后续的个性化推荐模型能够使用更加干净、更加高质量的数据,从而产生更好的推荐。频次为什么效果好?为观察频次贡献的来源,我们有两个经验洞察:
- 首先可以看到:对于单独的
baseline predictor,引入频次项的效果非常强大。但是在后面我们将会看到,它们在完整的predictor中贡献小得多。当添加了user-item交互项(矩阵分解方法或邻域方法)时,它们的大部分收益都会消失。 - 其次,频次与
item bias配合使用时似乎有所帮助,但是与user bias配合使用时却毫无帮助。
- 首先可以看到:对于单独的
频次有助于区分用户对大量电影进行评分的日期,通常这些评分日期和用户观看电影的日期有一定的距离,这使得评分日期的评分和观看日期的评分存在一定差异。我们认为:当用户进行大量评分时,用户仍然会反映其正常偏好,但是电影会呈现不对称的评分。
某些电影被部分用户喜欢,并能很长时间内记住(印象深刻);但是另一部分用户不喜欢它们,并逐渐遗忘掉,即沉默的负样本。因此,只有非常喜欢它们的用户才会在观看日期之后一段时间对其进行评分,而不喜欢它们的用户则压根不会想起它们。
这在热门电影上表现得非常明显,即:要么被用户喜欢且记忆深刻,要么被用户遗忘或忽略。
某些电影很糟糕,不喜欢它们的用户总是做出负面评价;但是另一部分喜欢的用户会逐渐将其遗忘,即沉默的正样本。因此,在观看电影很长时间之后,只有不喜欢该电影的用户才对其进行评分。
这就解释了这种
bias和电影相关联,和用户无关联。这也解释了为什么当添加了user-item交互项时,大多数效果消失了:这些交互项已经 “了解” 用户对于电影是喜欢还是不喜欢。因此,我们假设高频次并不能代表用户偏好的较大变化,但是我们假设大多数情况下高频次会对电影的频分带来
bias:有些电影会带来大量的正面评价(沉默的负样本)、有些电影会带来大量的负面评价(沉默的正样本)。进一步验证我们的假设具有实际意义。如果频次确实代表了选择性的偏见
biased selection,则应该将它们视为噪声,并在进行推荐的时候分离出来。即:训练的时候考虑频次项,但是推荐的时候剔除这一项。因为我们考虑的是:给用户推荐的时候,用户的当时的评价(而不是经过一段时间之后)。
14.1.3 预测未来
我们的模型包含大量的
day-specific具体于日期的参数,如 。在训练期间我们可以从训练数据中学得它们的值,但是在预测期间,尤其时在未来的日期(如明天),如何选择它们的取值?比如在训练集中 最大为300,但是预测时 。一种简单的方法是:将这些具体于日期的参数设为默认值,如 默认为零, 默认为零。
一个问题是:如果我们不能用这些具体于日期的参数来预估未来的评分,那么它们存在的意义是什么?我们大费周章的建立模型、训练参数,结果在预测期间将它们都置为零,似乎这些参数存在的意义不大。
事实上,我们对时间的建模并未尝试捕获未来的变化,它捕获的是短时效应,这些短时效应对用户的历史反馈产生了重大影响。当模型识别出这类影响时,必须对其进行打压以便让我们能够对更长期的信号进行建模。这使得我们的模型可以更好的捕获数据的长期特征,同时让这些
day-specific参数吸收掉短期的波动。因此,
day-specific参数完成了训练数据的清理,从而改善了模型对将来的预测。
14.1.4 混合模型
我们最终的混合模型包含了时间效应的
baseline predictor:为学习参数 我们最小化目标函数,并通过随机梯度下降法来优化:
我们对每个参数都是用独立的学习率、对每个参数使用独立的正则化系数:

注意: 的正则化尽可能接近
1.0,其它正则化则尽可能接近0.0。另外,除了 的初始值为1.0之外, 所有其它参数的初始化值为0.0。该
predictor在Quiz数据集上的RMSE为0.9555。我们最终的混合模型包含了频次效应的
baseline predictor:我们也是用随机梯度下降进行优化,并使用独立的学习率、正则化系数。

对于超参数 我们选择为
6.76。该
predictor在Quiz数据集上的RMSE为0.9278。我们将这个模型记作[PQ1]。
14.2 MF Predictor
MF模型假设每个用户 关联一个用户因子向量 ,每个item关联一个item因子向量 , 为向量的维度。另外,可以将 视为用户 隐式反馈的item集合(知道有评分,但是不知道评分的具体取值)。因此,每个item还关联一个item隐式反馈因子向量 。进一步的,我们考虑时间效应,即:用户的偏好随着时间改变,即 。这里我们认为
item的特质是时不变的。因此得到timeSVD ++模型:其中 为考虑时间效应的
baseline predictor:注意:这里的归一化形式为 ,我们选择了 。
我们对 的每个分量进行建模:
类似于
user bias,我们有:其中:
- 捕获了用户因子的时不变部分,即用户兴趣的稳定部分。
- 捕获了用户因子的时间线性变化部分,即用户兴趣的长期变化部分。
- 捕获了用户因子的瞬时变化部分,即用户的兴趣的
day-specific部分。
我们还可以使用内存效率更高的版本,此时没有
day-specific部分:我们还可以引入频次效应。由于频次会影响电影的感知,因此我们尝试将频次诸如到
item因子向量中。因此,我们为每个电影因子建立另一个版本:这里 为引入频次效应的
baseline predictor:这里 。
注意:虽然引入了频次效应的
item bias效果非常显著,但是引入了频次效应的item因子(即 )的增益非常小。我们在最终混合模型中包含了矩阵分解的多个变种。所有模型都是通过直接应用于原始数据的随机梯度下降来学习,无需任何预处理或后处理。
在对模型混合的过程中,我们发现 每个
predictor的过拟合是有益的。即:让每个predictor训练更长的step, 从而对训练集过拟合。第一个
MF predictor为:bias相关参数的学习率和正则化系数如下:
对于因子向量 ,我们使用
0.0015的正则化系数,初始学习率为0.008并以0.9的衰减系数在每轮迭代中衰减。 对于 ,其学习率为1e-5,正则化系数为50。该
predictor的三个变种,以及各自在Quiz数据集上的RMSE为:xxxxxxxxxx31d=20, 迭代step = 40, RMSE = 0.89142d=200, 迭代step = 40, RMSE = 0.88143d=500, 迭代step = 50, RMSE = 0.8815第二个
MF predictor为:的学习率为
0.004,正则化系数为0.001。其它参数的学习率和正则化系数如前所述。每个predictor也针对训练集过拟合。该
predictor的两个变种,以及各自在Quiz数据集上的RMSE为:xxxxxxxxxx21d=200, 迭代step = 80, RMSE = 0.88252d=500, 迭代step = 110, RMSE = 0.8841第三个
MF predictor为:的学习率为
2e-5,正则化系数为0.02。其它参数的学习率和正则化系数如前所述。每个predictor也针对训练集过拟合。该
predictor的六个变种,以及各自在Quiz数据集上的RMSE为:xxxxxxxxxx61d = 200, 迭代step =40, RMSE=0.87772d = 200, 迭代step =60, RMSE=0.87873d = 500, 迭代step =40, RMSE=0.87694d = 500, 迭代step =60, RMSE=0.87845d = 1000, 迭代step =80, RMSE=0.87926d = 2000, 迭代step =40, RMSE=0.8762我们将其中 以及迭代
step为40的变种记作[PQ2]。
14.3 Neighborhood Predictor
除了矩阵分解之外,邻域模型也是协同过滤常用的方法。尽管邻域方法的准确性通常不如矩阵分解方法,但是邻域方法具有可解释性、对新输入的评分无需重新训练模型等优点而受到欢迎。
邻域模型通常分为
Userbased CF和Itembased CF,这里我们主要基于Itembased CF。我们考虑邻域模型:
其中:
为
baseline predictor,它给出了user-item交互以外的预估部分。为基于显式反馈得到的
item-item相似度。为根据经验公式得到的基准预估:
为基于隐式反馈得到的
item-item相似度。这里它和 的主要区别在于:在计算隐式反馈时仅考虑是否产生评分,而不考虑评分的具体数值。事实证明使用两组相似度是有益的:一组 与评分值相关;另一组 与是否评分相关。
注意:这里的相似度 以及
baseline predictor中的biase都是从数据中学到。当考虑时间效应时,需要考虑两个部分:
一个是
baseline predictor,它解释了大多数观测到的信号。这部分和因子模型没有什么区别,可以根据下面两种方式来考虑时间效应。另一个是捕获
user-item交互的部分,这部分需要采用不同的时间效应处理策略。item-item相似度 反映了item的固有属性,因此不会随着时间变化。因此学习过程应该确保它们能够捕获无偏的长期价值,而不会受到漂移drifting的影响。实际上如果处理不当,数据的时变性质
time-changing nature会掩盖很多长时间的item-item关系:- 一方面, 如果用户在短时间内将
item都给予很高的评分,这使得它们的相似度很高从而具有较高的 。 - 另一方面,如果用户在很长时间(如
3年)内将item都给予很高的评分,则由于用户的口味很可能发生变化,因此这两个item之间可能没有任何关系。这时它们应该具有较低的相似度从而具有较低的 。
因此我们考虑同一个用户 评价的两个
item之间的相似性进行时间衰减加权:时间间隔越大权重越小,时间间隔越小权重越大。这里我们考虑指数时间衰减:其中 控制了用户 的衰减系数,并且从数据中学习。
- 一方面, 如果用户在短时间内将
最终我们考虑时间效应的
ItemBased CF模型为:我们采用随机梯度下降法来最优化带正则化的平方误差代价函数,与
bias相关参数的学习率、正则化系数如前所述。这里 的学习率都为0.005,正则化系数为0.002。 使用了一个非常小的学习率1e-7,正则化系数为0.01。我们还尝试了其它的时间衰减模式,如对计算更友好的 ,这导致了相同的准确率并大大降低了训练时间。
引入时间效应之后,邻域模型的准确率得到提高。相比静态领域模型,考虑时间的邻域模型在
Quiz数据集上的RMSE从0.9002降低到了0.8870。从某种角度来看,通过使用混合方法,其结果甚至比报告的结果要更好。如:在其它算法的残差上应用邻域方法,比如在
baseline predictor的残差上。我们从中得到的一个经验教训是:与设计更复杂的模型相比,解决数据中的时间动态性可能对结果准确性产生更大的影响。
我们在最终混合模型中包含了邻域分解的多个变种。
第一个
Neighborhood Predictor为:该
predictor的三个变种,以及各自在Quiz数据集上的RMSE为:xxxxxxxxxx31迭代 step = 20, RMSE = 0.88872迭代 step = 25, RMSE = 0.88853迭代 step = 30, RMSE = 0.8887最终迭代
20和30次的变种进入到最终混合模型中。第二个
Neighborhood Predictor为:我们使用随机梯度下降法迭代
20步,在Quiz数据集上的RMSE为0.8870。该predictor被记作[PQ3]。
我们还尝试扩展了邻域模型:添加一个没有归一化的
item-item相似性 :我们认为同一个用户给出的评分都比较相似,因此 使用较高的初始值
0.5来初始化(相比而言 采用0.0来初始化)。对于 我们使用较慢的学习率1e-5。我们采用随机梯度下降法迭代
25步,最终在Quiz数据集上的RMSE为0.8881。我们认为:如此微不足道的RMSE收益并不能证明第三个item-item相似度 的引入是合理的。该
predictor也包含在最终的blend中。
14.4 RBM 扩展
我们扩展了受限玻尔兹曼机
Restricted Boltzmann Machines:RBM模型。原始模型通过使隐单元成为当前用户对电影评分的条件,从而显著提升性能。但我们发现,通过调节可见单元也可以达到类似的显著性能提升。直观的讲,每个
RMB可见单元都对应于一个特定电影,因此它们的bias代表了电影bias。但是我们知道其它类型的bias在数据中更为重要,即user bias、single-day user bias、以及frequency-based movie bias。因此我们根据当前用户和日期,把这些bias添加到可见单元。首先,我们使用条件多项式分布对观察到的二元评分矩阵 的每一列进行建模:
其中:
为隐向量, 为隐单元数量。
表示对
item评分为 , 为:和 对应于模型的
bias和权重。
我们扩展了原始的条件分布。令当前的用户为 ,当前的日期为 ,则我们添加了
user-date bias:其中 为
user-specific参数, 为user-date-specific参数。我们通过随机梯度下降来训练模型,其中 的学习率为
0.0025, 的学习率为0.008。另外我们这里采用online学习,即每次仅对一个训练样本进行更新。注意:除非另有说明,否则我们将使用原始论文中建议的相同学习率权重衰减
weight decay,即0.001。考虑到频次的显著影响,我们这里进一步考虑频次。假设用户 在日期 关联了一个评分频次 ,则调整后的
RBM为:其中 是一个
movie-frequency-specific变量,其学习率为0.0002。这里也采用online learning。受到
Pragmatic Theory团队的启发,我们在使用频次时,也对visible - hidden权重进行修改。我们使用frequency-dependent权重 来代替原始权重 :我们通过
online-learning来学习新的参数 ,其学习率为1e-5。但是事实证明:当存在
frequency-bias时,权重的这种扩展几乎不会提高性能,并且还提高了训练时间,因此我们不太推荐。但是这仍然是我们frequency-aware RBM实现的一部分。受到
day-specific用户因子(即 )的影响,我们尝试创建day-specific RBM隐单元:在 个隐单元的基础上,我们还添加 个day-specific隐单元。如果一个用户在 个不同日期进行评分,则我们创建这 个day-specific隐单元的 个并行的拷贝,所有这些拷贝共享相同的hidden-visible权重、hidden bias、conditional connection。同样地,每个并行的拷贝仅连接到与其对应日期给出评分相应的可见单元。即:设当前日期为 ,对应的
day-specific隐单元为 。定义指示向量 表示当前用户在日期 对哪些电影产生评分。因此建模用户特征的隐单元为:
在我们的实现中,我们将该模型和
frequency-biased RBM一起使用。所有该day-specfic单元相关的参数都是通过mini-batch随机梯度下降来学习,学习率为0.005,权重衰减为0.01。事实表明,这种方法的效果不大理想,并且需要进一步完善。
我们在最终混合模型中包含了
RBM的多个变种。第一个
RBM Predictor为:根据我们的参数配置,
RBM通常在Quiz数据集上大约迭代60~90轮就可以收敛。但是为了最终的模型混合我们继续对训练集训练从而过拟合。该
predictor的四个变种,以及各自在Quiz数据集上的RMSE为:xxxxxxxxxx41F=200, 迭代 step = 52, RMSE = 0.89512F=200, 迭代 step = 62, RMSE = 0.89423F=400, 迭代 step = 82, RMSE = 0.89444F=400, 迭代 step = 100, RMSE = 0.8952最终迭代
20和30次的变种进入到最终混合模型中。第一个
RBM Predictor为:该
predictor的两个变种,以及各自在Quiz数据集上的RMSE为:xxxxxxxxxx21F = 200, 迭代 step =90, RMSE=0.89282F = 200, 迭代 step =140, RMSE=0.8949这两个变种分别称作
[PQ4]和PQ[5]。
有意思的是:仅仅通过
RBM最好的结果是RMSE=0.8928,但是通过利用kNN来进一步拟合RBM的残差,则可以进一步显著降低RMSE。但是,我们并未针对这个现象进行专门的试验。最后,一个具有
50个隐单元,以及50个day-specific隐单元的RBM迭代70轮,产生的RMSE = 0.9060。该模型被称作[PQ6]。
14.5 GBDT 混合
在
Netflix数据集上获得有竞争力的结果,其关键在于使用精细sophisticated的混合方案blending scheme。这些混合方案将很多单独的predictor合并为最终的解决方案solution。我们的混合技术应用于三组不同的
predictor:- 第一组由
454个predictor组成,代表了BellKor的Pagmatic Chaos小组的所有predictor。 它们匹配了Probe和Qualifying的结果。 - 第二组由
75个predictor组成,它们从前面454个predictor中选择而来。 - 第三组由
24个predictor组成,它们匹配了Probe和Qualifying结果。
- 第一组由
尽管通过挖掘数据的新特征可以在竞赛中取得重大突破,但是这些新特征越来越稀少(绝大多数好用的特征都已经被人们发现)并难以获取。当进入比赛尾声时我们意识到:即使是一些新颖和准确的
predictor(采用新特征、新模型),它也难以对混合结果产生重大影响。因为在上百个predictor之间,单个predictor的影响太小。我们推断:通过探索新的混合技术,或改进现有的混合技术,可以获得更好的效果。混合技术提供了在很短的时间内以较低的代价来改善预测性能:
- 首先,与单个
predictor不同,更好的混合技术与最终结果直接相关。 - 其次,混合技术同时涉及多个
predictor,而不是一次影响一个predictor,影响范围更大。
- 首先,与单个
我们利用
GBDT来混合我们的众多predictor,我们将每个predictor的输出作为一路特征,并额外增加了四路特征:user support(用户所有评分的电影总数)、movie support(电影所有被评分的总数)、频次frequency(用户当天评分的电影总数)、评分日期(数据集中最早一个评分到当前的天数)。我们将
GBDT应用于上述454个predictor和75个predictor。我们将Probe数据集用于训练GBDT,并将其应用于Qualifying数据集。GBDT的参数配置为num_tree = 200、tree_size=20、学习率0.18、采样率0.9。最终得到Quiz数据集上的RMSE为:454个predictor的RMSE=0.8603、75个predictor的RMSE=75。当
GBDT应用在更小的24个predictor上时,GBDT的参数配置为num_tree = 150、tree_size=20、学习率0.2、采样率1.0。最终得到Quiz数据集上的RMSE为0.8664。注意:我们的实验并未对
GBDT的四个参数(num_tree子树的数量、tree_size子树大小、学习率、样本采样率)进行敏感性分析。引入用户和电影的聚类也是有益的,这可以在
GBDT中引入用户或电影的 “类别” 特征(即用户/电影是属于哪个类簇)。我们可以根据用户的
user support将用户分为多个桶,然后同一个桶内的用户视为同一个粗。由于我们在GBDT中已经增加了用户支持度特征,因此这一能力已经被GBDT实现:GBDT本身就有分桶并划分样本到各个桶的能力。但是,我们也可以引入其它类型的聚类,如:根据矩阵分解模型计算用户因子向量,然后根据用户因子向量来聚类。
item因子向量也可以类似地进行聚类。我们在
24个predictor的GBDT中实验了以下三种聚类形式:从
timeSVD ++模型中得到因子向量: ,其中维度 。另外所有的单个
bias项都作为GBDT的特征。另外,每个
user-item组合 ,我们增加了20维的电影因子 、以及20维的用户因子 作为GBDT的特征。最终导致模型的
RMSE = 0.8661。然后我们采用具有
20个隐单元的RBM,隐向量作为用户的embedding来代替timeSVD ++中的用户因子向量。电影的representation仍然使用timeSVD ++模型。最终导致模型的RMSE也是0.8661。最后,我们在
timeSVD++特征的基础上增加了kNN特征,即:对每对 ,我们找到与 最相似的top 20部电影,并由 对其进行评分。我们添加了这些电影的评分乘以对应的相似度作为额外的特征,这些相似度是通过归一化的Pearson相关性计算而来。最终模型的RMSE略微降低到0.8860。
上述的
GBDT用于用户对电影评分的类别:1~5一共五类。这是作为分类任务来处理。另一种用法是视为回归问题来处理。对每个用户,我们计算了由相应
RBM的50个隐单元的值组成的50维特征向量。对每部电影,我们使用GBDT来将50维用户向量来拟合真实的用户评级,从而解决回归问题,最终RMSE = 0.9248。该模型记作[PQ7]。
14.6 总结
广泛的参与、广泛的新闻报道、许多出版物都反映了
Netflix大奖赛的巨大成功。处理 “电影” 这个贴近老百姓身边的话题,绝对是一个好的开端。然而,由于以下几个因素,大赛最终取得了成功:第一个成功因素是在
Netflix的组织方面。他们发布了一个珍贵的数据集,从而为推荐领域做出了巨大的贡献。除此之外,比赛的设计和进行都是完美的。例如,数据集规模正好符合目标:比同类型数据集大得多、更具代表性,但是又小到足以让任何拥有商业
PC的人都能参与比赛。再举个例子,前面提到将数据集分为三个部分:Probe, Quiz, Test,这对于确保比赛的公平性至关重要。第二个成功因素是众多选手的广泛参与。该比赛引起了巨大的轰动,导致更多的人进一步参与。选手之间广泛有着的合作精神,他们在网络论坛和学术期刊上公开发表和讨论了他们的创新成果。这是一个大社区的共同进步,使得所有参与者的体验更加愉悦和高效。事实上,这提升了比赛的性质,比赛就像一场长距离马拉松,而不是一系列短距离冲刺。
另一个有帮助的因素是运气。最突出的一个是
10%提升目标的设定。这个数字的任何微小偏差都会使得比赛过于简单或者过于复杂从而难以进行。推荐系统科学是这场比赛的主要受益者。许多新人开始涉足该领域并做出了贡献,相关出版物数量明显激增,
Netflix数据集是该领域开发更好算法的直接催化剂。在众多新算法的贡献中,我想强调一个:那些不起眼的
baseline预测器(或者bias),它们捕获数据中的主要影响。当大多数文献集中于更复杂的算法方面,但是我们知道:对主要效应的精确处理,至少与提出突破性的模型同样重要。