深度强化学习
一、PPO [2017]
近年来,人们提出了几种不同的方法从而用神经网络函数近似器来进行强化学习。领先的竞争者是
deep Q-learning(《Human-level control through deep reinforcement learning》)、平凡的策略梯度policy gradient方法(《Asynchronous methods for deep reinforcement learning》),以及trust region / natural策略梯度方法(《Trust region policy optimization》)。然而,在开发一种scalable(用于大型模型和并行实现)、数据高效和鲁棒(无需超参数调优即可在各种问题上取得成功)的方法方面仍有改进空间:Q-learning(带function approximation)在许多简单的问题上都失败了,而且人们对其理解不深。- 平凡的策略梯度方法的数据效率和鲁棒性很差。
trust region policy optimization: TRPO相对复杂,而且与包含噪声(如dropout)或参数共享(在策略函数和价值函数之间参数共享、或与辅助任务之间参数共享)的架构不兼容。
论文
《Proximal Policy Optimization Algorithms》试图通过引入一种算法来改善目前的状况,这种算法可以达到TRPO的数据效率和可靠性能,同时只使用一阶优化first-order optimization。论文提出了一个具有clipped probability ratio的新目标,它形成了对策略性能的悲观估计(即,下限)。为了优化策略,作者在来自策略的数据采样、以及对被采样的数据进行若干个epoch的优化之间交替进行。论文的实验比较了各种不同版本的代理目标
surrogate objective的性能,发现具有clipped probability ratio的版本表现最好。论文还将PPO与之前文献中的几种算法进行了比较:- 在
continuous control任务上,PPO比baseline算法表现得更好。 - 在
Atari任务上,PPO的表现(就样本复杂度而言)明显优于A2C,与ACER相似,但是PPO要简单得多。
1.1 背景:策略优化
策略梯度方法:策略梯度方法的工作原理是,计算策略梯度的估计值并应用到随机梯度上升算法中。最常用的梯度估计器的形式是 :
其中:
timestepadvantage function的一个估计,其中batch上样本的经验均值。这里的样本是在一个交替执行采样和优化的算法中获取。
推导过程:
定义回报
定义动作状态价值函数:
如果一个策略很好,那么对于所有的状态
因此策略学习可以描述为最优化问题:
策略梯度为:
根据:
因此:
为了训练更稳定,我们用
advantage function用采样值来估计
其中
使用自动微分软件的实现方法是构建一个目标函数,这个目标函数的梯度是策略梯度估计器
policy gradient estimator。估计器虽然使用相同的轨迹
trajectory对这个损失函数large policy update(见实验部分;结果没有显示,但与"no clipping or penalty"的setting相似或更差)。Trust Region方法:在TRPO方法中,一个目标函数(即,surrogate objective)被最大化,同时约束了policy update的大小。具体而言:其中:
KL为KL距离函数,注意,对于
因此,后者在分母上用更新之前的策略参数
在对目标函数进行线性近似、以及对约束进行二次近似之后,这个问题可以有效地使用共轭梯度算法进行近似解决。
证明
TRPO的理论实际上建议使用惩罚项而不是约束,也就是说,解决无约束的优化问题:其中
KL惩罚项的系数。这源于这样一个事实:即某个
surrogate objective(计算状态上的最大KL值,即KL值,即TRPO使用硬约束而不是惩罚,因为很难选择一个TRPO的单调改进monotonic improvement),实验表明,仅仅选择一个固定的惩罚系数SGD优化这个无约束优化问题的目标函数是不够的,还需要进行额外的修改。
1.2 PPO
1.2.1 Clipped Surrogate Objective
令
probability ratio:则有
因此
TRPO最大化一个surrogate objective:上标
CPI指的是保守的策略迭代conservative policy iteration: CPI(《Approximately optimal approximate reinforcement learning》)。如果没有约束,最大化
large policy update。因此,我们现在考虑如何修改目标从而惩罚那些使1的策略更新。我们提出的主要目标函数为:其中
这个目标函数的动机如下。
min函数内的第一个项是probability ratio从而修改surrogate objective,clipped objective和unclipped objective的最小值,所以最终的目标函数是unclipped objective的下限(即,悲观的下界)。注意:
- 当
- 然而,当
下图描绘了
probability ratioadvantageadvantage function,而不是Action)是正还是负。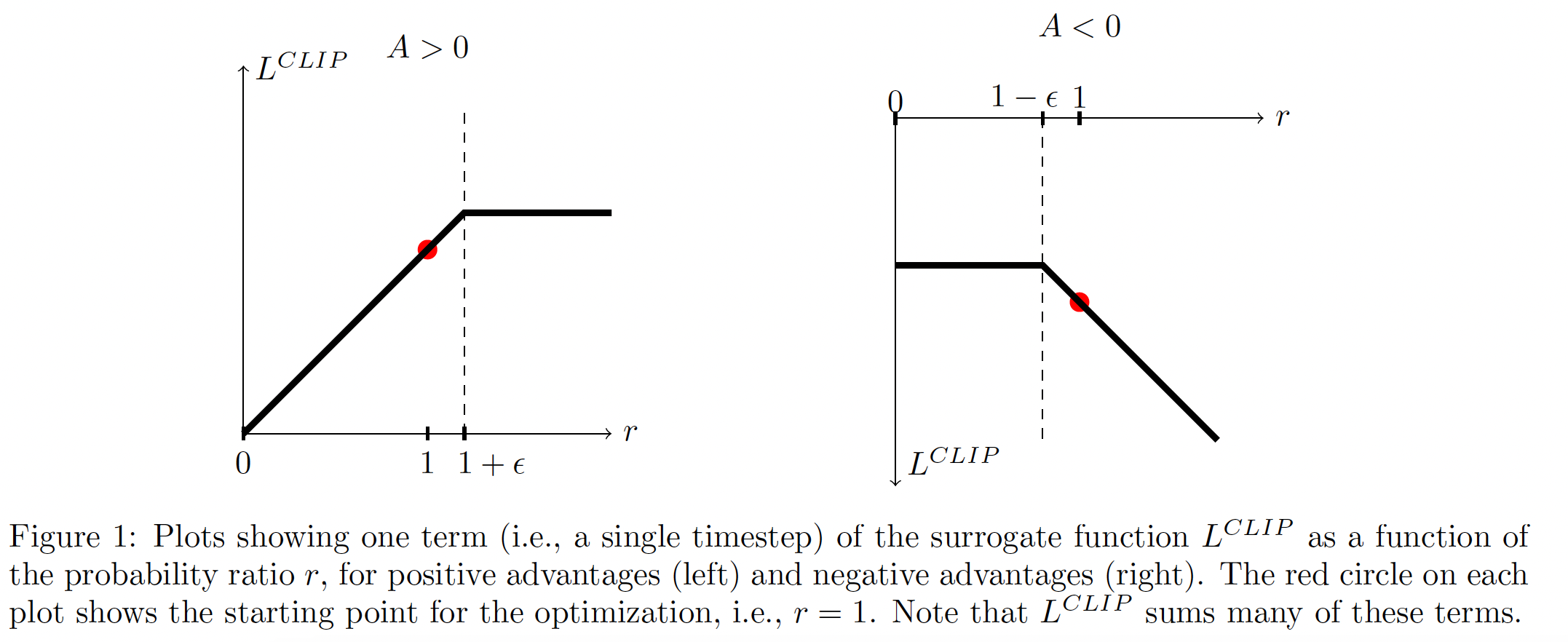
- 当
下图提供了关于
surrogate objectivecontinuous control problem上的proximal policy optimization(我们很快将介绍的算法)得到的。我们可以看到,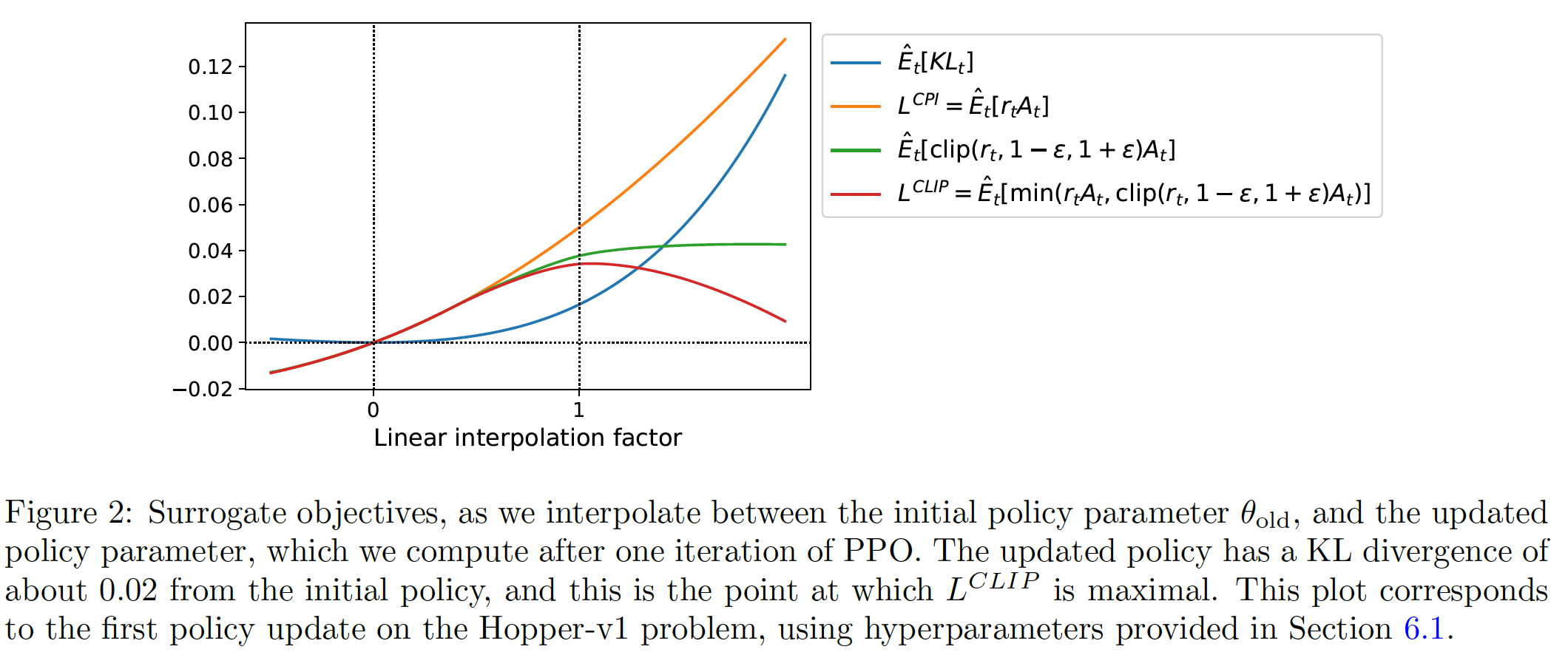
1.2.2 Adaptive KL Penalty Coefficient
另一种方法,可以作为
clipped surrogate objective的替代品,或者作为它的补充,是使用作用在KL散度上的惩罚,并调整惩罚系数从而使我们在每次策略更新时达到KL散度的某个目标值KL惩罚的表现比clipped surrogate objective更差。然而,我们在这里包括它,因为它是一个重要的baseline。在这个算法的最简单的实现中,我们在每次策略更新中执行以下步骤:
执行
minibatch SGD若干个epoch从而优化KL-penalized objective:计算
- 如果
- 如果
- 如果
更新后的
KL散度与KL散度靠近上面的超参数
1.5和2是启发式选择的,但该算法对它们并不十分敏感。
1.2.3 PPO
前面几节的
surrogate loss可以通过对典型的策略梯度进行的微小改变来计算和微分。对于使用自动微分的实现方式,我们只需构建损失大多数用于方差缩减
variance-reduced的advantage-function estimators的技术都使用了学到的状态价值函数state-value functiongeneralized advantage estimation(《High-dimensional continuous control using generalized advantage estimation》)、或者《Asynchronous methods for deep reinforcement learning》中的inite-horizon estimators。如果使用一个在策略函数和价值函数之间共享参数的神经网络架构,我们必须使用一个损失函数来结合policy surrogate和value function error。这个目标函数可以通过增加熵奖励entropy bonus来进一步增强,从而确保充分的探索,正如过去的工作《Asynchronous methods for deep reinforcement learning》和《Simple statistical gradient-following algorithms for connectionist reinforcement learning》所建议的。结合这些项,我们得到以下目标,它在每轮迭代中都被最大化(或被近似地最大化):这里有两个函数:策略函数
其中:
第一项对应于
entropy bonus(鼓励
有一种策略梯度的实现方式,在
《Asynchronous methods for deep reinforcement learning》中得到了推广并且很适合用于RNN网络:在episode长度),并使用收集的样本进行更新,这个时间段被称作trajectory segment。这种方式需要一个advantage estimator,该estimator不会查看超出时间步《Asynchronous methods for deep reinforcement learning》中使用的estimator为:其中:
trajectory segment中位于[0, T]之间的时间索引。推广这一选择,我们可以使用
generalized advantage estimation的截断版本:其中
当
generalized advantage estimation就简化回原始的形式。一个使用固定长度
trajectory segment(长度为proximal policy optimization: PPO算法如下所示。每次迭代,actors中的每一个都收集T timesteps的数据。然后,我们在这NT timesteps的数据上构建surrogate loss,并用minibatch SGD(或者通常为了更好的性能,用Adam)对其进行优化epochs。PPO Actor-Critic Style:输入:
- 初始的策略
- 外层迭代次数
actor数量trajectory segment长度minibatch size
- 初始的策略
输出:更新后的策略
算法步骤:
外层迭代:
iteration=1,2,...O:内层迭代:
actor = 1,2,..., N:在环境中执行策略
T timesteps。计算
advantage estimates
关于
surrogate loss,一共优化epoch,其中minibatch size
1.3 实验
1.3.1 Surrogate Objective 的比较
首先,我们在不同的超参数下比较几个不同的
surrogate objective:- 对于
KL penalty,可以使用一个固定的惩罚系数target KL value - 我们也尝试过在
log space(而不是线性空间)中进行剪裁,但发现其性能并没有提高。
因为我们正在为每个算法搜索超参数,所以我们选择了一个计算量小的
benchmark来测试算法。也就是说,我们使用了在OpenAI Gym中实现的7个模拟机器人任务,它们使用了MuJoCo物理引擎。我们在每个任务上做1M timesteps的训练。除了用于裁剪的超参数(KL penalty(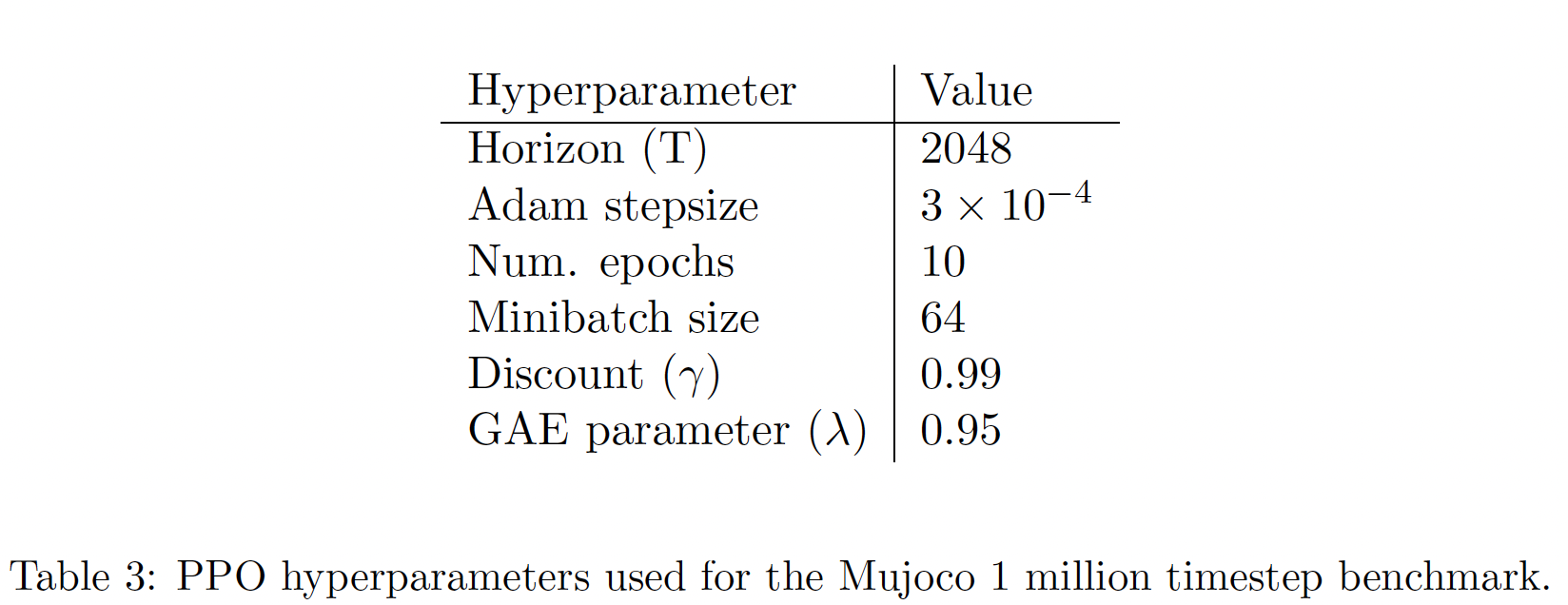
- 对于
我们使用了一个全连接的
MLP来表示策略函数。这个MLP有两个隐藏层,隐层维度为64,采用tanh非线性激活函数,输出高斯分布的平均值,并有可变的标准差。我们不在策略函数和价值函数之间共享参数(因此irrelevant的),我们也不使用entropy bonus。意思是
每个算法都在所有
7种环境下运行,每种环境下有3个随机种子。我们通过计算最后100个episodes的平均总奖励来评估算法的每次运行。我们对每个环境的分数进行shift和scale,使随机策略给出的分数为0、最好策略给出的分数为1,并对21次运行进行平均,从而为每个算法setting产生一个单一的标量。结果如下表所示。请注意,对于
No clipping or penalty的setting,得分是负的,因为在其中一个环境(half cheetah)上它导致了一个非常负的分数,这比最初的随机策略更糟糕。Clipping的效果在这三者之间最好。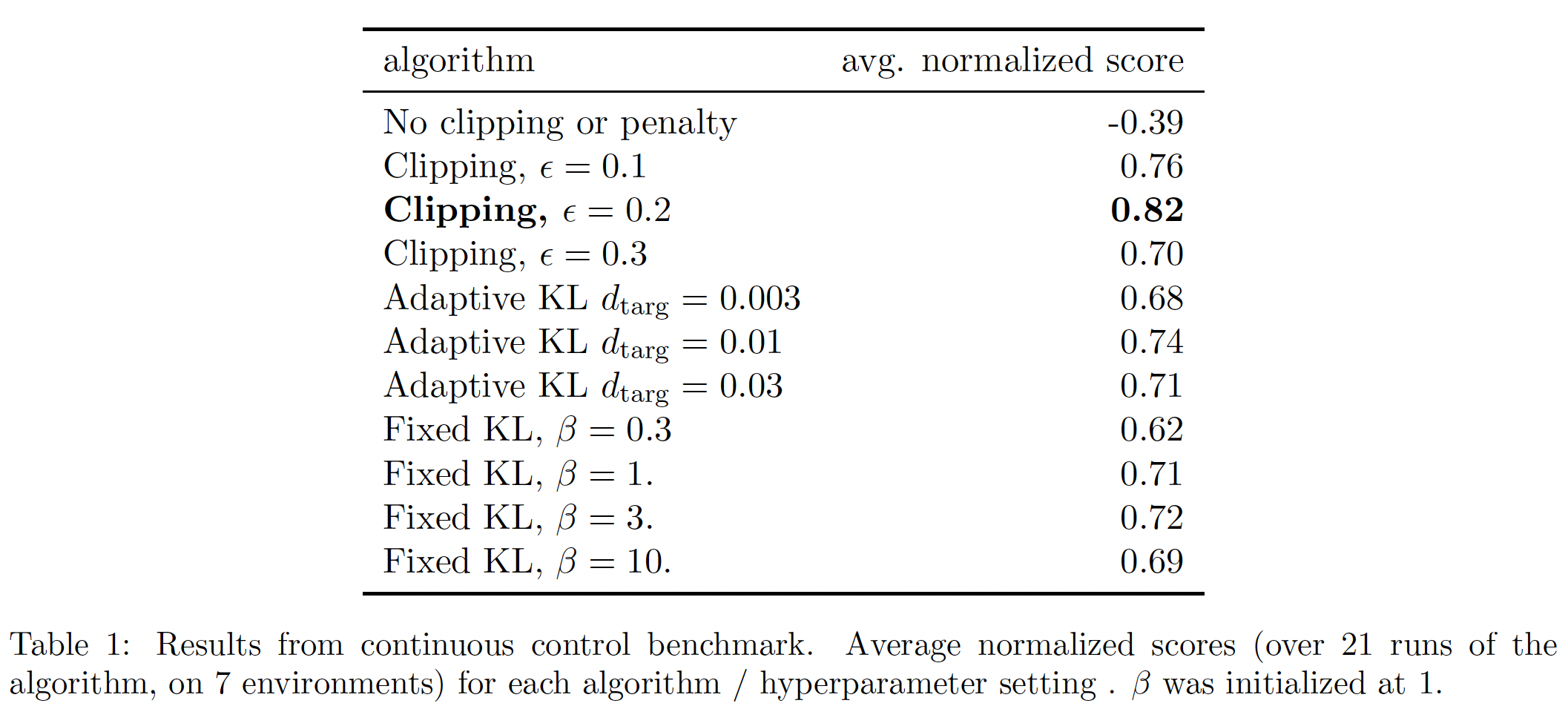
1.3.2 Continuous Domain 中的算法比较
接下来,我们将
PPO(具有clipped surrogate objective)与文献中的其他几种方法进行比较,这些文献中的方法被认为对continuous problems有效。我们与以下算法的超参数调优的实现进行了比较:trust region policy optimization(《Trust region policy optimization》)。cross-entropy method: CEM(《Learning Tetris using the noisy cross-entropy method》)。- 带有自适应步长的平凡策略梯度。
A2C(《Asynchronous methods for deep reinforcement learning》)。- 带有
trust region的A2C(《Sample Efficient Actor-Critic with Experience Replay》)。
A2C代表advantage actor critic,是A3C的一个同步版本,我们发现它的性能与异步版本(即A3C)相同或更好。对于PPO,我们使用了上一节中的超参数,其中PPO在几乎所有的continuous control environments上都优于以前的方法。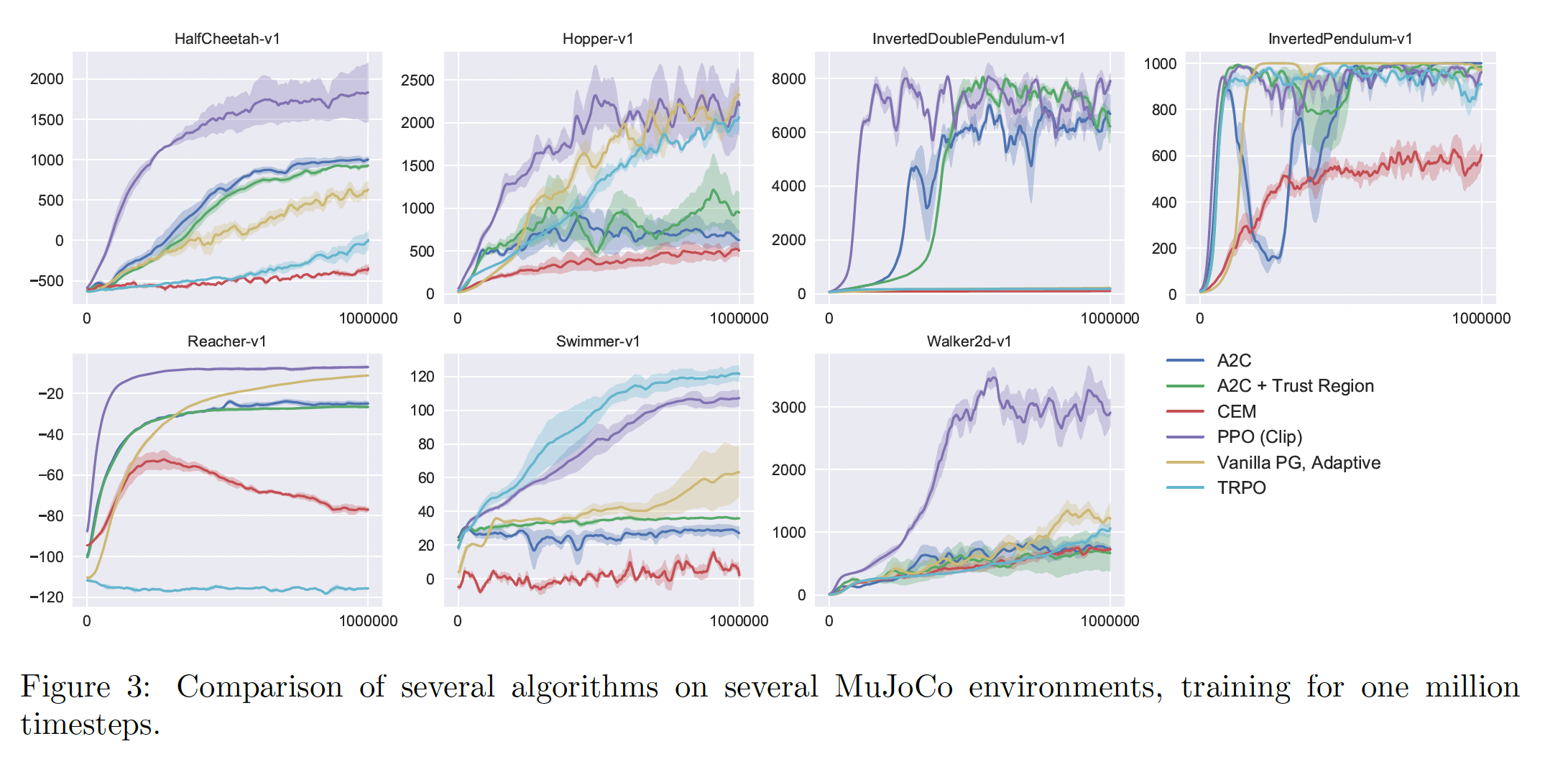
1.3.3 Continuous Domain 中的示例
为了展示
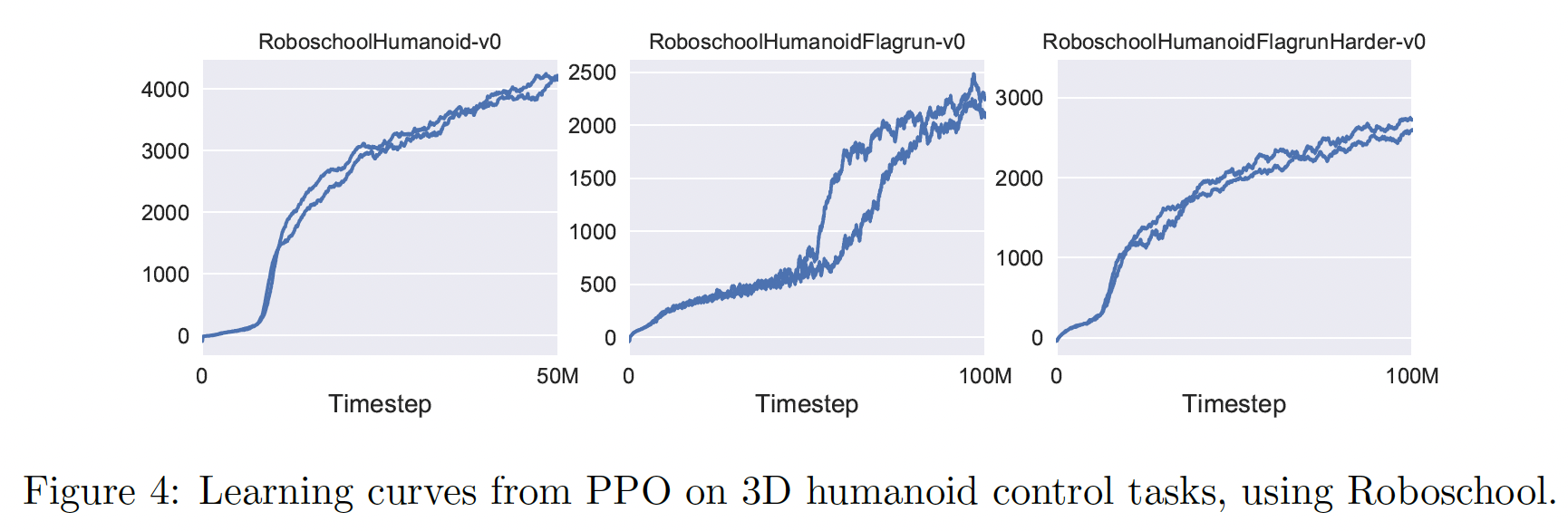
PPO在高维连续控制问题high-dimensional continuous control problems上的性能,我们对涉及三维人形机器人的一组问题进行了训练,在这些问题中,机器人必须跑动、转向、并从地面上站起来,并且同时可能被方块击中。我们测试的三个任务是:RoboschoolHumanoid:仅向前运动。RoboschoolHumanoidFlagrun:每隔200个timestep则position of target随机变化,或只要达到目标则position of target就随机变化。RoboschoolHumanoid-FlagrunHarder:机器人被方块砸中,需要从地上站起来。
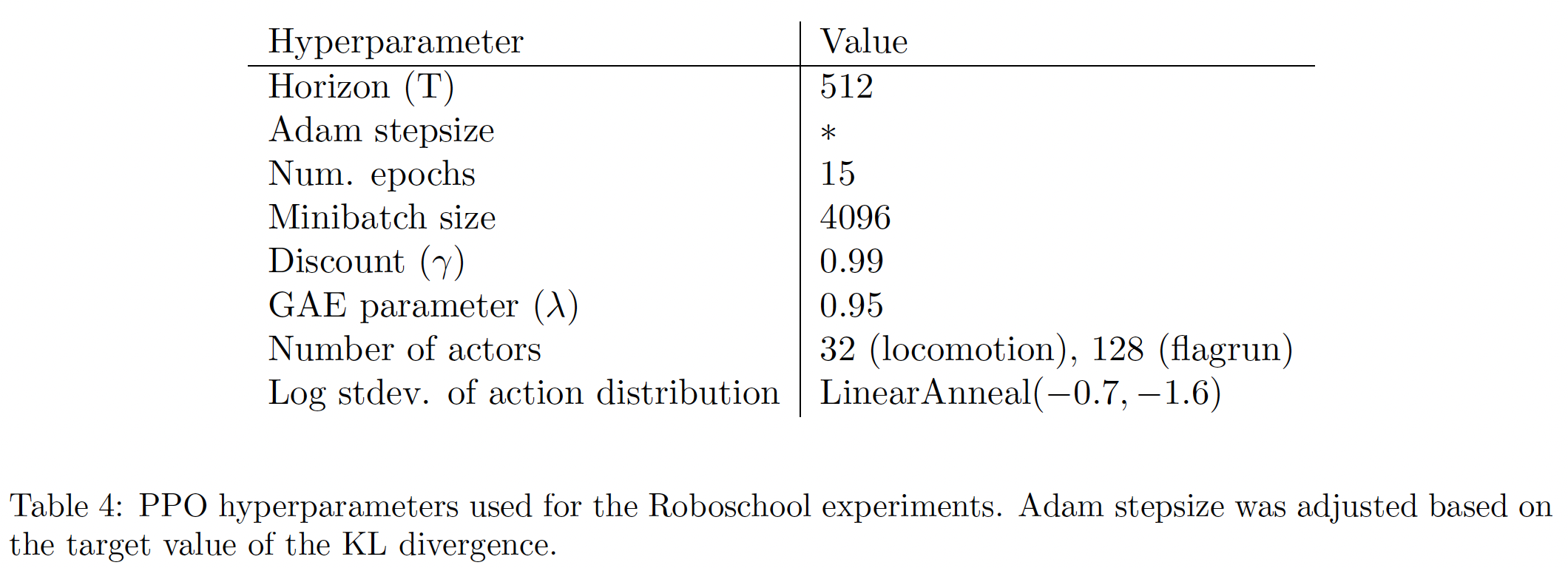
Figure 5是学习策略的静止画面,Figure 4是这三个任务的学习曲线。下表中提供了超参数。在同期的工作中,《Emergence of Locomotion Behaviours in Rich Environments》使用PPO的自适应KL变体来学习三维机器人的运动策略。
1.3.4 Atari Domain 中的算法比较
我们还在
Arcade Learning Environment这个benchmark上运行PPO,并与A2C(《Asynchronous methods for deep reinforcement learning》)和ACER(《Sample Efficient Actor-Critic with Experience Replay》)的well-tuned实现进行比较。对于这三种算法,我们使用了与《Asynchronous methods for deep reinforcement learning》相同的策略网络架构。下表中提供了PPO的超参数。对于其他两种算法,我们使用了经过调优的超参数,从而在该benchmark上的性能最大化。
下表和下图提供了所有
49个游戏的结果和学习曲线。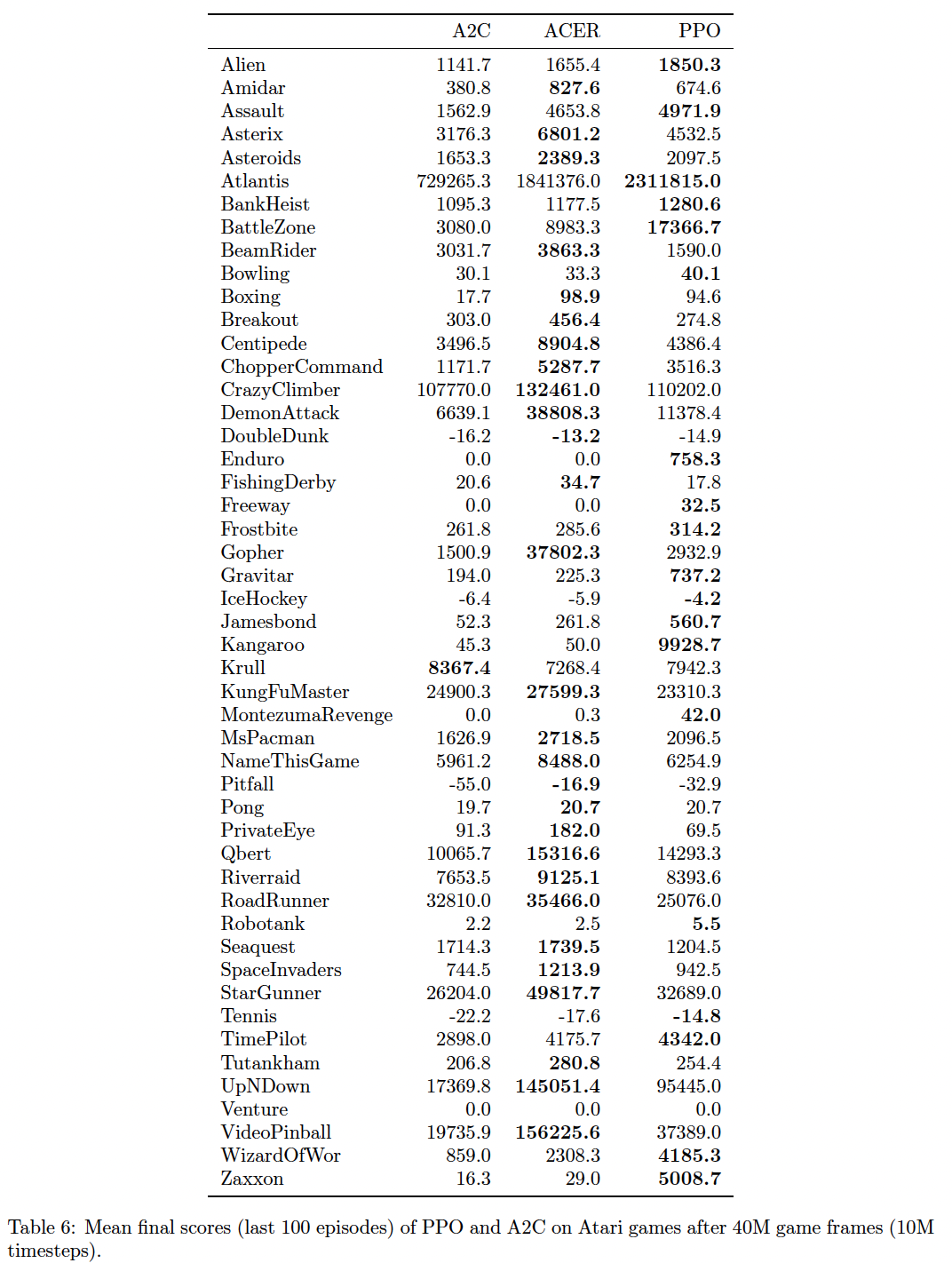
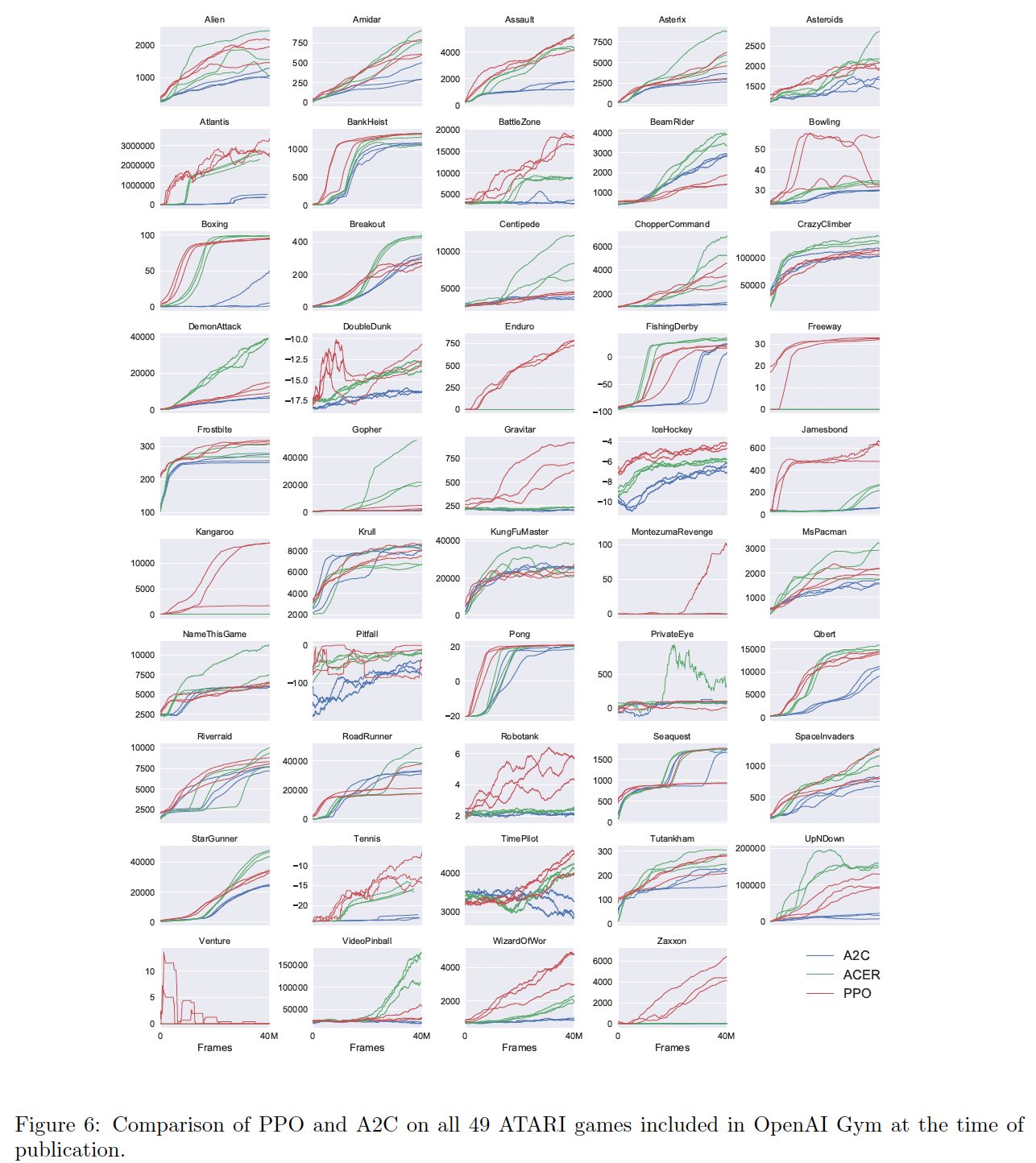
我们考虑了以下两个评分指标:
- 整个训练期间每个
episode的平均奖励(有利于快速学习)。 - 训练的最后
100个episodes的每个episode平均奖励(有利于最终表现)。
下表显示了每种算法 "获胜" 的游戏数量,我们通过对三次试验的平均得分指标来计算胜利者。

- 整个训练期间每个