七、LUT-GEMM[2022]
论文:
《LUT-GEMM: Quantized Matrix Multiplication based on LUTs for Efficient Inference in Large-Scale Generative Language Models》修改之前的论文标题:
《nuQmm: Quantized MatMul for Efficient Inference of Large-Scale Generative Language Models》
近年来,大型语言模型在各种自然语言处理(
NLP)任务上呈现出SOTA的性能。这种NLP性能的快速进步在很大程度上得益于自监督学习方法。由于预训练主导了整个训练过程而不需要昂贵的标注过程,训练数据集的规模可以大幅增加。结合效率较高的sequence-to-sequence模型架构(如Transformer),模型参数数量也显著增加。之前的研究(
《Language models are few-shot learners》、《Training compute-optimal large language models》、《Scaling Laws for Neural Language Models》)报告称:LM的性能随着模型大小遵循可预测的power-law scaling。因此,近年来出现了几种大型生成式语言模型,包括GPT-3(175B)、HyperCLOVA(204B)、Gopher(280B)、Chinchilla(70B)、Megatron Turing NLG(530B)、和PaLM(540B),从而进一步提升SOTA性能。然而,数十亿参数的模型由于GPU内存大小有限,无法容纳在单个GPU上,GPU内存通常被牺牲以提高带宽(《8-bit Inference with TensorRT》、《Up or Down? Adaptive Rounding for Post-Training Quantization》)。为解决这一问题,研究人员提出了模型并行(model parallelism),通过GPU-to-GPU通信将计算分布在多个GPU上(《Efficient large-scale language model training on GPU clusters using megatron-LM》、《Megatron-lm: Training multi-billion parameter language models using model parallelism》)。如Figure 1所示,模型并行将大型LM模型的参数分布到多个GPU上,允许训练/推理期间通过专用通道在GPU之间共享信息。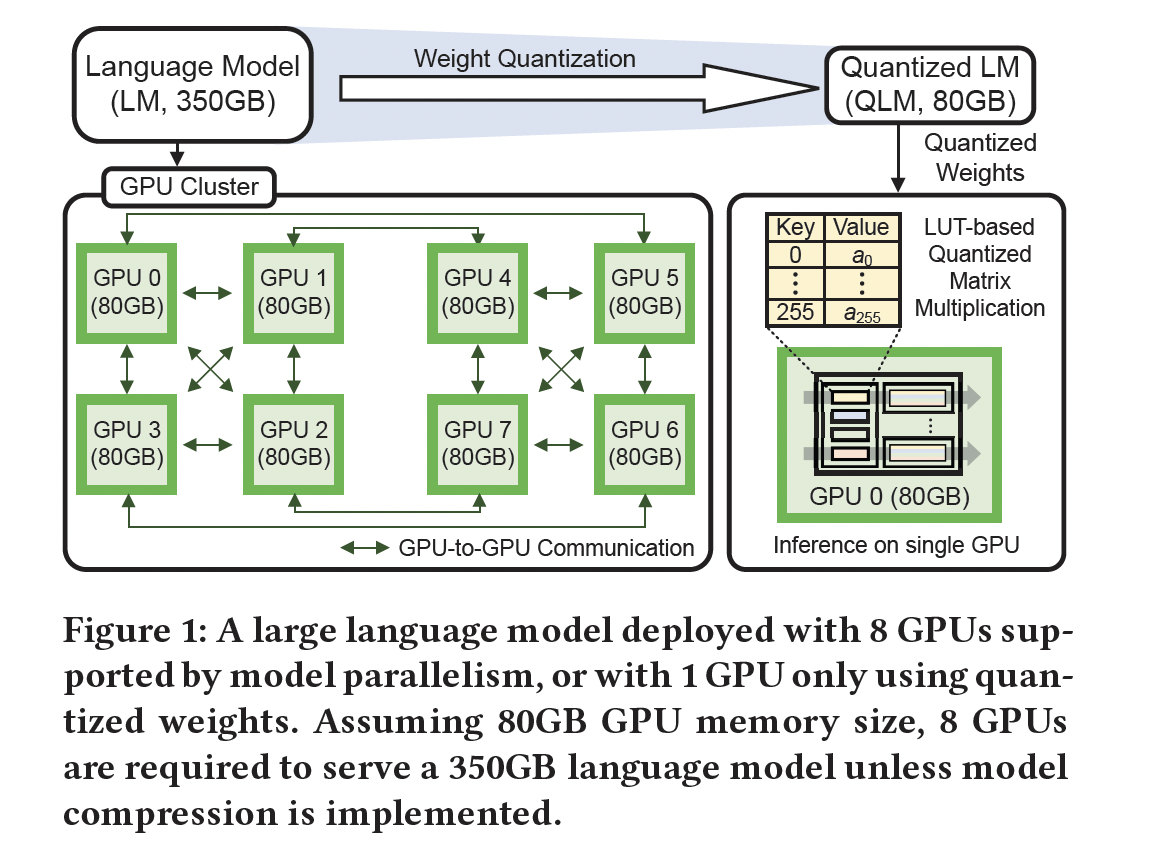
模型并行可以分为张量并行和流水线并行,从而分别提高延迟和吞吐量。但是,这种并行方案需要各种通信原语来同步
GPU产生的部分输出,如AllReduce、Reduce、Broadcast和AllGather(《Optimized broadcast for deep learning workloads on dense-GPU InfiniBand clusters:MPI or NCCL?》)。尽管GPU-specific的外部通信协议(如NVLink)可以减少通信延迟,但GPU性能的固有variance(由各种随机因素引起,如制程variance和操作系统条件)仍是另一个性能瓶颈(《Pathways: Asynchronous Distributed Dataflow for ML》)。此外,由于大型矩阵被分成子矩阵,每个GPU面临高纵横比(tall-and-skinny)的矩阵乘法,资源利用率较低(《Efficient sparse matrix-vector multiplication on CUDA》、《Biqgemm: matrix multiplication with lookup table for binary-coding-based quantized dnns》)。因此,模型并行获得的性能提升随GPU数量呈亚线性(sublinear)函数。为了缓解模型并行相关的挑战,参数量化(
parameter quantization)提供了最小化模型大小的实用解决方案,从而减少推理所需的GPU数量,如Figure 1所示。在各种量化方案中,均匀量化(uniform quantization)受青睐,可以利用基于整数的算术单元(integer-based arithmetic units)。尽管如此,均匀量化实际上被限制在8-bit,非线性操作(如softmax和normalization))可能产生不精确的结果(《Efficient 8-Bit Quantization of Transformer Neural Machine Language Translation Model》、《I-bert: Integer-only bert quantization》)。此外,为了充分利用整数算术单元,实现activation的实时量化/逆量化、以及对activation分布的精确估计是必要的(《LLM.int8 (): 8-bit Matrix Multiplication for Transformers at Scale》、《ZeroQuant: Efficient and Affordable Post-Training Quantization for Large-Scale Transformers》)。近期研究提出了4-bit weight-only quantization作为内存压缩方法(《GPTQ: Accurate Post-Training Quantization for Generative Pre-trained Transformers》、《GLM-130B: An Open Bilingual Pre-trained Model》),需要实时转换为full-precision。尽管这牺牲了使用整数算术的计算优势,但大型语言模型中weight-only quantization提供了经验证据,即与同时量化weights and activations相比,可以在给定目标准确率下获得明显更高的weight compression ratio(GPTQ, GLM-130B)。各种采用non-uniform格式的weight-only quantization方法也被提出以提高压缩率(《Biqgemm: matrix multiplication with lookup table for binary-coding-based quantized dnns》、《AlphaTuning: Quantization-Aware Parameter-Efficient Adaptation o fLarge-Scale Pre-Trained Language Models》)。在本文中,我们介绍了
LUT-GEMM kernel,旨在促进当权重使用uniform或non-uniform方法量化而保持full-precision activations时的quantized matrix multiplications。如Figure 2所示,LUT-GEMM有效地解决了之前量化方法中存在的两个问题:1):因quantized activations导致的不可避免的准确率降低。2):额外的dequantization implementation的需要。
LUT-GEMM本质上适用于quantized weights and full-precision activations,可以在保持所需precision level的同时加速推理过程。具体而言,LUT-GEMM采用binary-coding quantization: BCQ格式(《XNOR-Net: ImageNet Classification Using Binary Convolutional Neural Networks》),从而利用简单的算术操作。值得注意的是,BCQ最初是为支持non-uniform量化而提出的,需要定制硬件进行bit-level操作。在本文中,我们证明了以前的uniform量化可以重构为BCQ形式,使LUT-GEMM能同时支持non-uniform量化和uniform量化格式。因此,LUT-GEMM能够执行各种weight-only quantization方案的矩阵乘法,实现低的inference latency、以及消除对activation quantization的需要。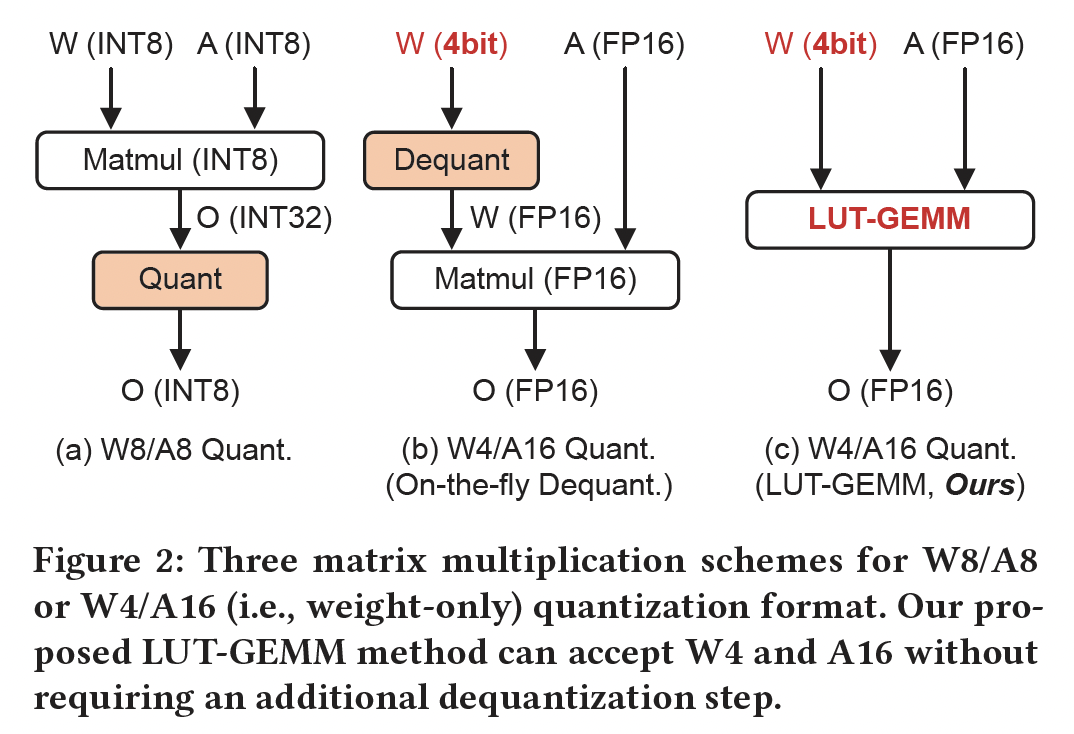
我们在本工作中的主要贡献包括:
我们证明了
BCQ能同时表示uniform and non-uniform weight quantization。我们展示了对于
BCQ格式,LUT-GEMM可以提供压缩率和延迟之间的广泛trade-offs(基于GPU-specific的高效硬件利用的方法来实现各种BCQ配置)。对大型语言模型,我们演示
LUT-GEMM可以显着加速small quantization bits的矩阵乘法,同时通过减少GPU数量从而大幅节省功耗。因此,LUT-GEMM实现了低能耗。假设对
OPT-175B的权重采用3-bit BCQ格式,由单个GPU来serve,我们的实验结果显示:与GPTQ(《GPTQ: Accurate Post-Training Quantization for Generative Pre-trained Transformers》)结果相比,LUT-GEMM可以将生成每个token的延迟加速2.1倍。
7.1 背景知识
7.1.1 生成式语言模型
大型生成式语言模型,如
GPT-3,是一种自回归模型,它以feed-forward方式使用previous tokens来预测future tokens。例如,Figure 3所示,如果提供了input context(如in-context learning中所做的,参考《Language models are few-shot learners》),则可以使用先前所生成的tokens来预测next token。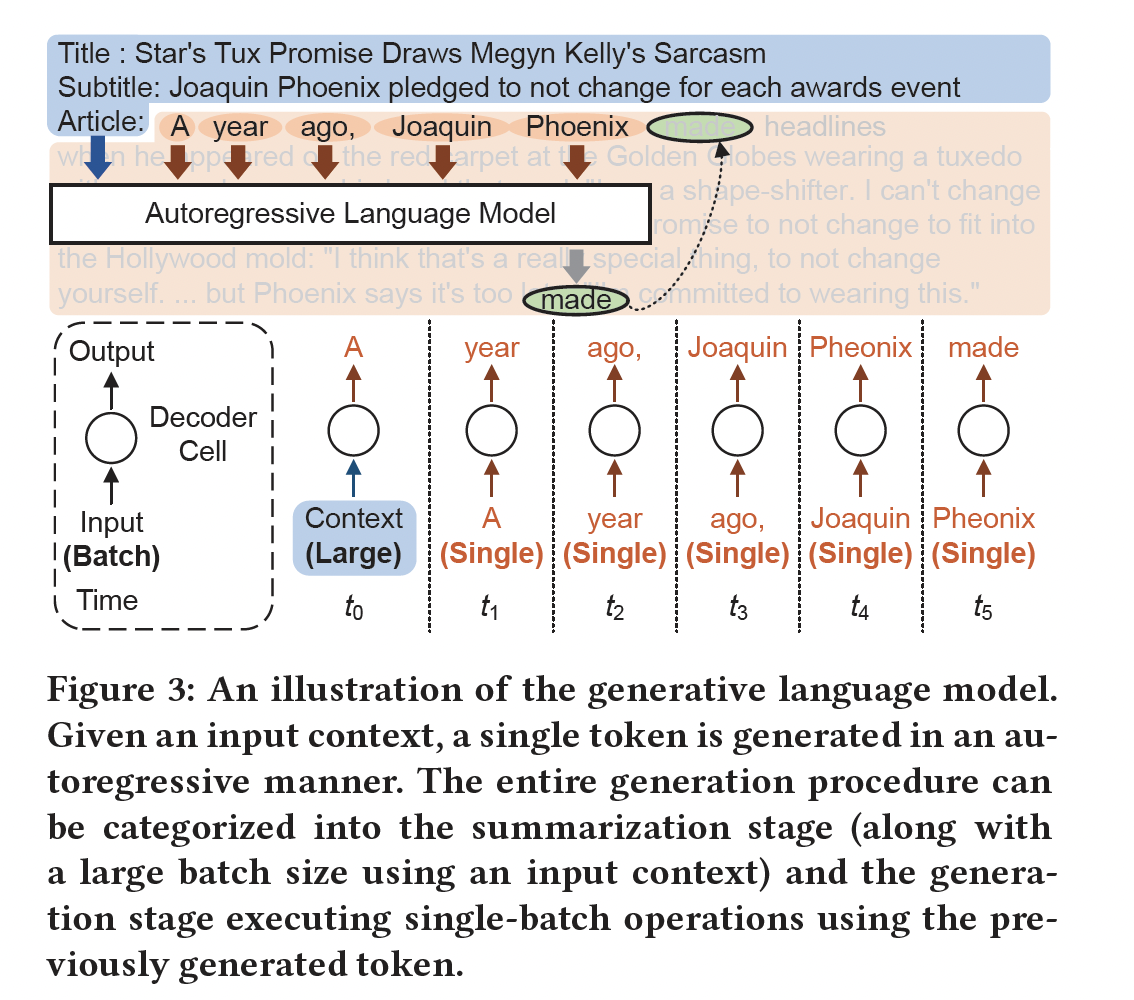
采用自注意力机制和并行训练算法的
Transformer架构在大型生成式语言模型中被广泛使用。多亏了自监督学习和scaling-law(《Language models are few-shot learners》、《Scaling Laws for Neural Language Models》),可以在增加模型大小时预测交叉熵损失,生成式语言模型中的参数数量也在不断增加。一些超大规模语言模型令人惊讶的定性评估结果(例如human-like writing)也推动了模型大小的竞争(《What Changes Can Large-scale Language Models Bring? Intensive Study on HyperCLOVA: Billions-scale Korean Generative Pretrained Transformers》、《Scaling Language Models: Methods, Analysis & Insights from Training Gopher》)。
7.1.2 GPU-Accelerated Generative LMs
对于大型语言模型,矩阵乘法的处理时间主导了整个
inference latency,因为与激活函数、normalization layers等相比,矩阵乘法的时间复杂度更高(《LLM.int8 (): 8-bit Matrix Multiplication for Transformers at Scale》)。为了验证这一结论,Figure 4展示了不同大小(OPT 6.7B/13B/30B/66B/175B)的各种大规模生成式语言模型,在不同input tokens数量下的延迟的分解。OPT模型遵循Transformer架构,由相同的层组成。设hidden sizemulti-head attention和一个feed-forward network,包括四个主要的线性计算,其时间复杂度更高(与其他非线性操作相比)。这些操作包括将一个(activation matrix与下列四个矩阵相乘:1):一个 (key, query, value。2):一个 (3):一个 (feed-forward sub-layer。4):一个 (feed-forward sub-layer。
所有层具有相同的结构,矩阵乘法主导整个推理延迟(
《Extremely Low Bit Transformer Quantization for On-Device Neural Machine Translation》)。Figure 4是用A100(80GB)和FasterTransformer(Nvidia的推理框架)获得的。对于各种规模的语言模型、以及不同的input token lengths,矩阵乘法至少占用了75%的处理时间(请注意,由于单个GPU的内存容量有限,大型语言模型可能需要多个GPU,从而增加了通信延迟)。GPU常被采用从而加速推理,因为GPU内嵌了大量算术单元(arithmetic units),并支持多个线程,这对加速矩阵乘法至关重要(《8-bit Inference with TensorRT》、《Efficient large-scale language model training on GPU clusters using megatron-LM.》)。但是,从GPU中获取高性能取决于算术强度(arithmetic intensity),因此batch size必须足够大,从而确保从主内存(main memory)中获得高的reuse ratio(《Nvidia tensor core programmability, performance & precision》)。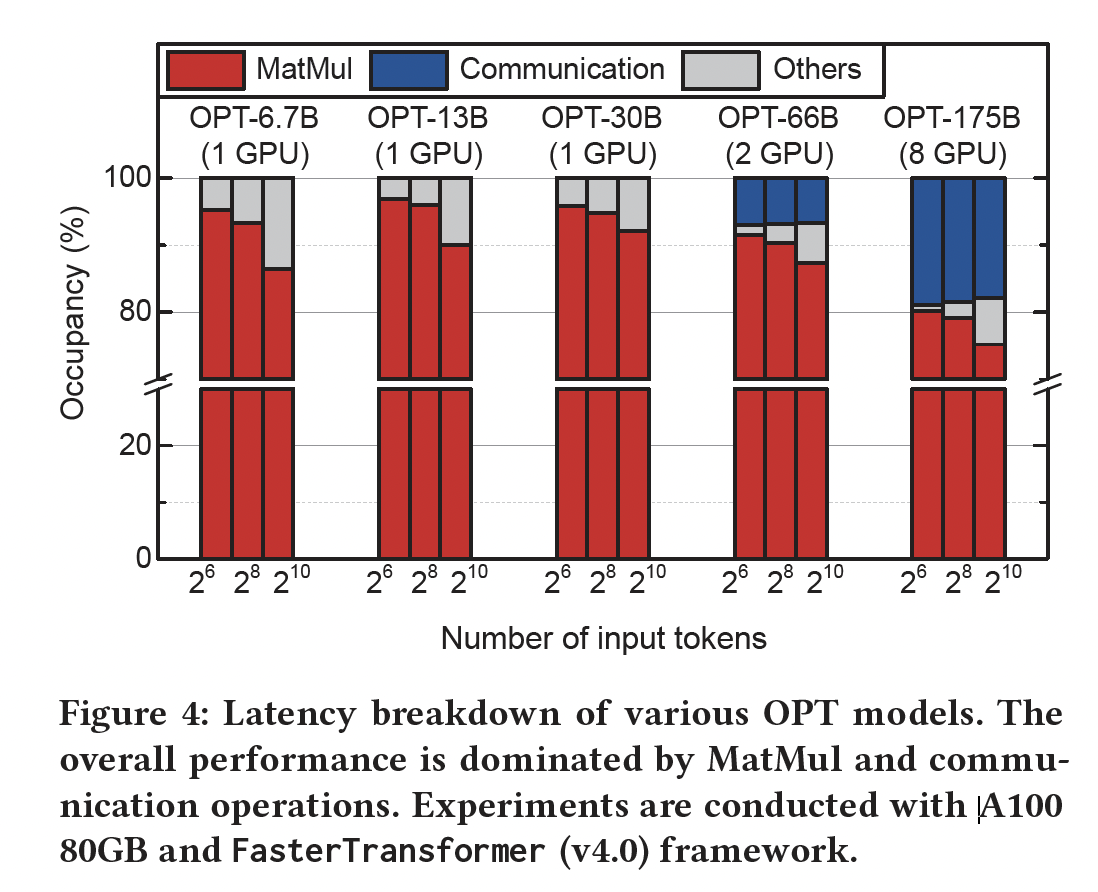
张量并行:对于高度并行的计算系统,高内存带宽对于为大量算术单元提供数据从而维持高资源利用率至关重要。因此,
GPU的主内存系统倾向于关注高带宽而不是大容量。相应地,即使提出了崭新的内存架构(如HBM,参考《Zero-infinity: Breaking the gpu memory wall for extreme scale deep learning》),单个GPU的最大内存容量仍然只有几十GB(《Evaluating modern gpu interconnect: Pcie, nvlink, nv-sli, nvswitch and gpudirect》)。这种有限的GPU内存容量导致了各种并行思想从而在多个GPU上划分大型语言模型(《Efficient large-scale language modeltraining on GPU clusters using megatron-LM》、《Megatron-lm: Training multi-billion parameter language models using model parallelism》)。张量并行可以将矩阵乘法划分到多个GPU上,从而同时生成更小的子任务。请注意,这种并行会引入额外的同步(synchronization)开销、和GPU-to-GPU通信开销。内存受限的
Text Generation:Figure 3中summarization阶段对计算资源有很大需求,权重重用的可能性也很高。因此,在多个GPU上采用张量并行可能会有效提高推理性能。相反,Figue 3中的generation阶段由于其自回归特性而呈现受限于内存的工作负载(memory-bound workload)。因此,增加GPU数量且结合张量并行可能不是一个经济有效的解决方案,特别是考虑到GPU之间的通信开销。随着ChatGPT等服务的日益重要,解决有限内存带宽的问题变得至关重要。不幸的是,通过hardware advancements来增加内存带宽通常会遇到物理限制,并与高功耗相关(《Digital integratedcircuits- A design perspective》、《Cambricon-S: Addressing Irregularity in Sparse Neural Networks through A Cooperative Software/Hardware Approach》)。因此,关注能够缓解内存瓶颈的模型压缩技术的研究工作势在必行。
7.1.3 量化方法及其局限性
各种研究工作致力于通过改进延迟和吞吐量来增强大型且笨重的深度神经网络的
serving性能。这些工作包括量化、剪枝、知识蒸馏、以及低秩近似。在这些方法中,量化是研究最广泛的领域,它涉及使用更快的、更高效的计算单元,以及减少内存使用。特别是采用INT8算子的uniform quantization在各种量化格式中研究最充分,目前正被积极应用于大语言模型中(《LLM.int8 (): 8-bit Matrix Multiplication for Transformers at Scale》、《SmoothQuant: Accurate and Efficient Post-Training Quantization for Large Language Models》、《ZeroQuant: Efficient and Affordable Post-Training Quantization for Large-Scale Transformers》)。与
FP16相比,当代计算系统中常见的INT8算术单元提供了降低延迟(得益于其较低的面积和功耗)和高达50%的内存减少。因此,目前的NVIDIA GPU采用支持INT8操作的Tensor cores来加速计算(《Nvidia tensor core programmability, performance & precision》)。但是,利用INT8需要activation quantization,这对采用INT8单元实现压缩和加速的模型提出了重大挑战。例如,当scaling factors离线确定时,由于异常值被近似,activation quantization可能导致模型准确率大幅下降。为了避免这种准确率下降,token-based dynamic quantization已成为量化大语言模型的关键技术(《LLM.int8 (): 8-bit Matrix Multiplication for Transformers at Scale》、《ZeroQuant: Efficient and Affordable Post-Training Quantization for Large-Scale Transformers》)。LLM.int8()方法(《LLM.int8 (): 8-bit Matrix Multiplication for Transformers at Scale》)通过提出分解方法,大部分计算用INT8进行,只对有限数量的异常值用FP16,解决了大语言模型中异常值系统性出现的问题,从而仅导致语言模型延迟轻微下降。SmoothQuant(《SmoothQuant: Accurate and Efficient Post-Training Quantization for Large Language Models》)采用了更高级的方法,通过数学方法将activations中的方差转移到权重中,而权重相对更容易量化;activations更难量化,因为存在异常值。该技术使得采用INT8计算单元(如W8A8)高效地计算大语言模型成为可能,即使在对activations进行静态量化的情况下。根据SmoothQuant的结果,当系统性地出现异常值时,大语言模型的加速可以达到1.5倍、GPU使用量减少2倍。然而,应注意的是,要在新的大语言模型中应用SmoothQuant,有必要在应用迁移技术之前经验性地观察和验证异常值的出现。另一方面,如前所述,
token generation过程的自回归特性限制了硬件的最大吞吐量,即使采用INT8 precision。因此,需要生成大量token的服务(如chatGPT),可能不会通过采用INT8 precision获得显著的性能改进。最近的研究关注
generation步骤的低效率,并相应地提出了利用W4A16格式(《GPTQ: Accurate Post-Training Quantization for Generative Pre-trained Transformers》、《GLM-130B: An Open Bilingual Pre-trained Model》),即将模型权重压缩为4-bit整数而不量化activations。鉴于当前计算系统无法加速W4A16格式,GPTQ(《GPTQ: Accurate Post-Training Quantization for Generative Pre-trained Transformers》)通过首先即时地将权重逆量化为FP16格式、然后执行矩阵乘法操作来解决此问题。通过利用generation步骤的受限于内存的特点,这种方法可以减少GPU的数量并改进generation latency,尽管存在逆量化的开销。
7.1.4 Binary-Coding Quantization
在本文中,我们提出了
binary-coding quantization: BCQ的应用。BCQ是一种通用的non-uniform quantization方案,它包含了uniform quantization,正如我们在后面的部分所讨论的。BCQ首先在《XNOR-Net: ImageNet Classification Using Binary Convolutional Neural Networks》中被提出,作为一种与传统uniform quantization方法形成对比的可行方案。当权重向量BCQ量化,且quantization bits数量为其中:
scaling factor。binary vector。
1 bit来表示,因此整个向量只需要n bit来表示。对于
bit来表示,因此quantization bits数量。注意,
scaling factorscaling factors。量化过程大致包括找到
scaling factors和binary vectors以最小化量化误差,即:其中
上式就是
LUT-GEMM的核心思想。后面的技巧都是为了加速这个求解过程而设计的。除非
scaling factors和binary vectors是通过迭代搜索(iterative search)方法(《Network sketching: exploiting binary structure in deep CNNs》、《Alternating Multi-bit Quantization for Recurrent Neural Networks》)、或量化感知训练(quantization-aware training)获得的(《Extremely Low Bit Transformer Quantization for On-Device Neural Machine Translation》)。最近,《AlphaTuning: Quantization-Aware Parameter-Efficient Adaptation of Large-Scale Pre-Trained Language Models》提出了AlphaTuning,一种结合parameter-efficient adaptation和BCQ方案的方法,展示了各种生成式语言模型可以在微调下游数据集的同时实现极端的low-bit quantization、甚至低至1-bit或2-bit。
7.2 LUT-GEMM的设计方法
LUT-GEMM是为了开发高性能、低能耗的大语言模型推理系统而设计的。为实现此目标,LUT-GEMM采用了几种创新方法。首先,我们通过添加
bias项来扩展常规的BCQ方法,这显著增强了表达能力。这个简单的addition使得extended BCQ格式可以同时表示non-uniform and uniform quantization方法,允许我们利用各种量化方法(依赖于具体的LLM要求)。其次,我们进一步
refine了BCQ方案的实现细节,使压缩比(compression ratio)与量化误差之间的权衡更好地利用语言模型的特点。最后,由于大多数
non-uniform quantization方法通常涉及低并行度的复杂操作,并且可能缺乏硬件支持,我们设计了LUT-GEMM以高效适配BCQ格式。我们提出的LUT-GEMM kernel直接利用BCQ格式,消除了额外的开销(如dequantization)。因此,LUT-GEMM展示了降低的延迟、和/或减少的语言模型推理所需GPU数量,同时本质上适配各种weight-only quantization的方法。
7.2.1 Extension of Binary-Coding Quantization
非对称的
Binary-Coding Quantization:常规的BCQ方法基本上局限于相对于零点呈现对称的quantization shape。BCQ方法的另一个约束源于其无法表示零值,这是由于其对称量化的特性。为增强BCQ的表达能力,我们通过引入bias项BCQ方法:因此, 修改后的
BCQ格式可以表示以asymmetry quantization,如Figure 5(a)所示。因为
{+1, -1},因此下图展示为一棵二叉树。假设考虑如果
假设考虑右子树。如果
以此类推,最终的叶节点代表
所有的叶节点代表
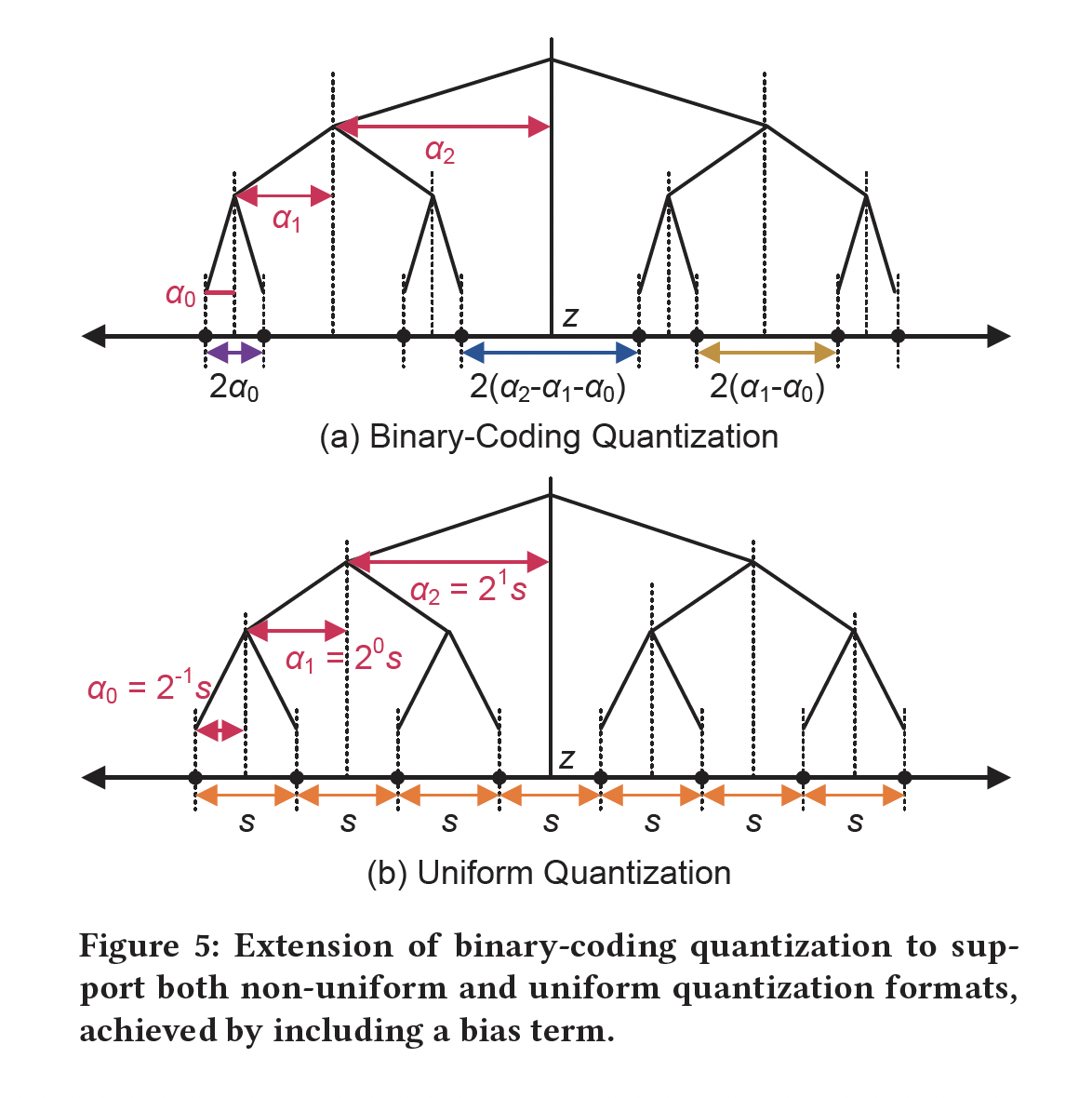
Uniform Quantization:我们表明,在BCQ格式中引入bias项使其能表示uniform quantization,方法是通过仔细调整scaling factors和bias项(Figure 5(b))。让我们详细说明如何将asymmetric uniform quantization转换为具有bias项的symmetric BCQ。一个b-bit的uniformly quantized weightscaling factor然后,
给定
BCQ格式的binary weight则这可以视为
BCQ的一个特例,其中:从
Figure 5中我们可以看到,对于q-bit量化,uniform quantization方法采用单scaling factor,而non-uniform量化技术需要使用scaling factors。因此,由于采用了extended BCQ格式,我们提出的LUT-based的矩阵乘法方案同时适用于uniform quantization和binary-coding-based non-uniform quantization方法。
7.2.2 Group-wise
在实践中,常规的
BCQ方法假设每个权重矩阵的行(甚至整个矩阵)共享一个scaling factor,从而支持CPU或GPU的向量指令 (vector instructions)(《XNOR-Net: ImageNet Classification Using Binary Convolutional Neural Networks》、《Alternating Multi-bit Quantization for Recurrent Neural Networks》)。但是,随着大型语言模型引入更深的和更宽的模型结构、以及参数数量的不断增加(《Scaling Language Models: Methods, Analysis & Insights from Training Gopher》、《Megatron-lm: Training multi-billion parameter language models using model parallelism》),我们认为这种常规的row-wise BCQ格式面临各种挑战。假设选择了一个相对较小的
hidden size(例如OPT 350M的scaling factors的row-wise assignment可能是合理的,以获得低的量化误差。另一方面,如果
hidden size迅速增加(例如GPT-3 175B的scaling factors从而与更多权重共享,这将更具挑战性。
为实现
low-bit quantization方案,我们有必要研究assigning scaling factors的不同方式,只要这些新的分配方式可以实现。作为
row-wise quantization的替代方案,我们提出了group-wise quantization,其中一个scaling factor可以由任意数量的权重共享。我们提出的新的BCQ格式引入了一个新的超参数group size,表示要共享一个scaling factor的权重数量。在本文中,row-wise quantization)。由于hidden size不影响我们的group-wise BCQ格式。group-wise quantization的物理意义:对于权重矩阵的给定行然后针对每个
其中,
scaling factor在各个分组内部共享。为什么按列进行分组,而不是按行进行分组?论文并未说明原因。
对压缩比(
Compression Ratio)的影响:设quantization bits数量。对于给定的group sizescaling factors的内存占用为代价来降低量化误差。然后,target quantization error作为约束来确定scaling factors和binary vectors的数量作为trade-off过程。请注意,如果矩阵宽度足够大,row-wise quantization的内存占用主要由binary vectors的大小决定,因为scaling factors的大小通常可以忽略。与常规方案相比,我们提出的
group-wise BCQ为满足target compression ratio提供了新的大搜索空间。Figure 6以两个quantization bits数量group sizescaling factors)时,内存占用也可能很大。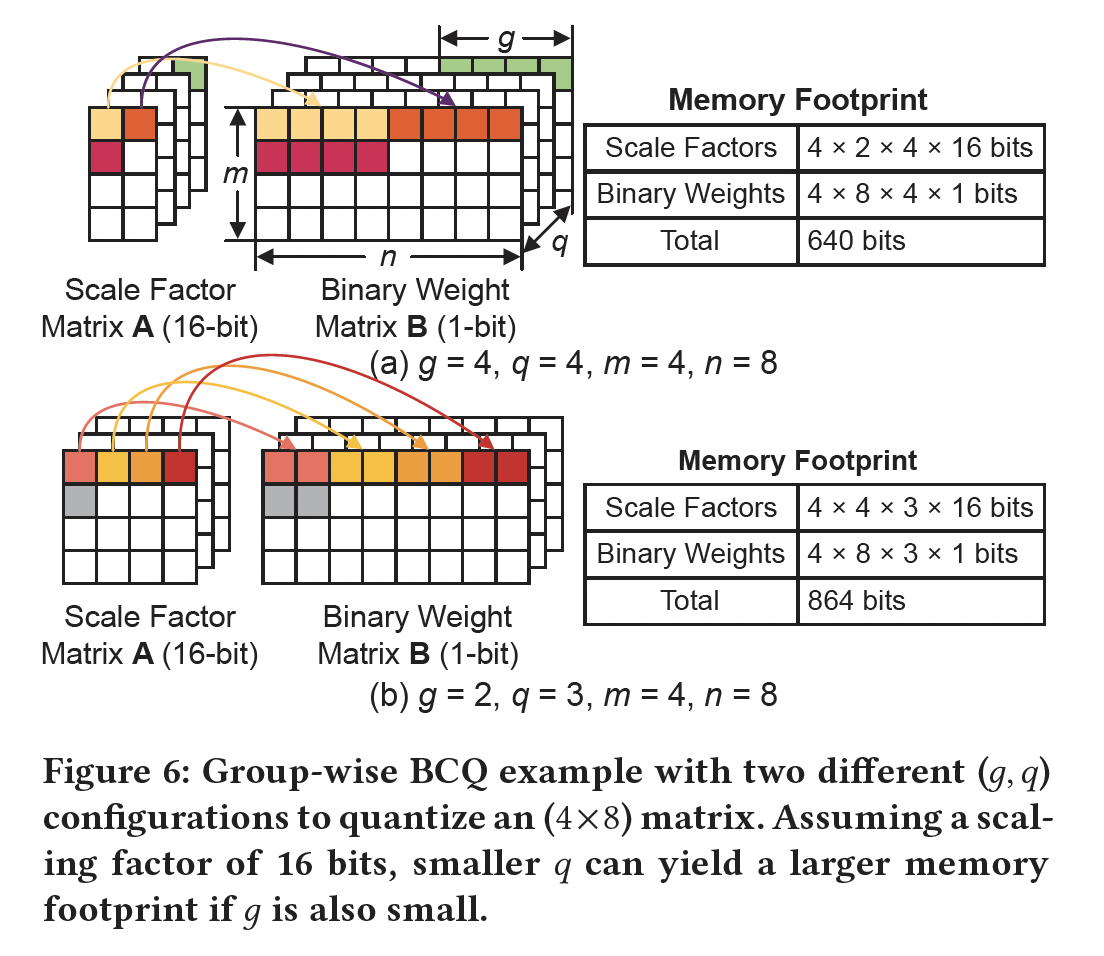
7.2.3 LUT based Quantized Matrix Multiplication
我们采用
BCQ格式用于weight quantization而为activations保持full precision的量化方案,会导致朴素的矩阵乘法中出现重复的和冗余的部分计算(partial computations)。为说明这一点,假设给定binary matrixactivation vector则计算
scaling factors相乘)会重复计算bit-level的内存访问,这对商用CPU和GPU来说可能较慢。为避免
bit-level的内存访问并高效计算full-precision activations和binary patterns的所有可能组合。请注意,当大量计算产生的值集中在一个受限集合时,lookup table: LUT已被广泛用于节省处理时间(《LUT filters for quantized processing of signals》、《LUT Optimization for Memory-Based Computation》、《Multiplication Through a Single Look-Up-Table (LUT) in CNN Inference Computation》)。当从LUT中检索一个值要比进行原始计算要快得多时,基于LUT的计算尤其合理。BCQ格式也适合LUT-based的方法实现。注意,这里的BCQ格式没有quantizing activations,其中quantizing activations需要大量修改训练代码和模型结构(《Quantization and training of neural networks for efficient integer-arithmetic-only inference》、《Training and Inference with Integers in Deep Neural Networks》)。例如,对
3个元素Table 1所示预先计算LUT中。假设LUT的子向量长度(因此Table 1中LUT的LUT检索操作所替代;同时,检索的key由binary elements拼接而成。为完成
partial products)被累加起来,然后乘以scaling factors。当row dimension增加时(例如随着生成式LM越来越大),LUT的利用率增加,因为出现了越来越多的冗余计算。这个
lookup table的存储会消耗大量资源;同时lookup table的预先生成需要消耗大量时间。更重要的是,在推断过程中,lookup table是一次性的消耗品:针对不同的输入需要生成不同的lookup table。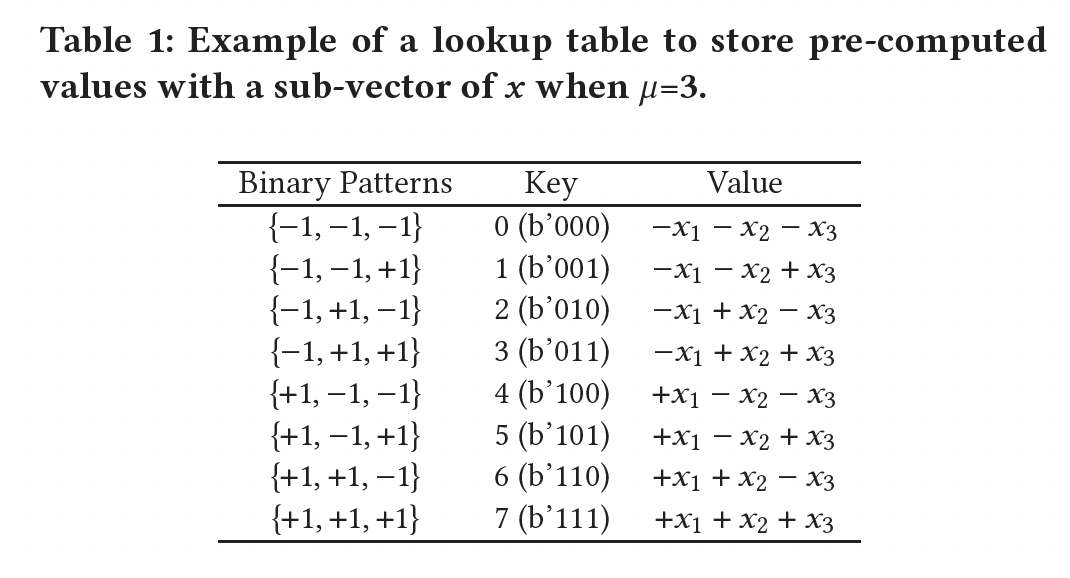
让我们简要解释一下如何优化
《Biqgemm: matrix multiplication with lookup table for binary-coding-based quantized dnns》中也有讨论。如果LUT的构建成本也会增加LUT检索操作取代FP16 additions操作。因此,正如《Biqgemm: matrix multiplication with lookup table for binary-coding-based quantized dnns》所报告的,存在一个最优的aligned memory accesses。在我们的工作中,
7.2.4 Proposed LUT-GEMM
除了
LUT-based的方案(消除冗余计算和bit-level内存访问)之外,我们提出的LUT-GEMM还需要与group-wise quantization配合,从而在给定GPU上优化single-batch operations的策略如下:为提高并行度,我们创建尽可能多的线程,同时每个线程都可以执行独立的
LUT访问。一个线程所访问的
binary weights可以共享一个公共scaling factor,这样scaling factors相关的操作不会降低线程的性能。如果向线程分配的资源太小,则
LUT利用率会很低,synchronization开销会增加。因此,我们需要经验性地优化线程配置。
为了简单起见,我们将提出的
group-wise quantized matrix multiplication公式化为:其中:
FP16的scaling matrix。FP16的binary matrix。FP16的长度为input vector。
请注意,在实际情况下,由于每
scaling factor,因此整体架构:对于
LUT-GEMM,我们将LUT分配给GPU的一个线程块(thread block: TB)。然后,分配给每个TB的TB内LUT的利用率。因此,2048是一个实用数字)。请注意,分配给每个TB的资源足够小,使得只要TB就可以共享一个scaling factor。Figure 7展示了在GPU上实现LUT-GEMM的整体方案,其中我们假设Figure 7的整个过程迭代该方案需要硬件级的编程支持,因此读者觉得实践的价值不大。因为换一种硬件(如手机芯片),算法是否仍然可行,是个未知数。
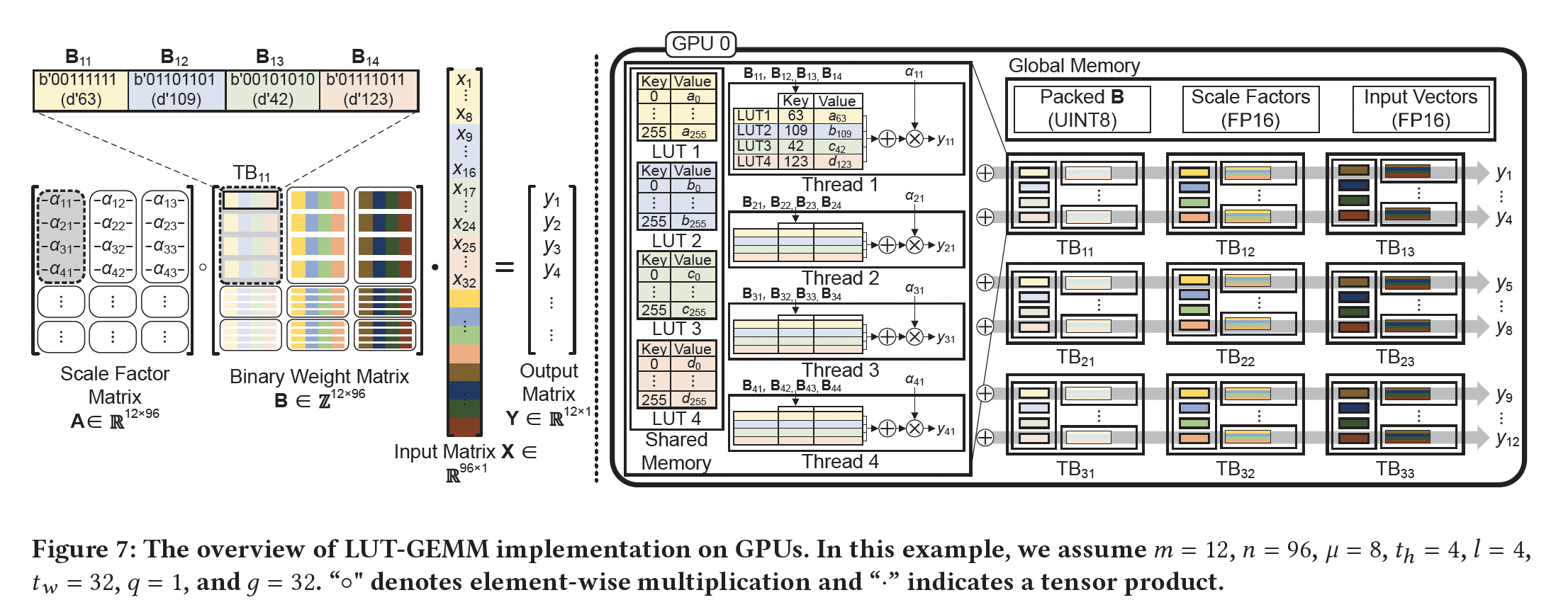
详细实现:
首先,每个
TB使用分配的部分LUT。然后,
TB中的所有线程可以共享LUT(以减少全局内存访问);多个线程可以并行处理当线程完成检索、以及对
LUT的值求和之后,获取scaling factors(每个线程只获取一次)并将其乘以产生partial outputs。最后,将来自不同
TB的partial outputs累加(通过atomicAdd操作,如Figurer 7所示)以生成最终输出。
LUT存储在GPU中的共享内存中,共享内存提供高带宽(例如A100的19TB/s)。因此,LUT的高内存访问(同时,一次LUT访问可以代替多个FLOPs)实现了快速的矩阵计算。关于LUT内存大小,every 8 hidden dimensions只需要1KB,共享内存大小超过几MB(例如A100 with 192KB per SM的共享内存大小是20MB,一共108 SMs),因此整个LUT可以安全存储在共享内存中。例如,对于A100,hidden dimension最多可达324,000,而GPT-3 175B的hidden dimension为12,288。为研究
LUT-GEMM对group sizeFigure 8中,对每个row-wise(即,BCQ格式进行了比较。有趣的是,当group-wise LUT-GEMM都与row-wise LUT-GEMM一样快。换句话说,合理的大128和256)可以使LUT-GEMM很快,同时group-wise可以大幅提高准确率。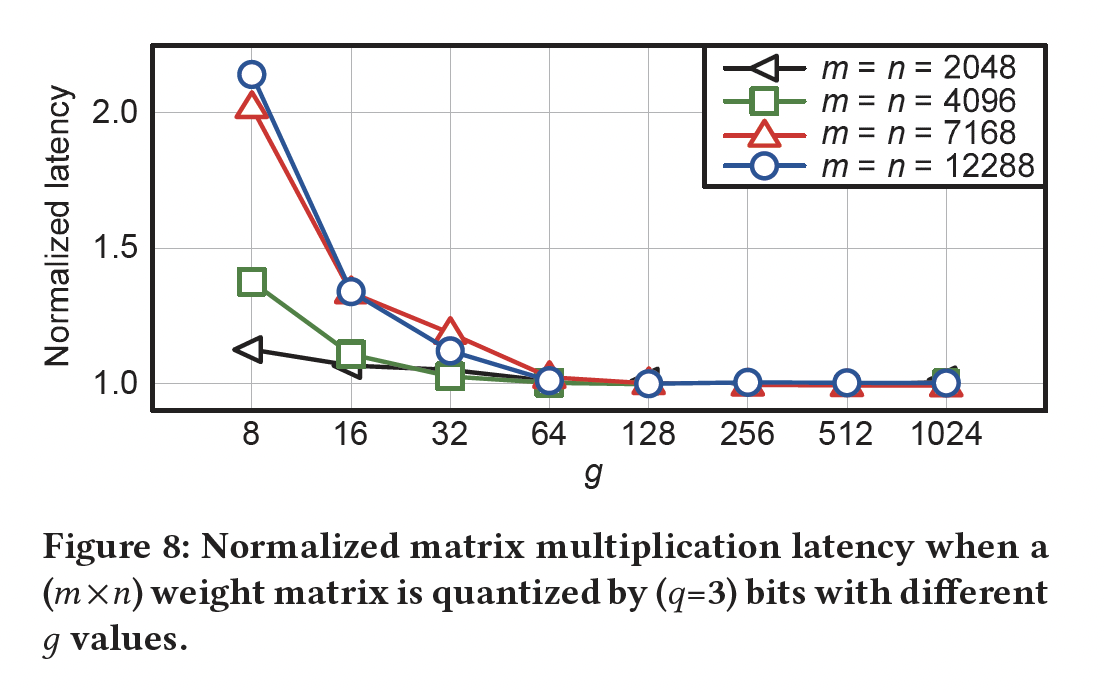
为深入理解
Figure 8中的机制,我们分析了LUT-GEMM的内存占用,因为single-batch operations主要受限于内存,而延迟与内存占用成正比。设binary weights和scaling factors的空间复杂度分别为因此,如果
single-batch operations下LUT-GEMM延迟与内存占用成正比的说法,在(q, g) pair以及相应的压缩比,并测量了矩阵乘法的延迟,如Figure 9所示。可以注意到,超参数
Figure 9中的所有可用压缩比中,latency是压缩比的函数。例如,如果两个不同的pairsLUT-GEMM得到相似的延迟。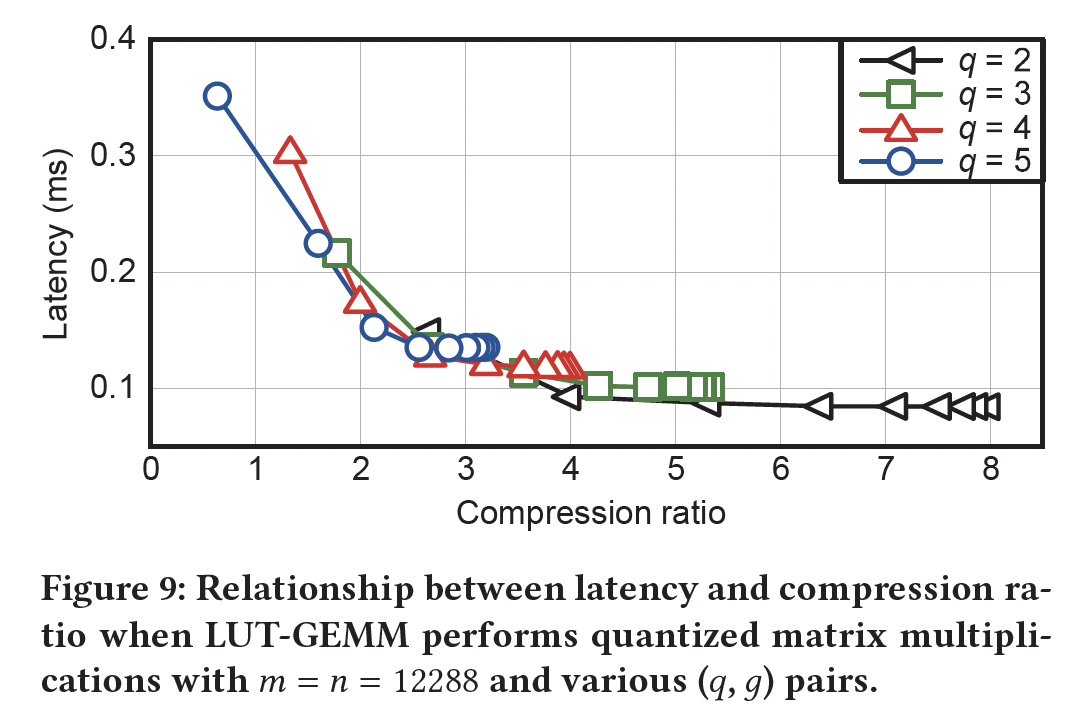
7.3 实验
在本节中,我们介绍在各种复杂度水平上使用
LUT-GEMM获得的实验结果,从single-layer experimental setup(不考虑group size)、到完整的model level。首先,我们在不考虑
group size的情况下检查LUT-GEMM对特定layer的影响。接下来,我们比较张量并行与
LUT-GEMM,然后研究group size的影响。最后,我们分析
OPT模型的端到端延迟,以确定LUT-GEMM整体对性能的影响。
7.3.1 与各种 Kernels 的简单比较
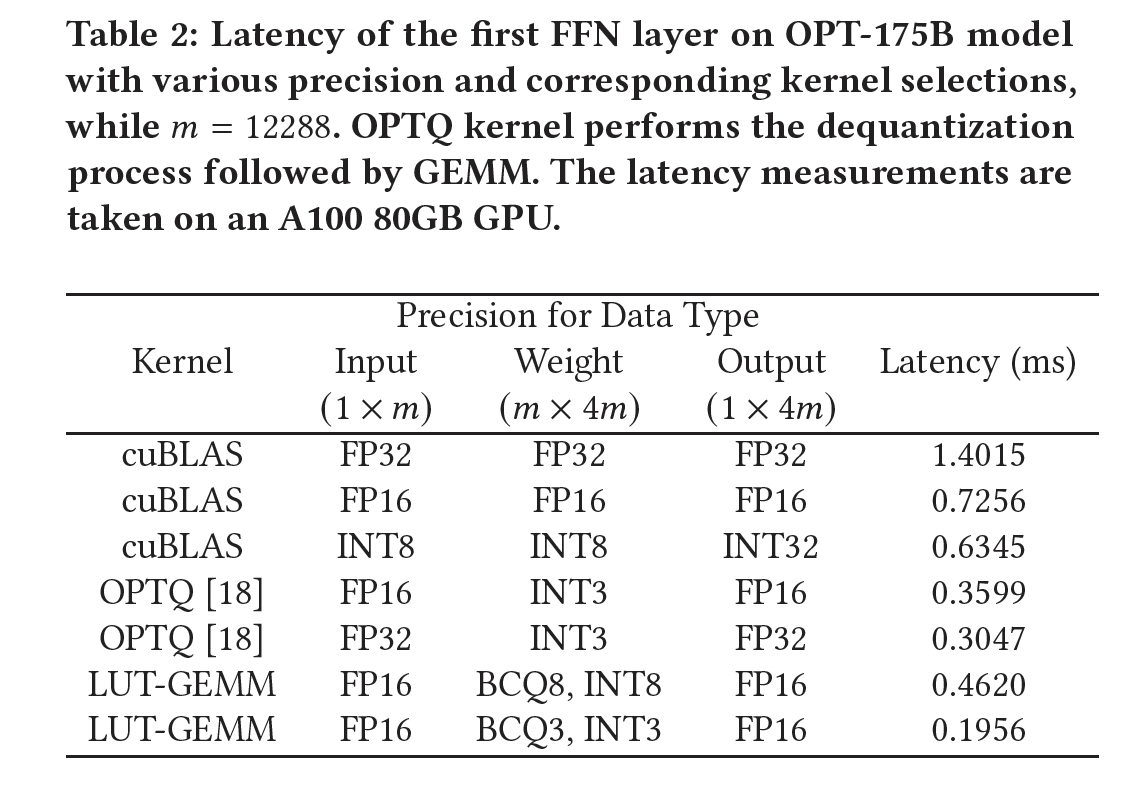
Table 2给出了在OPT-175B模型的前馈神经网络(Feedforward Neural Network: FFN)第一层上的延迟测量结果。结果是通过各种input and weight quantization方法获得的,包括FP-FP(baseline)、INT-INT、FP-INT和FP-BCQ。所选kernels包括:cuBLAS(用于FP-FP或INT-INT)、GPTQ(用于FP-INT)、或LUT-GEMM(用于FP-INT或FP-BCQ)。注意,GPTQ kernel包括dequantization过程,然后紧跟着GEMM;而LUT-GEMM直接接受row-wise quantized weights,不需要dequantization。我们可以观察到:
INT8-INT8(使用cuBLAS)实现的延迟相比FP-FP仅略有改善,因为cuBLAS没有针对single-batch operations进行很好的优化。与
INT8-INT8量化相比,GPTQ kernel延迟更低,但由于dequantization开销,其速度慢于LUT-GEMM。支持
BCQ和INT量化的所提出的LUT-GEMM kernel在考虑的kernels中实现了最低延迟。
7.3.2 与 FP16 张量并行的比较
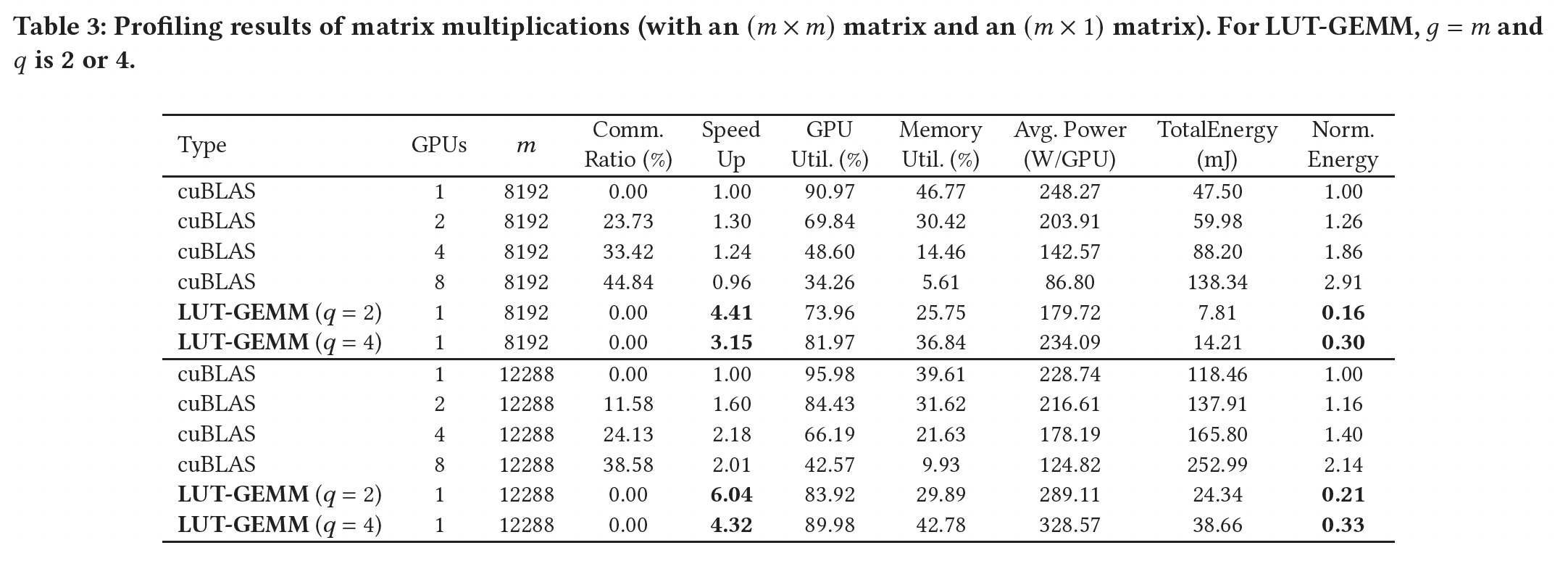
Table 3总结了使用cuBLAS(具有张量并行)或LUT-GEMM(具有一个GPU)执行的矩阵乘法的分析结果。使用nvidia-smi工具收集了GPU功率和其他指标。同样,一个8192和12288。这个操作与我们对GPT-3 175B的研究相关,其hidden size为12288。我们对LUT-GEMM包含BCQ格式的quantization-aware training,一些文献报告对Transformer的2-bit量化是可行的(《Extremely Low Bit Transformer Quantization for On-Device Neural Machine Translation》)。我们注意到:cuBLAS中张量并行使用额外的GPU会显著降低GPU利用率、内存利用率、以及computation latency ratios。如通信延迟占比的增加所示,这种利用率的降低表明一些GPU可能暂时闲置,直到所有GPU都被同步。相应地,张量并行可以获得的加速程度远小于GPU的数量。因此,使用更多GPU的cuBLAS会增加矩阵乘法的能耗。另一方面,
LUT-GEMM(具有一个GPU)可以提供高速加速(这是张量并行无法实现的),同时保持高的GPU/memory利用率。因此,LUT-GEMM通过结合低延迟和减少GPU数量,极大地节省了矩阵乘法的能耗。例如,当cuBLAS,LUT-GEMM(GPU)实现了4.8倍的能耗降低、以及6.0倍的加速。
7.3.3 压缩比的探索
为研究
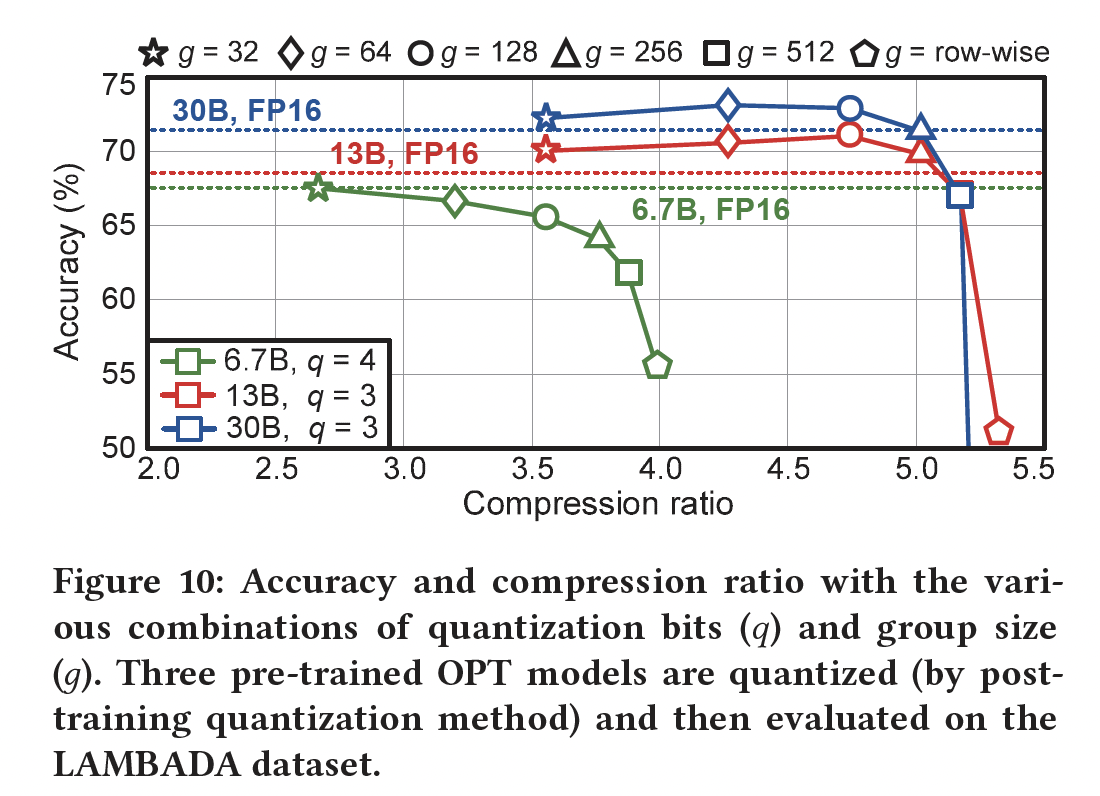
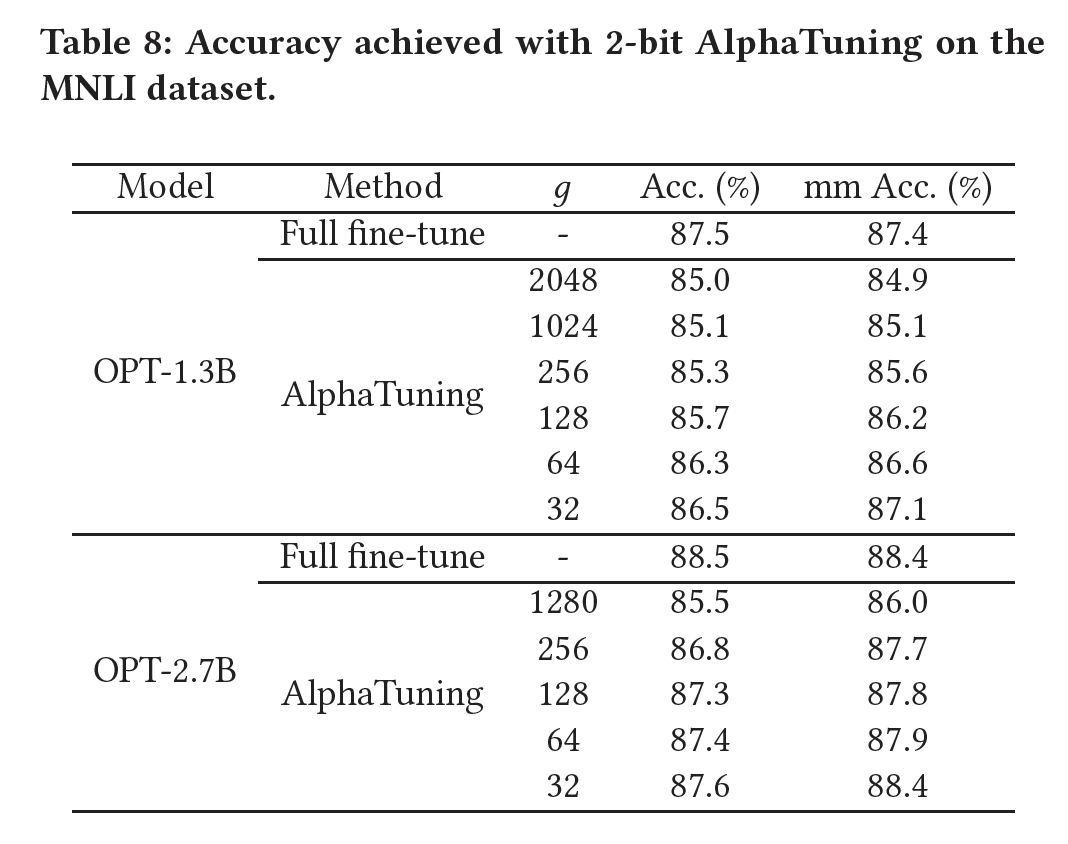
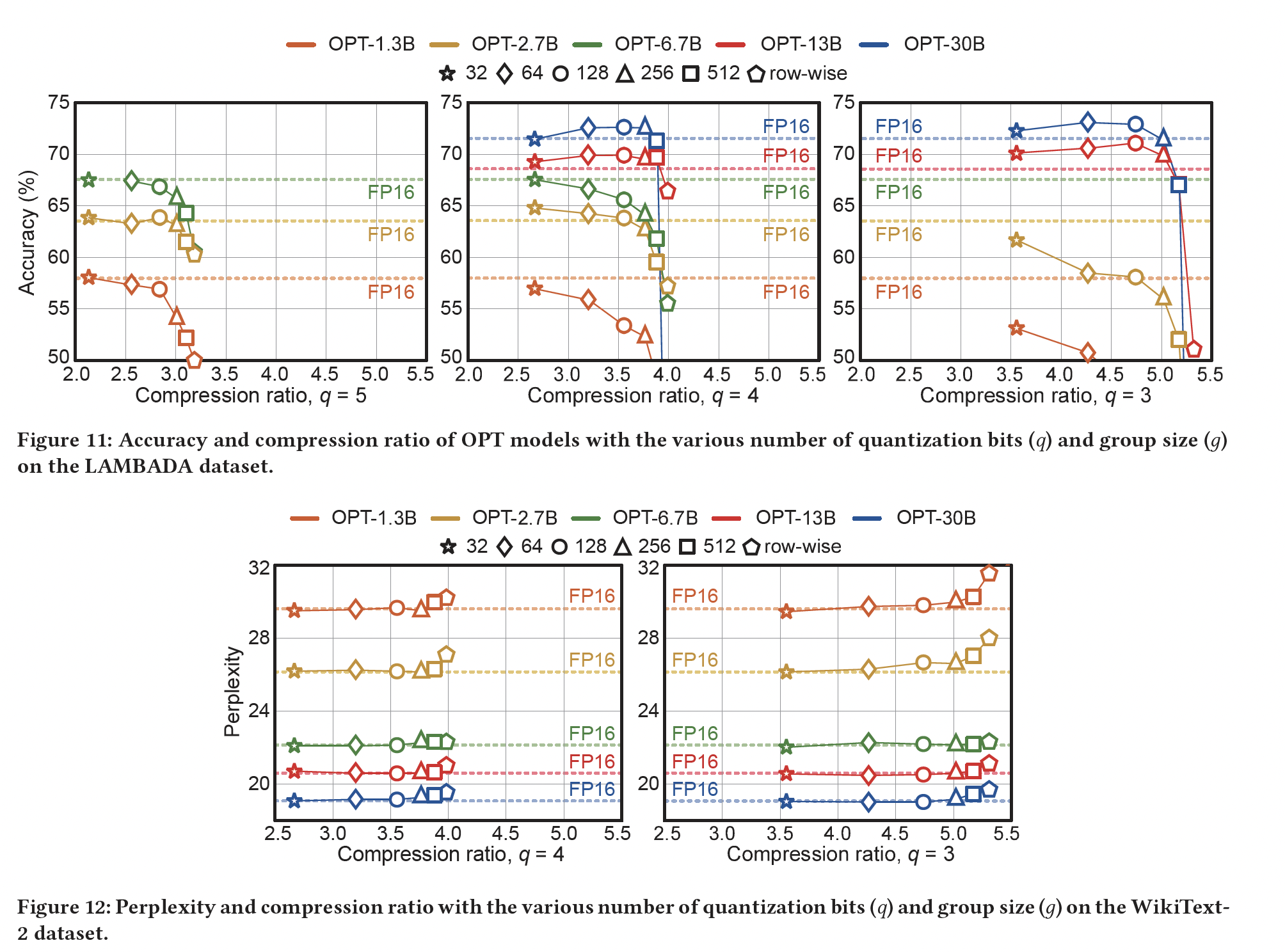
group-wise BCQ从而扩大compression的搜索空间的能力,我们在三个公开可用的pre-trained OPT模型上进行了实验。具体而言,我们在pre-trained OPT模型上应用post-training quantization(使用《Alternating Multi-bit Quantization for Recurrent Neural Networks》中介绍的iterative solver),同时调整quantized model在LAMBADA数据集上进行评估,找到压缩比和准确率之间的关系。Figure 10显示了尝试各种Figure 10可以观察到:与传统的
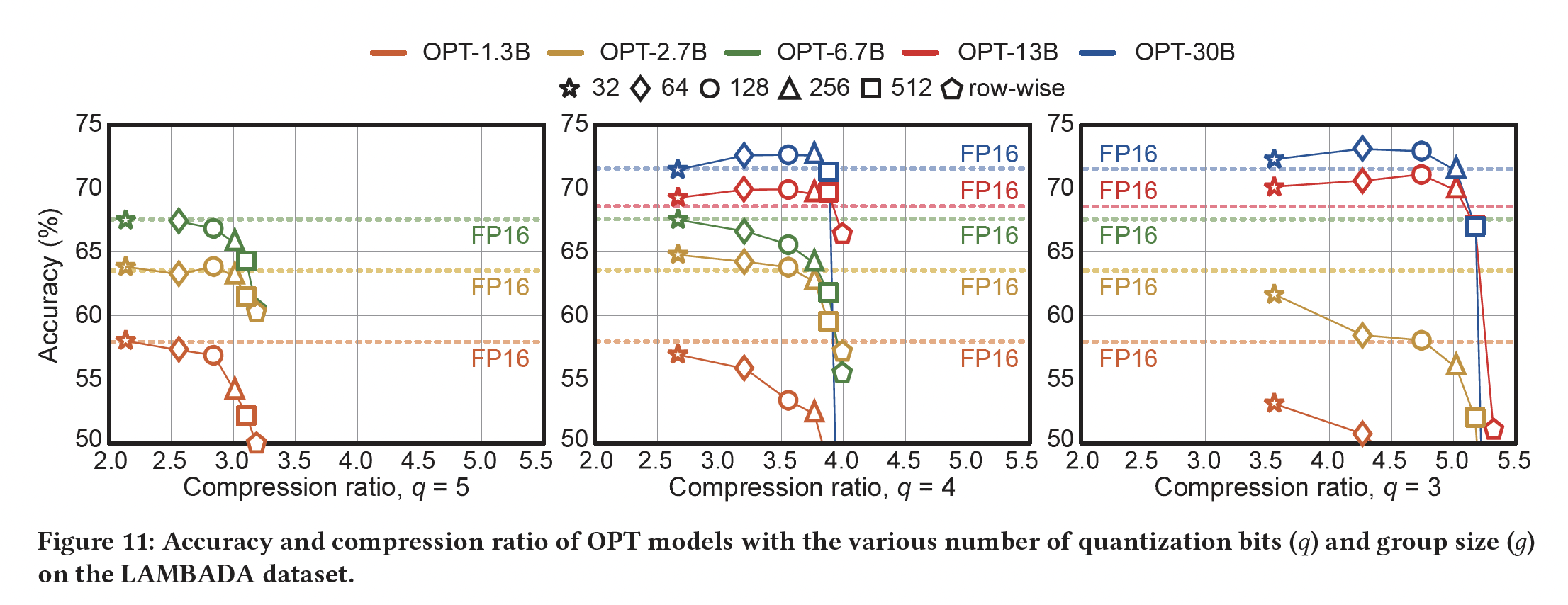
row-wise quantization相比,group-wise BCQ提供了新的最优配置(见附录中的Figure 11从而查看更广泛的结果)。因此,为了实现最佳压缩比(或最小的准确率退化),有必要同时探索不同的注意,对于
OPT-13B和OPT-30B,正如我们讨论的大型语言模型的row-wise quantization的局限性,小的
总之,对每个模型,
7.3.4 端到端延迟
现在,我们评估保持
full precision activations并采用quantized weights下,各种OPT模型的single-batch size端到端的推理延迟。Table 4展示了使用round-to-nearest: RTN方法进行均匀量化时,end-to-end latency per token和困惑度。注意,延迟测量是在FasterTransformer框架内进行的。我们利用不同数量的GPU来获得model parallelism可以实现的潜在加速增益。从Table 4的观察我们可以得出以下结论:1):减小group size(RTN量化方案,代价是延迟略有增加。2):增加GPU数量(即,并行度增加)并不能显著降低延迟,因为存在各种开销,如GPU-to-GPU通信成本,如Figure 4所述。值得一提的是,在LUT-GEMM的case中(其中矩阵乘法被加速),相较cuBLAS,GPU-to-GPU相对通信开销更加突出。因此,对于LUT-GEMM,模型并行似乎不太有效。换言之,对于高性能的矩阵乘法引擎,通信开销更加突出。
以
OPT-30B模型为例,使用FP16权重可以在单个GPU上执行端到端推理。但是,对于具有FP16权重的OPT-66B模型,由于模型大小超过单个GPU的内存容量(A100为80GB),必须使用模型并行技术。然而,当OPT-66B模型的权重被量化到3-bit或4-bit时,这被证明是可行的(《GPTQ: Accurate Post-Training Quantization for Generative Pre-trained Transformers》),推理可以容纳在单个GPU上。假设采用3-bit量化、以及用LUT-GEMM,可以对OPT-30B(使用1个GPU)实现2.43倍的加速、对OPT-66B(使用2个GPU)实现2.25倍的加速。请注意,我们在Table 4中展示LUT-GEMM性能的方法依赖于basic post-training quantization,而大语言模型有更高级的量化方法。例如,在构建pre-trained模型后进行微调,如ChatGPT中所展示的,更有效的量化技术如AlphaTuning(《AlphaTuning: Quantization-Aware Parameter-Efficient Adaptation of Large-Scale Pre-Trained Language Models》)甚至可以实现2-bit量化。当与先进的量化方法相结合以减少quantization bits时,LUT-GEMM的效用进一步增强。附录A.1中提供了额外的评估结果。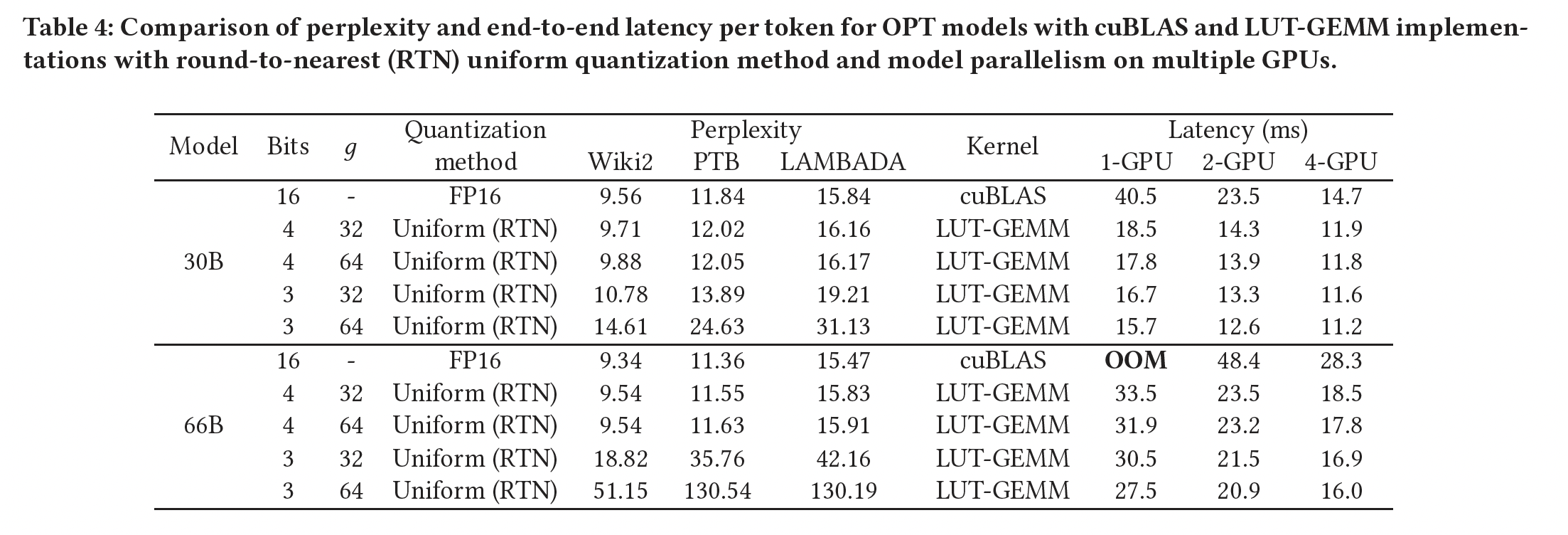
7.4 加速 Quantized OPT-175B
Table 5比较了在FasterTransformer框架中生成OPT-175B的一个token的端到端延迟。我们评估了三种不同的实现:1):原始FP16 cuBLAS。2):集成了FP16 cuBLAS(使用GPTQ的library)的dequantization(从3-bit)。3):假设uniform quantization的LUT-GEMM。
通过只关注前面讨论的四个特定矩阵乘法,
LUT-GEMM展示了它降低所需GPU数量的能力,同时随着GPU的增加从而降低延迟。对于具有FP16的OPT-175B,运行推理至少需要8个GPU。但是,应用BCQ格式进行量化后,LUT-GEMM能够只使用单个GPU执行推理,同时保持可比的整体延迟。值得注意的是,当比较相同的3-bit量化场景时(weight-only和row-wise),使用LUT-GEMM的latency for token generation比GPTQ库降低了2.1倍。这种显著的延迟减少主要归因于LUT-GEMM可以直接接受quantized weights的能力,从而消除了dequantization的需要。
让我们证明
LUT-GEMM的灵活特性(归因于extended BCQ格式)可以加速现有的uniform quantization方法。Table 6显示了使用GPTQ方法在各种OPT-175B的困惑度。该Table还显示了LUT-GEMM(不包括FP16)实现的相应延迟(per generated token)。结果清楚地表明:随着LUT-GEMM提供了更低的延迟,尽管过小的总之,通过集成
LUT-GEMM和GPTQ,以可接受的困惑度增加为代价,可以将运行OPT-175B推理所需的GPU数量从8个降低到1个,同时保持高性能。值得强调的是,如果包含dequantization,则无法实现这样的性能改进。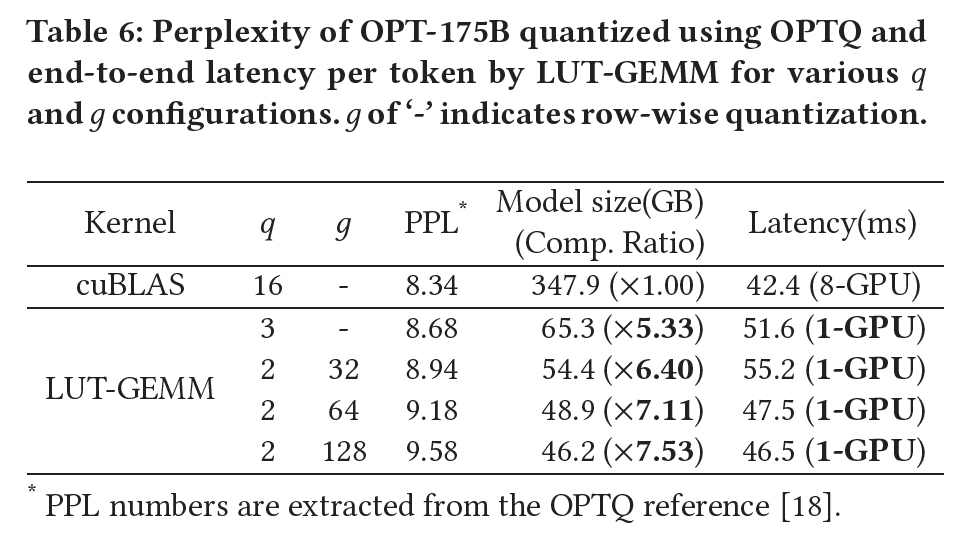
7.5 使用 Quantized Weights 的上下文处理
如前所述,生成式语言模型推理由两个阶段组成:使用
input context的summarization、以及generation,如Figure 3所示。这些阶段需要不同的batch size。summarization允许并行处理多个tokens,而generation由于其自回归特性是single-batch operation。因此,生成式语言模型的推理需要平衡:受限于计算(高并行的上下文处理)和受限于内存(低并行的generation)。我们提出的推理策略涉及存储
quantized weights(使用extended BCQ)。然后这些权重:1):在上下文处理(context processing)阶段dequantized从而执行full-precision cuBLAS的矩阵乘法。2):并在generation阶段作为LUT-GEMM的输入。
请注意,即使在上下文处理过程中,
weight quantization对有效的内存使用也是必不可少的。此外,由于weight reuse ratio很高,context processing阶段的dequantization latency相比generation阶段较低。因此,LUT-GEMM是generation阶段的理想方法,因为generation阶段通常主导整体推理延迟,因为需要生成更多的tokens(生成式语言模型的常见要求)。
八、K-bit Inference Scaling Laws [2022]
论文:
《The case for 4-bit precision: k-bit Inference Scaling Laws》
大型语言模型(
LLM)广泛用于zero/few-shot inference,但由于其庞大的内存占用(175B参数的模型高达352GB GPU内存)和高延迟,这些模型使用起来具有挑战性。然而,内存和延迟主要由模型的参数中的比特总数决定。因此,如果我们通过量化来减少model bits,我们可以期望模型的延迟会相应地减少,可能以任务准确率为代价(《Gptq: Accurate post-training quantization for generative pretrained transformers》、《nuqmm: Quantized matmul for efficient inference of large-scale generative language models》、《Zeroquant: Efficient and affordable post-training quantization for large-scale transformers》)。由于我们可以将训练好的模型的参数量化到任意
bit-precision,这引出了一个问题:给定当前的base方法从而用于model quantization,为了在准确率和total model bits之间取得最佳trade-off,应该使用多少比特?例如,如果我们有一个4-bit精度的60B参数模型、以及一个8-bit精度的30B参数模型,哪个模型的准确率会更高?为了研究这种trade-offs,采用scaling laws(《Scaling laws for neural language models》、《Scaling laws for autoregressive generative modeling》) 的角度是很有帮助的,它们评估变量的基本趋势从而推广单个数据点。在本文中,我们研究了
zero-shot quantization的bit-level inference scaling laws,以确定在给定模型total bits数量的情况下,什么精度可以最大化zero-shot accuracy。我们的主要发现是:在所有测试的模型规模和模型族中,4-bit参数都可以为固定数量的model bits提供最佳性能。我们研究了五个不同的模型族,
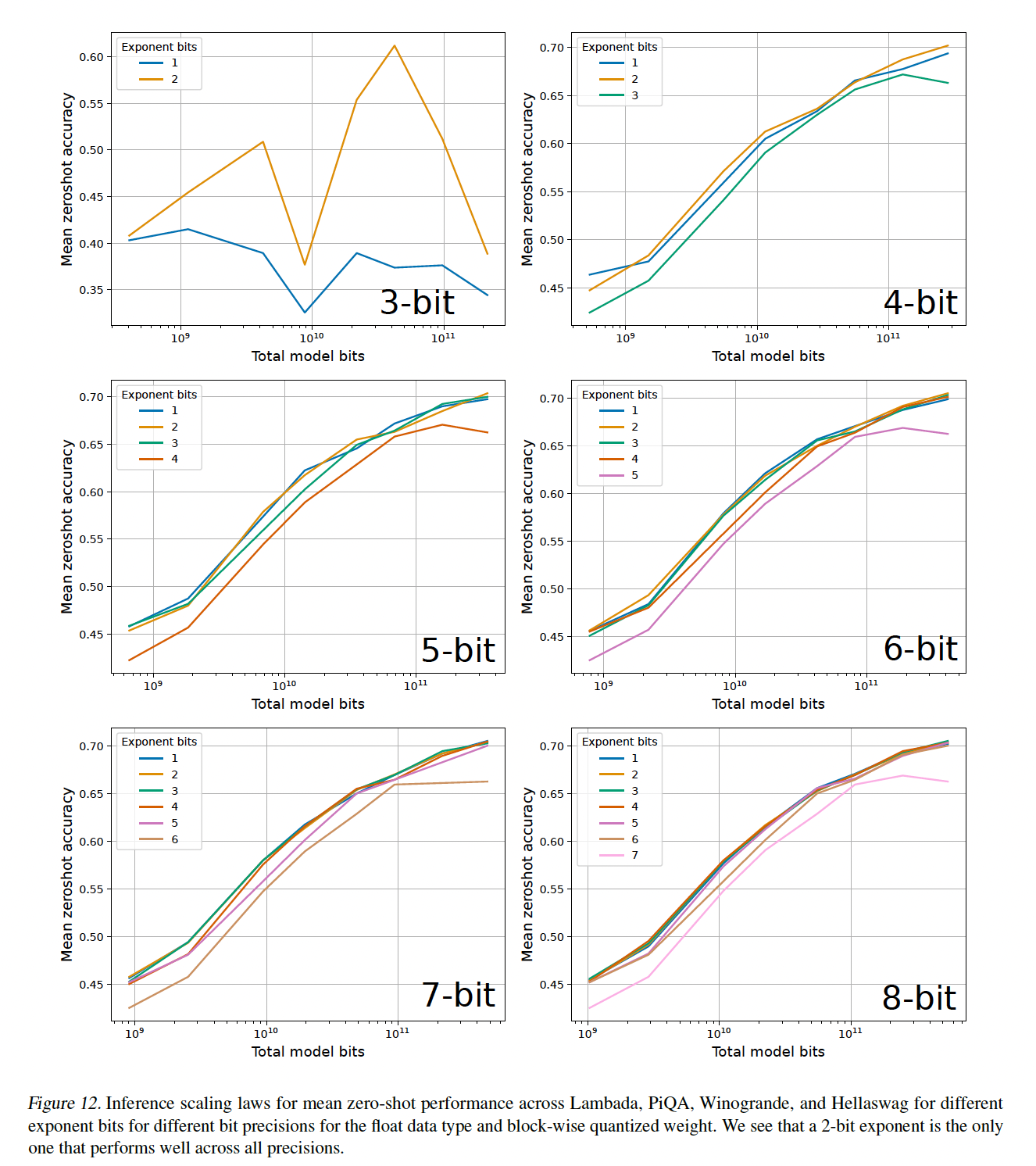
OPT、Pythia/NeoX、GPT-2、BLOOM和BLOOMZ,参数范围从19M到176B不等,精度范围从3-bit到16-bit。此外,我们运行了超过35,000个zero-shot experiments,以测试量化精度的许多最近研究的进步,包括底层数据类型和quantization block size。我们发现,将精度稳步从16-bit降低到4-bit可以在固定数量的model bits下提高zero-shot性能;而在3-bit时,zero-shot性能会下降。这种关系贯穿了所有被研究的模型,并且在从19M参数扩展到176B参数时没有改变,这使得4-bit量化在所有测试案例中都是通用的最佳选择。此外,我们分析了哪些量化方法可以改进
bit-level scaling、而哪些量化方法会降级(degrade)bit-level scaling。我们发现,在6-bit到8-bit精度下,我们测试的所有量化方法都无法改进scaling behavior。对于4-bit精度,数据类型和小的quantization block size是增强bit-level scaling趋势的最佳方法。我们发现quantile quantization数据类型和浮点数据类型是最有效的,而整数类型和dynamic exponent数据类型通常产生较差的scaling趋势。对于大多数4-bit模型,在我们的研究中,64到128之间的block size是最佳的。根据我们的结果,我们可以对使用
zero-shot quantized models进行推理提出直接的建议:始终使用4-bit模型、以及小的block size、以及浮点数据类型。如果需要在total model bits和预测性能之间进行trade-off,保持4-bit精度但改变模型的参数数量。尽管早期的工作已经表明,通过使用
outlier-dependent quantization可以显着提高quantized models的预测性能(《LLM.int8(): 8-bit matrix multiplication for transformers at scale》、《Smoothquant: Accurate and efficient post-training quantization for large language models》),但我们发现这对于bit-level scaling并不有效。具体而言,我们分析了3-bit OPT and Pythia模型的不稳定性,并表明尽管这些模型可以通过outlier-dependent quantization(我们称之为proxy quantization)来稳定,但与4-bit精度相比,这并没有改进bit-level scaling。另一方面,我们强调one-shot quantization方法,即该方法通过a single mini-batch of data来优化quantization,潜在地可以扩展到4-bit level以下。总体而言,这些发现表明,改进zero-shot bit-level scaling laws的最有希望的方向是开发新的数据类型和技术,这些技术可以用高精度来量化异常值而不需要大量的additional bits。我们还强调了one-shot quantization方法的潜力,作为一种实现low-bit transformers的方法,如果与我们的见解相结合。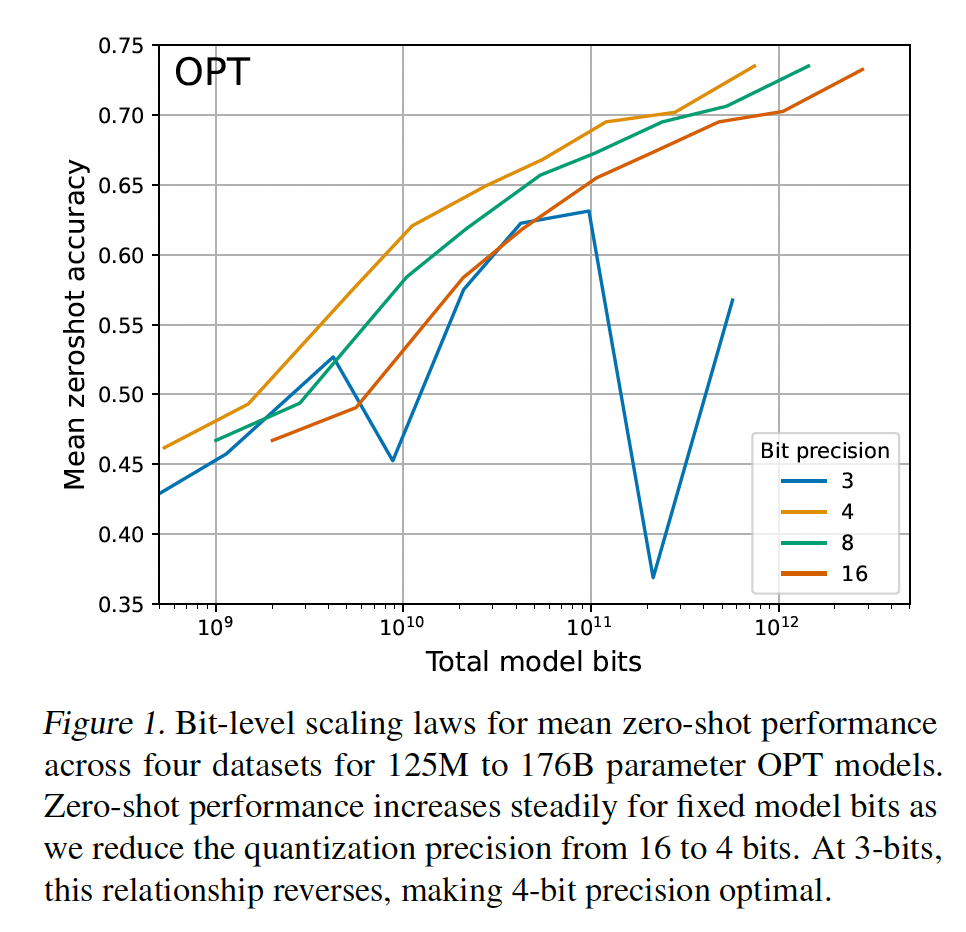
相关工作:
大型语言模型的量化:最相关的工作是针对具有十亿级以上参数的大型语言模型的量化。与小型模型相比,
LLM量化具有一些独特的挑战,例如出现的异常值、以及针对LLM的optimized low-bit inference。方法之间的一个主要区分因素是:zero-shot quantization方法(它直接量化一个模型而不需要任何额外信息),以及one-shot quantization方法(它需要a mini-batch of data进行量化)。虽然one-shot方法更加准确,例如GPTQ通过a mini-batch of data来优化量化期间的rounding(《Gptq: Accurate post-training quantization for generative pretrained transformers》),但它们也更复杂,可能需要几个小时的优化才能使用模型。另一方面,zero-shot方法的优点是它们可以立即使用,这使它们很容易使用,但zero-shot量化方法在更低的精度下通常会失败。量化方法:与我们的工作相关的另一个方面是量化方法,可以分为几类。例如,存在与
blocking and grouping相关的方法、centering相关的方法、通过聚类找到learned data types的方法、或direct codebook optimization的方法。虽然我们的工作研究了grouping and blocking,但我们只研究了一种通过整个input tensor的分位数(quantiles)对相似权重进行分组的数据类型(《8-bit optimizers via block-wise quantization》)。虽然我们没有深入研究learned data types,但我们是第一项工作来展示这些对改进LLM的bit-level scaling是至关重要的。Scaling Laws for Inference:早期关于scaling laws的工作强调了研究变量随规模变化的重要性,因为规模是模型性能的最佳预测指标之一(《Scaling laws for neural language models》、《A constructive prediction of the generalization error across scales》、《Deep learning scaling is predictable, empirically》)。特别是对于推理,已经有工作研究了4-bit与16-bit模型的zero-shot性能的scaling趋势(《Glm-130b:An open bilingual pre-trained model》)。我们研究了从3-bit到16-bit的精度,并分解了改善scaling的因素。《Efficiently scaling transformer inference》的工作查看了production setting(其中large batch size很常见)中的scaling inference。虽然他们只对量化进行了基本研究,但他们分解了导致更好model FLOPS utilization: MFU的因素。由于减少模型的bit-precision可以提高MFU,这与我们研究bit-level scaling的方法类似。主要区别在于:我们改变模型的bit-width,并研究消费者和小型组织常见的small batch size。
8.1 背景知识
对于
LLM,减少模型的bits数量与推理延迟(inference latency)直接相关,这一点可能并不直观。接下来将阐述这种关系的背景知识。之后,我们将介绍quantization的数据类型和方法。
8.1.1 Inference Latency 和 Total Model Bits 的关系
尽管我们的工作的主要目标是为大型语言模型找到
model bits和zero-shot accuracy之间的最佳trade-offs,但total model bits也与inference latency密切相关。整体的计算延迟(从计算开始到结束的时间)主要由两个因素决定:(1):从主内存(mainn memory)加载数据到缓存和寄存器需要多长时间。(2):执行计算需要多长时间。
例如,对于现代硬件(如
GPU),加载一个number通常需要比用那个number进行算术运算花费100倍以上的时间(《Dissecting the nvidia turing t4 gpu via microbenchmarking》、《A not so simple matter of software》)。因此,减少从主内存加载数据的时间通常是加速整体计算延迟(overall computation latency)的最佳方法。这种减少主要可以通过caching、以及更低精度的numbers来实现。如果两个矩阵都不完全适合设备的
L1缓存,caching可以将矩阵乘法的总延迟减少10倍或更多(《Dissecting the nvidia turing t4 gpu via microbenchmarking》)。在矩阵乘法中,batched input,global memory)进行多次加载,可以被缓存。如果
L1缓存,则不可能进行重用,因为RTX 3090 or RTX 4090 GPU,这发生在inference batch size低于60 or 200时。因此,在这些batch size以下,caching是无效的,inference latency完全由从加载因此,在
mini-batch适合L1缓存的情况下,可以通过使用较小的lower bit-precision per parameter)从而来减少推理延迟。例如,除了为quantization改善rounding的算法创新之外,《Gptq:Accurate post-training quantization for generative pretrained transformers》还为 “16-bit浮点输入且3-bit整数型权重” 开发了inference CUDA kernels,与“16-bit浮点输入且16-bit浮点权重” 相比,这为OPT-175B带来了高达4.46倍的inference latency改善,接近5.33倍的model bits减少。因此,对于small inference batch sizes,total model bits的减少与inference latency高度相关。我们在附录E中提供了roofline model和初步的unoptimized implementations的数据。
8.1.2 数据类型
这里我们简要概述被研究的的数据类型。有关这些数据类型的完整规范,请参见附录
A。我们使用四种不同的数据类型:对于整数类型和浮点数据类型,使用
IEEE标准。我们的浮点数据类型具有exponent bias,其中exponent bits。我们还使用分位数量化(
quantile quantization),这是一种无损最大熵量化数据类型(lossy maximum entropy quantization data type)(《8-bit optimizers via block-wise quantization》),其中每个quantization bin包含相等数量的值。这确保每个bit pattern出现的频率相等。quantile quantization可以被定义为:其中:
quantile function,它是累计分布函数的逆函数bit数量;bin,quantile quantization的第value。
我们使用
SRAM Quantiles算法来估计input tensor的经验累计分布函数来逼近input tensor的quantiles。最后,我们使用动态指数量化(
dynamic exponent quantization)(《8-bit approximations for parallelism in deep learning》),它使用indicator bit将exponent bit region和linear quantization region分开。通过移动indicator bit,exponent可以在不同的值之间变化。这种数据类型对于数值变化跨越多个数量级的张量具有较低的量化误差。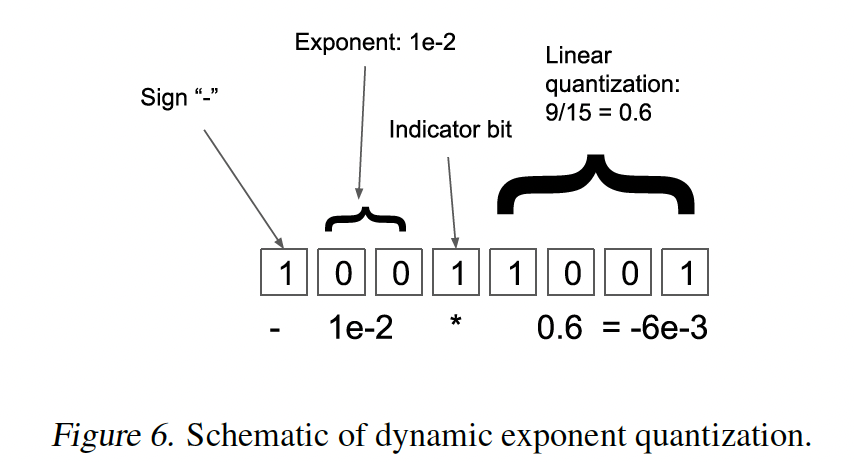
8.1.3 Blocking / Grouping
量化精度(
quantization precision)在一定程度上取决于是否所有quantization bins被均匀地使用。例如,4-bit数据类型有16个bins,但如果平均只使用了8个bins,那么就相当于3-bit数据类型。因此,帮助增加数据类型中所有quantization bins的平均使用率的方法可以增加量化精度。在这一小节中,我们介绍了blocking。blocking/grouping方法将张量分割成更小的blocks,并独立地对每个block进行量化。这有助于将异常值限制在特定的blocks中,从而增加其他blocks使用的bins的平均数量,进而提高平均的量化精度。Blocking/Grouping:blocking和grouping是相似的概念。在
grouping中,我们沿着某个维度将张量细分为group)分配其自己的归一化常数absolute maximum)。在
blocking中,我们将张量看作是一个一维的数值序列,并将这个序列划分为大小为blocks。
在我们的工作中,我们使用
blocking,因为与grouping不同,它提供了additional bits per parameter的指标,独立于hidden dimension。例如,使用16-bit normalization constants和block size 64意味着,我们每64个参数有额外的16 bits,或者说使用block-wise quantization的每个参数增加了16/64=0.25 bit的成本;这对于每个模型都是成立的,与hidden dimension无关。对于grouping,确切的成本将取决于每个模型的hidden dimension大小。对于
block-wise quantization,我们使用《8-bit optimizers via block-wise quantization》的符号,其中定义了:具有k bits的block-wise quantization、block-sizeblocks。如果并且我们用索引
block在block-wise quantization可以通过找到quantization map的值的最小距离来定义:其中:
block,
8.2 通过 Proxy Quantization 实现 Outlier-dependent Quantization
大型语言模型中出现的异常值特征会导致大的量化误差和严重的性能退化。尽管已经证明使用
16-bit输入和8-bit权重就足以避免这种破坏(《Glm-130b:An open bilingual pre-trained model 》),但如果我们使用16-bit输入和低于8-bit精度的权重,异常值特征是否仍会导致性能退化还不清楚。为此,我们通过
proxy quantization开发了outlier-dependent quantization,其中我们对与outlier feature dimensions对应的权重进行更高精度的量化,以测试权重需要多少精度。一个重大挑战是,每个模型具有不同数量的异常值特征,异常值部分地取决于每个zero-shot task不同的输入。因此,我们寻求一个model-independent的方法,该方法在所有模型和任务上都具有恒定的内存占用。在初步实验中,我们注意到
《LLM.int8(): 8-bit matrix multiplication for transformers at scale》开发的准则(即,用阈值来衡量hidden states从而检测异常值特征)是不可靠的,因为它取决于hidden state的标准差。这会引起问题,因为对于诸如OPT之类的模型,hidden state的标准差在后面的层中增加,这会导致检测到太多的异常值。这也已经得到《Glm-130b: An open bilingual pre-trained model》的注意。通过检查OPT模型中的这种异常情况,我们发现检测outlier dimensions的更好测量是:previous layer中每个hidden unit权重的标准差。产生异常值的hidden unit权重的标准差,要比其他维度的标准差高出20倍。我们在附录D中提供了标准差与异常值大小之间关系的相关性分析的进一步数据。由于神经网络的全连接特性,每一个
hidden unit会与多个下一层的hidden unit相连接。因此,每个hidden unit对应了多个权重。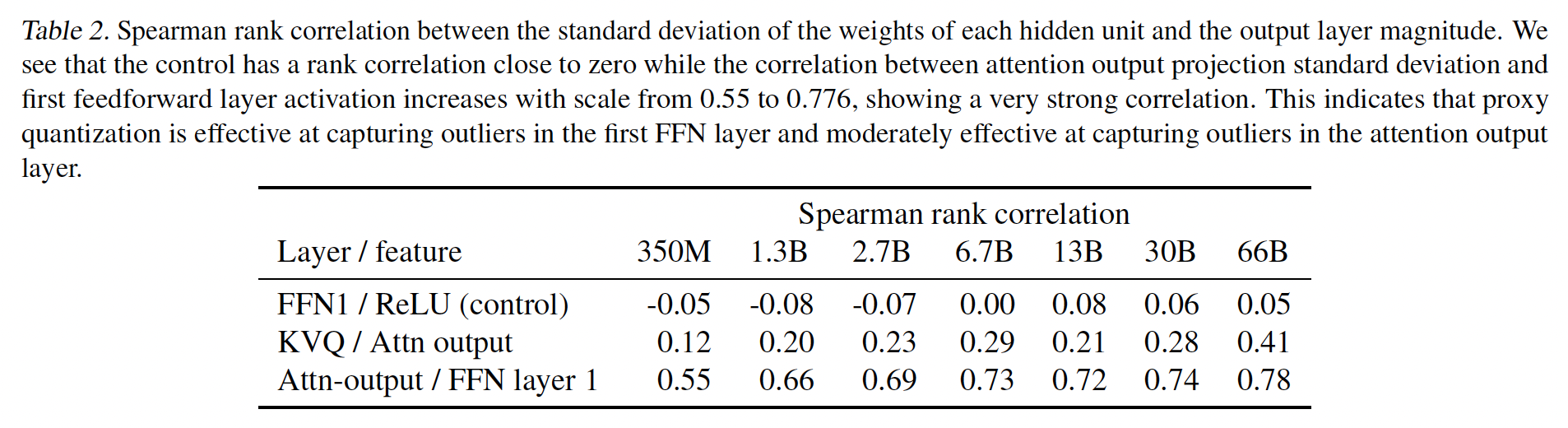
有了这一见解,我们开发了所谓的
proxy quantization。proxy quantization与输入无关,因此与任务无关,因为它使用每个层hidden unit权重的标准差作为哪些维度具有异常值特征的代理。例如,给定一个具有FFN和注意力投影层)的transformer,权重矩阵hidden units)。对于第其中:
上式的物理含义为:寻找
如果
16-bit;否则为k-bit。第
8.3 实验
配置:
在我们的实验中,我们使用
16-bit inputs和k-bit quantized parameters,16-bit baseline(16-bit浮点数)。为了衡量
k-bit quantization方法的推理性能,我们使用The Pile的CommonCrawl子集上的困惑度指标,以及EleutherAI LM Evaluation harness上的平均zero-shot性能。具体而言,对于zero-shot setting,我们在GPT-2 setting下使用EleutherAI LM eval harness,在LAMBADA、Winogrande、HellaSwag和PiQA等任务。选择这些特定的
zero-shot任务主要是由于前人的工作。但是,在我们的评估中,我们发现困惑度是一个更好的指标,因为每个样本的continuous value导致less noisy evaluations。这也得到了《Gptq: Accurate post-training quantization for generative pretrained transformers》的注意。例如,当使用困惑度来评估数据类型时,quantile quantization是最佳的数据类型。然而,当我们使用zero-shot accuracy作为评估指标时,由于zero-shot accuracy存在更多噪声,浮点数据类型有时会较好。此外,我们发现在超过
35,000次zero-shot experiments中,CommonCrawl困惑度与zero-shot performance之间的皮尔逊相关系数为-0.94。这突出表明:困惑度用于评估已经足够,且更可取。一个严重的缺点是困惑度难以解释。因此,为了清楚起见,我们在论文主体中使用了
zero-shot accuracy,但鼓励读者使用附录中的困惑度指标进行复现和比较。由于困惑度评估非常可靠,我们可以通过评估a small number of samples的困惑度来复制我们的工作,这使得构建scaling laws的计算量不那么大。Scaling Laws:我们试图将power laws拟合我们的数据,但我们发现关于参数数量和bit-precision的双变量幂函数(bivariate power function)的拟合效果很差。但是,当我们拟合线性插值来表示scaling curves时,我们发现不同bit-precisions几乎是平行的,这表明不同精度的scaling趋势可以由一个base function、以及每个bit-precision的偏移量来准确表示。因此,我们选择使用线性插值来表示scaling趋势。
8.3.1 Bit-level Inference Scaling Laws
主要结果如
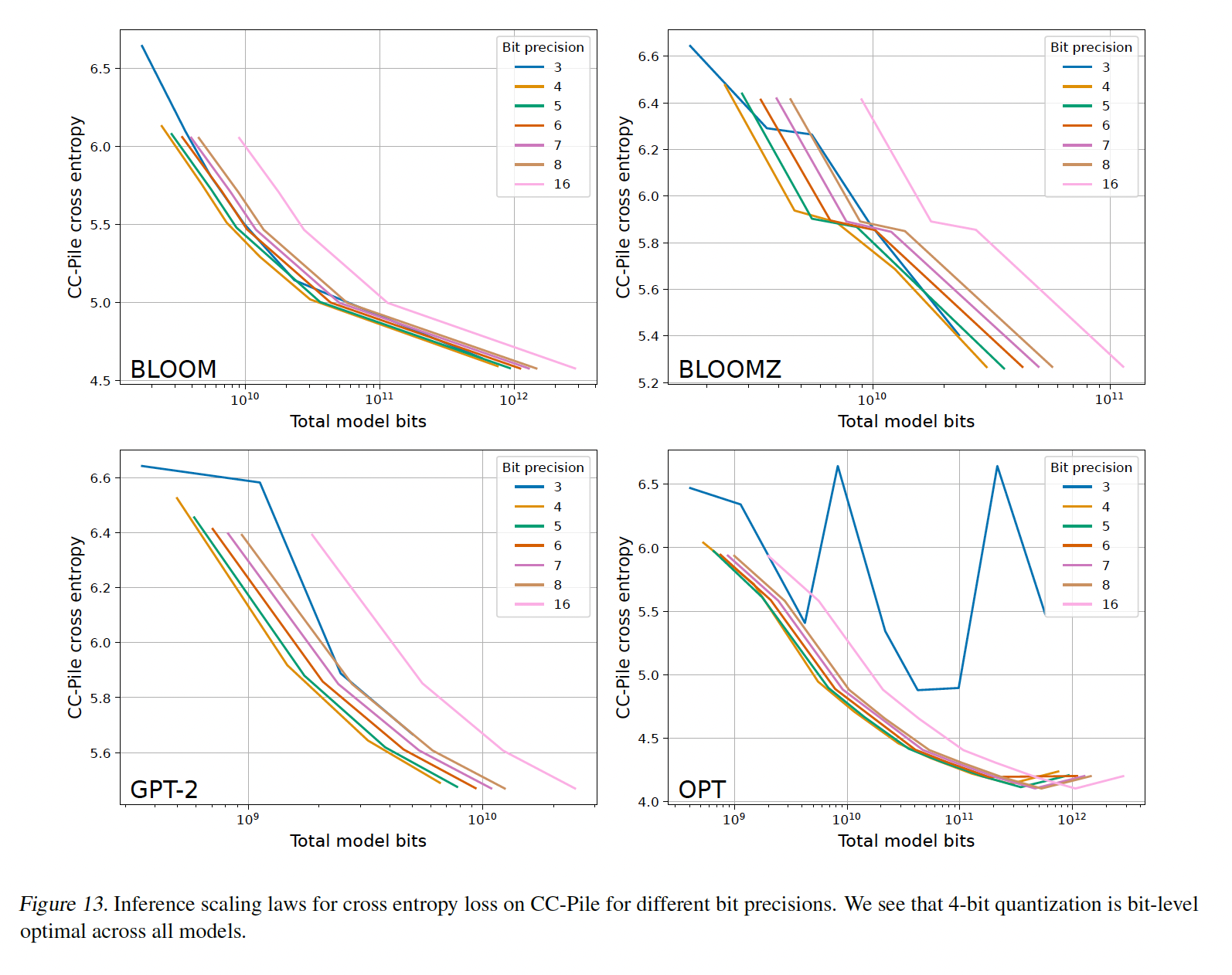
Figure 2所示,其中描绘了在Lambada、PiQA、HellaSwag和Winogrande任务上的平均zero-shot accuracy,给定OPT、BLOOM、Pythia和GPT-2的total number of bits,但是参数精度从3-bit到16-bit。我们得出以下观察:对于给定的
zero-shot性能,4-bit精度对于几乎所有模型族和模型规模都提供了最佳的scaling。唯一的例外是BLOOM-176B,其中3-bit略好但不明显。scaling curves几乎是平行的,这表明bit-level scaling在很大程度上与scale无关。3-bit量化是一个例外。即,
Bit-level Inference Scaling Law与bit无关。对于
3-bit推理,Pythia和OPT不稳定,其中最大的Pythia/OPT模型的性能接近随机的准确率。
这个实验的量化是采用类似于
LLM.int8()的方式进行的,其中高精度量化的权重矩阵列的集合为: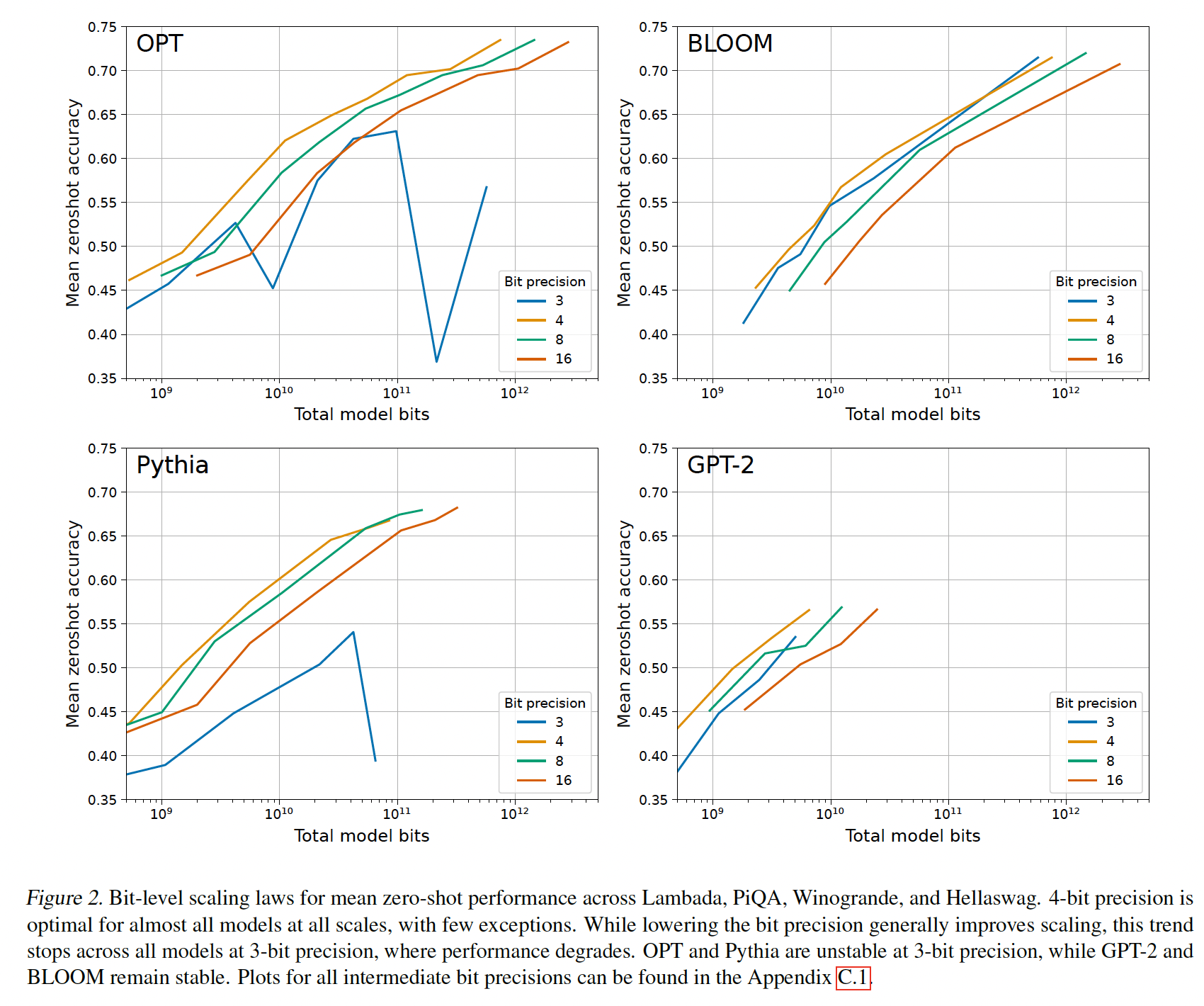
8.3.2 改进 Scaling Laws
鉴于
Figure 2中的main scaling results,一个重要的后续问题是我们如何进一步改进scaling趋势。为此,我们运行了超过35,000次zero-shot实验,以测试quantization precision的许多最近研究进展,包括基础数据类型、quantization block size、以及outlier-dependent quantization。这些方法通常以少量
additional bits为代价来改进量化误差。例如:block size = 64且使用16-bit quantization constant,意味着每64个参数增加16个additional bits(或每个参数增加16/64 = 0.25 bit)。outlier-dependent quantization以16-bit精度存储top p的权重向量,从而将每个参数的bits增加0.24 bits per parameter。
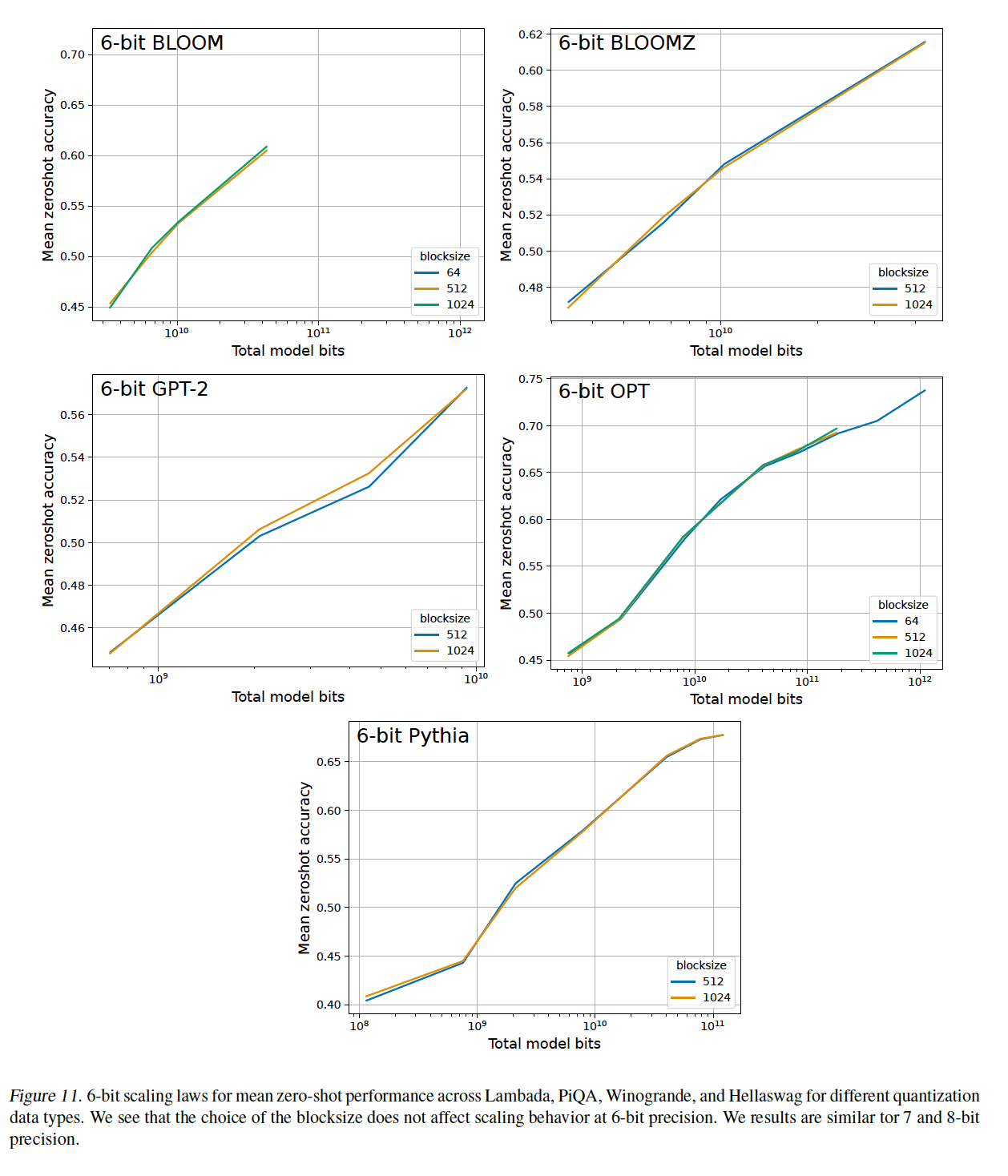
6-bit precision到8-bit precision没有改善scaling:我们将所有可能的量化方法(数据类型、blocking)与6-bit到8-bit量化组合,我们发现这些方法都没有改进bit-level scaling(参见附录C.3)。对于6-bit到8-bit精度,模型参数似乎有足够的精度,与16-bit权重相比,不会造成明显的性能降低。因此,scaling behavior只能通过其它方法使用低于6-bit的精度(而不是提高quantization precision)来改进。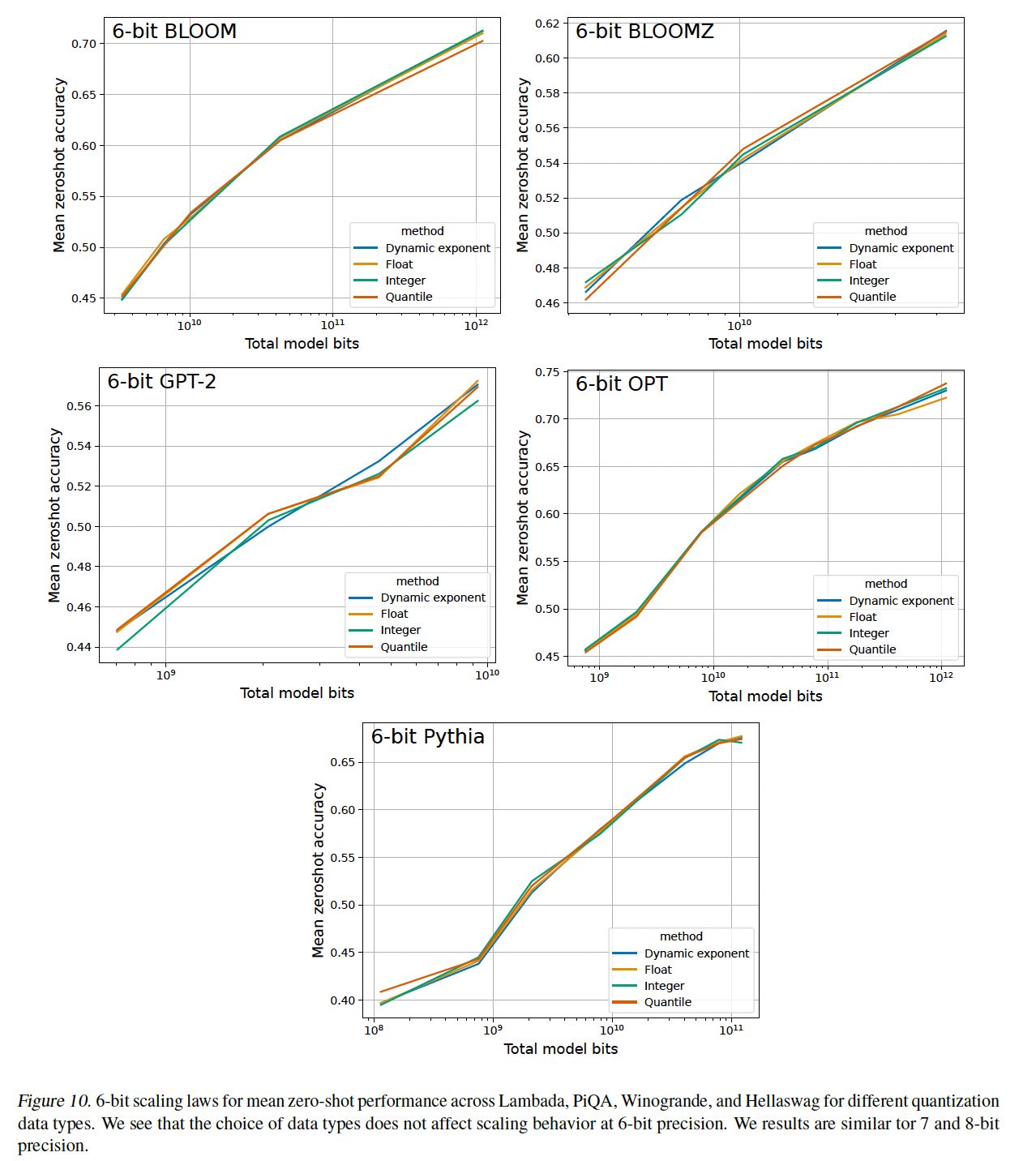
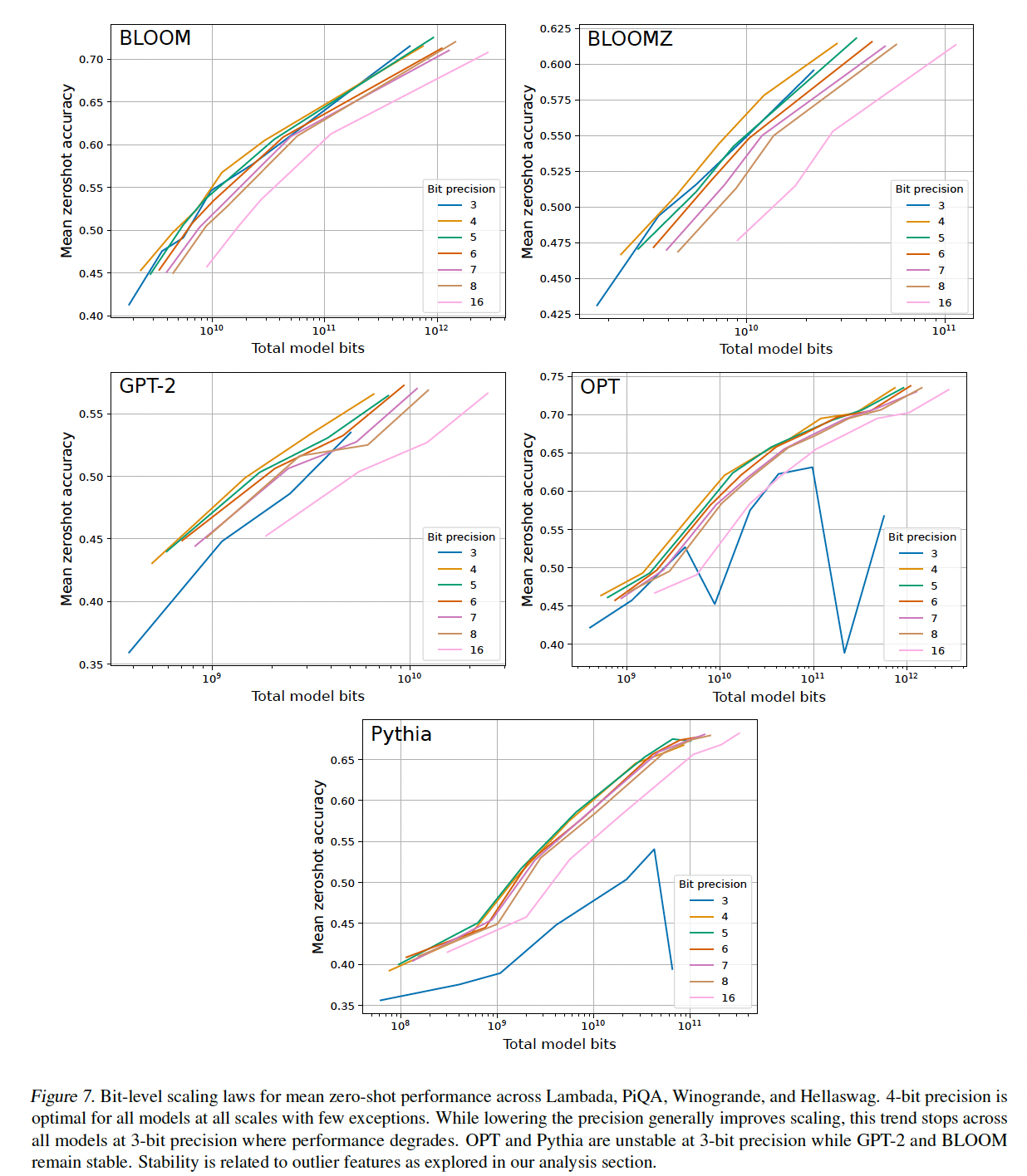
small block size改善了scaling:对于3-bit至5-bit精度,我们确实看到各种量化方法在scaling上的改进。Figure 3显示,对于4-bit Pythia模型,使用small block size可以实现可观的bit-level scaling改进。为了给出这一improvement的视角:从block size = 1024降低到block size = 64增加了0.24 bits per parameter,但zero-shot accuracy的改进几乎与从4-bit提升到5-bit一样大。因此,对于4-bit precision,使用small block size增加了几个extra bits从而提高了zero-shot accuracy。除了
Pythia之外,GPT-2模型也有很大程度的改进。BLOOM、BLOOMZ和OPT模型有明显改进,但与Pythia和GPT-2相比,改善的幅度较小,(参见附录C.2)。这种关系可能起源于emergent outlier features。对于
5-bit模型,使用small block size的改进很小但仍然显著。small block size可显著改进3-bit的scaling,但仍无法与4-bit precision的scaling相竞争。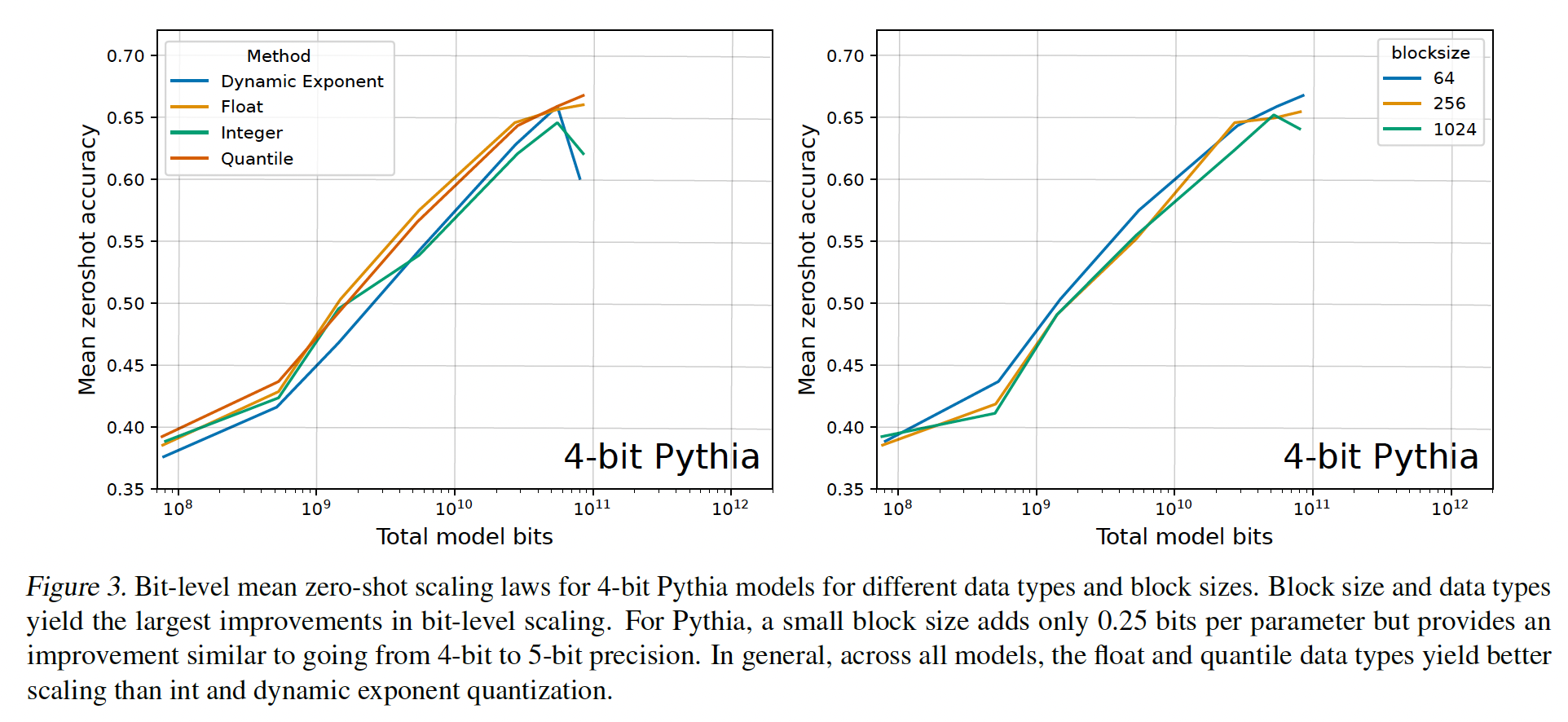
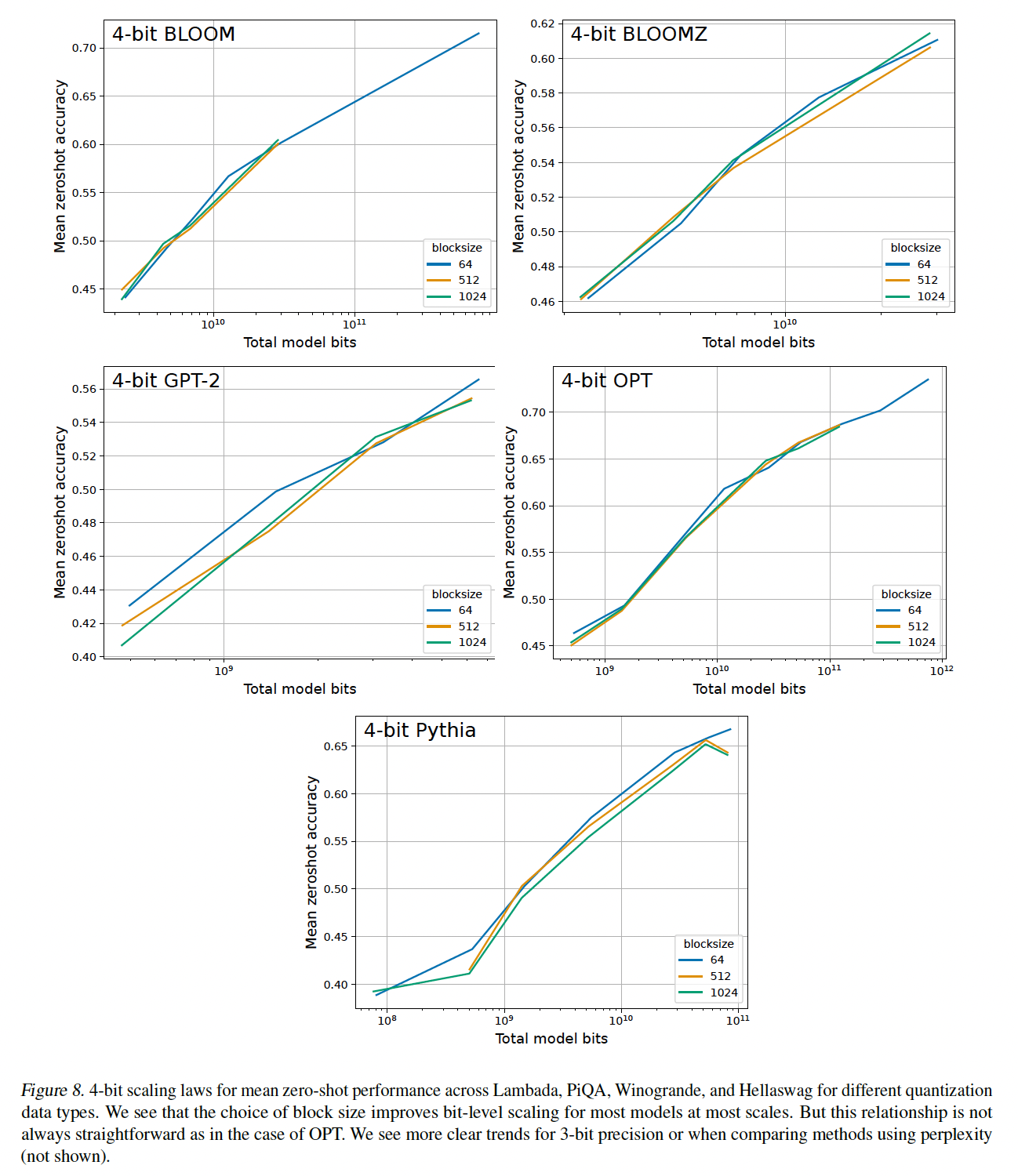
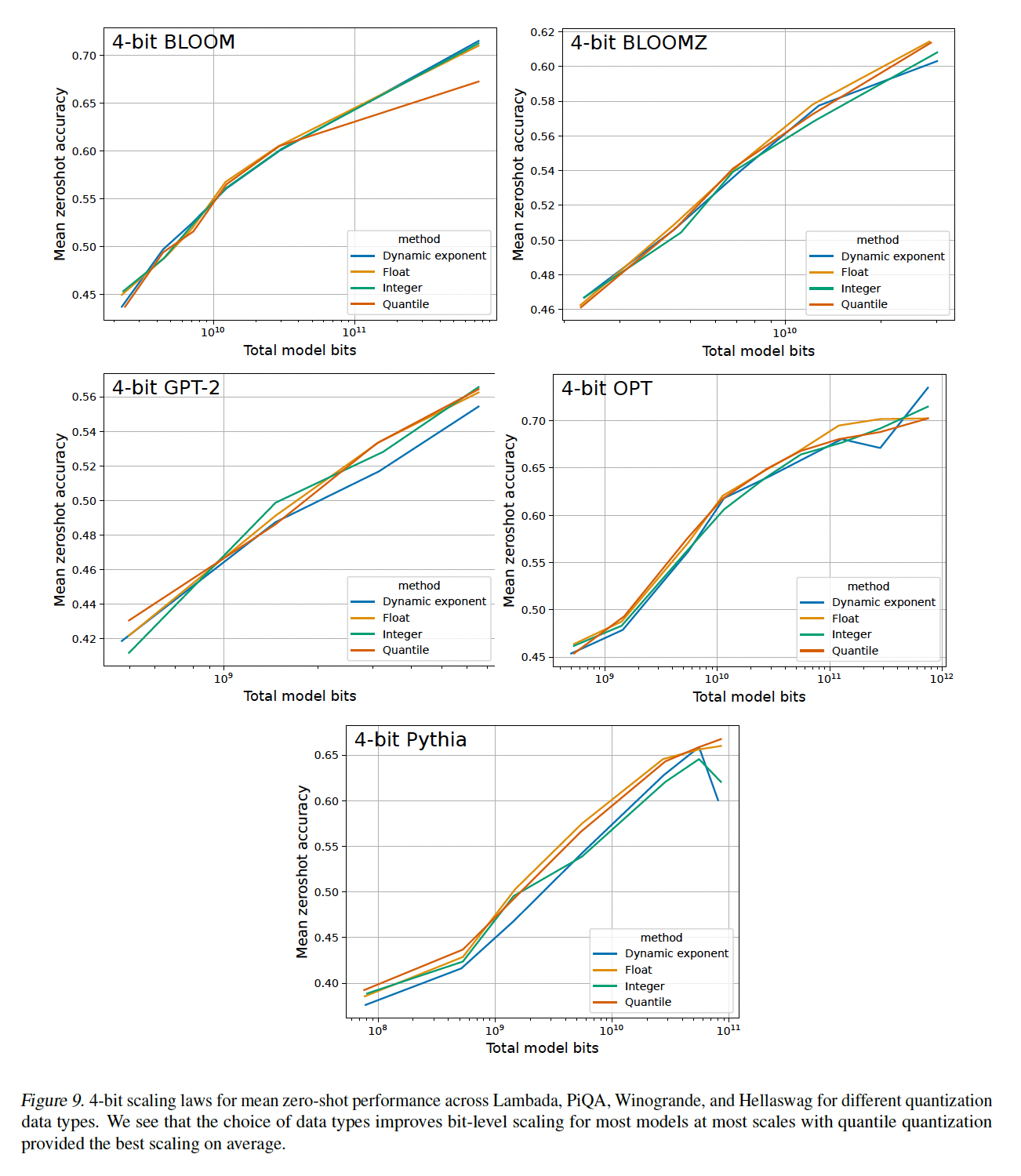
数据类型改善了
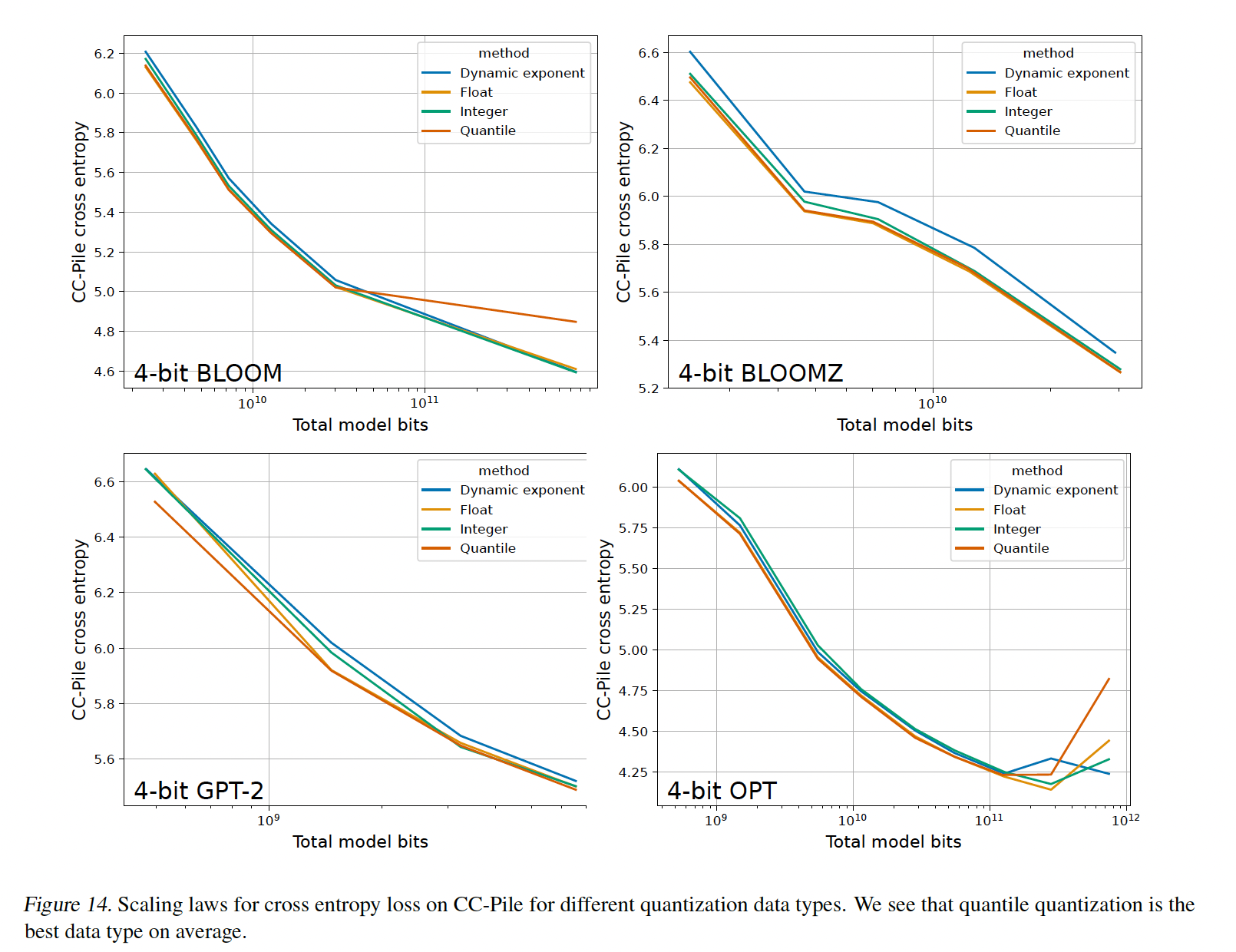
scaling:从Figure 3中可以看出,数据类型改善了4-bit Pythia的scaling趋势。具体而言,quantile quantization和浮点数据类型提供了比整数类型和dynamic exponent quantization更好的scaling。我们发现:
quantile quantization通常是所有模型、scales、精度中最好的数据类型(参见附录C.5)。浮点数据类型似乎优于整数类型,只有少数例外:整数类型对于
5-bit优于浮点类型。这似乎是因为浮点数据类型高度依赖指数位和小数位之间的平衡,根据特定的bit precision,浮点数据类型可以更好或更差。
outlier-dependent quantization提高了稳定性,但没有提高scaling:最后,我们注意到了OPT和Pythia中的3-bit不稳定性,并将其与emergent outlier features相关联(《LLM.int8(): 8-bit matrix multiplication for transformers at scale》、《Smoothquant: Accurate and efficient post-training quantization for large language models》)。如果我们使用proxy quantization将2%最重要的异常维度量化为16-bit而不是3-bit,我们可以提高3-bit Pythia and OPT模型的稳定性和整体scaling。这在Figure 4(left)的OPT中显示。然而,尽管有这一改进,4-bit precision仍然提供了更好的scaling。对于4-bit precision,Figure 4(right)所示的outlier-dependent quantization在scaling上没有好处,这意味着尽管使用proxy quantization时3-bit precision有可观的改进,但4-bit precision仍是最佳的。因此,似乎异值常特征不需要超过4-bit precision的权重就可以提供最佳的bit-level scaling。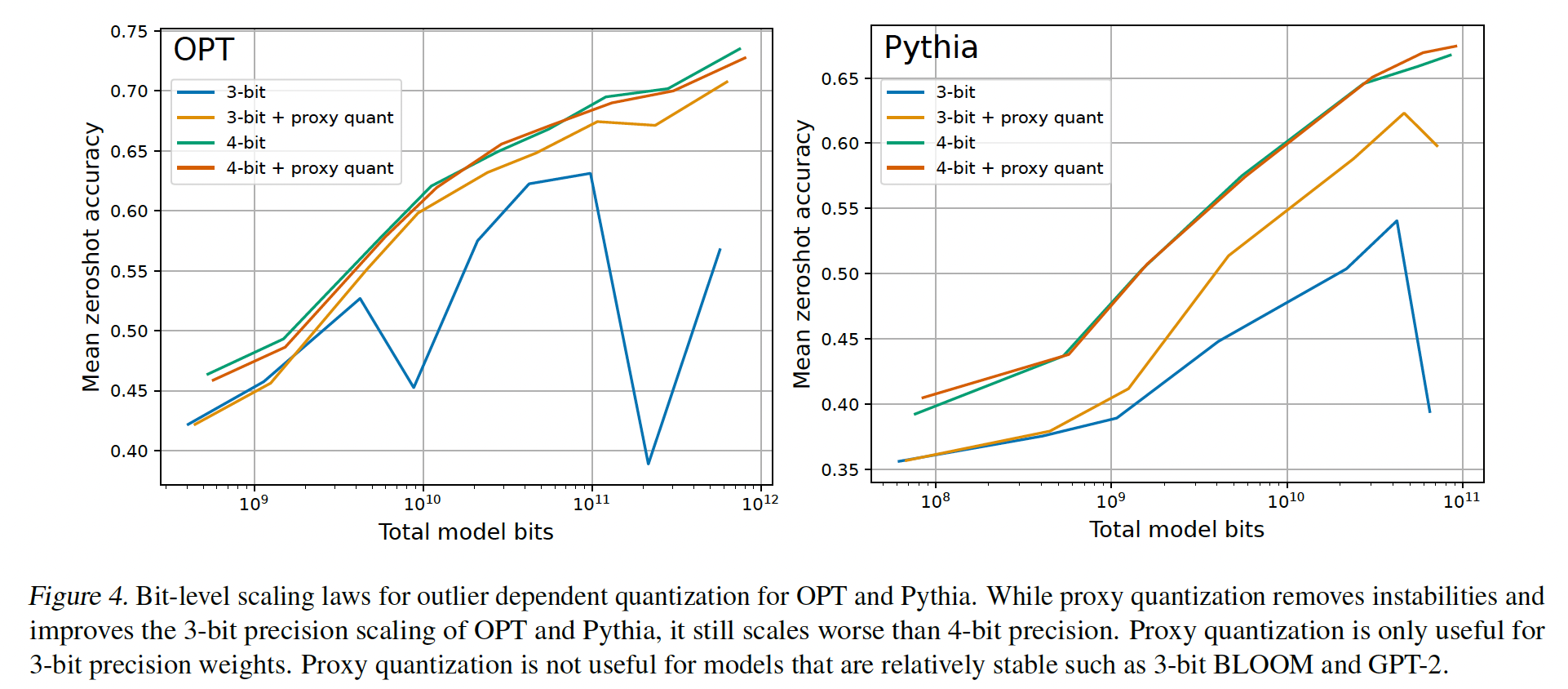
8.4 建议和未来工作
我们提出以下建议:
默认使用
4-bit quantization进行LLM推理,因为它在total model bits和zero-shot accuracy之间提供了最佳trade-offs。使用
128或更小的block size来稳定4-bit quantization并提高zero-shot性能。使用浮点类型或
quantile quantization数据类型。在某些情况下,整数类型可能更可取,从而改进inference latency(依赖于实现和硬件支持)。
需要高于
4-bit precision的一个场景是:当GPU具有足够的内存来容纳更高的bit precision而不是容纳更大的模型时。例如,48 GB GPU有足够的内存以5-bit precision使用66B参数模型,但不能以4-bit容纳175B参数模型。因此,如果需要最大化zero-shot accuracy,则对于这种场景,5-bit precision且66B参数模型是可取的。未来工作的有希望方向:
我们的结果表明当前
4-bit precision在bit-level是最有效率的,但我们也展示了3-bit scaling可以明显地被改进。因此,一个有希望的研究方向是关注4-bit以下的low-bit precisions并改善它们的scaling趋势。已经证明one-shot quantization(例如使用输入样本优化quantization的GPTQ)在low-bit precisions更有效(《Gptq: Accurate post-training quantization for generative pretrained transformers》)。Table 1显示,与zero-shot 3-bit Float相比,2-bit GPTQ with blocking可以获得更好的性能。这突出表明one-shot方法对于low-bit precisions非常有希望。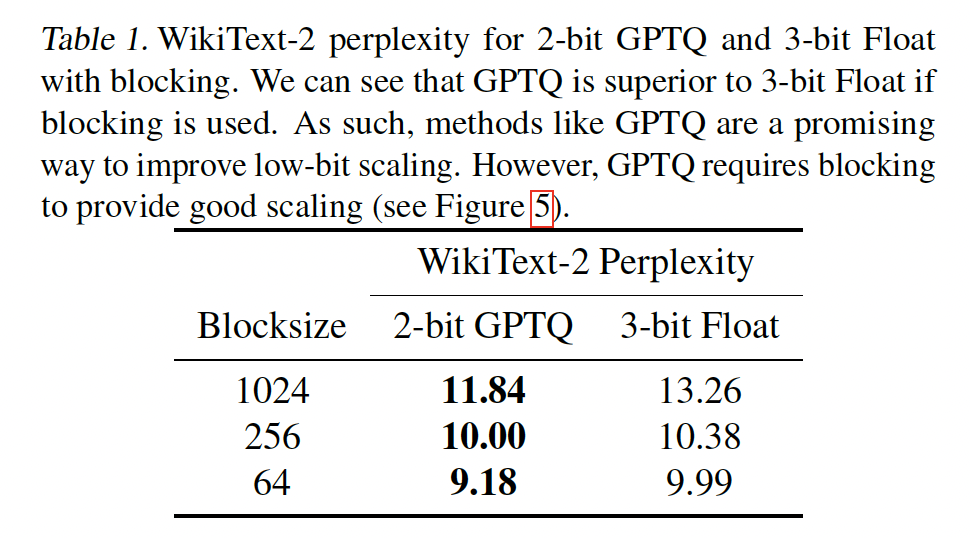
另一方面,
Figure 5也表明,与3-bit Float with a blocksize of 64相比,3-bit GPTQ without blocking的scaling更差;而4-bit GPTQ without blocking与4-bit Float with a blocksize of 64的scaling相似。从这些结果可以看出,我们从zero-shot scaling laws中获得的见解可以传递到one-shot quantization方法。这表明zero-shot quantization research非常适合于分离和理解quantization scaling中的各个因素,而one-shot方法可以最大化性能。相比之下,当前的one-shot方法研究起来非常昂贵。例如,仅对OPT-175B和BLOOM-176B模型重复我们的scaling experiments,估计需要5120 GPU days的计算。因此,zero-shot quantization scaling insights和one-shot quantization methods的组合可能产生最佳的未来方法。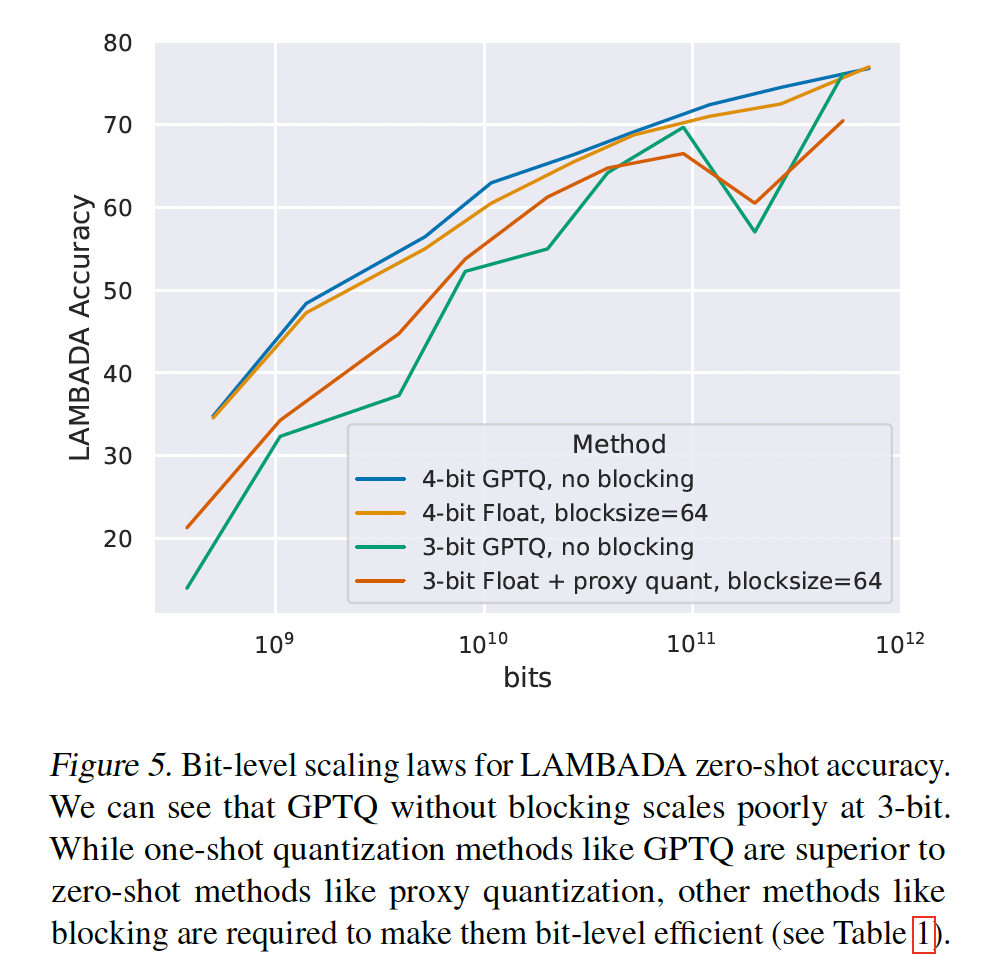
我们工作中未解决的一个挑战是数据类型也应该能在硬件级别上高效地使用。例如,尽管
quantile quantization数据类型展示最佳的scaling趋势,但它需要一个小的lookup table,这在高度并行的setup中很难实现,因为并行内存访问(parallel memory access)通常会由于序列化而导致性能较差。这个问题可以通过设计新的数据类型来解决,其中这个数据类型既具有bit-level scaling效率、又具有硬件效率。解决这个问题的另一种方法是硬件设计:我们能设计什么硬件来高效地使用quantile quantization等数据类型?block-size和outlier-dependent quantization都可以改进异常值的quantization precision。虽然outlier-dependent quantization在scaling上没有改进,但是有理由表明:存在unknown quantization方法可以帮助处理异常值,并同时改进scaling趋势。因此,未来研究的另一个重点应该集中在最大限度地保留异常值信息,但是最小化使用additional bits。
8.5 讨论和局限性
局限性:
尽管我们运行了超过
35,000次实验,但一个主要局限性是我们没有考虑某些类别的量化方法。例如,存在一些量化方法,其中数据类型使用额外的输入数据进行优化、或数据类型仅从模型的权重进行优化。仅从权重进行优化,与我们研究中最有效的quantile quantization类似。因此,这暗示这样的量化方法可以改进inference的scaling,但我们错过了将其纳入研究的机会。然而,我们的研究是重要一步从而认识到这些方法对于优化model-bits-accuracy trade-off的重要性,而这种视角以前不存在。另一个局限性是缺乏
optimized GPU implementations。目前还不清楚其他依赖lookup tables的数据类型是否能实现明显的加速。然而,我们的Int/Float数据类型可以实现高效的实现;即使对于其他数据类型,我们的结果对于未来产生strong scaling and efficient implementations的数据类型的开发仍然有用。虽然我们只通过研究
model-bits-accuracy trade-off间接地研究了latency-optimal视角,但latency-optimal视角的一个实际局限性是:low-bit models with 16-bit inputs可能是less latency efficient的,如果这样的模型被部署用于许多用户(《Efficiently scaling transformer inference》)。给定一个busy deployed API,其中每秒处理数千个请求,那么large mini-batch将不再fit cache。这意味着在这种情况下,bit-level scaling laws与inference latency的相关性会越来越小。对于这样的高吞吐量系统,需要建模low-bit weights and low-bit inputs的scaling laws来研究最佳的inference latency scaling。简而言之,我们的scaling laws仅对mini-batch不适合设备L1 cache的case有效;除此之外,需要一套新的scaling laws。最后一个局限性是,加载权重矩阵只是
inference latency优化的一部分。例如,如果不优化attention operations,多头注意力可以占据很大一部分推理延迟(《Sparseis enough in scaling transformers》、《Efficiently scaling transformer inf》)。然而,模型的整体内存占用仍然被减小,这使得在GPU内存有限时,大型语言模型更易于使用。
九、SparseGPT[2023]
论文:
《SparseGPT: Massive Language Models Can be Accurately Pruned in One-Shot》
来自
Generative Pretrained Transformer: GPT家族的大型语言模型(Large Language Models: LLMs)在广泛的任务中展现出了显著的性能,但由于其巨大的大小和计算成本而难以部署。例如,性能最佳的GPT-175B模型拥有175B个参数,即使以半精度(FP16)格式存储也至少需要320GB(以1024为基数计数)的存储空间,这意味着推理至少需要5个80GB A100 GPU。因此,通过模型压缩来降低这些成本自然受到了广泛的关注。到目前为止,几乎所有现有的GPT压缩方法都集中在量化(《LLM.int8(): 8-bit matrix multiplication for transformers at scale》、《ZeroQuant: Efficient and affordable post-training quantization for large-scale transformers》、《Smoothquant: Accurate and efficient post-training quantization for large language models》、《GPTQ: Accurate post-training compression for generative pretrained transformers》)上,即降低模型numerical representation的精度。与量化相辅相成的压缩方法是剪枝(
pruning),即移除网络元素,从移除单个权重(非结构化剪枝)到移除更高粒度的结构(如权重矩阵的行或列,即结构化剪枝)。剪枝具有悠久的历史(《Optimal brain damage》、《Optimal brain surgeon and general network pruning》),并且在计算机视觉模型、以及较小规模的语言模型中得到了成功的应用(《Sparsity in deep learning: Pruning and growth for efficient inference and training in neural networks》)。然而,性能最佳的剪枝方法需要对模型进行大量的重新训练以恢复准确率。反过来,这对于GPT-scale的模型来说非常昂贵。尽管存在一些准确的one-shot pruning方法(《Accelerated sparse neural training: A provable and efficient method to find N:M transposable masks》、《Optimal Brain Compression: A framework for accurate post-training quantization and pruning》),即无需重新训练模型就可以进行压缩,但不幸的是,这些方法在应用于数十亿参数的模型时也变得非常昂贵。因此,到目前为止,准确地剪枝数十亿参数模型的工作几乎为空白。在本文中,我们提出了
SparseGPT,这是第一种在成百上千亿参数模型规模上高效工作的accurate one-shot pruning方法。SparseGPT的工作原理是将剪枝问题简化为大量的稀疏回归(sparse regression),然后通过一种新的近似稀疏回归求解器(approximate sparse regression solver)来解决这些实例。该求解器足够高效,可以在几小时内在最大的公开可用GPT模型(175B参数)上单GPU执行。同时,SparseGPT足够准确,在裁剪后仅有微乎其微的准确率下降,无需任何微调。例如,当在最大的公开可用的生成式语言模型(OPT-175B和BLOOM-176B)上执行时,SparseGPT可以在one-shot中诱导(induce)50-60%的稀疏度,accuracy loss很小,无论是从困惑度还是zero-shot accuracy来衡量。我们的实验结果(我们在
Figure 1和Figure 2中提供了概览)得出以下观察。首先,如
Figure 1所示,SparseGPT可以在例如OPT家族的175B参数变体中诱导高达60%的uniform layer-wise sparsity,accuracy loss很小。相比之下,目前已知的可以轻松扩展到这种规模的唯一one-shot baseline(Magnitude Pruning,参考《A simple and effective method for removal of hidden units and weights》、《Learning both weights and connections for efficient neural networks》)只能在稀疏度达到10%时保持准确率,而在稀疏率超过30%时则完全崩溃。其次,如
Figure 2所示,SparseGPT还能在更严格但对硬件友好的2:4和4:8半结构化稀疏模式中准确地施加稀疏性(《Accelerating sparse deep neural networks》);不过对于更小的模型,相对于dense baseline,其准确率会有所下降。
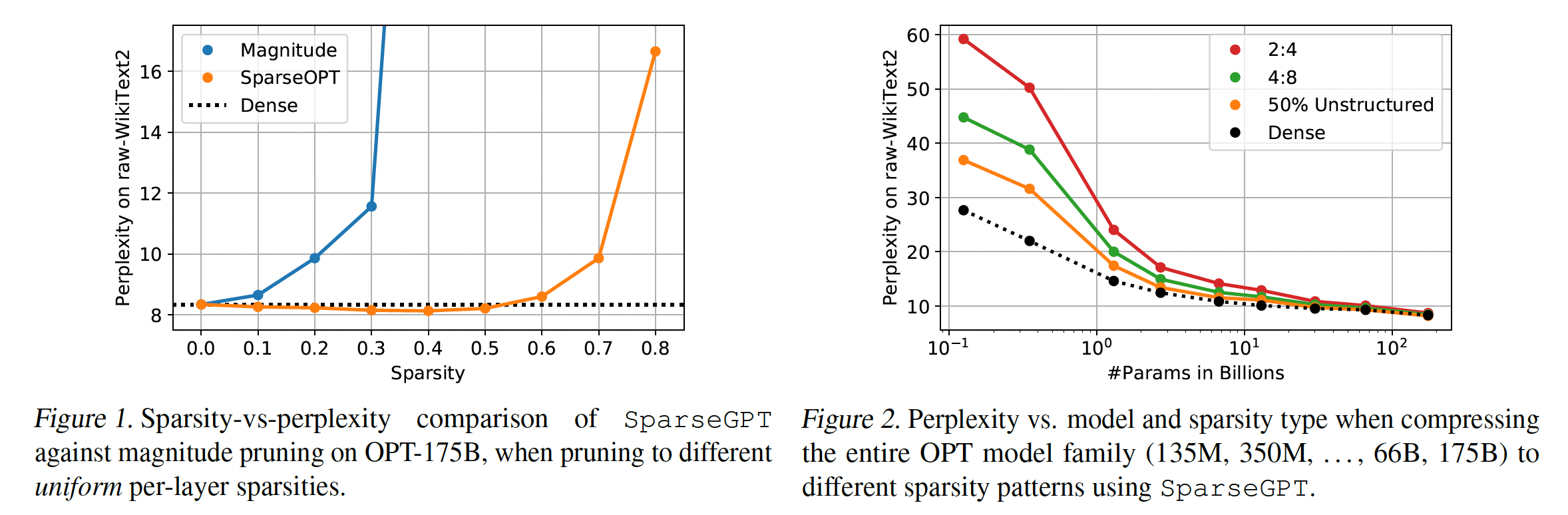
一个关键的
positive发现是,如Figure 2所示,更大的模型更容易压缩:在固定的稀疏度下,它们相对于较小的对应模型,损失更少的准确性。(例如,OPT和BLOOM家族中最大的模型可以稀疏化到50%而困惑度几乎无增加。)此外,我们的方法允许稀疏度与weight quantization技术(《GPTQ: Accurate post-training compression for generative pretrained transformers》)结合:例如,我们可以在OPT-175B上同时诱导50%的weight sparsity和4-bit weight quantization,而困惑度几乎无增加。一个显著的特点是,
SparseGPT完全是局部的,意味着它仅依赖于weight updates,而weight updates是为保留每个层的input-output relationship而设计的,而weight updates是在没有任何global gradient information的情况下计算的。因此,我们发现直接在dense pretrained models的 “邻域” 中识别这样的sparse models是令人惊讶的,其中sparse models的输出与dense model的输出有极高的相关性。相关工作:
剪枝的方法:据我们所知,我们是首次研究裁剪大型
GPT模型的,例如超过10B参数的模型。针对这个令人惊讶的gap的一个解释是:大多数现有的剪枝方法,例如(《Deep compression: Compressing deep neural networks with pruning, trained quantization and Huffman coding》、《The state of sparsity in deep neural networks》、《Well-tuned global magnitude pruning can outperform most bert-pruning methods》)在剪枝后需要大量的retraining从而恢复准确率,而GPT-scale的模型无论是训练还是微调通常都需要大量的计算和参数调优(《OPT: Open pre-trained transformer language models》)。SparseGPT是一种GPT-scale模型的post-training方法,因为它不执行任何微调。到目前为止,post-training pruning方法只在经典的CNN或BERT-style模型的规模下进行了研究,这些模型的参数比我们关注的模型少100-1000倍。我们在正文部分讨论了这些方法的scaling的挑战,以及其与SparseGPT的关系。Post-Training Quantization:相比之下,对公开的GPT-scale模型进行post-training quantization有大量工作。具体来说:ZeroQuant、LLM.int8()和nuQmm方法研究了对数十亿参数模型进行round-to-nearest quantization的可行性,表明通过这种方法可以实现权重的8-bit quantization;但由于存在outlier features,activation quantization可能很困难。《GPTQ: Accurate post-training compression for generative pretrained transformers》利用近似的二阶信息准确地将权重量化到2-4 bits;对于最大的模型,并展示了当与有效的GPU kernels相结合时,生成式的batch-size = 1的推理可以获得2-5倍的加速。后续工作
《Smoothquant: Accurate and efficient post-training quantization for large language models》研究了activation and weight quantization的联合8-bits量化,提出了一种平滑的方案,减少了activation quantization的困难,并配合高效的GPU kernels。《Quadapter: Adapter for gpt-2 quantization》通过quadapters(可学习参数的目标是channel-wise地缩放activations,同时保持其他模型参数不变)来解决量化activation outliers的困难。《The case for 4-bit precision: k-bit inference scaling laws》研究了模型大小、quantization bits和不同准确率概念之间的scaling relationships,观察到perplexity scores与跨任务汇总的zero-shot accuracy之间存在高度相关性。
正如我们在正文中所示,
SparseGPT算法可以与GPTQ(目前SOTA的weight quantization算法)结合使用,并且与activation quantization方法(Smoothquant、Quadapter)兼容。
9.1 背景知识
Post-Training Pruning:Post-Training Pruning是一个实际场景,其中我们得到一个经过良好优化的模型calibration data),并且必须获得sparse and/or quantized版本)。这一setting最初在quantization的背景下流行,最近也已成功地拓展到剪枝。Layer-Wise Pruning:post-training compression通常通过将full-model compression问题拆分为layer-wise子问题来完成,其solution quality通过如下的方式来衡量:给定输入uncompressed layer(权重为compressed layer的输出之间的《Accelerated sparse neural training: A provable and efficient method to find N:M transposable masks》将此问题表述为:对每个层target density),以及可能的updated weights其中
然后通过 “拼接” 各个
compressed layers来获得overall compressed model。Mask Selection & Weight Reconstruction:上式中layer-wise pruning问题的一个关键方面是:掩码remaining weightsNP-hard问题。因此,对较大的层(即,参数量较多)进行精确求解是不现实的,这导致所有现有方法都采用近似方法。一个特别流行的方法是:将问题分解为掩码选择(
mask selection)和权重重构(weight reconstruction)(《AMC: AutoML for model compression and acceleration on mobile devices》、《A fast post-training pruning framework for transformers》、《Accelerated sparse neural training: A provable and efficient method to find N:M transposable masks》)。具体来说,这意味着:首先根据一些显著性标准(如权重幅值)(
《To prune, or not to prune: exploring the efficacy of pruning for model compression》)选择一个pruning mask然后在保持掩码不变的情况下优化
remaining unpruned weights。重要的是,一旦掩码固定,上式变为一个易于优化的线性平方误差问题。
Existing Solvers:早期工作 (
《Hypothesising Neural Nets》)将迭代线性回归应用于小型网络。更近期的
AdaPrune方法(《Accelerated sparse neural training: A provable and efficient method to find N:M transposable masks》)通过magnitude-based weight selection、以及应用SGD steps来重构remaining weights,在现代模型上为此问题显示了良好的结果。后续工作表明,通过消除
mask selection和weight reconstruction之间的严格分离,可以进一步改进pruning accuracy。Iterative AdaPrune(《SPDY: Accurate pruning with speedup guarantees》)在gradual steps with re-optimization中进行剪枝。OBC(《Optimal Brain Compression: A framework for accurate post-training quantization and pruning》)引入了一个贪心求解器(greedy solver),每次移除一个权重,并在每次迭代后通过有效的闭式方程完全重构remaining weights。
扩展到
100B以上参数的困难:以前的post-training技术都是为了准确地压缩最多几亿参数的模型,计算时间在几分钟到几小时。然而,我们的目标是使规模高达1000倍的模型稀疏化。即使是
AdaPrune这种为理想的speed/accuracy trade-off而优化的方法,也需要几个小时才能使仅有1.3B参数的模型稀疏化(参见实验部分);如果线性扩展到175B Transformers,则需要数百个小时(几周时间)。比AdaPrune更准确的方法至少要贵几倍(《SPDY: Accurate pruning with speedup guarantees》),或者甚至表现出比linear scaling更糟的扩展性(《Optimal Brain Compression: A framework for accurate post-training quantization and pruning》)。这表明,将现有的
accurate post-training技术扩展到极大的模型是一项艰巨的任务。因此,我们提出了一种新的基于careful approximations to closed form equations的layer-wise求解器,SparseGPT,它可以轻松地扩展到巨大的模型,无论是运行时间还是准确性方面。
9.2 SparseGPT 算法
SparseGPT的核心思想与GPTQ一致:layer-by-layer地最小化重构误差:其中
为权重矩阵中的某一行。
可以是 quantized weights、可以是sparsified weights,甚至可以同时包含稀疏化和量化。
9.2.1 Fast Approximate Reconstruction
动机:如前所述,对于固定的
pruning maskmask中所有权重的最优值,可以通过求解对应于矩阵中每一行sparse reconstruction问题来精确地计算(即,采用闭式解)。一共有
总的时间复杂度为
Transformer模型,这意味着总运行时间随hidden dimmension4次方扩展;我们需要至少减少一个Equivalent Iterative Perspective:为了推导我们的算法,我们首先必须从不同的迭代视角来看待row-wise weight reconstruction,使用经典的OBS update。对于给定的行,假设损失函数的二次逼近,对于当前权重OBS updateremaining weights的最佳调整,从而来补偿移除索引由于对应于
layer-wise裁剪OBS公式在这种情况下是精确的。因此,optimal weight reconstruction。此外,给定对应于掩码optimal sparse reconstructionOBS来找到掩码optimal reconstruction。因此,这意味着:我们并不是直接地求解full maskOBS应用于逐个裁剪权重full maskregression reconstruction相同的最优解。Optimal Partial Updates:应用OBS更新all available parameters的值(在当前掩码remaining unpruned weights的权重会怎样呢?因此,我们仍然可以从误差补偿(error compensation)中受益,仅使用子集OBS的成本。这样的
partial update确实可以通过简单地使用对应于OBS update,并仅更新layer-wise问题的损失函数对于OBS update仍然是最优的:对approximation error,只是误差补偿可能不那么有效,因为可供调整的权重更少。与此同时,如果masked Hessians。Hessian Synchronization:接下来,假设输入特征的固定顺序换句话说,从包含所有索引的
inverse Hessians《Optimal Brain Compression: A framework for accurate posttraining quantization and pruning》,通过高斯消元法可以在updated inverse其中
inverse Hessians可以在一旦某个权重
unpruned weights以实现最大的误差补偿。这导致以下策略:对于所有的行inverse Hessiansinverse Hessiansreused从而在所有行中remove weight j(当权重pruning mask的一部分时)。该算法的可视化描述见Figure 4。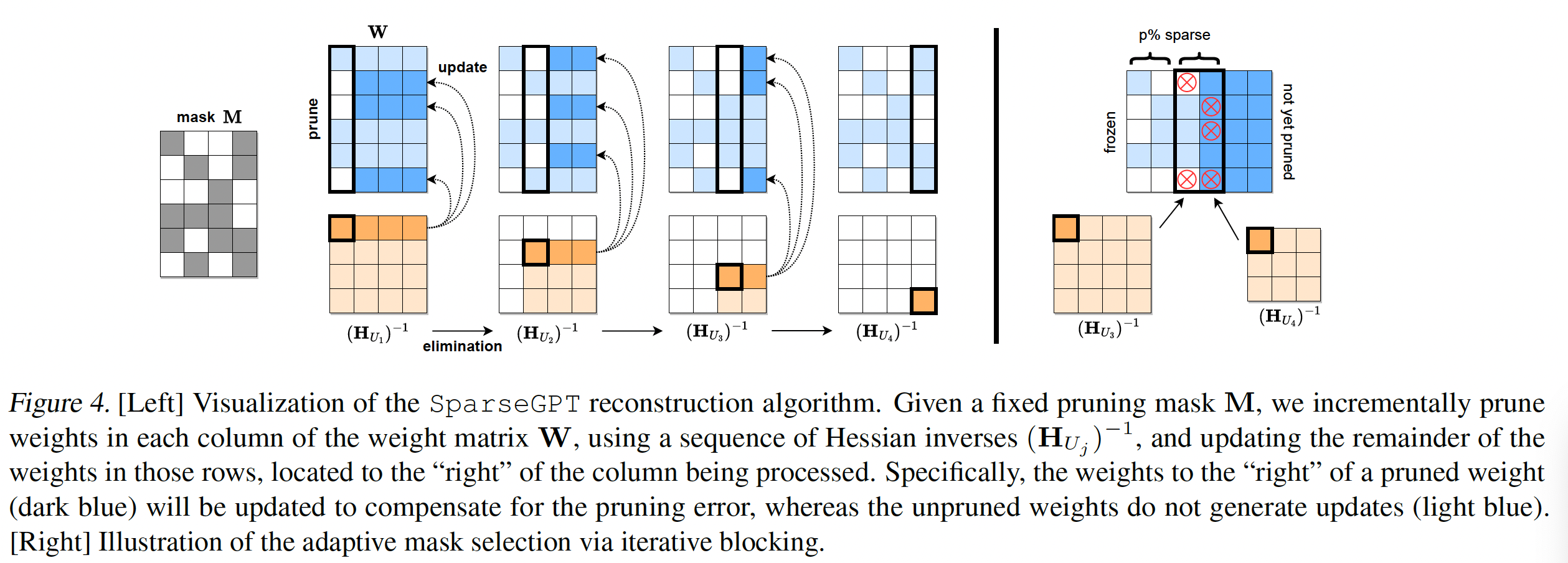
计算复杂度:总成本由三部分组成:
(a):计算初始海森矩阵,需要时间A)。(b):遍历inverse Hessian集合需要时间(c):reconstruction/pruning本身。后者成本可以用对
总共这些加起来为
Transformer模型,这简单地是exact reconstruction快了整整一个Weight Freezing Interpretation:虽然我们将SparseGPT算法表示为对exact reconstruction的逼近,使用optimal partial updates,但这个方案还有另一种有趣的视角。具体来说,考虑一个exact greedy framework,它按列压缩权重矩阵,在每一步总是最优地更新所有尚未压缩的权重。乍看之下,SparseGPT似乎不适合这个框架,因为我们在每列中只压缩一些权重,也只更新一部分未压缩的权重。然而,从原理上讲,“压缩”一个权重最终意味着将其固定为某个特定值,并确保它不会通过某些未来的更新再次 “解压缩”,即固定它。因此,将column-wise compression定义为:即,将不在掩码中的权重置零,并将其余权重固定为当前值,那么我们的算法可以解释为精确的
column-wise贪心方案。这种视角将允许我们干净地将sparsification和quantization合并为单个压缩过程。
9.2.2 Adaptive Mask Selection
到目前为止,我们仅关注
weight reconstruction,即假设固定的pruning maskAdaPrune(《Accelerated sparse neural training: A provable and efficient method to find N:M transposable masks》),一个简单的选择掩码的选项是:根据magnitude pruning(《To prune, or not to prune: exploring the efficacy of pruning for model compression》)。然而,最近的工作(《OptimalBrain Compression: A framework for accurate posttrainingquantization and pruning》)表明,剪枝过程中,updates由于correlations显着改变了权重,并且在mask selection中考虑这一点可以得到更好的结果。通过在reconstruction过程中自适应地选择掩码,可以将这一见解集成到SparseGPT中。一个明显的方法是在压缩列
p%权重,从而达到整体p%稀疏度。这个方法的最大缺点是:稀疏度无法在列之间非均匀分布,施加了额外的不必要结构。这对于拥有少量highly-sensitive outlier features(《LLM.int8(): 8-bit matrix multiplication for transformers at scale》、《Smoothquant: Accurate and efficient post-training quantization for large language models》)的大型语言模型来说尤其成问题。我们通过
iterative blocking来消除这一缺点。更准确地说,我们总是以pruning mask(见附录A),基于OBS的重构误差block的mask,并执行下一个non-uniform selection,特别是还使用了相应的海森矩阵信息,同时也考虑了先前的权重更新。(对于单个列怎么选择?读者猜测:选择重构误差最小的
9.2.3 Extension to Semi-Structured Sparsity
SparseGPT也可以容易地适配到诸如流行的n:m sparsity格式(《Learning N:M fine-grained structured sparse neural networks from scratch》、《Accelerated sparse neural training: A provable and efficient method to find N:M transposable masks》)等半结构化模式,其2:4 implementation在Ampere NVIDIA GPU上提供了速度提升。具体来说,每连续block sizemask selection中强制zeros-constraint,选择导致最低误差的最后,我们注意到,在这个半结构化场景中,较大的
column-sets之间非均匀地分布。
9.2.4 Full Algorithm Pseudocode
根据前面讨论的
weight freezing interpretation,SparseGPT reconstruction可以转化为最近的量化算法GPTQ的column-wise greedy framework。这意味着我们还可以继承GPTQ的几个算法增强,具体为:通过
Cholesky分解来预计算所有相关的inverse Hessian信息,从而实现数值稳定性。应用
lazy batched weight matrix updates从而提高算法的compute-to-memory ratio。
我们的
adaptive mask selection以及其向semi-structured pruning的扩展也与所有这些额外技术兼容。Algorithm 1以fully-developed的形式呈现了SparseGPT算法的unstructured sparsity,集成了GPTQ的所有相关技术。
9.2.5 联合 Sparsification 和 Quantization
Algorithm 1运行在GPTQ的column-wise greedy framework中,因此共享如下的计算密集步骤:计算Cholesky分解、连续地更新joint procedure成为可能。具体来说,所有被SparseGPT固定的权重额外地被量化,导致在后续update step中补偿以下泛化误差:其中,
quantization grid上的nearest value。关键是,在此方案中,single pass中几乎没有额外成本就可以联合地执行量化和剪枝。此外,联合执行量化和剪枝意味着后面的pruning decisions会受到前期的quantization rounding的影响;反之亦然。这与先前的joint技术(《Optimal Brain Compression: A framework for accurate post-training quantization and pruning》)形成对比,后者首先使层稀疏化,然后简单地量化remaining weights。
9.3 实验
配置:我们在
PyTorch中实现SparseGPT,并使用HuggingFace Transformers库来处理模型和数据集。所有剪枝实验都是在具有80GB内存的单个NVIDIA A100 GPU上进行的。在此设置下,SparseGPT可以在大约4小时内完全稀疏化175B参数模型。类似于ZeroQuant和GPTQ,我们顺序地剪枝Transformer layers,这大大减少了内存需求。我们的所有实验都是在one-shot操作中进行的,没有微调,与最近关于GPT-scale模型post-training quantization的工作(GPTQ、ZeroQuant、LLM.int8())采用了类似的设置。另外,在附录E中,我们使用现有工具研究了稀疏模型的实际加速效果。对于
calibration数据,我们遵循《GPTQ: Accurate post-training compression for generative pretrained transformers》,使用从C4数据集的第一个shard中随机选择的128个2048-token segments。这代表了从互联网上爬取的通用文本数据,并确保我们的实验仍然是zero-shot的,因为剪枝过程中没有看到特定任务的数据。模型、数据集和评估:
我们主要使用
OPT模型系列来研究scaling行为,但也考虑了BLOOM的176B参数版本。尽管我们的重点在于非常大的变体,但我们也在较小的模型上显示了一些结果。就指标而言,我们主要关注困惑度,已知困惑度是一个具有挑战性的和稳定性的指标,非常适合评估压缩方法的准确性。
我们考虑原始
WikiText2和PTB的测试集、以及C4验证数据的子集,这些都是LLM压缩的文献中的常用基准。为了增加解释性,我们还提供了
Lambada、ARC (Easy and Challenge)、PIQA和StoryCloze上的zero-shot accuracy结果。
我们注意,我们评估的重点在于稀疏模型相对于稠密
baseline的准确性,而不是绝对数字。不同的预处理可能影响绝对准确性,但对我们的相对论断几乎没有影响。困惑度的计算严格遵循HuggingFace描述的过程,使用full stride。我们的zero-shot evaluations是使用GPTQ的实现进行的,后者又基于流行的EleutherAI-eval harness。附录B中可以找到更多评估细节。所有稠密的和稀疏的结果都是使用完全相同的代码(在补充材料中提供)来计算的,以确保公平比较。baselines:我们与标准的
magnitude pruning baseline(《To prune, or not to prune: exploring the efficacy of pruning for model compression》)进行比较,layer-wise地应用,可扩展到最大模型。在高达
1B参数的模型上,我们还与AdaPrune进行了比较,后者是现有accurate post-training pruning方法中最高效的。为此,我们使用《SPDY: Accurate pruning with speedup guarantees》的内存优化重新实现,并进一步调优AdaPrune作者提供的超参数。因此,在我们关注的模型上,我们实现了约3倍的加速,而不影响解质量。
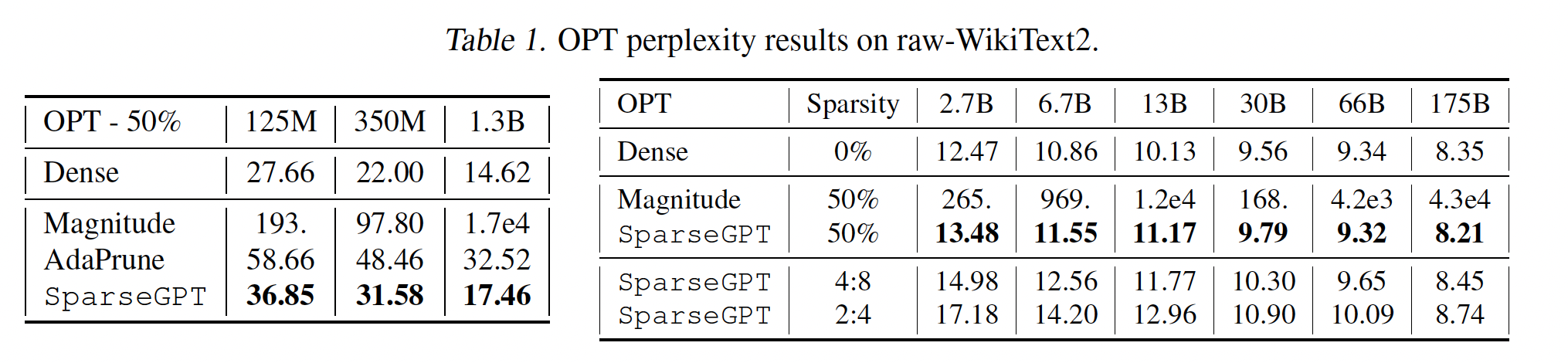
Pruning vs. Model Size:我们首先研究pruning LLMs changes与模型大小的关系。我们考虑整个OPT模型族,并统一地裁剪所有线性层,排除embedding layer和head layer,这是标准做法(《Movement pruning :Adaptive sparsity by fine-tuning》、《The Optimal BERT Surgeon: Scalable and accurate second-order pruning for large language models》),从而达到50% unstructured sparsity、full 4:8 or full 2:4 semi-structured sparsity(2:4模式是最严格的)。原始WikiText2性能指标如Table 1所示,并在Figure2中可视化。PTB和C4的对应结果可以在附录C中找到,并且整体显示出非常相似的趋势。一个直接的发现是:在不同规模上,
magnitude-pruned模型的准确率都崩溃了,通常较大的变体下降得比较小的变体更快。这与较小的视觉模型形成鲜明对比:后者通常可以通过简单的magnitude selection来裁剪到50%或更高稀疏度,但是损失很小的准确率。这突出了对大型生成式语言模型准确地裁剪的重要性,但也凸显出困惑度是一个非常敏感的指标。对于
SparseGPT,趋势非常不同:即使在
2.7B参数时,困惑度损失约为1点。在
66B参数时,损失基本为零。在最大规模上,甚至相对于
dense baseline略有准确性提升,然而这似乎与数据集有关(参见附录C)。
如预期的那样,相比
magnitude pruning,AdaPrune也产生了很大的改进,但不如SparseGPT准确。尽管AdaPrune的效率很高,但在350M模型上运行它大约需要1.3小时、在1.3B模型上运行它需要4.3小时;而SparseGPT可以在大致相同的时间内完全稀疏化66B和175B参数模型, 在相同的单块A100 GPU上执行。
总体来说,更大的模型更容易稀疏化的趋势是明显的,我们推测这是由过参数化(
overparametrization)导致的。对这一现象进行详细研究将是一个不错的未来工作方向。对于
4:8 and 2:4 sparsity,行为类似,但准确性下降通常更高,因为稀疏模式更受约束(《Accelerated sparse neural training: A provable and efficient method to find N:M transposable masks》)。尽管如此,在最大规模上,对于4:8 and 2:4 sparsity,困惑度分别仅仅增加仅为0.11和0.39。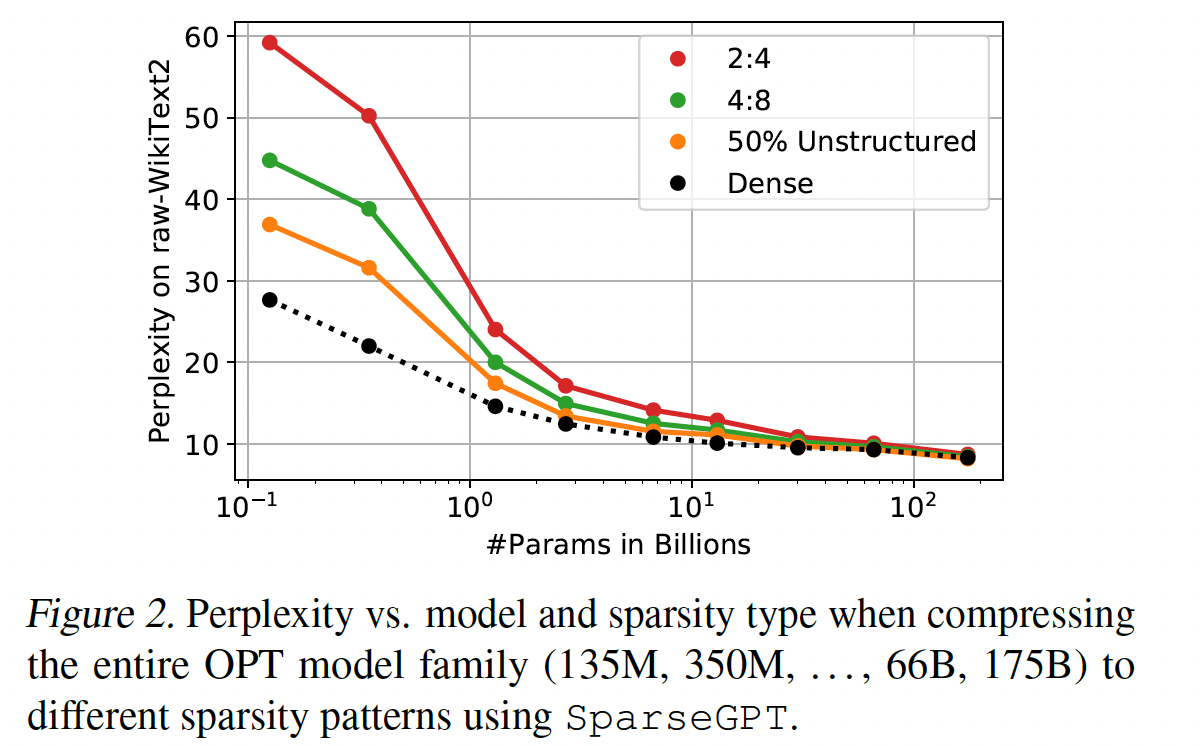
超过
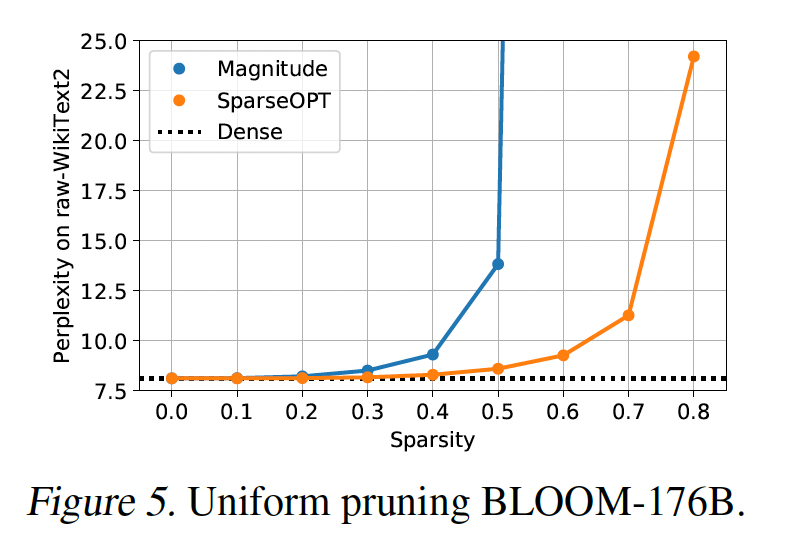
100B参数模型的Sparsity Scaling:接下来,我们仔细研究目前最大的公开稠密模型OPT-175B和BLOOM-176B,并研究SparseGPT或magnitude pruning引起的稀疏度对其性能的影响。结果如Figure 1和Figure 5所示。对于
OPT-175B模型(Figure 1),magnitude pruning最多只能达到10%的稀疏度,然后发生显著的accuracy loss。同时,SparseGPT可以在类似的perplexity increase下达到60%的稀疏度。BLOOM-176B(Figure 5)对magnitude pruning似乎更有利,允许30%的稀疏度而不会重大损失。尽管如此,在类似水平的perplexity degradation下,SparseGPT可以提供50%的稀疏度,提高了1.66倍。即使在80%的稀疏度下,SparseGPT压缩的模型仍取得合理的困惑度,而magnitude pruning分别对OPT和BLOOM在40/60%的稀疏度下就已经导致完全崩溃( 大于100的困惑度)。
值得注意的是,
SparseGPT从这些模型中删除了大约100B个权重,对准确率的影响很小。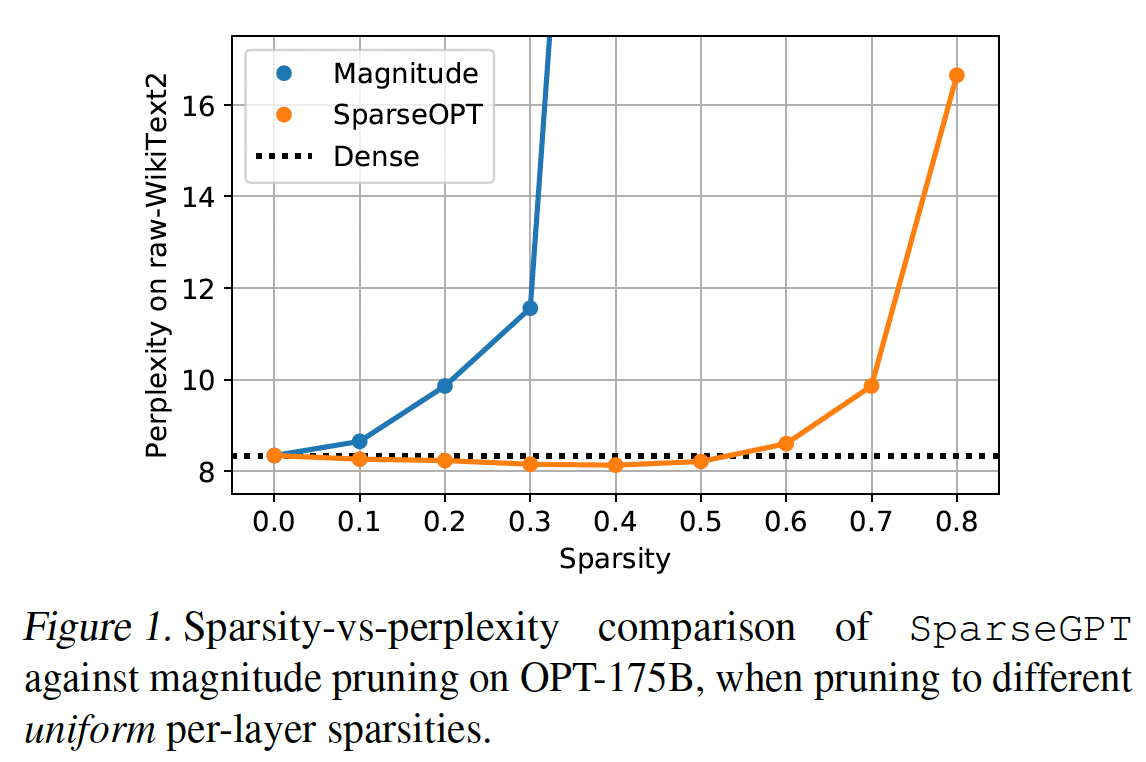
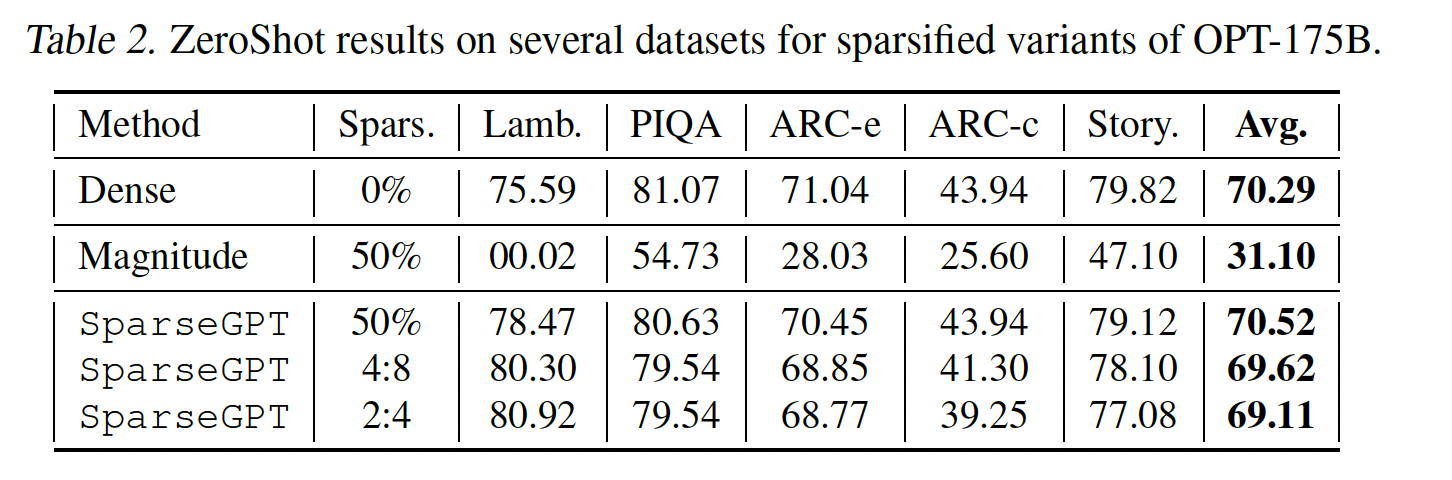
ZeroShot实验:为补充perplexity的评估,我们在几个zero-shot任务上提供了结果。已知这些评估相对地noisy(《LLM.int8(): 8-bit matrix multiplication for transformers at scale》),但更具解释性。请参阅Table 2。整体上,类似的趋势保持不变:
magnitude-pruned的模型崩溃到接近随机性能,而SparseGPT模型保持接近原始准确率。然而,如预期的那样,这些数字更加
noisy:尽管是最受约束的稀疏模式,2:4 pruning在Lambada上似乎实现了明显高于稠密模型的准确率。考虑许多不同任务时,这些效应最终会平均化,这与文献一致。
Joint Sparsification & Quantization:另一个有趣的研究方向是稀疏性和量化的组合,这将允许组合来自稀疏性的计算加速、以及来自量化的内存节省。具体来说,如果我们压缩模型到50% sparse + 4-bit weights,只存储非零权重并使用bitmask指示其位置,那么这与3-bit量化具有相同的总体内存消耗。因此,在Figure 6中,我们将SparseGPT 50% + 4-bit与目前SOTA的GPTQ 3-bit进行了比较。可以看出:对于2.7B+参数的模型,SparseGPT 50% + 4-bit模型比各自的GPTQ 3-bit版本更准确,包括在175B模型上的8.29 vs. 8.68。我们还在
OPT-175B上测试了2:4 and 4:8 in combination with 4-bit,分别得到了8.55和8.85的困惑度,这表明4-bit权重量化仅在semi-structured sparsity之上带来约0.1的困惑度增加。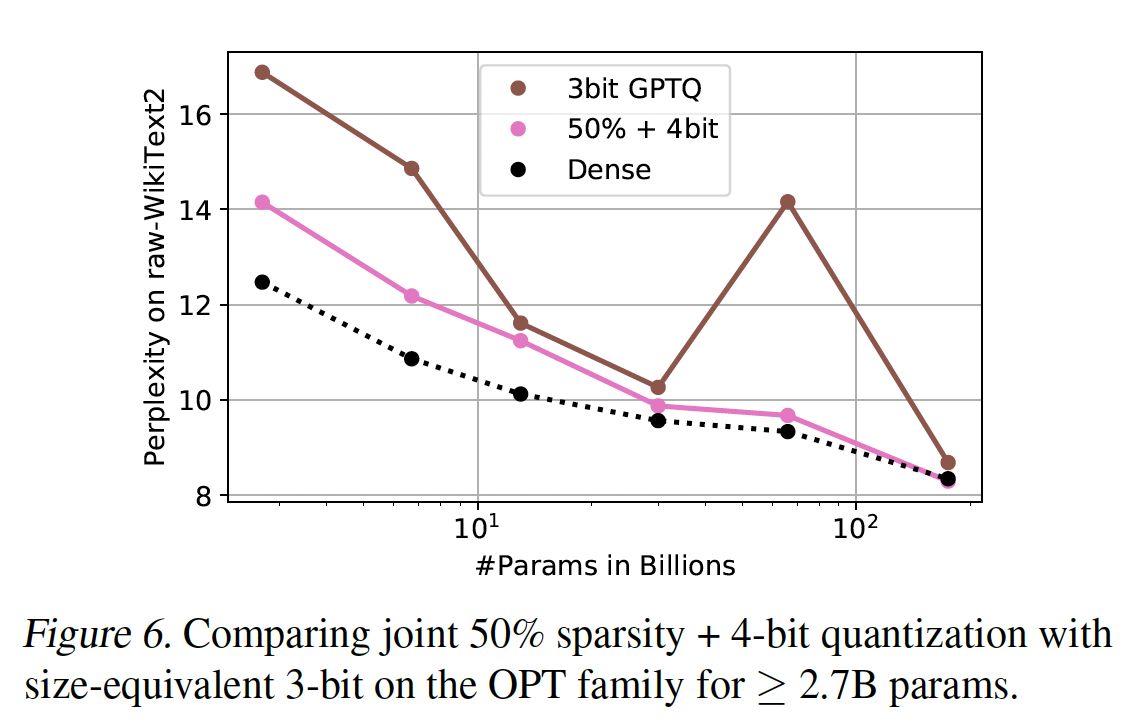
Sensitivity & Partial N:M Sparsity:关于n:m pruning的一个重要实际问题是,如果fully sparsified model不够准确,该怎么办?overall sparsity level不能简单地统一降低,相反,必须选择layers的一个子集进行完全地n:m-sparsify。我们现在研究极端大语言模型背景下做出good selection的问题:我们假设OPT-175B/BLOOM-176B的layers中,三分之二的层应裁剪为2:4 sparsity,并考虑跳过某种类型的所有层(attention layer、fully-connected-1 layer、或者fully-connected-2 layer)、或跳过占总层数三分之一的连续层(前面三分之一、中间三分之一、最后三分之一)。结果如Figure 7所示。尽管模型之间的
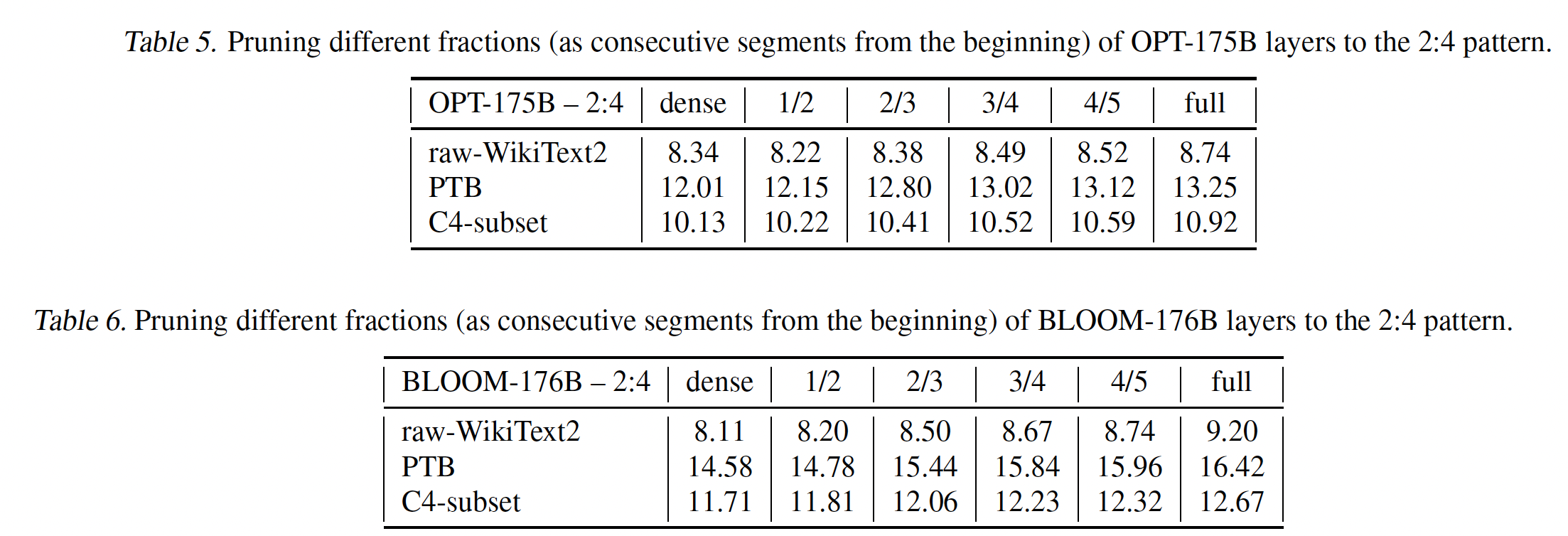
layer-types敏感性差异显著,但模型部分方面似乎存在明确的趋势:later layers比earlier layers更敏感;跳过最后三分之一层的模型可以获得最佳准确率。这对实践有非常重要的意义,那就是由于SparseGPT的顺序性质(sequential nature),我们能够生成稀疏性逐渐增加的2:4 sparsified模型的一个序列(如1/2, 2/3, 3/4, ...),通过在single pruning pass中结合两种方式:在前面SparseGPT,以及原始模型的最后model sequences的准确性如附录D所示。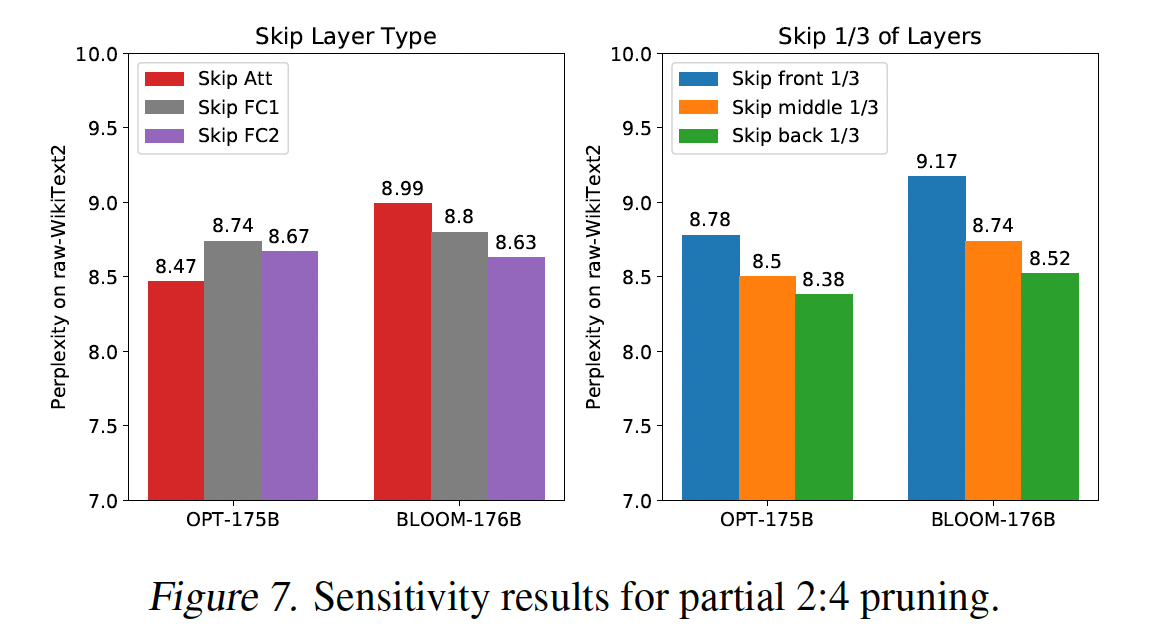
消融研究:
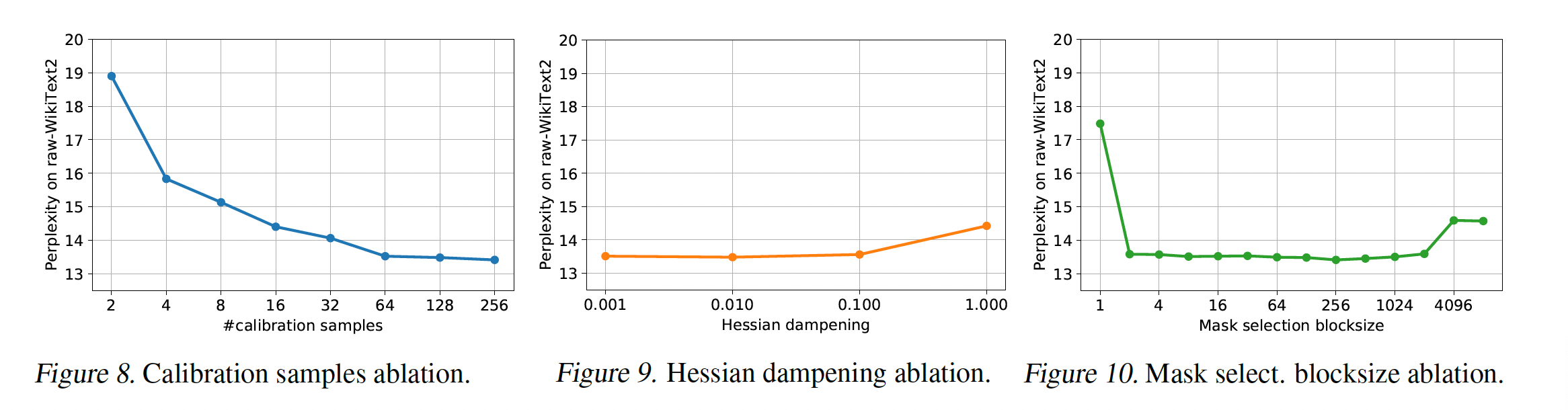
Calibration Data数量:随着calibration样本数量的增加,准确性得到改善。但是当数量超过某个点时,困惑度曲线逐渐变平缓。由于更多的样本数量增加了计算代价和内存代价,因此在实验中我们选择128个calibration样本。Hessian Dampening:整体而言,dampening参数不太敏感,除非它非常高。我们选择1%(即,0.01)的dampening。Mask Selection Blocksize:block_size = 1(对应于column-wise)、以及block_size = 4096 and 8192(接近full blocksize)效果最差。block_size在100附近获得更好的准确性,因此我们选择block_size = 128。此外,block_size = 128也简化了算法的实现,因为它匹配了默认的lazy weight update batchsize。
9.4 讨论
局限性:
我们主要关注
uniform per-layer sparsity,但non-uniform distributions是有前景的未来工作主题。此外,
SparseGPT目前在非常大的变体上的准确性还不如在最小的和中等大小的变体上。我们认为这可能通过仔细的部分微调或完全微调来解决,这在数十亿参数的模型规模上已经开始成为可能。最后,虽然我们在本文中研究了
pretrained foundation models的稀疏化,但我们认为研究诸如指令微调、或具有reinforcement learning with humanfeedback: RLHF等额外post-pretraining技术如何影响可压缩性也将是一个重要的未来研究领域。