二十六、AutoInt[2018]
由于几个原因,
CTR预测问题非常具有挑战性:首先,输入特征是极其稀疏和高维的。
在现实世界的应用中,相当比例的用户人口统计学和
item属性通常是离散的。为了应用监督学习,这些特征首先被转换为one-hot embedding向量,这很容易导致特征具有数百万的维度。面对如此稀疏的、高维的输入特征,机器学习模型很容易过拟合。其次,正如大量文献所示,高阶特征交互
feature interaction对良好的性能至关重要。然而,寻找这种有意义的高阶组合特征在很大程度上依赖于领域专家。此外,几乎不可能手工制作出所有有意义的组合。有人可能会问,我们可以列举出所有可能的高阶特征,让机器学习模型选择有意义的特征。然而,枚举所有可能的高阶特征将指数级地增加输入特征的维度和稀疏度,导致更严重的模型过拟合问题。
Factorization Machine: FM结合了多项式回归模型和因子分解技术从而建模特征交互,并在各种任务中证明了有效性。然而,受其多项式的限制,它只对低阶特征交互建模有效,而无法捕获高阶特征交互。最近,人们提出许多基于深度神经网络的工作从而建模高阶特征交互。具体而言,通常使用多层非线性神经网络来捕获高阶特征交互。然而,这类方法有两个局限性:
- 首先,全连接的神经网络在学习乘性
multiplicative的特征交互方面效率低下。 - 其次,由于这些模型是以隐式的方式学习特征交互,它们缺乏对哪些特征组合是有意义的良好解释。
在论文
《AutoInt: Automatic Feature Interaction Learning via Self-Attentive Neural Networks》中,作者提出了一种基于多头自注意力机制的方法。具体而言:categorical特征和numerical特征首先被嵌入到低维空间中,这降低了输入特征的维度,同时允许不同类型的特征通过向量运算(如求和和内积)来交互。然后,
AutoInt提出了一个新的交互层interacting layer,以促进不同特征之间的交互。在每个交互层内,允许每个特征与所有其他特征进行交互,并能够通过多头注意力机制自动识别相关特征以形成有意义的高阶特征。此外,多头机制将一个特征投射到多个子空间中,因此它可以在不同的子空间中捕获不同的特征交互。论文使用注意力机制来度量特征之间的相关性,这提供了良好的模型可解释性。
论文贡献:
- 论文提议研究显式学习高阶特征交互的问题,同时为该问题找到具有良好解释能力的模型。
- 论文提出了一种基于自注意力神经网络的新方法,它可以自动学习高阶特征交互,并有效地处理大规模高维稀疏数据。
- 论文在几个真实世界的数据集上进行了广泛的实验。在
CTR预测任务上的实验结果表明,所提出的方法不仅优于现有的SOTA的预测方法,而且还提供了良好的模型解释能力。
相关工作:
Learning Feature Interactions:学习特征交互是一个基本问题,因此在文献中得到了广泛的研究。Factorization Machine: FM用于捕获一阶特征交互和二阶特征交互,并被证明对推荐系统的许多任务是有效的。Field-aware Factorization: FFM建模不同field的特征之间的细粒度交互。GBFM和AFM考虑了不同二阶特征交互的重要性。
然而,所有这些方法都集中在建模低阶特征交互。最近有一些工作建模高阶特征交互:
NFM将深度神经网络堆叠在二阶特征交互的输出之上,从而建模高阶特征交互。PNN, FNN, DeepCrossing, Wide&Deep, DeepFM也利用前馈神经网络来模拟高阶特征交互。
然而,所有这些方法都是以隐式的方式学习高阶特征交互,因此缺乏良好的模型可解释性。相反,有三类工作是以显式方式学习特征交互:
- 首先,
Deep&Cross和xDeepFM分别在bit-wise level和vector-wise level上对特征进行外积outer product。虽然它们进行了显式的特征交互,但要解释哪些组合是有用的并不简单。 - 其次,一些基于树的方法结合了
embedding-based模型和tree-based模型的力量,但不得不将训练过程分成多个阶段。 - 第三,
HOFM提出了高效的高阶分解机的训练算法。然而,HOFM需要太多的参数,只有它的低阶(通常小于5)形式可以实际使用。
与现有工作不同的是,我们以端到端的方式显式地用注意力机制建模了特征交互,并通过可视化的方式探究学到的特征组合。
Attention and Residual Networks:我们的模型利用了深度学习文献中的最新技术:注意力机制和残差网络。
26.1 模型
定义
CTR Prediction:令itemcategorical features用one-hot encoding来表示。点击率预测问题旨在根据特征向量item针对
CTR预测问题的一个直接的解决方案是:将此外,如现有文献所示,利用高阶组合特征来产生良好的预测性能是至关重要的。
定义
p阶组合特征:给定输入特征向量p阶组合特征定义为distinct field,feature fields的数量,non-additive的组合函数,如乘法或外积。例如,field传统上,有意义的高阶组合特征是由领域专家手工制作的。然而,这非常耗费时间,而且很难推广到其他领域。此外,几乎不可能手工制作出所有有意义的高阶特征。因此,我们的目标是开发一种能够自动发现有意义的高阶组合特征的方法,同时将所有这些特征映射到低维的连续空间。
问题定义:给定一个用于
CTR预测的输入特征向量representation,它建模了高阶组合特征。我们的方法的目标是:将原始稀疏的高维特征向量映射到低维空间,同时建模高阶特征交互。如下图所示:
我们的方法将稀疏的特征向量
embedding layer,将所有的特征(即categorical特征和数值特征)投影到同一个低维空间。接下来,我们将所有
field的embedding馈入一个新的交互层interacting layer,该层被实现为一个多头自注意力神经网络。对于每个交互层,高阶特征通过注意力机制进行组合,不同种类的组合可以通过多头机制进行评估,这些多头机制将特征映射到不同的子空间。
最后一个交互层的输出是输入特征的低维
representation,它建模了高阶组合特征,并进一步通过一个sigmoid函数来估计CTR。
核心思想:将
Transformer Encoder Block作用到feature field embedding上。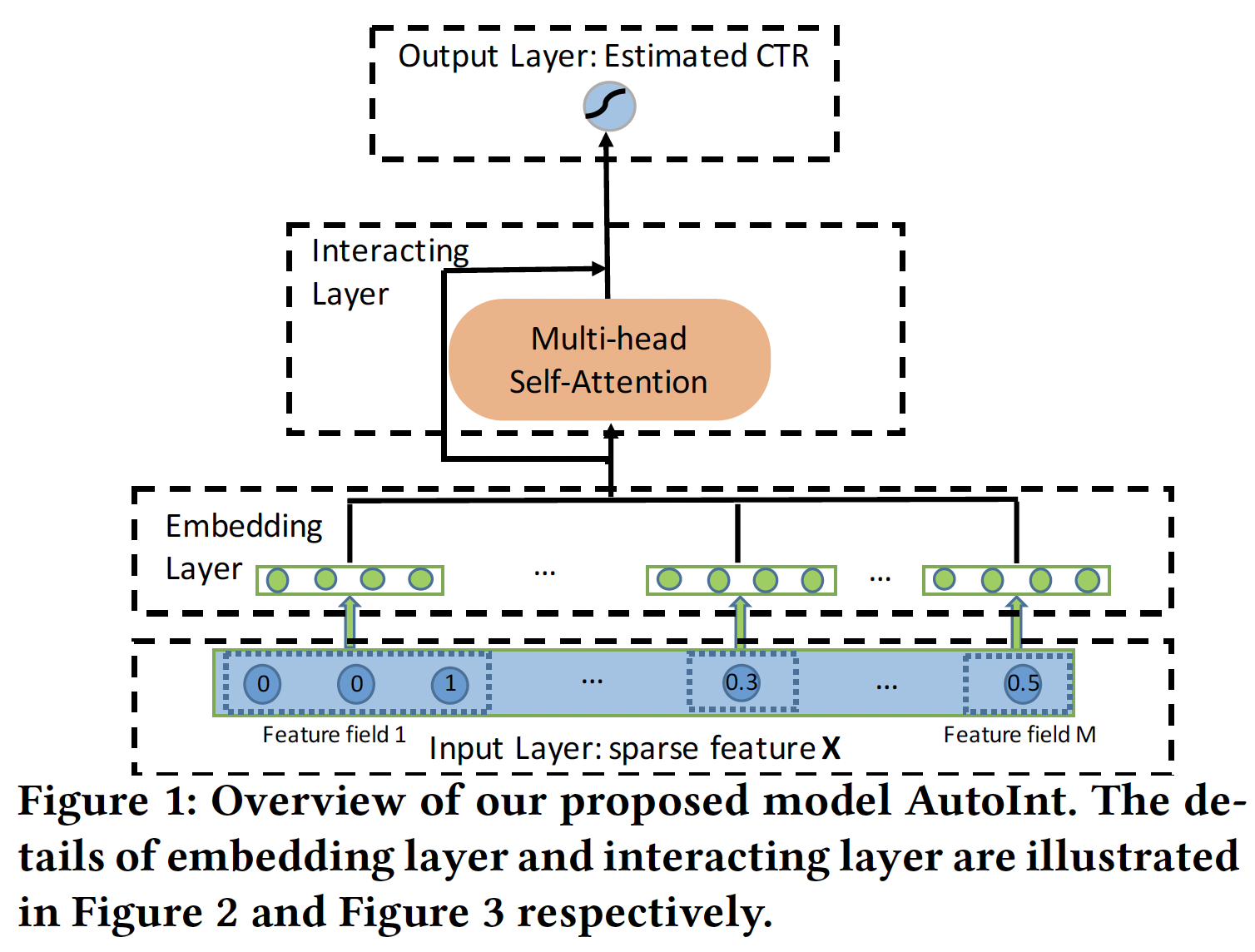
Input Layer:我们首先将用户画像和item属性表示为一个稀疏向量,它是所有field的拼接:其中:
feature fields的总数;field的feature;如果第
field是categorical特征,则one-hot向量。如果第field是numerical特征,则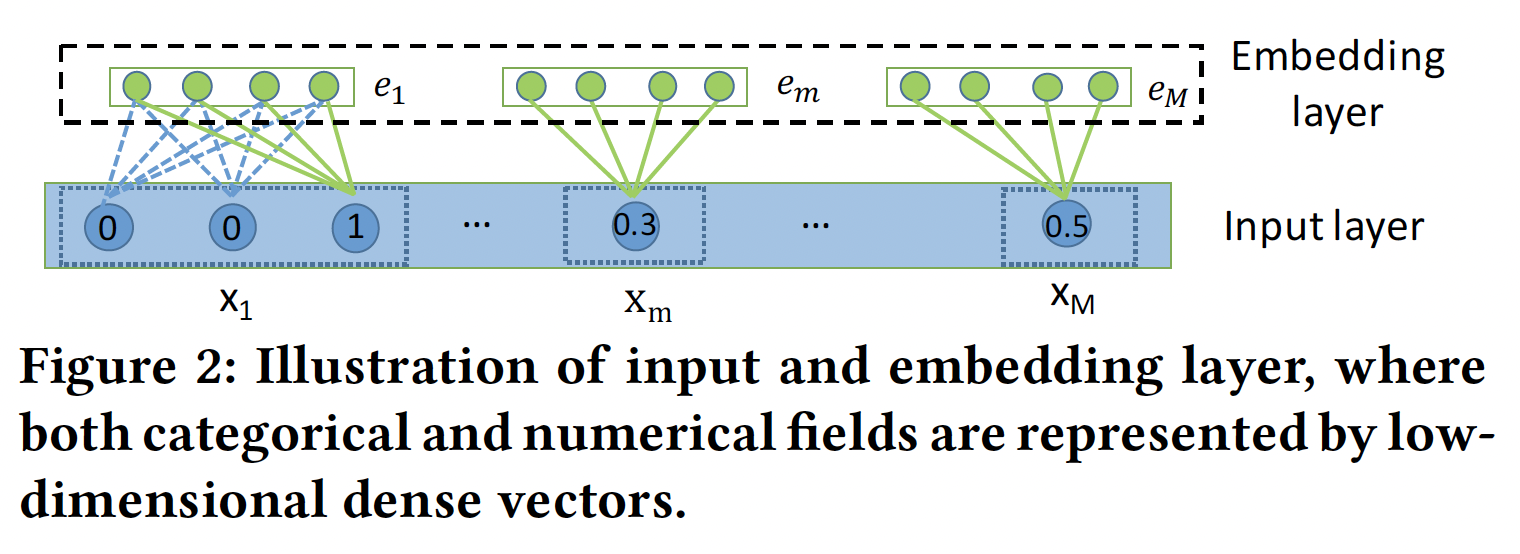
Embedding Layer:我们用一个低维向量来表示每个categorical特征,即:其中:
fieldembedding matrix;fieldone-hot向量。很多时候,
categorical特征可以是多值的,即,multi-hot向量。因此,我们将multi-valued feature field表示为相应feature embedding vectors的平均值:其中:
field的取值的数量,multi-hot向量。可以用更复杂的、有效的操作来代替均值操作。
为了允许
categorical特征和numerical特征之间的交互,我们也在同一个低维特征空间中表示numerical特征。我们将numerical特征表示为:其中:
fieldembedding向量,这里
field最终,
embedding layer的输出将是多个嵌入向量的拼接。Interacting Layer:我们采用注意力机制来确定哪些特征组合是有意义的。以特征其中:
embedding空间投影到新的空间。field的原始embedding size,embedding size。
然后,我们通过
representation:其中
这其实就是标准的
Transformer Encoder Block:我们通过使用多个头来创建不同的子空间,分别学习不同的特征交互。我们收集在所有子空间学到的组合特征如下:
其中:
为了保留先前学到的组合特征,包括原始特征(即,一阶特征),我们在网络中加入了标准的残差连接:
其中
标准的
Transformer中也包含残差连接。通过这样的交互层,每个特征的
representationrepresentation这就是标准的
Transformer Encoder Block,将其应用到feature field embedding上。Output Layer:交互层的输出是一组特征向量CTR预估,我们简单地将它们全部拼接起来,然后应用非线性投影:其中:
bias,sigmoid函数。训练:损失函数为
log loss:其中:
ground-truth、CTR、
26.2 分析
建模任意阶次的组合特征:可以看到,
AutoInt是以hierarchical的方式学习特征交互,即从低阶交互到高阶交互,所有的低阶特征交互都由残差连接来承载。具体分析参考原始论文。空间复杂度:
embedding层的参数规模为embedding size,- 交互层的参数为
- 输出层的参数数量为
因此,总的空间复杂度为
field embedding维度,field embedding维度,vocab size的总和)。论文的结论是:空间复杂度几乎被交互层的参数所统治。结论不正确,实际上空间复杂度几乎是被
embedding table所统治。时间复杂度:
- 一个
head中,注意力权重的时间复杂度为 - 然后,构建一个
head中的组合特征的时间复杂度也是
考虑有
field数量。- 一个
26.3 实验
数据集:
Criteo、Avazu、KDD12、MovieLens-1M。我们对
MovieLens-1M进行了二元化:我们将评分小于3的样本视为负样本,将评分大于3的样本视为正样本,并删除中性样本(即评分等于3的样本)。我们删除不经常出现的特征(出现次数少于阈值),并将其作为一个单一的特征
"<unknown>",其中阈值对Criteo、Avazu和KDD12数据集分别设置为{10,5,10}。由于数值特征可能有很大的方差,对机器学习算法造成伤害,我们采用
Criteo竞赛的冠军提出的方案进行数值特征归一化:我们随机选择
80%的样本进行训练,并将剩下的样本随机分成大小相同的验证集和测试集。
数据集的统计信息如下表所示。
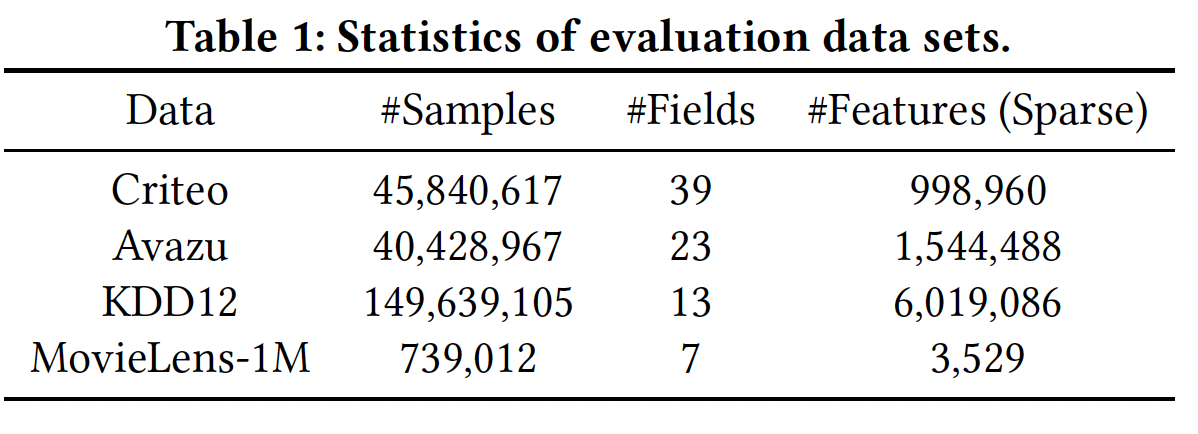
评估指标:
AUC, Logloss。baseline方法:LR:仅建模原始特征的线性组合。FM:使用因子化技术建模二阶特征交互。AFM:通过注意力机制来区分二阶组合特征的重要性,从而扩展了FM。DeepCrossing:采用带残差连接的深度全连接神经网络,以隐式的方式学习非线性的特征交互。NFM:将深度神经网络堆叠在二阶特征交互层之上。通过神经网络隐式地捕获高阶特征。CrossNet:CrossNet是Deep&Cross的核心,它在bit-wise level上执行concatenated特征向量的外积,从而显式地建模特征交互。CIN:Compressed Interaction Network: CIN是xDeepFM模型的核心,在vector-wise level上对堆叠的特征矩阵进行外积。HOFM:提出了高效的kernel-based算法来训练高阶FM。我们实现了一个三阶FM。
实现细节:
对于
AutoInt和所有baseline方法,我们根据经验将embedding维度16,batch size = 1024。AutoInt有三个交互层,隐单元的数量为了防止过拟合,我们用网格搜索法在
{0.1 - 0.9}范围内为MovieLens-1M数据集选择dropout rate,我们发现dropout对其他三个大数据集来说是没有必要的。对于
baseline方法,我们按照他们的论文建议:- 在
NFM的Bi-Interaction层上使用一个大小为200的隐藏层。 - 对于
CN和CIN,和AutoInt一样,我们使用三个交互层。 DeepCrossing有四个前馈层,隐单元的数量为100,因为它在使用三个前馈层时表现很差。
一旦所有的网络结构都固定下来,我们还对
baseline方法应用网格搜索,以获得最佳的超参数。- 在
我们使用
Adam来优化所有基于深度神经网络的模型。
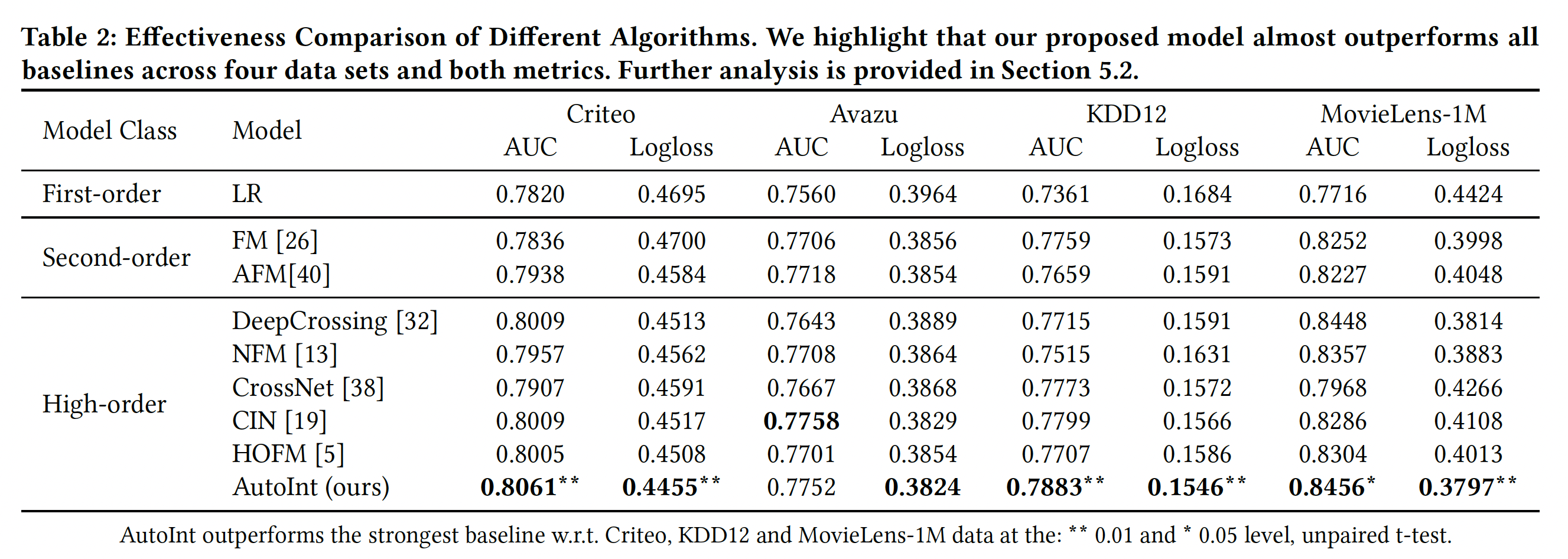
模型效果:我们将
10次不同运行的平均结果总结到下表,可以看到:探索二阶特征交互的
FM和AFM在所有的数据集上都以很大的幅度超过LR,这表明单个特征在CTR预估中是不够的。一个有趣的观察是:一些捕捉高阶特征交互的模型的劣势。例如:
DeepCrossing和NFM使用深度神经网络作为学习高阶特征交互的核心组件,但它们并不能保证比FM和AFM有更大的改进。这可能是由于它们是以隐式的方式学习特征交互的。相反,CIN显式地做到了这一点,并持续优于低阶模型。此外,尽管
HOFM可以学习比FM更高阶的特征交互,但是HOFM在Avazu, KDD12上的效果比FM更差。AutoInt在四个真实世界的数据集中的三个上取得了最佳性能。在Avazu数据集上,CIN在AUC评估中的表现比AutoInt好一点,但我们得到的Logloss更低。请注意,我们提出的
AutoInt与DeepCrossing共享相同的结构,除了特征交互层,这表明使用注意力机制来学习显式的组合特征是至关重要的。
模型效率:我们在下图中展示了不同算法在四个数据集上的运行时间。可以看到:
LR由于其简单性而成为最高效的算法。FM和NFM在运行时间方面表现相似,因为NFM只在二阶交互层之上堆叠了一个前馈隐藏层。- 在所有列出的方法中,
CIN在所有baseline中实现了最好的预测性能,但由于其复杂的交叉层,它要耗费更多的时间。 AutoInt有足够的效率,这与高效算法DeepCrossing和NFM相当。
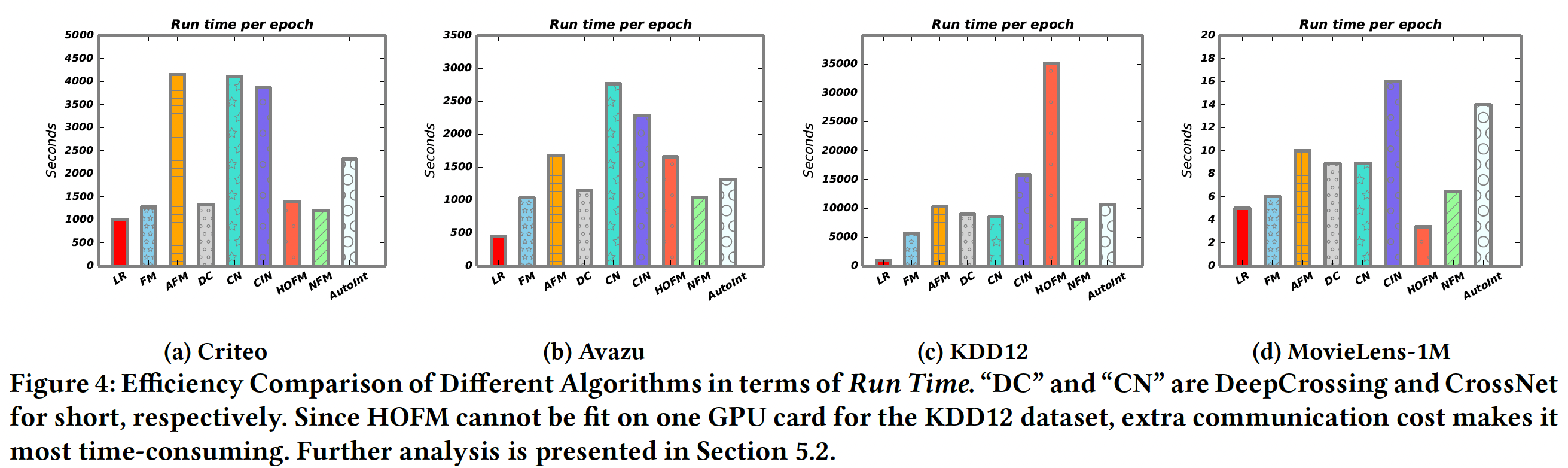
我们还比较了不同模型的大小(即参数的数量),作为效率评估的另一个标准。如下表所示,与
baseline模型中的最佳模型CIN相比,AutoInt的参数数量要小得多。综上所述,
AutoInt在所有baseline模型中取得了最好的性能。与最具竞争力的baseline模型CIN相比,AutoInt需要的参数要少得多,而且在在线推理过程中效率更高。
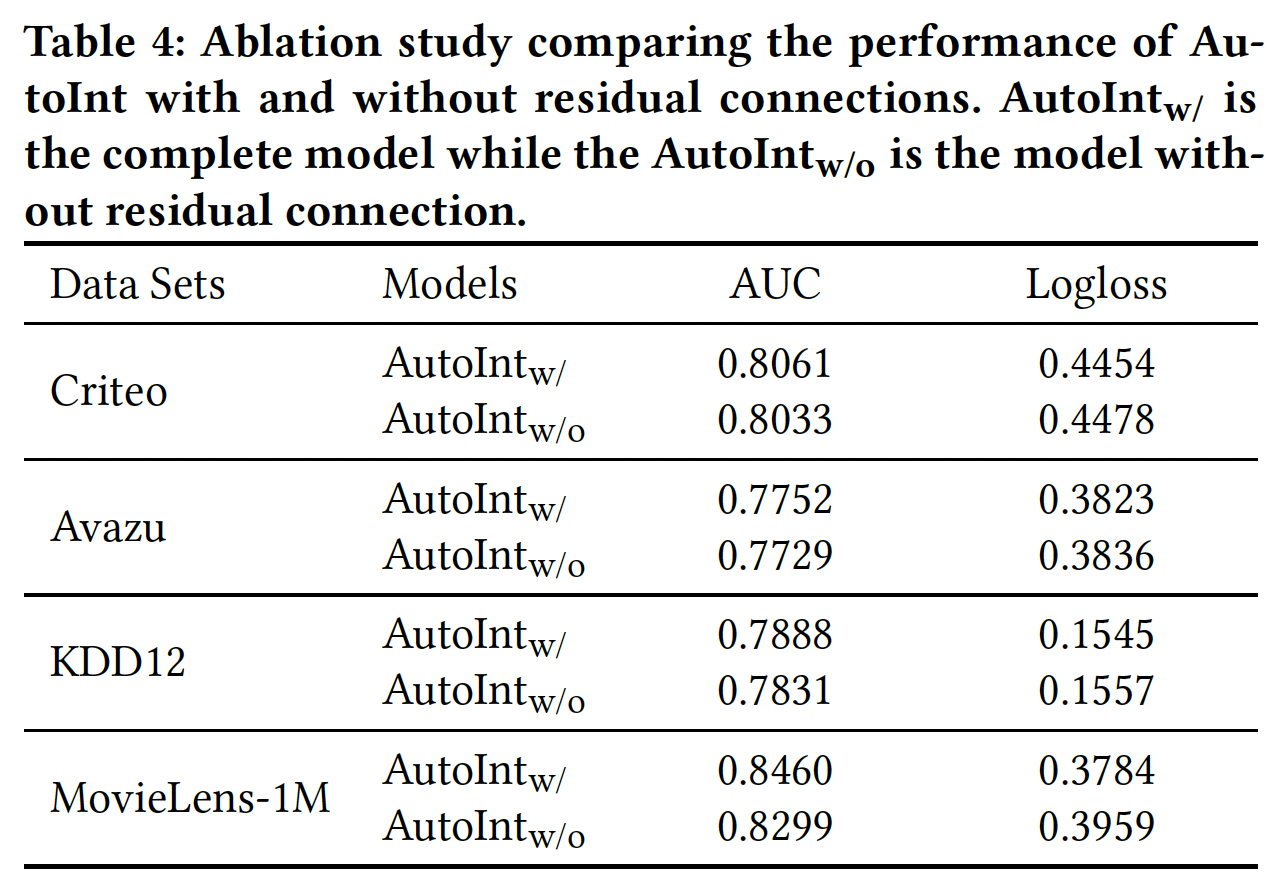
消融研究:
残差结构的影响:为了证明残差单元的贡献,我们把它们从标准模型中分离出来,并保持其他结构不变。如下表所示,如果去除残差连接,所有数据集的性能都会下降。
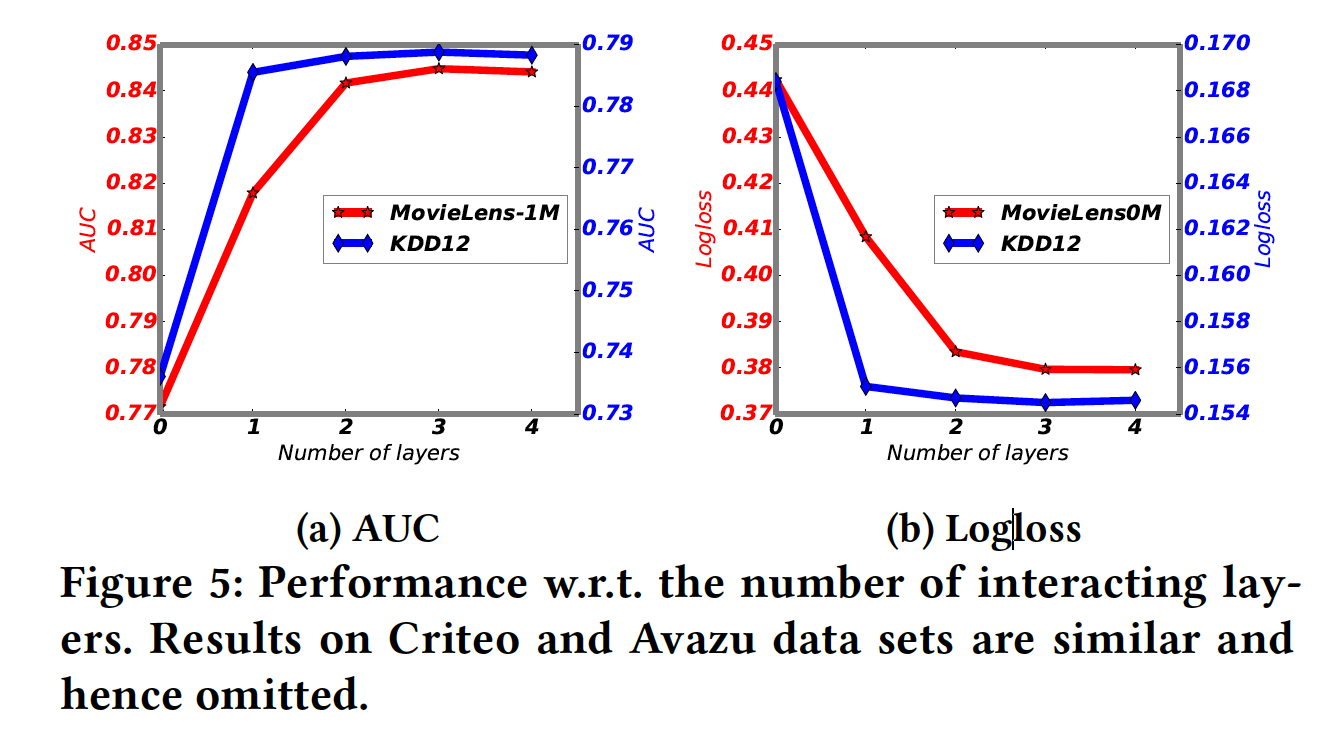
网络深度的影响:我们考虑不同交互层的数量的影响。注意,当交互层的数量为零时,意味着不考虑组合特征。结果如下图所示。
- 如果使用一个交互层,即考虑到特征交互,在两个数据集上的性能都会大幅提高,这表明组合特征对于预测来说是非常有参考价值的。
- 随着交互层数量的进一步增加,即高阶组合特征被考虑在内,模型的性能进一步提高。
- 当层数达到三层时,性能变得稳定,表明增加更高阶特征对预测没有参考价值。
embedding维度的影响:我们考虑不同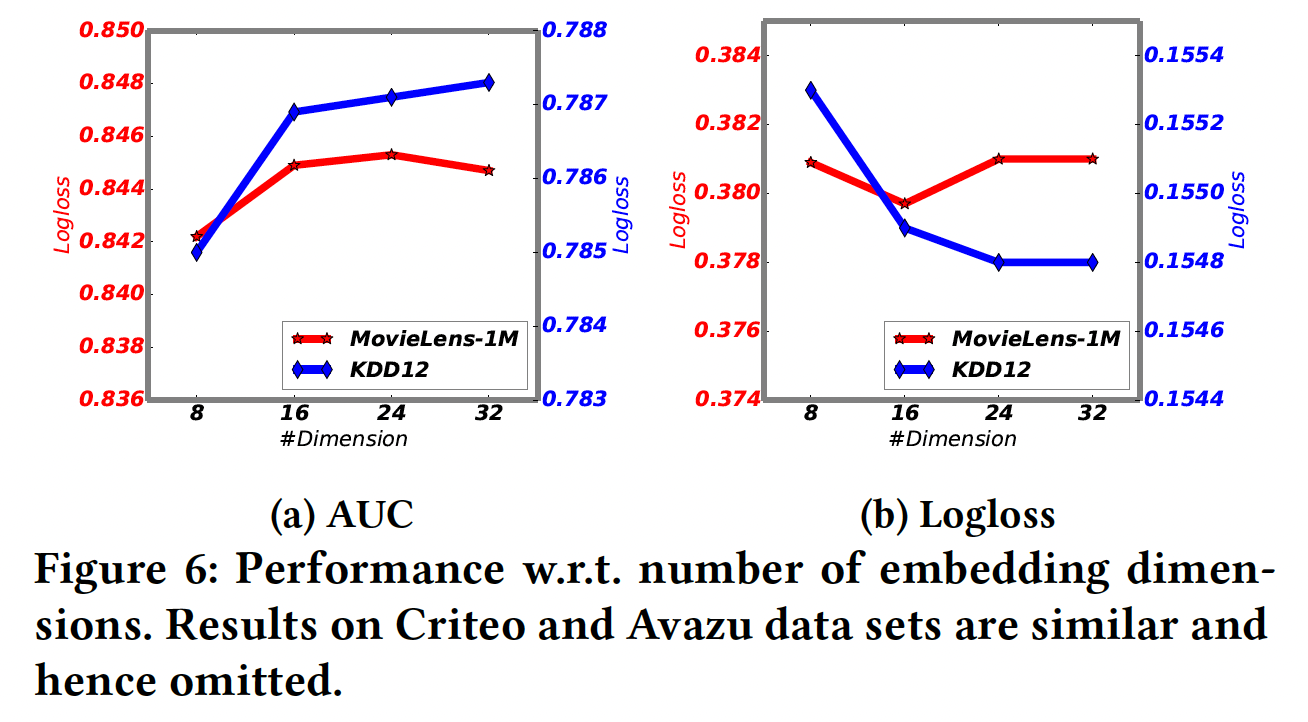
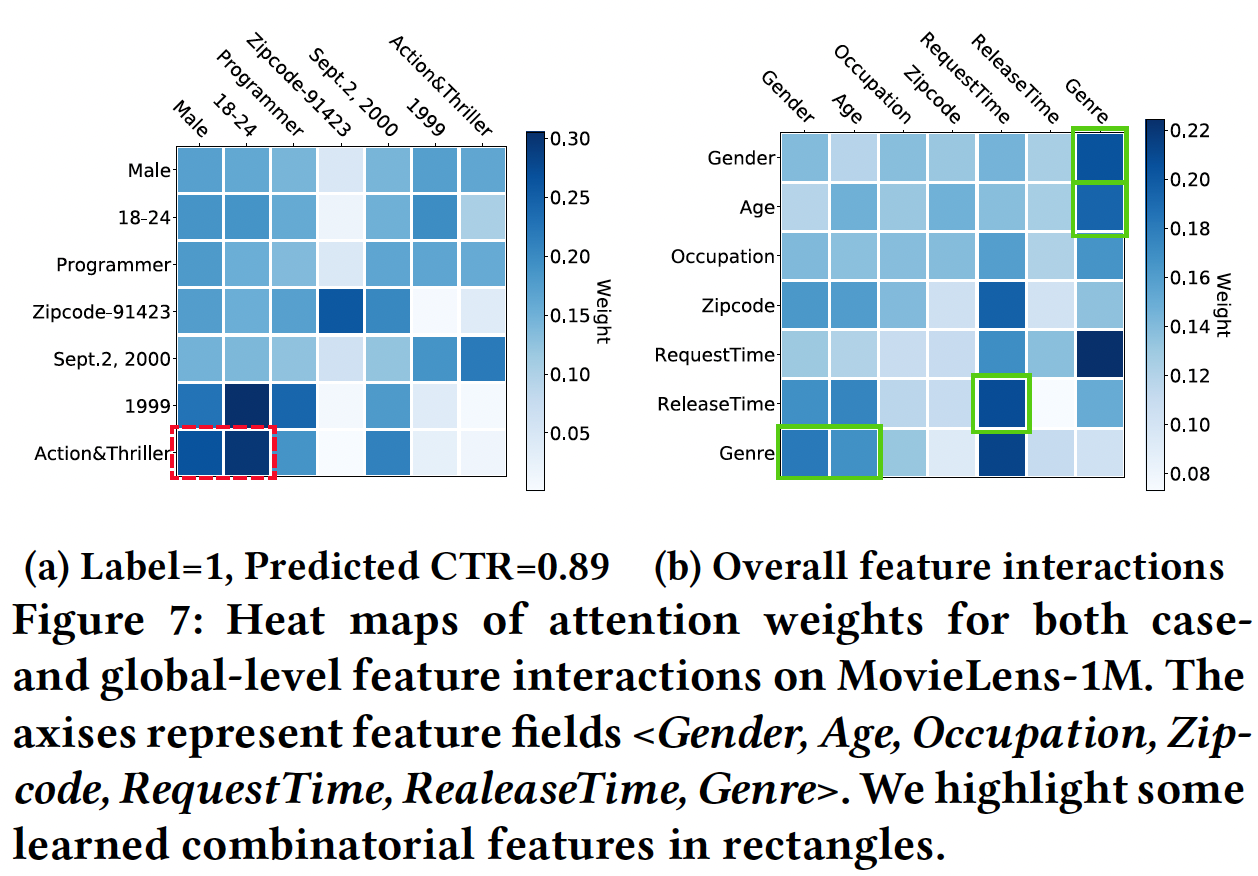
可解释性:我们以
MovieLens-1M数据集为例。case-level:下图(a)展示了不同field的输入特征之间的相关性,这些相关性是由注意力得分得到的,其中该样本的label = 1。我们可以看到:AutoInt能够识别出有意义的组合特征<Gender=Male, Age=[18-24], MovieGenre=Action&Triller>(即红色的虚线矩形)。这是非常合理的,因为年轻男子很可能喜欢动作片和惊悚片。这种相关性是怎么计算的?如果是利用了
attention矩阵,那么对于多个交互层,使用哪一层的结果?读者猜测是第一个交互层的attention矩阵。global-level:下图(b)展示了不同feature field之间在整个数据中的平均注意力得分,从而衡量各feature field之间的相关性。可以看到:<Gender, Genre>, <Age, Genre>, <RequestTime, ReleaseTime>, <Gender, Age, Genre>是强相关的(即,绿色的实心区域),这是推荐的可解释性规则。是考虑所有样本还是仅考虑正样本?读者猜测是仅考虑正样本。
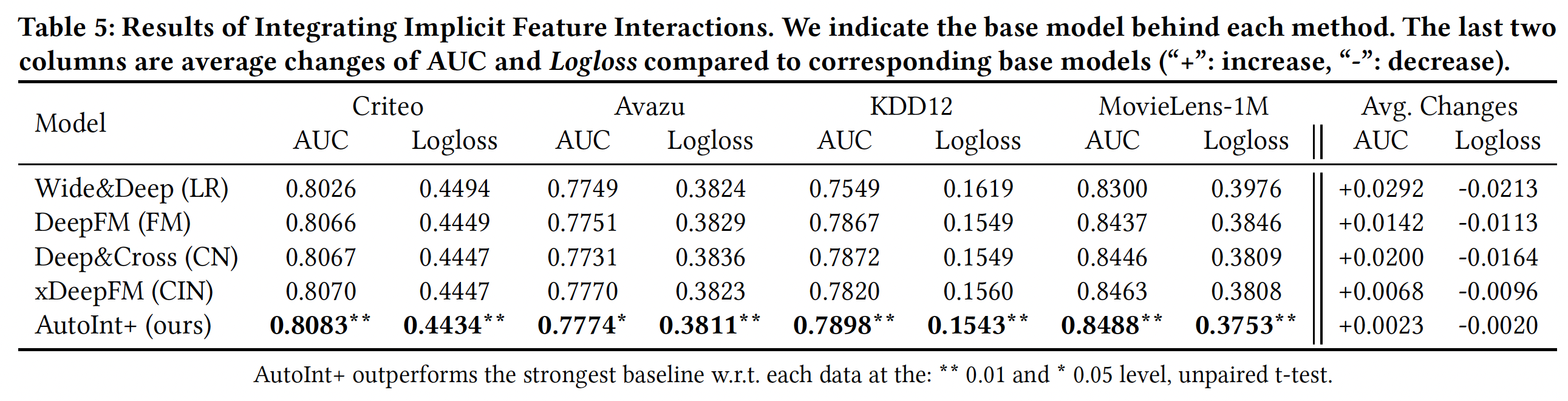
集成隐式交互:前馈神经网络能够建模隐式的特征交互,并被广泛集成到现有的
CTR预测方法中。为了研究集成隐式的特征交互是否能进一步提高性能,我们通将AutoInt与两层前馈神经网络相结合(并行集成,而不是堆叠)。我们将这个联合模型命名为AutoInt+,并将其与以下算法进行比较:Wide&Deep、DeepFM、Deep&Cross、xDeepFM。结果如下表所示。可以看到:
通过集成前馈神经网络,我们的方法在所有数据集上的性能都有所提高。这表明,集成隐式的特征交互确实提高了
AutoInt的预测能力。然而,从最后两栏可以看出,与其他模型相比,性能提高的幅度相当小,表明我们的单个模型
AutoInt是相当强大的。集成了隐式的特征交互之后,
AutoInt+的性能超过了所有的baseline方法,并取得了新的SOTA的性能。
二十七、Fi-GNN[2019]
建模复杂的特征交互,对
CTR预测的成功起到了核心作用。FM是一个著名的模型,它通过向量内积来建模二阶特征交互。FFM进一步考虑了field信息并引入了field-aware embedding。然而,这些FM-based模型只能建模二阶交互。最近,许多基于深度学习的模型被提出来从而学习高阶特征交互,这些模型遵循一个通用的范式:简单地拼接
field embedding向量,并将其馈入DNN或其他专门设计的模型,从而学习交互。例如FNN, NFM, Wide&Deep, DeepFM等。然而,这些基于DNN的模型都是以bit-wise的、隐式的方式来学习高阶特征交互,这缺乏良好的模型解释。一些模型试图通过引入专门设计的网络来显式地学习高阶交互。例如,
Deep&Cross]引入了Cross Network: CrossNet,xDeepFM引入了压缩交互网络Compressed Interaction Network: CIN。尽管如此,它们仍然不够有效和显式,因为它们仍然遵循将feature field组合在一起的通用范式来建模交互。简单的unstructured combination将不可避免地限制了灵活地、显式地建模不同feature field之间复杂交互的能力。在论文
《Fi-GNN: Modeling Feature Interactions via Graph Neural Networks for CTR Prediction》中,作者考虑了multi-field feature的结构。具体来说,作者用一个名为feature graph的图结构来表示multi-field feature。直观而言,图中的每个节点对应于一个feature field,不同field可以通过边进行交互。因此,建模feature field之间复杂交互的任务可以转化为建模feature graph上的节点交互的任务。为此,作者在Graph Neural Network: GNN的基础上设计了一个新的Feature interaction Graph Neural Network: Fi-GNN,它能够以灵活的、显式的方式建模复杂的节点交互(即,特征交互)。在Fi-GNN中,节点将通过与邻居节点交流node state来进行交互,并以recurrent的方式更新自己。AutoInt用Transformer Encoder Block建模multi-field feature,而这里用GNN来建模multi-field feature。Transformer Encoder Block可以视为一个简单的GNN。在每一个
time step中,模型与邻居节点进行one-hop的交互。因此,interaction step的数量等同于特征交互的阶次。此外,在feature graph中,边的权重反映了不同feature interaction对于CTR预测的重要性,而节点的权重反映了每个feature field对于CTR预测的重要性。这可以提供很好的解释。总的来说,论文提出的模型能够以显式的、灵活的方式建模复杂的特征交互,并提供良好的可解释性。论文贡献如下:
- 论文指出了现有工作的局限性,即把
multi-field feature视为feature field的unstructured combination。为此,作者首次提出用图结构来表示multi-field feature。 - 论文设计了一个新的模型
Feature interaction Graph Neural Network: Fi-GNN,从而以更灵活的、显式的方式建模graph-structured feature上feature field之间的复杂交互。 - 论文在两个真实世界的数据集上进行的广泛实验表明:所提出的方法不仅可以超越
SOTA的方法,而且可以提供良好的模型解释。
- 论文指出了现有工作的局限性,即把
相关工作:
Feature Interaction in CTR Predict:建模特征交互是CTR预测成功的关键,因此在文献中得到了广泛的研究。LR是一种线性方法,它只能对原始单个特征的线性组合建模一阶交互。FM通过向量内积来建模二阶特征交互。之后,FM的不同变体也被提出:Field-aware factorization machine: FFM考虑了field信息并引入了field-aware embedding。AFM考虑了不同二阶特征交互的权重。
然而,这些方法只能建模二阶交互,这是不够的。
随着
DNN在各个领域的成功,研究人员开始用它来学习高阶特征交互,因为它有更深的结构和非线性激活函数。一般的范式是将field embedding向量拼接在一起,并将其馈入DNN来学习高阶特征交互。《A convolutional click prediction model》利用卷积网络建模特征交互。FNN在应用DNN之前,在field embedding上使用预训练的FM。PNN通过在field embedding layer和DNN layer之间引入一个product layer来建模二阶交互和高阶交互。- 类似地,
NFM通过在field embedding layer和DNN layer之间引入一个Bi-Interaction Pooling layer来建模二阶交互,但是随后的操作是sum操作,而不是像PNN中的拼接操作。
另一个方向上的一些工作试图通过混合架构来联合建模二阶交互和高阶交互:
Wide&Deep和DeepFM包含一个wide组件来建模低阶交互、一个deep组件来建模高阶交互。然而,所有这些利用
DNN的方法都是以隐式的、bit-wise的方式学习高阶特征交互,因此缺乏良好的模型解释能力。 最近,一些工作试图通过专门设计的网络以显式的方式学习特征交互:Deep&Cross引入了一个在bit-level上对特征进行外积的CrossNet。- 相反,
xDeepFM引入了一个在vector-level对特征进行外积的CIN。
然而,他们仍然没有解决最根本的问题,即把
field embedding向量拼接起来。对
feature field进行简单的unstructured combination将不可避免地限制了以灵活的、显式的方式建模不同field之间复杂交互的能力。为此,我们提出用图结构表示multi-field feature,每个节点代表一个field,不同的feature field可以通过边进行交互。因此,我们可以在图上建模不同feature field之间的灵活交互。Graph Neural Network:图是一种数据结构,它对一组对象(节点)和它们的关系(边)进行建模。早期的工作通常将图结构的数据转换成序列结构的数据来处理。- 无监督的
DeepWalk算法受word2vec的启发,用于学习基于random walk的node embedding。 - 之后,
LINE算法保留了图的一阶结构信息和二阶结构信息。 node2vec引入了一个有偏的随机行走。
然而,这些方法的计算成本很高,而且对于大型图而言也不是最优的。图形神经网络(
graph neural network: GNN)就是为了解决这些问题而设计的,它是基于深度学习的方法,在graph domain上运行。现在已经有很多GNN的变种,这里我们只介绍一些有代表性的经典方法:Gated Graph Neural Network: GGNN使用GRU作为更新器。Graph Convolutional Network: GCN考虑了图的spectral structure并利用卷积聚合器。GraphSAGE考虑了空间信息,并引入了三种聚合器:mean aggregator, LSTM aggregator, Pooling aggregator。graph attention network: GAT将注意力机制纳入消息传播步骤。
由于
GNN具有令人信服的性能和较高的可解释性,GNN已经成为一种广泛应用的图分析方法。在这项工作中,我们提出了一个基于GGNN的模型Fi-GNN来为CTR预测建模特征交互。- 无监督的
27.1 模型
假设训练数据集由
field的categorical feature、以及表示用户点击行为的labelCTR预测任务是对输入特征(包含field)来预测用户点击的概率下图是我们所提出方法的概览(
- 输入的
sparse m-field feature vector首先被映射成稀疏的one-hot向量,然后通过embedding layer和multi-head self-attention layer嵌入到稠密的field embedding向量中。 - 然后,
field embedding向量被表示为一个feature graph,其中每个节点对应于一个feature field,不同的feature field可以通过边进行交互。因此,建模交互的任务可以转换为建模feature graph上的节点交互。因此,feature graph被馈入Fi-GNN从而建模节点交互。 - 最后,在
Fi-GNN的输出上应用一个Attentional Scoring Layer来估计点击率
这里的
Multi-head Self-Attention Layer就是单层的AutoInt,因此,Fi-GNN相当于是AutoInt和GNN的堆叠。实验并没有表明AutoInt在这里的贡献,而且即使是AutoInt + Fi-GNN,模型在所有数据集上的整体效果提升也不明显,因此论文价值不大。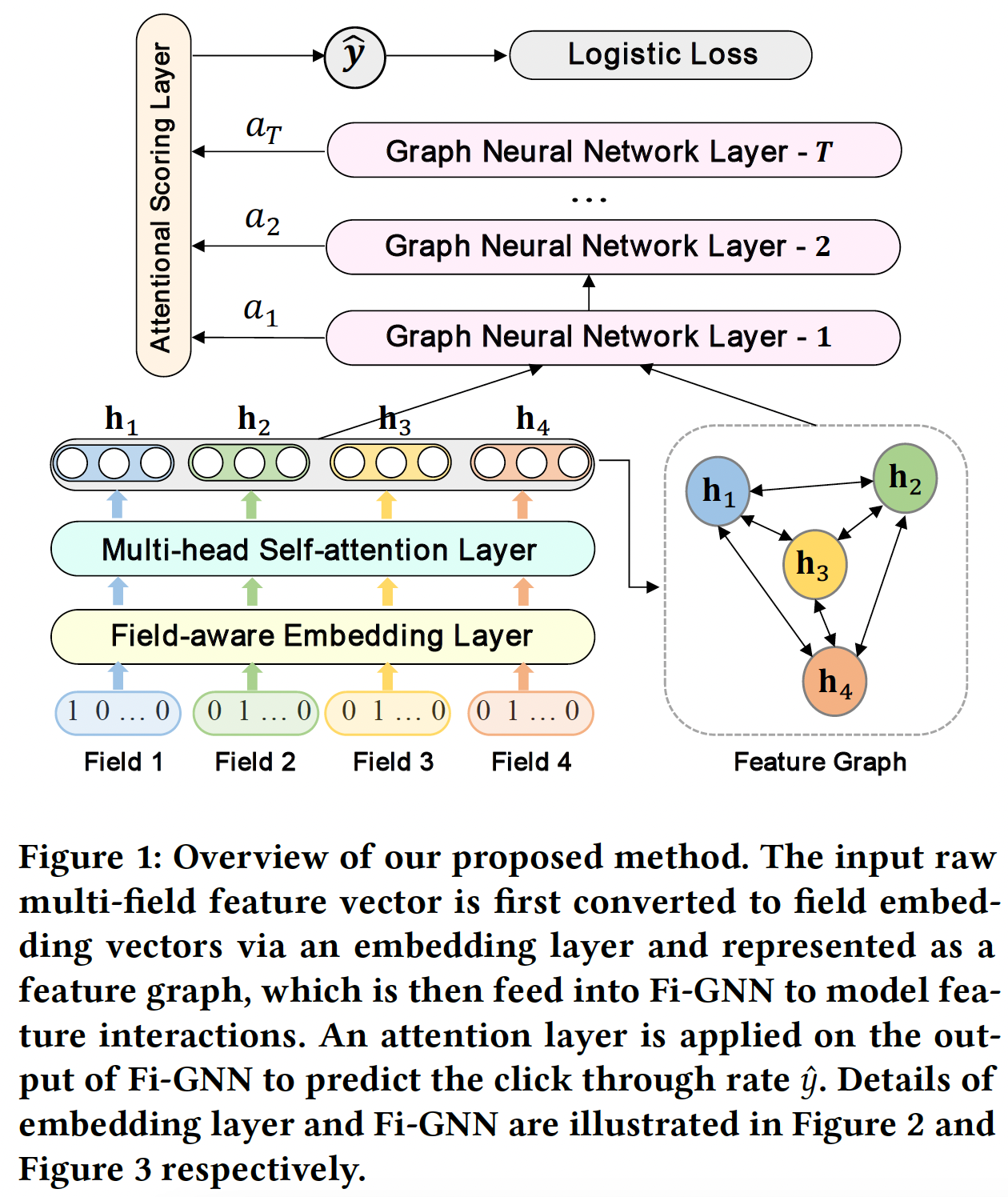
- 输入的
Embedding Layer:我们将每个field表示为一个ont-hot encoding向量,然后将其嵌入到一个稠密向量中,记做field embedding向量 。field的field embedding向量被拼接为(沿着feature field维度拼接):其中:
fieldembedding向量,field embedding向量的维度,feature field维度拼接。Multi-head Self-attention Layer:我们利用多头自注意力机制来捕获不同语义子空间中的pairwise特征交互。遵从
《AutoInt: Automatic Feature Interaction Learning via Self-Attentive Neural Networks》,给定feature embedding矩阵feature representation,它覆盖了attention headpairwise interaction:其中:
attention headhead然后,我们将学到的每个
head的feature representation结合起来,以保留每个语义子空间中的pairwise feature interaction:其中:
embedding维度),attention head数量,embedding维度。Feature Graph:与以往简单地将field embedding向量拼接在一起并将其馈入模型中从而学习特征交互所不同的是,我们用图结构来表示feature field。具体而言,我们将每个输入的multi-field feature表示为一个feature graphfeature fieldfield可以通过边进行交互,所以每个样本对应一张图,因此这是一个
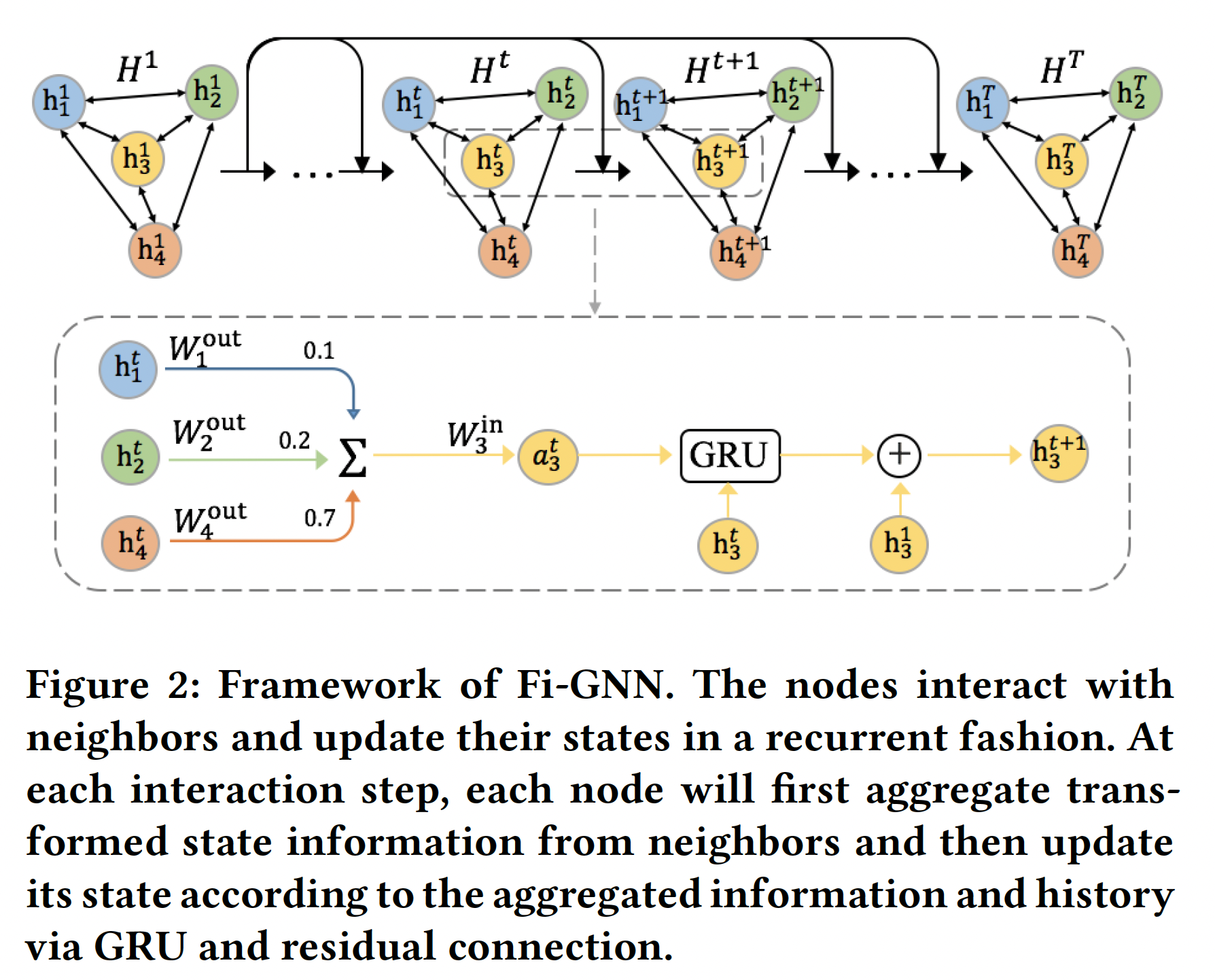
graph-level分类任务(二分类)。Feature Interaction Graph Neural Network:Fi-GNN旨在以一种灵活的、显式的方式建模feature graph上的节点交互。在Fi-GNN中,每个节点hidden state其中
interaction step。由多头自注意力层学到的feature representation作为图的初始状态如下图所示,节点以循环方式进行交互并更新其状态。在每一个
interaction step中,节点聚合邻居节点的状态信息(经过变换之后),然后根据聚合信息、以及节点历史状态通过GRU和残差连接来更新节点状态。State Aggregation:在interaction step其中:
显然,投影矩阵和邻接矩阵决定了节点之间的交互。由于每条边上的交互应该是不同的,我们的目标是建模边上的交互,这需要对每条边有一个
unique的权重和投影矩阵。基于注意力的边权重:为了推断不同节点之间交互的重要性,我们建议通过注意力机制来学习边权重。具体而言,从节点
field embedding向量)来计算:其中:
embedding维度)。利用softmax函数进行归一化,使不同节点的权重容易比较。最终邻接矩阵为:
由于边的权重反映了不同交互的重要性,
Fi-GNN可以很好地解释输入样本的不同feature field之间的关系,这一点将在实验部分进一步讨论。edge-wise变换:如前所述,所有边上的固定的投影矩阵无法建模灵活的交互,对每个边进行unique的变换是必要的。然而,我们的图是完全图complete graph(即,任意两个节点之间都存在边),因此包含大量的边。简单地给每条边分配一个unique的投影矩阵将消耗太多的参数空间和运行时间。为了减少时间和空间的复杂性,同时实现edge-wise transformation,我们为每个节点因此聚合信息
这样一来,参数的数量与节点的数量成正比,而不是与边的数量成正比,这就大大降低了空间复杂性和时间复杂性,同时也实现了
edge-wise interaction。
State Update:聚合状态信息之后,节点将通过GRU和残差连接来更新状态向量。通过
GRU进行状态更新:根据传统的GGNN,节点step的状态通过GRU更新的:通过残差连接进行状态更新:我们引入了额外的残差连接(来自初始状态),与
GRU一起更新节点状态,这可以促进低阶特征重用和梯度反向传播:注意,这里是
Attentional Scoring Layer:经过propagation step之后,我们得到了final node state:由于节点已经与它们的
Fi-GNN建模了graph-level output来预测CTR。我们分别对每个
field的final state预测一个得分,并通过注意力机制将它们相加,这个注意力机制衡量它们对整体预测的影响。正式地,每个节点attentional node weight可以通过两个MLP分别得到:整体预测是所有节点的预测的加权和:
训练:损失函数为
logloss,即:其中:
label;CTR。我们采用
RMSProp优化器。此外,为了平衡正负样本比例,在训练过程中,对于每个batch我们随机选择相同数量的正样本和负样本。
27.2 实验
数据集:
Criteo, Avazu。对于这两个数据集:我们移除了低频特征,并将低频特征替换为
"<unknown>"。频次阈值分别为:Criteo数据集为10、Avazu数据集为5。即出现频次低于该阈值则移除。由于数值特征可能具有较大的方差,因此我们进行对数变换:
这是由
Criteo竞赛的获胜者提出的。数据集以
8:1:1的比例随机拆分为训练集、验证集、测试集。
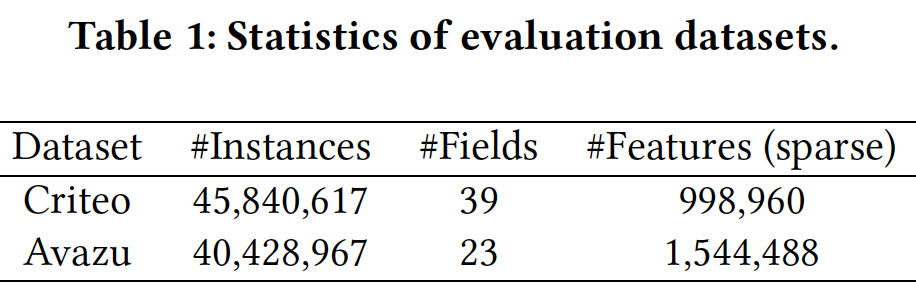
数据集的统计信息如下表所示。
评估指标:
AUC, LogLoss, Relative Improvement (RI)。应该注意的是,对于真实世界的
CTR任务来说,AUC方面的微小改进被认为是显著的。为了估计我们的模型相对于baseline模型的相对改进,我们在此测量RI-AUC和RI-Logloss:其中
X为AUC或LogLoss。baseline方法:LR:通过原始特征的线性组合来建模一阶特征交互。FM:通过field embedding向量的内积来建模二阶特征交互。AFM:是FM的一个扩展,利用注意力机制考虑不同二阶特征交互的权重。DeepCrossing:利用具有残差连接的DNN以隐式的方式学习高阶特征交互。NFM:利用Bi-Interaction Pooling layer来建模二阶特征交互,然后将拼接的二阶组合特征馈入DNN来建模高阶特征交互。CrossNet(Deep&Cross):是Deep&Cross模型的核心,它通过采用拼接的feature vector的外积,从而显式地在bit-wise level上建模特征交互。CIN(xDeepFM):是xDeepFM模型的核心,它通过采用堆叠的feature matrix的外积,从而显式地在vector-wise level上建模特征交互。
实现细节:我们使用
Tensorflow实现我们的方法。最优超参数由网格搜索策略确定。baseline的实现遵循《AutoInt: Automatic Feature Interaction Learning via Self-Attentive Neural Networks》。- 对于所有方法,
field embedding向量的维度是16,batch size = 1024。 DeepCrossing有四个前馈层,每层有100个隐单元。NFM在Bi-Interaction layer之上有一个大小为200的隐层,如原始论文中所推荐的。CrossNet和CIN都有三个交互层。- 所有实验都是在配备了
8个NVIDIA Titan X GPU的服务器上进行的。
- 对于所有方法,
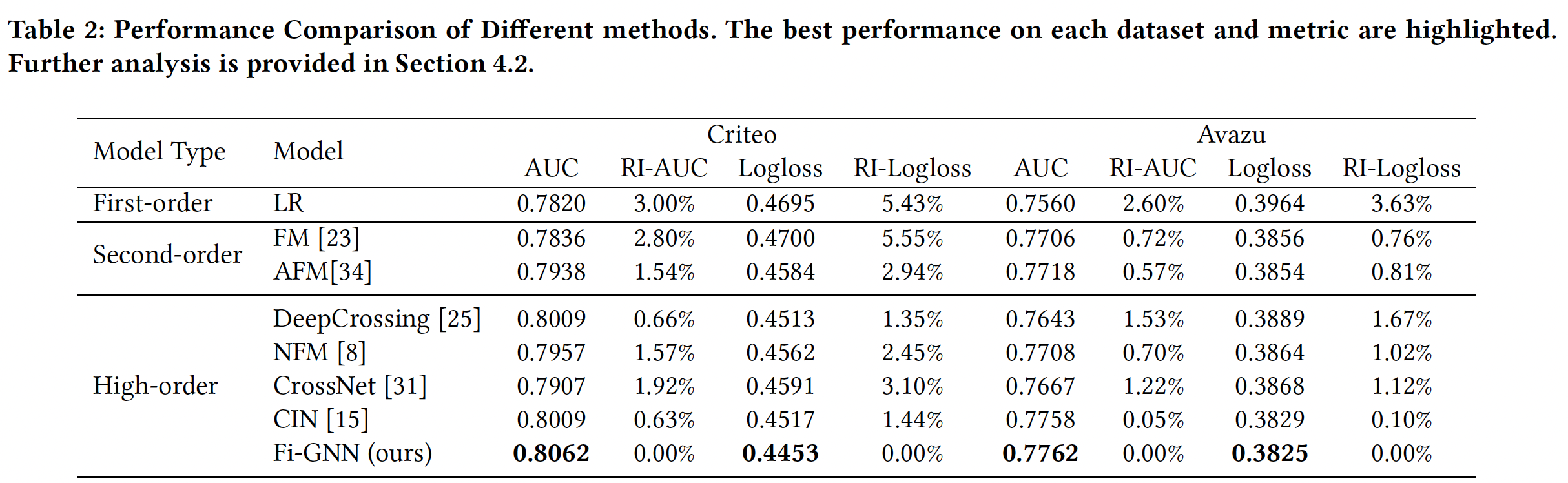
不同模型的性能比较,如下表所示。可以看到:
LR在这些baseline中效果最差,这证明了单个特征在CTR预测中是不够的。- 在所有数据集上,建模二阶特征交互的
FM和AFM优于LR,这表明建模feature field之间的pairwise交互是有效的。此外,AFM比FM具有更好的表现,证明了在不同交互上的注意力的有效性。 - 建模高阶特征交互的方法大多优于建模二阶特征交互的方法。这表明二阶特征交互是不够的。
DeepCrossing优于NFM,证明了残差连接在CTR预测中的有效性。- 在两个数据集上,
Fi-GNN在所有这些方法中取得了最好的性能,尤其是在Criteo数据集上。 Fi-GNN在Criteo数据集上取得的相对改进,高于在Avazu数据集上取得的相对改进。这可能是因为Criteo数据集中有更多的feature field,可以更好地利用图结构的表达能力。
消融研究:我们提出的
Fi-GNN模型是基于GGNN的,在此基础上我们主要做了两个改进:- 通过
attentional edge weight和edge-wise transformation实现edge-wise node interaction。 - 引入残差连接从而与
GRU一起更新节点状态。
为了评估两种改进的有效性,我们对比了三个变体:
Fi-GNN(-E/R):同时没有上述两个改进的变体。Fi-GNN(-E):没有edge-wise interaction: E的变体。即,用二元邻接矩阵、以及所有边上共享的投影矩阵。Fi-GNN(-R):没有residual connection: R的变体。
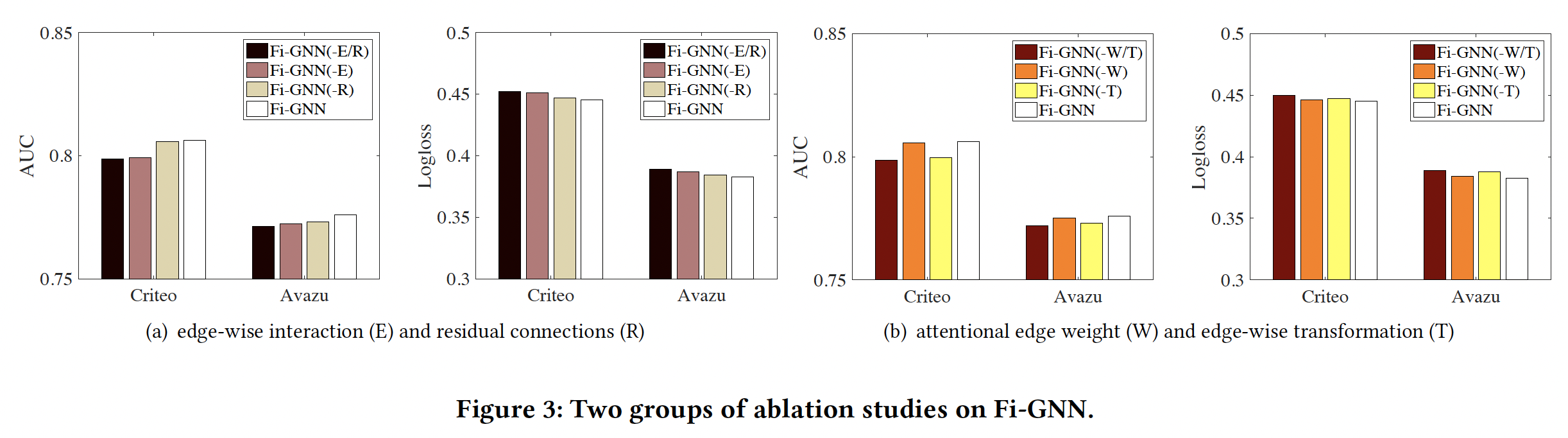
对比结果如下图
(a)所示。可以看到:Fi-GNN(-E)的性能相比完整的Fi-GNN大幅下降,这表明建模edge-wise interaction是至关重要的。Fi-GNN(-E)取得了比Fi-GNN(-E/R)更好的性能,证明了残差连接确实可以提供有用的信息。- 完整的
Fi-GNN优于三种变体,表明我们所做的两种改进,即残差连接和edge-wise interaction,可以联合提高性能。
在
Fi-GNN中,我们采用两种方法来实现edge-wise node interaction:attentional edge weight: W、edge-wise transformation: T。为了进一步研究巨大的改进来自哪,我们比较了另外三个变体:Fi-GNN(-W/T):即Fi-GNN-(E)。Fi-GNN(-W):没有attentional edge weight。Fi-GNN(-T):没有edge-wise transformation,即所有边上共享投影矩阵。
对比结果如下图
(b)所示。可以看到:Fi-GNN(-T)和Fi-GNN(-W)都优于Fi-GNN(-W/T),这证明了它们的有效性。Fi-GNN(-W)比Fi-GNN(-T)实现了更大的改进,这表明在建模edge-wise interaction方面,edge-wise transformation比attentional edge weight更有效。这是非常合理的,因为投影矩阵应该比标量的attentional edge weight对edge-wise interaction有更强的影响。
- 通过
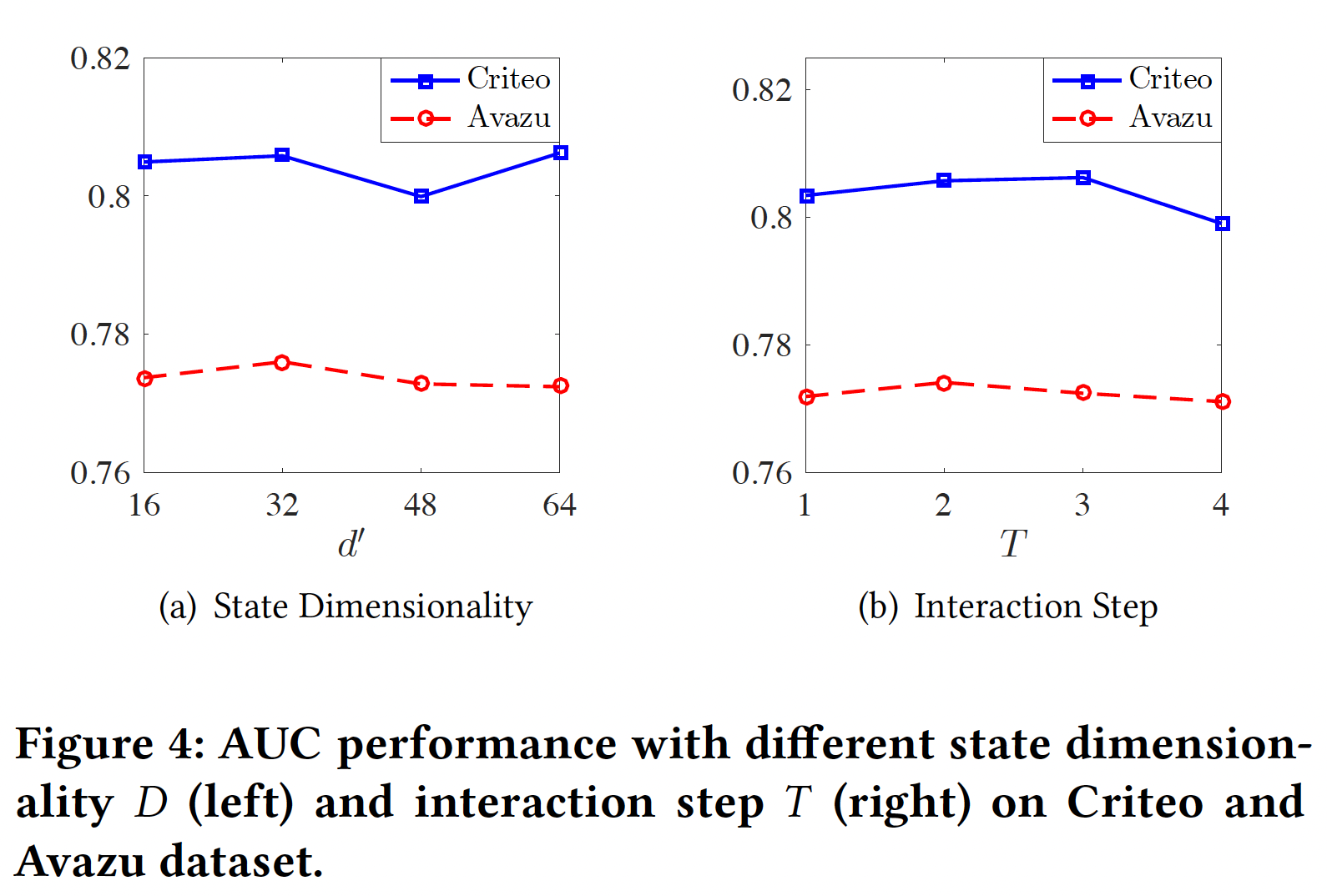
超参数研究:
state维度32(Avazu数据集)、64(Criteo数据集)时性能最佳。这是合理的,因为Criteo数据集更复杂,需要更大的维度来保持足够的信息。没有考虑
attention head的影响?interaction stepinteraction step等于特征交互的最高阶次。模型性能随着2(Avazu数据集)、3(Criteo数据集)时性能最佳。这是合理的,因为Avazu数据集有23个feature field、Criteo数据集有39个feature field。因此,Criteo数据集需要更多的interaction step来使field node与feature graph中的其他节点完全交互。
模型可解释性:我们在
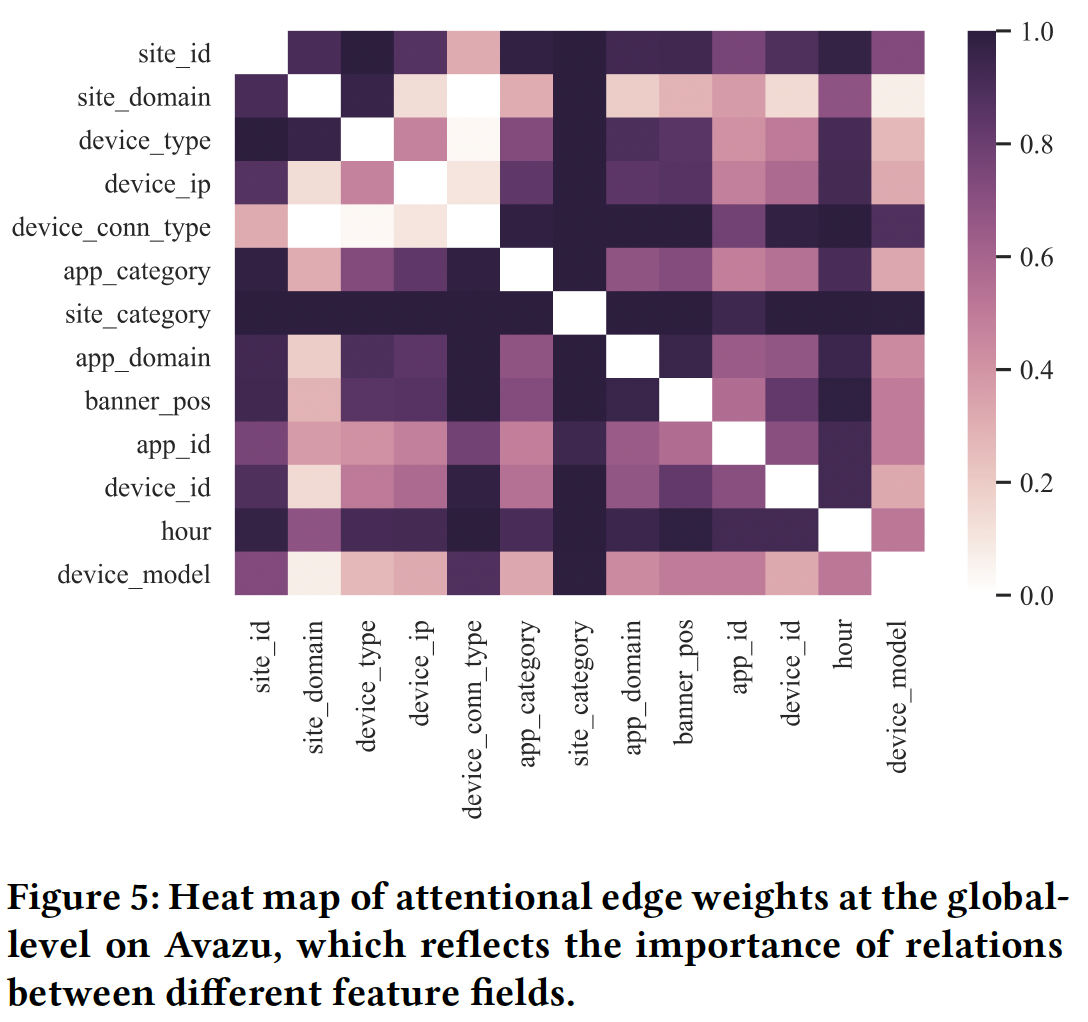
feature graph的边上和节点上都应用了注意力机制,分别得到了attentional edge weight和attentional node weight,可以从不同的角度给出解释。Multi-head Self-attention Layer捕获的pair-wise交互是否也是可解释的?论文并没有说明这一点。attentional edge weight:attentional edge weight反映了两个相连的field node之间交互的重要性,也反映了两个feature field之间的关系。下图展示了Avazu数据集中所有样本的全局平均邻接矩阵的热力图,它可以在全局水平上反映不同field之间的关系。 由于有一些field是匿名的,我们只显示剩余的13个具有真实含义的feature field。可以看到:
- 一些
feature field倾向于与其他field有很强的关系,例如site_category和site_id。这是有意义的,因为两个feature field都对应于投放广告的网站。 hour是另一个与其他field有密切关系的特征。这是合理的,因为Avazu专注于移动场景,用户可以在一天的任何时间在线冲浪。上网时间对其他的广告特征有很大的影响。- 另一方面,
device_ip和device_id似乎与其他feature field的关系较弱。这可能是因为它们几乎等同于user id,相对固定,不易受其他特征的影响。
- 一些
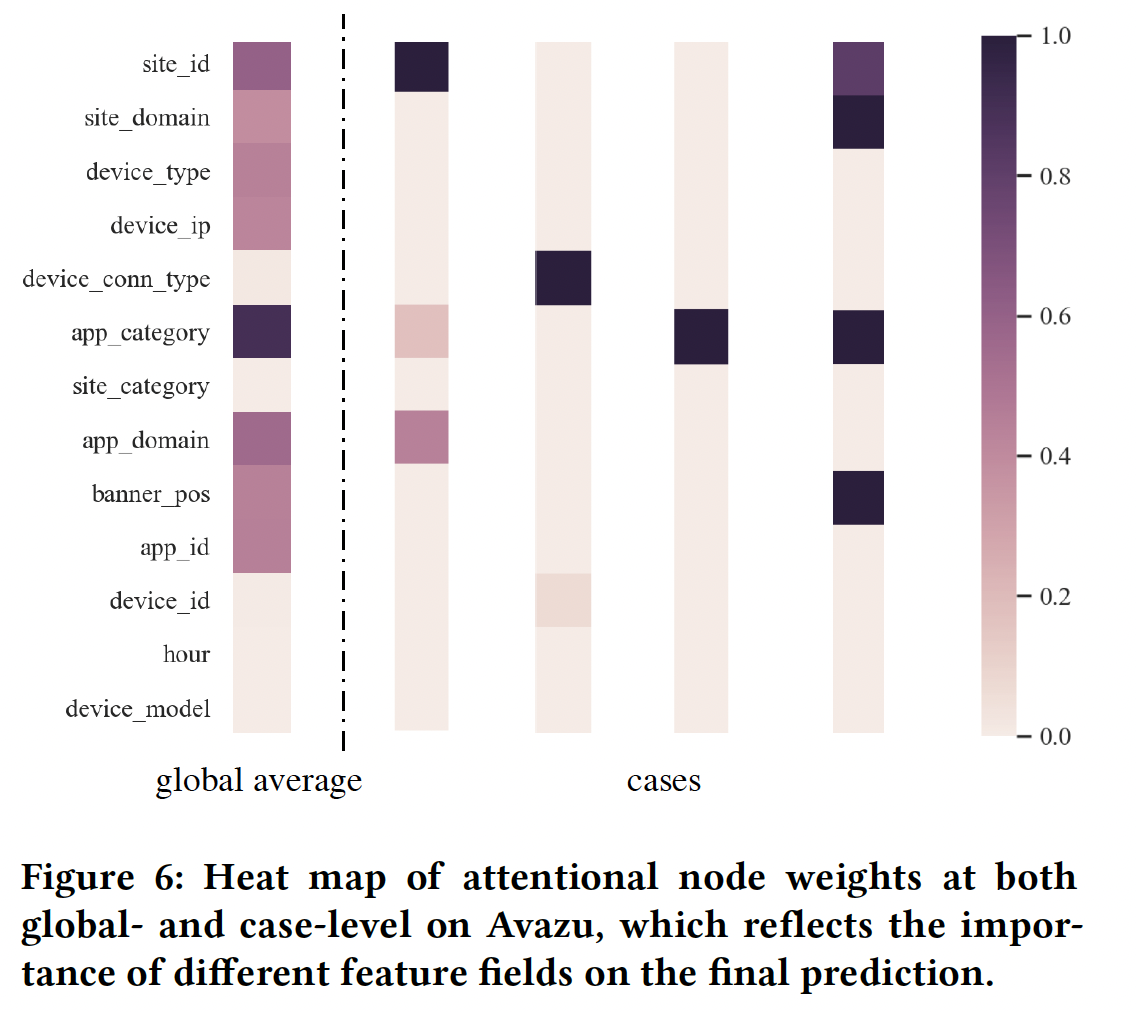
attentional node weight:attentional node weight反映了feature field对整体预测分数的影响的重要性。下图显示了global-level和case-level的attentional node weight的热力图。左边的是Avazu数据集中所有样本的全局平均值,右边的是Avazu数据集中随机选择的四个样本(预测分数分别为[0.97, 0.12, 0.91, 0.99],标签分别为[1, 0, 1, 1])。- 在
global level,我们可以看到featuer field app_category对点击行为的影响最大。这是合理的,因为Avazu专注于移动场景,而app是最重要的因素。 - 在
case level,我们观察到,在大多数情况下,最终的点击行为主要取决于一个关键的feature field。
- 在
二十八、FwFM[2018]
CTR预估所涉及的数据通常是multi-field categorical data,这类数据具有以下特性:- 首先,所有的特征都是
categorical的,并且是非常稀疏的,因为其中许多是id。因此,特征的总数很容易达到数百万或数千万。 - 其次,每个特征都唯一地属于一个
field,而且可能有几十到几百个field。
下表是一个用于
CTR预估的现实世界multi-field categorical data set的例子。
multi-field categorical data的特性对建立有效的机器学习模型进行CTR预测提出了几个独特的挑战:- 特征交互
feature interaction是普遍存在的,需要专门建模。在和标签关联方面,特征拼接feature conjunction与单个特征不同。例如,nba.com上展示的耐克广告的点击率,通常比所有网站上耐克广告的平均点击率、或nba.com上展示的所有广告的平均点击率高很多。这种现象在文献中通常被称为特征交互。 - 来自一个
field的特征往往与来自其他不同field的特征有不同的交互。例如,我们观察到,来自field GENDER的特征通常与field ADVERTISER的特征有很强的交互,而它们与field DEVICE_TYPE的特征交互却相对较弱。这可能是由于具有特定性别的用户更偏向于他们正在观看的广告,而不是他们正在使用的设备类型。 - 需要注意潜在的高模型复杂性。由于实践中通常有数以百万计的特征,模型的复杂性需要精心设计和调整,以适应模型到内存中。
为了解决这些挑战的一部分,研究人员已经建立了几个解决方案,
Factorization Machine: FM和Field-aware Factorization Machine: FFM是其中最成功的:FM通过将pairwise特征交互的影响建模为两个embedding向量的内积来解决第一个挑战。然而,field信息在FM中根本没有被利用。- 最近,
FFM已经成为CTR预估中表现最好的模型之一。FFM为每个特征学习不同的embedding向量,从而用于当特征与其他不同field的特征进行交互。通过这种方式,第二个挑战被显式地解决了。然而,FFM的参数数量是特征数量乘以field数量的数量级,很容易达到数千万甚至更多。这在现实世界的生产系统中是不可接受的。
在论文
《Field-weighted Factorization Machines for Click-Through Rate Prediction in Display Advertising》中,作者引入了Field-weighted Factorization Machines: FwFM来同时解决所有这些挑战。论文贡献:- 经验表明,不同的
field pairs与label的关联程度明显不同。按照同样的惯例,论文称它为field pair interaction。 - 基于上述观察,论文提出了
Field-weighted Factorization Machine: FwFM。通过引入和学习field pair weight matrix,FwFM可以有效地捕获field pair interaction的异质性。此外,FwFM中的参数比FFM中的参数少几个数量级,这使得FwFM成为现实世界生产系统中的首选。 FwFM通过用embedding vector representation取代线性项的binary representation而得到进一步的增强。这种新的处理方法可以有效地帮助避免过拟合,提高预测性能。- 论文在两个真实世界的
CTR预估数据集上进行了综合实验,以评估FwFM与现有模型的性能。实验结果表明:FwFM仅用FFM的4%的参数就能达到有竞争力的预测性能。当使用相同数量的参数时,FwFM比FFM的AUC提升了0.9%。
- 首先,所有的特征都是
28.1 模型
假设有
unique特征fieldsfield,记做给定数据集
label表示是否点击;active的。例如,假设有两个
field:性别、学历,那么field,field,它们的取值都是0或1。LR模型为:其中:
注意,因为这里将
label取值空间设为{1, -1}而不是{1, 0},因此这个损失函数与交叉熵不同,而是指数损失函数。Poly2:然而,线性模型对于诸如CTR预估这样的任务来说是不够的,在这些任务中,特征交互是至关重要的。解决这个问题的一般方法是增加feature conjunction。已有研究表明,Degree-2 Polynomial: Poly2模型可以有效地捕获特征交互。Poly2模型考虑将其中:
FM:Factorization Machine: FM为每个特征学习一个embedding向量FM将两个特征embedding向量其中:
在涉及稀疏数据的应用中(如
CTR预估),FM的表现通常优于Poly2模型。原因是,只要特征本身在数据中出现的次数足够多,FM总能为每个特征学习到一些有意义的embedding向量,这使得内积能很好地估计两个特征的交互效应interaction effect,即使两个特征在数据中从未或很少一起出现。FFM:然而,FM忽略了这样一个事实:当一个特征与其他不同field的特征交互时,其行为可能是不同的。Field-aware Factorization Machines: FFM通过为每个特征(如embedding向量来显式地建模这种差异,并且只使用相应的embedding向量field虽然
FFM比FM有明显的性能改进,但其参数数量是FFM的巨大参数数量是不可取的。因此,设计具有竞争力的和更高内存效率的替代方法是非常有吸引力的。
field pair的交互强度:我们特别感兴趣的是,在field level,交互强度是否不同。即,不同feature pair的平均交互强度是否不同。这里的平均交互强度指的是:给定一个field pair,它包含的所有feature pair的平均交互强度。例如,在
CTR预估数据中,来自field ADVERTISER的特征通常与来自field PUBLISHER的特征有很强的交互,因为advertiser通常针对一群有特定兴趣的人,而PUBLISHER的受众自然也是按兴趣分组的。另一方面,field HOUR_OF_DAY的特征往往与field DAY_OF_WEEK的特征没有什么交互,这不难理解,因为凭直觉,它们的交互对点击量没有什么贡献。为了验证
field pair interaction的异质性,我们使用field pairfield pair的交互强度:其中:
下图是每个
field pair和标签之间的互信息的可视化,由Oath CTR数据计算得出。不出所料,不同field pair的交互强度是相当不同的。一些field pair有非常强的交互,如(AD_ID,SUBDOMAIN)、(CREATIVE_ID,PAGE_TLD),而其他一些field pair有非常弱的交互,如(LAYOUT_ID,GENDER)、(Day_OF_WEEK,AD_POSITION_ID)。虽然分析结果并不令人惊讶,但我们注意到,现有的模型都没有考虑到这种
field level interaction的异质性 。这促使我们建立一个有效的机器学习模型来捕获不同field pair的不同交互强度。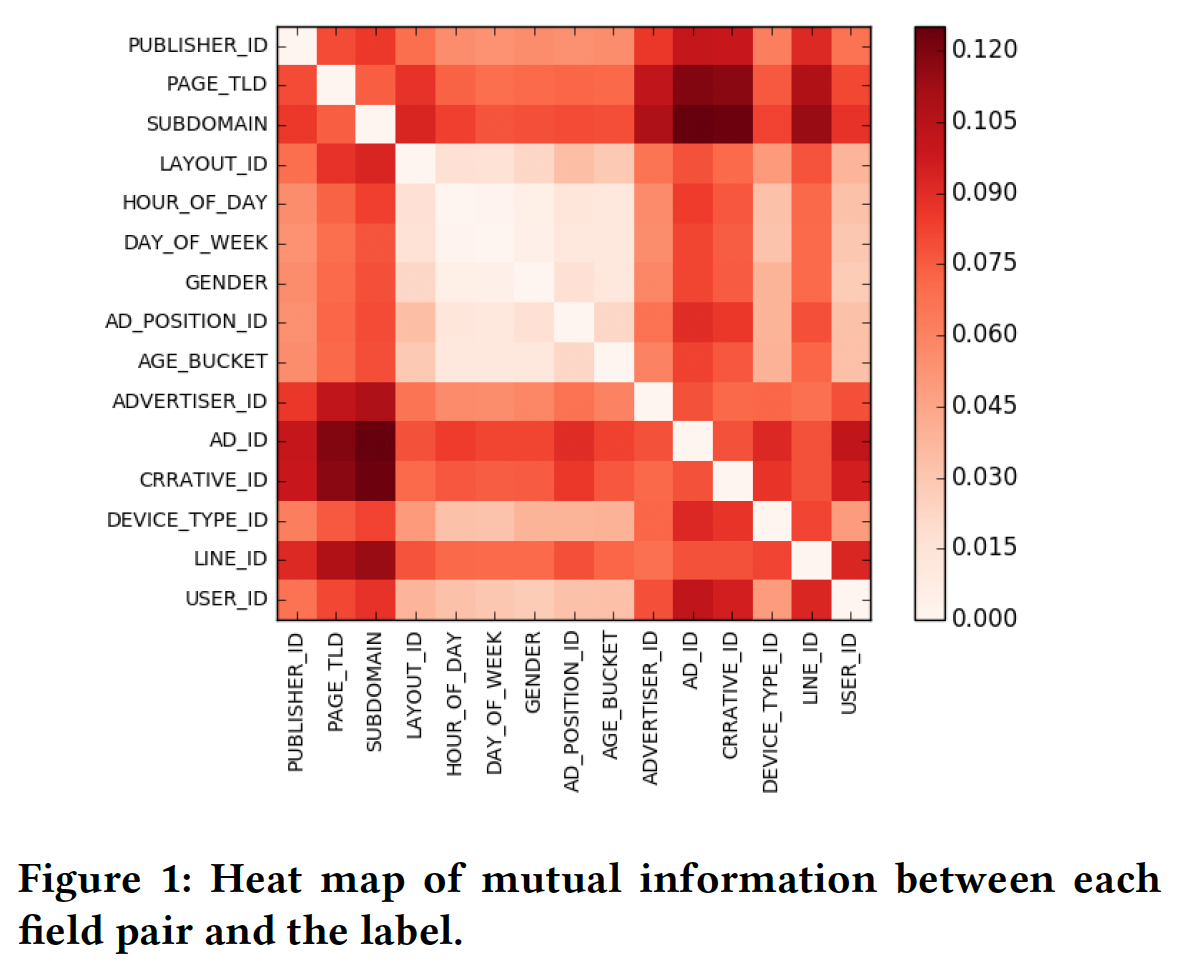
FwFM:我们提出对不同field pair的不同交互强度进行显式的建模,其中feature pair其中:
field pair核心要点:在
FM基础上乘以进一步地,我们是否可以在
field的概念之上继续遵循这种做法。比如,可以把field进行分组:用户年龄、性别等等field是一组,item类别、品牌等等是另一组、用户历史行为序列是其它一组,然后设定field group的权重:其中
field group之间的权重。我们将得到的模型称为
Field-weighted Factorization Machine: FwFM。模型复杂度:
FM的参数数量为embedding向量的参数数量。FwFM使用了额外的field pair,因此总的参数数量为FFM的参数数量为embedding向量。考虑到通常
FwFM的参数与FM相当,显著少于FFM。
线性项:我们认为,
embedding向量我们为每个特征学习一个线性权重
FwFM的线性项变为:这需要
FwFM的总参数数量为FwFM_FeLV。这相当于为每个特征学习两个
embedding:embeddingembedding- 首先,这种方法的表达能力更强。
- 其次,实现起来更简单。原始的线性项需要把特征表示成
sparse形式从而节省内存和计算量(大量的零存在),在实现的时候需要特殊的逻辑(稀疏张量的转换和计算)。而这里直接用embedding lookup,与现有的逻辑保持一致。
或者,我们为每个
field学习一个线性权重此时总的参数数量为
FwFM_FiLV。这相当于为每个
field学习一个embedding。原始线性权重的
FwFM记做FwFM_LW。或者我们是否可以用
1的向量,一定程度上降低了参数规模同时缓解过拟合。原因如下:考虑在后面的实验部分,确实发现参数更少的
FwFM_FiLV的测试AUC更高。那么是否1的向量时效果还要好?
28.2 实验
数据集:
Criteo CTR数据集:我们将数据按60%: 20%: 20%随机分成训练集、验证集和测试集。Oath CTR数据集:我们使用两周的点击日志作为训练集,下一天的数据作为验证集、下下一天的数据作为测试集。对于
Oath CTR数据集,正样本的比例通常小于1%。我们对负样本进行降采样,使正负样本更加平衡。对验证集和测试集不做降采样,因为评估应该在反映实际流量分布的数据集上进行。
对于这两个数据集,我们过滤掉所有在训练集中出现少于
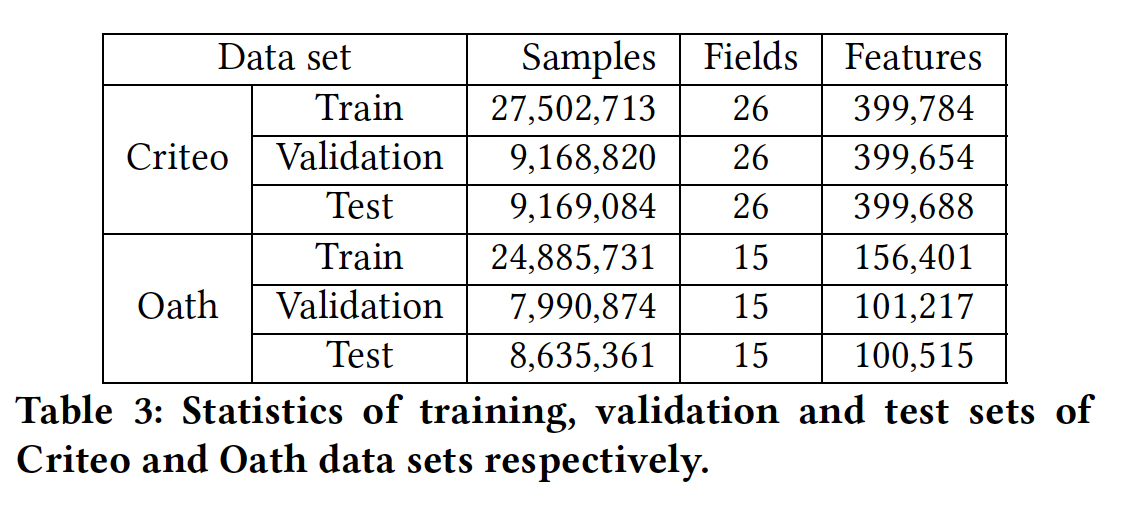
NULL特征代替,其中Criteo数据集中被设置为20,在Oath数据集中为10。这两个数据集的统计数字如下表所示:
实现:我们使用
LibLinear来训练Poly2,并使用哈希技巧将feature conjunctions哈希到Tensorflow中实现。Tensorflow中FwFM的结构如下图所示。输入是一个稀疏的二元向量
field。对每个样本而言每个field都有一个且只有一个活跃的特征。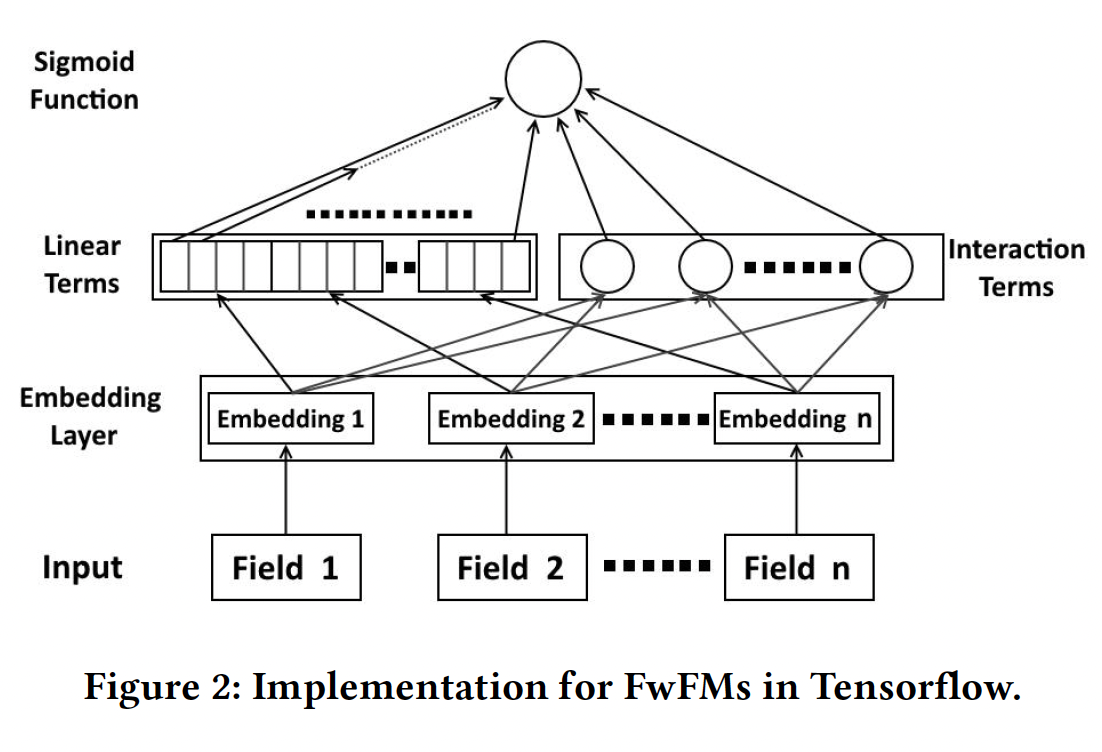
FwFM和已有模型的比较:我们评估了带原始线性项的FwFM,即FwFM_LW。对于所有的超参数,我们在验证集上进行调优,然后在测试集上进行评估。可以看到:- 在两个数据集上,
FwFM都能取得比LR、Poly2和FM更好的性能。这种改进来自于FwFM显式地建模了field pair的不同交互强度。 FFM总是在验证集和测试集上获得最佳性能。然而,FwFM的性能相比FFM具有相当的竞争力。
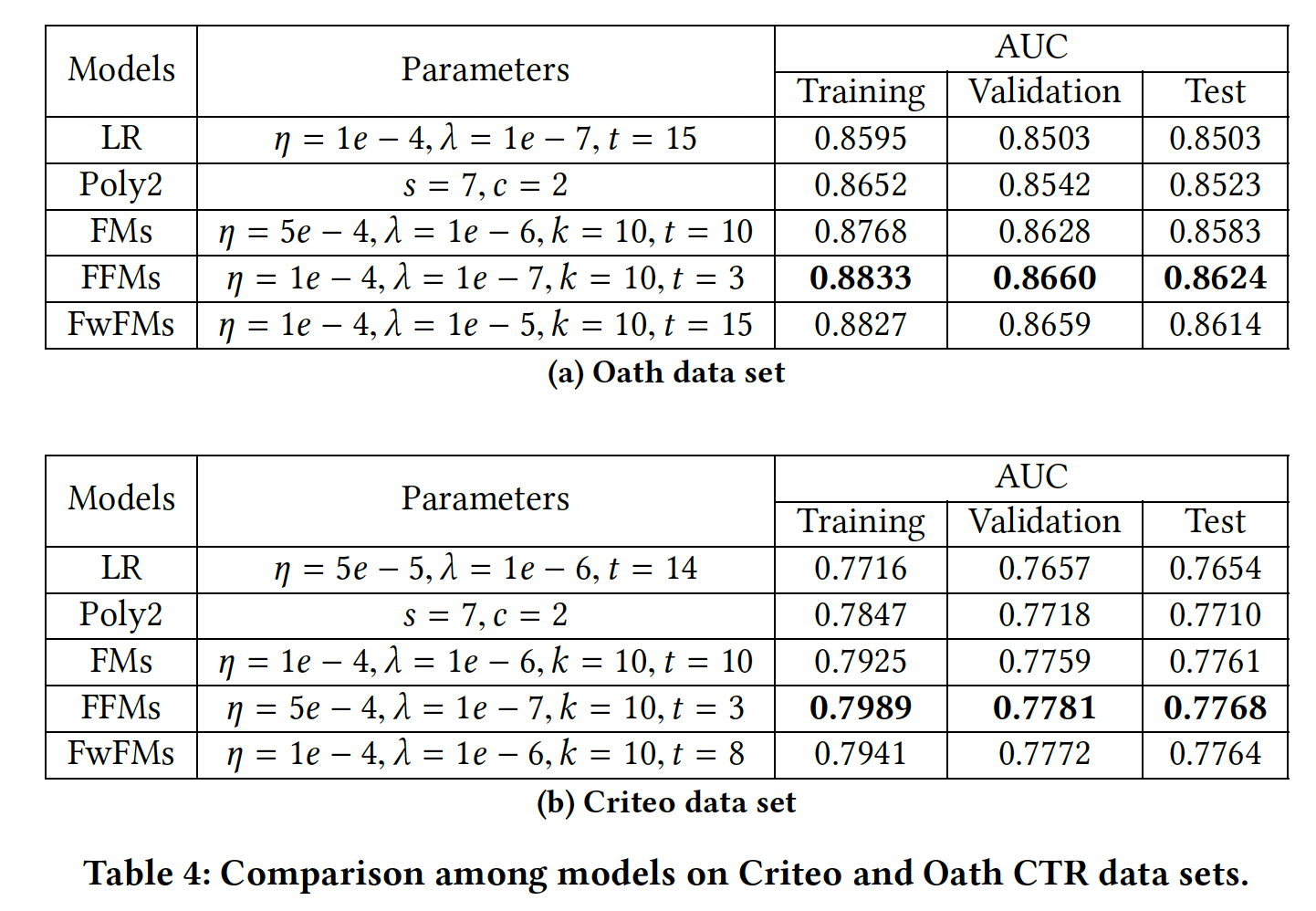
- 在两个数据集上,
FwFM与FFM在具有相同参数规模的情况下的比较:FFM的一个关键缺点是其参数数量在FFM的参数数量:使用较小的《Field-aware factorization machines in a real-world online advertising system》提出对FFM使用较小的这里我们通过选择合适的
FFM和FwFM的参数数量相同。我们不计算线性项的参数,因为它们与交互项的数量相比可以忽略。我们选择FwFM在Criteo和Oath数据集的测试集上得到更好的表现,提升幅度分别为0.70%和0.45%。
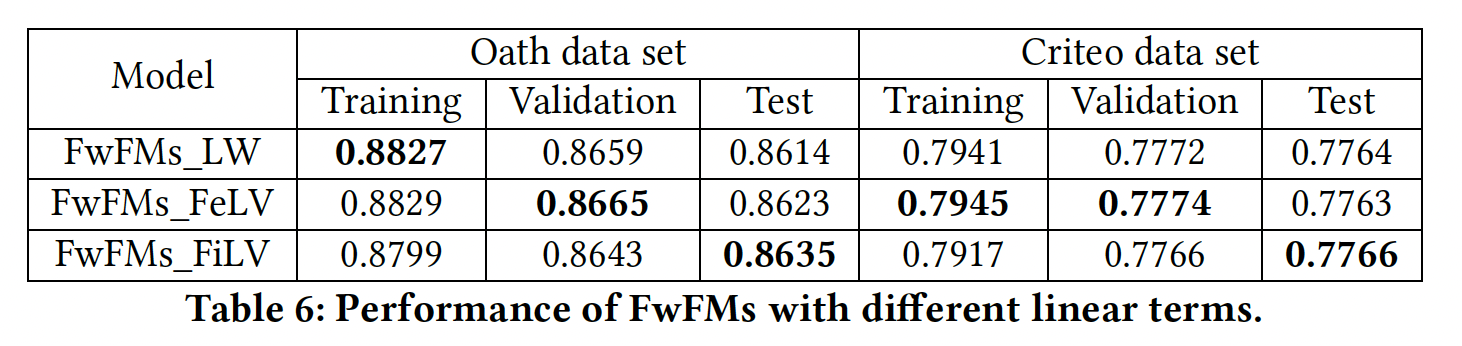
具有不同线性项的
FwFM:下表给出了不同线性项的FwFM的性能。可以看到:FwFM_LW和FwFM_FeLV在训练和验证集上比FwFM_FiLV能取得更好的性能。原因是这两个模型的线性项(FwFM_FiLV(FwFM_FiLV更好地拟合训练集和验证集。- 然而,
FwFM_FiLV在测试集上得到了最好的结果,这表明它有更好的泛化性能。 - 此外,当我们使用相同数量的参数将
FwFM_FiLV与FFM进行比较时,在Oath数据集和Criteo数据集上的AUC提升分别为0.92%和0.47%。
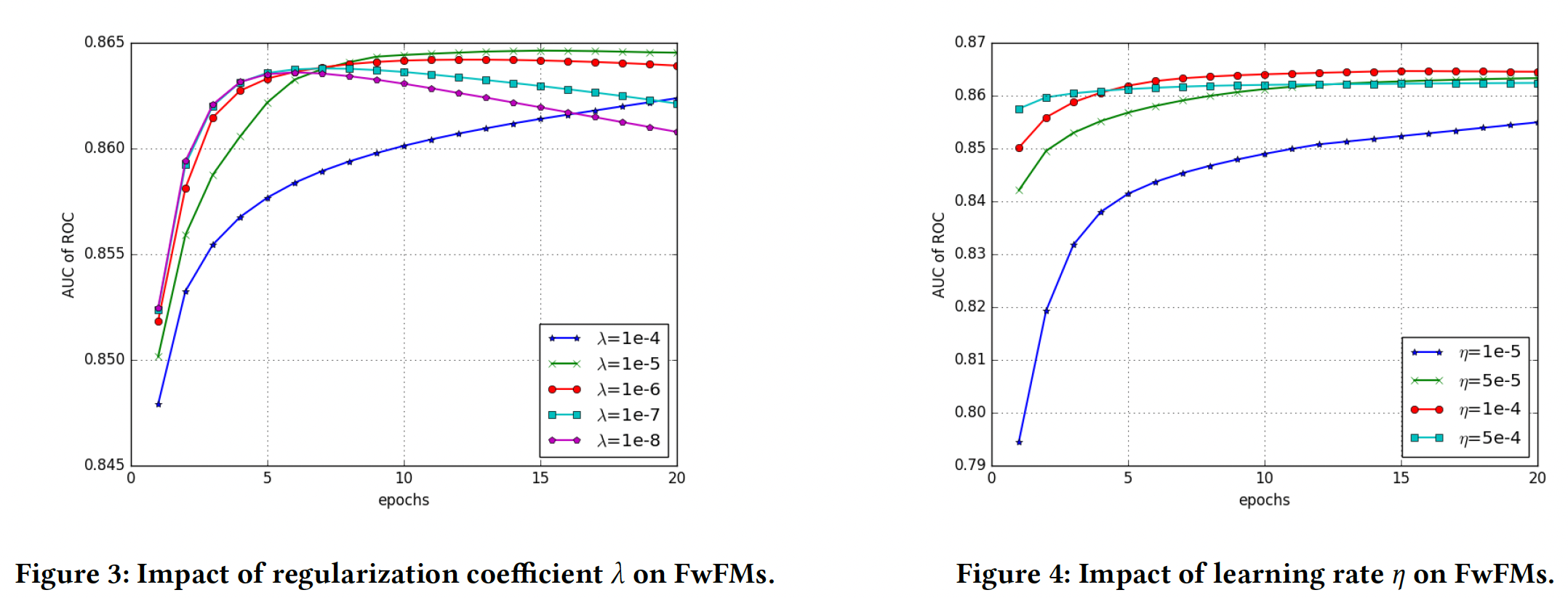
超参数调优:以下所有的评估都是
FwFM_FiLV模型在Oath验证集上进行的。L2正则化系数Figure3所示,正则化系数作用于所有的
parameters。学习率
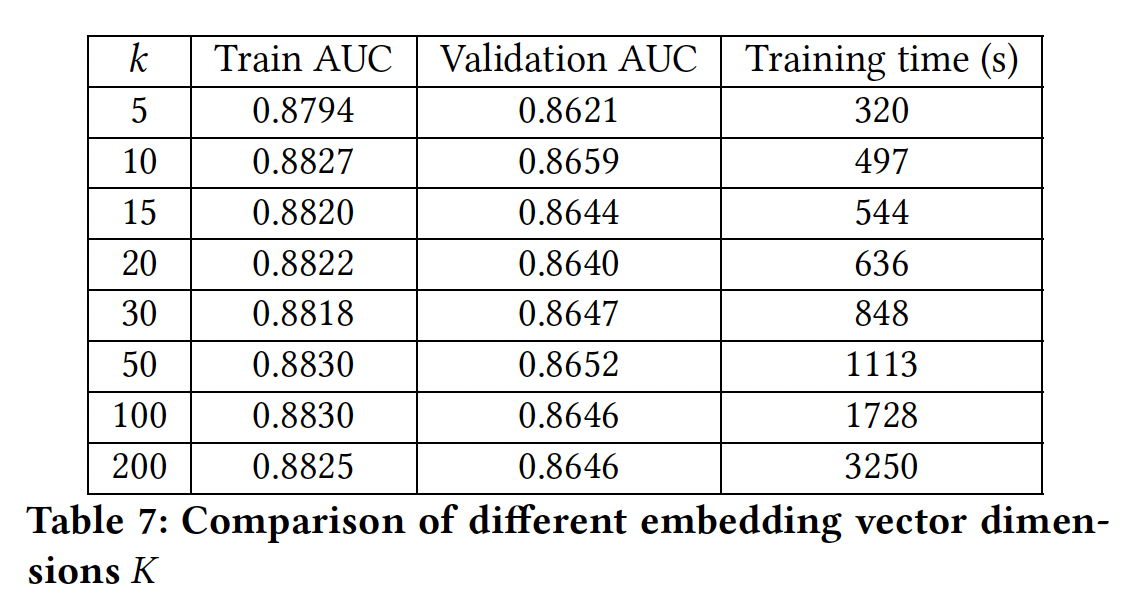
Figure4所示,我们选择embedding维度
学到的
field交互强度:这里我们比较了FM、FFM和FwFM在捕获不同field pair的交互强度方面的能力。我们的结果表明,由于field pair交互权重FwFM可以比FM和FFM更好地建模交互强度。field pair的交互强度通过互信息(field pair和标签之间的互信息Figure 5(a)中通过热力图进行了可视化。为了衡量学到的
field交互强度,我们定义了以下指标:其中:
feature pairfeature pair- 对于
FM, - 对于
FFM, - 对于
FwFM,
- 对于
注意,我们将内积项的绝对值相加,否则正值和负值会相互抵消。
如果一个模型能够很好地捕捉到不同
field pair的交互强度,我们期望其学习到的field交互强度接近于互信息Figure 5中以热力图的形式绘制了由FM, FFM, FwFM学到的field交互强度,以及field pair和标签之间的互信息field交互强度与互信息的匹配程度。- 从
Figure 5(b)中我们观察到:FM学到的交互强度与互信息完全不同。这并不奇怪,因为FM在建模特征交互强度时没有考虑field信息。 - 从
Figure 5(c)中我们观察到:FFM能够学习与互信息更相似的交互强度。 - 从
Figure 5(d)中我们观察到:FwFM学到的交互强度的热力图与互信息的热力图非常相似。
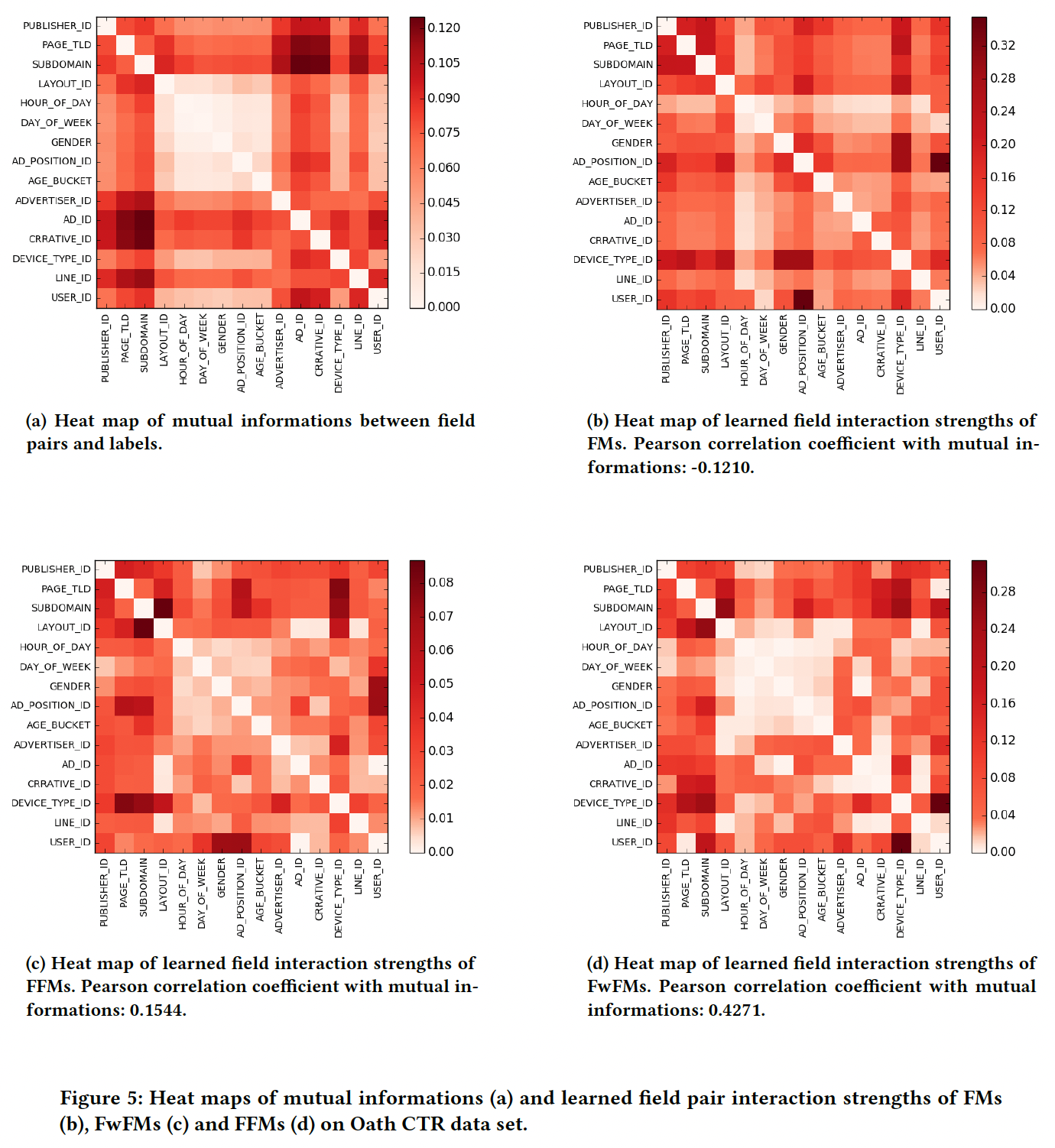
为了了解权重
field pair的交互强度方面的重要性,我们在Figure 6中绘制了FwFM(退化回FM)的学到的field交互强度。可以看到:Figure 5(a)的互信息热力图、Figure 5(d)的FwFM学到的field交互强度都非常相似。这意味着field pair的不同交互强度。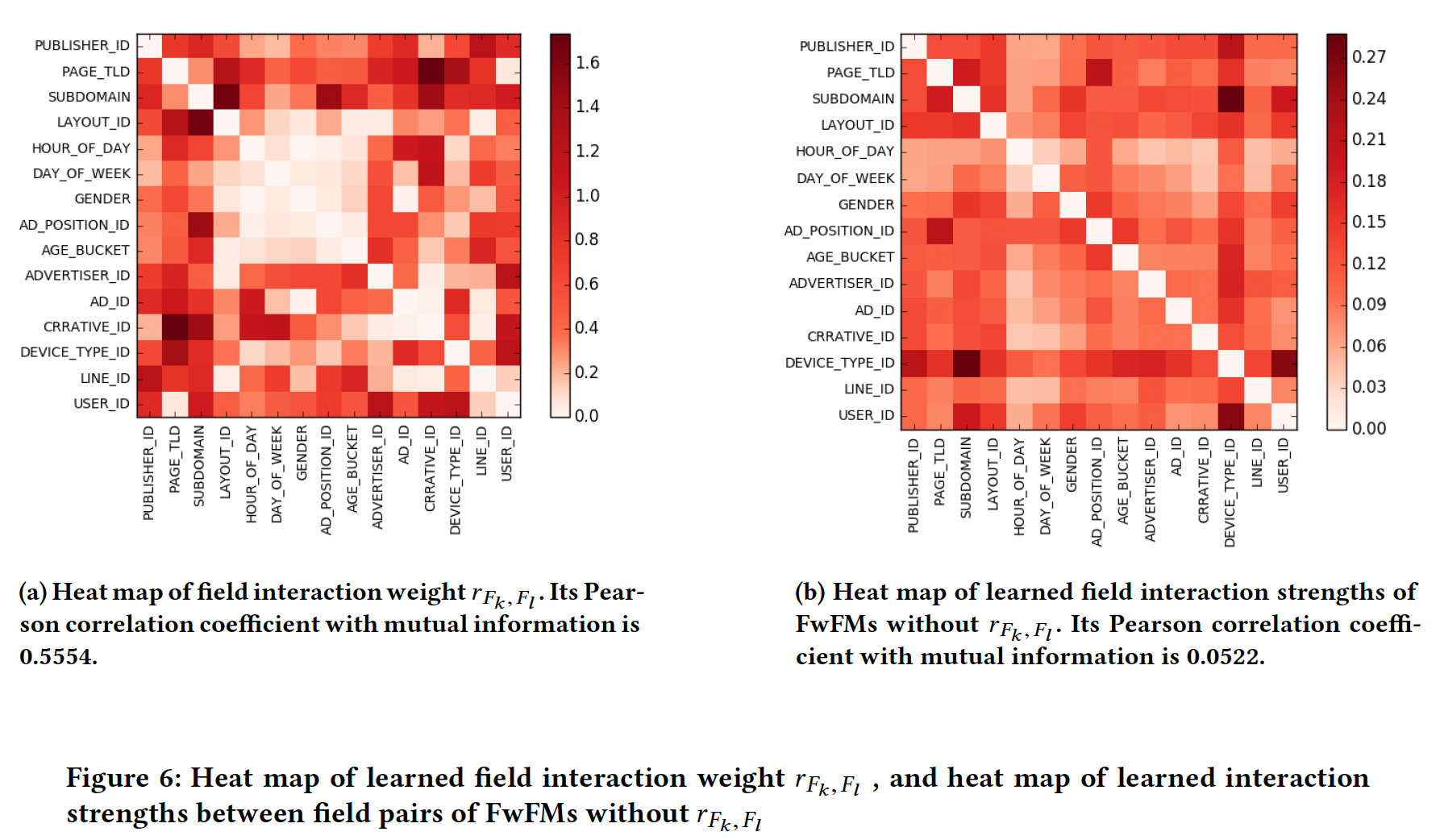
二十九、FM2[2021]
CTR预估所涉及的数据通常是multi-field categorical data,这类数据具有以下特性:- 首先,所有的特征都是
categorical的,并且是非常稀疏的,因为其中许多是id。因此,特征的总数很容易达到数百万或数千万。 - 其次,每个特征都唯一地属于一个
field,而且可能有几十到几百个field。
针对
ctr预测问题的一个卓越模型是具有交叉特征的逻辑回归。当考虑到所有的交叉特征时,产生的模型等同于二阶的多项式核。然而,要考虑所有可能的交叉特征需要太多的参数。为解决这个问题,人们提出了matrix factorization: MF和factorization machine: FM,这些方法通过两个feature embedding向量的点乘来学习交叉特征的影响。在FM的基础上,人们提出了Field-aware Factorization Machine: FFM,从而考虑field信息来建模来自不同field pair的不同的特征交互。最近,人们又提出了Field-weighted Factorization Machine: FwFM模型,以一种更加parameter-efficient的方式来考虑field信息。现有的考虑
field信息的模型要么有太多的参数(如FFM),要么不是很有效(如FwFM)。论文《FM2: Field-matrixed Factorization Machines for Recommender Systems》建议使用两个特征向量之间的field matrix来建模这两个特征向量之间的交互,其中矩阵是为每个field-pair单独学习的。论文表明,field-pair matrix方法在保持计算空间和时间效率的同时,实现了良好的准确性。- 首先,所有的特征都是
29.1 模型
假设有
unique特征fieldsfield,记做给定数据集
label表示是否点击;active的。LR模型为:其中:
然而,线性模型缺乏表示特征交互的能力。由于交叉特征可能比那些单一特征更重要,在过去的几十年里,人们提出了许多改进。
Poly2:然而,线性模型对于诸如CTR预估这样的任务来说是不够的,在这些任务中,特征交互是至关重要的。解决这个问题的一般方法是增加feature conjunction。已有研究表明,Degree-2 Polynomial: Poly2模型可以有效地捕获特征交互。Poly2模型考虑将其中:
FM:Factorization Machine:FM为每个特征学习一个embedding向量FM将两个特征embedding向量其中:
在涉及稀疏数据的应用中(如
CTR预估),FM的表现通常优于Poly2模型。原因是,只要特征本身在数据中出现的次数足够多,FM总能为每个特征学习到一些有意义的embedding向量,这使得内积能很好地估计两个特征的交互效应interaction effect,即使两个特征在数据中从未或很少一起出现。FFM:然而,FM忽略了这样一个事实:当一个特征与其他不同field的特征交互时,其行为可能是不同的。Field-aware Factorization Machines: FFM通过为每个特征(如embedding向量来显式地建模这种差异,并且只使用相应的embedding向量field虽然
FFM比FM有明显的性能改进,但其参数数量是FFM的巨大参数数量是不可取的。因此,设计具有竞争力的和更高内存效率的替代方法是非常有吸引力的。FwFM:在FwFM中,feature pair其中:
field pairFwFM的公式为:FwFM是FM的扩展,即它使用额外的权重feature pair的不同交互强度。FFM可以隐式地建模不同feature pair的不同交互强度,因为FFM为每个特征embedding向量,每个向量fieldfield特征的不同交互。
最近,也有很多关于基于深度学习的
CTR预测模型的工作。这些模型同时捕获了低阶交互和高阶交互,并取得了明显的性能改进。然而,这些模型的在线推理复杂性比浅层模型要高得多。通常需要使用模型压缩技术,如剪枝、蒸馏或量化来加速这些模型的在线推理。在本文中,我们专注于改进低阶交互,所提出的模型可以很容易地作为这些深度学习模型中的浅层组件。我们提出了一个新的模型,将
field pair的交互表达为一个矩阵。与FM和FwFM类似,我们为每个特征学习一个embedding向量。 我们定义一个矩阵fieldfield其中:
featureembedding向量。featurefield。fieldfield注意:
embedding向量不同。此外,考虑到 “fieldfieldfieldfield
我们称这个模型为
Field-matrixed Factorization Machine: FmFM(也叫做FM2):FmFM是FwFM的扩展,它使用一个二维矩阵FwFM中的标量field pair的交互。通过这些矩阵,每个特征的embedding空间可以被转换到另外的embedding空间。我们将这些矩阵命名为Field-Matrix。核心思想:将
FwFM中的标量下图展示了
feature pairfield。计算可以分解为三步:Embedding Lookup:从embedding table中查找feature embedding向量- 转换:将
fieldfield - 点乘:最终的交互项将是
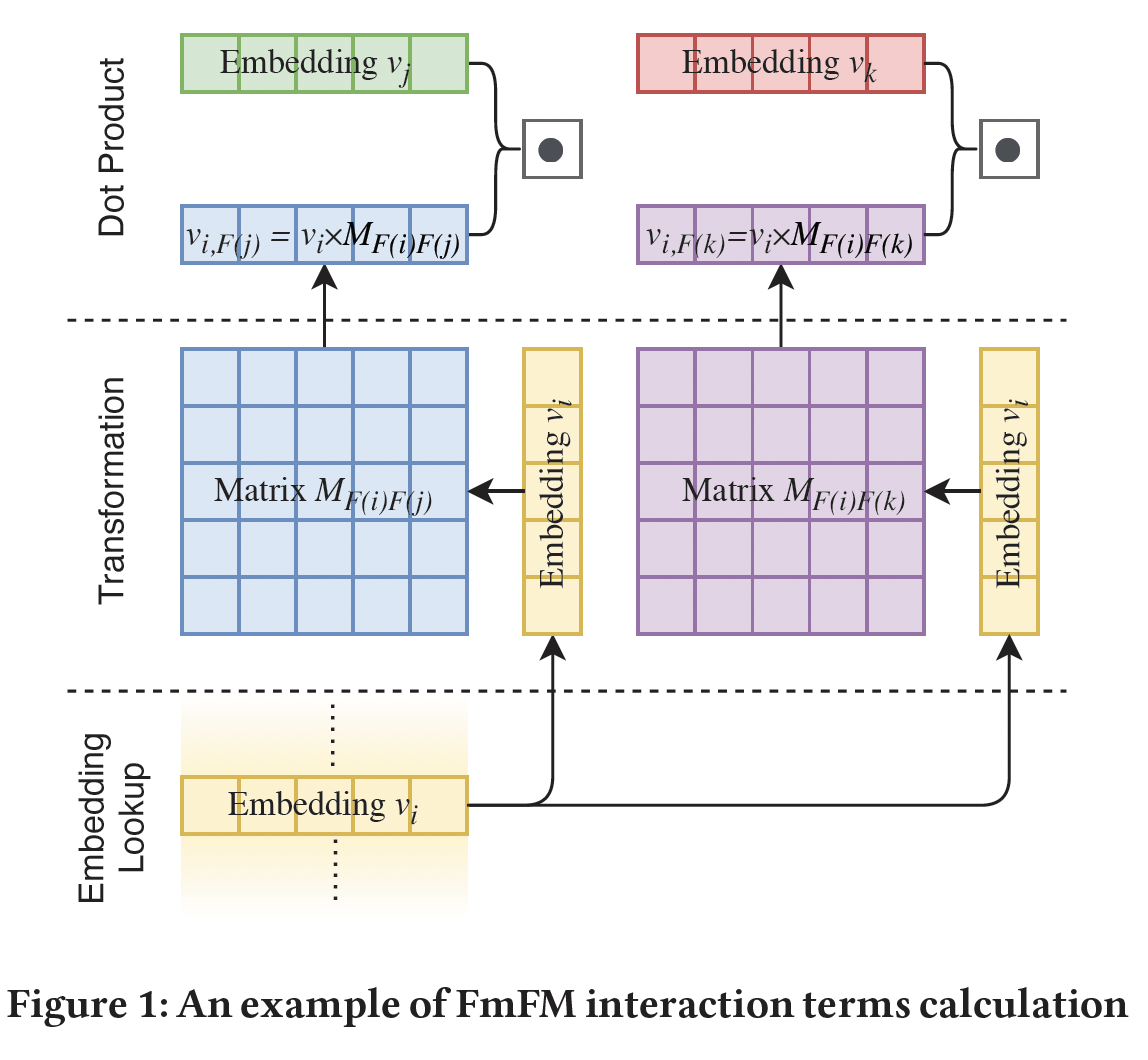
29.2 FM2 作为统一框架
FM家族的统一框架:FM:下图展示了FM中特征交互的计算。如果将FmFM中所有的field matrix都固定为单位矩阵,那么FmFM将退化为FM。由于单位矩阵是固定的、不可训练的,因此我们定义其自由度为0。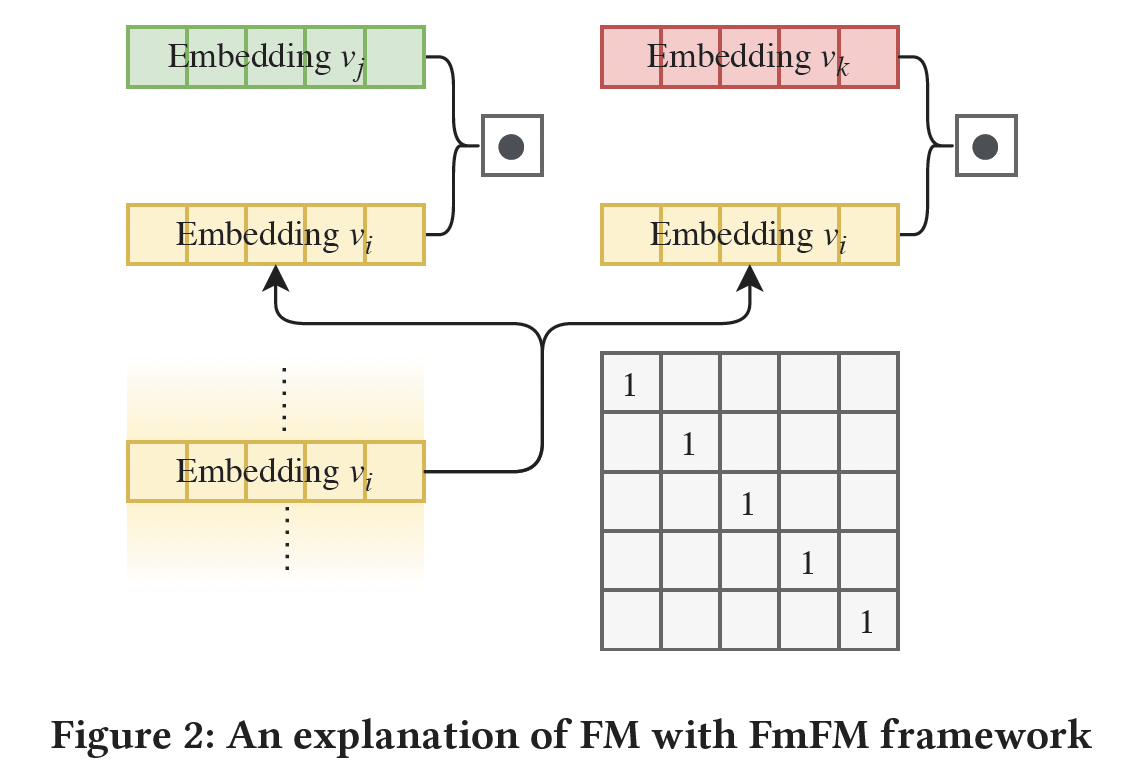
FwFM:下图展示了FwFM中特征交互的计算。如果将FmFM中的field pair取不同的值,那么FmFM将退化为FwFM。我们定义FwFM的自由度为1。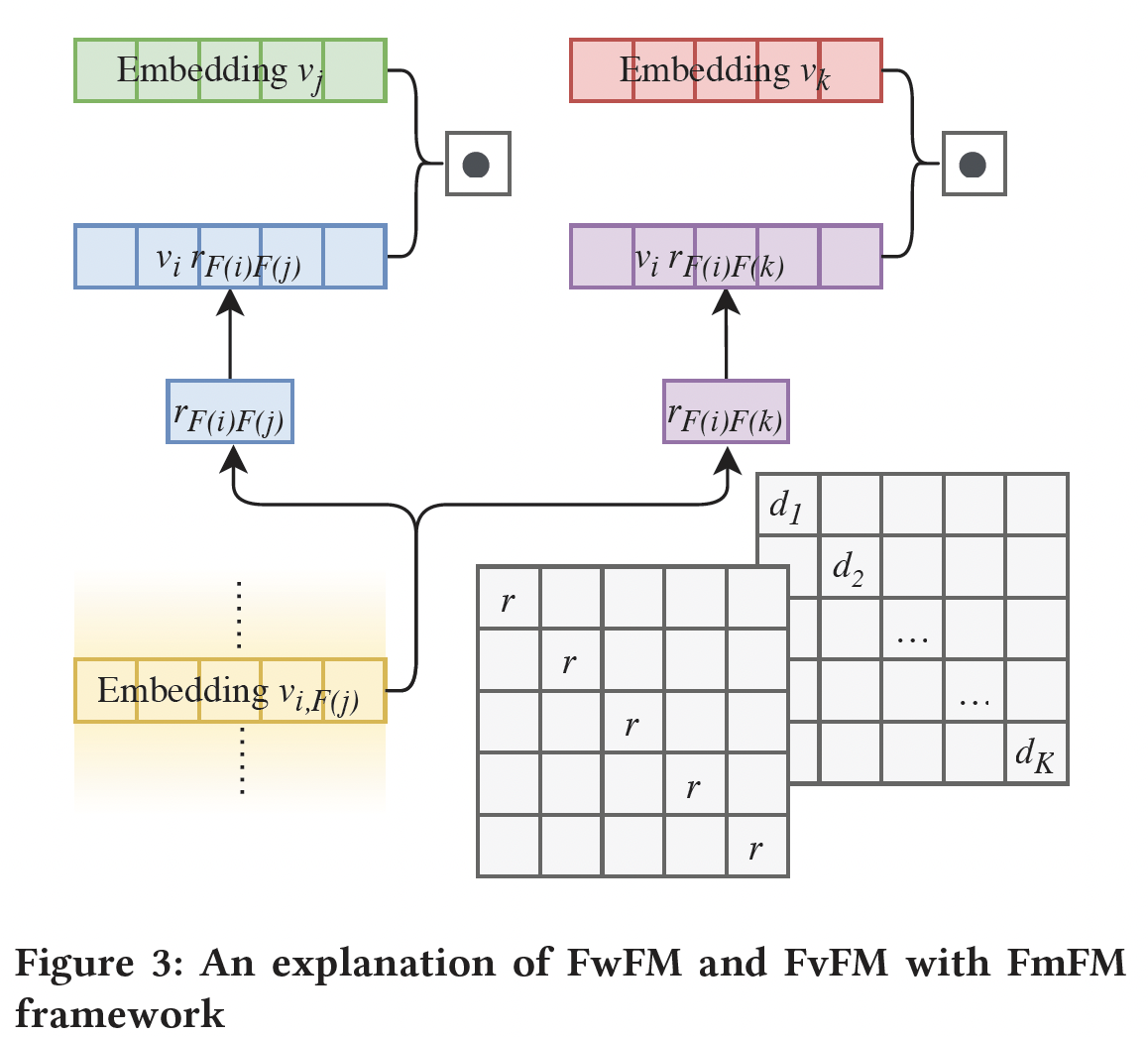
FvFM:根据Figure 3的线索,我们将FmFM中的field pair选择不同的对角矩阵,如Figure3的右边的矩阵所示,那么:其中:
我们将这种方法命名为
Field-vectorized Factorization Machine: FvFM,它的自由度为2。FmFM:它具有一个矩阵的所有自由度,即自由度为3。我们预期FmFM比其他FM模型有更强大的预测能力。
总之,我们发现
FM、FwFM、FvFM都是FmFM的特例,唯一的区别是它们的field matrix的限制。根据它们的灵活性,我们把它们总结在下表中。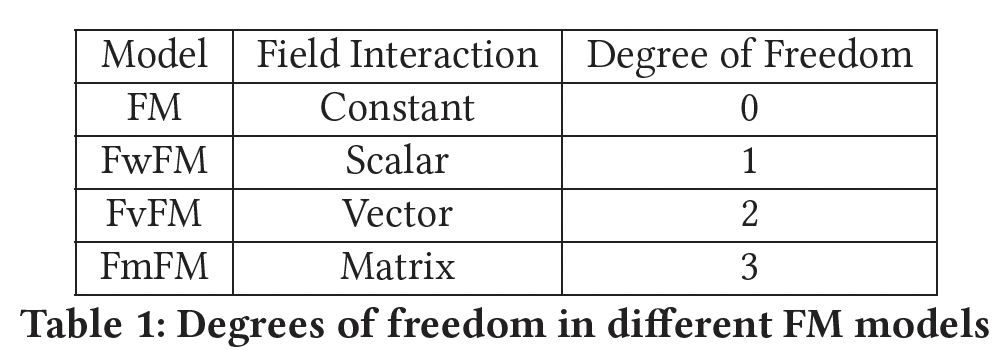
FmFM与OPNN的关系:FmFM也可以看做是通过加权外积来建模两个feature embedding vector的交互:OPNN也提出通过外积来建模特征交互。然而,FmFM在以下两个方面与OPNN不同:- 首先,
FmFM是一个简单的浅层模型,没有像OPNN中那样的全连接层。我们可以将FmFM作为任何深度CTR模型的一个浅层组件或构建块。 - 其次,
FmFM支持针对不同feature field的可变embedding size。
- 首先,
FFM vs FmFM,即Memorization vs Inference:与上述其他FM不同,FFM不能被改造成FmFM框架。下图展示了FFM中特征交互的计算。FFM不共享feature embedding,因此对于每个特征都有embedding从而分别与其它field进行交叉。在训练过程中,这些field-specific embedding将被独立学习,而且这些embedding之间没有任何限制,即使它们属于同一特征。这种
FFM机制给了模型最大的灵活性来拟合数据,而且大量的embedding参数也具有惊人的记忆能力。同时,即使有数十亿的样本需要训练,也总是存在着过拟合的风险。特征分布的属性是一个长尾分布,而不是均匀分布,这使得feature pair的分布更加不平衡。以下图为例。假设
feature pairembedding,因此embeddingfeature pair可能占据了训练数据的绝大部分,而低频的feature pair(占据了feature pair中的绝大多数)则不能被很好地训练。FmFM使用共享embedding向量,因为每个特征只有一个embedding向量。它利用一个变换过程,将这一个embedding向量投影到其他field。这基本上是一个推理过程,那些embedding向量embedding向量field matrix,向量是可以前向变换和反向变换。这就是FFM和FmFM的根本区别:在同一特征中那些可变换的中间向量(即,feature pair。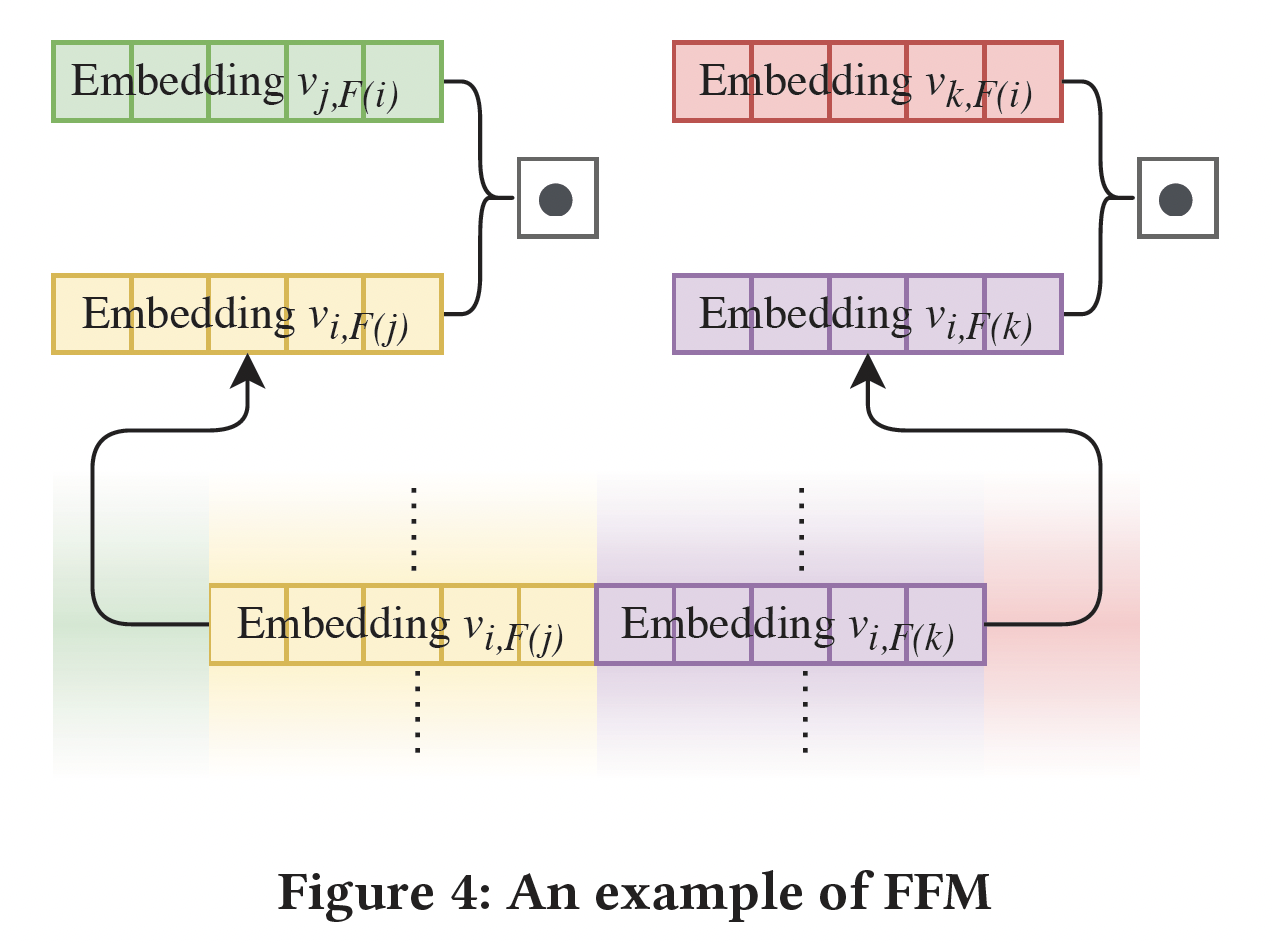
回到
Figure 1的例子。即使feature pairfeature embeddingfeature pair(如field matrixfieldfieldfeature pair尽管
FFM和FmFM之间有这种差异,但它们有更多的共同点。Figure 4和Figure 1之间一个有趣的观察是:当所有变换完成后,FmFM模型变成了FFM模型。我们可以缓存那些中间向量,避免在运行时进行矩阵操作。细节将在下一节讨论。相反,
FFM模型无法被改造成FmFM模型。那些field feature embedding table是独立的,因此很难将它们压缩成单个feature embedding table,并在需要时恢复它们。模型复杂度:
FM的参数数量为embedding向量。FwFM对每个field对使用FwFM的参数总数为FmFM对每个field对使用FwFM的参数总数为FFM的参数数量为embedding向量。
在下表中,我们比较了到目前为止提到的所有模型的复杂度。我们还列出了每个模型的估计参数规模(模型配置,如
embedding size,参考实验部分),这些模型使用了公共数据集Criteo。这些数字可以让我们对每个模型的规模有一个直观的印象。FM、FwFM和FmFM的规模相近,而FFM的规模比其他模型大十几倍。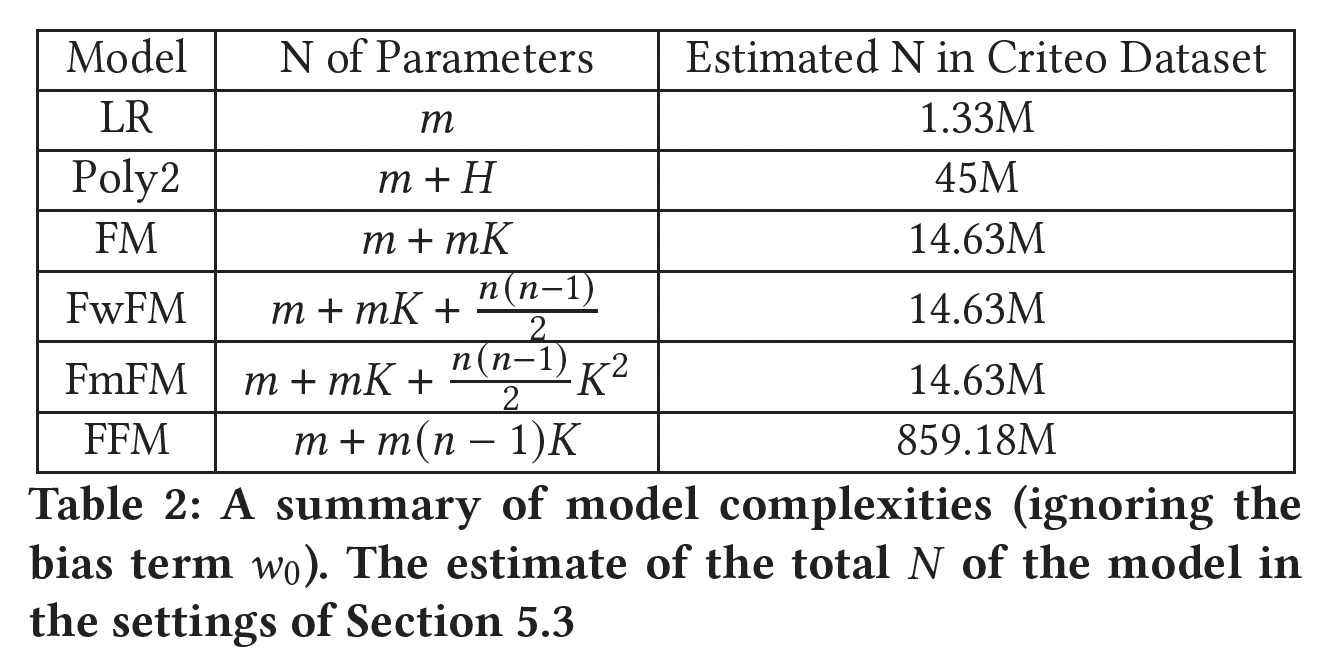
29.3 模型优化
这里我们可以设计出
3种策略来进一步降低FmFM的复杂度:field-specific embedding dimension:它是FmFM的一个独特属性,允许我们在embedding table中使用field-specific的维度,而不是全局的固定长度这里
field-specific的维度是通过对训练好的embedding table进行降维来实现的。因此需要训练两遍。缓存中间向量:避免矩阵运算从而在运行时减少
FmFM的计算复杂度(仅用于推断期间)。减少线性项:用
field-specific权重来代替。
这里面提到的优化方法大多数都不实用,无法优化训练速度,而仅聚焦于优化推断速度。实际上,如果想优化推断速度,那么可以用模型剪枝、模型量化、模型蒸馏技术。
Field-specific Embedding Dimension:为了进行点积,FM要求所有feature embedding的向量维度field。改进后的模型如FwFM、FvFM也采用了这个特性。然而,向量维度当我们利用
FmFM中的矩阵乘法时,它实际上并不要求field matrix是方阵:我们可以通过改变field matrix的shape来调整输出向量的维度。这一特性给了我们另一种灵活性,可以在embedding table中按需设置field-specific维度,如下图所示。embedding向量的维度决定了它所能携带的信息量。例如,field user_gender可能只包含3个值(male, female, other),field top_level_domain可能包含超过1M个特征。因此,user_gender的embedding table可能只需要5维,而field top_level_domain的embedding table可能需要7维,因此它们之间的field matrix的shape为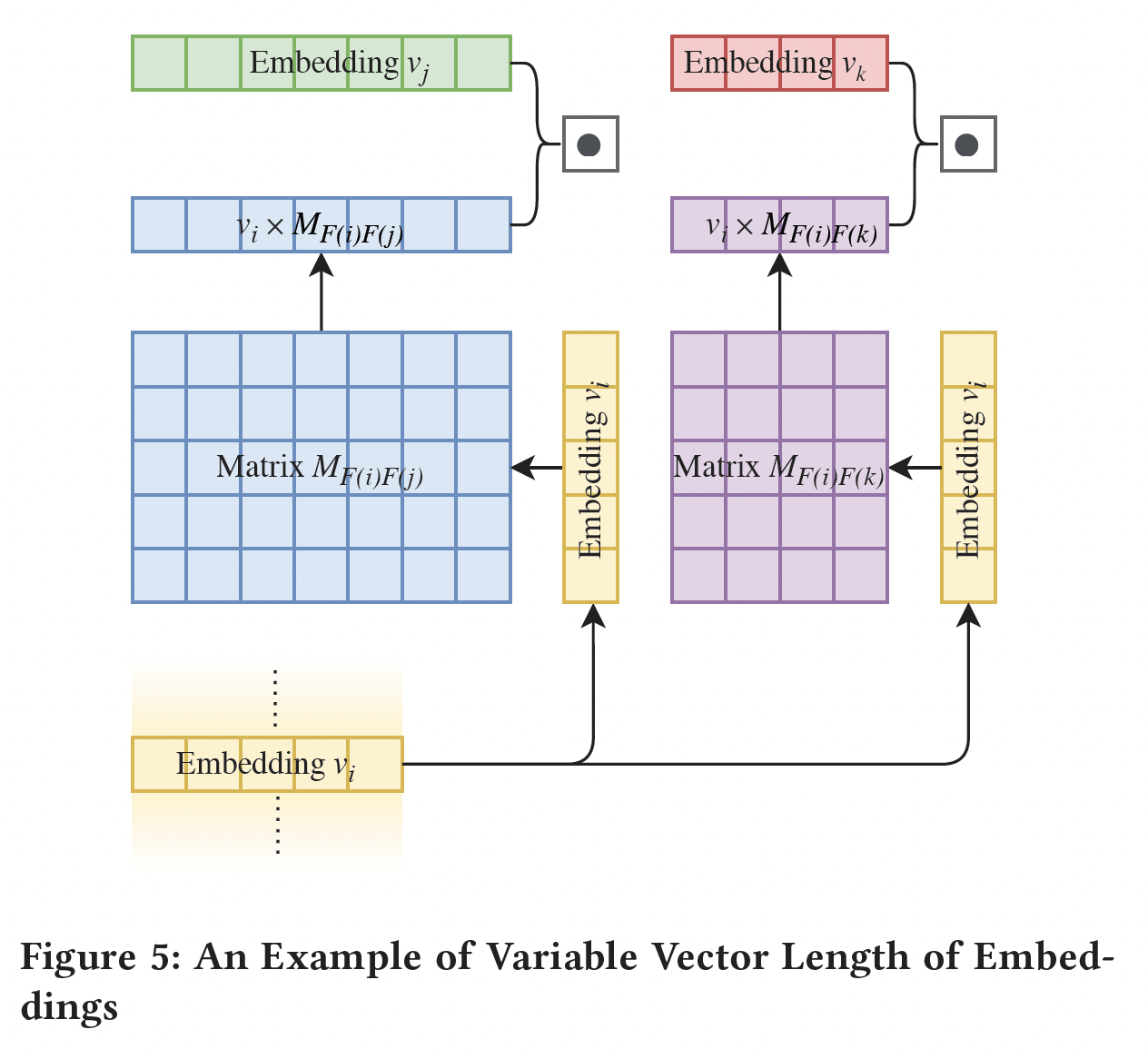
为了在不损失模型性能的前提下设计
field-specific embedding vector dimension,我们提出了一种2-pass方法:- 在第一个
pass,我们对所有field使用较大的固定的embedding向量维度,如FmFM训练为完整模型。从完整的模型中,我们了解到每个field有多少信息(方差),然后我们在每个field的embedding table上应用标准的PCA降维方法。从实验部分中我们发现,包含95%原始方差的新维度是一个很好的tradeoff。 - 有了这个新的
field-specific的维度设置,我们在第二个pass中从头开始训练模型。与第一个完整的模型相比,所得到的第二个模型没有任何明显的性能损失。
这种方法训练时间翻倍。一般而言,
CTR预测任务的数据集很大、模型也比较复杂,因此整体训练时间会很长。翻倍的训练时间不太有利。并且,这种方法还需要仔细设计
field matrix的shape,增加了开发成本。下表显示了
Criteo数据集中每个field通过PCA进行优化后的维度。可以看到,这些维度的范围很大,从2到14,而且大部分维度都小于10。平均7.72,低于FwFM的最佳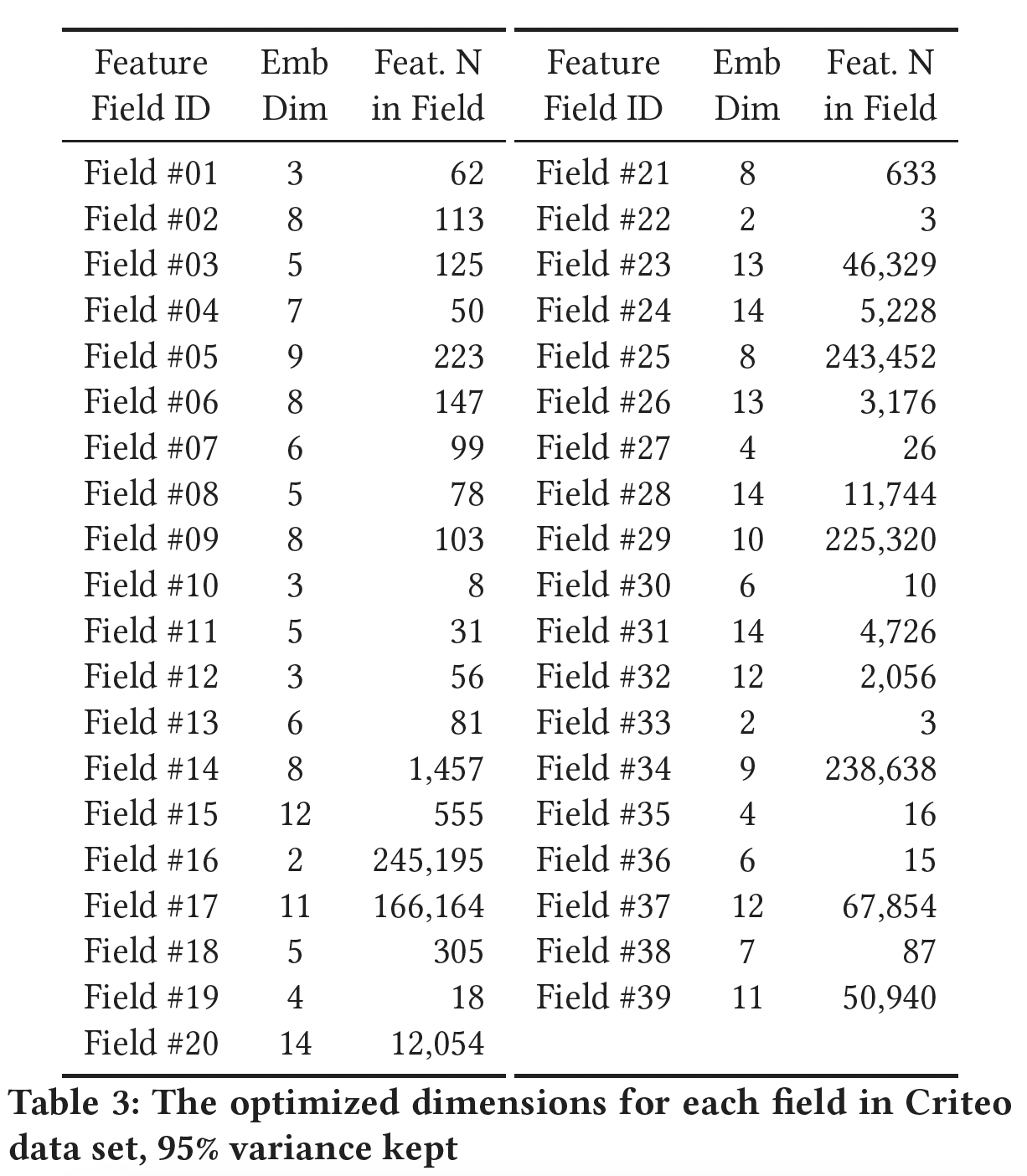
- 在第一个
Intermediate Vectors Cache:在参数数量上,FmFM是一个比FFM更低复杂度的模型。但是FmFM在变换步骤中需要昂贵的矩阵运算。在下表中,我们列出了每个模型的浮点运算(Floating Point Operations: FLOPs)的数量,并以典型的设置对其进行估计。注:典型设置为:
DNN隐层的单元数,DNN的隐层数量,AutoInt中新空间的维度,DeepLight中FwFM和DNN组件的稀疏率。在这些
FM模型中,FmFM需要最多的操作来完成其计算,大约是FwFM和FFM的DNN模型快。如前所述,我们已经表明,通过缓存所有的中间向量,可以将FmFM模型转化为FFM模型。在这个意义上,我们可以把它的操作数量减少到与FM和FFM相同的量级,这几乎是20倍的速度。首先,如何缓存?论文并未提到细节。
其次,缓存中间向量仅在推理期间有效,因为此时所有参数都已经学好并固定不动。然而在训练期间,每经过一个
training iteration参数都发生更新,因此缓存的中间向量到下一个iteration就没有意义。因此,读者估计,FmFM的训练时间会非常的长。最后,这里给的计算复杂度及其估计值是针对推理期间的,而不是训练期间的。而
95% variance是在训练完成之后进行的,在训练期间不可用。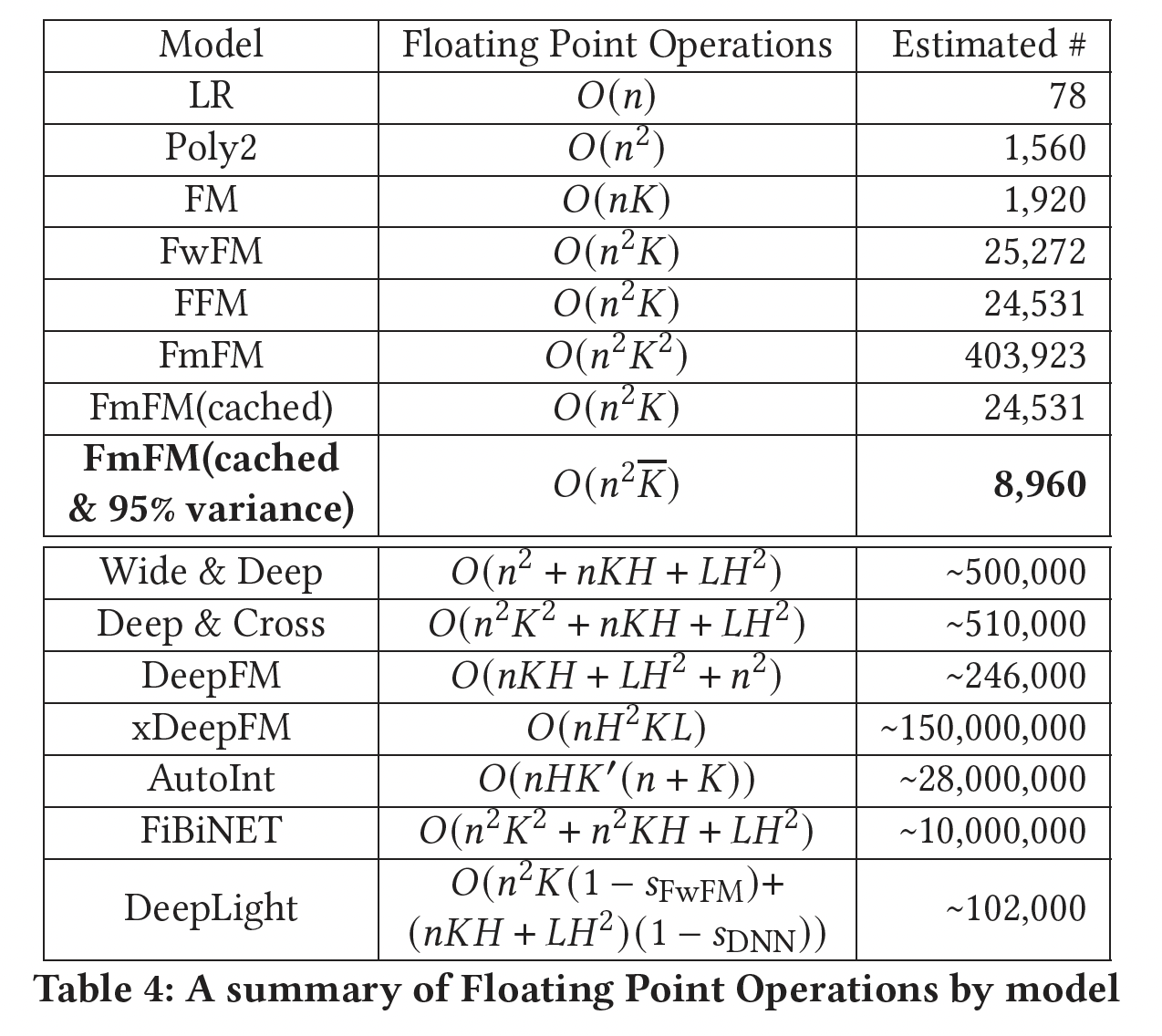
Embedding Dimension and Cache Optimization Combined:当我们把field-specific embedding dimensional optimization和缓存优化结合起来时,推理速度可以快得多,而且所需的内存也可以大大减少。这得益于FmFM的另一个特性:交互矩阵是对称的。这意味着:证明见原始论文。
因此,我们可以选择缓存那些
field embedding维度较低的中间向量,并在推理过程中与其他特征向量进行点乘。例如,在Table 3中,两个特征field #16和field #28。有了这个对称性,当我们计算- 由于
field matrix2(field #16)增加到14(中间向量),然后与维度也为14的14个单位的内存用于中间向量的缓存,在推理过程中需要2*14个FLOPs。 - 相比之下,后者
14(field #28)缩减到2(中间向量),然后与维度也是2的2个单位的内存,并在推理中花费2*2 FLOPs。因此缓存维度为2的中间向量,可以节省7倍的内存和时间,而没有任何精度损失。
通过这两种优化技术的结合,
FmFM模型的时间复杂度大大降低。在Table 4中,我们估计优化后的模型只需要8,960个FLOPs,这只是FFM的1/3左右。在实验部分中,我们将说明这个优化的模型可以达到与完整模型相同的性能。- 由于
Soft Pruning:field-specific embedding dimension实际上也起到了类似于剪枝的作用。传统的剪枝,如DeepLight,给出了保留或放弃一个field或一个field pair的二元决定。而field-specific embedding dimension给了我们一个新的方法:按需确定每个field和field pair的重要性,并给每个field分配一个系数(即,emebdding维度)来代表其重要性。例如,在Table 3的FmFM模型中,cross field#17和#20是一个高强度的field pair,它在推理过程中需要11个单位的缓存和2*11个FLOPs;相反,一个低强度的field pair,即cross field#18和#22,只需要2个单位的缓存和2*2个FLOPs。缓存空间大小就是
field pair中最短的那个emebdding维度。在传统的剪枝方法中,当我们放弃一个
field pair时,它的信号就完全消失了。而在我们的方法中,一个field pair仍然以最小的代价保留主要信息(即,很小的embedding维度)。这是一个soft pruning的版本,类似于Softmax。它的效率更高,在soft pruning过程中性能下降更少。然后这种剪枝方法依赖于
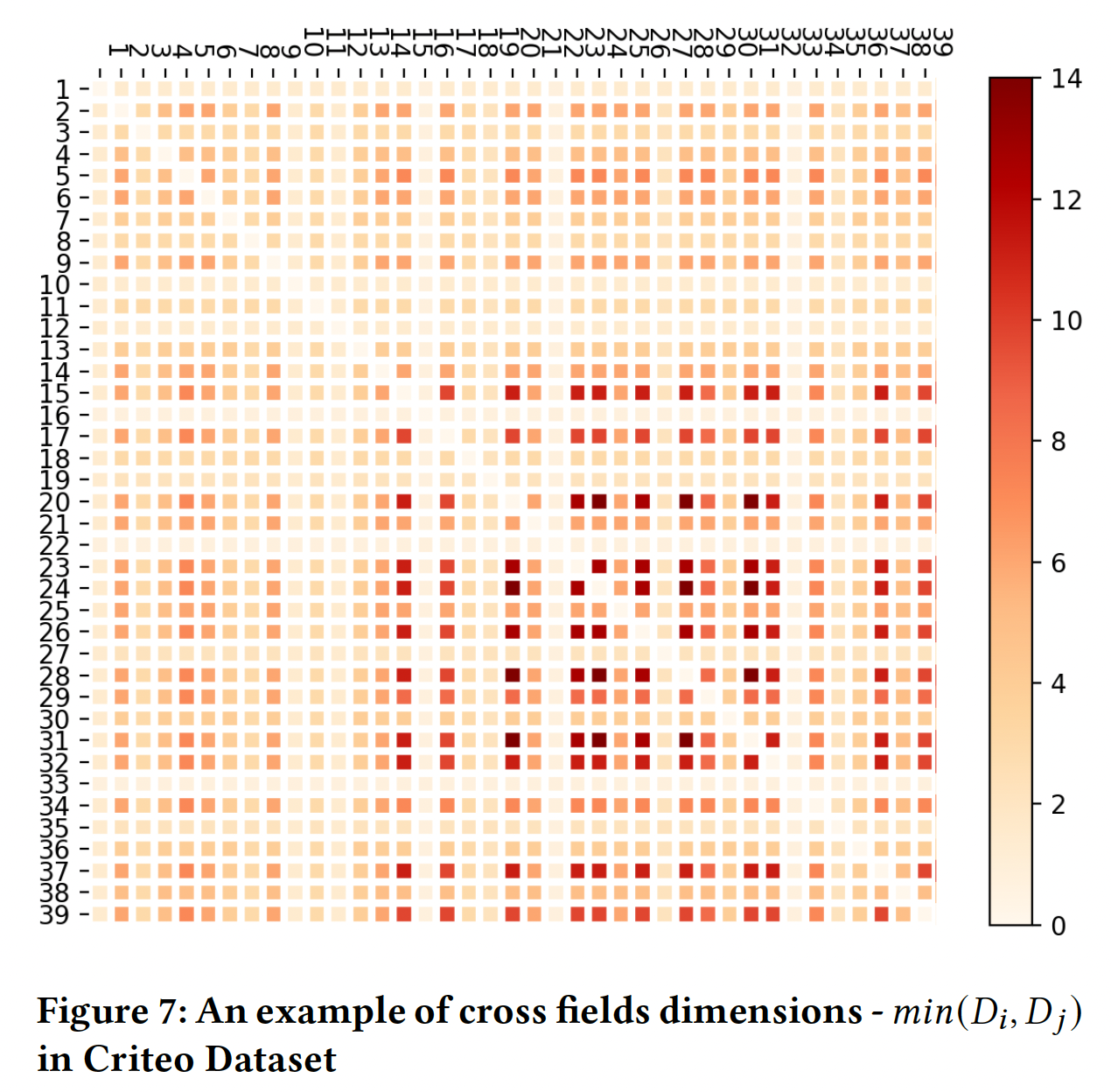
emebdding维度,而embedding维度是针对embedding table进行降维而得到的。这意味着在正式训练之前,先要完成一个训练从而得到embedding table。此外,PCA降维方法无法应用到大规模embedding table。Figure 6显示了Criteo数据集中field pair和label之间的互信息分数的热力图,它代表了field pair在预测中的强度。Figure 7显示了cross field dimension,这是两个field之间的较低维度,它表示每个field pair的参数和计算成本。显然,这两个热力图是高度相关的,这意味着优化后的FmFM模型在那些强度较高的field pair上分配了更多的参数和更多的计算,而在强度较低的field pair上分配了较少的参数和较少的计算。
线性项:线性部分为:
这需要为每个特征
embedding向量embedding向量。我们遵从
FwFM的方法,通过学习一个field-specific向量field在本文的其余部分,我们默认对
FwFM、FvFM和FmFM应用这种线性项优化。
29.4 实验
数据集:
Criteo、Avazu。我们遵循那些已有的工作,将每个数据集随机分成三部分,
80%用于训练、10%用于验证、10%用于测试。对于
Criteo数据集中的数值特征,我们采用Criteo竞赛冠军提出的对数变换来归一化数值特征:对于
Avazu数据集中的date/hour特征,我们将其转换为两个特征:day_of_week(0-6)、hours(0-23)。我们还删除了两组数据中那些低于阈值的低频特征,并用该
field的默认"unknown"特征来替换。Criteo数据集的阈值为8,Avazu数据集的阈值为5。
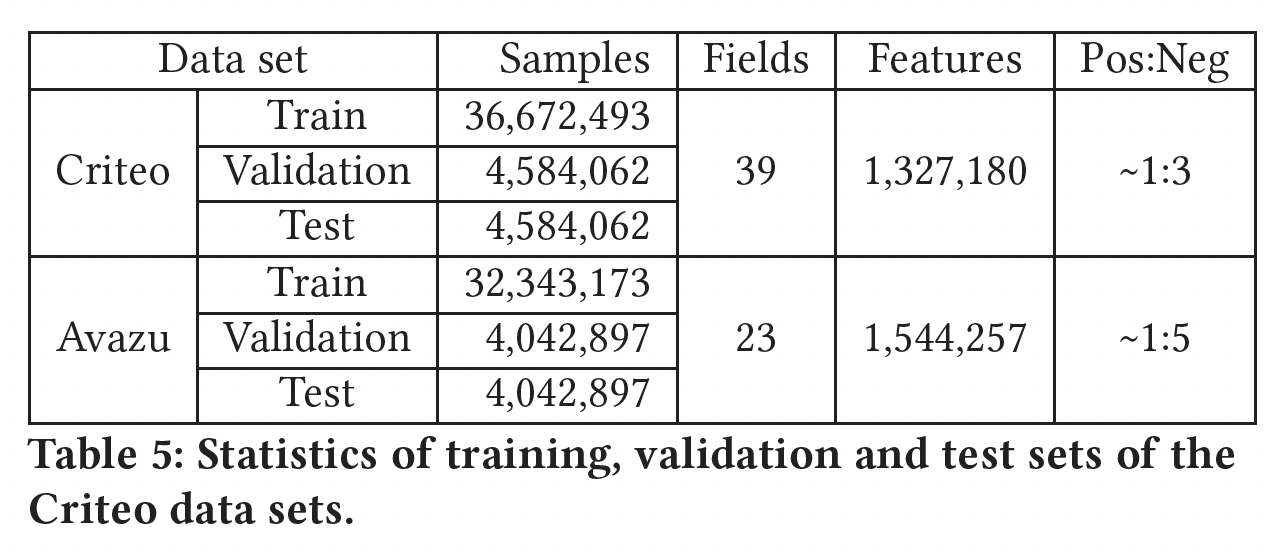
归一化后的数据集的统计数字如下表所示:
baseline方法:LR、FM、FwFM、FFM、FvFM、FmFM。我们遵循
PNN原始论文中LR和FM的实现,并遵循FwFM原始论文中FFM和FwFM的实现。评估指标:验证集的
AUC, logloss。模型配置:对于那些
SOTA模型,它们都是DNN模型,可能需要更多的超参数调优,我们从它们的原始论文中提取它们的性能(AUC和Log Loss),以保持它们的结果最佳。我们列出他们的结果只是为了参考。Deep & Cross网络是一个例外,因为他们的论文只列出了logloss而没有列出AUC。因此,我们实现了他们的模型,得到了类似的性能。对于所有模型中的正则化系数
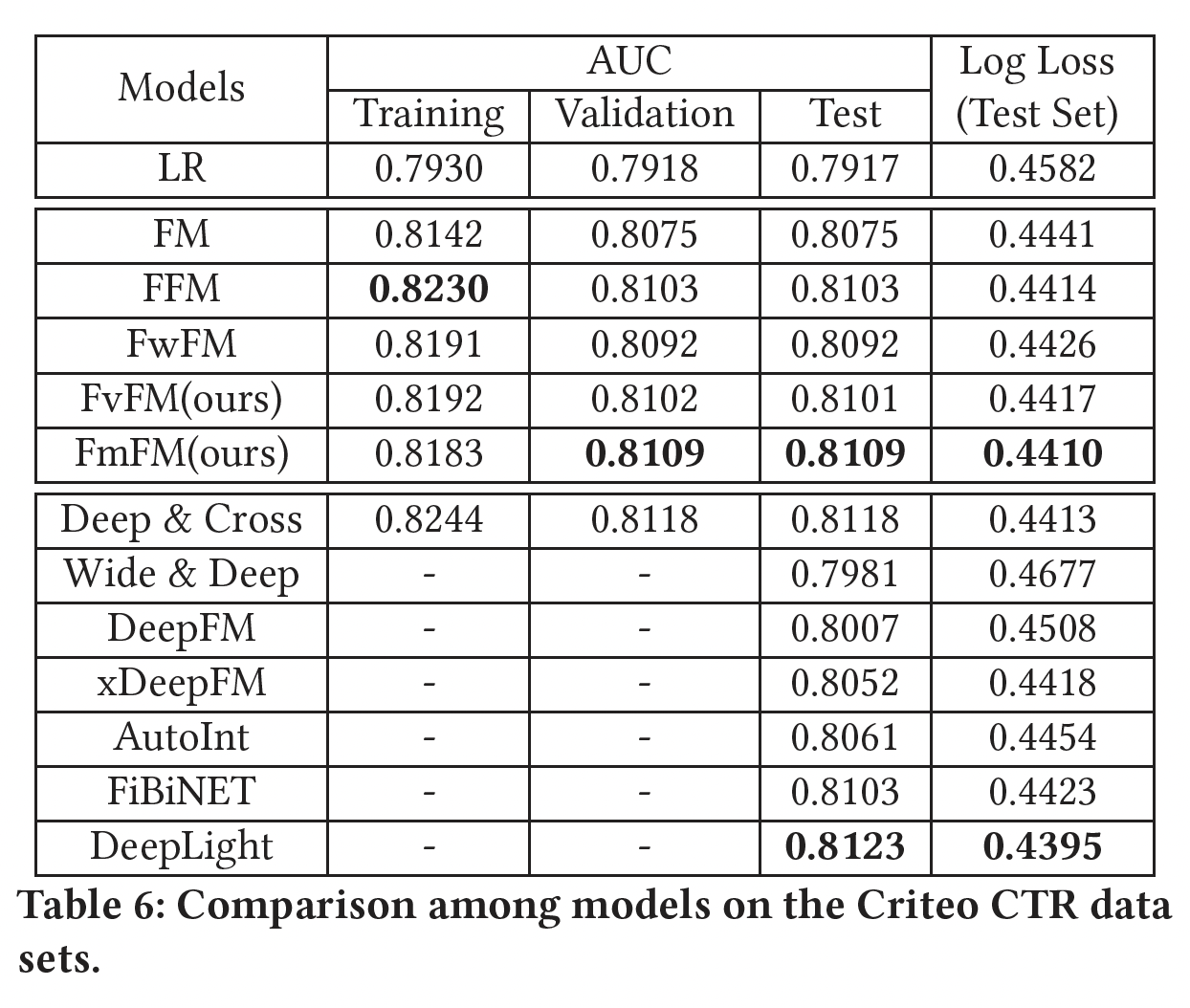
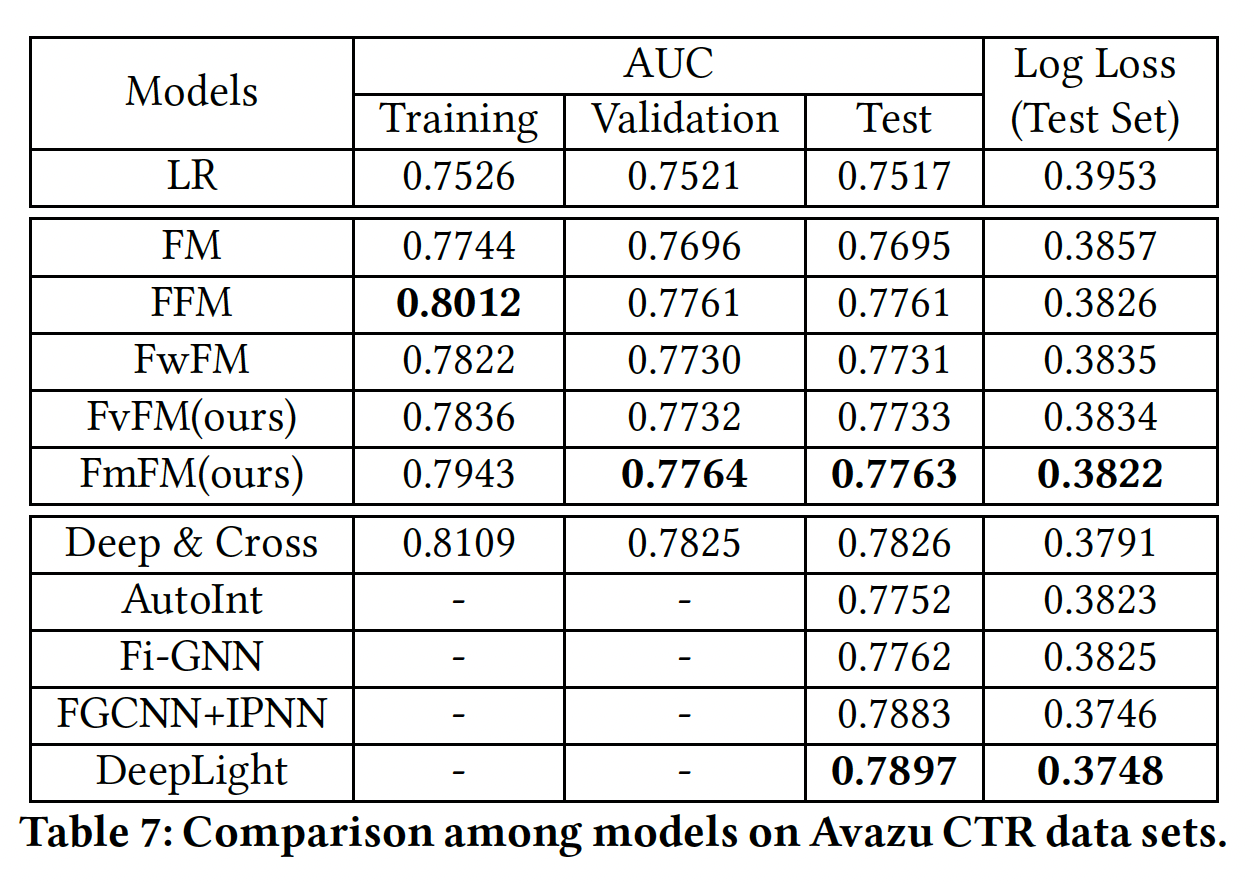
模型评估结果如下所示,其中对于
FmFM我们不采用任何优化手段。可以看到:在这两个数据集上,
FvFM和FmFM都能取得比LR、FM和FwFM更好的性能,这也是我们所预期的。令人惊讶的是,
FmFM在两个测试集上都能取得比FFM更好的性能。正如我们之前提到的,即使FFM是一个比FmFM大几十倍的模型,我们的FmFM模型仍然在所有浅层模型中得到最好的AUC。FmFM和FFM的性能相差无几,非常接近。此外,如果我们比较训练集和测试集之间的
AUC差异,我们发现factorization machine模型中最低的一个,这肯定了我们前面的假设:那些低频特征在交互矩阵的帮助下也被训练得不错,这种机制帮助FmFM避免过拟合。这里的数据和结论都不正确,
0.0074,最低的是LR模型。
Embedding Dimension Optimization:在这一部分,我们前面描述的方法,即我们有一个full size的模型,我们可以为每个field提取其embedding table,然后我们利用标准的PCA降维。在这里,我们做了几个实验,比较降维对模型性能的影响,并试图在模型大小、速度和性能之间找到一个平衡点。我们使用
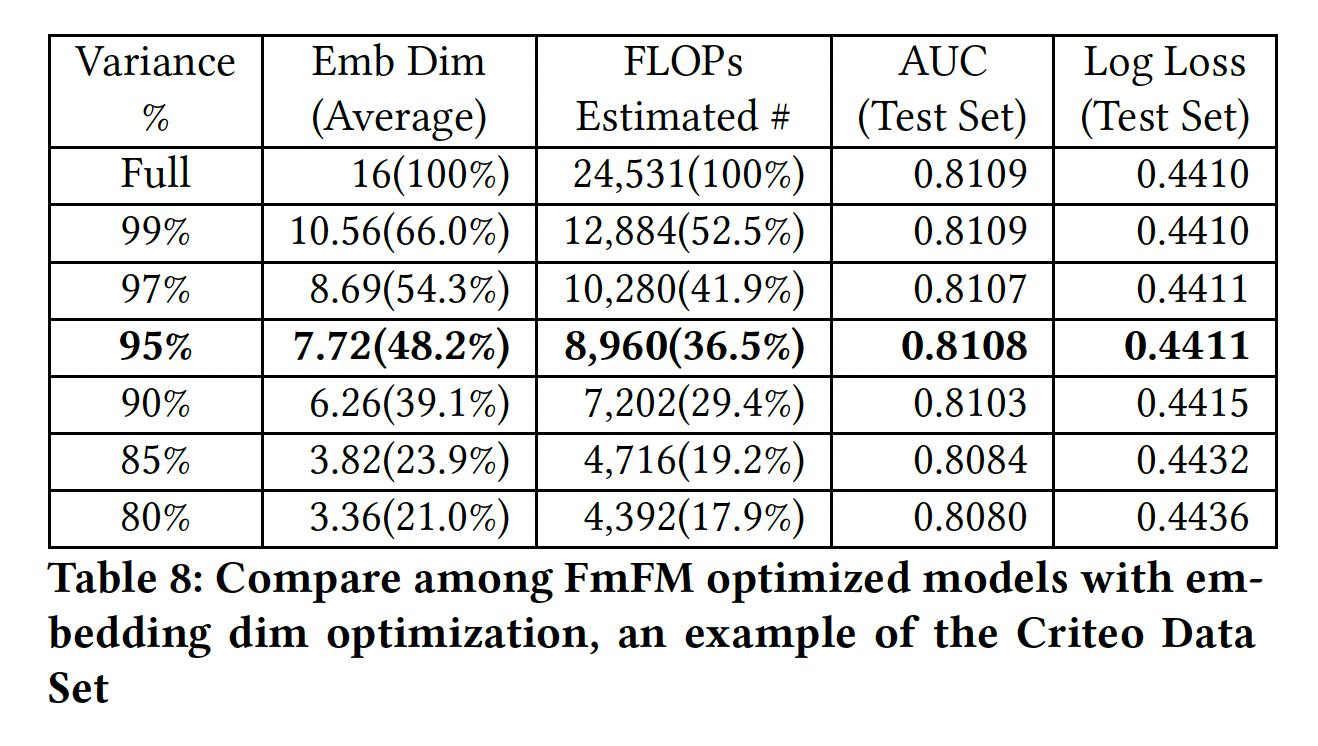
Criteo数据集,PCA降维中分别保持99%, 97%, 95%, 90%, 85%, 80%的方差,并估计平均embedding维度和FLOPS(具有缓存的中间向量)。在新的维度设置下,我们分别训练这些FmFM模型的第二遍,并观察测试集的AUC和Log Loss变化。结果如下表所示。可以看到:- 当我们保持较少的
PCA方差时,平均embedding维度明显减少。 - 当我们保持
95%的方差时,与full size模型相比,只有不到1/2的emebdding维度和1/3的计算成本,而模型的性能没有明显变化。因此,当我们优化FmFM的embedding维度时,95%的方差是一个很好的tradeoff。
- 当我们保持较少的
下图 显示了这些模型的性能(
AUC)和它们的计算复杂性(FLOPs)。与所有的baseline模型相比,作为一个浅层模型,优化后的FmFM模型得到了更高的AUC以及更低的FLOPs,除了Deep&Cross和DeepLight。然而FmFM的计算成本比这两个ensemble了DNN模块和浅层模块的复杂模型(即,Deep&Cross和DeepLight)要低得多,其FLOPs分别只有它们的1.76%和8.78%。较低的FLOPs使得FmFM在计算延迟受到严格限制时更受欢迎,这也是实时在线广告CTR预测和推荐系统中的常见情况。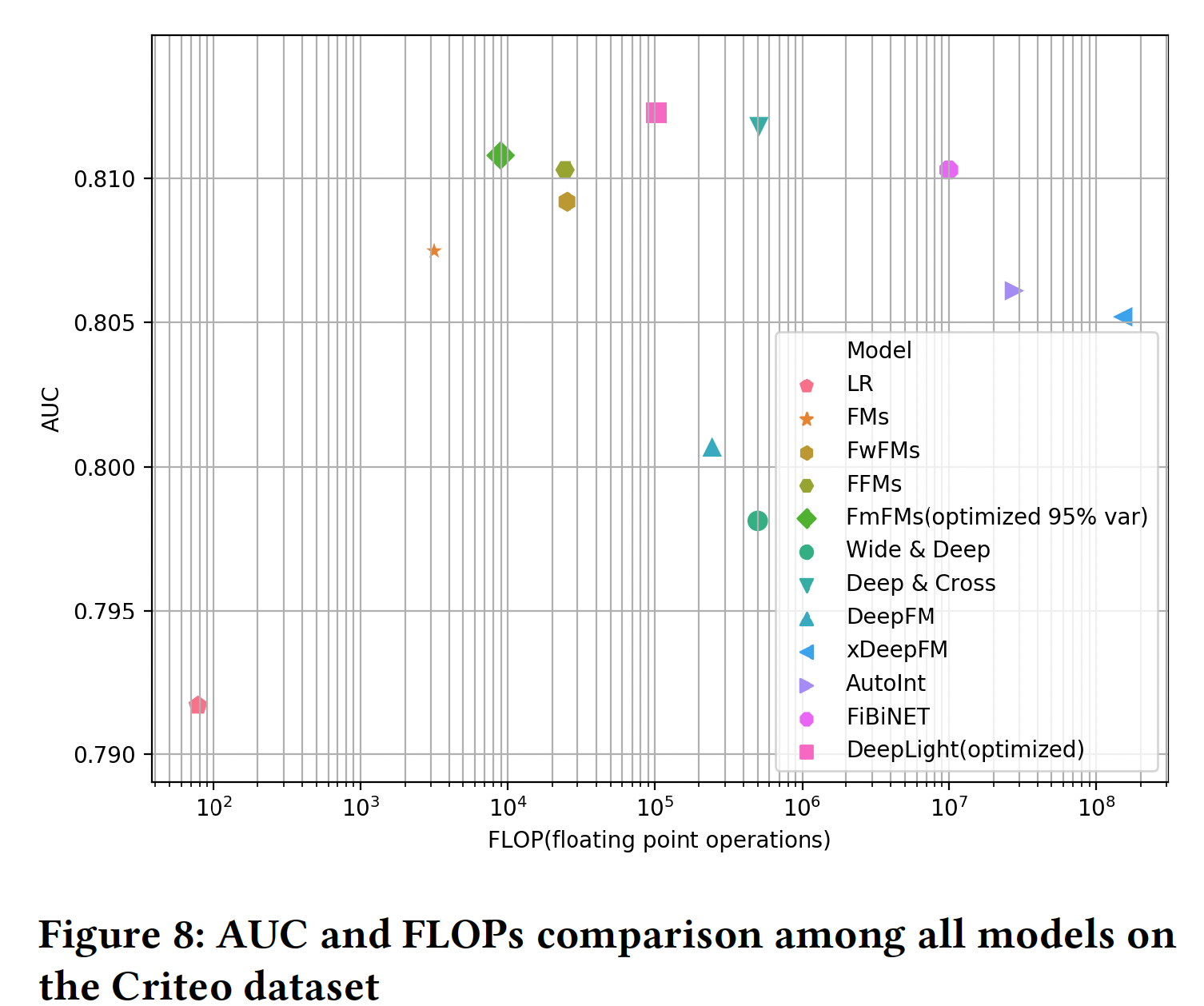
29.5 讨论
未来方向:
FmFM仍然是一个线性模型,我们可以将非线性层引入到field交互中,让模型成为非线性模型,这样就更加灵活。- 所有的
FM模型实际上都是二阶模型,它最多允许2个field交互。这种限制主要是因为点积的原因。在未来,我们可以引入三维张量,允许3个field的交互,或者甚至更高阶次。这项工作可能需要更多的模型优化,因为有太多的三阶交互。 - 我们可以结合
DNN模型,如Wide & Deep、DeepFM、DeepLight,并尝试将FmFM作为DNN模型的一个构建模块,以进一步提高其性能。
三十、FiBiNET[2019]
近年来,许多基于深度学习的
CTR模型被提出并取得了成功,如Factorization-Machine Supported Neural Network: FNN、Wide&Deep model: WDL、Attentional Factorization Machine: AFM、DeepFM、XDeepFM等等。论文
《FiBiNET: Combining Feature Importance and Bilinear Feature Interaction for Click-Through Rate Prediction》提出了一个叫做FiBiNET的新模型,它是Feature Importance and Bilinear feature Interaction NETwork的缩写,用于动态地学习特征重要性和细粒度的特征交互。- 众所周知,不同的特征对目标任务有不同的重要性。例如,当我们预测一个人的收入时,职业这个特征比爱好这个特征更重要。考虑到这一点,论文引入了
Squeeze-and-Excitation network: SENET来动态地学习特征的权重。 - 此外,特征交互是
CTR预测领域的一个关键挑战,许多相关工作以简单的方式计算特征交互,如Hadamard积和内积。论文提出了一种新的细粒度的方法采用双线性函数来计算特征交互。
论文主要贡献:
- 受
SENET在计算机视觉领域的成功启发,论文使用SENET机制来动态地学习特征的权重。 - 论文引入了三种类型的双线性交互层
Bilinear-Interaction layer,以一种精细的方式学习特征交互。而之前的工作用Hadamard积或内积来计算特征交互。 - 结合
SENET机制和双线性特征交互,论文的浅层模型在Criteo和Avazu数据集上的浅层模型之间(如FFM)实现了SOTA。 - 为了进一步提高性能,论文将经典的深度神经网络组件与浅层模型相结合,构成一个深度模型。深度
FiBiNET在Criteo和Avazu数据集上的表现一直优于其他SOTA的深度模型。
- 众所周知,不同的特征对目标任务有不同的重要性。例如,当我们预测一个人的收入时,职业这个特征比爱好这个特征更重要。考虑到这一点,论文引入了
相关工作:
FM及其变体:factorization machine: FM和field-aware factorization machine: FFM是两个最成功的CTR模型。FM使用因子化的参数建模所有的特征交互。它的时间复杂度和空间复杂度都很低,在大型稀疏数据上表现很好。FFM引入了field-aware的潜在向量,并赢得了由Criteo和Avazu主办的两个比赛。然而,FFM的空间复杂度太高,不容易在互联网公司中使用。
Deep Learning based CTR Models:近年来,许多基于深度学习的CTR模型被提出。大多数基于神经网络的CTR模型的关键因素是:如何有效地建模特征交互。Factorization-Machine Supported Neural Network: FNN是一个前馈神经网络,使用FM来预训练embedding layer。然而,FNN只能捕获高阶的特征交互。Wide & Deep model: WDL联合训练wide linear model和deep neural network,从而为推荐系统来结合memorization和generalization的好处。然而,对于WDL的wide部分的输入,仍然需要专业的特征工程,这意味着cross-product transformation也需要手工设计。- 为了减轻特征工程中的人工努力,
DeepFM用FM取代了WDL的wide部分,并在FM和deep组件之间共享feature embedding。DeepFM被认为是CTR预估领域中的SOTA模型之一。 Deep & Cross Network: DCN以一种显式的方式有效地捕捉了有界阶次的特征交互。eXtreme Deep Factorization Machine: xDeepFM也通过提出一个新颖的Compressed Interaction Network : CIN组件来显式地建模低阶特征交互和高阶特征交互。- 正如
《Attentional factorization machines: Learning the weight of feature interactions via attention networks》所提到的,FM的一个不足是它对所有特征交互采用相同的权重,然而并不是所有的特征交互都同样有用和具有预测性。因此,他们提出了Attentional Factorization Machine: AFM模型,该模型使用注意力网络来学习特征交互的权重。 Deep Interest Network: DIN用兴趣分布interest distribution表示用户的多样化兴趣,并设计了一个类似注意力的网络结构从而根据候选广告局部地激活相关的兴趣。
SENET Module:《Squeeze-and-excitation networks》提出了Squeeze-and-Excitation Network: SENET,通过显式地建模卷积特征通道之间的相互依赖关系,从而提高网络的表达能力。SENET被证明在图像分类任务中是成功的,并在ILSVRC 2017分类任务中赢得了第一名。除了图像分类,
SENET还有其他的应用。《Recalibrating Fully Convolutional Networks with Spatial and Channel’Squeeze & Excitation’Blocks》介绍了三种用于语义分割任务的SE模块的变体。- 对常见的胸部疾病进行分类,以及对胸部
X光片上的可疑病变区域进行定位(《Weakly Supervised Deep Learning for Thoracic Disease Classifcation and Localization on Chest X-rays》)是另一个应用领域。 《Global-andlocal attention networks for visual recognition》用global-and-local attention: GALA模块扩展了SENET模块,在ILSVRC上获得SOTA的准确性。
30.1 模型
我们的目标是以一种细粒度的方式动态地学习特征的重要性和特征交互。为此,我们提出了用于
CTR预估任务的Feature Importance and Bilinear feature Interaction NETwork: FiBiNET。我们的模型结构如下图所示。为了清晰起见,我们省略了
logistic regression的部分,这部分可以很容易地纳入。我们的模型由以下部分组成:sparse input layer, embedding layer, SENET layer, Bilinear-Interaction layer, combination layer, multiple hidden layers, output layer。sparse input layer和embedding layer与DeepFM相同,它对输入特征采用稀疏表示并将原始特征嵌入到稠密向量中。SENET layer可以将embedding layer转换为SENET-Like embedding feature,这有助于提高特征的discriminability。由于原始
Embeddings和SENET-Like Embeddings都作为后续模块的输入,因此SENET-Like Embeddings仅仅是作为原始Embeddings的补充(类似于残差机制),而不是作为原始Embeddings重要性的解释。如果仅仅将
SENET-Like Embeddings作为后续模块的输入,这时候才具有可解释性。接下来的
Bilinear-Interaction layer分别对原始embedding和SENET-Like embedding的二阶特征交互进行建模。combination layer拼接了Bilinear-Interaction layer的输出。最后,我们将
combination layer的输出馈入一个深度神经网络从而得到预测分数。
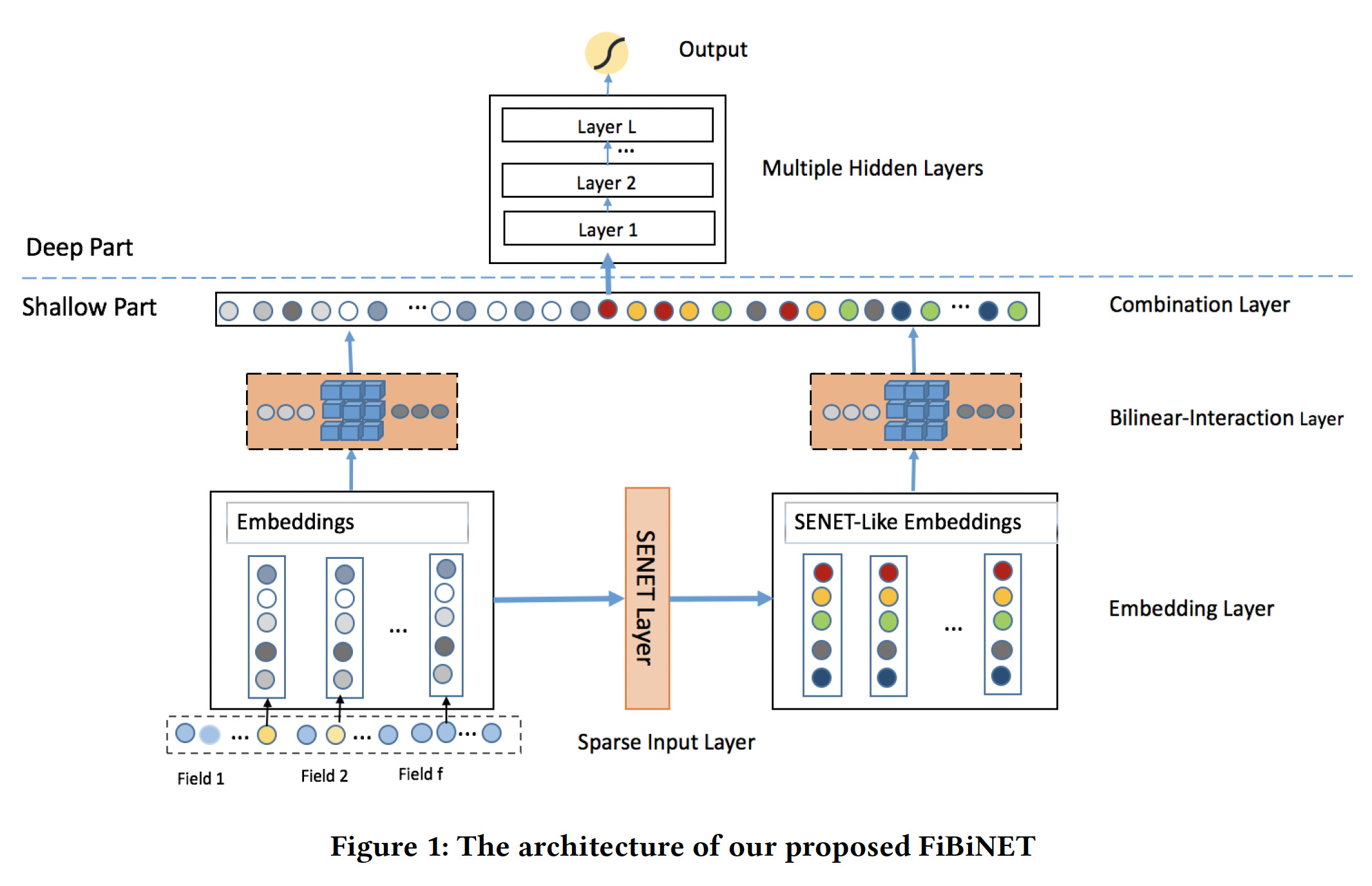
Sparse Input and Embedding layer:sparse input layer对原始输入特征采用了sparse representation,embedding layer将sparse feature嵌入到一个低维稠密的实值向量中。embedding layer的输出是由field embedding向量所拼接而来:field数量,field embedding维度。SENET Layer:我们都知道,不同的特征对目标任务有不同的重要性。例如,当我们预测一个人的收入时,职业这个特征比爱好这个特征更重要。受到SENET在计算机视觉领域的成功启发,我们引入了SENET机制,让模型更加关注特征的重要性。对于特定的CTR预估任务,我们可以通过SENET机制动态地增加重要特征的权重、减少不重要特征的权重。以
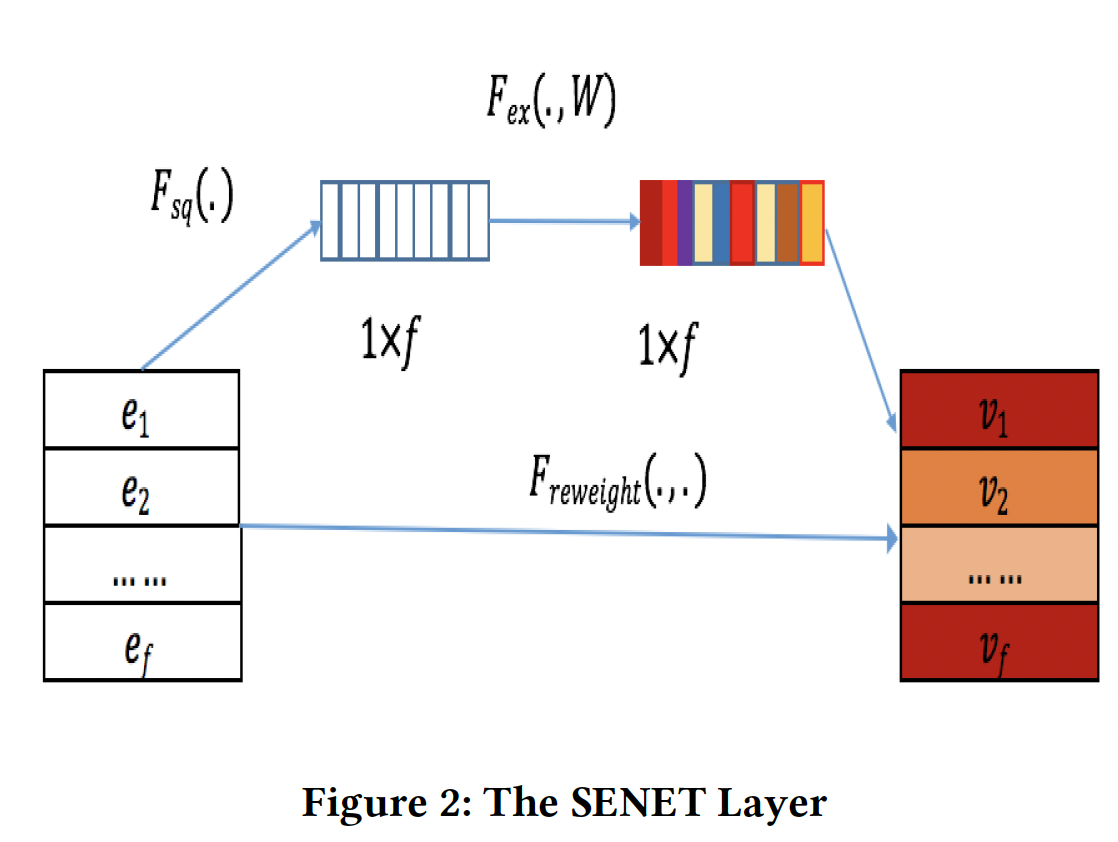
feature embedding作为输入,SENET针对field embedding产生权重向量embeddingembedding(即,SENET-Like embedding):其中:
field的权重;field的SENET-Like embedding。如下图所示,
SENET由三个步骤组成:squeeze step、excitation step、re-weight step。squeeze:这一步是用来计算每个field embedding的summary statistics的。具体而言,我们使用一些池化方法(如max/mean)从而将原始的embeddingsum池化、或者最大池化。原始
SENET论文中的squeeze函数是最大池化。然而,我们的实验结果表明,均值池化的性能比最大值池化的性能更好。excitation:这一步可以用来基于统计向量field embedding的权重。我们使用两个全连接层来学习权重:- 第一个全连接层是一个降维层,参数为
- 第一个全连接层是一个升维层,参数为
正式地,
field embedding的权重的计算公式为:其中:
这一步是降维,从而最多保留最重要的
- 第一个全连接层是一个降维层,参数为
re-weight:SENET的最后一步是reweight,在原始论文中被称为re-scale。SENET-Like embedding
Bilinear-Interaction Layer:Interaction layer用于计算二阶的特征交互。特征交互的经典方法是内积和Hadamard积,其形式分别为:Hadamard积过于简单,不能有效地建模稀疏数据集中的特征交互。因此,我们提出了一种更加细粒度的方法来结合内积和Hadamard积,如下图(c)所示。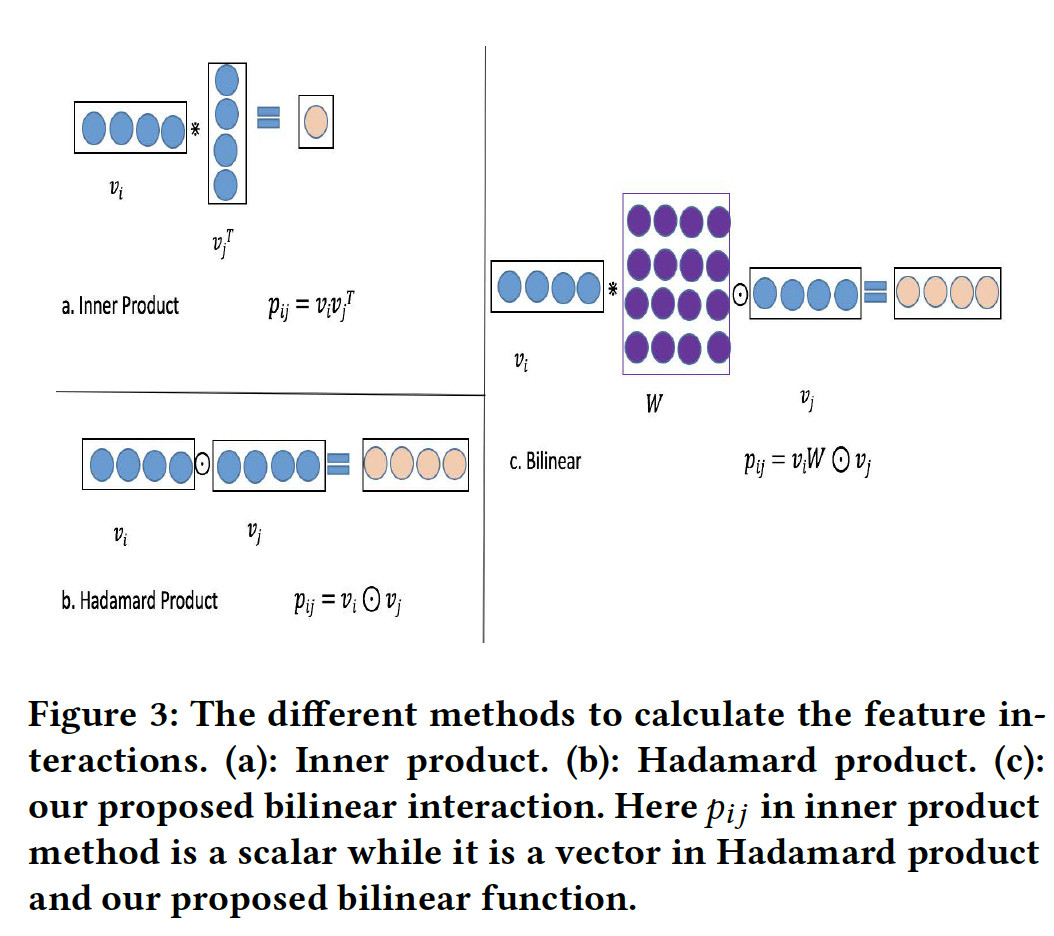
具体来说,我们在
Interaction layer提出了三种类型的双线性函数,并称这一层为Bilinear-Interaction layer。以第field embeddingfield embeddingField-All Type:其中:
field interaction pair之间共享。Field-Each Type:其中:
field都有一个。Field-Interactoin Type:其中:
field interaction pair都有一个。
如
Figure 1所示,我们有两种embedding:原始embedding、SENET-like embedding。对于每一种embedding,我们可以选择采用bilinear函数或Hadamard积。最终,
Bilinear-Interaction layer可以从原始embeddigninteraction vectorSENET-like embeddinginteraction vectorCombination Layer:combination layer将interaction vector如果我们将向量
sigmoid函数来输出预测值,我们就有了一个浅层的CTR模型。为了进一步提高性能,我们将浅层组件和
DNN组件组合成一个统一的模型,形成深度网络结构。这个统一的模型在本文中称为深度模型。而更好的办法是:拼接
Deep Network:深度网络由多个全连接层组成,隐式地捕获了高阶的特征交互。Deep Network的输入是什么?论文没有说明。但是根据Figure 1,应该是Output Layer:我们模型的输出为:其中:
sigmoid函数,deep part的输出,wide part的输出。目标函数为交叉熵损失:
其中:
ground-truth。与
FM, FNN的联系:- 假设我们去掉
SENET layer和Bilinear-Interaction layer,不难发现我们的模型将退化为FNN。 - 当我们进一步去掉
DNN部分,同时使用常数的sum,那么浅层FiBiNET就退化为传统的FM模型。
- 假设我们去掉
30.2 实验
数据集:
Criteo:包含有4500万个样本的点击日志。在Criteo数据集中有26个匿名的categorical feature field和13个continuous feature field。我们将数据集随机分成两部分:90%用于训练,其余用于测试。Avazu:包含有4000万个样本的点击日志。对于每个点击数据,有24个feature field。我们将其随机分成两部分:80%用于训练,而其余部分用于测试。
评估指标:
AUC, LogLoss。baseline方法:- 浅层
baseline模型:LR、FM、FFM、AFM。 - 深层
baseline模型:FNN、DCN、DeepFM、XDeepFM。
- 浅层
实现细节:
- 所有模型用
TensorFlow来实现。 embedding layer的维度:Criteo数据集设为10、Avazu数据集设为50。- 使用
Adam优化器,Criteo数据集的batch size = 1000,Avazu数据集的batch size = 500,学习率设为0.0001。 - 对于所有的深度模型,层深度都是
3、激活函数都是RELU、dropout rate都是0.5。Criteo数据集的隐层维度为400、Avazu数据集的隐层维度为2000。 - 对于
SENET部分,两个全连接层中的激活函数是RELU函数,缩减率设置为 - 硬件配置:
2个Tesla K40 GPU。
- 所有模型用
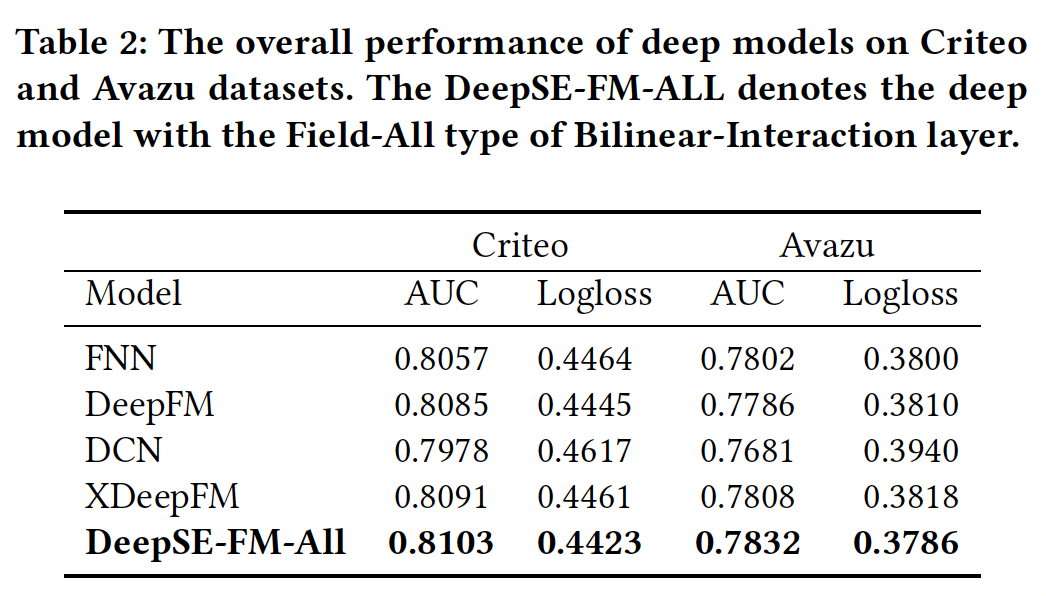
Table 1和Table 2中分别总结了浅层模型和深层模型在Criteo测试集和Avazu测试集上的总体表现。这里
Interaction layer使用Field-All双线性函数,如表格的标题所示。浅层模型:我们的浅层
SE-FM-All模型一直优于其他模型,如FM、FFM、AFM等。- 一方面,结果表明,将
SENET机制与稀疏特征上的bilinear interaction结合起来,对于许多现实世界的数据集来说是一种有效的方法。 - 另一方面,对于经典的浅层模型来说,
SOTA的模型是FFM,但是它受到大内存的限制,不能轻易用于互联网公司。我们的浅层模型的参数较少,但仍然比FFM表现更好。因此,它可以被视为FFM的一个替代方案。

- 一方面,结果表明,将
深层模型:
将浅层部分和
DNN结合成一个统一的模型,浅层模型可以获得进一步的性能提升。我们可以从实验结果中推断,隐式的高阶特征交互有助于浅层模型获得更多的表达能力。在所有的比较方法中,我们提出的深度
FiBiNET取得了最好的性能。在Criteo数据集上和Avazu数据集上,我们的深度模型以0.222%和0.59%的AUC(0.494%和0.6%的logloss)优于DeepFM。结果表明,将
SENET机制与DNN中的Bilinear-Interaction相结合进行预测是有效的。一方面,
SENET固有地引入了以输入为条件的动态性,有助于提高特征的discriminability;另一方面,与内积或Hadamard积等其他方法相比,双线性函数是一种有效的方法来建模特征交互。
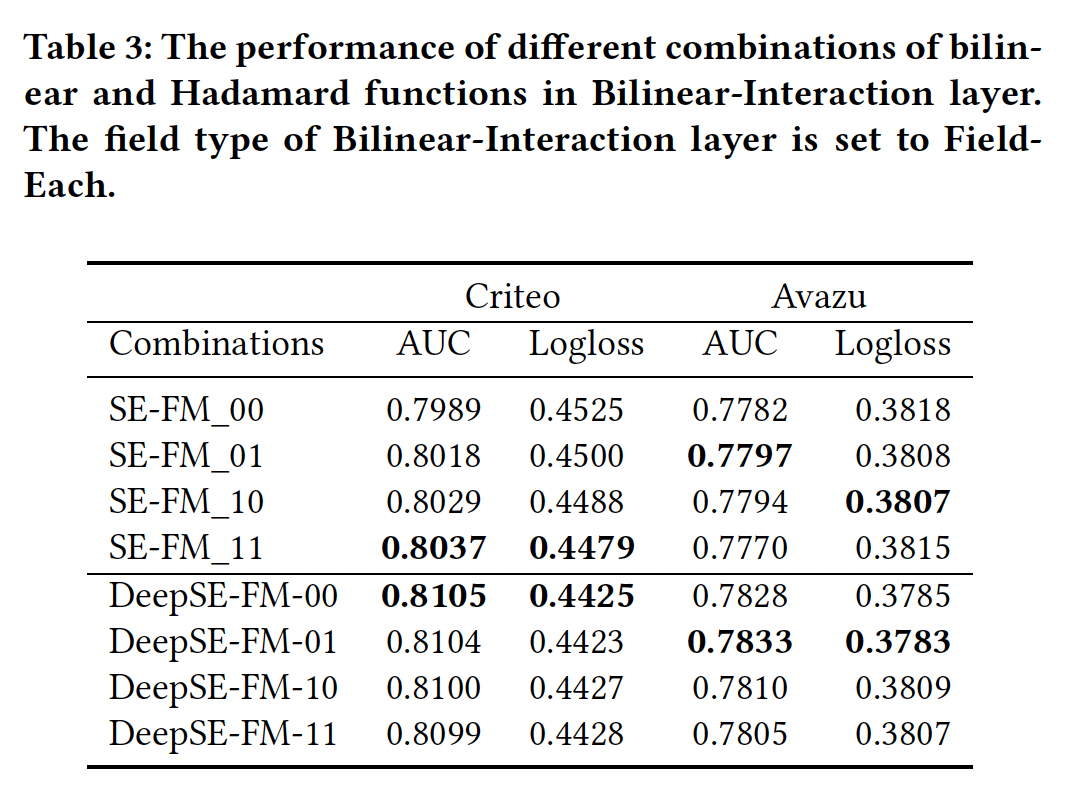
不同的特征交互方式:我们将讨论在
Bilinear-Interaction layer中,双线性函数和Hadamard积不同类型的组合的影响。为方便起见,我们用0和1来表示在Bilinear-Interaction layer使用哪种函数:1表示使用双线性函数,而0表示使用Hadamard积。Interaction layer使用Field-Each双线性函数。很奇怪Table3和Table1/2使用了不同的双线性函数。我们有两个
embedding,所以使用两个数字。第一个数字表示用于原始embedding的特征交互方法,第二个数字表示用于SENET-like embedding的特征交互方法。例如:10表示双线性函数被用作原始embedding的特征交互方法、Hadamard函数被用作SENET-like embedding的特征交互方法。实验结果如下表所示。可以看到,在
Criteo数据集上:11的组合在浅层模型中表现最好,但是在深度模型中表现最差。- 深层模型中的首选组合应该是
01。这种组合意味着双线性函数只适用于SENET-Like embedding layer。
不同数据集的结论不同,因此这个双线性函数的组合方式需要根据不同的数据进行调优。
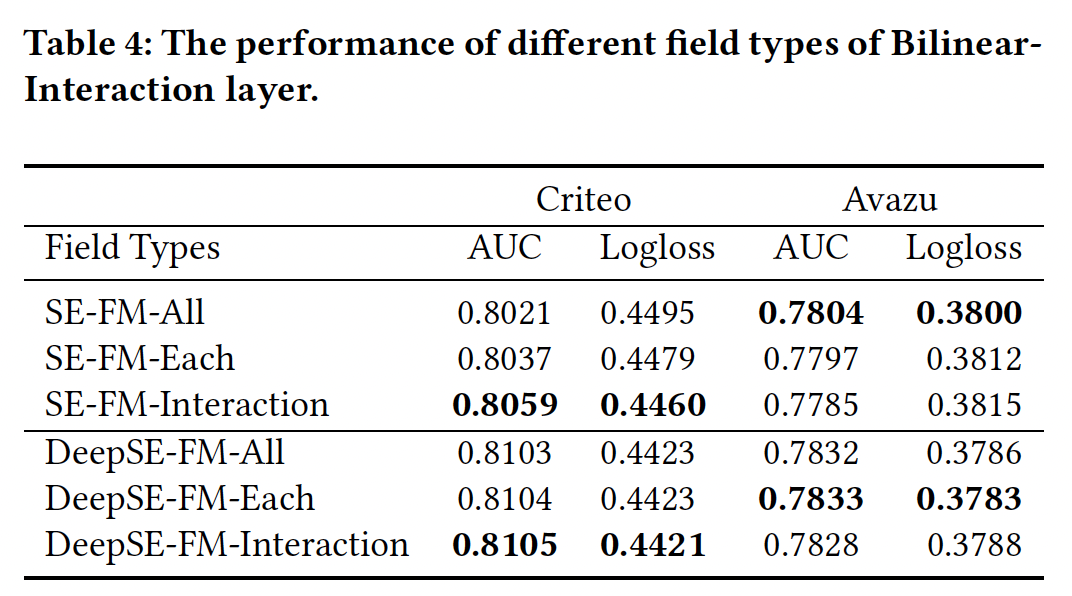
Bilinear-Interaction的Field Types:这里我们研究了Bilinear-Interaction layer的不同field类型(Field-All, Field-Each, Field-Interaction)的影响。对于深层模型,Bilinear-Interaction layer的组合被设置为01;对于浅层模型,Bilinear-Interaction layer的组合被设置为11。- 对于浅层模型,与
Field-All类型相比(见Table 1),Field-Interaction类型可以在Criteo数据集上获得0.382%(相对提升0.476%)的AUC改进。 - 对于深层模型,与
Field-All类型相比(见Table 2),Criteo数据集的Field-Interaction类型、以及Avazu数据集的Field-Each类型可以分别获得一些改进。 - 不同类型的
Bilinear-Interaction layer的性能取决于数据集。
- 对于浅层模型,与
超参数:
Embedding部分:我们将embedding size从10改变到50。可以看到:随着维度从
10扩大到50,在Avazu数据集上我们的模型可以获得大幅改善。当我们增加
Criteo数据集的embedding size时,性能就会下降。扩大
embedding size意味着增加embedding layer和DNN部分的参数数量。我们猜测可能是Criteo数据集的特征比Avazu数据集多得多,导致了优化的困难。有两个原因:过拟合、以及优化困难。因为这两个数据集的样本量都在
4000万以上,因此二者的过拟合程度应该相差无几。
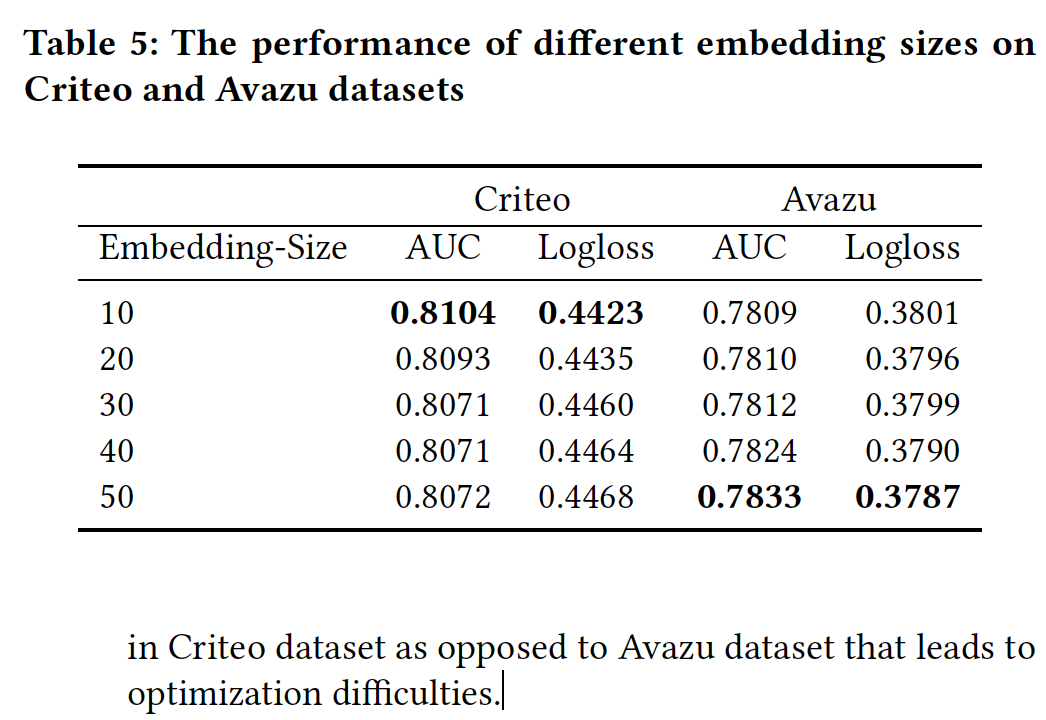
SENET部分:squeeze函数:下表总结了不同squeeze函数的性能,我们发现GlobalMeanPooling在Criteo数据集和Avazu数据集上优于GlobalMaxPooling或GlobalSumPooling。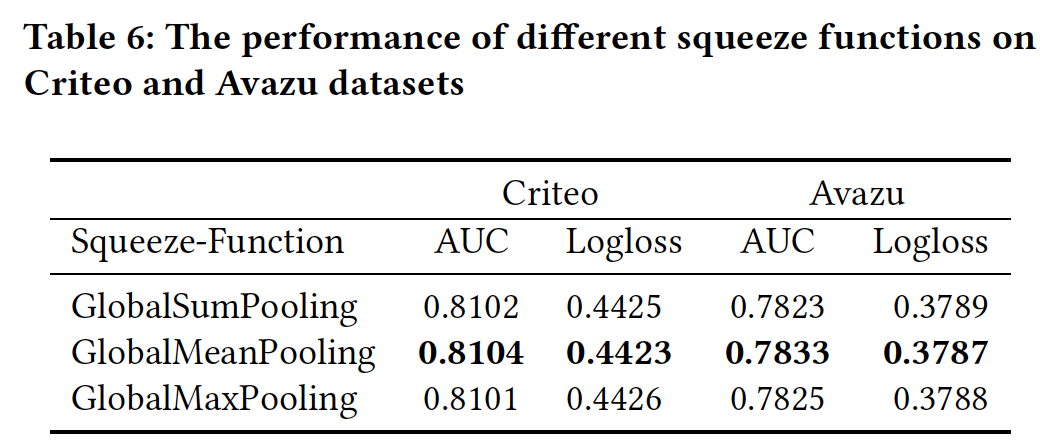
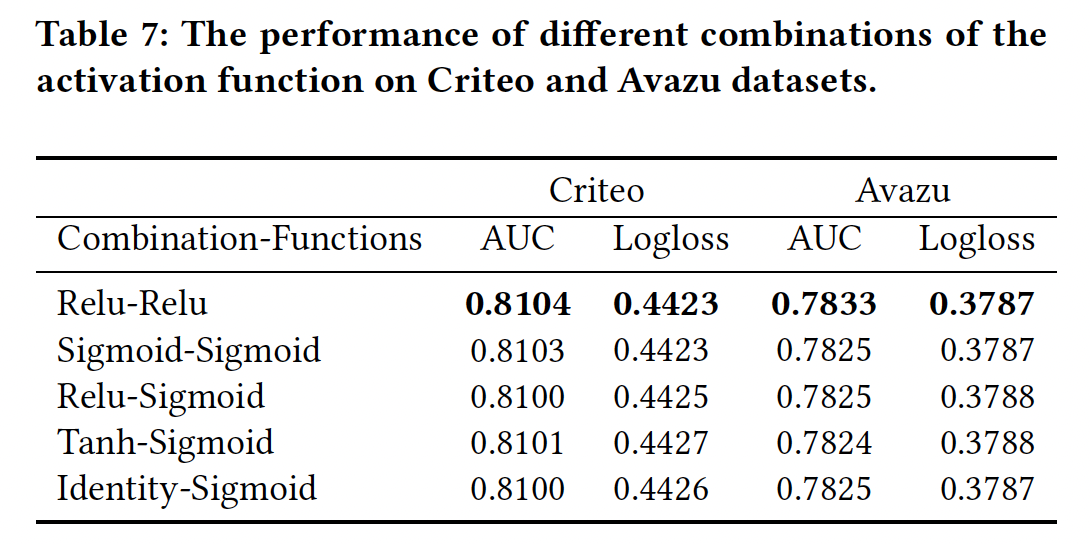
激活函数:我们改变了激活函数的组合,如下表所示。
- 在这些激活函数的组合中,
Relu-Relu略胜于其他组合。 - 与原始
SENET的设置不同,FiBiNET的SENET组件中的第二个激活函数是Relu函数,其性能比sigmoid函数更好。
- 在这些激活函数的组合中,
此外,我们还改变了压缩率(
DNN部分:网络层数:增加层数可以增加模型的复杂性。我们可以从下图中观察到,增加层数在开始时可以提高模型性能。然而,如果层数不断增加,性能就会下降。这是因为过于复杂的模型很容易过拟合。对于
Avazu数据集和Criteo数据集,将隐藏层的数量设置为3是一个不错的选择。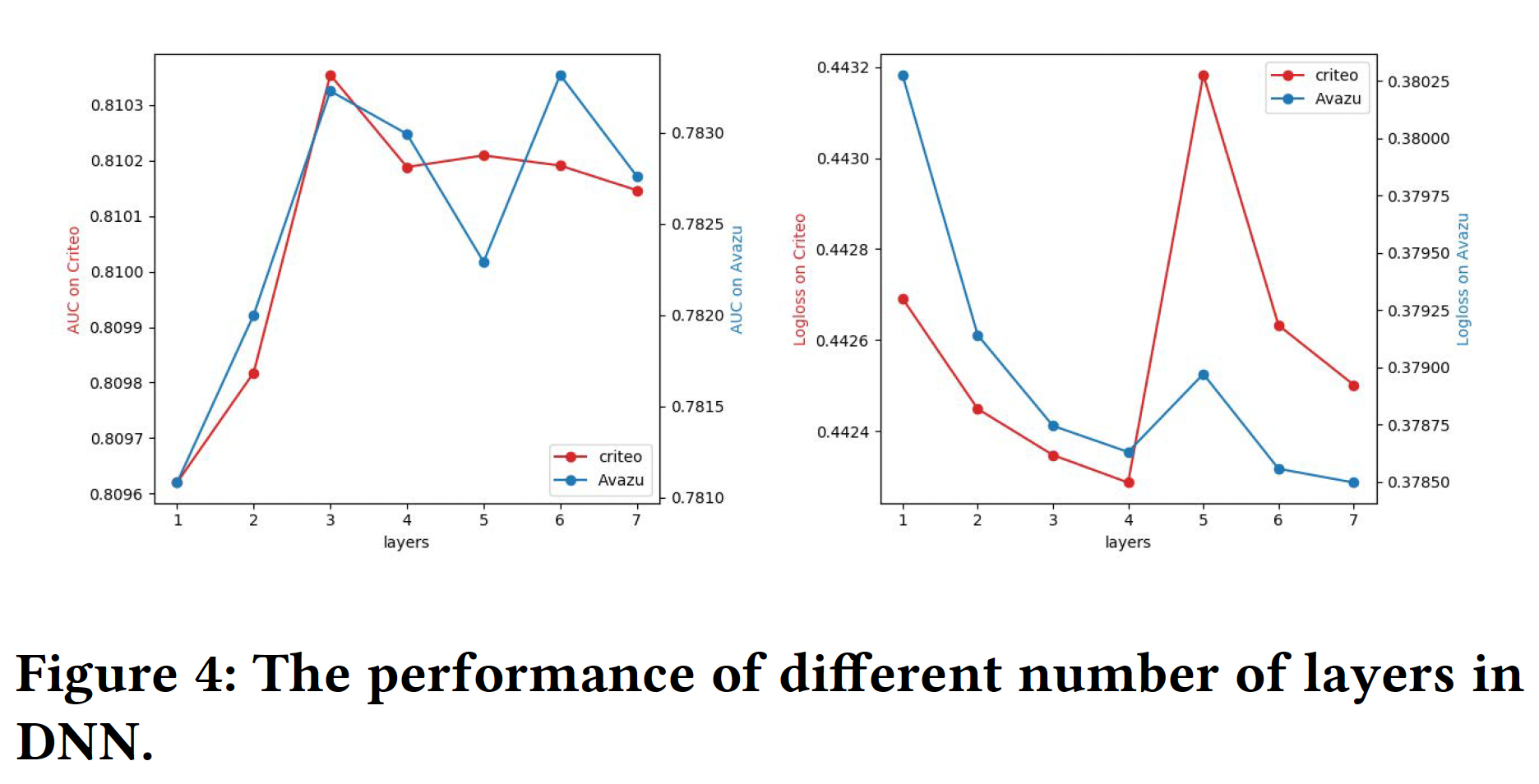
隐层神经元数量:同样,增加每层的神经元数量也会引入复杂性。在下图中,我们发现对于
Criteo数据集,每层设置400个神经元比较好;对于Avazu数据集,每层设置2000个神经元比较好。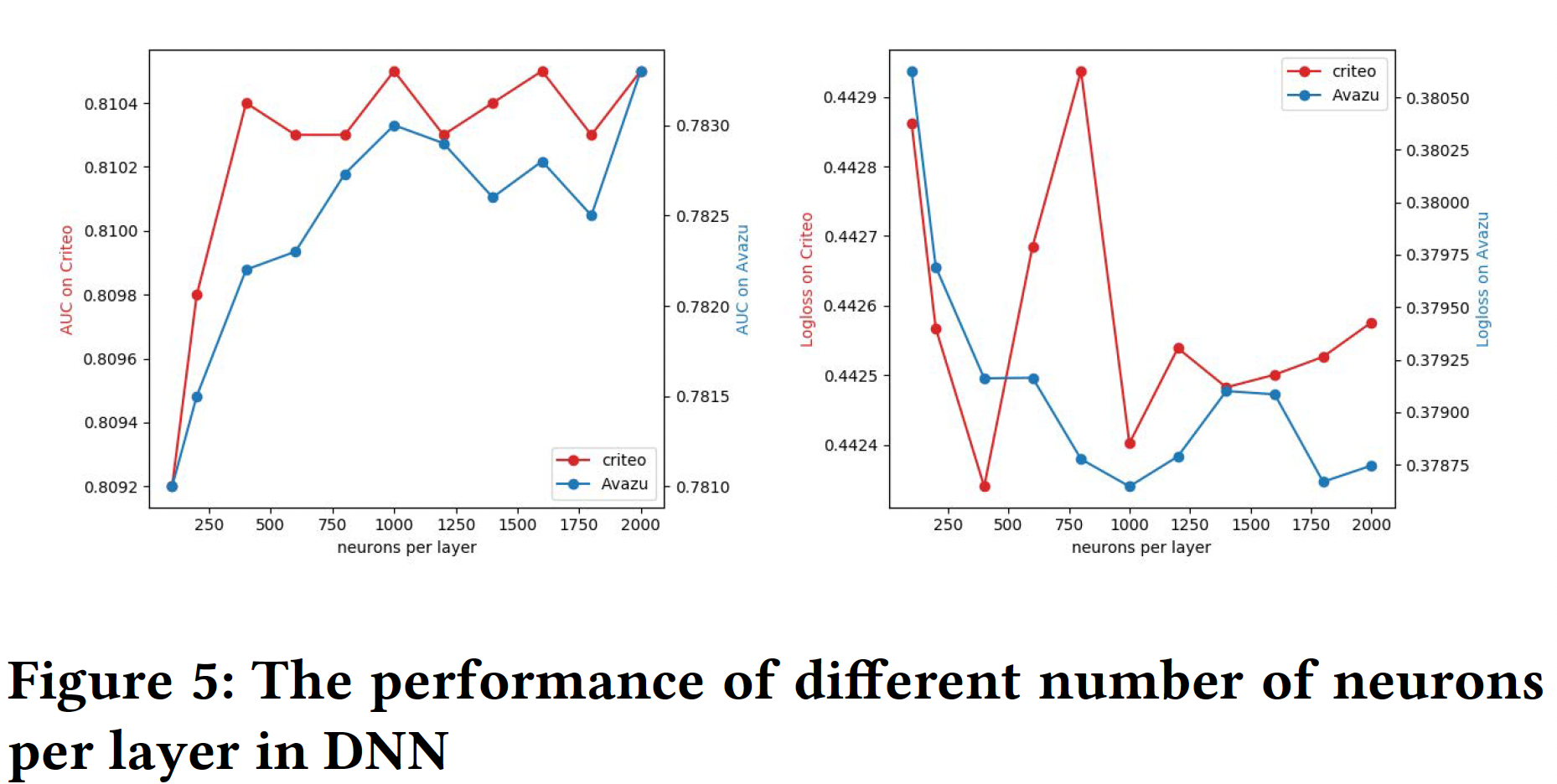
消融研究:目前为止,我们还没有分离出
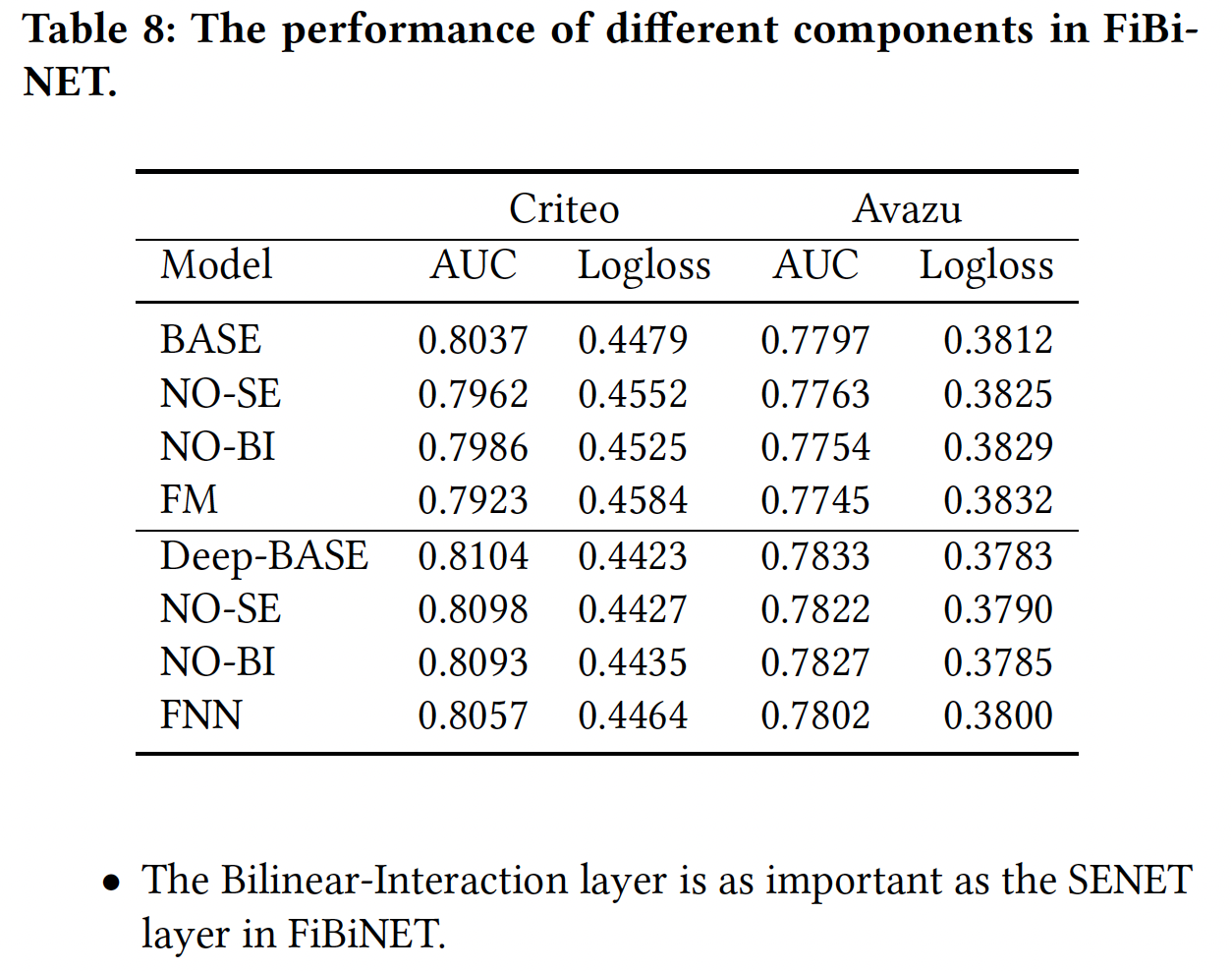
FiBiNET的每个组件的具体贡献。在本节中,我们对FiBiNET进行了消融实验,以便更好地了解它们的相对重要性。我们将DeepSE-FM-Interaction设定为基础模型,并以下列方式进行:No BI:从FiBiNET中删除Bilinear-Interaction layer。No SE:从FiBiNET中删除SENET layer。
如果同时我们删除
SENET layer和Bilinear-Interaction layer,我们的浅层FiBiNET和深层FiBiNET将降级为FM和FNN。实验结果如下表所示。Bilinear-Interaction layer和SENET layer对于FiBiNET的性能都是必要的。我们可以看到,当我们删除任何组件时,性能将明显下降。- 在
FiBiNET中,Bilinear-Interaction layer与SENET layer一样重要。
三十一、AutoFIS[2020]
显式的特征交互可以显著提高
CTR模型的性能。早期的协同过滤推荐算法,如矩阵分解matrix factorization: MF和分解机factorization machine: FM,用一个bi-linear learning model抽取二阶信息。然而,并非所有的交互都有利于性能。一些基于树的方法已经被提出来,以自动找到有用的特征交叉。
gradient boosting decision tree: GBDT试图找到损失函数梯度较高的交互。AutoCross在一个树状结构的空间中搜索有效的交互。但是树型模型在multi-field categorical data的推荐系统中只能探索所有可能的特征交互中的一小部分,所以它们的探索exploration能力受到限制。同时,深度神经网络
DNN模型被提出。它们的表达能力更强,而且根据通用近似特性universal approximation property,它们可以探索大多数的特征交互。然而,使用基于梯度的优化,并不能保证DNN自然地收敛到任何预期的函数。简单的DNN模型可能无法找到合适的特征交互。因此,人们提出了各种复杂的架构,如深度兴趣网络Deep Interest Network: DIN、深度分解机Deep Factorization Machine: DeepFM、Product-based Neural Network: PNN、以及Wide & Deep。因子分解模型Factorization Model(如FM, DeepFM, PNN, Attention Factorization Machine: AFM, Neural Factorization Machine: NFM),已被提出采用feature extractor来探索显式的特征交互。然而,所有这些模型要么是简单地枚举所有的特征交互,要么是需要人为的努力来识别重要的特征交互。前者总是给模型带来巨大的内存和计算成本,并且难以扩展到高阶交互。此外,无用的特征交互可能带来不必要的噪音,使训练过程复杂化。后者,如在
Wide & Deep中手动识别重要的特征交互,具有很高的人力成本,并有可能错过一些反直觉的(但重要的)特征交互。如果在这些因子分解模型中可以事先识别出有用的特征交互,那么模型就可以专注于对它们的学习而不必处理无用的特征交互。通过去除无用甚至有害的特征交互,我们期望模型能在降低计算成本的情况下表现得更好。
为了自动学习哪些特征交互是必要的,我们为每个特征交互引入了一个
gate(处于打开或关闭状态),以控制其输出是否应该被传递到下一层。在以前的工作中,gate的状态要么是由专家知识事先指定、要么是设置为全部打开。从数据驱动的角度来看,一个gate是打开还是关闭,应该取决于每个特征交互对最终预测的贡献。显然,那些贡献小的特征交互应该关闭,从而防止给模型学习引入额外的噪音。然而,要找到模型性能的最佳open gate集合是一个NP-Hard问题,因为我们面临着一个巨大的空间(如果我们只考虑2阶特征交互, 则搜索空间为feature field的数量)来搜索。受最近用于神经架构搜索的
DARTS的启发,论文《AutoFIS: Automatic Feature Interaction Selection in Factorization Models for Click-Through Rate Prediction》提出了一个两阶段的方法AutoFIS,用于自动选择因子分解模型中的低阶特征交互和高阶特征交互:- 在搜索阶段,
AutoFIS不是在一组离散的候选特征交互上进行搜索,而是通过引入一组架构参数architecture parameters(每个特征交互一个)从而将choice松弛为连续的,这样就可以通过梯度下降学习每个特征交互的相对重要性。架构参数与神经网络权重由GRDA优化器(一种容易产生稀疏解的优化器)联合优化,这样训练过程可以自动丢弃不重要的特征交互(架构参数为零)而保留那些重要的特征交互。 - 之后,在
re-train阶段,AutoFIS选择架构参数值非零的特征交互,用选定的特征交互重新训练模型,同时将架构参数作为注意力单元attention unit,而不是交互重要性的指标。
论文在三个大规模的数据集上进行了广泛的实验(两个公开的
benchmark、一个是private数据集)。实验结果表明:AutoFIS可以显著提高所有数据集上因子分解模型的CTR预估性能。由于AutoFIS可以去除大约50%-80%的二阶特征交互,原始模型总是可以实现效率的提升。通过学习每个三阶特征交互的重要性,论文还将AutoFIS应用于三阶交互的选择。实验结果表明:在选择了大约1%-10%的三阶交互之后,因子分解模型的AUC可以提高0.1%-0.2%,而不会引入很多计算成本。实验结果表明,使用
AutoFIS进行高阶特征交互的自动选择是一个很有前景的方向。实验还表明,重要的二阶特征交互和三阶特征交互,通过在FM中由AutoFIS所识别,也可以大大提升目前SOTA模型的性能,这意味着我们可以使用一个简单的模型进行交互选择interaction selection,并将选择结果应用于其他模型。此外,论文在真实数据和人工合成数据上分析了AutoFIS所选择的特征交互的有效性。此外,在华为应用商店的推荐服务中进行了为期十天的online A/B test,其中AutoFIS产生的推荐模型比DeepFM实现了20.3%的CTR改善、以及20.1%的CVR改善,这为业务收入的增长做出了巨大贡献。综上所述,本文的主要贡献如下:
论文通过经验验证:在训练因子分解模型时,去除冗余的特征交互是有益的。
论文提出了一个两阶段的算法
AutoFIS来自动选择因子分解模型中重要的低阶特征交互和高阶特征交互。- 在搜索阶段,
AutoFIS可以在一个完整的训练过程中通过架构参数学习每个特征交互的相对重要性。 - 在重训练阶段,移除不重要的交互,作者重新训练得到的神经网络,同时保留架构参数作为注意力单元从而帮助模型的学习。
- 在搜索阶段,
在三个大规模数据集上的离线实验证明了
AutoFIS在因子分解模型中的优越性能。此外,AutoFIS还可以找到一组重要的高阶特征交互,以提升现有模型的性能,而没有引入太多的计算成本。一个为期十天的online A/B test表明,AutoFIS在CTR和CVR方面将DeepFM模型平均提高了约20%。
- 在搜索阶段,
相关工作:
factorization machine: FM将每个特征投影到一个低维向量中,并通过内积来建模特征交互,这对于稀疏的数据来说效果很好。Field-aware factorization machine: FFM进一步使每个特征有多个vector representation从而与其他field的特征进行交互。最近,深度学习模型在一些公共
benchmark上取得了SOTA的性能。有几个模型使用MLP来改进FM,如Attention FM、Neural FM。Wide & Deep联合训练了一个wide模型(采用人工特征)、和一个deep模型(采用原始特征)。DeepFM使用一个FM layer来代替Wide & Deep中的wide组件。PNN使用MLP来建模FM layer和feature embeddings的交互,而PIN引入了network-in-network架构来建模pairwise特征交互,而不是PNN和DeepFM的内积操作。PNN用内积/外积来建模feature embeddings的交互。
需要注意的是:现有的因子分解模型都是简单地枚举所有二阶的特征交互,其中包含了许多无用的和噪音的交互。
gradient boosting decision tree: GBDT是一种通过决策树算法进行特征工程和搜索交互的方法。然后,转换后的特征交互可以被送入逻辑回归或FFM模型。在实践中,树状模型更适合于连续数据,但不适合推荐系统中的高维categorical data,因为categorical feature的使用率很低。同时,也有一些工作使用
AutoML技术来处理推荐系统中的问题。人们提出了AutoCross在许多候选特征的子集上进行搜索,从而识别有效的交互。这需要训练整个模型来评估每一个所选择的特征交互,但候选集多得令人难以置信:例如,对于一个有field的数据集,仅仅考虑二阶特征交互就有AutoCross通过两个方面的近似来加速:- 它通过树状结构中的
beam search贪心地构建局部最优的特征集合。 - 它通过
field-aware LR模型来评估新生成的特征集合。
由于这两种近似,从
AutoCross中提取的高阶特征交互可能对深度模型没有用。与
AutoCross相比,我们提出的AutoFIS只需要执行一次搜索阶段来评估所有特征交互的重要性,这要高效得多。此外,AutoFIS学到的有用的交互将改善深度模型,因为这些特征交互是在该深度模型中直接学习和评估的。- 它通过树状结构中的
最近,
one-shot架构搜索方法(如DARTS)已经成为最流行的神经架构搜索neural architecture search: NAS算法,以有效地搜索网络架构。在推荐系统中,这种方法被用来为协同过滤模型搜索适当的交互函数。《Efficient Neural Interaction Function Search for Collaborative Filtering》中的模型主要是为特征交互识别适当的交互函数,而我们的模型主要是搜索和保留重要的特征交互。受最近用于神经架构搜索的
DARTS工作的启发,我们将搜索有效特征交互的问题表述为一个包含架构参数architecture parameters的连续搜索问题。与DARTS使用two-level optimization来交替优化架构参数和模型权重,并通过训练集和验证集进行迭代不同,我们使用one-level optimization来联合训练这两类参数,并以所有数据作为训练集。
31.1 模型
31.1.1 Factorization Model: Base Model
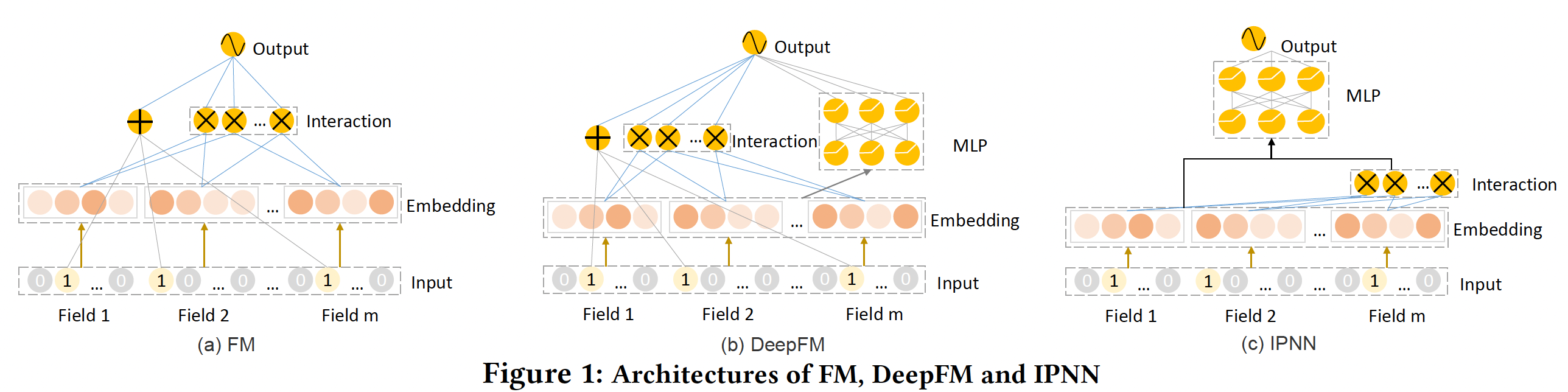
因子分解模型是指:通过内积或神经网络等操作将来自不同特征的几个
embedding的交互建模为一个实数。我们将FM、DeepFM和IPNN作为实例来描述我们的算法,并探索在各种数据集上的性能。下图展示了FM、DeepFM和IPNN模型的结构。FM由一个feature embedding layer和一个feature interaction layer组成。DeepFM和IPNN模型除了feature embedding layer、feature interaction layer之外,还有一个额外的MLP layer。DeepFM和IPNN的区别在于:在DeepFM中,feature interaction layer和MLP layer是并行工作的,而在IPNN中是堆叠排列的。
Feature Embedding Layer:在大多数CTR预测任务中,数据是以multi-field categorical form收集的。一个典型的数据预处理是:通过one-hot encoding或multi-hot encoding将每个数据实例转化为高维稀疏向量。只有当一个field是multivariate的时候,它才被表示为multi-hot encoding vector。一个数据样本可以被表示为:其中:
field数量,field的one-hot/multi-hot encoding vector。feature embedding layer用于将encoding vector转化为低维向量,即:其中:
field的embedding矩阵;field的feature value数量;- 如果
one-hot encoding vector,其中第1,那么 - 如果
multi-hot encoding vector,其中第1,那么:sum池化)或者
feature embedding layer的输出为多个embedding向量的拼接:- 如果
Feature Interaction Layer:将特征转换到低维空间后,可以用feature interaction layer在这样的空间中建模特征交互。首先,计算
pairwise特征交互的内积:其中:
field的feature embedding;这里
pairwise特征交互的数量为可以根据
然后,在
FM和DeepFM模型中,feature interaction layer的输出为:在这里,所有的特征交互以相同的贡献被传递到下一层。正如前面内容所指出的(并将在实验部分得到验证),并非所有的特征交互都具有同等的预测性,无用的特征交互甚至会降低性能。因此,我们提出了
AutoFIS算法来有效选择重要的特征交互。为了研究我们的方法是否可以用来识别重要的高阶特征交互,我们将具有三阶交互(即三个
field的组合)的feature interaction layer定义为:其中
MLP Layer:MLP Layer由若干个带激活函数的全连接层组成,它学习特征的relationship和combination。单层MLP Layer的输出为:其中:
bias;relu为relu激活函数。Output Layer:FM模型没有MLP Layer,它直接将feature interaction layer和prediction layer相连:其中:
predicted CTR。DeepFM以并行的方式将feature interaction layer和MLP layer进行组合:IPNN以堆叠的方式将feature interaction layer和MLP layer进行组合:请注意,
IPNN的MLP layer也可以作为不同特征交互的re-weighting,从而捕获其相对重要性。这也是IPNN比FM和DeepFM有更高容量的原因。然而,在IPNN的公式中,人们无法检索到对应于每个特征交互的相对贡献的精确值。因此,IPNN中无用的特征交互既不能被识别、也不能被丢弃,这给模型带来了额外的噪声和计算成本。
Objective Function:FM、DeepFM和IPNN有着相同的目标函数,即最小化预测值和标签的交叉熵:其中:
label;
31.1.2 AutoFIS
AutoFIS自动选择有用的特征交互,可以应用于任何因子分解模型的feature interaction layer。AutoFIS可以分为两个阶段:- 搜索阶段
search stage:检测有用的特征交互 - 重训练阶段
re-train stage:对具有选定特征交互的模型进行重训练。
核心思想:根据
data-driven的权重field交互特征的重要性,并裁剪不重要的field交互特征。AutoFIS和AFM很类似,它们都是学习每个交互特征的重要性,然而:AutoFIS通过自由参数来描述交互特征的重要性,可以视为global-level的建模。AFM通过attention机制来描述交互特征的重要性,可以视为sample-level的建模。理论上而言,对于给定的field-pair,我们可以统计所有样本在它上面的注意力权重,从而得到global-level的重要性。- 此外,
AFM用逐元素乘积来描述交互特征,而AutoFIS用内积。
- 搜索阶段
a. 搜索阶段
为了便于介绍算法,我们引入了
gate操作来控制是否选择一个特征交互:一个打开的gate对应于选择一个特征交互,而一个关闭的gate则导致丢弃一个特征交互。所有二阶特征交互对应的gate的总数为open gate的集合是非常具有挑战性的,因为我们面临着一个难以置信的巨大空间在这项工作中,我们从不同的角度来处理这个问题:我们不是在一个离散的
open gate的集合上进行搜索,而是通过引入架构参数choice放宽为连续的,这样就可以通过梯度下降学习每个特征交互的相对重要性。下图显示了所提出的AutoFIS的概览。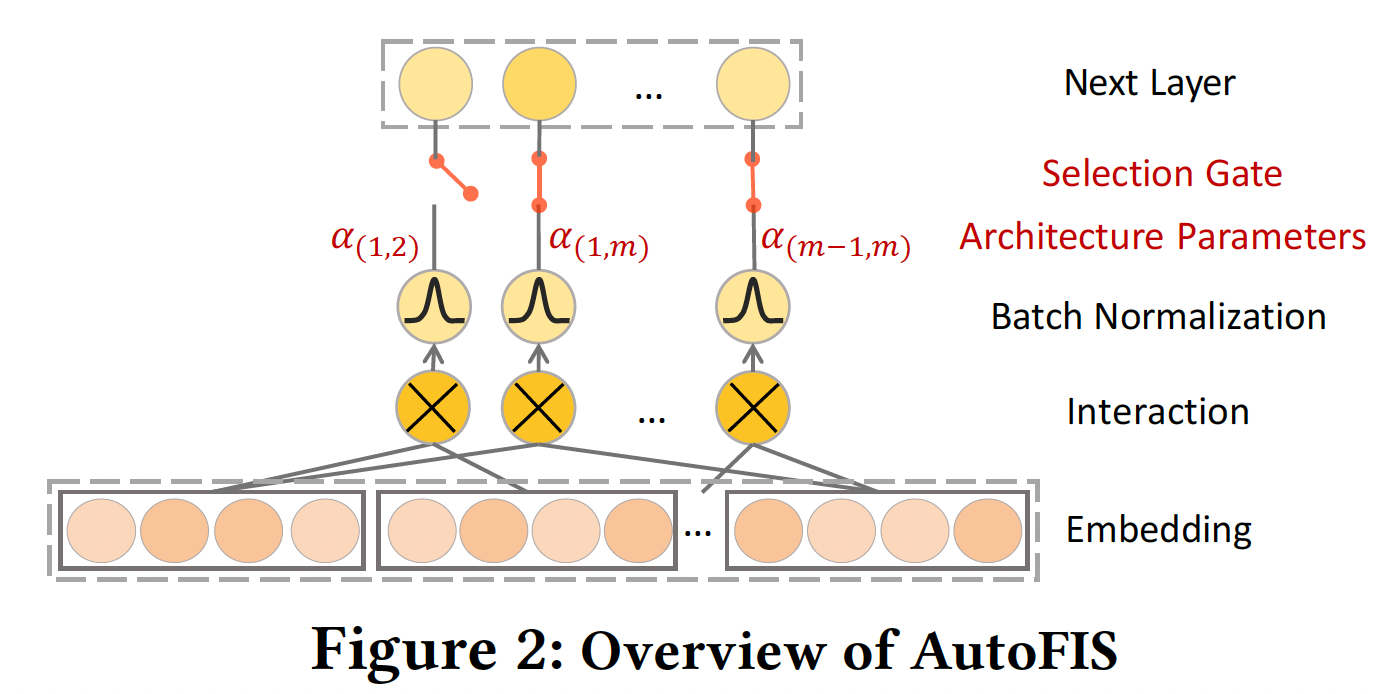
这种通过梯度学习的架构选择方案受到
DARTS的启发,其中,DARTS的目标是从卷积神经网络架构的一组候选操作中选择一个操作。具体而言,我们将因子分解模型中的interaction layer重新表述为:其中:
在
AutoFIS的搜索阶段,我们可以学习gate状态。如何确保
GRDA Optimizer来实现。此外,是否可以保留最重要的
field,而不仅仅是最重要的field pair?实际上,如果fieldfieldBatch Normalization:从整个神经网络的角度来看,特征交互的贡献由由于
scale耦合会导致对Batch Normalization: BN来消除其scale问题。原始的
BN采用mini-batch统计量从而对activated output进行标准化。具体而言:其中:
BN层的输入;BN层的输出;mini-batchBN层的可训练的scale/shift parameters;为了获得对
scale/shift parameters分别设为1和0。对每个特征交互BN操作计算如下:其中:
mini-batchGRDA Optimizer:generalized regularized dual averaging: GRDA优化器旨在获得一个稀疏的深度神经网络。为了在每个梯度step其中:
在搜索阶段,我们使用
GRDA优化器来学习架构参数除了
Adam优化器学习。One-level Optimization:为了在AutoFIS的搜索阶段学习结构参数DARTS不同。DARTS将higher-level决策变量、将网络权重lower-level变量,然后用bi-level优化算法对其进行优化。在DARTS中,假设只有当网络权重被正确学习后,模型才能选择操作,从而使在
AutoFIS的公式中,这意味着我们可以在网络权重被正确训练后决定gate应该打开还是关闭,这使我们回到了问题:完全训练DARTS建议只用一个梯度下降步来近似计算网络权重的最优值,并迭代地训练我们认为,这种近似的不精确性可能会降低性能。因此,我们建议不使用
bi-level优化,而是用one-level优化来联合优化在这种情况下,
在实验部分中,我们将展示
one-level optimization比two-level optimization的优越性。
b. 重训练阶段
在搜索阶段的训练结束后,根据搜索阶段的架构参数
gate状态,当gate状态被固定为永久关闭。在移除这些不重要的交互后,我们重新训练新的模型。具体来说,
feature interaction layer被替换为:注意这里
Adam优化器学习。这里
0或1(根据特征交互的选择的结果),并且在训练过程中保持不变。重训练阶段,所有参数(包括
Adam优化器来优化。
31.2 实验
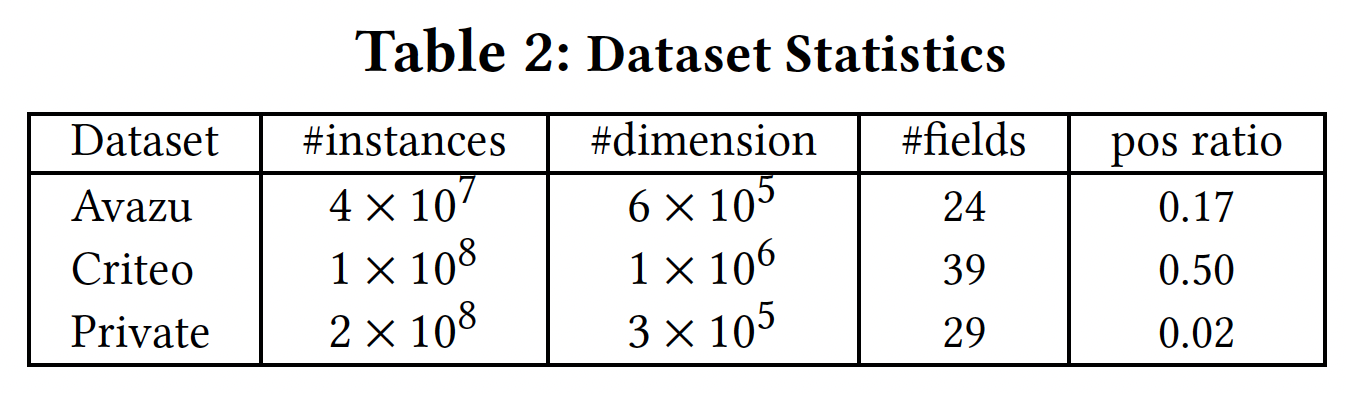
数据集:两个
public数据集(Avazu, Criteo)、一个private数据集。Avazu:在Kaggle的CTR预估竞赛中被发布。随机拆分80%的数据作为训练和验证,剩余20%用于测试。出现次数少于20次的categories将被删除从而进行降维。Criteo:包含一个月的点击日志,有数十亿的数据样本。我们选择"data 6-12"作为训练集和验证集,同时选择"day-13"进行评估。为了应对标签的不平衡,我们采用了负降采样的方法,使正样本比例大致保持在50%左右。13个数值字段通过分桶被转换为one-hot特征,其中某个字段中出现少于20次的特征被设置为dummy feature "other"。如何分桶?论文并未说明。
Private:从华为应用商店的游戏推荐场景中收集的。该数据集包含app特征(如ID, category),用户特征(如用户的行为历史)和上下文特征。
数据集统计结果如下表所示。
baseline:我们将AutoFIS应用于FM和DeepFM模型以显示其有效性(分别表示为AutoFM和AutoDeepFM)。baseline方法为:GBDT-based的方法(GBDT+LR, GBDT+FFM),FM模型(AFM, FwFM, FFM, IPNN)。由于其巨大的计算成本和源代码的不可用,我们没有将我们的模型与
AutoCross进行比较。评估指标:
AUC, Log loss。超参数配置:
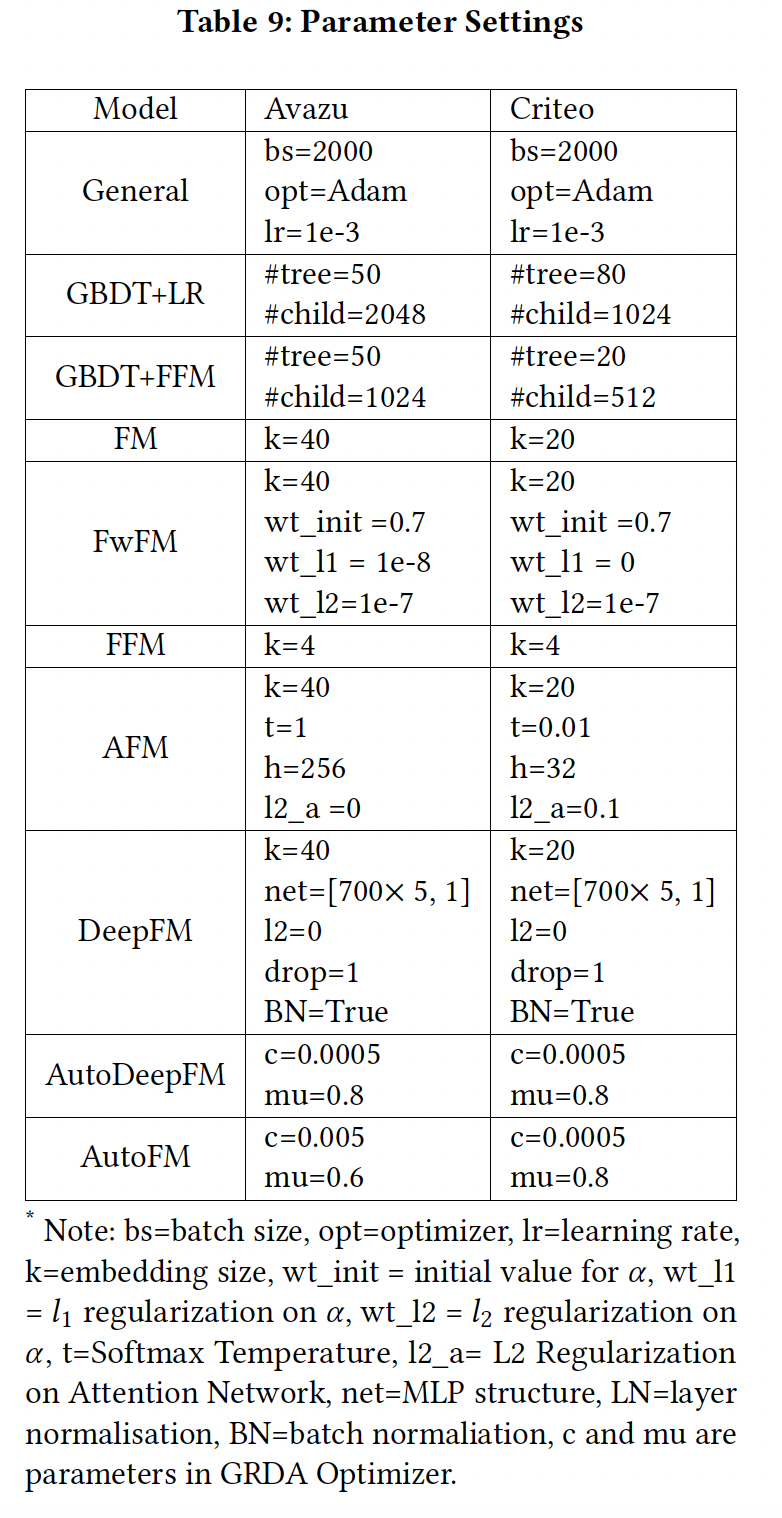
实现细节:
- 为
AutoFM和AutoDeepFM选择二阶特征交互:在搜索阶段,我们首先在所有训练数据上联合训练 - 为
AutoFM和AutoDeepFM选择三阶特征交互:我们复用所选中的二阶交互,并在搜索阶段枚举三阶特征交互从而学习其重要性。最后,我们用选中的二阶交互和三阶交互来重新训练我们的模型。
注意,在搜索阶段,架构参数
GRDA优化器优化,而其他参数Adam优化器优化。在重新训练阶段,所有参数都由Adam优化器优化。- 为
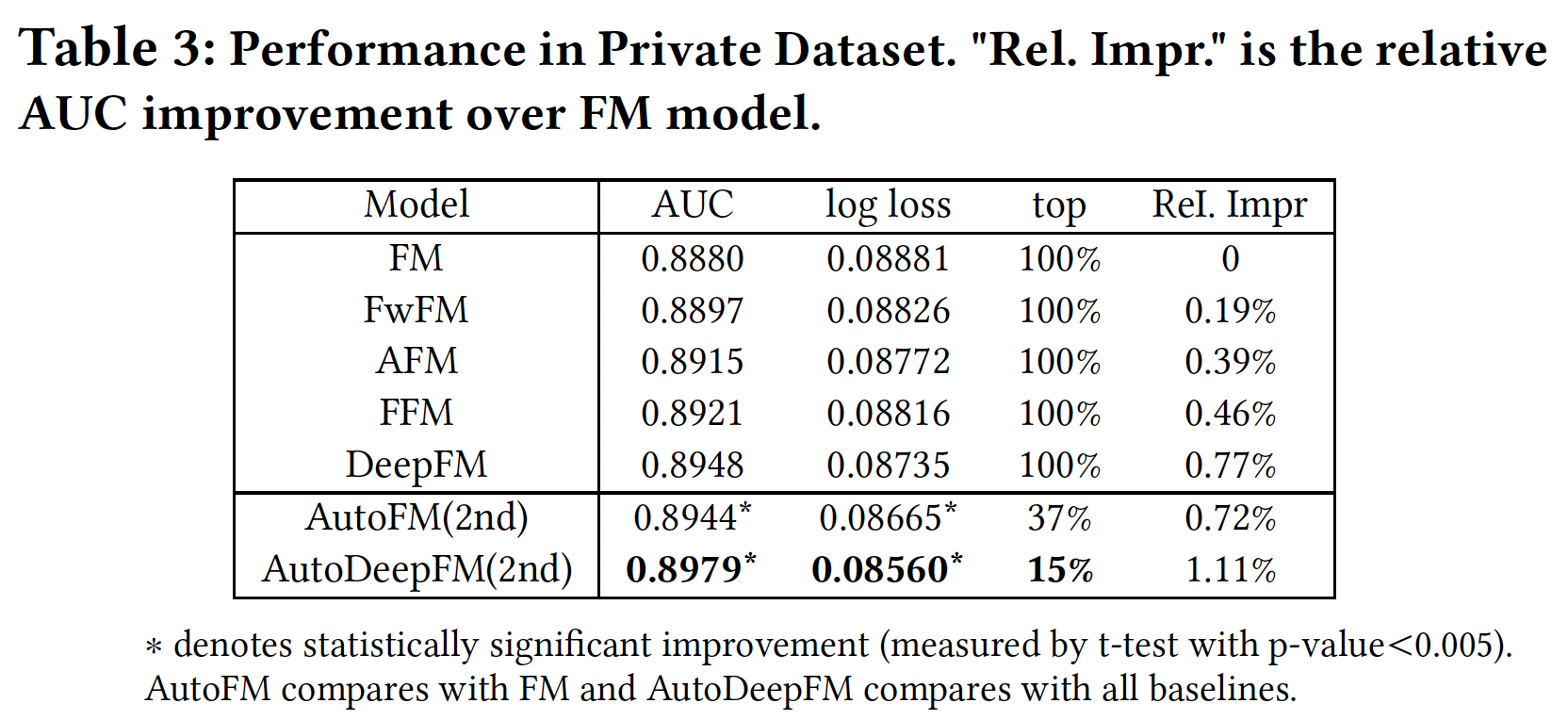
AutoFIS选择的特征交互:Table 1和Table3总结了AutoFM和AutoDeepFM在Avazu, Criteo, Private数据集上自动选择二阶重要交互和三阶重要交互的性能。可以看到:对于
Avazu数据集,FM/DeepFM分别可以移除71%/76%的二阶交互。移除这些无用的交互:- 不仅可以使模型在推理时更快:
AutoFM(2nd)和AutoDeepFM(2nd)的推理时间明显少于FM和DeepFM。 - 而且可以明显提高预测准确性:从
AUC来看,AutoFM(2nd)比FM的相对性能提高了0.49%、AutoDeepFM(2nd)比DeepFM的相对性能提高了0.20%。
类似的改进也可以从其他数据集中得出。
- 不仅可以使模型在推理时更快:
对于高阶特征交互的选择,只有
2%-10%的三阶特征交互需要包含在模型中。AutoFM(3rd)和AutoDeepFM(3rd)的推理时间远远少于FM(3rd)和DeepFM(3rd)(与FM和DeepFM相当)。同时,通过移除不重要的三阶特征交互,准确率得到了显著的提高。即在
Avazu上的AUC指标上,AutoFM(3rd)比FM(3rd)的相对性能提高了0.22%、AutoDeepFM(3rd)比DeepFM(3rd)提高了0.20%。对
Criteo的观察也是如此。
所有这些性能提升都是以边际时间成本
marginal time cost实现的。例如,AutoDeepFM(3rd)在Avazu和Criteo用一块GPU卡搜索重要的二阶特征交互和三阶特征交互需要24分钟和128分钟。同样的结果可能需要人类工程师花很多小时或几天的时间来手动识别这些重要的特征交互。
注意,在
FM和DeepFM中直接枚举三阶特征交互会使推理时间增加7到12倍,这在工业应用中是不可接受的。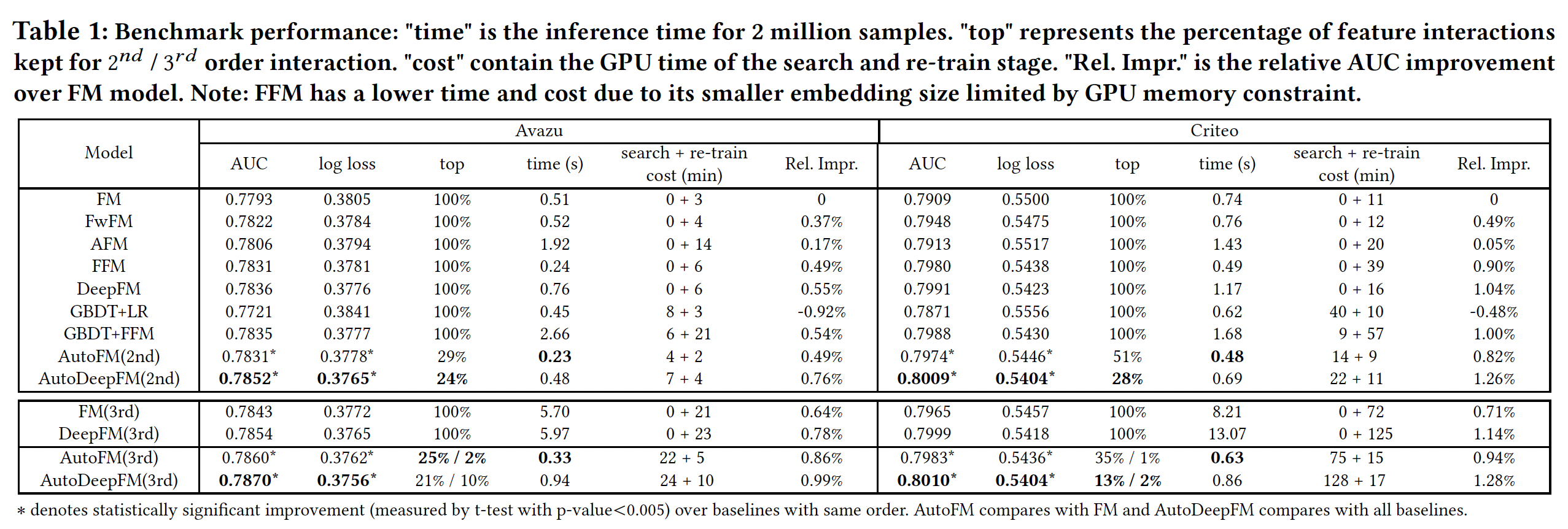
所选特征的可迁移性:我们研究了由
AutoFM(这是一个简单的模型)所学到的特征交互是否可以迁移到SOTA的模型(如IPNN)从而提高其性能。如下表所示:
- 使用
AutoFM选择的二阶特征交互(即AutoIPNN(2nd))实现了与IPNN相当的性能,在Avazu和Criteo的所有交互中约占30%和50%。 - 使用
AutoFM选择的二阶特征交互和三阶特征交互(即AutoIPNN(3rd)),性能得到明显改善。
这两个证据都验证了
AutoFM所选择的特征交互的可迁移性。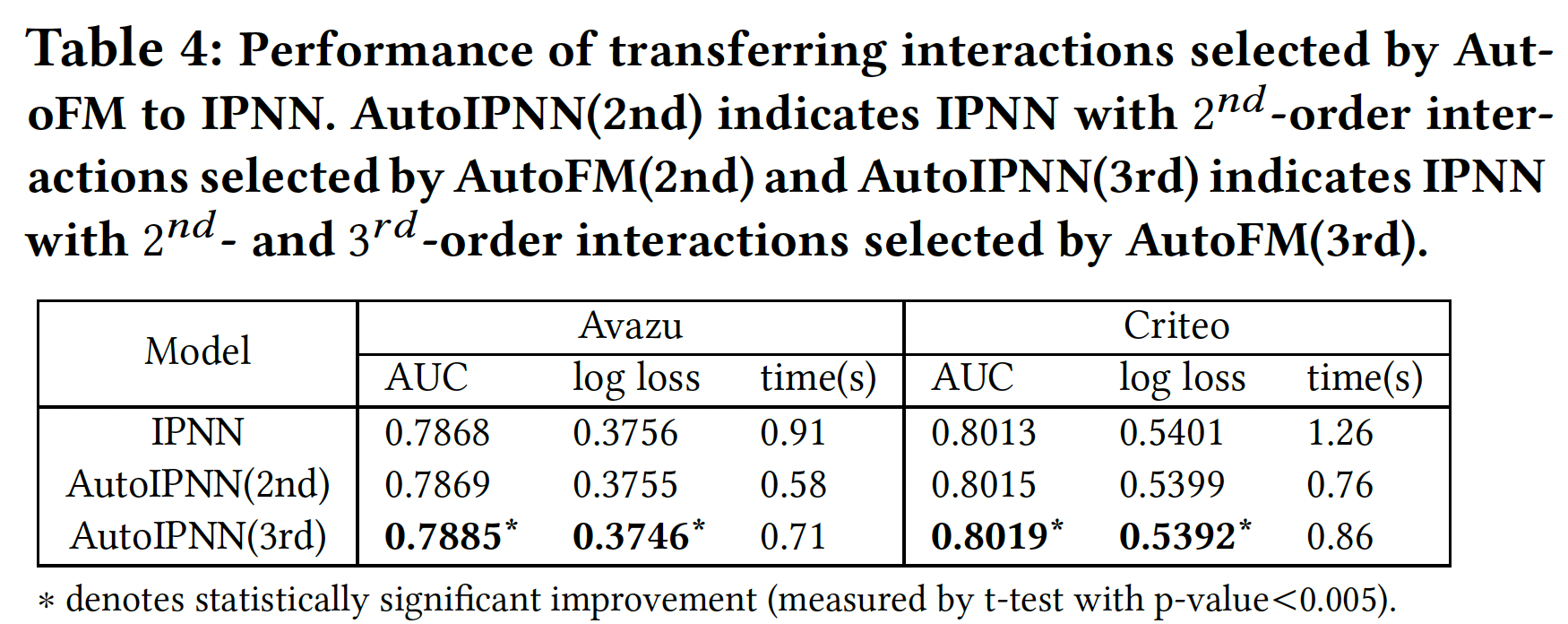
- 使用
所选特征的效果:
在真实数据上:我们定义
statistics_AUC来表示一个特征交互对最终预测的重要性。对于一个给定的特征交互。我们构建一个只考虑该交互的predictor,其中prediction为训练集中特定特征交互的statistical CTR(#downloads/#impressions)。然后,这个predictor的AUC是相对于这个给定的特征交互的statistics_AUC。statistics_AUC越高,表明该特征交互在预测中的作用越重要。然后,我们将statistics_AUC和即,仅仅以这一对特征作为输入,
label不变。这个predictor如何构建?论文并未说明。可以选择LR或FM模型。如下图所示,我们可以发现,被我们模型选中的大多数特征交互(绝对值较高的
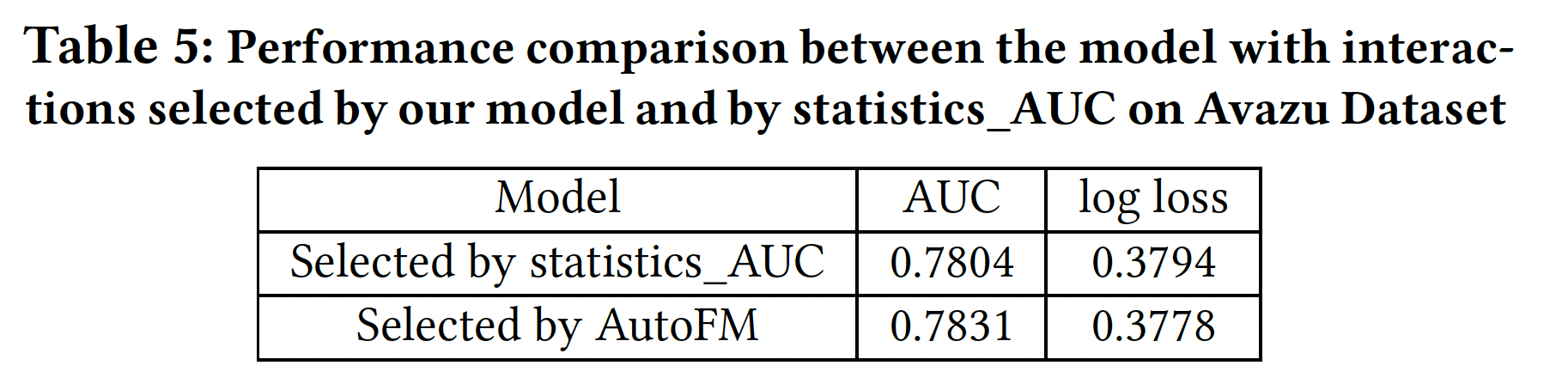
statistics_AUC,但并非所有具有高statistics_AUC的特征交互都被选中。这是因为这些交互中的信息也可能存在于其它交互中,而这些其它交互也被我们模型所选中。为了评估我们的模型所选择的特征交互的有效性,我们还根据
statistics_AUC选择了top-N特征交互(statistics_AUC选择的特征交互的模型。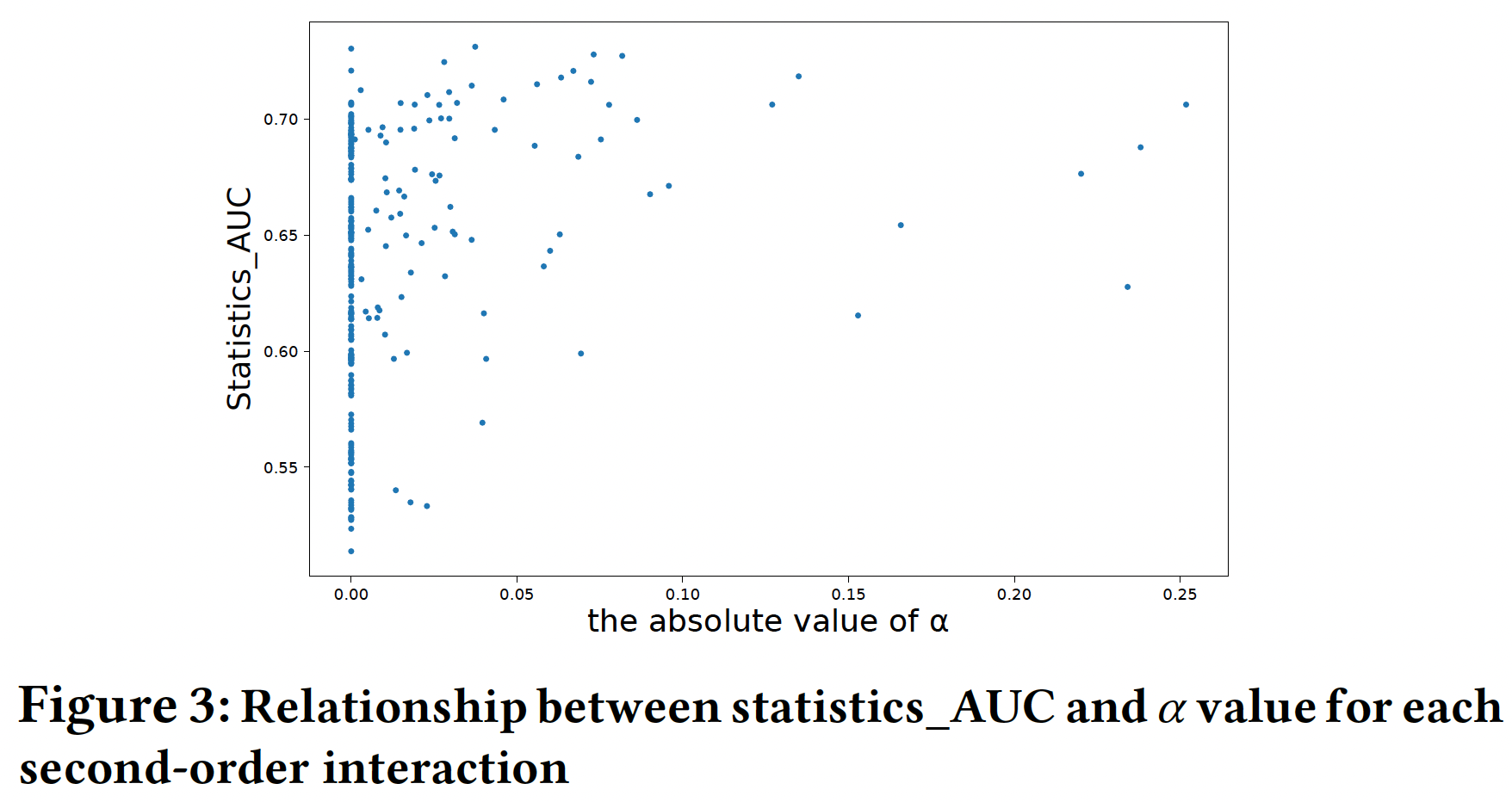
在人工合成数据上:合成数据集是由一个不完整的
poly-2函数产生的,其中的双线性项类似于categories之间的交互。基于这个数据集,我们研究了:我们的模型是否能够找到重要的交互、我们的模型与其他FM模型相比的性能。数据集的输入
field的binary标签:其中,数据分布
data pair是独立同分布采样来构建训练集和测试集。我们还在采样的数据中加入一个小的随机噪声我们使用
FM和我们的模型来拟合人工合成数据。我们在测试数据集上使用AUC来评估这些模型。我们选择
Figure 4展示了我们的模型与FM的性能比较,这表明了我们的模型的优越性。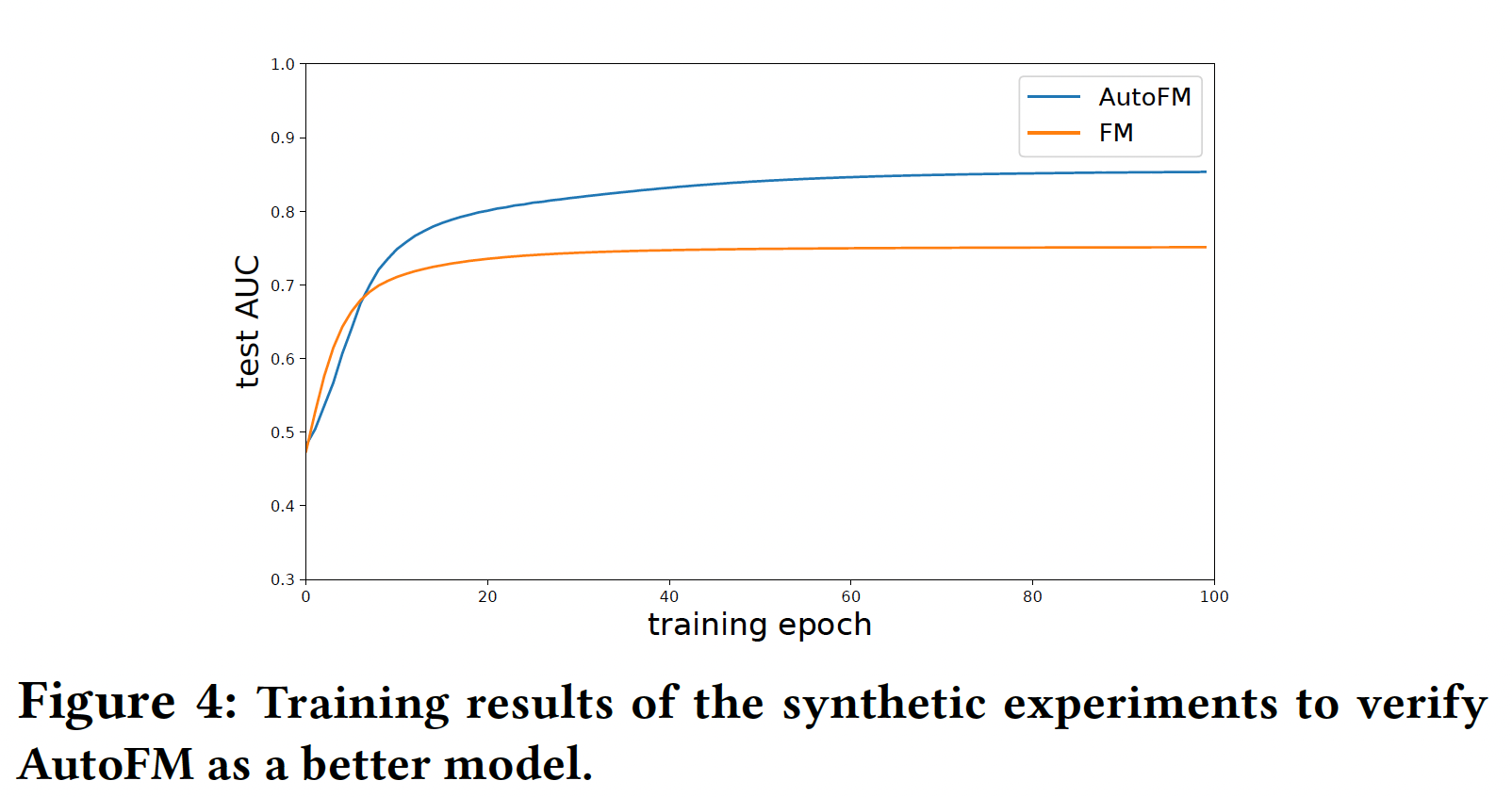
如
Figure 5所示,我们的模型可以精确地提取重要的特征交互: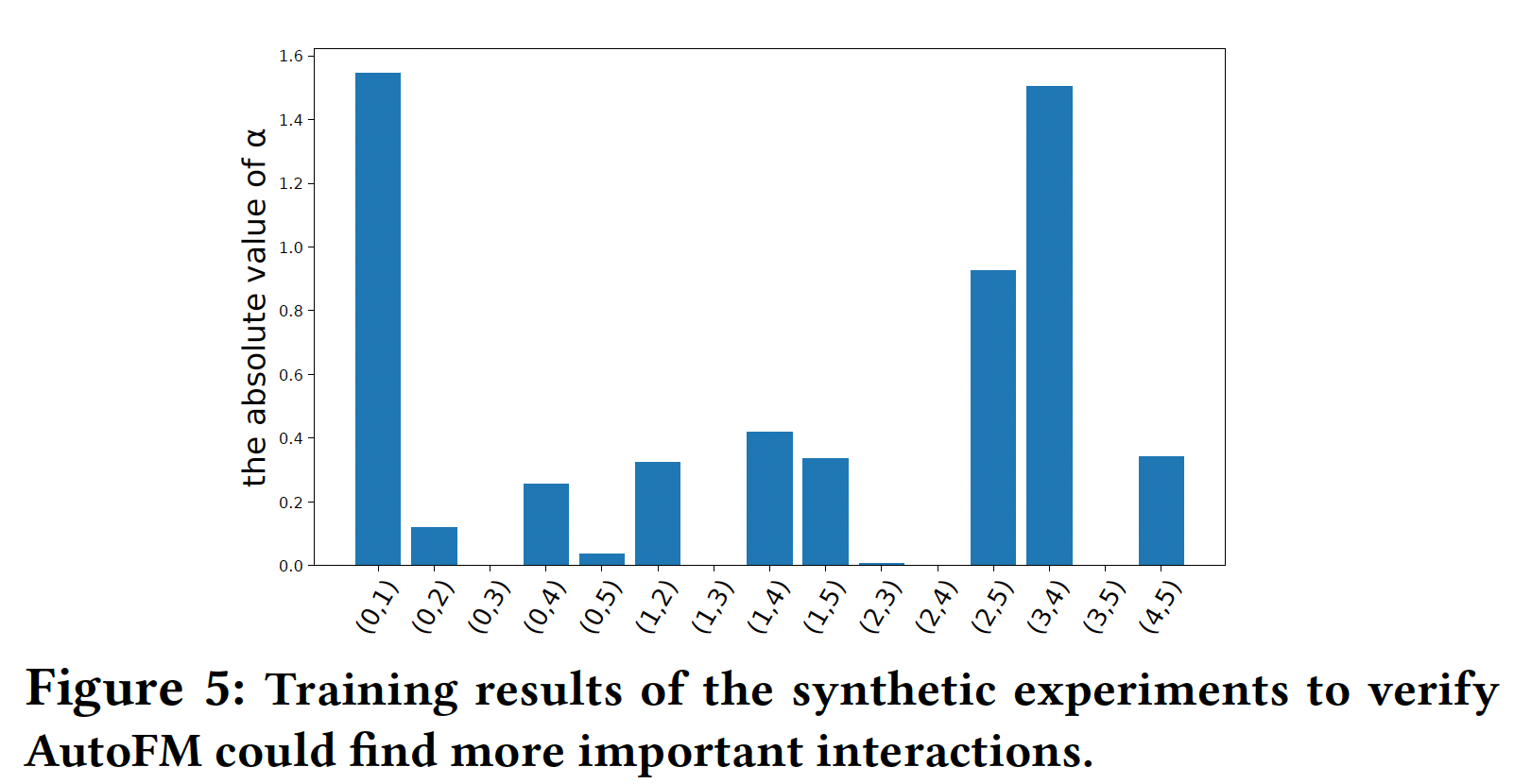
在线实验:我们在华为应用商店的推荐系统中进行了在线实验,以验证
AutoDeepFM的卓越性能。具体而言,在
App Store的游戏推荐场景中进行了为期10天的A/B test。我们在线实验的baseline是DeepFM,这是一个强大的baseline,因为它具有优秀的准确性和高效率,已经在商业系统中部署了很长一段时间。- 对照组:随机选择
5%的用户,并向他们展示由DeepFM生成的推荐。 - 实验组:随机选择
5%的用户,并向他们展示由AutoDeepFM生成的推荐。
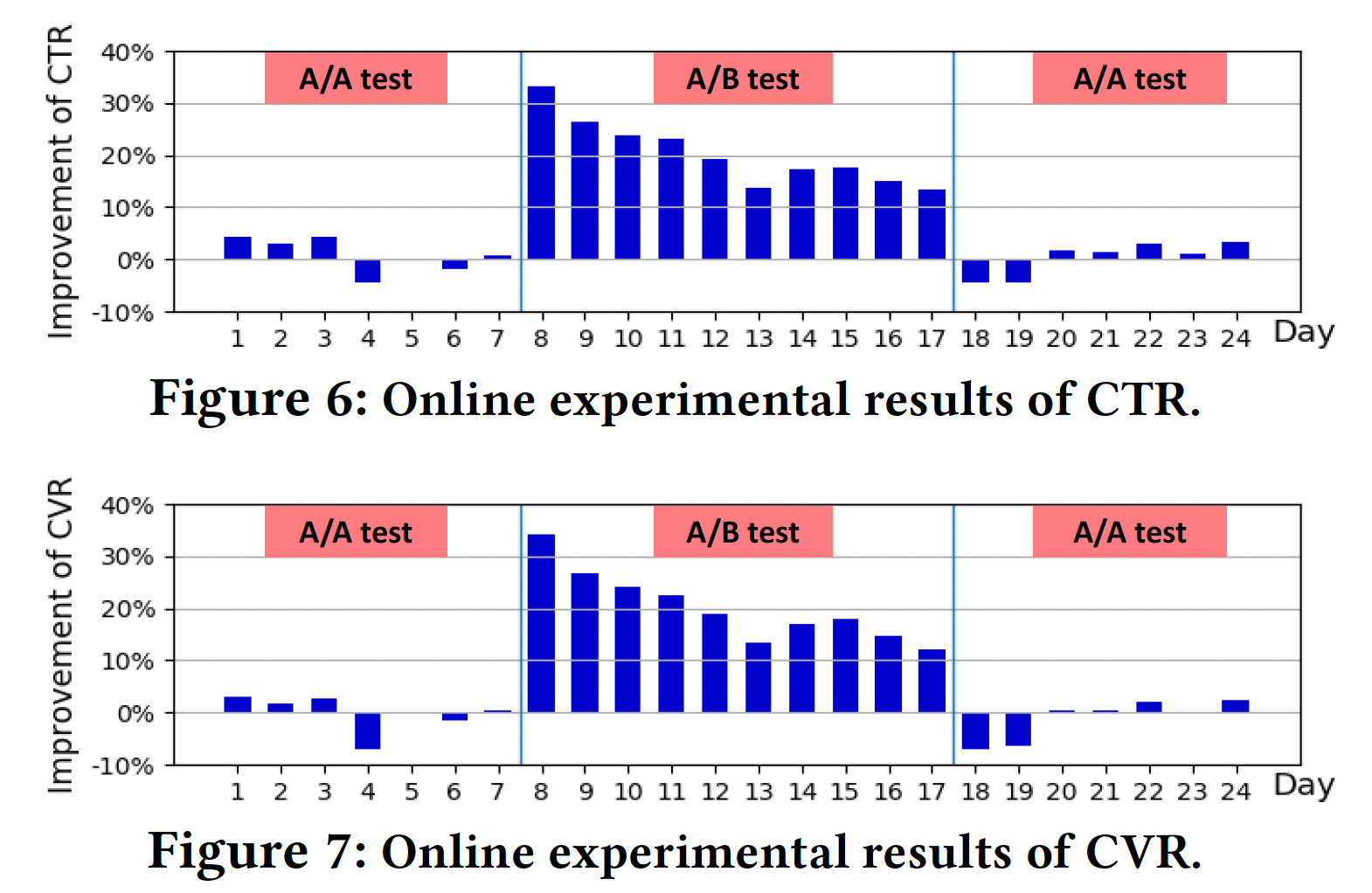
Figure 6和Figure 7显示了实验组比对照组在CTR(#downloads/#impressions)和CVR(#downloads/#user)上的改进。可以看到:- 该系统是相当稳定的,在
A/A test期间,CTR和CVR都在8%以内波动。 - 我们的
AutoDeepFM模型在第8天被启动到实时系统中。从第8天开始,我们观察到在CTR和CVR方面比baseline模型有明显的改善。在10天的A/B test中,CTR的平均改进为20.3%,CVR的平均改进为20.1%。这些结果证明了我们所提出的模型的巨大有效性。 - 从第
18天开始,我们再次进行A/A test,在实验组中用baseline模型替换我们的AutoDeepFM模型。我们观察到实验组的性能急剧下降,这再次验证了实验组在线性能的改善确实是由我们提出的模型引入的。
- 对照组:随机选择
消融研究:
不同随机数种子下
Avazu上用不同的随机数种子运行AutoFM的搜索阶段。由不同随机数种子估计的
Pearson相关性约为0.86,这验证了BN,这个Pearson相关性会下降到0.65左右。AutoFIS组件的效果:为了验证AutoFIS中各个组件的有效性,我们提出了几个变体,如Table 6所示。- 为了验证
AutoFIS搜索阶段的有效性,我们将其与"Random"策略(即,随机选择特征交互)进行比较。 - 在重训练阶段,我们验证了
BN和
注意,对于
AutoFM-BN,仅仅是在重训练阶段没有BN,而在搜索阶段还是用了BN的。
Table 7列出了这些变体的性能。对于"Random"策略,我们选择与AutoFM相同的交互数量,我们尝试了10种不同的"Random"策略,并对结果进行了平均。结论:
比较
AutoFM-BN-𝛼和Random+FM,我们可以看到:在相同数量的交互下,AutoFIS的选择总是能取得比随机选择更好的性能。这说明在搜索阶段AutoFIS就能识别出重要的交互。在
Criteo数据集中,Random+FM和FM之间的性能差距表明:在某些情况下,随机选择的特征交互可能优于保留所有特征交互的模型。这支持了我们的说法:移除一些无用的特征交互可以提高性能。类似于
xgboost中的feature sample。在
Avazu数据集中,Random+FM略逊于FM。AutoFM和AutoFM-BN之间的比较验证了BN在重训练阶段的有效性,其中的原因在AutoFIS章节已经说明。AutoFM-BN和AutoFM-BN-𝛼之间的性能差距表明:
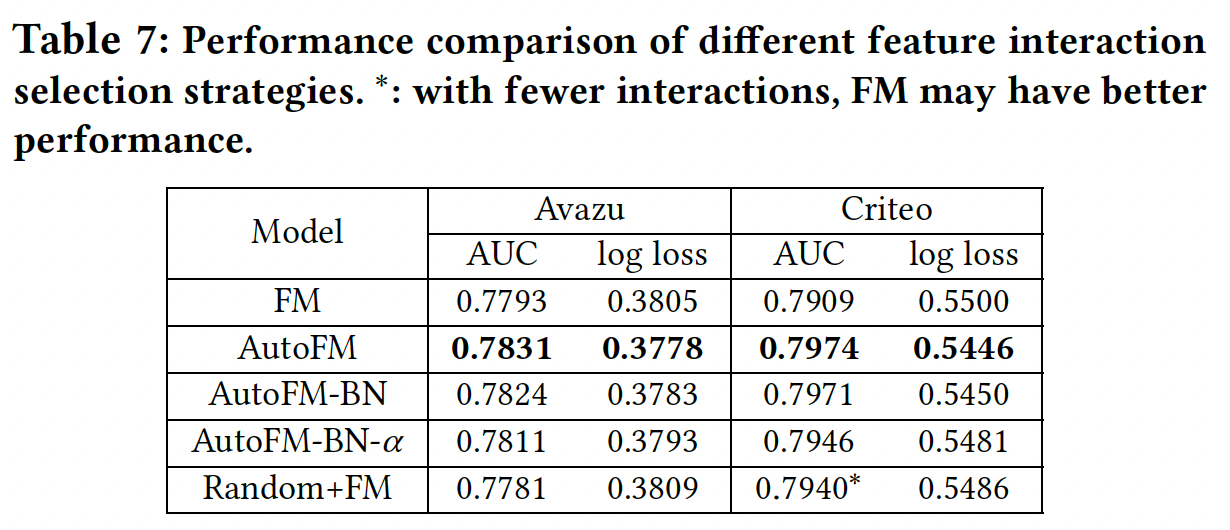
- 为了验证
one-level optimization vs bi-level optimization:结果如Table 8所示。可以看到:AutoFM和Bi-AutoFM(以及AutoDeepFM和Bi-AutoDeepFM)之间的性能差距表明了one-level optimization比bi-level optimization的优越性,其原因在one-level optimization章节已经说明。
三十二、DCN V2[2020]
有效的特征交叉
feature cross对于许多learning to rank: LTR模型的成功至关重要。特征交叉提供了单个特征之外的额外交互信息。例如,"国家" 和 "语言" 的组合比其中单个特征更有信息量。在线性模型时代,机器学习从业者依靠手动识别这种特征交叉来增加模型的表达能力。不幸的是,这涉及到一个组合搜索空间,在数据大多是categorical的web-scale的应用中,这个搜索空间很大而且很稀疏。在这种情况下的搜索是耗时耗力的,往往需要领域的专业知识,并使模型更难以泛化。后来,
embedding技术被广泛采用,将特征从高维稀疏向量投影到更低维的稠密向量。Factorization Machine: FM利用embedding技术,通过两个latent vector的内积来建模pairwise特征交互。与那些传统的线性模型中的特征交叉相比,FM带来了更多的泛化能力。在过去的十年中,随着更大的算力和巨大的数据规模,工业界的
LTR模型已经逐渐从线性模型和FM-based的模型迁移到深度神经网络(DNN)。这使得搜索和推荐系统的模型性能得到了全面的提升。人们普遍认为DNN是通用的函数近似器,可以潜在地学习各种特征交互。然而,最近的研究(《Latent cross: Making use of context in recurrent recommender systems》、《Deep & Cross Network for Ad Click Predictions》)发现:DNN甚至对二阶特征交叉或三阶特征交叉进行近似建模都是低效的。为了更准确地捕捉有效的特征交叉,常见的补救措施是通过更宽或更深的网络进一步提高模型容量。这自然是一把双刃剑:
- 我们在提高模型性能的同时也使模型的服务速度大大降低。在许多生产环境中,这些模型正在处理极高的
QPS,因此对实时推理有非常严格的延迟要求。可能,serving系统已经被推到了一个极限,无法承受更大的模型。 - 此外,更深的模型往往引入可训练性问题,使模型更难训练。
这已经揭示了设计一个能够有效地学习
predictive特征交互的模型的关键需求,特别是在一个处理数十亿用户的实时流量的资源限制环境中。 最近的许多工作试图解决这一挑战。共同的思想是:利用那些从DNN学到的隐式高阶交叉、以及显式的和有界的特征交叉(在线性模型中已经发现,显式的和有界的特征交叉是有效的)。隐式交叉是指通过端到端的函数来学习交互,而没有任何明确的公式来建模这种交叉。另一方面,显式交叉是通过一个具有可控交互阶次的显式公式来建模的。在所有这些方法中,
Deep & Cross Network: DCN是有效和优雅的。然而,在大规模工业系统中部署DCN面临许多挑战。DCN的cross network是有局限性的:cross network代表的多项式仅由random cross patterns的灵活性。- 此外,
cross network和DNN之间的分配容量是不平衡的。当将DCN应用于大规模生产数据时,这种差距明显增加。绝大部分的参数将被用于学习DNN中的隐式交叉。
在论文
《DCN V2: Improved Deep & Cross Network and Practical Lessons forWeb-scale Learning to Rank Systems》中,作者提出了一个新的模型DCN-V2,改进了原来的DCN模型。作者已经在整个谷歌的相当多的learning to rank system中成功部署了DCN-V2,在离线模型准确性和在线业务指标方面都有显著的提高。DCN-V2首先通过cross layer学习输入(通常是embedding layer)的显式特征交互,然后与深度网络相结合从而学习互补的隐式交互。DCN-V2的核心是cross layer,它继承了DCN中cross network的简单结构,然而在学习显式的和有界的交叉特征方面的表达能力显著增强。论文研究了以点击为正标签的数据集,然而DCN-V2与标签无关,可以应用于任何learning to rank system。论文贡献:
论文提出了一个新的模型
DCN-V2来学习有效的显式特征交叉和隐式特征交叉。与现有的方法相比,DCN-V2更具有表达能力,但仍然是高效和简单的。观察到
DCN-V2中所学到的矩阵的低秩性质,论文提出利用低秩技术从而在子空间中近似feature cross,以获得更好的性能和延迟的trade-off。此外,论文提出了一种基于
Mixture-of-Expert架构的技术,以进一步将矩阵分解为多个较小的子空间。然后,这些子空间通过一个门控机制被聚合起来。论文利用人工合成数据集进行并提供了广泛的研究,证明了传统的基于
ReLU的神经网络学习高阶特征交叉的低效率。通过全面的实验分析,论文证明了的
DCN-V2模型在Criteo和MovieLen-1M基准数据集上的表现明显优于SOTA算法。论文提供了一个案例研究,并分享了在一个大规模工业
ranking系统中部署DCN-V2的经验,这带来了显著的离线收益和在线收益。
- 我们在提高模型性能的同时也使模型的服务速度大大降低。在许多生产环境中,这些模型正在处理极高的
相关工作:最近
feature interaction learning工作的核心思想是利用显式的和隐式的特征交叉。为了建模显式交叉,最近的工作引入了乘法运算(pairwise interaction。我们根据他们如何结合显式部分和隐式部分来组织相关工作。并行结构:一个工作方向是联合训练两个并行网络,其灵感来自于
wide and deep模型,其中wide组件将原始特征的交叉作为输入,而deep组件是一个DNN模型。然而,为wide组件选择交叉特征又回到了线性模型的特征工程问题。尽管如此,wide and deep模型已经激发了许多工作从而采用这种并行的架构并改进wide部分。DeepFM通过在wide组件采用FM模型从而自动进行feature interaction learning。xDeepFM通过生成多个feature map增加了DCN的表达能力,每个feature map都编码了当前level和输入level的特征之间的pairwise交互。此外,它还将每个feature embeddingunit,而不是将每个元素unit。不幸的是,它的计算成本很高(#params的10倍),使得它在工业规模的应用中不实用。此外,
DeepFM和xDeepFM都要求所有的feature embedding具有相同的大小,这在应用于工业数据时又是一个限制,因为工业数据的词表大小(categorical features的大小)从AFM通过一个注意力网络为每个特征交互分配重要性。AutoInt利用带残差连接的multi-head self-attention机制。InterHAt进一步采用了分层注意力。
堆叠结构:另一个工作方向是在
embedding layer和DNN模型之间引入一个interaction layer,该interaction layer创建了显式的特征交叉。这个interaction layer在早期阶段捕捉到了特征交互,并促进了后续隐层的学习。product-based neural network: PNN引入了inner product layer(IPNN)和outer product layer(OPNN)作为pairwise interaction layer。OPNN的一个缺点在于其高计算成本。Neural FM: NFM通过用Hadamard积代替内积来扩展FM。DLRM遵从FM,通过内积来计算特征交叉。
这些模型只能创建到二阶显式交叉。
AFN将特征转化为对数空间,并自适应地学习任意阶的特征交互。
与
DeepFM和xDeepFM类似,这些方法只接受大小相等的embedding size。
尽管这些年经过了许多发展,我们的综合实验表明,
DCN仍然是一个强大的基线。我们将此归因于其简单的结构,它促进了optimization。然而,正如所讨论的,其有限的表达能力使其无法在web-scale的系统中学习更有效的特征交叉。在下文中,我们提出了一个新的架构,它继承了DCN的简单结构,同时提高了它的表达能力。
32.1 模型
这里描述了一个新颖的模型架构
DCN-V2来学习显式特征交互和隐式特征交互。DCN-V2从一个embedding layer开始,然后是一个包含多个cross layer的cross network(用于建模显式特征交互),然后结合一个深度神经网络(用于建模隐式特征交互)。DCN-V2中的改进对于将DCN用于高度优化的生产系统至关重要。DCN-V2极大地提高了DCN在web-scale的生产数据中在建模复杂的显式的交叉项的表达能力,同时保持其优雅的公式,便于部署。DCN-V2所建模的函数族是DCN所建模的函数族的严格超集。模型整体架构如下图所示,有两种方式将
cross network与deep network结合起来:堆叠式、并行式。此外,考虑到cross layer的低秩性质,我们建议利用low-rank cross layer的混合来实现模型性能和效率之间更健康的trade-off。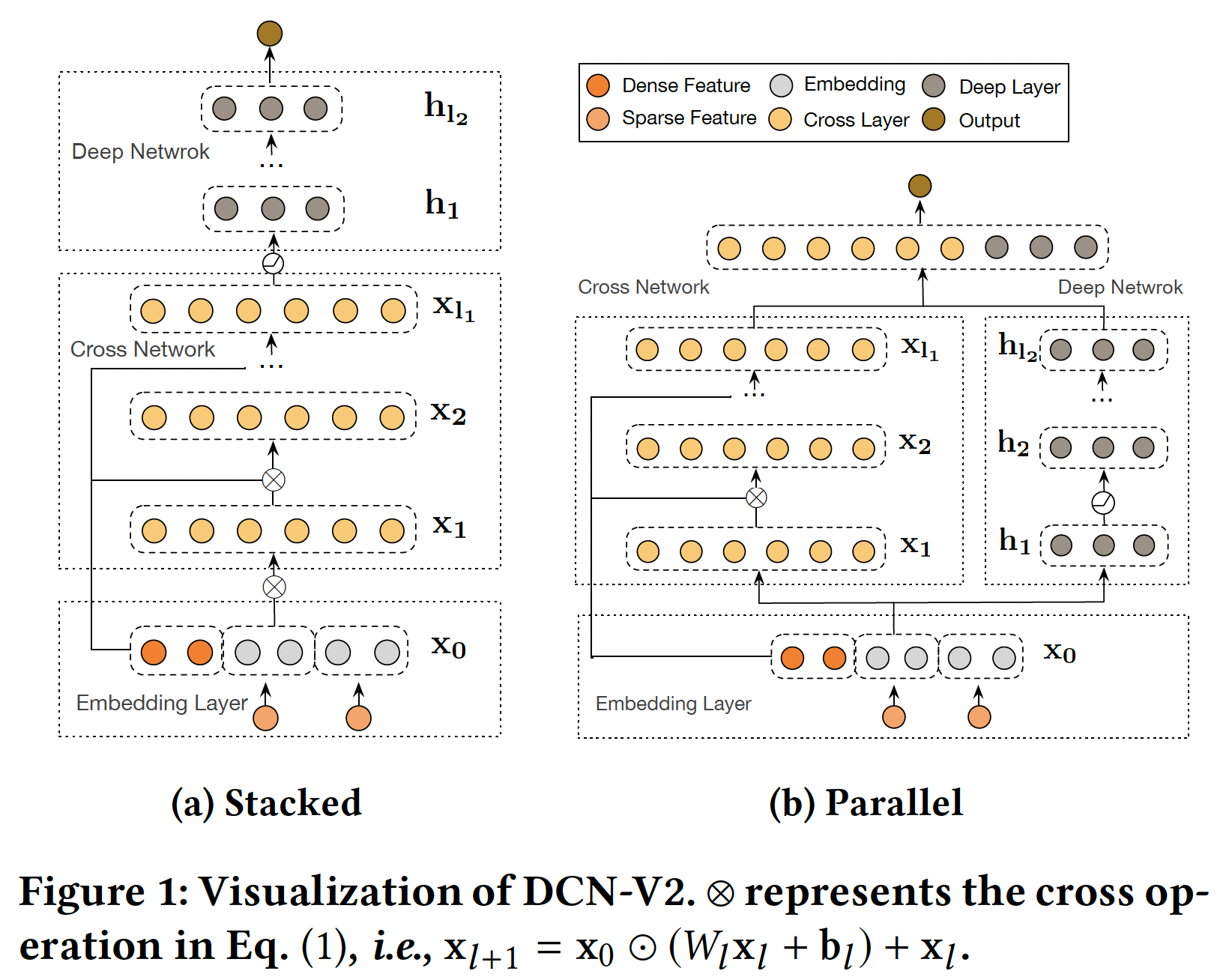
Embedding Layer:embedding layer将categorical (sparse)特征和dense特征的组合作为输入,并输出DCN类似的setting。与DeepFM, NFM, xDeepFM, DLRM, IPNN, FM不同的是,DCN-V2接受任意的embedding size。这对于词表规模从Cross Network:DCN-V2和核心在于cross layer,它创建了显式的特征交叉。其中第cross layer如下所示:其中:
base layer,它包含原始的一阶特征,通常被设置为embedding layer。bias向量。
下图展示了一个单独的
cross layer。
对于一个
cross network,最高的多项式阶数是DCN-V2退化到DCN。cross layer仅能建模有界的多项式类,而其他任何复杂的函数空间只能被近似。因此,我们接下来引入了一个deep network来补充数据中固有分布的建模。DCN V1的公式为:DCN V2的公式为:bias项即:
DCN V1中,DCN V2中,DCN V2的模型容量更高。DCN V2的核心:用Deep Network:第deep layer的公式为:其中:
deep layer的的输入和输出。bias向量。ReLU。
Deep and Cross Combination:我们提出了两种结构:Stacked Structure(如Figure 1a):输入cross network,然后是deep network,最后是输出层输出Parallel Structure(如Figure 1b):输入cross network和deep network,然后这两个网络的输出拼接起来作为最终输出
prediction为:其中:
sigmoid函数。对于损失函数,我们使用
logloss(带正则化项)。注意,DCN-V2本身是对prediction-task和损失函数无关的。Cost-Effective Mixture of Low-Rank DCN:对于那些生产模型来说,模型容量往往受到有限的serving资源、严格的latency要求的限制。因此,我们寻求使DCN-v2更具cost-efficient的方法。DCN-V2结构简单,计算瓶颈在于matrix-vector乘法,这使得我们可以利用矩阵近似技术来降低成本:通过两个低秩矩阵gap或快速的谱衰减时,该方法是最有效的。在许多情况下,我们确实观察到所学的矩阵下图
(a)显示了DCN-V2中来自生产模型的学到的矩阵因此,我们定义第
cross layer的低秩版本为:其中:
这个新的公式有两种解释:
我们在一个子空间中学习特征交叉。
这个解释启发我们采用
Mixture-of-Experts: MoE的思想。MoE-based模型由两部分组成:experts(通常是一个小网络)和gating(输入的一个函数)。在我们的案例中,我们不是依靠一个单一的专家来学习特征交叉,而是利用多个这样的专家,每个专家在不同的子空间学习特征交互,并使用门控机制(取决于输入mixture的公式如下(如下图(b)所示):其中:
sigmoid或softmax函数。
我们将输入
这个解释激励我们利用投影空间的低维性质。我们不是立即从
refine the representation:其中:
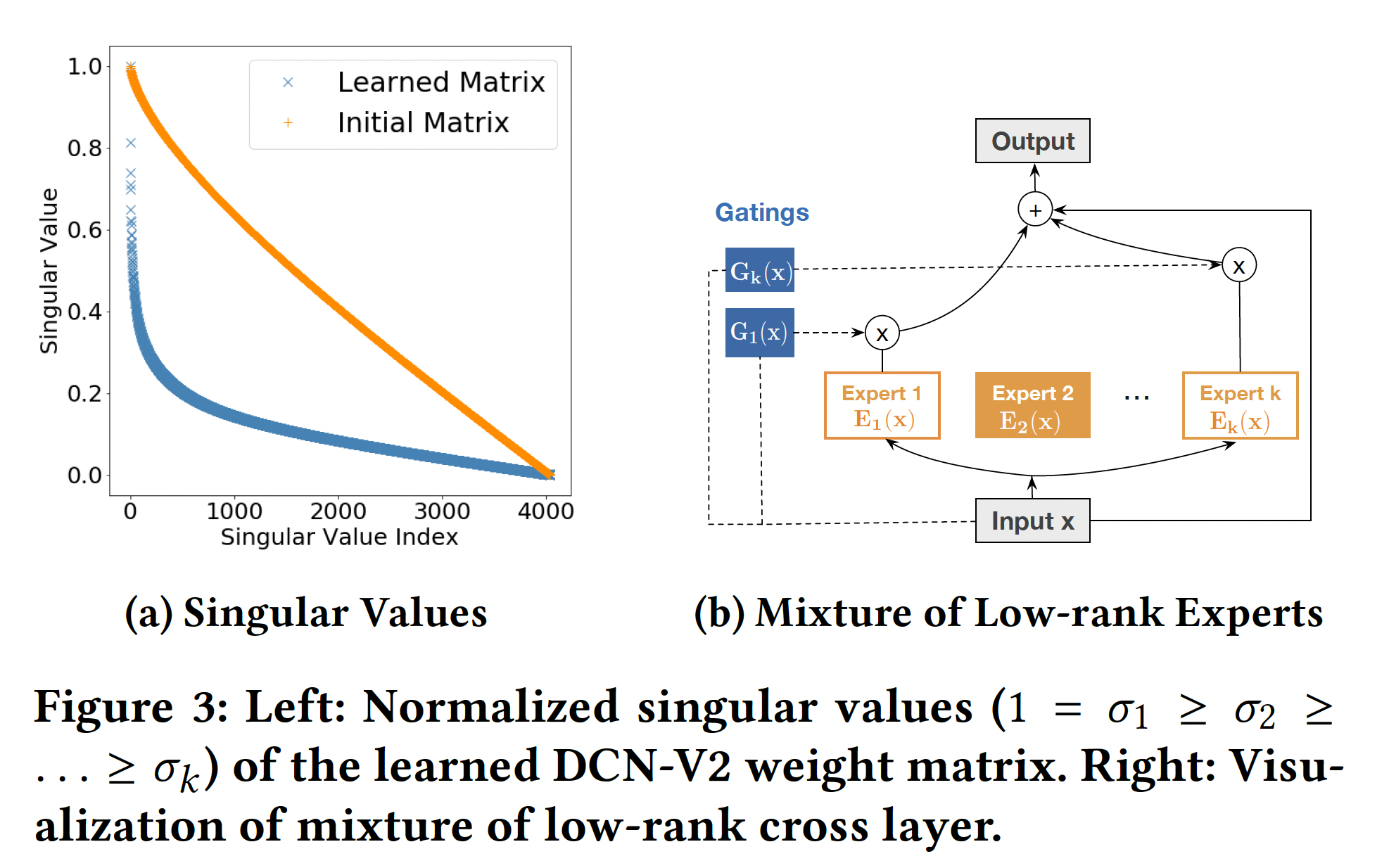
我们旨在有效利用固定的内存/时间预算来学习有意义的特征交叉。以下公式从上到下都代表一个严格意义上的、逐渐增大的函数族:
这一组模型有比较大的工程参考意义,它描述了从简单模型到复杂模型的升级路径,同时也具有一定的物理意义。
算法复杂度:令
embedding size,cross layers数量,DCN专家的数量。此外,我们假设每个专家具有相同的小维度cross network的时间复杂度和空间复杂度为mixDCN(低秩DCN) 的时间复杂度和空间复杂度为从
bit-wise和feature-wise的角度来看,对于cross network,cross network能够创造出直到与
DCN相比,DCN-V2用更多的参数来刻画相同的多项式类,表达能力更强。此外,DCN-V2中的特征交互具有更强的表达能力,可以从bit-wise和feature-wise两方面来看;而在DCN中,它只是从bit-wise的角度来看。
32.2 实验
"CrossNet"或"CN"代表cross network,"Mix"代表低秩混合版本。
32.2.1 人工合成数据集
大多数工作只研究了具有未知交叉模式和噪音的数据的公共数据集。很少有工作在一个干净的环境中用已知的
ground-truth模型进行研究。因此,重要的是要了解:- 在哪些情况下,传统的神经网络会变得没有效率。
- 在我们提出的模型
DCN-V2中每个组件的作用。
我们用
DCN模型中的cross network来表示那些特征交叉方法,并与工业推荐系统中常用的ReLU进行比较。为了简化实验和便于理解,我们假设每个特征难度增加时的性能:仅考虑二阶特征交叉,令
ground-truth model为- 稀疏性 (
- 交叉模式的相似性(
因此,我们创建了难度不断增加的人工合成数据集:
其中:
[-1, 1]之间均匀采样的。下表报告了
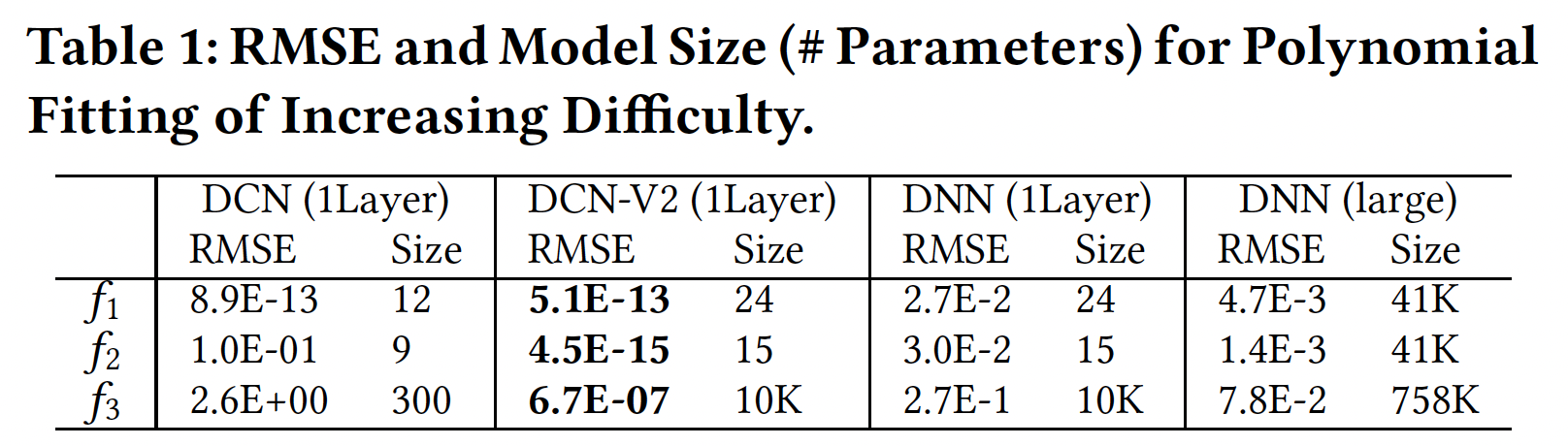
5次运行和model size的平均RMSE。可以看到:- 当交叉模式很简单时(即,
DCN-V2和DCN都很有效。 - 当模式变得更加复杂时(即,
DCN-V2仍然准确,而DCN则准确性下降了。 - 即使采用更宽更深的结构,
DNN的性能仍然很差。这表明DNN在建模单项式模式时效率不高。
- 稀疏性 (
每个组件的作用:我们还分别对
3阶和4阶的同质多项式进行了消融研究。对于3阶和4阶,我们从20个交叉项。下图展示了层深度对于平均RMSE的影响。- 显然,
2层对3阶多项式取得的最佳性能得到验证(4阶多项式也是类似的)。在其他层,性能明显下降。 DCN(红色虚线)在复杂的交叉模式建模方面的有限表达能力。
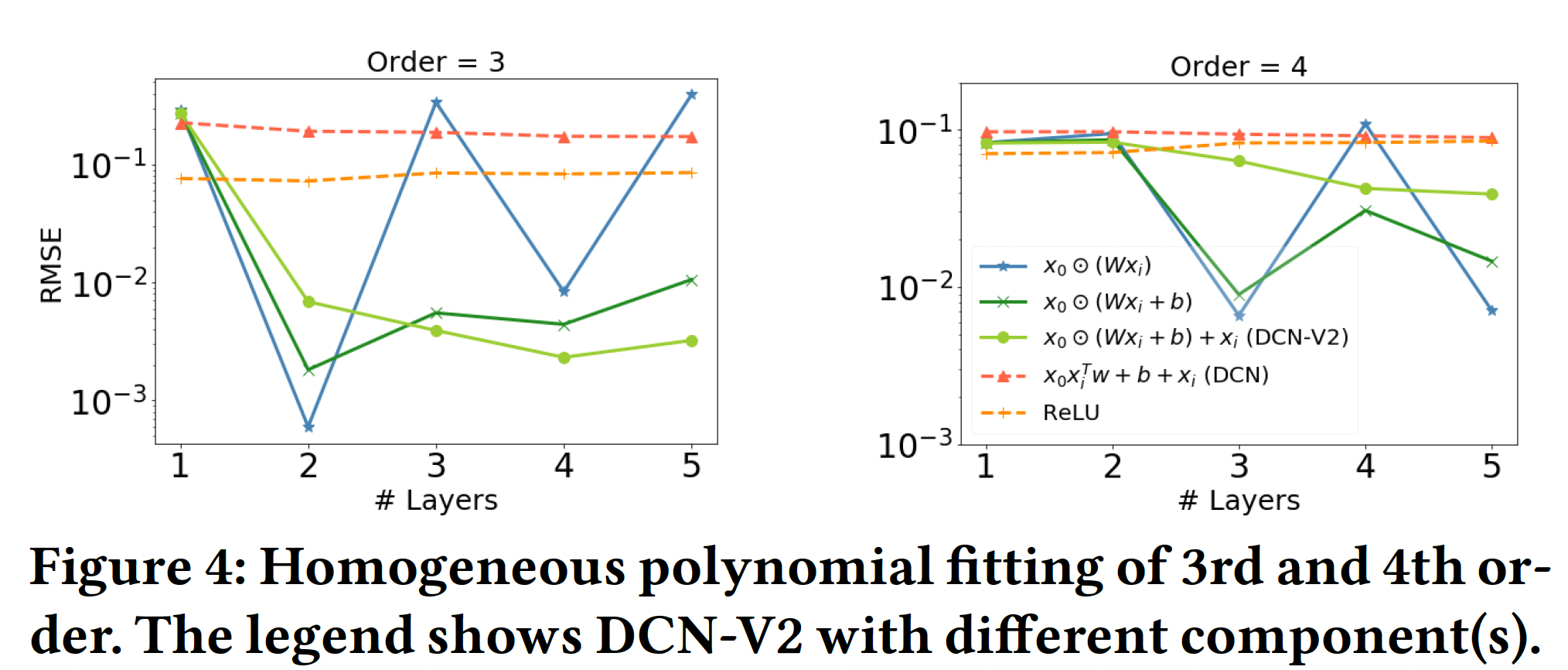
- 显然,
总而言之,
ReLU(即,ReLU激活函数的DNN)在捕获显式的特征交叉(乘法关系)方面效率不高,即使有更深更大的网络。DCN准确地捕捉到了简单的交叉模式,但在更复杂的模式中却失败了。DCN-V2对于复杂的交叉模式仍然是准确和有效的。
32.2.2 真实数据集
数据集:
Criteo:包含7天内的用户日志,包含45M个样本和39个特征。我们使用前6天的数据进行训练,并将最后一天的数据随机平均分成验证集和测试集。我们对13个dense特征执行log归一化(feature-2为26个categorical feature。MovieLen-1M:包含740k个样本和7个特征。每个训练样本包括一个<user-features, movie-features, rating>三元组。我们将任务形式化为一个回归问题:所有一分和两分的评分都被归一化为0、四分和五分被归一化为1、三分被删除。使用和嵌入6个non-multivalent categorical feature。数据被随机分成80%用于训练、10%用于验证、10%用于测试。
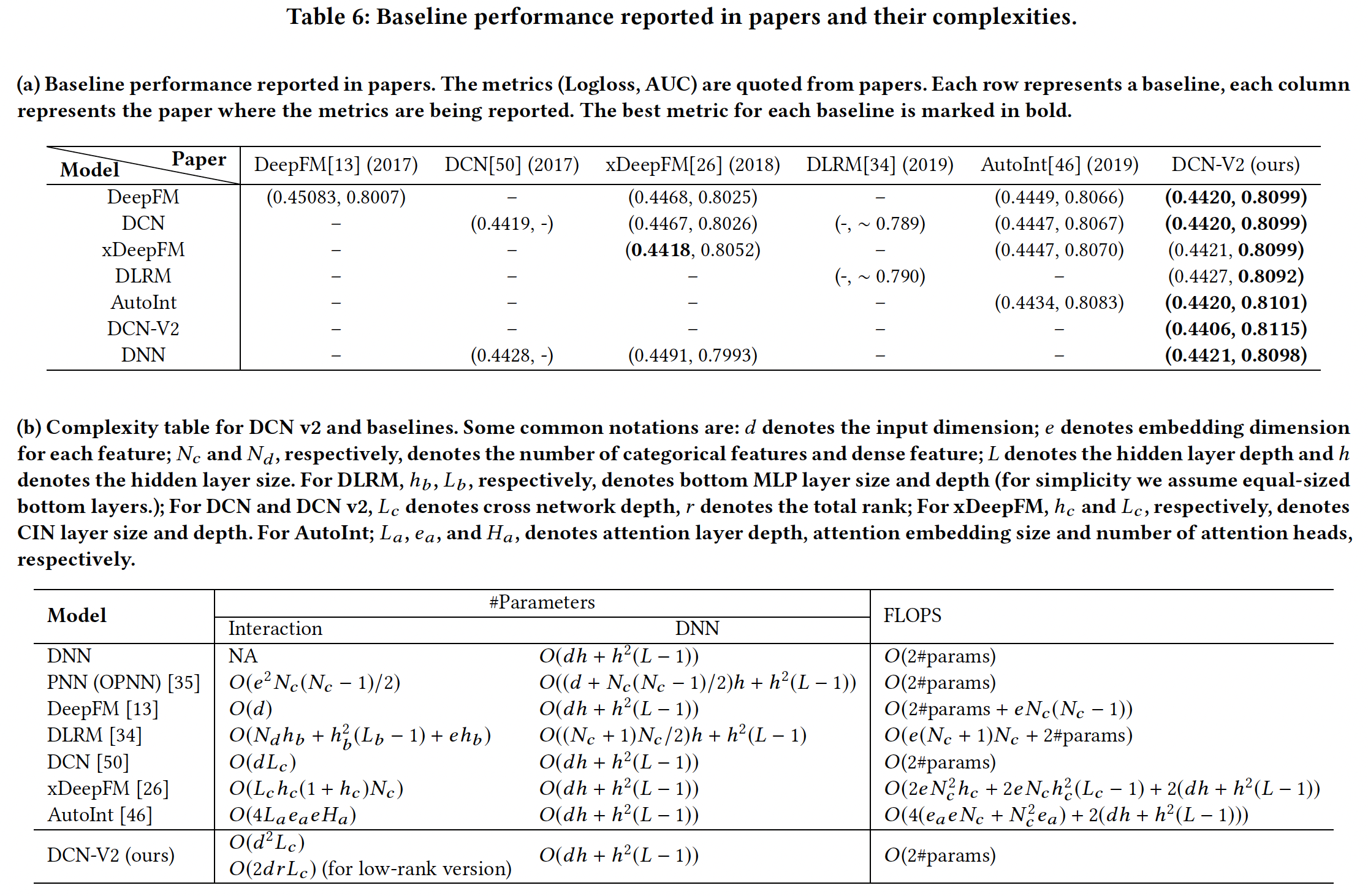
baseline方法:SOTA的feature interaction learning算法,如下表所示。
实现细节:所有
baseline和我们的方法都在TensorFlow v1中实现。为了公平比较,除了特征交互组件,所有模型的实现都是相同的。embedding:除了DNN和DCN模型,所有的baseline都要求每个特征的embedding size是相同的。因此,我们将所有的模型固定为Criteo为39、Movielen-1M为30)。optimization:Adam优化器,batch size = 512(MovieLen batch size = 128)。权重以He Normal来初始化,bias被初始化为零,梯度被截断为范数10。对参数采用decay = 0.9999的指数移动平均。超参数调优:对于所有的
baseline,我们对超参数进行了粗粒度(大范围)的网格搜索,然后再进行细粒度(小范围)的搜索。为了确保可重复性和减少模型方差,对于每个方法和数据集,我们报告了最佳配置的5次独立运行的均值和标准差。我们在下面描述了Criteo的详细设置。对于MovieLens,我们也遵循类似的过程。对于
Criteo的所有baseline:- 学习率调优范围:对数尺度上从
- 训练步数调优范围:
{150k, 160k, 200k, 250k, 300k} - 隐层深度调优范围:
{1, 2, 3, 4}。 - 隐层维度调优范围:
{562, 768, 1024}。 - 正则化参数调优范围:
每个模型自己的超参数:
DCN:交叉层的数量调优范围{1, 2, 3, 4}。AutoInt:注意力层的数量调优范围{2, 3, 4};attention embedding size调优范围{20, 32, 40};attention head数量调优范围{2, 3};残差连接调优范围{enable, disable}。xDeepFM:CIN layer size调优范围{100, 200},CIN layer depth调优范围{2, 3, 4},激活函数为恒等映射,计算为direct或indirect。DLRM:bottom MLP layer size和数量的调优范围{(512,256,64), (256,64)}。PNN:我们运行了IPNN、OPNN和PNN*,对于后两者,kernel type调优范围{full matrix, vector, number}。
对于所有的模型,参数总数上限为
- 学习率调优范围:对数尺度上从
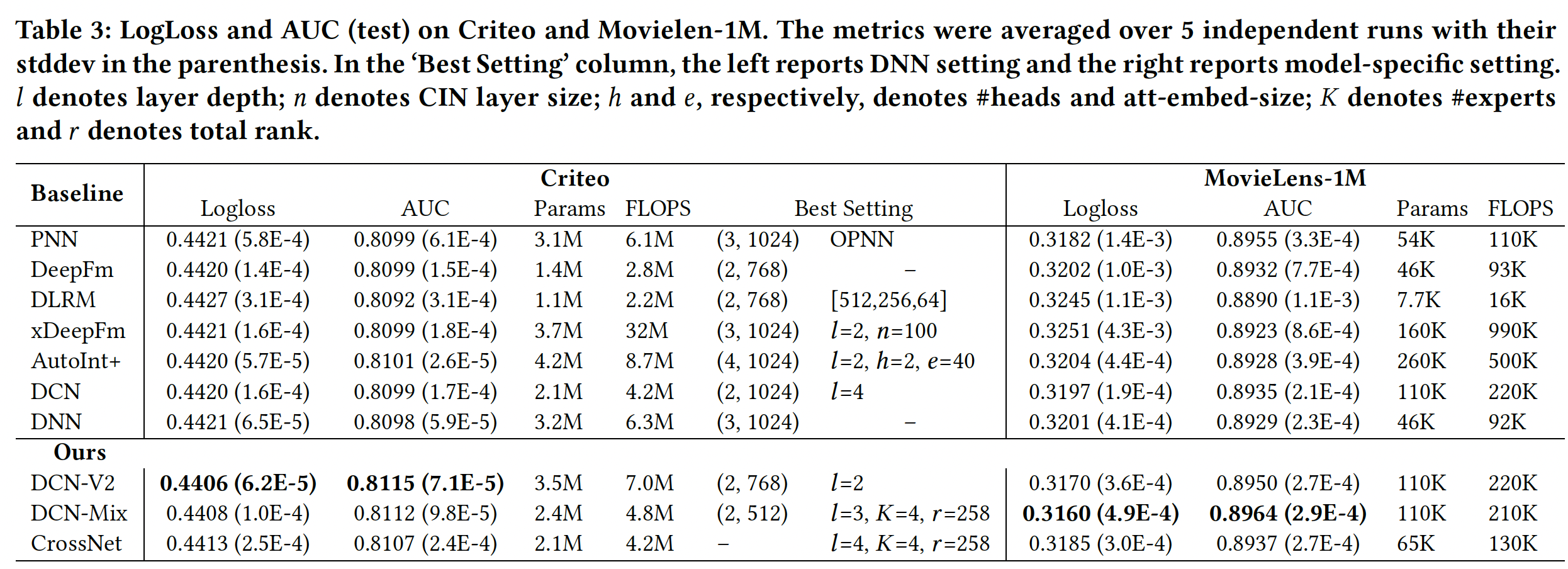
DCN-V2和baseline比较结果:每个模型的最佳setting是超参数空间中搜索出来的。如果两个setting的性能相当,我们就报告成本较低的那个。可以看到:我们看到,
DCN-V2的表现一直优于baseline(包括DNN),并实现了健康的quality/cost trade-off。注意,在我们为
baseline模型的最佳setting而进行的彻底的超参数搜索中,我们确实探索了更宽、更深的模型。然而,更大的模型也不能产生更多的质量收益,清楚地表明许多bseline的瓶颈是质量而不是效率。Best Setting:对于
DCN-V2模型,"stacked"和"parallel"结构都优于所有baseline,而"stacked"在Criteo上效果更好、"parallel"在Movielen-1M上效果更好。在实践中,我们发现:
"stacked"结构更能提高质量,而"parallel"结构有助于减少模型方差。
与
baseline的比较:- 对于二阶方法,
DLRM的表现不如DeepFM,尽管它们都来自FM。这可能是由于DLRM在点积层之后省略了一阶稀疏特征。 - 对于高阶方法,
xDeepFM、AutoInt和DCN在Criteo上的表现相似;而在MovieLens上,xDeepFM在Logloss上表现出很高的方差。 DCN-V2在Criteo上取得了最好的性能,它显式地建模三阶特征交互。DCN-Mix有效地利用了内存,并在保持准确性的同时减少了30%的成本。单独的CrossNet在两个数据集上的表现都优于DNN。
- 对于二阶方法,
与
DNN的比较:我们调优了DNN模型,并使用了更大的layer size。令我们惊讶的是,DNN的表现与大多数baseline相差无几,甚至超越了某些模型。我们的假设是:那些来自
baseline的显式特征交叉的模型并不是以一种富有表达能力、以及易于优化的方式建立的。前者使其性能容易被具有大容量的DNN所匹配,后者则容易导致可训练性问题从而使模型不稳定。因此,当与DNN组合时,整体性能被DNN组件所支配。在表达能力方面,考虑二阶方法。
PNN的模型比DeepFM和DLRM更具有表达能力,这导致它在MovieLen-1M上的表现更出色。这也解释了DCN与DCN-V2相比性能较差的原因。在可训练性方面,某些模型可能天生就比较难训练,导致性能不尽如人意。
在
Criteo上,PNN的平均性能与DNN相当。这是由PNN的不稳定性造成的。虽然它的最好成绩比DNN好,但它在多次试验中的高标准差推高了平均损失。
模型效率:
- 对于大多数模型,
FLOPS大约是参数数量的2倍。然而,对于xDeepFM,FLOPS要高出参数数量一个量级,这使得它在工业规模的应用中难以部署。 - 在所有的方法中,
DCN-V2提供了最好的性能,同时保持了相对的效率。 DCN-Mix进一步降低了成本,在模型效率和质量之间取得了更好的trade-off。
- 对于大多数模型,
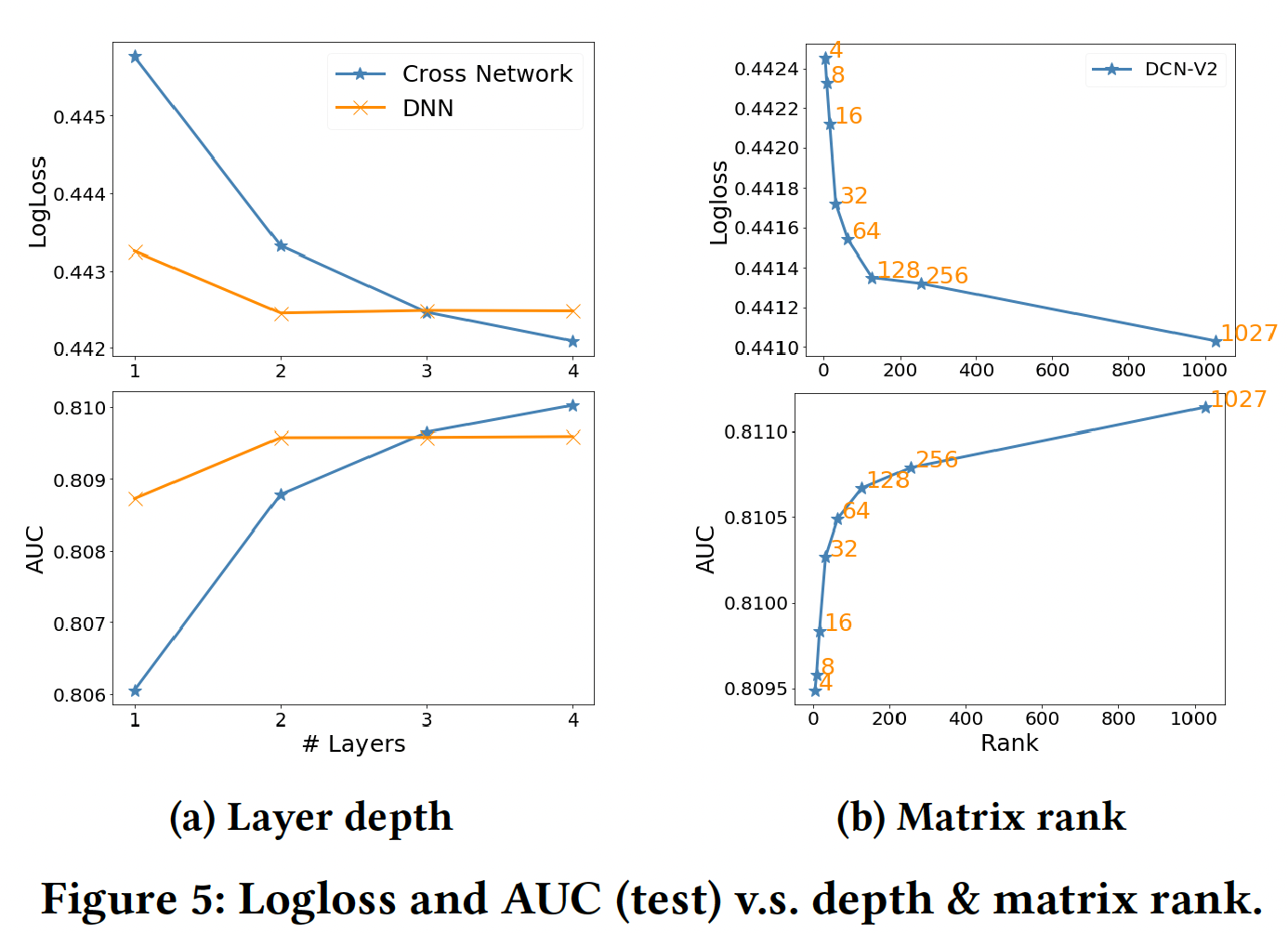
超参数研究:
Depth of Cross Layer:根据设计,cross network捕获的最高阶特征交叉随着层深的增加而增加。如图Figure 5 (a)所示:- 随着
cross network的加深,质量有了稳定的提高,表明它能够捕捉到更多有意义的交叉。 - 然而,当使用更多的层时,改善的速度放缓了。这表明高阶交叉的贡献比低阶交叉的贡献要小。
我们还用一个同样大小的
DNN作为参考。当有≤2层时,DNN的表现优于交叉网络;当有更多层时,cross network开始缩小性能差距,甚至优于DNN的表现。- 随着
矩阵的秩:模型是
3个交叉层,然后是3个512-size ReLU层。如图Figure 5 (b)所示:- 当
4时,性能与其他baseline持平。 - 当
4增加到64时,LogLoss几乎随 - 当
64进一步增加到满时,LogLoss的改善速度减慢了。
我们把
64称为rank阈值。从64开始的明显放缓表明:刻画特征交叉的重要信号可以在前64个奇异值中捕获。- 当
专家数量:我们观察到:
- 表现最好的
setting(专家数量、gate类型、激活函数类型)受到数据集和模型架构的影响。 - 每种
setting的最佳表现模型产生了相似的结果。更多的lower-rank experts并没有比单个higher-rank expert表现更好,这可能是朴素的gating函数、以及采取的optimizations所导致。我们相信更复杂的gating和optimization会在mixture of experts架构下产生更好的结果。
- 表现最好的
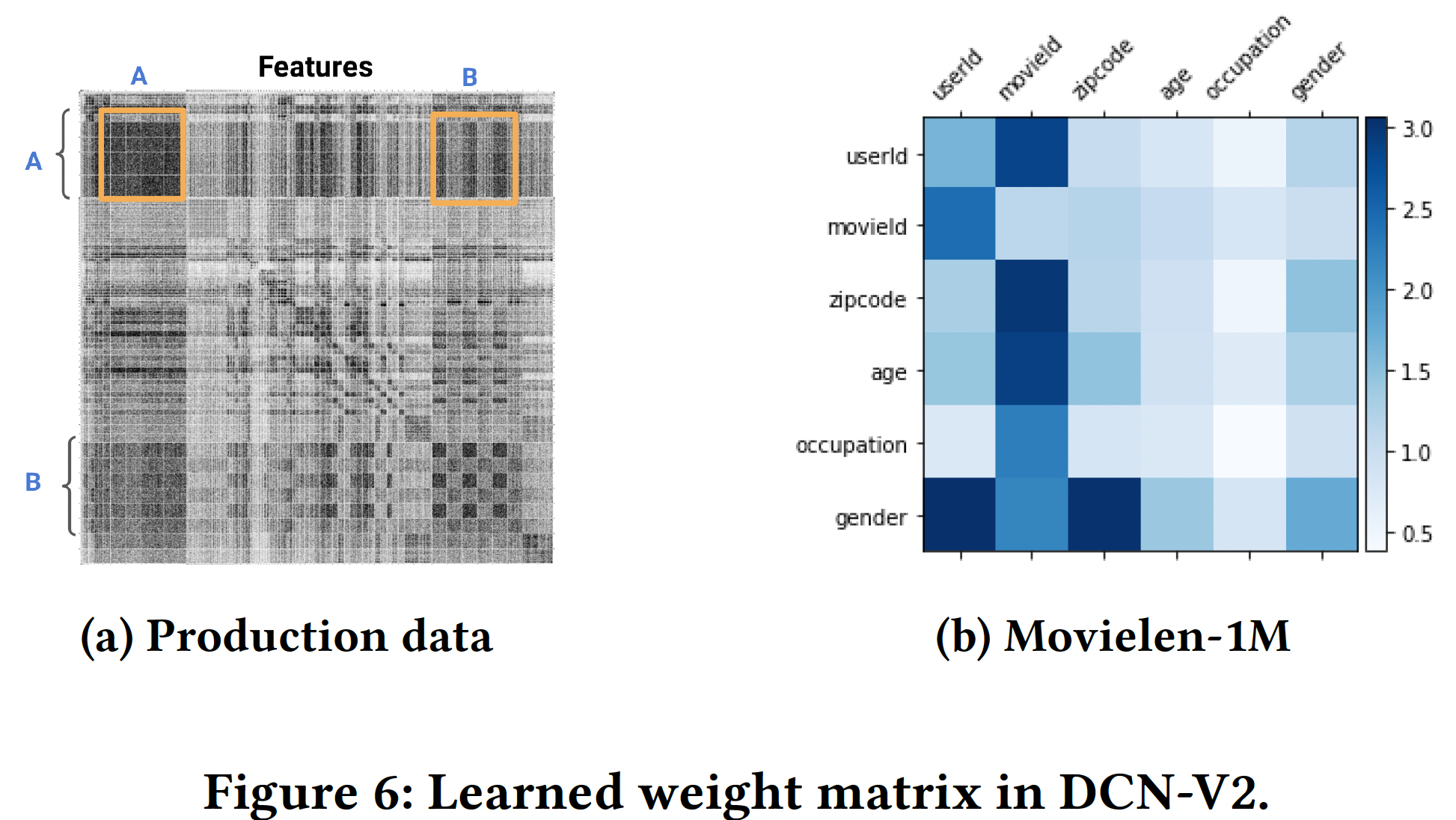
模型可视化:
DCN-V2中的权重矩阵block-wise视图(由下图展示了第一个交叉层中学到的权重矩阵
(a)中,由于版权的原因,特征名称被省略了;深色的像素代表较大的权重。在图(b)中,每个block代表它的Frobenius范数。图
(a)展示了整个矩阵,橙色方框突出了一些值得注意的特征交叉。非对角线的block对应于重要的交叉,这表明DCN-V2的有效性。对角线的block对应于self-interaction(即,图
(b)表现学到的一些强交互,如Gender × UserId、MovieId × UserId。图
(a)包含的特征更多,因此方块更小;图(b)包含很少的特征,因此方块显得很大。
DCN-V2在谷歌中的产品化:我们通过DCN-V2同时在离线模型的准确性、以及在线关键业务指标方面都取得了显著的收益。与公共数据集相比,收益也更加明显,这可能是由于生产数据集的数据量明显更大,数据分布更复杂。生产数据和模型:生产数据是由数以千亿计的训练样本组成的抽样用户日志。稀疏特征的词表规模从
2到数百万不等。baseline模型是一个全连接的多层感知机,采用ReLU激活函数。与生产模型的比较:与生产模型相比,
DCN-V2产生了0.6%的AUCLoss(即,1.0 - AUC)改进。我们还观察到显著的在线关键业务指标收益。baseline为多层感知机,所以DCN-V2表现好是符合预期的。为什么不和DeepFM进行比较?
我们分享一些我们通过产品化
DCN-V2学到的实际经验:- 最好在
DNN的输入层和隐层之间插入交叉层。 - 我们看到,通过堆叠或拼接
1-2个交叉层,准确性得到了一致的提高。超过2个交叉层,收益开始趋于平稳。 - 我们观察到,堆叠交叉层和拼接交叉层的效果都不错。堆叠层
stacking layers可以学到高阶的特征交互,而拼接层concatenating layers(类似于多头机制)可以捕获到互补的交互。 - 我们观察到,使用
rank = (input size)/4的low-rank DCN始终保持了full-rank DCN-V2的准确性。