主题模型
给包含 篇文档的定语料库 ,其中 为第 篇文档,包含 个单词。
语料库的所有单词来自于词汇表 ,其中 表示词汇表的大小,第 个单词为 。
注意:文档中的单词标记为 ,它表示文档中第 个位置的单词为 。如:文档中第1个位置的单词为 (假设 ),则文档中第一个位置的单词为
我。因此这里将 来表示文档中的单词(也称作
token),用 表示词表中的单词。BOW:Bag of Words:词在文档中不考虑顺序,这称作词袋模型。
一、Unigram Model
假设有一个骰子,骰子有 个面,每个面对应于词典中的一个单词。
Unigram Model是这样生成文档的:- 每次抛一次骰子,抛出的面就对应于产生一个单词。
- 如果一篇文档有 个单词,则独立的抛掷 次骰子就产生着 个单词。
令骰子的投掷出各个面的概率为 ,其中 为抛出的面是第 面的概率:。满足约束:
就是待求的参数。
假设文档包含 个单词,这些单词依次为 : ,其中 。用 代表文档, 则生成这篇文档的概率为:
在 中, 称作 的上下文。由于采取的是词袋模型,没有考虑上下文,所以有:
于是有:
- 如果考虑了上下文(即抛弃词袋模型),则各种单词的组合会导致爆炸性的复杂度增长。
- 由于是词袋模型,因此 并不构成一个概率分布。 仅仅是生成该文档的一种非归一化概率。
假设单词 中,有 个 ,有 个 ,...有 个 ,其中 ,则:
参数估计:就是估计骰子的投掷出各个面的概率
1.1 最大似然估计
假设数据集 包含 篇文档 。对文档 ,假设其单词依次为 , 用 来表示。其中:
- 表示文档 的第 个单词为单词 。
- 表示文档 一共有 个单词。
由于每篇文档都是独立的且不考虑文档的顺序和单词的顺序,则数据集发生的概率
假设数据集的所有单词 中,有 个 ,有 个 ,...有 个 。其中 , 为所有文档的所有单词的数量。则有:
使用最大似然估计法,也就是最大化对数的 :
于是求解:
用拉格朗日乘子法求解,其解为:
其物理意义为:单词 出现的概率 等于它在数据集 中出现的频率,即:它出现的次数 除以数据集 所有单词数 。
1.2 最大后验估计
根据贝叶斯学派的观点, 参数 也是一个随机变量而不再是一个常量,它服从某个概率分布 , 这个分布称作参数 的先验分布。
此时:
根据前面的推导有: ,则有:
此处先验分布 有多种选择。注意到数据集条件概率 刚好是多项式分布的形式,于是选择先验分布为多项式分布的共轭分布,即狄利克雷分布:
其中: 为参数向量, 为
Beta函数:显然根据定义有:
令 为词频向量,其每个元素代表了对应的单词在数据集 中出现的次数。
此时有:
因此 仅由 决定,记作:
后验概率 :
可见后验概率服从狄利克雷分布 。
因为这时候的参数 是一个随机变量,而不再是一个固定的数值,因此需要通过对后验概率 最大化或者期望来求得。
这里使用期望值 来做参数估计。
由于后验分布 服从狄利克雷分布 , 则有期望:
即参数 的估计值为:
考虑到 在狄利克雷分布中的物理意义为:事件的先验的伪计数。因此该估计式物理意义为:估计值是对应事件计数(伪计数+真实计数)在整体计数中的比例。
这里并没有使用最大似然数据集 来做参数估计,因为 中并没有出现参数 。
1.3 文档生成算法
文档生成算法:根据主题模型求解的参数来生成一篇新的文档。
最大似然模型的
Unigram Model生成文档步骤:根据词汇分布 ,从词汇表 中独立重复采样 次从而获取 个单词。则这些单词就生成一篇文档。
最大后验估计的
Unigram Model生成文档的步骤为:根据参数为 的狄利克雷分布 随机采样一个词汇分布 。
所谓随机采样一个词汇分布,即:根据狄里克雷分布生成一个随机向量。选择时要求 :
根据词汇分布 ,从词汇表 中独立重复采样 次从而获取 个单词。则这些单词就生成一篇文档。
二、pLSA Model
Unigram Model模型过于简单。事实上人们写一篇文章往往需要先确定要写哪几个主题。如:写一篇计算机方面的文章,最容易想到的词汇是:内存、CPU、编程、算法等等。之所以能马上想到这些词,是因为这些词在对应的主题下出现的概率相对较高。
因此可以很自然的想到:一篇文章由多个主题构成,而每个主题大概可以用与该主题相关的频率最高的一些词来描述。
上述直观的想法由
Hoffman在 1999 年的probabilistic Latent Semantic Analysis:pLSA模型中首先进行了明确的数学化。主题
topic:表示一个概念。具体表示为一系列相关的词,以及它们在该概念下出现的概率。- 与某个主题相关性比较强的词,在该主题下出现概率较高
- 与某个主题相关性比较弱的词,在该主题下出现概率较低
主题示例:给定一组词:
证明,推导,对象,酒庄,内存,下列三个主题可以表示为:- 数学主题:
- 计算机主题:
- 红酒主题:
证明 推导 对象 酒庄 内存 数学 0.45 0.35 0.2 0 0 计算机 0.2 0.15 0.45 0 0.2 红酒 0 0 0.2 0.8 0
2.1 文档生成算法
假设话题集合 有 个话题,分别为 。
pLSA模型的文档生成规则:以概率 选中第 个话题 ,然后在话题 中以概率 选中第 个单词 。
重复执行上一步
挑选话题--> 挑选单词次,则得到一篇包含 个单词 的文档,记作 。其中: , 表示文档的第 个单词为 。
对于包含 篇文档的数据集 ,假设所有文档都是如此生成。则数据集 的生成规则:
以概率 选中第 篇文档。这个概率仅仅用于推导原理,事实上随着公式的推导,该项会被消掉。
通常选择均匀选择,即
对于第 篇文档,以概率 选中第 个话题 ,然后在话题 中以概率 选中第 个单词 。
重复执行上一步
挑选话题--> 挑选单词次,则得到一篇包含 个单词 的文档,记作 。重复执行上述文档生成规则 次,即得到 篇文档组成的文档集合 。
2.2 模型原理
令
- 表示:选中第 篇文档 的条件下,选中第 个话题 的概率
- 表示:选中第 个话题 的条件下,选中第 个单词 的概率
待求的是参数 和 :
根据
pLSA概率图模型(盘式记法),结合成对马尔可夫性有:即:文档和单词关于主题条件独立。
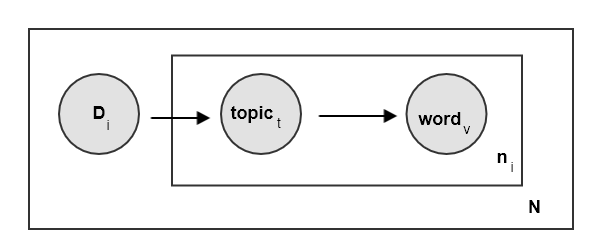
对于文档 ,给定其中的单词 ,有:
根据该等式,可以得到:
即:给定文档 的条件下,某个的单词 出现的概率可以分成三步:
- 首先得到给定的文档 的条件下,获取某个话题 的概率
- 再得到该话题 生成该单词 的概率
- 对所有的话题累加 即得到给定的单词 在给定文档 中出现的概率
对于给定文档 中主题 生成的单词 ,有:
则已知文档 中出现了单词 的条件下,该单词由主题 生成的概率为:
其物理意义为:给定文档 的条件下,单词 由主题 生成的概率占单词 出现的概率的比例。
2.3 参数求解
pLSA模型由两种参数求解方法:矩阵分解、EM算法。
2.3.1 矩阵分解
根据前面的推导,有: 。其中文档 和单词 是观测到的,主题 是未观测到的、未知的。
令 ,根据:
则有:
令:
则有: 。
由于 是观测的、已知的,所以
pLSA对应着矩阵分解。其中要求满足约束条件:.
2.3.2 EM 算法
在文档 中,因为采用词袋模型,所以单词的生成是独立的。假设文档 中包含单词 ,其中:
- 表示文档 的单词总数。
- 表示文档 的第 个单词为 。
则有:
根据前面的推导,有:。则:
则有:
假设文档 的单词 中,单词 有 个, 。 则有:
的物理意义为:文档 中单词 的数量。
考虑观测变量 ,它表示第 篇文档 以及该文档中的 个单词。
则有:
由于文档之间是相互独立的,因此有:
要使得观测结果发生,则应该最大化 。但是这里面包含了待求参数的乘积,其最大化难于求解,因此使用
EM算法求解。考虑完全变量 ,其中 为文档中 中每位置的单词背后的话题。
- 由于采用词袋模型,所以生成单词是相互独立的,因此有:
根据 有:
于是:
- 由于文档之间是相互独立的,因此有:
假设在文档 中,单词 不论出现在文档的哪个位置,都是由同一个话题 产生的。
则有:
则有:
则完全数据的对数似然函数为:
E步:求取Q函数,为 关于后验概率 的期望。根据前面的推导,有:
其中 均为上一轮迭代的结果,为已知量。
则有:
M步:最大化Q函数,同时考虑约束条件:对每个参数进行求导并使之等于0 ,联立方程求解得到:
文档-主题概率 更新方程
其物理意义:文档 中每个位置背后的、属于主题 的频数(按概率计数),除以位置的个数。也就是主题 的频率。
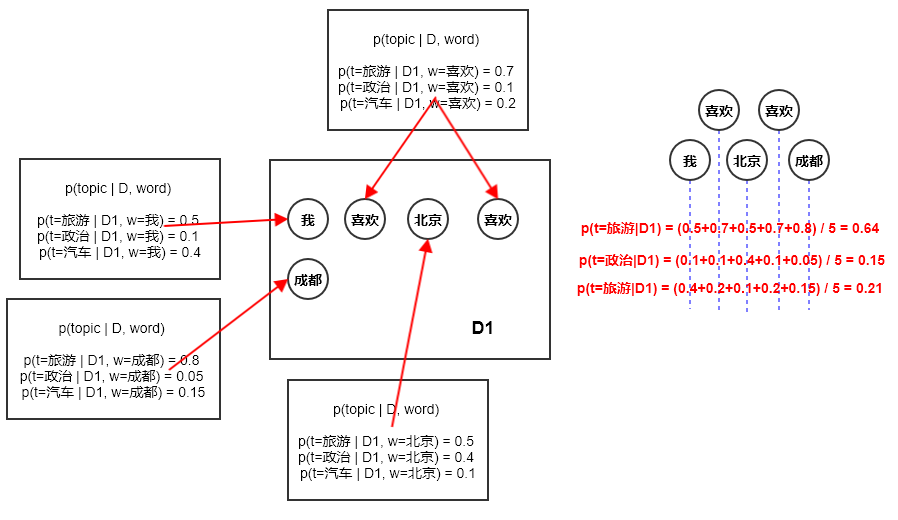
主题-单词概率 更新方程
其物理意义为:单词 在数据集 中属于主题 的频数(按概率计数),除以数据集 中属于主题 的频数(按概率计数)。即单词 的频率。
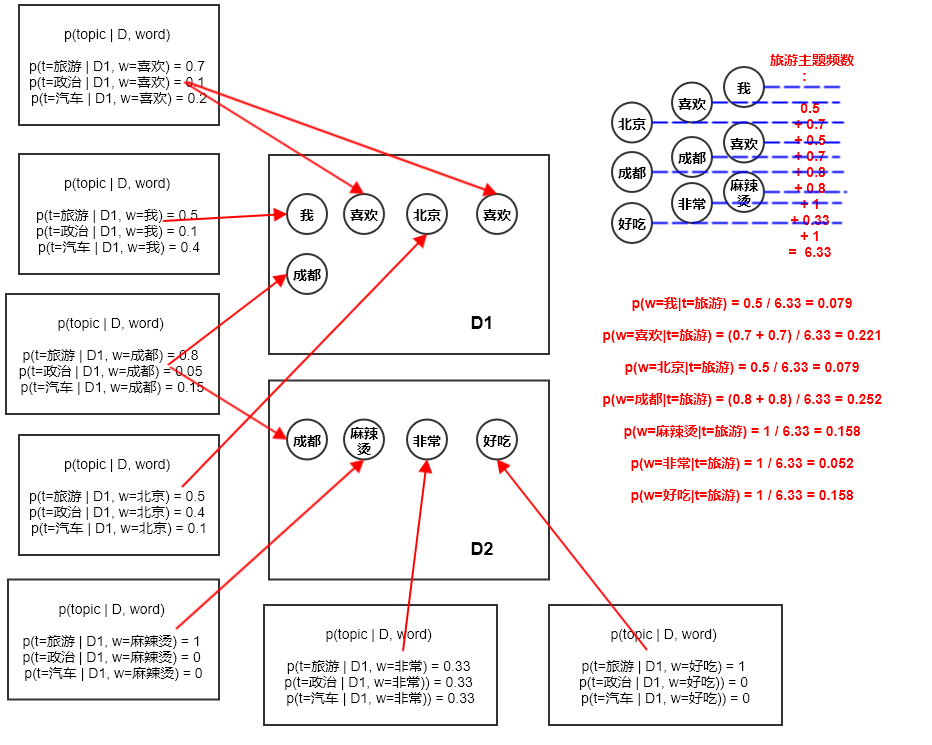
pLSA的EM算法:输入:文档集合 ,话题集合 ,字典集合
输出:参数 和 ,其中:
算法步骤:
初始化: 令 , 为 和 赋初值, 。
迭代,迭代收敛条件为参数变化很小或者
Q函数的变化很小。迭代步骤如下:E步:计算 函数。- 先计算后验概率:
再计算 函数:
M步:计算 函数的极大值,得到参数的下一轮迭代结果:重复上面两步直到收敛
三、LDA Model
在
pLSA模型中,参数 是常数。而在LDA模型中,假设 也是随机变量:- 参数 为文档 的主题分布(离散型的),其中 。该分布也是一个随机变量,服从分布 (连续型的)。
- 参数 为主题 的单词分布(离散型的),其中 。该分布也是一个随机变量,服从分布 (连续型的)。
因此
LDA模型是pLSA模型的贝叶斯版本。例:在
pLSA模型中,给定一篇文档,假设:- 主题分布为
{教育:0.5,经济:0.3,交通:0.2},它就是 。 - 主题
教育下的主题词分布为{大学:0.5,老师:0.2,课程:0.3},它就是 。
在
LDA中:给定一篇文档,主题分布 不再固定 。可能为
{教育:0.5,经济:0.3,交通:0.2},也可能为{教育:0.3,经济:0.5,交通:0.2},也可能为{教育:0.1,经济:0.8,交通:0.1}。但是它并不是没有规律的,而是服从一个分布 。即:主题分布取某种分布的概率可能较大,取另一些分布的概率可能较小。
主题
教育下的主题词分布也不再固定。可能为{大学:0.5,老师:0.2,课程:0.3},也可能为{大学:0.8,老师:0.1,课程:0.1}。但是它并不是没有规律,而是服从一个分布 。即:主题词分布取某种分布的概率可能较大,取另一些分布的概率可能较小。
- 主题分布为
3.1 文档生成算法
LDA模型的文档生成规则:- 根据参数为 的狄利克雷分布随机采样,对每个话题 生成一个单词分布 。每个话题采样一次,一共采样 次。
- 根据参数为 的狄利克雷分布随机采样,生成文档 的一个话题分布 。每篇文档采样一次。
- 根据话题分布 来随机挑选一个话题。然后在话题 中,根据单词分布 来随机挑选一个单词。
- 重复执行
挑选话题--> 挑选单词次,则得到一篇包含 个单词 的文档,记作 。其中: , 表示文档的第 个单词为 。
对于包含 篇文档的数据集 ,假设所有文档都是如此生成。则数据集 的生成规则:
以概率 选中第 篇文档。
根据参数为 的狄利克雷分布随机采样,对每个话题 生成一个单词分布 。每个话题采样一次,一共采样 次。
生成文档 :
- 根据参数为 的狄利克雷分布随机采样,生成文档 的一个话题分布 。每篇文档采样一次。
- 在文档 中,根据话题分布 来随机挑选一个话题。然后在话题 中,根据单词分布 来随机挑选一个单词。
- 重复执行
挑选话题--> 挑选单词次,则得到一篇包含 个单词 的文档,记作 。
重复执行上述文档生成规则 次,即得到 篇文档组成的文档集合 。
由于两次随机采样,导致
LDA模型的解会呈现一定程度的随机性。所谓随机性,就是:当多次运行LDA算法,获得解可能会各不相同当采样的样本越稀疏,则采样的方差越大,则
LDA的解的方差越大。- 文档数量越少,则文档的话题分布的采样越稀疏。
- 文档中的单词越少,则话题的单词分布的采样越稀疏。
3.2 模型原理
由于使用词袋模型,
LDA生成文档的过程可以分解为两个过程::该过程表示,在生成第 篇文档 的时候,先从
文档-主题分布 中生成 个主题。其中:
- 表示文档 的第 个单词由主题 生成。
- 表示文档 一共有 个单词。
:该过程表示,在已知主题为 的条件下,从
主题-单词分布 生成 个单词。其中:
- 表示由主题 生成的的第 个单词为 。
- 为由 生成的单词的数量。
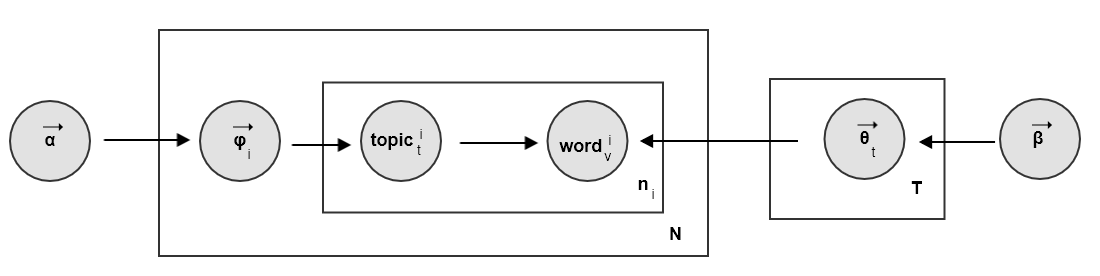
3.2.1 主题生成过程
主题生成过程用于生成第 篇文档 中每个位置的单词对应的主题。
:对应一个狄里克雷分布
:对应一个多项式分布
该过程整体对应一个
狄里克雷-多项式共轭结构:
合并文档 中的同一个主题。设 表示文档 中,主题 出现的次数。则有:
则有:
其中 表示文档 中,各主题出现的次数。
由于语料库中 篇文档的主题生成相互独立,则得到整个语料库的主题生成概率:
.
3.2.2 单词生成过程
单词生成过程用于生成数据集 中所有文档的所有主题的单词。
:对应一个狄里克雷分布
:对应一个多项式分布,其中 为数据集 中(将所有单词拼接在一起)由主题 生成的单词。
数据集 中,由主题为 生成的所有单词的分布对应一个
狄里克雷-多项式共轭结构:
合并主题 生成的同一个单词。设 表示中主题 生成的单词中, 出现的次数。则有:
则有:
其中 表示由主题 生成的单词的词频。
考虑数据集 中的所有主题,由于不同主题之间相互独立,则有:
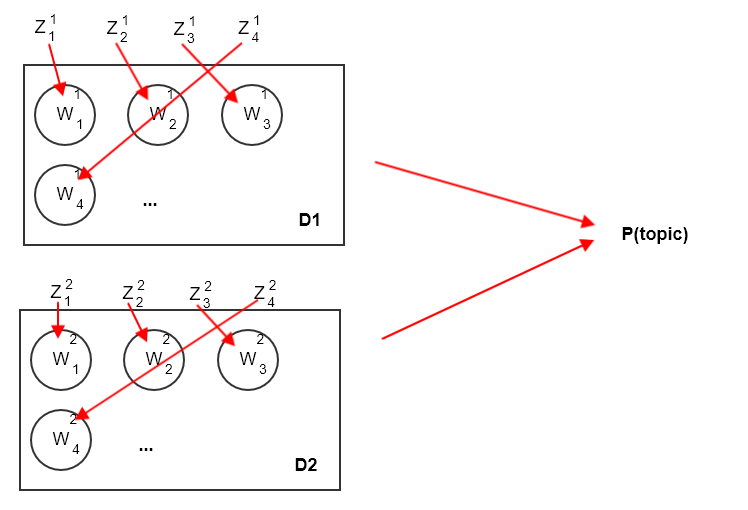
这里是按照主题来划分单词,如果按照位置来划分单词,则等价于:
注意:这里 的意义发生了变化:
- 对于前者, 表示由主题 生成的第 个单词。
- 对于后者, 表示文档 中的第 个单词。
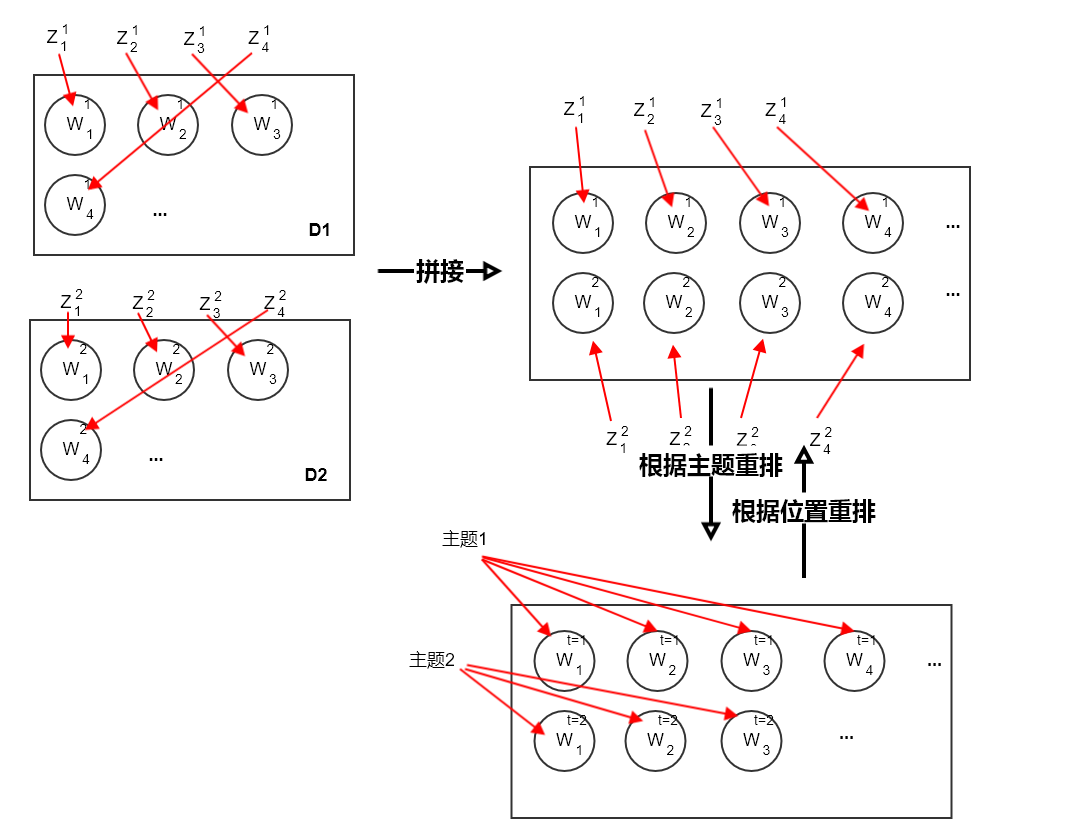
3.2.3 联合概率
数据集 的联合概率分布为:
其中:
- 表示文档 中,各主题出现的次数。
- 表示主题 生成的单词中,各单词出现的次数。
3.2.4 后验概率
若已知文档 中的主题 ,则有:
则有: 。这说明参数 的后验分布也是狄里克雷分布。
若已知主题 及其生成的单词 则有:
则有: 。这说明参数 的后验分布也是狄里克雷分布。
3.3 模型求解
LDA的求解有两种办法:变分推断法、吉布斯采样法。
3.3.1 吉布斯采样
对于数据集 :
- 其所有的单词 是观测的已知数据,记作 。
- 这些单词对应的主题 是未观测数据,记作 。
需要求解的分布是: 。其中: 表示文档 的第 个单词为 , 表示文档 的第 个单词由主题 生成。
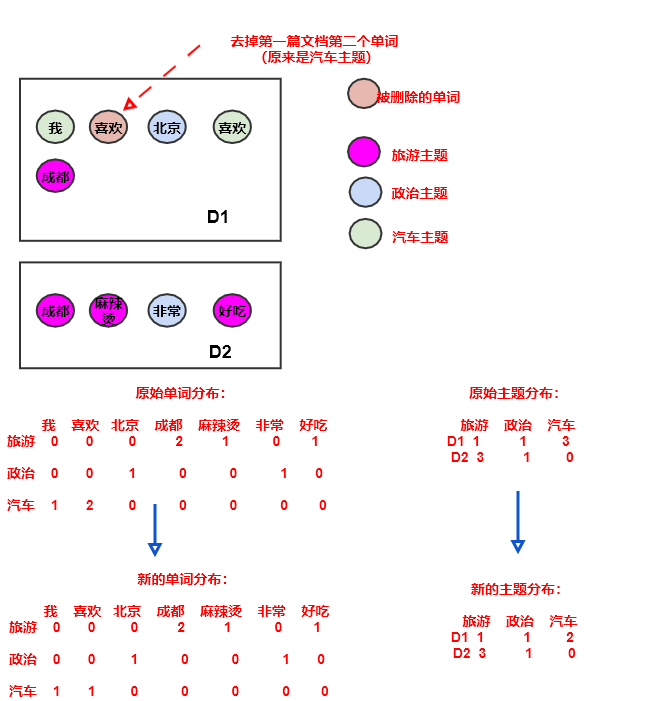
定义 为:去掉 的第 个单词背后的那个生成主题(注:只是对其频数减一):
定义 为:去掉 的第 个单词:
根据吉布斯采样的要求,需要得到条件分布:
根据条件概率有:
则有:
对于文档 的第 个位置,单词 和对应的主题 仅仅涉及到如下的两个
狄里克雷-多项式共轭结构:- 文档 的主题分布
- 已知主题为 的情况下单词的分布
对于这两个共轭结构,去掉文档 的第 个位置的主题和单词时:
先验分布(狄里克雷分布):保持不变。
文档 的主题分布:主题 频数减少一次,但是该分布仍然是多项式分布。其它 个文档的主题分布完全不受影响。因此有:
主题 的单词分布:单词 频数减少一次,但是该分布仍然是多项式分布。其它 个主题的单词分布完全不受影响。因此有:
根据主题分布和单词分布有:
其中:
- 表示去掉文档 的第 个位置的单词和主题之后,第 篇文档中各主题出现的次数。
- 表示去掉文档 的第 个位置的单词和主题之后,数据集 中,由主题 生成的单词中各单词出现的次数。
考虑 。记 ,则有:
考虑到主题生成过程和单词生成过程是独立的,则有:
考虑到文档 的第 个位置的单词背后的主题选择过程和其它文档、以及本文档内其它位置的主题选择是相互独立的,则有:
考虑到文档 的第 个位置的单词选择过程和其它文档、以及本文档内其它位置的单词选择是相互独立的,则有:
则有:
根据狄里克雷分布的性质有:
则有:
其中: 为文档 的第 个位置的单词背后的主题在主题表的编号; 为文档 的第 个位置的单词在词汇表中的编号。
根据上面的推导,得到吉布斯采样的公式():
- 第一项刻画了:文档 中,第 个位置的单词背后的主题占该文档所有主题的比例(经过 先验频数调整)。
- 第二项刻画了:在数据集 中,主题 中,单词 出现的比例(经过 先验频数调整)。
- 它整体刻画了:文档 中第 个位置的单词为 ,且由主题 生成的可能性。
令:
- 为数据集中所有主题的先验频数之和
- 为数据集中所有单词的先验频数之和
- 表示去掉文档 位置 的主题之后,文档 剩下的主题总数。它刚好等于 ,其中 表示文档 中单词总数,也等于该文档中的主题总数。
- 表示:数据集 中属于主题 的单词总数。
- 表示去掉文档 位置 的单词之后,数据集 中属于主题 的单词总数,则它等于 。
则有:
考虑到对于文档 来讲, 是固定的常数,因此有:
事实上,上述推导忽略了一个核心假设:考虑到采取词袋假设,
LDA假设同一篇文档中同一个单词(如:喜欢)都由同一个主题生成。定义 为:已知所有单词,以及去掉文档 中单词 出现的所有位置(对某个单词,如
喜欢,可能在文档中出现很多次)背后的主题的条件下,单词 由主题 生成的概率。则有:
其中:
表示:去掉单词 出现的所有位置背后的主题之后,文档 剩余的主题中,属于主题 的总频数。则根据定义有:
其中 表示文档 中单词总数,也等于该文档中的主题总数; 为文档 中单词 出现的次数。
表示:去掉文档 单词 出现的所有位置背后的主题之后,数据集 中由主题 生成的单词 总数。则根据定义有:
其中 表示数据集 中属于主题 的单词总数。
因此得到:
这称作基于单词的采样:每个单词采样一次,无论该单词在文档中出现几次。这可以确保同一个文档中,相同的单词由同一个主题生成。
前面的采样方式称作基于位置的采样:每个位置采样一次。这种方式中,同一个文档的同一个单词如果出现在不同位置则其主题很可能会不同。
3.3.2 模型训练
定义
文档-主题计数矩阵 为:其中第 行代表文档 的主题计数。
定义
主题-单词计数矩阵 为:其中第 行代表 主题 的单词计数
LDA训练的吉布斯采样算法(基于位置的采样)输入:
- 单词词典
- 超参数
- 主题数量
- 语料库
输出:
文档-主题分布 的估计量
主题-单词分布 的估计量
因为这两个参数都是随机变量,因此使用它们的期望来作为一个合适的估计
算法步骤:
设置全局变量:
- 表示文档 中,主题 的计数。它就是 ,也就是 的第 行第 列。
- 表示主题 中,单词 的计数。它就是 ,也就是 的第 行第 列。
- 表示各文档 中,主题的总计数。它也等于该文档的单词总数,也就是文档长度,也就是 的第 行求和。
- 表示单主题 中,单词的总计数。它也就是 的第 行求和。
随机初始化:
对全局变量初始化为 0 。
遍历文档:
对文档 中的每一个位置 ,其中 为文档 的长度:
- 随机初始化每个位置的单词对应的主题:
- 增加“文档-主题”计数:
- 增加“文档-主题”总数:
- 增加“主题-单词”计数:
- 增加“主题-单词”总数:
迭代下面的步骤,直到马尔科夫链收敛:
遍历文档:
对文档 中的每一个位置 ,其中 为文档 的长度:
删除该位置的主题计数,设 :
根据下面的公式,重新采样得到该单词的新主题 :
记新的主题在主题表中的编号为 ,则增加该单词的新的主题计数:
如果马尔科夫链收敛,则根据下列公式生成
文档-主题分布的估计,以及主题-单词分布 的估计:
如果使用基于单词的采样,则训练过程需要调整为针对单词训练,而不是针对位置训练:
对文档 中的每一个词汇 ,其中 为出现在文档 的词汇构成的词汇表的大小。:
- 随机初始化每个词汇对应的主题:
- 增加“文档-主题”计数:
- 增加“文档-主题”总数:
- 增加“主题-单词”计数:
- 增加“主题-单词”总数:
其中 表示文档 中单词 出现的次数。
采样公式:
主题更新公式:
通常训练时对 和 进行批量更新:每采样完一篇文档或者多篇文档时才进行更新,并不需要每次都更新。
- 每次更新会带来频繁的更新需求,这会带来工程实现上的难题。如分布式训练中参数存放在参数服务器,频繁更新会带来大量的网络通信,网络延时大幅增加。
- 每次更新会使得后一个位置(或者后一个单词)的采样依赖于前一个采样,因为前一个采样会改变文档的主题分布。这使得采样难以并行化进行,训练速度缓慢。
这使得训练时隐含一个假设:在同一篇文档的同一次迭代期间,
文档-主题计数、主题-单词矩阵保持不变。即:参数延迟更新。
3.3.3 模型推断
理论上可以通过最大似然估计来推断新的文档 的主题分布。设新文档有 个单词,分别为 。 假设这些单词背后的主题分别为 。则有:
由于单词的生成是独立的,且主题的单词分布是已经求得的,因此有:
由于主题的选择是独立的,但是文档的主题分布未知,该主题分布是从狄里克雷分布采样。因此有:
其中 为文档中主题 的频数。
因此有:
由于 取值空间有 个,则新文档中可能的主题组合有 种,因此最大似然 计算量太大而无法进行。
有三种推断新文档主题分布的策略。假设训练文档集合为 ,待推断的文档集合为 ,二者的合集为 。
完全训练:
- 首先单独训练 到模型收敛。
- 然后加入 ,并随机初始化新文档的主题,继续训练模型到收敛。
这种做法相当于用 的训练结果为 的主题进行初始化( 的部分仍然保持随机初始化)。其推理的准确性较高,但是计算成本非常高。
固定主题:
- 首先单独训练 到模型收敛。
- 然后加入 ,并随机初始化新文档的主题,继续训练模型到收敛。训练过程中固定 的主题。
这种做法只需要在第二轮训练中更新 的主题。
固定单词:
- 首先单独训练 到模型收敛。
- 然后训练一篇新文档 。训练过程中,使用训练集合 的主题-单词计数矩阵 。
这种做法可以在线推断,它每次只处理一篇新文档(前面两个版本每次处理一批新文档)。
四、LDA优化
标准
LDA的模型训练过程中,对于文档 (令 ,采用基于位置的更新) :常规的采样方式是:
- 计算
- 将采样空间划分为:第一段 , 第二段 ,... 第 段 ,称作分桶。
- 在 之间均匀采样一个点,该点落在哪个桶内则返回对应桶的主题。
常规
LDA采样算法:- 在 之间均匀采样一个点,假设为 。其算法复杂度为 ,因为需要计算 。
- 查找下标 ,使得满足 ,返回 。通过二分查找,其算法复杂度为 。
事实上如果执行非常多次采样,则常规
LDA采样算法第一步的成本可以分摊到每一次采样。因此整体算法复杂度可以下降到 。如果仅执行一次采样,则整体算法复杂度为 。与 有关,而 在文档 的不同位置 取值不同。这意味着每一次采样的概率分布都不同,因此采样每个主题的算法复杂度为 。
有三种算法对采样过程进行了加速:
SparseLDA和AliasLDA使用基于位置的采样,这是为了方便对采样概率进行有效分解。LightLDA使用基于单词的采样,这种采样更能够满足LDA的假设:LDA假设同一篇文档中同一个单词都由同一个主题生成。
4.1 SparseLDA
sparseLDA推断比传统LDA快大约20倍,且内存消耗更少。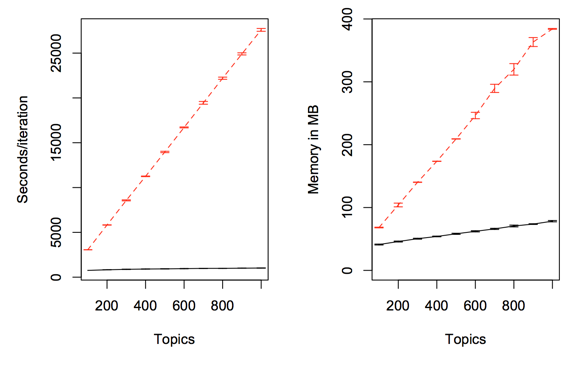
4.1.1 概率分解
SparseLDA主要利用了LDA的稀疏性。事实上,真实场景下的一篇文档只会包含少数若干个主题,一个词也是参与到少数几个主题中。因此可以将采样公式分解(令 ,采用基于位置的更新):令:
其中: 仅仅和主题的单词统计有关; 和文档 的主题统计、主题的单词统计都有关; 和文档 的主题统计、主题的单词统计、文档 的单词统计都有关。
假设 为常数,即:主题的所有单词的先验频数都为常数 。现在仅考虑一篇文档的训练,因此忽略角标 ,有:
令 ,原始
LDA的采样方式为:- 将 划分为 个桶,将每个桶根据其 分解继续划分为三个子桶。
- 根据从均匀分布 中采样一个点。该点落在那个桶,则采样该桶对应的主题。
假设该点落在桶 ,则有三种情况:
- 若该点落在
r对应的子桶,其概率为 。 - 若该点落在
s对应的子桶,其概率为 。 - 若该点落在
q对应的子桶,其概率为 。
考虑重新组织分桶,按照 划分为
[0,R)、[R,R+S)、[R+S,U)三个桶。将第一个桶根据 划分为T个子桶; 将第二个桶根据 划分为T个子桶;将第三个桶根据 划分为T个子桶。则上述采样过程的三种情况等价于:从均匀分布 中采样一个点。该点落在那个桶,则就在桶内的子桶中继续采样主题。
- 该桶落在
R桶的子桶t,其概率为: 。 - 该桶落在
S桶的子桶t,其概率为: 。 - 该桶落在
Q桶的子桶t,其概率为: 。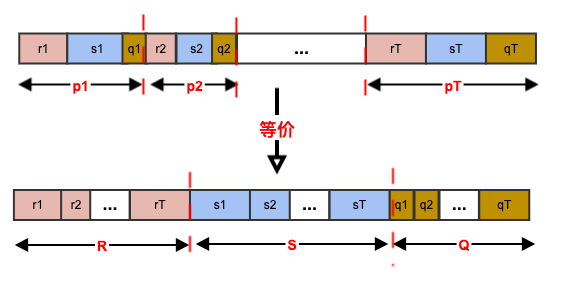
- 该桶落在
4.1.2 采样过程
sparseLDA采样过程中假设:在同一篇文档的同一次迭代期间,文档-主题计数、主题-单词矩阵保持不变。即:参数延迟更新。sparseLDA采样过程:从均匀分布 中采样一个点 。如果 ,则从 中继续均匀采样一个点,设该点落在子桶 ,则返回主题 。
考虑到 对于同一篇文档中的所有位置都相同,这使得对桶 采样的平摊算法复杂度为 。
如果 ,则从 中继续均匀采样一个点,设该点落在子桶 ,则返回主题 。
此时只需要考虑当前文档中出现的主题,因为对于其它未出现的主题有 ,则 。
因此对桶 采样的算法复杂度为 , 为文档中出现的主题数量。 同时内存消耗更少,因为只需要保存非零值对应的分量。
如果 ,则从 中继续均匀采样一个点,设该点落在子桶 ,则返回主题 。
此时只需要考虑使得当前单词 的
主题-单词计数非零的那些主题。因为对于其它主题有 ,则 。因此对桶 采样的算法复杂度为 , 为当前单词 涉及到的主题数量 。 同时内存消耗更少,因为只需要保存非零值对应的分量。
整体推断的算法复杂度为 。
对于小数据集, ,但是对于大数据集可能发生 。即:单词 出现在了几乎所有主题中。
假设单词 由主题 生成的可能性为 ,则 篇文档中 至少由主题 生成的一次的概率为:
因此对于非常大的数据集对于
sparseLDA是不利的。
4.2 AliasLDA
4.2.1 概率分解
AliasLDA通过引入Alias Table和Metropolis-Hastings方法来进一步加快采样速度。AliasLDA对采样公式进行不同的分解(令 ,采用基于位置的更新):其中 与文档无关。
AliasLDA采样过程是:从均匀分布 中采样一个点 。如果 ,则从 中继续均匀采样一个点,设该点落在子桶 ,则返回主题 。
此时只需要考虑当前文档中出现的主题,因为对于其它未出现的主题有 ,则 。
因此对桶 采样的算法复杂度为 , 为文档中出现的主题数量。 同时内存消耗更少,因为只需要保存非零值对应的分量。
如果 ,则从 中继续均匀采样一个点,设该点落在子桶 ,则返回主题 。
如果能够使得该子采样的算法复杂度为 ,则整体采样的算法复杂度为 ,要大大优于
sparseLDA的 。
4.2.2 Alias Table
Alias Table用于将离散的、非均匀分布转换成离散的、均匀的分布。这是为了采样方便:离散均匀分布的采样时间复杂度为 。假设一个离散、非均匀分布为 。
常规的采样方式为:
- 分桶:
1:[0,1/2), 2:[1/2,5/6), 3:[5/6,11/12), 4:[11/12,1)。 - 采样:从
0~1之间均匀生成一个随机数x,x落在哪个桶(二分查找),则返回对应的桶的编号。
其平均每次采样的复杂度为 ,其中 为事件的数量。
- 分桶:
一个改进的方法是:
建立四个分桶,桶的编号分别为
1~4。从
1~4中均匀采样一个整数,决定落在哪个桶。假设在第 个桶。从
0~1之间均匀采样一个小数 ,则:- 计算非归一化概率: (即:归一化概率除以其中的最大值)。
- 若 ,则接受采样,返回事件 ;若 ,则拒绝接受,重新采样(重新选择分桶、重新采样小数)。
理想情况下其算法复杂度为 ,平均情况下算法复杂度为 。
可以看到:事件 被选中的概率(非归一化)为:,归一化之后就是 。

Alias Table在上述思想指导下更进一步,它对概率除以均值而不是最大值。构建
Alias Table(算法复杂度 ):初始化数组 ,第 个桶的容量 表示事件 发生的概率; , 存放第 个桶中的另外一个事件的编号。
第 个桶要么完全由事件 组成,要么由事件 和另外一个事件组成(由 给出)。每个桶最多包含2个事件。
将每个桶的容量乘以 : 。即:计算非归一化概率。
构建队列
A,存放容量大于1的桶编号;构建队列B,存放容量小于1的桶编号。处理每个桶,直到满足条件:队列
B为空。处理方式为:从队列
A取出一个桶,假设为 ;从队列B取出一个桶,假设为 。将 填充到容量为1,填充的容量从 消减。假设消减的容量为- 记录容量: ;登记: 。
注意:此时不需要更新 , 存放的是事件 的非归一化概率,也等于它在桶中的比例。
- 若 ,则继续放入队列
A;若 ,则放入队列B;若 ,则桶 处理完成。
最终每个桶的容量都是1,桶内最多存放两个事件(由 记录)。
从
1~N中均匀采样一个整数,决定落在哪个桶。从
0~1之间均匀采样一个小数 。假设在第 个桶:若 ,则返回事件 ;否则返回事件 。
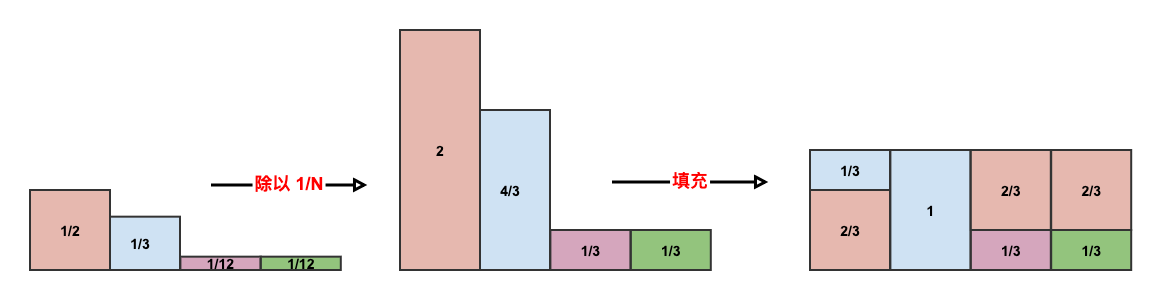
Alias Table的算法复杂度:- 构建
Alias Table步骤复杂度 ,采样步骤复杂度 - 如果采样1次,则算法复杂度为 。如果采样非常多次,则构建
Alias Table的代价会被平均,整体的平摊复杂度为 。
- 构建
4.2.3 MH 采样算法
如果直接对 采用
Alias Table采样,则会发现一个严重的问题:对于文档中不同位置 的单词 不同,因此概率分布 随位置 发生变化。这就相当于采样 1 次的Alias Table算法,完全没有发挥出Alias Table的优势。解决方式是:提出一个不随位置 变化的概率分布 ,它近似原始分布 但是更容易采样。然后采用基于
MH的MCMC采样算法。标准的
MH算法需要构建状态转移矩阵,但是这里的状态转移比较特殊:状态转移概率仅与最终状态有关,与前一个状态无关,即: 。算法输入: 近似概率分布 ,原始概率分布
算法输出:满足原始分布的采样序列
算法步骤:
从概率分布 中随机采样一个样本
对 执行迭代。迭代步骤如下:
根据 采样出候选样本
计算接受率 :
根据均匀分布从 内采样出阈值 ,如果 ,则接受 , 即 。否则拒绝 , 即 。
由于 近似于 ,因此大多数情况下会接受 。
返回采样序列 。
注意:返回的序列中,只有充分大的 之后的序列 才是服从原始分布的采样序列。
4.2.4 AliasLDA
AliasLDA综合采用了AliasTable和MH采样算法。对分桶 采样的算法步骤:构建不随文档中的位置 变化的概率分布 ,算法复杂度 。
根据 构建
AliasTable,算法复杂度 。循环:遍历文档的所有位置 :
对于文档的当前位置 根据前述的
MH算法采样出主题 ,其算法复杂度为 。
考虑到前面两步的代价可以平摊到每次采样过程,因此平摊算法复杂度为 。
4.3 LightLDA
web-scale规模的预料库非常庞大也非常复杂,通常需要高容量的主题模型(百万主题、百万词汇表,即:万亿参数级别)来捕捉长尾语义信息。否则,当主题太少时会丢失这些长尾语义信息。这种规模数据集的训练需要上千台机器的集群,而
LightLDA允许少量的机器来训练一个超大规模的LDA主题模型,它可以用 8 台机器训练一个包含百万主题&百万词汇表(万亿级参数)、包含千亿级单词的数据集。LightLDA主要采用了以下方法:- 更高效的
MH采样算法,其算法复杂度为 ,并且与当前最先进的Gibbs采样器相比收敛效率快了近一个量级。 structure-aware的模型并行方案,其利用主题模型中的依赖关系,产生一个节省机器内存和网络通信的采样策略。- 用混合数据结构来存储模型,其针对高频单词和低频单词采用不同的数据结构,从而使得内存可以放置更大规模的模型,同时保持高效的推断速度。
- 有界异步数据并行方案,其可以降低网络同步和通信的成本,从而允许通过参数服务器对海量数据进行有效的分布式处理。
- 更高效的
4.3.1 structure-aware 模型并行
数据并行:分割数据集,将不同文档集交给不同的
worker来处理。所有worker共享同一份模型参数,即:共享同一份全局主题-单词矩阵 。如:
YahooLDA和 基于参数服务器的LDA实现就是采取数据并行。数据并行+模型并行:分割数据集,将不同文档集交给不同的
worker来处理。同时分割模型,不同worker处理不同的主题-单词分布。即:每个worker只会看到并处理本地文档出现过的单词的主题-单词分布。如:
PLDA和Peacock,以及LDA就是采取这种策略。为了解决模型内存需求太大与
worker内存较小的问题,LightLDA提出了structure-aware模型并行方案。在每个
worker中,采样算法执行之前先将本worker分割到的数据集进一步划分为数据块Data Block 1,Data Block 2,...。同时计算每个数据块包含的单词的词汇表,并将该词汇表作为元数据附加到数据块上。该操作只需要线性扫描,其计算复杂度为 。
在
worker对Data Block i执行采样时:首先加载数据块
Data Block i到worker的内存,取得该block的元数据。然后根据元数据,将该数据块的词汇表划分为集合 。
对每个词表集合 ,拉取参数服务器中的全局
主题-单词矩阵 中涉及 的单词的部分,称作模型切片,记作 。因此worker仅仅需要保存模型的一个切片。然后对
Data Block i中的所有文档执行采样并更新 ,采样时仅仅考虑出现在 中的单词。当对 更新完毕时,将本次更新同步到参数服务器中的全局
主题-单词矩阵 。然后继续处理下一个词汇集合 。
一旦对
Data Block i处理完毕,继续采样下一个数据块Data Block i+1。
如下图所示为
Data Block 2的采样过程, 表示该数据块包含的文档数量。在d1,d2,...中的箭头给出了主题采样的顺序。每个文档通过灰色块表明出现对应的单词(出现一次或多次)、白色块表明没有出现对应的单词。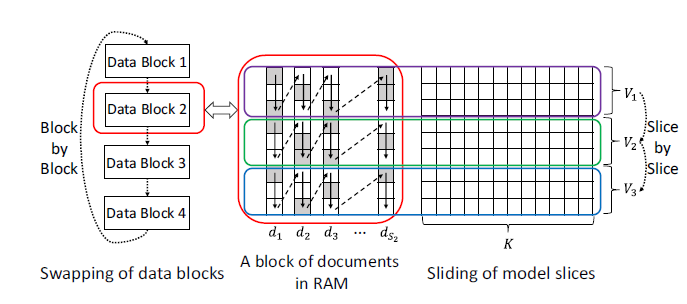
structure-aware除了降低worker内存需求之外,还通过以下方式减轻网络通信瓶颈:在处理数据块
Data Block i时,只有当前模型切片相关的所有单词都被采样时,才会移动到下一个模型切片。这使得在处理数据块
Data Block i时,每个模型切片只需要被换入换出内存一次,而不是反复换入换出内存。模型切片的换入换出需要和参数服务器进行同步,因此多次交换会增大通信压力。在利用当前模型切片对数据块采样时,可以同步进行下一个模型切片的加载(从参数服务器拉取到本地)、上一个模型切片的同步更新(从本地推送到参数服务器)。
这进一步降低了网络通信的时间延迟。
4.3.2 高效的 MH 采样算法
AliasLDA采样的计算复杂度为 ,因此它不擅长处理比较长的文档,比如网页。这是因为:在初始迭代中,文档每个位置的主题都是随机初始化的,因此对于较长的文档 非常大。这会使得AliasLDA在迭代初期非常缓慢,消耗大量时间。当利用分布 对 进行采样时,一个好的 需要满足两个条件(从而加速采样速度):从 中采样相对更加容易;马尔科夫链更快混合
mix。因此在设计分布 时,存在一个折中:
- 如果分布 和 更接近,则马尔科夫链混合的更快,但是从 采样的代价可能与 相差无几。
- 如果分布 非常容易采样但是与 很不一样,则马尔科夫链混合的很慢。
所谓马尔科夫链的良好的混合意味着:马尔科夫链能够收敛,且收敛速度不会太长。
当拒绝率太高时,
MCMC采样很可能长期处于某些值附近(如下图所示的平摊区域),搜索整个参数空间要花非常多的时间。下图中,横轴为迭代次数,纵轴表示采样结果。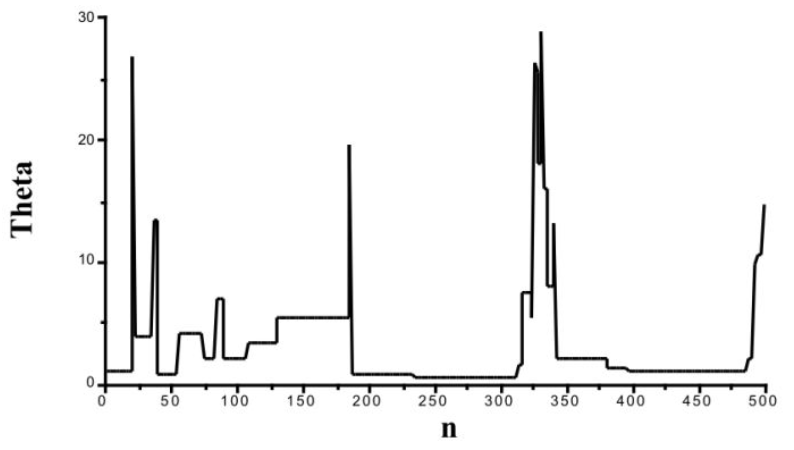
与
AliasLDA和SparseLDA不同,LightLDA用两个近似分布 来对 进行采样。考虑采样概率:
定义 :
其中 为文档内主题 的频次, 为文档长度。则接受率为:
定义:
其中 表示数据集 中由主题 生成的单词中单词 的次数, 表示数据集 中由主题 生成的单词总频数。则接受率为:
为了提高对 的采样效率,对 进一步拆分:
因此采样步骤为:
首先从均匀分布 中采样一个点。
如果该点落在 之间,则使用 进行采样。此时无需建立
AliasTable,直接从文档中均匀随机选择一个单词,其背后的主题就是采样得到的主题,该分布刚好就是 。如果该点落在 之间,则使用 进行采样。
- 如果 为常数,则此时 为均匀分布,无需建立
AliasTable。 - 如果 并不是全部相等,则由于 与单词、文档都无关,因此可以建立全局
AliasTable,它可以跨单词、跨数据块共享,其平均时间、空间复杂度为 。
- 如果 为常数,则此时 为均匀分布,无需建立
因此从 采样的平摊时间、空间复杂度均为 。
为了提高对 的采样效率,采用类似于
AliasLDA的Alias Table方式,从而使得对 的采样复杂度为 。注意:虽然在文档内部, 在不同位置处不同,是变化的,因此不满足
Alias Table的要求。但是在同一个数据块中,对于同一个单词 , 是相同的,是不变的,因此满足Alias Table的要求。因此 是在同一个数据块内,跨文档共享。建立 的空间复杂度是 ,因为它需要存储 个分桶的边界,以及桶内的值。为了降低空间复杂度,可以进一步拆分:
其采样步骤为:
- 首先从均匀分布 中采样一个点。
- 如果该点落在 之间,则使用 进行采样。此时只需要考虑单词 涉及的主题即可,空间复杂度为 。
- 如果该点落在 之间,则使用 进行采样。它与单词 无关,因此可以在所有单词之间共享,这使得平均的空间复杂度为 。
因此对 的采样的平摊时间复杂度为 ,平摊空间复杂度为 。
考虑到 , 为
文档-主题概率,与 比较接近; 为主题-单词概率,与 比较接近。- 如果仅仅用 采样,则有可能出现 较小、 很大的情形。此时 较大,而 较小,使得接受率较低,收敛速度较慢。
- 同理:如果仅仅用 采样,则有可能出现 较小、 很大的情形。此时 较大,而 较小,使得接受率较低,收敛速度较慢。
因此:虽然单独利用 或者单独利用 都可以对 进行采样,但是单独使用时收敛速度较慢。
LightLDA联合采用 来加速采样的收敛速度,它轮流在二者之间采样。这等价于用 进行采样,其接受率较大、收敛速度较快。算法输入:原始函数分布 ,
文档-主题近似分布,主题-单词近似分布算法输出:满足原始分布的采样序列
算法步骤:
从 中随机采样一个样本
对 执行迭代。迭代步骤如下:
根据 采样出候选样本 ,计算接受率 :
根据均匀分布从 内采样出阈值 ,如果 ,则接受 , 即 。否则拒绝 , 即 。
根据 采样出候选样本 ,计算接受率 :
根据均匀分布从 内采样出阈值 ,如果 ,则接受 , 即 。否则拒绝 , 即 。
返回采样序列 。
4.3.3 混合数据结构
对于百万词汇表 x 百万主题,如果每一项(
单词-主题计数)是32 bit,则需要4 TB内存才能存放。假设一台机器有128 G内存,则至少需要32台参数服务器。因此如果能够大幅降低内存,则对硬件资源的需求也能够下降。考虑词频统计,在数十亿网页文件中:
- 在删除停用词之后,几乎所有单词的词频不超过 32 位无符号整数的上限。因此
主题-单词矩阵的元素采用 32 位无符号整数存放。 - 大多数单词出现的次数少于 次, 为主题数量(论文中为一百万)。这意味着
主题-单词矩阵中,大多数单词列是稀疏的,如果采用稀疏表示( 如hash映射) 将显著减少内存需求。
- 在删除停用词之后,几乎所有单词的词频不超过 32 位无符号整数的上限。因此
采用稀疏表示存在一个问题:其随机访问性能很差,这会损害
MCMC采样的速度。为了保持高采样性能、低内存需求,LightLDA提出了混合数据结构:- 对于词频较高的单词,其对应的主题计数列是不做修改的、方便随机访问的
dense表示。这部分单词占据词表的10%,几乎覆盖了语料库中95%的位置。 - 对于词频较低的长尾单词,其对应的主题计数列经过
hash映射的sparse表示,使得内存需求大幅降低。这部分单词占据词表的90%,仅仅覆盖了语料库中5%的位置。
这就使得:
- 在
MCMC采样中,对大多数主题-单词列的访问都是dense表示,这使得采样的吞吐量很高。 - 在存储方面,大多数
主题-单词列的存储是sparse表示,这使得内存需求较低。
- 对于词频较高的单词,其对应的主题计数列是不做修改的、方便随机访问的
4.3.4 系统实现
LightLDA使用开源的分布式机器学习系统Petuum来实现,特别使用其参数服务器来进行有界异步数据并行。参数服务器用于存放
LDA的两类模型参数:主题-单词矩阵 ,主题频次向量 ,其中 为主题 生成的单词的总数(它也等于 第 行的求和)。因为语料库的规模远大于模型的大小,所以在网络中交换文档的代价对网络压力非常大。因此
LightLDA并不是交换数据,而是交换模型:先将语料库随机分配到各个worker的磁盘上,然后在整个算法期间每个worker仅仅访问本地磁盘上的部分语料库。交换数据的做法是:每轮迭代时,将语料库分发到不同
worker,每个worker在不同迭代步处理的数据会有所不同。LightLDA整体架构如下图所示:各参数的意义位(这里采用论文中的符号表示):
- :文档 的长度; :数据分片中包含的文档数量。 :文档 的第 个词汇的主题。
- :语料库中主题 生成的单词 的数量,即 。 :语料库中主题 的频次,即 第 行的求和。:文档 的主题 的频次。
- :数据分片。 :模型分片。 :主题频次向量。
数据分片从
worker的磁盘加载到worker的内存,模型分片由worker从参数服务器进行获取。考虑到每个数据分片可能仍然非常巨大,无法一次性加载进
worker内存。因此LightLDA将每个数据分片继续划分成数据块Data Block,并将这些数据块依次加载进内存处理。
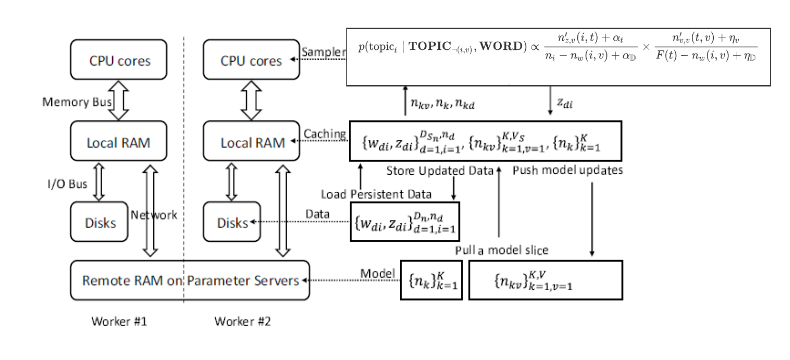
为了加速并行处理,
LightLDA进行了如下优化:通过流水线来消除IO的延迟:在采样的同时可以加载数据块、拉取下一个模型分片、更新上一个模型分片。
这需要根据采样器的吞吐量、数据块大小、模型切片大小仔细安排参数。
为防止模型切片之间的数据不均衡(热门词和冷门词),需要对词汇表按照词频进行排序,然后对单词进行混洗来生成模型切片。
在生成数据块时,将文档中的单词按照它们在词表中的顺序进行排序,从而确保同一个模型切片的所有单词在数据块中是连续的。这个操作只需要执行一次,与
LDA整体消耗时间相比该操作非常快。使用有界异步数据并行来消除在相邻迭代边界处发生的网络等待时间。
LightLDA在每个worker内部开启多线程来进一步加速算法:- 每个数据块在内存中被划分为不相交的区域,每个区域由不同的线程进行采样。
- 所有线程之间共享模型切片,且采样期间模型切片不变。在将模型切片更新到参数服务器之前,对各线程的更新结果进行聚合。
通过保持模型切片不变,这避免了竞争条件和加锁/解锁等并发问题。虽然这种延迟更新方式需要更多的迭代步才能收敛,但是由于这种方式消除了并发问题,提高了采样器吞吐率,使得每个迭代步的速度快得多,因此整体上仍然可以加速收敛速度。
五、sentence-LDA
5.1 sentence-LDA
LDA认为每个单词对应一个主题,但是针对短文本可能每句话表示一个主题,这就是Sentence-LDA的基本假设。Sentence-LDA的文档生成过程:根据参数为 的狄利克雷分布随机采样,对每个话题 生成一个单词分布 。每个话题采样一次,一共采样 次。
对每篇文档 :
根据参数为 的狄利克雷分布随机采样,生成文档 的一个话题分布 。每篇文档采样一次。
对文档 中的每个句子:
从话题分布中 中采样一个话题 ,然后从话题的单词分布 采样 个单词 。 为句子的编号。
此时这些单词的话题都是 。
重复生成 个句子,得到一篇包含 个句子的文档。
重复执行上述文档生成规则 次,即得到 篇文档组成的文档集合 。
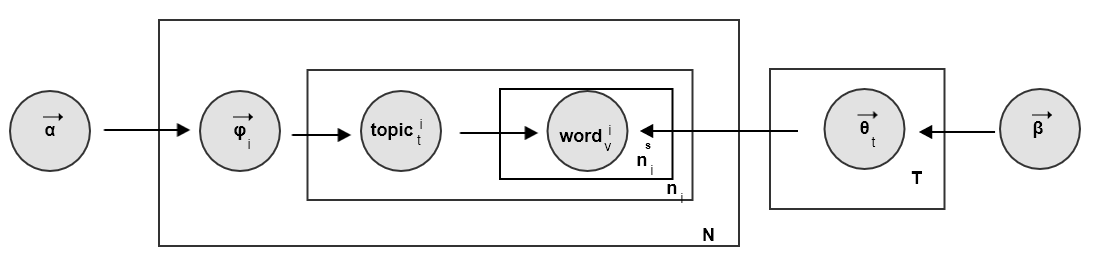
Sentence-LDA的吉布斯采样概率为:各参数的意义为:
- :已知所有单词,以及除了第 篇文档的第 个句子之外的所有句子的主题的情况下,第 篇文档的第 个句子的主题为 的概率。
- :排除第 篇文档的第 句之外,第 篇文档中属于主题 的句子的数量。
- :排除第 篇文档的第 句之外,数据集 中属于主题 的词汇 的数量。
- :文档-主题计数中,主题 的先验计数; :主题-单词计数中,单词 的先验计数。
- :第 篇文档的第 句的单词总数;:第 篇文档的第 句的词汇 的总数。
Sentence-LDA得到的文档-主题概率分布为:主题-单词概率分布为:
其中:
- :文档 中,属于主题 的句子数量;:数据集 中,属于主题 的单词 的数量。
- 其实分别是 的期望值,因为 均为随机变量。
5.2 ASUM
论文
Aspect and sentiment unification model for online review analysis中提出了sentence-LDA以及扩展了sentence-LDA的ASUM模型。ASUM(Aspect and Sentiment Unification Model)同时对评论的主题以及评论的情感进行建模。它认为客户撰写评论的方式为:(以餐馆评论为例):- 首先决定餐馆评价的好坏概率分布,如:70%是满意的,30%是不满意的。
- 然后对每个情感给出其评价主题概率分布。如:满意的主题概率分布为:50%是服务,25%是食物,25% 是价格。
- 最后对每个句子,表达一个主题和一个情感。即:每个句子中所有的单词背后都是同一个主题,也是同一个情感。
ASUM文档生成过程:对每一个
主题-情感对(情感为 ,主题为 ),从 的狄利克雷分布随机采样,得到该主题和该情感下的单词分布: 。每个主题-情感采样一次,一共采样 次。其中 为情感的总数。
对每篇文档 :
根据参数为 的狄利克雷分布随机采样,生成文档 的一个情感分布 。每篇文档采样一次。
对每个情感 ,根据参数为 的狄利克雷分布随机采样,生成生成文档 的一个话题分布 。每篇文档采样一次。
对文档 中的每个句子:
从情感分布 中采样一个情感 ,然后从话题分布中 中采样一个话题 ,然后从
主题-情感的单词分布 采样 个单词 。 为句子的编号。此时这些单词的话题都是 。
重复生成 个句子,得到一篇包含 个句子的文档。
重复执行上述文档生成规则 次,即得到 篇文档组成的文档集合 。
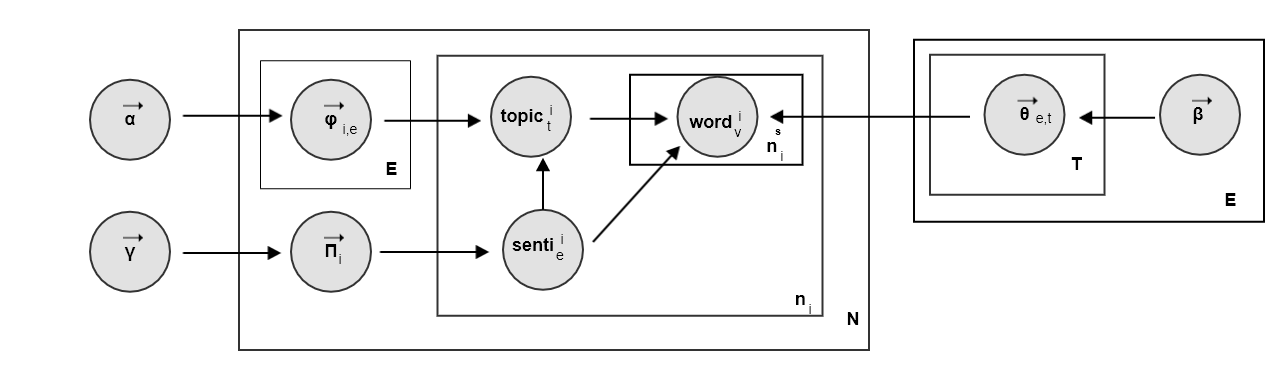
与
LDA模型不同,ASUM模型中的 参数是非对称的:如good,great不大可能会出现在负面情感中,bad,annoying不大可能出现在正面情感中。ASUM的吉布斯采样概率为:各参数的意义为:
- :已知所有单词、除了第 篇文档的第 个句子之外的所有句子的主题,以及除了第 篇文档的第 个句子之外的所有句子的情感的情况下,第 篇文档的第 个句子的情感为 、主题为 的概率。
- :排除第 篇文档的第 句之外,第 篇文档中属于情感 的句子的数量。
- :排除第 篇文档的第 句之外,第 篇文档中情感 的且属于主题 的句子的数量。
- :排除第 篇文档的第 句之外,数据集 中属于情感 且属于主题 的词汇 的数量。
- :文档-情感计数中,情感 的先验计数; :文档-主题计数中,主题 的先验计数; :主题-单词计数中,属于情感 的单词 的先验计数。
- :第 篇文档的第 句的单词总数;:第 篇文档的第 句的词汇 的总数。
ASUM得到的文档-情感概率分布为:文档的情感-主题分布为:
主题-单词概率分布为:
其中:
- :文档 中,属于情感 的句子数量;:文档 中,属于情感 和主题 的句子数量;:数据集 中,属于情感 和主题 的单词 的数量。
- :文档中,属于情感 和主题 的
情感-主题二元对的先验计数。 - 其实分别是 的期望值,因为 均为随机变量。
ASUM和SLDA可以用于以下用途:利用
SLDA进行评论的主题抽取。利用
ASUM进行情感-主题的抽取。自适应的扩展特定主题下的情感词。
- 首先进行
情感-主题合并。以词的分布为向量,计算情感-主题的两两余弦相似度。如果结果超过一个阈值,则认为二者是相同的。 - 计算词的出现概率。如果一个单词在所有
情感-主题下都有高概率,则它是一个通用词;如果它仅仅在一个情感-主题下有高概率,则它是一个特定主题下的情感词。
- 首先进行
无监督情感分类。根据 中,各情感的分布来执行分类。
其中需要引入先验知识: 的取值是多少才代表正面情感。这需要观察
情感-主题词的分布,由人工指定。
六、模型讨论
pLSA容易陷入过拟合。pLSA认为:- 文档-主题分布 不是随机变量,而是未知的常量。
- 主题-单词分布 也不是随机变量,也是未知的常量。
pLSA通过拟合训练数据集来求解这些参数,这意味着这些参数只能表征当前的训练集的文档的特征。对于未知的文档,pLSA认为它也符合训练集的文档特征。事实上这就是一种过拟合,尤其是当训练集的文档数量太少时,非常容易陷入过拟合。
LDA会给 加入一些先验性的知识。当数据量较小,先验性的知识会占据主导地位;当数据量较大,真实数据占据主导地位。以人口抽样问题为类比。
pLSA认为:人口的男女比例是一个常数。给出一个人口集合,
pLSA先统计男女比例(假如训练集是从医院获取的)。假如结果为2 :1, 则pLSA会断言:所有的人口比例都是2 : 1。于是训练集越小,
pLSA越容易陷入过拟合,离真实结果也就越远。LDA会首先假设男女比例为1000:1000。 然后再统计人口集合中男女的人数,最终得到的结果。假设人口集合中男女的人数分别为
200:100,则最终LDA得到男女比例为1200:1100。虽然该结果离真实的结果可能有偏差,但是它比pLSA的结果要更好。
当数据量足够大的时候,
pLSA跟LDA的结果相差无几。这是因为当数据量足够大时,真实数据的信息会淹没掉先验知识。假设有词表共有 3 个单词,主题表共有 3个主题。下面一张图形比较了
Unigram Model,pLSA与LDA的区别。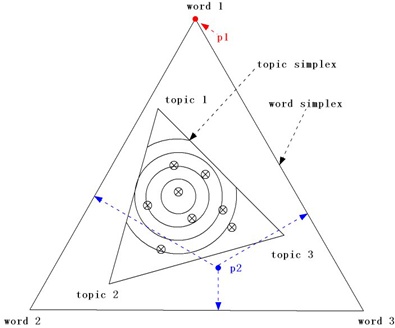
最外的三角形为单词三角形。内部每个点(如 )表示一个单词概率分布,表示产生
word1,word2,word3这三个词的概率的大小;靠内的三角形为主题三角形。内部每个点表示一个主题概率分布,表示产生topic1,topic2,topic3这三个主题的概率的大小。Unigram模型:该模型由生成各单词的概率决定,因此单词三角形内部任意一点(如 )代表了一个Unigram模型。pLSA模型:主题三角形内任意一些点(如带叉的点所示)就是一个pLSA模型。模型先根据主题概率分布采样一个主题,然后根据该主题的单词概率分布采样一个单词。重复执行
选择主题-选择单词的过程,即可得到一篇文档。LDA模型:主题三角形内,每一条曲线表示了一个pLDA模型。模型首先根据曲线(它代表主题概率分布的分布,即主题概率分布选择某类分布的概率较大)选择主题三角形内的一个点(它代表一个主题概率分布);然后根据该主题概率分布随机采样一个主题;然后根据该主题的单词概率分布采样一个单词。重复执行
选择主题 - 选择单词的过程,即可得到一篇文档。topic分布的分布,即topic分布取某些值的概率较大,取另外一些值的概率较小。它刻画了LDA模型选择主题的过程。