贝叶斯分类器

一、贝叶斯定理

1.1 贝叶斯定理

1. 设 $\mathbb S$ 为试验 $E$ 的样本空间； $B_1,B_2,\cdots,B_n$ 为 $E$ 的一组事件。若 ：

   • $B_i \bigcap B_j=\phi,i \ne j,i,j=1,2,\cdots,n$
   • $B_1 \bigcup B_2 \bigcup \cdots \bigcup B_n=\mathbb S$

   则称 $B_1,B_2,\cdots,B_n$ 为样本空间 $\mathbb S$ 的一个划分。

2. 如果 $B_1,B_2,\cdots,B_n$ 为样本空间 $\mathbb S$ 的一个划分，则对于每次试验，事件 $B_1,B_2,\cdots,B_n$ 中有且仅有一个事件发生。

3. 全概率公式 ：设试验 $E$ 的样本空间为 $\mathbb S$ ， $A$ 为 $E$ 的事件， $B_1,B_2,\cdots,B_n$ 为样本空间 $\mathbb S$ 的一个划分，且 $p(B_i) \ge 0(i=1,2,\cdots,n)$ 。则有：

   $$p(A)=p(A\mid B_1)p(B_1)+p(A\mid B_2)p(B_2)+\cdots+p(A\mid B_n)p(B_n)=\sum_{j=1}^{n}p(A\mid B_j)p(B_j)$$

4. 贝叶斯定理 ：设试验 $E$ 的的样本空间为 $\mathbb S$， $A$ 为 $E$ 的事件， $B_1,B_2,\cdots,B_n$ 为样本空间 $\mathbb S$ 的一个划分，且 $p(A) \gt 0,p(B_i) \ge 0(i=1,2,\cdots,n)$ ，则有：$p(B_i\mid A)=\frac{p(A\mid B_i)p(B_i)}{\sum_{j=1}^{n}p(A\mid B_j)p(B_j)}$ 。

1.2 先验概率、后验概率

1. 先验概率：根据以往经验和分析得到的概率。

   后验概率：根据已经发生的事件来分析得到的概率。

2. 例：假设山洞中有熊出现的事件为 $Y$ ，山洞中传来一阵熊吼的事件为 $X$ 。

   • 山洞中有熊的概率为 $p(Y)$ 。它是先验概率，根据以往的数据分析或者经验得到的概率。
   • 听到熊吼之后认为山洞中有熊的概率为 $p(Y\mid X)$ 。它是后验概率，得到本次试验的信息从而重新修正的概率。

二、朴素贝叶斯法

1. 朴素贝叶斯法是基于贝叶斯定理与特征条件独立假设的分类方法。

   对给定的训练集：

   • 首先基于特征条件独立假设学习输入、输出的联合概率分布。
   • 然后基于此模型，对给定的输入 $\mathbf {\vec x}$ ，利用贝叶斯定理求出后验概率最大的输出 $y$ 。

2. 朴素贝叶斯法不是贝叶斯估计，贝叶斯估计是最大后验估计。

2.1 原理

1. 设输入空间 $\mathcal X \subseteq \mathbb R^{n}$ 为 $n$ 维向量的集合 ，输出空间为类标记集合 $\mathcal Y =\{ c_1,c_2,\cdots,c_k\}$ 。

   令 $\mathbf{\vec x} =(x_1,x_2,\cdots,x_n)^T$ 为定义在 $\mathcal X$ 上的随机向量，$y$ 为定义在 $\mathcal Y$ 上的随机变量。

   令 $p(\mathbf{\vec x},y)$ 为 $\mathbf{\vec x}$ 和 $y$ 的联合概率分布，假设训练数据集 $\mathbb D=\{(\mathbf {\vec x}_1,\tilde y_1),(\mathbf {\vec x}_2,\tilde y_2),\cdots,(\mathbf {\vec x}_N,\tilde y_N)\}$ 由 $p(\mathbf{\vec x},y)$ 独立同分布产生。

   朴素贝叶斯法通过训练数据集学习联合概率分布 $p(\mathbf{\vec x},y)$。具体的学习下列概率分布：

   • 先验概率分布： $p(y)$ 。
   • 条件概率分布： $p( \mathbf {\vec x}\mid y)=p(x_1,x_2,\cdots,x_n \mid y)$ 。

2. 朴素贝叶斯法对条件概率做了特征独立性假设：$p( \mathbf{\vec x}\mid y )=p(x_1,x_2,\cdots,x_n\mid y )=\prod_{j=1}^{n}p(x_j\mid y )$ 。

   • 这意味着在分类确定的条件下，用于分类的特征是条件独立的。
   • 该假设使得朴素贝叶斯法变得简单，但是可能牺牲一定的分类准确率。

3. 根据贝叶斯定理：

   $$p(y\mid \mathbf {\vec x})=\frac{p( \mathbf {\vec x}\mid y)p(y)}{\sum_{y^\prime} p( \mathbf {\vec x}\mid y^\prime)p(y^\prime)}$$

   考虑分类特征的条件独立假设有：

   $$p(y\mid \mathbf {\vec x})=\frac{p(y)\prod_{i=1}^{n}p(x_i\mid y)}{\sum_{y^\prime} p( \mathbf {\vec x}\mid y^\prime)p(y^\prime)}$$

   则朴素贝叶斯分类器表示为：

   $$f(\mathbf {\vec x})=\arg \max_{y \in \mathcal Y}\frac{p(y)\prod_{i=1}^{n}p(x_i\mid y)}{\sum_{y^\prime} p( \mathbf {\vec x}\mid y^\prime)p(y^\prime)}$$

   由于上式的分母 $p(\mathbf {\vec x})$ 与 $y$ 的取值无关，则分类器重写为：$f(\mathbf {\vec x})=\arg \max_{y \in \mathcal Y} p(y)\prod_{i=1}^{n}p(x_i\mid y)$ 。

2.2 期望风险最小化

1. 朴素贝叶斯分类器是后验概率最大化，等价于期望风险最小化。

2. 令损失函数为：

   $$L(y,f(\mathbf{\vec x}))= \begin{cases} 1, & y \ne f(\mathbf{\vec x}) \\ 0, & y=f(\mathbf{\vec x}) \end{cases} \\ R_{exp}(f)=\mathbb E[L(y,f(\mathbf{\vec x}))]=\sum_{\mathbf {\vec x} \in \mathcal X}\sum_{y \in \mathcal Y}L(y,f(\mathbf {\vec x}))p(\mathbf {\vec x}, y)$$

3. 根据 $p(\mathbf{\vec x},y)=p(\mathbf{\vec x})p(y \mid \mathbf{\vec x})$ 有：

   $$R_{exp}(f)=\mathbb E[L(y,f(\mathbf{\vec x}))]=\sum_{\mathbf {\vec x} \in \mathcal X}\sum_{y \in \mathcal Y}L(y,f(\mathbf {\vec x}))p(\mathbf {\vec x}, y) =\mathbb E_X[\sum_{y\in \mathcal Y} L(y,f(\mathbf {\vec x}))p(y\mid \mathbf {\vec x})]$$

   为了使得期望风险最小化，只需要对 $\mathbb E_X$ 中的元素极小化。

   令 $\hat y=f(\mathbf{\vec x})$ ，则有：

   $$\arg\min_{\hat y} \sum_{y\in \mathcal Y}L(y,\hat y) p(y\mid \mathbf{\vec x})=\arg\min_{\hat y} \sum_{y\in \mathcal Y}p(y\ne \hat y\mid \mathbf{\vec x} )\\ =\arg\min_{\hat y}( 1-p( \hat y\mid \mathbf{\vec x} )) = \arg\max_{\hat y}p( \hat y\mid \mathbf{\vec x} )$$

   即：期望风险最小化，等价于后验概率最大化。

2.3 算法

1. 在朴素贝叶斯法中，学习意味着估计概率：$p(y)$， $p( x_i\mid y)$ 。

2. 可以用极大似然估计相应概率。

   • 先验概率 $p(y)$ 的极大似然估计为：$p(y=c_k)=\frac {1}{N} \sum_{i=1}^{N}I(\tilde y_i=c_k)$

   • 设第 $j$ 个特征 $x_j$ 可能的取值为 $\{a_{j,1},a_{j,2},\cdots,a_{j,s_j}\}$，则条件概率 $p(x_j=a_{j,l}\mid y=c_k)$ 的极大似然估计为：

     $$p(x_j=a_{j,l}\mid y=c_k)=\frac{\sum_{i =1}^{N}I(x_{i ,j}=a_{j,l},\tilde y_{i }=c_k)}{\sum_{i =1}^{N}I(\tilde y_{i }=c_k)}\\ j=1,2,\cdots,n; \;l=1,2,\cdots,s_j; \;k=1,2,\cdots,K$$

     其中：$I$ 为示性函数， $x_{i ,j}$ 表示第 $i$ 个样本的第 $j$ 个特征。

3. 朴素贝叶斯算法 ：

   • 输入 ：

     • 训练集 $\mathbb D=\{(\mathbf {\vec x}_1,\tilde y_1),(\mathbf {\vec x}_2,\tilde y_2),\cdots,(\mathbf {\vec x}_N,\tilde y_N)\}$ 。

       $\mathbf {\vec x}_i=(x_{i,1},x_ {i,2},\cdots,x_ {i,n})^{T}$, $x_{i,j}$ 为第 $i$ 个样本的第 $j$ 个特征。其中 $x_{i,j} \in \{a_{j,1},a_{j,2},\cdots,a_{j,s_j}\}$， $a_{j , l}$为第 $j$ 个特征可能取到的第 $l$ 个值。

     • 实例 $\mathbf {\vec x}$ 。

   • 输出 ：实例 $\mathbf {\vec x}$ 的分类

   • 算法步骤：

     • 计算先验概率以及条件概率：
     $$p(y=c_k)=\frac {1}{N} \sum_{i=1}^{N}I(\tilde y_i=c_k),k=1,2,\cdots,K\\ p(x_j=a_{j,l}\mid y=c_k)=\frac{\sum_{i =1}^{N}I(x_{i ,j}=a_{j,l},\tilde y_{i }=c_k)}{\sum_{i =1}^{N}I(\tilde y_{i }=c_k)}\\ j=1,2,\cdots,n; \;l=1,2,\cdots,s_j; \;k=1,2,\cdots,K$$
     • 对于给定的实例 $\mathbf {\vec x}=(x_1，x_2,\cdots,x_n)^{T}$，计算：$p(y=c_k)\prod_{j=1}^{n}p( x_j\mid y=c_k)$ 。
     • 确定实例 $\mathbf {\vec x}$ 的分类：$\hat y= \arg\max_{c_k}p(y=c_k)\prod_{j=1}^{n}p( x_j\mid y=c_k)$ 。

2.4 贝叶斯估计

1. 在估计概率 $p( x_i\mid y)$ 的过程中，分母 $\sum_{i =1}^{N}I(\tilde y_{i }=c_k)$ 可能为 0 。这是由于训练样本太少才导致 $c_k$ 的样本数为 0 。而真实的分布中， $c_k$ 的样本并不为 0 。

   解决的方案是采用贝叶斯估计（最大后验估计）。

2. 假设第 $j$ 个特征 $x_j$ 可能的取值为 $\{a_{j,1},a_{j,2},\cdots,a_{j,s_j}\}$ ，贝叶斯估计假设在每个取值上都有一个先验的计数 $\lambda$ 。即：

   $$p_{\lambda}(x_j=a_{j,l}\mid y=c_k)=\frac{\sum_{i =1}^{N}I(x_{i ,j}=a_{j,l},\tilde y_{i }=c_k)+\lambda}{\sum_{i=1}^{N}I(\tilde y_i=c_k)+s_j\lambda}\\ j=1,2,\cdots,n; \;l=1,2,\cdots,s_j; \;k=1,2,\cdots,K$$

   它等价于在 $x_j$ 的各个取值的频数上赋予了一个正数 $\lambda$。

   若 $c_k$ 的样本数为0，则它假设特征 $x_j$ 每个取值的概率为 $\frac{1}{s_j}$，即等可能的。

3. 采用贝叶斯估计后，$p(y)$ 的贝叶斯估计调整为:

   $$p_\lambda(y=c_k)=\frac{\sum_{i=1}^{N}I(\tilde y_i=c_k)+\lambda}{N+K\lambda}$$
   • 当 $\lambda=0$ 时，为极大似然估计当 $\lambda=1$ 时，为拉普拉斯平滑
   • 若 $c_k$ 的样本数为 0，则假设赋予它一个非零的概率 $\frac{\lambda}{N+K\lambda}$ 。

三、半朴素贝叶斯分类器

1. 朴素贝叶斯法对条件概率做了特征的独立性假设：$p( \mathbf{\vec x}\mid y )=p(x_1,x_2,\cdots,x_n\mid y )=\prod_{j=1}^{n}p(x_j\mid y )$ 。

   但是现实任务中这个假设有时候很难成立。若对特征独立性假设进行一定程度上的放松，这就是半朴素贝叶斯分类器semi-naive Bayes classifiers 。

2. 半朴素贝叶斯分类器原理：适当考虑一部分特征之间的相互依赖信息，从而既不需要进行完全联合概率计算，又不至于彻底忽略了比较强的特征依赖关系。

3.1 独依赖估计 OED

1. 独依赖估计One-Dependent Estimator:OED是半朴素贝叶斯分类器最常用的一种策略。它假设每个特征在类别之外最多依赖于一个其他特征，即：

   $$p( \mathbf{\vec x}\mid y)=p(x_1,x_2,\cdots, x_n\mid y) =\prod_{j=1}^{n}p(x_j\mid y,x_j^P)$$

   其中 $x_j^P$ 为特征 $x_j$ 所依赖的特征，称作的 $x_j$ 父特征。

2. 如果父属性已知，那么可以用贝叶斯估计来估计概率值 $p(x_j\mid y,x_j^P)$ 。现在的问题是：如何确定每个特征的父特征？

   不同的做法产生不同的独依赖分类器。

3.1.1 SPODE

1. 最简单的做法是：假设所有的特征都依赖于同一个特征，该特征称作超父。然后通过交叉验证等模型选择方法来确定超父特征。这就是SPODE:Super-Parent ODE方法。

   假设节点 Y 代表输出变量 $y$ ，节点 Xj 代表属性 $x_j$ 。下图给出了超父特征为 $x_1$ 时的 SPO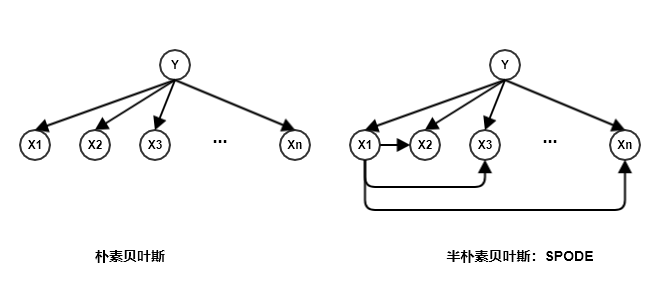DE 。

   

3.1.2 TAN

1. TAN:Tree Augmented naive Bayes是在最大带权生成树算法基础上，通过下列步骤将特征之间依赖关系简化为如下图所示的树型结构：

   • 计算任意两个特征之间的条件互信息。记第 $i$ 个特征 $x_i$ 代表的结点为 $\mathbf X_i$，标记代表的节点为 $\mathbf{Y}$ 则有:

     $$I(\mathbf X_i,\mathbf X_j\mid \mathbf Y)=\sum_y\sum_{x_i}\sum_{x_j} p(x_i,x_j\mid y)\log \frac{p(x_i,x_j\mid y)}{p(x_i\mid y)p(x_j\mid y)}$$

     如果两个特征 $x_i,x_j$ 相互条件独立，则 $p(x_i,x_j\mid y)=p(x_i\mid y)p(x_j\mid y)$ 。则有条件互信息 $I(\mathbf X_i,\mathbf X_j\mid \mathbf Y)=0$，则在图中这两个特征代表的结点没有边相连。

   • 以特征为结点构建完全图，任意两个结点之间边的权重设为条件互信息 $I(\mathbf X_i, \mathbf X_j\mid \mathbf Y)$ 。

   • 构建此完全图的最大带权生成树，挑选根结点（下图中根节点为节点 $\mathbf X_1$)，将边置为有向边。

   • 加入类别结点 $\mathbf Y$ ，增加 $\mathbf Y$ 到每个特征的有向边。因为所有的条件概率都是以 $y$ 为条件的。

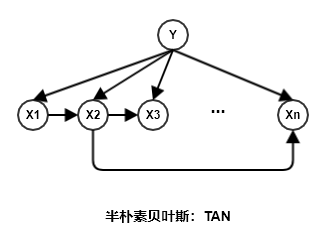
四、其它讨论

1. 朴素贝叶斯分类器的优点：

   • 性能相当好，它速度快，可以避免维度灾难。
   • 支持大规模数据的并行学习，且天然的支持增量学习。

2. 朴素贝叶斯分类器的缺点：

   • 无法给出分类概率，因此难以应用于需要分类概率的场景。