k 近邻法

一、k 近邻算法

$k$ 近邻法（k-Nearest Neighbor:kNN）是一种基本的分类与回归方法。
- 分类问题：对新的样本，根据其 $k$ 个最近邻的训练样本的类别，通过多数表决等方式进行预测。
- 回归问题：对新的样本，根据其 $k$ 个最近邻的训练样本标签值的均值作为预测值。
$k$ 近邻法不具有显式的学习过程，它是直接预测。它是“惰性学习”(lazy learning)的著名代表。
- 它实际上利用训练数据集对特征向量空间进行划分，并且作为其分类的"模型"。
- 这类学习技术在训练阶段仅仅将样本保存起来，训练时间开销为零，等到收到测试样本后再进行处理。
  那些在训练阶段就对样本进行学习处理的方法称作“急切学习”(eager learning)。
$k$ 近邻法是个非参数学习算法，它没有任何参数（ $k$ 是超参数，而不是需要学习的参数）。
- $k$ 近邻模型具有非常高的容量，这使得它在训练样本数量较大时能获得较高的精度。
- 它的缺点有：
  - 计算成本很高。因为需要构建一个 $N\times N$ 的距离矩阵，其计算量为 $O(N^{2})$ ，其中 $N$ 为训练样本的数量。
    当数据集是几十亿个样本时，计算量是不可接受的。
  - 在训练集较小时，泛化能力很差，非常容易陷入过拟合。
  - 无法判断特征的重要性。
$k$ 近邻法的三要素：
- $k$ 值选择。
- 距离度量。
- 决策规则。

1.1 k 值选择

当 $k=1$ 时的 $k$ 近邻算法称为最近邻算法，此时将训练集中与 $\mathbf {\vec x}$ 最近的点的类别作为 $\mathbf {\vec x}$ 的分类。
$k$ 值的选择会对 $k$ 近邻法的结果产生重大影响。
- 若 $k$ 值较小，则相当于用较小的邻域中的训练样本进行预测，"学习"的偏差减小。
  只有与输入样本较近的训练样本才会对预测起作用，预测结果会对近邻的样本点非常敏感。
  若近邻的训练样本点刚好是噪声，则预测会出错。即： $k$ 值的减小意味着模型整体变复杂，易发生过拟合。
  - 优点：减少"学习"的偏差。
  - 缺点：增大"学习"的方差（即波动较大）。
- 若 $k$ 值较大，则相当于用较大的邻域中的训练样本进行预测。
  这时输入样本较远的训练样本也会对预测起作用，使预测偏离预期的结果。
  即： $k$ 值增大意味着模型整体变简单。
  - 优点：减少"学习"的方差（即波动较小）。
  - 缺点：增大"学习"的偏差。
应用中， $k$ 值一般取一个较小的数值。通常采用交叉验证法来选取最优的 $k$ 值。

1.2 距离度量

特征空间中两个样本点的距离是两个样本点的相似程度的反映。
$k$ 近邻模型的特征空间一般是 $n$ 维实数向量空间 $\mathbb R^{n}$ ， $k$ 其距离一般为欧氏距离，也可以是一般的 $L_p$ 距离：
$L_p(\mathbf {\vec x}_i,\mathbf {\vec x}_j)=(\sum_{l=1}^{n}|x_{i,l}- x_{j,l}|^{p})^{1/p},\quad p \ge 1\\ \mathbf {\vec x}_i,\mathbf {\vec x}_j \in \mathcal X=\mathbb R^{n};\quad \mathbf {\vec x}_i=(x_{i,1},x_{i,2},\cdots,x_{i,n})^{T}$
- 当 $p=2$ 时，为欧氏距离： $L_2(\mathbf {\vec x}_i,\mathbf {\vec x}_j)=(\sum_{l=1}^{n}|x_{i,l}- x_{j,l}|^{2})^{1/2}$
- 当 $p=1$ 时，为曼哈顿距离： $L_1(\mathbf {\vec x}_i,\mathbf {\vec x}_j)=\sum_{l=1}^{n}|x_{i,l}- x_{j,l}|$
- 当 $p=\infty$ 时，为各维度距离中的最大值： $L_{\infty}(\mathbf {\vec x}_i,\mathbf {\vec x}_j)=\max_l|x_{i,l}- x_{j,l}|$
不同的距离度量所确定的最近邻点是不同的。

1.3 决策规则

1.3.1 分类决策规则

分类决策通常采用多数表决，也可以基于距离的远近进行加权投票：距离越近的样本权重越大。
多数表决等价于经验风险最小化。
设分类的损失函数为 $0-1$ 损失函数，分类函数为 $f:\mathbb R^{n} \rightarrow \{c_1,c_2,\cdots,c_K\}$ 。
给定样本 $\mathbf {\vec x} \in \mathcal X$ ，其最邻近的 $k$ 个训练点构成集合 $\mathcal N_k(\mathbf {\vec x})$ 。设涵盖 $\mathcal N_k(\mathbf {\vec x})$ 区域的类别为 $c_m$ （这是待求的未知量，但是它肯定是 $c_1,c_2,\cdots,c_K$ 之一），则损失函数为：
$L = \frac {1}{k}\sum_{\mathbf {\vec x}_i \in \mathcal N_k(\mathbf {\vec x})}I(\tilde y_i \ne c_m)=1-\frac{1}{k}\sum_{\mathbf {\vec x}_i \in \mathcal N_k(\mathbf {\vec x})}I(\tilde y_i = c_m)$
$L$ 就是训练数据的经验风险。要使经验风险最小，则使得 $\sum_{\mathbf {\vec x}_i \in \mathcal N_k(\mathbf {\vec x})}I(\tilde y_i = c_m)$ 最大。即多数表决： $c_m=\arg \max_{c_m} \sum_{\mathbf {\vec x}_i \in \mathcal N_k(\mathbf {\vec x}) } I(\tilde y_i=c_m)$ 。

1.3.2 回归决策规则

回归决策通常采用均值回归，也可以基于距离的远近进行加权投票：距离越近的样本权重越大。
均值回归等价于经验风险最小化。
设回归的损失函数为均方误差。给定样本 $\mathbf {\vec x} \in \mathcal X$ ，其最邻近的 $k$ 个训练点构成集合 $\mathcal N_k(\mathbf {\vec x})$ 。设涵盖 $\mathcal N_k(\mathbf {\vec x})$ 区域的输出为 $\hat y$ ，则损失函数为：
$L = \frac 1k\sum_{\mathbf {\vec x}_i \in \mathcal N_k(\mathbf {\vec x})} (\tilde y_i - \hat y)^2$
$L$ 就是训练数据的经验风险。要使经验风险最小，则有： $\hat y = \frac {1}{k}\sum_{\mathbf{\vec x}_i\in \mathcal N_k(\mathbf{\vec x})}\tilde y_i$ 。即：均值回归。

1.4 k 近邻算法

$k$ 近邻法的分类算法：
- 输入：
  - 训练数据集 $\mathbb D=\{(\mathbf {\vec x}_1,\tilde y_1),(\mathbf {\vec x}_2,\tilde y_2),\cdots,(\mathbf {\vec x}_N,\tilde y_N)\},\mathbf {\vec x}_i \in \mathcal X \subseteq \mathbb R^{n},\tilde y_i \in \mathcal Y=\{c_1,c_2,\cdots,c_K\}$
  - 给定样本 $\mathbf {\vec x}$
- 输出：样本 $\mathbf {\vec x}$ 所属的类别 $y$
- 步骤：
  - 根据给定的距离度量，在 $\mathbb D$ 中寻找与 $\mathbf {\vec x}$ 最近邻的 $k$ 个点。定义涵盖这 $k$ 个点的 $\mathbf {\vec x}$ 的邻域记作 $\mathcal N_k(\mathbf {\vec x})$ 。
  - 从 $\mathcal N_k(\mathbf {\vec x})$ 中，根据分类决策规则（如多数表决）决定 $\mathbf {\vec x}$ 的类别 $y$ ： $y=\arg \max_{c_m} \sum_{\mathbf {\vec x}_i \in\mathcal N_k(\mathbf {\vec x}) } I(\tilde y_i=c_m)$ 。
$k$ 近邻法的回归算法：
- 输入：
  - 训练数据集 $\mathbb D=\{(\mathbf {\vec x}_1,\tilde y_1),(\mathbf {\vec x}_2,\tilde y_2),\cdots,(\mathbf {\vec x}_N,\tilde y_N)\},\mathbf {\vec x}_i \in \mathcal X \subseteq \mathbb R^{n},\tilde y_i \in \mathcal Y \subseteq \mathbb R$
  - 给定样本 $\mathbf {\vec x}$
- 输出：样本 $\mathbf {\vec x}$ 的输出 $y$
- 步骤：
  - 根据给定的距离度量，在 $\mathbb D$ 中寻找与 $\mathbf {\vec x}$ 最近邻的 $k$ 个点。定义涵盖这 $k$ 个点的 $\mathbf {\vec x}$ 的邻域记作 $\mathcal N_k(\mathbf {\vec x})$ 。
  - 从 $\mathcal N_k(\mathbf {\vec x})$ 中，根据回归决策规则（如均值回归）决定 $\mathbf {\vec x}$ 的输出 $y$ ： $y= \frac {1}{k}\sum_{\mathbf{\vec x}_i\in \mathcal N_k(\mathbf{\vec x})}\tilde y_i$ 。

二、 kd树

实现 $k$ 近邻法时，主要考虑的问题是：如何对训练数据进行快速 $k$ 近邻搜索。
最简单的实现方法：线性扫描。此时要计算输入样本与每个训练样本的距离。
当训练集很大时，计算非常耗时。解决办法是：使用 $kd$ 树来提高 $k$ 近邻搜索的效率。
$kd$ 树是一种对 $k$ 维空间中的样本点进行存储以便对其进行快速检索的树型数据结构。
它是二叉树，表示对 $k$ 维空间的一个划分。
构造 $kd$ 树的过程相当于不断的用垂直于坐标轴的超平面将 $k$ 维空间切分的过程。
$kd$ 树的每个结点对应于一个 $k$ 维超矩形区域。

2.1 kd树构建算法

平衡 $kd$ 树构建算法：
- 输入： $k$ 维空间样本集 $\mathbb D=\{\mathbf {\vec x}_1,\mathbf {\vec x}_2,\cdots,\mathbf {\vec x}_N\},\mathbf {\vec x}_i \in \mathcal X \subseteq \mathbb R^{k}$
- 输出： $kd$ 树
- 算法步骤：
  - 构造根结点。根结点对应于包含 $\mathbb D$ 的 $k$ 维超矩形。
    选择 $x_1$ 为轴，以 $\mathbb D$ 中所有样本的 $x_1$ 坐标的中位数 $x_1^*$ 为切分点，将根结点的超矩形切分为两个子区域，切分产生深度为 1 的左、右子结点。切分超平面为： $x_1=x_1^*$ 。
    - 左子结点对应于坐标 $x_1<x_1^*$ 的子区域。
    - 右子结点对应于坐标 $x_1>x_1^*$ 的子区域。
    - 落在切分超平面上的点( $x_1=x_1^*$ ) 保存在根结点。
  - 对深度为 $j$ 的结点，选择 $x_l$ 为切分的坐标轴继续切分， $l=j\pmod k+1$ 。本次切分之后，树的深度为 $j+1$ 。
    这里取模而不是 $l=j+1$ ，因为树的深度可以超过维度 $k$ 。此时切分轴又重复回到 $x_l$ ，轮转坐标轴进行切分。
  - 直到所有结点的两个子域中没有样本存在时，切分停止。此时形成 $kd$ 树的区域划分。

2.2 kd 树搜索算法

$kd$ 树最近邻搜索算法（ $k$ 近邻搜索以此类推）：
- 输入：
  - 已构造的 $kd$ 树
  - 测试点 $\mathbf {\vec x}$
- 输出： $\mathbf {\vec x}$ 的最近邻测试点
- 步骤：
  - 初始化：当前最近点为 $\mathbf{\vec x}_{nst}=null$ ，当前最近距离为 $\text{distance}_{nst}=\infty$ 。
  - 在 $kd$ 树中找到包含测试点 $\mathbf {\vec x}$ 的叶结点：从根结点出发，递归向下访问 $kd$ 树（即：执行二叉搜索）：
    - 若测试点 $\mathbf {\vec x}$ 当前维度的坐标小于切分点的坐标，则查找当前结点的左子结点。
    - 若测试点 $\mathbf {\vec x}$ 当前维度的坐标大于切分点的坐标，则查找当前结点的右子结点。
    在访问过程中记录下访问的各结点的顺序，存放在先进后出队列 Queue 中，以便于后面的回退。
  - 循环，结束条件为Queue 为空。循环步骤为：
    - 从Queue 中弹出一个结点，设该结点为 $\mathbf{\vec x}_q$ 。计算 $\mathbf {\vec x}$ 到 $\mathbf{\vec x}_q$ 的距离，假设为 $\text{distance}_q$ 。
      若 $\text{distance}_q\lt \text{distance}_{nst}$ ，则更新最近点与最近距离：
      $\text{distance}_{nst}=\text{distance}_q,\quad \mathbf{\vec x}_{nst}= \mathbf{\vec x}_q$
    - 如果 $\mathbf{\vec x}_q$ 为中间节点：考察以 $\mathbf {\vec x}$ 为球心、以 $\text{distance}_{nst}$ 为半径的超球体是否与 $\mathbf{\vec x}_q$ 所在的超平面相交。
      如果相交：
      - 若Queue 中已经访问过了 $\mathbf{\vec x}_q$ 的左子树，则继续二叉搜索 $\mathbf{\vec x}_q$ 的右子树。
      - 若Queue 中已经访问过了 $\mathbf{\vec x}_q$ 的右子树，则继续二叉搜索 $\mathbf{\vec x}_q$ 的左子树。
      二叉搜索的过程中，仍然在Queue 中记录搜索的各结点。
  - 循环结束时， $\mathbf{\vec x}_{nst}$ 就是 $\mathbf {\vec x}$ 的最近邻点。
$kd$ 树搜索的平均计算复杂度为 $O(\log N)$ ， $N$ 为训练集大小。
$kd$ 树适合 $N >> k$ 的情形，当 $N$ 与维度 $k$ 接近时效率会迅速下降。
通常最近邻搜索只需要检测几个叶结点即可：
但是如果样本点的分布比较糟糕时，需要几乎遍历所有的结点：

2.3 示例

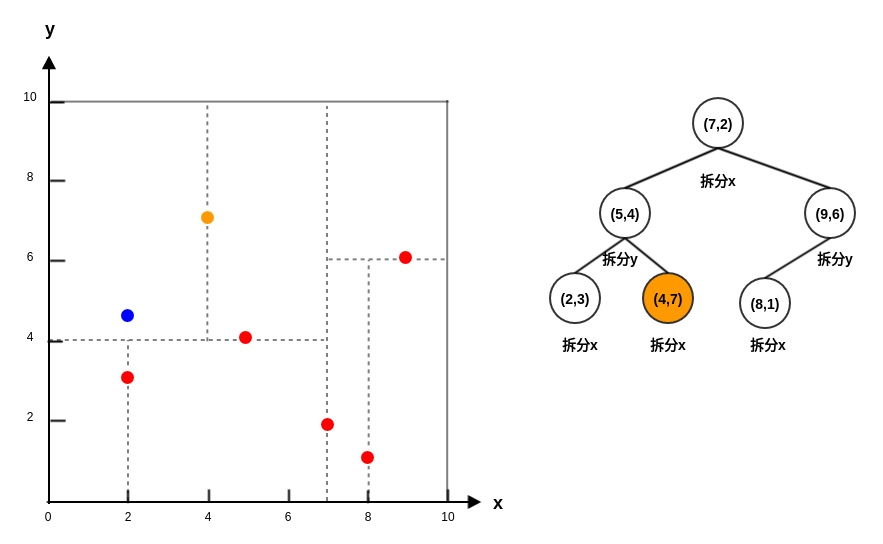
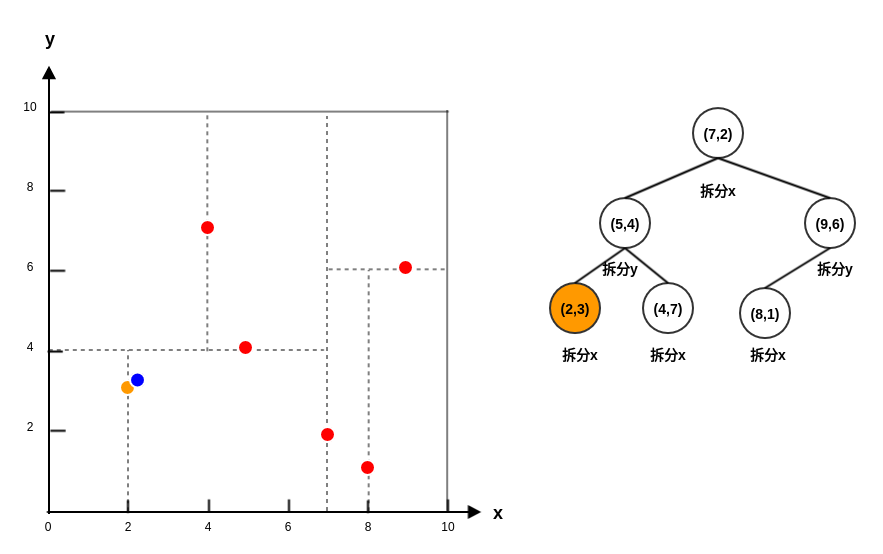
假设有 6 个二维数据点： $\mathbb D=\{(2,3),(5,4),(9,6),(4,7),(8,1),(7,2)\}$ 。
构建kd 树的过程：
- 首先从 x 轴开始划分，根据x 轴的取值2,5,9,4,8,7 得到中位数为 7 ，因此切分线为： $x=7$ 。
  可以根据x 轴和y 轴上数据的方差，选择方差最大的那个轴作为第一轮划分轴。
- 左子空间（记做 $\mathbb D_1$ ）包含点 (2,3),(5,4),(4,7)，切分轴轮转，从y 轴开始划分，切分线为： $y=4$ 。
- 右子空间（记做 $\mathbb D_2$ ）包含点 (9,6),(8,1)，切分轴轮转，从y 轴开始划分，切分线为： $y=6$ 。
- $\mathbb D_1$ 的左子空间（记做 $\mathbb D_3$ ）包含点(2,3)，切分轴轮转，从x 轴开始划分，切分线为： $x=2$ 。
  其左子空间记做 $\mathbb D_7$ ，右子空间记做 $\mathbb D_8$ 。由于 $\mathbb D_7,\mathbb D_8$ 都不包含任何点，因此对它们不再继续拆分。
- $\mathbb D_1$ 的右子空间（记做 $\mathbb D_4$ ）包含点(4,7)，切分轴轮转，从x 轴开始划分，切分线为： $x=4$ 。
  其左子空间记做 $\mathbb D_9$ ，右子空间记做 $\mathbb D_{10}$ 。由于 $\mathbb D_9,\mathbb D_{10}$ 都不包含任何点，因此对它们不再继续拆分。
- $\mathbb D_2$ 的左子空间（记做 $\mathbb D_5$ ）包含点(8,1)，切分轴轮转，从x 轴开始划分，切分线为： $x=8$ 。
  其左子空间记做 $\mathbb D_{11}$ ，右子空间记做 $\mathbb D_{12}$ 。由于 $\mathbb D_{11},\mathbb D_{12}$ 都不包含任何点，因此对它们不再继续拆分。
- $\mathbb D_2$ 的右子空间（记做 $\mathbb D_6$ ）不包含任何点，停止继续拆分。
最终得到样本空间拆分图如下：
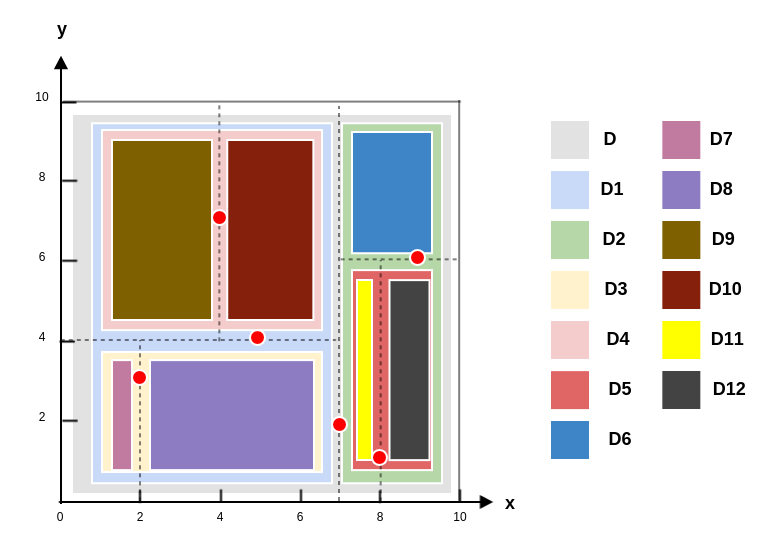
样本空间结构图如下：
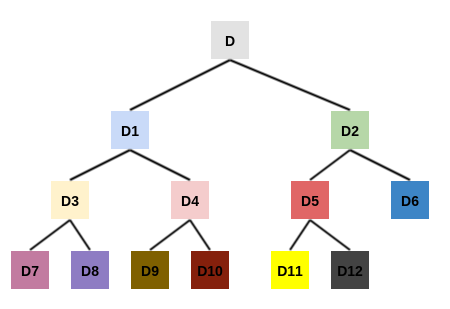
kd 树如下。
- kd 树以树的形式，根据样本空间的拆分，重新组织了数据集的样本点。每个结点都存放着位于划分平面上数据点。
- 由于样本空间结构图 中的叶区域不包含任何数据点，因此叶区域不会被划分。因此kd 树的高度要比样本空间结构图 的高度少一层。
- 从kd 树中可以清晰的看到坐标轮转拆分。
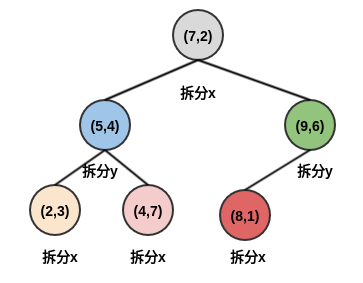
假设需要查询的点是P=(2.1,3.1) 。
- 首先从kd 树进行二叉查找，最终找到叶子节点(2,3)，查找路径为：Queue=<(7,2),(5,4),(2,3)> 。
- Queue 弹出结点(2,3)：P 到 (2,3)的距离为0.1414 ，该距离作为当前最近距离，(2,3) 作为候选最近邻点。
- Queue 弹出结点(5,4)：P 到 (5,4)的距离为3.03 。候选最近邻点仍然为(2,3)，当前最近距离仍然为0.1414 。
  因为结点(5,4)为中间结点，考察以P 为圆心，以0.1414 为半径的圆是否与y=4 相交。结果不相交，因此不用搜索(5,4) 的另一半子树。
- Queue 弹出结点(7,2)：P 到 (7,2)的距离为5.02 。候选最近邻点仍然为(2,3)，当前最近距离仍然为0.1414 。
  因为结点(7,2)为中间结点，考察以P 为圆心，以0.1414 为半径的圆是否与x=7 相交。结果不相交，因此不用搜索(7,2)的另一半子树。
- 现在Queue 为空，迭代结束。因此最近邻点为(2,3) ，最近距离为0.1414 。
假设需要查询的点是P=(2,4.5) 。
- 首先从kd 树进行二叉查找，最终找到叶子节点(4,7)，查找路径为：Queue=<(7,2),(5,4),(4,7)> 。
- Queue 弹出结点 (4,7) ：P 到 (4,7) 的距离为3.202 ，该距离作为当前最近距离， (4,7) 作为候选最近邻点。
- Queue 弹出结点 (5,4) ：P 到 (5,4) 的距离为3.041 ，该距离作为当前最近距离， (5,4) 作为候选最近邻点。
  因为(5,4) 为中间结点，考察以P 为圆心，以3.041 为半径的圆是否与y=4 相交。
  结果相交，因此二叉搜索(5,4) 的另一半子树，得到新的查找路径为：Queue=<(7,2),(2,3)> 。
  二叉查找时，理论上P 应该位于结点(5,4) 的右子树。但是这里强制进入(5,4) 的左子树，人为打破二叉查找规则。接下来继续维持二叉查找规则。
- Queue 弹出结点 (2,3) ：P 到 (2,3) 的距离为1.5 ，该距离作为当前最近距离， (2,3) 作为候选最近邻点。
- Queue 弹出结点(7,2)：P 到 (7,2)的距离为5.59 。候选最近邻点仍然为(2,3)，当前最近距离仍然为1.5 。
  因为结点(7,2)为中间结点，考察以P 为圆心，以1.5 为半径的圆是否与x=7 相交。结果不相交，因此不用搜索(7,2)的另一半子树。
- 现在Queue 为空，迭代结束。因此最近邻点为(2,3) ，最近距离为1.5 。